I.2.2.1. Représentation avec STRIPS
Dans ce qui suit, nous introduisons dans un premier temps les
principaux concepts du domaine de la planification en utilisant
STRIPS; le langage basique de représentation des
planificateurs classiques.
Pour mieux comprendre les choses, la présentation de
cette représentation sera illustrée à travers l'exemple le
plus fameux des domaines de planification : le monde de blocs.
Il consiste en un ensemble de blocs, de forme cubique posés sur une
table « figure1.1 >> :
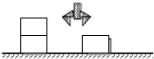
C
A
B
Figure1.1: Exemple du monde de blocs
· Les blocs peuvent s'entasser les uns sur les autres, mais
seulement un bloc peut être mis directement sur un autre bloc ;
· Un bras de robot peut tenir seulement un bloc à la
fois, donc il ne peut pas tenir un bloc qui a un autre bloc sur lui ;
· L'objectif sera toujours de bâtir une ou plusieurs
piles de blocs, spécifiées en termes de quels blocs sont au
dessus d'autres blocs.
· Représentation des états :
Les planificateurs décomposent le monde en conditions logiques
et représentent un état comme une conjonction de
littéraux positifs. Des restrictions sont
permises dans cette représentation :
· On peut considérer des littéraux
propositionnels: BrasVide peut représenter l'état : le bras du
robot est vide ;
· On peut considérer des littéraux du
premier-ordre: Sur(C,B)?Sur(B,A) peuvent représenter
l'état : le bloc C est sur le bloc B et B est sur A ;
· Les littéraux du premier-ordre doivent être
instanciés (ground) et libres de
fonctions; des littéraux comme sur(x,y) ou
habite(père(Paul), Paris) ne sont pas permis ; et
· L'hypothèse du monde-clos est
utilisée; cela signifie que toute condition non mentionnée dans
un état est considérée fausse.
Pour l'exemple de la « figure1.1 >> la
représentation de l'état sera :
S =

SurTtable(A) , SurTable(B) , Sur(C, A) BrasVide ,
Dégagé(B) , Dégagé(C)
SurTtable(A) , SurTable(B) , Sur(C, B)
BrasVide ,
Dégagé(A)
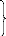
· Représentation des actions :
Une action est définie par l'application d'un
opérateur de transformation. Le principe de la
représentation d'un opérateur consiste à spécifier
les préconditions qui doivent être valables avant
qu'il puisse être exécutée et les effets
qui s'ensuivent quand il est exécuté. Les
précondition peuvent être positives ou négatives : les
préconditions positives expriment les propriétés qui
doivent être vérifiées, par exemple Sur(C,
A) et les préconditions négatives expriment celles
qui doivent être absentes de l'état pour que l'action soit
appliquée, par exemple not(SurTable(A)).
Un opérateur avec variables est appelé un
schéma d'opérateur. Il ne correspond pas
à une seule action exécutable, mais à une famille d'action
différentes qui peuvent être dérivées en
instanciant les variables à des constantes
différentes.
Plus généralement un schéma
d'opérateur est constitué de trois parties:
Le nom de l'opérateur et une liste de
paramètres : définis par une expression de la forme
n(x1, . . ., xk) où n est le nom de l'opérateur
et x1, . . ., xk représentent les paramètres de
l'opérateur.
Les préconditions : définies
par une conjonction de littéraux (positifs), libres de fonctions,
faisant état de ce qui doit être vrai dans un état avant
que l'opérateur puisse être exécutée. Toute variable
apparaissant dans les préconditions doit aussi apparaître dans la
liste de paramètres de l'opérateur.
Les effets : définis par une
conjonction de littéraux (positifs ou négatifs), libres de
fonctions décrivant les faits à ajouter et les faits à
supprimer de l'état du monde après l'exécution de
l'opérateur : l'effet P?not(Q) signifie ajouter P et
supprimer Q. Les variables dans les effets doivent aussi
apparaître dans la liste de paramètres de l'opérateur.
Certains systèmes de planification divisent les effets en liste
d'addition (add list) pour les littéraux positifs et
en liste de suppression (delete list) pour les
littéraux négatifs.
Pour notre exemple des blocs, on peut définir les deux
opérateurs suivants :
Déplacer(b, x, y) ;;
L'opérateur pour déplacer le bloc b du dessus de x au dessus de y
Precond : Sur(b,
x)?Dégagé(b)?Dégagé(y)
Effet : Sur(b,
y)ADégagé(x)A#172;Sur(b, x)A#172;Dégagé(y)
DéplacerSurTable(b, x) ;;
L'opérateur pour déplacer un bloc b de x à la table
Precond : Sur(b, x)ADégagé(b)
Effet : Sur(b,
Table)ADégagé(x)A#172;Sur(b, x)
Une action est une instance d'un opérateur. Si a est
une action et si un état tel que Precond+(a) appartient à si et
precond-(a) si, alors a est applicable à si, et le résultat de
cette application App est l'état si+1 tel que :
App(si,a) = si+1 = (si - effets-(a)) U effets+(a).
Dans le modèle de l'état « s » de la
figure1.1 décrit précédemment, l'action «
Déplacer(C, A,
B) » peut être appliquée ; le nouveau
état « s' » engendré après son exécution
sera :
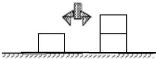
A
C
B
Figure1.2: L'exemple du monde de blocs dans
l'état S'
Le résultat Res de l'application d'une
séquence d'actions ?= <a1, a2, ..., an> sur un état s est
récursivement défini par :
Res(s, < >) = s
Res(s, <a1, a2, ..., an>) =
Res(App(s,a1), <a2, a3, ..., an>)
Remarques :
Il faut noter que si un effet positif est déjà dans
s celui-ci n'est pas ajouté deux fois et si un effet négatif
n'est pas dans s alors cette partie de l'effet est ignorée.
Chaque littéral non mentionné dans l'effet reste
inchangé. De cette façon STRIPS évite le frame
problem (c.a.d. représenter toutes les choses qui restent les
mêmes)
· Représentation des objectifs :
Un objectif est un état partiellement spécifié,
représenté comme une conjonction des littéraux
instanciés positifs comme BrasVide ou Sur(A, C). Un
état propositionnel s satisfait un objectif g si s
contient tous les atomes dans g (et possible d'autres);
l'état Sur(A, C)?Sur(C, B)?Sur(E, D) satisfait l'objectif
Sur(A, C)?Sur(C, B).
· Représentation des domaines : En
planification, un domaine de planification définit l'ensemble des
opérateurs qui peuvent s'appliquer sur le monde.
· Représentation des problèmes :
En planification Un problème P doit spécifier
l'état initial ainsi que le but à atteindre. Il peut être
défini comme un triplet P = (O, s0, g) où :
- s0, l'état initial, est un état quelconque de S
;
- g, le but, définit un ensemble cohérent de
prédicats instanciés, i.e. : les propriétés du
monde devant être atteintes ;
- O, est l'ensemble des opérateurs applicables.
· Représentation des plans : Un
plan solution pour un problème de planification P = (O, s0, g) est une
séquence d'actions ?= <a1, a2, ..., an> décrivant un chemin
d'un état initial s0 à un état final sn tel que le but g
soit inclus dans sn. Autrement dit, le plan ?= <a1, a2, ..., an> est une
solution pour le problème P si Res(s0, ?) satisfait g.
Pour notre exemple une représentation d'un
problème de planification et d'une solution peut être
décrite comme suit :
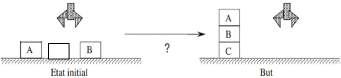
C
Figure1.3 : Exemple d'un problème de
planification dans le monde des blocs
Init (
Sur(A,Table)?Sur(B,Table)?Sur(C,Table)?Bloc(A)?
Bloc(B)?Bloc(C)?Dégagé(A)?Dégagé(B)?Dégagé(C)
) Objectif ( Sur(A, B)?Sur(B, C) )
Action ( Déplacer(b, x,
y)
Precond : Sur(b,
x)?Dégagé(b)?Dégagé(y)
Effet : Sur(b, y)?Dégagé(x)?#172;Sur(b,
x)?#172;Dégagé(y) )
Action (
DéplacerSurTable(b, x)
Precond : Sur(b, x)?Dégagé(b)
Effet : Sur(b, Table)?Dégagé(x)?#172;Sur(b, x)
)
Une solution possible est:
<Déplacer(B, Table, C), Déplacer(A, Table,
B)>
Avec ces aspects, STRIPS impose des restrictions sur la
représentation de la planification ; il est donc assez expressif pour
certains domaines du monde réel. Des extensions sont donc apparues pour
remédier à cette insuffisance de STRIPS. Il s'agit des deux
langages ADL et PDDL.
| 


