Contrôle actif robuste d'une structure flexible

4.2. Application du contrôle 8 au modèle de la suspension quart de véhicule

Après avoir présenté la synthèse 8 standard, nous allons dans cette section appliquer cette technique de commande sur le modèle linéaire quart de véhicule afin de synthétiser une loi de commande permettant d'assurer, à la fois, un bon confort et une bonne tenue de route.

4.2.1. Mise sous forme standard

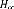
Pour pouvoir synthétiser une commande , il faut au préalable mettre le système considéré

sous forme standard. Pour cela nous avons besoin de déterminer quelles sont les entrées
exogènes , les entrées de commande , les sorties à contrôler et les sorties mesurées . Dans

notre cas la seule mesure disponible est le débattement de la suspension ( ) - ( ) , qui est

mesurée par un capteur électronique auquel s'ajoute un bruit de mesure. Celle-ci est à la fois facile à effectuer sur un véhicule et utile pour le correcteur. Les entrées exogènes sont le bruit de mesure d'une part et le profil de la route d'autre part. La seule entrée de contrôle correspond à la force de l'actionneur actif. Enfin, pour les sorties contrôlées nous cherchons à limiter

l'accélération verticale de la caisse ( ( ) ), l'écrasement du pneu ( ) - ( ) , le débattement
de la suspension ( ) - ( ) et celui de la commande . Cependant, nous voulons limiter ces

sorties différemment selon les fréquences. Les sorties à contrôler correspondent donc à ces sorties affectées de pondérations. Les fonctions de pondération sont donc choisies de façon à améliorer les fonctions de transfert dans les domaines de fréquence intéressants.

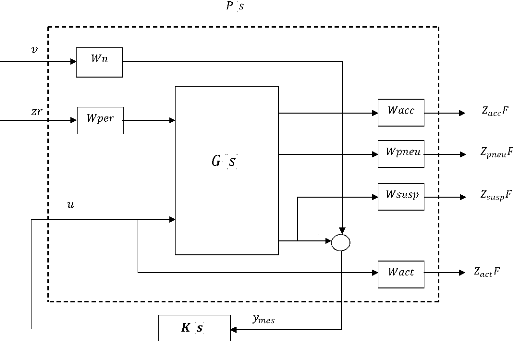
Le schéma suivant montre l'emplacement des fonctions de pondérations fréquentielles permettant de gérer les compromis.

( )

( )

( )

+ +

69

Figure 4.3 - Mise sous forme standard du problème avec les pondérations

Le système ( ) représente la dynamique du quart de véhicule à 2DDL. Les pondérations fréquentielles ajoutés aux entrées et sorties du système conservent les fréquences prédominantes et atténuent les fréquences moins importantes. Pour les critères de performance, la pondération conserve les fréquences les plus sensibles et atténue les fréquences moins importantes.

4.2.2. Choix des pondérations

L'objectif principal est de réduire l'accélération de la caisse (pour le confort des passagers), de réduire l'écrasement du pneu (pour garder le contrôle du véhicule en toute sécurité), de réduire le débattement de la suspension (contrainte matérielle), et la commande en force de l'actionneur (afin de ne pas trop le solliciter en hautes fréquences). Le filtrage du bruit de mesure n'étant pas notre principal objectif, la pondération est très faible. A cet effet, une pondération constante

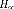
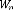
est choisie pour le bruit de mesure. La pondération est aussi choisie comme constante

pour l'écrasement du pneu. La nécessité de conserver l'adhérence des pneus sur toute la gamme des fréquences explique ce choix.

Comme les perturbations de la route sont importantes pour la conception du contrôleur, la

pondération agissant ( ) - ( ) sur correspond à un filtre passe bas avec une fréquence

de coupure de 1Hz. Il permet de modéliser la densité spectrale de la route pour qu'elle soit représentative du cas réel.

La pondération fréquentielle agissant sur ( ) - ( ) correspond à un filtre passe bas

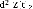
avec une fréquence de coupure de 5Hz. Il permet de contrôler la déflexion de suspension en basses fréquences là où elle est la plus importante et facilement contrôlable par l'actionneur. Il permet aussi de réduire la force appliquée en hautes fréquences, car l'actionneur a une fréquence maximale d'opération limitée. De plus, en pondérant la commande par un passe haut ( ) pénalise l'utilisation de l'actionneur en hautes fréquences.

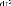
La pondération agissant sur ( ( ) ) correspond au filtre de sensibilité humaine.

Pour représenter l'importance relative de chaque critère, un poids multiplie l'amplitude de chaque filtre. Le tableau suivant donne les valeurs des poids utilisés :

poids	variable	critère	valeur
		Bruit de mesure	0.0001
		Perturbation de la route	1
		Déflexion de suspension	25
		Déflexion du pneu	6000
		Accélération du passager	1
		Force de l'actionneur	0.00000001

Tableau 4.1 - Poids des pondérations

Chapitre IV synthèse

Les pondérations choisies sont les suivantes :

= ; =

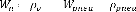
(4.19)

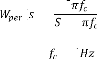
2

( ) = (4.20)

+ 2

Avec = 1

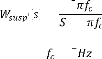
2

( ) = (4.21)

+ 2

Avec = 5

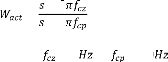
12

(4.22)

+ 30.02 + 901.3

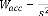
Avec = 30.02 ; = 4.78 ; = 0.5

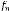
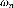
+ 2

= (4.23)

+ 2

Avec = 3 , = 30

71

Nous pouvons construire le système augmenté ( ) en utilisant la commande sysic du ^<<robust control Toolbox^>> de ^<<Matlab^>>.

Le correcteur est synthétisé avec la commande ^<<hinfsyn^>> sous Matlab. Il est donné par sa

fonction de transfert :

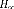
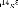
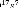
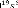
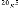
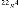
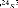
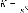
4.134 10 + 1.327 10 + 1.433 10 + 9.434 10 + 4.094 10 + 1.169 10 +

2.164 10 + 2.203 10 + 6.533 10

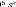
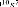
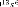
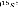
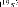
+ 2.006 10 + 2.011 10 + 2.678 10 + 7.173 10 + 6.718 10 + 2.948 10 +

7.488 10 + 1.012 10 + 3.267 10

Après avoir réalisé la synthèse du correcteur, nous obtenons = 15.133. Il faut noter que

l'ordre du correcteur ( ) est la somme de celle du modèle et des filtres. Par conséquent, le correcteur obtenu pour le quart de véhicule est d'ordre 9.

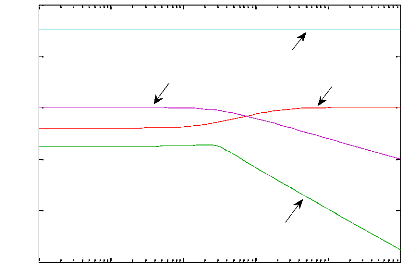
Les pondérations fréquentielles sur l'accélération de la caisse, sur l'écrasement du pneu, sur le débattement de la suspension et de la force de l'actionneur sont représentées sur la figure 4.4.

Bode des ponderations Wpneu, Wsusp, Wact et Wacc

10^-1 10⁰ 10¹ 10² 10³ 10⁴

Magnitude (dB)

-100

-150

100

-50

50

0

Wsusp Wact

Wpneu

W acc

Frequence (Hz)

72

Figure 4.4 - Pondérations fréquentielles appliquées sur les critères de performances

73

Chapitre IV synthèse

4.2.3. Présentation des résultats de simulation

Les figures 4.5 à 4.8 montrent les réponses fréquentielles et temporelles des critères de performances.

Nous rappelons que, le test temporel simule le passage sur une bosse d'amplitude maximale de 5cm.

10⁰ 10¹

Magnitude (abs)

Diagramme de Bode du trasnfert Yacc(s)/w (s)

10²

10¹

10⁰

10^-1

passif

actif

Frequence (Hz)

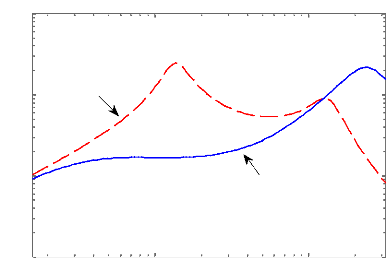
Figure 4.5 - Réponse fréquentielle du transfert entre l'accélération verticale de la caisse et le
profil de la route.

Chapitre IV synthèse

10⁰ 10¹

Magnitude (abs)

Diagran-me de Bode du transfert Ypneu(s)/w (s)

10^-1

10^-2

10^-3

passif

actif

Frequence (Hz)

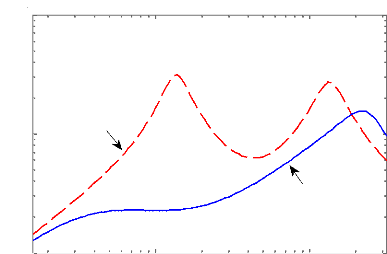
Figure 4.6 - Réponse fréquentielle du transfert entre l'écrasement du pneu et le profil de la route.

10⁰ 10¹

Magnitude (abs)

Diagran-me de Bode du transfert Ysusp(s)/w (s)

10⁰

10^-1

10^-2

10^-3

passif

actif

Frequence (Hz)

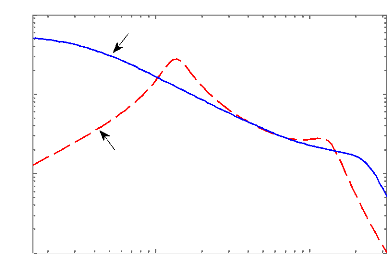
Figure 4.7 - Réponse fréquentielle du transfert entre le débattement de la suspension et le profil de la route.

75

Chapitre IV synthèse

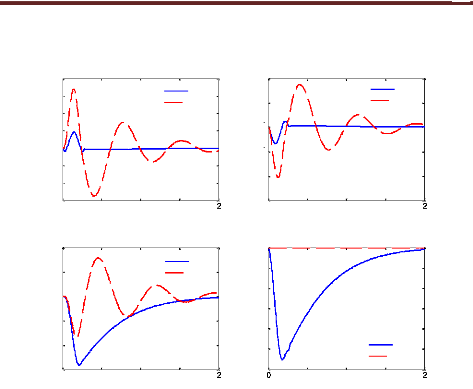
x 10-4 Ecrasement du Pneu

AccOlOration Verticale de Caisse

0

-20

Amplitude (N)

-40

-60

-80

-100

-120

temps (s)

x 10-3 DObattement de Suspension

0 0.5 1 1.5

4

riccati
passif

2

Amplitude (m)

0

-2

-4

-6

temps (s)

temps (s)

Force de Contrôle

0.5 1 1.5

temps (s)

riccati
passif

riccati
passif

0 0.5 1 1.5

4

2

Amplitude (m)

0

-2

-4

-6

0 0.5 1 1.5

0.4

riccati
passif

0.3

0.2

Amplitude (m/s²)

0.1

0

-0.1

-0.2

-0.3

Figure 4.8 - Réponses temporelles

Les réponses fréquentielles et temporelles du contrôle par Riccati, nous montre clairement

une nette amélioration des performances de la suspension active comparativement au cas passif (sans contrôle).

En effet, les deux modes de résonance principaux, autour de 1Hz et autour de 10 Hz respectivement de la masse suspendue et de la masse non suspendue sont complètement ou pratiquement éliminés pour les trois critères. Ceci montre que la loi de commande élaborée assure de bonnes performances en termes d'isolation vibratoire vis-à-vis des perturbations (un bon confort pour les passagers) et de maintien du niveau d'adhérence au sol suffisamment important (une bonne tenue de route). Cependant, ces améliorations sont amenées au détriment du débattement de suspension en basses fréquences.

Chapitre IV synthèse

4.3. Résultats pour le contrôle actif du quart de véhicule à deux degrés de liberté

Afin d'apprécier l'amélioration apportée par les lois de commandes appliquées au système de la suspension active du modèle quart de véhicule. On compare ces dernières avec le cas passif (qu'on appelle aussi boucle ouverte).

Les figures 4.9 à 4.15 montrent le résultat des réponses en fréquence et le résultat des réponses temporelles obtenues pour la suspension passive et les différentes stratégies de contrôle.

Diagrarrire de Bode du transfert Yacc(s)/w (s)

passif LQG

LQG/LTR

LQR

Hinfini

10²

10^-1

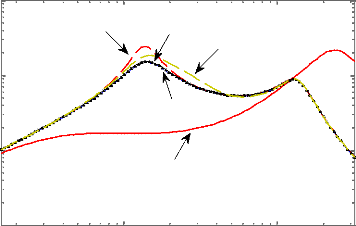
10⁰ 10¹

10¹

Magnitude (abs)

10⁰

Frequence (Hz)

Figure 4.9 - Réponse fréquentielle du transfert entre l'accélération verticale de la caisse et le
profil de la route.

77

Chapitre IV synthèse

Diagramme de Bode du transfert Ypneu(s)/w (s)

passif

LQG

LQG/LTR

LQR

Hinfini

10^-3

Magnitude (abs)

10^-1 10^-2

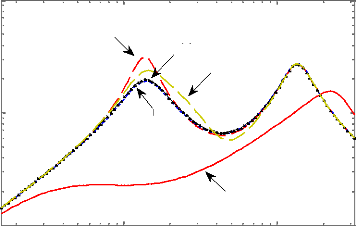
10⁰ 10¹

Frequence (Hz)

Figure 4.10 - Réponse fréquentielle du transfert entre l'écrasement du pneu et le profil de la route.

10⁰ 10¹

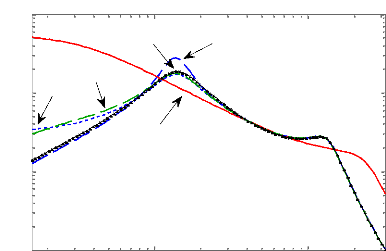
Magnitude (abs)

Diagramme de Bode du transfert Ysusp(s)/w (s)

10⁰

10^-1

10^-2

10^-3

LQR

LQG

LQG/LTR passif

Hinfini

Frequence (Hz)

Figure 4.11 - Réponse fréquentielle du transfert entre le débattement de la suspension et le profil
de la route.

Chapitre IV synthèse

Accélération Verticale de la Caisse

Amplitude (m/s²)

-0.1

-0.2

-0.3

0.4

0.3

0.2

0.1

0

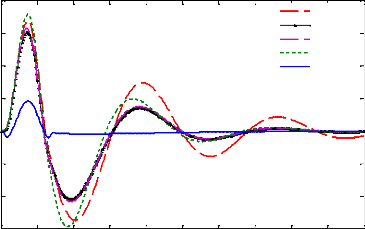
passif LQR

LQG LQG/LTR Hinfini

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

temps (s)

Figure 4.12 - L'accélération verticale de la caisse obtenus pour les différentes lois de
commande.

x 10^-4 Ecrasement du pneu

Amplitude (m)

-1

-2

-3

-4

-5

4

5

3

2

0

1

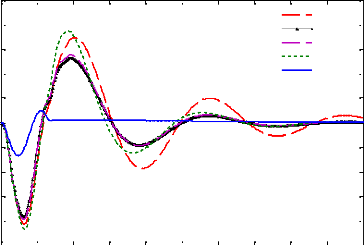
passif LQR

LQG LQG/LTR Hinfini

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

temps (s)

Figure 4.13 - L'écrasement du pneu obtenus pour les différentes lois de commande

79

Chapitre IV synthèse

x 10-3 Débattement de suspension

Amplitude (m)

-1

-2

-3

-4

-5

-6

4

3

2

0

1

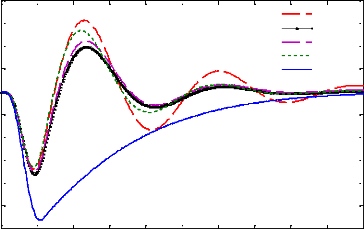
passif LQR

LQG LQG/LTR Hinfini

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

temps (s)

Figure 4.14 - Débattement de la suspension obtenus pour les différentes lois de commande

Force de contrOle

Amplitude (N)

-100

-120

-20

-40

-60

-80

20

0

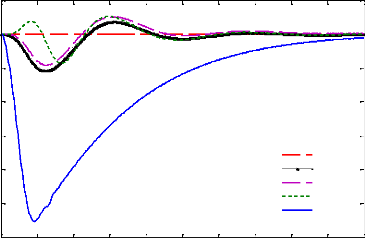
passif LQR

LQG LQG/LTR Hinfini

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

temps (s)

Figure 4.15 - Force de contrôle obtenu pour les différentes lois de commande

Chapitre IV synthèse

Le tableau suivant donne la valeur de l'indice de performance J :

Contrôle	Critère J
Passif	0.0362
LQR	0.0263
LQG	0.0268
LQG/LTR	0.0319
	0.2771

Tableau 4.2 - Performance des différents contrôleurs pour le modèle à 2DDL

Le contrôle par (LQR, LQG, LQG/LTR) permet effectivement de minimiser le critère J, ce qui améliore sensiblement la performance de la suspension. Le contrôle par offre un indice de performance J le plus élevé. Par contre, la réponse est beaucoup mieux modelée en fréquence, surtout pour l'accélération verticale de la caisse et l'écrasement du pneu. Cette observation nous permet de noter que la distribution en fréquence de la réponse est importante dans l'évaluation de la performance d'une suspension.

81

Chapitre IV synthèse

4.4. Conclusion

Dans ce chapitre, la synthèse d'une loi de commande pour la suspension active du modèle

quart de véhicule a été présentée. Dans un premier temps nous avons mené une étude bibliographique sur la synthèse , Puis nous avons détaillé les pondérations choisies de façon à améliorer les fonctions de transfert dans les domaines de fréquence intéressants. Nous pourrons dire, d'après ce qui a précédé que les objectifs sont pleinement atteints avec le contrôle .