Contrôle actif robuste d'une structure flexible

.République Algérienne Démocratique et Populaire
Ministère de l'Enseignement Supérieur et de la Recherche Scientifique
Université Mouloud MAMMERI, Tizi-Ouzou

Faculté de Génie Electrique et d'Informatique
Département d'Automatique

Mémoire de Fin d'Etudes

En vue de l'obtention du diplôme

Master acalémique en )4utomatique
Option commanie des systèmes

Theme

Proposé par : M^r DJENNOUNE Said Présenté par:

Mr HADJOU Lyes

Dirigé par : M^r DJENNOUNE Said M^r BELHOCINE Mohamed

Soutenu le : 15 /07 /2010

Résumé

L'objectif du travail réalisé est de mieux comprendre la suspension active de véhicule automobile et plus précisément de développer des stratégies de contrôle optimal. Afin d'atteindre cet objectif, un modèle analytique a été mis au point pour simuler la réponse de la suspension à une perturbation correspondant au profil vertical de la route.

Le modèle représente un système de suspension quart de véhicule, équipé d'un actionneur qui génère des forces sous la demande d'une stratégie de contrôle, dont la présence confère à la suspension, un caractère actif. Un travail de simulation sur le logiciel Matlab permet de visualiser des résultats satisfaisants par rapport à la suspension passive.

Abstract

The objective of this work is to better understand the active suspension of motor vehicle and more specifically to develop strategies for optimal control. To achieve this objective, an analytical model was developed to simulate the response of the suspension to a disturbance corresponding to the vertical profile of the road.

The model represents a quarter of a suspension vehicle equipped with an actuator that generates forces under the application of a control strategy, whose presence gives the suspension, active character. A working simulation on the Matlab software allows visualizing satisfactory results compared to the passive suspension.

Introduction générale. 1

Chapitre 1: Modélisation du système physique .3

1. Modèle quart de véhicule 3

1.1. Introduction 3

1.2. La suspension 3

1.3. Description du modèle quart de véhicule 5

1.3.1. Équations de la dynamique 6

1.3.2. Mise sous forme d'état 7

1.3.2.1. Le formalisme d'état 7

1.3.2.2. La formalisation des équations sous forme d'état 9

1.3.3. Relation entrée-sortie 15

1.4. Notion de stabilité 17

1.4.1. Conditions de stabilité 18

1.5. Résultats de simulation 20

1.6. Conclusion 24

Chapitre 2 : outils d'analyse des systèmes bouclés 25

2. Introduction 25

2.1. Propriétés du système nominal 25

2.1.1. Performances nominales 26

2.1.1.1. Matrices de sensibilité 26

2.1.1.2. Objectifs de commande 27

2.1.2. Stabilité nominale 28

2.1.2.1. Critère de Nyquist (cas multivariable) 28

2.1.2.2. Théorème du faible gain 30

2.2. Notions de robustesse 31

2.2.1. Incertitudes de modèle 31

2.2.2. Robustesse en stabilité : analyse non structurée 34

Chapitre 3 : commandes linéaires (LQR, LQG, LQG/LTR) ...35

3.1. Introduction 35

3.1.1. Contrôle optimal 35

3.2. Commande Linéaire Quadratique 35

3.2.1. Formulation du problème de commande (LQR) 35

3.3. Commande linéaire quadratique gaussienne (LQG) 38

3.3.1. Formulation du problème de commande (LQG) 38

3.3.2. Synthèse d'une commande LQG 39

3.3.3. Structure de la de commande LQG 40

3.4. Commande LQG/LTR (Loop Transfert recovery) 42

3.4.1. Formulation du problème de commande (LQG/LTR) 42

3.4.1.1. Recouvrement en entrée 43

3.4.1.2. Recouvrement en sortie 43

3.4.2. Synthèse d'un correcteur LQG/LTR 44

3.5. Application des commandes linéaires au modèle quart de véhicule 45

3.5.1. Objectifs de contrôle 45

3.5.2. Contrôle LQR 46

3.5.3. Contrôle LQG 47

3.5.4. Contrôle LQG/LTR 48

3.6. Simulations 50

3.6.1. Résultats de simulation LQR 50

3.6.2. Résultats de simulations LQG 53

3.6.3. Résultats de simulations LQG/LTR 55

3.7. Conclusion 57

Chapitre 4 : synthèse . 58

4.1. Introduction 58

4.1.1. La Synthèse o 58

4.1.2. Outils de calcul nécessaire à la synthèse o 58

4.1.3. Formulation du problème o 61

4.1.4. Résolution du problème o standard par Riccati : 64

4.2. application de la commande o au modèle de la suspension quart de véhicule 68

4.2.1. Mise sous forme standard 68

4.2.2. Choix des pondérations 69

4.2.3. Présentation des résultats de simulation 73

4.3. Résultats pour le contrôle actif du quart de véhicule à deux degrés de liberté 76

4.4. Conclusion 80

Liste des symboles, Figures et tableaux

Liste des figures

Figure 1.1 - Modèle de la suspension active quart de véhicule 5

Figure 1.2 - Diagramme pôles-zéros du système 21

Figure 1.3 - Réponse fréquentielle des critères de performances 22

Figure 1.4 - Réponse temporelle des critères de performances 23

Figure 2.1 - Schéma bloc pour l'étude de la performance nominale 25

Figure 2.2 - Schéma bloc pour l'étude de la stabilité nominale 28

Figure 2.3 - Bouclage d'une matrice de transfert ( ) 29

Figure 2.4 - Critère de Nyquist multivariable 30

Figure 2.5 - Représentation généralisée des incertitudes de modélisation 32

Figure 2.6 - Schéma d'analyse de la robustesse de la stabilité 33

Figure 3.1 - Schéma général de la commande linéaire quadratique (LQR). 40

Figure 3.2 - Théorème de séparation 43

Figure 3.3 - Structure d'un régulateur LQG 45

Figure 3.4 - Schéma bloc du régulateur et du modèle 48

Figure 3.5 - Critères fréquentiels du modèle quart de véhicule 54

Figure 3.6 - Réponses temporelles du modèle quart de véhicule avec le contrôleur LQR à l'excitation

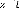
Do . 55

Figure 3.7 - Critères fréquentiels du modèle quart de véhicule 56

Figure 3.8 - Réponse temporelle du modèle quart de véhicule avec le contrôleur LQG à l'excitation

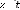
Do . 57

Figure 3.9 - Critères fréquentiels du modèle quart de véhicule 58

Figure 3.10 - Réponse temporelle du modèle quart de véhicule avec le contrôleur LQG/LTR à

l'excitation D( ) 59

Figure 4.1-- Problème DO standard 61

Figure 4.2 - Problème o standard incluant les pondérations 63

Figure 4.3 - Mise sous forme standard du problème avec les pondérations 69

Figure 4.4 - Pondérations fréquentielles appliquées sur les critères de performances 72

Figure 4.5 - Réponse fréquentielle du transfert entre l'accélération verticale de la caisse et le profil de

la route... 73

Figure 4.6 - Réponse fréquentielle du transfert entre l'écrasement du pneu et le profil de la route 74

Figure 4.7 - Réponse fréquentielle du transfert entre le débattement de la suspension et le profil de la

route 74

Figure 4.8 - Réponses temporelles 75

Figure 4.9 - Réponse fréquentielle du transfert entre l'accélération verticale de la caisse et le profil de la route... 76
Figure 4.10 - Réponse fréquentielle du transfert entre l'écrasement du pneu et le profil de la

route 77
Figure 4.11 - Réponse fréquentielle du transfert entre le débattement de la suspension et le profil de la

route... 77

Figure 4.12 - L'accélération verticale de la caisse obtenus pour les différentes lois de commande 78

Figure 4.13 - L'écrasement du pneu obtenus pour les différentes lois de commande 78

Figure 4.14 - Débattement de la suspension obtenus pour les différentes lois de commande 79

Figure 4.15 - Force de contrôle obtenu pour les différentes lois de commande 79

Liste des tableaux

Tableau 1.1 - Valeurs numériques des paramètres du modèle quart de véhicule 20

Tableau 1.2 - Pôles du modèle de la suspension quart de véhicule en boucle ouverte 20

Tableau 3.1 - Poids des pondérations multipliant les critères 50

Tableau 3.2 - Marges de stabilité pour déférentes valeurs de . 52

Tableau 3.3 - Marges de stabilité obtenus pour les différentes lois de commande 52

Liste des symboles

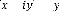
Im : Partie imaginaire d'un nombre complexe, c'est-à-dire Im( + ) = Re : Partie réelle d'un nombre complexe, c'est-à-dire Re( + ) =

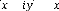
= v-1

S : Variable de Laplace.

: Temps.

: Masse non suspendue.

: Masse suspendue (caisse).

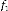
: Amortisseur du pneu.

: Amortisseur de la suspension.

: Ressort de la suspension.

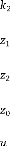
: Ressort du pneu.

: Déplacement verticale de la caisse. : Déplacement verticale de la roue.

: Profit de la route.

: Force de commande.

? ? : La somme des forces qui agissent sur la masse

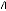
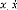
, : Vecteur d'état, dérivée du vecteur d'état. : Pulsation.

: Matrice d'évolution du système.

: Matrice d'application de la commande.

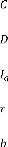
: Matrice d'observation.

: Matrice de transmission directe. : Matrice identité de dimension q. : Signal de référence.

: Perturbation à l'entrée.

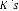
( ) : Fonction du transfert du correcteur.

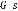
( ) : Matrice de transfert en boucle ouverte.

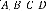
( , , , ) : Représentation minimale de ( ).

E I1 La sortie du système.

E I1 La commande (sortie du correcteur).

E I1 L'effet sur la sortie des perturbations affectant le système.

E I1 Les bruits de mesure.

: Matrice de sensibilité (en sortie).

: Matrice de sensibilité complémentaire en sortie.

: Matrice de sensibilité (en entrée).

: Matrice de sensibilité complémentaire en entrée.

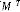
[ ] : Transposée de la matrice .

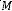
[ ]* : Transposée conjuguée de la matrice .

i ( ) : Représente les incertitudes de modélisation.

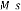
( ) : La matrice de transfert nominale du système.

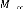
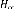
II II : Norme de la matrice .

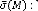
Valeur singulière maximale de la matrice . ( ): Valeur singulière minimale de la matrice . : Critère linéaire d'optimisation.

* : Commande optimale

: Horizon

: Temps final

Etat estimé

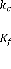
: Gain du retour d'état LQR : Gain du filtre de Kalman

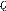
: Gain du recouvrement du correcteur LQG/LTR

: Matrice symétrique définie positive : Matrice symétrique définie positive et : Bruits blancs.

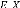
[ ] : Espérance mathématique de .

Abréviations

LQ : Commande linéaire quadratique

LQG : Commande linéaire quadratique gaussienne

LQG/LTR : Commande linéaire quadratique par recouvrement LFT : Transformation linéaire fractionnelle

LTI : Linear Time Invariant (linéaire temps invariant)