Contrôle actif robuste d'une structure flexible

.République Algérienne Démocratique et Populaire
Ministère de l'Enseignement Supérieur et de la Recherche Scientifique
Université Mouloud MAMMERI, Tizi-Ouzou

Faculté de Génie Electrique et d'Informatique
Département d'Automatique

Mémoire de Fin d'Etudes

En vue de l'obtention du diplôme

Master acalémique en )4utomatique
Option commanie des systèmes

Theme

Proposé par : M^r DJENNOUNE Said Présenté par:

Mr HADJOU Lyes

Dirigé par : M^r DJENNOUNE Said M^r BELHOCINE Mohamed

Soutenu le : 15 /07 /2010

Résumé

L'objectif du travail réalisé est de mieux comprendre la suspension active de véhicule automobile et plus précisément de développer des stratégies de contrôle optimal. Afin d'atteindre cet objectif, un modèle analytique a été mis au point pour simuler la réponse de la suspension à une perturbation correspondant au profil vertical de la route.

Le modèle représente un système de suspension quart de véhicule, équipé d'un actionneur qui génère des forces sous la demande d'une stratégie de contrôle, dont la présence confère à la suspension, un caractère actif. Un travail de simulation sur le logiciel Matlab permet de visualiser des résultats satisfaisants par rapport à la suspension passive.

Abstract

The objective of this work is to better understand the active suspension of motor vehicle and more specifically to develop strategies for optimal control. To achieve this objective, an analytical model was developed to simulate the response of the suspension to a disturbance corresponding to the vertical profile of the road.

The model represents a quarter of a suspension vehicle equipped with an actuator that generates forces under the application of a control strategy, whose presence gives the suspension, active character. A working simulation on the Matlab software allows visualizing satisfactory results compared to the passive suspension.

Introduction générale. 1

Chapitre 1: Modélisation du système physique .3

1. Modèle quart de véhicule 3

1.1. Introduction 3

1.2. La suspension 3

1.3. Description du modèle quart de véhicule 5

1.3.1. Équations de la dynamique 6

1.3.2. Mise sous forme d'état 7

1.3.2.1. Le formalisme d'état 7

1.3.2.2. La formalisation des équations sous forme d'état 9

1.3.3. Relation entrée-sortie 15

1.4. Notion de stabilité 17

1.4.1. Conditions de stabilité 18

1.5. Résultats de simulation 20

1.6. Conclusion 24

Chapitre 2 : outils d'analyse des systèmes bouclés 25

2. Introduction 25

2.1. Propriétés du système nominal 25

2.1.1. Performances nominales 26

2.1.1.1. Matrices de sensibilité 26

2.1.1.2. Objectifs de commande 27

2.1.2. Stabilité nominale 28

2.1.2.1. Critère de Nyquist (cas multivariable) 28

2.1.2.2. Théorème du faible gain 30

2.2. Notions de robustesse 31

2.2.1. Incertitudes de modèle 31

2.2.2. Robustesse en stabilité : analyse non structurée 34

Chapitre 3 : commandes linéaires (LQR, LQG, LQG/LTR) ...35

3.1. Introduction 35

3.1.1. Contrôle optimal 35

3.2. Commande Linéaire Quadratique 35

3.2.1. Formulation du problème de commande (LQR) 35

3.3. Commande linéaire quadratique gaussienne (LQG) 38

3.3.1. Formulation du problème de commande (LQG) 38

3.3.2. Synthèse d'une commande LQG 39

3.3.3. Structure de la de commande LQG 40

3.4. Commande LQG/LTR (Loop Transfert recovery) 42

3.4.1. Formulation du problème de commande (LQG/LTR) 42

3.4.1.1. Recouvrement en entrée 43

3.4.1.2. Recouvrement en sortie 43

3.4.2. Synthèse d'un correcteur LQG/LTR 44

3.5. Application des commandes linéaires au modèle quart de véhicule 45

3.5.1. Objectifs de contrôle 45

3.5.2. Contrôle LQR 46

3.5.3. Contrôle LQG 47

3.5.4. Contrôle LQG/LTR 48

3.6. Simulations 50

3.6.1. Résultats de simulation LQR 50

3.6.2. Résultats de simulations LQG 53

3.6.3. Résultats de simulations LQG/LTR 55

3.7. Conclusion 57

Chapitre 4 : synthèse . 58

4.1. Introduction 58

4.1.1. La Synthèse o 58

4.1.2. Outils de calcul nécessaire à la synthèse o 58

4.1.3. Formulation du problème o 61

4.1.4. Résolution du problème o standard par Riccati : 64

4.2. application de la commande o au modèle de la suspension quart de véhicule 68

4.2.1. Mise sous forme standard 68

4.2.2. Choix des pondérations 69

4.2.3. Présentation des résultats de simulation 73

4.3. Résultats pour le contrôle actif du quart de véhicule à deux degrés de liberté 76

4.4. Conclusion 80

Liste des symboles, Figures et tableaux

Liste des figures

Figure 1.1 - Modèle de la suspension active quart de véhicule 5

Figure 1.2 - Diagramme pôles-zéros du système 21

Figure 1.3 - Réponse fréquentielle des critères de performances 22

Figure 1.4 - Réponse temporelle des critères de performances 23

Figure 2.1 - Schéma bloc pour l'étude de la performance nominale 25

Figure 2.2 - Schéma bloc pour l'étude de la stabilité nominale 28

Figure 2.3 - Bouclage d'une matrice de transfert ( ) 29

Figure 2.4 - Critère de Nyquist multivariable 30

Figure 2.5 - Représentation généralisée des incertitudes de modélisation 32

Figure 2.6 - Schéma d'analyse de la robustesse de la stabilité 33

Figure 3.1 - Schéma général de la commande linéaire quadratique (LQR). 40

Figure 3.2 - Théorème de séparation 43

Figure 3.3 - Structure d'un régulateur LQG 45

Figure 3.4 - Schéma bloc du régulateur et du modèle 48

Figure 3.5 - Critères fréquentiels du modèle quart de véhicule 54

Figure 3.6 - Réponses temporelles du modèle quart de véhicule avec le contrôleur LQR à l'excitation

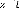
Do . 55

Figure 3.7 - Critères fréquentiels du modèle quart de véhicule 56

Figure 3.8 - Réponse temporelle du modèle quart de véhicule avec le contrôleur LQG à l'excitation

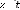
Do . 57

Figure 3.9 - Critères fréquentiels du modèle quart de véhicule 58

Figure 3.10 - Réponse temporelle du modèle quart de véhicule avec le contrôleur LQG/LTR à

l'excitation D( ) 59

Figure 4.1-- Problème DO standard 61

Figure 4.2 - Problème o standard incluant les pondérations 63

Figure 4.3 - Mise sous forme standard du problème avec les pondérations 69

Figure 4.4 - Pondérations fréquentielles appliquées sur les critères de performances 72

Figure 4.5 - Réponse fréquentielle du transfert entre l'accélération verticale de la caisse et le profil de

la route... 73

Figure 4.6 - Réponse fréquentielle du transfert entre l'écrasement du pneu et le profil de la route 74

Figure 4.7 - Réponse fréquentielle du transfert entre le débattement de la suspension et le profil de la

route 74

Figure 4.8 - Réponses temporelles 75

Figure 4.9 - Réponse fréquentielle du transfert entre l'accélération verticale de la caisse et le profil de la route... 76
Figure 4.10 - Réponse fréquentielle du transfert entre l'écrasement du pneu et le profil de la

route 77
Figure 4.11 - Réponse fréquentielle du transfert entre le débattement de la suspension et le profil de la

route... 77

Figure 4.12 - L'accélération verticale de la caisse obtenus pour les différentes lois de commande 78

Figure 4.13 - L'écrasement du pneu obtenus pour les différentes lois de commande 78

Figure 4.14 - Débattement de la suspension obtenus pour les différentes lois de commande 79

Figure 4.15 - Force de contrôle obtenu pour les différentes lois de commande 79

Liste des tableaux

Tableau 1.1 - Valeurs numériques des paramètres du modèle quart de véhicule 20

Tableau 1.2 - Pôles du modèle de la suspension quart de véhicule en boucle ouverte 20

Tableau 3.1 - Poids des pondérations multipliant les critères 50

Tableau 3.2 - Marges de stabilité pour déférentes valeurs de . 52

Tableau 3.3 - Marges de stabilité obtenus pour les différentes lois de commande 52

Liste des symboles

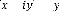
Im : Partie imaginaire d'un nombre complexe, c'est-à-dire Im( + ) = Re : Partie réelle d'un nombre complexe, c'est-à-dire Re( + ) =

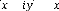
= v-1

S : Variable de Laplace.

: Temps.

: Masse non suspendue.

: Masse suspendue (caisse).

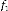
: Amortisseur du pneu.

: Amortisseur de la suspension.

: Ressort de la suspension.

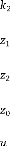
: Ressort du pneu.

: Déplacement verticale de la caisse. : Déplacement verticale de la roue.

: Profit de la route.

: Force de commande.

? ? : La somme des forces qui agissent sur la masse

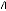
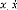
, : Vecteur d'état, dérivée du vecteur d'état. : Pulsation.

: Matrice d'évolution du système.

: Matrice d'application de la commande.

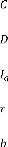
: Matrice d'observation.

: Matrice de transmission directe. : Matrice identité de dimension q. : Signal de référence.

: Perturbation à l'entrée.

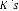
( ) : Fonction du transfert du correcteur.

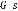
( ) : Matrice de transfert en boucle ouverte.

( , , , ) : Représentation minimale de ( ).

E I1 La sortie du système.

E I1 La commande (sortie du correcteur).

E I1 L'effet sur la sortie des perturbations affectant le système.

E I1 Les bruits de mesure.

: Matrice de sensibilité (en sortie).

: Matrice de sensibilité complémentaire en sortie.

: Matrice de sensibilité (en entrée).

: Matrice de sensibilité complémentaire en entrée.

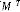
[ ] : Transposée de la matrice .

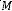
[ ]* : Transposée conjuguée de la matrice .

i ( ) : Représente les incertitudes de modélisation.

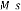
( ) : La matrice de transfert nominale du système.

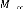
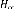
II II : Norme de la matrice .

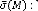
Valeur singulière maximale de la matrice . ( ): Valeur singulière minimale de la matrice . : Critère linéaire d'optimisation.

* : Commande optimale

: Horizon

: Temps final

Etat estimé

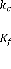
: Gain du retour d'état LQR : Gain du filtre de Kalman

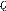
: Gain du recouvrement du correcteur LQG/LTR

: Matrice symétrique définie positive : Matrice symétrique définie positive et : Bruits blancs.

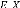
[ ] : Espérance mathématique de .

Abréviations

LQ : Commande linéaire quadratique

LQG : Commande linéaire quadratique gaussienne

LQG/LTR : Commande linéaire quadratique par recouvrement LFT : Transformation linéaire fractionnelle

LTI : Linear Time Invariant (linéaire temps invariant)

Introduction

1

Les vibrations des structures mécaniques sont souvent sources de problèmes affectant le bon fonctionnement de nombreux systèmes, c'est le cas des structures flexibles. La maitrise du comportement dynamique d'une structure flexible lorsque celle-ci opère près de ses fréquences de résonances, devient un problème majeur auquel les constructeur sont confrontés.

Plusieurs études ont donc été effectuées afin d'éliminer l'effet néfaste de ces vibrations. Les premières solutions techniques adoptées furent celles dites passives en adoptant la méthode dite de découplage, ou isolation vibratoire, ce qui consiste à désorganiser la propagation des vibrations en alternant des milieux d'impédances mécaniques très contrastées, ou alors celle de l'amortissement, qui consiste à dissiper en chaleur, du fait d'une forte hystérésis du matériau, les ondes vibratoires qui le sollicitent. Dans les deux cas, nous introduisons des dispositions constructives pour minimiser l'effet des vibrations.

De nombreux travaux de recherche ont portés sur le développement des techniques qui permettent de réduire significativement voir éliminer les vibrations, l'idée étant d'introduire des éléments de tel sorte à éliminer ces vibrations cette méthode de contrôle est appelées contrôle actif.

Le contrôle actif permet de repousser les limites de la maitrise du comportement dynamique des structures flexibles au delà de celles permises par le contrôle passif. Des critères économiques (gain d'énergie, gain de matière, ...), de confort, de sécurité, ...peuvent être introduits. Pour cela la structure doit être équipée d'éléments actifs qui assurent l'échange d'énergie avec le milieu environnant. Les automobiles, comme toutes les structures mécaniques, n'échappent pas aux vibrations et c'est pour cette raison que toutes les automobiles sont munies de suspension. La suspension automobile a pour but de réduire et ultimement d'éliminer ces vibrations qui sont néfastes pour les passagers et pour le véhicule. Le but de ce travail est de mieux comprendre la suspension active et plus précisément de développer des stratégies de contrôle permettant de satisfaire des spécifications face aux perturbations de la route.

Le premier chapitre présente la modélisation du système de suspension quart de véhicule à deux degrés de liberté servant à l'application des commandes ainsi que les entrées du système et les critères de performances.

Le deuxième chapitre est consacré à l'outil d'analyse des systèmes bouclés où nous définissons la stabilité et l'aspect robustesse.

Le troisième chapitre est dédié à la présentation et la comparaison des différentes stratégies de contrôle linéaires quadratique qui sont la commande LQR, la commande LQG et en fin la commande LQG/LTR. Un contrôleur utilisant chaque stratégie est conçu pour un modèle quart de véhicule. Le processus de synthèse et la comparaison avec le modèle passif permettent de faire ressortir les particularités associées à chaque type de contrôle.

Dans le chapitre quatre, nous allons présenter la synthèse 8 qui est une technique de commande robuste qui a fait ces preuves parmi les techniques de commande les plus utilisées, cette technique est basée sur la minimisation de la norme 8 d'un critère de robustesse dans le domaine fréquentiel, c'est donc un problème d'optimisation résolu selon deux approches que sont, l'approche classique basée sur la transformation du problème d'optimisation en deux équations de Riccati, la deuxième approche plus récente est basée sur la solution d'un problème d'optimisation sous forme d'inégalité matricielle (LMI) cette dernière ne sera pas abordée . Une application au modèle quart de véhicule est présentée en fin de chapitre.

Chapitre I

Modelisation du systems physique

3

5

Il est traité dans ce chapitre la modélisation d'un système de suspension active quart de véhicule. Après une brève présentation de la structure, nous élaborons un modèle dynamique tout en considérant un comportement à deux degrés de liberté. Ce dernier est synthétisé à partir de l'analyse du mouvement vertical du quart de véhicule par une méthode classique basée sur les théorèmes généraux de la mécanique. Ensuite, nous introduisons une formulation des équations de la dynamique sous forme d'état. Les automaticiens sont plus familiers avec cette représentation car elle correspond à une paramétrisation de la relation entrée-sortie du système. Pour finir, nous présentons pour ce type de suspension les critères de performances qui seront utilisés dans les chapitres 3 et 4 pour l'analyse et la comparaison des déférentes stratégies de commande. Ces critères serviront donc de référence pour celles des systèmes bouclés par les différentes commandes.

1. Modèle quart de véhicule 1.1. Introduction

L'objectif principal de la conception des systèmes de suspension des véhicules est d'atténuer les perturbations causées par les imperfections de la route, qui sont néfastes pour les passagers et pour le véhicule (sources d'inconfort et d'insécurité).

Suivant le type de système de suspension qu'on veut analyser et suivant l'objectif de l'analyse, la modélisation diffère. Pour des questions de simplicité, et de sens physique, lors de cette étude nous utilisons un modèle quart de véhicule à deux degrés de liberté. Ce modèle permet de prendre en compte le mouvement vertical de la caisse ainsi que celui de la roue quel que soit le système de suspension en question. De plus, concernant la dynamique du véhicule, le modèle est valide pour l'étude du confort routier et de la tenue de route du véhicule.

1.2. La suspension

On désigne sous le nom de suspension l'ensemble des éléments mécaniques qui relient les
roues à la structure principale d'un véhicule (caisse). Le système de suspension verticale

permet de supporter le poids du véhicule et de filtrer les irrégularités de la route, tout en maintenant une garde au sol convenable, et les pneumatiques en contact avec le sol.

Dans les systèmes à suspension automobile, nous distinguons trois types:

? Suspension passive:

Les systèmes à suspension passive traditionnelle sont conçus à base des éléments passifs, c.à.d. équipée généralement d'un ressort et d'un amortisseur de valeurs fixes (invariant dans le temps), et ils sont choisis en fonction des exigences de conception des véhicules.

? Suspension semi-active:

Les systèmes à suspension semi-active, sont constitués d'un élément passif (ressort) et d'un amortisseur contrôlé. L'amortisseur semi-actif, tout comme l'amortisseur passif, ne peut que dissiper de l'énergie en produisant une force qui s'oppose à la vitesse relative entre la caisse et la roue. Mais contrairement à un amortisseur passif, cette force est modulable, d'où le nom «semi-actif».

? Suspension active:

Les suspensions passive et semi-active produisent des forces qui sont limitées par les positions et les vitesses relatives entre la caisse et la roue et qui ne peuvent que dissiper de l'énergie. Cela peut se traduire par la limitation de leurs aptitudes en termes de confort (isolation vibratoire) et de sécurité (stabilité de conduite).

Les systèmes à suspension active peuvent améliorer leurs qualités à travers le rajout d'un amortisseur actif, qui génère des forces instantanées permettant de supporter les charges et d'assurer la sécurité et le confort contre les contraintes (mauvaise route, surcharge, ...etc.).

Tout au long de notre étude, nous nous consacrons donc à la suspension active, constituée par des éléments passifs (ressort et amortisseur) en parallèle avec un amortisseur actif (actionneur).

1.3. Description du modèle quart de véhicule

Une représentation très utilisée dans la littérature d'un système de suspension active est de prendre le cas d'une roue, c'est-à-dire un quart de véhicule. Ce modèle est semblable au modèle passif mais inclut un actionneur tel qu'illustré à la figure ci-dessous [1.1]. La simplicité de ce modèle en facilite l'optimisation et l'analyse.

Figure 1.1 - Modèle de la suspension active quart de véhicule

L'entrée du système est le mouvement vertical de la route sous le pneu z0. Le modèle est composé de deux masses distinctes. La masse non suspendue M1 représente la masse de la roue avec tous ses éléments (pneu, la jante et les axes...etc.). La masse suspendue M2 représente la masse du châssis supportée par la roue en question. Le pneu est modélisé par un ressort en parallèle avec un amortisseur linéaire de constante situés entre la masse non-suspendue et la route. La suspension est composée d'un ressort et d'un amortisseur linéaire de constante en parallèle avec un actionneur de force situés entre la masse suspendue et non-suspendue. L'amortisseur actif (actionneur) génère des forces appliquées au système (entre les masses suspendue et non suspendue) sous la demande d'une stratégie de contrôle.

1.3.1. Équations de la dynamique

Il existe un nombre important de méthodes pour établir les équations dynamiques d'un système mécanique. Dans notre cas, on utilise une formulation classique basée sur les théorèmes généraux de la mécanique s'appuyant sur l'emploi du principe fondamental de la dynamique.

1.3.1.1. Déterminations des équations du mouvement

Le modèle considéré [Figure 1.1] prend en compte le mouvement vertical de la caisse (z2) ainsi que celui de la roue (z1). C'est donc un modèle quart de véhicule à deux degrés de liberté. Il est régis par des équations linéaires à coefficients constants;

La dynamique du système est décrite par les équations différentielles suivantes :

I

I

I I I F

I I I F

Z H - - -

Z H H

(1.1)

Z -â I F F - 1 F F

1 1 F F - 1 1 F F

z -É

Les équations sont obtenues en additionnant les forces appliquées sur les masses suspendue et non suspendue.

Les forces des ressorts et des amortisseurs sont données par:

7

Z -â I l F 1 F F (1.2)

I E F F - 1 1 F F

z -É

Avec :

: Sont respectivement les coefficients de raideur et d'amortissement verticaux de la suspension.

	: Sont respectivement les coefficients de raideur et d'amortissement verticaux du
pneu.

: La force développée par l'actionneur.

N.B. Le temps apparaît comme une variable qui évolue continûment. Sur un horizon de durée , la variable prend toutes les valeurs de cette période en croissant.

Les équations différentielles obtenues ci-dessus (1.1) peuvent être mis sous forme d'état.

1.3.2. Mise sous forme d'état

1.3.2.1. Le formalisme d'état [1]

Le formalisme d'état est une vision élargie de la théorie des systèmes reposant sur le concept d'énergie. La démarche est naturelle et complète puisque découlant d'une logique considérant que l'évolution de tout système est directement liée à celle du volume énergétique qu'il renferme. Pour un système considéré, ce volume représente l'état du système alors spécifié par des grandeurs caractéristiques ; modifier l'évolution revient donc à agir sur l'état grâce aux facteurs d'énergie potentielle et cinétique que sont les grandeurs caractéristiques.

Il s'agit de la formalisation des équations linéaires sous forme matricielle pour représenter la dynamique du système. Cette représentation fait appel aux propriétés de l'algèbre matricielle linéaire pour mener une étude plus fine du système considéré.

1.3.2.1.1. Équations d'état

L'équation d'état se présente comme une forme d'une équation différentielle du premier ordre. L'équation prend la forme suivante :

= [ ] H 2 (1.3)

Avec :

: Vecteur d'état à n composantes, tel que :

Z , KKI 2 (1.4)

: Vecteur d'entrée à r composantes, tel que :

Z , KKI 2. (1.5)

: Matrice d'évolution du système, carrée de dimension (n x n).

: Matrice d'application de la commande, de dimension (n x r).

N.B. La dimension d'une matrice est donnée par: (nombre de lignes, nombre de colonnes).

1.3.2.1.2. Équation d'observation

Les grandeurs d'état ne sont pas nécessairement celles intéressant l'utilisateur du système ;
toutefois, la simple raison suffit à comprendre que les variables choisies ou désignées comme

9

sorties sont fonction de l'état et des entrées. L'équation d'observation détermine alors les relations qui existent entre ces diverses grandeurs, soit :

Z , 2 H , 2 (1.6)

Avec :

: Vecteur de sortie ou d'observation à m composantes, tel que :

Z , KKK 2 (1.7)

: Matrice d'observation, de dimension (m x n).

: Matrice de transmission directe, de dimension (m x r).

? En pratique, on repère le nombre de grandeurs d'état d'un système au nombre

d'éléments susceptible d'accumuler de l'énergie, potentielle ou cinétique.

1.3.2.2. La formalisation des équations sous forme d'état

Pour formuler la dynamique du système en fonction de variables d'état, nous débutons par

définir le vecteur d'état i F.

Suivant la figure 1.1, Les deux masses et la liaison élastique sont les éléments susceptibles d'accumuler respectivement de l'énergie cinétique et de l'énergie potentielle. Le vecteur d'état le plus naturel est donc, constituer de quatre variables: la vitesse de déplacement vertical de chacune des masses, l'effort transmit par le débattement vertical (ressort) de la suspension et l'écrasement vertical du pneu. Le vecteur d'état a été choisi tel que :

I E F FI E F F

I F Z E F f F , , E F 1 1 , EN1UF

Par la suite, les équations sont décomposées en fonction du vecteur d'état I F, de l'entrée contrôlée et de l'entrée perturbatrice F F . L'équation d'état associée aux équations (1.1) est sous la forme.

P F Z [ ] I F H 2 I F H 2 f F EN.9F

Avec les matrices suivantes :

0

0

L

1

-N

0

0

I

0

- /

z

z

z

10)

0

0

- /

0

N1

0

0

1

-I H FT

-N

I-

10

Le vecteur d'entrée , I F I F2 est constitué de la variation du profil de la route vertical et

de la force active produite par l'actionneur (commande).

Afin de déterminer la qualité de la suspension, il est nécessaire de définir des critères, ces critères permettent de caractériser les performances de la suspension. Rappelons que dans ce chapitre, nous nous intéressons uniquement à l'analyse en boucle ouverte (sans contrôle). Le système est donc soumis à la seule sollicitation externe, qui est le profil de la route vertical.

1.3.2.3. Critères de performances

Dans la conception des systèmes de suspension des véhicules, l'objectif double est d'assurer une bonne isolation vibratoire vis-à-vis des sollicitations de la route pour le confort des passagers et de maintenir un niveau d'adhérence au sol suffisamment important pour garder le contrôle du véhicule en toute sécurité.

Les critères de performance sont spécifique aux suspensions et concerne principalement le confort, la tenue de route et le débattement des suspensions. Nous présentons dans cette partie des critères usuels de la littérature portant sur l'étude d'un modèle quart de véhicule à deux degrés de liberté équipé d'une suspension active. Ils permettent de définir les performances nominales du système, c'est-à-dire, les performances obtenues pour un système nominal sans incertitudes.

1.3.2.3.1. Confort

La notion du confort est liée au bien-être des passagers dans le véhicule. Sur mauvaise route, les irrégularités de la route excitent en déplacement les ressorts. Ces derniers transforment par leur compression ce déplacement en effort qui se traduit par l'accélération verticale de la caisse, et qui affecte le confort. Selon l'accélération à laquelle est soumis le passager, ce dernier peut ressentir des malaises. Lorsque l'accélération varie à une certaine fréquence, des malaises, dus aux vibrations de certains organes du corps humain, peuvent être ressentis. De plus, l'allongement de la durée d'exposition aux vibrations augmente sa sensibilité. Pour un meilleur confort vertical, l'accélération subie par le passager doit être minimisée.

1.3.2.3.2. Tenue de route

La tenue de route peut être définie par l'aptitude que possède un véhicule à adhérer à la route. Elle représente la stabilité d'un véhicule.

Le pneumatique représente le seul lien du véhicule avec le sol. Il génère des forces
longitudinale (en cas d'accélération ou de freinage) et/ou latérale (en manoeuvre de
changement de voie) nécessaires donc aux changements et aux corrections de trajectoire.

12

Cette force d'adhérence au sol varie largement en fonction de la force de contact (normale). Pour assurer la continuité du contact entre le pneumatique et le sol (force du pneu constante), la suspension doit réduire les variations de la force de contact appliquée sur le pneu. Celle-ci passe par la minimisation de la composante dynamique de l'écrasement du pneu. Une bonne tenue de route correspond à un écart nul entre le déplacement vertical de la roue et du sol.

1.3.2.3.3. Débattement de la suspension

Une bonne isolation vibratoire vis-à-vis des sollicitations de la route et un maintien de niveau d'adhérence au sol suffisamment important sont réalisés sous un certain débattement de la suspension. Or celui-ci est limité par des butées de choc (compression) et de rebond (détente) pour des aspects d'encombrement. Afin de réduire la hauteur du centre de gravité et d'éviter l'impacte de ces butées, il est donc important de prendre en compte le débattement maximal de la suspension dans la synthèse d'une stratégie de contrôle afin d'éviter les chocs qui surviennes lorsque la suspension arrive en fin de cours. Le but est uniquement de le contraindre à rester dans un certain intervalle tel que les butées ne soient pas atteintes.

1.3.2.3.4. Autre critère

Dans le cas d'une suspension active, on s'intéresse aussi à la commande I F en vérifiant qu'elle satisfait les contraintes technologiques de l'actionneur. En effet, ce dernier génère une force qui est appliquée sur les masses suspendue et non suspendue. Cependant, la puissance requise pour générer cette force est limitée puisqu'elle provient généralement du moteur. Il est doc important que celle-ci soit également minimisée.

En résumé, dans le cas de la suspension active, pour maximiser les performances, quatre critères déférents doivent être minimisés :

1' Accélération verticale de la caisse 1' Ecrasement du pneu

1' Débattement de la suspension 1' Force générer par l'actionneur

Ces critères de performances nous servirons donc à introduire le vecteur de sortie ou

d'observation F F.

Chaque critère de performance cité ci-dessus, on lui associe une matrice d'observation et une matrice de transmission directe. Ces matrices sont donnée par:

- Accélération vertical de la caisse I E F F z x? (tF :

Z xM - - ]

Z x1v (1.11)

Z x z

- Ecrasement du pneu I F - F F Z f (tF :

Z xN 0 0 1]

Z x1v (1.12)

Z x1V]

- Débattement de la suspension F F - I F Z (tF :

Z xM 0 1 0]

Z [dV] (1.13)

z x1V]

- Force de l'actionneur I F :

Z xM 0 0 IVk

Z x1v (1.14)

Z xN]

l'équation d'observation est donnée par :

( FZ 3 2 E FH 3 2 E FH 3 2 E F (1.15)

avec les matrices suivantes:

0

0

/

0

0 0

=

0

0

- L

0

1

- L

0

0

=

=

0

0

0

0

NL

0

0

1

(1.16)

on obtient ainsi le système d'équation suivant :

(1.17)

E FZ 3 2 1 FH3 2 1 FH3 2 EF

E FZ 3 2 1 FH3 2 1 FH 3 2 EF

Le quadruplet lb ]z ,b ] ,3 z, 3 zF est une représentation d'état du système

14

considéré. Cette représentation interne n'est pas unique, il en existe une infinité qui sont équivalentes et qui dépendent du vecteur d'état choisi.

(1.19)

E F Z I F H I F H I F

I F Z I F H I F H I F

> Avec l'approche par représentation d'état, les problèmes de commande reviennent à

étudier les propriétés algébriques des matrices réelles et de leurs valeurs propres.

Le système d'équations (1.17) peut également être décrit de façon externe (matrice de transfert) :

1.3.3. Relation entrée-sortie

Le comportement dynamique d'un système linéaire étant défini par l'évolution de ses variables d'état, on sait que les variables d'observations (sortie) s'expriment alors par une forme linéaire des variables d'état et des variables d'entée (1.15).

La relation entrée-sortie temporelle (système d'équations différentielles) est présentée sous la forme opérationnelle en appliquant aux équations d'état et d'observation la transformation de Laplace.

Soit I Fla transformé de Laplace de I F xM, oox , alors :

{ ( 1} Z I F - (1.18)

À l'instant Z 0 le système est au repos, c'est-à-dire que son énergie emmagasinée est nulle, il en découle ;

Z 0 , le système d'équation (1.17) devient :

16

que l'on peut encore écrire :

I F Z 1 1 F F (1.20)

d'où l'on tire la matrice de transfert :

I F Z , - H (1.21)

Avec F F Z , I F F F] , Z , z , Z , z

La matrice I F est une matrice rationnelle, c'est-à-dire que ses composantes sont des fractions de polynômes en .

Il existe plusieurs façons de représenter la matrice I F. Une possibilité consiste à calculer le
plus petit commun multiple de tous les polynômes dénominateurs de I F, que nous noterons

par I F. La matrice I F peut alors s'écrire :

I F Z E F (1.22)

E F

Où F F est une matrice polynomiale, c'est-à-dire que ses composantes sont des polynômes
en . Une troisième représentation I F consiste à utiliser des fractions de matrices

polynomiales.

Nous pouvons alors écrire :

I F Z I I I F Z I F I F (1.23)

Où I F, I F, I F et I F sont des matrices polynomiales avec I F et I F carrées

inversibles. Le couple I F, I F est une fraction de matrices polynomiales à droite. Le

couple I F, I F est une fraction de matrices polynomiales à gauche. En particulier, nous

avons :

I F Z CEi F F (1.24)

Les zéros du polynôme I F, c'est-à-dire les valeurs pour lesquelles le polynôme s'annule,
sont les pôles du système multivariables (racines de I F Z 0). Ce sont également les zéros

des matrices polynomiales I F et I F.

> Avec l'approche par matrice de transfert, les problèmes de commande reviennent à

étudier les propriétés algébriques des matrices polynomiales et de leurs zéros.

Dans ce qui suit, nous introduirons une définition de la notion de stabilité des systèmes linéaires et invariants et les outils mathématiques de base nécessaires pour l'analyse. Ces outils concernent essentiellement le calcul matriciel dans le domaine complexe.

1.4. Notion de stabilité

La notion de stabilité est fondamentale dans le développement des systèmes de commande et particulièrement pour les architectures de commande à contre-réaction. En effet, en l'absence de cette propriété qualitative, aucun système n'est utilisable en pratique. Ce concept dont chacun a une compréhension intuitive s'avère délicat à définir de manière uniforme dans sa généralité. Il est le plus souvent nécessaire de définir les propriétés particulières du système que l'on souhaite caractériser à travers une notion de stabilité qui sera adéquate.

Qualitativement, on dit qu'un système est dans un état stable quand à la suite d'une
perturbation (de durée limitée) il tend à retrouver son état initial ; cette définition est

18

satisfaisante pour les systèmes linéaires qui évoluent selon une réponse transitoire amortie lorsqu'ils sont stables.

Un autre point de vue peut être adopté où la stabilité d'un système est définie simplement au
sens d'un critère entrée-sortie ; un système sera dit stable si sa réponse à toute entrée bornée

est bornée : on parle de stabilité _ f 1 I gl am faél i gl am 1 l fél IF. Cette définition

ne met en jeu que les signaux exogènes ; aucune variable interne n'est directement concernée.

1.4.1. Conditions de stabilité

Dans le cas des systèmes linéaires invariants I F, la propriété de stabilité peut être testée en

vérifiant la localisation des valeurs propres de la matrice (racines du déterminant de la

matrice I C F, encore appelé polynôme caractéristique) ou de façon équivalente, des

pôles de la matrice de transfert I F, dans une certaine région du plan complexe. Pour les systèmes continus, cette région est le demi-plan complexe gauche. D'autres régions plus complexes peuvent également être considérées pour assurer une certaine performance du système. Il existe différents critères algébriques permettant de tester cette localisation des pôles, comme par exemple, le critère de Routh-Hurwitz.

· La Stabilité

Un système au repos (conditions initiales nulles) est stable au sens _ f1 si et seulement si

pour toute entrée I F bornée la sortie I F est bornée.

Théorème 1.1 : un système i of possédant entrées et sorties de matrice de réponse

impulsionnelle DI F est _ f 1 stable si et seulement s'il existe une constante [ M telle que :

5 --fi I I CI CI II DD

Il est à noter que la stabilité EIED n'impose pas à la réponse impulsionnelle d'être bornée.

Seule l'aire sous la courbe de la réponse impulsionnelle doit l'être. Toutefois, cette

caractérisation n'est pas facile à utiliser en pratique (calcul de l'intégrale de la valeur absolue de la réponse impulsionnelle). Cela nous conduit à chercher une caractérisation plus simple utilisant la fonction de transfert (matrice de transfert cas multivariables) qui est l'équivalent opérationnel de la réponse impulsionnelle, soit :

( ) = ( ) Fonction de transfert entre la é sortie et la é entrée.

Cette caractérisation peut être développée à partir de la localisation des pôles du système dans

le plan complexe. Alors, le système est BIBO stable si les pôles (zéros du polynôme ( )

définis au paragraphe 1.3.3), satisfont les trois conditions du théorème 1.2.

Théorème 1.2 : le système est BIBOstable si et seulement si :

) Les pôles de ( ) sont à partie réel négative

) ( ) Ne possède pas de pôles à l'origine

) Les pôles à partie réel nulles doivent être simples

20

1.5. Résultats de simulation

Nous présentons dans cette partie les résultats de simulation des différents critères de performances. Les valeurs des paramètres constants du modèle utilisés pour la simulation sont données par le tableau suivant :

symbole	paramètre	valeur	unité
	Masse non suspendue	30	kg
	Masse suspendue	250	kg
	Ressort de la suspension	20000	N/m
	Ressort du pneu	200000	N/m
	Amortisseur de la suspension	1000	N.S/m
	Amortisseur du pneu	100	N.S/m

Tableau 1.1 - Valeurs numériques des paramètres du modèle quart de véhicule

Afin d'analyser le comportement du système en boucle ouverte (sans contrôle) sur le plan fréquentiel et temporel, nous allons calculer ses valeurs propres, ensuite tracer les réponses fréquentielles de chaque critère de performance ainsi que les réponses temporelles.

? Valeurs propres

Valeurs propres	amortissements	Pulsations (rad/s)
-1.64 #177;48.43	0.195	8.59
-18.7 #177; 82.9	0.219	85

Tableau 1.2 - Pôles du modèle de la suspension quart de véhicule en boucle ouverte

Le système possède quatre valeurs propres complexes conjuguées à partie réelle négative, signifiant qu'il est donc stable.

Partie imaginaire

100 80 60 40 20 0 -20 -40 -60 -80 -100

La figure suivante présente le diagramme pôles zéros du système :

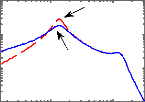
modes lents

modes rapides

-20 -18 -16 -14 -12 -10 -8 -6 -4 -2 0

Fartie réelle

Figure 1.2 - Diagramme pôles-zéros du système

Nous constatons sur la figure 1.2, deux modes oscillatoires (pôles complexes conjugués), ces modes correspondent respectivement au mode lent de la caisse (masse suspendue) et au mode rapide de la roue (masse non suspendue).

? Réponses fréquentielles

Comme nous l'avons vu au paragraphe (1.3.2.3), nous devons surveiller l'accélération

verticale de la caisse ( ( ) ), le débattement de la suspension ( ) - ( ) et l'écrasement

du pneu ( ) - ( ) .

La figure suivante montre les résultats fréquentiels de simulation en boucle ouverte :

Diagramme de Bode du transfert Yacc(s)/w (s)

10²

10¹

10⁰

10^-1

10⁰ 10¹

Magnitude (abs)

liagramme de Bode du transfert Ypneu(s)/w (s)

1

10^-2

10^-3

10⁰ 10¹

Magnitude (abs)

10

Fréquence (Hz) Fréquence (Hz)

Diagramme de Bode du transfert Ysusp(s)/w (s)

10⁰

10^-1

10^-2

10^-3

10⁰ 10¹

Magnitude (abs)

22

Fréquence (Hz)

Figure 1.3 - Réponse fréquentielle des critères de performances

Le test temporel simule le passage du véhicule sur un profil de la route ayant comme équation :

(

33

33333 333 3 33333 3 3 33 33 3 3 3 333 (1.26)

3 33333

Dans notre cas est considérée comme étant le profil de la route 2 3, ceci s'explique par le fait que l'amortissement du pneu peut être négligé.

Accélération Verticale de Caisse

0 0.5 1 1.5 2

temps (s)

x 10-4 Ecrasement du pneu

passif

0 0.5 1 1.5 2

tamps (s)

Amplitude (m)

4

2

0

-2

-4

-6

Amplitude (m/s²)

-0.2

-0.4

0.4

0.2

0

passif

x 10-3 Débattement de suspension

Amplitude (m)

-2

-4

4

2

0

passif

0 0.5 1 1.5 2

temps (s)

Figure 1.4 - Réponse temporelle des critères de performances

24

1.6. Conclusion

Dans ce chapitre et dans un premier temps, nous avons présenté brièvement les différents types de suspension d'un véhicule ainsi que la structure du système étudié. Également, la modélisation et la mise sous forme d'état de la structure ont été abordées.

Nous avons abouti à un modèle de quatrième ordre. Toutefois, ce modèle servant par la suite à l'application des commandes ne représente pas parfaitement le modèle réel.

Chapitre II

Outils d'analyse des systemes boucles

25

2. Introduction

Ce chapitre est consacré à un rappel des outils d'analyse des systèmes bouclés. Après un bref rappel sur l'analyse de la stabilité et de la performance du système bouclé nominal, nous nous intéressons à la notion de robustesse. Nous différentions deux types d'incertitudes : les incertitudes non structurées, seulement caractérisées par une borne de leur norme, et les incertitudes structurées qui correspondent à une représentation beaucoup plus fine des incertitudes. Nous rappelons le théorème du faible gain appliqué à l'analyse de la robustesse face à des incertitudes non structurées.

2.1. Propriétés du système nominal

Considérons le système bouclé de la Figure 2.1, où ( ) est un modèle sous forme de matrice
de transfert d'un système multivariable, de dimension X et ( ) le correcteur de

dimension X . On appelle :

consigne ou signal de référence.

la sortie du système.

la commande (sortie du correcteur).

perturbations affectant la sortie du système. des bruits de mesure.

= - l'écart d'asservissement.

Figure 2.1 - Schéma bloc pour l'étude de la performance nominale

27

29

31

( ) = ( )'( ) ( )'( ) ) : ) (2.6)

( )

Avec : ( ) = ( )

La référence , la perturbation et le bruit de mesure sont les signaux exogènes qui

agissent sur le système bouclé. Le signal est généralement la consigne générée qui dirige la sortie . Les signaux et sont en général les signaux non désirés dont l'influence sur le système devrait être limitée.

2.1.1. Performances nominales

La performance nominale consiste à assurer, pour le système en boucle fermée correspondant au modèle utilisé pour le calcul de la commande, des propriétés convenables, notamment de précision et de rapidité.

Pour traduire mathématiquement ces propriétés, un certain nombre de matrices de transfert caractéristiques du système en boucle fermée sont définies :

2.1.1.1. Matrices de sensibilité

On peut, à partir du schéma de la Figure 2.1, exprimer les transformées de Laplace des

signaux ( , , et ) en fonction des transformées de Laplace des signaux ( et ) :

( ) = + ( ) ( ) ( ) ( ) -- ( ) + ( ) ( ) ( ) (2.1)

( ) = + ( ) ( ) -- ( ) f. ( ) ( ) ( ) ( ) ( ) (2.2)

( ) = ( ) + ( ) ( ) -- ( ) -- ( ) (2.3)

Ces relations font intervenir les matrices de transfert suivantes :

. Matrices de sensibilité en sortie:

( ) = ( ) ( ) appelée matrice de sensibilité en sortie. Elle représente la

matrice de transfert entre la consigne et l'écart . Ainsi que l'influence des perturbations sur la sortie et l'écart .

( ) = ( ) ( ) ( ) est appelée matrice de sensibilité complémentaire en

sortie. Elle représente la matrice de transfert entre la consigne et la sortie , ainsi que

l'influence des bruits de mesure sur la sortie et l'écart .

2.1.1.2. Objectifs de commande

L'objectif de commande est de concevoir un correcteur ( ) qui rend

( ) , ( ) et ( ) ( ) le plus faible possible, tout en assurant la stabilité interne du

système bouclé.

Compte tenue du sens donné à ( ) et ( ) , il est clair que lorsqu'en effectue la synthèse du correcteur ( ) on doit chercher à :

· rendre ( ) le plus faible possible afin de réduire l'influence des perturbations et d'assurer un bon suivi de consigne.

· rendre ( ) le plus faible possible afin de réduire l'influence des bruits de mesure.

rendre ( ) ( ) le plus faible possible afin de réduire l'effort de commande.

·

Le système en boucle fermée devra donc satisfaire un certain nombre de spécification sur les
différents transferts caractérisant le système. Ces transferts étant liés, notamment à travers la

relation ( ) + ( ) = , il faudra donc établir un compromis entre ces spécifications.

En effet, du fait de la contrainte ( ) + ( ) = , il est impossible de rendre faible

simultanément ( ) et ( ) .

Cependant, Les perturbations sont des signaux qui agissent en basses fréquences et le bruit en

haut fréquence. Il est donc possible de concevoir un correcteur ( ) qui rend faible ( ) en basse fréquence et ( ) en haute fréquence.

( )

- Comportements de ( )

Ces deux matrices de sensibilité s'expriment uniquement en fonction de la matrice de transfert

de la boucle ouverte ( ), définie par:

( ) = ( ) ( ) (2.4)

Dans les zones où la boucle ouverte présente un gain élevé, ce qui se produit en général aux

basses fréquences, ( ) ) ( ) ( ) .

Réciproquement, dans les zones où la boucle ouverte présente un gain faible, ce qui se produit

en général aux hautes fréquences, ( ) et ( ) ( ) ( ).

2.1.2. Stabilité nominale [8]

Soit le système bouclé de la figure 2.2, où G(s) représente la matrice de transfert d'un système

multivariable de dimension x , et ( ) le correcteur de dimension x ; et sont

respectivement la référence et la sortie reçue du système bouclé.

+

( )

( )

-

Figure 2.2 - Schéma bloc pour l'étude de la stabilité nominale

2.1.2.1. Critère de Nyquist (cas multivariable)

Le critère de Nyquist est un critère graphique qui permet de ramener l'étude de la stabilité d'un système en boucle fermée à l'étude de certaines caractéristiques de la réponse fréquentielle de la fonction ou matrice de transfert en boucle ouverte.

( )

+

-

Figure 2.3 - Bouclage d'une matrice de transfert ( )

( ) = ( ) ( ) est le transfert en boucle ouverte, supposée strictement propre ( ( )

est matrice carrée de dimension ).

Pour appliquer correctement le critère de Nyquist, il faut s'assurer qu'il n'y ait pas de simplification pôle/zéros instables dans la chaine d'asservissement (modes cachés).

Théorème 2.1 : (critère de Nyquist multivariable) - dans le cas où la matrice de fonctions de
transfert ( ) ne possède pas de pôles imaginaires purs, le système bouclé multivariable
(figure 2.3) est stable si et seulement si l'image du contour d'exclusion (figure 2.4) de

Nyquist par det + ( ) encercle l'origine (dans le sens inverse des aiguilles d'une

montre) un nombre de fois égale au nombre de pôles instables de ( ).

( ) ( )

( ) det + ( ) ( )

Figure 2.4 - Critère de Nyquist multivariable

Contrairement à ce que suggère l'énoncé du critère de Nyquist, son principal intérêt n'est pas, en général, de vérifier à partir de la boucle ouverte si le système en boucle fermée correspondant est stable ou non. On peut en effet aisément déterminer si le système en boucle fermée est stable en calculant ses pôles. L'intérêt du critère de Nyquist est autre et double. Dans le contexte de la recherche d'un correcteur qui stabilise un système , le critère de Nyquist appliqué à = permet de choisir graphiquement de façon à assurer la stabilité du système bouclé. L`autre grande application est d'étudier pour un système bouclé stable ses marges de stabilité (marges de phase et de gain).

L'application du critère de Nyquist est complexe. En pratique, on utilise le plus souvent la méthode dite du faible gain.

2.1.2.2. Théorème du faible gain [14]

Supposons que ( ) et ( ) ont tous les pôles à partie réelle négative, alors le système

bouclé de transmittance en boucle ouverte ( ) = ( ) ( ) est stable si ? ?8 < 1.

Ou bien si : V JZ )

Où valeur singulière maximale de ( ) calculée à la pulsation

2.2. Notions de robustesse

La mise en équation d'un processus physique nécessite des approximations, d'où résultent par conséquent des incertitudes de modèle. De plus la synthèse du correcteur fait généralement appel à un modèle simplifié, dans lequel sont, par exemple négligées les dynamiques hautes fréquences du système, celles des capteurs ou actionneurs, d'éventuels retards purs...etc. Enfin, les paramètres du modèle ainsi obtenus sont plus au moins entachés d'incertitudes.

On dit qu'une propriété du système asservi est robuste si cette propriété est garantie malgré la présence d'incertitudes. En particulier, on cherchera au moins à assurer au système asservi la robustesse de la stabilité. Une exigence plus importante consiste à garantir la robustesse d'une performance (telle que le taux de rejet d'une perturbation par exemple).

2.2.1. Incertitudes de modèle [4]

On ne peut parler de robustesse que par rapport à un objectif donné et aux types d'incertitudes considérées. Dans le cadre linéaire, celles-ci sont généralement regroupées en deux classes:

1' Incertitudes non-structurées:

Elles représentent les incertitudes influant sur le système mais pour lesquelles aucune information structurelle n'est disponible. Elles peuvent traduire par exemple des phénomènes hautes fréquences comme des dynamiques négligées dans un modèle (incertitudes dynamiques).

1' Incertitudes structurées :

Elles représentent des incertitudes dont on peut déterminer l'influence sur la structure du système étudié. Elles peuvent traduire des phénomènes basses fréquences comme des variations paramétriques dues à l'usure du système (incertitudes paramétriques).

Une représentation générale d'un système soumis à des incertitudes de modèle est donnée sur la figure 2.5.

?( )

( )

Figure 2.5 - Représentation généralisée des incertitudes de modélisation

Toutes les incertitudes de modèle sont rassemblées dans la matrice L( ). La matrice de
transfert ( ) modélise les interconnexions entre les entrées , les sorties , et les signaux

et qui permettent de faire intervenir les incertitudes.

En écrivant les relations entre les déférents signaux :

( ) = ( ) ( ) + ( ) ( )

( ) = ( ) ( ) + ( ) ( ) (2.5)

( ) = i( ) ( )

On calcul le transfert entre et :

33

L'expression (2.6) est appelée une Transformation Fractionnaire Linéaire LFT. Elle est

notée ,i(s)

Pour écrire l'expression (2.6), il faut que la matrice ( )L( ) inversible pour

presque tout .

L'étude de la robustesse consiste à chercher à garantir une propriété particulière (par exemple la stabilité) pour un ensemble d'incertitudes L( ). On peut imaginer 2 degrés de complexité différents pour aborder ce problème :

- Soit en ignore la structure de i ( ), en cherchant simplement quelle est la plus grande

valeur admissible de sa norme. L'outil adéquat pour traiter le problème de cette façon est la norme 8.

- Soit on prend compte de la structure de L( ), ce qui conduit à des résultats plus

précis. Il faut pour cela définir un nouvel outil : la valeur singulière structurée.

Remarque :

Si la propreté qu'on cherche à garantir est la stabilité, et si par hypothèse ( ) et L( ) sont
stable, la seul source d'instabilité provient du bouclage par L( ), et il est donc équivalent

d'étudier la stabilité du système de la figure 2.6, avec ( ) = ( ).

i( )

( )

Figure 2.6 - Schéma d'analyse de la robustesse de la stabilité

2.2.2. Robustesse en stabilité : analyse non structurée

Nous faisons l'hypothèse que le système nominal est stable. Notre but est alors de vérifier que le système demeure stable en présence d'une incertitude vérifiant 2.6. Une solution simple à ce problème est donnée par le théorème du faible de gain, qui donne une condition nécessaire et suffisante de stabilité.

Théorème 2.2 : (théorème du faible gain) - Si ( ) et L( ) sont stables, le système de

la figure 2.6 est stable pour tout L( ) tel que IIL( )II() < 1 si et seulement si

II ( )ILo ~ 1 V JZ )

Chapitre III

Commandes linealres (LOR_I LOG, LQGILTR)

35

Dans ce chapitre, nous nous penchons sur l'aspect contrôle optimal de la suspension active par les commandes linéaires (LQR, LQG, LQG/LTR). Dans un Premier temps, nous présentons la théorie du contrôle optimale de chacune de ces techniques de commande. Ensuite, chaque stratégie de contrôle est appliquée au modèle quart de véhicule et comparée à la suspension dite passive (en boucle ouverte).

3.1. Introduction

3.1.1. Contrôle optimal

La théorie de contrôle moderne se présente comme la synthèse de la matrice de gain du contrôle par retour d'état. Le contrôle intervient dans l'équation d'état comme une donnée que l'on peut choisir, en imposant une énergie de contrôle, afin de minimiser l'énergie mécanique de la structure. Le problème du contrôle optimal consiste essentiellement à déterminer le contrôle *( ), admissible, apte à conduire le système vers un état désiré *( ), tout en minimisant une fonctionnelle coût. Afin de déterminer la solution d'un problème du contrôle optimal, il existe plusieurs approches dont deux sont principales, la première, constituée de la théorie de Hamilton-Jacobi, consiste à établir des conditions suffisantes d'optimalité global et la deuxième se base sur le principe de minimum de Pontriaguine qui est un principe de variation, le contrôle optimal doit minimiser une fonction appelée Hamiltonien.

3.2. Commande Linéaire Quadratique

3.2.1. Formulation du problème de commande (LQR)

Nous considérons le système linéaire continu, invariant dans le temps, stabilisable et observable décrit par les équations d'états suivantes :

( ) = ( ) + ( )

( ) = ( ) + ( ) (3.1)

( ) = ( ) + ( )

où :

( ) : Vecteur d'état, de dimension x 1.

( ) : Vecteur de commande, de dimension x 1.

( ) : Vecteur de sortie ou d'observation, de dimension x 1. ( ) : Vecteur de sorties contrôlées, de dimension x 1.

, , , ,

,

Sont des matrices de dimensions appropriées indépendantes du temps.

La synthèse linéaire quadratique dénommée LQ ou LQR (linear quadratic regulator) consiste

en la recherche d'une matrice gain , telle que la commande par retour d'état ( ) =
- ( ) stabilise le système et minimise l'expression quadratique à horizon infini ^[1] de la

fonction coût suivante :

8

( ( ) ( ) + ( ) ( ))

2

=

1

(3.2)

2 ( ( ) ( ) + ( ) ( ) + ( ) ( ) + ( ) ( ))

=

1

(3.3)

où les matrices de pondérations ,

, p p

satisfont :

= ( + )

= ~ 0, = > 0, =

, =

que l'on peut réécrire sous la forme:

Est une matrice carrée symétrique définie semi-positive et est une matrice symétrique définie positive. , , Sont respectivement les matrices de pondération sur l'état, de couplage état-action et sur l'action.

Comme nous l'avons vu précédemment, l'objectif de la commande quadratique est de minimiser une fonctionnelle définie par l'équation (3.2) à l'aide de la matrice gain optimale placée dans la boucle de réaction. La solution à ce problème d'optimisation à horizon infini¹ est donnée par l'expression de suivante :

= ( + ) (3.4)

où est une matrice constante, solution de l'équation algébrique de Riccati suivante :

+ - + = 0 (3.5)

Avec = -

, = p - -

37

L'obtention du gain passe donc par la recherche de la solution symétrique définie

positive de l'équation de Riccati (3.5). La structure du système de commande est conforme au schéma fonctionnel suivant :

( ) = 0 +

+

+

+

( )

( )

Figure 3.1 - Schéma général de la commande linéaire quadratique (LQR).

¹ Lors de contrôle a horizon infini, aucune condition n'est imposée sur l'état final

La force de cette méthode réside dans sa simplicité, mais c'est aussi sa faiblesse, car à tout instant, l'intégralité du vecteur d'état doit être observée, ce qui n'est pas réalisable sur des systèmes mécaniques complexes. Dans la majorité des problèmes de commande, on ne dispose que d'une connaissance partielle du vecteur d'état. Dans le cas de la suspension active, la déflexion du pneu en est un bon exemple.

3.3. Commande linéaire quadratique gaussienne (LQG)

Dans le cas de la commande LQR, la loi de commande est basée sur la représentation d'état du système. La difficulté de mesurer l'état ( ) fait que l'on préfère utiliser la commande LQG. Cette dernière est bien adaptée lorsque l'état du système n'est pas directement mesurable ou que les mesures sont affectées par le bruit, et la synthèse de cette commande prend en compte les propriétés statistiques de perturbations, sans affecter la stabilité.

La synthèse LQG consiste donc à rechercher, à partir de cette mesure partielle, un régulateur qui minimise un critère quadratique de nature stochastique.

La commande LQG associe un observateur d'état basé sur le filtre de Kalman à la commande LQR. L'observateur est un système dynamique, dont les entrées sont constituées de l'entrée et de la sortie du système à commander, et qui a pour fonction de reconstruire l'état du système.

3.3.1. Formulation du problème de commande (LQG)
Soit le système linéaire décrit par les équations suivantes :

( ) = ( ) + ( ) + ( ) (3.6)

( ) = ( ) + ( )

où et représentent respectivement les perturbations sur le modèle d'évolution et les bruits de mesures sur . Ils sont supposés être blancs centrés. Il vient alors :

[ ] = 0, [ ] = 0 (3.7)

Nous introduisant alors les matrices de variance pour la variance du bruit d'état et pour

la variance du bruit de mesure, et la matrice de covariance pour la corrélation entre les

:

bruits d'état ( ) et de mesures ( )

=

( ) = [ ] = ~ 0 , ( ) = [ ] = ~ 0 ( , ) = [ ]

39

Avec [...] l'opérateur espérance mathématique.

On note aussi = la matrice de covariance du bruit d'état.

Le problème de commande LQG est de déterminer la loi de commande optimale *( ) qui minimise le critère suivant :

1

= Iim

-*8

( + ) (3.8)

Avec ~ 0 > 0

3.3.2. Synthèse d'une commande LQG [13]

La solution de ce problème est connue sous le nom du théorème de séparation. Ce théorème établit que la commande optimale est obtenue :

1. En recherchant l'estimé de soit de telle sorte que : {[ ( ) - )] [ ( ) - )]}

est minimale. L'estimateur d'état optimal est donner par le filtre de Kalman (il est

indépendant de et ).

2. En employant cet estimé pour résoudre le problème de commande optimale linéaire

déterministe dans le cas de la régulation (méthode LQR), c'est-à-dire et sont ignorés.

Ainsi, le problème de la commande LQG et sa solution peuvent être séparés en deux étapes distinctes, comme le montre la figure suivante :

-

Système

Filtre de Kalman

( ) ( )

Figure 3.2 - Théorème de séparation

Où = - Le contrôle est donc proportionnel à l'estimateur d'état du système.

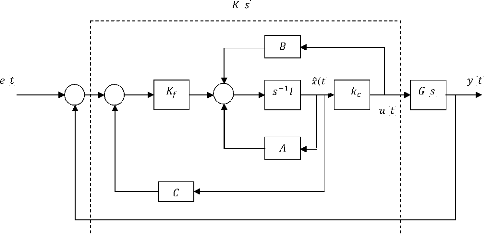
3.3.3. Structure de la de commande LQG

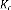
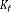
Le régulateur LQG qui réalise l'optimisation du critère quadratique (3.8), est constitué de l'association d'un retour d'état et d'un filtre de Kalman , soit :

?

= -

) = ) + ( ) + - )

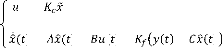
(3.9)

Où désigne le gain de l'observateur de Kalman, calculé de telle sorte qu'il minimise la

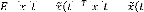
quantité : {[ ( ) - )] [ ( ) - )]}

Le gain du contrôle optimal et du filtre sont donnés par:

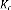
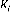
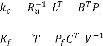
= ( + ) (3.10)

= ( + ) (3.11)

Où et sont solution des deux équations de Riccati suivantes :

( - ) + ( - ) - + - = 0 (3.12)

( - ) + ( - ) - + - = 0 (3.13)

Avec = > 0 représentant la covariance de l'erreur d'estimation - )

régime permanent.

41

Si l'état du système est entièrement mesurable, le filtre de Kalman n'est pas nécessaire. On

obtient alors le régulateur en appliquant directement la commande ( ) = - ( ).

Lorsque l'état du système n'est pas entièrement mesurable, on implante la commande par
l'intermédiaire d'un observateur. Le correcteur équivalent ( ) réalisant le rebouclage

( ) = - ( ) ( ) est alors :

( ) = - ( - + + ) (3.14)

La structure de la commande LQG est illustrée par la figure suivante :

( ) = 0

+ + +

+

-

+

+

( )

)

-

( )

( )

( )

Figure 3.3 - Structure d'un régulateur LQG

3.4. Commande LQG/LTR (Loop Transfert recovery) [13, 5]

La présence d'un observateur fait perdre les propriétés de robustesse de la méthode LQR. Pour se remédier a ce problème la synthèse d'une commande de type LQG qui recouvre asymptotiquement soit les propriétés de robustesse de la méthode LQ, soit celles du filtre de KALMAN est nécessaire.

La méthode LTR (recouvrement du transfert de la boucle) fait tendre asymptotiquement le transfert de boucle de la méthode LQG afin de se rapprocher du transfert qui serait obtenu avec un réglage LQ qui présente d'excellentes marges de stabilité.

3.4.1. Formulation du problème de commande (LQG/LTR)

La méthode LTR ne concerne que les systèmes propres définis par la représentation d'état ( , , , ) et qui vérifie :

1' = 0 (strictement propre).

1' ( - ) à minimum de phase.

?

= (nombre égal d'entrées et de sorties).

3.4.1.1. Recouvrement en entrée

Cette première approche consiste à effectuer le réglage des matrices et du filtre de

Kalman à partir d'un réglage nominale et en faisant augmenter le paramètre du
nouveau réglage :

= +

, =

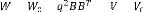
(3.15)

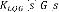
Afin que le transfert de boucle ( ) ( ) recouvre asymptotiquement le transfert de

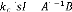
boucle - ( - ) de la méthode LQR.

uirn 8 ( ) ( ) = - ( - ) (3.16)

où

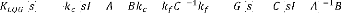
( ) = - ( - + + ) , ( ) = ( - ) (3.17)

3.4.1.2. Recouvrement en sortie

Cette seconde approche consiste à régler les matrices et du retour d'état LQ à partir d'un

43

réglage nominale et en faisant augmenter le paramètre du nouveau réglage :

= (3.18)

= +

,

Afin que le transfert de boucle ( ) ( ) recouvre asymptotiquement le transfert

- ( - ) du filtre de Kalman.

uim

-*8

( ) ( ) = -- ( - ) (3.19)

3.4.2. Synthèse d'un correcteur LQG/LTR

La démarche à suivre pour la synthèse du correcteur consiste à :

1.

Synthétiser une loi de commande LQR par un choix approprier des matrices et puis appliquer la première approche.

2.

Synthétiser le filtre du Kalman par un choix approprié des matrices et puis
appliquer la deuxième approche.

45

3.5. Application des commandes linéaires au modèle quart de véhicule

L'ensemble contrôleur et modèle de la structure peut être représenté par le schéma bloc suivante :

+

-

( )

( )

Figure 3.4 - Schéma bloc du régulateur et du modèle.

3.5.1. Objectifs de contrôle

L'objectif double est d'assurer une bonne isolation vibratoire vis-à-vis des sollicitations de la route pour le confort des passagers et de maintenir un niveau d'adhérence au sol suffisamment important pour garder le contrôle du véhicule en toute sécurité.

Comme nous l'avons vu au chapitre 1 (paragraphe 1.3.2.3.), nous devons donc surveiller l'accélération verticale de la caisse, le débattement de la suspension et l'écrasement du pneu. On s'intéresse aussi à la commande en vérifiant qu'elle satisfait les contraintes technologiques de l'actionneur.

3.5.2. Contrôle LQR

Le critère de performance s'écrit en fonction des variables d'état sous la forme suivante :

+ + + ) (3.20)

1

2 (

est ensuite converti sous forme matricielle

+ + + ) (3.21)

1

2 (

Nous obtenons les matrices , et des équations:

(3.22)

0 0 0

- -

0 -

0 -

0

?

?

?

?

?

?

?

= - -

(3.23)

= + (3.24)

Les poids sont donnés dans le tableau suivant :

Poids	Variable	Critère	valeur
		Accélération du châssis	1
		Déflexion de la suspension	10 000
		Déflexion du pneu	100 000
		Force de l'actionneur	0.0001

Tableau 3.1 - Poids des pondérations multipliant les critères Après résolution de l'équation de Riccati nous obtenons :

= (-1431.1 22.1 761.4 642.1) (3.25)

alors :

* = 1431.1 * - 22.1 * - 761.4 * - 642.1 * (3.26)

3.5.3. Contrôle LQG

Les matrices de pondération , , et sont choisies comme suit:

0 1 0 0

0 0 1 0

0 0 0 , 1

1

10 0

0 0

0

0 0

0 1

,

= 100 *

0

1 0

0 0

0

0 0

0 1

= 1 (3.27)

10

10

10

47

10

Après résolution de l'équation de Riccati nous obtenons :

(3.28)

= 10 *

0.0372

-2.2349

0.0644

-0.2107

alors, le correcteur de la loi de commande LQG est donné par sa fonction de transfert :

1.888
· 10 + 1.431
· 10 + 1.347
· 10 + 3.454
· 10

( ) =

(3.29)

+ 106.9 + 1.227
· 10 + 7.376
· 10 + 2.605
· 10

3.5.4. Contrôle LQG/LTR

L'objectif de la procédure de réglage LTR est de restaurer les marges de stabilité initiales du retour d'état LQR (ou dualement du filtre de Kalman).

L'inconvénient de cette approche réside dans le fait qu'augmenter revient à accorder plus d'importance au bruit d'état, et donc à dégrader le filtrage de bruit de mesure. Pour pouvoir donc limiter la sensibilité à ce bruit, on va tolérer en pratique, un écart entre la matrice de transfert du régulateur LQR et celle du régulateur LQG, il convient donc d'arrêter l'augmentation de lorsqu'on a obtenu le recouvrement dans une bonde de fréquence garantissant le niveau de performances et de robustesse souhaité.

On utilisant un recouvrement en entrée, le tableau suivant donne les marges de stabilité obtenue pour les différentes valeurs du paramètre :

	Marge de gain (dB)	Marge de phase ( °)
0	4.1865	Co
10	4.1867	Co
10	10.1149	Co
10	824.9638	Co

Tableau 3.2 - Marges de stabilité pour déférentes valeurs de .

La valeur du paramètre , qui permet de satisfaire le compromis performance/robustesse est

de = 10 .

Alors, le correcteur de la loi de commande LQG/LTR est donné par sa fonction de transfert :

1.571
· 10 + 6.848
· 10 + 1.172
· 10 - 6.226
· 10

( ) =

+ 77.77 + 9583 + 1.974
· 10 + 3.149
· 10

Le tableau 3.3 permet de visualiser les marges de stabilité du transfert de boucle ( ) ( )

pour les différentes lois de commande appliquée :

Lois de commande	Marge de gain (dB)	Marge de phase ( °)
LQR	Co	Co
LQG	2.3124	Co
LQG/LTR	10.1149	Co

49

Tableau 3.3 - Marges de stabilité obtenus pour les différentes lois de commande.

0.025 * (1 - cos(8 * * )) si 0 ~ ~ 0.25 (3.30)

0 si non

( ) =

3.6. Simulations

Dans ce qui va suivre, nous allons présenter les différents résultats de simulation obtenus avec les lois de commande élaborées précédemment pour le modèle de la suspension active quart de véhicule.

3.6.1. Résultats de simulation LQR

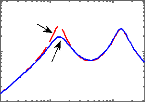
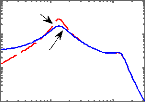
Les figures 3.5, 3.6 montrent les réponses fréquentielles et temporelles des critères. Le test temporel simule le passage sur une bosse d'amplitude maximale de 5cm. Ce test permet d'analyser la sensibilité du système contrôlé en présence de perturbations en entrée.

L'entrée de perturbation correspondant au profil de la route est donnée par l'équation :

Diagramme de Bode du transfert Yacc(s)/w (s)

10²

passif

10¹

actif

10⁰

10^-1

10⁰ 10¹

Magnitude (abs)

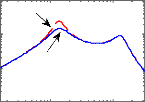
Diagramme de Bode du transfert Ypneu(s)/w (s)

1

passif

10^-2

actif

10^-3

10⁰ 10¹

Magnitude (abs)

10^-

Frequence (Hz) Frequence (Hz)

Magnitude (abs)

10^0 10^-1 10^-2 10^-3

Diagramme de Bode du transfert Ysusp(s)/w (s)

10⁰ 10¹

passif

actif

Frequence (Hz)

Figure 3.5 - Critères fréquentiels du modèle quart de véhicule

51

Amplitude (rn/s^2)		0.4 0.2 0 -0.2 -0.4
Amplitude (m)	4 2 0 -2 -4 -6

Accélération Verticale de Caisse

passif actif

0 0.5 1 1.5 2

temps (s)

x 10-3 Débattement de suspension

x 10-4 Ecrasement du pneu

passif actif

0 0.5 1 1.5 2

tamps (s)

Force de contrôle

Amplitude (N)

-10

-20

-30

10

0

passif actif

Amplitude (m)

-2

-4

4

2

0

passif actif

0 0.5 1 1.5 2

temps (s)

0 0.5 1 1.5 2

temps (s)

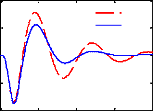
Figure 3.6 - Réponses temporelles du modèle quart de véhicule avec le contrôleur LQR à

l'excitation ( )

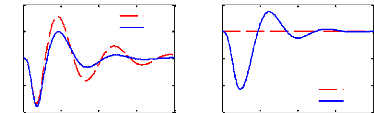
D'après la figure 3.5, on observe que la loi de commande obtenue permet effectivement d'amortir la résonance de la masse suspendue autour de 1 Hz, ce qui améliore sensiblement les performances (confort en basse fréquences), sans pour autant détériorer la capacité de filtrage en hautes fréquences.

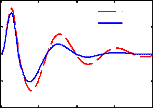
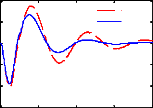
Ainsi, d'après la figure 3.6, nous remarquons en effet une atténuation rapide des oscillations comparativement à la boucle ouverte, ce qui améliore aussi ses performances en temps de réponse.

Le signal de commande est ajouté dans les figures de réponses temporelles afin d'observer la force développée par l'actionneur et son comportement.

3.6.2. Résultats de simulations LQG

Les figures 3.7 et 3.8 montrent les réponses fréquentielles et temporelles des critères.

Diagrarwme de Bode du transfert Yacc(s)/w (s)

10²

passif

10¹

actif

10⁰

10^-1

10⁰ 10¹

Magnitude (abs)

Diagranne de Bode du transfert Ypneu(s)/w (s)

1

passif

10^-2

actif

10^-3

10⁰ 10¹

Magnitude (abs)

10^-

Frequence (Hz) Frequence (Hz)

10⁰

Diagranne de Bode du transfert Ysusp(s)/w (s)

10^-2

10^-3

10⁰ 10¹

Magnitude (abs)

10^-1

passif

actif

Frequence (Hz)

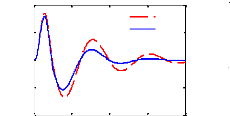
Figure 3.7 - Critères fréquentiels du modèle quart de véhicule

53

Amplitude (m/s²)

0.4

0.2

4

2

passif actif

Accélération Verticale de Caisse

x 10-4 Ecrasement du pneu

-0.2

-0.4

0

Amplitude (m)

-2

-4

-6

0

Amplitude (N)

20 10 0 -10 -20

0 0.5 1 1.5 2

temps (s)

Amplitude (m)

4 2 0 -2 -4

x 10^-3Débattement de suspension

passif actif

0 0.5 1 1.5 2

temps (s)

0 0.5 1 1.5 2

temps (s)

Force de contrôle

passif actif

0 0.5 1 1.5 2

temps(s)

passif actif

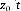
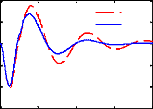
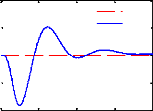
Figure 3.8 - Réponse temporelle du modèle quart de véhicule avec le contrôleur LQG à
l'excitation ( )

Comparativement au cas passif, on constate que le contrôle LQG permet aussi d'améliorer les critères fréquentiels autour de la fréquence de résonance de la masse suspendue ainsi que le temps d'atténuation des oscillations sans pour autant détériorer la capacité de filtrage en hautes fréquences. Cependant, il offre une marge de gain relativement faible.

3.6.3. Résultats de simulations LQG/LTR

Les figures 3.9 et 3.10 montrent les réponses fréquentielles et temporelles des critères.

Diagrannie de Bode du transfert Yacc(s)/w (s)

10²

passif

10¹

10⁰

10^-1

10⁰ 10¹

Magnitude (abs)

actif

Diagramme de Bode du transfert Ypneu(s)/w (s)

1

passif

actif

10^-2

10^-3

10⁰ 10¹

Magnitude (abs)

10^-

Frequence (Hz) Frequence (Hz)

Diagrannie de Bode du transfert Ysusp(s)/w (s)

10⁰

Magnitude (abs)

10^-1

10^-2

10^-3

10⁰ 10¹

passif

actif

Frequence (Hz)

Figure 3.9 - Critères fréquentiels du modèle quart de véhicule

55

Accélération Verticale de la Caisse x 10-4 Ecrasement du pneu

Amplitude (m)

-2

-4

-6

4

2

0

passif actif

Amplitude (m/s²)

-0.2

-0.4

0.4

0.2

0

passif actif

0 0.5 1 1.5 2

0 0.5 1 1.5 2

temps (s)

x 10-3 Débattement de suspension Force de contrôle

0 0.5 1 1.5 2

temps (s)

0 0.5 1 1.5 2

temps (s)

Amplitude (N)

-10

-20

20

10

0

passif actif

Amplitude (m)

-2

-4

4

2

0

passif actif

Figure 3.10 - Réponse temporelle du modèle quart de véhicule avec le contrôleur LQG/LTR à
l'excitation ( )

Le contrôle LTR permet lui aussi d'améliorer les performances de la suspension active. Il offre une légère atténuation de la résonance de la masse suspendue mais le débattement de suspension en basse fréquence est plus raisonnable. Cependant, on remarque une légère détérioration de la capacité de filtrage de l'accélération verticale de la caisse ainsi que de l'écrasement du pneu dans les moyennes fréquences.

57

3.7. Conclusion

Dans ce chapitre, l'étude nous montre clairement l'apport de ces commandes linéaires en terme de minimisation des vibrations liées au confort. Pour des considérations pratiques, on a vu aussi que la commande LQ peut être implémentée via un observateur. Néanmoins, une restauration des marges de stabilité s'impose pour augmenter la robustesse du système. Ainsi, la méthode LTR à été appliquée.

Notons qu'en pratique, les commandes linéaires quadratiques, restent les plus utilisées, car elles présentent l'avantage d'être faciles à implémentées et d'avoir un gain fixe.

En résumé, nous pouvons affirmer, d'après ce qui a précédé que les lois de commande élaborées jusqu'ici sont valables sur le modèle linéaire de la suspension active quart de véhicule. Notons aussi, que la force de contrôle appliquée est plus que satisfaisante.

Chapitre IV

Synthese H_00

58

Dans ce chapitre, nous allons décrire la synthèse 8 standard en présentant les outils nécessaires à cette approche (les valeurs singulières d'une matrice de transfert, la norme infinie d'un système linéaire), la notion de problème standard et enfin nous présentons une méthode de résolution par équations de Riccati. Différentes simulations ont été réalisées et commentées en fin de ce chapitre.

4.1. Introduction

4.1.1. La Synthèse 8

La synthèse 8 propose un cadre général pour le calcul d'un correcteur, en manipulant des concepts fréquentiels. Elle permet de prendre en compte des objectifs de stabilité, de marges de stabilité et de modelage de différents transfert, voir certains objectifs de robustesse, en retour dynamique de sortie. Une vision plus réaliste est de considérer cette approche comme une façon particulière de calculer un correcteur, sans que toutes les demandes de performance et de robustesse soient prises en compte a priori.

La recherche de la loi de commande du correcteur se fera algorithmiquement par la résolution du problème d'optimisation (minimisation de la norme 8 d'un critère mathématique). La tache de l'automaticien sera donc d'établir le critère mathématique qui reflète au mieux le cahier des charges.

4.1.2. Outils de calcul nécessaire à la synthèse 8 [4]

a) Valeurs singulière d'une matrice de transfert

Considérons un système linéaire invariant avec un vecteur d'entrée ( ) et de sortie ( ) de
dimension respectivement et . Soit ( ) sa matrice de transfert. En réponse à une excitation

harmonique ( ) = , la sortie du système s'écrit :

( ) = ( ) (4.1)

Chapitre IV synthèse

Pour un système monovariable, on définit à partir de cette relation le gain du système à la

pulsation par le module I ( )I. Dans le cas multivariables, on utilise la notion de valeurs

singulières, elles constituent une généralisation de la notion de gain et définies comme étant les racines carrée des valeurs propres positives de ( ) multipliée par sa tansconjuguée :

) ( (-- ) ) ( ) = ( )( (-- ) ) , = 1, min ( , ) (4.2)

Où est la é valeur propre.

On notera ) grande valeur singulière et ( ( )) la plus petite :

) ) ) ) (4.3)

Remarque : Pour un système monovariable, il n'existe qu'une valeur singulière, qui est donnée par:

) ) )I (4.4)

b) Norme 8 d'un système linéaire invariant

Soit le système linéaire invariant décrit par la représentation d'état :

( ) = ( ) + ( ) (4.5)

( ) = ( ) + ( )

De matrice de transfert ( ) = ( - ) + . Nous posons l'hypothèse que le système est

stable. L'ensemble des matrices de transfert ( ) correspondant à un système stable est noté usuellement R 8.

Pour toute matrice ( ) dans R , on définit une norme notée I ( )I, et qui est appelée

norme 8. Celle-ci est calculée de la manière suivante :

I ( )I_L = ))| R (4.6)

La norme ( ) est donc la valeur la plus élevée du gain du système sur l'ensemble des
pulsations . Sur la base de la définition (4.6), on peut facilement obtenir une borne inférieure de

( )?8 en cherchant la valeur la plus élevé du 2^ême membre de l'équation (4.6) pour un ensemble de valeurs de choisies a priori. Mais si celui-ci présente un maximum très »pointu», on risque de sous évaluer la norme 8.

La propriété suivante fournit un majorant de la norme , :

Propriété 4.1 : soit un réel positif > ( ). Alors ( )?8 < si et seulement si la matrice

Hamiltonienne :

= -

= -

-

=

-

(4.7)

n'a pas de valeur propre sur l'axe imaginaire.

Pour déterminer la norme 8 du système, il suffit alors de rechercher le plus petit tel

que ( )?8 < . Pour cela on peut effectuer une recherche linéaire sur le paramètre en

60

faisant par exemple une approche par dichotomie.

61

4.1.3. Formulation du problème 8[6, 3]

Toute méthodologie de commande avancée consiste à trouver un régulateur ( ) qui permet de contrôler efficacement le système, de telle sorte que le système en boucle fermée ait de bonnes propriétés de performances et de robustesse.

Sous sa forme la plus simple, le problème 8 est un problème de réjection de perturbations. A partir du système exprimé sous la forme standard de la figure (4.1), il consiste à minimiser l'effet d'une perturbation sur le comportement du système. Son effet sur le système est mesuré par la norme € du vecteur de sortie (sorties à contrôler), sachant que l'on peut agir sur le système par une commande (éléments actifs) et que l'on dispose d'une observation (mesures

disponibles). Il s'agit donc de synthétiser une loi de commande = ( ) qui minimise

l'impacte de sur . On mesurera cet impacte par le rapport . La stabilité interne du

système devra bien sûr être assurée.

( )

( )

Figure 4.1- Problème 8 standard

La matrice de transfert ( ) modélise les interactions dynamiques entre deux ensembles

d'entrées et deux ensembles de sorties, tendis que ( ) désigne le correcteur que l'on cherche à calculer.

Le système (plant) admet pour équation d'état :

?( ) = ( ) + ( ) + ( )

?( ) = ( ) + ( ) + ( ) (4.8)

( ) = ( ) + ( ) + ( )

Comme le système ( ) a deux entrées et deux sorties, il peut être partitionné de la manière suivante :

( ) =

( ) ( )

( ) ( )

(4.9)

Dans le domaine de Laplace, les équations du système dynamique se réécrivent :

( )

t ( ) = ( ) ( ) (4.10)

( )

Ainsi, la matrice de transfert entre et du système bouclé est donné par la Transformation Linéaire Fractionnelle (LFT) :

( ) = ( , ) ( ) (4.11)

( , ) = ( ) + ( ) ( ) - ( ) ( ) ( ) (4.12)

Le problème décrit ci-dessus peut se formuler mathématiquement comme suite:

63

? Etant donné > 0, existe-il un une loi de commande ( ) telle que :

1. Le système bouclé figure (4.1) soit stable de manière interne (c.-à-d. tous les pôles
du système bouclé sont à partie réelle strictement négative).

2.

( , )?00 < .

Assure

Le correcteur permettant d'atteindre la plus petite valeur de sera dit optimal. Cette valeur minimale, notée , peut être approchée par dichotomie.

En pratique, le système généralisé (dit augmenté) est en faite constitué du système étudié ( )

et des pondérations fréquentielles ( ) et ( ) associé respectivement aux entrées

exogènes et aux sorties contrôlées , représentant les spécifications de performance. Soit :

( )

( )

( )

( )

( )

Figure 4.2 - problème ₀₀ standard incluant les pondérations

Ces pondérations en fréquences permettent de privilégier certains transferts pour certains domaines fréquentiels.

Deux approches peuvent être envisagées pour résoudre le problème ₀₀ standard. La première approche est fondée sur la résolution des équations de Riccati. Elle est aussi connue sous le nom de l'algorithme de Glover-Doyle ou -itérations, apparue à la fin des années 80. C'est la solution la plus simple et la plus fiable numériquement. Une deuxième solution de ce problème de commande 00 peut être aussi utilisée, elle est basée sur la résolution d'un problème d'optimisation convexe sous contraintes d'inégalités matricielles linéaires (LMI). Nous présentons ci-dessous l'approche par équations de Riccati.

4.1.4. Résolution du problème 8 standard par Riccati [4]

Cette approche permet de résoudre le problème 8 standard définie plus haut, à partir de la représentation d'état (4.13) du système augmenté . Soit :

?( )

?( )

?( )

=

( )

( )

( )

(4.13)

Avec R ; R ; R ; R ; R .

Considérons les matrices symétriques = et Q = Q ayant les mêmes dimensions que la

matrice . on note:

=

(4.14)

la solution symétrique définie positive, si elle existe, de l'équation de Riccati :

+ - + = 0 (4.15)

de telle sorte que les valeurs singulières de ( - ) ont une partie réelle strictement négative.

Le problème 8 standard a une solution si les quatres hypothèses suivantes sont vérifiées :

H1) La paire ( , ) est stabilisable et ( , ) est détectable : condition nécessaire et suffisante pour qu'il existe un régulateur ( ) stabilisant de manière interne le système en boucle fermée. Elle implique notamment la stabilité des pondérations fréquentielles ( ) (figure (4.2)).

H2) ( ) = et ce sont des conditions suffisantes pour assurer que la loi

de commande ( ) est propre.

, + : garantit que la matrice de transfert ( ) entre

H3)

les entrées de commandes ( ) et les sorties à réguler ( ) n'a pas de zéros sur l'axe imaginaire.

, + : assure que la matrice de transfert ( ) n'a

H4)

pas de zéros sur l'axe imaginaire.

Le théorème suivant donne les conditions nécessaires et suffisantes pour résoudre le problème 8 standard. Ces conditions correspondent à un cas simplifié pour lequel les formules sont simples.

Théorème 4.1 : Sous les hypothèses H1 à H4, le problème de commande 8 a une solution si et seulement si les cinq conditions suivantes sont remplies :

( ) La matrice Hamiltonienne 8 =

-

propre sur l'axe imaginaire.

n'a pas de valeur

-

( ) Il existe une matrice 8 = ( ) 0 ; telle que + +

) + = 0

( ) La matrice Hamiltonienne 8 =

-

- -

n'a pas de valeur propre

( ) Il existe une matrice , = ( ) 0 ; telle que + + -

65

= 0

( ) ( 8 8) < Où représente le module de la valeur propre maximale (rayon spectral).

sur l'axe imaginaire.

Le théorème suivant permet, alors, de calculer la solution du problème 8 standard:

Théorème 4.2 : Sous les conditions du théorème 4.1, le régulateur ( ) stabilisant le système et

satisfaisant ( , )?8 < est donné par:

c C

- 0

8

(4.16)

Où

= +

8 - 8 - c C

(4.17)

o = ( - C ) (4.18)

La mise en oeuvre de cette solution consiste donc à utiliser tout à d'abord les résultats du théorème 4.1 de façons à estimer la valeur minimale du niveau d'atténuation . Cela se fait en utilisant l'algorithme de dichotomie. On calcule ensuite le régulateur central en utilisant le théorème 4.2 et la valeur obtenue.

Remarques :

·

L'ordre du correcteur est de , c'est-à-dire l'ordre de ( ) soit le système à commander ( ) augmenté des différentes pondérations (éventuellement) introduites.

·

On peut essayer de rechercher le plus petit , noté tel que le problème 8 standard
admette une solution à l'optimum.

? La valeur peut être approchée par dichotomie, en suivant le processus :

a. Choix d'un niveau de tolérance et de deux valeurs et telles que, pour

, le problème 8 problème admette une solution et que, pour = , le

=

67

problème 8 standard n'admette pas de solution;

b. On test si pour = , le problème 8 standard admet une solution. Si

oui alors = sinon

= ;

c. Si - lors retourner à b.

d. Calcul de la représentation d'état de la loi de commande permettant d'obtenir la

norme 8 proche de .

4.2. Application du contrôle 8 au modèle de la suspension quart de véhicule

Après avoir présenté la synthèse 8 standard, nous allons dans cette section appliquer cette technique de commande sur le modèle linéaire quart de véhicule afin de synthétiser une loi de commande permettant d'assurer, à la fois, un bon confort et une bonne tenue de route.

4.2.1. Mise sous forme standard

Pour pouvoir synthétiser une commande , il faut au préalable mettre le système considéré

sous forme standard. Pour cela nous avons besoin de déterminer quelles sont les entrées
exogènes , les entrées de commande , les sorties à contrôler et les sorties mesurées . Dans

notre cas la seule mesure disponible est le débattement de la suspension ( ) - ( ) , qui est

mesurée par un capteur électronique auquel s'ajoute un bruit de mesure. Celle-ci est à la fois facile à effectuer sur un véhicule et utile pour le correcteur. Les entrées exogènes sont le bruit de mesure d'une part et le profil de la route d'autre part. La seule entrée de contrôle correspond à la force de l'actionneur actif. Enfin, pour les sorties contrôlées nous cherchons à limiter

l'accélération verticale de la caisse ( ( ) ), l'écrasement du pneu ( ) - ( ) , le débattement
de la suspension ( ) - ( ) et celui de la commande . Cependant, nous voulons limiter ces

sorties différemment selon les fréquences. Les sorties à contrôler correspondent donc à ces sorties affectées de pondérations. Les fonctions de pondération sont donc choisies de façon à améliorer les fonctions de transfert dans les domaines de fréquence intéressants.

Le schéma suivant montre l'emplacement des fonctions de pondérations fréquentielles permettant de gérer les compromis.

( )

( )

( )

+ +

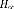
69

Figure 4.3 - Mise sous forme standard du problème avec les pondérations

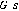
Le système ( ) représente la dynamique du quart de véhicule à 2DDL. Les pondérations fréquentielles ajoutés aux entrées et sorties du système conservent les fréquences prédominantes et atténuent les fréquences moins importantes. Pour les critères de performance, la pondération conserve les fréquences les plus sensibles et atténue les fréquences moins importantes.

4.2.2. Choix des pondérations

L'objectif principal est de réduire l'accélération de la caisse (pour le confort des passagers), de réduire l'écrasement du pneu (pour garder le contrôle du véhicule en toute sécurité), de réduire le débattement de la suspension (contrainte matérielle), et la commande en force de l'actionneur (afin de ne pas trop le solliciter en hautes fréquences). Le filtrage du bruit de mesure n'étant pas notre principal objectif, la pondération est très faible. A cet effet, une pondération constante

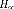
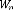
est choisie pour le bruit de mesure. La pondération est aussi choisie comme constante

pour l'écrasement du pneu. La nécessité de conserver l'adhérence des pneus sur toute la gamme des fréquences explique ce choix.

Comme les perturbations de la route sont importantes pour la conception du contrôleur, la

pondération agissant ( ) - ( ) sur correspond à un filtre passe bas avec une fréquence

de coupure de 1Hz. Il permet de modéliser la densité spectrale de la route pour qu'elle soit représentative du cas réel.

La pondération fréquentielle agissant sur ( ) - ( ) correspond à un filtre passe bas

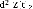
avec une fréquence de coupure de 5Hz. Il permet de contrôler la déflexion de suspension en basses fréquences là où elle est la plus importante et facilement contrôlable par l'actionneur. Il permet aussi de réduire la force appliquée en hautes fréquences, car l'actionneur a une fréquence maximale d'opération limitée. De plus, en pondérant la commande par un passe haut ( ) pénalise l'utilisation de l'actionneur en hautes fréquences.

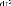
La pondération agissant sur ( ( ) ) correspond au filtre de sensibilité humaine.

Pour représenter l'importance relative de chaque critère, un poids multiplie l'amplitude de chaque filtre. Le tableau suivant donne les valeurs des poids utilisés :

poids	variable	critère	valeur
		Bruit de mesure	0.0001
		Perturbation de la route	1
		Déflexion de suspension	25
		Déflexion du pneu	6000
		Accélération du passager	1
		Force de l'actionneur	0.00000001

Tableau 4.1 - Poids des pondérations

Chapitre IV synthèse

Les pondérations choisies sont les suivantes :

= ; =

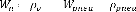
(4.19)

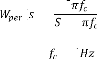
2

( ) = (4.20)

+ 2

Avec = 1

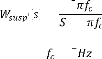
2

( ) = (4.21)

+ 2

Avec = 5

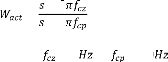
12

(4.22)

+ 30.02 + 901.3

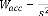
Avec = 30.02 ; = 4.78 ; = 0.5

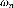
+ 2

= (4.23)

+ 2

Avec = 3 , = 30

71

Nous pouvons construire le système augmenté ( ) en utilisant la commande sysic du ^<<robust control Toolbox^>> de ^<<Matlab^>>.

Le correcteur est synthétisé avec la commande ^<<hinfsyn^>> sous Matlab. Il est donné par sa

fonction de transfert :

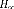
4.134 10 + 1.327 10 + 1.433 10 + 9.434 10 + 4.094 10 + 1.169 10 +

2.164 10 + 2.203 10 + 6.533 10

+ 2.006 10 + 2.011 10 + 2.678 10 + 7.173 10 + 6.718 10 + 2.948 10 +

7.488 10 + 1.012 10 + 3.267 10

Après avoir réalisé la synthèse du correcteur, nous obtenons = 15.133. Il faut noter que

l'ordre du correcteur ( ) est la somme de celle du modèle et des filtres. Par conséquent, le correcteur obtenu pour le quart de véhicule est d'ordre 9.

Les pondérations fréquentielles sur l'accélération de la caisse, sur l'écrasement du pneu, sur le débattement de la suspension et de la force de l'actionneur sont représentées sur la figure 4.4.

Bode des ponderations Wpneu, Wsusp, Wact et Wacc

10^-1 10⁰ 10¹ 10² 10³ 10⁴

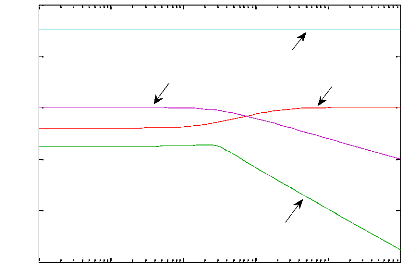
Magnitude (dB)

-100

-150

100

-50

50

0

Wsusp Wact

Wpneu

W acc

Frequence (Hz)

72

Figure 4.4 - Pondérations fréquentielles appliquées sur les critères de performances

73

Chapitre IV synthèse

4.2.3. Présentation des résultats de simulation

Les figures 4.5 à 4.8 montrent les réponses fréquentielles et temporelles des critères de performances.

Nous rappelons que, le test temporel simule le passage sur une bosse d'amplitude maximale de 5cm.

10⁰ 10¹

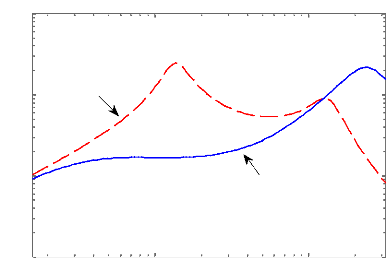
Magnitude (abs)

Diagramme de Bode du trasnfert Yacc(s)/w (s)

10²

10¹

10⁰

10^-1

passif

actif

Frequence (Hz)

Figure 4.5 - Réponse fréquentielle du transfert entre l'accélération verticale de la caisse et le
profil de la route.

Chapitre IV synthèse

10⁰ 10¹

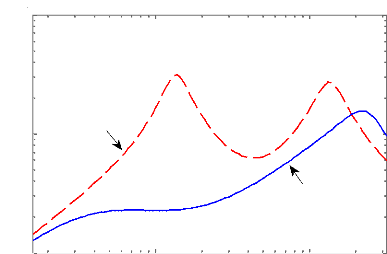
Magnitude (abs)

Diagran-me de Bode du transfert Ypneu(s)/w (s)

10^-1

10^-2

10^-3

passif

actif

Frequence (Hz)

Figure 4.6 - Réponse fréquentielle du transfert entre l'écrasement du pneu et le profil de la route.

10⁰ 10¹

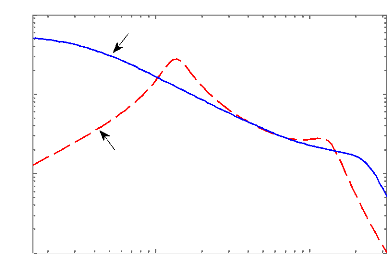
Magnitude (abs)

Diagran-me de Bode du transfert Ysusp(s)/w (s)

10⁰

10^-1

10^-2

10^-3

passif

actif

Frequence (Hz)

Figure 4.7 - Réponse fréquentielle du transfert entre le débattement de la suspension et le profil de la route.

75

Chapitre IV synthèse

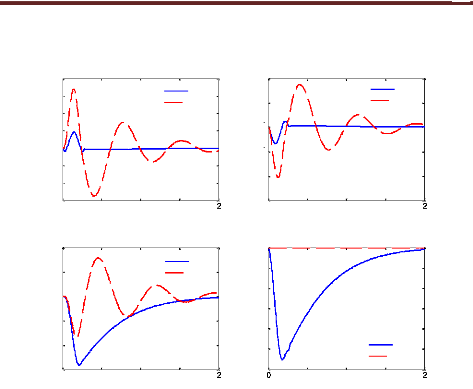
x 10-4 Ecrasement du Pneu

AccOlOration Verticale de Caisse

0

-20

Amplitude (N)

-40

-60

-80

-100

-120

temps (s)

x 10-3 DObattement de Suspension

0 0.5 1 1.5

4

riccati
passif

2

Amplitude (m)

0

-2

-4

-6

temps (s)

temps (s)

Force de Contrôle

0.5 1 1.5

temps (s)

riccati
passif

riccati
passif

0 0.5 1 1.5

4

2

Amplitude (m)

0

-2

-4

-6

0 0.5 1 1.5

0.4

riccati
passif

0.3

0.2

Amplitude (m/s²)

0.1

0

-0.1

-0.2

-0.3

Figure 4.8 - Réponses temporelles

Les réponses fréquentielles et temporelles du contrôle par Riccati, nous montre clairement

une nette amélioration des performances de la suspension active comparativement au cas passif (sans contrôle).

En effet, les deux modes de résonance principaux, autour de 1Hz et autour de 10 Hz respectivement de la masse suspendue et de la masse non suspendue sont complètement ou pratiquement éliminés pour les trois critères. Ceci montre que la loi de commande élaborée assure de bonnes performances en termes d'isolation vibratoire vis-à-vis des perturbations (un bon confort pour les passagers) et de maintien du niveau d'adhérence au sol suffisamment important (une bonne tenue de route). Cependant, ces améliorations sont amenées au détriment du débattement de suspension en basses fréquences.

Chapitre IV synthèse

4.3. Résultats pour le contrôle actif du quart de véhicule à deux degrés de liberté

Afin d'apprécier l'amélioration apportée par les lois de commandes appliquées au système de la suspension active du modèle quart de véhicule. On compare ces dernières avec le cas passif (qu'on appelle aussi boucle ouverte).

Les figures 4.9 à 4.15 montrent le résultat des réponses en fréquence et le résultat des réponses temporelles obtenues pour la suspension passive et les différentes stratégies de contrôle.

Diagrarrire de Bode du transfert Yacc(s)/w (s)

passif LQG

LQG/LTR

LQR

Hinfini

10²

10^-1

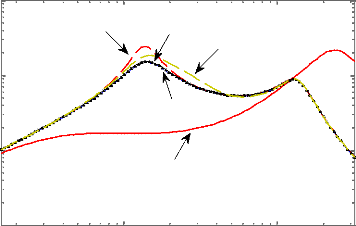
10⁰ 10¹

10¹

Magnitude (abs)

10⁰

Frequence (Hz)

Figure 4.9 - Réponse fréquentielle du transfert entre l'accélération verticale de la caisse et le
profil de la route.

77

Chapitre IV synthèse

Diagramme de Bode du transfert Ypneu(s)/w (s)

passif

LQG

LQG/LTR

LQR

Hinfini

10^-3

Magnitude (abs)

10^-1 10^-2

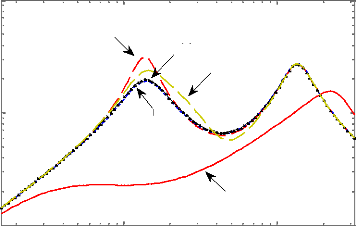
10⁰ 10¹

Frequence (Hz)

Figure 4.10 - Réponse fréquentielle du transfert entre l'écrasement du pneu et le profil de la route.

10⁰ 10¹

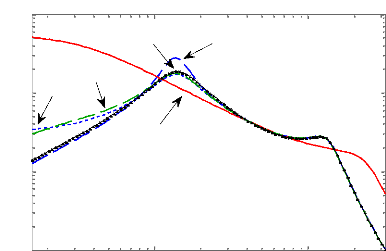
Magnitude (abs)

Diagramme de Bode du transfert Ysusp(s)/w (s)

10⁰

10^-1

10^-2

10^-3

LQR

LQG

LQG/LTR passif

Hinfini

Frequence (Hz)

Figure 4.11 - Réponse fréquentielle du transfert entre le débattement de la suspension et le profil
de la route.

Chapitre IV synthèse

Accélération Verticale de la Caisse

Amplitude (m/s²)

-0.1

-0.2

-0.3

0.4

0.3

0.2

0.1

0

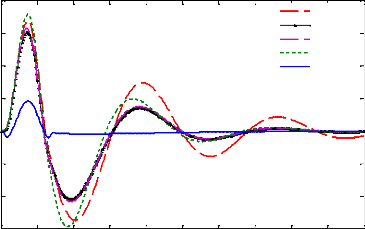
passif LQR

LQG LQG/LTR Hinfini

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

temps (s)

Figure 4.12 - L'accélération verticale de la caisse obtenus pour les différentes lois de
commande.

x 10^-4 Ecrasement du pneu

Amplitude (m)

-1

-2

-3

-4

-5

4

5

3

2

0

1

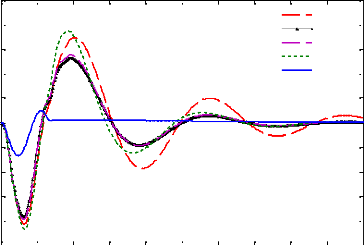
passif LQR

LQG LQG/LTR Hinfini

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

temps (s)

Figure 4.13 - L'écrasement du pneu obtenus pour les différentes lois de commande

79

Chapitre IV synthèse

x 10-3 Débattement de suspension

Amplitude (m)

-1

-2

-3

-4

-5

-6

4

3

2

0

1

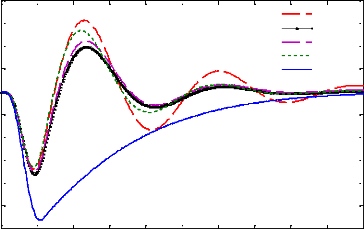
passif LQR

LQG LQG/LTR Hinfini

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

temps (s)

Figure 4.14 - Débattement de la suspension obtenus pour les différentes lois de commande

Force de contrOle

Amplitude (N)

-100

-120

-20

-40

-60

-80

20

0

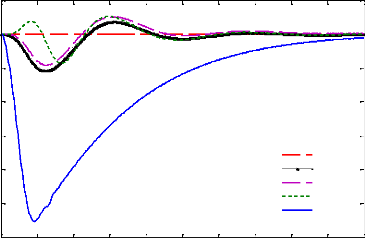
passif LQR

LQG LQG/LTR Hinfini

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

temps (s)

Figure 4.15 - Force de contrôle obtenu pour les différentes lois de commande

Chapitre IV synthèse

Le tableau suivant donne la valeur de l'indice de performance J :

Contrôle	Critère J
Passif	0.0362
LQR	0.0263
LQG	0.0268
LQG/LTR	0.0319
	0.2771

Tableau 4.2 - Performance des différents contrôleurs pour le modèle à 2DDL

Le contrôle par (LQR, LQG, LQG/LTR) permet effectivement de minimiser le critère J, ce qui améliore sensiblement la performance de la suspension. Le contrôle par offre un indice de performance J le plus élevé. Par contre, la réponse est beaucoup mieux modelée en fréquence, surtout pour l'accélération verticale de la caisse et l'écrasement du pneu. Cette observation nous permet de noter que la distribution en fréquence de la réponse est importante dans l'évaluation de la performance d'une suspension.

81

Chapitre IV synthèse

4.4. Conclusion

Dans ce chapitre, la synthèse d'une loi de commande pour la suspension active du modèle

quart de véhicule a été présentée. Dans un premier temps nous avons mené une étude bibliographique sur la synthèse , Puis nous avons détaillé les pondérations choisies de façon à améliorer les fonctions de transfert dans les domaines de fréquence intéressants. Nous pourrons dire, d'après ce qui a précédé que les objectifs sont pleinement atteints avec le contrôle .

Conclusion Generale

Conclusion générale

Dans cette approche, nous pouvons conclure que les commandes linéaires LQR et LQG permettent de réduire efficacement le pic de résonance de la masse suspendue, sans détériorer le filtrage en hautes fréquences, seulement que, cette dernière est fort peu robuste. La commande LTR quant à elle permet effectivement d'améliorer les marges de stabilité. L'atténuation de la résonance de la masse suspendue est moins importante mais le débattement de la suspension est plus raisonnable en basses fréquences. Cependant, le filtrage est tout de même détérioré dans les moyennes fréquences.

La commande 8 est, elle, reconnue dans le domaine de l'Automatique pour son potentiel à prendre en compte les spécifications de performances dans le domaine fréquentiel, et la robustesse de la loi de commande. Pour les trois critères, les deux modes de résonances principaux sont pratiquement éliminés, ce qui est un avantage non négligeable. Mais, ces améliorations sont amenées au détriment de la suspension en basses fréquences. Le contrôle

8 offre des résultats bien plus supérieurs aux autres contrôleurs, mais son ordre élevé est une source de problèmes potentiels. Les résultats obtenus démontrent l'importance de la pondération en fréquence des critères de performances.

Plusieurs compromis sont possibles entre les critères. Les commandes sont donc aussi jugées sur leur capacité à gérer ces compromis.

Comme pour toute optimisation multivariable, les poids et les filtres utilisés ont une grande influence sur la réponse du système. Plusieurs autres contrôleurs réalistes peuvent être aussi conçus en modifiant les poids et les filtres utilisés.

81

Références bibliographiques

[1] PHILIPPE DE LARMINA, Analyse des Systèmes Linéaires, Edition Lavoisier, 2002.

[2] PIERRE-JEAN BARRE, JEAN- PIERRE CARON, JEAN-PAUL HAUTIER, MARC LEGRAND, Systèmes Automatiques, Edition Ellipse, 1995.

[3] DANIEL ALAZAR, CHRISTELLE CUMER, PIERRE APKARIAN, MICHEL GAUVRIT, GILLES FERRERES, robustesse et commande optimale, Edition Cépaduèse ,1999.

[4] Gilles Duc, Stéphane Font, commande et -analyse, Edition HERMES, Paris, 1999.

[5] N'OUALI, L, MEZAR, S, commande linéaire quadratique gaussienne de la suspension active d'un véhicule, présentée en vue de l'obtention du titre d'ingénieur en automatique, soutenue en 2006.

[6] Damien SAMMIER, sur la modélisation et la commande de suspension de véhicules automobiles, présentée en vue de l'obtention du grade de docteur de L'INPG spécialité : Automatique- Productique, soutenue le 9 novembre 2001.

[7] STEPHANIE HARARI, contrôle modale semi-actif et actif à faible consommation énergétique par composants piézoélectriques, présentée en vue de l'obtention du grade de docteur spécialité : Génie Mécanique, soutenue le 12 octobre 2009 ;

[8] HADDAD Madjid, contrôle actif robuste d'une structure mécanique flexible, présentée en vue de l'obtention du diplôme de magister en génie mécanique, soutenue le 12 octobre 2009.

[9] GHERBI Sofiane, la commande robuste (technique -analyse et -synthèse), présentée en vue d'obtention du diplôme de doctorat, option : Automatique, soutenue 2009.

[10] Alessandro ZIN, sur la commande robuste de suspension automobile en vue du contrôle global de châssis, présentée en vue d'obtention du grade de docteur de L'INPG, soutenue le 3 novembre 2005.

[11] Othman Ben Mekki, Amortissement semi-actif des structures flexibles, présentée en vue d'obtention du diplôme de docteur de l'école nationale des ponts et chaussées, soutenue en mai 2006.

[12] Emmanuel Marie ARNOUX, lois des commandes et systèmes de suspension adaptatifs théorie et application à la mécanique automobile, présentée en vue d'obtention du titre de docteur de l'école centrale de Lyon, soutenue le 11 avril 2003.

[13] A.MAIDI, Cours de la théorie de l'optimisation et de la commande optimale, Département Automatique. 2009-2010.

[14] S.DJENNOUNE, cours d'analyse des systèmes multivariables, Département Automatique 2007-2008.

[15] Ales Kruczek, Anonin Stribrsky, control of automotive active suspension with linear
motor, CTU, Faculty of Electrical Engineering Department of Control Engineering Karlovo namesti 13, 121 35 Praha 2.

[16] Yahaya Md. Sam, Mohd. Ruddin Hj. AB.Ghani, Nasarudin Ahmad, LQR Controller for Active Car Suspension, Control and Instrumentation Eng. Dept. Faculty of Electrical Engineering University Technology Malaysia.