Modèlisation d'un prototype et commande vectorielle avec et sans capteur mécanique du moteur couple

Annexe 1: Essais expérimentaux et validation du modèle.

3.2. Tableau des relevés : Moteur à vide en fonctionnement moteur. n=46,8 tr/min (synchrone)= 50 Hz

Mesures

N°	Uab (V)	Ia0 (A)	Ib0 (A)	P0 (W)	Q0 (var)
1	340	10,85	10,9	1 440	6 131
2	320	9,9	10	1 260	5 196
3	307	9,3	9,4	960	4 677
4	280	8,3	8,1	750	3 741
5	260	7,4	7,25	624	3 076
6	240	6,9	6,7	525	2 728
7	220	6,6	6,4	460	2 321
8	200	5,8	5,65	374	1 916
9	180	5,2	5,1	294	1 535
10	160	4,65	4,55	226	1 154
11	145	4,2	4,1	185	927
12	120	3,2	3,1	125	580

Calculs

tan (p	cos (p	Uab2 x10^3	PJ (W)	Pméca + Pmag (W)	Pmag (W)	S0	Vas (V)
						2 2 ? ( P 0 Q ) 0
4,26	0,229	116	343	1 097	1 050	6 298	196,3
4,12	0,24	102,4	283	977	930	5 347	184,8
4,87	0,20	94,4	249	711	664	4 775	177
4,98	0,20	78,4	199	551	504	3 815	162
4,93	0,20	67,6	158	466	419	3 139	150
5,20	0,19	57,6	137	388	341	2 778	139
5,05	0,19	48,4	126	334	287	2 366	127
5,12	0,19	40,0	97,0	277	230	1 952	115
5,22	0,19	32,4	780	216	169	1 563	104
5,11	0,19	25,6	62,3	164	117	1 176	92,4
5,01	0,20	21,0	50,9	134	87	945	83,7
4,64	0,21	14,4	29,5	96	49	593	69,3

Tab.An1-3 Nota : P J = 3 R sI ⁰² avec R s = 961 m ? à 20°C Pmag+ mé ca ? P ₀ - P J

3.3. Tracé de la courbe : U P _mag P mé c

² F-> +

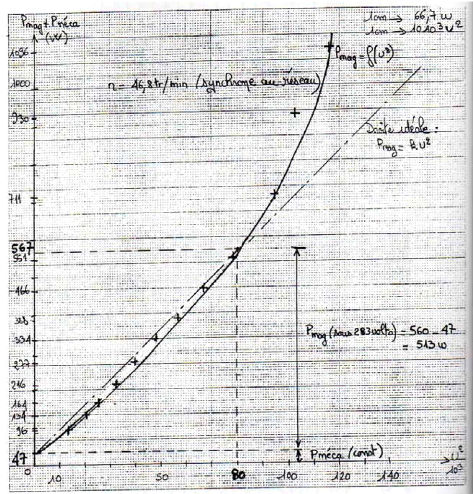
Fig.An1-5

4. ESSAI EN CHARGE EN FONCTIONNEMENT MOTEUR.

4.1. Essais à couples constants (Fonctionnement en boucle ouverte) :

4.1.a) Tableaux des relevés ; Essai à T_u = 100,6 N.m (Constant) ? Pu ? 0,48 kW

n=46,8 tr/min (synchrone)= 50 Hz

Mesures

N°	Uab (V)	Vas (V)	Ia (A)	Ib (A)	Pabs (W)	Qabs (var)
1	312,4	180	9,75	10	1 590	5 040
2	304	174,6	9,40	9,50	1 506	4 645
3	296	170	9,12	9,21	1 437	4 380
4	288	166	8,80	8,91	1 341	4 204
5	280	162	8,50	8,51	1 290	4 001
6	278	Décrochage du rotor

Calculs

(1) cos q	(2) PJ 3RsIb ^2 (W)	(3) Pmag (W)	S	Pu Tu(2in) (W)	11 Pu/Pabs (%)	PmajPabs (%)
			2 2 + ? P abs Q abs ) (VA)
0,30	339	760	5 285	493	31	48
0,31	306	667	4 883	493	33	44
0,31	288	640	4 610	493	34	45
0,30	269	587	4 413	493	37	44
0,31	245	486	4 204	493	38	38

Tab.An1-4

(1) : Cos q = Cos [Arc tan (Qabs /Pabs)]

(2) : A chaud, R_s = 1,13Q

(3) : D'aprés les essais à vide, on a k =6,20.10^-3 W/V² pour une tension inférieure à 283 volts.

4.1.b) Tracé des coubes : I b ? Uab pour différentes valeurs de T_u

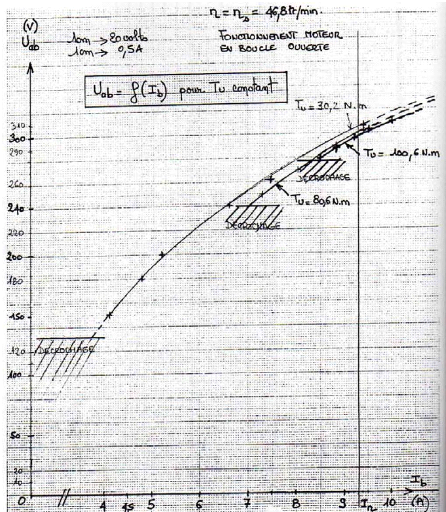
Fig.An1-6

4.2. Essais à tensions constantes (Fonctionnement en boucle ouverte) :

4.2.a) Tableaux de relevés ; Essai à Uab = 300 volts (Constant) =0 ~Tu ~138 N.m

n=46,8 tr/min (synchrone)= 50 Hz Pmag = 667 W(constante)

Vas = 172 volts

Mesures

N°	Tu (N.m)	Pu (kW)	Ia (A)	Ib (A)	Pabs (W)		Qabs (var)
1	0	0	9,02	9,10	1	005	4	547
2	20,4	0,09	9,02	9,12	1	089	4	536
3	40,1	0,19	9,10	9,20	1	185	4	547
4	66,8	0,32	9,25	9,33	1	308	4	583
5	82,1	0,39	9,30	9,40	1	383	4	619
6	100,6	0,48	9,35	9,46	1	464	4	614
7	111	0,54	9,41	9,51	1	500	4	666
8	120	0,57	9,50	9,60	1	554	4	687
9	130,3	0,63	9,56	9,67	1	605	4	703
10	138	Décrochage du rotor

Calculs

(1) cos q	(2) PJ 3RsIb^2 (W)	S	Pu Tu(2in) (W)	TI Pu/Pabs (%)	Pmag/Pabs (%)
		2 ^2 + ( ( P abs Q abs ) (VA)
0,22	281	4 657	0	0	66,3
0,23	282	4 665	100	9,1	61,2
0,25	287	4 699	197	16,6	56,3
0,27	295	4 766	327	0,25	51,0
0,29	300	4 822	402	29,1	48,2
0,30	303	4 841	493	33,7	45,6
0,31	307	4 901	544	36,3	44,5
0,31	312	4938	588	37,8	42,9
0,32	310	4 969	639	39,8	41,6

Tab.An1-5

(1) : Cos q = Cos [Arc tan (Qabs /Pabs)]

(2) : A chaud, R_s = 1,13Q

4.2.b) Tableaux de relevés ; Essai à U_ab = 340 volts (Constant) =0 <_Tu <_138,5 N.m :

n=46,8 tr/min (synchrone)= 50 Hz Pmag = 717 W (constante)

Vas = 196 volts

Mesures

N°	Tu	Pu	Ia	Ib	Pabs	Qabs
	(N.m)	(kW)	(A)	(A)	(W)	(var)
1	104,6	0,50	11,25	11,3	1 890	6 287
2	138,5	0,64	11,3	11,32	1 995	6 365
3		Limite du banc d'essais 3

Calculs

(1) cos cp	(2) PJ 3RsIb^2 (W)	S	Pu Tu(27Cn) (W)	n Pu/Pabs (%)	Pmag/Pabs (%)
		( P abs + Q2 abs) ( (VA)
0,29	433	6 565	513	27,1	37,9
0,29	434	6670	678	34,0	36,0

Tab.An1-6

(1) : Cos cp = Cos [Arc tan (Qabs /Pabs)]

(2) : A chaud, R_s = 1,13n

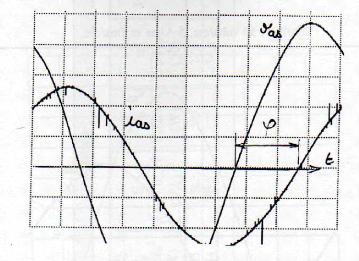
4.3. Relevé des oscillogrammes vas( t ) et i as ( t ) : moteur chargé : 4.3.a) T u = 40 ,1 N. m, U ab = 300 volts à n_n =46,8 tr/min (50 Hz) Echelles : 50 volts/cm, 5 A/cm et 2ms/cm

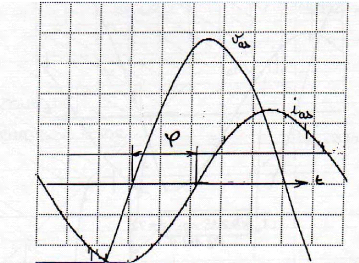
I as = 8 , 8 A p = - 77 ,1°

Fig.An1-7
Echelles : 50 volts/cm, 5 A/cm et 5ms/cm

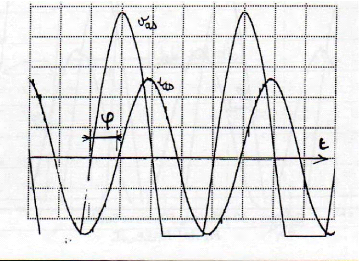
Annexe 1: Essais expérimentaux et validation du modèle. 4.3.b) T u = 100 N. m, U ab = 300 volts à n_n =46,8 tr/min (50 Hz)

Echelles : 50 volts/cm, 5 A/cm et 2ms/cm

I as ? 9 , 2 A ? p = 72°
Fig.An1-9

Echelles : 50 volts/cm, 5 A/cm et 5ms/cm

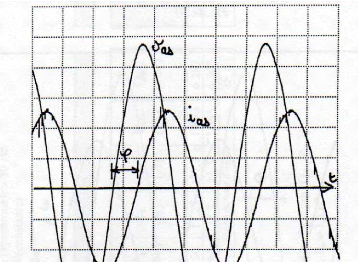
Fig.An1-10

Comparé au précédent relevé, on remarque un déphasage, du courant statorique, amélioré de 5° environ. Le courant est resté toutefois très inductif.

Annexe 1: Essais expérimentaux et validation du modèle. 4.3.c) Tracé des coubes : I b > T_u pour différentes valeurs de U ab

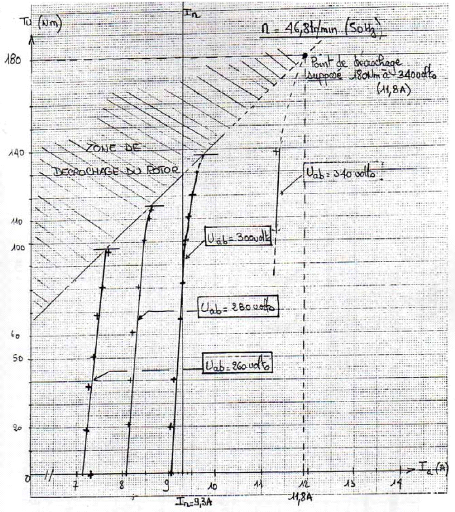
Fig.An1-11

5. DETERMINATION DE LA CONSTANTE THERMIQUE.

Sonde platine n°1
Stator n°1

Sonde platine n°2
Stator n°2

t (min) 0	r' (() 1,704	r (n) 110,2	r-r' -3 0° (°C)	r' (n)	r (n)	r-r' -3 0° t° Ambiant (°C) à 1cm du moteur (°C)
			22	1,384	109,9	22	22,2
5	1,570	117,2	40	1,432	119,8	47,5	/
10	1,587	123,9	58	1,464	125	61	23,4
15	1,591	127,1	66	1,490	128,3	79	24,9
20	1,598	129,5	72	1,513	131,0	76	25,8
25	1,606	131,9	78,5	1,530	133,7	83,5	26,7
30	1,610	134,6	85	1,550	136,4	90,5	27,4
35	1,622	138,1	95	1,576	140,2	100	/
43	1,628	141,6	104	1,608	144,2	111	/
45	1,629	142,5	106	1,614	145,1	113	29,9

5.1. Tableau des relevés

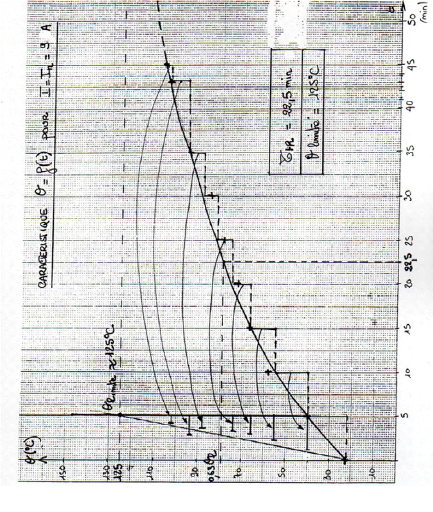
Fig.An1-12

5.2. Tracé de la courbe : t + 0 pour I I n

- ANNEXE 2 -

COMMANDE SANS CAPTEUR MECANIQUE DU
MOTEUR FINTRONIC.

FILTRE DE KALMAN

QUELQUES NOTIONS SUR LES VARIABLES ALEATOIRES

Il nous semble important d'apporter quelques précisions sur les signaux aléatoires pour comprendre le fonctionnement du filtre de Kalman.

· L'espérance (moyenne arithmétique):

Nous allons définir l'espérance d'une variable aléatoire à travers un exemple simple. Considérons n relevés de mesure sur une variable aléatoire réelle notée X, (x ₁ , x ₂ , x ₃, . . ., x_n) et effectuons la moyenne de ces valeurs. On obtiendrait pour n

mesures finies :

une valeur moyenne : x

? ? lim

n n ?? n

x x

? ? ?

. . . x

1 2 n 1 ?

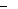
i =n

xi

i

=

1

Or, si on faisait plusieurs séries de mesures, avec n relevés tendant vers l'infini, on verrait que la valeur moyenne obtenue pour chaque série de mesures aurait tendance à converger vers une valeur unique et non pas plusieurs valeurs dépendants du nombre de relevés . Et c'est justement cette valeur unique qui caractérise l'espérance de la variable aléatoire X. L'espérance de X sera notée :

1

E{ X} ou X avec E{ x( t)} = lim ? x ? t ?

t =n

=

= Cste

(An2-1)

Nota : A noter que l'espérance des bruits blancs, est nulle.

· La variance :

La variance correspond à l'espérance mathématique du carré des écarts par rapport à la valeur moyenne (espérance).

La variance de X sera notée :

?_x ? E ? ? X ? X ? 2 ?

Avec

? ? ? ? ? ? ?

2 1 i n ? 2 ? x ? E X ? X ? lim ? x i ? X ? n ?? n i =1

2

(Carré de l'écart type).

(An2-2)

Plus clairement et en reprenant l'exemple précédent, cette variance permet d'apprécier la dispersion des valeurs mesurées par rapport à son espérance. C'est ce qu'on appelle la variance de la variable aléatoire X.

Nota:

L'écart type d'une variable aléatoire correspond à la racine carrée de sa variance.

· Le coefficient de covariance :

le coefficient de covariance caractérise l'interdépendance éventuelle entre 2 variables aléatoires X et Y. Ce coefficient est défini et noté par:

1 ?xy ? ? ? ? ? ?

? E X ? X Y ? Y ? lim ? ? ? ?

x i ? X y i ? Y

n ?? n ? i= 1

i n

?

(An2-3)

Cette valeur correspond à l'espérance de la multiplication de l'écart type des 2 variables aléatoires.

Nota :

On pourra considérer par la suite que la notion d'espérance, de variance et de covariance suffisent pour définir une variable aléatoire.

· La matrice de variance-covariance :

Si un système différentiel quelconque est tributaire de plusieurs variables aléatoires, il est possible de représenter ces variables aléatoires, sous la forme d'un vecteur.

Dès lors, il est possible de représenter la variance et la covariance des différentes composantes de ce vecteur sous la forme d'une matrice dite de « variance-covariance ».

Soit X

?

F I L

X X X

1 2 3

1 ? I J

: vecteur de 3 variables aléatoires,

(An2-4)

F I

[

C

xx

On a la matrice de variance-covariance suivante:

x 1 x

x 2 x

i

3 ?

3 ? ? ?

Dx 1 cx 1 x2 c

cx 2 x1 ⁰x 2 g

cx 3 x1 cx 3 x2 ⁰ x 3

(An2-5)

Si on remplace chaque terme par leur expression, on a :

??

Cxx = E

L

?

? ? ? ? ? ? ? ? ? ? ?

X X X X X X X X

? ? ? ? X X

?

? 2 2 1 1 3 3 2 2 3 3

^-11

? ?

? ?

? ??

? ?

? ? ? ? ? ? ? ? ?

2

? X X

? X X X X

? ? X X X

?

1 1 1 1 2 2 1 1 3

? ? ? ? ?

? X 3 ?

? ? ? ? ? ? ? ? ? ?

2

X X X X X X X X X X

?

2 2 1 1 2 2 2 2 3 3

2

(An2-6))

De plus si on remplace ? ? Xi

X i ? X _i par pour simplifier les notations, on obtient

02

r

0

11 I 1 ? ?? ?

? ? ? ?

3

X1

0

o o

??? ?

?

?

E

?

1 ?

L

C xx = E

3

X2

r 1 1 ? ? ? ?

0

2

r

? i ? ?

X3

r 1

?

1

[

L

? ? ? ? ?

X X X

?? 1 2 3

?? ?

? i

o o o o

X 1 X ₁ X ₂ X ₁ X

₀ 2 0 0

X ₂ X 1 X 2 X ₂ X

0 0 0 0 0

X ₃ X ₁ X ₃ X 2 X3

(An2-7)

Soit :

Matrice de variance-covariance du vecteur aléatoire : gxx

f 0 0 T = E iX X ???

(An2-8)

.

Nota : Dans le cas particulier des bruits blancs, X = X.

- ANNEXE 3 -

COMMANDE SANS CAPTEUR MECANIQUE DU
MOTEUR FINTRONIC.

FILTRE DE KALMAN

CHANGEMENTS DE REPERE : (a_s, b_s,c_s) ~~ (ct_s, _3sos) et (d, q, o) ~~ (ct_s, 3_s, o_s)

TRANSFORMATIONS DE CLARKE ET DE CONCORDIA.

1. DETERMINATION DE LA MATRICE DE PASSAGE DU REPERE (a_s, b_s,c_s) AU REPERE (a_s, O_s, o_s).

Afin d'eviter des calculs longs et fastidieux, il est essentiel de tenir compte de la remarque suivante:

· Le referentiel (a_s, r3_s, o_s) correspond au referentiel de Park (d, q, o) pour lequel, on a immobilise le système d'axes (d, q, o) et oriente l'axe a_s suivant la même orientation que l'axe a_s.

On peut donc considerer que le referentiel (a_s, (3_s, o_s) est un cas particulier du referentiel de Park avec lequel, on a remplace les lettres du système d'axes d, q par a_s et p_s. Il suffit donc de reprendre la matrice de Park et de remplacer 0 par 0. On obtient ainsi, la nouvelle matrice de passage.

Dans la litterature courante, cette transformation est appelee « transformation de

CLARKE ». La matrice de cette transformee sera notee [ _Cla] .

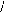
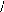
1

?

?

i

[ P] =

2 3

1^- [

cose cos(0 -- 2 7c 3 ) cos(0 -- 4 7c 3)

--sine --sin(0 -- 2 7c 3 ) --sin(e -- 4 7c 3

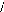
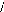
1 2 1 2 1 2

(An3-1) : Matrice de PARK : Repère (d, q, o). En remplaçant 0 par 0, on obtient :

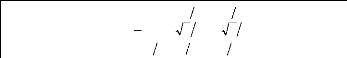
1 -- 1 2 --1 2

2

0 3 2 -- 3

1 2 1 2 1 2

1 ?

?

? ?

r I

[

2

3

[ C _la ] .

(An3-2): Matrice de CLARKE : Repère (as, fi_s, o_s). Les expressions de tensions, courants et flux deviennent :

i _as = 1 3(

i ? s = 1 3

( i bs -- ics)

2i as -- i bs -- ics)

1³

?

s

? ? ? ?? ?

i ? C i

?? o s la abc

? ? ? ?? ?

v ? C v

?? o s la abc

v_as =1 3(

2v _as --v bs ^--vcs)

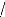
v' s = 1 3

( v bs -- v cs )

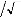
1³

?

s

? ? ? 1 3 ?

? s

? ? ? 1 3

? s

( Tbs ^--"cs)

[If alio s [ la abc
] = C IT ]

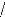
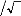
²Tas ^--Tbs ^--Tcs)

?

s

(An3-3)

Nota :

On ne fait pas apparaître volontairement les expressions, sur l'axe o. Cet axe intervient uniquement pour l'inversion de la matrice de transformation (matrice carree).

L'unicité de la matrice de transformation [ _Cla] , pour les tensions, les courants et les flux, nous oblige à tenir compte des changements de variables, identiques à la transformation de Park.

2

2

3 Ilj_a s

i i

? ? v ? ? v ? ? ?

? s ? s ? s ? s ? s

3

2 2

s

i ' = i v' = v Ill' = Ill'

li

s

P

s

^P

^s 3

P

s

li

1³

s

³

(An3-4)

2. DETERMINATION DE LA MATRICE DE PASSAGE DU REPERE (as, Ps) AU REPERE (a_s, b_s, cs).

Avec les mêmes arguments que précédemment, on remplace 0 par 0, dans la matrice de Park inverse.

r
[

_[P]-1. =

i

?

?

? ?

4

i

3 ) -- sin(9 --

4

7c

3

)

1

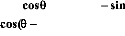
1

0

2 7c 3) -- sin(9 -- 2 7c 3 ) 1

(An3-5)

On remplace 0 par 0 et on obtient :

[

[C_lar¹ = --

--1 2 --

_ii
L

1

1 0

1 2 3 2 1

3 2 1

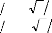
(An3-6): Matrice de CLARKE inverse. Les expressions de tensions, courants et flux deviennent :

i _as ^--i as ^--ias

i bs = P_bs = 1 2(
i cs = Pcs = 1 2(

i as + 3 ifts)

i as -- 3 ifts)

[i abo ]_s =[C la ]^-licoo]

s

v as =vas

US

v as = 3 2v

Us

? ? ? v 3 v ? ?

? s ? s

v _as -- 3 va_s)

? ? v 3 v ?

? s ? s

? v 3 v ?

? s ? s

?

v bs = 3 4(

v cs = 3 4(

[v abo ]_s = [C la ] ¹[vafid

v bs = 1 2(

v cs = 1 2(

s

s

?

ⁱl^las = 3 2ijas

^IPbs = 3 4( ^IPcs = 3 4(

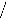
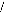
cos e -- sin

cos(9 --

cos(9 --

l^jas + ³¹Pris)

? ?? 3 ? ?

? s ? s

? ?

? ?

as ? s

[Tabo ]_s =[C la ]^-1[Tcoo]

? ? ? ?

? 1 2 ? ? ? 3 ?

bs ? s ? ? s

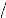
? ? 1 2 ? ? ? ?

? 3 ? ? ?

cs ? s ? s

(An3-7)

3. REPRESENTATION VECTORIELLE DES SYSTEMES D'AXES

Rs

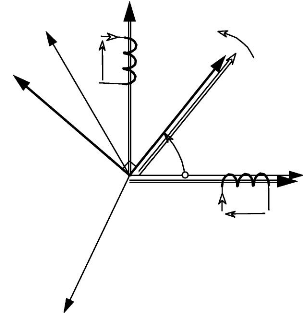
b_s

i ?s

CO

Axe
du
rotor

d

q

vas

-->

^IP aim

0 + 00

O

i as

v_as

a_s

(Fixes)

as

c_s

Fig.An3-1

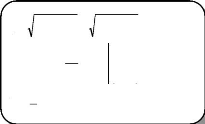
s cos9

i i I

? ? ?

? s ? s

?

2

?

? ? arctan ?? ?

i ? s ?

? ?? ?

i ? ? s

V = ₃v

OLs

? ? ? ?

i i

? ? ? ?

2 ² i i

2 2

s s s ?

? ? ? ? s

?

?

i i I

? ? ? ?

? ?

s s s

since

?

I s =

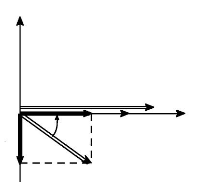
i^?as

a_s

i^?Ys

?

->

V_s

->

I _s

v_as

Rs

a_s

?

Cas particulier où v s = V_s cosco_st

Fig.An3-2

La représentation vectorielle de la figure 3.2 correspond à un cas particulier oil la tension est colinéaire à l'axe as à l'instant initial. Dans le cas général, on aurait :

· v _s = ? V _scos(w_st + O s0)

s 0

= arcta --

?
· Non pas (p mais (p-O_s0 avec cp -- ips

· Non pas

2 " 2 2 2 Vs = 3 v. 3 mais Vs = (v + vPs) et Os 0 = arcta as v

s,

? s ?? s

Os0 : Position du vecteur "tension", par rapport à l'axe a_s ou par rapport à l'axe a_s,

l'instant t=0.

En gardant 0 , comme l'angle représenté par la position du rotor par rapport à l'axe fixe a_s et par conséquent par rapport à l'axe a_s, on peut représenter les projections du flux produit par les aimants sur les axes a_s et r3_s :

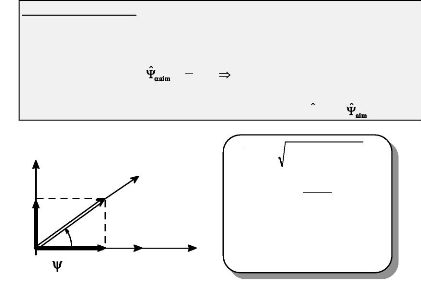
3^,'
= 2 Taim

te^taim = ⁴aim

pour Ta'aim = D'après la nouvelle notation, on a :

Vaaim =

Fig.An3-3

R_s

?

T_aim

?

a_s

aaim

?

? ? arctan ??

waaim = T_aim cos°
xvpaim = ''aim sin°

? ?2 2
? ?
aim ? ?
? ? aim

W?

Raim

??

? ? aim

^d

--)

Waim

11aim

0

a_s

Remarque importante:

Transposé sur l'axe a_s, le flux créé par les aimants (déterminé par un essai) doit être normalement majoré du coefficient 3/2 (unicité de la matrice de Clarke). On aurait donc :

Etant donné que nous utilisions des valeurs non primées, on fera de même

·
·

" coW]

[ Cla ][¹¹¹abc .1 aim ^=111a4 sinO^li

(An3-8)

Il faudra faire ATTENTION que dans tout ce qui suit, nous utiliserons
des notations non primées pour simplifier les écritures (Sauf indication
contraire).

Pour retrouver les vraies valeurs de flux et de tensions sur les axes a et 13, il faudra multiplier chaque résultat par 3 2 (les résultats sur les courants restent identiques).

4. EQUATIONS ELECTRIQUES DANS LE REPERE (as, 13s, os).
L'expression matricielle des tensions dans le repère (a_s, b_s, c_s) correspond à :

? v ? R ? i ? d ? ?

? ? ?

abc s s abc s abc s

dt

(An3-9)

On multiplie chaque terme par la matrice de CLARKE et on remplace ? par

?abc ? s

[ Cla] ? o ? aim ?1 ???

. On obtient :

? v ? R ? i ? d ? ?

? ? ?

abc s s abc s abc s

dt

[ v ? R ? i ? ? C ? d ? ? ? ?

?1

? ? C la ? ?? ?

?? o s s ?? s ^la dt o _s

? v ? R ? i ? d ? ?

?? ? ?? ? ? ??

o s s s dt o s

(An3-10)

Il faut exprimer les flux en fonction des courants. Pour cela, nous utilisons la même démarche que précédemment, en partant de l'expression des flux dans le repère (a_s, b_s, c_s). [''abc] s ? s ?? abc ? s ? ? abc ? aim

? L i ?

On multiplie chaque terme par la matrice de CLARKE et on remplace l'expression des flux par celle de l'expression 3.1:

?1

? C la ? ? abc ? s ? C la ? ? L s ? ? i abc ? s ? C la ? ? abc ? aim

? ? ? ? . Sachant que ? i abc ? s ? C la ? ? i o ? s

? ??

On a : ['I^j_ap_o ] s = [ C la] [ L s ] [ C la ] 1 [i apo ] _s #177;[Illapo ]aim

· Détermination de [ C la ] [ L_s] :

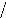
1 2(

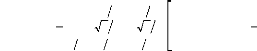
1 ? ?

? ?

2

=

3

p

M M L

? 1 ? 1 2 ? 1 2 ?

? ?

0 3 2 ? 3 2

? ?

? ? 1 2 1 2 1 2 ? ?

3

2

[C _la ][Ls]

=

L p M M

M L p M

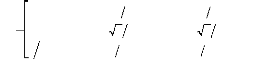
1 2

=

3

0 3 2

^{1 2}(

L

p -- M --1 2 (L p -- M) --1 2(L p -- M)

(L p -- M) -- 3 2(L p -- M)

L _p + 2 M) 1 2 (L _p + 2 M ) 1 2 (L _p + 2M)

1 ?

? ?

? ?

? ?

, ?

(An3-11)

· Détermination de [ C la ][ L_s] [ C_la] ^-1:

[C _la ][L _s ][Cla]

(An3-12)

L p -- M --1 2 (L p -- M) --1 2(L p -- M)

1 ? ? ? J

0 3 2 (L p -- M) -- 3 2(L p -- M)

L _p + 2 M) 1 2 (L _p + 2 M ) 1 2 (L _p + 2M)

1 --12 --121

?

0 3 2 -- 3 2 ?

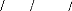
1 2 1 2 1 2 ? ?

? 1

? ?? ? ? ?

C L C ? ? 0 ? ?

L M
?

la s la p

?

0 0

?

0

(L _p + 2M)

L p -- M 0 0

? ?

f ?

s

? L 0 0 ?

0 L 0 ? s ?

? ? 0 0 L ?

1

?

?

?

J

=

Matrice que l'on notera ? L o ? s

??

?

r 1

[

1 ?

?

? ?

e
e

cos
sin
0

Taim

L_s

0 0

L_f

0 0

[ ja1 o ] s ? ?? o ? s ? ?? o ? s ? ? ?? o ? aim ? L i ?

Avec

0 L s 0

r 1

[

1 ?

?

? ?

Llio]

[_a=

et [T' ] = alio _aim

(An3-13)

On dérive l'expression précédente pour obtenir :

d? ? ? ? ? ?

d

? ? L i o

?? ??

dt o s o s dt ??

?

+ maim

s

r
[

cos

0

? ?

? ?

aim

?

?

sin

(An3-14)

On rappelle que 0 = wt dO = co dt

On remplace l'expression de la dérivée du flux dans l'expression (4.1) pour obtenir l'expression finale des tensions :

?

? v ? R ? i ? ? L ? d ? ?

? ? i o s ?

?

?? o s s ?? ??

s o s dt ?? aim

Soit

v _as = R _s i _ss + L_s

AN

cotPaim sine

di a s

dt

v 0 s = R _s i D_s + L_s
v os = R _s i _os + L_f

AN

+ _cotPaim cose

di 0 s

dt

di os

dt

(Attention aux valeurs primées)

r 1

[

sin

cos

0

0

0

1 ?

?

? ?

aim

(An3-15)

Sous une autre forme, on obtient un système de 2 équations différentielles linéaires à coefficients constants aux 1ers membres et avec les seconds, variables en fonction du temps:

?

(4.5) :

di

0

? aim

? sin ?

L L

s

?

Taim

0) cos0

L s L

di

R

dt

L _s

R

dt

L s

? s

v

Qs s Qs

#177; i = #177; #177;

Qs

s

v

s s ? s

? i ? ?

s

(An3-16) (Attention aux valeurs primées)

5. DETERMINATION DE LA MATRICE DE PASSAGE DU REPERE (d, q, o) AU REPERE (as, (_s,o_s).

En reprenant la figure 3.1, on remarque que l'on peut passer d'un système d'axes (d, q) au système d'axes (c_s, J_s) très facilement. La matrice de cette transformée que l'on appelle « matrice de CONCORDIA » et notée [ C 0] , correspond à :

[ C o ] .

r [

cose -- sin ? 0 ? ? sin cos ? ? 0 ? 0 0 1 ? _I

(An3-17) : Matrice de CONCORDIA : Repère (as, fi_s, os).

En inversant cette matrice, on obtient :

[C _o]^-1. --

r 1

cose sine

sin e cose

0 0

0_ll

0 ?

?_I

1

(An3-18):Matrice inverse de CONCORDIA : Repère (as, ?_s, o_s).

On remarque que cette matrice inverse correspond à la transposé de la matrice de

Concordia : ? ?

C o ? C

? ? t

1 ? . Il y a donc conservation de la puissance instantanée et de

^ol'amplitude des grandeurs vectorielles.

On obtient ainsi :

i _ds = i_ds cose -- i qs

i 13s = i_ds sin e + iqs

Nota :Expressions valables aussi pour les tensions et les flux

sine cose

?

i ds = i_as cos ° + ip_s

i qs = -- i _ns sin e + iPs

sine

cose

(An3-19)

6. EXPRESSION DU COUPLE ELECTROMAGNETIQUE DANS LE REPERE (as, (_s,o_s).

En reprenant l'expression du couple électromagnétique dans Park, nous avions :

¹aim

3

T_em = KT i_qs avec K _T = 2 Np

Or, en remplaçant i_qs par son expression en (An3-19), on obtient une nouvelle expression du couple électromagnétique :

T_em = K _T ( i p s cos e -- i_es sine)

avec

3

KT= ₂ Np

...taim

(An3-20)

7. EQUATION MECANIQUE DANS LE REPERE (as, (3s, os).

T _em ( Trm a #177; T r f #177; T r 0 )

?

? N J J

( m ? r )

??

p

dco 1

dt ^I]

1

Avec

T r f = f co

T r0 = Cste

T rma = k co² ou k co³ ou k co ou Cste

(An3-21)

En remplaçant T_em par son expression, on obtient :

?

K ? i i ? f ? T T ? N J J d

1

? ? ? ? ? ? ?

? ? ? ? ? ( ? )

T s cos s sin rma r 0 ?? m ^r dt ??

p

soit

Attention : f est en rad/s^-1 électrique

[K _T (i p_s cos 9 -- i _es sin e) -- f o)-- T rma -- Tr0]

J m + J

dco

?

dt

N p

(An3-22)

- ANNEXE 4 -

COMMANDE SANS CAPTEUR MECANIQUE DU
MOTEUR FINTRONIC.

FILTRE DE KALMAN

Schéma général sous Simulink : commande du moteur avec filtre de Kalman (fichier "bfesmli.m").

Schéma-blocs sous Simulink et masque de S-Function du filtre.

Fichier metafile : bfesmlim.m.
Fichier metafile : Filtre1m.m.

Annexe 4 : Commande sans capteur mécanique - Filtre de Kalman - Mémoire CNAM Patrick BOIDIN. Fichier : bfesmli1.m

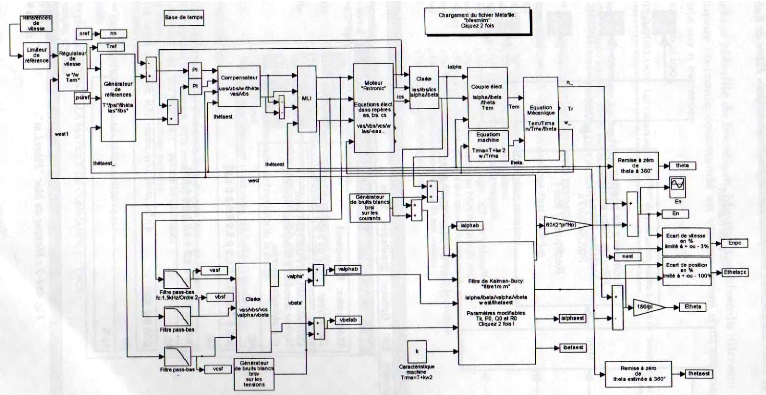
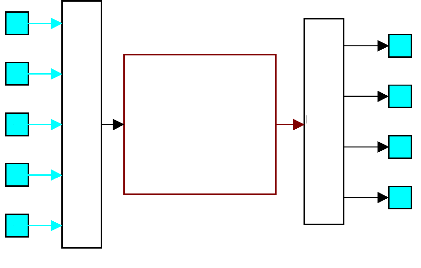
Fig.An4-1 : Schéma général de la commande sous Matlab-Simulink.

Filtre de Kalman

1

west

2

ibeta

thetaest

3

ialphaest

4

ibetaest

Mux

Demux

ialpha

valpha

vbeta

5

k

1

2

3

4

Fig.An4-2 : Bloc "filtre de Kalman".

Estimateur de position: Filtre de Kalman-Bucy

Metafile: "filtre1m"

P0/Q0/R0/Tk

Recliquez 2 fois !

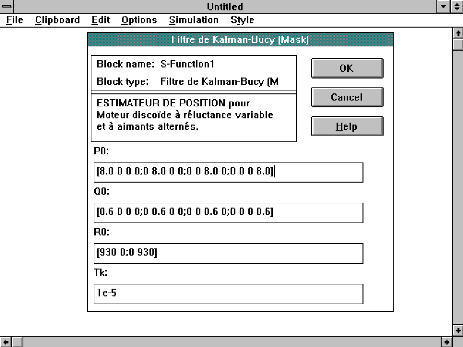
Fig.An4-3 : Masque du bloc "Filtre1.m".
- 152 -

%Fichier Métafile de boesti5.m, bfesti5.m et bfesmli1 :filtre1m %Moteur Fintronic commandé en vitesse, muni d'un estimateur et régulé sur n estimée

%20:23 16.11.1995

%

%NOTE IMPORTANTE: Les valeurs suivies de "**" doivent correspondre à ceux de "boesti5.m" et autres

%***********************************************************

%%

function[sys,X0]=filtre1m(t,X,u,flag,P0,Q0,R0,Tk);

%P0=700 / Q0=6 / R0=500 / Tk=30 microseconde

%********************* FILTRE DE KALMAN ********************

%

%**** DECLARATION DES CONSTANTES ESTIMEES:

%

Ld=0.0537 ;%**(mH) - Inductance synchrone d'axe d (Ld=Ls)

Ls=Ld ;

Rs=1.13 ; %**Ohms - Résistance d'une phase statorique

phiaim=0.141 ; %**Wb - Flux créé par les aimants

f=0.0306 ; %**N.m/rad.s-1 - Frottements visqueux

KT=13.536 ; %**N.m/A - Constante de couple : KT=3/2*phiaim*Np

Np=64 ; %**Nombre de pas, assimilé au Nbre de paire de pôles

Jm=0.141 ; %**kg.m2 - Moment d'inertie des masses tournantes du moteur

Jr=0.1 ; %**kg.m2 - Moment d'inertie des masses tournantes de la machine

Tr0=3 ; %**N.m - Couple résistant résiduel dû aux aimants

T=0 ; %**N.m - Couple résistant à n=0

%

J=Jm+Jr ; %kg.m2 - Moment d'inertie total: Moteur/machine

%

pL=phiaim/Ld ; %Simplification des notations

RL=Rs/Ld ; %Simplification des notations

KJ=KT*Np/J ; %Simplification des notations

%

Q=Q0 ; %Matrice de variance-covariance représentatif des

%bruits sur le système v (coefficients de la diagonale)

R=R0 ; %Matrice de variance-covariance représentatif des

%bruits sur les mesures w (coefficients de la diagonale)

%

% k ;%Constante représentative de l'évolution de la charge

;%Trma=T+kw2

% Tk ;%Pas d'échantillonnage: 10 micro sec.(déclaré dans simulink)

%

%**** NOTATIONS :

%

% X(1): dialphaest/dt, X(2): dibetaest/dt, X(3): dwest/dt, X(4): dthétaest/dt

% X(5): ialphaest, X(6): ibetaest, X(7): west, X(8): thétaest

% F: matrice des dérivées partielles, C: matrice de commande

% Fd: matrice de transition des dérivées partielles

% u(1): ialpha, u(2): ibeta, u(3): valpha, u(4): vbeta, u(5): k

% Y: Matrice de sortie;

%

%**** DECLARATION DE LA MATRICE UNITE (4,4) :

I=eye(4);

%

%**** DECLARATION DE LA MATRICE DE COMMANDE C : Y=CX :

%y1=ialpha, y2=ibeta

%

C=[1 0 0 0

0 1 0 0];

if flag==2

n=t/Tk;

m=floor(n+1e-13*(1+n));

if abs(round(m-n))<1e-8

%

%**** EVOLUTION DE f(x)- VARIABLES D'ETATS ESTIMEES X(5),X(6),X(7),X(8) :

%Méthode d'Euler

%

% Variation de ialpha estimé X(5): X(1);

X(1)=X(5)+Tk*(-RL*X(5)+pL*X(7)*sin(X(8))+u(3)/Ls);

%

% Variation de ibeta estimé X(6): X(2);

X(2)=X(6)+Tk*(-RL*X(6)-pL*X(7)*cos(X(8))+u(4)/Ls);

%

% Variation de w estimée X(7): X(3); xm3=KJ*X(6)*cos(X(8))-KJ*X(5)*sin(X(8))-Np/J*f*X(7)-Np/J*(Tr0+T)*sign(X(7))- Np/J*u(5)*X(7)*abs(X(7));

X(3)=X(7)+Tk*xm3;

%

% Variation de théta estimée X(8): X(4);

X(4)=X(8)+Tk*(X(3)+X(7))/2;

%

%**** PREMIERE ESTIMATION DU VECTEUR D'ETAT (avant les mesures et correction):

% XM=Xest(k/k-1)

% XM=[X(1)

X(2)

X(3)

X(4)];

%

%**** MISE EN MEMOIRE DE LA MATRICE DE VARIANCE COVARIANCE DE L'ERREUR

% SUR LA DEUXIEME ESTIMATION PP=P(k/k):

%

PP=[X(9) X(10) X(11) X(12)

X(13)	X(14)	X(15)	X(16)
X(17)	X(18)	X(19)	X(20)
X(21)	X(22)	X(23)	X(24)];

%

%**** CALCUL DE LA MATRICE DES DERIVEES PARTIELLES DE f(x), F(x): %

F(1,1:4)=[-RL 0 pL*sin(X(8)) pL*X(7)*cos(X(8))];

F(2,1:4)=[0 -RL -pL*cos(X(8)) pL*X(7)*sin(X(8))];

F(3,1:3)=[-KJ*sin(X(8)) KJ*cos(X(8))-Np/J*f-2*Np/J*u(5)*abs(X(7))]; F(3,4)=[-KJ*X(5)*cos(X(8))-KJ*X(6)*sin(X(8))];

F(4,1:4)=[0 0 1 0];

%**** CALCUL DE LA MATRICE DE TRANSITION Fd(x) de F(x)

% par la méthode du développement limité: I+FT+(FT)2/2!+... :

% Fd=I+Tk*F;

%

%**** DISCRETISATION DE LA MATRICE DE VARIAN. COV. Q

% par la méthode des trapèzes :

% Qd=(Fd*Q*Fd'+Q)*Tk/2;

%

%**** DETERMINATION DE LA MATRICE DE VARIANCE COVARIANCE DE L'ERREUR

% SUR LA PREMIERE ESTIMATION PM=P(k/k-1) :

% PM=Fd*PP*Fd'+Qd;

%**** CALCUL DE LA MATRICE DE KALMAN K (correction) :

%

K=PM*C'*inv(C*PM*C'+R);

%

%**** MESURE DES COURANTS REELS ialpha ET ibeta POUR COMPARAISON :

%

Y=[u(1);u(2)];

%

%**** CORRECTION DE L'ESTIMATION DU VECTEUR D'ETAT ESTIME APRES MESURES:

% XP=Xest(k/k) et XM=Xest(k/k-1)

% XP=XM+K*(Y-C*XM);

%

%**** DETERMINATION DE LA MATRICE DE VAR. COVAR. DE L'ERREUR

% SUR LA DEUXIEME ESTIMATION PP=P(k/k):

% PP=(I-K*C)*PM*(I-K*C)'+K*R*K';

% ou

%PP=PM-(K*C*PM)

%

%**** MISE EN MEMOIRE DE XP=Xest(k/k) et PP=P(k/k)

X(5)=XP(1);

X(6)=XP(2);

X(7)=XP(3);

X(8)=XP(4);

X(9:24)=[PP(1,1:4)';PP(2,1:4)';PP(3,1:4)';PP(4,1:4)'];

sys=X;

else

sys=X;

end

%

%**** RETOUR AU VARIABLES DE SORTIE west et thétaest

% + ialphaest ET ibetaest :

%

elseif flag==3

sys=[X(7);X(8);X(5);X(6)];

%

%**** RETOUR AUX CONDITIONS INITIALES :

%

elseif flag==0

%

%**** DECLARATION DU NOMBRE DE PARAMETRE A TRAITER :

%

sys=[0,24,4,5,0,0];

%

%**** DECLARATION DES CONDITIONS INITIALES

% dialpha0, dibeta0, dw0, dthéta0, ialpha0, ibeta0, w0, théta0 :

%

X0(1:8)=[0;0;0;0;0;0;0;0]; %**

%P0=P(0/0)

X0(9:24)=[P0(1,1:4)';P0(2,1:4)';P0(3,1:4)';P0(4,1:4)'];

%

else sys=[];

end

%*********** Fichier Métafile de bfesmli1.m ******************

%Moteur Fintronic commandé en boucle fermée dans le repère as, bs, cs

%Filtre de Kalman (filtre1m.m) fonctionnant en paralléle %Régulation de vitesse, avec onduleur, avec nest et thetaest %Machine: Tr=T+kw2

%18:17 13/10/1995

%NOTE IMPORTANTE: Les valeurs suivies de "**" doivent correspondre à ceux de "filtrem.m" %PARAMETRES DE SORTIE GRAPHIQUE ET DE SIMULATION:

%********** Méthode : EULER ***************

STT =0.0 ; %s - Start Time

ST =0.08 ; %s - Stop Time

MISS=2*1e-4 ; % - Min Step Size

MASS=2*1e-4 ; % - Max Setp Size

TOL =1e-4 ; % - Tolérance

bt=10000 ; %Base de temps de l'horloge

p1=10000 ; %Nbre de points (sortie graphique)

%

%MODULATEUR MLI:

e=0 ; % Entrée des relais, changement d'état

U=810 ; %volts - u/2 : Valeur maxi de la modulante

son=U/2 ; % Sortie relais (Amplitude de l'impulsion)

soff=-U/2 ;

%Up=410 ; %volts - Valeur crête de la porteuse

%f=2400 ; %Hz soit un rapport des fréquences m=39

%Remarque: La dent de scie est réalisée par un bloc fonction pré-défini par Simulink%

%

%PARAMETRES DU MOTEUR A RELUCTANCE VARIABLE ET A AIMANTS ALTERNES "FINTRONIC":

%In=9,3A / Imax=13A / n(nominale)= 60tr/min / Tn=200N.m / fn=64Hz/ Vn=220volts

Ld=0.0537 ; %**(mH) - Inductance synchrone d'axe d (Ld=Ls)

Rs=1.13 ; %**Ohms - Résistance d'une phase statorique

phiaim=0.141 ; %**Wb - Flux créé par les aimants

f=0.0306 ; %**N.m/rad.s-1(élec) - Frottements visqueux

KT=13.536 ; %**N.m/A - Constante de couple: KT=3/2*Np*phiaim

Np=64 ; %**Nombre de pas du moteur

Jm=0.141 ; %**kg.m2 - Moment d'inertie du moteur

%

%PARAMETRES MACHINE:

Jr=1.2 ; %**kg.m2 - Moment d'inertie de la machine entrainée

Tr0=3 ; %**N.m - Couple statique du aux aimants

T=0 ; %**N.m - Couple résistant

J=Jr+Jm ; %kg.m2 - Moment d'inertie de l'ensemble

%

% PARAMETRES DES CONDITIONS DE FONCTIONNEMENT

Tmax=130 ; %N.m pour

nref=60 ; %tr/min

wref=2*pi*Np*nref/60; k=(Tmax-T)/wref/wref; %

theta0=0*pi/180 ; %degré;

%Vmin=-600 ; %volts - Limitation de la tension

%Vmax= 600 ; %volts - Limitation de la tension

psiref=0*pi/180 ; %Degré - Couple maxi pour psi=0;

%

tec1=0 ; %s - A-coups de couple machine;

ec1 =0 ; %N.m - A-coups de couple machine;

%---- Régulateur de courant

kp=150 ; %Gain des correcteurs

ki=80 ; %Coef d'intégration des correcteurs

%

%---- Régulateur de vitesse

kvp=20 ; %Gain des correcteurs;

kvi=80 ; %Coefficient d'intégration;

Lmin=-300 ; %N.m

Lmax=300 ; %N.m

tnref=0.00 ; % s - Limitation de la référence de vitesse

tev1=0.04 ; % - A-coups de vitesse n°1 (s / tr/min)

ev1=0 ; % - A-coups de vitesse n°2

tev2=0 ;

ev2=0 ;

tev3=0 ; % - A-coups de vitesse n°3

ev3=0 ;

%

% Génération des bruits blancs

brsi=1/3 ; %x3 maxi A - bruits de mesures sur les courants

brsv=0.2 ; %x3 maxi volts - bruits de mesures sur les tensions

%

%Bruits sur le système:

brdias=140 ; %x3 maxi A - bruits sur la variation de ias

brdibs=150 ; %x3 maxi A - bruits sur la variation de ias

brdics=160 ; %x3 maxi A - bruits sur la variation de ias

brdw=20 ; %x3 maxi rad/s - bruits sur la variation de w

brdt=20 ; %x3 maxi ° - bruits sur la variation de théta

%

%Filtrage des tensions vas, vbs et vcs par filtres pass-bass:

%fc=1500 ;%Hz - Fréquence de coupure

%ordre=2 ;% - Ordre

%

%CONDITIONS INITIALES:**

ias0=0 ;ibs0=0 ;ics0=0; w0=0 ;kvi0=0 ;ki0=0; %

%Grandeurs de sortie (plot):

%nn / n / nref / En / Enpc / nest / vas / vbs / vcs

%valpha / vbeta / valphab / valphaest / Vs / eas

%Enthetapc / theta / thetaest / Etheta

%ias / ialpha / ibeta /Is / ialphab (bruité) / ialphaest / ibetaest

%Tref / Trma / Tem / Tr

%ds (porteuse) / vasreg / vbsreg / vcsreg / vasf (filtré) / vbsf / vcsf

%vasmli / vbsmli / vcsmli / sr1 / sr2 / sr3

QUELQUES PHOTOS

Photo 1

Photo 2

Photo 3

Photo 4

Photo 5

Photo 6

- 161 -

Photo 7

Photo 8

Photo 9