Modèlisation d'un prototype et commande vectorielle avec et sans capteur mécanique du moteur couple

Chapitre 2 : Essais expérimentaux et validation du modèle - Mémoire CNAM Patrick BOIDIN.

.

Aimants P.

Marche/Arrêt

J r = 1 0244 10 ²

. _ kg m ²

, .

Trma

T_u P_u

Dispositif de Frein :

Capacité de réglage du couple résistant de 0 à 135 N.m

Couple résistant à peu prés constant par rapport à la vitesse de rotation

n

Frein

ea

Poudre

T

n

n = 46,8 tr/ min

v a ( t)

i a ( t)

1'

1

U

20A

W

I

220V-3ph
Réseau

N

2'

MS

3

2

W

I

3'

3

Régulateur d'induction

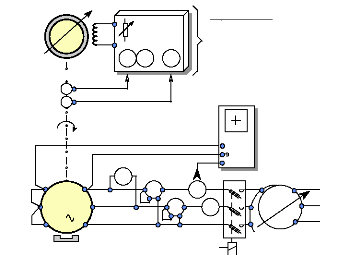
Fig. II-3.1 : Schéma de montage des essais en charge.

D'après les résultats obtenus et présentés en annexe 1, on fait les remarques suivantes:

· Quelle que soit le couple résistant, appliqué à l'arbre, le moteur a pu démarrer directement sur la fréquence du réseau. Il suffit d'appliquer une tension suffisante aux bornes du moteur.

Une charge équivalente à un couple résistant constant de 138 N.m n'a pas empêché de démarrer le moteur. Il faut noter que le moment d'inertie des masses tournantes de la charge (frein à poudre) est relativement faible et s'oppose peu à la variation de la vitesse.

1ère constatation:

? Les conditions de démarrage du moteur Fintronic en boucle ouverte dépendent essentiellement du moment d'inertie des masses tournantes et dépend beaucoup moins du couple résistant.

· Le courant nominal de 9,3A limite le couple utile à environ 100 N.m pour une fréquence d'alimentation de 50 Hz. =

1. Pour un fonctionnement en service continu, il n'est pas possible d'obtenir un couple utile supérieur à 100N.m sans échauffements excessifs.

2. Pour un fonctionnement en service intermittent, il est possible d'atteindre des couples utiles très élevés (environ 180 N.m). Il faut cependant accepter un dépassement du courant nominal.

2ème constatation :

? On tend à proposer ce type de moteur pour des applications nécessitant des couples élevés durant des cycles intermittents.

Dans ce cas de fonctionnement, il est important de connaître les contraintes thermiques du moteur, compte tenu des courants imposés. On pourrait prévoir une commande tenant compte à chaque instant, de l'état thermique du moteur.

· Le courant à vide du moteur augmente très vite avec la tension. Pour une tension de 300 volts, les courants correspondent aux courants nominaux. Ce sont les pertes magnétiques qui contribuent à absorber de tels courants.

3ème constatation :

? Pour une charge donnée, iI est essentiel de limiter les pertes magnétiques dans les tôles du moteur. Il faut réduire au mieux les tensions aux bornes du moteur. On applique des tensions justes suffisantes pour maintenir le couple électromagnétique maximale correspondant au couple résistant.

· Les courants absorbés dans les phases du moteur sont très inductifs. Par conséquent, le vecteur représentatif de la f.e.m induite au stator tend à se retrouver en avance sur le vecteur courant [9]. Dans le cas d'une commande par onduleur « commutateur de courant », la position de la f.e.m ne favorise pas l'annulation et l'inversion des courants (cas où l'inductance synchrone est en court-circuit sur sa f.e.m). L'amplitude et le signe de cette f.e.m ne sont pas aptes à s'opposer efficacement à ce courant. Il faut insérer, dans le circuit, des condensateurs qui permettent de transférer l'énergie stockée dans les inductances vers les condensateurs.

4ème constatation :

? L'utilisation d'un onduleur de tension est moins coûteuse et plus appropriée. Il n'est pas nécessaire d'équiper le système d'un dispositif particulier de commutation forcée puisque l'énergie stockée dans l'inductance est dissipée au moyen des diodes de roue libre.

· Le flux créé par les aimants est faible devant le flux nécessaire dans l'entrefer. On doit donc renforcer ce flux par une réaction d'induit. C'est pourquoi, les courants statoriques sont très inductifs. Par conséquent, il serait utopique de vouloir améliorer le facteur de puissance sans réduire sensiblement les performances du moteur en couple. Le rendement du moteur se trouve pénalisé et les meilleurs résultats obtenus pour ce rendement ont été de 40%. Toutefois, cette valeur ne peut pas être considérée comme mauvaise compte tenu des conditions de fonctionnement. En effet, pour des fréquences de rotation aussi faibles, des couples aussi importants et des encombrements aussi faible, les solutions utilisants le moteur asynchrone ne donnerait pas d'aussi bons résultats, même muni d'une commande vectorielle de flux. Une étude comparative serait intéressante à faire.

5ème constatation :

? Pour ce type de machine, il vaut mieux favoriser le contrôle du couple instantanéau détriment du facteur de puissance.

· Au démarrage, les courants de pointe, absorbés par le moteur n'ont jamais dépassé plus de 2,3 fois le courant nominal. Dans la majorité des cas, ces courants sont restés voisins du courant nominal.

· A l'arrêt, le flux constant créé par les aimants tend à vouloir figer le rotor par rapport au stator. On est en présence d'un couple"résiduel" qu'il ne faut pas oublier de rajouter au couple résistant. Ce couple, obtenue par un essai (bras de levier et poids),

prend une valeur approximative de 3N.m. Ce couple est constant par rapport à la vitesse.

3.2. Résultats obtenus pour U ab = 340 volts et T u = 138 ,5 N . m :

Ce relevé particulier va permettre, par la suite, de vérifier la validité du modèle mathématique du moteur. Avant cela, nous présentons les résultats expérimentaux obtenus par ce relevé :

Mesures

Tu	Pu	Ias	Ibs	Pabs	Qabs	Vas
(N.m)	(kW)	(A)	(A)	(W)	(var)	(V)

138,5

0,64

11,3

11,3

1 995

6 365

196,2

n = 46 , 8 tr/ min. => 50Hz. Pmag = 717 W.

Calculs

(1) cosg ( ( ' )	(2) PJ 3 2 R s I bs (W)	S	Pu T u ( 2i n ) (W)	? P u P abs (%)	Pmag Pabs (%)
		2 2 + P abs Q abs (VA)
0,299 72,6	434	4 969	639	34,0	36,0

(1) : cos q = cos[ Arc tan( Q abs Pabs)].

(2) : A chaud, R_s = 1 ,1 3 ?.

4. SIMULATIONS EN BOUCLE OUVERTE ET VALIDATION DU MODELE.

Toutes les simulations, précisées dans ce paragraphe, sont réalisées numériquement avec le module « SIMULINK » du logiciel « MATLAB SOUS WINDOWS » version 4.2c.1 d'Octobre 1994 (MathWorks). Ce logiciel est un outil informatique qui permet de réaliser des simulations pour des systèmes définis sous la forme d'équations algébrodifférentielles. La méthode de résolution numérique retenue pour notre application est celle de Runge et Kutta d'ordre 5 et d'Euler.

4.1. Modèle mathématique du moteur et valeur numérique des paramètres :

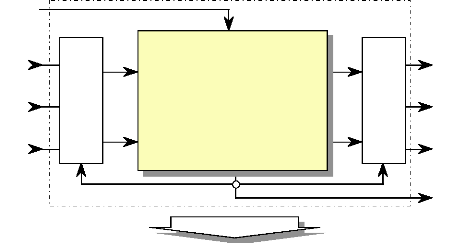
vas

v_cs

vbs

T_rma

Matrice
de
Park

[P]

vqs

vds

Modéle mathématique

du moteur
FINTRONIC
dans Park
Avec

sa machine iqs

ids

Matrice
inverse
de
Park

[ P] --1

ias

ibs

ics

0

Fig. II-4.1.

d i _ds ( t)

v _ds ( t ) = R _s i _ds ( t ) + L_d

? ? ( )

t L i t

( )

d qs

dt

v t R i t L qs ( ) ? ?

s qs ( ) d

dt +w ( t)

(L _d i _ds ( 0+ taim)

di _qs ( t)

3

T t K i t

( ) avec ?

K ? N

em T qs ( ) ?

? T p daim

2

T _em ( t ) -- T _r (t

avec T t T t f t T

? ?

r ( ) rma ( ) ( )

? ? r 0

dt

) - )

? ?

J J

?

m r

N

p

d o) (t

(II-15)

di _ds (t

) R v t

ds ( )

? ? L i t

^s ( ) ( ) ( )

? ? t i t ?

ds qs

dt L

d d

di t

qs (

dt

)

) R v ( t ) ? ? daim

? ? L i t

s ds

? ? t i t ? ? ? t

qs ( ) ( ) ( ) (

^ds L L

d d

d

d o) ( t) N_p

dt J _m + J_r

T _em ( t ) = K _T i _qs 0 )

[T _em ( 0-- T _rma ( t ) -- f o) ( t ) -- Tr0]

(II-16)
Pour effectuer les différentes simulations, on définit les paramètres J_r et Trma ( t) ainsi

que les valeurs initiales i _ds0 , i_qs0 , ⁽¹⁾ 0 et 90 :

· En charge, on prend un moment d'inertie de la machine, équivalent à celui du frein à poudre : 1,0244.10^-2 kg.m² . Cette valeur correspond à une roue pleine en acier, de diamètre 0,1 m et d'épaisseur 0,06m.

J		an R ^4L	avec acier = 8 930 kg / m^3.
	ü --	2

(II-17)

· Le couple résistant _Trma, dû à la machine entraînée, est supposé proportionnel au carré de la fréquence de rotation avec une condition à vitesse nulle, non nulle : Trma (t ) = k o)² (t) + T

(II-18)

· Les valeurs initiales de i _ds , i _qs ,00 et co0 sont supposées nulles.

· Les phases du moteur seront soumises à un système triphasé de tensions de la forme :

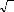
v as = V_s 2 cosco_st

2n1 3 4n1 3

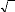
v bs = V_s 2 cos(co_st

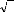
v cs = V_s 2 cos(co_st

(II-19)

En réunissant toutes les valeurs numériques, on obtient :

R =1 , 13n / L d = 53 , 7 mH / ''daim = 141 mW / N_p = 64
K T = 13 , 5 N . m / A / J m = 0 , 141 kg . m ² / T r0 = 3 N .m

f = 0 , 0306 N . m / rad^-1 (é lec) / i ? ?

i ? ?

? ? 0

ds 0 qs 0 0 0

En charge:

T t k t T J 2 ? 2 ? ? ? ? 1 0244 10 kg m . rm a ( ) ( ) / , . r

2

(II-20)