Modèlisation d'un prototype et commande vectorielle avec et sans capteur mécanique du moteur couple

CHAPITRE 2

ESSAIS EXPERIMENTAUX
ET
VALIDATION DU MODELE

1. INTRODUCTION.

Dans cette partie d'étude, nous avons tout d'abord déterminé par des essais expérimentaux, l'ensemble des valeurs numériques définissant les éléments du modèle. C'est à dire :

· La résistance de l'enroulement des phases du stator : R_s .

· L'inductance synchrone du moteur : L_s qui correspond aussi à l'inductance synchrone d'axe d du référentiel de Park L_d. Avec les 2 paramètres précédents, on en déduit la constante électrique statorique du moteur : t_s.

· La f.e.m à vide, induite dans les phases du stator et provoquée par la variation du flux créée par les aimants du rotor : e 0 s . On en déduit le flux maximal, produit par les

aimants : ??aim et la constante de couple du moteur : K_T.

· Le coefficient de frottement visqueux du moteur : f .

· Le moment d'inertie des masses tournantes du moteur (rotor) : J_m et d'en déduire la constante mécanique du moteur, à vide : ' m0.

· La constante thermique d'échauffement du moteur, compte tenu que le moteur est démuni de tout système de refroidissement : tth.

· La température limite d'échauffement des enroulements de phases : 0lim.

Ensuite et pour compléter les résultats obtenus, nous avons émis une série de remarques sur le comportement du prototype, face aux différents essais.

Pour finir ce chapitre et valider le modèle mathématique du moteur, nous avons comparé les résultats obtenus par des simulations, sous MATLAB-SIMULINK, avec les résultats des essais.

2. DETERMINATION NUMERIQUE DES ELEMENTS DU MODELE. 2.1. Essai à vide du moteur en fonctionnement générateur :

Cet essai permet de construire la caractéristique de la f.e.m en fonction de la fréquence de rotation (Annexe 1) et d'en déduire la valeur du flux dans l'entrefer, produit par les aimants. Pour effectuer cet essai, nous entraînons le moteur FINTRONIC avec un moteur à courant continu à excitation séparée.

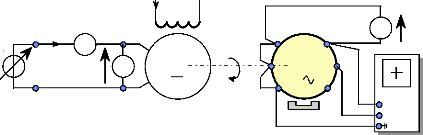
Ea 0s

V

1

I

1'

n

+

A

U

2'

V

2

M

GS

J= 0,8A

3

Chronomètre 3'
et
Tachymètre

3

Aimants P.

e a 0 s (t )
e b 0 s (t )

Fig. II-2.1 : Schéma de montage de l'essai à vide en générateur.

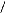
Les résultats et les remarques sur cet essai, sont les suivants :

· Sur une moyenne de 10 relevés, on obtient une constante de vitesse de 0,67volts efficace par tour par minute. Soit :

?

0 ,6 7 volts / tr . min -1 = E a 0s = 40 ,2 volts pour n = 60 tr / min

(II-1)

· Pour un fonctionnement à vide, on a :

v as = e a 0 s ?Vs = E0 s =⁰) aim

co = 27c N _p n

avec N p : Nombre de pas du moteur (64 dans notre cas).

On en déduit la valeur maximale du flux produit par les aimants et la valeur de la

constante de couple sachant que KT = 3 2 NpTdaim :

^·?aim = 141 mWb soit Taim = 99 ,7 mWb
K_T = 13 ,5 N . m / A

(II-2)

· Les ondes de tensions, obtenues sur les oscillogrammes, sont quasiment sinusoïdales. Echelles : 20 volts/cm et 2ms/cm :

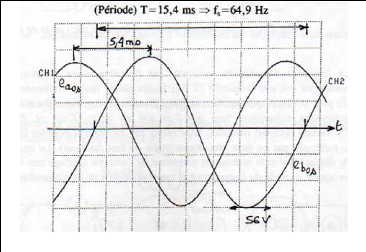
Fig. II-2.2 : Ondes de tensions. e a 0 s ( t ), e b 0 s ( t) et e c 0s ( t) à n =61 tr/min

· Au moment de cet essai, on remarque que la fréquence de rotation du moteur varie sensiblement et de façon périodique. Cet effet néfaste (parasite) impose à la machine des vibrations et des à-coups de couple qui nuisent au bon fonctionnement du moteur. Ce phénomène se produit quelle que soit la fréquence de rotation du moteur. A l'oscilloscope, on observe cet effet parasite par l'intermédiaire de l'onde de tension induite au stator.

La machine tourne à 14 tr/min (15Hz) soit à peu prés au quart de sa vitesse nominale. La base de temps est de 0,5s par cm.

1 tour mécanique

Fig. II-2.3 : Oscillations parasites détectées sur l'onde de fe.m.

La fréquence d'oscillation, constatée sur l'oscillogramme, équivaut au demi-tour mécanique soit une fréquence 32 fois moins élevée que la fréquence électrique (2,2 Hz pour 69,3 Hz). Contrairement aux apparences, ce phénomène n'est pas dû à des frottements mécaniques bien que l'on soit en limite. Ceci est dû à des forces d'attraction (axiales) parasites, provoquées par les aimants dont les lignes de champs se referment par les plots statoriques (règle du flux maximal). Le manque de rigidité du disque rotor et le manque de constance de l'entrefer (réglage très difficile à mettre en oeuvre = voile du disque) sont la cause principale de ce phénomène.

Chapitre 2 : Essais expérimentaux et validation du modèle - Mémoire CNAM Patrick BOIDIN.

.

Stator
N°1

Stator
N°2

Les forces
d'attraction ne sont
plus
équilibrées

Disque
rotor

Aimants

N

S

Stator
N^°1

Stator
N^°2

Entrefer
constant

Axe de rotation

S

N

Entrefer mécanique

Entrefer non constant

Position du rotor

0 = 0⁰

Position du rotor
0 = 1 80^?

Les forces

d'attraction s'équilibrent

Stator
N°1

Stator
N°2

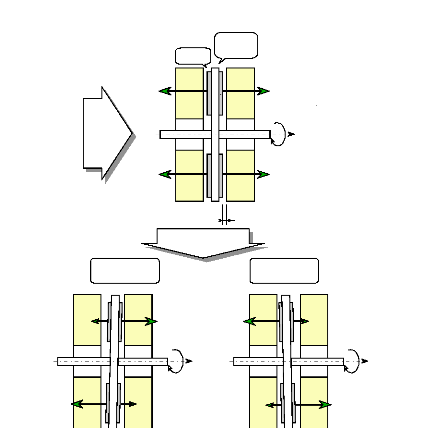
Fig. II-2.4 : Explication du phénomène d'oscillations sur la fréquence de rotation.

2.2. Essai avec les enroulements statoriques en court-circuit :

Cet essai permet de déterminer la valeur de l'inductance synchrone du moteur et d'en déduire la constante de temps électrique.

J= 0,8A

V

M

Chronomètre
et
Tachymètre

n

I

+

A

U

1'

1

2'

GS

3

Icc

2

A

3

3'

Aimants P.

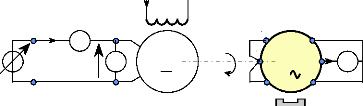
Fig. II-2.5 : Schéma de montage de l'essai en cc.

· Des mesures sur la résistance des phases statoriques, par la méthode voltampèremétrique, nous donne les résultats suivants :

R s = 961 m ? à 20°C et 1,13Q à 80°C.

· En convention générateur, on a : V E R I j L I

= -- -- co

s s

-- s -- s -- s -- s

(II-3)

? 2

0 ( ) ( )

2 2

E R I j L I ? ?

= -- -- co ? E R I

? ? L I

?

s s s s cc s c c

? ? ?

s cc cc

2

E ? 2 ? ( )

?

R I

L s ?

s s cc

?
Co I cc

(II-4)

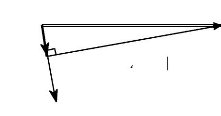
soit dans la construction de Fresnel :

--)

s 0) I cc

90^?

--)

E_s

0

Fig.II-2.6

--)

R _s I cc

--)

Icc

Sachant que w = 2 i N _p n , on a l'expression de l'inductance synchrone en fonction de la fréquence de rotation (tr/s) :

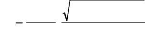
L s

?

2 ?

1

N n I

p

.

2

E --

s

( )

R I

s cc

cc

2

(II-5)

· Par l'essai à vide, on a obtenu E a 0 s = 40 , 2 volts pour n = 1 tr / s. Quelque soit la fréquence de rotation du moteur, l'essai en court-circuit nous donne : I cc = 1 ,8 6 A. D'où,

L'inductance synchrone correspond à :L s = 53 ,7 mH

(II-6)

L s

? La constante de temps électrique du moteur 'r_s = est de 47,5 ms. Cette valeur est

R s

importante, comparée à celle obtenue pour un moteur classique de même puissance qui est de quelques ms seulement.

2.3. Essai à vide du moteur FINTRONIC en fonctionnement moteur :

Cet essai permet de déterminer les pertes mécaniques et d'en déduire le coefficient de frottement visqueux du moteur. Tous les essais sont réalisés sous une alimentation de tension à 50 Hz pour une fréquence nominale de 64 Hz.

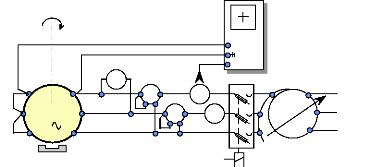
Aimants P.

Marche/Arrêt

n = 46,8 tr / min

v a 0 s (t ) i a 0 s (t )

1'

1

U

W

I

20A

220V-3ph
Réseau

N

2'

MS

3

2

W

I

3'

3

Régulateur d'induction

Fig.II-2.7 : Schéma de montage de l'essai et vide en moteur.

· En prolongeant la courbe de la caractéristique U ² i--> Pmag + Pmé ca, au point

d'abscisse égal à zéro (Annexe 1), on obtient les pertes mécaniques. Elles sont supposées constantes par rapport à la tension et sont proportionnelles au carré de la vitesse mécanique. On en déduit le coefficient de frottement viqueux f :

P_m

f -- LIé ^2ca et Pmé ca = Tfr n ? f = 1 ,96 N . m / rad . s-1(méca)

Coefficient de frottement visqueux.

mé _ca

ou f -- ?

2 et Pmé ca = Tfr ( 27c n) = f = 0 , 205 N. m / tr. min ^-1

P

(2 7c n)

2 et Pmé ca = Tfr (0) N_p) = f = 0 ,0306 N. m / rad . s^-1(élec)

mé ca

ou f --

P

(o) N_p)

(II-7)

· Pour effectuer cet essai, on couple la machine sur le réseau par la méthode habituelle : Moteur à courant continu et lampes de mise en phases sur le réseau. Le moteur à courant continu entraîne la machine à 47 tr/min. Ensuite, elle est couplée au réseau, par l'intermédiaire d'un régulateur d'induction réglé à l'avance à une tension composée de 115 volts. En fonctionnement générateur, la machine fournit entre les 2 bornes de son stator, une tension composée de 55 volts.

? La machine se couple au réseau sans problème et fonctionne en moteur.

Dans un deuxième temps, on tente de démarrer le moteur en forçant sa rotation à la main.

? Le moteur s'accroche au réseau sans et-coups, ni problème. La fréquence de synchronisme du moteur est très facilement atteinte et la main.

Pour finir, nous tentons de demarrer le moteur sous 115V en direct et sans aucune aide exterieure. L'essai est concluant et le moteur démarre à chacune de nos tentatives. Il en est de même pour tous les essais effectues.

? Le moteur est apte à démarrer en direct sur le réseau.

· La tension limite de decrochage du moteur, à vide, se situe à environ 110 volts soit une tension de phase de 63,5 volts.

· Le moteur vibre sensiblement pour des tensions elevees, voisines de la tension nominale.

· On suppose que les pertes magnetiques sont proportionnelles au carre de la tension (droite ideale sur la caracteristique en annexe). On en deduit le coefficient de proportionnalite :U _ab = 67 , 6 . 10³ --> P_mag = 419 W = k=6,20.10 ^-3 W/volts^2.

De 0 à 283 volts, on peut effectivement considerer cette proportionnalite comme
realiste. Au-delà, il faut reconsiderer cette hypothèse, il suffit de comparer les
courbes de la caracteristique U ² i--> P_mag + Pmé ca, en annexe 1, pour s'en convaincre.

· Le couple de frottement visqueux correspond à : T_fr = 9 ,5 7 N . m
2.4. Essai de ralentissement du moteur fonctionnant à vide :

Connaissant le coefficient de frottement visqueux f, cet essai permet de determiner le moment d'inertie des masses tournantes du moteur, à vide.

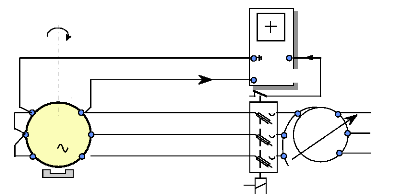
220V-3ph
Réseau

2

2'

N

3

3'

Aimants P.

Marche/Arrêt

n(t0 ) = 48tr/min

n(t₁ ) =0tr/min

MS

3

Synch

e a 0 s (t ₀ à t₁)

1'

1

20A

Régulateur d'induction

Fig. II-2.8 : Schéma de montage de l'essai de ralentissement du moteur.

· e a 0 s ( t) dans l'intervalle de temps compris entre t0 (correspondant à n = 48 tr / min) et t1 à n = 0 tr / min :

Echelle : 20ms/cm

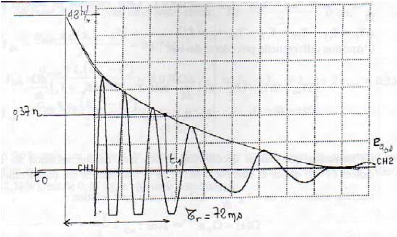
Fig. II-2.9 : Relevé de l'oscillogramme e a 0 s (t ).

· Le niveau de tension aux basses vitesses, fourni par la dynamo-tachymétrique, est trop faible pour obtenir des mesures significatives. De plus, les à-coups de couple ont tendance à transformer le signal continu du capteur, en un signal modulé inexploitable. Or, pour réaliser cet essai, on décide d'observer l'évolution de la f.e.m aux bornes d'une phase du moteur dans son fonctionnement générateur et en phase de décélération.

· En régime dynamique, le système mécanique, constitué par un moteur accouplé en direct sur une machine, est régi par l'équation différentielle suivante :

d ?
dt

T T ( J J )

em ? r _m + _r

(II-8)

Nota : Généralement, le premier terme de l'expression est non linéaire.

Pour supprimer la non-linéarité du premier terme, on linéarise le système autour d'un
point fonctionnement sur la vitesse : ?₀ . Pour cela, on découpe la période de

décélération en intervalles de temps A t donnés. On obtient ainsi [8] :

· A t₀=0, la condition initiale de l'essai ?₀

? 1

·

A t 1 = A t , T _ T ( J J ) t

= +

em 0 r 0 m ^r A

Q 2

·

A t 2 = t ₁ + A t , T _ T ( J J ) t

= +

em 1 r 1 m r ?

· A t 3 = t ₂ + At ...

Dans de nombreux cas, la variation du couple moteur est supposée constante autour de son point de fonctionnement et la variation du couple résistant, proportionnelle à la vitesse. D'où :

AT_em = Tem 1 -- Tem 0 = T_{em 2} -- T_em1 =... = cte=T. Cette variation ne dépend pas de n. AT_r = Tr 1 -- Tr 0 = T_r 2 -- Tr1 =...= fn

L'équation différentielle précédente devient :

AT em -- AT r =	? ? ?? J J ? soit T f ? ? m ? r ? ? ? J J m r At		di2 dt

n(t = 0 ) = n 0

(II-9)

En supposant que chaque décélération a lieu sans aucune variation du couple moteur
(T=0) et que le moment d'inertie de la machine est nul (décélération sans machine

entrainée), on a J

m

di2 dt

+ fn = 0, qui a pour solution :

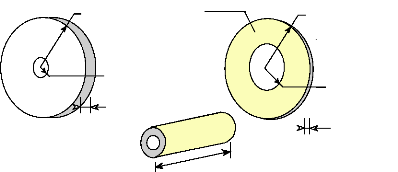
Taux d'occupation des aimants

tocc = ⁷⁶%

R=155 mm

aacier = 7850 kg / m3

(Densité)

r=30 mm

Ra=149 mm

caim = 8300 kg / m3

(Densité Récoma 28)

+ 2 x

ra=122 mm

e=10,5 mm

R=80 mm r=30 mm

+

Acier

L=141 mm

ea=1,75 mm

Jm

? ? t ? ? ? e ? t mo

? avec ?m 0 ? .

⁰ f(II-10)

On en déduit ainsi :

n(t = T m 0 ) = 0 ,3 7 n₀

(II-11)

L'essai nous donne t m 0 = 72 ms. Or, sachant que f=1,96 N.m/rad.s^-1, on obtient:

J _m = f T = 0 ,14 1 kg .m² : Moment d'inertie des masses tournantes du moteur
FINTRONIC.

(II-12)

· Vérification du résultat précédent par un calcul approximatif :

On sait que le rotor est constitué d'un disque métallique muni d'un arbre creux et de 2 couronnes d'aimants collées sur les faces du disque.On peut donc calculer le moment d'inertie de l'ensemble.

Fig.II-2.10 : Les éléments de constitution du rotor.

Moment d'inertie pour un cylindre creux : J = an e (R 4 -- r4). D'où,

2

J dis

J aim

J arb

?

aaciern

aim a

? ?

aaciern

e

e R-- r⁴)

L (R ⁴ - r⁴)

2 = 0 ,0746

(R a 4 -- r_a⁴)

2 = 0 ,070

2 ti occ= 0 ,0047

? ?

??

?

?
?

? ?

??

J J J

? ? 2 J ? 0 154

, kg m

.

m isc arb aim

A 10% prés, on retrouve le même résultat. Par comparaison, le moment d'inertie d'un moteur asynchrone, pouvant fournir un couple nominal de 95N.m à 750tr/min (7,5kW), est de 0,13 kg.m² (donnée constructeur).

2.5. Essai d'échauffement du moteur FINTRONIC :

Cet essai permet de déterminer :

· La température limite _elim atteinte par les enroulements statoriques pour un régime de fonctionnement permanent donné.

· La constante thermique tith.

Chaque enroulement des 12 secteurs est équipé d'une double sonde de température du
type thermo-résistance au platine PT100n. On utilise 2 de ces sondes pour effectuer cet

essai. Une table de conversion conforme à la norme permet de convertir les valeurs de résistance en valeurs de température (en degrés Celsius).

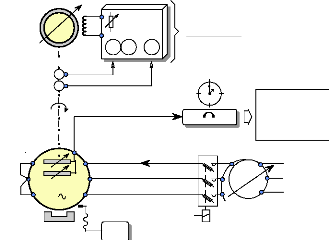
n = 46,8 tr / min

N

3'

2'

1'

Aimants P.

Frein
ea
Poudre

MS

3

e

T

n

Résistances variables par
sonde platine

3

1

Thermomètre

2

oC

T_u P_u n

Trma

I = 9A

Marche/Arrêt

Dispositif de Frein : Réglé à 87 N.m

Ohmmètre

20A

SL

Régulateur d'induction

Table de correspondance
de la norme
DIN 43 760

CPC

220V-3ph
Réseau

Fig.II-2.11

· D'après les relevés effectués (Annexe 1), on obtient une température limite des enroulements statoriques de 125°C. La température ambiante était de 22,2°C au moment de l'essai.

1ère constatation :

En prenant une marge de sécurité d'environ 10%, les parties isolantes du moteur doivent tenir 140°C, au minimum. Ce qui correspond d'après la norme NFC à la catégorie F des matières isolantes (155°C).

Nota :

Il faut préciser que le prototype est démuni de tout système de refroidissement. En effet, un dispositif d'auto-ventilation serait inutile compte tenu des faibles vitesses de rotation du moteur.

L'enveloppe du moteur est constitué d'une résine de moulage « DAMIVAL 13 576 » dont la plage thermique d'utilisation est de -70°C à +130°C. La notice technique du matériau concerné précise une tenue thermique en continu de 140°C, sans dégradation.

? Le matériau utilisé est limite en tenue thermique. Il faut réduire les pertes magnétiques afin de limiter les échauffements. La commande se chargera de réduire ces pertes.

· La constante thermique d'échauffement est de 22,5min. La température limite du moteur est atteinte après environ 112 min de fonctionnement (1h52 min).

°lim ? 1 2 5° C et rth = 22 ,5 min.

(II-13)

2.6. Paramètres du modèle :

Equations électriques dans le repère (d,q) de Park :

v R i L

=

ds s ds + d

v R i L

=

qs s qs + q

ds

di

dt

qs

di

dt

avec

e qs = w ( L _d i _ds + _daim ) e ds ? L q qs

?? et co i

3

L d = L q = L s = l _f + 2 s

L m

et
R_s = 1 , 1 3 ?, L d = L q = L s = 53 ,7 m H

? ? aim ? ? ? aim = 141 mWb

Equation mécanique dans Park :

3

T em = K _T i _qs avec K T = N p

2

H

T T _N J J

1 (

- =

em r ?? m +

p

T r = T _rma + T r 0 + f O)

? e ds
+ e qs

^??daim

_r)

do) 1 dt I?

Tous les essais effectués permettent de déduire l'ensemble des paramètres numériques du modèle. On obtient ainsi :

Constante de couple : KT = 13 ,5 N . m / A Nombre de pas du moteur : Np=64 Couple résiduel dû aux aimants : Tr0 = 3 N . m Moment d'inertie du rotor : J m = 0 ,14 1 kg .m^2 Coefficient de frottement visqueux du moteur : f = 0 , 0306 N . m / rad . s ^-1 0 lec)ou f = 0 ,205 N . m / tr.min^-1

(II-14)

Nota:

· Jr et Trma sont à définir selon la machine entraînée.

· Le modèle ne tient pas compte :

des pertes magnétiques,

de la saturation du circuit magnétique,

de la variation du flux _Taim, due aux parties saillantes des plots statoriques.

· Attention : v_ds et v_qs sont en réalité des valeurs primées.

3. ESSAIS EN CHARGE EN FONCTIONNEMENT MOTEUR.

Cette série d'essais, effectuée en boucle ouverte, permet de juger les capacités et les performances du prototype. Par obligation, on a augmenté l'entrefer de la machine pour éliminer les contraintes mécaniques et magnétiques observées au début de nos essais. Cette modification a pour conséquence de réduire sensiblement les performances de la machine. Les améliorations mécaniques et magnétiques nécessaires n'ont pas pu être réalisées dans le cadre de nos travaux.

On notera clue les performances réelles sont en réalité bien supérieures à celles annoncées dans ce mémoire.

Pour réaliser ces essais, on utilise un banc d'essai dynamométrique. Ce banc est équipé d'un frein à poudre magnétique (couple résistant constant par rapport à la vitesse) du type PB115 et de marque « Vibro-meter ».

3.1. Remarques sur les essais en charge :