Influence de la dispersion aléatoire faible sur la transmission par solitons et du mélange à quatre ondes dans les fibres optiques

RÉPUBLIQUE DU CAMEROUN REPUBLIC OF CAMEROON

Paix - Travail - Patrie Peace - Work - Fatherland

UNIVERSITÉ DE YAOUNDE I

UNIVERSITY OF YAOUNDE I

FACULTE DES SCIENCES

FACULTY OF SCIENCE

DÉPARTEMENT DE PHYSIQUE

DEPARTMENT OF PHYSICS

LABORATOIRE DE MECANIQUE

Influence d e la dispersion aléatoire faib le sur la
transmission par solitons et du Mélange a quatre
ondes dans les fibres optiques

MÉMOIRE
Présenté en vue de l'obtention du
Diplôme d'Etudes Approfondies en Physique
(D.E.A)
Par
Lucien MANDENG MANDENG, Maître es sciences
Option : Mécanique Matricule : 02Q076

Sous la direction du Sous la supervision du

Dr. Laurent NANA Pr. Timoléon Crépin KOFANE

Chargé de cours Professeur

Université de Douala Université de Yaoundé I

Année académique 2006 - 2007

D édicace

Ce mémoire est dédié a toute ma famille en partant des lointains ancetres aux descendants a venir_' particulièrement a la mémoire de feu mon frère ainé IVI A N D ~N G

Clément Hervé.

Re mercie ments

M es re mercie ments s'ad ressent a tous ceux qui d e p rès ou d e loin quelques soient les moyens ont eu a m'aid er pour la réalisation d e ce travail.

Je p ense p articulière ment :

- Au personnel enseignant d u d ép arte ment d e physique d e la faculté des sciences a

l'U niversité d e YAOUNDE I_' aux Professeurs_' D octeurs et d octorants qui ont eu

à m'encad rer : Pr. Timoléon C rép in KO FAN E_' Pr. Paul WO AFO ' Pr. Claude Marie N GABIREN G ...

- Au D r. Laurent NANA.

- A M . FEWO .

- A M . N change AD AM O U .

- A mes parents M . et Mme MAN D EN G qui m'ont toujours soutenus.

- A toute ma famille.

- A la Famille YANA.

- A mes ami(e)s : Jacques Christian KO TTA ' Fredy FEZEU ' Patrick NJIO N O U ' Placid e O M BO LO ' C hristelle NAN G N E_' Yoland e KEMA G O UA ' MAYEGA ' Bernard BIN D EG ' Laurent FO TZE_' Patrick NYAN DJO U .

- A tous ceux qui ont eu a c euvrer pour que ma soutenance d e sortie d e l'E.N .S d e YAOUNDE soit une réussite : Rev. Pasteur Emile MAN D EN G et sa fe mme_' ma famille (mes p arents_' Mme Emilienne NYO BE_' Mme BIEN D ' Mama Franc_' Mlle Bénédicte N G O N LEN D ' Gabriel M INYEM EC K_' Dora AN D EM E_' ma sc eur S ylvie_' mon frère ainé Antoine_' mon petit frère Patrick_' Louis - C ésaire_' S eh BADJE_' M arthe_' Yoland e KEMAG O UA ' Hans NWAHA ' Placid e O M BO LO ' Jean - Baptiste N DJIN GU E_' Fredy FEZEU ' Patrick NJIO N O U ' Annie....

Bref a tous ceux d ont j'oub lie certaine ment les no ms ici_' merci a tous.

Table des matières

D édicace					2
Re mercie ments					3
Table des matieres					4
Résumé					5
Abstract					6
Introduction Générale					7
1 G énéralités sur les ondes solitaires et les téléco mmunications op tiques haut débit					9
1.1 Bref historique sur les ondes solitaires [4'6'17] 8 8 8 8 8 8	8	8	8	8	8 9
1.2 Téléco mmunications optiques haut d éb it [7]8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8	8	8	8	8	.10
2 L'équation de SNL et un modele pour l'évolution du Mélange a quatre ondes					19
2.1 O rigine d e l'équation modele non linéaire d e Schrodinger [4]					19
2.2 Equation modele et parametres de trans mission8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8	8	8	8	8	.23

2.3 Modele de l'évolution du mélange a quatre ond es (FWM ) et la condition d e résonance [1]8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 .8 8 8 8 8 8 8 8 8 8 8 8 8 28

3 L'évolution du FWM et la dispersion stochastique faible comparée a la gestion de dispersion 3 7

3.1 Equation S N L avec la dispersion stochastique faib le [1_'19]8 8 ..8 8 8 8 8 8 8 8 8 8 8 8 .37

3.2 Résultats numériques pour l'évolution du FWM en p résence d 'une faible dispersion stochastique ou aléatoire8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 .38 3.3 C o mp araison entre la dispersion stochastique faib le et la dispersion gérée8 8 8 8 8 8 ..41

Conclusion G énérale 47

Annexe 1 49

Annexe 2 54

Bib liograp hie 59

Résumé

Dans ce mémoire, il est question de présenter les effets de la dispersion aléatoire faible sur les solitons¹ enveloppes de transmission dans les fibres optiques et sur les produits du mélange à 4 ondes.

Il s'agit du développement de l'article des chercheurs Rudy L. HORNE , C.K.R.T Jones et Tobias SCHAFER, les deux premiers étant du département des mathématiques de l'Université de la Caroline du Nord à Chapel Hill aux Etats - Unis , le dernier appartenant au Staten Island College à New - York aux Etats - Unis. Cet article est apparu dans la revue internationale de physique « PHYSICA D » et a pour référence: Physica D 205 (2005) 70 - 79.

Ce sujet est intéressant dans la mesure oil dans plusieurs applications de la physique qui utilisent les solitons comme véhicules de l'information, ceux - ci peuvent être détruits après une ou plusieurs interactions entre - eux (collisions inter - solitons de fréquences voisines). Ces interactions peuvent résulter de la dégradation du signal initial autant que de l'apparition des sous - produits non linéaires parasites qui affectent la performance du système de transmission optique. Dans les systèmes de communication optique non linéaires, particulièrement ceux utilisant le multiplexage en longueur d'onde (WDM)², les interactions entre deux solitons de fréquences voisines induisent la croissance des composantes du Mélange à 4 ondes (FWM)³. Il est montré dans ce travail que l'introduction d'un bruit faible (processus stochastique) dans le système considéré (à travers le terme de dispersion) réduit la croissance des composantes dudit Mélange à 4 ondes. La dispersion aléatoire affecte aussi la condition de résonance concernant le Mélange à 4 ondes. Ce qui est surprenant, c'est qu'on constate que l'effet du bruit faible dans le terme de dispersion a un impact comparable (sinon encore meilleure) à la technique déterministe usuellement utilisée pour résoudre le même problème notamment celle de la gestion de dispersion.

¹ Solitons : ondes solitaires

² WDM : Wavelength - Division Multiplexing

³ FWM : Four - wave mixing

Abstract

In this work, it is question to present the effects of weak randomness on pulse interactions and four - wave mixing products.

In fact, It is a development of the paper of researchers Rudy L. HORNE , C.K.R.T Jones, Tobias SCHAFER , the two first being in Mathematics' s department of North Carolina University at Chapel Hill in U.S.A , the last one belonging to Mathematics ` s Department of Staten Island College at New - York in U.S.A. This paper has appeared into the international review of physic «PHYSICA D» and has the following reference: Physica D 205 (2005) 70 - 79.

This research subject is very important in the case that, in many physical applications that use pulses as information carriers, pulses may be distorted after one or many interactions (collisions between solitons having neighbours frequency). These interactions can result in initial pulse degradation as well as the production of non linear by - products that affect system performance. In nonlinear optical communications systems, particularly wavelength - division multiplexing (WDM), pairwise pulse interactions induce Four - Wave Mixing (FWM) components growth. It is shown here that, the introduction of small noise (stochastic process) in the underlying system (trough the dispersion term) reduces the growth of this FWM. The weak random dispersion also affects the resonance condition concerning Four - Wave Mixing. What is surprising, is that we note effect of weak randomness in the dispersion term is shown to have a comparable impact as that of using the much more drastic deterministic dispersion management (DM) technique.

Introduction Générale

L'on ne saurait se tro mp er en disant que les téléco mmunications sont l'invention la plus p rolifique_' utile et imp ortante de ces d ernières décennies : p artant de la télép honie_' en passant par internet... b ref tous les médias modernes d e communication a distance [1-7]. Plusieurs travaux de recherche subventionnés par des grand es Entreprises d e téléco mmunications_' se retrouvent dans ce do maine [7_'20(5)]. D e plus en plus_' des techniques pour améliorer les communications sur des longues distances ( milliers d e km) a des débits d e plus en élevés (Gb its/s)_' sont mises au p oint_' ceci_' du d o maine théorique au do maine exp érimentale. C ela p eut exp liquer la p rolifération d 'articles scientifiques sur les téléco mmunications [7]. C e qu'on ap p elle 0 cable coaxial » a été pendant une certaine époque le meilleur moyen pour transporter les informations sur d e longues distances. D ep uis quelques années_' la fibre op tique_' après avoir sup planté ce d ernier_' est devenue un des médias les plus utilisés pour transporter tous les types d e données (audio_' vid éo_' Internet). C e choix est dil aux efforts soutenus des chercheurs dans le do maine des téléco mmunications op tiques. Puisque l'on s'est rendu co mp te que la lumière (étant une ond e électro magnétique se prop ageant a la plus grande vitesse existante dans l'Univers d 'après le Relativité Restreinte d 'Alb ert EINSTEIN) p ouvait servir a transporter les informations sur d e longues distances a des vitesses non envisageab les jusqu'à lors. C e qui a pour conséquence l'augmentation presque exp onentielle des déb its dans les téléco mmunications [1-7].

Les télécommunications optiques sont la première application d 'un champ d 'investigation extrèmement pro metteur pour le chercheur et l'ingénieur. H éritières d e la radioélectricité_' les transmissions op tiques ont vu leur développ e ment b asé sur l'existence de trois notions a priori indép endantes : le canal d e trans mission_' le signal a trans mettre et le bruit [17]. Quelques dérogations a ce grand princip e sont bien silr app arues_' co mme les non - linéarités parasites (par exe mple en ce qui concerne ce travail_' l'on considère co mme canal de transmission les systè mes mono modes a très hauts d éb its utilisant la technique du multiplexage en longueur d 'onde_' l'une des non - linéarités parasites est le mélange a quatre ond es) [17]. Les recherches dans ce d o maine sont donc axés dans l'amélioration de la transmission d e d onnées par fibre op tique que l'on p eut diviser en deux catégories : a) l'étude des co mp osants b ) l'étude d e propagation. Notre mé moire s'inscrit dans la d euxiè me catégorie qui est plus théorique que pratique_' notamment ici nous montrons par exe mp le que l'introduction des

p rocessus stochastiques (avec une faib le intensité) dans l'équation régissant la propagation d e la lumiêre (plus précisé ment dans le terme d e dispersion) dans les fibres mono modes utilisant le multiplexage en longueur d 'onde réduit de maniêre comparable l'effet non - linéaire parasite qu'est le mélange a quatre ondes et par conséquent améliore la transmission des signaux op tiques dans la fibre [1].

Tout d 'ab ord co mpte tenu du fait que le do maine des téléco mmunications op tiques est un vaste champ d 'investigation encore jeune et donc pas três b ien connu_' nous jugeons utile de p résenter dans le premier chap itre des généralités sur les ond es solitaires_' téléco mmunications op tiques_' fibres op tiques_' technique du multiplexage en longueur d 'onde_' mélange a quatre ond es... ' afin d'être ap te a b ien app réhend er l'objet focal de ce travail qui est une fois de plus exp osée a la fin dudit chap itre.

Ensuite dans le second chapitre_' nous d évelop p ons l'équation modêle de S N L⁴ qui sera utilisée tout au long de ce travail ainsi que un modêle pour l'évolution du Mélange a quatre ond es et la condition de résonance.

Dans le troisiê me chapitre_' nous montrons par des résultats numériques comment la dispersion stochastique faib le réduit les co mp osantes du FWM . Nous testons cette hyp othêse en co mp arant ce résultat a celui de la méthode usuelle qu'est la gestion d e dispersion ou D M ⁵ [2]_' ceci_' pour le cas des fibres optiques réelles⁶. Tout ce travail nous p ermet a la fin d e ce chap itre d 'éb aucher des perspectives d 'investigation ultérieure qui p ourraient en découler. ...

⁴SNL : Schrödinger Non Linéaire

⁵ DM : Dispersion management

⁶ Fibres optiques réelles : Fibres avec pertes

Chapitre 1 Généralités sur les ond es solitaires et les

téléco mmunications op tiques haut d éb it

1.1 Bref historique sur les ond es solitaires [4' 6' 17]

En 1834_' John SCOTT RUSSEL ob serva une onde hydrodynamique (vague) se d éplacant le long du canal Edinburgh - Glasgow. Il suivit (sur le dos d 'un cheval) la vague le long du canal et ob serva que la vague conservait sa forme. Il voulut plus tard app eler ce p héno mène : < translation d 'une grande onde ». C eci est connu co mme étant la première observation de ce qu'on connait aujourd 'hui sous le nom de < S oliton ».

L'histoire des solitons de 1834 a 1970 a été écrite par p lusieurs auteurs. En 1973_' les solitons étaient aussi prédits co mme étant susceptib les d'apparaitre dans les systè mes de fibres op tiques. Dans les articles de HASEGAWA et TAPPERT_' ces derniers montraient que les équations de MAXWELL p euvent ètre app roximées par une équation d e SCHRODINGER non linéaire. Ils montraient ensuite que l'équation p ossédait des solutions (solitons) : les ond es solitaires dans les fibres corresp ond ant a une dispersion anormale ap p elées solitons b rillants (< bright » ou encore de type envelopp e) et les ond es solitaires dans les fibres corresp ondant a une dispersion normale app elées solitons somb res (< dark » ou encore d e type trou). Dans une ond e solitaire b rillante_' l'intensité décroit vers zéro aux grand es distances tandis que pour une ond e solitaire sombre on a une d écroissance locale en intensité a p artir d 'une valeur d e base non nulle.

Mème avec la p rédiction théorique de l'existence des solitons dans les fibres optiques_' ce n ' est que vers 1980 que les solitons sont pour la première fois ob servés dans une fibre par M O LLENAU ER_' STOLEN et GORDON.

Dans ce travail_' on se réfère aux ondes solitaires sous la déno mination d e solitons. Les solitons app araissent dans l'équation S N L co mme un résultat de l'équilib re entre la dispersion et la non linéarité. Aussi_' l'imp ortance pour les objectifs d e transmission par impulsions lumineuses résident dans le fait que les solitons p ossèdent deux propriétés re marquables :

(i) Les solitons sont stables sous d e faib les perturbations et p euvent se prop ager sur d e

très grand es distances.

(ii) C es ond es préservent (avec des p aramètres dynamiques convenab les) leur

structure après d 'éventuelles collisions entre elles.

1.2 Téléco mmunications op tiques haut débit [7] 1.2.1 Historique

Les réseaux d e téléco mmunication dans les années 70 rep osent sur deux types d e systè mes : le cable coaxial et les faisceaux hertziens.

Le réseau hertzien est b asé sur une infrastructure de relais (distant d 'environ 50 km les uns des autres) et utilise diverses b andes de fréquences essentielle ment autour de 6/7 G Hz et 11 GHz. D e 1975 a 1985_' la recherche se concentre sur les prob lè mes que pose l'augmentation de la b and e p assante liée au passage d e l'analogique au numérique_' et des d évelopp e ments imp ortants voient le jour. Ainsi_' des faisceaux hertziens p ermettant la transmission de 8 canaux (7 plus un canal de secours) a 140 Mb it/s_' soit environ 1 Gb it/s sur un lien sont disp onibles dès la fin des années 80. Le rend e ment sp ectral_' qui rep résente l'efficacité dans l'utilisation du sp ectre_' atteint alors environ 4 b it/s/H z_' grace a des sché mas d e modulation p erformants.

Les lignes d e transmission utilisant le cable coaxial p ossèdent_' quant a elles_' une longueur du pas d e régénération b eaucoup plus faib le du fait de la très forte atténuation du milieu. Le systè me de base de ces réseaux a une cap acité de 140 Mb it/s avec un esp ace ment entre chaque rép éteur de l'ordre de 2 km. Les d erniers d évelop p e ments sur ces lignes d e transmission ont p ermis d 'ob tenir une cap acité d e 560 Mb it/s avec le mème esp ace ment entre rép éteurs. C o mme a l'ép oque les cables interurb ains disp osaient typique ment de 8 a 12 p aires_' la cap acité d'une ligne atteignait 2 ou 3 Gb it/s.

C 'est vers la fin des années 80 que vont apparaitre les premiers systè mes d e transmission optique : une p ériod e d e coexistence commence avec les autres réseaux. C e d évelopp e ment commercial est l'ab outisse ment de plus de deux d écennies de recherche de base pour ob tenir des co mp osants et disp ositifs (en p articulier des sources)_' mais aussi des fibres dont l'atténuation est compatible avec les exigences d'un réseau d e téléco mmunication.

Les premières années d e l'op tique sont marquées par des évolutions imp ortantes :

· Le passage de la fibre multi mode⁷_' utilisée dans les premières exp érimentations_' a la fibre mono mod e qui propose des d éb its sans rapport avec la première.

· Le passage successif de la première fenétre d e transmission autour d e 850 nm (fibre multi mode) a la d euxiè me autour de 1310 nm (minimum d 'atténuation d'environ 0_'3 a 0_'4 dB/km)_' puis a celle autour de 1550 nm (minimum d 'atténuation de 0_'2 dB/km)_' qui est la norme aujourd 'hui en matière d e réseau. C es change ments de fenétre d e transmission ont été rendus p ossib les par l'amélioration des techniques de fabrication des préformes et au développ e ment des sources op tiques.

S i_' dans les premières années_' le réseau optique a un déb it qui ne surp asse pas encore celui des lignes d e transmission utilisant le cable coaxial_' il p résente quand méme un avantage indéniab le face a ce dernier : l'esp ace ment entre chaque rép éteur est plus imp ortant_' d e l'ordre

d e quelques dizaines d e kilo mètres (par exe mple environ 70 km pour un systè me a 560 Mb it/s a 1550 nm).

Les réseaux d e téléco mmunications rep osent donc toujours sur deux systè mes_' la radio et le cable qui d e coaxial est devenu op tique. L'avantage de la fibre op tique par rapport au cable coaxial (augmentation du pas de régénération et d onc diminution des rép éteurs et des cofits d e fabrication des lignes de transmission) va trouver un champ d 'ap plication dans le

d o maine des téléco mmunications très longues distances (en p articulier dans les lignes de transmission sous-marines) : des cables optiques furent envisagés dès lors que la fiab ilité des co mp osants optiques permit d e les immerger. Le premier cable sous- marin transatlantique⁸ TAT 8 utilisant des fibres optiques fut p osé en 1988 et offre une cap acité d e 280 Mb it/s par p aire de fibres a 1310 nm. TAT 9 qui suivit en 1991_' travaille quant a lui a 1550 nm_' avec une cap acité de 560 Mb it/s par p aire de fibres.

La notion d e ligne d e transmission otout-optique» faisant app el exclusive ment a la fibre op tique apparait au déb ut des années 1990.

D e 1992 a 1996_' vont se b -tir les réseaux 0 tout-op tique » d e grande cap acité utilisant la fibre mono mode standard ap p elée G-652⁹_' chaque fibre étant capable de transporter un d éb it

d e 2_'5 Gb it/s avec un pas moyen d e régénération de 90 km. C ette évolution technologique

⁷ La fibre multimod e conserve cep end ant sa pertinence dans d 'autres d o maines tels que l'aéronautique par exe mp le.

⁸ TAT : Câble sous - marin transatlantique

⁹ Norme ITU - T.

des réseaux 0 tout-optique » a été rendue possible par la mise au point d 'amp lificateurs op tiques des la fin des années 80. En général_' l'amplificateur utilise une fibre ED FA¹⁰; ainsi cela p ermet d e contrô ler sans conversion électro-optique la puissance des signaux trans mis et co mp ense les p ertes sub ies lors de la propagation.

En 1995 le premier réseau sous-marin utilisant la technologie d e l'amp lification op tique a fibre d op ée a l'erb ium (ED FA) est mis en service. C ette liaison longue d e 6300 km (TAT 12_' TAT 13) co mp orte 133 rép éteurs en ligne et propose un d éb it total de 10 Gb it/s trans mis sur deux fib res_' équip ées chacune d 'une longueur d'onde modulée a 5 Gb it/s.

Enfin la véritab le révolution technologique va se produire avec l'app arition du multiplexage en longueur d'onde ou WD M qui amene donc une multiplication par un facteur consid érab le de la cap acité du réseau. Lintérét principal de cette technique_' qui a fait sa p opularité_' est d e p ouvoir réutiliser la fibre déjà installée_' ce qui n'entraine pas de surcout pour d e nouvelles infrastructures. Le p aragraphe suivant va nous exp liquer son fonctionne ment

1 .2.2 Multiplexage, modulation WDM

Un avantage des amplificateurs op tique a fibres dop ées a l'Erb ium (ED FA) est le fait qu'ils présentent une b ande sp ectrale d 'amplification de 30 a 40 nm. 1l est donc possible d 'amplifier simultané ment p lusieurs canaux d e longueurs d 'ond e voisines dans cette plage sur une méme fibre. C ette technique app elée multiplexage en longueur d 'ond e ou WD M p ermet d e multiplier le d éb it des réseaux d e téléco mmunications par le no mb re de canaux.

Dans toute trans mission_' il est d onc intéressant d e faire passer au méme moment dans le méme conducteur (ici une méme fibre) un maximum d e communications concurrentes_' sans que l'une ne vienne b rouiller l'autre. O n les ache mine d onc chacune sur une longueur d'onde différente : c'est le multiplexage.

Le multip lexage et sa fonction inverse sont assurés par des M ux/D e mux. Les différentes longueurs d 'ond e sont générale ment asse mb lées et sép arées par des p rocédés optiques_' co mme les filtres en couches minces (les plus co mmuné ment rép andus). Plusieurs trains d e signaux numériques a la méme vitesse de modulation sont associés_' mais chacun a une longueur d 'ond e distincte.

¹⁰ Dans laquelle se p roduit un mécanisme d e transfert d e puissance entre une p o mp e op tique et le signal a transporter.

Fibre

MULTIPLEXEUR

DEMULTIPLEXEUR

Récepteur 2

Emetteur A2

1, 2, ..., N

Récepteur AN

Emetteur X1

Récepteur X1

Emetteur AN

Compensateur de dispersion

Amplificateur optique

Figure 1.1. Principe dXune liaison WD M11

C ette figure 1.1 montre le fonctionne ment la technique WD M : p lusieurs signaux sont multiplexés^1A_' ensuite drainés dans la méme fibre dans laquelle ils sont amplifiés a chaque fois par des amp lificateurs optiques. Arrivés a la réception les signaux sont d é multip lexés et trans mis chacun vers le récep teur corresp ondant.

¹¹ Toutes les figures apparaissant dans ce chapitre sont inspirées de la référence [7], sauf les figures 1.3, 1.4, 1.5

¹² Technique analogue à celle de modulation/démodulation de fréquences usuelle.

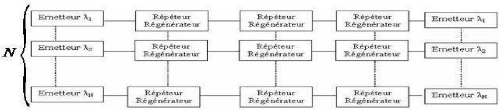
Figure 1. 2. Opportunité d 'utilisation du multiplexage couplée a l'amp lification optique

C ette figure 1.2 montre le principal profit de la technique du multiplexage en longueur

d 'onde (WD M )' a savoir le fait qu'elle rend inutile l'utilisation des rép éteurs/régénérateurs intermédiaires^1B .

Il est a noter que la technologie du multiplexage en longueur d 'onde (WDM) et en p articulier le multiplexage en longueur d 'onde dense (DWD M)^1C_' du fait des fortes p uissances op tiques guidées va introduire des effets non linéaires qui en dégradent les performances dont les plus imp ortants sont :

· L'auto modulation de phase ou S PM ^1D.

· La modulation de phase croisée ou diaphonie entre canaux_' app elée XPM ^1E.

¹³ Qui eux obligent l'utilisation de plusieurs fibres optiques, ce qui n'est pas le cas de la WDM, celle - ci est donc non seulement plus économique mais plus performante et réalise la même opération.

¹⁴ DWDM : Dense Wave - length Multiplexing

¹⁵ SPM : Self Phase Modulation

· Le mélange a quatre ondes noté FWM ¹⁷ qui créerait de lXinter-modulation op tique entre les différents canaux.

· La diffusion RAMAN stimulée ou S RS ¹⁸ qui augmente les écarts de puissance revue entre canaux et par conséquent produit une trop grande dispersion du rapport signal/b ruit_' il y a égale ment la diffusion RAMAN auto - induite dans laquelle on assiste a un transfert d 'énergie des courtes aux grand es longueurs d 'ondes par vibrations moléculaires (phonons op tiques) dans la silice [18].

· La diffusion BRILLO U IN stimulée ou S BS ^1H_' il y a p erte de puissance du signal a l'ap proche du seuil par transfert de puissance a l'ond e STO KES ' cet effet est similaire a la diffusion RAMAN stimulée [18].

Pour ce qui est de notre travail on s'intéresse unique ment a l'effet non linéaire du élange a quatre ondes.

1.2.3 Le mélange a quatre ondes (FWM) [20(4)]

Le mélange a quatre ond es est un effet optique non linéaire_' qui consiste en une inter - modulation entre deux ou trois ondes électro magnétiques qui en générent ou amp lifient une ou deux autres. C 'est un processus du troisiéme ordre qui est générale ment d 'intensité faible et intéressant seule ment en l'ab sence de p rocessus d e second ordre.

L'accord de phase est en général réalisé non colinéaire ment dans les solides et colinéaire ment en utilisant la dispersion anormale dans les gaz. Le p rocessus p eut étre large ment plus efficace en présence d 'une résonance a un ou deux photons.

Le mélange a quatre ondes joue un role important dans la génération de super continuum dans les fibres op tiques a cristal photonique_' particuliérement dans le cas

d 'impulsions longues. C 'est égale ment une cause d e géne majeure dans le do maine d e téléco mmunications par fibre op tique particuliérement dans le cas du multiplexage en longueur d 'onde co mme nous le mentionnons d ep uis le d éb ut et c'est pour annuler cet effet négatif qu'on introduit ici une dispersion aléatoire faib le dans l'équation d'évolution des solitons dans les fibres optiques.

¹⁶ XPM : Cross Phase Modulation

¹⁷ FWM : Four Wave Mixing

¹⁸ SRS : Stimulated RAMAN Scattering

¹⁹ SBS : Stimulated BRILLOUIN Scattering

1.2.4 Fibre optique [7' 12' 20] a) Description

Une fibre op tique est un guide d 'ond e diélectrique qui posséde générale ment une symétrie de révolution. Une fibre classique est constituée par deux couches de matériaux transp arents a base d e silice ap p elées le coeur_' d 'indice d e réfraction n1_' et la gaine op tique qui entoure le coeur_' d'indice n2. L'indice n1 est sup érieur a n2 ce qui garantie la réalisation de la condition de réflexion totale a l'interface gaine - co eur c'est - a - dire qu'un rayon lumineux p énétrant dans le coeur d e la fib re_' a l'une de ses extré mités_' se p rop age longitudinale ment jusqu'a l'autre extré mité grace aux réflexions totales qu'il sub it a l'interface entre le verre d e coeur et le verre de gaine.

O n distingue :

> Les fibres multi modes_' dans ce type de fibres on a :

· la fibre a saut d 'indice 200/380 constituée d'un coeur et d'une gaine op tique en verre d e différents indices de réfraction. C ette fibre p rovoque de par l'i mp ortante section du coeur_' une grand e dispersion des signaux la traversant_' ce qui génére une d éformation du signal reçu :

Figure 1.3 S ché matisation de la propagation dans la fibre a saut d'indice

· la fibre a gradient d'indice dont le coeur est constitué de couches de verre successives ayant un indice de réfraction p roche. Bande p assante typique 200- 1500Mhz par km.

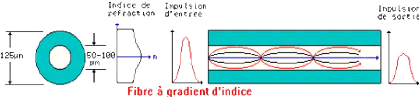
Figure 1.4 Schématisation d e la propagation dans la fibre a gradient d'indice

> Les fibres monomodes^A0 dont le coeur est si fin que le chemin de propagation des différents modes est pratique ment direct. La dispersion nodale d evient quasi ment nulle. La b and e p assante trans mise est p resque infinie (sup érieur 10Ghz/km). C ette fibre est utilisée essentielle ment pour les sites a distance. Le petit diamétre du coeur (10um) nécessite une grande puissance d 'é mission_' d onc des diodes au laser qui sont relative ment onéreuses.

Figure 1.5 S ché matisation d e la propagation dans la fibre a saut d 'indice mono mode

C es figures^A1 présentent les fibres citées ci - dessus ainsi que leurs caractéristiques géo métriques et de propagation. Le type sur laquelle nous app liquons notre hypothése est le d ernier type : Fibre mono mode dans les systémes du multip lexage en longueur d 'ond e (WD M).

b ) La dispersion dans les fibres optiques

Lorsqu'une impulsion se p rop age en régime linéaire dans une fibre op tique_' elle sub it un phénoméne de dispersion qui se traduit par un étale ment te mp orel de celle-ci (figure 1.5).

Figure 1.6 . Evolution de l'impulsion pendant sa propagation dans la fibre optique

O n voit b ien qu'il y a étale ment te mp orel de l'impulsion initial a la sortie de la fibre.

Plusieurs types d e dispersion existent_' contribuant tous a l'étale ment d e l'imp ulsion au cours de sa propagation dans le guide : la dispersion intermodale_' la dispersion du matériau_' la dispersion du guide. La so mme des dispersions du guide et du matériau_' rep résente générale ment ce qu'on app elle : Dispersion chro matique [7].

²⁰ Ces fibres sont à sauts d'indice.

²¹ Elles proviennent de la référence [20(9)] : figures 1.3, 1.4, 1.5.

Nous allons maintenant dans le second chap itre_' dévelop p er l'équation modele d e Schrodinger non linéaire (S N L) qui sera utilisée tout au long d e ce travail ainsi qu'un modele pour l'évolution du Mélange a quatre ond es et la condition de résonance.

C hap itre 2 L'équation d e SNL et un modele pour l'évolution du Mélange a quatre ond es

2.1 Origine d e l'équation modèle non linéaire de Schrödinger [4]

Nous l'avons dit p récéde mment_' la dynamique des ond es solitaires dans les fibres op tiques_' a pour origine les équations qui régissent celle de l'onde électro magnétique qu'est la lumiére a savoir les équations d e MAXWELL :

,...

rotE

at

,...

divB

a

I

A

( 2.1)

0

,...

D

,rotH = J

l ^l+aat

oil E et H représentent les champ s électrique et magnétique resp ective ment_' tandis que_' D et B rep résentent resp ective ment le vecteur d ép lace ment électrique et l'induction magnétique. D ans une fib re optique_' on a J_l = 0 et p_l = 0 . D et B sont reliés a E et H p ar les relations :

D = e0E +P ii= u0H +M

( 2.2.a) ( 2.2.b)

M est le vecteur magnétisation et est nulle dans notre cas (l'usage des fibres a silice) ; on a la relation : e0 u₀ = 1 c ² oil c = 2, 9997 × 10 ⁸ m
· s ^-1 est la vitesse de la lumiére dans le vide ' alors

que e₀ et u₀ sont resp ective ment la p ermittivité électrique et la p erméab ilité magnétique du
vide. P est le vecteur polarisation ' ce d ernier est constitué d 'une polarisation linéaire P L et

d 'une polarisation non linéaire PAIL : P = PL + PAIL .

En p articulier_' la p artie linéaire est d onnée par :

S.V.P Ne pas distribuer / Please Do not distribute

~~~ ~

( ) ( ) ( ) ( ) ( )

~~ ~

+? ~ - ~

= ~ -

1 0 '

? ? ~ i t t ~

?

P_L r t

, t t E r t e

' , dt ' 2.3

( )

0

-?

x⁽¹⁾ est la susceptib ilité électrique d e premier ordre.

La p artie non linéaire est plus co mp liquée. Il est suffisant pour notre objectif d 'approximer

P NL par :

~~ ~

( ) ( ) ( )

~~ ~

2

P NL r , t ? ? 0 ? NL E E r , t (2.4)

La non linéarité d e E _NL en E 2 rep résente la non linéarité de KERR²² dans une fibre mono mod e ; ici on a_' E _NL E ² = 2 n₂ E ² et n₂ est la p artie non linéaire d e l'indice d e

réfraction. En p renant le rotationnel de la première équation du systè me (2.1) et en utilisant les relations (2. 2)_' on a :

~~ ~~ ~~

2 2

? ~ ? ? ~

2

1 E P L P NL

( 2.5)

--
·2

u

2 2 0 ~ + ~

2 2

? ~ ? ? ~

? -

E =

c t t t

Nous consid érons que VD V(E₀ E).--0 ' car VE contrib ue seule ment aux ordres sup érieurs. Nous d éfinissons la transformée de FOURIER :

~ ~

( ) ( ) ( )

~ ~ - ~

i t

0 ~

, ? ? +?

F r

~ ? ?

- = ~ F r t e

, dt 2.6.a

( )

0 -?

~ 1 ~

+?

( ) ~ ( ) ( )

~ - - ~

i ? ? t

0 ~

F r t

, = ~ -

F r , ? ? e ~ d ? 2.6.b

( )

0

2 ? -?

w₀ est la fréquence princip ale. La transformée d e FOURIER (TF) est prise au regard de t associée a la variation w - w₀ de fréquence. En p renant la transformée de FOURIER d e l'équation (2.5) on a :

~ ' a

0 ~ I a ² +*.

AE + CO E = u₀ TF f eoz( 1 )( t , t )e [ ia( ")] + _t2 k0 e E]lNL 2

at2 J

.

car TF at 2 2 2 _m2 ,

=-co_o² P A m

É + 7 È =- 7 V( 1) É+ g _NL E)

_aF

c c

22

Voir annexe 2.

Tout si mple ment p arce que TF ( f * g ) = f * g~ ' on p eut égale ment simplifier en

consid érant le vecteur de propagation ? k ₀ =⁰et en p osant que :

c

E ? , E = 1 + ? ~ ? + ? ~ NL E 2.7

( ) ( ) ( ) ( )

2 1 ² ( )

O n ob tient :

~ AE+E

( ) ? , E k 0 E ~ = 0 2.8 2 ^2 ( )

Nous p ouvons effectuer une sép aration d e variables (x , y , z) de la maniere suivante :

- L'évolution du champ E le long d e la fibre p eut etre décrite suivant l'axe z (c'est cette dynamique là qui nous intéresse).

- L'évolution transverse du champ est représentée par la fonction F (x , y) .

O n écrit :

~

~ i z

0

E r

( ) ( ) (

, ? - ? = F x y W z

, ~ , ? - ? ) e ? 2.9

( )

0 0

oft fl₀ est le no mb re d 'ond e et r = (x, y , z) . En re mplaçant l'expression de E(r , (0-(0₀) dans l'équation (2.8) on aura^2B :

~
~~~

~

~~

~ a2 F a^2F axe ) x^2+ay2 +

( ( ( ) ( ) ) ) 2 k 2 1 1 + ? ? ? ~ - F = 0 2.10.a ( ) 0 0

~ 2 2 F a²* F

2k, -

W az 2 + W az

0 ( 2.10.b)

~ ~ =

~

- 2 n 2F ³ W

~

~

O n simp lifie la relation (2.10.b ) par F et on la multiplie par W				' ensuite on la divise par
-2' on ab outit a :
^23 Voir annexe 1
O0W -^1 - zz+ + n 2 0147 F ^2 k ^2 W- W		2 =
			0 2.11 ( )

Posons E ( Z , T ) W( z ,t) ' T = t - Az ' Z = z ; l'équation (2.11) d evient donc²⁴ :

2 AEZ + ^161 Ems.+ n 2 F ^2 k 0^2E 2	E	2=	0 2.12 ( )
O n divise cette relation (2.12) p ar 130 ' tout en sachant que O n aura :				1 ? ? 0 0 ? 0 = = = 20 c 2/1c

iE _Z + E _TT + 2zn ₂ F2w0 E

1⁶1²

2₁6₀

c

E 2 =

0 2.13

( )

2

O n p osera ₁32 =- ¹⁶¹ =-AZ) ' ofi

fl0

1

?₁ = ' v_g est la vitesse de group e du soliton. ₎0₂ et

g

v

iE Z + 13( 2Z) E TT + yE

E

2 = 0

( 2.14)

f(Z) representent le p rofil d e la disp ersion . F (x , y) est la distrib ution transversale dans la fib re ' ici (cas d 'une fib re monomode) co mp te tenu d e la symetrie cylindrique F (x, y) est constante tout le long du cceur de la fib re et contrib ue a definir le terme concernant la non

linearite cub ique ; on d efinit A_eff = 1 co mme etant la section du cceur d e la fib re qui varie

2AF²

entre 50 - 80 um ² aux longueurs d 'onde de 1_'55 um ' l'indice de refraction non lineaire n 2 = 3, 2 × 10^-16cm² /W et la frequence centrale w₀ de l'impulsion a une valeur de 1200Thz a

0

2 = 1,55um . O n considere d onc le coefficient non linéaire y = n 2 qui p our les fib res

cAeff

op tiques a des valeurs entre 2 et 30 W - 1 km^-1 [4].

En prenant en co mpte de tout ceci_' (2.13) devient :

₂₄ co

a a a

₂a

az = aZ ; az 2 -/31 a T2

2 2

L'équation (2.14) est l'équation S N L avec non linéarité cub ique²⁵ sans amp lification^2E. Quand on y ajoute l'amplification on a :

? ( )

Z 2

iE + E + ? E E = - i ? E 2.15

( )

Z TT

2

C ette dernière équation est l'équation p rincip ale^2F de notre analyse.

2 .2 Equation mod èle et paramètres de transmission

Nous co mmençons notre analyse avec l'équation mod èle de SCHRODINGER non linéaire (S N L) (2.15) p récéd ente qui inclut la disp ersion_' la non linéarité cub ique et l'amplification :

? ( )

Z 2

iE + E + ? E E = - i ? E 2.16

( )

Z TT

2

Le soliton envelop p e du champ électrique est E (Z , T) oil Z (mesurée en km) est la variable sp atiale de propagation et T (mesuré en ps) est le temps.

Les coefficients de p erte ou de non linéarité et d 'amplification sont resp ective ment d onnés par : 7 et a ; le coefficient de dispersion est représenté par ?(Z) .

Nous introduisons les variables adimensionnées : c = Z / z * ' 2 = T / t * ' Pav et

Q(4", 'r) = E(Z , T ) / P_* oil

P_* dénotent resp ective ment l'échelle de longueur

z * , t * , 1⁶ av , et

caractéristique_' l'échelle d e temps caractéristique ' la dispersion moyenne et la puissance
maximale. Nous d éfinissons les échelles d e longueur associées avec la dispersion ( _zflav ) et la

non linéarité ( zNL ) données par

zflav t / = * 2

1^6 av

et zNL = 1 / P* . Ainsi' nous définissons le pas

d 'amplification sans dimension par z _a = L_a / z_* . ici_' L_a est le pas d 'amplification en

²⁵ Elle est matérialisée par le terme en 7 .

²⁶ Généralement due à un apport extérieur, ceci pour pallier à l'effet de l'amortissement. Dans ce mémoire on considèrera - iaE dans le second membre de (2.14) pour matérialiser l'amplification :a est le coefficient d'amplification.

²⁷ On a eu à ignorer les filtres.

dimension de longueur et est égal a 40Km [1]. Avec ce change ment d e variab les_' l'équation (2.16) devient :

iQ 4. + d ( Z ) z* z* v-rr+ zNL 2 z fl av

Q

2

Q = - i FQ

( 2.17)

, _ia( Z)zfl_av

oft nous avons p osé d ( Z )= ₂ , z_*ot = F et on sait que z_NL = 1 / )4³.

t_*

Une forme plus convenante d e l'équation (2.16) est ob tenue en effectuant des calculs

[ 1 dg ( c) = -Fg( ()

2 d

c

supp lé mentaires : on prend Q(4^-, r) = g(4)u(4^-,r) qu'on re mplace dans (2.16)_' on forme deux équations dont l'une en g(4) et l'autre en u (4, r) ' ce qui nous raméne au systéme suivant :

( 2.17)

L

_W. d ( Z ) z_* z

u ,,,+* g ( c)u ²u=0 ^C+ 2 z fl zNL

av

Dans la deuxiéme relation de (2.17) le coefficient d e la non linéarité est la fonction p ériodique g(4) qui incorp ore de maniére implicite le coefficient d 'amplification. C ette fonction est relative au pas d 'amp lification sans dimension z_a et satisfait l'équation suivante:

dg

d4-

= - 2Fg ( 2.18)

S i on se trouve a l'amplificateur d e numéro d 'ordre n ' celui qui le suit directe ment est celui de numéro d 'ordre n+1_' par conséquent la fonction g p eut étre intégrée entre nz_a et

(n + 1 )z_{a '}c'est - a - dire que la grandeur adimensionnée 4^- varie entre ces deux b ornes :

nz a < 4 < ( n + 1 )z_a ( 2.19)

O n aura

fg

0 g( ) g dg ( y4) = - 2 FI^C d ` l4<sup>g</sup> )= - 2F(` - nz_a)
nzag0

En prenant l'exp onentiel des deux me mb res de cette relation on a :

g = g₀ exp [- 2F(` - nz_a )]

Pour une convenance d 'écriture_' on consid érera p our la suite que : 4 z et r --> t ' ce qui nous p ermet d 'écrire l'expression explicite d e g (4) :

g z = g exp ~ - 2 ? z - nz a ~ , nz a ? z ? n + 1 z a 2.20

( ) 0 ( ) ( ) ( )

~ ~

La valeur d e g _max est telle que la valeur de g ( z) pour une p ériod e sp atiale z_a soit égale a 1 : (g ( z) )= 1 la g( c) dc =1 1 la g₀ exp[ - 2r( c - nz_a )] d4^- =1

z a 0 z_a 0

L'intégration conduit a :

1

g 0 [ exp

z_a

1^-

2

z a g

[ ( ) ] ~ 0 2

2 nz 1 [ e 2 nz 2 nz

- ? -

? = ~ - e - ? z ? ?

a

a a a

? - e ] 1

=

a ~~ 2 ? z

0

Pour cela on d oit consid érer qu'entre deux amplificateurs successifs n=0 donc on aura :

g 0 21^-z

21^-z ( ) 2 z a - e - ? a 1 = ~ = 1 g 0 a 1- exp( -^21"za )

.

O n a en so mme :

( ) 2

2 ? z a

g z = ? ~ - ? - ~

exp 2 ( )

z nz , 1 2.21

nz z n z

? ? +

( ) ( )

z a a a

a

1 - _e- ? ~ ~

A cause du fait que nous aurons a étab lir la condition de résonance du Mélange a quatre ond es (FWM) associée au cycle d 'amplification_' on utilise souvent [2_'3] l'extension en série de FOURIER d e g ( z) :

+Da

g ( z) = E g _max exp ( -ink _az) ( 2.22)

n

=-0

dz

1 z a

oil k a = 27c/ z_a est le no mb re d 'onde caractéristique ; et g max = f g( n = 0, z)e^inkaz

za 0

Ici le terme g (n = 0, z) provient de la relation (2.21) :

g n z g e - ?

( )

= = 2 z

0, 0

C e qui conduit a l'expression suivante^2M :

g	max = I"z a - inz rza ( 2.23)

Pour arriver a réaliser un équilib re entre les termes disp ersif et non linéaire_' on choisit nos paramétres d e la maniére suivante : z * = zfl av = z_NL .

C ette analyse nous p ermet de p rendre co mme modéle l'équation d e S N L découlant d e la deuxiéme relation du systéme (2.17):

u + g z u u =

( ) ² 0 2.24

( )

tt

2

iu _z + d

( z)

oft on a effectué le change ment C z et r --> t . O n note que d ( z ) = (d) + F( z) oft (d) est
la dispersion moyenne et F ( z) est une fonction donnée. Tout au long de ce travail_' on va
consid érer que (d) 1 . Dans les sections et chap itres suivants on étudiera les cas oft

F ( z ) = 0 et F(z)# 0 .

Lorsqu'on p ose^2H g ( z ) = 1 et F ( z ) = 0 ' l'équation (2.24) d evient :

1

iu _z + ₂u_tt + u

0 2.25

( )

2

u=

Pour d éterminer la forme des solutions solitons de cette équation (2.25)_' on pose

u ( z , t ) = Af( z ,t ) exp[im( z ,t )]

qu'on re mplace dans la dite équation. O n ob tient 3K:

i

( ) ( ) ( )

~ ~

2

u z t A h A t z T 2

( , ) sec

= ~ - ? + ~ exp exp ( )

~ ~ ~ A - ? z ?

i t 2.26

~

~ 2 ~

N ous tracons cette solution soliton en 3 dimensions³¹ sur la figure 2.1 suivante :

²⁸ Voir annexe 1.

²⁹ Cas des fibres optiques sans pertes, les solutions solitons sont donc des solitons idéals.

³⁰ Voir annexe 1.

Ici_' A est l'amp litud e du soliton_' T est la p eriode te mp orelle et n = Ac2t*2 ^All est la frequence³² du soliton_' c est la vitesse d e la lumiere_' t_* est l'echelle de temps caracteristique

precedemment d efinie_' 'lest la longueur d 'onde du soliton et A2 denote la largeur du canal de la fibre.

Dans ce travail_' nous p rendrons les valeurs des parametres d e transmission co mme vues a la reference [1].

Ici le no mb re 1_'763 represente la moitie d e la largeur maximale du soliton ideale [1]. S i

on prend n = 3,9 on aura ? = 0, 62 × 10 - 9 m = 0,62 nm

? car

? 2

? =

? ?

.

Tct

*

Figure 2.1 Evolution de l 'amplitude de la solution soliton (2.26 ) en fonction d e z et de t O n a eu a prendre pour cette figure A=1_' SI = 3 . 9 ' T=O.

Bien silr ici z et t sont sans dimensions_' il en est d e méme pour l'amp litude de la solution soliton.

O n note sur la figure 2.1 que la solution soliton ainsi représentée selon l'évolution sur le temps t_' a la forme (profil du soliton suivant z) d 'un soliton type 0 pulse » (soliton envelopp e). O n observe alors une croissance de la norme de -5 a 0 et une décroissance (symetrique a la croissance par rapport a 0) de 0 a 5 suivant z_' ceci_' quelque soit t.

³¹ La norme par rapport à la distance z et au temps t

³² Voir référence [4].

2.3 Modèle de l'évolution du mélange a quatre ondes (FWM) et la condition de résonance [1]

Le mélange a quatre ondes_' nous l'avons déjà dit est un p rocessus non linéaire qui apparait suite aux collisions entre solitons lors du multiplexage en longueur d 'ond e (méthod e WD M). C 'est un p rocessus qui d égrad e la performance de la transmission du signal impulsion véhiculant des informations (données) a travers la fibre op tique. C et effet p eut étre faib le_' mais p eut étre amp lifié de plus en plus que les collisions inter - solitons ont lieu. Pour un cas intégrab le (fibre sans p ertes) de l'équation (2.24) c'est - a - dire g ( z ) = 1 et d ( z ) = ( d) = 1 ' les termes du Mélange a quatre ondes (FWM ) sont connus pour croitre jusqu'à une valeur maximale a p artir d e z --> -. ' ensuite pour décroitre vers zéro quand z --> +. (voir figure 2.2) [4_' 5]. Essentielle ment_' le produit FWM est réab sorb é dans les co mp osantes du soliton aprés que la collision soit compléte.

Pour un cas non idéal d e l'équation (2.2.10) c'est - a - dire g ( z ) # 1 et d ( z ) = ( d) = 1 '

les produits du FWM croissent a p artir de z --> -0. et se saturent a une valeur non triviale (voir figure 2.3) [1 - 5]. Dans ce cas_' un produit permanent FWM interagit avec les impulsions p rincip ales et affecte la transmission du signal dans les systémes WD M .

Tout au long de ce mé moire la L ²- norme d 'une fonction f ( z , t) est d onnée p ar[1_'3] :

f 2 Log.^' f (z , t ) 2 dt ( 2.27)

Nous notons que_' nous p ouvons exp rimer la L ² - norme dans le d o maine d e FOURIER en utilisant le théoréme de PARS EVAL. Nous éb auchons maintenant la dérivation d 'un modele linéaire d 'une équation aux d érivées p artielles qui décrit l'évolution du FWM permanent dans le cas non id éal ( g ( z ) # 1 ) ; en utilisant ce modéle_' nous dérivons une condition d e résonance qui relie la fréquence du soliton s_' l'amplitude A et le pas d 'amplification sans dimension z_a . Nous suivons l'analyse originelle ment p résentée dans les

références [2_' 3].

Nous déco mp osons la solution d e l'équation (2.24) de la maniére suivante :

u ( z , t ) -'="-" u soliton + u FWM oi1 usoliton 7.--. u1 + ^u2 et uFWM -.=-" u112 + u₂₂₁ .

D onc on p eut ecrire que :

u (z,t):=-- u ₁ ( z , t ) + u ₂ ( z , t ) + u ₁₁₂ ( z , t ) + u ₂₂₁ ( z , t) + ( 2.28)

u ₁ ( z , t) et u ₂ ( z , t) sont nos signaux solitons d'entree ayant les frequences resp ectives 51₁ et 52₂. Nous p renons n₂ = -n 1 = n ; cela implique que la difference entre les frequences des signaux est AD = 51₂ - n 1 = 251 ; les termes u 112 ( z,t) et u 221 ( z,t) sont les co mp osantes

resp ective ment Stokes et Anti - Stokes des residus FVVM avec les frequences resp ectives^BB :

n112 = 252₁ - n 2 = -3n et n221 = 2522 -n 1 = 3n donc ⁵²221 = -5 ₁₁₂ .

~

~

~

~

~

~

~

~

~

~

~

1=0 ( 2.29.c)

u 1 + u 2 2 + u * u2 1 1 2

= 0 ( 2.29.d)

Lorsqu'on p rend u ( z , t) de la relation (2.28) et on le place dans l'equation (2.24) on a^B4 :

u₁

2 2

+ 2

u₂

u₁

2 2

+ 2

u 2

1

iu + u g z u

+ ( ) (

1, z 1, tt 1

2

1

iu + u g z u

+ ( ) (

2, z 2, tt 2

2

) 0 2.29.a

= ( )

) 0 2.2

= ( )

9.b

2 2 *

iu 112, z + 1 u 112, tt s-, + 2 ( z )[u ₁₁₂ u ₁ + u ₂ + u ₁ u2

2
1

iu 221, z + 2 u + 2 ( z )

221, tt ..-. [u221

S eule nous interesse la derniere equation (2.29.d)_' celle qui correspond a la dynamique de la co mp osante Anti - Stokes du FVVM : tout si mple ment p arce qu'elle represente suffisamment l'evolution sp atiote mp orelle du Melange a quatre ondes. O n va pour la suite

assimiler u ₂₂₁ ( z,t) a q ( z , t) et on va o mettre le terme en u ₂₂₁ u₁ + u2 2 p arce que celui - ci est négligeable. C e qui conduit a la forme suivante pour l'équation (2.29.d) :

1 = - g

* ( z )u ₁ u ²² ( 2.30)

iqz +q tt

²

C o mp te tenu de la solution (2.26)_' on p eut écrire u₁ et u₂ d e la maniere suivante :

³³ Il s'agit ici de la condition d'accord de phase sans laquelle il n'y a pas apparition du Mélange à quatre ondes.

³⁴ Voir annexe 1

? ~

2

~

( ) (

, = 0 , - ? - ) exp ? - =

j

u _j z t u _j z t j z T j i _j t i z j ,

, 1 2 2.31

( )

~

2

~ ~

avec

A²_;

u j 0 ( z ,t ) = A _j sec h ( A _jt) exp 2

[i ' z (2.32)

oir A ₁= A ₂? A ' T ₁= -T₂ T₀

C e qui nous amene^3D a :

~ u 1 * u 2 2 = A ³ sec h ² [A ( t -52z + T0]sec h [A ( t +52z - T 0 ) ]exp ii [3nt + 1 ( A2 -52²)z 2 ~ ~

g-12 ~

= u 10 u20 exp 3i nt - i z

~ 2 ~

Pour determiner la solution d e l'equation (2.30) on p eut poser que :

q

? 2( z , t ) = H ( z , t)ex43i nt - i 2 z)

(2.33)

O n prend la forme (2.33) qu'on p orte dans l'equation (2.30) et on cherche^3E une equation pour H ( z , t) :

1 [ H _tt + 6 i S2H t - 2(2 51) ² H ] = - g

( z )u 22 0 u 10 ( 2.34)

iH _z +

2

avec

52^2 /44 = u1 * /4 exp - 3i 52t +i z ~ 2

( 2.35)

³⁵ Voir annexe1

³⁶ Voir annexe1

En utilisant la relation (2.34)_' on p eut d ériver la condition d e résonance_' elle relie la fréquence du soliton1 ' l'amp litude A et le pas d 'amplification sans dimension z_a [10]. Pour cela on doit prendre la transformée de FOURIER (T.F) d e l'équation (2.34) :

I 1 T . F iiH z + tt + 6i 52H t - 2(2 5I) 2

^2 H ]} = T. F { -g ( z ) u 22 0 u10 } (2.36)

O n a T . F ( H ) = f He- ^i° dt = H^à . Ainsi la relation (2.36) devient:

-?

oft

iH - 1 0 2

.(2^2 i z ( co, n)H= - à , 2.37.a g z e F z ( ) ( ) 2 ? ( )

+--

2 * 2 * - i t

F z

( )

, = ~

T F u u

. exp 3

( )

- ? ~ =

i t u u

2 1 exp 3

( )

i t e dt

?

? 2.37.b

( )

~ 2 1 ~ ~ - ?

-?

avec

? ? , ? = ? + 6 ? ? + 2 2 ? 2.37.c

2 2

( ) ( ( ) ) ( )

Pour ob tenir la condition de résonance on doit d évelop p er³⁷ F ( z, w) :

?

~ 1 ~ +? - i b

2

( ) ( )

2 - ? - ? +

2 2

F z , ? = A exp ~ i A z i z i T

? ? sec [ ] [

sec 2 ] 2.38

( )

0 ~ h b h b A e ^A db

+ ? 0

~~

2 -?

~

S i l'on re mplace cette expression (2.38) dans l'équation (2.37.a)_' on ob tient :

iH

^z

-

2

1 i [A2 z - ailz +aT0)

( WO =--A ² g (Z)e ² Z sec h ( _2A )I (2 AA₀,_A^w) (2.39)

on ³⁸

³⁷ Voir annexe 1

I ( z , w) = kosh( z) + i wsinh ( z) - exp(i az)]cos ech² ( z) (2.40)

O n introduit le developpement de FOURIER d e g ( z) dans l'equation (2.39) et on l'integre par rapport a z. Il vient :

~ ~ ?i t⁴⁶40 +4) 2 (w)z ) p

z_{w z}

( z, CO) = A ² e sec h (

2A 1E-- g ni ex

(

CO

( 2.41)

)

2+

Pour effectuer l'integration du second me mb re de la relation (2.41) on fait le change ment de variab le suivant : = 52z ' ' dz' = ' ce qui donne :

H

oft

+?

~

z ~ ~g

~

co

n ×

( z, (0) = ² e^i`dT0 sec h (" 2 A lexp (- i ( co² + MD+ 2 ( 2a)²)

2

icn

dce

OD

L

~ ~ ~ ~

? ?

I A

~ ? ~ ~ ~

2 , 2.42

( )

~ ~ ? ~ ~

⁰ A

son	A 2 - 2nka+O(co) (?)= 2.43 ( ) 251

O n constate une grand e contribution d e H^à ( z , ?) lorsqu'on se rapp roche des w_n ' qui

.

2n

sont les racines de p_n (w) = A 2 - 2 nk _a + 0( 0

En effet on a :

?#177; = - ? #177; ? + nk_a - A

2 2

n 3 2 2.44

( )

Pour que H à ( z , ?) soit exp onentielle ment p etit_' il faut choisir la solution positive wn + et la faire tendre vers zero [4] : con + 0 .

³⁸ Voir référence [2, 3]

(0 5.

A 2 27cn

wz I (2 AA0, )dz'

2 -

z a A

La condition de résonance est donc :

2 z_a 2

1 2 n7/- A2 ~

SZ =

( 2.45)

2

₂ (2.46)

R

uFWM

=

usoliton

oil les expressions

uFWM

2

et

u soliton

2

sont prises selon la relation

f

2

+? = ~ -?

f (z , t )

2

dt

.

N otons encore que fréquence du soliton estn ' l'amplitude est A ' la distance entre deux amplificateurs z_a et n est un entier p ositif . Quand z_a = 0,1 et A = 1 ' les valeurs

prédites de n sont : 52 3,95 ; 5 _'59 ; 6_'86 et 7_'92 pour n = 1_' 2_' 3 et 4 resp ective ment. Nous tracons sur la page suivante le ration Mélange a quatre ondes / signal en module élevée au carré. O n le d éfinit par :

2

Figure 2.2 Variation d u rapport R = uFWM2 en fonction d e z cas des fibres sans pertes

u soliton

d(z)=1 et g(z)=1

2

Figure 2.3 Variation d u rapport R = uFWM2 en fonction d e z cas des fibres réelles d(z)=1

u soliton

et g ( z ) # 1 ' z est sans dimension.

Sur la figure 2.2_' on a tracé la variation du rapport R en fonction de z. La forme ob tenue est celle d 'un . pulse . (croissance de -2.5 a 0 et d écroissance symétrique d e 0 a 2.5 suivant z). C ette courb e a été ob tenue en p renant l'exp ression du Mélange a quatre

ond es (FWM) et celle du soliton des fibres sans p ertes [4_' 5]. O n voit b ien que le rapport croit jusqu'à une valeur maximale a p artir de z --> -. ' ensuite pour décroitre vers zéro quand z --> -F. ' en conclusion le Mélange a quatre ondes aprés la collision en z=0 disparait d e lui - méme : on a d onc pas b esoin d e le supp rimer.

Tandis que sur la figure 2.3_' la forme ob tenue est celle d 'un « kink » (forme d 'une marche). L'exp ression du Mélange a quatre ondes (FWM ) est celle d e la relation (2.33) et celle du soliton correspond a la so mme des deux impulsions u1 et u2. O n voit b ien que les p roduits du Mélange a quatre ondes (FWM ) croissent a p artir de z --> -. et se saturent " une valeur non nulle. C e qui signifie qu'ils subsistent méme aprés l'interaction : ceci est néfaste a la transmission des imp ulsions^3H. Dans l'intervalle d e -1 a 1 sur la figure 2.3 on observe des ondulations qui montrent que si la fibre est id éale on retrouve la forme de la figure 2.2.

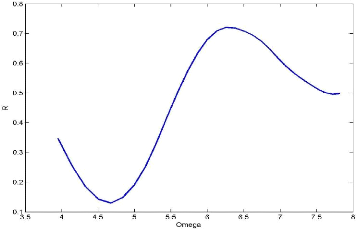
2

Figure 2.4 Evolution du rapp ort R = uFWM 2 en fonction de n ' qui ici est sans

usoliton

dimension.

La figure 2.4 montre la condition d e résonance_' décrite par la relation (2.45). Nous avons tracé ici le rapport R en fonction d en . O n observe (pour notre cas d e figure)

³⁹ Pour remédier à ce problème, on introduit un faible bruit dans le terme de la dispersion (voir chapitre 3).

l'app arition du premier maximum local entre^4K 6 et 6.5. L'exp ression du FWM et celle du soliton sont les mémes que celles de la figure 2.3.

Les figures 2.2_' 2.3 et 2.4 n'ont pas été faciles a ob tenir (surtout les figures 2.3 et 2.4). C eci est dit a la p résence dans les algorithmes corresp ondants_' de plusieurs boucles d 'instructions concernant des sommations discrétes et continues. Pour les figures 2.3 et 2.4_' il fallait attendre un temps d 'exécution b ien long (des heures p arfois une journée !!!) d e l'ordinateur pour avoir au moins une courb e que nous retouchions en modifiant les paramétres du programme⁴¹ avant de le relancer.

Dans le chapitre 3_' nous examinons comment l'équation (2.24) est p erturb ée en présence d 'une dispersion stochastique faib le. Il s'agit de réduire l'amplitude des co mp osantes du Mélange a quatre ondes (FWM) c'est - a - dire celle qui apparait sur la figure 2.3_' de +1 a + 00 suivant z. Pour cela_' nous introduisons d 'ab ord cette dispersion aléatoire dans le modéle et nous regardons comment elle affecte l'évolution des co mp osantes du FWM .

⁴⁰ La prévision est 3.95 pour le premier maximum local, nous comptons améliorer l'approche utilisée.

⁴¹ Voir annexe 2.

C hap itre 3 L 'évolution du FWM et la dispersion

stochastique faible comparée a la dispersion gérée

3 .1 Equation SNL avec la dispersion stochastique faib le [1_'19]

Dans le chapitre p récédent_' nous avons résumé quelques résultats connus concernant l'évolution des co mp osantes du FWM en p résence d e l'amortisse ment / amplification avec dispersion constante. Nous avons dérivé un modéle linéaire d 'une équation aux dérivées p artielles qui d écrit l'influence d e l'évolution d e la co mp osante Anti - Stokes identifiée co mme étant une condition d e résonance qui relie la fréquence du soliton_' son amplitude et la distance entre deux amplificateurs.

Dans un tel systé me_' l'interaction inter impulsions p eut étre étudiée directe ment co mme la dynamique d 'une p aire de solitons. Les solitons sont connus pour survivre a une telle interaction avec seule ment un change ment dans les paramétres co mme la phase. C 'est une conséquence directe d e l'intégrab ilité [15]. Tout systéme de communication réel_' cep end ant_' va voir apparaitre en son sein des effets physiques qui détruisent cette structure intégrab le. Le cas échéant on a l'atténuation et l'amplification requise pour annihiler celle - ci_' cela méne a un systéme non - intégrab le dans lequel les effets du mélange a quatre ond es sont manifestes [1 - 4].

Nous examinons maintenant l'évolution du mélange a quatre ond es en p résence d 'une faible dispersion stochastique a travers des simulations numériques.

Nous consid érons une version modifiée de l'équation (2.24) :

d z ( ) ( ) iu + u + g z z tt 2

u

2 u = 0

( 3.1)

oft d ( z) représente maintenant un terme de dispersion qui varie stochastique ment :

d ( z ) = ( d) + ( z) (3.2)

Ici ( d ) = 1 et ( z) est un terme du bruit b lanc gaussien donné co mme suit :

((z)) = ⁰ ' (?( z ),( z' )) = D8( z-z ') (3.3)

oft D d énote le paramétre intensité du bruit. G énérale ment les valeurs de D sont rangées entre 0_'005 et 0_'05. Dans notre analyse_' nous nous intéressons a la faib le dispersion stochastique qui est définie ici co mme le cas oft D << 1 dans les équations (3.2) et (3.3).

Il a été montré aup aravant [10]_' que la distance a laquelle le signal d 'entrée commence a se d égrad er sous les effets de la faible dispersion aléatoire est inverse ment p rop ortionnelle " l'intensité du b ruitD .

C ette distance d e dégradation est d éfinie par :

z deg r

1 ? D (3.4)

oft z _deg r = 20 - 200 correspond a notre intervalle de valeurs d e D .

3.2 Résultats numériques pour l'évolution du FWM en p résence d 'une faib le dispersion stochastique ou aléatoire

Dans les simulations suivantes_' les valeurs des différents paramétres sont d onnées co mme dans le p aragrap he 11.2 du chap itre précéd ent : z_a = 0,1 ; = 1 0 ; c/₂ = -? 1 = 3,9 .

Nos impulsions optiques entrent en collision a z = 1 pour des valeurs 0 z zfinal oft z final = 2,5 << zdegr. C es valeurs des paramétres de transmissions correspondent a pas

d 'amplification en dimension de longueur L_a = 40 km avec une distance d e dispersion d e 400 km [1].

Nous intégrons l'équation (2.24) sur 25 fois cette distance soit une distance de 1000 km. Dans notre analyse de l'évolution du FWM ' nous résolvons les équations (3.1) a (3.3) _'en

e mployant une méthode app ropriée a la résolution d 'une équation différentielle stochastique (S D E) [19] en utilisant les conditions aux limites suivantes du signal :

_n2

j

u j( z = 0, t ) =u 0 ( z = 0, 0exp(i n_jt- z) ; j=1 ,2 ( 3 . 5) 2

oft u ₀ ( z , t )= A sec h(At) exp(i 2 z)

et n 2 = -n ₁ ?n .

L'intégration des équations (3.1) a (3. 3) est améliorée sur l'intervalle b alayé par z (ci -

d essus). A chaque valeur de z_' la valeur de dispersion est la so mme d 'un paramétre d e dispersion moyenne ( d ) = 1 et d 'une p artie aléatoire ( z) . En p renant deux impulsions_' qui entrent en collision en z = 1 . Nous réalisons des simulations numériques dans l'esp rit de résolution numérique d 'une équation différentielle stochastique (S D E) [19] pour intégrer l'équation (3.1) incorp orant la dispersion aléatoire décrite par les relations (3.2) et (3.3).

R

2

Figure 3.1 Evolution d u rapport R = uFWM 2 en fonction de z_' qui est sans di mension.

u soliton

Nous utilisons ici la dispersion aléatoire pour des intensités du bruit D = 0,0 1 ; 0_'03 ; 0_'05.
Nous incluons le cas oft la dispersion aléatoire est ab sente (cas g ( z ) # 1 et d ( z ) = ( d) = 1 ) pour
des raisons de co mp araison.

C ette figure 3.1 montre que la dispersion aléatoire réduit les co mp osantes du FWM co mme une fonction de l'intensité du bruit D ; on observe une diminution d e R_' au fur et " mesure que l'on augmente D : d 'ab ord D =0.00 (cas de la figure 2.3)_' ensuite D =0.01 (le rapport commence a diminuer)_' il diminue d avantage pour D =0.03 et D =0.05.

S i l'on observe cette figure_' on note que :

(i) l'amplitude du FWM est réduite lorsque D varie.

(ii) l y a un étale ment d e l'évolution du FWM du a la dispersion aléatoire.

⁴² Ce qui est fait en créant un bruit blanc gaussien suivant la transformation de BOX - MULLER [19]

(iii) Il y a un change ment de l^-amplitude d e la co mp osante Anti - Stokes du FWM co mme une fonction de D .

O n p eut alors tirer co mme conclusion que la dispersion stochastique faib le réduit les co mp osantes du Mélange a quatre ondes (FWM ) donc améliore la transmission des solitons dans les fibres optiques.

Plus loin_' nous voyons que cette réduction est comparable a celle p rovenant d e l^-utilisation d e méthode d e la dispersion gérée.

Dispersion aléatoire faible

Distance z
Figure 3.2 Variations de la dispersion aléatoire faible en fonction d e la distance z (bruit créé

selon la transformation de BOX - MULLER). D =0.005_' z est sans dimension_' la dispersion aléatoire égale ment.

La figure 3.2_' donne le tracé de la variation par rapport a la distance z_' de la dispersion aléatoire faib le avec un bruit b anc gaussien introduit selon la transformation d e BOX - MULLER [19]. Nous voyons b ien que la variation est désord onnée (chaotique) caractéristique du bruit.

Figure 3.3 Rep résentation du bruit blanc gaussien pour différentes valeurs de D en fonction d e z

La figure 3.3_' montre la variation du bruit blanc gaussien pour D =0.005 ; 0.01 ; 0.03 ; 0.05 en fonction de la distance z. O n observe que plus D est grand ' plus l'amp litude du bruit est grand e (on le voit a travers les p ics ob tenus sur la figure). C e qui signifie que D rep résente b el et b ien l'intensité du bruit.

Nous examinons maintenant comment la faib le dispersion stochastique est co mp arée a la technique de la gestion d e dispersion.

3.3 Comparaison entre la dispersion stochastique faib le et la dispersion gérée

3.3.1 Introduction

En 1995_' la technique de la dispersion gérée était d 'ab ord e mployée par SUZUKI et al. dans les lab oratoires KD D [1_'3] ; la méthode impose essentielle ment a la dispersion une d ép endance a un terme p ériodique variant rapid e ment qu'on ob tient en grand es valeurs négatives ou positives. La gestion de la dispersion (D M ^C3) a été avec succés re marquable dans l'amélioration de la performance des systémes de transmission par fibre optique mono mod e. C ette technique a montré qu'elle était efficiente dans la réduction du p rocessus non linéaire d e la modulation d e phase croisée et d e la génération des co mp osantes du Mélange a quatre ond es (FWM).

⁴³ DM : Dispersion management

Toutefois_' la dép end ance de la dispersion de la fréquence fait d e l'utilisation d e la technique d e la dispersion gérée_' une utilisation p rovisoire vicieuse d evant étre dép assée pour les systémes du multiplexage en longueur d 'ondes (WD M ) [1].

3.3.2 Comparaison entre la dispersion stochastique faib le et la dispersion gérée

Nous revisitons l'équation de Schrodinger non linéaire (S N L) adimensionnée (3.1) :

iu z +d

( z) g ( z ) u2 u =0 3.6 ( ) tt 2

oft la dispersion d ( z) est prise co mme variant en fonction de z dans deux directions différentes. Le cas d e la faib le dispersion stochastique prescrit que le coefficient d e dispersion s'écrive co mme selon les relations (3.2) et (3.3) ; le cas de la gestion de dispersion (D M ) est d onné par la forme [3] :

d ( z) = 1 + ¹ 4 z (3.7)

z_a za ~

oft z_a est le pas d 'amplification sans dimension ( z_a = 0,1 ) et :

~

A( c)H A₂

~

A₁ 0

~

1.

A₁ -0<

C

C

C

?

?

?

1

1
4

3

4

(3.8)

Ici	z ?= ; A 1 = 4s et A2 = -4s oft «s » est app elée paramétre « force de la carte d e

z_a

dispersion » ou « map strength ».

Figure 3.4 Représentation des 3 cas de dispersion utilisés dans ce mé moire. s= 0.125_' z est sans dimension.

A la figure 3.4 nous visualisons trois cas d e dispersion :

(i) dispersion constante ( d ) = 1

(ii) dispersion p ériodique a force de la carte d e dispersion s = 0,1 25

(iii) dispersion aléatoire faib le avec intensité du bruit D = 0,005

Pour le cas d e dispersion p ériodique_' on a une variation brusque d e la dispersion suivie d 'une dispersion constante_' ensuite le cycle recommence mais de maniere ord onnée et contrô lée. C 'est contraire a la dispersion aléatoire qui elle est une succession d e variations b rusques désordonnées. O n re marque égale ment que la dispersion p ériodique est d éfinie co mme ayant deux valeurs d e signe contraires. Elle est donc a la fois négative et positive par intervalle. Pour ce qui est d e la dispersion stochastique_' elle est plus en clin a etre positive que négative.

Nous prouvons cela en utilisant une théorie d e prob ab ilité élé mentaire [8].

O n se sert des relations (3.2) et (3.3)_' nous définissons la variable aléatoire X :

X d( z ) --( d) (3.9)

Ici X est une variable aléatoire normale ment distrib uée qui représente le p rocessus du bruit b lanc gaussien donné par ( z) . En p renant ( d) = 1 ' nous calculons la prob ab ilité pour qu'on ait X < -- 1 (équivalent a la prob ab ilité d e trouver d ( z ) < 0 d énoté P ( X < -- 1) ):

x 2

-

( ) ~-

1

P X 1

< - =

1 e ²

-?

27rDz

(3.10)

^Dz dx

2

En p osant u 2 = ^x= dx = 2Dzdu
2Dz

' x = - 1 u = ; x --> -0 u --> -0

2Dz

1

1 1

1

( ) ~ - ~ -

e du

- u 2 -

< - =

1 Dz = 2 ~ Dz u 2

2 Dz

P X 2 2

~ e du

2/rDz -- 2R- --

1

~ - ~

u 2

1 -

P X 2

( )

< - = ~

1 2 Dz e du ~ 3.11

( )

2 ? ~ -?

~ ~

D est l'intensité du bruit et z = zfinal est la distance entre les différentes localisations des

interactions inter - solitons considérées ici. En p renant les parametres concrets : D = 0,05 et z = zfinal = 2,5 . Nous avons^" :

1

~ 1 -

~

2

P X

( )

< - = ~-

1 2 2

~ Dz e ^u du ~ = 0, 0023

~

2R- -- ~

P ( X < - 1 ) = 0,0023 ( 3.12)

C ela décrit que la prob ab ilité pour que d ( z ) > 0 est extremement grand e.

Plus haut (p aragraphe 2.2 du chapitre 2) nous avons montré l'existence d 'une condition d e résonance qui p eut etre utilisée pour p rédire a quelles fréquences les co mp osantes d eviennent imp ortantes. C ette condition de résonance a été montrée co mme tenant du cas d e la gestion d e dispersion (D M ) [3].

⁴⁴ Nous avons intégré cette expression numériquement sur MATLAB en utilisant la fonction « trapz »

S.V.P Ne pas distribuer / Please Do not distribute

R

2

Figure 3.5 C o mparaison d e la variation d u rapport R = uFWM2 en fonction de z p our le cas

u soliton

d e la faible dispersion aléatoire pour D = 0,0 1 ; 0_'03 ; 0_'05 et pour le cas de la gestion d e la dispersion (D M ) s=1. z est sans dimension.

La figure 3.5_' montre la co mp araison entre l'efficacité d e la dispersion gérée et celle d e la dispersion aléatoire faib le sur le FVVM . O n observe que pour la valeur D = 0,0 1 ' la technique d e la dispersion contro lée est plus efficace que celle d e la dispersion stochastique. C ep endant pour D = 0.03 et 0.05_' la dispersion aléatoire faib le est plus efficace que la gestion d e la disp ersion_' ceci_' pour z 1 . O n re marque que pour D = 0,03 ' la technique d e gestion d e la dispersion (D M ) est comparable a celle de la dispersion aléatoire.

C e résultat est surp renant puisque les types de dispersion utilisés sont grand e ment différents.

Dans le cas de la dispersion gérée (D M )' le coefficient d e dispersion d ( z) est une fonction p ériodique du p aramètre d 'évolution z_' qui varie rapid e ment.

Pour le cas de la dispersion stochastique faib le_' toutefois_' d ( z) est une fonction non p ériodique qui a une très grand e prob ab ilité a être positive ap rès la collision.

En résumé_' nous p ouvons dire que la dispersion stochastique faib le est grand e ment utile dans la réduction des co mp osantes du mélange a quatre ondes (cas D = 0.03 et 0.05) et nous affirmons que cette méthode est b ien plus efficace que celle générale ment utilisée et plus

connue_' a savoir la dispersion contrô lée (cas D = 0.05). La propagation dans les fibres op tiques mono modes utilisant le multip lexage en longueur d 'onde (WD M )' se trouve améliorée si l'on introduit des processus stochastiques de faib le intensité dans les parametres d e transmission.

Conclusion G énérale

En définitive_' dans ce mé moire il était question d 'analyser_' en utilisant les techniques numériques_' comment des faib les perturbations stochastiques de la dispersion affecte la transmission des solitons d e type «pulse ».

Tout d 'ab ord ' nous avons introduit une variante de l'équation de S N L oft nous avons inclus les effets provenant de l'atténuation / l'amplification et d 'une dispersion variable. Nous avons d érivé ensuite une version adimensionnée de l'équation avec les p aramètres appropriés et les échelles définies. Après_' nous avons décrit comment l'évolution des co mp osantes du FWM apparait dans les interactions inter solitons et avons éb auché une d érivation d 'un modèle qui d écrit cette évolution. L'analyse de ce modèle nous a mené a une condition d e résonance concernant l'évolution des co mp osantes du FWM relative a la fréquence d e transmission du soliton (cette condition d e résonance d éterministe est utilisée co mme moyen d e prédiction quand l'évolution des résidus du FWM sera plus imp ortante que la largeur de la b and e p assante d e l'imp ulsion). En observant l'évolution des résidus du FWM et la condition d e résonance associée_' nous avons montré que l'introduction d 'une dispersion aléatoire faib le réduisait l'évolution du FWM .

Finale ment_' nous avons co mp aré l'efficacité de la dispersion stochastique faib le dans la réduction des co mp osantes du Mélange a quatre ond es (FWM ) avec celle d e la méthod e plus connue d e la gestion d e dispersion. Dans la méthode d e la dispersion gérée_' on a e mp loyé une dispersion p ériodique variant rap ide ment (plus connue sous le nom d e force d e la carte d e dispersion) oft la dispersion p eut être imp ortante en magnitude avec soit un signe p ositif soit un signe négatif. La réduction du Mélange a quatre ondes (FWM) due a la faib le dispersion aléatoire diffère d e celle de la dispersion gérée dans la mesure oft il y a une grande p rob ab ilité pour que la dispersion soit positive^' au - dela du p rocessus d e collision inter - solitons. Traditionnelle ment_' la présence d 'un bruit aussi faible soit - il au sein d 'une fibre a toujours été pris co mme étant négatif dans la propagation des solitons optiques. Dans ce cas au contraire_' le bruit (via le terme disp ersif) joue un rô le plutô t b énéfique a la

⁴⁵ Bien sûr, nous parlons de la dispersion stochastique faible.

propagation des solitons en réduisant l'amp litude d e génération des co mp osantes du Mélange a quatre ond es (FWM ) dans les fibres monomodes utilisant la technique du multiplexage en longueur d 'onde (WD M ).

C ep end ant_' étant d onné que le bruit e mp loyé ici est le bruit b lanc gaussien_' il serait intéressant pour un dévelop p e ment futur d 'étudier l'évolution du mélange a quatre ondes en fonction d e la fréquence dans le cadre d e la dispersion aléatoire faible_' d 'étudier le cas de l'utilisation d 'un autre type de bruit par exe mple un bruit coloré... ' et aussi analyser une autre équation modéle d e Schrodinger non linéaire (S N L) co mme celle d 'une non linéarité d 'ordre sup érieure a 3.

Annexe 1

1.1 O b tention du systseme d 'équations (2.10)

2

? z

2

?

F a F

aY)

2

x

2

F

+ ~

W

~

W

+ ( k0 ² E -₁3₀² )F

a

a

0

=

F

~

W

2

+

i/i0

~

aW

az

~2 ₂ ) e

az az

+W

az + k ² E FWe^iAz

0

a2 _F a² FA₄₇~ Az + F a aW eifl0 z~ae 4z

x

a

y

a2 _F a² F

_a 2_/7_/7

+ e i Az + F +24F - FT/VA² e ^iAz + k ⁰² E FIVe^iAz

ax ² ay² az ² az

O n simplifie p ar e ^iAz et on divise p ar W on obtient :

~ ~

~

a

0

=

0

=

~ ~ =

~

2

~

3

2 n ₂F

W

~F a2W ~ F avf⁷

² 2k 0 + iflo

az² W az

0 ( 2.10.b)

O n identifie les deux me mbres de cette derniere relation a 0 pour trouver une solution compatible a l'équation (2.1.8) ' ce qui nous mene au systeme :

~ ? ? ~

2 2

F F

~ + ~ +

~ ? ? ~

2 2

x y

(k 0 2 ( 1 + e) ( 0)- ₁3₀²)F = 0 (2.10.a)

~

2

1 + -1( ¹⁾( 0+

2

?2 0

+

F

2n₂

W

k ²

0

~~ ~

~~ ~

~ ~~ F

a

~ ~~

a

~ ~

~F ? 2 W F ? W ~

~ ~ + 2 ~

i ? ~

2 0

~ W ? z W ? z ~

F a F

aY)

x

2

2

x

2

2

F a²F

? y 2 ~

+( k( 1 +,f( 1 )( 0)- x)F

~ ~

~ F ? 2 WF ? W ~

~ ~ + 2 ~

i ? ~

2 0

~ W ? z W ? z ~

a

~

2

3

W

F

2n₂

k ²

0

=

a

za

1.2 O b tention de l'équation (2.23)

gmax

g z g

0 a - ?

2 z ink z 0

a

= ~ ×

e = ~

e dz

0 z 0

a a

~

za

z

~

~~

0

( ) g

2 1

- ?+ ink z 0 ( 2 ink )

a a

e dz =
· e - ?+

~~

z - ? +

2 ink

a a

2rz

1 1

[ ( - ?+ ) ] ? z

a 2 ink z a

a a [ ]

z a × × × e 1 = e - ?

2

g max gmax

-

- × × - 1

z a

e z a

- ?

1

-

2 n = 0 a

2 ? ni z

e - ?

2 ?

+

z_a

2

1 - - ? +

z i ? n

a

?

z a

×

2 ? z a

1

e

-

rz _a-iAn

[ a ]

2 z

e - ?

1

× -

g max

rz_a

rz _a-ing

( 2.23)

1. 3 Obtention de l'équation (2.26)

[ ( ) ( ) ] [

A

im im im

im

f e if m e

+ + f e ifm e

+ ]

z z t t t

2

iA

im

0

=

+ A³ f e

3

~ifz - fmz+

1 2

^2( f tt + 2Y^.t mt -fm ) + A^2 f 3 = t

~ ~~

~~

~

2

1

0

=

m t

f _z + f_t

-

fm + 1 ftt

z

fm_t² + A² f 3 = 0

O n p eut considérer cette forme d e m ( z , t) : m ( z , t ) = c₁z + c ₂t

~

~
~~

~~

f_z +c₂ f_t

c₁

f + 2ftt

=

0

-

2

c₂

2

f

+

A2 f

3 =

0

?

az as

a a

=; ;la apre miire erelation ns'écriraa t t as

Posons s = t - 52z + T

a =

a

donc : - 52f_s + c₂ f_s = 0 c₂ - 52 = 0 ;croil c₂ =

1 g-12

+ 2 ^fss- 2 f + _A2 f3 =0 f _ss- (2 c ₁ + n² ) f + 2A² f ³ =0.

N ous voulons co mme solution des solitons de typ es sech_' alors on prend f = sec h(c ₃s)

sinh ( c₃s)

cosh ² ( )

c s

3

cosh ³ ( c₃ s )- 2 sinh ² ( c₃ s ) cosh( c₃s)

cosh 4 ( )

c s

₃ )

^1---sinhk

cosh

2( c3s)i

3( c3s))

=

fs

c₃

=

~

_c2

3

fss

=

-

c^2Z₃

² ( c₃s ) c [ h ( c s ) h ( c s ) ] c [ f f]

2 3 2 3

= - 2 sec - sec = - 2 -

3 3 3 3

2 - cosh

cosh 3 ( c₃s)

=

_c2

3

fss

Doncfinale mentt la relation f_ss, ---(2 c₁ 1++ ²) ff++2A^{2 2}f f³³== 0 deviendra :2 + - + ? +

2 ( 2 ) 2

2

- f A f

2 3

c f c f c

2 3 = 0

3 3 1 0

i

[- --224f f^{3 3}+ +2A² 2ff33==00C e equi ip ermet tde efaire eles séquivalences ssuivantes s:: 4f f- --(2 c₁₁++5²) ff==00 ~ c 3 = A '

2 ² , on prendra c₃ = A ; la seconde relation conduit a A² ---2 c1₁--- 5²²==0o

Doncc ₁ 1= =₂₂¹ 1( A^{2 2}--- 5²²) ). .C e equi ip ermet tdonc cd 'écrire eque e::

=

sec

f

h( c ₃s) = sec h( As ) = sec h[ A (t - 52z + T)]

m = c1 z + c2

^1 ( ) 2 = - ? 2 t A z 2

+ Elt

Nous p ouvons donc ecrire que la forme des solutions solitons a l'equation modèle de Schrodinger non lineaire (S NL) (2.25) est :

u ( z , t ) = Af ( z , t)exp [ im ( z , t)]
u ( z , t ) = Af ( z , t)exp [ im ( z , t)]

A sec h [A ( t -Cz + T) ]exp [i ( A ² -51²) z exp ( i nt)

= A sec h [A ( t -Cz + T) ]exp [i ( A ² -51²) z exp ( i nt) (2.26)

(2.26)

=

1.4 Obtention du système (2.29)
1.4 Obtention du système (2.29)

(u ₁ +u ₂ + u ₁₁₂ + u₂₂₁ ) z 2 + (u₁ +u ₂ + u ₁₁₂ + u₂₂₁ ) _tt +g( z )u ₁ +u ₂ + u ₁₁₂ + u 221 2( u₁ +u ₂ + u ₁₁₂ + u₂₂₁ )

1

0

i

=

1

( u u u

+ + + u ) (

+ u u u

+ + + u ) ( ) (

+ g z u u u u

[ + + + )

1 , z 2 , z 1 1 2 , z 22 1 , z 1 , tt 2 , tt 1 1 2 , tt 22 1, tt 1 2 112 221

2

×

( u₁ +u ₂ + u ₁₁₂ + u ₂₂₁ ) *]u+u ₂ + u ₁₁₂ + u₂₂₁ )

0

=

( u u u

+ + + u ) (

1

+ u u u

+ + + u ) ( )

+ g z [

1 , z 2 , z 1 1 2 , z 22 1 , z 1 , tt 2 , tt 1 1 2 , tt 22 1, tt

2

2

u *

1

*

+ _u112u1 + u

u *

1

+u

+

u 1

2

221

2

2

_u*

2

*

+ u112u 2 +u

_u*

2

*

*

+u

+u

u ₁₁₂ + _u2u112 + u

+u

221u 112 u1u221

u 2

1

221

112

2

(u₁ + u ₂ + u ₁₁₂ + u221) = 0

*

*

]

+ u₁₁₂ u ₂₂₁ + u

u₂

u 221

221

O n d oit co mpte tenu du fait que u FWM << u soliton ' négliger dans le d ernier facteur ci - dessus

uFWM . Ce qui revient à avoir :

( u u

+ + + u ) (

1 2

u + u u

+ + u + u ) ( )

+ g z u

[

1, z 2 , z 1 1 2, z 22 1, z 1 , tt 2 , tt 1 1 2 , tt 22 1 , tt

2

u *

1

*

+u112u 1 +u

u *

1

+u

+

1

2

221

2

2

_u*

2

*

+ u112u 2 + u

_u*

2

*

*

*

+u

+u

+ u2u ₁₁₂ + u ₁₁₂ +u

+ u

u+

1221

u 2

u 112

1u112

1

221

221

2

( u ₁ + u₂) =0

*

*

]

+ u112u 221 + u

u 221

u₂

221

~ (+ + + u ) (

1

i u u u + u u

+ + u + u ) ( )

+ g z u

[

1 , z 2 , z 1 1 2 , z 22 1 , z 1 , tt 2 , tt 1 1 2 , tt 22 1 , tt 1

2

2

2

2

+u

+

+u

u₁

u₂

u 1

112

1

2

2

u u ₂ +u

u u

*

2 1

*

*

2

1

2 1

u ₂ u1

+ u

+u

+u

+ u u u +

1 2 112

u₁

u 1

u 112

u221

2

112

221

2

2

2

* + u2u * u

1 221 +

*

1u ₂ u ₂₂₁ + u1u 112 u221 + u

+u

+ u

+

u₁

u 221u112

u 221

u112

u₂

1

1

1

2

2

2

2

u ² 2

u *

1

*

1

*

+u

+ u1u2u 221 + u

+u

u 2 +u112 u2+u

+ u

u 2

u 112

u 2

u 2

u 112

u₂

2

1

221

1

2

2

+ u _2u1*12 + u 2

* 2

221u 112u 2 + u1u ₂ u ₂₂₁ + u₂

*

*

] =0

+u

+ u221u 112u 2 + u

u 221

u 2

u₂

112

221

En simplifiant encore par rapport aux termes FWM négligeables (les termes non linéaires en

u1 1 2 et u 22 1 ) :

2

i u u u

( + + + u ) (

1

+ u u

+ + u + u ) ( ) (

+ g z u u

[ + 2 u

1 , z 2 , z 1 1 2 , z 22 1, z 1 , tt 2 , tt 1 1 2 , tt 22 1, tt 1 1 2

2

²)

2

+ u u u

* +

1 2

_u*

2

2 1

2 2

u

( 2

+ u

2 2 )1

2

2

]=0

+u

+u

+u

+u

+u

u₁

u₁

112

2

221

2

C e qui conduit au système :

~

~

~

~

~

~

~

~

~

~

~

+ + ~ =

2

u u u u

2 *

1 2 1 2 ~

~ = 0

~

) 0 2.2

= ( )

9.b

1 2

iu _1z + u 1 tt + u + 2 u 2 2) = 0

2

2 2

1

u₁

iu 2, z + u 2, tt + g ( z ) u ₂ ( u₂ + 2

2

1

iu + u + ~

g z u

( )

112, z 112, tt ~ 112

2

1 2 * 2

iu + + ~ + +

u g z u u u u u

( )

221, z 221, tt ~ 221 1 2 1 2

2

( 2.29.a)

0 2.29.c

( )

( 2.29.d)

1.4 Obtention du p roduit u1 *u 22

~ ? 2 ~

1

u z t u z t

( ) (

, = , - ? -

z T ) exp ~ i t i z

? - ~

1 10 1 1 1

~ 2 ~

=

sec

A₁

1

h A t

[ ( - ? - ) ] exp ( ) ~

- ?

~~~ ~ ? + ~~~

1 z T i t A 2 2

1 z

1 1 1 ~~

1

~~ 2

1

( )

, [ ( ) ] exp ~~~ ( )

2 ~

2

~ = sec + ? - ~ - ? +

u z t A h A t z T i t A - ? z ~~ ~~~

1 0 ~~

2

u2

( z ,t ) = u20 (z,t-n2 z -T 2)

exp

~ ? 2 ~ ~ i t i z 2 ? - ~ 2 ~ 2 ~

=

sec

A₂

1

h A t

[ ( - ? - ) ] exp ( ) ~

- ?

~~~ ~ ? + ~~~

2 z T i t A 2 2

2 z

2 2 2 ~~

2

~~ 2

( ) [ ( ) ] ~ ? + 1

, exp ~~~ ( )

2 ~

2

~ u z t A h A t z T

= sec - ? + i t A - ? z ~~ ~~~

2 0 ~~ 2

*

1

u

1

= [ ( ) ] exp ~~~ ( ) ~

2

sec + ? - A

~ ? -

A h A t z T i t - ? 2 z ~~ ~~~

0 ~~ 2

u A h [ A ( t z T ) ] { i [ t ( A ) z ] }

2 2 2 2 2

= sec - ? + exp 2 ? + - ?

2 0

~ u

* 1

u ^22 = A

3

sec

1 2 [ ( ) ] [ ( ) ] exp 3 ~~~ ( ) ~ 2 h A t z T 2 ~ ? + sec - ? + h A t z T + ? - i t A - ? z ~~~ 0 0 ~~ ~~ 2

*

=

exp

u10

2

u 20

~ ? ² ~

~ 3 i t i z

? - ~

~2 ~

1.5 Obtention de l'équation (2.34)

- g z u u

( ) *

2

2 1

t

~ ~~ ¹J

~ ? 2 ~ ~ ? 2 ~ ~ ? 2

~ ~ ~ ? 2 ~

i t

~~ 3 ? - ~~ ~~ ~ ~

z ~~ 3 3

? 2 i t

~~ 3 ? - z i t

? - z

1 ~~ i t

~~ ? - z ~~

2 ~ 2 ~ 2 2

~~

i H e

~ ~ - i He ~ ~ ~ ~

+ H e ~ + ?

3 i He ~

z t

~ 2 ~ 2

~ ~ ~~

~ ~~
~

1

^I

~

~

~

[Htt

+

2

~ ? 2 ~ ~ ? 2

i t

~~ 3 ? - z ~~ ~~ 3 ? -

? 2 i t z

~ 2 ~ - ~ 2

H e i He

z

~ ? 2 ~

i t

~~ 3 ? - z ~~

~ 2 ~

e

+ 6i51H _t

2

i

~ ~

~

~

2

-

?

]

e

He

9

~ ? 2 ~

i t

~~ 3 ? - z ~~

~ 2 ~

~ ? 2 ~

i t

~~ 3 ? - z ~~

~ 2 ~

~ ? 2 ~

~~ 3 ? - z ~~

i t

( ) 20 10

2 ~ 2 ~

g

*

z u u e

2

i[3 S2t-

^g2 z 2

O n simp lifie p ar e on a :

?

2

iH + 2 2 H +¹ [H tt

+ 6i52H t - 9 51 H ]=-g

( z

)u 2 20

u 10

2

~ iH + z

1 2

[ H tt + 6i52Ht - 951^2 H + 51^2H] =-g

( z

)u 2 20

* u 10

iH +1 2 [Htt

+ 6i52H t - 8 51 H ]=-g

( ₁,2 ,₄* _Vz P4'20'10

2

D 'oh. l'équation p our H ( z , t) s'écrit :

1 [ H _tt + 6 0-H t - 2(2 51) ² H ] = - g

²

z u 22 0 u 10 ( 2.34)

iH _z +

1.6 Obtention de la relation (2.41)

. 1

( z , co) = f +.0A³ sec h² [ A ( t - + T₀ )] sec h[ A (t + - T ₀ )] expit[352t + ( A² - n² )z_. Li} ×

2

exp

(- 3int

) e

ict

dt

-

ict

~ ~~ e

dt

+? 1

3

~ ( ) = ~ [ ( - ? + ) ] [ (

sec + ? - ) ] ( )

~ - ?

F z ? A h A t z T

² h A t z T ~~ i A 2 2

, exp

sec z

0 0

-? 2

1 ~

3

( ) ( ) ~ [ (

+?

2 2 2 -

~ F z = A exp ~ - ?

i A

~~ z ~~ sec h A t z T

- ? + ) ] [ (

sec h A t z T e dt

i ? t

, ? + ? - ) ]

0 0

2 -?

Posons b = A(t - 52z + T₀ ) ' t = + 52z - T 0 dt =

db

A A

2

cT0

db

co

- i _Ab-i aglz+i

A

F( z , co) = A³ exp(i ¹ ( A² -n²)z_l^+*sech²[ b ] sec h[b+252Az -2AT₀]e -?

?

1 ~

( ) ( ) ~ [ ] [ ( ) ]

i

+? - b

2

~ ? = exp ~ - ? - ? +

F z A ~~ i A 2 2 ?

z i z i T

? ~~ sec h b h b A z T e db

2

, sec + ? -

2 A

0 0

2 -?

Soit A₀ = (52z - T₀) on a

?

~ 1 ~ +? - i b

2

( ) ( )

2 - ? - ? +

2 2

F z , ? = A exp ~ i A z i z i T

? ? sec [ ] [

sec 2 ] 2.38

( )

0 ~ h b h b A e ^A db

+ ? 0

~~

2 -?

~

2

~ ~~×

aT₀

Donc

1 z 2

( ) ( ) ⁱ

- ? ? = -

? ~ - ? - ? +

1

à , 2

à exp ~~ ( )

2 2

iH H g z e A i A z i z i

z ?

2 2

sec h²[ b ] sec h[b + 2 AA₀

- i

^cob

A

db

] e

~ - ? +

A 2 ~

i

-

CO_b

A

db

] e

i ~ z ? ?

~

à iH z

-

1 2

z T ~

0

( ) ( ) ~ [ ] [

+?

~ ~

? ? = -

? , à sec

2 2 2

H A g z e h b h b A

sec + ?

2 0

-?

~ ? + ? ~ ~

( ? )

- ~

i ? z +?

0 ~ ~ ? 2

~ ~

?? z ( ? ) A 2 ? n ~ ~ ?

à ~ ~

2 2

H z

( )

, ? ?

= ~ ~

i A e sec h ~ ~ exp ~ ~ ' 2 , dz' 2.41

( )

n 0

~ ~

g i + - ~ ~ ?

z I A

~ ~

~ ~

2 A -? 2 2 z A ~

n =-? ~ ~ ~ ~ ~ ~ ~

a

Annexe 2

2.1 L'effet KERR [18]

La rép onse d 'un matériau diélectrique est non-lineaire pour un champ électro magnétique tres intense. L'indice de réfraction devient : n = n₁ + n₂I oh. n₁ représente l'indice classique et n₂ est l'indice non-lineaire (a ne pas confondre avec l'indice de la gaine). I est l'intensité dans la fib re_' exprimée en W / m² .

Pour ce qui est des fibres optiques mono modes_' la valeur de n₂ est relative ment faib le dans la silice_' l'intensité est tres élevée_' car la puissance est confinée dans le coeur de fiab le dimension. O n a une grand e distance d 'interaction_' grace au phénomene de guidage et une atténuation tres faib le (0_'2 dB/km a 1_'55 pm)

2.2 Description breve de la méthod e utilisée pour la réalisation d e certaines simulations (courbes) présentes dans ce mémoire

2.2.1 " AlgorithmeCE " de la simulation numérique d e la courb e (figure 2.3)

On veut q ( z , t ) = u221 = uF solution de l'équation :

* ( z ) u ₁ u ²² ( 2.30)

iqz +

1

2q

2

u

Pour tracer ( )

R = FWM = f z

2

' ilfaut " q " et u soliton

u soliton

usoliton ?u₁ +u₂

. 1 11

u ₁ ( z , t )= A sec h[ A ( t + - T ₀ )] expit[- nt + _vt² - n² m_il

2

111

u ₂ ( z , t ) = A sec h[ A ( t - + T₀ )] expii[nt + ( A² - n² m_il 2 C o mme A=1 ' T0 =0 '

z

[ ] ( )₂

i 1 -? 2

i t

u sec ( )

- ? - ? + sec ( )

+ ? ?

i t

? + =

u u h t z e h t z e e

soliton 1 2

2

O r co mme

( z, t)

( , )
z t

dt

f

f

_f+oo

J-00

= -

g

⁴⁶ Pas au sens où l'entendent les informaticiens, il s'agit juste ici des diverses étapes dans la réalisation des simulations.

~usoliton 2 = [ sec h( t - 51z) e^-iat + sec h( t + 51z)e ^iat ]× [ sec h( t - 51z)e ^-iat + sec h( t + 51z)e iat ]* ~ usoliton 2 = [ sec h( t - nz)e ^-iat + sec h( t + 51z)e ^iat]× [ sec h( t - 51z) e ^iat + sec h( t + 51z)e ^-iat]

~ usoliton

( t - 51z) + 2 sec h

t z h t z

- ? sec ( ) cos( ) sec ( )

+ ? ? +

t h t z

² + ?

( )

2

2

sec

h

=

~ usoliton

2 + ? 2 +? = u dt soliton ~ = ~ -? -?

[sec h^22( t t---5z))+ +2 2sec ch( t t--- 5z ))sec ch( t t++ 5z))cos((5t ))++secch^22( t t++5z)]dtt

Pour q ( z , t ) = u221 = u _FWM on a

? ~( z , t ) = =H H( z , t)exx3i it t- i 22zz

2.33))

_q

²

2

^+?

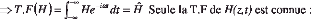
~ z ~ ~^g~

--co

nn×X

i _ir 2

à

H

~ ~ ~

?? i 2

0

( ) ( ( ) )

2

z , ? e i ? T

= sec h ~ ~ ~ -

exp ? ?

+ ? + ?

8 2 2

? ~ ~ ~

2 A 2

5n.

zz

((05^.

ddee

_OD

L

~ ~ ~ ~

? ?

I A

~ ? ~ ~ ~

2 , 2.42

( )

~ ~ ? ~ ~

⁰ A )

Avec I ( z , co) = kosh( z) + i wsinh ( z) - exp(icoz)]cosech² ( z)

·

A 2 - 2 nk + cD( w) a? ( ? ) ?

252

n

( (c, ,5)= ( (2 + 66(01+ 2 ( 2 25)²) ) 2.37.a))

On doit trouver d'a bor H à ( z , w) ensuite_', on cherche H(z_'t) ' puis on déterminee

_? 3i

2 ~

H(z, t ) ) 2

q ( z, t) 2 = H ( z, t) exp

2

i

t

t

i i

2
2

2

₌

Ensuite

^+.0q ( z , t) )2 2= = j q(z , t ) )^22dtt== fH( z ,t) -? )

2

dt

₂

_u

Pour prendre enfin le rappor ( )

R = FWM = f z

2 )

usoliton

2.2.2 « Algorithme » de la simulation numérique de la cour be (figure 2.4)

Ils'agitt ici du cas des fibres réelles casoùt d(z)=1 et g ( z ? 1 , ontrace e

~T . F H

( ) = f dt = Hà Seule la T.F de H(z,t) est connue : -?

2

R= uFWM 2 = f( SI) pour un zfixe; ;

usoliton

Ici on fait varier maintenant 52 , suivant l'expression :

=

1 2 n 7t- A2

~ - ~

2 z_a 2 ~

( 2.45)

Nous avons juste modifier le programme précédent celui de la figure 2.3) : maintenant n va de 1 à 4.

2.2.3 Algorithme » de la simulation numérique de la courb e (figure 3.1)

N ous avons discrétisé p artielle ment sur la variable t » l'équation :

d iu z +

( z) u tt + g ( z) 2

u

2 u = 0

( 3.1)

+?

d ( z ) = (d) + ( z) , (d) = 1 , ((z)) = 0 , ((z)(z')) = Dö(z - z ') , g( z ) = E g exp( - ink_az)

n=-.

O n a p osé que u ( z , t ) = X (z , t ) + iY (z , t )

) = 0

+

L

?

iX z - Yz +1 2 (Xtt + iY_tt ) + g(z )( X ² + Y² )(X +iY On obtient le système suivant :

+co

-

Y_z +

0

=

)]

Xtt + 1 Xtt +E ₂ (X ² + Y ² )[( X - na^-Y)cos(20 7inz ) + (n7rX + Y) sin( 207inz

1

2

n

=-?

(1)

1

Ytt + 2Ytt

¹ +E2 2 +

X_z +

?

2

+.0

n

=-?

Y²) [-(

0

=

)]

X n Y

- ? ) sin( 20 ? nz

) + (nzX +

Y)cos(207inz

2 1+ n² 71^-

On discrétise X_tt et Y_tt selon les différences finies centrées :

X z X z X z

- +

+ 1 ( ) 2 ( ) 1 ( )

j j j -

X z t

( , ) =

tt

( ) ²

? t Y z Y z Y z

-

j + 1 ( ) 2 ( ) ( )

+

j j 1

, 2

Y z t

( , ) = -

tt (

) ? t

}

~~

+o

On pose pour la deuxième équation de ce système

1 1f 1 ( z , t) = - Y_tt+ L 2 ₂ (X ² + Y ² )[(niff+Y) cos(20 n7z) - (X - na^-Y)sin( 20 n71z)]

2 =-00 1 n 71^-

Donc

+ex,

2( At ) n= -pp 1 + n

_x-1 1

₂ + 2a 2 2 [ X.2 / (z ) +Y_j²

?

Y z Y z Y z

( ) 2 ( ) ( )

- +

j

f1,

j + 1 j j - 1

( )

) +

z = - { (z )] [ -( X ( z ) - itnYj (z)) sin(2070nz

( nizX (z ) + Y(z)) cos(207inz

j

j

1 Y z Y z Y z

( ) 2 ( ) ( )

- +

j + 1 j j 1

Et on pose ( , )

g ₁ ( z , t ) = - Y _tt z t donc g z

( ) = - -

1 , j

2( At)²

D e mê me on a p our la pre miere équation :

f₂( z ) -{ X ₁ (z ) - 2 X_j (z )+ X -1j(z) ^+0. 1

=

( )][( ( )

- ? ( )) cos( 20 ? nz

z X z nY z

j j

) +

2 2 2 [ X_.² /(z )+Y

2(

A

t ) n=-

co

1+n

)] }

( (z ) + Y_j (z)) sin(202nz

n2tX

(2)

(3)

(4)

g 2 , j ( z) = (z ) - 2 X (z ) + (z)

2( At) ²

C e qui signifie que le systè me ED P precedent se ramène a un système S D E ordinaire :

dX z

j ( ) =

dz

dY z

j ( ) =

dz

( )

z + ? ( )

z g z

j ( )

1 , j

( )

z + ? ( )

z g z

j ( )

2 , j

f 1 ,

f 2 ,

~

O n est dans un cas typique S D E d éjà résolu d ans la reference [19] :

X k =X k,

z z

+ ? z z

k +?

'

z dz

' )

(

'

z dz

' )

k

+ ~ f z dz

( ' ) ' + ~ ? ( )

z g
'

j z 1 , j 1 , j

z

k k

(

z z

+? z z

k +?

Y_k +1, j = Y_k

k

+ ~ f z dz

( ' ) ' + ~ ? ( )

z g
'

j z 2 , j 2 , j

z

k k

Lorsqu'on s'intéresse d 'ab ord a première equation de ce dernier systè me :

'

? z

~
~~

)

~
~~

)

? f z

(

1 , j

( )

z z

' - k

z k

( )

z z

' - k

z k

~
~~

'

+

+

( ' )

z g z

= ( )

j 1 , j k

+

g1,

~

L

( ' ) ( )

z f z

=

j 1 , j k

f1,

+

'

z

(

1 ,

? g

j

'

? z

~
~~

O n re mplace ces expressions d ans la première equation du systè me (3) on aura

X k + 1, j = X k,j f1, j (z k)Az

~
~~

+

? f z

j (

'

) ~ z z

+? z z

+?

k

1 , k

~ ( ' ) ' ( )

z z dz g z

- + ~ ? ( )

z dz

' ' +

k 1 , j k

z k zk

a

z '

z k

z

+Az

)

j

ag

1,

zk

az

zk

'

? ( z')( z ' -z k

Par analogie on écrit pour la d euxiè me equation du système (3) :

§ f2, j (zk)Az ,

Y_k

Y_k

j

1,

~
~~

+

? f z

j (

'

)

~
~~

z z z z

2 , k +? k +?

~ ( ' ) ' ( )

? z

z z dz g z

- + ~ ? ( )

z dz

' ' +

k 2 , j k

z k zk

'

z k

z

+Az

)

j

ag

2,

az

_fzk
zk

zk

?( z')(z ' -z_k ) dz '

O n sait que :

z _k +Az

a) Le terme Az ')(z'-z _k )dz' est d e moyenne nulle et de fonction d e correlation :

f

z k

<

z k

~ z k

+Azz z

' '

>

)dz

l +?

? ( )( )

z z z dz

' ' - '
· ? ( )(

z z z

' ' ' ' -

k k

~ z l

+Az

=

fzl z l

D⁸kl

3

( )

? z

( )

z z dz D

2

' - ' = ?

k kl

3

3

_ez k+Az

D c jAz ')(z ' -z _k )dz' est d 'ordre ( Az ) ²

zk

b ) Le terme

_fzk +Az

J 4^.( z )d.Z est de moyenne nulle et de fonction de corrélation :

Z,

<

z k

~ z k

' '

>

)dz

+Azz z

l +?

? ( )

z dz

' '
· ~ ? ( z ' '

+Az

=

₁zl_z

l

Db^.kl

)

z l

1

2 .

dz'= D ⁸kl Az

_rzk+Az

Alors jg ( z ' )dz ' est d 'ordre ( Az )

k

z

D e ces d eux termes on va négliger celui qui d 'ordre sup érieur a Az a savoir f z k+Az ( z ')( z '-

z _k )dz' .

z k

D 'o11notre systè me de S D E (3) se résume a :

~ ~~

~~

(5)

X =k 1 , j X k, j ,j (z _k ) Az+ g 1(zk)71k

Yk +1, j = Yk , j + f2,j (z _k) Az+ g2, j z k )'7k

z k+Az

O11 k = f ( z')dz' < 77_k
· ¹71 >= DgkiAz ce qui signifie que ¹7k = DAz
· rk rk est nombre

k

z

aléatoire gaussien de moyenne 0 et de variance 1.

O n numérise le systè me (5) en prenant pour différentes valeurs d e l'intensité du bruit

D = 0,005 - 0.0 1 - 0.03 - 0.05 sur l'intervalle de 0 a 2.5 d e z.

2.2.3 Code MATLAB pour l'obtention de la figure 3.2

z=0; dz=0.01; k=1; D =0.005;

while z<=0.5 x1=rand (1); x2=rand (1); b =sqrt(-2*log(x1))*cos(2*pi* x2); %génération du bruit b lanc gaussien

d 3(k)=1+(sqrt(D *dz)*b ); %dispersion stochastique faib le

x(k)=z;

z=z+dz;

k=k+1;

end

plot(x_'d3)

Bib lio grap hie

[1] Rudy L.H orne_' Christopher K .R.T Jones_' Tobias Schafer « The effects ofweakrandomness on pulse and four - wave mixing products»_' Physica D 205 (2005) 70.

[2] M .J. Ab lowitz_' G . Biondini_' S . C hakravarty_' R.B. Jenkins_' J.R. Sauer « Four - wave mixing in wave - length - multiplexing soliton systems :damping and amplification »' Optics letters 21 (1996) 1646.

[3] M .J. Ab lowitz_' G . Biondini_' S . C hakravarty_' Rudy L.H orne_' « Four - wave mixing in dispersion - managed return - to - zero systems »' J. Opt. Soc. Am. B 20 (2003) 831.

[4] Rudy L.H orne_' « Collision - induced timing jitter and four - wave mixing in wavelength - division multiplexing soliton » ' Thesis of PH D ' University of C olorado_' 2001.

[5] M .J. Ab lowitz_' G . Biondini_' S . C hakravarty_' R.B. Jenkins_' J.R. Sauer « Four - wave mixing in wave - length - multiplexing soliton systems : ideal fibers »' J. Opt. Soc. Am. B 14 (1997) 1788.

[6] T.C . KO FAN E_' « Théorie des solitons »' notes d e cours_' C hapitre 1 a 5_' 2007.

[7] Julien Maury_' «Etude et caractérisation dXune fibre optique amplificatrice et compensatrice de dispersion chromatique »' These de doctorat_' U niversité de Limoges_' 2003.

[8] David A . M eyer_' « Introduction to mathematical modelling lectures 314: basic probability theory »' 2004_' Page 7.

[9] T. S chafer_' R.O . Moore_' C .K.R.T. Jones_' « Pulse propagation in media with deterministic and random dispersion variations »' Optics Communications 214 (2002) 353.

[10] M . Chertkov_' Y. Chung_' A . Dyachenko_' I. G ab itov_' I. Kolokolov_' V . Leb edev_' « Shedding and interaction in weakly disordered optical fibers »' Physical Review E 67 (2003) 036615.

[11] Xavier Godivier_' François C hap eau-Blondeau_' « La résonance stochastique ou la transmission non linéaire du signal favorisée par le bruit» C olloque de Recherche D octorale Auto matique_' Génie informatique_' image_' signal. Angers_' France_' 9 - 11 D éce mbre 1997.

[12] Bertrand PO U MELLEC ' ,,, Les fibres optiques monomodes : Quand la science des materiaux et de l'optique se propagent à la meme vitesse »' Nouvelles s c i e n t i f i q u e s_' M ai - Juin - Juillet 1998.

[13] Ph. Loub aton_' . Notions sur les signaux aleatoires ». Filière Reseau.

[14] Cedric WARE_' . Recuperation dXhorloge par boucle a verrouillage de phase utilisant le melange a quatre ondes dans un amplificateur optique a semi1conducteurs »' S p ecialite : Electronique et C o mmunications_' These de doctorat_' Ecole nationale sup erieure des teleco mmunications et electronique de Paris_' 2003.

[15] Vincent C audrelier_' . Equation de Schrodinger non - lineaire et impuretes dans les systemes non integrables »' S p ecialite : Physique theorique. These de doctorat_' Universite de S avoie_' 2005.

[16] R. Ab ab ou_' C ours de prob ab ilites_' . Processus aleatoires et equations differentielles stochastiques »' 1. Bruit b lanc gaussien.

[17] Patrick Vandamme_' Jean-Baptiste Tho mine_' Philippe G allion_' . La transmission par solitons ».

[18] G . H IN C ELIN ' . Effets non lineaires dans les fibres optiques ». P 1 - 20.

[19] N change Kouotou Adamou_' . Methodes de simulation numerique des systemes dynamiques sous l'influence des excitations stochastiques »' Me moire d e D .E.A_' U niversite de YAOUNDE I_' 2005.

[20] Liens des pages web visitees :

· http :// www.w3.org/TR/xhtml1/D TD/xhtml1-transitional.dtd

· http ://fr.wikip edia.org/wiki/S oliton

· http ://fr.wikip edia.org/wiki/Bruit blanc

· http ://fr.wikip edia.org/wiki/ Melange a quatre ond es

· http :// www.telcite.fr/fibre.htm

· http://www.httr.ups-tlse.fr/pedagogie/cours/fibre/cortail.htm

· http ://www.httr.up s-tlse.fr/p edagogie/cours/fibre/connect.htm

· http://www.httr.ups-tlse.fr/pedagogie/cours/fibre/folac.htm

· http :// christian.caleca.free.fr/fib roptique/

· http :// christian.caleca.free.fr/fib roptique/fib re_optique.htm

· http :// christian.caleca.free.fr/fib roptique/methodes.htm

· http :// www.telcite.fr/fibre.htm

· http ://www.httr.up s-tlse.fr/p edagogie/cours/fibre/welco me.htm

· http ://www.httr.up s-tlse.fr/p edagogie/cours/fibre/fotheori.htm

· http ://www.httr.up s-tlse.fr/p edagogie/cours/fibre/mesures.htm

· http://www.httr.ups-tlse.fr/pedagogie/cours/fibre/exemples.htm

· http ://michaud .chez-alice.fr/intro_fib re.html

· http ://michaud .chez-alice.fr/so mmaire.html

· http ://p erso.orange.fr/michel.hubin/p hysique/fib re/chap _fo1.htm

· http ://michaud .chez-alice.fr/princip e.html

· http ://www. mines.inp l-nancy.fr/^- tisseran/cours/teleco m/printable.html

· http ://michaud .chez-alice.fr/appl.html

Lors de la réalisation d e ce mé moire l'Auteur était affilié au Lab oratoire
de Mécanique du département de Physique a la Faculté des sciences d e
l'U niversité de YAOUNDE I

Version reconstituée_' adaptée pour la mise en ligne le 24Janvier 2008

Edité par Lucien M.MANDENG

Contact de l'Auteur :

Tel. Fire: ([phone] Cell. : ([phone]

Emails: [e-mail] ' [e-mail]_' [e-mail] B.P: 30815 Biyem - assi YAOUNDE CAMEROUN

(c) Copyrigth 2007 / Manluro Corporation - Tous droits réservés (All rights reserved) Disponible sur : www.physiques-manluro.kokoom.com