1.3 Exponentiation dans CPO
Soient A et B deux opcs.
Posons [A -* B] := { f: A -* B , continue
}. Munissons [A -* B] de l'ordre point par point
défini par
f g ssi f (x) g
(x) pour tout x E A.
Nous nous demandons si ([A -* B], ) est un opc.
Soit F une partie dirigée de [A -* B]. On a
:
Proposition 1.10. Pour tout x E A,
Ix = {f (x), f E F} est une
partie dirigée de B.
Preuve. Soient f (x) et g
(x) deux éléments de I. f, g
E F impliqu'il existe h E F tel que f h
et g h. i.e, pour tout x E A, f(x)
h(x) et g(x) h(x). Donc
Ix est une partie dirigée de
B.

De ce résultat, il ressort que VB
Ix existe et que la correspondance
V F : A -* B
qui à tout x E A associe
VB Ix ; est une application.
Nous nous proposons de montrer que V F est le
supremum de la partie dirigée F de [A -*
B]. C'est l'objectif du lemme ci-dessous.
Lemme 1.7. V F = V[A?B]
F.
Preuve. Soit f un élément de
F.
Pour tout x E A, f(x) E
{f(x), f EF} et f(x)
VF(x) pour tout x E A. Donc VF
est un majorant de F. Soit W un majorant de F.
Pour tout f E F, f W. i.e, pour tout x E
A, f (x) W (x). Donc
VB Ix W (x) pour rout x E
A. Partant, V F W. Donc VF=
V[A?B] F.

Ceci conduit au résultat suivant.
Corollaire 1.2. [A -* B] est un opc.

Nous allons à présent montrer que CPO
admet des exponentiels.
Lemme 1.8. Soient A et B deux
opcs. Pour tout a E A, l'application.
åA
B

[A--*B]xA --* B (f, a) F--*
f(a)
est continue.
Preuve. Soit D une partie
dirigée de [A * B] x A. D'après le
lemme(1.5).
)V[A?B]×A D = (V[A?B]
D1, VA D2
)[A?B] D=VB åA B
(D).
où les Di sont définis comme au lemme(1.5)
pour i = 1, 2. (V Nous allons montrer que
åA B
) )

åA (V[A?B] D
= åA (V[A?B] D1 ,
VA D2
B B
= V[A?B] D1 (VA D2
) par définition de åA B
= VBV[A?B] D1(D2)
= VB {V[A?B] D1 (a) , a E
D2o, (car V[A?B] D1 est continue) =
VB (VB {f(a), a E D2, f E
D1})
= VB{f(a), a E
D1} = VB åA B (D1)

Ce qui traduit la continuité deåA
B .
Par ailleurs åA B est caractérisée
par la propriété universelle suivante :

Lemme 1.9. Soient A, B et C trois
opcs. Pour toute application continue
h:CxA-*B
il existe une unique application continue
bh: C -* [A*B]
rendant commutatif le diagramme ci-dessous.
[A * B] x A ;v;
vvvvvvvvvvvvvvvvvvv
h

EA
73
// B

bh×1A
CxA
Preuve. Soit bh: C -* [A
* B] continue.
Montrons que l'unique application
donnée par la propriété universelle de l'exponentiation de
B par A dans ENS, définie par
bh:C -* [A*B]
|
c i-*
|
bh(c): A-*B
ai-*h(c, a)
|
est continue.
Soit D une partie dirigée de
C, pour tout a E A,
((WC D, a
= h(vC D, WA { =
h
)
a})
= h (VC×A D x {a}
bh (WC D (a) ) ))
= W B {h ( d , a) , d E D} , (car h
est continue)
(WB bh (D) )
= (a)
.
On conclut également d'après la
propriété universelle de åA B dans ENS que
bh rend commutatif le diagramme ci-dessous.
[A?B] xA;v;

bh×1A
vvvvvvvvvvvvvvvvvvv
h
CxA

De la proposition(1.10) et du lemme(1.9) nous pouvons conclure
que CPO est exponentiable. Ayant montré
que CPO est une sous catégorie de TOP et sachant
que TOP n'est pas exponentiable, nous avons là un exemple de
sous catégorie de TOP sur laquelle l'on peut
définir des espaces fonctionnels.
1.3.1 Graphe d'un homomorphisme d'opcs
Etant donnée une application f de A
vers B, le graphe de f est le sous ensemble
G (f) de A x B défini par G
(f) = {(x, f (x)), x E A}. La
notion de graphe d'un morphisme d'opc5
nécessite celle de sous opc.
Dans ce paragraphe, nous allons définir la
notion de sous opc et montrer que si f est une application
continue de l'opc A vers l'opc B, G (f) =
{(x, f (x)), x E A} est un sous opc de
A x B. C'est le graphe de f.
Définition 1.8. Soit A un opc. Un sous opc de
A est une partie S de A qui munie de
l'ordre induit est un opc.
Exemple 1.5. i) Soit n0 un entier naturel. L'ensemble
Xn0 = {n E N,n0 n}) est un
sous opc de N.
ii) Soit X un ensemble non vide. Soit x E X la
collection < x > des sous ensembles de X contenant
x est un sous opc de l'opc (P (X),
Ç).
iii) L'ensemble des entiers naturels N n'est pas un sous opc de
(N, =); car la partie dirigée, P =
{2n, n E N} n'admet pas de supremum dans N.
iv) Le sous ensemble P2 = {n2, n E
N} U {oc} de N est un sous opc de N.
En effet, si D est une partie dirigée
de P2, alors elle admet un plus grand élément si elle
est finie. Si non elle admet oc comme supremum.
Remarquons que pour tout opc A.
Un sous ensemble S de A est un sous opc de A si et
seulement si S est non vide et stable par suprema
dirigés. C'est-à-dire que toute famille
dirigée D de S admet un supremum dans
S.
Le résultat suivant montre que le
graphe d'un morphisme d'opc f : A -? B est un sous opc
de A x B :
Lemme 1.10. Soit f : A ? B une application
continue entre deux opcs. Le sous ensemble
G (f) = {(x, f (x))x E A}
de A x B est un sous opc de A x B.
Preuve. Il faut montrer que toute partie
dirigée de G (f) = {(x, f
(x)) ; x E A} admet un supremum. Soit D une famille
dirigée de G (f) = {(x, f
(x)) ; x E A}. D'après le lemme (1.5), il existe
D1 et D2 définies par :
D1 = {x E A tel qu'il existe y E
B, (x, y) E G (f)} et
D2 = {y E B tel qu'il existe
x E A, (x, y) E G (f)} tels que
VG(f) D = (VA
D1, VB D2) .
L'on remarque que tout couple (x, y) E
A x B est élément de G (f) si et seulement
si y= f (x)
Ceci étant, D2 = f (D1).
D1 étant une partie dirigée de A,
VA D1 existe. f étant
continue, f (D1) = {f (d) ; d E D}
est une partie dirigée de B et f
(VB D1) = VB f
(D1) .D'où
(VA D1, VB f
(D1)) 1A
V D1, f (VB
D1)) qui est bien un élément de G
(f) . Donc G (f)

est un sous opc de A x B.

Exemple 1.6. * Sur l'opc N = N U {oc},
l'application s :N -? N définie par
½s (n) = n +1 si n oc

ocsin=oc
est continue et a pour graphe G (s)
= {(n, n +1); (oc, oc) ; n E N}
.
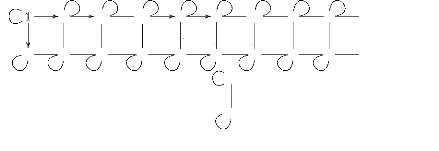
** L'application ci-dessous
schématisée est continue de l'opc P2 vers N
²²
22 >
f
· //
f
V
2n //
f
· //
f
· //
2
V
23
f
·
11 011//1 11 // 2 //
11 3 11 //
· // 11
·
// 22 n // 11
·
11-/
·
·
·
·
oc
f
et a pour graphe
G (f) = {(2n,
n) ; et (oc, oc) ; n E N}
f
f
f
f
²²
²²
oc
²²
²²
·
·
·
* * *
v) Le graphe du morphisme ci-dessous
représenté :

FF
77y
y
f ;;
gg
::
f
x
§§
§§

77
z gg
f
··
""
Ir
77
z gg
§§
est : G (f) = {(y,
y), (x, z), (z, y)}.
| 


