Systeme de transition sur les ordre Partiellement complet

1.1.5 Caractérisation des monos et épis dans la catégorie CPO.

Proposition 1.7. Les monos de CPO sont exactement les injections continues_; alors _que ses épis sont les surjections continues.

Preuve.

i) Monos de CPO.

* Soit m : A -? B une injection continue entre deux opc^s A et B. Montrons _que m est un monomorphismes.

m étant continue, il suffit de montrer _que pour tout opc C et pour toutes applications continues f, g : C -? A, m o f = m o g impli_que f = g.

Supposons m o f = m o g. Pour tout c E C,

m o f (c) = m o g (c) par h_ypothèse m(f(c)) = m(g(c))

f (c) = g (c) car m est injective .

Donc f = g.

** Soit m: A -? B un mono.

Montrons _que m est une injection continue.

La continuité de m découle du fait _que m est un morphisme. Il suffit de montrer _que m est injective. Soient a et a' deux éléments de A tels _que m (a) = m (a'). Considérons l'opc trivial à un seul élément_; {*}, et définissons les applications continues suivantes : f: {*}-?Apar f(*) = aet g: {*} -? Apar f(*)= a'. On a

m (a) = m (f (*)) et m (a') = m (g (*)). De m (a) = m (a'), on a m (f (*)) = m (g (*)). m étant un mono, f (*) = g (*). i.e, a = a'.

ii) Épis de CPO.

* Soit e : A -? B une surjection continue.

Montrons _que e est un épimorphisme. e étant continue, il suffit de montrer _que pour tout opc C et pour toutes applications continues f, g : B -? C, f o e = g o e impli_que f =g.

Supposons f o e = g o e. Pour tout b E B, il existe a dans A tel _que b = e (a). (car e est surjectif. )

f(b) = f(e(a))

= g (e (a)) par h_ypothèse

= g(b) pour tout b E B.

D'où f = g.

Donc e est un épimorphisme.

** Soit e : A -? B un épimorphisme.

Montrons _que e est surjective en montrant _que Im (e) = B.

Pour cela, il suffit de montrer _que Xe(A) = X13. où XC dési_gne l'application caractéristi_que de C pour tout ensemble C. Il suffit de remar_quer _que {0, 1} muni de l'ordre ci-dessous représenté :

1 _ee

0 //

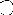
est un opc, pour le_quel la topolo_gie _grossière {{0, 1}, } est de Scott. Pour

Xe(A) : B :-? ({{0, 1}, {{0, 1}, }}) et X13 : B :-? ({{0, 1}, {{0, 1}, }}). On a pour tout a E A, _Xe(A) o e (a) = X13 o e (a) = 1.

Donc Xe(A) = X13 .

1.2 Produits d'opcs .

Soient A et B deux opc. Munissons A x B de l'ordre point par point" défini par (x, y) = (x', y') si et seulement si x = x' et y = y'.

Il est clair _que (A x B, =) est un ordre.

Nous nous proposons de montrer _que A x B muni de la première et de la seconde projection est l'opc produit de A et B.

Lemme 1.5. Soient A et B deux opc^s.

Soit D une partie diri_gée de A x B. On pose :

D1 = {x1 E A tel _qu' il existe x2 E B; (x1,x2) E D} et

D2 = {x2 E B tel _qu' il existe x1 E A; (x1, x2) E D}. Alors,

(i) D1 (respD2) est une partie diri_gée de A (resp B). (ii)V^A×B D=(V^A D1, VB D2)

Preuve.

(i) Soient x1 et y1 deux éléments de D1. Cherchons x E D1 tel _que x1 = x et y1 = x. Comme x1 E D1, il existe x2 E D2 tel _que (x1, x2) E D. De même il existe y2 E D2 tel _que (y1, y2) E D. D étant diri_gée de Ax B, il existe (x, y) E D tel _que (x1, x2) = (x, y) et (y1, y2) = (x, y). Donc x1 = x et y1 = x. Ce _qui montre _que D1 est une partie diri_gée de A.

De même, on montre _que D2 est une partie diri_gée de B.

(ii) * Montrons _que (V^A D1, ^VB D2) est un majorant de D. Soit (x, y) E D, alors x = V^A D1 et y = V^B D2. Donc (x, y) = (V^A D1, V^B D2). Ce _qui prouve _que _(V A D1, V^B D2) est un majorant de D.

** Montrons _que (V^A D1, VB D2) est le plus petit majorant de D.

Soit (a, b) un majorant de D. Pour tout x E D1 il existe y E D2 tel _que (x, y) E D. (a, b) étant un majorant de D, (x, y) = (a, b). Donc x = a pour tout x E D1. Partant, a est un majorant de D1 et, V^A D1 = a.

De même, on montre _que V^B D2 = b. Ce _qui montre _que (V^A D1, V^B D2) = (a, b). Donc (V^A D1, V^B D2) = VA×B D.

Lemme 1.6. Soient A et B deux opc^s (i) Les projections

ð1: A x B ----> A (a, b) 1----> a

et

ð2 : A x B ----> B (a, b) 1----> b

sont continues .

(ii) Pour tout opc C, une application f :C ---> A x B est continue si et seulement si r1 o f et r2 o f sont continues.

Preuve.

(i) Soit D une partie diri_gée de AxB. D'après le lemme(1.5), (V^A D1, V^B D2) = VAXB D. (VAXB D) = VA r1 (D).

Montrons _que r1
Nous savons _que

(_VAXB D) = (VA _D1, ^VB D2 )

_=VA

D1

=VA r1 ^(D) .

Donc r1 est continue.

(ii) ) Si f est continue, r1 o f et r2 o f sont continues comme composées d'applications continues.

?)Supposons r1 o f et r2 o f continues et montrons _que f est continue.

Soit D une partie diri_gée de C. Nous allons montrer _que f (VC ^D) VA X B f (D)

f (VC D) = ir1 o f ^(VC , r2 o f (VC _D) )

VA r1 o _{f (D)} , VB r2

o f (D)) car ri o f est continue pour i E {1, 2}

=

= VAXB f (D) d'après lemme (1.5)

On conclut _que f est continue.

Remar_que 1.2. Soit L un opc muni de deux applications continues q1 : L ---> A et q2 : L---> B , d'après la propriété universelle de A x B dans ENS, il existe une uni_que

application < q1,q2 >:L --> A x B

l 1---> (q1 (l), q2 (l))

rendant commutatif le dia_gramme suivant :.

Q2	//B
		.

A< L

CC_CC<Q1,Q2>
ð1_V ð2

AxB

D'après lemme (1.6), < q1, q2 > est continue

De cette remar_que et des lemmes (1.5) et (1.6), nous déduisons _que : Corollaire 1.1. La caté_gorie CPO admet des produits binaires.

Remar_que 1.3. L'opc trivial (réduit à un seul élément ) est un objet final de la caté_gorie CPO.

A présent, l'on désire montrer _que CPO admet des produits finis. Pour cela, nous avons besoin du résultat classi_que ci-après.

Théorème 1.2. (f4J)Si une caté_gorie C admet des produits binaires et un objet final alors elle admet des limites finies.

De ce résultat et des lemmes et corollaires ci-dessus, nous déduisons _que : Proposition 1.8. CPO est cartésienne.

Pour faciliter la compréhension de cette notion, construisons _quel_ques exemples de produits.

Exemple 1.4. 1) A la remar_que(1.1), nous avons défini sur A = {x, y, z} une structure

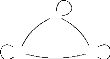
d'opc représentée par :

₇₇

z ^qq hh

%%

x

3₃ y

_ee

Le produit A x A est illustré par :

¼¼

(z,z)

_'t

_AA

]]

_R

¼¼

(y,x)

(x,y)

(y,y)

_jj

₇₇

_Lt

]]

_AA

(x,x)

_YY

¼¼

₇₇

_MM

_gg

(y,z)

(z,y)

_XX

¼¼

(z, x)

(x,z)

_JJ

Dans cette représentation, les flèches dési_gnent l'ordre composante par composante.

2) Le produit N x N est illustré par :

·

>
·

·

(0, 2)

₇₇

¼¼

··

·

·

//

₇₇

₇₇

(0,1)

(1,1) //

_JJ

(2, 2)

··

··

(1, 2)

//

(0, 0)

Ji

(1,0)

''

11

''

//

(2,1)

·

·

· >
·

J'

''

(2, 0)

4

Proposition 1.9. Soient A, B et C trois opc^s. Une application f: A x B ? C est continue si et seulement si ses applications partielles f (--, b) et f (a, -) sont continues pour tout a E A et b E B.

Preuve.

i) Supposons f (-, b) et f (a, -) continues pour tout a E A et b E B.

* Soient (x, y) et (x', y') deux éléments de A x B ; tels _que (x, y) = (x', y') alors, f (x, y) = f (x, y') car f est monotone en son deuxième ar_gument

= f (x', y') car f est monotone en son premier ar_gument

Ce _qui montre _que f est monotone.

** Soit D une partie diri_gée de A x B.

D'après le lemme (1.5), V^A×BD = (V^A D1, V^B D2). Où D1 et D2 sont définies comme au lemme(1.5). Par ailleurs,

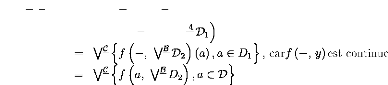
f ^(V- D)f VAD1, VB D2)

( -,

f

V

BD2)(

V

A

= WC n (f-VB D2) (a), a E D1o , carf (-, y) est continue

= WC nf (a, --) (VB D2) , a E Do , carf (x, -) est continue = _WC nVC If (a, b) , a E D1, b E D2}o

= WC f (D1 x D2)

Comme D ? D1 x D2, WC f (D) = WC f (D1 x D2) .

Pour démontrer l'iné_galité inverse, notons _que tout élément (x, y) de D1 x D2 est inférieure ou é_gal à un élément de D.

D1)

= WC n f(a, VBD2) , a E Do

En effet, comme x E D1, il existe y^f E D2 tels _que (x; y^f) E D. De même, il existe x^f E
D1 tel _que (x^f, y) soit dans D. Comme D est une partie diri_gée, il existe (x^ff, y^ff) E D

(_xf _y) < (x» y") ; ff et y =

tel _que (x, y^f) = (x^ff , , y") et ) en particulier, x = x y^ff.

\

i.e, (x, y) = (xff, y^ff ) . Comme tout élément (x, y) de D1 x D2, est majoré par un élément de D, et comme f est monotone, tout majorant de f (D) est aussi majorant de f (D_oo x DE). On a donc ^We f (D1 x D2) = We f (D).

D'où ^We f (D) = f (y 'Ax8 D. Ce _qui montre _que f est continue.

ii) Récipro_quement, supposons f continue de A x B dans C. Pour toute partie diri_gée D de B, et pour tout x E A, la partie {x} x D de A x B est une partie diri_gée de A x B. Soit f (x, -) l'application _qui à tout y E B associe f (x, y). Comme f

est continue, f ^(\tAx8 {x} D) = We f ({x}

x D). Donc f (x, -) est continue. De

même, on montre, par un ar_gument similaire _que l'application f (-, y) _qui à tout x E A associe f (x, y) est continue.

observation 1.1. Ce résultat est un cas particulier car en topolo_gie _générale, il est démontré _que la continuité d'une application définie sur un produit impli_que celle de ses fonctions partielles. La récipro_que de ce résultat est fausse. L'exemple t_ype est le cas de la fonction f :118 xl -?R définie par :

½20)+y xy

f (x, y)=x 2 si (x, y) (0, 0)

(

0 les applications partielles f(0,--) et f(--, 0) sont des
, fonctions nulles et sont donc continues. En revanche, pour y = ax, a E IR et x =6 0, on a

f (x, ax) = 1%2 _qui ne tend pas vers 0 avec x. La fonction n'est donc pas continue en (0, 0). C'est ce _qu'illustre son _graphe ci-dessous.

Nous allons à présent établir un lien entre la topolo_gie de Scott sur les produits et celle de T_ychonoff.

Théorème 1.3. La topolo_gie de Scott sur les produits est plus fine _que celle de T_ychonof.

Preuve. Soit A et B deux opc^s.

Soit U un ouvert de T_ychonoff de A x B, il existe U1 (resp U2) ouvert de A

(resp ouvert de B) tels _que U = 7r1^-1 (U1) n 7r2^-1 (U2)

Montrons _que U est un ouvert de Scott.

* Soient (a, b) et (á, â) deux éléments de A x B tels _que (a, b) = (á, â) et (a, b) E U. Nous devons montrer _que (á, â) E U. Comme U = 7r₁^-1 (U1) n 7r2¹ (U2), alors (a, b) EU impli_que (a, b) E 7ri¹ (U1) et (a, b) E 7r2¹ (U2) . Donc (á, â) E 7ri¹ (U1) n 7r2¹ (U2) car cha_que 7r_i^-1 (Ui) est filtrant pour i = 1, 2 . Partant, (á, â) E U.

.

** Montrons _que U est inaccessible par suprema diri_gés.

Soit D une partie diri_gée de A x B telle que _VA× B

D E U. Il faut montrer _que D n U =6 ç Cependant, il existe D1 et D2 définis comme au lemme (1.5) tels _que

.

VA×B (VA D1, ^VB D2) .

Ainsi

VA×B D E U é_quivaut à (V^A D1, V^B D2) E 7r₁^-1 (U1) n 7r2^-1 (U2)

implique ^(VA D1, ^VB D2) E-1(U1) ^(VA D1,V^B D2) E 7r₂ (U2) impli_que V^A D1 E U1 et V^B D2 E U2

impli_que D1 n U1 =6 ç et D2 n U2 =6 ç

impli_qu'ils existent d1 E D1 n U1 et d2 E D2 n D2

D'après la définition de Di, il existe a E D2 (resp b E D2) tel _que (d1, a) E D et (b, d2) E D. D étant une partie diri_gée de A x B, il existe (x, y) E D tel _que (d1, a) = (x, y) et (b, d2) = (x, y) . Donc d1 = x et d2 = y. Comme di EUi et Ui est filtrant, d1 = x et d2 = y impli_que x E U1 et y E U2. Partant, (x, y) E 7r^-1 (U1) n E 7r^-1 (U2) n D.

Ce _qui montre _que U est inaccessible par suprema diri_gés. Par consé_quent, tout ouvert de T_ychonoff est é_galement ouvert de Scott.

Ce résultat était prévisible car la topolo_gie de T_ychonoff est la moins fine des topolo_gies définies sur A x B rendant continues les projections 7r1 et 7r2. Or nous avons montré au lemme(1.6) _que A x B muni de la topolo_gie de Scott rendait continue ces projections. Donc par minimalité, la topolo_gie de Scott est plus fine _que celle de T_ychonoff.

Pour démontrer la récipro_que de ce théorème, nous allons utiliser la propriété universelle du produit A x B. C'est l'objet du théorème suivant.

Théorème 1.4. La topolo_gie de Scott est moins fine _que celle de T_ychonof.

Preuve. Posons S (resp T) la topolo_gie de Scott (resp T_ychonoff) sur AxB. Le théorème précédent montre _que T C S. Ce _qui si_gnifie _que l'identité

idA×B : (A x B, S) -? (A x B, T) (_que nous noterons idS?T) est continue. Il suffit de montrer _que l'identité idA×B : (A x B, T) -? (A x B, S) (_que nous noterons idT?S) est continue pour conclure _que S C T. D'après la P.0 de (A x B, S) (resp (A x B, T)), il existe une uni_que application continue ? (resp ) rendant commutatif le dia_gramme ci-dessous. i.e, 7rio ? = 7ri et 7ri o = 7ri pour i = 1, 2. Comme idS?T est continue, on déduit l'unicité de ? _que ? = idS?T. D'après la P.0 de (A x B, S) , idS?S est la seule application f continue de (A x B, S) vers (A x B, S) telle _que 7ri o f = 7ri pour i = 1, 2. Cependant, 7ri o?o = 7ri pour i = 1,2. On conclut d'après l'unicité de idS?S _que ? o = idS?S. Comme ? = idT ?S,

on déduit _que b = idS?S. Ce _qui montre _que S Ç T. (A, SA)(A x B, T )

ð2 // (B, SB)

oo ð1

ça

_OO

ø

²²

^eeJJJJJJJJ_JJJJJ

ð1 JJJJJJJJ

_9t9

_ttttttt^tttttttttttt

ð2

(AxB, S)