2.1.6 Quelques exemples de morphismes de
systèmes de transi-
tion.
1) Pour tout système de transition S,
l'application identitité 1S : S -? S est un morphisme
de systèmes de transition.
2) Considérons l'application : N -? 2 ?
définie par (n)={ n+2
sin=68 8 sinon
ç') est continue et pour tout n, m E
N,n /> m implique 2 + n
2? /> m + 2.
N
Donc ç') préserve les transitions.
Par ailleurs, pour tout n E 2 ?,
l'équation en x :
2+x =n
admet une unique
solution dans N. D'où ç') est un morphisme de
système de transition.
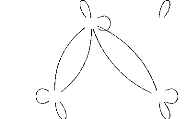
3) Soient S et T deux
systèmes de transition ci-dessous
représentés.
Soit G (f) ={(x, v),
(z, u), (y, o), (t, o)}
le graphe de f:S-?T.
Nous nous proposons de construire à partir de S
et T des systèmes de transition pour
lesquels f est un morphisme de systèmes
de transition.
et

S=
S
££
S
z
99 FF OO
§§
x \\
t \\
y
S
yy
u T
o
T
T
v \\
w \\
££
T=
;; G²G UU ^^=======T
T ====
²²²²²²²²²²²²²=
T ==
T ====
%% {{
xx
L'application f est continue par construction. La
transition x S />z est préservée par
f car , f (x) = v T /> u
= f (z). De même, la transition z
S />x, est préservée par
f car f (z) = u T /> v
= f (x). De façon
analogue, l'on montre que f préserve les
transitions x S />x et z S
/>z. Partant, f est continue et préserve les
transitions
de S. Pour que f soit un morphisme
de systèmes de transition, il faudrait qu'elle
réfléchisse les transitions de T.
· Les transitions v T
/> u et u T /> v sont
naturellement réfléchies par f. La seule
transition qui fait problème est u T
/> w; qui n'est pas réfléchie
par f, car w n'est
image d'aucun état de S. Pour
que celle-ci soit réfléchie, nous devons affaiblir les
transitions de T. Le plus simple serait de supprimer la transition
u T /> w.
Ainsi, pour T' ci-dessous représenté,
f est un morphisme de systèmes de transition.

yy
u T
T
T
v \\
w \\
;; G²G UU ^^<<<<<<<
T <<<
²²²²²²²²²²²²²²<
T <<
T <<<<
{{
T' =
%%
xx
££
o
·
· Nous pouvons aussi modifier
S et G (f) de manière à obtenir un
morphisme tout en conservant la transition u
T> w. Si la transition u
T> w est maintenue, pour
que l'on ait un morphisme, il faudrait simplement que
w soit image d'un état 0 de S
où 0 est tel que z T>
0. Comme y et t ont la même image
par f, nous pouvons changer dans G (f) le
couple (y, o) par (y, w) . Ceci étant, on
imposerait simplement la transition z S> y. La
nouvelle application f' ainsi construite sur le nouveau
système S' ci-dessous représenté est
un morphisme.
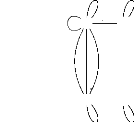
S' =
S
S
S
z
££
S //
y .
99FFJO
k
x \\
t \\
Ce morphisme a pour graphe : G (f')
= {(x, v), (z, u), (y,
w), (t, o)}.

S
S
S' =
S
uu
k§
S
z
££
S//
y
.
99FFA
x \\
t \\
·
·
· En conservant
l'application f', l'on peut modifier le système
S' en S» ci-dessous représenté
Remarque 2.3. On démontre sans peine
que la composée des morphismes de systèmes
de transition est un morphisme de systèmes de transition. Les
identitités étant des morphismes de systèmes de
transition, l'on conclut que les systèmes de
transition et les morphismes de systèmes de transition
forment une catégorie.
| 


