Etude et implémentation d'un système sans fil multi-antennes dans un contexte MC-CDMA

Chapitre 3

Implémentation matérielle et analyse de

performances

1. Introduction

Dans le chapitre précédent, on a étudié et évalué les performances d'une chaîne de transmission utilisant le multiplexage spatial dans un contexte MC-CDMA en utilisant l'outil Matlab. Dans ce chapitre, on aborde la phase de l'implémentation matérielle des différents blocs de la chaîne. Cette implémentation consiste tout d'abord à concevoir pour chaque bloc une structure simplifiée pour le traitement de données garantissant ainsi la facilité de l'implémentation, de test, de validation et du bon fonctionnement de la structure tout en satisfaisant les contraintes temporelles exigées en fonction de l'application. Le second objet de l'implémentation matérielle consiste à l'optimisation progressive de la description matérielle de la structure de chaque bloc en fonction de son assemblage avec les autres blocs de la chaîne.

L'implémentation de la chaîne MIMO-MC-CDMA est destinée pour le développement d'une bibliothèque d'IP « propriété intellectuelle » (Intellectual Property) reconfigurable et réutilisable afin de pouvoir implémenter toute la chaîne. Ce développement des IPs à TELNET est basé sur une méthodologie de conception basée sur une plateforme de prototypage destinée pour une architecture cible « FPGA » de technologie Altera.

Dans ce chapitre, on commence par présenter l'architecture cible FPGA « Stratix.II.GX » ainsi que ses ressources internes. Puis, on décrit l'environnement de synthèse et le flot de conception adopté. Ensuite, on présente les architectures proposées et le rapport d'implémentation des différentes composantes des circuits d'émission et de réception de la chaîne MIMO-MC-CDMA. Enfin, on examine le résultat des performances de l'architecture proposée en termes de complexité et de rapidité.

2. Le circuit FPGA Stratix II.GX

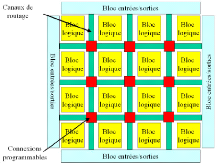
Un FPGA (Field Programmable Gate Array) est un circuit programmable qui se compose généralement de blocs logiques reliés entre eux via un réseau d'interconnexion (figure 3.1). Ces blocs logiques sont regroupés sous la forme d'une matrice.

47

Figure 3.1. Bloc diagramme d'un FPGA

Basée sur une unité logique configurable, un FPGA est une matrice composée d'un grand nombre d'éléments configurables qui interagissent via des ressources de routage également reconfigurables. Un bloc logique est composé de 2 à 4 LUT, d'une chaîne de propagation de la retenue et de bascules D. Entre les blocs, des lignes d'interconnexion sont disposées pour établir les liaisons. Finalement, autour de la matrice à deux dimensions, nous trouvons les blocs d'entrées/sorties. Pour mieux comprendre le fonctionnement des FPGAs actuels, il paraît évident de connaître leur architecture interne ainsi que leurs modes de configuration.

La famille Stratix II.GX disponible à Telnet est une plateforme FPGA du constructeur ALTERA. Elle offre plusieurs fonctionnalités à travers un certain nombre de composantes prédéfinies, qui caractérisent la puissance de traitement de l'FPGA. Parmi ces composantes on cite :

- Le module ALM : Le bloc logique structurel de base dans Stratix II.GX est l'ALM (Adaptative

Logic Module), qui fournit des traitements avancés. Chaque ALM contient une variété de LUT (Look-Up-Table). En plus des ressources LUT-Basées adaptatives, chaque ALM contient deux registres programmables, deux additionneurs, trois signaux d'entrées venant des ALM du même LAB sachant qu'un LAB est composé de huit ALM. A travers ces ressources l'ALM peut configurer plusieurs fonctions arithmétiques.

- Le module DSP : ces modules intègrent des fonctions matérielles telles que multiplieurs,

accumulateurs, additionneurs, multiplexeurs et registres et permettent, entre autre, de réaliser des multiplieurs 36 bits. Ainsi, les DSP contiennent des unités de calcul nécessaires lors de la conception des filtres RIF et RII, la transformée de fourier rapide et son inverse ainsi que, la transformée en cosinus discrète.

48

- Le module PLL : Le rôle des PLL consiste à assurer la gestion des réseaux globaux d'horloge.

Ces PLL servent dans l'amélioration de performances, dans la synthèse des fréquences et dans le timing des systèmes configurés.

- Le module Trimatrix : Il s'agit d'un module mémoire constitué de trois types de bloc RAM : M512 RAM, M4K RAM et M-RAM.

3. Flot de conception adopté et environnement de synthèse

Dans la phase d'implémentation nous avons adopté un flot de conception proposé par ALTERA spécifique pour ces FPGAs. Ce flot décrit toutes les étapes nécessaires pour l'implémentation matérielle comme illustré dans la figure 3.2. L'outil de conception qui met en oeuvre ce flot est Qua rtus II de ALTERA.

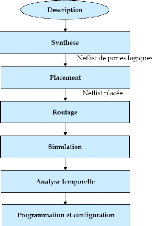
Figure 3.2. Flot de conception de l'outil Quartus

Nous décrivons brièvement les différentes étapes de ce flot dans ce qui suit :

- La description des blocs avec un langage d'un haut niveau d'abstraction (VHDL, Verilog..) ;

- La synthèse logique qui consiste à convertir cette description en une netlist de portes

logiques selon une bibliothèque de cellules relatives à la cible ;

- Le placement consiste à choisir des endroits spécifiques sur le FPGA pour les blocs logiques

de la netlist ;

49

50

51

- Le routage consiste à choisir les lignes d'interconnexion nécessaires afin d'établir les

connexions électriques entre les blocs ;

- La simulation fonctionnelle est une vérification du fonctionnement du système ne prenant pas en compte les aspects temporels du circuit ;

- La validation temporelle consiste en une simulation temporelle du circuit tenant compte des

temps de propagation, recouvrement de signaux, etc.

4. Spécification fonctionnelle et résultats d'implémentation

Dans cette partie du rapport, on s'intéresse à décrire les spécifications fonctionnelles, le schéma en bloc et le résultat d'implémentation de chaque bloc de la chaîne MIMO-MC-CDMA.

4.1. Architecture de la chaîne MIMO associée au MC-CDMA

La chaîne MIMO-MC-CDMA qu'on se propose d'implémenter comporte les paramètres suivants : - Nombre d'antennes à l'émission : Nt=2 ;

- Nombre d'antennes à la réception : N_r=2 ;

- Nombre de sous-porteuses : L_c=64 ;

- Nombre d'utilisateurs : N_u=64 (à pleine charge).

L'architecture de la chaîne de transmission MIMO associée au MC-CDMA est décrite par un circuit émetteur et un circuit récepteur présentés dans les deux figures suivantes.

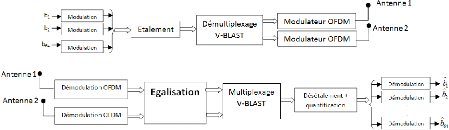
Figure 3.3. Circuits d'émission et de réception implémentés Le diagramme en bloc du circuit d'émission se compose de 4 blocs principaux :

- Bloc de modulation : Ce bloc effectue la modulation numérique 256-QAM ;

- Bloc étalement : ce bloc réalise l'étalement de donnés de 64 utilisateurs utilisant les codes de

Walsh-Hadamard de longueur égale à L_c=64 ;

- Bloc démultiplexage V-BLAST : Ce bloc comporte 64 entrées relatives à 64 utilisateurs.

Chaque entrée i représente les symboles d'un utilisateur i, i=1,...,64. Le rôle du démultiplixeur V-BLAST est de transformer chaque séquence de 2 symboles reçus, pour chaque entrée, en parallèle afin de les répartir sur les deux antennes d'émission.

- Bloc modulateur OFDM : Ce bloc effectue la modulation OFDM des symboles reçus à son entrée.

Le diagramme en bloc du circuit de réception se compose de 5 blocs principaux :

- Bloc démodulation OFDM : Ce bloc reçoit les symboles émis du circuit d'émission et effectue la démodulation OFDM.

- Bloc d'égalisation : Les symboles reçus sont altérés par l'effet du canal et par le bruit

complexe BBAG. Le rôle de ce bloc consiste à estimer les symboles émis connaissant le canal et le rapport signal sur bruit.

- Bloc multiplexage V-BLAST : ce bloc réordonne les données démultiplexées.

- Bloc désétalement + quantification : ce bloc effectue le désétalement des données par les

mêmes séquences de Walsh-Hadamard utilisées en émission. Les données sont par la suite quantifiées selon la constellation de la modulation 256-QAM.

- Bloc démodulation : ce bloc effectue la démodulation numérique des symboles pour récupérer les données binaires reçus.

4.2. Architecture des blocs utilisés dans la chaîne

Dans cette partie, on se propose de détailler l'architecture interne de chaque bloc de la chaîne MIMO-MC-CDMA. On note que l'implémentation de cette chaîne a nécessité l'implémentation des opérations arithmétiques élémentaires telles que l'addition et la multiplication. Les schémas RTL correspondants à ces opérateurs seront fournis en annexe.

4.2.1. Bloc de modulation 256-QAM

Ce bloc effectue la modulation numérique des données binaires pour 1 utilisateur. On rappelle qu'un symbole issu d'un modulateur numérique 256-QAM est de la forme :

ckakjbk (3.1)
où ak et bk appartiennent à l'alphabet {#177;1, #177;3, ..., #177;15}.

Le bloc du modulateur numérique 256-QAM délivre un symbole correspondant à chaque 8 bits successifs reçus à son entrée. Le fonctionnement de ce modulateur est décrit par l'organigramme de la figure 3.4.

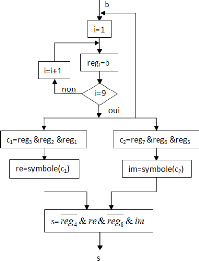
Figure 3.4. Organigramme du modulateur 256-QAM

code	000	001	011	010	110	111	101	100
symbole	15	13	11	9	7	5	3	1

Tableau 3.1. Table d'assignation des symboles en fonction du code

La génération des symboles en fonction des codes composés de trois bits est décrite par le tableau 3.1. Les paramètres d'entrées sorties du bloc "Modulation" sont présentés dans le tableau 3.2. Le résultat de synthèse au niveau RTL du bloc modulation est fournit dans le tableau 3.3.

4.2.2. Bloc étalement

Ce bloc effectue l'étalement simultané des symboles des 64 utilisateurs. Les séquences d'étalement utilisées pour notre chaîne sont les séquences de Walsh-Hadamard. Le processus d'étalement peut être effectué par une multiplication par la matrice de Walsh-Hadamard en se référant à l'équation

Nom du signal	E/S	Description	Taille	Groupement logique
b	Entrées	Donnée binaire d'un utilisateur	1 bit	Interface entrée
s	sortie	Symbole délivré	64 bits

Tableau 3.2. Table des paramètres entrées/sorties du bloc de modulation

Famille de FPGA	Nombre de LUT	Nombre de registres	Nombre total de pin	Nombre de DSP	Nombre de bloc mémoire
Stratix.II.GX	21	11	64	0	0

Tableau 3.3. Résultat de synthèse du bloc modulation

(1.31) du chapitre 1. Donc l'étalement d'un vecteur de 64 symboles dk=[ ⁽⁰⁾

d_k , ..., ⁽⁶³⁾

dk ]^T est calculé

par :

xk=C64.dk, (3.2)

où _C64 est la matrice de Walsh-Hadamard d'ordre 64 et xk est le vecteur résultant de l'opération d'étalement de longueur 64.

Ce calcul peut-être simplifié en effectuant un algorithme de transformée de Hadamard Rapide (Fast Hadamard Transform FHT) du vecteur dk. En effet, d'après les équations (1.24) et (1.26) du chapitre 1 :

xk=

1 1 H 8 8 64

H H 32 32 H H 32 32

.dk (3.3)

52

En décomposant le vecteur dk en d1, k=[ (0)

d_k , ..., ⁽³¹⁾

dk ]^T et d2 ,k=[ (32)

d_k , ..., ⁽⁶³⁾

d_k ]^T, on obtient :

(3.4)
xk=		11 H H d H d H d 32 32 1, 32 1, 32 2, k kk 8 8 H H d H d H d 32 32 2, 32 1, 32 2, k k k

On remarque que la transformée de Hadamard d'ordre 64 du vecteur dk peut se simplifier par une transformée de Hadamard d'ordre 32 de _d1,k et une transformée de Hadamard d'ordre 32 de _d2,k puis effectuer la somme et la différence de ces deux transformées.

Ainsi le FHT est un algorithme récursif, d'où la transformée de Hadamard d'ordre 32 peut être
calculée de la même manière en fonction de la transformée de Hadamard d'ordre 16. L'architecture

proposée pour le bloc d'étalement est représenté dans la figure 3.5. On représente aussi la

1

transformée de Hadamard d'ordre 2 en tenant compte de la multiplication par le facteur de 8 dans

la figure 3.6. A titre d'illustration, on montre le schéma RTL du circuit effectuant la transformée de Hadamard d'ordre 8 dans la figure 3.7.

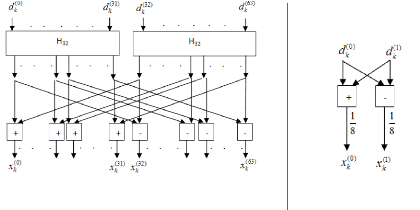
Figure 3.5. Architecture du bloc Etalement

Figure 3.6. FHT d'ordre 2

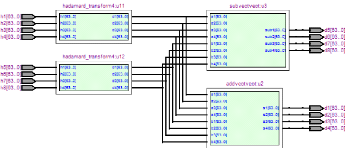
53

Figure 3.7. Schéma RTL du FHT à l'ordre 8

Les paramètres d'entrées sorties du bloc "Etalement" sont présentés dans le tableau 3.4.

Nom du signal	E/S	Description	Taille	Groupement logique
h[1..64]	Entrées	Symboles des utilisateurs	64 bits	Interface entrée
d[1..64]	Sorties	Symboles étalés	64 bits	Interface sortie

Tableau 3.4. Table des paramètres entrées/sorties du bloc de Etalement

Le résultat de synthèse au niveau RTL du bloc FHT à l'ordre 8 est fournit dans le tableau 3.5.

Famille de FPGA	Nombre de LUT	Nombre de registres	Nombre total de pin	Nombre de DSP	Nombre de bloc mémoire
Stratix.II.GX	44772	0	1024	0	0

Tableau 3.5. Résultat de synthèse du bloc FHT 8

4.2.3. Bloc de démultiplexage spatial V-BLAST pour 2 antennes

Le bloc de démultiplexage spatial pour les 2 antennes est composé de 64 démultiplexeurs relatifs aux 64 sous-porteuses où les sorties de chaque démultiplexeur génère les symboles vers les 2 antennes. Le schéma bloc du démultiplexage spatial V-BLAST est représenté dans la figure 3.8. L'organigramme de chaque démultiplexeur pour chaque sous-porteuse est présenté dans la figure 3.9.

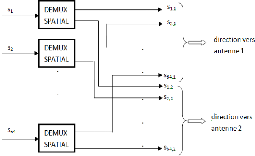
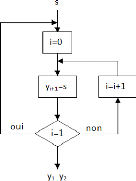
Figure 3.8. Bloc de Démultiplexage V-BLAST

Figure 3.9. Organigramme d'un "DEMUX

54

SPATIAL"

Le schéma RTL du DEMUX SPATIAL est représenté dans la figure 3.10.

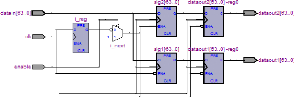
Figure 3.10. Schéma RTL du Bloc "DEMUX SPATIAL"

Les paramètres d'entrées sorties du démultiplexeur spatial sont présentés dans le tableau 3.6.

Nom du signal	E/S	Description	Taille	Groupement logique
clk	Entrée	Horloge de système	1 bit	Interface système
enable	Entrée	Validation de fonctionnement	1 bit
datain[1..64]	Entrées	Données du système	64 bits	Interface entrée
enable[1..2]	sorties	Validation de sortie de données	1 bit	Interface sortie
dataout[1..128]	sorties	données démultiplexées	64 bits

Tableau 3.6. Table des paramètres entrées/sorties du bloc de démultiplexage V-BLAST

Le résultat de synthèse au niveau RTL du bloc de démultiplexage V-BLAST est fournit dans le tableau 3.7.

Famille de FPGA	Nombre de LUT	Nombre de registres	Nombre total de pin	Nombre de DSP	Nombre de bloc mémoire
Stratix.II.GX	2	16385	12290	0	0

Tableau 3.7. Résultat de synthèse du bloc de démultiplexage V-BLAST

4.2.4. Bloc modulateur OFDM

Le rôle principal de ce bloc est d'effectuer la modulation OFDM des 64 symboles reçus en parallèles à son entrée. L'architecture d'un modulateur OFDM est représentée dans la figure 3.11.

55

Figure 3.11. Architecture du modulateur OFDM Le bloc "Modulateur OFDM" est composé de 2 sous-blocs :

- Bloc IFFT : ce bloc est utilisé dans les chaînes utilisant la technique de modulation OFDM. Son

rôle consiste à effectuer la transformée de Fourier rapide inverse d'un vecteur de 64 symboles.

- Bloc P/S+ACe bloc effectue la sérialisation des données reçus en parallèle en introduisant

l'intervalle de garde qui consiste à un préfixe cyclique de longueur Lc .

4

4.2.4.1. Architecture du bloc IFFT

Pour définir une architecture du bloc IFFT. On définit tout d'abord la Transformée de Fourier Discrète Inverse (TFDI) d'un vecteur x de longueur N où x =(x0, x1, ..., xN-1).

La TFDI de x est définit par :

N 1

A w x

k N n

n k

. , pour k=0,..,N-1, (3.5)

n 0

2i

avec w N

N e . L'expression de Ak peut être décomposée en 2 expressions l'une à indice paire et

l'autre à indice impair. On obtient les équations (3.6) et (3.7).

N 1 2

A x x w ^nk

. (3.6)

2 k n N N

n

n 0 2 2

2

k

N

A x x w

2 1 n N

0 2

n nk

N N
. w

n

n 2

1

(3.7)

56

L'expression _A2k+1 (équation 3.7) peut être décomposé en 2 expressions : l'une à indice 4k+1 et l'autre à indice 4k+3. On obtient les équations (3.8) et (3.9).

N

1

(3.8)

4 n n k

.

. . 3

A x ^j x x j x

N N N N

w w

4 1

k n n n n N

N

n 0 4 2 4 4

1

43 .

n n k

. . 3

A x ^j x x j x

N N N N (3.9)

4 3

k n n n n N

w w

n 0 4 2 4 4

Le système formé par les équations (3.6), (3.8) et (3.9) est un système appelé Split Radix qui permet le calcul de la transformée de Fourier rapide inverse du vecteur x.

On observant la TFDI, on peut remarquer que les équations (3.6), (3.8) et (3.9) sont aussi des TFDI de certaines combinaisons de x.

57

En effet :

N N

11

22

A x x W a W TFDI

. . ( )

nk ^nk a (3.10)

2 k n N N n N

n

22 0 2

n

⁰

n

où a=(a0, a1, ..., _aN/2-1) ^avec _an=xn + _xn+N/2. On a encore :

N N 1 1 4 4 n n k n k . . A x ^j x x j x b k n n n n N n . . N N N N N 3 W W W 4 1 n0^4 2 4 4 4 n 0	TFDI b ( ) , (3.11)
n n où b=(b0, b1, ..., bN/4-1) avec b j j 3 n n n n n N n n n n N 3 x x x x W x x j x j x N N N . . N N N . . W 4 2 4 2 4 4		.

On écrit également :

N N

1 1

4 3 . 4 .

A x x x x c_n

n n k n k

j j

. .

N N 3 N N N N

W W W TFD c

( ) , (3.12)

4 3

k n n n n

n 0 4 2 4 4 n0 4

3n 3 n

avec c=(c0, c1, ..., _cN/4-1) et cj j 3

n n n n n N n n n n N

3

x x x x W x x j x j x

N N N

. .

N N N . . W

4 2 4 2 4 4

D'après les équations (3.10), (3.11) et (3.12), on peut conclure que la Transformée de Fourier Inverse
à l'ordre N du vecteur x peut être décomposée en une Transformée de Fourier Inverse à l'ordre

N du vecteur a et une Transformée de Fourier Inverse à l'ordre N des vecteur b et c.

2 4

Pour notre cas, on a besoin d'une IFFT à l'ordre 64. Donc les expressions des vecteurs a, b et c sont données dans les équations suivantes :

an=xn + _xn+32 , n=0, ..., 31 (3.13)

. n j

16 . 48

x n W _N , n=0, ...,16 (3.14)

n

b n x _n x n j x

32

3

n x n x n W N , n=0, ...,16 (3.15)

n

c n x 32 . 16 . 48

j x n j

Et par suite, l'architecture du bloc de l'IFFT peut être déduite par la figure 3.12. Les architectures des sous-blocs IFFT32 et IFFT16 peuvent être déduites à partir des équations (3.10), (3.11) et (3.12) en remplaçant respectivement N par 32 et par 16. Les blocs d'IFFT à l'ordre 2 et 4 sont représentés dans les figures 3.13 et 3.14.

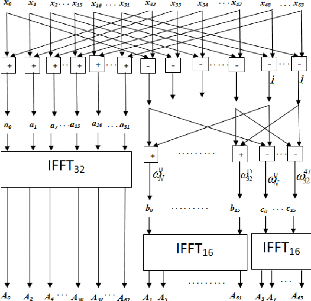
Figure 3.12. Architecture du bloc IFFT

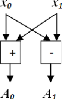
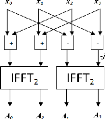
Figure 3.13. Bloc d'une IFFT à l'ordre 2

Figure 3.14. Bloc d'une IFFT à l'ordre 4

58

Les paramètres d'entrées/sorties du bloc " IFFT " sont présentés dans le tableau 3.8.

Nom du signal	E/S	Description	Taille	Groupement logique
d[1..64]	Entrées	Données du système	64 bits	Interface entrée
f[1..64]	sorties	Sorties modulés en IFFT	64 bits	Interface sortie

Tableau 3.8. Table des paramètres entrées/sorties du bloc IFFT Le schéma RTL d'une IFFT à l'ordre 8 est illustré dans la figure 3.15.

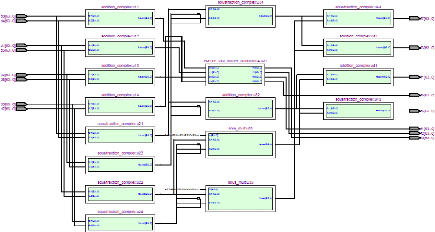
59

Figure 3.15. Schéma RTL d'une IFFT à l'ordre 8

Le résultat de synthèse au niveau RTL du bloc IFFT à l'ordre 8 est fournit dans le tableau 3.9.

Famille de FPGA	Nombre de LUT	Nombre de registres	Nombre total de pin	Nombre de DSP	Nombre de bloc mémoire
Stratix.II.GX	52259	0	1024	0	0

Tableau 3.9. Résultat de synthèse du bloc IFFT

4.2.4.2. Bloc de conversion parallèle/série avec introduction de l'intervalle de garde

Le convertisseur P/S avec introduction de l'intervalle de garde est le deuxième sous-bloc de la composante "Modulateur OFDM". Il consiste, dans un premier temps à envoyer successivement les 16 derniers symboles des 64 symboles à transmettre. Puis, il envoie tous les symboles successivement. L'organigramme de ce bloc est présenté dans la figure 3.16. Ainsi, le résultat de synthèse au niveau RTL du bloc conversion P/S +est fournit dans le tableau 3.10.

Famille FPGA	de	Nombre de LUT	Nombre registres	de	Nombre de pin	total	Nombre DSP	de	Nombre mémoire	de	bloc
Stratix.II.GX		1352	71		4162		0		0

Tableau 3.10. Résultat de synthèse du bloc P/S +

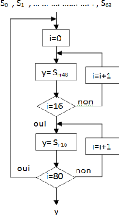
60

Figure 3.16. Organigramme du bloc de conversion P/S +

4.2.5. Bloc démodulateur OFDM

Ce bloc est composé des blocs de la chaîne de démodulation OFDM. Son diagramme en bloc est représenté dans la figure 3.17.

Figure 3.17. Diagramme en bloc du démodulateur OFDM Le bloc "démodulateur OFDM" est composé des deux sous-blocs suivants :

- Bloc S/P-: Le rôle de se bloc consiste à supprimer l'intervalle de garde de chaque symbole

OFDM reçu tout en effectuant la conversion série/parallèle.

- Bloc FFT : ce bloc calcule la transformée de Fourier rapide d'un vecteur de 64 symboles.

4.2.5.1. Bloc de conversion série/parallèle avec suppression de l'intervalle de garde

Le convertisseur S/P avec suppression de l'intervalle de garde est le premier bloc de la partie de réception de la chaîne MC-CDMA. Il consiste à recevoir les 16+64 symboles émis (en série) en éliminant les 16 premiers symboles reçus qui correspondent à l'intervalle de garde introduit lors de l'émission. L'organigramme de ce bloc est présenté dans la figure 3.18. Ainsi, le résultat de synthèse au niveau RTL du bloc conversion S/P -est fournit dans le tableau 3.11.

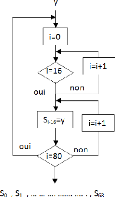
61

Figure 3.18. Organigramme du bloc de conversion S/P -

Famille FPGA	de	Nombre de LUT	Nombre registres	de	Nombre de pin	total	Nombre DSP	de	Nombre mémoire	de	bloc
Stratix.II.GX		84	8199		4162		0		0

Tableau 3.11. Résultat de synthèse du bloc S/P -

4.2.5.2. Bloc de Transformée de Fourier rapide FFT

Pour définir l'architecture du bloc FFT. On doit d'abord expliciter l'expression de la transformée. Soit un vecteur x de dimension N tel que x =( x0, x1, ..., xN-1).

La Transformée de Fourier Discrète (TFD) de x est égal à :

~ 1 A x TFD x ~ ù 1 ( ) n k . k ~ n n 0

avec

2i ù N ~ e pour k=0,..,N-1

Donc l'architecture du FFT aura une architecture semblable à celle de l'IFFT avec les changements suivants :

- Les multiplications par ^k

ù₁ deviennent des multiplications par ~ù k ;

- Les multiplications par j deviennent des multiplications par -j ;

62

- L'architecture du FFT à l'ordre 2 en tenant compte de la multiplication par le facteur N est

décrite dans la figure 3.19 dans le cas d'une FFT à l'ordre 64.

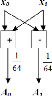
Figure 3.19. Architecture d'une FFT à l'ordre 2.

Les paramètres d'entrées sorties du bloc "FFT" sont présentés dans le tableau 3.12.

Nom du signal	E/S	Description	Taille	Groupement logique
f[1..64]	Entrées	Données reçue	64 bits	Interface entrée
d[1..64]	Sorties	données modulés en FFT	64 bits	Interface sortie

Tableau 3.12. Table des paramètres entrées/sorties du bloc FFT

Le résultat de synthèse au niveau RTL du bloc IFFT à l'ordre 8 sont fournit dans le tableau 3.13.

Famille de FPGA	Nombre de LUT	Nombre de registres	Nombre total de pin	Nombre de DSP	Nombre de bloc mémoire
Stratix.II.GX	71179	0	1024	0	0

Tableau 3.13. Résultat de synthèse du bloc IFFT

4.2.6. Bloc de l'égalisation

Nous avons décrit en VHDL les blocs d'égalisation suivants :

- Egalisation mono-utilisateur à critère ZF ;

- Egalisation multi-utilisateurs à critère MMSE ;

- Algorithme SIC à critère MMSE.

Nous ne développons dans cette partie que les spécifications fonctionnelles de l'égaliseur multiutilisateurs à critère MMSE. Pour une égalisation multi-utilisateurs le vecteur xà correspondant à la décision des symboles émis est égale à :

xà =.y (3.16)

où y est le vecteur reçu et Q est la matrice d'égalisation donnée par :

~ =(eTc9-(†c9-(e+ 1 r

5 )^-1 eTc9-( † (3.17)

avec e est une matrice diagonale en bloc, dont les matrices sur la diagonale de e sont des matrices de Hadamard, c9-( est une matrice formée par des matrices diagonales Hrt , avec H_rt=diag _(hrt,n; n=0,...,63), r est le SNR estimé. Pour une transmission à plein charge, on a :

e^T=e et e^-1 = e (3.18)

Donc :

e+ 1 xà =(ec9-( ^†c9-( r	5)^-1 e^Tc9-(^†.y (3.19)
= e~~(c9-( ^†c9-( + 1 r + 1 = e (c9-( ^†c9-( r		5)-1 e~~ e c9-(^†.y 5)^-1 c9-( ^†.y

La matrice (c9-( ^†c9-( + 1 5 )^-1 c9-( † est une matrice formée par des sous-matrices diagonales.

r

On pose:

+ 1 v=(c9-( ^†c9-( r

5 )^-1 c9-( ^†.y (3.20)

Le calcul de xà consiste donc à calculer le vecteur v, puis lui appliquer la transformée de Hadamard.

L'inverse d'une matrice formée par des sous-matrices diagonales est aussi une matrice formée par des sous-matrices diagonales. On pose:

63

+ 1 P= c9-( ^Hc9-(

r

5 (3.21)

On décrit par la suite la méthode qu'on a suivi pour inverser la matrice P. On rappelle que la matrice équivalente du canal de taille 128x128 s'écrit :

~ = 11 12

[ ? ,

H H

21 22

H H

(3.22)

et :

T

y= ? ? . (3.23)

y y y y y

1,0 1,1 1,63 2,0 2,63

On décompose ~ en 64 sous-matrices Ki ,0= i =63 de la forme : Alors :

Ki = 11, 12,

h h

i

[ h h

21, 22,

i

i Ò , 0= i =63. (3.24)

i

64

La matrice Ki représente la matrice qui regroupe les i^ème éléments diagonaux de chaque matrice Hrt 1=r,t=2.

yi= y 1, i , 0= i =63 (3.25)

y 2, i

avec yi est le vecteur qui rassemble le i^ème élément reçu par la première antenne et le i^ème élément reçu par la deuxième antenne.

On montre que, le calcul de vi (les sous vecteurs de v avec 0= i =63) se déroule de la manière suivante :

vi =(Ki † Ki+ 1 ã

I)^-1 Ki^† yi . (3.26)

L'architecture qu'on propose pour l'égaliseur multi-utilisateurs à critère MMSE est représentée dans la figure 3.20.

D'après cette figure, le bloc de l'égaliseur se compose de 64 sous-blocs de "calculateur de vi". L'architecture de ce sous-bloc sera définie en fonction de l'équation 3.26 sachant les équations 3.24 et 3.25. En développant vi, on obtient :

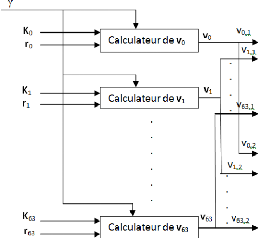
Figure 3.20. Architecture de l'égaliseur multi-utilisateurs à critère MMSE.

1 0

* * * *

L h h y

h h ã h h

?

11, 21, 1,

i i i

11, 12,

i i 11, 21,

i i

L H ? ?

?

* * * *

h h y

h h

1 h h

12, 22, 2,

i i i

21, 22,

i i 12, 22,

i i

0

? ?

1

vi=

. (3.27)

ã

qui s'écrit sous cette forme :

v_i = M _i .w i (3.28)

1

2 2 1

avec Mi=

h h h h h h

* *

? 1 1, 21, 11, 12, 21, 22,

i i i i i i

ã

? h h h h

? i i i i

* 2 2 1

* *

11, 12, 21 , 22, 12, 22 ,

h h

i i

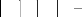
ã

?

65

T

et

*

h y

11, 1,

i i

h h y h y

* * *

11, 21, 1, 21, 2,

i i i i i

w ? ?

ⁱ h h y h y

* * T

*

12, 22, 2,

i i i 12, 1,

i i

h y

*

22, 2,

i i

D'où le calculateur de vi consiste à : calculer la matrice Mi, calculer l'inverse de la matrice Mi, calculer wi et calculer le produit wi par Mi.

66

L'architecture du calculateur de vi est représentée dans la figure 3.21.

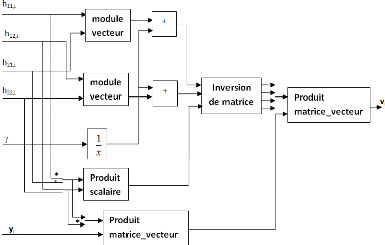
Figure 3.21. Architecture du calculateur de vi en fonction de _hrt,i , yi et ã

Les schémas RTL des sous-blocs du calculateur de vi sont représentés dans les figures (3.22), (3.23), (3.24) et (3.25).

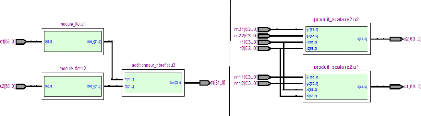
Figure 3.22. Schéma RTL du sous-bloc Figure 3.23 Schéma RTL du sous-bloc "Produit

"module vecteur" matrice_vecteur"

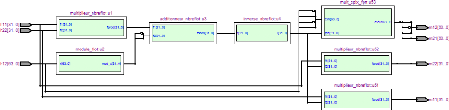
Figure 3.24. Schéma RTL du sous-bloc inversion de matrice

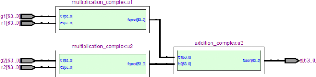
67

Figure 3.25. Schéma RTL du sous-bloc produit scalaire

Le résultat de synthèse au niveau RTL du bloc calculateur est fournit dans le tableau 3.14.

Famille de FPGA	Nombre de LUT	Nombre de registres	Nombre total de pin	Nombre de DSP	Nombre de bloc mémoire
Stratix.II.GX	93672	0	544	0	0

Tableau 3.14. Résultat de synthèse du bloc-bloc calculateur utilisé pour le bloc égaliseur

Les paramètres d'entrées sorties du bloc "Egaliseur multi-utilisateurs à critère MMSE" sont présentés dans le tableau 3.15.

Nom du signal	E/S	Description	Taille	Groupement logique
snr	Entrée	Rapport signal sur bruit estimé	32 bit
h11_[1..64]			64 bit
h12_[1..64]	Entrées	Les coefficients du canal estimés		Interface système
h21_[1..64]
h22_[1..64]
r1_[1..64]	Entrées	Vecteur reçu après démodulation	64 bits	Interface entrée
r2_[1..64]		OFDM
s1_[1..64]	Sorties	Vecteur obtenu après égalisation	64 bits	Interface sortie
s2_[1..64]

Tableau 3.15. Table des paramètres entrées/sorties du bloc Egaliseur multi-utilisateurs

4.2.7. Bloc de multiplexage spatial de 2 antennes

Le bloc de multiplexage spatial de 2 antennes est composé de 64 multiplexeurs où les entrées de chaque multiplexeur proviennent de la première antenne et de la deuxième antenne. Son diagramme en bloc est représenté dans la figure 3.26. L'organigramme de chaque multiplexeur est représenté dans la figure 3.27.

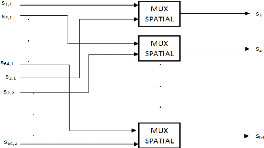
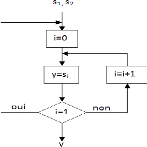
Figure 3.26. Diagramme du bloc de multiplexeur spatial

Figure 3.27. Organigramme d'un

68

multiplexeur

Le schéma RTL d'un multiplexeur est représenté dans la figure 3.28.

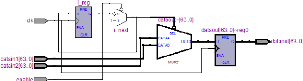
Figure 3.28. Schéma RTL d'un multiplexeur spatial

Les paramètres d'entrées sorties du multiplexeur spatial sont présentés dans le tableau 3.16. Ainsi, le résultat de synthèse au niveau RTL du bloc multiplexeur spatial est fournit dans le tableau 3.17.

4.2.8. Bloc "désétalement + quantification"

Ce bloc effectue désétalement des symboles reçus à son entrée qui consiste à effectuer la transformée de Hadamard inverse d'un vecteur de symbole, puis effectue la procédure de quantification en fonction de la technique de modulation numérique utilisée (256-QAM).

69

Nom du signal	E/S	Description	Taille	Groupement logique
clk	Entrée	Horloge de système	1 bit	Interface système
enable[1..2]	Entrée	Validation de fonctionnement	1 bit	Interface entrée
datain[1..128]	Entrées	Données Démultiplexées	64 bits
enout	sorties	Validation de sortie de données	1 bit	Interface sortie
dataout[1..64]	sorties	données réordonnées	64 bits

Tableau 3.16. Table des paramètres entrées/sorties du bloc multiplexeur spatial

Famille FPGA	de	Nombre de LUT	Nombre registres	de	Nombre de pin	total	Nombre DSP	de	Nombre mémoire	de	bloc
Stratix.II.GX		3	4098		12292		0		0

Tableau 3.17. Résultat de synthèse du bloc-bloc calculateur utilisé pour le bloc multiplexeur spatial

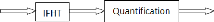
Figure 3.29. Schéma bloc de "désétalement + quantification"

4.2.8.1. Bloc IFHT

Ce bloc calcule la transformée de Hadamard inverse d'un vecteur. Puisqu'on est dans le cas d'une transmission à pleine charge, alors C est une matrice carrée et elle est égale à son inverse. Ainsi, l'architecture du calculateur de la transformée de Hadamard rapide inverse est semblable à l'architecture de la transformée de Hadamard rapide FHT définie dans 3.2.2 de ce chapitre.

4.2.8.2. Bloc de quantification

La procédure de quantification est effectuée en fonction de la modulation numérique 256-QAM. Cette procédure consiste à renvoyer en sortie le symbole qui est à une distance minimal du symbole reçu en entrée. La figure 3.30 présente l'organigramme du quantificateur 256-QAM.

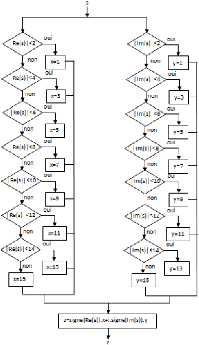
70

Figure 3.30. Organigramme du quantificateur 256-QAM

Le résultat de synthèse au niveau RTL du bloc quantificateur 256-QAM est fournit dans le tableau 3.19.

Famille de FPGA	Nombre de LUT	Nombre de registres	Nombre total de pin	Nombre de DSP	Nombre de bloc mémoire
Stratix.II.GX	12	0	128	0	0

Tableau 3.19. Résultat de synthèse du bloc-bloc calculateur utilisé pour le bloc quantificateur

4.2.9. Bloc démodulation

Ce bloc effectue la démodulation 256-QAM des symboles. Son principe consiste à renvoyé en sortie les bits qui correspondent au symbole reçu à son entrée en fonction de la constellation 256-QAM. L'organigramme de ce bloc est représenté dans la figure 3.31.

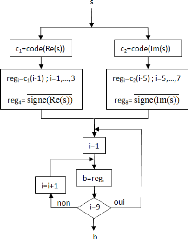
71

Figure 3.31. Organigramme du bloc de démodulation

Les paramètres d'entrées sorties du bloc démodulation sont présentés dans le tableau 3.20.

Nom du signal	E/S	Description	Taille	Groupement logique
s	Entrée	symbole	64 bits	Interface entrée
b	Sortie	bit d'information	1 bit	Interface sortie

Tableau 3.20. Table des paramètres entrées/sorties du bloc démodulation

Le résultat de synthèse au niveau RTL du bloc démodulation est fournit dans le tableau 3.21.

Famille de FPGA	Nombre de LUT	Nombre de registres	Nombre total de pin	Nombre de DSP	Nombre de bloc mémoire
Stratix.II.GX	53	4	67	0	0

Tableau 3.21. Résultat de synthèse du bloc-bloc calculateur utilisé pour le bloc démodulation

5. Optimisation et analyse de performances de la chaîne

Dans cette partie, on s'intéresse à la synthèse et à l'analyse temporelle des circuits d'émission et de réception de la chaîne MIMO-MC-CDMA implémentée. La phase d'optimisation de la conception commence dans les étapes de simulations fonctionnelles et d'analyse temporelle.

Dans le flot de conception adopté, l'optimisation d'un tel système revient à :

- la réduction de l'utilisation de ressources inférées ;

- l'amélioration des performances de « timing » ;

- la réduction du temps de compilation (utilisation de la compilation incrémentale pour alléger

l'espace d'exploration des solutions dans le placement et routage) ;

- l'estimation et la gestion optimale de la puissance dissipée en consommation statique et

dynamique ;

- la création des partitions pour préparer la synthèse incrémentale.

Pour l'optimisation de notre chaîne d'émission, on a recours aux étapes suivantes :

- Synthèse incrémentale qui consiste à donner la priorité pour la synthèse aux blocs de mémorisation (spécialement des registres et des mémoires de type SRAM) de façon qu'ils soient contigus dans leurs emplacements dans l'FPGA.

- Une phase d'exploration d'architecture qui nécessite la définition d'un vecteur de contrainte

dont ses composants reflètent les valeurs pondérées souhaitées sur la surface, la consommation et la fréquence.

- Les différentes phases qui précèdent la génération optimale des résultats de synthèse de toute la chaîne d'émission consistent en une paramétrisation et une configuration des contraintes du système à implémenter par :

- la fixation de l'architecture cible, dans notre cas c'est le circuit FPGA « Stratix II GX

EP2GXX90FF1508C3N » équipé de 1508 pins et de douze transmetteurs pour la sérialisation et la désérialisation des données;

- La configuration de l'exigence de « timing » : l'ajout d'un fichier des contraintes temporelles

force le synthétiseur à accomplir des optimisations dans la synthèse physique (après le placement et routage). Cette configuration doit se baser sur la connaissance des paramètres technologiques des « LUTs » et « ALMs », dans notre cas ce sont les temps "tsu" , "th", "tco", "tpd" et la fréquence nominale des étages séquentielles dans la chaine d'émission, ici la fréquence est fixée à 500M Hz.

- Lire les différents temps de latence de la chaîne et qui correspondent aux différents chemins

critiques du système. Cette étape consiste à corriger les violations des paramètres

72

73

74

technologiques temporelles et de déceler la fréquence maximale de la chaîne par le temps de latence entre l'entrée et la sortie (ou « tpd »).

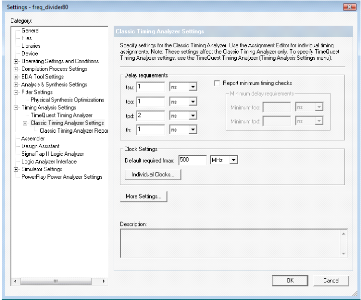
Figure 3.32. Configuration des paramètres de Timing

Dans le cas où il y a une insatisfaction des résultats attendus spécialement en terme d'aspect fréquentiel, on sera obligé de refaire l'étape de la configuration des contraintes de la synthèse et d'analyser de nouveau les résultats de post-placement et routage.

Les figures 3.32 et 3.33 résument le résultat de synthèse et l'analyse de Timing pour le cas de deux utilisateurs qui émettent leurs données pour un système MIMO-MC-CDMA.

On conclut que la fréquence fonctionnelle (ou de cadencement des données et ses traitements) maximale est de 174,672 MHz obtenue après avoir suivi les différentes optimisations citées auparavant.

Les figures 3.34 et 3.35 résument le résultat de synthèse et l'analyse de Timing pour le circuit de réception du système MIMO-MC-CDMA récupérant les données de deux utilisateurs.

On conclut que la fréquence fonctionnelle (ou de cadencement des données et ses traitements)
maximale est de 54,29 MHz obtenue après avoir suivi les différentes optimisations citées auparavant.

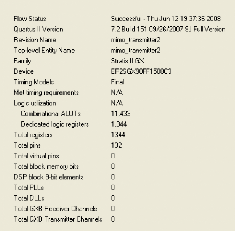
Figure 3.32. Résultat de synthèse de la chaîne d'émission du système MIMO-MC-CDMA

Figure 3.33. Analyse de Timing de la chaîne d'émission du système MIMO-MC-CDMA

Figure 3.34. Résultat de synthèse de la chaîne de réception du système MIMO-MC-CDMA

75

Figure 3.35. Analyse de Timing de la chaîne de réception du système MIMO-MC-CDMA

6. Conclusion

A travers ce chapitre, on a d'abord présenté la plateforme FPGA cible Stratix.II.GX et l'architecture de ses ressources internes. Puis, on a expliqué le flot de conception adopté pour la réalisation matérielle des différents blocs de la chaîne MIMO-MC-CDMA. Ensuit, on a détaillé les architectures des différentes composantes de la chaîne. Ces architectures, malgré leurs efficacités de traitement rapides des signaux, présentent des inconvénients en termes de consommation en ressources internes du FPGA. Pour cela, on a eu besoin de chercher des solutions permettant l'optimisation des architectures implémentées.

76