Etude et analyse paramétrique des echangeurs de chaleur dans une machine tritherme - cas du condenseur-

III.2.D. Condensation en film à l'intérieur des tubes horizontaux :

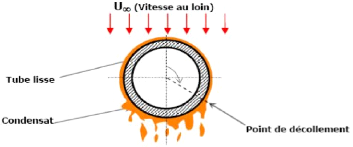
Du fait du ruissellement du condensât sur la paroi interne d'un tube horizontal, il peut y avoir une accumulation du condensât dans la partie basse du tube comme le montre la figure suivante :

Figure I.07 : Condensation a l'intérieur d'un tube horizontal

De plus le débit vapeur introduit une contrainte tangentielle à l'interface liquide-vapeur du condensât accumulé. Il en résulte une interaction compliquée donnant naissance à différents régimes d'écoulement diphasique, notamment :

ü Ecoulement annulaire ;

ü Ecoulement à bouchon ;

ü Ecoulement avec ondes ;

ü Ecoulement avec bulles de vapeur (figure I.08)

Figure I.08 : Les différents écoulements de condensation à l'intérieur d'un tube horizontal

On peut calculer le coefficient de transfert de chaleur lors de la condensation dans les tubes horizontaux par la corrélation de CHATO [05]:

1

é

ê

ëê

0.555

h

4

L ù

( ) ( )

3 v

g r r r l ú

l l v f

- (I.31)

m f sat p i

T T d

- û ú

Régimes d'écoulement diphasique :

Plusieurs auteurs ont cherché à établir les régimes d'écoulement diphasique lors de la condensation de vapeur. Soliman et Azer [06] ont observé les régimes suivants lors de la condensation de R12 et R134a :

· Ecoulement dispersé : dans lequel il n'ya pas de film de condensat visible ; tout le liquide formé est entrainé par la vapeur sous forme de petites gouttes ;

· Ecoulement annulaire : dans lequel un film liquide annulaire se forme, la vapeur s'écoule dans la partie centrale ;

· Ecoulement semi annulaire : qui ressemble à l'écoulement annulaire, mais l'épaisseur du film liquide varie sur la circonférence du tube et est maximale en bas du tube.

· Ecoulement avec ondes : dans lequel le liquide coule sur la partie base du tube tandis que la vapeur se trouve bien séparé du liquide dans la partie supérieur. L'interface liquide- vapeur pour le régime d'écoulement est ondulée ;

· Ecoulement formant des bouchons liquides : dans ce régime l'onde sur la surface du liquide s'amplifie et touche la partie supérieur du tube formant ainsi un bouchon pour le passage de la vapeur ;

· Ecoulement a bouchons : dans lequel la section du tube est remplie de liquide, mais il n'ya de longues bulles de vapeur qui appauvrissent de temps à autre et qui semblent avoir la même vitesse que le liquide ;

· Ecoulement semi annulaire avec ondes : sur la surface du film liquide

· Ecoulement dispersé et annulaire : dans ce régime le film liquide se forme d'une façon intermittente et disparait ensuite à cause de l'arrachement du liquide sous forme de gouttes par l'écoulement de vapeur ;

· Ecoulement annulaire avec ondes sur la surface du film liquide : dans ce régime l'épaisseur du film liquide est plus importante dans la partie basse du tube tandis que la partie supérieur s'emble parfois sèche.

I. ETAT DE L'ART SUR LES PHENOMENES DE CONDENSATION :

Dans cette étude on se base sur les travaux théoriques et expérimentaux relatifs aux calculs des coefficients de transfert de chaleur lors de la condensation (coté fluide frigorigène), et des coefficients de transfert de chaleur par convection (coté fluide de refroidissement).

Puis on va voir le principe de fonctionnement des condenseurs et leurs principales technologies.

I.1 Coté fluide frigorigène :

I.1.1. Condensation a l'extérieur des tubes verticaux :

§ NUSSELT [3] a établi en 1916, les relations théoriques pour le calcul des coefficients d'échanges de chaleur, dans le cas de la condensation des vapeurs pures en couche mince, sur des tubes ou sur des plaques. Et il a montré que la conductance par unité de surface, décroît lorsque la distance compté à partir du sommet de la plaque ou tube, et par conséquent l'épaisseur du film augmente. Il à aussi remarqué qu'une augmentation de la différence de température ( T _sat - T _p ) entraîne une diminution de la conductance par unité

de surface.

Nusselt est le premier auteur qui a donné les formules qui permet le calcul du coefficient d'échange moyen.

2

r l ³

g L

l v l (II.01)

ù ú û ú

4T - T L

m ( )

l sat p

é

ê

ëê

h

0,943

1

4

§ La théorie de Nusselt à été modifier par ROHSENOW [07], afin de tenir compte de la convection d'enthalpie. Son analyse conduit à l'expression suivante pour le coefficient d'échange moyen lors de condensation d'une vapeur stagnante sur une plaque isotherme de longueur L :

1

4

l r r r

³ g L

( )

- cents ù

l l l

ú(II.02)

ûú

é

ê

ëê

0.943

h

( )

T T L

- p

m l sat

Dans laquelle _vL^cents [j/kg] : Représente la chaleur latente équivalente donnée par :

é -

( )

T T ù

sat p

L L Cp

cents = +

êë 1 0 . 6 8 (II.03)

v v ^l L úû

v

NB : Les relations de Nusselt et Rohsenow sont aussi valable pour la condensation à l'intérieur des tubes verticaux.

§ KUTATELADZE et GOGONIN [08] ont présenté les mesures des coefficients d'échange thermique en présence des ondes, et ils proposent l'expression suivante ont prenant compte des ondes lors de la condensation sur une surface verticale de langueur L :

	hondes	Re f 0 .04	(II.04)
Pour :5< Ref <100	hNusselt

q L

cents

Re = (II.05)

^f L

m

Avec:

l v

q cents : Densité de flux thermique [w/m²]

§ Les équations gouvernant l'écoulement du film de condensât sur une plaque vertical ont été résolues par MIYARA [09]. Les résultats de ses calculs montrent que la valeur moyenne de l'épaisseur du film liquide est légèrement plus faible que la solution donnée par la théorie de Nusselt. Les nombres de Nusselt calculés sont comparés aux valeurs obtenues l'aide des expressions suivantes proposées par différents auteurs sur la Figure II.01

Figure II.01 : L'influence des ondes sur la surface du film

- Kutateladze: Nu * = 0.557Re f *0 .22 (II.06)

- Chun-Seban: Nu = f

* 0.606Re - 0.22 (II.07)

-Uehara-Kinoshita: * 0 .707 Re - 0 .25

Nu = f (II.08)

1

h v 2 3

æ ö

*

Avec : Nu l

= g

^x ç ÷ (II.09)

l l è ø

et

q cents

Re

v

^f L

m l

§ SHEKRILADZE et GOMELAURI [10] admettent que l'aspiration de la couche limite vapeur par la condensation rend l'écoulement de vapeur laminaire et font l'hypothèse que la contrainte tangentielle à l'interface liquide-vapeur est égale a la perte de quantité de mouvement de la vapeur condensée cette hypothèse n'est valable que pour un taux de condensation infini, mais possède l'avantage de rendre inutile la résolution des équations de la phase vapeur pour assurer légalité des contrainte tangentielles à l'interface et simplifie considérablement l'analyse lorsqu'on néglige le gradient de pression. Ainsi sans tenir en compte des termes d'inertie et de convection d'enthalpie et en effectuent une analyser du type Nusselt, Shekriladze et Gomelauri proposent la relation suivante :

Plaque plane verticale :

h_m

16 gL ù ÷ ú

2 2 1

ç + ^é +

1 ç ê_ë úû ÷ ú

U H

2

l r

æ ö

è ø ú

l l

1

æ 2 ö ù

2 2

ç (II

U .10)

÷ 1 ú

L ø 1

æ 2 ö

ç 16 ù ÷

1 1

+ ^é + gL ç êë U H

2 ú_û ÷

è ø û

Avec :

H

Ja Prl

(II.11)

Ja = CpDT L_v

U : La vitesse du fluide loin de la paroi [m/s]

§ FUJII et UEHARA [11] ont utilisée la méthode de Polhausen pour résoudre les équations intégrales pour étudier la condensation en film laminaire sur une plaque verticale. Ils négligent les termes d'inertie et de convection d'enthalpie dans le film liquide et adoptent une équation de second degré pour définir le profile de vitesse dans la phase vapeur. Les équations sont résolues par la méthode numérique de Range Kutta et Gill. Les résultats de leurs calculs sont représentés par l'équation suivante :

Nu

1

3 4

é 4

2

= = æ + ö

1 ~ Gr

æ ö ù

h L

^m ê Re 0 .790

0 . 65 6 1 . 20 ú (II.12)

^m l ç_è ç_{è ø}÷

ê RH _ø÷ + H û ú

^l ë

Avec :

L g

3

, 2

Gr = (II.13)

v_l

H

Ja

Pr_l

~

U L

=

Re

,

v_l

æ r m ö

l l

, R r m

= ç ÷

è v v ø

1

2

Pour la condensation laminaire sur un cylindre les résultats de Fujii et Coauteurs sont représentés par l'expression :

1

0 .27 6 ~

ù ⁴ 1

Nu_m x 2

1 ú û

₄ Re (II.14)

= é + x FrH

êë

Avec :

~

U ²

Fr

=

(II.15)

, Re_D

gD

l

1

c 0 . 90 1 ,

= æ + RH ö

ç_{è ø}÷

r

l U D

m

I.1.2. Condensation à l'extérieur des tubes horizontaux :

Nu

Nu

^m l

Nu

^m l

§ Le coefficient moyen d'échange thermique lors de la condensation d'une vapeur stagnante sur un
cylindre lisse de diamètre D suivant la théorie de NUSSEL T-R OHSENO W est donné par :

é

ê

ëê

m l sat

( )

T T D

- p

l g r L cents

3 2

ù ú û ú

1

4

h 0.725

§ DHIR et LIENHARD [12] proposent une modification de la théorie de Nusselt-Rohsenow pour étudier la condensation sur un corps axisymétrique. Dans ce cas, l'écoulement de condensât est soumis à une force de pesanteur variable g(x) fonction de x

1

h x g L x 3 4

é

x eq l l v v

r r r

( )

- cents ù

= = ê ú (II.17)

^x T T

l _ê 4 m l ( )

-

l ë l l sat l û ú

Dhir et Lienhard ont ainsi proposé des formules pour plusieurs cas : - Condensation sur un cylindre horizontale :

1

3 4

h D gD

é ù

= = A

^m 0 . 729 úû (II.18)

*

ê_ë

l 0

- Condensation sur le semi-Cylindre supérieure :

1

3 4

h D gD

é ù

= = A

^m 0 . 8 66 úû (II.19)

*

ê_ë

l 0

- Condensation sur le semi-Cylindre inférieure :

Nu

1

3 4

h D gD

é ù

= = A

^m 0 . 592 úû (II.20)

*

^m l

ê_ë

l 0

§ JAKOB [13] a étendu l'analyse de Nusselt à un faisceau aligné en admettant que le condensât tombe sur le tube placé plus bas comme une nappe continue en écoulement laminaire. En admettant que la différence de température (T _sat - T _p )reste la même pour l'ensemble des tubes

en faisceaux il montre que le coefficient d'échange moyen pour un faisceau de n tubes (h _n )comparé à celui pour le premier tube est :

h n = n ⁴

( )

h m 1

- 1

(II.21)

Et le coefficient d'échange de tube n :

( ) ( ) ( ) úû

³ ù

h m n h m 1 n n 1

= é - - 4

3

⁴ (II.22)

êë

§ KERN [14] propose pour globaliser le coefficient d'échange de Nusselt à l'échelle du faisceau circulaire de tubes, des modèles empiriques de coefficient d'échange moyen définis à l'échelle du faisceau. Ils sont exprimés en fonction du coefficient d'échange de Nusselt pour un seul tube et des paramètres géométriques que sont le pas entre les tubes, le rayon de faisceau, du type d'arrangement des tubes (carré, triangle, carré pivoté,...), et le type d'écoulement du film d'un tube sur l'autre (continu, discontinu). Pour les condenseurs constitués de faisceaux circulaires à pas carré pivoté. Les deux corrélations retenues sont les suivantes :

ü Ecoulement continu du film d'un tube sur l'autre :

hfaisceau₌ - - - + -

( ) [ ( ) ( )

11

0 .972 ¹ 1 0 . 25 1 0 .223 3

4 8 2 ]

R P R P R P(II.23)

h

ü Ecoulement discontinu du film d'un tube sur l'autre :

hfaisceau = - - - + -

( ) [ ( ) ( )

17

0 .97 5 ¹ 1 0 .242 0 . 223 3

6 12 2 ]

R P R P R P(II.24)

h

Avec : P: Distance l'entre axe des tubes [m] R : Rayon du faisceau de tubes [m]

Figure II.02 : Configuration géométrique du faisceau de tubes

§ KERN [15] observe que le condensât coule en bas du tube en régime de gouttes ou de colonnes ce qui perturbe la surface du film et diminue l'effet l'inondation, il propose donc:

h - 1

n = n ⁶ (II.25)

( )

h m 1

et le coefficient d'échange du tube n :

( ) ( ) ( ) úû

⁵ ù

h m n h m 1 n n 1

= é - - 6

5

⁶ (II.26)

êë

§ L'analyse de CHEN [16] utilise la méthode de perturbation donne l'expression suivante pour une nappe verticale de n tubes placés l'un en dessous de l'autre dans le domaine du nombre de Prandtl Pr_l > 1 ou Pr_l < 0.05 et des paramètres (n-1)

Ja

Ja

£ 2( = £

H 20)

Pr_l

1

( ) [

n n Ja

4 = + -

1 0 . 2( 1)

h m 00

1 0 . 68 0 . 02

] é + +

Ja H ù

êë 1 0 . 95 0 . 1 5

+ -

H JaH úû

( ) tube n

.

h m Chen

1

4

(II.27)

g ( )

r r

l v

-

mlCondenseur x

1

4

(II.28)

r l ³ L ù

l l v

( ) ^ú

T T

sat p

- û ú

é

ê

ëê

h B

=

L'indice 00 correspond à la solution de Nusselt pour Ja = H =0 Ja : Nombre adimensionnel de Jakob (CpDT L_v).

§ CHEN [17] a modifié le modèle de Nusselt dans le but de calculer des coefficients d'échange pour des configurations à faible vitesse de vapeur et de généraliser cette étude à M colonnes de N tubes, contrairement à Nusselt qui ne considère qu'une seule colonne de N tubes

Le modèle adapté aux faibles vitesses du modèle de Nusselt, garde globalement les mêmes hypothèses. La nouvelle hypothèse impose donc une faible vitesse de vapeur

Cette modification concerne l'intégration d'un facteur de correction (B) du coefficient
d'échange qui prend en compte l'accumulation et l'écoulement des condensats. Chen a introduit
également une nouvelle variable (xcondenseur ) pour tenir compte de la complexité de l'écoulement des

condensats d'un tube sur l'autre et de l'interférence entre deux rangées verticales proches. Cette variable est fonction du nombre de tubes verticaux coexistant dans le faisceau. Les condenseurs intègrent un faisceau de tubes à pas carré pivoté. Le modèle modifié s'écrit alors :

é ( ) ( )ú_û

T T

- ù

sat ^p N

B = +

0 .725 1 0 .2 1

- (II.29)

tub .Vert

êë L v

xCondenseur = N tub . Vert . D ext (II.30)

2 .

p R

N tubVert

.

2

P

(II.3 1)

§ BERMAN et TUMANOV [18] ont fait des travaux basés sur l'analyse expérimentale et la réalisation de modèles empiriques de coefficient d'échange en condensation prenant en compte l'effet de la vitesse de vapeur. Dans le cas d'une convection forcée, l'écoulement du condensât est très perturbé par les contraintes de cisaillement à l'interface vapeur - condensât.

D'après ces auteurs les phénomènes à prendre en compte dans cette configuration pour traduire le comportement du film de condensât (Figure II.03) sont :

(i) Les contraintes de cisaillement générées par la vapeur à la surface libre du film,

(ii) Le décollement de la couche limite de la vapeur à l'arrière du tube a un angle compris entre 80 et 180 degrés par rapport au point de stagnation de la vapeur.

Les expériences de Berman & Tumanov ont été réalisées sur un tube horizontal actif placé dans un faisceau de tubes non refroidis soumis à un flux de vapeur d'eau descendant. Le dépouillement des résultats et l'analyse à partir de nombre adimensionnels ont conduit à la formulation de modèles empiriques spécialisés par rapport aux domaines de variation des

paramètres opératoires.

Figure II.03 : Condensation contrôlée par cisaillement

§ SPAROW et GREGG [19] considèrent que l'angle du phénomène de la conduction peut être abordée en utilisent les équations de la couche limite de "Mécanique des fluides" et adoptent la

méthode de la transformation affine pour réduire les équations différentielles au dérivées partielles à des équations différentielles ordinaires.

En faisant l'hypothèse selon laquelle la contrainte tangentielle à l'interface liquide-vapeur est nulle. Mais sans négliger les termes d'inertie et de convection d'enthalpie, ils résolvent (par une méthode numérique) les équations gouvernant l'écoulement du film de condensât sur une plaque verticale placée dans une vapeur stagnante. Pour de faibles nombres de Jackob (Ja); ils obtiennent la relation suivante pour la condensation dune vapeur stagnante sur un cylindre lisse :

Nu

l l

0.733

^m m l

é

ê

ëê

g L D

r 2 3

( )

T T

sat p

-

l v (II.32)

ù ú û ú

1

4

Le coefficient 0.733 est peu différent de 0.725 données par l'analyse de Nusselt, mais les résultats de l'analyse numérique des équations de la couche limite afin de traiter le problème de la condensation et montrent une influence non négligeable du nombre de Prandtl du condensât sur le coefficient d'échange.

§ SHEKRILADZE et GOMELAURI [10] admettent que l'aspiration de la couche limite vapeur par la condensation rend l'écoulement de vapeur laminaire et font l'hypothèse que la contrainte tangentielle à l'interface liquide-vapeur est égale a la perte de quantité de mouvement de la vapeur condensée cette hypothèse n'est valable que pour un taux de condensation infini, mais possède l'avantage de rendre inutile la résolution des équations de la phase vapeur pour assurer légalité des contrainte tangentielles à l'interface et simplifie considérablement l'analyse lorsqu'on néglige le gradient de pression. Ainsi sans tenir en compte des termes d'inertie et de convection d'enthalpie et en effectuent une analyser du type Nusselt, Shekriladze et Gomelauri proposent les relations suivantes :

- Plaque plane Horizontale :

1

2

hm	é ê ëê	H
		H+

(II.33)
(II.34)

r l

L U ù

l v l

ú

1 ú

( )

T T L

sat p

- û

Avec : H

Ja

Pr_l

Nu

x

1

3

1 . 50 8 ú

~ - 1 ê 1

Re 0 .43 6

2 =

x

ù

ú

G ú

T ú

ú

L û

æ D

l ö

l

ç 1 + ÷

è m l v ø

3

2

+

(II.35)

§ ROSE [20] propose pour la condensation sur une plaque plane horizontale l'équation suivante :

1

2

æ r m ö

, R r m

l l

= ç ÷ (II.36)

è v v ø

G

=

JaR T

l D æ r m ö

Pr ÷

l l l

= ç

l L

m l v è r m

v v ø

1

2

~

, Re x

x

r U

m l

§ Les équations couplées de la phase liquide et de la phase vapeur pour la condensation laminaire sur un cylindre sont résolues par ASBIK et AL [21] en utilisant une méthode de différence finie implicite. Ces résultats montrant que l'hypothèse de Shekiladze et Gomelauri est acceptable pour un écoulement laminaire lorsque la différence de température est importante le gradient de pression dans leurs calculs pour un cylindre faisant partie d'une nappe est calculé par la méthode de singularité en admettant un écoulement potentiel.

§ Les équations couplées de la phase liquide et de la phase vapeur sont résolues par HOMNESCU et PANDA Y [22] en tenant compte de la turbulence dans les deux phases. L'équation suivante est proposée par Homenscu et Panday pour représenter les résultats numériques concernant la condensation turbulente sur un cylindre :

é ù

1

ê 1

~ - 1 ( ) ú

1 ö ³ 1 1 0 . 8

+ A 2

Nu_t Re 0 . 29 1 0 . 7 5 1

² ê _ø÷ + +

4

= æ + A ú

ç_è 0 . 25 (II.37)

1

ê G 4

ö ú

æ +

1

2

ê ç_è 0 . 25 1 .7 5

A A ø÷ ú

ë û

Avec :

Nu t

A=

hD

= Nombre de Nus selt pour la condensation Turbulente

:

l l

Pr l l v

m L Dg

= (II.38)

FrJa l

l

U T T

² ( sat p )

-

( ) 2

1

Pr R T T l r l ö l sat p l

- æ l l

G = = ç ÷

Ja L v v

m è r l

v v ø

(II.39)

§ MC NAUGHT [23] à développé la corrélation de Nusselt pour un condensat contrôlé par les forces de cisaillement dans le faisceau de tubes :

h

= tt

h_l

1 . 26 - 0 .78

X(II.40)

h_l : Coefficient de transfert de chaleur de la phase liquide [w/m²K]. Xtt : Paramètre de Lockhart-Maritineii a travers le long du faisceau.

Xtt

0 .9 0 .5 0. 1

æ -

1 x ö æ r Avec x @ 0 . 9

ö æ m ö

v l

ç è _ø÷ ç ÷ ç ÷ (II.41)

x èrlø èmvø

§ BEA TTY et KA TZ [24] ont développée la corrélation de Nusselt pour la condensation a l'extérieur des tubes ailettés horizontaux en introduisant la notion du Diamètre équivalent, par la corrélation suivantes :

1

3 4

l r r r

( )

l l l v v

- gL (II.42)

( )

m _l

T T

sat p

-

D e

ù

ú

û ú

é ê ë ê

0 . 6 89

h

- 0 .25 1 . 3

0 - -

h 0.25 0.25

ail ail net r

S E S D

+

h p tot

(II.43)

1 Pr

* l

A Fr Ga

= =

3

⁰ P

1

w 2 æ g 3

ö

^{0 ç} ÷

g v 2

r v

Pr_l
Pr v

(II.46)

Avec :

D_e : Diamètre équivalant [m]

hail : Rendement des ailettes.

h_p : Rendement de la paroi.

Sail : Surface des ailettes par unité de longueur [m²/m] Snet : Surface nette par unité de longueur [m²/m]

Sto t : Surface totale par unité de longueur [m²/m]

D_r : Diamètre racine des ailettes [m]

E : Paramètre dans l'équation de Beatty et Katz [m]

E = p r ₂ - r 2r

( ) ( ₂ )

2 ² (II.44)

1

r₁ : Rayon des racines des ailettes r 1 = D_r 2 [m]

r₂ : Rayon des ailettes [m]

I.1.3. Condensation à l'intérieur des tubes verticaux :

§ BORISHANSKI et AL [25] ont proposé la formule suivante pour le coefficient d'échange moyen ( h_m ) lors de la condensation complète de la vapeur d'eau à l'intérieur d'un tube verticale

:

h w ²

m = = +

⁰ Nu 0 . 1 7 A 0 . 2 A

*1 .7 *2 .8 (II.45)

0

l _l g

Avec :

centsL

w₀

4q

L D

vrl

(II.47)

qcents : La densité de flux thermique moyen [w/m²].

w₀ : Vitesse du condensât basée sur la longueur L [m/s]

§ IVASHCHENKO et AL [26] proposent d'utiliser un coefficient correcteur par rapport au nombre de Nusselt pour la condensation de vapeur stagnante donnée par :

h D

Nu l

0 0 . 925 Re Ga

0 0 .28

-

l

(II.48)

= l =

1

3

Avec :

3

centsL

_q gD

Re = , 2

Ga =

^l L

v l

m v_l

(II.49)

§ CA VALLINI et ZECCHIM [27] analysent les résultats expérimentaux de différents chercheurs et proposent la relation empirique suivante pour des vapeurs de fluides frigorifique :

0. 8

1

é 2 ù

0 .05 Pr 0. 3 3 Re Re

m æ r ö

ê v l

Nu m l v (II.50)

l

= r

ç +

÷ ú

ê m ú

l è vø

ë û_m

m: Indice représentant la moyenne entre l'entrée et la sortie du tube

§ SHEKRILADZE et MESTVIRISHVITI [28] utilisent l'hypothèse selon laquelle la contrainte tangentielle à l'interface liquide-vapeur est égale à la perte de quantité de mouvement de la vapeur condensée pour un écoulement turbulent du film liquide et pour une vitesse importante de la vapeur ils obtiennent la relation :

h x x

= 0 .2 [

ll l

PrRe^*

(II.51)

Pr ln 1 5 Pr

l ( l ) ]

+ +

Avec:

x

v_l

x

q cents ( )

U v

L v

r _l

Re *

ö ÷÷ ø

(II.52)

æ _çç è

§ SHAH [29] adopte la correction de Dittus-Boelter et considère que l'échange thermique lors de a condensation s'effectue à travers l'écoulement monophasique du film liquide l'analyse des résultats expérimentaux de différents chercheurs lui permet de déterminer correcteurs en fonction du titre vapeur et de la pression réduite, ainsi il propose l'équation empirique suivante :

h l é *0 .8 l m l l = êë 0 . 023 Re Pr D

ù úû

æ ç ( ) ( ) ( ) 0. 04 0 .76 ç * * 0. 8 3 . 8 1 x x - m m 1 - + x * ç m 0. 3 8 ç æ P ö ç ç ÷ è è P cr ø

ö ù ÷ ú ú ÷ ÷ ú (II.53) ÷ ú ø ú ÷ û

Avec :

x_m Titre moyen entre l'entrée et la sortie [%]

* :

Pcr : Pression critique du fluide [bar] MD

& S p D ²

m l

l₄

S

Re ,

* = = (II.54)

M& : Débit masse totale à l'entrée du tube est du liquide [kg/s].

§ CHEN, TIEN et GERNER [30] tiennent compte de la contrainte tangentielle à l'interface, de l'influence des ondes ainsi que du transport turbulent et adoptent les corrélations proposées par d'autres chercheurs afin de développer une équation générale :

- Pour une condensation laminaire avec ondes sur la surface du condensât, ils admettent la relation de Chen et Seban :

1

3

( ) ( ) 0 .22

h v ²

æ ö

* = l x

x l

Nu l ç ÷ = 0 . 823 Re -

xLam g

l è ø

(II.55)

Avec :

t

* I

t =

I

r_l

( ) 3

2

gv l

3

h v ²

æ ö 0 .65 * 1

x l 2

ç ÷ = 0 . 03 6 Pr l I

t

{ ( ) }

Nu * =

x Lam t

1

l g

l è ø

(II.57)

(II.58)

- Pour une condensation turbulente (Re_l )_x > 3500 et en l'absence de contrainte inter faciale, ils utilisent les résultats de BLANGTTI et SCHLUMDER [31] :

1

h v 2 3

æ ö

( ) ( ) 0 .4 065

Nu =

x ^l 0 . 00402 Re l l Pr l

= l ÷ (II.56)

x tur g

ç

l è ø

- Pour la condensation laminaire avec une contrainte tangentielle importante, ils adoptent la relation de SOLIMAN et AL [06]:

§ Ainsi, en utilisent la technique de Churchill et Usagi, CHEN, TIEN et GERNER [30] développent d'abord une expression pour la condensation de vapeur stagnante dominées par la gravité en posent :

( ) [ ( ) ( ) ] 1

1

n 1 1

* * * n n

Nu x g = Nu Lam + Nu (II.59)

turb

Une corrélation générale est ensuite établie en combinaison l'expression précédente avec une contrainte tangentielle importante ainsi ils écrivent :

[ ( ) ( ) ] 2

1

n 2 2

x = Nu _g + Nu t

* * * n n

0 Lam

Nu

(II.60)

§ En se basent sur les résultats expérimentaux de BLANGETTI et SCHUMDER [31], ils obtiennent l'équation suivante avec n1=6 et n2=2

(II.61)

l x 14 I

l l

1 é 2 3

h v

æ ö = æ

* x

Nu =

x

l ê

ç ÷ _çç

ê

è g ø ë è

1 1

1

2

( ) ( )

Re Pr

2 3 .9 3 ù

ö 3

1 .32 l x l l

Pr

- *

0 . 3 1 Re + ÷÷ + t ú

2 . 3 7 10 77 1 . 6 ú

ø û

En ce qui concerne l'estimation de *

t _I CHEN et AL [30] proposent d'utiliser l'équation suivante basée sur les résultats de Dukler concernant la perte de charge en régime annulaire concernant (dans le sens de gravité) d'un écoulement diphasique isotherme :

t I = B Re l T - Re l x Re l x

* * [ ( ) ( ) ] ( ) ^0.4

1 4 (II.62)

Avec :

r r

0 .553 0. 78

l v

3

B

* 0 .252 m

D

2

g

2

1.177 0.156

l v

m

(II.63)

(Re_l ) T : Le nombre de Reynolds du film liquide de condensât pour une condensation totale.

§ La première modification de la théorie de Nusselt pour la condensation à l'intérieur des tubes verticaux est introduite par CARPENTER et COLBURN [32] qui considèrent que la résistance thermique est due seulement à une sous couche laminaire dans le film de condensât et proposent l'équation d'échange suivante pour déterminé le coefficient d'échange local :

1

2

l r

h x c

l l

= Pr l

m_l

1

2

( ) 2

1

t I x

(II.64)

Avec : c = 0.043