CHAPITRE 2 ETUDE
THEORIQUE ET DIMENSIONNEMENT D'UN GENERATEUR PIEZOELECTRIQUE
2.3 Principe de fonctionnement
2.3.1 Théorie de la
piézoélectricité
Le mot
« piézoélectricité » vient de la
contraction des mots grecs piezen et eleckron qui veulent
dire respectivement pression et électron. La
piézoélectricité est la capacité de certains
matériaux de pouvoir transformer une énergie mécanique en
une énergie électrique et vice-versa. Elle a été
observée qualitativement pour la première fois par René
Just Haüy en 1817, mais on en attribue la découverte à
Pierre et Jacques Curie qui ont été les premiers à en
faire l'étude en 1880. On distingue deux effets de la
piézoélectricité : l'effet direct et l'effet inverse
(Ahmed-Seddik, 2012). L'effet piézoélectrique direct correspond
à l'apparition de charges électriques sous une contrainte
mécanique et l'effet piézoélectrique inverse qui
correspond à une déformation du matériau lorsqu'on
applique un champ électrique au matériau (Figure 9). Cet effet a
deux propriétés : lorsque la contrainte est nulle, les charges
s'annulent, et lorsque le sens des contraintes est inversé, le signe des
charges est inversé (Defosseux, 2011).
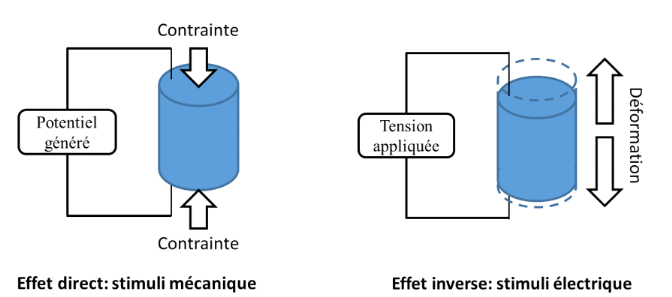
Figure 9 : Effets
piézoélectriques direct à gauche et inverse à
droite (JUSTEAU, 2020)
On retrouve cet effet piézoélectrique dans
certains cristaux (Un cristal est un solide dont les constituants
molécules sont assemblés de manière
régulière, c'est-à-dire qu'un même motif est
répété à l'identique un grand nombre de fois selon
un réseau régulier. La plus petite partie du réseau
permettant de récompenser l'empilement est appelée une maille).
Il résulte du décalage des barycentres de charge positives et
négatives de la maille cristalline suite à la déformation
mécanique de cette maille.
Ainsi la piézoélectricité est fortement
liée à la symétrie de la maille comme le montre la Figure
10, un matériau centrosymétrique (est celui constitué de
mailles dont les barycentres de charges positives et négatives demeurent
confondus peu importe la sollicitation mécanique à laquelle la
maille est soumise) ne peut donner lieu à un cristal
piézoélectrique.
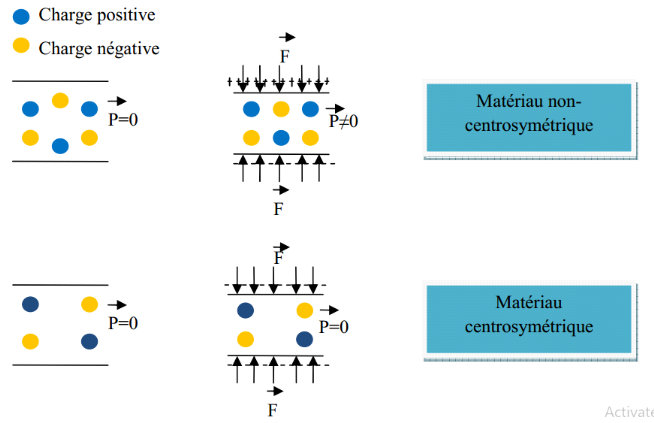
Figure 10 : Effet
piézoélectrique direct à l'échelle microscopique
(Ahmed-Seddik, 2012)
2.3.2 Mise en équation de la
piézoélectricité
Par sa définition même, la
piézoélectrique met en relation des propriétés
électriques et mécaniques.
L'effet piézoélectrique direct est l'apparition
de charges lorsque le matériau est soumis
à une contrainte.
Ces charges sont proportionnelles à la contrainte, et s'inversent
lorsqu'on
inverse le sens de la contrainte. L'effet
piézoélectrique direct se traduit par :
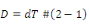
L'effet piézoélectrique inverse se traduit par
une déformation du matériau sous l'application d'un champ
électrique :
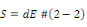
Avec :
|
Grandeur Physique
|
Symbole
|
Unité
|
|
Contrainte
|
T
|
N.m-2
|
|
Déformation
|
S
|
-
|
|
Champ électrique
|
E
|
V.m-1
|
|
Induction électrique (Polarisation)
|
D
|
C.m-2
|
|
Souplesse
|
s
|
m2.N-1
|
|
Constante piézoélectrique
|
D
|
m.V-1
|
|
Permittivité électrique
|
E
|
F.m-1
|
Tableau 2-1 : Les
grandeurs physiques
En plus de ces deux effets décrits par les relations
(2-1) et (2-2) s'ajoute les propriétés élastiques et
diélectriques du matériau qui se traduisent par les relations
suivantes :
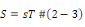
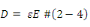
En y regardant de plus près on remarque que
l'équation 2-3 n'est qu'une réécriture de la loi de Hooke
appliquée au matériau piézoélectrique.
La figure suivante résume graphiquement les relations
entre les différentes gradeurs physiques entrant en jeu qui sont :
- Les grandeurs électriques : le champ
électrique et l'induction électrique
- Les gradeurs mécaniques : la contrainte et la
déformation
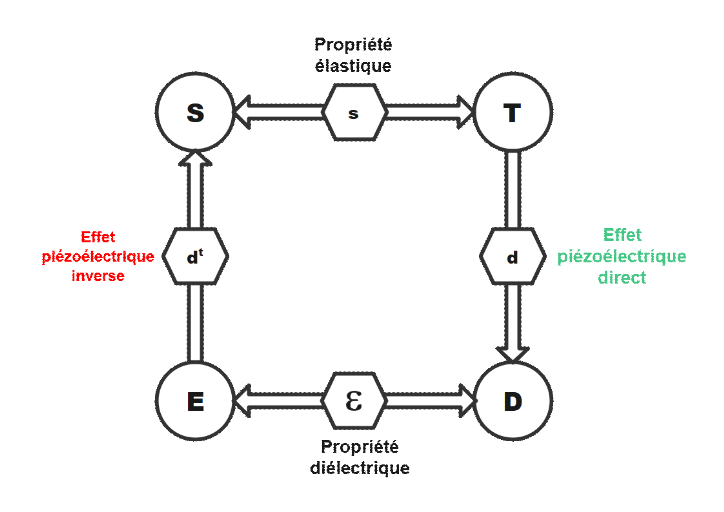
Figure 11 : Relations
entre les grandeurs physiques
Le comportement fondamental de la
piézoélectricité s'écrit donc par couple
d'équation :
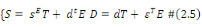
- La notation d'une grandeur avec un exposant autre que
« t » veut dire que la grandeur est
considérée lorsque l'exposant est nul ou constant, il ne s'agit
pas d'une puissance mais plutôt d'une représentation
symbolique.
- Le « t » veut dire la transposée
de la grandeur.
Le comportement fondamental de la
piézoélectricité peut s'écrire aussi par trois
autres couples d'équations qui s'équivalent :
|
|
Grandeurs mécaniques
|
|
Variables indépendantes
|
T
|
S
|
|
Grandeurs électriques
|
E
|
|
|
|
D
|
|
|
Tableau 2-2 : Equations
constitutives de la piézoélectricité (Carlioz,
2009)
|
Paramètre
|
Définition
|
Unité
|
Dimension
|
|
Electrique
|
e
|
Permittivité diélectrique
|
|
3*3
|
|
b
|
Perméabilité électrique
|
|
3*3
|
|
Mécanique
|
s
|
Souplesse
|
|
6*6
|
|
c
|
Raideur, rigidité élastique
|
|
6*6
|
|
Piézoélectrique
|
d
|
Constante de charge
|
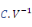 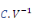 ou ou 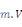 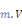
|
3*6
|
|
e
|
Constante piézoélectrique
|
|
3*6
|
|
g
|
Constante de tension
|
|
3*6
|
|
h
|
Constante piézoélectrique
|
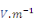 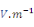 ou ou 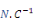 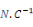
|
3*6
|
Tableau 2-3 :
Définition de différentes constantes (Ahmed-Seddik, 2012)
Les 4 couples d'équations du Tableau 2-2 étant
équivalents, il existe des relations entre les différentes
constantes électriques, mécaniques et
piézoélectriques.
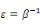
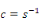
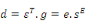
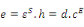
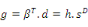
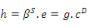
Nous utiliserons dans la suite du travail le couple
d'équations 2-5 car il fait varier directement les grandeurs intensives
T et E.
Le champ électrique E et l'induction électrique
D sont des vecteurs avec 3
composantes. La contrainte T et la
déformation S sont des tenseurs avec 6 composantes : les 3 axes du
repère, et les axes croisés correspondant aux rotations. De ce
fait, la souplesse s
s'exprime sous la forme d'un tenseur 66, les
coefficients piézoélectriques d sous la forme
d'un tenseur 63,
et la permittivité électrique sous la forme d'un tenseur 33.
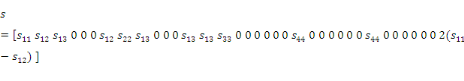
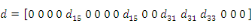
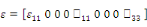
| 


