2. Méthodologie de travail
Cette partie consistera à présenter la
démarche économétrique utilisée pour l'estimation
de nos modèles et les principaux tests utilisés.En effet, nous
présentons une application directe des données réelles des
recettes fiscales de Côte d'Ivoire en utilisant la méthode de box
et Jenkins à l'aide d'un modèle ARIMA (p, d, q), nous terminerons
par des prévisions à l'horizon
« n » à déterminer avec le
logiciel Eviews 9.
La méthode box-Jenkins
Cette méthodologie vise à formuler un
modèle économétrique permettant de représenter une
série chronologique avec pour objectif de prévoir des valeurs
futures à court terme, d'où l'objet de notre étude. Cette
démarche se fonde sur le modèle ARIMA.
L'approche box-Jenkins suggère une démarche
à trois phases.
· La phase d'identification d'un
modèle préliminaire
C'est une étape délicate qui conditionne la
prévision d'une chronique. Elle est fondée sur l'analyse des
corrélogrammes (représentations graphiques des fonctions
d'autocorrélation) simple et partiel. Avant de modéliser par un
processus ARIMA, la série doit être stationnaire après cela
nous passons à l'identification des paramètres p et q du
modèle de type ARIMA (p, d, q) le modèle adéquat.
· La phase d'estimation des
paramètres
Cette phase consiste à estimer les paramètres du
modèle retenu, puis à vérifier à parti de certains
tests statistiques que le modèle est valide.
· La phase de validation et choix du
modèle
On doit d'abord vérifier que le modèle n'a aucun
défaut à travers des tests statistiques qui consistent à
tester que les résidus du modèle estimé ne suivent pas le
bruit blanc autrement dit qu'ils soient non corrélés et ne
présentent pas d'hétéroscédasticité
(variance constante).
· Tests de spécification du modèle
ü Test de bruit blanc
ü Test de Breusch-Goldfrey pour
l'autocorrélation
ü Test d'hétéroscédasticité
d'Arch
ü Test de significativité des coefficients
ü Test de normalité de Jarque-Bera
Si plusieurs modèles réussissent cette
dernière phase, on passe au choix du modèle. Deux critères
de choix de meilleur modèle existent :
3. Modélisation
Les modèles choisis pour ce présent travail sont
Le modèle ARIMA et le modèle ARIMAX, car selon Peter (2012) et
al, le modèle ARIMA est plus précis que le modèle
ARIMAX.
3.1. Le
modèle ARIMA
En effet, ARIMA est un modèle qui comprend trois
processus :
ü Le processus autorégressif
AR(p)
Il est constitué par une combinaison linéaire
finie des valeurs passées d'un processus aléatoire. Il est
noté AR(p) ou p désigne le degré autorégressif.
Sa formule générale est :
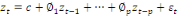 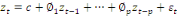 (11) (11)
Avec t 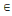 Z , Où Z , Où
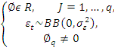
On peut donc réduire notre formule à :
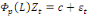 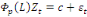 (12) (12)
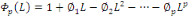 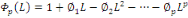 (13) (13)
Où
Avec c, une constante. Cette formule peut aussi être
ramenée par une simple translation. Cette translation consiste à
considérer :
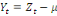 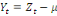 (14) (14)
Avec  , l'espérance de , l'espérance de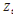 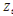 . On a alors : . On a alors :
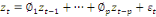 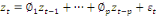 (15) (15)
Exemple :
· Si p=1 alors AR(1) : 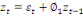 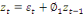
· Si p=2 alors AR(2) : 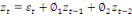 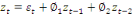
ü Le processus moving average MA(q)
Aussi appelé moyenne mobile en français, ce
processus tient compte des valeurs passées du bruit blanc. On la note
MA(q) avec q, l'ordre de moyenne mobile.
Sa formule générale est :
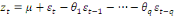
Cette formule peut être réduire
à :
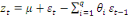 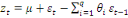 (16) (16)
Pour tout t 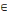 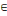 Z et Z et  , la moyenne, Où , la moyenne, Où
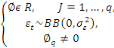
Ce processus peut être réécrire de la
manière suivante :
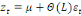 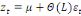 (17) (17)
Par un opérateur mobile :
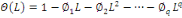 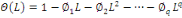 (18) (18)
Exemple
· Si q=1 alors MA(1) : 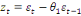 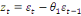
· Si q=2 alors MA(2) : 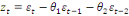 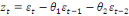
NB : Le processus MA(q) est stationnaire quelles que
soient les valeurs de  
MA(q) : 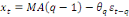 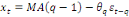 (19) (19)
ü Le processus mixte auto régressive
moving average ARMA (p.q.)
L'incorporation simultanée des composantes AR et MA
dans un même processus conduit à un processus mixte nommé
ARMA (p, d) d'où p est l'ordre autorégressif et d est l'ordre des
moyennes mobiles. Le modèle s'écrit :
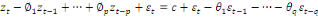 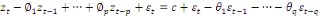 (20) (20)
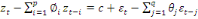 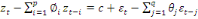 (21) (21)
Pour t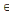 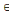 Z Z
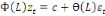 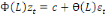 (22) (22)
Avec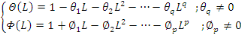 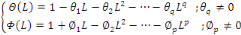
NB :
Si le processus est non stationnaire donc il convient de le
rendre stationnaire par passage aux différences selon l'ordre
d'intégration I. le processus devient alors un processus Auto
Régressive Integreted Moving Average ARIMA (p, d, q) avec d, le nombre
de fois qu'il a fallu différencier la série pour la rendre
stationnaire.
Un processus est ARIMA (p, d, q) s'il vérifie la
relation suivante :
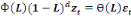 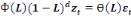 (23) (23)
Ou 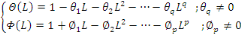 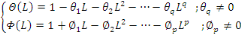
| 


