Tableau 6 : Résultats du Modèle à
Correction d'Erreurs
|
Dependent Variable: D(LCPR)
|
|
Method: Least Squares
|
|
Date: 06/23/15 Time: 14:29
|
|
Sample(adjusted): 1985 2013
|
|
Included observations: 29 after adjusting endpoints
|
|
Variable
|
|
Coefficient
|
|
Std. Error
|
t-Statistic
|
Prob.
|
|
C
|
|
-0.004757
|
|
0.015559
|
-0.305752
|
0.7633
|
|
D(LFDRE)
|
|
-0.030848
|
|
0.080527
|
-0.383082
|
0.7061
|
|
D(LFDRM)
|
|
-0.141783
|
|
0.126386
|
-1.121825
|
0.2767
|
|
D(LFIR)
|
|
0.159068
|
|
0.131275
|
1.211710
|
0.2413
|
|
D(LPIBR)
|
|
0.750126
|
|
0.313976
|
2.389117
|
0.0280
|
|
D(LCPR(-1))
|
|
-0.164225
|
|
0.241088
|
-0.681184
|
0.5044
|
|
D(LFDRE(-1))
|
|
0.000497
|
|
0.075549
|
0.006573
|
0.9948
|
|
D(LFDRM(-1))
|
|
-0.082602
|
|
0.178522
|
-0.462699
|
0.6491
|
|
D(LFIR(-1))
|
|
-0.043396
|
|
0.131178
|
-0.330820
|
0.7446
|
|
D(LPIBR(-1))
|
|
0.585633
|
|
0.443019
|
1.321915
|
0.2028
|
|
Q(-1)
|
|
-0.725349
|
|
0.314051
|
-2.309653
|
0.0330
|
|
R-squared 0.737653
Adjusted R-squared 0.591905
F-statistic 5.061152
Prob(F-statistic) 0.001442
|
Source : L'auteur à partir
des résultats de la régression.
Le coefficient du résidu décalé d'une
période, qui est la force de rappel vers l'équilibre de long
terme est statistiquement négatif et significatif au seuil de 5%. Cela
valide donc le MCE dans notre cas. La force de rappel vers l'équilibre
de long terme est égale à -0.725349 avec une probabilité
équivalente à 0.0330.
Le coefficient de détermination trouvé (R2
= 0.737653) et la probabilité associée à la
statistique de Fisher (soit 0.001442) nous permettent d'apprécier notre
modèle. Ces indicateurs montrent que dans le court terme, la variation
de la consommation privée réelle en cours D(LCPR) est fonction
de la variation des variables explicatives retenues à 73,76% et que ces
dernières sont globalement significatives en se référant
à la probabilité associée à la statistique de
Fisher. Ainsi, les résultats trouvés nous conduisent à
valider notre modèle à correction d'erreurs.En calculant le
délai de rattrapage, on trouve les résultats contenus dans le
tableau suivants :
Tableau 7 : Calcul du délai de rattrapage
|
Valeur
|
Année
|
Mois
|
Jours
|
|
72,5349%
|
1
|
0
|
0
|
|
100%
|
1
|
4
|
16
|
Source : nous-mêmes à
partir du coefficient de la force de rappel.
Le calcul du délai de rattrapage nous permet de
constater que vu que les 72,5349% du choc se résolvent pour une
période d'une année, le retour à l'équilibre,
c'est-à-dire les 100% du choc, se réalise après un
délai d'un an, quatre mois et seize jours.
III.2.2.5. Résultats des Tests de stabilité du
modèle
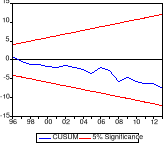
Pour analyser la stabilité de notre modèle, nous
avons fait recours aux tests des résidus récursifs, CUSUM et
CUSUM of squares tests.
Le CUSUM test analyse la présence ou non de la
stabilité systématique et le CUSUM of squares test quant à
lui, teste la présence ou non de la stabilité
aléatoire.
| 


