Le marché de change marocain. évaluation et couverture des options européennes et américaines de change et modélisation du taux de change du dirham.

Année universitaire : 2019-2020

Royaume du Maroc

UNIVERSITÉ MOHAMMED V AGDAL - RABAT
ÉCOLE MOHAMMADIA D'INGÉNIEURS

Département Modélisation et Informatique Scientifique

Mémoire de Projet de Fin d'Études

Le Marché de Change Marocain:

Évaluation et Couverture des Options

Européennes et Américaines de Change et

Modélisation du Taux de Change du Dirham

En vue de l'obtention du diplôme d'Ingénieur d'État

Soutenu le : 06 Juillet 2020
Présenté par : M^T. TOUFIK Youness

Devant le jury composé de :

M^T. Mohamed RYAD P.E.S. EMI Président

M^T. Hassane EL MANOUNI P.E.S. EMI Rapporteur

M^T. Mohamed RYAD P.E.S. EMI Encadrant

M^T. Abderrahmane HATIMY Forex & Commodities Derivatives Trader Parrain

i

Résumé

L'instauration d'un marché des changes au Maroc en 1996 constitue incontestablement une des principales manifestations concrètes de l'intégration de l'économie marocaine dans le circuit de la mondialisation et de la globalisation financière. Le Maroc est actuellement dans la deuxième phase du processus de réforme du régime de change, qui a été initié en Janvier 2018. Cette réforme va engendrer une diversification de la palette des produits financiers de change, notamment les produits dérivés complexes qui servent à satisfaire les besoins des clients en matière de couverture contre le risque de change. C'est dans l'optique de répondre au besoin des traders du marché de change, à savoir évaluer les options sur devises et immuniser leurs portefeuilles d'options contre le risque de taux de change, que ce projet de fin d'études a été réalisé.

Ce mémoire présente les différents modèles et méthodes pour la valorisation des options de change Européennes et Américaines, ces modèles se basent principalement sur différentes méthodes de résolution analytique ou numérique de l'équation aux dérivées partielles de Black-Scholes ou de ses extensions. Il présente aussi les stratégies de couverture qui peuvent être utilisés par les investisseurs particuliers ou les opérateurs du marché afin d'immuniser leurs portefeuilles d'options. Une partie de ce mémoire sera consacrée à la modélisation du taux de change du Dirham.

ii

Abstract

The establishment of a foreign exchange market in Morocco in 1996 is undoubtedly one of the main concrete manifestations of the integration of the Moroccan economy into the circuit of financial globalization. Morocco is currently in the second phase of the process of reforming the exchange rate regime, which was initiated in January 2018. This reform will lead to a diversification of the range of foreign exchange financial products, including complex derivatives that serve to meet the needs of customers in terms of hedging against foreign exchange risk. It is with a view to meeting the needs of Foreign Exchange Traders, i.e. to evaluate currency options and immunize their option portfolios against exchange rate risk, that this end-of-study project was carried out.

This dissertation presents the different models and methods for valuing European and American currency options. These models are mainly based on different analytical or numerical methods for solving the Black-Scholes partial derivative equation or its extensions. It also presents hedging strategies that can be used by individual investors or market operators to immunize their option portfolios. A part of this paper will be devoted to the modelling of the Dirham exchange rate.

Remerciements

À l'issue de ce Projet de Fin d'Études, mes remerciements vont tout d'abord à Dieu le tout puissant, qui m'a donné la force et la patience pour accomplir ce travail.

Il me tient à coeur d'adresser mes sincères remerciements à toutes les personnes qui ont pris part à ce projet, à celles qui ont oeuvré pour sa réussite, et à tous ceux qui m'ont soutenu ne serait-ce que par leur présence.

Je souhaiterai exprimer ma profonde gratitude envers mon tuteur de stage, M^r. Abderrah-mane HATIMY, Trader Dérivés FX et Matières Premières chez Attijariwafa Bank, pour avoir accepté de m'encadrer, pour tout le temps qu'il m'a consacré malgré sa charge de travail, pour le savoir qu'il m'a transmis, pour sa contribution à l'avancement de ce rapport, pour son aide précieuse et son encouragement. Je n'omettrai de remercier toute l'équipe de la salle des marchés d'Attijariwafa Bank pour son accueil, ses conseils et sa collaboration.

Je tiens à exprimer mes considérations distinguées à mon encadrant académique, le Professeur Mohamed RYAD pour son encadrement, ses conseils, sa disponibilité et sa participation à l'acheminement de ce rapport.

Mes sincères remerciements aux membres du jury pour l'intérêt qu'ils ont porté à ce sujet en acceptant d'examiner le travail et de l'enrichir par leurs propositions. Aussi, faut-il remercier l'ensemble du corps professoral du département Modélisation et Informatique Scientifique pour les efforts déployés à notre formation.

J'exprime pareillement mes profonds remerciements et mes profondes reconnaissances à mes chers parents, à mes chères soeurs et à mon cher frère. Merci pour votre soutien et merci pour votre amour.

iii

A vous ce modeste travail.

iv

Table des matières

Liste des figures vii

Liste des tableaux viii

Introduction 1

Présentation du cadre de travail 3

1 Généralités sur les options sur devises 6

1.1 Définition 6

1.2 Les spécificités d'un contrat d'option sur devise 7

1.3 Notions sur le pricing des options sur devises 8

1.3.1 Valeur intrinsèque 8

1.3.2 Valeur Temps 9

2 Pricing des options Européennes sur devises 12

2.1 Notations et hypothèses 12

2.2 L'évaluation risque-neutre 13

2.3 Modèle de Black-Scholes 14

2.3.1 L'équation aux dérivées partielles de Black-Scholes 14

2.3.2 Les formules d'évaluation de Black-Scholes 15

2.4 Modèle de Garman-Kohlhagen 16

2.5 Les lettres grecques 17

2.5.1 Delta 17

2.5.2 Gamma 18

2.5.3 Thêta 19

2.5.4 Vega 20

2.5.5 Rhô 20

2.6 Application 21

3 Surface de volatilité : Modèle de Vanna-Volga 24

3.1 Volatilité historique et volatilité implicite 24

3.1.1 Volatilité historique 24

3.1.2 Volatilité implicite 25

3.2 Estimation de la volatilité implicite 27

3.2.1 Méthode de Newton-Raphson 27

3.2.2 Méthode de Vanna-Volga 28

3.3 Application 32

v

4 Pricing des options Américaines sur devises 35

4.1 Généralités sur les options Américaines 35

4.1.1 Définition 35

4.1.2 L'exercice anticipé d'un call 36

4.1.3 L'exercice anticipé d'un put 36

4.2 Méthode des différences finies 37

4.3 Approximation de Barone-Adesi et Whaley (1987) 42

4.4 Approximation de Bjerksund et Stensland (1993) 44

4.5 Approximation de Bjerksund et Stensland (2002) 46

4.6 Application 49

5 Portefeuille d'options: Couverture et gestion des risques 51

5.1 Stratégies statiques de couverture 51

5.1.1 Forward synthétique 52

5.1.2 Risk Reversal 53

5.1.3 Butterfly spread 55

5.1.4 Condor 56

5.1.5 Résultats numériques 58

5.2 Stratégies dynamiques de couverture 59

5.2.1 Delta Hedging 60

5.2.2 Optimal Delta Hedging 66

6 Modélisation du taux de change Marocain 74

6.1 Introduction 74
6.2 Modélisation du taux de change marocain dans le cadre d'un régime de change

flottant administré 76

6.2.1 Le modèle de Krugman 77

6.2.2 Le modèle STARTZ Smooth Transition Autoregressive Target Zone . . . 80

6.2.3 Méthodologie d'estimation du modèle STARTZ 82

6.2.4 Modélisation du taux de change du Dirham par le modèle STARTZ . 83

6.2.5 Conclusions 94

Conclusion 95

vi

Table des figures

1.1 Impact des variations du taux de change, du prix d'exercice et de durée de vie jusqu'à l'échéance sur la valeur d'une option lorsque S0 = 50, K = 50, r =

5%, ó = 30% et T = 1, [14]. 10
1.2 Impact des variations de la volatilité et taux d'intérêt sans risque sur la valeur

d'une option lorsque S0 = 50, K = 50, r = 5%, ó = 30% et T = 1, [14] 11

2.1 Représentation de N(x),[14]. 16

2.2 Représentation du delta, [14]. 17
2.3 Variation du delta en fonction du cours du sous-jacent: (a) option d'achat; (b)

option de vente, [14] 18

2.4 Variation du gamma en fonction du cours du sous-jacent, [14] 19

2.5 Variation du thêta en fonction du cours du sous-jacent, [14]. 19

2.6 Variation du vega en fonction du cours du sous-jacent, [14]. 20

2.7 Interface de pricing des option Européennes sur devises. 23

3.1 Le smile de volatilité pour les options sur devises, [14]. 26

3.2 La distribution implicite et la distribution log-normale des taux de change, [14]. 26

3.3 Principe de le méthode de Newton-Raphson 27

3.4 Données du marché pour les 3 volatilités óATM, óRR ^et óBF 32

3.5 Matrice de volatilité pour l'EURUSD. 33

3.6 Surface de volatilité pour l'EURUSD. 33

3.7 Smiles de volatilité pour l'EURUSD. 34

4.1 Représentation du schéma numérique de résolution, [14] 38

4.2 Différence entre le schéma implicite et le schéma explicite. 39

4.3 Frontière d'exercice [7] 47

4.4 Interface de pricing des option Américaines sur devises. 50

5.1 Payoffs d'un forward sythétique : (a) position longue, (b) position courte. . 53

5.2 Payoff d'un Butterfly Spread. 55

5.3 Payoff d'un Condor. 57

5.4 Profit & Loss Delta Hedging 61

5.5 Aperçu de l'interface de saisie. 63

5.6 Aperçu du portefeuille d'options 64

5.7 Extrait de la base de données des options 64

5.8 Interface Mark-To-Market du portefeuille. 65

5.9 Extrait de la feuille d'ajustement 65

5.10 Profit & Loss du portefeuille 66

5.11 Évolution de l'EURUSD du 22 Avril 2019 au 20 Mai 2020 69

5.12 Estimation des paramètres des calls entre le 23 Juillet 2019 et le 20 Mai 2020. 70

5.13 Estimation des paramètres des puts entre le 23 Juillet 2019 et le 20 Mai 2020. 70

5.14 R² pour les calls et les puts entre le 23 Juillet 2019 et le 20 Mai 2020 72

vii

6.1 Représentation de s en fonction de v, [20] 79

6.2 Représentation de s en fonction de v, [20] 79

6.3 La déviation en pourcentage de l'USDMAD du cours de référence. 83

6.4 Représentation de la de la série de l'USDMAD et de ses composantes 84

6.5 Représentation de la de la série y⁰_t. 85

6.6 Les fonctions de transition G'^- et G¹' pour la moyenne conditionnelle 90

6.7 Les fonctions de transition G'^- et G¹' pour la variance conditionnelle. 90

6.8 Représentation des données observés et ajustés par le modèle pour la série yt 91

6.9 L'histogramme et le graphe quantile-quantile des résidus du modèle STARTZ. 92

6.10 Représentation des données observés et prévues par le modèle pour yt 94

viii

Liste des tableaux

1.1 Comparaison entre les options de change et les forwards de change. 7

1.2 Les différentes appellations d'une option selon son prix d'exercice. 7

1.3 Les différentes valeurs intrinsèques selon les types d'options. 9

1.4 Résumé des effets de l'augmentation d'une variable, lorsque les autres restent

fixes, sur le prix des options sur devises 9

2.1 Les inputs des 6 options utilisées pour tester le pricer 22

2.2 Comparaison des prix des options 22

2.3 Comparaison des lettres grecques. 22

4.1 Prix de options Américaines sur l'EURUSD pour K = 1, 08 et rf = 0, 04. . . . 50

5.1 Revenus d'une position longue sur forward synthétique. 52

5.2 Revenus d'une position courte sur forward synthétique. 52

5.3 Revenus d'une position longue sur Risk Reversal 53

5.4 Revenus d'une position courte sur Risk Reversal. 53

5.5 Revenus d'une position longue sur Butterfly Spread. 55

5.6 Revenus d'une position longue sur Condor. 57

5.7 Résultats numériques des stratégies zero-cost 59

5.8 Simulation de la couverture dynamique par delta 61

5.9 Nombre de contrats utilisés en fonction de leur Moneyness et de leur échéance. 69

5.10 Statistiques descriptives de a, b, c et CMV pour les calls. 71

5.11 Statistiques descriptives de a, b, c et CMV pour les puts. 71

5.12 Gain du Minimum Variance Hedging par rapport au Delta Hedging. 72

6.1 Test de Dickey-Fuller Augmenté (ADF) sur la série yt 85

6.2 Test de Dickey-Fuller Augmenté (ADF) sur la série y⁰_t 85

6.3 Comparaisons des modèles AR(n), n = 1, . . . , 5, par les critères AIC et BIC.. 86

6.4 Test de Shapiro-Wilk pour les résidus du modèle AR(1). 86

6.5 Test de Ljung-Box pour les résidus du modèle AR(1). 87

6.6 Test de White pour les résidus du modèle AR(1) 87
6.7 Comparaisons des modèles GARCH(p,q), p = 1, 2, q = 1, 2, par les critères

AIC et BIC 88

6.8 Paramètres du modèle AR(1)-GARCH(1,1) 88

6.9 Test de ARCH LM pour les résidus carrés du modèle AR(1)-GARCH(1,1). . 88

6.10 Test de Pearson Goodness-of-Fit du modèle AR(1)-GARCH(1,1) 89

6.11 Résultats d'estimation des paramètres du modèle STARTZ 89

6.12 Indicateurs d'écart du modèle STARTZ. 92

6.13 Test de Shapiro-Wilk pour les résidus du modèle STARTZ. 93

6.14 Test de Ljung-Box pour les résidus du modèle STARTZ 93

6.15 Test de White pour les résidus du modèle STARTZ. 93

1

Introduction

Notre projet de fin d'études traite les problématiques liées au pricing des options Européennes et Américaines à travers marché de change (FOREX), qui s'est développé récemment pour aider les entreprises à se protéger contre une partie de l'incertitude des fluctuations des taux de change. Ce marché est considéré en général comme l'un des plus grands marchés financiers avec plus de 5 000 milliards de dollars de transactions quotidiennes, soit plus que les marchés des contrats à terme et des actions réunis. Plusieurs produits financiers sont négociés sur ce marché, nous allons cependant nous intéresser aux dites options, car dans la littérature des mathématiques financières, les options sont considérées comme le produit financier qui a sollicité le plus de travaux de recherche. Au Maroc, les options de change n'ont fait leur apparition qu'à partir de 2005. Depuis, le marché de ces produits a connu un vif intérêt aussi bien de la part des banques qui proposent des transactions en devises que des investisseurs qui les demandent.

Le but de notre projet de fin d'études est entre autres de mettre en application l'ensemble des connaissances acquises pendant notre cursus d'ingénieur, que ce soit en Informatique, en Finance ou en Mathématiques. Ces trois compétences étant très recherchées, elles doivent être mises en avant afin de nous mettre en valeur, surtout au vu de la situation économique actuelle. C'est pourquoi ce projet, le plus important de notre cursus scolaire, devait les mettre en relation. La finalité étant d'obtenir des outils informatiques pratiques d'utilisation reposant sur des recherches financières et mathématiques afin de pouvoir montrer une réalisation concrète de notre savoir-faire. Le sujet de ce rapport aborde des notions utilisées par les équipes du Front Office au sein des salles des marchés, telles que les options Européennes, les options Américaines, le modèle de Black-Scholes, la volatilité, les algorithmes de minimisation, les grecques, etc. Avec ce sujet, nous étions sûrs d'acquérir des connaissances qui nous seraient utiles dans notre parcours professionnel.

Avant de mettre en évidence notre problématique, il convient de préciser que tout trader qui opère sur le marché doit balancer deux considérations opposées - le profit et le risque. Un trader qui vend une option à un client est confronté au problème de gestion du risque. Même avec l'utilisation des bons modèles de pricing, il est indispensable de suivre des stratégies de couverture strictes et bien étudiées, car un trader qui ne tient pas compte des risques liés sa position va certainement avoir une carrière courte et malheureuse. Ce qui nous ramène aux questions traitées tout au long de ce rapport, à savoir comment évaluer et couvrir une option sur devises.

Pour répondre à cette problématique avec le souci de l'équilibre entre les éléments théoriques et les aspects opérationnels, nous avons adopté un plan scindé en six chapitres. Nous introduirons dans un premier chapitre quelques généralités sur les options sur devises. Pour ce faire, nous définirons les options sur devises, puis nous citerons les spécificités de ce type d'option et enfin nous présenterons des notions sur l'évaluation des options sur devises, car avant de se lancer dans les différents modèles de pricing des options sur devises, il faut

2

avoir une bonne compréhension des facteurs et des paramètres qui déterminent le prix de ces options.

Le deuxième chapitre sera consacré au pricing des options Européennes sur devises, donc il sera nécessaire de présenter le modèle de Black-Scholes et celui de Garman-Kohlhagen qui est une extension du premier de manière à ce que le modèle puisse faire face à la présence de deux taux d'intérêt sans risque. La présentation du modèle de Black-Scholes doit naturellement nous conduire à parler des lettres grecques, pour cela, nous consacrons une section pour présenter les lettres grecques qui quantifient différents aspects du risque dans une position sur options.

Le modèle de Black-Scholes repose sur l'hypothèse selon laquelle la volatilité est un paramètre constant. Or, une telle hypothèse est loin d'être réaliste. La réalité a mis en évidence le lien direct entre la volatilité, la maturité et le prix d'exercice d'une option, illustré par une courbe de volatilité convexe nommée Smile de volatilité, c'est le point que nous traiterons dans le troisième chapitre ,qui présentera la méthode de Vanna-Volga utilisée pour la construction de la surface de volatilité.

Le quatrième chapitre sera consacrée au pricing des options Américaines sur devises. Ce chapitre examine d'abord les caractéristiques des options Américaines, puis présente quelques méthodes utilisées afin de les évaluer, sachant qu'elle n'existe pas une formule fermée qui donne le prix exact d'une option Américaine. Dans ce sens, nous allons utiliser une approche par la méthode des différences finies afin de résoudre l'EDP de Black-Scholes, ensuite, nous allons présenter trois autres modèles qui permettent de donner des formules fermées approximatives pour évaluer les options Américaines.

La gestion des risques est une problématique très importante en finance de marché. Pour cette raison nous avons consacré le cinquième chapitre à la couverture et gestion des risques d'un portefeuille d'option, qui se divise en deux grandes catégories : Gestion statique est gestion dynamique. Ce chapitre a donc pour objectif de présenter quelques exemples de stratégies statiques utilisées au niveau des salles des marchés, le chapitre contient aussi un volet traitant la gestion dynamique d'un portefeuille d'options dans lequel nous allons présenter le Delta Hedging classique, largement utilisé, puis nous présenterons ensuite une nouvelle approche appelée Optimal Delta Hedging définie par John Hull et Alan White (2017) [15]; cette approche vise à remédier aux faiblesses de la couverture de le delta de Black-Scholes.

Le Maroc, en décidant de passer d'un régime de change fixe à un régime de change flottant administré, va subir une hausse au niveau des volatilités des cours de change. Pour cela le sixième chapitre aura comme objectif de modéliser le taux de change Marocain. Un modèle de séries temporelles appelé STARTZ (Smooth Transition Autoregressive Target Zone), présenté par Lundbergh et Teräsvirta (2005) [22], sera conçu pour modéliser les fluctuations des du Dirham à l'intérieur d'une bande de fluctuation.

3

Présentation du cadre de travail

Présentation du groupe Attijariwafa Bank

Le groupe Attijariwafa Bank est classé 1^er groupe bancaire au Maroc et 6^me en Afrique. Créé en 2003 suite à une fusion entre Wafabank (1904) et la Banque Commerciale du Maroc (BCM) (1911), le groupe Attijariwafa Bank accompagne aujourd'hui près de 10 millions de clients particuliers, professionnels, entreprises et institutionnels et mobilise 20 125 collaborateurs dans 25 pays en Afrique, en Europe et au Moyen-Orient.

Attijariwafa Bank a su, depuis plus d'un siècle, se réinventer en diversifiant ses métiers, en renouvelant ses offres et en adaptant ses organisations, pour répondre à son ambition de devenir la banque relationnelle de référence. Banque de Détail pour particuliers et professionnels, Banque Privée, Banque de Financement et d'Investissement, Assurances, le groupe s'appuie sur la complémentarité de ses métiers pour accompagner une clientèle diversifiée. Le groupe opère aujourd'hui à travers 19 filiales:

-- Attijari Factoring

-- Attijari Finances Corp.

-- Attijari Global Research

-- Attijari Intermédiation

-- Attijari International bank

-- Attijari Invest

-- Attijari Titrisation

-- Bank Assafa

-- Wafa Assurance

-- Wafa Bourse

-- Wafa Courtage

-- Wafa Gestion

-- Wafa IMA Assistance

-- Wafa Immobilier

-- Wafa LLD

-- Wafabail

-- Wafacash

-- Wafasalaf

-- Attijari Payment Processing

Le Conseil d'administration d'Attijariwafa Bank, à sa tête M. Mohamed EL KETTANI Président Directeur Général du groupe, est responsable de la solidité financière de la banque. Il définit ses orientations stratégiques, y compris sa politique de développement, tant au niveau local

4

qu'à l'international, et assure la surveillance de la gestion de ses activités. Le système de gouvernance a également institué le principe de collégialité des décisions dans la gestion du groupe, s'appuyant sur un Comité Exécutif et un Comité de Coordination et de Synergies.

Au 31 Décembre 2018, le groupe Attijariwafa Bank est détenu par 5 actionnaires:

-- Groupe Al Mada (46,4%)

-- Institutionnels nationaux (28,3%)

-- Flottant et autres (17,1%)

-- Santusa Holding S.L (Grupo Santander) (5,1%)

-- Personnel de la banque (3,1%)

Présentation de la salle des marchés

La salle des marchés du groupe Attijariwafa Bank fut inaugurée au début de l'année 2007, c'est le lieu où sont rassemblés les opérateurs de marché intervenant sur les marchés financiers. C'est un espace regroupant les différents services spécialisés permettant à la banque d'intervenir sur les marchés des capitaux internationaux. Elle sert deux types de métiers:

-- Trading,

-- Sales et courtage.

La salle des marchés est répartie en trois pôles distincts qui sont le Front Office dont la mission principale est la négociation directe avec les clients, le Middle Office qui s'en charge du contrôle des opérations et les risques ainsi que l'analyse des résultats et le Back Office qui est chargé de la saisie des opérations et des contrôles comptables.

Front Office

Le Front Office représente l'interface de la banque vis-à-vis du marché. Il centralise et traite tous les besoins de la salle des marchés et de ses clients en termes de couverture et de financement, investissement, gestion de position, trading et arbitrage. Il se distingue du Back Office qui exécute l'ensemble des tâches administratives ou logistiques liées à la vente. Le Front Office du groupe Attijariwafa Bank peut être décomposé en quatre Desks:

-- Desk change : Plus communément appelé FOREX (Foreign Exchange), est le Desk du marché des changes sur lequel les devises sont échangées l'une contre l'autre, à des taux de change qui varient sans cesse. Ce Desk se charge du trading aussi bien pour le propre compte de la banque que pour le compte des particuliers qui représentent essentiellement les entreprises marocaines qui ont accès à la salle des marchés. Ce Desk est le plus important en termes d'effectif et de revenu, du fait qu'il représente presque le tiers des revenus de la salle des marchés.

-- Desk actions : Il a pour mission majeure de fructifier le compte propre de la banque en actions. Le rôle du trader au sein du Front Office s'avère être primordial, puisqu'il est amené à tout moment à assurer une rentabilité en faveur de la banque en profitant

5

des situations favorables des cours, il achète ainsi au cours le plus bas possible et vendent avec au cours le plus haut possible.

-- Desk taux: Ce Desk se décompose en trois Desks : Le Desk taux trésorière qui s'occupe de l'optimisation de la trésorerie de la banque en Dirham et en devises, le Desk taux trader et sales qui a pour mission assurer la liquidité de la banque et la gestion du portefeuille de la banque, et finalement le Desk structuration qui a pour mission de répondre aux exigences financières des clients en leurs offrant des produits personnalisés.

-- Desk matières premières : Se charge du trading pour le compte propre de la banque en prenant des positions sur les différentes matières premières (métaux, céréales,...) sur les marchés essentiellement Anglo-saxons, Londonien et Américain (CBOT).

Les opérations conclues en Front Office engagent la banque de manière irrévocable vis-à-vis des contreparties. Pour prendre au mieux les décisions en respectant les limites de marché et de contreparties qui leur sont fixées, les opérateurs doivent s'appuyer sur des systèmes leur permettant de s'informer sur l'activité de marché et de mesurer et d'analyser leurs positions et leur résultat, la salle des marchés a été pour cet effet équipée d'écrans projetant les cotations et les dernières nouvelles économiques à travers la chaîne Bloomberg et de postes disposant de licences Reuters.

Middle Office

Le Middle Office est le service chargé de nommer les opérations initiées par les traders dans la salle des marchés, plus exactement dans le Front Office, après avoir vérifié qu'elles sont conformes à la réglementation. Il est chargé de faire la jonction entre le Front et le Back Office. Il saisit sur une base de données toutes les transactions effectuées par les traders et les sales. Et enfin, il met en place avec le Front et le Back Office des méthodes d'analyse des risques et définit les procédures homogènes par lignes de produits.

Back Office

L'opérateur Back Office est chargé d'assurer le suivi administratif et comptable des opérations conclues au Front Office. Il enregistre les transactions, informe les clients (entreprises ou institutions), effectue le règlement et la livraison des titres, gère le versement des dividendes des actions et des intérêts des obligations. Il participe aussi à la mise en place et à l'évolution des procédures et des systèmes informatiques.

6

Chapitre 1

Généralités sur les options sur devises

Le marché des changes s'est développé pour aider les entreprises à se protéger contre une partie de l'incertitude des mouvements des taux de change, mais les contrats futures ou forward sur devises sont approprié pour des expositions connues. Leur utilisation pour couvrir les expositions contingentes, variables ou de translation pourrait forcer une entreprise à accepter des pertes sur des opérations de change inutiles. Non seulement cela, mais les entreprises rivales qui laissent leur exposition non couverte peuvent soudainement acquérir un avantage concurrentiel. Cela a donc en partie conduit à l'expansion du marché des options sur devises, cette expansion a été encore plus spectaculaire que l'énorme croissance de l'ensemble du marché des changes au cours des dernières années.

1.1 Définition

Une option sur devises est un contrat qui donne à son détenteur le droit - et non l'obliga-tion - d'acheter ou vendre un montant donné d'une devise spécifique à un taux de change défini à l'avance, appelé prix d'exercice et à une date ou pendant une période déterminée, moyennant le paiement d'une prime. Lorsque l'option implique un achat d'une quantité de devises contre une autre, elle est appelée Call ou option d'achat. Mais lorsque le détenteur de l'option veut vendre une devise contre l'acquisition d'une autre, on parle d'un Put ou option de vente.

Dans toutes les opérations de change, on achète une devise contre une autre. Par conséquent, chaque paire de devises s'échange à la fois comme Call et Put.

Les caractéristiques essentielles d'une option sur devises pour son propriétaire sont celles de la limitation des risques et du potentiel de profit illimité. Elle est similaire à une assurance, dans laquelle, au lieu de payer une prime pour assurer sa maison contre le risque d'incendie, le propriétaire paie une prime pour s'assurer contre les mouvements défavorables du taux de change.

TABLE 1.1 - Comparaison entre les options de change et les forwards de change.

Options de change Forwards de change

Droit mais non obligation d'ache- Obligation d'acheter/vendre une devise ter/vendre une devise

Prime à payer Aucune prime à payer

Large gamme de prix d'exercice Un seul taux à terme pour une date donnée

Conserve un potentiel de profit illimité tout en limitant risque de perte

Date de livraison flexible de la devise (possibilité d'acheter une option plus longtemps que nécessaire)

Élimine le potentiel de hausse ainsi que les risques de perte

Date de livraison fixe de la devise

1.2 Les spécificités d'un contrat d'option sur devise

L'actif sous-jacent

L'actif sous-jacent est l'actif sur lequel porte l'option, il peut être acheté ou vendu par le détenteur de l'option qui exerce son droit.

Dans notre cas, l'actif sous-jacent est la devise. Pour une paire de devises cotée ccy1ccy2, le taux de change au comptant St à l'instant t est le nombre d'unités de ccy2 (également connu sous le nom de devise domestique, ou de devise de cotation) requis pour acheter une unité de ccy1 (la devise étrangère ou parfois la devise de base), le taux au comptant est fixé aujourd'hui et le règlement a lieu à la date prévue. Le taux au comptant est donc égal aux unités de ccy2 par ccy1.

Par exemple la cotation de la GBPUSD signifie dollars Américains par livre sterling, donc si la GBPUSD est de 1,63935, alors une livre sterling peut être achetée pour 1, 63935$ sur le marché au comptant. Il s'agit d'un prix en USD par GBP. C'est le coût d'une livre, en dollars.

Le prix d'exercice

Le prix d'exercice appelé aussi Strike est le taux de change auquel les deux devises de la paire de devises sous-jacente doivent être échangées si l'option est exercée.

Une option peut avoir différentes appellations selon son prix d'exercice s'il est supérieur, inférieur ou égal au prix spot:

TABLE 1.2 - Les différentes appellations d'une option selon son prix d'exercice.

Option Call Put

En dehors de la monnaie Strike > Spot Strike < Spot

A la monnaie Strike = Spot Strike = Spot

Dans la monnaie Strike < Spot Strike> Spot

7

8

La date d'échéance

La date d'échéance est la seule date où cette option peut être exercée s'il s'agit d'une option Européenne, ou avant laquelle cette option peut être exercée s'il s'agit d'une option Américaine.

La prime de l'option

La prime d'une option représente le montant payé par l'investisseur pour l'acquisition d'une option d'achat ou de vente, elle reste acquise au vendeur qu'il y ait ou pas exercice de l'op-tion par l'acheteur. La prime d'une option est calculée en tenant compte de plusieurs paramètres:

-- Le prix au comptant, appelé Spot

-- Le prix d'exercice, appelé Strike

-- Le temps restant jusqu'à la maturité

-- Le taux d'intérêt sans risque domestique

-- Le taux d'intérêt sans risque étranger

-- La volatilité du taux de change

1.3 Notions sur le pricing des options sur devises

Avant de se lancer dans les différent modèle de pricing des options sur devises, il faut avoir une bonne compréhension des facteurs et des paramètres qui déterminent le prix de ces options. En effet, le prix d'une option ne dépend pas uniquement du gain obtenu en décidant de l'exercer immédiatement, mais aussi, de la probabilité que cette option devienne bénéfique. De ce fait, la valeur d'une option se décompose en deux éléments : La valeur intrinsèque et la valeur temps.

Prix de l^'option = Valeur intrinsque + Valeur temps

1.3.1 Valeur intrinsèque

La valeur intrinsèque correspond à la valeur minimale de la prime; elle correspond au gain immédiat, sans risque, que ferait l'acheteur de l'option en faisant simultanément une opération sur le marché des changes (le marché au comptant ou le marché à terme).

La valeur intrinsèque représente la différence entre le prix d'exercice et le cours à terme, pour une option Européenne, et la différence entre le prix d'exercice et le cours le plus avantageux des cours au comptant ou à terme, pour une option Américaine. Lorsque cette différence est négative la valeur intrinsèque est nulle. Le tableau ci-dessous présente les différentes valeurs intrinsèques selon les types d'options:

9

TABLE 1.3 - Les différentes valeurs intrinsèques selon les types d'options.

Type Positon???Call		Put
Achat	Max(ST - K; 0)	Max(K - ST; 0)
Vente	-Max(ST - K; 0)	-Max(K - ST; 0)

1.3.2 Valeur Temps

La valeur temps reflète la probabilité que l'option devienne dans la monnaie. Elle est égale à la différence entre le prix de l'option et sa valeur intrinsèque.

Comme cela a été évoqué dans la section précédente, le prix des options de change est en général fonction de 6 paramètres. Dans cette section, nous nous intéressons à ce qu'il advient du prix des options lorsque l'un de ces facteurs change, tandis que les autres restent constants. Les résultats sont résumés dans le tableau ci-dessous :

TABLE 1.4 - Résumé des effets de l'augmentation d'une variable, lorsque les autres restent fixes, sur le prix des options sur devises.

Variable	Call	Put
Taux de change au comptant	+	-
Prix d'exercice	-	+
Date d'échéance	+	+
Taux d'intérêt sans risque domestique	+	-
Taux d'intérêt sans risque étranger	-	+
Volatilité du taux de change	+	+

"+" signifie qu'une croissance de la variable provoque une augmentation de la valeur de l'option. "-" signifie qu'une croissance de la variable provoque une baisse de la valeur de l'option.

Taux de change au comptant et prix d'exercice

Si une option d'achat est exercée à une date future, le flux engendré, appelé Payoff, est égal à la différence entre le taux de change au comptant et le prix d'exercice. Par conséquent, la valeur d'un call augmente lorsque le taux de change croît. Elle est faible quand le prix d'exercice est élevé. Pour une option de vente, le Payoff à l'exercice est égal à la différence entre le prix d'exercice et la taux de change. La valeur de ce type d'option diminue si le taux de change s'accroit. 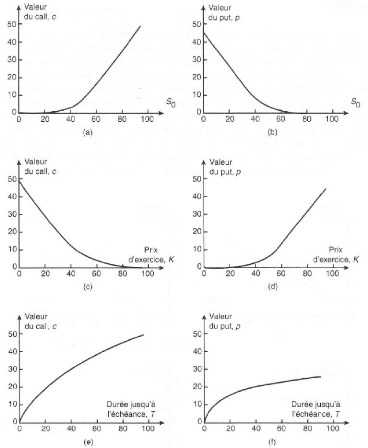Elle augmente au contraire, lorsque le prix d'exercice est élevé. Les graphiques a, b, c, d de la figure 1.1 illustrent la façon dont les valeurs d'un call et d'un put dépendent du taux de change et du prix d'exercice.

Date d'échéance

Étudions à présent les effets de la date d'échéance sur les options. Les options d'achat, aussi bien que les options de vente, voient leur valeur s'accroitre (ou au moins ne pas baisser) lorsque la date de maturité s'éloigne, c'est à dire quand la durée restant à courir jus-qu'à l'échéance augmente. Considérons deux options qui diffèrent seulement par la date d'échéance. Le propriétaire de l'option à durée de vie plus longue profite de toutes les opportunités d'exercice ouvertes ouvertes au propriétaires des options à durée de vie plus

10

FIGURE 1.1 - Impact des variations du taux de change, du prix d'exercice et de durée de vie jusqu'à l'échéance sur la valeur d'une option lorsque S0 = 50, K = 50, r = 5%, ó = 30% et T = 1, [14].

courte, et plus encore. La valeur de l'option à l'échéance plus longue est toujours supérieur à celle de l'option à l'échéance plus courte. Les graphiques e, f de la figure 1.1 illustrent de quelle manière la valeur des options d'achat et de vente dépend de la date d'échéance.

Volatilité du taux de change

La volatilité du taux de change mesure l'incertitude quant aux variations futures de ce taux. Plus la volatilité est grande, plus la probabilité que le taux de change atteigne des sommets, ou subisse de fortes baisses, est importante. Le détenteur d'un call bénéficie d'une hausse du taux de change, mais limite son risque de perte, puisqu'en cas de chute du taux de change, il ne subit qu'une perte liée à la valeur de son option. Réciproquement, le détenteur d'un put bénéficie de la baisse du taux de change, mais il limite également son risque en cas de hausse du taux. Par conséquent, la valeur des calls, comme celle des puts, augmente avec la volatilité du sous-jacent (voir graphiques a et b de la figure 1.2).

11

Taux d'intérêt sans risque

Le taux d'intérêt sans risque affecte la valeur de l'option d'une façon moins évidente. Lorsque les taux d'intérêt augmentent, l'espérance de rendement, attendu par les investisseurs, tend à s'élever également. Mais la valeur actuelle des flux de trésorerie futurs reçus par les détenteurs d'options diminue. L'impact combiné de ces deux effets entraîne une baisse de la valeur des options de vente et un accroissement de la valeur des options d'achat (voir graphiques c et d de la figure 1.2).

Il est important de souligner que nous envisageons ici une variation des taux d'intérêt tandis que toutes les autres variables demeurent inchangées.

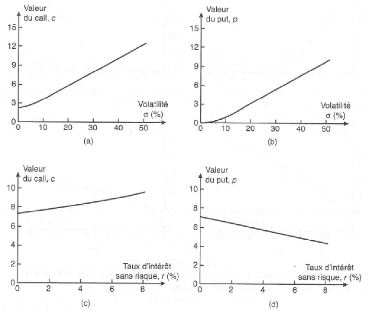
FIGURE 1.2 - Impact des variations de la volatilité et taux d'intérêt sans risque sur la valeur d'une option lorsque S0 = 50, K = 50, r = 5%, ó = 30% et T = 1, [14].

12

Chapitre 2

Pricing des options Européennes sur

devises

Pour évaluer les options sur devises, nous avons besoin d'un modèle pour les taux de change au comptant qui leur permet d'avoir un comportement stochastique et une stricte positivité. Nous suivons donc les travaux de Black et Scholes (1973) et les travaux associés de Garman et Kohlhagen (1983) appliqués aux options sur devises, et décrivons le taux au comptant par un mouvement Brownien géométrique:

dSt = uStdt + óStdWt (2.1)

2.1 Notations et hypothèses

Notations

Nous utiliserons dans ce chapitre et dans toute la suite de ce rapport les notations suivantes:

-- S0 : Le taux de change à la date t = 0.

-- K : Le prix d'exercice de l'option.

-- T : Le temps restant à courir jusqu'à l'échéance de l'option.

-- St : Le taux de change à l'instant t.

-- rd : Le taux sans risque domestique.

-- rf : Le taux sans risque étranger.

-- c : La valeur d'un call Européen.

-- p : La valeur d'un put Européen.

-- C : La valeur d'un call Américain.

-- P : La valeur d'un put Américain.

Hypothèses

Les hypothèses de ce chapitre sont valides pour reste de ce rapport sauf mention contraire, elle sont les mêmes hypothèses citées dans la section 15.5 de Hull (2017) [14].

-- Le taux de change aux comptant St (en devise domestique) d'une unité de devise étrangère suit un processus lognormal (2.1), conduit par une volatilité constante ó.

13

-- La vente à découvert est autorisée.

-- Absence de frais de transaction et de taxes.

-- Les devises domestique et étrangères ont des taux sans risque rd et rf, constants sur

toutes les échéances.

-- Absence d'opportunités d'arbitrage.

-- Le marché fonctionne en continu.

2.2 L'évaluation risque-neutre

Le principe d'évaluation risque-neutre stipule que, lors de la valorisation d'un dérivé, nous pouvons supposer que les investisseurs sont indifférents vis-à-vis du risque; par abus de langage, on dit qu'ils sont risque-neutre. Cette hypothèse signifie qu'ils n'exigent pas une espérance de rentabilité supérieure pour compenser le risque accru d'un investissement. Un monde où les investisseurs sont neutres vis-à-vis du risque est appelé univers risque-neutre. Celui dans lequel nous vivons n'est évidemment pas un univers risque-neutre. Plus les investisseurs prennent de risques, plus ils exigent un taux de rentabilité élevé. Cependant, il s'avère que l'hypothèse d'un univers risque-neutre fournit une valeur des options identiques à celle que l'on obtiendrait dans notre univers réel. Cela résout le problème lié au fait que nous ignorons quasiment tout degré d'aversion au risque des acheteurs et des vendeurs d'options.

L'évaluation risque-neutre semble un résultat surprenant lorsqu'on l'aborde pour la première fois. Les options sont des investissements risqués. Le degré d'aversion au risque d'un investisseur ne devrait-il pas affecter la façon dont elles sont évaluées? La réponse est qu'en réalité, lorsque nous évaluons une option en fonction du prix du sous-jacent, le degré d'aversion au risque n'a aucune importance si le prix du sous-jacent est un prix d'équilibre. Lorsque les investisseurs deviennent plus "riscophobes", le cours baisse, mais les formules évaluant le prix des options restent inchangés [14].

Un univers risque-neutre présente deux caractéristiques qui simplifient l'évaluation des produits dérivés:

-- La rentabilité espérée de tous investissement est le taux sans risque.

-- Le taux d'actualisation utilisé pour l'espérance des flux procurés par une option est le taux sans risque.

14

2.3 Modèle de Black-Scholes

2.3.1 L'équation aux dérivées partielles de Black-Scholes

Dans cette section, nous aborderons la démonstration de l'équation aux dérivées partielles de Black-Scholes pour une action ne versant pas de dividendes

Le processus suivi par l'action est un mouvement brownien géométrique, caractérisé par l'équation :

dS = uSdt + óSdz (2.2)
Notons f le prix d'une option d'achat ou de tout autre produit dérivé lié au titre S. La variable f est alors une fonction de S et t. En utilisant la formule d'Itô nous déduisons la relation suivante :

df = (?f?2f

?S^uS+ ??t f + ¹_?S2ó²S²)dt + ? f

_?SóSdz (2.3)

2

Sous leur forme discrète, les équations (2.2) et (2.3) s'écrivent :

OS = uSOt + óSOz (2.4)

et

O f = (?fuS+ ^?f + ¹ ?2ó2S2)Ot+ ^?f crSOz (2.5)

?S ?t 2 ?S²?S

où OS et Of représentent les variations de f et S pendant un court intervalle de temps de longueur Ot. Les variations aléatoires de f et S sont gouvernées par le même processus de Wiener. En d'autres termes, les Oz des équations (2.4) et (2.5) sont identiques. Ainsi, en choisissant un portefeuille composé d'une action et de l'un de ses produits dérivés, la composante aléatoire peut être éliminée.

Un portefeuille approprié peut être défini de la façon suivante :

Vente d'une unité su produit dérivé.

Achat de _??Sf action.

Le détenteur du portefeuille est alors en position courte (vendeur) sur le produit dérivé et en position longue (acheteur) sur ?f/?S actions. La valeur du portefeuille, notée H, s'écrit

alors :

? f

H = -f + _?SS (2.6)

La variation OH de la valeur du portefeuille au cours d'un intervalle de temps Ot est donnée par :

? f

OH = -Of + _?SOS (2.7)

En substituant O f et OS, dans l'équation (2.7), par leurs valeurs, nous obtenons :

OH = (-?f- 1 ?22 ²₅²)Ot (2.8)

?t 2 ?S²

cette équation ne comporte pas l'expression Oz, le portefeuille doit être sans risque pendant l'intervalle de temps Ot. Les hypothèses énoncées à la section précédente impliquent qu'un tel portefeuille doit procurer une rentabilité égale au taux sans risque. Dans

le cas contraire, les investisseurs profiteraient d'une opportunité d'arbitrage. Nous pouvons donc écrire :

OH = rHOt (2.9)

où r représente le taux sans risque. Si nous remplaçons les termes H et OH de cette équation par leurs expressions données dans les équations (2.6) et (2.8), nous obtenons :

(af+1a2fcr2S2)Ot=r af Ot

at 2 aS2 (f _aS) (2.10)

et donc :

af +rS^af + ¹cr²S^2a22 = rf (2.11)

at as 2 aS

L'équation (2.11) est l'équation aux dérivées partielles de Black-Scholes. Cette équation a plusieurs solutions correspondant à tous les produits dérivés qui peuvent avoir S comme actif sous-jacent. La solution de l'équation dépend alors des conditions aux bornes qui caractérisent le produit dérivé considéré. Ces conditions précisent les valeurs de l'actif dérivé analysé aux bornes des ensembles de valeurs possibles de S et t.

Par exemple, dans le cas d'un call Européen, la condition aux bornes est :

f = max(S - K; 0), quand t = T Dans le cas d'un put Européen, elle s'écrit :

f = max(K - S; 0), quand t = T

Notons que 1e portefeuille utilisé dans la dérivation de l'équation (2.11) n'est pas un portefeuille sans risque de façon permanente. Il est sans risque uniquement pendant un intervalle de temps infinitésimal. En effet, dès que S et t varient, af /aS varie aussi. Ainsi, afin de conserver le caractère non risqué du portefeuille, il est nécessaire d'ajuster fréquemment les positions relatives de l'action et du produit dérivé au sein du portefeuille.

2.3.2 Les formules d'évaluation de Black-Scholes

Les formules de Black-Scholes permettant de calculer, à l'instant t = 0,la valeur d'un call Européen ou d'un put Européen sur une action qui ne verse pas de dividendes, sont les suivantes :

c = S0N(d1) - Ke-^rTN(d2) (2.12)

p = Ke^-rTN(-d2) - S0N(-d1) (2.13)

avec :

d1 = _v/

cr T

ln(S0/K) + (r + cr²/2)T

et :

ln(S0/K) + (r - cr²/2)T

_v/

cr T

d2 =

_v/

= d1 - cr T

15

La fonction N(x) désigne la fonction de répartition d'une loi normale centrée-réduite. En d'autres termes, c'est la probabilité qu'une variable suivant une loi normale, 0(0, 1), soit inférieure à x. Cette idée est illustrée dans la figure 2.1.

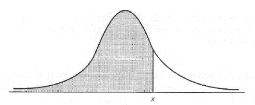
FIGURE 2.1 - Représentation de N(x),[14].

2.4 Modèle de Garman-Kohlhagen

Le modèle Garman-Kohlhagen est une modification du modèle d'évaluation des options de Black-Scholes. Il a été proposé en 1983 par Garman et Kohlhagen. Ils ont modifié le modèle Black-Scholes de manière à ce que le modèle puisse faire face à la présence de deux taux d'intérêt sans risque. La différence avec le modèle BS est que le modèle GK corrige la différence entre les taux d'intérêt domestiques et étrangers. En même temps, le modèle Garman-Kohlhagen partage les mêmes limites que le modèle Black-Scholes.

Le modèle Garman-Kohlhagen traite les devises étrangères comme s'il s'agissait de titres de placement qui fournissent un rendement en dividendes connu. Le propriétaire de la devise étrangère (domestique) reçoit un rendement en dividendes égal au taux sans risque du pays étranger (domestique).

Notons S le taux de change actuel (la valeur d'une unité de la devise étrangère mesurée en devise domestique). S est supposé suivre un mouvement Brownien géométrique semblable à celui des actions. Dans l'univers risque-neutre, la dynamique du processus s'écrit:

dS = (rd - rf)Sdt + óSdz (2.14)

En suivant les même démarche de la section précédente, on aboutit à l'équation aux dérivées partielles suivante

? f + (rd - rf)S ? f ?S2 = rd f (2.15)
?S + ¹ 2ó2S2 ?2 f

?t

Les valeurs d'un call Européen ou d'un put Européen sur devise deviennent: c = S0e^-rf ^TN(d1) - Ke^-rdTN(d2) (2.16)

p = Ke^-rd^TN(-d2) - S0e^-rf ^TN(-d1) (2.17)

avec:

d1 =

ln(S0/K) + (rd - rf + ó²/2)T

/

ó T

et :	d2 =	ln(S0/K) + (rd - rf - ó^2/2)T			/ = d1 - ó T

16

Le taux d'intérêt domestique, rd, et le taux d'intérêt étranger, rf, sont tous deux des taux continus pour la maturité T. Le put et le call sur une devise sont symétriques. De ce fait, un put permettant de vendre la devise A au taux de change K est équivalent à un call permettant d'acheter la devise B au prix 1/K.

17

2.5 Les lettres grecques

Une institution financière qui vend une option à un client est confrontée au problème de gestion de son risque. L'institution financière doit donc neutraliser son exposition au risque du marché afin de ne pas subir des pertes importantes dans le cas où le client exerce cette option.

Les stratégies les plus sophistiqués utilisées par les traders, nécessitent le calcul de mesures telles que le delta, le gamma et le vega. Ces mesures sont communément appelées lettres grecques. Elles quantifient différents aspects du risque dans une position sur options.

Cette section examine les propriétés de certaines lettres grecques les plus importantes. Pour calculer une lettre grecque, il faut utiliser un modèle de valorisation d'option. Les traders retiennent le modèle de Black-Scholes ou ses extensions, dans notre cas le modèle de Gar-man-Kohlhagen, pour les options Européennes.

2.5.1 Delta

Le delta d'une option est défini comme le taux de variation de la valeur de l'option par rapport à celle du sous-jacent. C'est la pente de la courbe reliant la valeur de l'option à celle du sous-jacent. La figure 2.2 montre la relation entre la valeur du call et le cours du sous-jacent. Lorsque 1e cours du sous-jacent est au point A, la valeur de l'option est au point B, et est la pente de la tangente indiquée dans la figure.

Plus généralement:

?c

= ?S

Pour un call Européen sur devise, on peut montrer que:

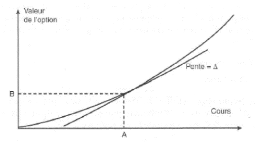
FIGURE 2.2 - Représentation du delta, [14].

(c) = e^-rf ^TN(d1)

où d1 est défini dans l'équation (2.16).

Pour un put Européen sur devise, le delta est égal à :

(p) = e^-rf ^T(N(d1) - 1)

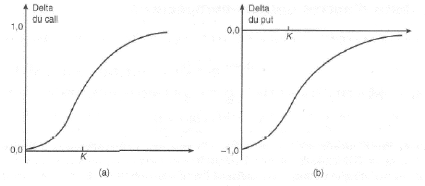
La figure 2.3 montre les variations du delta d'un call et d'un put en fonction du cours du sous-jacent.

18

FIGURE 2.3 - Variation du delta en fonction du cours du sous-jacent: (a) option d'achat; (b) option de vente, [14].

2.5.2 Gamma

Le gamma d'un portefeuille d'options, noté F, est le taux de variation du delta du portefeuille en fonction de la valeur de l'actif sous-jacent. C'est la dérivée seconde de la valeur du portefeuille par rapport au cours de l'actif:

?²Ð

F = ?S2

Si le gamma est faible, le delta varie lentement, et il n'est pas nécessaire d'ajuster fréquemment le portefeuille pour maintenir un portefeuille delta-neutre. Par contre, si le gamma est important en valeur absolue, le delta est très sensible aux variations du cours de l'actif sous-jacent. Il est alors risqué de laisser un portefeuille delta-neutre inchangé trop longtemps.

Pour un call ou un put Européens sur devise, le gamma s'écrit:

N0(d1)e-rf T

F = v

S0ó T

où d1 est défini dans l'équation (2.16). Et N'(x) par:

1

N'(x) = v2ð e-x2/2 (2.18)

Le gamma est toujours positif, la figure 2.4 montre les variations du gamma en fonction du cours du sous-jacent.

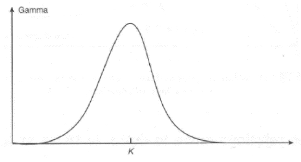
FIGURE 2.4 - Variation du gamma en fonction du cours du sous-jacent, [14].

2.5.3 Thêta

Le thêta d'un portefeuille d'options, È, se définit comme le taux de variation de la valeur du portefeuille par rapport à la durée de vie de l'option.

Pour un call Européen sur devise, le thêta s'écrit:

v

2 T

Pour un put Européen sur devise, on obtient:

È(c) =

-S0N0(d1)óe-rf T+ rfS0N(d1)e-rf T - rdKe^-rd^TN(d2)

19

È(p) =

-S0N0(d1)óe-rf T	rfS0N(-d1)e-rf ^T+ rdKe^-rd^TN(-d2)

où d1 et d2 sont définis dans l'équation (2.16) et N⁰(x) dans l'équation (2.18).

Le thêta d'une option est généralement négatif car la valeur de l'option diminue lorsqu'on se rapproche de l'échéance. La variation du thêta en fonction du cours du sous-jacent, pour un call, est illustrée dans la figure 2.5.

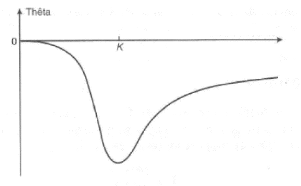
FIGURE 2.5 - Variation du thêta en fonction du cours du sous-jacent, [14].

20

2.5.4 Vega

Nous avons supposé, jusqu'à présent, que la volatilité du sous-jacent reste constante pendant toute la durée de vie de l'option. En réalité, c'est loin d'être vrai car la volatilité varie au fil du temps. Cela signifie que la valeur de l'actif dérivé est susceptible de changer à cause des variation de la volatilité.

Le vega d'un portefeuille de d'options, y, représente le taux de variation de la valeur du portefeuille en fonction de la volatilité de l'actif sous-jacent:

y =

aÐ

acr

Si la valeur absolue du vega est importante, la valeur du portefeuille est très sensible au moindre changement de volatilité. Si le vega est faible, en valeur absolue, un changement de la volatilité n'aura qu'un léger impact sur la valeur du portefeuille.

Pour un call ou un put Européens sur devise, le vega est obtenu par:

v

y = S0 TN0(d1)e-rf T

où d1 est défini dans l'équation (2.16) et N'(x) dans l'équation (2.18).

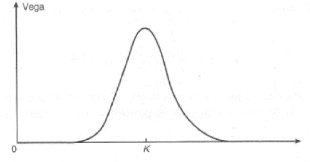
Le vega d'une option est toujours positif. La variation du vega en fonction du cours du sous-jacent est illustrée dans la figure 2.6.

2.5.5 Rhô

Le rhô d'un portefeuille d'options est en fonction du taux d'intérêt sans risque:

aÐ

rhào =

FIGURE 2.6 - Variation du vega en fonction du cours du sous-jacent, [14].

ard

Il mesure la sensibilité de la valeur du portefeuille d'options par rapport à une variation du taux d'intérêt.

Pour un call Européen sur devise, le rhô s'écrit:

rhào(c) = KTe^-rd^TN(d2)

21

Pour un put Européen sur devise, on obtient:

rhào(p) = -KTe^-rdTN(-d2)

où d2 est défini dans l'équation (2.16)

2.6 Application

Après avoir présenté les différente notions théoriques, nécessaires au pricing des options Européennes sur devises, nous allons passer maintenant à l'application de ces notions pour élaborer un pricer de ces options.

La première tâche réalisée dans ce projet était le développement d'un pricer des options Européennes sur devises. Dans un premier lieu, nous avons réalisé une librairie de pricing sous le langage Python, cette librairie contient des fonctions qui permettent le calcul des prix des options, ainsi que leurs différentes sensibilités en fonctions des différents inputs : Prix spot, prix d'exercice, temps restant jusqu'à l'échéance, taux sans risque domestique, taux sans risque étranger et enfin, la volatilité. Les fonction créées en Python on été ensuite utilisés comme étant des fonctions Excel à l'aide d'un outil qui permet de relier les deux plateformes. Tout cela dans le but de profiter en même temps de la rapidité offerte par le langage Python, ainsi que la facilité d'utilisation d'Excel.

Résultats et validation

Les résultats obtenus par notre pricer doivent être testés et comparés avant d'être validés. Pour cela nous avons comparé les résultats de notre pricer avec celles du logiciel DerivaGem - Version 4.00, c'est un logiciel développé par A-J Financial Systems Inc, ce logiciel permet d'effectuer des calculs détaillés pour différents produits dérivés tels que les dérivés de crédit et les dérivés de taux d'intérêt, ainsi que pour les options sur les actions, les indices, les devises, les prix, les volatilités implicites et les contrats à terme en saisissant les données de base et en appliquant des filtres automatisés.

DerivaGem - Version 4.00 est basé sur VBA-Excel, ces pricipale fonctionnalités sont:

-- Effectuer des calculs pour les dérivés de crédit et les dérivés de taux d'intérêt, ainsi

que pour les options sur les actions, les indices, les devises et les contrats à terme.

-- Calculer les prix, les volatilités implicites et les lettres grecques.

-- Mettre en oeuvre des modèles de taux d'intérêt normaux et lognormaux pour évaluer

les options Américaines sur taux d'intérêt.

-- Afficher des graphiques montrant les relations entre les variables.

-- Afficher les arbres binomiaux/trinomiaux utilisés pour l'évaluation

Pour tester notre pricer, nous avons choisis 6 options pour lesquelles nous allons calculer le prix et les trois sensibilités, delta, gamma et vega, et nous allons comparer les résultats de notre pricer avec celles du logiciel.

Le tableau suivant contient les inputs de nos 6 options:

22

TABLE 2.1 - Les inputs des 6 options utilisées pour tester le pricer.

Option	Type	S0	K	T	rd	rf		ó	1
Call	1,07	1,08	0,5013	1,681%	-0,383%	5%		2
Put	1,11	1,09	2	1,708%	-0,195%	15%		3
Call	1,09	1,09	1	1,69%	-0,32%	10%		4
Put	1,1	1,1	1,5013	1,699%	-0,258%	10%		5
Call	1,13	1,11	1	1,69%	-0,32%	15%		6
Put	1,11	1,12	0,7534	1,686%	-0,351%	5%

Le tableau ci-dessous contient les prix donnés par notre pricer et le logiciel DerivaGem - Version 4.00, pour chacune des 6 options:

TABLE 2.2 - Comparaison des prix des options.

Option	Prix du pricer		Prix du logiciel DerivaGem	1
1,5699%	1,5698%		2
6, 4266%	6, 4268%		3
5,4923%	5,4920%		4
3,8698%	3,8696%		5
8, 9740%	8, 9737%		6
1, 5876%	1, 5878%

Le tableau suivant contient une comparaison des résultats obtenus pour le calcul des lettres grecques (delta, gamma, vega) entre notre pricer et le logiciel DerivaGem - Version 4.00 :

TABLE 2.3 - Comparaison des lettres grecques.

Option	Pricer				Logiciel DerivaGem
	Gamma		Vega	Delta	Gamma	Vega	1
0, 5104	10,5484		0, 003027	0, 5198	10, 5404	0, 003024	2
-0, 2298	1, 2911		0, 004772	-0, 3566	1, 5876	0, 005868	3
0,6010	3,5578		0,004227	0,6010	3,5578	0,004227	4
-0, 3269	2, 6828		0, 004873	-0, 3831	2, 8397	0, 005158	5
0,6305	2,2374		0,004285	0,6305	2,2374	0,004285	6
-0,4506	8,2364		0,003822	-0,4341	8,1860	0,003799

On peut donc remarquer que les valeurs des prix et des lettres grecques, données par notre pricer, sont très proches de celles données par le logiciel DerivaGem - Version 4.00. On pourra donc valider ces résultats.

23

Interface

L'interface utilisateur de notre pricer est représentée dans la figure 2.7. Dans cette interface, l'utilisateur peut évaluer plusieurs options en même temps, chacune dans une ligne Excel, afin de permettre à l'utilisateur de gagner du temps en effectuant plusieurs opérations à la fois.

FIGURE 2.7 - Interface de pricing des option Européennes sur devises.

24

Chapitre 3

Surface de volatilité : Modèle de

Vanna-Volga

De façon générale, le modèle de Black-Scholes et ses extensions restent l'outil fondamental utilisé par les traders des options. Cependant, il existe des inconsistances qui rendent impossible son application directe sur le marché des options:

-- Le modèle de Black-Scholes suppose une volatilité constante tout au long de la durée de vie de l'option, ce qui n'est pas le cas dans la réalité.

-- Contrairement à l'hypothèse centrale du modèle, le prix du sous-jacent ne varie pas de façon continue.

C'est pourquoi le modèle est utilisé comme une approximation de premier ordre au fonctionnement des marchés.

Dans ce chapitre, nous décrivons les courbes de volatilité utilisées par les opérateurs des marchés d'options sur devises. Nous expliquons la relation entre le Smile de volatilité et la distribution de probabilité risque-neutre de la valeur future d'un actif. Nous examinons également de quelle manière ces opérateurs adaptent la volatilité en fonction de la maturité de l'option, et comment ils utilisent des surfaces de volatilités comme outils d'évaluation.

3.1 Volatilité historique et volatilité implicite

Dans le modèle de Black-Scholes, ou de Garman-Kohlhagen, tous les paramètres sont connus (K, T) ou observables (S, rd, rf) sauf la volatilité ó qui doit être estimée, Il y a plusieurs façons de la calculer.

3.1.1 Volatilité historique

La volatilité historique est calculée à partir de l'historique des prix du sous-jacent. Le paramètre de volatilité n'est pas observable mais son estimation empirique est facile si les rendements sont indépendants et identiquement distribués. Le calcul n'est pas compliqué, mais la détermination de la période sur laquelle on veut estimer la volatilité reste très délicat.

25

Afin d'estimer empiriquement la volatilité d'une action, des relevés de cours périodiques sont nécessaires.

Notons:

-- n + 1 : Le nombre d'observations.

-- Si : Le cours du sous-jacent au terme du i-ème intervalle de temps. -- T : La durée des intervalles de temps en années.

On pose alors:

ui = ln( ^Si )

Si-1

pour i = 1,2,..., n.

L'estimation, s, de l'écart-type des ui est donnée par la formule:

s =

soit:

\/

n

1 (ui - u)²
n - 1 ? i=1

s = n(n - 1)⁽

\/ n - 1 ? u2 i - 1 ? ui)
1

i=1 i=1

n n

2

où u est la moyenne des ui.

Nous savons que l'écart-type des ui est égal à crVT . La variable s est donc un estimateur de crVT. Nous pouvons donc estimer cr par crà avec:

crà =

s

_VT

Il peut être démontré que l'écart-type de cet estimateur est approximativement égal à àcr/V2n.

Déterminer une valeur optimale de n reste très délicat. Généralement, plus le nombre de données est important, meilleure est la qualité de l'estimation. Mais la volatilité historique, cr, varie au fil du temps, et la prise en compte de données trop anciennes n'est pas pertinente pour une bonne prédiction de la valeur future. Une règle générale très utilisée consiste à faire coïncider le nombre de jours sur lequel on se base pour le calcul de la volatilité historique avec l'horizon d'investissement. Ainsi, si l'investisseur cherche à estimer une volatilité pour calculer le prix d'une option d'échéance deux ans, il utilisera des données quotidiennes relevées sur une période de deux ans.

3.1.2 Volatilité implicite

En connaissant le prix du marché d'une option, il est possible d'obtenir une valeur unique pour la volatilité. Il suffit de trouver la volatilité, notée crimp, telle que l'estimation donnée par le modèle de Black-Scholes corresponde à celle du marché. Cette valeur est appelée volatilité implicite. Plus généralement, la volatilité implicite d'une option est la volatilité permettant, quand elle est injectée dans le modèle de Black-Scoles, de donner le prix de l'option sur le marché.

26

La courbe de volatilité utilisée par les traders pour évaluer les options sur devises a généralement la forme d'un sourire, représenté dans la figure 3.1, d'où le nom Smile. La volatilité est relativement faible pour des options à la monnaie, et elle s'élève progressivement au fur et à mesure que l'option devient davantage dans la monnaie ou en dehors de la monnaie. On peut donc déterminer la distribution de probabilité risque-neutre du prix d'un actif à

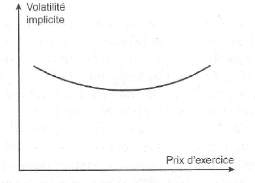
FIGURE 3.1 - Le smile de volatilité pour les options sur devises, [14].

une date future T à partir du Smile de volatilité déduit des prix d'options d'échéance T. Cette loi est appelée distribution implicite. Le Smile de volatilité de la figure 3.1 correspond à la distribution de probabilité indiquée en gras dans la figure 3.2. Une distribution log-normale avec la même moyenne et le même écart-type est reportée en pointillé dans la figure 3.2.

On peut voir que la distribution implicite a des extrémités plus épaisses que celles de la loi log-normale.

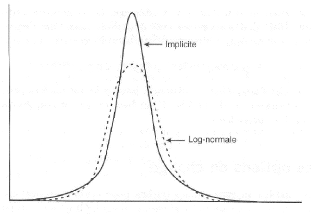
FIGURE 3.2 - La distribution implicite et la distribution log-normale des taux de change, [14].

27

3.2 Estimation de la volatilité implicite

La volatilité implicite est calculée à partir des prix de marché des produits les plus liquides et de la formule théorique d'évaluation d'option. Elle est obtenue en inversant la formule de Black-Scholes qui donne le prix _cBS du call par rapport au prix _cobs du call observé sur le marché, à un niveau de cours actuel donné, pour une maturité et un strike donné. Cette volatilité implicite crimp est donc donnée par la relation:

cBS(K, T, crimp) = cobs(K, T)

C'est donc un problème dit inverse et qui définit bien de manière unique crimp puisque le prix _cBS de Black-Scholes est une fonction strictement croissante de la volatilité.

Il n'y a pas de formule explicite pour crimp et on a recours à des méthodes numériques pour la calculer : Méthode de Newton Raphson, méthodes par dichotomie, méthode de splines cubiques, modèle de Vanna-Volga.

Notons que crimp dépend du strike et de la maturité liés au prix du call observé. Souvent, on calcule cette volatilité implicite pour différents strikes et/ou différentes maturités de call et on représente alors son graphe en fonction du strike et/ou de la maturité.

Dans cette section nous allons présenter brièvement la méthode de Newton-Raphson, puis nous allons se concentrer sur le modèle de Vanna-Volga car il est le plus adapté pour le marché de change.

3.2.1 Méthode de Newton-Raphson

L'algorithme de Newton-Raphson est utilisé pour trouver une approximation de la solution d'une fonction f(x) = 0. Le principe étant de partir d'une valeur initiale et d'approximer le résultat espéré à l'aide de la tangente en ce point. En effet, une tangente T étant affine, il est facile de trouver une solution x telle que T(x) = 0. Ainsi on peut définir la récurrence

suivante:

f(x_n)

xn+1 = x_n - f ⁰(x_n)

La figure 3.3 représente le principe de cette méthode:

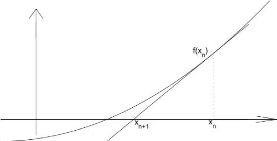
FIGURE 3.3 - Principe de le méthode de Newton-Raphson.

Afin de calculer la volatilité implicite à l'aide de la méthode de Newton-Raphson, on cherchera donc à minimiser la fonction suivante:

f(wimp) = cBS(K, T, wimp) - cobs(K, T)

A chaque itération il faut calculer wn+1 à partir du w_n obtenu dans l'itération précédente, tel que:

wn+1 = w_n

cBS(K, T, w_n) - cobs(K, T)

c0 BS(K, T, w_n)

Or, dériver cBS(K, T, wimp) - cobs(K, T) par rapport à wimp revient à calculer le Vega défini dans le chapitre précédent, on peut donc réécrire l'équation sous la forme:

wn+1 = wn		cBS(K, T, wn) - cobs(K, T)

Ci-dessous l'algorithme de Newton-Raphson:

Algorithm 1: Algorithme de Newton-Raphson.

wimp ? w0 e ? 10-⁴

while cBS(K, T, wimp) - cobs(K, T) = e do

wimp ? wimp

cBS(K,T,wimp)-cobs(K,T) c0 BS(K,T,wimp)

end

return wimp

28

3.2.2 Méthode de Vanna-Volga

La méthode de Vanna-Volga est une méthode populaire d'interpolation/extrapolation des smiles de volatilité. Cette technique est largement utilisée dans le contexte des marchés des changes, en raison de sa capacité à construire de manière cohérente tout le smile de volatilité en utilisant seulement trois cotations de marché.

Cette méthode consiste à ajouter une correction au modèle de Black-Scholes, pour ce faire, la méthode utilise les cotations les plus liquides sur le marché, généralement des options à la monnaie, des stratégies Risk Reversal et Butterfly (un chapitre sera consacré à ces stratégies de couverture). Elle consiste ensuite à construire un portefeuille de couverture qui annule le Vega, Vanna et Volga de l'option du modèle de Black-Scholes. Le choix de ces lettres grecques est lié au fait qu'ils offrent tous une mesure de la sensibilité de l'option par rapport à la volatilité, et donc le portefeuille de couverture construit vise à prendre l'effet du smile en compte.

Le smile de volatilité est fonction du strike K. Sur les marchés de change, les stratégies les plus liquides sont:

-- Straddle : C'est une stratégie consistant à acheter ou à vendre un put et un call sur le même sous-jacent, avec les mêmes dates d'échéance et prix d'exercice.

-- Strangle : Il s'agit en effet d'une variation du straddle, et qui correspond à acheter et un call et un put sur le même sous-jacent, même échéance, et ayant des prix d'exercice

différents, traditionnellement, le strike du call est au dessus du strike du put.

29

Butterfly : C'est une stratégie qui combine l'achat et la vente de 3 options de mêmes types (calls ou puts) et qui portent sur le même sous-jacent, ayant les mêmes échéances, mais 3 prix d'exercice différents K1, K2 et K3 tels que : K1 < K2 < K3. Le butterfly se compose donc de l'achat d'une option de strike K1, la vente de 2 options de strike K2 et l'achat d'une option de strike K3.

Normalement, les brokers cotent les volatilités au lieu des prix direct des instrument financiers. Elles sont exprimées en fonction de 0, par exemple, une volatilité à 250-call ou put fait référence à la volatilité aux strikes K_c, K_p qui satisfait 0call(Kc, U(K_c)) = 0, 25 et 0put(Kp, U(K_p)) = -0, 25 respectivement. Les cotations les plus liquides de la volatilité sont :

La volatilité à la monnaie : UATM

La volatilité 250-Risk Reversal (RR) : URR

La volatilité 250-Butterfly (BF) : UBF

La volatilité óATM

Elle est cotée sur le marché pour un Straddle à la monnaie de delta 0%. Le delta de ce Straddle est la somme des deltas du call et du put qui le composent : 0(c) + 0(p) = 0%

La volatilité óRR

Elle est estimée comme étant la différence entre la volatilité d'un call et celle d'un put. Il est convenu d'utiliser un call et un put de delta égal à 25% en valeur absolue pour calculer cette volatilité :

URR = U250c - U250p

La volatilité óBF

Elle est égale à la différence entre la volatilité d'un Strangle, qui est la moyenne des volatilités du put et du call de deltas respectivement -25% et 25%, et la volatilité à la monnaie :

UBF =	U250c + U250p		UATM

UBF

2

UBF

2

Calcul de la volatilité implicite On peut déduire que :

U250c = UATM + _UBF + U250p = UATM + UBF

Notons KATM, K250c ^et _K250p les strikes correspondant aux volatilités UATM, U250c ^et U250p respectivement. On peut monter que :

KATM = S0 e(rd-rf +U2

^AZ^M)T

(rd-r ^{c M})T-N^-1(0,25e^rf ^T)a_z50_c\T

K250c = S0 e f +

30

K254 = S0 e(rd --rf+^°ZA_ZM)T-N^-1(-0,25e^'f^T+1)v_z5o_p\T

Nous avons ainsi 3 couples :(ó25Äp, K25Äp), (óATM, KATM) ^et (ó25Äc, K25Äc). Pour des raisons de simplification on les notes : (ó1, K1), (ó2, K2) et (ó3, K3) respectivement.

Le modèle de Black-Scholes permet de donner le prix d'une option. Sous les hypothèses du modèle, l'utilisation d'une stratégie delta-neutre pour cette option permet de se couvrir contre le risque lié à la variation du prix du sous-jacent, ceci supposons que la volatilité est une donnée constante durant la vie de l'option.

Dans la réalité du marché, afin de contourner l'imperfection du modèle Black-Scholes au niveau de la volatilité, les traders couvrent ce risque en construisant un nouveau portefeuille.

Soit Ð un portefeuille constitué de :

La vente d'un call cK de strike K.

L'achat d'une quantité Ä du sous-jacent.

L'achat de 3 calls _cKi de strikes Ki, en proportions ùi, avec i = {1, 2, 3}.

On a donc:		3
Ð = cK - ÄS -	? i=1	ùicKi

On choisit Ä et ùi de telle sorte que notre portefeuille vérifie le système suivant :

Vega-neutre : ?Ð?ó = 0

Vanna-neutre : ?2Ð ?ó?S = 0

Volga-neutre : ?2Ð

?2ó = 0

La solution de ce système est :

ù1 =	V(cK) V(cK1)	ln(K2 K )ln(K3 K ) ù2 = ln(K2 K1 )ln(K3 K1 )	V(cK) V(cK2)	ln(K1 K )ln(K3 K ) ù3 = ln(K2 K1 )ln(K3 K2 )	V(cK) V(cK3)	ln( K1K)ln(K2 K )
						ln(^K3 K1 )ln(K3 K2 ) (3.1)

Avec : V(cK_i) = Vega(cK_i)

Une volatilité notée í, déduite à partir de la méthode de Vanna-Volga, pour un call de strike K est obtenue en ajoutant le prix du modèle de Black-Scholes au coût de la mise en place de la couverture ci-dessus :

3

c(K, í) = c(K, ó) + ? ùi(c(Ki, ói) - c(Ki, ó)) (3.2)

i=1

Avec c(K, ó) est le prix, par le modèle de Black-Scholes, d'un call de strike K et de volatilité constante ó.

Une courbe de volatilité implicite peut être construite en inversant l'équation (3.2), pour chaque valeur de strike K.

Approximation au 1^er ordre de la volatilité implicite On utilise l'approximation suivante :

c(Ki, ói) - c(Ki, ó) (ói - ó)V(cK_i)

On a donc:

3

c(K, í) c(K, ó) + L ùi(ói - ó)V(cK_i)

i=1

En substituant les ùi les résultats de (3.1), et en utilisant le fait que V(cK) = a donc:

3 L i=1

ùiV(cKi), on

3

c(K, í) c(K, ó) + V(cK)( L yiói - ó) c(K, ó) + V(cK)(í - ó) i=1

Avec :

3

í = L yiói (3.3)

i=1

Est l'approximation au 1^er ordre de la volatilité implicite í pour le strike K, et les coefficients yi sont donnés par :

ln(K2 _K )ln(K3 _K )

y2 =

ln(K2 _K1 )ln(K3 _K1 )

ln(K2 K )ln(K3 _K )

y3 =

ln(^K2 K1)ln(K3 _K2 )

y1 =

(3.4)

ln(^K3

K1 )ln(K3 _K2 )

ln(K1 K )ln(K2 ^K )

Cela montre que la volatilité implicite í peut être approximée par une combinaison linéaire des trois smiles de volatilité ói

Approximation au 2^nd ordre de la volatilité implicite

Une approximation au second ordre plus pertinente, peut être obtenue en utilisant l'approxi-mation suivante :

c(K, í) c(K, ó) + V(cK)(í - ó) + ₂Vó(cK)(í - ó)²

1

c(K, ó) +

3 L i=1

ùi(V(cKi)(ói - ó) + 2Vó(cKi)(ói - ó)^2) 1

Avec :

V(cKi)d1(Ki)d2(Ki)

Vó(cKi) = ó

Donc :

1 V(cK)d1(K)d2(K)

V(cK)(í - ó) + (í - ó)²

2 ó

3

- V(cK)ó + V2U) Lyid1(Ki)d2(Ki)(ói - ó)²

i=1 i=1

V(cK)

3

( 1d1(K)d2(K)(í - ó)^2 + (í - ó) - í - ó + 2 ó	3 L i=1	yid1(Ki)d2(Ki)(ói - ó)^2	~ 0
		2ó

31

D'où :

La résolution de cette équation quadratique donne l'approximation au second ordre de la volatilité implicite:

d1(K)d2(K)

Avec cr souvent prise égale à cr2 et y représente l'approximation au premier ordre de l'équa-tion (3.3).

y = cr +

s ( 3

-cr + cr² + 2cr(y - cr) + ? yid1(Ki)d2(Ki)(cri - cr)²) d1(K)d2(K) i=1

(3.5)

3.3 Application

Après avoir présenté les notions théoriques derrière la méthode de Vanna-Volga, nous allons maintenant les appliquer pour développer un outil qui permet de calculer la volatilité implicite de l'EURUSD pour un strike K et une maturité T données.

L'outil à été développé sous Python, il a été ensuite utilisé comme étant une fonction Excel à l'aide d'un outil qui permet de relier les deux plateformes.

Les inputs de cette outil sont le strike K et la maturité T, il permet ensuite de faire une interpolation bilinéaire par rapport à ces deux variables.

Comme nous avons mentionné dans la section précédente, les cotations utilisés pour la méthodes de Vanna-Volga sont : crATM, crRR ^et crBF. Les données de ces trois cotations sont représentées dans la figure 3.4, pour des maturités allant jusqu'à 10 ans.

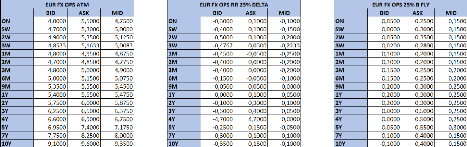
32

FIGURE 3.4 - Données du marché pour les 3 volatilités crATM, crRR ^et crBF.

En plus du smile de volatilité, les traders tiennent compte de la structure par termes des volatilités lorsqu'ils évaluent des options. Concrètement, la volatilité utilisée pour évaluer une option à la monnaie dépend de la durée de vie de cette option. Elle tend à être une fonction croissante de la maturité lorsque les volatilités historiques à court terme sont faibles. Cela traduit le fait que les opérateurs anticipent une hausse de la volatilité. Symétriquement, la

volatilité tend à être une fonction décroissante de la maturité lorsque les volatilités historiques à court terme sont élevées. Cela traduit également l'anticipation d'une baisse future de la volatilité.

Une surface de volatilité combine les smiles de volatilité et la structure par termes des volatilités, elle est souvent présentée sous la forme d'un tableau donnant les volatilités implicites en fonction du prix d'exercice et de la durée de vie. Un exemple de surface de volatilité pour l'EURUSD est représentée dans la figure 3.5.

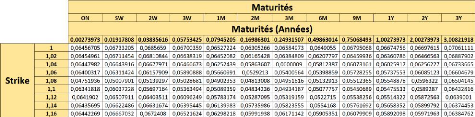
FIGURE 3.5 - Matrice de volatilité pour l'EURUSD.

Une des dimensions de ce tableau est le prix d'exercice, l'autre la durée de vie résiduelle de l'option. Les éléments du tableau donnent les différentes valeurs de volatilité implicite calculées par la méthode de Vanna-Volga. Pour chaque maturité, certaines données correspondent à des options liquides pour lesquelles les prix de marché sont fiables. Les autres éléments du tableau sont calculés par interpolation linéaire.

La surface de volatilité qui correspond à ce tableau est représentée dans la figure 3.6.

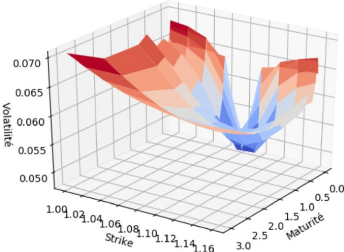
FIGURE 3.6 - Surface de volatilité pour l'EURUSD.

33

34

Les smiles de volatilité correspondant à chaque maturité sont représentés dans la figure 3.7.

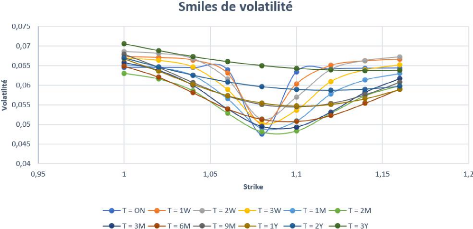
FIGURE 3.7 - Smiles de volatilité pour l'EURUSD.

On peut dire que l'impact, sur les options, des variations extrêmes et de l'instabilité de la volatilité du sous-jacent dépend de l'échéance des options. L'impact relatif de l'instabilité de la volatilité sur les cours des options croît avec la durée de vie de l'option, mais le Smile de volatilité créé par l'instabilité de la volatilité devient généralement moins prononcé.

35

Chapitre 4

Pricing des options Américaines sur

devises

Après avoir présenté les options Européennes sur devises, nous allons consacrer ce chapitre au options Américaines sur devises. Ces options donnent à leur détenteur le droit de les exercer à n'importe quelle date avant l'échéance de l'option.

Ce chapitre examine d'abord les caractéristiques des options Américaines, puis présente quelques méthodes utilisés afin de les évaluer, sachant qu'elle n'existe pas une formule fermée qui donne le prix exact d'une option Américaine. Nous allons utiliser une approche par la méthode des différences finies afin de résoudre l'EDP de Black-Scholes, ensuite, nous allons présenter trois autres modèles qui permettent de donner des formules fermées approximatives pour évaluer les options Américaines.

4.1 Généralités sur les options Américaines

4.1.1 Définition

Une option Américaine donne à son détenteur le droit de l'exercer à tout instant à partir de la date d'ouverture initiale jusqu'à la date d'échéance. Elle est donc plus flexible qu'une option Européenne ce qui explique le fait qu'elle est plus chère.

La valeur Ct d'un call Américain à l'instant t peut donc s'écrire:

Ct = ct + ec,t

Avec ct est la valeur d'un call Européen correspondant et _ec,t est la prime d'exercice prématuré. De même on pourra écrire la valeur d'un put Américain Pt à l'instant t comme suit:

Pt = pt + ep,t

Avec pt est la valeur d'un call Européen correspondant et _ep,t est la prime d'exercice prématuré.

36

4.1.2 L'exercice anticipé d'un call

Cas d'absence de dividendes

Nous allons montrer qu'il n'est jamais optimal d'exercer un call Américain sur un sous-jacent ne versant pas de dividendes.

On peut montrer que:

c > S0 _ Ke_^rT

Puisque les détenteurs d'options Américaines disposent d'opportunités d'exercice plus avantageuses que les détenteurs d'options Européennes équivalentes, la valeurs des calls Américains est supérieure ou égale à celle des calls Européens:

C > c

et par conséquent:

C > S0 _ Ke_^rT

Sachant que r > 0, il en découle que C > S0 _ K. S'il était optimal d'exercer plus tôt, on aura C = S0 _ K. Nous pouvons donc en déduire qu'il n'est jamais optimal d'exercer par anticipation en cas d'absence de dividendes.

Cas de présence de dividendes

Les dividendes entraînent une baisse des cours à la date de détachement. Leur annonce est une mauvaise nouvelle pour la valeur des calls. Par conséquent, lorsqu'un dividende est attendu, l'exercice prématuré du call Américain peut être optimal juste avant la date de détachement du dividende. Il n'est cependant pas optimal d'exercer à un autre moment.

4.1.3 L'exercice anticipé d'un put

Il peut être optimal d'exercer prématurément un put Américain portant sur un sous-jacent ne versant pas de dividendes. En effet, à tout moment un put devrait être exercé s'il est suffisamment dans la monnaie.

Pour démontrer la condition d'exercice optimal d'un put Américain, on utilisera la parité call-put:

p = c + Ke_^rT _ S0

En ajoutant et en soustrayant K dans cette équation, on peut écrire:

p = K_S0+c_K(1 _ e_^rT)

Si le sous-jacent ne verse pas de dividendes, le prix d'un call Européen sera donc égal au prix d'un call Américain correspondant, c = C, l'équation devient:

p = K _ S0 + C _ K(1 _ e_^rT)

Quand C > K(1 _ e_^rT) on a p > K _ S0, donc:

P > p > K _ S0

Donc l'exercice anticipé n'est pas optimal sous cette condition.

37

38

En général, l'exercice anticipé d'un put devient d'autant plus intéressant lorsque S0 baisse, r augmente et que la volatilité cT diminue.

4.2 Méthode des différences finies

La méthode des différences finies peut être utilisé pour évaluer les produits dérivés à travers la résolution de l'équation aux dérivées partielles (EDP), satisfaite par le prix de ces actifs. Pour cela l'EDP est convertie en un ensemble d'équation de différence, ces équations sont ensuite résolues de manière itérative.

Dans cette section, nous allons appliquer la méthode des différences finies pour l'évaluation d'options Américaine sur devises. Cette option doit vérifier l'EDP (2.15),déjà démontrée plus haut:

a at f + (rd - rf )S a f (4.1)

aS + ¹ 2cT2S2 a2 f

aS2 = rd f

Discrétisation

Considérons tout d'abord un maillage en espace (qui représente le prix du sous-jacent) et en temps, nous nous en servons pour écrire le schéma numérique nécessaire à la résolution.

Discrétisation en temps

La durée de vie de l'option, T, est divisée en N intervalles de durées:

T

L\t = N

Nous avons donc:

t_n = nL\t Vn E [0, N]

Discrétisation en espace

Notons _Smax un taux de change suffisamment élevé pour qu'une fois celui-ci atteint, l'option n'ait virtuellement aucune valeur. L'intervalle [0, _Smax] est aussi divisé en M intervalles de longueur:

Smax

L\S = M

On considère donc M + 1 taux de change régulièrement espacés:

S_n = nL\S Vn E [0, M]

La valeur de _Smax doit être choisie de façon que l'un de ces taux de change soit le taux de change spot de la devise sous-jacente.

Schéma numérique

Les dates et les taux de change définissent une grille de dimension (N + 1) x (M + 1), représentée dans la figure 4.1. Le point (i, j) de la grille correspond à la date iL\t et au taux de change jL\S, et _fi,j désigne la valeur de l'option en ce point.

FIGURE 4.1 - Représentation du schéma numérique de résolution, [14].

Schéma explicite des différences finies

Dans le schéma explicite, pour tout point intérieur (i, j) de la grille, on peut approximer af/aS par :

af aS

fi+1,j+1 - fi+1,j-1 =(4.2)

20S

L'approximation de a²f /aS² par différences finies peut être donnée par :

a^2f aS2 =

fi+1,j+1 - 2fi+1,j + fi+1,j-1 (4.3) 20S^2

Pour af/at l'approximation suivante est retenue :

af at

fi+1,j - fi,j =(4.4) 0t

En substituant les équation (4.2), (4.3) et (4.4) dans l'équation aux dérivées partielles (4.1) et en remarquant que S = j0S, on obtient

fi+1,A_t f + (rd - rf )j0Sfi+1,j+20S -1 ₊1

02j20S2 fi+1,j+1 - 220S2j rdfid

j

pour j = 1,2, , M - 1 et i = 0,1, , N - 1.

Un réarrangement des termes conduit à :

fi,j = aj _fi+1,j-1 + bj _fi+1,j + cj fi+1,j+1 (4.5)

avec :

aj = 1 + r0t(- 12(rd-rf)j0t+12~2j20t)

39

( )

1

bj = 1 - ó²j²Lt
1 + rLt

cj =

1 ₍₁ )

₂(rd - rf )jLt + ¹ 2ó2j2Lt

1 + rLt

La figure 4.2 représente la différence entre le schéma explicite et le schéma implicite.

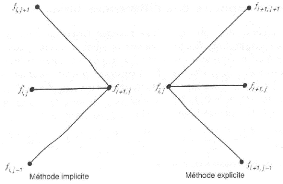
FIGURE 4.2 - Différence entre le schéma implicite et le schéma explicite.

Le schéma implicite donne une relation entre trois valeurs différentes de l'option à la date iLt qui sont fi,j-1, fi,j ^et _fi,j+1, et une valeur de l'option à la date (i + 1)Lt qui est _fi+1,j. Par contre, le schéma explicite donne une relation entre la valeur de l'option à la date iLt qui est fi,j et trois valeurs différentes de l'option à la date (i + 1)Lt qui sont fi+1,j-1, fi+1,j ^et fi+1,j+1

L'avantage de la méthode implicite est qu'elle est indéfiniment stable, mais elle nécessite la résolution d'un système de M - 1 équation, à chaque pas du temps, afin de déterminer la valeur de _fi,j à partir des _fi+1,j. Pour cette raison on a choisi d'utiliser la méthode explicite afin de simplifier les calculs, mais cette méthode nécessite une étude de stabilité.

Conditions initiales et aux limites

Conditions initiales

Puisque nous avons utilisé un schéma rétrograde, la condition initiale correspond à la condition à la date d'expiration de l'option.

-- Pour un call : À la date t = T on a :

fN,j = max(S - K;0) = max(jLS - K;0) j = 0,1, , M (4.6)

-- Pour un put : À la date t = T on a :

fN,j = max(K - S;0) = max(K - jLS;0) j = 0,1, , M (4.7)

40

Conditions aux limites

On suppose qu'il n'existe pas de convexité aux bords, de sorte que les valeurs aux bords n'affectent pas les calculs de manière significative, on impose pour cela les conditions Zero-Gamma aux deux extrémités de l'espace, on a : ?2 f

?S2 = 0 pour j = 0 et j = M, on aura donc:

fi,0 - 2 _fi,1 + fi,2 = 0 (4.8)

fi,M-2 - 2fi,M-1 + fi,M = 0 (4.9)

Formulation matricielle

Afin d'implémenter le code de résolution numérique de l'EDP avec le schéma explicite, il nous faut tout d'abord faire la formulation matricielle de l'équation (4.5).

La formulation matricielle de l'équation (4.5) et des condition initiales et aux bords est donnée par:

Fi = AFi+1 + Ki+1 (4.10)

?

? ? ? ? ? ?

Avec i = 0,1, , N - 1 et

fi,1

Fi =

fi,2

...

..

.

i,M-1

Ki+1 =

? ? ? ? ? ? ?

a1 fi+1,0 0 ... ... cM-1 fi+1,M

? ? ? ? ? ? ?

A = ? 0 a3 b3 ··· ··· 0 0

?b1 c1 0 ··· ··· 0 0

? ? a2 b2 c0 ··· ··· 0 0

? ? .

? .. ....

0 0 0 · · · ··· aM-1 bM-1

. . ....

. ..

. . ... ?

? ? ? ? ? ?

Stabilité et convergence

La méthode de différences finies traitée ci-dessus est stable et fiable sous certaines conditions. En effet, pour une équation aux dérivées partielles bien posée, un schéma d'approxi-mation numérique convergent nous donnera sa vraie solution, tant que le schéma est stable. Les paragraphes suivants décrivent ce que l'on entend par chacun de ces termes techniques: schéma numérique bien posé, convergent et stable.

Il faut d'abord déterminer si le problème mathématique pour lequel une solution est recherchée a non seulement une solution, mais aussi si cette solution est facile à trouver. On sait qu'un tel problème est bien posé, et ces problèmes ont généralement une solution qui change peu lorsqu'on se déplace dans son voisinage à petits pas . Les mathématiciens appellent cela stable sous l'effet de petites perturbations. Le fait que notre problème de pricing des options

est bien posé est intuitivement évident: L'économie derrière nous dit qu'il n'y aura qu'un seul prix pour le contrat d'option à un et ce prix évoluera lentement en fonction des petites variations des variables économiques.

Un schéma numérique est dit convergent si, au fur et à mesure que la taille du maillage et les tailles des pas de temps diminuent, le schéma de différences finies se rapproche de plus en plus des équations différentielles qui tentent de l'approcher. Nous avons donc choisi une bonne discrétisation du problème considéré. C'est également le cas pour le schéma de différences finies explicite pour déterminer les prix des options ci-dessus. Au fur et à mesure que la taille des pas devient de plus en plus petite, nos approximations des dérivés s'améliorent.

En passant du problème à la méthode d'approximation que nous adoptons, nous trouvons que les idées de stabilité sont également importantes. La stabilité d'une méthode d'approxi-mation mise en oeuvre fait référence à l'impact que de petites erreurs dans la méthode ont sur les résultats. Si ces petites erreurs peuvent produire de grandes fluctuations dans les résultats - en déplaçant la solution approximative loin de la vraie solution - alors la méthode a une faible stabilité. Un système de différences finies efficace doit donc satisfaire les conditions de stabilité.

Lemma 4.2.1. On peut montrer que le schéma explicite des différences finies est stable ssi

0 < (ÄS)2 = 1

Ät

2

Lemma 4.2.2. On peut montrer que le schéma implicite des différences finies est stable ssi

Ät

0 < (ÄS)2

D'après le lemme 4.2.1 et le lemme 4.2.2, nous savons que la méthode implicite est toujours stable pour l'EDP de Black-Scholes car Ot et OS sont tous deux positifs, mais la méthode explicite n'est pas toujours stable. Ainsi, la stabilité et la précision de ces deux méthodes à différences finies exigent que ces conditions soient satisfaites pour les valeurs assez petites de Ot et OS.

Résolution

Pour évaluer les options Américaines à l'aide de la méthode des différences finies nous devons faire respecter l'exigence selon laquelle, à chaque noeud, la valeur de l'option est supérieure à son payoff (valeur intrinsèque) à cet instant.

Cas d'un call

La valeur d'un call Américain, à chaque instant i, doit vérifier la condition suivante:

fi,j ~ max(jÄS - K;0)

car sinon, l'exercice à la date à la date T - iÄt est optimal. Donc:

fi,j = max(max(jÄS - K;0); aj _fi+1,j-1 + bj _fi+1,j + cj fi+1,j+1)

41

42

Cas d'un put

La valeur d'un put Américain, à chaque instant i, doit vérifier la condition suivante:

fi,j = max(K - jÄS;0)

car sinon, l'exercice à la date à la date T - iÄt est optimal. Donc:

fi,j = max(max(K - jÄS; 0); aj _fi+1,j-1 + bj _fi+1,j + cj fi+1,j+1)

4.3 Approximation de Barone-Adesi et Whaley (1987)

Barone-Adesi et Whaley (1987) [2] écrivent le prix de l'option Américaine comme la somme du prix de l'option Européenne correspondante et d'une quantité appelée prime d'exer-cice anticipé. Le prix de l'option Européenne est donné par la formule de Black-Scholes et la prime d'exercice anticipé est approximée par la solution d'un problème à frontière libre pour une équation différentielle ordinaire. Cette équation différentielle ordinaire est obtenue en ignorant le terme de la dérivé par rapport au temps dans l'équation aux dérivées partielle satisfaite par la prime d'exercice anticipé.

Barone-Adesi et Whaley donnent une formule simple pour la solution du problème à frontière pour une équation différentielle ordinaire. De plus, ils déterminent une approximation de la frontière libre en résolvant numériquement une équation non linéaire qui dépend de la variable temporelle comme paramètre. Cette solution approximative du problème de pricing des options Américaines est appelé approximation quadratique de Barone-Adesi et Whaley, elle est largement utilisé sur les marchés financiers par les praticiens.

L'approximation quadratique donnée par Barone-Adesi et Whaley sera utilisée pour évaluer des calls et des puts Américains sur devises. Le modèle est rapide et précis pour la plupart des valeurs d'entrée pratiques. Pour une démonstration détaillé des formules, se référer à Barone-Adesi, G. and Whaley, R.E. (1987) [2].

Call Américain sur devises

Le prix d'un call Américain est donnée par:

_f

c(S, K, T) + A2(S/S^*)q² si S < S*

C(S, K, T) = S - K si S = S*

Avec c(S, K, T) est le prix d'un call Européen correspondant, donnée par la formule de Black-Scholes, et

_S*

A2 = (1 - e^-rf ^TN(d1(S^*)))
q2

d1(S) =

ln(S/K) + (rd - rf + ó^2/2)T v ó T

43

q2 =	\ -(N - 1) + (N - 1)^2+ 4M/X 2
2rd M= N = 0^-^2		2(rd - rf)	X = 1 - e-rdT
		0^-^2

Put Américain sur devises

(

p(S, K, T) + A1(S/S^**)q¹ si S > S**

P(S, K, T) =

K - S si S = S**

Avec p(S, K, T) est le prix d'un put Européen correspondant, donnée par la formule de Black-Scholes, et

_S**

A1 = (1 - e^-rf ^TN(-d1(S^**)))
q1

q1 =

\

-(N - 1) - (N - 1)² + 4M/X

2

Pour le call Américain, S^* est le prix critique du sous-jacent qui vérifie :

_S*

S* - K = c(S^*, K, T) + (1 - e^-rf ^TN(d1(S^*))) (4.11)
q2

Même si S^* est le seul inconnu dans l'équation (4.11), il doit être déterminé de manière itérative. Pour commencer, nous allons commencer par calculer les deux cotés de l'équation (4.11) pour une valeur initiale S1. Notons :

LHS(Si) = Si - K

Si

RHS(Si) = c(Si, K, T) + (1 - e^-rf ^TN(d1(Si)))

q2

Nous allons utiliser l'algorithme de Newton-Raphson, décrit plus haut, pour résoudre cette équation.

La pente de RHS en Si est :

?RHS	1 1 1 C e-rf Tn(d1(Si))~ = bi = e^-rf ^TN(d1(Si))(1 - ) + - v q2 q2 0- T
?Si

où n(.) est la fonction densité de la loi normale.

Étant donnée une valeur initiale Si, il en découle directement de la méthode Newton-Raphson que la prochaine et meilleure estimation, _Si+1, est :

K - RHS(Si) - biSi

Si+1 =

1 - bi

La procédure itérative doit se poursuivre jusqu'à ce que l'erreur relative absolue se situe dans un niveau de tolérance acceptable. Par exemple :

|LHS(Si - RHS(Si| < 10^-5 K

44

Pour le put Américain, S^** est le prix critique du sous-jacent qui vérifie :

S**

K - S^** = p(S^**, K, T) - (1 - e^-rf ^TN(-d1(S^**))) (4.12)
q1

Notons :

VS(Sj) = K - Sj

Sj

HS(Sj) = p(Sj, K, T) - (1 - e^-rf ^TN(-d1(Sj)))

q1

La pente de HS en Sj est :

?HS ?Sj

= bj = -e^-rf ^TN(-d1(Sj))(1 - 1₎ 1 (1 + e-rf ^Tn(-d1(Sj))) -

v

q1 q1 ó T

Étant donnée une valeur initiale Sj, il en découle directement de la méthode Newton-Raphson que la prochaine et meilleure estimation, _Sj+1, est :

Sj+1 =

K - HS(Sj) + bjSj 1 + bj

Comme toujours avec l'utilisation de la méthode Newton-Raphson, nous avons besoin d'une valeur de départ. Barone-Adesi et Whaley suggèrent d'utiliser :

v ( K )

S* 1 = K + (S^*(co) - K)(1 - e^h2) avec h2 = -((rd - rf)T + 2ó T) S^*(co) - K

Si* = S^**(co) + (K - S^**(co))e^h1 avec h1 = ((rd - r)T - 2cr.\/T) ( )

f K - S^K**(co)

Avec S(co) est le prix critique du sous-jacent quand la date d'échéance tend vers l'infini :

S^*(co) =					K
1	-	2(-(N	-	1)	+ (N - 1)^2 + 4M)-^1 / -K
S**(co) 1	-	2(-(N	-	1)	/(N - 1)^2 + 4M)-^1

4.4 Approximation de Bjerksund et Stensland (1993)

L'approximation de Bjerksund et Stensland (1993) [6] peut être utilisée évaluer des options Américaines sur actions, futures et devises. La méthode est analytique et extrêmement efficace et économique sur le plan informatique. L'approximation de Bjerksund et Stensland est basée sur une stratégie d'exercice correspondant à une frontière plane X (prix de déclenchement).

45

Les résultats numériques montrent que le prix donnée par l'approximation est très proche de la véritable valeur de l'option. Pour les options à court terme, la méthode est aussi précise que l'approximation quadratique par Barone-Adesi et Whaley, alors que cette méthode méthode est nettement plus performante avec les options à long terme. Cependant, une approximation encore plus précise est l'approximation de Bjerksund et Stendsland (2002) [7] qui sera bientôt présentée. Pour une démonstration détaillé des formules, se référer à Petter Bjerksund and Gunnar Stensland Colsed-Form Approximation Of American Options (1993) [6].

Call Américain sur devises

Il est bien connu dans la littérature que la valeur d'une option peut être représentée comme l'espérance, dans l'univers risque-neutre, du payoff actualisé au taux sans risque.

Considérons un call Américain ayant une maturité T est un strike K. Pour une stratégie d'exercice donnée, représentée par un temps d'arrêt ô ? [0, T], la valeur de cette option pour cette stratégie est donnée par:

C = E0(e^-rd^ômax(S_ô - K;0))

En conséquence, le prix d'un call Américain est:

C(S, K, T,rd,rf, ó) = sup E0(e^-rd^ômax(S_ô - K;0))

ô?[0,T]

Bjerksund et Stensland (1993) obtiennent la valeur du call Américain sous réserve d'un exercice anticipé lorsque le prix de l'actif sous-jacent atteint une frontière plane X > K par le bas. Le call Américain peut être décomposé de :

-- Un call Européen up-and-out avec une barrière knock-out X, de strike K et de maturité T.

-- Un rabais X - K réceptionné à la date du knock-out si l'option atteint la barrière knockout avant sa date de maturité.

L'approximation d'un call Américain donnée par Bjerksund et Stensland (1993) est:

C = C(S, K, T, rd, rf, ó)

où

C = áSâ - áÖ(S, T, â, X, X) + Ö(S, T,1, X, X) - Ö(S, T,1, K, X)

- KÖ(S, T, 0, X, X) + KÖ(S, T, 0, K, X) (4.13)

Avec:

á = (X - K)X^-â

₍₁ \ ₍rd - rf \2

2 - rd - rf + 2rd

â = + ó2 - 1

ó2 2 ó2

La fonction Ö(S, T, ã, H, X) est donnée par:

_\ê (

Ö(S, T, ã, H, X) = eëSã( ( X d - 2ln(X/S) \\

N(d) - N v

S ó T

46

( ₂ã(ã - 1)ó²)

ë = - rd + ã(rd - rf ) + 1 T

d=

( 2)ó2)

ln(S/H) + rd - rf + (ã - 1 T

ê =

v

ó T

2(rd - rf)

ó2 + (2ã - 1)

La frontière libre X est définie par:

X = B0 + (B₈ - B0)(1 - eh(T))

v ( _B0 )

h(T) = -((rd - rf )T + 2ó T) B₈ - B0

B₈ = â

â - 1K

( )

K; rd

B0 = max K

rf

Si S = X, il est optimal d'exercer l'option immédiatement, et sa valeur doit être égale à la valeur intrinsèque S - K. En revanche, si rf = 0, il ne sera jamais optimal d'exercer le call Américain avant l'expiration, et sa valeur peut être déduite de la formule de Black-Scholes.

Put Américain sur devises

Le prix d'un put Américain peut être déduit de la formule d'approximation donnée dans l'équation (4.13) pour un call Américain, le prix est donnée par la transformation suivante:

P(S, K, T, rd, rf, ó) = C(K, S, T, rf, rd, ó) (4.14)

Avec C(.) est la valeur d'un call Américain sur devises avec un taux sans risque domestique rd et un taux sans risque étranger rf. En utilisant cette transformation, il n'est pas nécessaire de développer une formule séparée pour évaluer un put Américain.

4.5 Approximation de Bjerksund et Stensland (2002)

L'approximation de Bjerksund et Stensland (2002) [7] divise le temps jusqu'à la maturité en deux parties, chacune ayant une frontière d'exercice plane distincte. Il s'agit donc d'une simple généralisation de l'algorithme de Bjerksund et Stensland (1993). La méthode est rapide et efficace et devrait être plus précise que les approximations de Barone-Adesi et Whaley (1987) et de Bjerksund et Stensland (1993). Pour une démonstration détaillé des formules, se référer à Petter Bjerksund and Gunnar Stensland Colsed-Form Valuation Of American Options (2002) [7].

47

Call Américain sur devises

Cette section étend l'approximation de la frontière plane, mentionnée dans la section précédente, en permettant une frontière plane X qui sera valide de la date 0 à la date t, et une autre frontière plane x valide de la date t à la date T, avec 0 < t < T. Il est bien connu que la frontière optimale est une fonction décroissante (et concave) du temps, d'où on choisi X > x > K.

La frontière d'exercice pour le call est composée des lignes en gras de la figure 4.3. On peut voir que la frontière d'exercice peut être vue comme des escaliers ayant 2 pas différents. La ligne verticale pointillée dans la figure 4.3 représente la frontière de non-exercice, qui correspond à l'exercice non-prématuré de l'option.

FIGURE 4.3 - Frontière d'exercice [7]. On défini le temps d'arrêt par :

ô = inf {{ inf : S_ô > X}, { inf : S_ô > x}, T }

ôE[0,8[ ôE[t,8[

La valeur d'un call Américain pour cette stratégie est :

C(S, K, T, rd, rf, ó, X, x, t) = E0(e^-rdômax(S_ô - K; 0))

Bjerksund et Stensland (2002) on donnée le prix d'un call Américain par la formule :

C = á(X)Sâ - áÖ(S, t, â, X, X) + Ö(S, t,1, X, X) - Ö(S, t,1, x, X) - KÖ(S, t, 0, X, X)

+ KÖ(S, t,0, x, X) + á(x)Ö(S, t, â, x, X) - á(x)Ø(S, T, â, x, X, x, t) + Ø(S, T,1, x, X, x, t)

- Ø(S, T,1, K, X, x, t) - KØ(S, T,0, x, X, x, t) + KØ(S, T,0, K, X, x, t) (4.15)

Avec :

á(X) = (X - K)X^-â á(x) = (x - K)x^-â

(1 rd rf_{l (}rd - rf 1_l2 2rd

â = \ 2 -U2 / + \ ó2 -2 / + ó2

La fonction Ö(S, T, ã, H, X) est donnée par :

Ö(S, T, ã, H, X) = e^ëSã(N(-d) - ()^êN(-d2))

S

ë = -rd + ã(rd - rf) + ₂ã(ã - 1)ó²

1

ê =

2(rd - rf)

ó2 + (2ã - 1)

d=

d2 =

( 2)ó2)

ln(S/H) + rd - rf + (ã - 1 T

_V

ó T

( 2)ó2)

ln(X²/SH) + rd - rf + (ã - 1 T

_V

ó T

Les deux frontières libres x et X sont définies par :

x = B0 + (B₈ - B0)(1 - eh(t))
X = B0 + (B₈ - B0)(1 - eh(T))

_K2

h(t) = -((rd - rf)t + 2óVt) ((B₈ - B0)B0 )

_K2

h(T) = -((rd - rf)T + 2óVT) ((B₈ - B0)B0)

1 V

t = ₂( 5 - 1)T

B₈ = â âK

- 1

B0 = max (K; rd K)

rf

La fonction Ø(S, T, ã, H, X, x, t) est donnée par :

Ø(S, T, ã, H, X, x, t) = e^ëTSã(M(- e1, -f1,11T) - (X/S)^êM(- e2, -f2,11_T)

- (x/S)^êM(- e3, -f

3, -11_T) + (x/X)^êM(- e4, -f4, -11;))

Avec M(., ., .) est la fonction de distribution de la loi normale bivariée, et :

e1 =

( 2)ó2)

ln(S/x) + rd - rf + (ã - 1 t

óVt

e2 =	( 2)ó2) ln(X^2/Sx) + rd - rf + (ã - 1 t
	óVt 48

e3 =

49

( 2)cr2)

ln(S/x) - rd - rf + ('r - 1 t

cr/t

e4 =

f1 =

( 2)cr2)

ln(X²/Sx) - rd - rf + ('r - 1 t

cr/t

( 2)cr2)

ln(S/H) + rd - rf + ('r - 1 T

/ cr T

f2 =

( 2)cr2)

ln(X²/SH) + rd - rf + ('r - 1 T

/ cr T

( 2)cr2)

f3 =

ln(x²/SH) + rd - rf + ('r - 1 T

/ cr T

f4 =

( 2)cr2)

ln(Sx²/HX²) + rd - rf + ('r - 1 T

/ cr T

Put Américain sur devises

Le prix d'un put Américain peut être aussi déduit de la formule d'approximation donnée dans l'équation (4.15) pour un call Américain, le prix est donnée par la transformation suivante:

P(S, K, T,rd,rf, cr) = C(K, S, T,rf,rd, cr) (4.16)

Avec C(.) est la valeur d'un call Américain sur devises avec un taux sans risque domestique rd et un taux sans risque étranger rf.

4.6 Application

Après avoir présenté les méthodes utilisées pour l'évaluation des options Américaines, à savoir la méthode des différences finies, l'approximation de Barone-Adesi et Whaley (1987), l'approximation de Bjerksund et Stensland (1993) et l'approximation de Bjerksund et Stens-land (2002), nous allons présenter dans cette section une comparaison des résultats de ces méthodes, ainsi que le pricer des options Américaines de change élaboré dans le cadre de ce rapport de fin d'études.

Nous avons procédé de la même manière que les chapitres précédents, dans un premier lieu, nous avons réalisé une librairie de pricing sous le langage Python, cette librairies contient des fonctions qui permettent le calcul des prix des options Américaines de change en fonctions des différents inputs, à savoir le taux de change spot, prix d'exercice, temps restant jusqu'à l'échéance, taux sans risque domestique, taux sans risque étranger et la volatilité. Les fonction créées en Python on été ensuite utilisés comme étant des fonctions Excel à l'aide d'un outil qui permet de relier les deux plateformes.

Résultats numériques

Le tableau ci-dessous contient les prix des call et put Américains sur EURUSD données par la méthode des différences finies, l'approximation de Barone-Adesi et Whaley (1987), l'ap-proximation de Bjerksund et Stensland (1993) et l'approximation de Bjerksund et Stensland (2002), ceci pour différents paramètres.

TABLE 4.1 - Prix de options Américaines sur l'EURUSD pour K = 1,08 et rf = 0,04.

Paramètres S =	Diff. finies		B-W 87		B-S 93		B-S 02
	Call	Put	Call	Put	Call	Put	Call	Put
rd = 0,08 1,04	0,0284	0,0594	0,0287	0,0593	0,0287	0,0590	0,0287	0,0592
o- = 0,20 1,06	0,0372	0,0479	0,0376	0,0480	0,0376	0,0476	0,0376	0,0478
T = 0,25 1,08	0,0475	0,0380	0,0479	0,0382	0,0479	0,0378	0,0479	0,0380
1,10	0,0594	0,0298	0,0597	0,0300	0,0597	0,0296	0,0597	0,0298
1,12	0,0726	0,0230	0,0729	0,0232	0,0729	0,0229	0,0729	0,0230
rd = 0,12 1,04	0,0325	0,0553	0,0329	0,0552	0,0329	0,0547	0,0329	0,0549
o- = 0,20 1,06	0,0421	0,0440	0,0425	0,0440	0,0425	0,0434	0,0425	0,0437
T = 0,25 1,08	0,0531	0,0344	0,0536	0,0346	0,0536	0,0340	0,0536	0,0342
1,10	0,0658	0,0266	0,0662	0,0268	0,0662	0,0262	0,0662	0,0264
1,12	0,0796	0,0202	0,0800	0,0205	0,0800	0,0199	0,0800	0,0200
rd = 0,08 1,04	0,0689	0,0994	0,0695	0,0997	0,0695	0,0994	0,0695	0,0996
o- = 0,40 1,06	0,0789	0,0894	0,0795	0,0897	0,0795	0,0894	0,0795	0,0896
T = 0,25 1,08	0,0894	0,0800	0,0902	0,0805	0,0902	0,0802	0,0902	0,0803
1,10	0,1011	0,0716	0,1016	0,0720	0,1016	0,0717	0,1016	0,0718
1,12	0,1132	0,0638	0,1138	0,0643	0,1137	0,0639	0,1137	0,0641
rd = 0,08 1,04	0,0490	0,0711	0,0493	0,0711	0,0493	0,0704	0,0493	0,0707
o- = 0,20 1,06	0,0589	0,0606	0,0592	0,0607	0,0592	0,0600	0,0592	0,0603
T = 0,5 1,08	0,0698	0,0513	0,0702	0,0515	0,0702	0,0508	0,0702	0,0510
1,10	0,0818	0,0432	0,0821	0,0435	0,0821	0,0427	0,0821	0,0429
1,12	0,0947	0,0361	0,0950	0,0364	0,0950	0,0357	0,0950	0,0359

Interface

L'interface utilisateur de notre pricer est représentée dans la figure 4.4. De la même façon que l'interface des options Européennes présentée plus haut, dans cette interface l'utilisa-teur peut évaluer plusieurs options en même temps, chacune dans une ligne Excel, tout en choisissant le modèle approprié, afin de permettre à l'utilisateur de gagner du temps en effectuant plusieurs opérations à la fois.

FIGURE 4.4 - Interface de pricing des option Américaines sur devises.

50

51

Chapitre 5

Portefeuille d'options : Couverture et

gestion des risques

Tout trader qui entre sur le marché doit balancer entre deux considérations opposées - le profit et le risque. Un trader espère que son analyse du marché conduira à des stratégie de trading rentables. Mais tout trader rationnel ne peut ignorer la possibilité de l'erreur. S'il se trompe et les conditions du marché changent d'une manière qui affecte négativement sa position, à quel point le trader pourrait-il être affecté? Un trader qui ne tient pas compte des risques liés à sa position va certainement avoir une carrière courte et malheureuse.

Un trader qui vend une option à un client est confronté au problème de gestion du risque. Si cette option se révèle identique à une autre option échangée sur le marché, le trader peut neutraliser son risque en achetant, sur le marché, la même option que celle qui est vendue au client. Mais lorsque l'option existe pour répondre exclusivement au besoin de ce client, la couverture contre le risque devient bien plus compliquée.

Afin de gérer les risques liés aux options, il est indispensable de suivre des stratégies de couverture qui peuvent généralement être classées selon deux catégories à savoir les stratégies statiques et les stratégies dynamiques. Les premières sont basées sur la prise de positions sur d'autres options afin de couvrir celles du portefeuille; le second type est une gestion en temps continu du portefeuille basée sur l'analyse des sensibilités des options qui composent le portefeuille.

Ce chapitre à pour objectif de présenter quelques exemples de stratégies statiques utilisées au niveau des salles des marchés, le chapitre contient aussi un volet traitant la gestion dynamique d'un portefeuille d'options.

5.1 Stratégies statiques de couverture

Les stratégies statiques de couverture sont des combinaisons de calls et de puts, permettant de mettre en place des stratégies adaptées aux anticipations des fluctuations du sous-jacent. Par exemple, supposons qu'un trader anticipe un forte variation du prix d'un actif, mais en ignore le sens, un certain nombre de stratégies s'offre à lui. Ces stratégies vont lui offrir un gain si son intuition est correcte, et limiter sa perte sinon.

52

Cette section sera consacré aux stratégies statiques les plus utilisée, en présentant leurs définitions et leurs profils de gain et de perte. Une autre contrainte s'ajoute, c'est que les investisseurs ne sont pas toujours prêt à payer la prime de l'option afin d'acquérir l'une de ces stratégies. Pour cela il faut choisir le paramètre qui permet d'annuler la prime en combinant les options qui constituent cette stratégie. Le paramètre sur lequel il faut agir dans ce cas c'est le strike K des options. Donc pour chaque stratégie que nous allons citer, il faut trouver le strike de chaque option qui constitue la stratégie afin d'annuler la prime totale de cette stratégie. Ce type de stratégies est appelé stratégies zero-cost.

5.1.1 Forward synthétique

Un contrat forward synthétique utilise des options d'achat et de vente ayant le même prix d'exercice et la même date d'échéance pour créer une position à terme équivalente. Un investisseur peut acheter/vendre un call et vendre/acheter un put avec le même prix d'exercice et la même date d'échéance, dans le but d'imiter un contrat future ou forward régulier.

-- Position longue sur forward synthétique : Achat d'un call et vente d'un put de même strike K et de même date d'échéance T.

-- Position courte sur forward synthétique : Achat d'un put et vente d'un call de même strike K et de même date d'échéance T.

Un avantage majeur des forwards synthétiques est qu'une position sur contrat future régulière peut être maintenue sans les mêmes types d'exigences pour les contreparties. Toutefois, contrairement à un contrat à terme, un contrat à terme synthétique exige que l'investisseur paie une prime d'option nette lors de l'exécution du contrat.

TABLE 5.1 - Revenus d'une position longue sur forward synthétique.

Taux de change Payoff achat du call Payoff vente du put Payoff total

ST = K ST-K 0 ST - K

ST = K 0 ST-K ST-K

TABLE 5.2 - Revenus d'une position courte sur forward synthétique.

Taux de change Payoff vente du call Payoff achat du put Payoff total

ST = K K-ST 0 K-ST

ST = K 0 K-ST K-ST

Pour que cette stratégie soit zero-cost, on doit trouver le strike K0 qui permet d'annuler la coût de cette stratégie. Pour cela nous allons utiliser la parité call-put.

c + Ke-rdT = p + S0e-rf T

donc

c - p = S0e-rf T - Ke-rdT

Pour annuler la prime de la stratégie, on doit avoir c - p = 0 donc:

S0e-rf T - K0e^-rd^T = 0

ce qui implique que:

K0 = S0e(rd-rf )T

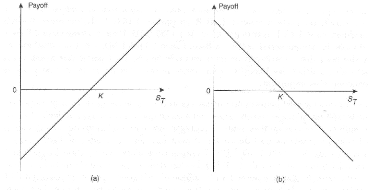
53

FIGURE 5.1 - Payoffs d'un forward sythétique : (a) position longue, (b) position courte.

5.1.2 Risk Reversal

Une stratégie Risk Reversal consiste à acheter/vendre un call en dehors de la monnaie et vendre/acheter un put en dehors de la monnaie, les deux ayant la même date d'échéance.

Dans cette stratégie, l'investisseur fait d'abord une intuition du marché; si cette intuition est haussière, il voudra être long. Cependant, au lieu d'être long sur le sous-jacent, il achètera un call hors de la monnaie de strike K2 et vendra simultanément un put hors de la monnaie de strike K1 avec K1 < K2. Si son intuition est baissière, il vaudra être court sur Risk Reversal en achetant un put hors de la monnaie de strike K1, et en vendant un call hors de la monnaie de strike K2.

TABLE 5.3 - Revenus d'une position longue sur Risk Reversal.

Taux de change	Payoff achat du call	Payoff vente du put	Payoff total
ST = K2	ST - K2	0	ST - K2
K1 < ST < K2	0	0	0
ST = K1	0	ST - K1	ST - K1

TABLE 5.4 - Revenus d'une position courte sur Risk Reversal.

Taux de change	Payoff vente du call	Payoff achat du put	Payoff total
ST = K2	K2 - ST	0	K2 - ST
K1 < ST < K2	0	0	0
ST = K1	0	K1 - ST	K1 - ST

Pour que cette stratégie soit zero-cost il faut trouver les deux strikes _K01 ^et _K02 du put et du call respectivement, qui permettent d'annuler la prime de la stratégie Risk Reversal. Pour cela if faut résoudre l'équation suivante:

p(K01) - c(K02) = 0 (5.1)

L'équation (5.1) peut être résolue numériquement en utilisant l'algorithme de Newton-Raphson d'écrit plus haut.

Nous avons d'après le modèle de Garman-Kohlhagen :

c(K) = S0e^-rf ^TN(d1) - Ke^-rdTN(d2)
p(K) = Ke^-rdTN(-d2) - S0e^-rf ^TN(-d1)

avec :	d1(K) =	ln(S0/K) + (rd - rf + cr^2/2)T
et :		v cr T

d2(K) = v

cr T

ln(S0/K) + (rd - rf - cr²/2)T

v

= d1(K) - cr T

On initialise l'algorithme en choisissant :

K01 = S0 et K02 = S0

Pour chaque itération de l'algorithme de Newton-Raphson, on calcule Kn+1

01 et Kn+1

02 à partir

de Kⁿ₀₁ et _Kn02, tels que :

Kn+1 = Kn

01 01 p0(Kn01)

p(Kⁿ₀₁) - c(Kⁿ₀₁)

et

02)

_Kn+1

02 = Kn 02 + p(Kn ₀₂) - c(Kⁿ c⁰(Kⁿ₀₁)

Avec :

c⁰(K) = S0e^-rf ^Td⁰₁(K)N⁰(d1) - e^-rd^T(N(d2) + Kd⁰₂(K)N⁰(d2) (5.2)

et

p⁰(K) = S0e^-rf ^Td⁰₁(K)N⁰(-d1) + e^-rdT(N(-d2) - Kd⁰2(K)N⁰(-d2)) (5.3)

où :

d⁰₁(K) = d⁰2(K) = -cr1

KvT

Ci-dessous l'algorithme de Newton-Raphson pour trouver les deux strikes _K01 ^et K02 :

Algorithm 2: Algorithme de Newton-Raphson pour _K01 ^et K02.

K01 ? S0

K02 ? S0 e ? 10-⁸

while |p(K01) - c(K02)| = e do

K01 ?K01 - p(K01)-c(K02)

p⁰(K01)

while |p(K01) - c(K02)| = e do

K02 ?K02 + p(K01)-c(K02)

c⁰(K02)

end

end

return K01, K02

54

55

5.1.3 Butterfly spread

Un Butterfly Spread implique des positions sur des options de trois prix d'exercice différents. Il peut être créé en achetant un call au prix d'exercice bas K1, en achetant un call au prix d'exercice plus élevé K3 et en vendant deux calls de prix d'exercice K2, situé entre K1 et K3.

Généralement, K2 est proche du prix spot du sous-jacent. Le profil de gain de cette stratégie est représenté dans la figure 5.2.

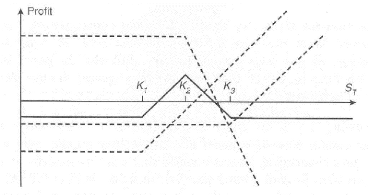
FIGURE 5.2 - Payoff d'un Butterfly Spread.

Un Butterfly Spread produit un bénéfice si le cours de l'action reste proche de K2, mais conduit à de faibles pertes si le cours du sous-jacent varie de façon significative à la hausse comme à la baisse. C'est, par conséquent, une stratégie judicieuse pour un investisseur qui pense qu'une variation importante du cours est improbable.

TABLE 5.5 - Revenus d'une position longue sur Butterfly Spread.

Taux de change	Payoff achat du premier call	Payoff achat du second call	Payoff vente des deux calls	Payoff total
ST < K1	0	0	0	0
K1 < ST < K2	ST - K1	0	0	ST - K1
K2 < ST < K3	ST - K1	0	-2(ST - K2)	K3 - ST
ST > K3	ST - K1	ST - K3	-2(ST - K2)	0

Ces revenus sont calculés en considérant K2 = 0, 5(K1 + K3)

Pour que cette stratégie soit zero-cost il faut trouver les trois strikes K01, K02 ^et _K03 des calls qui constituent cette stratégie, et qui permettent d'annuler la prime de la stratégie Butterfly Spread. Pour cela if faut résoudre l'équation suivante :

2c(K02) - c(K01) - c(K03) = 0 (5.4)

De la même manière que la stratégie précédente, nous allons résoudre l'équation (5.4) numériquement en utilisant l'algorithme de Newton-Raphson.

56

On fixe K02 = S0, et on initialise l'algorithme en choisissant:

K01 = S0 - 0,01 et K02 = S0 + 0,01

Pour chaque itération de l'algorithme de Newton-Raphson, on calcule Kn+1

01 et Kn+1

03 à partir

de Kn 01 et _Kn03, tels que:

03)

_Kn+1

01 = Kn 01 + 2c(Kn ₀₂) - c(Kn ₀₁) - c(Kⁿ

c⁰(Kⁿ₀₁)

et

03)

_Kn+1

03 = Kn 03 + 2c(Kn ₀₂) - c(Kn ₀₁) - c(Kⁿ

c⁰(Kⁿ₀₃)

Avec c⁰(K) définie dans l'équation (5.2).

Ci-dessous l'algorithme de Newton-Raphson pour trouver les trois strikes K01, K02 ^et K03 :

Algorithm 3: Algorithme de Newton-Raphson pour K01, K02 ^et K03.

K01 ? S0 - 0,01

K02 ? S0

K03 ? S0 + 0,01

e ? 10-⁸

while |2c(K02) - c(K01) - c(K03)| = e do

K01 ? K01 + 2c(K02)-c(K01)-c(K03)

c⁰(K01)

while |2c(K02) - c(K01) - c(K03)| = e do

K03 ? K03 + 2c(K02)-c(K01)-c(K03)

c⁰(K03)

end

end

return K01, K02, K03

5.1.4 Condor

Un Condor est une stratégie qui implique des positions sur des options de quatre prix d'exer-cice différents, ayant la même date d'échéance T, cette stratégie peut être créée en achetant deux calls de strikes respectifs K1 et K4 et en vendant deux autres calls de strikes K2 et K3, avec K1 < K2 < K3 < K4.

Le profil de gain de la stratégie Condor est représentée dans la figure 5.3

Le maximum de profit que peut dégager cette stratégie est obtenu si le cours du sous-jacent se situe entre K2 et K3. Cette stratégie ressemble beaucoup à celle du Butterfly Spread, elle permet de limiter les pertes si le cours du sous-jacent varie de manière significative à la hausse comme à la baisse.

57

FIGURE 5.3 - Payoff d'un Condor.

TABLE 5.6 - Revenus d'une position longue sur Condor.

Taux de change	Payoff achat premier call	Payoff achat second call	Payoff vente premier call	Payoff vente second call	Payoff total
ST = K1	0	0	0	0	0
K1 < ST = K2	ST - K1	0	0	0	ST - K1
K2 < ST < K3	ST - K1	0	K2 - ST	0	K2 - K1
K3 = ST < K4	ST - K1	0	K2 - ST	K3 - ST	K4 - ST
ST = K4	ST - K1	ST - K4	K2 - ST	K3 - ST	0

Ces revenus sont calculés en considérant K2 + K3 = K1 + K4

Pour que cette stratégie soit zero-cost il faut trouver les quatre strikes K01, K02, K03 ^et K04 des calls qui constituent cette stratégie, et qui permettent d'annuler la prime de la stratégie Condor. Pour cela if faut résoudre l'équation suivante:

c(K02) + c(K03) - c(K01) - c(K04) = 0 (5.5)

Pour résoudre l'équation (5.5) nous allons utiliser, encore une fois, l'algorithme de Newton-Raphson.

On initialise l'algorithme en choisissant:

K01 = S0 - 0,02 K02 = S0 - 0,01 K03 = S0 + 0,01 K04 = S0 + 0,02

Pour chaque itération de l'algorithme de Newton-Raphson, on calcule Kn+1

01 , Kn+1 ₀₂ Kn+1

03 et

_Kn+1

04 à partir de Kⁿ01^, Kⁿ02^, Kn03 ^et _Kn04, tels que:

04)

_Kn+1

01 = Kn 01 + c(Kn ₀₂) + c(Kn ₀₃) - c(Kn ₀₁) - c(Kⁿ

c⁰(Kⁿ₀₁)

c(Kⁿ₀₂) + c(Kⁿ₀₃) - c(Kⁿ₀₁) - c(Kⁿ₀₄)

_Kn+1

02 = Kn 02 c0(Kn 02)

04)

_Kn+1

03 = Kn 03 - c(Kn ₀₂) + c(Kn ₀₃) - c(Kn ₀₁) - c(Kⁿ

c0(Kn 03)

58

+ c(Kⁿ₀₂) + c(Kⁿ₀₃) - c(Kⁿ₀₁) - c(Kô₄)

44

⁺¹ nÔ4 1 = Kn04 c⁰(Kⁿ₀₄) Avec c⁰(K) définie dans l'équation (5.2).

Ci-dessous l'algorithme de Newton-Raphson pour trouver les quatre strikes K01, K02, K03 et

K04 :

Algorithm 4: Algorithme de Newton-Raphson pour K01, K02, K03 ^et K04.

K01 ? S0 - 0, 02

K02 ? S0 - 0, 01

K03 ? S0 + 0,01

K04 ? S0 + 0, 02 e ? 10-⁸

while |c(K02) + c(K03) - c(K01) - c(K04)| = e do

K01 ?K01 + c(K02)+c(K03)-c(K01)-c(K04)

c⁰(K01)

while |c(K02) + c(K03) - c(K01) - c(K04)| = e do

K02 ?K02 - 2c(K02)-c(K01)-c(K03)

c⁰(K02)

while |c(K02) + c(K03) - c(K01) - c(K04)| = e do

K03 ? K03 - 2c(K02)-c(K01)-c(K03)

c⁰(K03)

while |c(K02) + c(K03) - c(K01) - c(K04)| = e do

K04 ?K04 + 2c(K02)-c(K01)-c(K03)

c⁰(K04)

end

end

end

end

return K01, K02, K03, K04

5.1.5 Résultats numériques

Le tableau ci-dessous présente les résultats numériques des stratégies citées ci-dessus. Pour chaque stratégie, et pour certains paramètres, nous allons calculer les strikes qui permettent d'annuler la prime totale de la stratégie en utilisant les méthodes citées plus haut.

D'après les résultats du tableau 5.7 on peut remarquer que les strikes trouvés, pour chacune des méthodes citées plus haut, permettent d'annuler les primes totales de la stratégie. Ainsi, un investisseur pourra donc profiter de la couverture statique gratuitement en achetant l'une de ces stratégies, car les prime des options qui les constituent se compensent.

L'algorithme de Newton-Raphson a prouvé son efficacité dans ce genre de calculs, il permet de donner des approximations très pertinentes, un autre avantage de cet algorithme c'est le temps de calcul largement réduit par rapport aux autres algorithmes de résolution.

59

TABLE 5.7 - Résultats numériques des stratégies zero-cost.

Stratégie	Paramètres	Srikes	Prix des options	Prix de la stratégie
Forward synthétique	S0 = 1,08 T = 0,5 rd = 0,08 r1 = 0,04 o- = 0,20	K0 = 1,1018	c(K0) = 0,0596 p(K0) = 0, 0596	0
Risk Reversal	S0 = 1,08	K01 = 1,0594	c(K01) = 0,0541	0
	T = 0,5	K02 = 1, 0803	p(K02) = 0, 0541
	rd = 0,04
	r1 = 0,06
	o- = 0,20
Butterfly Spread	S0 = 1,08	K01 = 1,07	c(K01) = 0,0753	0
	T = 0,5	K02 = 1,08	c(K02) = 0,0701
	rd = 0,08	K03 = 1, 0907	c(K03) = 0, 0649
	r1 = 0,04
	o- = 0,20
Condor	S0 = 1,08	K01 = 1,06	c(K1) = 0,0807	0
T = 0,5	K02 = 1,0701	c(K2) = 0,0752
	rd = 0,08	K03 = 1,09	c(K03) = 0,0652
	r1 = 0,04	K04 = 1,1018	c(K04) = 0,0596
	o- = 0,20

5.2 Stratégies dynamiques de couverture

Notre discussion jusqu'à présent devrait permettre de comprendre pourquoi les traders utilisent des modèles théoriques pour évaluer les options. Tout d'abord, un modèle nous renseigne sur la valeur d'une option. Nous pouvons comparer cette valeur avec le prix de l'op-tion sur le marché et, à partir de là, choisir une stratégie appropriée. Deuxièmement, une fois que nous avons pris position, le modèle nous aide à quantifier un grand nombre des risques que comporte la négociation de l'option. En comprenant ces risques, nous serons mieux préparés à minimiser nos pertes lorsque les conditions du marché jouent contre nous et à maximiser nos profits lorsque les conditions du marché jouent en notre faveur, c'est ce qu'on appelle la couverture dynamique.

La couverture dynamique se différencie des stratégies de couverture statiques, vues dans la section précédente, dans lesquelles la couverture est définie dès le départ et n'est plus jamais ajustée. La couverture dynamique est réalisée par le biais des lettre grecques, vues plus haut dans ce rapport, telles que le delta, le gamma et le vega. Ces mesures quantifient les différents aspects du risque dans une position en options.

60

5.2.1 Delta Hedging

Le delta d'une option, noté , a été introduit plus haut dans le chapitre 2. C'est le taux de variation de la valeur de l'option par rapport à celle du sous-jacent. C'est aussi la pente de la courbe reliant la valeur de l'option à celle du sous-jacent (voir figure 2.2). Le delta d'un call est donné par:

ac

= aS

où c est la valeur du call et S le cours de l'action. Le delta d'un portefeuille d'options est:

aLI
aS

où LI représente la valeur du portefeuille.

Le delta du portefeuille peut être calculé à partir des deltas de chacune des options du portefeuille prises individuellement du fait de la linéarité du passage aux dérivées partielles.

Si un portefeuille est constitué d'une quantité wi d'une option i (1 i n), le delta du
portefeuille est obtenu par:

où i représente le delta de l'option i.

=

n ? i=1

wi i

Le delta est étroitement lié au modèle de Black-Scholes, ils ont montré qu'il était possible d'établir un portefeuille sans risque consistant sur une position sur le sous-jacent, et une position sur l'option. Le portefeuille de Black-Scholes est constitué par:

-- La vente d'une option.

-- L'achat d'une quantité du sous jacent.

Une position dont de delta est nul est appelée position delta-neutre. Il est important de comprendre que, puisque le delta varie, la position de l'investisseur reste couverte en delta-neutre seulement dans un intervalle de temps relativement court. La couverture doit être réajustée périodiquement, d'où l'appellation de couverture dynamique.

Exemple

Pour illustrer plus clairement cet aspect dynamique de la couverture, nous allons travailler sur un exemple dans lequel un call Européen sur EURUSD est vendu. La couverture est sensée être ajustée chaque semaine jusqu'à l'échéance de l'option. Les inputs du call sont:

-- Notionnel: 100000

-- Spot : 1,1177

-- Strike : 1,08

-- Maturité : 20 semaines

-- Taux domestique : 1,679%

-- Taux étranger: -0,398%

-- Volatilite : 5,0492% (Donnée par le modèle de Vanna-Volga)

Nous Avons donc d'après le modèle de Garman-Kohlhagen :

Prix de l'option : 4 773,41

Delta : 0, 701

Le tableau ci-dessous présente les différentes opérations de couverture pendant la durée de vie de l'option :

TABLE 5.8 - Simulation de la couverture dynamique par delta.

Sem	Taux EURUSD	Delta	Emprunt USD	Placement EUR	P&L Intérêt	P&L Devise	P&L Option	P&L Total
0	1,1177	0, 701	73 590, 83	70112, 05	-	-	-	-
1	1,1160	0, 689	72 208, 48	68 873, 39	-29, 76	-119,19	209, 25	60, 31
2	1,1122	0, 668	69 944, 93	66 838,18	-29, 23	-261, 72	398, 70	107, 76
3	1,1090	0, 650	67957, 05	65 045, 68	-28, 33	-213, 88	341, 28	99, 07
4	1,1025	0, 620	64 620, 06	62 018, 93	-27, 55	-422, 80	619, 40	169, 05
5	1,1094	0, 641	66 874, 04	64 050, 65	-26, 20	427, 93	-539, 78	-138, 06
6	1, 0945	0, 580	60 289, 94	58 035, 03	-27,17	-954, 35	1313,10	331, 57
7	1, 0832	0, 535	55 335, 71	53 461, 33	-24, 48	-655, 80	867, 34	187, 07
8	1, 0845	0, 536	55 537, 32	53 647, 23	-22, 46	69, 50	-10, 84	36, 21
9	1,1026	0, 595	61972, 96	59 484, 01	-22, 57	971, 01	-1325, 21	-376, 76
10	1,1286	0, 669	70 343, 68	66 900, 92	-25, 26	1546, 58	-2 407, 73	-886, 41
11	1,1106	0, 608	63 608, 55	60 836, 51	-28, 79	-1204, 22	1800, 66	567, 65
12	1, 0695	0, 480	49 849, 98	47 972, 02	-26, 00	-2 500, 38	3 000, 32	473, 93
13	1,1142	0, 602	63 496, 20	60 219, 57	-20, 26	2144, 35	-3 240, 98	-1116, 89
14	1, 0809	0, 510	53 496, 46	50 968, 27	-25, 98	-2 005, 31	2 847,11	815, 81
15	1, 0936	0, 537	56 506, 65	53 720, 82	-21, 79	647, 30	-825, 64	-200,14
16	1, 0878	0, 520	54 654, 02	52 017, 72	-23, 09	-311, 58	540, 90	206, 23
17	1, 0821	0, 506	53149, 56	50 627, 41	-22, 34	-296, 50	477, 08	158, 24
18	1, 0985	0, 527	55 448,17	52 719, 90	-21, 72	830, 29	-1246, 69	-438,13
19	1, 0841	0, 505	53 008, 73	50 469, 71	-22, 75	-759, 17	1375, 63	593, 71
20	1, 0815	1, 000	106 575, 74	100 000, 00	-21, 71	-131, 22	429, 52	276, 59

Le graphe du Profit & Loss est représenté dans la figure ci-dessous :

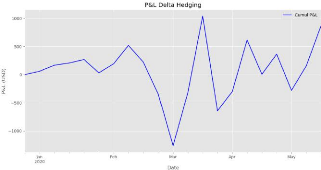
FIGURE 5.4 - Profit & Loss Delta Hedging.

61

62

Pour bien expliquer d'où proviennent les coûts, nous allons détailler les opération effectuées pour les deux premières semaines, on suit la même démarche pour les semaines qui suivent:

Semaine 0

-- Taux de change EURUSD : 1,1177.

-- Prix de l'option : 4773,41 USD.

-- Delta : 0,701 ce qui est équivalent à 70112,05 EUR, et 78364,24 USD.

Pour couvrir cette position, le trader doit acheter la quantité delta en EUR qui est 70112,05 EUR. Pour réaliser cette opération il doit:

-- Emprunter 73590,83 USD (78 364,24 USD -4773,41 USD) à un taux de 1,679%. -- Placer 70112,05 EUR à un taux de -0,398%.

Semaine 1

-- Taux de change EURUSD : 1,1160.

-- Prix de l'option : 4564,15 USD.

-- Delta : 0,689 ce qui est équivalent à 68873,39 EUR, et 76862,70 USD.

La différence entre le delta de la semaine 0 et le delta de la semaine 1 est:

ÄS1 - ÄS0 = -0,012

Pour couvrir cette position, le trader doit vendre l'équivalent de la différence de delta qui est 1238,657 EUR. Les nouvelle valeurs de placement et emprunt seront donc:

-- Placement: 68873,39 EUR. -- Emprunt: 72208,4857 USD.

Le Profit & Loss total de l'opération de couverture entre les deux semaines se divise en trois parties:

-- P&L Option : Se calcule de la manière suivante:

P&L OptionS1 = Prix de l⁰optionS0 - Prix de l⁰optionS1 Dans notre cas on a : P&L OptionS1 = 209,25 USD.

-- P&L Sous-jacent: Se calcule de la manière suivante:

P&L Sous jacentS1 = ÄS0 × Notionnel × (Taux de changeS1 - Taux de changeS0) Dans notre cas on a : P&L Sous - jacentS1 = -119,19 USD.

-- P&L Intérêts : Se calcule de la manière suivante:

P&L Int'eràetsS1 = EmpruntS0 × (1 - erd/52) - Taux de changeS0 × PlacementS0 × (1 - _erf /52₎ Dans notre cas on a : P&L Int'eràetsS1 = -29,76 USD.

63

Application

Le même raisonnement présenté dans l'exemple précédent peut être appliqué sur un portefeuille contenant plusieurs options. Nous avons développé un outil qui permet la gestion dynamique d'un portefeuille d'options Européennes sur devises, en prenant en compte tous les facteurs dynamiques entrant dans la gestion des options à savoir : Les taux d'intérêt, le taux de change et la surface de volatilité. Cet outil est composé des éléments suivants:

-- Une interface qui permet l'ajout ou la suppression d'une option de la base de données. -- Une base de données qui contient les différentes options qui constituent le portefeuille.

-- Une composante qui donne le Mark-To-Market du portefeuille.

-- Une feuille Excel qui permet de faire l'ajustement quotidien du portefeuille, et permet aussi de calculer le Profit & Loss journalier.

Interface d'ajout/suppression

Cette interface ce compose de deux fenêtres : "Interface de saisie" et "Portefeuille".

La première fenêtre, représentée dans la figure 5.5, permet de remplir tous les champs requis afin d'ajouter l'option à la base de données, puis en cliquant sur "Ajouter" l'option sera enregistrée dans le portefeuille, cette interface permet aussi d'afficher le prix et les sensibilités de l'option ajoutée.

La deuxième fenêtre, représentée dans la figure 5.6, est un aperçu du portefeuille, elle contient toute les informations des options existante, elle sert aussi à supprimer une option du portefeuille en la sélectionnant et en cliquant dur "Supprimer".

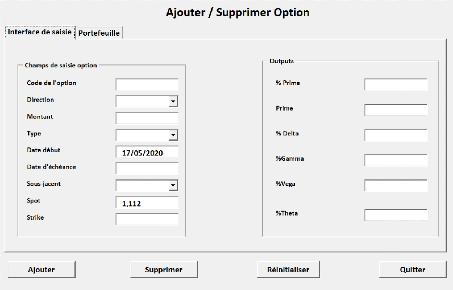
FIGURE 5.5 - Aperçu de l'interface de saisie.

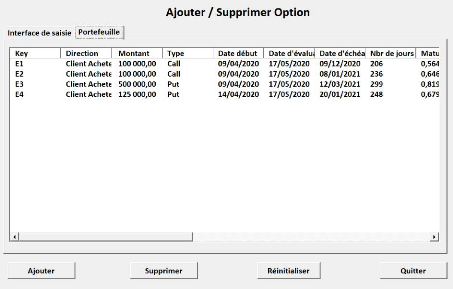
64

FIGURE 5.6 - Aperçu du portefeuille d'options.

Base de données

Notre base de données est une feuille Excel, représentée dans la figure 5.7, qui contient toutes les options du portefeuille, après avoir rempli les champs dans l'interface d'ajout/suppression et cliquer sur "Ajouter", l'option s'ajoute automatiquement sur la feuille Excel, cette feuille contient aussi les prix de chaque option et ses sensibilités au jour le jour.

FIGURE 5.7 - Extrait de la base de données des options.

Mark-To-Market

La composante qui donne le Mark-To-Market du portefeuille, représentée dans la figure 5.8, permet de donner la valeur et les sensibilités du portefeuille au jour le jour. Elle contient aussi un bouton "Ajuster le portefeuille" qui permet de faire les calculs présentées dans l'exemple précédent, en ajoutant une ligne qui correspond à la date du jour dans la feuille d'ajustement.

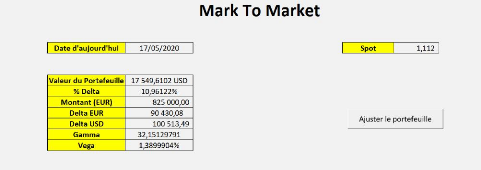
65

FIGURE 5.8 - Interface Mark-To-Market du portefeuille.

Feuille d'ajustement

La feuille d'ajustement, représentée dans la figure 5.9, contient les mêmes informations présentées dans l'exemple précédent, elle sert à ajuster le portefeuille quotidiennement afin de se couvrir par le delta. Elle permet aussi le suivi du Profit & Loss quotidien depuis la date d'ouverture de la première option jusqu'à la date au jour le jour.

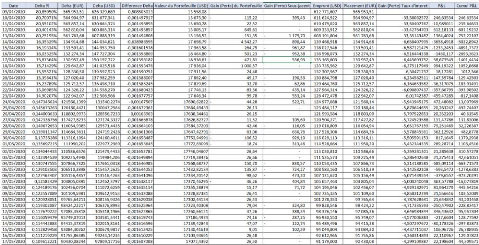
FIGURE 5.9 - Extrait de la feuille d'ajustement.

La figure 5.10 représente le graphe du Profit & Loss cumulé de la stratégie depuis la date d'ouverture de la première option jusqu'à la date au jour le jour.

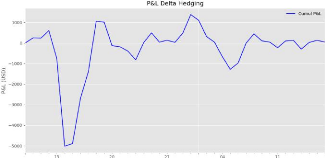
66

FIGURE 5.10 - Profit & Loss du portefeuille.

5.2.2 Optimal Delta Hedging

Le delta est de loin le paramètre de couverture le plus important et heureusement, c'est celui qui peut être le plus facilement ajusté car il ne nécessite qu'un achat/vente de l'actif sous-jacent. Depuis la naissance des marchés d'options négociés en bourse en 1973, la couverture delta a joué un rôle majeur dans la gestion des portefeuilles d'options. Les traders en options ajustent fréquemment le delta, le rendant proche de zéro, en négociant l'actif sous-jacent.

Plusieurs chercheurs et praticiens on remarqué que le delta du modèle de Black-Scholes ne minimise pas la variance des changement de la valeur de la position d'un trader. Cela est dû au fait qu'il existe une corrélation non nulle entre les mouvements du prix de l'actif sous-jacent et les mouvements de la volatilité de cet actif.

John Hull et Alan White (2017) [15] proposent une nouvelle approche pour optimiser la couverture des option, appelée Minimum Variance Delta qui tient compte à la fois des changements de prix et de la variation attendue de la volatilité conditionnée par un changement de prix.

Dans cette section nous allons reprendre les travaux de John Hull et Alan White (2017) [15] et nous les appliquerons sur les options sur l'EURUSD. Nous allons présenter d'abord la théorie de ce modèle, puis le choix des données sur lesquelles nous allons tester le modèle, et enfin les résultats et la discussion de ces résultats.

Étude théorique

Dans le modèle de Black-Scholes, le prix de l'actif sous-jacent suit un processus de diffusion avec une volatilité constante. De nombreuses alternatives au modèle Black-Scholes ont été développées pour tenter d'expliquer les prix des options qui sont observés dans la pratique. Il s'agit de la volatilité stochastique, des sauts dans le prix de l'actif ou de la volatilité, de l'aversion au risque, etc. Dans cette section nous allons présenter l'approche théorique pour la détermination du Minimum Variance Delta, äMV, à partir du delta du modèle de Black-Scholes, äBS.

Définissons ÄS comme une petite variation du prix du sous-jacent et Äf la variation correspondante du prix de l'option. Le Minimum Variance Delta, äMV, est la valeur qui minimise la

variance de :

Of = äMVOS (5.6)

La volatilité implicite est définie comme la volatilité qui, lorsqu'elle est insérée dans la formule de Black-Scholes, donne un prix qui est égal au prix du marché de l'option. Supposons que nous observions le prix d'une option, f, lorsque le prix du sous-jacent est S. La volatilité implicite est définie implicitement par :

f = fBS(S, óimp) (5.7)

où _fBS est la fonction d'évaluation du modèle de Black-Scholes et óimp est la volatilité implicite. La fonction d'évaluation de Black-Scholes est continue et continuellement différen-tiable.

Un développement en séries de Taylor au premier ordre de l'équation (5.7) donne :

? ^fOf = ?S + ?~f Oóimp + O(OS²)

p

ce qui est équivalent à :

Of = äBSOS + _íBSOóimp + e (5.8)

avec äBS ^et íBS sont le delta et le vega du modèle de Black-Scholes et e désigne les termes résiduels d'ordre supérieur dans le développement en séries de Taylor.

En substituant äMVOS des deux côtés de l'équation (5.8) on obtient :

Of - äMVOS = (äBS - äMV)OS + _íBSOóimp + e (5.9)
En conditionnant sur OS et en prenant les espérances que nous obtenons :

äMV = äBS + íBS

E(Oóimp) OS +

E(e) OS

Dans le cas des processus de diffusion, lorsque OS se rapproche de zéro, le dernier terme est infinitésimal, de ce fait :

äMV = äBS + íBS

E(Oóimp) OS

ce qui conduit à :

äMV = äBS + íBS

(5.10)

?E(óimp)

?S

avec _E(óimp) est l'espérance de la volatilité implicite en fonction de S.

John Hull et Alan White montrent qu'on peut approximer _E(Oóimp) par :

E(Oóimp) =

₍a + _bäBS + cäBS) OS vT S

avec a, b et c des constantes que nous cherchons à déterminer. Nous avons donc :

67

äMV = äBS + ^SBT (a + _bäBS + cä²_BS) (5.11)

Nous commençons par une implémentation basée sur l'équation (5.6) appliquée aux variations quotidiennes des prix :

Of = äMVOS + e (5.12)

Le seul élément inconnu dans le modèle est l'équation quadratique en äBS dans l'équa-tion (5.11). Nous estimons les paramètres du modèle, a, b et c, en utilisant un modèle de régression basé sur les équations (5.12) et (5.11).

68

Of - äBSOS = S~_T(a + _bäBS + cä²_BS) + e (5.13)

avec O f est la variation journalière du prix de l'option, OS est la variation du prix de l'actif sous-jacent correspondante, T est le temps jusqu'à la maturité, et äBS ^et íBS sont le delta et le vega du modèle de Black-Scholes.

Nous allons estimer le Minimum Variance Delta en utilisant les données historiques des option, ensuite, nous utilisons cette estimation pour réduire la variance de l'erreur de couverture au futur.

Le modèle est ajusté pour toutes les option sur une période considérée, les trois coefficients â, b^à et cà obtenus pour cette période vont être utilisés pour la couverture de l'option pour le jour suivant.

L'erreur de couverture en se basant sur ce modèle est :

eMV = Of - äBSOS -SA_T (â + _bäBS + M2BS)

L'erreur de couverture en se basant sur le modèle de Black-Scholes est :

eBS = O f - äBSOS

Lors de la présentation de nos résultats, nous définirons l'efficacité d'une couverture comme le pourcentage de réduction de la somme des carrés des résidus résultant de la couverture. Nous désignons le Gain d'une couverture Minimum Variance comme le pourcentage d'aug-mentation de l'efficacité d'une couverture Minimum Variance par rapport à l'efficacité de la couverture par le modèle de Black-Scholes.

SSE(Of - äMVOS)

Gain = 1 - (5.14)
SSE(Of - äBSOS)

où SSE désigne Sum of Squared Errors.

ce qui est équivalent à :

SSE(eMV)

Gain = 1 - SSE(eBS)

Data

Pour notre analyse, nous avons utilisé les option sur l'EURUSD. Nous avons extrait les données depuis https://fr.investing.com/currencies/eur-usd-historical-data, les données s'étendent du 22 Avril 2019 au 20 Mai 2020.

Le prix, le delta et le vega de chaque option ont été dérivés du modèle de Black-Scholes en utilisant la volatilité implicite de cette option, donnée par le modèle de Vanna-Volga, comme étant le paramètre de volatilité.

Nous définissons Initial Moneyness d'un contrat comme étant le ratio suivant:

K

Initial Moneyness = S0

où K est le strike du contrat et S0 est le prix spot du sous-jacent à la date de début du contrat.

Nous considérons que les calls en dehors de la monnaie (OTM) et les puts dans la monnaie (ITM) ont une Initial Moneyness supérieure strictement à 1; les calls et les puts à la monnaie (ATM) ont une Initial Moneyness égale à 1; et les calls dans de la monnaie (ITM) et les puts en dehors la monnaie (OTM) ont une Initial Moneyness inférieure strictement à 1. En outre, les contrats d'options à court terme sont des options dont la durée de vie totale est inférieure ou égale à 3 mois et les options à long terme sont des options dont la durée de vie totale est supérieure à 3 mois.

TABLE 5.9 - Nombre de contrats utilisés en fonction de leur Moneyness et de leur échéance.

Moneyness		Contrats d'options (Call/Put)
		Court terme			Long terme
K	1	284	/	284	282	/	282
S0 <
K =	1	283	/	283	283	/	283
S0
K >	1	282	/	282	284	/	284
S0

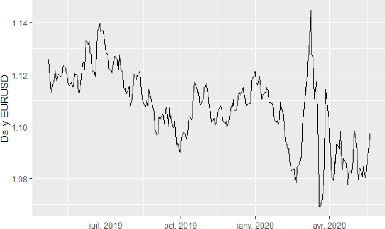
69

FIGURE 5.11 - Évolution de l'EURUSD du 22 Avril 2019 au 20 Mai 2020.

70

Résultats

Les paramètres du modèle a, b et c dans l'équation (5.11), sont estimés en utilisant toutes les options négociées dans une fenêtre mobile de 3 mois, puis appliqués pour déterminer la couverture pour chaque jour qui suit. La première fenêtre utilisée pour estimer les paramètres s'étend du 22 Avril 2019 au 22 Juillet 2019.

Les figures 5.12 et 5.13 représentent les estimations des paramètres de l'équation (5.13) pour les calls et puts respectivement, entre le 23 Juillet 2019 et le 20 Mai 2020.

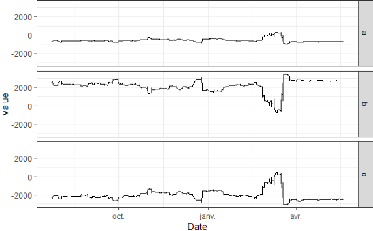
FIGURE 5.12 - Estimation des paramètres des calls entre le 23 Juillet 2019 et le 20 Mai 2020.

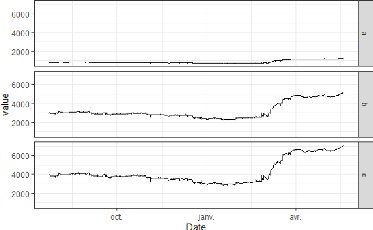
FIGURE 5.13 - Estimation des paramètres des puts entre le 23 Juillet 2019 et le 20 Mai 2020.

71

Généralement, les paramètres du modèle quadratique le mieux adapté changent lentement au fil du temps, mais d'après la figure 5.11 nous remarquons des variations extrêmes du cours de l'EURUSD entre Février 2020 et Avril 2020, ceci est dû à la crise du COVID-19. Ces variations extrêmes ont affecté l'estimation des paramètres a, b et c pendant cette période.

Les tables 5.10 et 5.11 ci-dessous présentent les statistiques descriptives des paramètres a, b et c, et de l'erreur de couverture CMV, pour les calls et le put respectivement.

TABLE 5.10 - Statistiques descriptives de a, b, c et CMV pour les calls.

	Paramètre a	Paramètre b	Paramètre c	Erreur CMV
Minimum	-959,9	-736,5	-3064	4,039 x 10-^5
1er Quartile	-712,4	1975,8	2 423	5,739 x 10-^5
Médiane	-598,0	2297,5	-2099	7,904 x 10-^5
Moyenne	-561,4	2 171,6	-2003	1,237 x 10-^4
3me Quartile	-498,8	2675,1	-1838	9.208 x 10-^5
Maximum	298,5	3463,5	441	3,697 x 10-^4

TABLE 5.11 - Statistiques descriptives de a, b, c et CMV pour les puts.

	Paramètre a	Paramètre b	Paramètre c	Erreur CMV
Minimum	712,0	2235	2850	-2,920 x 10-^3
1er Quartile	786,6	2649	3453	-1,507 x 10-^3
Médiane	831,9	2897	3795	-1,253 x 10-^3
Moyenne	888,8	3203	4232	-1,475 x 10-^3
3me Quartile	879,7	3150	4128	-9,419 x 10-^4
Maximum	1257,3	5203	7107	-6,132 x 10-^4

Pour pouvoir visualiser la qualité de l'ajustement de notre modèle de régression au données utilisés, nous avons calculé le coefficient de détermination, R², pour toute la période considérée, les résultats sont présentés dans la figure 5.14. Nous remarquons que pour les calls, le R² est supérieur à 0,5 pour la majorité de la période considérée, il atteint parfois 0,8, cela signifie que le modèle de régression explique jusqu'à 80% de la variabilité des données des call. Par contre, entre Février 2020 et Avril 2020 nous avons remarqué un faible R², cela peut être dû au variations extrêmes sur l'EURUSD observées pendant cette période suite à la crise du COVID-19. Pour les puts le coefficient de détermination, R², est proche de 1 pour la totalité de la période considérée, cela signifie que le modèles de régression explique presque l'ensemble de la variabilité des données pour les puts.

Nous allons maintenant étudier le gain obtenu par le Minimum Variance Hedging par rapport au Delta Hedging du modèle de Black-Scholes, les résultats seront obtenus pour chaque Mo-neyness, OTM, ITM et ATM, et pour les options long terme et cours terme.

Considérons un ensemble de n observations des variations quotidiennes des prix des options. Ces changements de prix peuvent être couvert en utilisant le delta de Black-Scholes, ou le Minimum Variance delta présenté dans cette section.

Soit xi le carré du résidu de la couverture de la ^i`eme variation d'un jour du prix de l'option en utilisant le Minimum Variance delta et soit zi le carré du résidu de la couverture par le delta du modèle de Black-Scholes.

Le gain de la couverture par le Minimum Variance delta, äMV, par rapport au delta du modèle de Black-Scholes, äBS, est:

Gain = 1	n ? i=1	xi
	n ? i=1	zi

72

Les résultats sont présentés dans le tableau 5.12 ci-dessous.

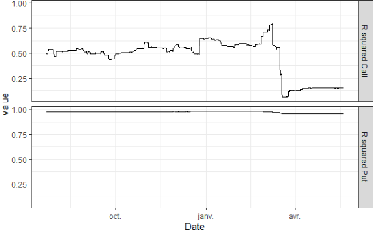
FIGURE 5.14 - R² pour les calls et les puts entre le 23 Juillet 2019 et le 20 Mai 2020.

TABLE 5.12 - Gain du Minimum Variance Hedging par rapport au Delta Hedging.

Moneyness	Type d'option	Temps jusqu'à maturité
		Long terme	Court terme	Tout
En dehors de la monnaie (OTM)	Call	47,8%	94,6%	90,3%
	Put	93,3%	56,9%	88,4%
À la monnaie (ATM)	Call	91%	91%	91%
	Put	61%	61%	61%
Dans la monnaie (ITM)	Call	83,5%	96,4%	94,1%
	Put	99,9%	99, 1%	99,8%
Tout l'échantillon	Call	69%	95,2%	91,2%
	Put	99,2%	94,2%	98,3%

73

Conclusion

Delta est de loin la lettre grecque la plus importante. Elle joue un rôle clé dans la gestion des portefeuilles d'options. Les traders d'options prennent des mesures pour s'assurer qu'ils sont proches du delta-neutre au moins une fois par jour. Ce document a étudié empiriquement la différence entre le delta de Black-Scholes et le Minimum Variance delta. John Hull et Alan White (2017) [15] ont fait l'étude sur les options sur indices, dans ce travail nous avons essayé d'appliquer leur étude sur les options sur l'EURUSD.

La principale contribution du travail de John Hull et Alan White (2017) est de montrer qu'une bonne estimation du Minimum Variance delta peut être obtenue à partir du delta de Black-Scholes et d'une estimation empirique de la relation historique entre les volatilités implicites et les prix des actifs. Ils ont montré que l'espérance de la volatilité implicite peut être approximé sous la forme d'une fonction quadratique sur le delta de Black-Scholes, divisé par la racine carrée du temps. Cela conduit à une formule pour convertir le delta de Black-Scholes en Minimum Variance delta.

74

Chapitre 6

Modélisation du taux de change Marocain

6.1 Introduction

Auparavant, le Maroc adoptait un régime de change fixe, ce dernier n'a pas pu escompter tous les objectifs principaux des autorités monétaires, qui ne sont autres que d'améliorer la compétitivité du pays, d'assurer la stabilité de la monnaie nationale tout en réduisant le risque de change. Le Maroc est resté sur le choix d'un ancrage à un panier constitué essentiellement de deux devises : euro et dollar. Un tel régime de change a permis au pays de lutter contre l'inflation et d'éviter l'inflation emportée.

En janvier 2018, le ministère de l'économie et des finances après avis de Bank Al-Maghrib, a décidé d'adopter, un nouveau régime de change où la parité du dirham est déterminée à l'intérieur d'une bande de fluctuations de #177;2,5% contre #177;0,3% précédemment, par rapport à un court centrale fixé par Bank Al-Maghrib sur la base d'un panier de devises composé de l'Euro et du Dollar Américain à hauteur respectivement de 60% et 40%. Depuis le 9 mars 2020, le Maroc est passé à la deuxième phase de sa réforme du régime de change. Le ministère de l'Économie et des Finances a ordonné, après avis de Bank Al-Maghrib, un élargissement de la bande de fluctuation du dirham qui passe d'une marge de manoeuvre de #177;2,5% à #177;5% par rapport à un cours central.

Il est essentiel de noter que le passage à un régime flottant requiert une bonne préparation de l'économie ainsi que des intervenants. En effet, une transition brusque ne permet pas aux acteurs sur le marché de s'adapter aux risques du flottement et de développer les instruments nécessaires pour faire face à ceux-ci. Cette transition peut s'étaler sur plusieurs années et ce pour garantir un bon fonctionnement des marchés internes et une préparation de la politique monétaire. Et c'est bien la démarche suivie dans le cas du Maroc, selon Mr Abdellatif Jouahri, Wali de Bank Al-Maghrib.

Évolution du régime de change au Maroc

Le Dirham Marocain a passé par plusieurs étapes depuis sa création en 1959 :

-- 1959 : C'est la date de création du Dirham, avec un rattachement au Franc français, ce dernier a connu une forte volatilité au début de 1970 provoquant des déséquilibres dans la valeur du dirham.

75

-- 1973 : Les autorités marocaines ont choisi de déterminer la valeur du Dirham à partir d'un panier de devises des principaux partenaires du pays. Le panier du de devises était constitué de la manière suivante 38% du Franc Français, 15% du Dollar Américain, 15% de la Peseta Espagnole, 8% de la Lire Italienne, 8% du Livre Sterling, 7% du Deutsch Mark, 4% du Franc Suisse, 3% du Franc Belge et 2% du Florin Hollandais.

-- 1980 : Les autorités marocaines on gardé le même panier de devises mais avec des pondérations différentes 25% du Franc Français, 32% du Dollar Américain, 15% de la Peseta Espagnole, 5% de la Lire Italienne, 8% du Livre Sterling, 7% du Deutsch Mark, 2% du Franc Suisse, 4% du Franc Belge et 2% du Florin Hollandais.

-- 1983 : L'adoption de la politique d'ajustement structurelle (PAS), imposée par le fonds monétaire international (FMI) en 1983, c'était le moment le plus difficile pour le Maroc, cette réforme avait comme but d'augmenter le budget de l'État, afin de régler ses dettes suite à une chute des prix de phosphate, elle a ainsi impliqué une série de réformes qui s'inscrit dans une optique d'ouverture de l'économie marocaine, et ceci par le biais d'une politique de libéralisation économique et financière progressive. Le Dirham Marocain a connu dans cette période une dépréciation de 37%.

-- 1996 : La création d'un marché monétaire qui était au départ seulement un marché de change interbancaire au Maroc en 1996 a représenté le couronnement de ces réformes. Les années 90 seront inscrites dans un processus de libéralisation.

-- 2001 : Réaménagement du panier limitant sa composition à l'Euro et au Dollar avec

des pondérations respectives de 80% et 20% impliquant une dévaluation de 5%.

-- 2015 : Révision de panier à 60% de l'Euro et 40% du Dollar.

-- 2018 : Élargissement de la bande de fluctuation de 0,3% à la hausse et à la baisse à 2.5% en janvier. Cette flexibilité vise à soutenir la compétitivité, améliorer la croissance et renforcer la résilience de l'économie nationale aux chocs exogènes (Selon MEF).

-- 2020 : Élargissement de la bande de fluctuation du Dirham de 2,5% à 5% par rapport au cous central fixé par Bank Al-Maghrib. Cet élargissement s'inscrit dans le cadre de la poursuite du processus de réforme du régime de change, qui a été initié en Janvier 2018, et intervient après l'atteinte des objectifs assignés à la première phase.

Implications du régime flottant sur l'économie marocaine

Le régime de change flottant aura plusieurs implications sur l'économie marocaine et sur le comportement des agents économiques.

Détermination de la valeur du dirham

La volonté de passer vers un régime de change flottant implique que la banque centrale ne déterminera plus la parité EURMAD et USDMAD mais c'est plus les jeux de l'offre et de la demande du marché de change qui vont déterminer la valeur du Dirham par rapport aux autres devises. En d'autres termes si des investisseurs étrangers viennent massivement au

76

Maroc, ils exprimeront une demande du Dirham ce qui le fera apprécier puisqu'ils chercheront à convertir leurs capitaux en devises en Dirham mais si au contraire on assiste à une délocalisation en Europe ou une fuite de capitaux, on aura une offre abondante du Dirham ce qui le fera déprécier.

Pouvoir d'achat des consommateurs

Quant au pouvoir d'achat des consommateurs marocains, si le Dirham venait à se déprécier ce qui sera surement le cas vu l'état déficitaire de la balance commerciale, les produits importés couteront plus chers incluant les matières premières qui viendront renchérir la production nationales de produits puisqu'ils incorporent ces matières premières, par conséquent le pouvoir d'achat des marocains qui n'est déjà pas souverain sous le régime fixe le sera encore moins puisqu'une partie de cette souveraineté sera déterminé par les mouvements de marché.

Avènement des fonds spéculatifs

Un autre phénomène qu'on risque d'observer est l'avènement de fonds spéculatifs. En effet , un Dirham flottant est livré à des mouvements spéculatifs extrêmement brutaux et rapides avec des mécanismes tel que la vente à découvert qui pourront mettre à mal notre économie puisqu'elle ne dispose ni de résilience ni de masse monétaire nécessaire pour absorber ces chocs.

Assèchement des liquidités

Le seul levier qui restera pour la banque centrale pour pouvoir continuer à soutenir sa monnaie en cas d'appréciation ou dépréciation brutale du Dirham sont les réserves stratégiques de change, elle devra donc puiser à chaque fois dans ces réserves internationales pour acheter le Dirham en contrepartie de devises, ce phénomène sera accentué par les mouvements spéculatifs et conduira à long terme à un assèchement des réserves de change.

6.2 Modélisation du taux de change marocain dans le cadre d'un régime de change flottant administré

Un régime de flottement administré est un système de taux de change convenu dans lequel certains pays, le Maroc faisant partie, s'engagent à maintenir leur taux de change dans une marge ou une bande de fluctuation spécifique. Cette marge peut être fixée par rapport à une autre devise ou à un panier de devises. L'amplitude de cette bande peut toutefois varier, donnant lieu à deux versions différentes:

-- Version forte : Également connue sous le nom Fixed Peg Arrangement. Le taux de change, qui fluctue dans des marges de #177;1% ou moins, est révisé assez rarement. L'autorité monétaire peut maintenir le taux de change dans les marges par une intervention directe (par exemple, en achetant et en vendant des devises domestiques et étrangères sur le marché) ou indirecte (par exemple, en influant sur les taux d'intérêt).

77

-- Version faible : Également connue sous le nom de Target Zone Exchange Rate. Dans ce cas, le taux de change fluctue de plus de #177;1% autour d'un cours de référence publié par la banque centrale. Une fois que le taux de change atteint une des deux extrémités, les autorités interviennent sur le marché de change en rachetant ou vendant un montant de devises suffisant pour maintenir le taux de change à l'intérieur de la bande.

La modélisation des taux de change sous un régime de flottement administré, est une tentative pour expliquer formellement comment le taux de change se comporte à l'intérieur de la bande de fluctuation. Il existe une vaste littérature sur les Target Zones, théorique et empirique. La littérature théorique moderne a son point de départ dans le modèle de la Target Zone de Krugman (1991) [20] qui sera décrit ci-dessous. Le modèle a ensuite été modifié pour les situations dans lesquelles son hypothèse de base, selon laquelle les interventions de la banque centrale ne se produisent qu'aux frontières de la bande de fluctuation, n'est pas satisfaite. Citons par exemple Delgado et Dumas (1992) [10] et Torres (2000) [30]. Le modèle Krugman a été testé de différentes manières dans de nombreuses contributions empiriques, et une observation générale est qu'il n'a pas réussi à caractériser les mouvements des taux de change à l'intérieur d'une bande de fluctuation, Target Zone.

Le modèle Krugman est un modèle à temps continu, et il y a eu de nombreuses tentatives de l'ajuster à diverses séries de taux de change quotidiens en utilisant la méthode des moments : voir par exemple Smith et Spencer (1992) [26], De Jong (1994) [18], Iannizzotto et Taylor (1999) [16] et Taylor et Iannizzotto (2001) [17]. Une autre approche, à temps discret, Bekaert et Gray (1998) [3], a été de modéliser la distribution conditionnelle de la dans une zone de fluctuation en supposant que la distribution est normale tronquée, la troncature étant le résultat de l'existence d'une zone crédible.

Dans ce chapitre, nous reprenons les travaux de Lundbergh et Teräsvirta (2005), où ils proposent un modèle à temps discret qu'il l'ont appelé Smooth Transition Autoregressive Target Zone (STARTZ). Leur objectif a été de développer un modèle qui permettra à la fois d'exa-miner la validité des hypothèses du modèle de Krugman et, en même temps, de caractériser adéquatement le comportement dynamique d'un taux de change fluctuant à l'intérieur d'une bande de fluctuation.

Le plan de ce chapitre est comme suit : Le modèle classique de Krugman est discuté dans la Section 1, le modèle STARTZ est défini dans la Section 2, la Section 3 est consacrée méthodologie d'estimation du modèle, la Section 4 à l'application et l'évaluation du modèle sur le taux de change marocain. Finalement, la Section 5 conclut.

6.2.1 Le modèle de Krugman

Krugman considère un modèle monétaire log-linéaire minimaliste du taux de change. Exprimant toutes les variables en logarithmes, le taux de change à tout chaque instant t est supposé égal à :

s(t) = f(t) + áE(^ds

dt |Ft) (6.1)

avec s(t) est le logarithme du taux de change spot à l'instant t, mesuré en unités de devise domestique par unité de devise étrangère ou un panier de devises étrangères. f(t) est ce qu'on appelle le fondamental et E(^ds

dt |Ft) est l'espérance conditionnelle de la variation du taux de change à l'instant t sachant la filtration Ft, qui représente l'information dispo-

78

nible à cet instant, celle-ci inclut la valeur actuelle du fondamental f(t), ainsi que toutes les restrictions explicites ou implicites que les autorités ont imposées à l'évolution future du fondamental.

Le fondamental f(t) peut s'écrire comme suit:

f(t) = m(t) + v(t) (6.2)

avec m(t) représente la masse monétaire à l'instant t, c'est un paramètre contrôlé par la banque centrale. v(t) contient tous les autres facteurs qui influent sur le taux de change. On suppose que cette composante suit un mouvement Brownien.

dv = ódz

avec z est un processus de Wiener standard.

La composante m(t) n'est modifié que pour maintenir le taux de change à l'intérieur de la bande. Plus précisément, l'autorité monétaire est prête à réduire m afin d'empêcher s de dépasser une certaine valeur maximale s^U, et à augmenter m pour empêcher s de tomber en dessous d'une certaine valeur minimale s^L. Tant que s^L < s < s^U, la composante m(t) reste inchangée.

S'il n'y a pas de bande de fluctuation et que la monnaie flotte librement, la banque centrale n'intervient pas (m = 0), et f, et donc s, suit un mouvement Brownien. Dans ce cas E(ds _dt |Ft) = 0.

Il n'y a aucune raison économique de supposer une mouvement Brownien sur v. L'hypo-thèse est faite ici pour deux raisons:

-- L'hypothèse d'une marche aléatoire permet de ce concentrer entièrement sur la dynamique causée par la présence d'une bande de fluctuation.

-- L'hypothèse de marche aléatoire donne lieu à une solution analytique simple.

Avant de passer à la solution analytique, il est utile de commencer par une approche intuitive des effets d'une bande de fluctuation sur le comportement des taux de change. La figure 6.1 représente le taux de change par rapport à v; la bande de fluctuation est indiquée par les lignes en pointillés qui définissent une bande qui limite le taux de change entre s^L et s^U. Nous considérons le comportement du taux de change lorsque l'on part d'une certaine masse monétaire initiale, disons m = 0.

Une vision naïve se présenterait comme suit: Puisque m est détenu localement constante et puisque v suit un mouvement Brownien, alors E(ds _dt |Ft) = 0. Ainsi, on pourrait simplement s'attendre à ce que le taux de change soit égal à m + v, c'est-à-dire que le taux de change flotte librement l'intérieur de la bande de fluctuation. Si les chocs successifs à v poussent le taux de change aux bords de la bande de fluctuation, alors la masse monétaire m sera ajustée pour éviter que s ne dérive davantage. Ainsi, cette vision naïve supposerait une relation entre v et s qui ressemble à la ligne épaisse de la figure 6.1.

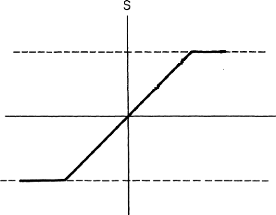
79

FIGURE 6.1 - Représentation de s en fonction de v, [20].

Krugman suppose l'existence d'une bande de fluctuation, s^L = s = s^U, et que les autorités interviennent à travers le paramètre m quand le taux de change atteint l'une des deux frontières s^L ou s^U. Cela change les anticipations des agents lorsque la zone est crédible. Lorsque le taux de change se trouve près de l'une des deux frontières, la probabilité que le taux de change se déplace vers le centre est perçue comme étant plus élevée que la probabilité qu'il se rapproche encore de la frontière. Les agents anticipent l'intervention, E(^ds

dt |Ft) =6 0, de sorte que la zone crée une non-linéarité appelée Honeymoon Effect dans le comportement du taux de change en fonction du fondamental. Au lieu d'une ligne droite, la relation entre le taux de change et fondamentale est caractérisée par une courbe en S lisse représentée dans la figure 6.2.

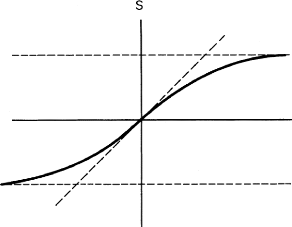
FIGURE 6.2 - Représentation de s en fonction de v, [20].

80

Nous voulons déterminer une relation,

s = g(m, v, s^L, s^U) (6.3)

qui est cohérente avec l'équation du modèle (6.1), et le comportement du taux de change supposé.

Supposons que nous maintenions m constant, c'est-à-dire que nous considérons une situation où s se situe à l'intérieur de la bande. Alors la seule source de changements espérés dans s réside dans le mouvement aléatoire de v. On a donc :

E(^ds

_dt|Ft) = ó22 g_vv(m, v, s^L, s^U) (6.4)

avec

g

g_vv(m, v, sL, sU a2 ) = av2

En substituant (6.4) dans (6.1), nous aurons :

g(m, v, s^L, s^U) = m + v + acr22 g_vv(m, v, s^L, s^U) (6.5)

La solution générale de l'équation (6.5) est de la forme :

g(m, v, s^L, s^U) = m + v + ^AeP(m+v) + Be-P(m+v) (6.6)

avec

_ /²a² P a

et A et B sont des constantes à déterminer à l'aide des conditions aux limites satisfaites par le taux de change s au moment de l'intervention.

Nous pouvons encore simplifier le problème en invoquant la symétrie. Supposons que m = 0; alors nous nous attendons sûrement à ce que la relation passe par le milieu de la figure 6.2, c'est-à-dire que s = 0 lorsque v = 0. Cela ne peut être vrai que si B = -A. L'équation (6.6) peut donc s'écrire :

g(m, v, s^L, s^U) = m + v + A(eP^(m+v) - e-P(m+v)) (6.7)

6.2.2 Le modèle STARTZ Smooth Transition Autoregressive Target Zone

Nous cherchons à estimer par ce modèle, l'écart yt du taux de change par rapport au taux

de référence, avec t = 1, 2 , T. Les limites inférieure et supérieure sont notées s^L et sU
respectivement.

Nous suivons Lundbergh et Teräsvirta (2005) [22], qui ont développé un modèle qui permet un changement de dynamique de la moyenne conditionnelle et la variance conditionnelle lorsque le processus s'approche de la limite de la zone cible.

Le degré de changement de la moyenne et de la variance conditionnelles dépend de façon

81

non linéaire de la distance entre la valeur du processus et le centre de la bande de fluctuation. Une hypothèse similaire sur la dynamique du processus des séries temporelles a été formulée par Bekaert et Gray (1998) [4] et Forbes et Kofman (2000) [11] qui introduisent une variable caractérisant la position du processus dans la bande de fluctuation.

Le modèle de Lundbergh et Teräsvirta (2005) est le suivant :

yt = mt + et (6.8)

avec

_p

et = zt ht (6.9)

où zt ~ iid(0, 1) et ht la variance conditionnelle de et.

La moyenne conditionnelle mt est définie par :

mt = ö^'xt + (us^L - ö^'xt)G^L(yt-1, ã_a, è_a, us^L) + (us^U - ö^'xt)G^U(yt-1, ã_a, è_a, us^U) (6.10)

avec xt = (1, yt-1, , _yt-n)0 est un vecteur d'interception-retard de dimension (n + 1) et

ö = (ö0, ö1, , ö_n)⁰ est le vecteur de paramètres correspondant. Le vecteur xt contient

implicitement toute l'information à propos du fondamental à l'instant t = 1.

Les fonctions G^L et G^U représentent les fonctions de transition, elle ont la forme suivante :

1

G^L(yt-1, ã, è, c) = ã > 0, è > 0
(1 + _e-ã(c-yt-1))è

1

G^U(yt-1, ã, è, c) = ã > 0, è > 0 (6.11)
(1 + _e-ã(yt-1-c))è

avec _yt-1 est la variable de transition, et ã, c et è sont les paramètres de pente, de localisation et d'asymétrie, respectivement. De plus, s^L et s^U définissent les frontières inférieure et supérieur de la bande de fluctuation, donc c = us^L et c = us^U sont les paramètres de localisation dans (6.10).

GL _et G^U sont des fonctions logistiques généralisées (Sollis, Leybourne et Newbold (1999) [27]). Le paramètre è est introduit pour l'asymétrie possible dans le processus de transition. Lorsque è = 1, les fonctions dans les équations (6.11) changent de façon monotone de 0 à 1, le changement étant symétrique autour de c. Sollis et al. (1999) soulignent que lorsque l'on s'approche de zéro, une asymétrie extrême est générée. Pour ã > 0 et è < 1, une transition commence plus lentement qu'elle ne se termine, mais c'est le contraire pour ã < 0. La vitesse de transition de _yt-1 dépend de la valeur de ã. Notons que :

?G^L(yt-1, ã, è, c) = è(c - yt-1)(1 + e-ã(c-yt-1))-(è+1)e-ã(c-yt-1) ?ã

et la valeur de la fonction logistique généralisée augmente à fur et à mesure que ã augmente si yt-1 < c. Par conséquent, une grande valeur de ã est associée à une transition rapide dans la dynamique du processus yt.

Le paramètre u, avec 0 < u < 1, ajoute une flexibilité au modèle et permet d'estimer une bande de fluctuation implicite à l'intérieur de la bande de fluctuation officielle. Le paramètre de pente ã_a > 0 et le paramètre d'asymétrie è_a > 0 nous indiquent le niveau de la variation

82

du comportement dynamique local du taux de change lorsque l'on passe du centre de la bande de fluctuation au voisinage de l'une ou l'autre des frontières.

La moyenne conditionnelle (6.10) a l'interprétation suivante. Près du centre de la bande de fluctuation, le comportement du taux de change est caractérisé, au moins approximative-

ment, par une combinaison linéaire de ses retards, cp'xt en tant que G^L 0 et G^U 0.
Proche de la limite supérieure et inférieure de la bande de fluctuation, le taux de change dépend non linéairement de xt. Par exemple, dans le cas où le taux de change se rapproche de la frontière supérieure, G^U 1 et il y a une transition de comportement autorégressif, représenté par cp'xt, vers un comportement de type "bruit blanc" autour de us^U. Évidemment la quantité 1 - u > 0 est petite. La vitesse de transition est déterminée par ã_a et è_a. Quand le taux de change s'approche de la frontière inférieure, G^L 1 et une conclusion similaire s'ensuit.

Selon les modèles théoriques de bande de fluctuation, la variance conditionnelle doit avoir une distribution en forme de n, car la variance conditionnelle du processus doit être faible à proximité des frontières si la bande est supposée crédible. Lundbergh et Teräsvirta (2005) [22] ont paramétré cette exigence d'une manière similaire à celle appliquée à la moyenne conditionnelle. L'écart conditionnel se présente sous la forme "GARCH local" suivante :

ht = rl^'wt + (ä - rl^'wt)G^L(yt-1, ãb, èb, us^L) + (ä - rl^'wt)G^U(yt-1, ãb, èb, us^U) (6.12)

où rl = (á0, á1, ... , á_q, â1, . . . , âp)' et wt = (1, e2t-1, . . . , e²t-q^, ht-1, . . . , _ht-p)'. En supposant que ä > 0 avec les restrictions á0 > 0, áj > 0, j = 1, 2, ... , q; âj > 0, j = 1, 2, ... , p; sont suffisantes pour la positivité de la variance conditionnelle. De plus, et = yt - mt de sorte que cp est supposé indépendant de rl. L'équation (6.12) implique que la variance conditionnelle est une fonction non linéaire des éléments de wt. Par exemple, dans le cas où l'écart par rapport au cours de référence augmente de telle sorte que G^U -* 1, il y a une transition d'un comportement standard de type GARCH représenté par rl'wt vers une constante ä > 0 qui devrait être proche de zéro.

Bien que le modèle STARTZ vise à modéliser des taux de change à l'intérieur d'une bande de fluctuation, il ne s'ensuit pas que le taux de change reste à l'intérieur de la bande avec une probabilité de 1. Près de la frontière, la variance conditionnelle du modèle STARTZ est faible mais toujours positive, comme ä > 0 : Ainsi, un choc tel que le taux de change franchit la frontière de la bande a une probabilité positive. Ce n'est pas irréaliste, même lorsqu'il n'y a pas de réalignement, le taux de change peut momentanément sortir de la bande de fluctuation avec une faible marge et être rapidement ramené à nouveau.

6.2.3 Méthodologie d'estimation du modèle STARTZ

Le modèle STARTZ défini dans les équations (6.8)-(6.12) est notre paramétrisation la plus générale du modèle du taux de change à l'intérieur d'une bande de fluctuation. Afin de réaliser les travaux empiriques de manière ordonnée, Lundbergh et Teräsvirta (2005) [22] proposent une stratégie de modélisation que l'on peut décrire comme suit :

1. Sélectionnez un modèle AR(n) pour la moyenne conditionnelle selon un critère approprié tel que l'AIC (Akaike, 1974) ou le BIC (Rissanen, 1978; Schwarz, 1978).

2. Sélectionnez un modèle ARCH ou GARCH d'ordre inférieur pour la variance conditionnelle.

3. Estimer un modèle AR(n)-GARCH(p,q), réduire la taille du modèle si nécessaire et ré-estimer pour la série afin d'obtenir les valeurs initiales pour l'estimation du modèle STARTZ.

4. Estimer les paramètres du modèle STARTZ et tester l'adéquation de la moyenne conditionnelle et de la de la variance conditionnelle à l'aide des test statistiques appropriés.

5. Si le modèle passe les tests avec succès, acceptez-le. Dans le cas contraire, essayez d'autres paramètres ou choisissez une autre famille de modèles.

Toutes les estimations des paramètres sont obtenues à l'aide de la méthode des moindres carrées non linéaires. Nous souhaitons donc estimer le vecteur des paramètres Ð = ('P0, . . . , 'P_n, Y, 'r_a, 0_a, '0, . . . , '_q, 130, . . . , 13p, , 'rb, 0b) qui ajuste au mieux les données, au sens des moindres carrés.

6.2.4 Modélisation du taux de change du Dirham par le modèle STARTZ

Dans cette section nous allons essayer de modéliser le taux de change USDMAD avec le modèle STARTZ, en suivant les étapes décrites dans la section précédente. Les données sont des observations quotidiennes du taux de change du 01 Juin 2015 au 01 Juin 2020, extraites de https://fr.investing.com/currencies/usd-mad-historical-data. Nous modélisons l'écart, en pourcentage, du taux de change par rapport au cours de référence. Nous nous sommes cantonnés au cas de l'USDMAD, puisque la même analyse pourra être faite pour le cas de l'EURMAD.

L'élargissement de la bande de fluctuation pour le Dirham de #177;2,5% à #177;5%, a été mis en place depuis le 09 Mars 2020, donc nous n'auront pas suffisamment de données historique pour estimer notre modèle. Pour remédier à ce problème nous avons supposé que la bande de fluctuation de #177;5% a été mise en place depuis le 01 Juin 2015, et nous avons estimé le cour de référence comme une moyenne géométrique des taux USDMAD sur toute la période considérée. La figure 6.3 représente l'évolution de l'écart de l'USDMAD par rapport au cours de référence considéré pour la période allant du 01 Juin 2015 au 01 Juin 2020, les lignes rouges en pointillés représentent la bande de fluctuation de #177;5% autour d'une cours de référence de 9,6597.

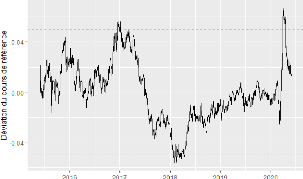
83

FIGURE 6.3 - La déviation en pourcentage de l'USDMAD du cours de référence.

Nous remarquons que le taux de change dépasse la bande pour quelques observation, mais cela ne contredit pas notre modèle, car on a prouvé que la probabilité que le taux de change dépasse la bande de fluctuation n'est pas nulle.

Estimation du modèle AR(n) pour la moyenne conditionnelle

La première étape de la modélisation est d'estimer un modèle AR(n) pour la moyenne conditionnelle mt, pour cela nous allons suivre la méthodologie de Box-Jenkins, c'est un outil systématique qui permet de déterminer le meilleur modèle de type ARMA décrivant le processus stochastique d'une série observée ou d'une transformation stationnaire de celle-ci, d'estimer ce modèle et de l'utiliser pour extrapoler les valeurs de la série. Les principales étapes de la méthodologie de Box-Jenkins sont:

1. Tracer la série des données et repérer ses principales caractéristique : Tendance, saisonnalité et résidu.

2. Transformer la série afin de stabiliser la variance (log, sqrt,...) et différenciation des données pour les rendre stationnaires.

3. Déterminer l'ordre n du processus AR à l'aide des critères AIC, BIC ou la fonctions ACF et PACF.

4. Estimer les paramètres du modèle.

5. Diagnostique et tests d'adéquation du modèle.

6. Prévision des valeurs futures à travers le modèle retenu.

Tout d'abord, il faut tracer la série temporelle et repérer ses principales caractéristique. Pour cela nous allons décomposer la série en 3 composantes : Tendance, saisonnalité et résidu. La figures 6.4 représente les différentes composantes de notre série.

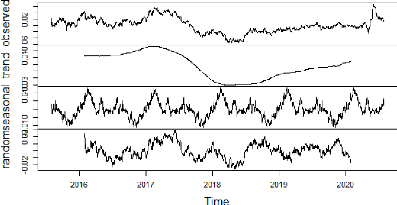
84

FIGURE 6.4 - Représentation de la de la série de l'USDMAD et de ses composantes.

85

Avant de travailler avec la série, il faut d'abord vérifier si elle est stationnaire ou pas, pour cela nous allons vérifier la stationnarité de la série à l'aide du test de Dickey-Fuller (1979) augmenté (ADF). Les hypothèses du test sont:

-- H0 : La série n'est pas stationnaire. -- H1 : La série est stationnaire.

TABLE 6.1 - Test de Dickey-Fuller Augmenté (ADF) sur la série yt.

Série Dickey-Fuller Test Lag Order p-value 5% Conclusion

yt -2,4992 10 0,367 Non Stationnaire

Nous remarquons que la p - value> 0,05 donc l'hypothèse H0 est retenue au seuil 5% pour la série temporelle yt.

D'après la méthodologie de Box-Jenkins, il faut stationnariser la série avant de l'utiliser pour estimer le modèle AR(n). La méthode utilisée pour stationnariser une série temporelle est la différenciation. Différencier une série temporelle signifie soustraire chaque point de données de la série de son successeur. Pour la plupart des modèles de séries chronologiques, une ou deux différences sont nécessaires pour en faire une série stationnaire. Notre nouvelle série temporelle, y⁰_t, différenciée une seule fois, représentée dans la figure 6.5, s'écrit:

y0 t = yt - yt-1

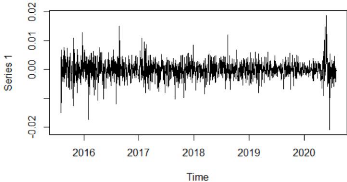
FIGURE 6.5 - Représentation de la de la série y⁰_t.

Nous allons vérifier de nouveau la stationnarité avec le test de Dickey-Fuller Augmenté (ADF).

TABLE 6.2 - Test de Dickey-Fuller Augmenté (ADF) sur la série y⁰_t.

Série Dickey-Fuller Test Lag Order p-value 5% Conclusion

y⁰_t -10,876 10 0,01 Stationnaire

86

Nous remarquons que la p - value < 0,05 donc l'hypothèse H0 est rejetée au seuil 5% pour la série temporelle y⁰_t.

Dans cette étape, ont doit déterminer l'ordre n du processus AR(n), pour cela nous allons utiliser les critères Akaike information criterion (AIC) et Bayesian Information Criterion (BIC). Nous allons estimer différents modèles : AR(1), AR(2), AR(3), AR(4) et AR(5), puis nous allons choisir le modèle de plus adéquat suivant ces deux critères. Les résultats sont présentés dans la tableau 6.3 ci-dessous.

TABLE 6.3 - Comparaisons des modèles AR(n), n = 1, . . . , 5, par les critères AIC et BIC.

Modèle	Critère AIC	Critère BIC
AR(1)	-11230,35	-11214,83		AR(2)
-11228,42	-11207,73	AR(3)
-11228,59	-11202,71	AR(4)
-11227,12	-11196,07	AR(5)
-11225,16	-11188,93

Le modèle choisi est celui qui aura les plus faible valeurs d'AIC et BIC. Ces critères reposent sur un compromis entre la qualité de l'ajustement et la complexité du modèle, en pénalisant les modèles ayant un grand nombre de paramètres. Pour le critère AIC la pénalité dépend seulement du nombre des paramètres, par contre pour le critère BIC la pénalité dépend à la fois de la taille de l'échantillon et du nombre de paramètres. Donc d'après le tableau 6.3 le modèle choisi est AR(1).

Avant de valider notre modèle il faut le diagnostiquer, pour cela il faut analyser les résidus du modèle, ces résidus doivent vérifier les trois hypothèses suivantes:

-- Normalité.

-- Absence d'auto-corrélation. -- Homoscédasticité.

La normalité peut être soit testée graphiquement, en représentant l'histogramme des résidus ou par le graphe quantile-quantile (qq-plot), soit testée statistiquement avec le test de Shapiro-Wilk, les hypothèses du test sont:

-- H0 : Les résidus sont normalement distribués.

-- H1 : Les résidus ne sont pas normalement distribués.

TABLE 6.4 - Test de Shapiro-Wilk pour les résidus du modèle AR(1).

Modèle Shapiro-Wilk Test p-value 5% Conclusion

AR(1) 0,96285 < 2,2 x 10-¹⁶ Non-normalité

Nous remarquons que la p - value < 0,05 donc l'hypothèse H0 est rejetée au seuil 5% pour le modèle AR(1). Cela ne posera pas de problème, car nous essayons seulement de trouver les valeur initiales pour notre modèle final STARTZ.

L'auto-corrélation des résidus peut être vérifiée avec le test de Ljung-Box (1978) ou celui de Box-Pierce (1970). Les hypothèses du test sont:

87

-- H0 : Absence d'auto-corrélation des résidus. -- H1 : Présence d'auto-corrélation des résidus.

TABLE 6.5 - Test de Ljung-Box pour les résidus du modèle AR(1).

Modèle ÷² Lag Order p-value 5% Conclusion

AR(1) 7,7444 x 10_⁵ 1 0,993 Pas d'auto-corrélation

Nous remarquons que la p _ value > 0.05 donc l'hypothèse H0 est retenue au seuil 5% pour le modèle AR(1).

L'homoscédasticité des résidus peut être vérifiée avec le test de White (1980). Les hypothèses du test sont:

-- H0 : Homoscédasticité des résidus. -- H1 : Hétéroscédasticité des résidus.

TABLE 6.6 - Test de White pour les résidus du modèle AR(1).

Modèle ÷² Lag Order p-value 5% Conclusion

AR(1) 5,1267 2 0,07705 Homoscédasticité

Nous remarquons que la p _ value > 0.05 donc l'hypothèse H0 est retenue au seuil 5% pour le modèle AR(1).

Estimation du modèle GARCH(p,q) pour la variance conditionnelle

La deuxième étape de la modélisation est d'estimer un modèle GARCH(p,q) pour la variance conditionnelle ht. Dans la première étape, nous avons vu que le modèle AR(1) était suffisant pour estimer la moyenne conditionnelle mt, nous allons donc utiliser cette conclusion et suivre les mêmes étapes afin de choisir le modèle GARCH(p,q) le plus adéquat.

De manière générale, on peut dire que la série yt suit le processus AR(1)-GARCH(p,q) suivant:

yt = ö0 + _{ö1yt_1} + et (6.13)

avec

\/

et = zt ht (6.14)

où zt iid(0, 1) et ht la variance conditionnelle de et qui suit le processus GARCH(p,q)

suivant:

ht = á0 + á1e2 _{t_1} + ... + ápe2 _{t_p} + _{â1ht_1} + ... + âqht_q (6.15)

De la même manière que l'étape précédente, ont doit décider les ordres p et q du modèle GARCH. pour cela nous allons estimer différents modèles : GARCH(1,1), GARCH(2,1), GARCH(1,2) et GARCH(2,2), puis nous allons choisir le modèle de plus adéquat suivant les critères AIC et BIC. Les résultats sont présentés dans la tableau 6.7 ci-dessous.

88

TABLE 6.7 - Comparaisons des modèles GARCH(p,q), p = 1,2, q = 1,2, par les critères AIC et BIC.

Modèle Critère AIC Critère BIC

GARCH(1,1) -8,7061 -8,6863 GARCH(2,1) -8,7029 -8,6792 GARCH(1,2) -8,7019 -8,6781 GARCH(2,2) -8,7026 -8,6749

Le modèle choisi est celui qui aura les plus faible valeurs d'AIC et BIC. Donc d'après le tableau 6.7 le modèle que nous allons choisir est GARCH(1,1).

Donc finalement nous avons un modèle AR(1)-GARCH(1,1) dont les paramètres sont représentés dans le tableau ci-dessous. Ces paramètres vont nous servir pour initialiser l'algo-rithme qui nous permettra d'estimer les paramètre de notre modèle STARTZ.

TABLE 6.8 - Paramètres du modèle AR(1)-GARCH(1,1).

Paramètres	Estimation	Std. Error	t-Statistic	Pr(> |t|)
P0	-1,527186 x 10-^5	0,000077	-0,198691	0,842504
P1	-0,022622	0,028974	-0,780754	0,434947
á0	7, 154863 x 10-^8	0, 000001	0, 096016	0, 923507
á1	0,046181	0,019789	2,333640	0,019615
â1	0,947683	0,019191	49,380824	0

Avant de valider notre modèle, on doit le diagnostiquer. Nous allons d'abord tester l'auto-corrélation des résidus avec le test de ARCH LM. Comme le test Ljung-Box, le test ARCH LM permet de tester la dépendance en série (auto-corrélation) due à un processus de variance conditionnelle en testant l'auto-corrélation dans le carré des résidus. Les hypothèses du test sont:

-- H0 : Absence d'auto-corrélation des résidus pour un ensemble de retards k. -- H1 : Présence d'auto-corrélation des résidus pour un ensemble de retards k.

TABLE 6.9 - Test de ARCH LM pour les résidus carrés du modèle AR(1)-GARCH(1,1).

Modèle Lag Order Statistic p-value 5% Conclusion

3 0,4118 0,5210 Pas d'auto-corrélation

AR(1)-GARCH(1,1) 5 1,2392 0,6635 Pas d'auto-corrélation

7 2,4429 0,6242 Pas d'auto-corrélation

Nous remarquons que pour tout les ordres de retard, la p - value > 0.05 donc l'hypothèse H0 est retenue au seuil 5% pour le modèle GARCH(1,1).

Nous allons maintenant tester si le modèle AR(1)-GARCH(1,1) ajuste bien les données en utilisant le test Pearson Goodness-of-Fit, ce test compare la distribution empirique des résidus standardisés avec la distribution théorique choisie. Les hypothèses du test sont:

-- H0 : Le modèle ajuste bien les données -- H1 : Le modèle n'ajuste pas les données.

TABLE 6.10 - Test de Pearson Goodness-of-Fit du modèle AR(1)-GARCH(1,1).

Modèle Échantillon Statistic p-value 5% Conclusion

AR(1)-GARCH(1,1)

20 34,43 0,01635 Modèle non-ajusté 30 38,53 0,11094 Modèle ajusté 40 45,30 0,22574 Modèle ajusté 50 58,47 0,16661 Modèle ajusté

Nous remarquons que pour un échantillon de 20, la p - value < 0.05 donc le modèle n'ajuste pas bien les données. Par contre pour un échantillon = 30, la p - value> 0.05 donc l'hypo-thèse H0 est retenue au seuil 5%, c'est-à-dire que le modèle AR(1)-GARCH(1,1) ajuste bien les données de la série.

Estimation du modèle STARTZ pour le taux de change

Dans les deux parties précédentes, nous avons estimé un modèle AR(1) pour la moyenne conditionnelle et un modèle GARCH(1,1) pour la variance conditionnelle. Donc nous avons un modèle AR(1)-GARCH(1,1) pour le taux de change, l'équation de ce modèle s'écrit:

yt = ö0 + _ö1yt-1 + et (6.16)

avec

\/

et = zt ht (6.17)

où zt ~ iid(0, 1) et ht la variance conditionnelle de et qui suit le processus GARCH(1,1) suivant:

ht = á0 + á1e2 _t-1 + â1ht-1 (6.18)

avec les paramètres initiaux (ö0, ö1, á0, á1, â1) sont définis dans la tableau 6.8.

Nous rappelons que le but de l'estimation d'un modèle AR(1)-GARCH(1,1) pour le taux change, est de trouver les paramètres initiaux qui nous permettrons d'initialiser notre algorithme pour estimer les paramètre finaux du modèle STARTZ. L'estimation des paramètres du modèle STARTZ est faite avec la méthode des moindres carrés non linéaires. Les résultats de l'estimation sont présentés dans le tableur ci-dessous.

TABLE 6.11 - Résultats d'estimation des paramètres du modèle STARTZ.

Modèle Paramètres

cP0 cP1

Initialisation			Résultat Final
-1,53	×	10-^5	1,10 × 10-^5
-2,26	×	10-^2	-1,13 × 10-^2
1				1
10				-2,93
0,5				0,5

y

Y_a V_a

STARTZ

á0 7, 15 × 10-⁸ -1, 19 × 10-³

á1 4,62 × 10-² 3,03 × 10-⁵

131 9,48 × 10-¹ 1,70

8 0,1 1,50 × 10-³

Yb 10 11,93

Vb 0,5 1,45

89

Les figures 6.6 et 6.7 ci-dessous représentent les fonctions de transition G'^- et G^1-' du modèle STARTZ, pour la moyenne et la variance conditionnelles.

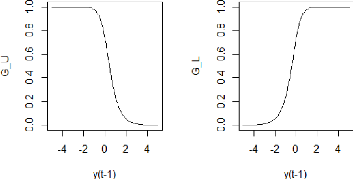
FIGURE 6.6 - Les fonctions de transition G'^- et G^1-' pour la moyenne conditionnelle.

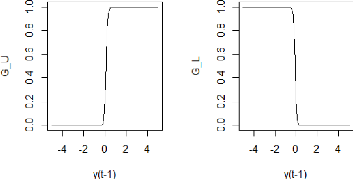
90

FIGURE 6.7 - Les fonctions de transition G'^- et G^1-' pour la variance conditionnelle.

Afin de tester l'adéquation de notre modèle STARTZ, les données historiques du cours de l'USDMAD ont été divisés en deux ensembles:

-- Ensemble d'apprentissage : Constitue 80% des données initialement choisies, cet ensemble représente l'écart yt du taux de change USDMAD par rapport au taux de référence pour la période allant du 01 Juin 2015 au 03 Juin 2019. Ce sont les données

qui ont été utilisés pour estimer les paramètres du modèle STARTZ représentés dans le tableau 6.11.

-- Ensemble de validation : Constitue les 20% restantes des données, cet ensemble représente l'écart yt du taux de change USDMAD par rapport au taux de référence pour la période allant du 04 Juin 2019 au 01 Juin 2020. Il sera utilisé pour évaluer la performance du modèle STARTZ.

Afin de voir si le modèle ajuste bien l'ensemble des donnée d'apprentissage, nous avons représenté dans la figure 6.8 ci-dessous, la série yt des donnée réellement observés contre les résultats de l'ajustement du modèle.

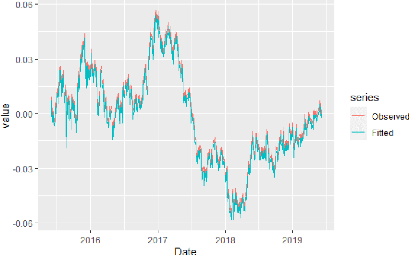
91

FIGURE 6.8 - Représentation des données observés et ajustés par le modèle pour la série yt.

Afin d'évaluer l'ajustement du modèle, nous allons calculer quelque indicateurs d'écart entre le valeur observés et les valeur données par le modèle. Ces indicateurs sont:

-- La somme des carrés des résidus (SSE) :

SSE = -- Le carré moyen des erreurs (MSE) :	n ? i=1		(yi - àyi)^2
1 MSE = n		n ? i=1		(yi - àyi)^2

-- L'erreur quadratique moyenne (RMSE) :

\/

n

1

RMSE = (yi - àyi)²

n ?

i=1

-- L'erreur absolue moyenne (MAE) : 1 MAE = n

n ? i=1

|yi - àyi|

-- L'erreur absolue moyenne en pourcentage (MAPE) :

1 MAPE = n

n ? i=1

|yi - àyi| |yi|

Les résultats sont présentés dans le tableau ci-dessous:

TABLE 6.12 - Indicateurs d'écart du modèle STARTZ.

SSE MSE RMSE MAE MAPE

2,094 x 10-² 2,003 x 10-⁵ 4,475 x 10-³ 3,501 x 10-³ 4,59%

D'après la figure 6.8 et le tableau 6.12, on peut remarque que l'écart entre le données observés et les données ajustés est très minime. Nous pouvons donc dire que le modèle ajuste bien les données.

Pour valider notre modèle STARTZ, et de la même façon que les deux premières étapes, il faut tester la normalité, l'auto-corrélation et l'homoscédasticité des résidus.

La normalité peut être testée graphiquement ou à l'aide du test de Shapiro-Wilk présenté plus haut, les résultats sont présentés dans la figure 6.9 et le tableau 6.13.

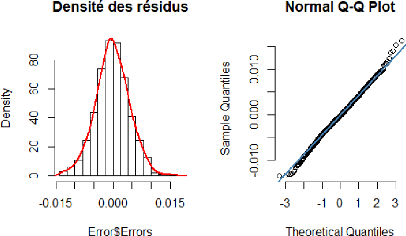
92

FIGURE 6.9 - L'histogramme et le graphe quantile-quantile des résidus du modèle STARTZ.

93

TABLE 6.13 - Test de Shapiro-Wilk pour les résidus du modèle STARTZ.

Modèle Shapiro-Wilk Test p-value 5% Conclusion

STARTZ 0,99774 0,1644 Normalité des résidus

Nous remarquons que la p - value> 0,05 donc l'hypothèse H0 est retenue au seuil 5% pour le modèle STARTZ, ce qui signifie que les résidus sont normalement distribués.

Nous allons maintenant vérifier l'auto-corrélation des résidus avec le test de Ljung-Box, présenté plus haut. Les résultats sont représentés dans le tableau 6.14 ci-dessous.

TABLE 6.14 - Test de Ljung-Box pour les résidus du modèle STARTZ.

Modèle ÷² Lag Order p-value 5% Conclusion

STARTZ 0,3607 1 0,5481 Pas d'auto-corrélation

Nous remarquons que la p - value > 0.05 donc l'hypothèse H0 est retenue au seuil 5% pour le modèle STARTZ, , ce qui signifie l'absence d'auto-corrélation des résidus.

L'homoscédasticité des résidus peut être vérifiée avec le test de White, présenté plus haut. Les résultats sont représentés dans le tableau 6.15 ci-dessous.

TABLE 6.15 - Test de White pour les résidus du modèle STARTZ.

Modèle ÷² Lag Order p-value 5% Conclusion

STARTZ 1,1744 2 0,5559 Homoscédasticité

Nous remarquons que la p - value > 0.05 donc l'hypothèse H0 est retenue au seuil 5% pour le modèle STARTZ, ce qui signifie l'homoscédasticité des résidus.

On peut conclure que les résidus vérifient les trois hypothèses : Normalité, absence d'auto-corrélation et homoscédasticité, ce qui valide le modèle STARTZ.

Afin de s'assurer de la performance du modèle, nous allons l'appliquer sur l'ensemble de validation qui représente la période allant du 04 Juin 2019 au 01 Juin 2020. Nous avons représenté dans la figure 6.10 ci-dessous, la série yt des donnée réellement observés contre les résultats du modèle.

Cette représentation nous permet de visualiser la qualité de l'estimation des paramètre, car l'ensemble de validation n'a pas été utilisé pour ajuster le modèle, et malgré cela on peut remarquer que le modèle donne une très bonne approximation de yt en fonction de (yt-1, ht-1, Ct-1).

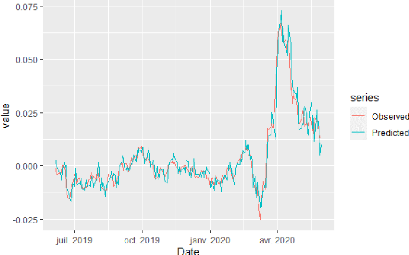
94

FIGURE 6.10 - Représentation des données observés et prévues par le modèle pour yt.

6.2.5 Conclusions

Dans la littérature sur les Target Zones, l'accent a été mis sur les modèles théoriques. Ce chapitre traite un modèle de série chronologique empirique assez souple, proposé par Lundbergh et Teräsvirta (2005) [22], capable de caractériser le comportement d'un taux de change à l'in-térieur d'une bande de fluctuation. Afin de modéliser les données empiriques de manière systématique, il est Il est important de disposer d'une stratégie de modélisation cohérente, et une telle stratégie a été conçue et appliquée aux données ici.

Le modèle a été appliqué au taux de change USDMAD, les résultats montrent que ce modèle ajuste bien les données. Plusieurs test statistiques ont été utiliser dans chacune des étapes de modélisation, le modèle a passé tous ces tests avec succès. Le modèle STARTZ peut également être utilisé pour modéliser d'autres variables économiques limitées par des frontières explicites ou implicites, telles que le taux chômage ou les séries de taux d'intérêt. Le modèle STARTZ à équation unique peut aussi facilement être rendu multivarié.

95

Conclusion

Notre projet s'inscrit parfaitement dans notre cursus académique. En effet, ce travail nous a permis de mettre en pratique l'ensemble des connaissances acquises au cours des enseignements théoriques de finance, de mathématiques, d'analyse des données ainsi qu'en séries chronologiques. De plus, nous nous sommes retrouvés dans un contexte différent et plus proche de la réalité que le cadre du modèle de Black-Scholes où la volatilité est constante.

Nous avons pu examiner dans une première partie le modèle de Garman-Kohlhagen, ce modèle n'est qu'une extension du modèle de Black-Scholes, adapté au marché de change de manière à ce que ce modèle puisse faire face à la présence de deux taux d'intérêt sans risque.Le modèle de Black-Scholes et ses extensions restent l'outil fondamental utilisé par les traders des options. Cependant, il existe des inconsistances, à savoir la volatilité constante, qui rend impossible son application directe sur le marché des options.

Pour pallier à cet inconvénient, nous nous sommes intéressés à la modélisation de la volatilité implicite. Cette courbe de volatilité utilisée par les traders pour évaluer les options sur devises a généralement la forme d'un sourire, d'où le nom Smile de volatilité. Comme il n'y a pas de formule explicite pour calculer la volatilité implicite, nous avons recours à des méthodes numériques pour la calculer, parmi lesquelles on trouve la méthode de Vanna-Volga; qui est largement utilisée dans le contexte des marchés des changes en raison de sa capacité à construire de manière cohérente tout le Smile de volatilité en utilisant seulement trois cotations de marché.

Le nouveau régime de change au Maroc a permis d'introduire de nouveaux produits plus complexes, notamment les options Américaines. L'évaluation de ce type d'options a sollicité de nombreux travaux de recherche. Sachant qu'elle n'existe pas une formule fermée qui donne le prix exact d'une option Américaine, nous avons présenté quatre méthodes largement utilisées en salles des marchés pour évaluer ce type d'options, à savoir la méthode des différences finies, l'approximation de Barone-Adesi et Whaley (1987), l'approximation de Bjerksund et Stensland (1993) et enfin l'approximation de Bjerksund et Stensland (2002). Nous avons constaté que les quatre méthodes donnent des résultats assez proches, mais d'un point de vue technique, l'approximation de Bjerksund et Stensland (2002) sera préférée.

Nous avons souligné tout au long de ce rapport l'importance capitale de la couverture et la gestion des risques. Afin de gérer les risques liés aux options, il est indispensable de suivre des stratégies de couverture, qui peuvent généralement être classées selon deux catégories à savoir les stratégies statiques et les stratégies dynamiques. Les premières sont basées sur la prise de positions sur d'autres options afin de couvrir celles du portefeuille. Ce type de stratégies est souvent utilisés par les investisseurs particuliers, donc ils seront toujours obligés de payer une prime afin d'acquérir l'une de ces stratégies. Pour cette raison nous avons élaboré un outil permettant de trouver le prix d'exercice optimal qui permet d'annuler la

96

prime totale de la stratégie. Le second type est une gestion en temps continu du portefeuille, souvent utilisée par les praticiens et les opérateurs du marché, basée sur l'analyse des sensibilités des options qui composent le portefeuille. La stratégie dynamique la plus populaire est le Delta Hedging, basée sur le modèle de Black-Scholes. Par contre, plusieurs chercheurs et praticiens ont remarqué que le delta du modèle de Black-Scholes ne minimise pas la variance des changements de la valeur de la position d'un trader. Cela est dû au fait qu'il existe une corrélation non nulle entre les mouvements du prix de l'actif sous-jacent et les mouvements de la volatilité de cet actif. Pour remédier à ce problème, nous avons présenté une nouvelle approche appelée Optimal Delta Hedging, introduite par John Hull et Alan White 2017. Cette approche est basée sur le calcul d'un Minimum Variance Delta qui tient compte à la fois des changements de prix et de la variation attendue de la volatilité conditionnée par un changement de prix.

La volonté de passer vers un régime de change flottant administré implique que la banque centrale ne déterminera plus la parité EURMAD et USDMAD, mais c'est plus les jeux de l'offre et de la demande du marché de change qui vont déterminer la valeur du Dirham par rapport aux autres devises. Dans ce nouveau régime,le taux de change fluctue autour d'un cours de référence publié par la banque centrale. Une fois que le taux de change atteint une des deux extrémités de la bande de fluctuation, les autorités interviennent pour réguler le marché de change en rachetant ou vendant un montant de devises suffisant pour maintenir le taux de change à l'intérieur de la bande. Le défi était donc de modéliser le taux de change à l'intérieur de cette bande de fluctuation. Un modèle de séries chronologiques appelé STARTZ (Smooth Transition Autoregressive Target Zone), basé sur les travaux de Lund-bergh et Teräsvirta (2005), a été conçu pour répondre à ce besoin. Ce modèle nous a permis de caractériser adéquatement le comportement dynamique d'un taux de change fluctuant à l'intérieur d'une bande de fluctuation.

Enfin, nous sommes satisfaits des résultats obtenus à travers ce projet, dans la mesure où ils concordent avec la réalité du marché de changes. De plus le fait de pouvoir tester dans un même projet des compétences en Mathématiques, en Finance et en Informatique ne pourra que nous servir dans notre vie professionnelle.

Suite à la nouvelle réforme du taux de change, le marché de change Marocain sera de plus en plus volatile. Afin de contourner ce risque lié à l'augmentation de la volatilité, de nouveaux produits plus complexes, notamment les options Asiatiques et Quanto, ont été introduites sur ce marché. Une suite logique de notre projet de fin d'études serait donc le pricing de ce type d'options dans le cadre du nouveau régime de change.

97

Bibliographie

[1] Clifford A. Ball and Antonio Roma. Target zone modelling and estimation for european monetary system exchange rates. Journal Empirical Finance, 1 :385-420, 1994.

[2] Giovanni Barone-Adesi and Robert E. Whaley. Efficient analytic approximation of ame-rican option values. The Journal of Finance, 42(2), 1987.

[3] Geert Bekaert and Stephen F. Gray. Target zones and exchange rates : An empirical investigation. Journal of International Economics, 45(1) :1-35, 1998.

[4] Geert Bekaert and Stephen F. Gray. Target zones and exchange rates : An empirical investigation. Journal of International Economics, 45 :1-35, 1998.

[5] Lorenzo Bergomi. Stochastic Volatility Modeling. Chapman and Hall, 1 ^st edition, 2015.

[6] Petter Bjerksund and Gunnar Stensland. Closed-form approximation of american options. Scandinavian Journal of Management, 9(1) :87-99, 1993.

[7] Petter Bjerksund and Gunnar Stensland. Closed form valuation of american options, 2002.

[8] Frédéric Bossens, Grégory Rayée, Nikos S. Skantzos, and Griselda Deelstra. Vanna-volga methods applied to fx derivatives : From theory to market practice. International Journal of Theoretical and Applied Finance, 13(8) :1293-1324, 2010.

[9] Iain J. Clark. Foreign Exchange Option Pricing : A Practitioner's Guide. Wiley, 1 ^st edition, 2011.

[10] Francisco Delgado and Bernard Dumas. Target zones broad and narrow. Exchange Rate Targets and Currency Bands, 1992.

[11] Catherine S. Forbes and Paul Kofman. Bayesian target zones. 2000.

[12] Naima El Haoudi and Oumaima Hali. Morrocan exchange rate modeling. International Journal of Business and Technology Studies and Research, 1(2), 2019.

[13] Espen Gaarder Haug. The Complete Guide to Option Pricing Formulas. McGraw-Hill Professional, 2 ^nd edition, 2007.

[14] John Hull. Options, futures et autres actifs dérivés. Pearson France, 10 ^th edition, 2017.

[15] John Hull and Alan White. Optimal delta hedging for options. Journal of Banking and Finance, 82 :180-190, 2017.

[16] Matteo Iannizzotto and Mark P. Taylor. The target zone model, non-linearity and mean reversion: is the honeymoon really over? Economic Journal, 109(454) :96-110, 1999.

[17] Matteo Iannizzotto and Mark P. Taylor. On the mean-reverting properties of target zone exchange rates : a cautionary note. Economics Letters, 71(1) :117-129, 2001.

[18] Frank De Jong. A univariate analysis of ems exchange rates using a target zone model. Journal of Applied Econometrics, 9(1) :31-45, 1994.

[19] Oleg Korenok and Stanislav Radchenko. The smooth transition autoregressive target zone model with the gaussian stochastic volatility and tgarch error terms with applications, 2008.

[20]

98

Paul R. Krugman. Target zones and exchange rate dynamics. The Quarterly Journal of Economics, 106(3) :669-682, 1991.

[21] Sandro Claudio Lera and Didier Sornette. Quantitative modelling of the eur/chf exchange rate during the target zone regime of september 2011 to january 2015. Journal of International Money and Finance, 2016.

[22] Stefan Lundbergh and Timo Teräsvirta. A time series model for an exchange rate in a target zone with applications. Journal of Econometrics, 131 :579-609, 2005.

[23] Terence C. Mills and Kerry Patterson. Palgrave Handbook of Econometrics, volume 2 : Applied Econometrics. Palgrave Macmillan, 2009.

[24] Sheldon Natenberg. Option Volatility and Pricing : Advanced Trading Strategies and Techniques. McGraw-Hill Education, 2 ^nd edition, 2014.

[25] Azar-Ibrahim Rabhi. Pricing et hedging dynamique des options asiatiques, quantos et américaines de change. Master's thesis, École Mohammadia d'Ingénieurs, Département Modélisation et Informatique Scientifique, 2017.

[26] G.W Smith and M.G Spencer. Estimation and testing in models of exchange rate target zones and process switching. Exchange Rate Targets and Currency Bands, pages 211-239, 1992.

[27] Robert Sollis, Stephen Leybourne, and Paul Newbold. Unit roots and asymmetric smooth transitions. Journal of Time Series Analysis, 20(6) :671-677, 2002.

[28] Nassim Taleb. Managing vanilla and exotic options. John Wiley & Sons, 1 ^st edition, 1997.

[29] Timo Teräsvirta. Specification, estimation, and evaluation of smooth transition autore-gressive models. Journal of the American Statistical Association, 89(425) :208-218, 1994.

[30] Jose L. Torres. An heterogeneous expectations target zone model. Economics Letters, 67(1) :69-74, 2000.

[31] Sami Vähämaa. Delta hedging with the smile. Financial Markets and Portfolio Management, (8) :241-255, 2004.

[32] Changwei Xiong. Foreign exchange implied volatility surface, 2011.

[33] Jia Zhou. Smooth transition autoregressve models : A study of the industrial production index of sweden. Master's thesis, UPPSALA UNIVERSITET, Department of Statistics, 2010.