II.2.
Approche méthodologique
Dans cette partie du travail, il a été
développé la démarche à suivre afin de bien
collecter les données relatives à cette étude.
II.2.1. Population
d'étude
La population d'étude désigne un ensemble dont
les éléments sont choisis parce qu'ils possèdent tous, une
même propriété et qu'ils sont de même nature
(GRAWITZ, 2001).
La population d'étude est un ensemble des
éléments parmi lesquels on aurait pu choisir
l'échantillon, c'est-à-dire l'ensemble des éléments
qui possèdent les caractéristiques que l'on veut
observer(D'HAINAUT, 1975).
Partant de ces différentes définitions, nous
pouvons donc dire que la population d'étude de cette recherche est
constituée de tous les ménages des quartiers Kahembe et
Kyeshero.
II.2.2. Echantillonnage
La population toute entière ne peut pas être
examinée ou étudiée parce qu'elle est nombreuse, et
surtout à cause des moyens matériels réduits dont dispose
le chercheur. Ce dernier se contentera d'un sous ensemble représentatif
de la population auquel seront faites les généralisations qu'on
appelle échantillon.
Un échantillon est une partie de la population
représentant les mêmes caractéristiques. Il est dit
représentatif lorsqu'il permet d'estimer les paramètres
étudiés avec une précision acceptable selon les objectifs
de l'enquête (BUGANDWA, 2017). Pour le cas de cette étude,
l'échantillon est extrait de la population d'étude.
II.2.2.1. Nature et type d'échantillonnage
L'enquête par questionnaire consiste à poser
à un ensemble de répondants, le plus souvent représentatif
d'une population, une série de questions relatives à leur
situation sociale, professionnelle ou familiale, à leur attitude
à l'égard d'opinions ou d'enjeux humains et sociaux, à
leurs attentes, à leur niveau de connaissance ou de conscience d'un
événement ou d'un problème, ou encore sur tout autre point
qui intéresse les chercheurs(QUIVY & CAMPENHOUDT, 1988).
La présente étude a cependant
utilisé l'échantillonnage de nature aléatoire. En effet,
l'échantillonnage aléatoire simple est un type
d'échantillonnage des probabilités où les observations
sont sélectionnées de façon aléatoire dans une
population qui a une probabilité ou une fraction
d'échantillonnage connue (STATSOFT, 2016).
II.2.2.2. Estimation de la taille de l'échantillon
Lorsqu'on effectue une enquête, on s'intéresse
à une population mère (population totale) dont on tire une partie
à interroger que l'on appelle échantillon qu'il faut
déterminer la taille soigneusement car elle a une grande importance sur
la précision des estimations réalisées sur les
caractéristiques de la population mère.
Pour des raisons économiques, il est nécessaire
d'utiliser une taille d'échantillon la plus réduite possible tout
en obtenant un taux de confiance et une marge d'erreur suffisants
(GIEZENDANNER, 1999).
Pour estimer cette taille de l'échantillon, nous nous
servirons de la formule de LYNCH qui est la suivante (NZABANDORA, 2019)
:
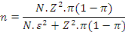
Ainsi l'estimation de l'échantillon sera :
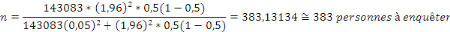
n = la taille de l'échantillon
N = nombre de la population des quartiers Kyeshero et Kahembe,
qui est estimé à 143083 selon les récents
recensements ;
Z= la valeur de déviation à degré de
confiance de 5% (c'est-à-dire, le paramètre lié au risque
d'erreur de 5%), tel qu'admis pour des études à caractère
social. Elle est ici égale à 1,96 ; cela correspond à
d'écart type.
  = prévalence qui est de 0,5.
  = Marge d'erreur qui est de 5 % (0,05).
q= 1-  ; c'est la probabilité, la proportion de n'ai pas avoir un
cas soit 1 - 0,5 = 0,5.
| 
