Test de validité de
l'échelle
Pour tester la validité de l'échelle, le
chercheur doit respecter les etapes suivantes envue de parfaire ces recherche
Étape 1: Déterminer l'approche selon le
type de problème
Approche exploratoire :Le
chercheur n'a pas d'a priori théorique sur la structure sous-jacente des
données et veut en explorer la structure. À ce titre, on peut
utiliser l'ACP pour deux motifs principaux:
§ Identifier la structure sous-jacente des
données
§ Réduire le nombre de variables en quelques
facteurs.
Approche confirmatoire :Le
chercheur a certain a priori théorique et désire confirmer une
structure factorielle documentée. Il cherche donc ici à confirmer
la présence de facteurs déjà connus et décrits dans
la littérature ou par d'autres analyses.
Étape 2: Préparation de
l'analyse
§ Nombre de variables :
Normalement, on effectue une ACP sur un ensemble de variables
substantiel. Extraire 8 facteurs à partir de 12 variables ne
permet pas vraiment de réduire de façon intéressante le
nombre de variables originales. Il faut donc avoir un minimum de variables.
§ Type de variables : De
plus, il est recommandé d'avoir des variables continues, malgré
que quelques variables de l'ensemble peuvent être dichotomiques (0-1). La
technique fonctionne également avec des variables ordinales.
§ Taille de l'échantillon :
Il est recommandé d'avoir un échantillon
relativement grand pour assurer une puissance statistique minimale. On
suggère 100 sujets et plus, mais Hair et al. (1998) donnent comme
règle générale d'avoir un ratio de 10 sujets par variable
insérée dans l'analyse.
Étape 3: Respect des postulats
Corrélations inter-items :
On doit s'assurer qu'il existe des corrélations minimales
entre les items ou les variables qui feront l'objet de l'analyse. Dans le
cas où les corrélations sont très faibles ou inexistantes,
il sera très difficile de faire émerger un ou des facteurs et
l'ACP n'est probablement pas l'analyse à conseiller. À cet
égard, on peut créer une matrice de corrélation avec
toutes les variables de l'analyse et examiner la magnitude des
coefficients. Cette matrice est une option disponible dans le menu SPSS de
l'analyse factorielle
ü Mesure de l'adéquation de
l'échantillonnage (KMO) : Cette mesure donne un
aperçu global de la qualité des corrélations
inter-items. L'indice KMO varie entre 0 et 1 et donne une
information complémentaire à l'examen de la matrice de
corrélation. Son interprétation va comme suit:
§ 0,80 et
plus Excellent
§ 0,70 et
plus Bien
§ 0,60 et
plus Médiocre
§ 0,50 et
plus Misérable
§ Moins de 0,50 Inacceptable
Cet indice augmente 1) plus la taille de l'échantillon
est grande, 2) plus les corrélations inter-items sont
élevées, 3) plus le nombre de variables est grand et 4) plus le
nombre de facteurs décroît.
ü Test de sphéricité de
Bartlett : Cette mesure indique si la matrice de
corrélation est une matrice identité à l'intérieur
de laquelle toutes les corrélations sont égales à
zéro. Nous espérons que le test soit significatif (p < 0,05)
pour que nous puissions rejeter l'hypothèse nulle voulant qu'il s'agisse
d'une matrice identité qui signifie que toutes les variables sont
parfaitement indépendantes les unes des autres.
Le tableau suivant présente les statistiques de la
validité de l'échelle de mesure
|
Tableau n°37. Indice KMO et test de
Bartlett
|
|
Indice de Kaiser-Meyer-Olkin pour la mesure de la
qualité d'échantillonnage.
|
0,889
|
|
Test de sphéricité de Bartlett
|
Khi-deux approx.
|
3155,075
|
|
Ddl
|
45
|
|
Signification
|
0,000
|
Source : Analyse avec SPSS
Il ressort de ce tableau qu'après analyse de la
validité de l'échelle de mesure, l'indice de KMO qui en
ressort de 0, 889et peut ainsi être qualifié de
méritoire car il est supérieur à 1
En outre, le test de sphéricité de
Bartlett ressort une valeur de 0.000, or si cette signification de
Bartlett tend vers 0, cela montre qu'il est fortement significatif. Ainsi,
l'analyse factorielle peut se poursuivre.
Tableau n°38. Analyse de la qualité de
représentation
Identification du poids le plus élevé
pour chaque variable : La prochaine étape est de prendre
chaque variable (ou item) en commençant par la première et
d'identifier sur la ligne le poids le plus élevé (en valeur
absolue). Pour des échantillons de moins de 100 individus, on
n'estime que la valeur absolue de 0,30 est le poids minimum qu'une variable
peut avoir pour être considérée significative. Cependant,
il arrive fréquemment que d'autres poids sont significatifs (plus de
0,30) sur une même ligne. Ceci complexifie le travail du chercheur
qui doit considérer ces poids dans son
interprétation. L'idéal est toujours de minimiser le nombre
de poids significatifs par variable. Une variable qui a des poids
significatifs sur plusieurs facteurs mérite probablement d'être
exclue de la matrice. Ceci implique que l'analyse en composantes
principales devra être exécutée de nouveau sans ces
variables.
|
|
Initiales
|
Extraction
|
|
Cette PME me permet de nourrir régulièrement mon
ménage en qualité et en quantité
|
1,000
|
,896
|
|
Cette PME me permet de scolariser mes enfants
|
1,000
|
,878
|
|
Cette PME me facilite l'accès à la
communication
|
1,000
|
,829
|
|
Cette PME me permet de vêtir mon ménage
|
1,000
|
,838
|
|
Cette PME me facilite l'accès aux loisirs quand j'en ai
envie
|
1,000
|
,657
|
|
Cette PME me permet de répondre aux différentes
obligations sociales
|
1,000
|
,902
|
|
Cette PME me permet d'épargner
|
1,000
|
,839
|
|
Cette PME me permet de réhabiliter ma maison
|
1,000
|
,624
|
|
Cette PME me permet d'engager une main d'oeuvre
extérieure pour mon ménage
|
1,000
|
,898
|
|
Cette PME me permet de développer mes
activités
|
1,000
|
,871
|
|
Méthode d'extraction : Analyse en composantes
principales.
Source : Analyse avec SPSS
Ce tableau présente 10 items acceptés par le
fait que leurs valeurs d'extraction est supérieur à 0,5 ou 50%.
Par contre 20/30 items ont été rejeté par le fait que
leurs valeurs d'extraction est inférieur à 0,5 ou 50%
|
|
Tableau n°39. Variance totale
expliquée
Examen de la matrice des composantes après
rotation : La rotation des facteurs consiste à faire
pivoter virtuellement les axes des facteurs autour du point d'origine dans le
but de redistribuer plus équitablement la variance à expliquer.
La solution factorielle alors obtenue est plus simple a interpréter et
est théoriquement plus pertinente que la solution sans rotation. La
rotation peut être orthogonale lorsque les facteurs sont pressentis comme
étant des dimensions indépendantes les unes des autres ou encore
oblique lorsque les facteurs peuvent être corrélés entre
eux.
Le but ultime de la rotation est toujours de simplifier la
lecture des poids des variables sur les facteurs. Dans la matrice de
poids, ceci signifie que dans chaque rangée, on trouve un maximum de
poids près de 0 et un minimum de poids très élevés
(idéalement un seul).
Dans la pratique, on utilise très
régulièrement la méthode de rotation orthogonale
VARIMAX. Cette méthode est privilégiée, entre autres,
lorsque l'on désire réduire le nombre de variables d'une matrice
de données en un plus petit nombre de facteurs non
corrélés entre eux et utilisés, par exemple, dans le cadre
d'une régression multiple.
Par ailleurs, si le but est d'obtenir des facteurs
représentant un construit théoriquement sensé, la rotation
oblique est suggérée, car il est difficile de postuler
l'orthogonalité (corrélation = 0) entre des facteurs d'un
même construit.
Ultimement, on suggère de procéder à
plusieurs types de rotation pour une même factorisation et de
sélectionner celle qui semble la plus intéressante à
interpréter et la plus robuste au plan conceptuel
|
|
Composante
|
Valeurs propres initiales
|
Sommes extraites du carré des chargements
|
|
Total
|
% de la variance
|
% cumulé
|
Total
|
% de la variance
|
% cumulé
|
|
1
|
8,233
|
82,327
|
82,327
|
8,233
|
82,327
|
82,327
|
|
2
|
,857
|
8,566
|
90,893
|
|
|
|
|
3
|
,345
|
3,446
|
94,339
|
|
|
|
|
4
|
,214
|
2,143
|
96,482
|
|
|
|
|
5
|
,116
|
1,158
|
97,640
|
|
|
|
|
6
|
,088
|
,883
|
98,523
|
|
|
|
|
7
|
,060
|
,598
|
99,121
|
|
|
|
|
8
|
,050
|
,495
|
99,616
|
|
|
|
|
9
|
,024
|
,238
|
99,855
|
|
|
|
|
10
|
,015
|
,145
|
100,000
|
|
|
|
|
Méthode d'extraction : Analyse en composantes
principales.
Source: Analyse avec SPSS
Il ressort de ce tableau qu'après l'analyse factorielle
sous la méthode Varimax, de tous les 10 items retenus dans
l'échelle de mesure de la présente étude, 1 composante a
été extraite et de ce fait, contribuent à 82,327% à
la variance totale du modèle global. De ce fait, cette composante est la
plus pertinente au regard de sa contribution au modèle.
|
Figure n°2. Tracé d'effondrement des
valeurs propres
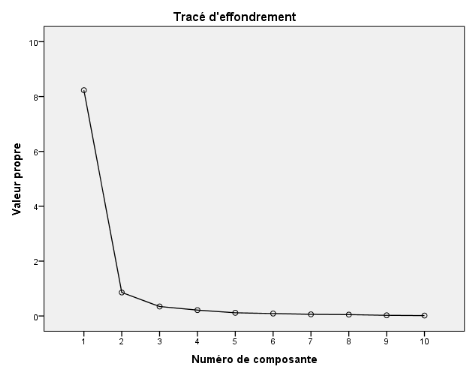 La figure ci-haut présente les valeurs propres des
composantes qui ont constitué cette étude. En effet, il en
ressort que si on relie tous les points par une tangente, seule 1 composante
est retenue pour l'étude de la contribution des PME à la
réduction de la pauvreté au sein des ménages des
propriétaires à Goma. La figure ci-haut présente les valeurs propres des
composantes qui ont constitué cette étude. En effet, il en
ressort que si on relie tous les points par une tangente, seule 1 composante
est retenue pour l'étude de la contribution des PME à la
réduction de la pauvreté au sein des ménages des
propriétaires à Goma.
Tableau n°40. Matrice des
composantes
|
|
Composante
|
|
1
|
|
Cette PME me permet de répondre aux différentes
obligations sociales
|
,950
|
|
Cette PME me permet d'engager une main d'oeuvre
extérieure pour mon ménage
|
,948
|
|
Cette PME me permet de nourrir régulièrement mon
ménage en qualité et en quantité
|
,947
|
|
Cette PME me permet de scolariser mes enfants
|
,937
|
|
Cette PME me permet de développer mes
activités
|
,933
|
|
Cette PME me permet d'épargner
|
,916
|
|
Cette PME me permet de vêtir mon ménage
|
,915
|
|
Cette PME me facilite l'accès à la
communication
|
,911
|
|
Cette PME me facilite l'accès aux loisirs quand j'en ai
envie
|
,811
|
|
Cette PME me permet de réhabiliter ma maison
|
,790
|
|
Méthode d'extraction : Analyse en composantes
principales.
Source : Analyse avec SPSS
|
|
a. 1 composante extraite.
|
Vu qu'il n'y a qu'une seule composante, il n'y aura pas de
rotation. Cependant, Tous les items sont bien corrélés sur la
première composante. Nous l'appelons « les aspects
socio-économiques de la contribution des PME (boutiques de birere)
à la réduction de la pauvreté au sein des ménages
des propriétaires à Goma ».
Tableau n°41. Indice ou niveau de
contribution de boutiques de Birere à la réduction de la
pauvreté dans les ménages de
propriétaires
|
N
|
Moyenne
|
Ecart type
|
|
Contribution des PME
|
171
|
3,8205
|
,89436
|
|
Indice
|
171
|
76,41%
|
|
|
|
|
|
Tableau n°42.Indice ou niveau de contribution
de boutiques de Birere à la réduction de la pauvreté dans
les ménages de propriétaires par rapport à l'existence de
sources secondaires de revenu des ménages
|
Votre conjoint (e) travail-t-il (elle) ?
|
Moyenne
|
N
|
Ecart type
|
|
Oui
|
68,0517
|
116
|
15,62709
|
|
Non
|
94,0364
|
55
|
4,54591
|
|
Total
|
76,4094
|
171
|
17,88712
|
Source : nos calculs sous SPSS
À l'issu de ce tableau il ressort que 116 individus
sur les 171 enquêtés confirment que leurs conjoint travaillent
alors que 55individus seulement sur les 171 enquêtés disent que
leurs conjoints ne travaillent pas. Bref, pour les ménages dans lesquels
les conjoints ont un travail, la boutique contribue à subvenir aux
besoins de ces derniers à 67,8% pendant que pour les ménages dans
lesquels les conjoints n'ont pas de travail, la boutique ne contribue
qu'à 32,2 dans la subvention aux besoins du ménage.
|
|



