Conclusion
Au terme de ce chapitre, nous avons expliqué ce que c'est
qu'un réseau de neurone, nous avons manipulé de très
grandes quantités de données et appris à faire du
prétraitement qui s'est avéré être la tâche la
plus difficile et la plus chronophage lors de la création d'un
algorithme, nous avons créé nos propres réseau de neurone.
Il ne nous reste plus qu'à les entraîner et mesurer les
performances.
CHAPITRE 3 :
SIMULATIONS ET INTERPRÉTATION DES RÉSULTATS
Introduction
Dans le cadre de notre recherche, nous avons
suggéré quelques métriques que nous allions utiliser pour
évaluer les performances des modèles que nous proposons. Nous
avons entrainé et testé nos modèles en utilisant le jeu de
données déjà traité. Nous avons obtenu des
résultats que nous avons comparés entre elles pour décider
du meilleur choix. Enfin nous avons testé le filtre de paquets à
partir des prédictions du modèle.
1. Métriques d'évaluation
des modèles
Pour évaluer l'efficacité de nos algorithmes,
nous nous sommes servis de métriques d'évaluations. Ils sont
très importants pour nous guider dans la conception de nos
modèles. Ils nous aident à nous rendre compte de la performance
d'un modèle ou pas !
Pour obtenir les métriques que nous voulons, nous avons
eu besoin du :
- Vrai Positif (True Positive TP) :
nombre de classification positive correcte. Un vrai
positif est un résultat où le modèle
prédit correctement la
classe positive.
- Vrai Négatif (True Negative
TN): Nombre de classification négative correcte.
un vrai négatif est un résultat
où le modèle prédit correctement la
classe négative.
- Faux Positif (False Positive FP):
Nombre de classification positif incorrecte qui devrait être
négative. Un faux positif est un
résultat où le modèle prédit la
classe positive alors qu'elle est négative.
- Faux Négatif (False Negative
FN): Nombre de classification négatif incorrecte qui devrait
être positif. un faux négatif est un
résultat où le modèle prédit la
classe négative alors qu'elle est positive.
Ensuite, nous pouvons donc calculer le reste des
métriques.
La précision, c'est la capacité d'un
classifieur à ne pas étiqueter une instance positive qui est en
fait négative. Pour chaque classe, il est défini comme le
rapport des vrais positifs à la somme des vrais et des faux positifs.
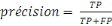 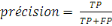 (6) (6)
Le rappel est défini comme le nombre de vrais positifs
sur le nombre de vrais positifs plus le nombre de faux négatifs.
C'est-à-dire qu'elle correspond au nombre de bonnes prédictions
ou d'éléments pertinents trouvés par rapport à
l'ensemble de ces éléments ou de bonnes prédictions au
total dans la base de données. Cela signifie que dans un jeu de
données où nous voulons prédire une classe par exemple,
plus on en obtient par rapport au nombre total de cette classe dans le jeu de
données, plus le rappel est élevé.
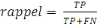 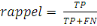 (7) (7)
Le score F1, également appelé score F
équilibré ou mesure F. Le score F1 peut être
interprété comme une moyenne pondérée ou harmonique
de la précision et du rappel, où un score F1 atteint sa meilleure
valeur à 1 et son pire score à 0. La contribution relative de la
précision et du rappel au score F1 est égale. La formule du
score F1 est:
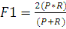 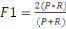 (8) (8)
Avec p mis pour précision et R mis pour rappel.
Dans le cas multi-classes et multi-étiquettes, il
s'agit de la moyenne du score F1 de chaque classe.
La matrice de confusion est une matrice qui montre
rapidement si un système de classification parvient à classifier
correctement.
Elle permet d'évaluer la qualité de la sortie
d'un classifieur sur l'ensemble de données. Les éléments
dans la diagonale représentent le nombre de points pour lesquels
l'étiquette prédite est égale. L'étiquette vraie,
tandis que les étiquettes hors diagonale sont celles qui sont mal
étiquetées par le classifieur. Donc plus les valeurs diagonales
de la matrice de confusion sont élevés, mieux
c'est, indiquant de nombreuses prédictions correctes.
Ensuite la perte correspond à la pénalité
pour une mauvaise prédiction. Autrement dit,
la perte est un nombre qui indique la
médiocrité de la prévision du modèle pour un
exemple donné. Si la prédiction du modèle est parfaite, la
perte est nulle. Sinon, la perte est supérieure à zéro.
Notre but est de trouver la perte la plus faible possible. Le calcul de la
perte dépend des fonctions de perte choisie. Dans notre cas nous avons
utilisé l'erreur quadratique moyenne qui est une mesure
caractérisant la « précision » d'un
estimateur. Elle mesure la moyenne des carrés entre les valeurs et
la valeur réelle [40].
Nous avons aussi pris compte du temps mis par chaque
algorithme pour fonctionner. Ce temps est très important pour
déterminer ses performances car il déterminera aussi le temps que
mettra un programme pour fonctionner et faire des prédictions.
| 


