Partie 2 : La cryptographie
II.4 Définition
La cryptographie est le composant le plus important de la
blockchain. C'est un domaine de l'utilisation des mathématiques pour
crypter et décrypter des données
[54]. La
23 Ce terme « Forks
» désigne la scission d'une blockchain donnant naissance à
deux nouvelles chaines partageant le même historique.
24 Un « Hard Fork
» permet de rompre définitivement avec la précédente
version de la blockchain, en déviante la chaîne de blocs initiale
sur la base d'un nouveau protocole créé à cet effet.
Le « soft fork » s'apparente pour sa
part à une simple modification du protocole existant, mais sans
création de monnaie nouvelle, le protocole antérieur pouvant
être encore utilisé.
Chapitre II Fonctionnement de la blockchain
[32]
cryptographie vous permet de stocker des informations
sensibles ou de les transmettre sur des réseaux non
sécurisés comme Internet afin qu'elles ne puissent être
lues par personne, à l'exception du destinataire
prévu [55]. Nous essaierons de
développer une solide compréhension de certains des concepts
cryptographiques de cette section, car différents problèmes
peuvent nécessiter des solutions cryptographiques différentes ;
c'est le composant le plus important pour assurer la sécurité du
système. De nombreux piratages ont été signalés sur
les portefeuilles et les échanges en raison d'une conception plus faible
ou de mauvaises implémentations cryptographiques.
La cryptographie existe depuis plus de deux mille ans.
Maintenant, c'est la science de garder les choses confidentielles en utilisant
des techniques de cryptage. Cependant, la confidentialité n'est pas le
seul objectif. En matière de cyber sécurité, il y a un
certain nombre de choses qui nous préoccupent en ce qui concerne les
données. Ceux-ci incluent la confidentialité,
l'intégrité, la disponibilité
et la non-répudiation, comme mentionné
dans la liste suivante, que nous explorerons plus loin :
§ La confidentialité signifie que
nos données ne peuvent pas être consultées / lues par des
utilisateurs non autorisés.
§ L'intégrité signifie que nos
données nous parviennent à 100% intactes et n'ont pas
été modifiées, que ce soit par un acteur malveillant, une
perte de données ou autre.
§ La disponibilité
(authentification) signifie que nos données sont accessibles en
cas de besoin.
§ La non-répudiation :
l'expéditeur, après avoir envoyé un message, ne peut pas
nier ultérieurement qu'il a envoyé le message. Cela signifie
qu'une entité (une personne ou un système) ne peut pas refuser la
propriété d'un engagement ou d'une action antérieure.
Toute information sous forme de message texte peut être
appelée texte en clair. L'idée est de chiffrer le texte en clair
à l'aide d'un algorithme de chiffrement et d'une clé qui produit
le texte chiffré. Le texte chiffré peut ensuite être
transmis au destinataire prévu, qui le déchiffre en utilisant
l'algorithme de déchiffrement et la clé pour obtenir le texte en
clair
[56].
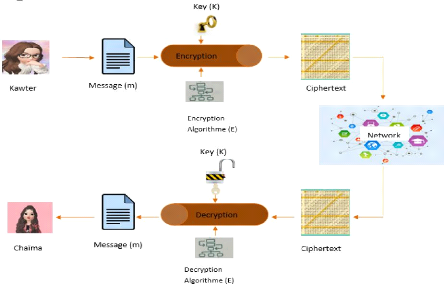
Prenons un exemple, Kawter veut envoyer un message (m)
à Chaima, si elle envoie simplement le message tel quel, tout
adversaire, disons, peut facilement intercepter le message et la
confidentialité est compromise. Donc, Kawter veut crypter le message en
utilisant un algorithme de cryptage (E) avec une clé secrète (k)
pour produire le message chiffré appelé "texte chiffré".
L'ennemie doit connaître l'algorithme (E) et la clé (k) pour
intercepter le message. Plus l'algorithme et la clé sont forts, plus
l'ennemie a de la difficulté à attaquer. Notez qu'il serait
toujours souhaitable de concevoir des systèmes de blockchain leurs
systèmes de sécurité s'adapteront également afin de
répondre aux besoins des différentes utilisations.
L'ensemble d'étapes commun à cette approche
peut être représenté comme illustré à la
figure suivante :
Chapitre II Fonctionnement de la blockchain
[33]
Chapitre II Fonctionnement de la blockchain
Figure II- 3: Comment fonctionne la cryptographie
en général
II.5 Les différents types de la
cryptographie
Nous examinerons les différentes formes de
cryptographie numérique et com ment elles peuvent nous aider à
atteindre les trois autres objectifs énumérés ci-dessus.
Lorsque nous parlons de cryptographie numérique, nous nous
référons généralement à l'un des
éléments suivants :
§ Cryptage symétrique.
§ Cryptage asymétrique.
§ Fonctions de hachage.
§ Signatures numériques.
Nous avons développé chacun de ces points
ci-dessous. Gardez également à l'esprit que ces exemples sont
destinés à illustrer les concepts et non à fournir les
meilleures pratiques en matière de sécurité des
données.
II.5.1 Cryptographie à clé
symétrique
II.5.1.1 Introduction
En cryptage, des clés symétriques
(également appelée cryptographie à clé commune,
cryptographie à clé secrète ou cryptographie classique)
sont utilisées pour crypter et décrypter des informations. En
d'autres termes, pour déchiffrer les informations, vous avez besoin de
la clé utilisée pour le chiffrement
[57]. Une "clé" ici est en fait un secret
partagé entre plusieurs parties, ce qui permet de maintenir un lien vers
des informations confidentielles. Cette exigence selon laquelle les deux
parties ont accès à la clé privée est
[34]
l'un des principaux inconvénients du cryptage à
clé symétrique par rapport au cryptage à clé
publique [57].
Bien que la vitesse de traitement de la cryptographie
à clé symétrique soit élevée, à
mesure que le nombre de personnes qui échangent des données
augmente, le nombre de clés à gérer augmente.
Il existe deux principaux types de cryptage symétrique
dans les temps modernes : le cryptage des flux de données et le cryptage
des blocs de données. Le cryptage du flux de données consiste
à générer un flux de code aléatoire avec
l'algorithme et la clé, puis à générer le flux de
données crypté avec le flux de données XOR. La partie de
déchiffrement n'a besoin que de générer le même flux
de code aléatoire. Le chiffrement des blocs de données divise les
données d'origine en blocs de données de taille fixe (tels que 64
bits), et le chiffreur utilise la clé pour traiter les blocs de
données. Le chiffrement des flux de données est
généralement plus rapide, mais le chiffrement par bloc est plus
sécurisé. Dans les méthodes de cryptage courantes, DES et
3DES sont les méthodes de cryptage par blocs les plus utilisées,
AES est une méthode de cryptage par blocs plus récente, RC4 est
le cryptage des flux de données, etc
[58].
Le schéma de chiffrement le plus courant utilisant la
cryptographie symétrique comprend cinq composants :
§ Texte brut : informations originales.
§ Algorithme de chiffrement : prenez la
clé comme paramètre, effectuez diverses règles et
étapes de substitution et de conversion sur le texte en clair et
transformez le résultat en texte chiffré.
§ Clé : Les paramètres des
algorithmes de chiffrement et de déchiffrement, qui affectent
directement le résultat de la transformation du texte en clair.
§ Ciphertext : résultat de la
transformation du texte en clair.
§ Algorithme de déchiffrement :
la transformation inverse de l'algorithme de chiffrement, avec le texte
chiffré comme entrée et la clé comme paramètres, et
le résultat de la conversion est en texte clair.
Il existe plusieurs opérations mathématiques
couramment utilisées en cryptographie symétrique. Le but commun
de ces opérations est de brouiller les chiffres en clair du texte en
clair aussi profondément que possible, augmentant ainsi la
difficulté de déchiffrement. Parmi ces opérateurs, on a
XOR connu sous le nom de "exclusive
or", il s'agit d'une opération
d'algèbre booléenne binaire. On peut également comprendre
simplement que si les deux chiffres participant à l'opération OU
exclusif sont égaux, le résultat est 0 et s'ils ne sont pas
égaux, le résultat est 1. Le symbole mathématique de XOR
est ? [59].

Chapitre II Fonctionnement de la blockchain
Figure II- 4: Opérateur XOR et sa table de
vérité
II.5.1.2 Les algorithmes de
chiffrement
Les algorithmes de chiffrement célèbres
incluent "DES", "RC4" et "AES". Dans ce qui suit, on va parler seulement des
algorithmes "DES" et "AES".
II.5.1.2.1 Data Encryption Standard « DES
»
DES est un chiffrement par blocs typique - un algorithme qui
convertit un texte en clair de longueur fixe en un texte chiffré de la
même longueur à travers une série d'opérations
complexes. Pour DES, la longueur de bloc est de 64 bits. Dans le même
temps, DES utilise des clés pour personnaliser le processus de
transformation, de sorte que l'algorithme estime que seuls les utilisateurs qui
détiennent la clé utilisée pour le chiffrement peuvent
déchiffrer le texte chiffré. La clé est de 64 bits en
surface, cependant, seuls 56 d'entre eux sont réellement utilisés
pour l'algorithme, et les 8 bits restants peuvent être utilisés
pour la parité et rejetés dans l'algorithme. Par
conséquent, la longueur de clé effective de DES n'est que de 56
bits [60J.
Deux principes de conception de chiffrement par blocs sont
utilisés dans la conception du DES : la confusion et la diffusion, dont
le but est de résister à l'analyse statistique du crypto
système par l'adversaire. Le rôle de la diffusion est d'appliquer
l'influence de chaque texte en clair à plus de bits de texte
chiffré en sortie le plus rapidement possible, afin d'éliminer la
structure statistique du texte en clair dans un grand nombre de textes
chiffrés et de rendre l'influence de chaque clé aussi rapide que
possible. Il y a plus de bits de texte chiffré pour éviter que la
clé ne soit décodée pièce par pièce.
[35]
Le cadre algorithmique du chiffrement DES est le suivant :

Chapitre II Fonctionnement de la blockchain
[36]
Figure II- 5: Structure DES
La vitesse des recherches exhaustives de clés contre
DES après 1990 a commencé à gêner les utilisateurs
de DES. Cependant, les utilisateurs ne voulaient pas remplacer DES car il faut
énormément de temps et d'argent pour changer les algorithmes de
chiffrement qui sont largement adoptés et intégrés dans de
grandes architectures de sécurité. L'approche pragmatique
n'était pas d'abandonner complètement le DES, mais de changer la
manière dont le DES est utilisé. Cela a conduit aux
schémas modifiés de Triple DES.
TDES (ou 3DES) est un algorithme qui
améliore DES. Il utilise trois clés de 64bits pour chiffrer trois
fois les données, et sa sécurité est
améliorée par rapport à l'algorithme DES. Cependant, les
performances de l'algorithme TDES sont bien inférieures à celles
de l'algorithme AES, et son efficacité d'implémentation
logicielle et matérielle n'est pas aussi bonne que l'algorithme AES. En
1999, le National Institute of Standards and Technologie (NIST) a
désigné TDES comme algorithme cryptographique pour la
période de transition. A l'heure actuelle, l'utilisation des algorithmes
TDES diminue, et on prévoit qu'ils seront éventuellement
remplacés par des algorithmes AES.
II.5.1.2.2 Advanced Encryption Standard «
AES »
L'Institut national des normes et de la technologie (NIST) a
travaillé à l'élaboration d'une nouvelle norme de
chiffrement pour sécuriser les informations gouvernementales.
L'organisation en est aux dernières étapes d'un processus ouvert
de sélection d'un ou
Chapitre II Fonctionnement de la blockchain
[37]
plusieurs algorithmes ou formules de brouillage des
données pour la nouvelle norme de chiffrement avancé (AES) et
prévoit de prendre des décisions.
AES est destiné à être un successeur plus
fort et plus efficace de la norme de chiffrement des données triple
(3DES), qui a remplacé le DES vieillissant, qui a été
fissuré en moins de trois jours en juillet 1998.
AES est une nouvelle génération de normes de
chiffrement NIST / FIPS25. Au cours des 30 prochaines années,
il remplacera DES en tant que norme de cryptage de mot de passe commune pour
les entreprises publiques et privées. Le texte chiffré
crypté peut protéger 100 ans de sécurité.
Il est utilisé pour protéger les données
sensibles. Le bloc de données est de 128 bits, et la longueur de la
clé peut être sélectionnée parmi 128/192/256
bits.

Figure II- 6: Structure AES
Le processus de cryptage AES fonctionne sur une matrice 4
× 4 octets. Cette matrice est également appelée «
état » et sa valeur initiale est un bloc de texte en clair. La
taille d'un élément de la matrice est l'un des blocs de texte en
clair. La méthode de chiffrement Rijndael prend en charge des blocs plus
grands et le "numéro de ligne" de sa matrice peut
25 FIPS (Federal
Information Processing Standards) sont des normes annoncées
publiquement développées par le National Institute of Standards
and Technology pour être utilisées dans les systèmes
informatiques par des agences gouvernementales américaines non
militaires et des entrepreneurs gouvernementaux.
Chapitre II Fonctionnement de la blockchain
[38]
être augmenté selon les besoins. Lors du
chiffrement, chaque tour de boucle de chiffrement AES (sauf le dernier tour)
comprend 4 étapes (61] :
§ AddRoundKey : chaque octet de la
matrice est associé à un sous-octet retour alliage de clé
fait (clé année) de l'opérateur OU EXCLUSIF, chaque
sous-clé générée par le système de
génération de clé.
§ SubBytes : Grâce à une
fonction de remplacement non linéaire, chaque octet est remplacé
par un octet correspondant par une table de recherche.
§ ShiftRows : tournez chaque ligne de la
matrice.
§ MixColumns : opérations pour
mélanger complètement les lignes individuelles dans la matrice.
Cette étape utilise une transformation linéaire pour
mélanger les quatre octets de chaque ligne. L'étape MixColumns
est omise dans la dernière boucle de chiffrement et remplacée par
une autre AddRoundKey.
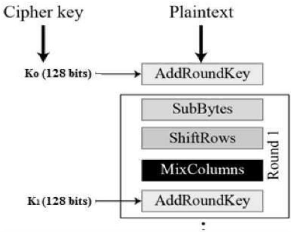
Figure II- 7: Processus du premier tour AES
II.5.1.2.3 Comparaison entre DES et AES
Depuis que l'algorithme DES a été rendu public,
la communauté universitaire a mené des recherches et lancé
des débats acharnés sur sa sécurité et d'autres
aspects. Techniquement, la critique du DES s'est concentrée sur les
domaines suivants (62] :
§ En tant que chiffrement par blocs, l'unité de
chiffrement de DES n'est que binaire 64 bits, ce qui est trop petit pour la
transmission de données, car chaque bloc ne contient que 8
caractères, et certains de ces bits sont également
utilisés pour la parité ou d'autres communications.
§ Le nombre de clés DES est trop court, seulement
56 bits, et les clés utilisées à chaque itération
sont générées récursivement, cette
corrélation réduit inévitablement la
sécurité du système cryptographique. La méthode
pour trouver la clé est devenue possible.
§ Le DES ne peut pas lutter contre la cryptanalyse
différentielle et linéaire.
§
Chapitre II Fonctionnement de la blockchain
[39]
La longueur de clé réelle utilisée par
les utilisateurs DES est de 56 bits et la force de cryptage maximale
théorique est de 256. Pour augmenter la force de chiffrement (telle que
l'augmentation de la longueur de clé) de l'algorithme DES, la surcharge
du système augmente de façon exponentielle. À l'exception
de l'amélioration des fonctions matérielles et de l'augmentation
des fonctions de traitement parallèle, la force de cryptage de
l'algorithme DES ne peut pas être améliorée à partir
de l'algorithme lui-même et de la technologie logicielle.
Par rapport à l'algorithme DES, l'algorithme AES
résout sans aucun doute les problèmes ci-dessus.
L'algorithme AES se manifeste principalement sous les aspects
suivants :
§ Vitesse de calcul rapide.
§ Les besoins en mémoire sont très faibles et
adaptés aux environnements contraints.
§ C'est un chiffrement itératif par blocs, avec
des conceptions de bloc et de longueur de clé flexibles.
§ La norme AES prend en charge une longueur de paquet
variable. La longueur du paquet peut être définie sur n'importe
quel multiple de 32 bits. La valeur minimale est de 128 bits et la valeur
maximale est de 256 bits.
§ La longueur de clé d'AES est supérieure
à celle de DES.
Ci-dessous, nous avons résumé la différence
entre DES et AES [62] :
Chapitre II Fonctionnement de la blockchain
[40]
|
DES
|
AES
|
Date
|
1996
|
1999
|
Taille de bloc
|
64
|
128
|
La longueur de la clé
|
56
|
128, 192, 256
|
Nombre de tours
|
16
|
9, 11, 13
|
Encryptions primitives
|
Substitution, permutation
|
Substitution, shifts, bit, mixing
|
Primitives cryptographiques
|
Confusion, diffusion
|
Confusion, diffusion
|
Conception
|
Ouvert
|
Ouvert
|
Justification de la conception
|
Fermé
|
Ouvert
|
Processus de sélection
|
Secret
|
Secretmais accepter les commentaires publics ouverts
|
Vitesse de calcul
|
Plus rapide
|
Rapide
|
La sécurité
|
Faible
|
Élevé
|
Source
|
IBM amélioré par NSA
|
Cryptographes indépendants
|
|
Tableau II- 2: Comparaison entre DES et
AES
II.5.2 Cryptographie à clé
asymétrique
II.5.2.1 Introduction
La cryptographie asymétrique trouve son origine dans
les travaux de recherche de Whitfield Diffie et Martin Hellma. Le papier qu'ils
ont publié en 1976 a complètement révolutionné la
cryptographie. L'algorithme qu'ils ont conçu évite aux
communicants de s'entendre sur une clé partagée au
préalable et a ainsi résolu le problème dit de
distribution de clé rencontré avec la cryptographie
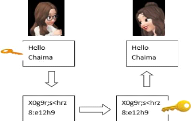
symétrique (63]. Voyons un
scénario pratique pour comprendre comment un tel système
fonctionnerait. Supposons que Kawter souhaite envoyer un message à
Chaima de manière confidentielle afin que personne d'autre que Chaima ne
puisse comprendre le message, alors cela nécessiterait les étapes
suivantes :
II.5.2.2 Principe de fonctionnement
Prenons l'exemple suivant (64]
Chapitre II Fonctionnement de la blockchain
[41]
Kawter l'expéditrice :
§ Crypter le message en clair m en utilisant l'algorithme
de cryptage E et la clé publique de Chaima pour préparer le texte
chiffré C.
§ Envoyer le texte chiffré C à Chaima
Chaima la réceptrice :
§ Déchiffrer le texte chiffré C en utilisant
l'algorithme de déchiffrement D et sa clé

privée pour obtenir le texte en clair d'origine m.
II.5.2.3 Illustration
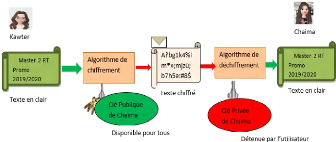
Figure II- 8: Cryptographie asymétrique
pour la confidentialité
Notez que la clé publique doit être
conservée dans un référentiel public accessible à
tous et la clé privée doit être gardée comme un
secret bien gardé. La cryptographie à clé publique fournit
également un moyen d'authentification.
Le réceptrice, Chaima, peut vérifier
l'authenticité de l'origine du message m de la même
manière.

Chapitre II Fonctionnement de la blockchain
Figure II- 9: Cryptographie asymétrique pour
l'authentification
Dans l'exemple de la figure II-17, le message a
été préparé à l'aide de la clé
privée de Kawter, afin de garantir qu'elle provienne uniquement de
Kawter. Le message entier a servi de signature numérique. De sorte que
la confidentialité et l'authentification sont souhaitables.
Le message doit d'abord être crypté avec la
clé privée de l'expéditeur pour fournir une signature
numérique. Ensuite, il doit être crypté avec la clé
publique de réceptrice pour assurer la confidentialité. Il peut
être représenté comme suit :
[42]
Comme vous pouvez le voir, le déchiffrement se produit
dans son ordre inverse uniquement. Notez que la cryptographie à
clé publique est utilisée quatre fois ici : deux fois pour le
chiffrement et deux fois pour le déchiffrement. Il est également
possible que l'expéditeur puisse signer le message en appliquant la
clé privée à un petit bloc de données
dérivé du message à envoyer, et non au message entier.
Nous avons examiné les utilisations des deux
clés en cryptographie asymétrique, qui peuvent être
résumées comme suit :
§ Une clé publique, qui crypte les données,
ou pour vérifier les signatures ;
§ Et une clé privée ou secrète
correspondante pour le décryptage ou pour créer des signatures
;
II.5.2.4 Les types d'algorithmes de chiffrement
et déchiffrement
II.5.2.4.1 L'algorithme de chiffrement
RSA
RSA est un algorithme de chiffrement mathématiquement
significatif et important. Sa difficulté à craquer est
basée sur la difficulté de décomposer un nombre composite
en deux grands nombres premiers [65].
Parce que la factorisation du produit de deux grands nombres
Chapitre II Fonctionnement de la blockchain
[43]
premiers est assez difficile (la preuve est un peu
compliquée et nécessite des concepts tels que la factorisation en
nombres premiers, les nombres premiers et la congruence).
Le chiffrement dit asymétrique signifie que
différentes clés peuvent être utilisées pour le
chiffrement et le déchiffrement. De cette façon, la clé
publique peut être envoyée à l'expéditeur et la
clé privée est conservée sur lui-même et
déchiffrée par la clé privée. Cela garantit que
vous seul pouvez déchiffrer le message
[66].
Le 12 décembre 2009, le RSA-768 (768 bits, 232
chiffres) a également été décomposé avec
succès. À l'heure actuelle, la longueur de clé la plus
sûre est RSA-1024 ou RSA-2048.Il s'agit actuellement de l'algorithme de
cryptage le plus important de la planète
[66].
II.5.2.4.1.1 Étapes pour la
génération de clés
Nous utilisons un exemple pour comprendre l'algorithme RSA.
Supposons que Kawter va avoir une communication cryptée avec Chaima.
Comment peut-elle générer des clés publiques et
privées ?
Figure II- 10: Étapes pour la
génération de clés
Dans la première étape, deux
nombres premiers inégaux p et q sont choisis au hasard. Chaima a choisi
61 et 53. En pratique, plus ces deux nombres premiers sont grands, plus il est
difficile de se fissurer.
Dans la deuxième étape, le produit
n de p et q est calculé. Chaima a multiplié 61 et 53.
n = 61 × 53 = 3233
Equation II- 1: Produit de n et p.
La troisième étape,
consiste à calculer la fonction d'Euler ö (n) de n. Selon la
formule
D (n) = (p-1) (q-1)
Equation II- 2: Calcule de la fonction
d'Euler
Chaima a calculé que ö (3233) est égal
à 60 x 52, ce qui correspond à 3120.
La quatrième étape, consiste
à choisir au hasard un entier e, à condition que 1 <e
<ö (n), et e et ö (n) soient des nombres premiers.
Chapitre II Fonctionnement de la blockchain
[44]
Chaima avait choisi entre 1 et 3120 et a été
choisie au hasard 17. En pratique, 65537 est souvent
sélectionné.
Dans la cinquième étape, calculez
l'élément inverse d de e pour ö (n).
Le soi-disant "élément inverse
modulaire" signifie qu'il existe un entier d, de sorte que le reste de
ed divisé par ö (n) est 1.
ed = 1 (mod ö (n))
Equation II- 3: Calcule d'élément
inverse d.
Par conséquent, trouver l'élément inverse
d revient essentiellement à résoudre l'équation
linéaire binaire suivante :
e.x + ö (n).y = 1
Equation II- 4: Equation linéaire binaire
Étant donné e = 17, ö (n) = 3120,
17x + 3120y = 1
Cette équation peut être résolue en
utilisant « l'algorithme euclidien étendu »,
et le processus spécifique est omis ici. En bref, Chaima a
calculé un ensemble de solutions entières comme (x,y) = (2753,
-15), c'est-à-dire d = 2753.
Jusqu'à présent, tous les calculs sont
terminés.
Dans la sixième étape, n et e
sont encapsulés dans une clé publique, et n et d sont
encapsulés dans une clé privée.
Dans l'exemple de Chaima, n = 3233, e = 17 et d = 2753, la
clé publique est donc (3233,17) et la clé privée est
(3233, 2753).
II.5.2.4.1.2 Chiffrement et
déchiffrement
Avec les clés publiques et secrètes, le chiffrement
et le déchiffrement sont possibles. (1) La clé publique
(n, e) est utilisée pour le chiffrement :
Supposons que Kawter veuille envoyer des informations
chiffrées m à Chaima, elle chiffrera m avec la clé
publique de Chaima (n, e). Notez ici que m doit être un entier (la
chaîne peut prendre des valeurs ascii ou Unicode), et m doit être
inférieur à n.
Le soi-disant "cryptage" consiste à calculer c :
La clé publique de Chaima est (3233, 17), et le m de
Kawter est supposé être 65, alors l'équation suivante peut
être calculée :
Donc, c'est égal à 2790, et Kawter envoie 2790
à Chaima.
Chapitre II Fonctionnement de la blockchain
[45]
(2) La clé privée (n, d) est utilisée
pour le déchiffrement :
Après que Chaima a obtenu 2790 de Kawter, elle a
utilisé sa clé privée (3233, 2753) pour la
décrypter. Il peut être prouvé que l'équation
suivante doit être vérifiée :
Autrement dit, le reste de la puissance de c divisé par
n est m. Maintenant, c'est égal à 2790 et la clé
privée est (3233, 2753), puis Chaima calcule :
À ce stade, le processus complet de «
chiffrement-déchiffrement » est terminé.
Nous pouvons voir que si nous ne connaissons pas d, il n'y a
aucun moyen de trouver m à partir de c. Comme mentionné
précédemment, savoir que d doit être
décomposé en n, ce qui est extrêmement difficile à
réaliser, donc l'algorithme RSA garantit la sécurité de la
communication.
Vous pourriez demander que la clé publique (n, e) ne
puisse chiffrer que des entiers m inférieurs à n, alors que faire
si vous voulez chiffrer des entiers supérieurs à n ?
Il existe deux solutions : l'une consiste à diviser le
message long en plusieurs messages courts, chacun étant chiffré
séparément, l'autre à choisir d'abord un "algorithme de
chiffrement symétrique" (tel que DES) et à utiliser la clé
de cet algorithme, chiffrez les informations, puis chiffrez la clé DES
avec la clé publique RSA.
La méthode de chiffrement à clé publique
RSA offre également une authentification à l'aide d'une signature
numérique. Notez ici qu'un algorithme différent appelé
algorithme de signature numérique (DSA) peut également être
utilisé dans de telles situations que nous verrons dans la section
suivante. RSA est largement utilisé avec HTTPS sur les navigateurs Web,
les e-mails, les VPNS et la télévision par satellite. En outre,
de nombreuses applications commerciales ou les applications dans les magasins
d'applications sont également signées numériquement
à l'aide de RSA. SSH utilise également la cryptographie à
clé publique ; lorsque vous vous connectez à un serveur SSH, il
diffuse une clé publique qui peut être utilisée pour
crypter les données à envoyer à ce serveur. Le serveur
peut ensuite décrypter les données à l'aide de sa
clé privée. L'algorithme de signature numérique DSA a
été conçu par la NSA26 dans le cadre de la
norme de signature numérique DSS et normalisé par le NIST. Notez
que son objectif principal est de signer les messages numériquement, et
non le cryptage. Juste pour paraphraser, RSA est à la fois
dédié pour la gestion des clés et l'authentification
tandis que DSA est dédié uniquement pour
l'authentification [67].
II.5.2.4.2 La signature
numérique
Lorsqu'une personne envoie des données via un document,
il devient important d'identifier son authenticité pour des raisons de
sécurité et de sûreté. Des signatures
numériques sont utilisées pour cette identification.
L'authentification des documents signifie savoir qui les a créés
et qu'ils n'ont pas interféré lors de leur transmission. Ces
signatures sont créées à l'aide de certains algorithmes.
L'algorithme de signature numérique (DSA) en
26 NSA : National
Security Agency est une agence de renseignement de niveau national du
Département de la défense des États-Unis, placée
sous l'autorité du directeur du renseignement national.
Chapitre II Fonctionnement de la blockchain
[46]
fait partie. DSA est un type d'algorithme de
chiffrement à clé publique et il est utilisé pour
générer une signature électronique
(68].
II.5.2.4.2.1 Introduction
Les signatures numériques sont idéales pour
l'intégrité et la non-répudiation. Une signature
numérique est une combinaison de hachage et de chiffrement
asymétrique. Autrement dit, un message est d'abord haché, et ce
hachage est chiffré avec la clé privée de
l'expéditeur. Cela constitue la signature, qui est envoyée avec
le message.
II.5.2.4.2.2 Fonctionnement d'algorithme de la
signature numérique
Il s'agit d'un algorithme de chiffrement à clé
publique conçu pour créer une signature électronique. Une
signature est créée « en privé » mais peut
être vérifiée « en public ». En d'autres termes,
il n'y a qu'un seul sujet qui peut créer une signature ajoutée
à un message, mais n'importe qui est en mesure de vérifier si la
signature est correcte ou non.
II.5.2.4.2.3 Schéma fonctionnel de la
signature numérique
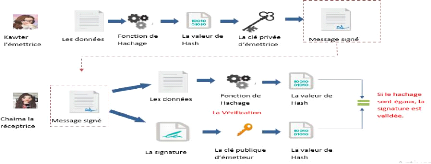
Figure II- 11: Schéma représente
comment la signature fonctionne II.5.2.4.2.4 Explication du schéma
fonctionnel
Premièrement, chaque
personne adoptant ce schéma possède une paire de clés
publique-privée en cryptographie
(69].
Les paires de clés utilisées pour le chiffrement
ou le déchiffrement et la signature ou la vérification sont
différentes pour chaque signature. Ici, la clé privée
utilisée pour la signature est appelée clé de signature et
la clé publique comme clé de vérification dans cet
algorithme.
Ensuite, les gens prennent le
signataire qui alimente les données à la fonction de hachage et
génère un hachage des données de ce message.
Maintenant, la valeur de
hachage et la clé de signature sont ensuite transmises à
l'algorithme de signature qui produit la signature numérique sur un
hachage donné de ce message. Cette signature est ajoutée aux
données, puis les deux sont envoyées au vérificateur pour
sécuriser ce message.
Ensuite, le
vérificateur alimente la signature numérique et la clé de
vérification dans l'algorithme de vérification de ce DSA. Ainsi,
l'algorithme de vérification donne une certaine valeur en sortie sous
forme de texte chiffré.
Chapitre II Fonctionnement de la blockchain
[47]
Ainsi, le vérificateur exécute
également la même fonction de hachage sur les données
reçues pour générer une valeur de hachage dans cet
algorithme.
Maintenant, pour la
vérification, la signature, la valeur de hachage et la sortie de
l'algorithme de vérification sont comparées avec chaque variable.
Sur la base du résultat de la comparaison, le vérificateur
décide si la signature numérique est valide pour cela ou non.
Par conséquent, la signature
numérique est générée par la clé
privée du signataire et personne d'autre ne peut avoir cette clé
pour sécuriser les données. Le signataire ne peut pas
répudier la signature des données à l'avenir pour
sécuriser ces données par la cryptographie.
II.5.2.4.2.5 Importance de la signature
numérique
Par conséquent, toute analyse cryptographique de la
signature numérique utilisant la cryptographie à clé
publique est considérée comme un outil très important ou
principal et utile pour assurer la sécurité des informations en
cryptographie en cryptanalyse [67].
Ainsi, outre la possibilité de fournir la
non-répudiation du message, la signature numérique fournit
également l'authentification du message et l'intégrité des
données en cryptographie.
Ceci est réalisé par la signature numérique
qui réalise :
o Authentification des messages
: Par conséquent, lorsque le vérificateur
valide la signature numérique à l'aide de la clé publique
d'un expéditeur, il est assuré que la signature n'a
été créée que par un expéditeur qui
possède la clé privée secrète correspondante et que
personne d'autre ne le fait par cet algorithme.
o Intégrité des données
: en fait, dans ce cas, un attaquant a accès aux
données et les modifie, la vérification de la signature
numérique à l'extrémité du récepteur
échoue dans cet algorithme. Ainsi, le hachage des données
modifiées et la sortie fournie par l'algorithme de vérification
ne correspondent pas à la signature de cet algorithme. Maintenant, le
récepteur peut refuser le message en toute sécurité en
supposant que l'intégrité des données a été
violée pour cet algorithme.
o Non-répudiation : Par
conséquent, c'est juste un nombre que seul le signataire connaît
la clé de signature, il ne peut que créer une signature unique
sur une donnée de ce message pour changer de cryptographie. Ainsi, le
destinataire peut présenter les données et la signature
numérique à un tiers comme preuve si un différend survient
à l'avenir pour sécuriser les données.
II.5.2.4.3 EllipticCurve Digital Signature
Algorithm
ECDSA c'est in algorithme de chiffrement à courbe
elliptique pour apprendre la signature numérique d'un
algorithme [70].
Chapitre II Fonctionnement de la blockchain
[48]
II.6 Comparaison entre cryptographie
symétrique et asymétrique
Le chiffrement asymétrique utilise deux types de
clés, tandis que le chiffrement symétrique utilise un seul type
de clé. Par conséquent, le traitement est plus simple dans ce
dernier cas, et les deux parties échangeant des données utilisent
la même clé secrète pour coder et décoder les
données reçues (71].
Le chiffrement symétrique est depuis longtemps la norme
en cryptographie, mais il existe plusieurs failles dans la
sécurité des communications qui ont créé une
cryptographie asymétrique. Cependant, le cryptage symétrique est
encore principalement utilisé pour transmettre de grandes
quantités de données.
La cryptographie à clé symétrique est
largement utilisée pour crypter des données telles que des
messages et des fichiers car le cryptage et le décryptage peuvent
être effectués à grande vitesse. La cryptographie à
clé publique présente l'inconvénient que le cryptage /
décryptage est plus lent que la cryptographie à clé
symétrique. Lors de l'échange de messages par e-mail, etc., la
vitesse élevée de la méthode de cryptage à
clé commune et la commodité de la méthode de cryptage
à clé publique sont combinées, le message est
crypté avec le cryptage à clé commune et la clé de
cryptage est cryptée avec le cryptage à clé publique.
II.7 Fonction de hachage
Le « hachage » est un concept qui se confond
facilement avec le chiffrement. Le hachage est une technologie qui convertit
les données d'origine en données de longueur fixe en effectuant
un traitement à l'aide d'une fonction de hachage. Il peut être
converti, mais ne peut pas être annulé. En d'autres termes, il n'y
a pas d'équivalent au "décryptage" dans le
hachage (72].
Le hachage a pour but de gérer les mots de passe et de
vérifier les fichiers. Le hachage et le stockage des mots de passe
éliminent la nécessité de gérer les mots de passe
bruts. Pour vous authentifier, il vous suffit de comparer la version
hachée du mot de passe entré avec le mot de passe haché
stocké. En outre, lorsque vous téléchargez un fichier
volumineux sur Internet, le hachage est utilisé pour comparer le fichier
sur le serveur avec le fichier téléchargé. Il est
difficile de comparer des fichiers volumineux tels qu'ils sont, nous les
hachons donc et les comparons (73].
Les fonctions de hachage incluent "MD5",
"SHA-1" et "SHA-256". Cependant, MD5 a
longtemps été souligné comme étant
vulnérable. Nous avons mentionné précédemment qu'il
n'y a pas d'équivalent au « déchiffrement » dans le
hachage, mais MD5 à une vulnérabilité où les
données d'origine avec une valeur de hachage spécifique sont
calculées. Une attaque qui exploite une telle
vulnérabilité est appelée attaque par collision. Par
conséquent, l'utilisation de MD5 n'est pas recommandée à
l'heure actuelle. L'utilisation d'une fonction de hachage permet de s'assurer
de l'intégrité des données et indirectement de les
authentifier. Il existe bien sûr de nombreuses autres applications pour
les fonctions de hachage, comme les MACs, certificats, etc
(73].
[49]
Chapitre II Fonctionnement de la blockchain
II.7.1 MD5
MD5 est une fonction de hachage largement utilisée dans
le domaine de la sécurité informatique pour assurer la protection
de l'intégrité des messages.
MD5 est largement utilisé pour l'authentification par
mot de passe et l'identification des clés de divers logiciels. MD5
utilise une fonction de hachage, et son application typique est de
générer un résumé de message pour une information
pour éviter toute falsification. Une application typique deMD5est de
générer des empreintes digitales sur un message pour
éviter qu'il ne soit "falsifié". S'il existe un organisme de
certification tiers, MD5 peut également empêcher l
'"autorité" de l'auteur du document, qui est la soi-disant application
de signature numérique. MD5 est également largement
utilisé pour l'authentification de connexion des systèmes
d'exploitation, tels qu'UNIX (74].
II.7.2 SHA-1
SHA1 est un algorithme de résumé de message
aussi populaire que MD5. Pour les messages de moins de 64bits, SHA1
génère un résumé de message de160bits. Lorsqu'un
message est reçu, ce résumé de message peut être
utilisé pour vérifier l'intégrité des
données. SHA1 ne peut pas récupérer les informations du
résumé de message, et deux messages différents ne
généreront pas le même résumé de message. De
cette façon, SHA1 peut vérifier l'intégrité des
données, alors on dit que SHA1est une technologie pour assurer
l'intégrité des fichiers
(75].
SHA1 est un algorithme plus sécurisé que MD5. En
théorie, tous les algorithmes de vérification numérique
qui utilisent la méthode "message digest" ont des "collisions",
c'est-à-dire que les résumés de messages calculés
par deux choses différentes sont les mêmes et
interopérables. La carte de triche est juste cela. Cependant, il est
très difficile pour un algorithme de haute sécurité de
trouver la "collision" des données spécifiées, et il est
encore plus difficile de calculer la "collision" à l'aide d'une formule.
Jusqu'à présent, seul MD5 a été craqué dans
les algorithmes de sécurité généraux.
II.7.3 Comparaison entre MD5 et SHA
La comparaison est conclue dans le tableau suivant
(76] :
Chapitre II Fonctionnement de la blockchain
[50]
|
SHA
|
MD5
|
|
SHA représente l'algorithme de hachage
sécurisé
|
MD5 signifie Message Digest
|
|
SHA est une famille de fonctions de hachage cryptographiques
développées par le NIST27
|
Il s'agit d'une fonction de hachage cryptographique largement
utilisée qui produit une valeur de hachage de 128 bits
|
|
Des versions plus sécurisées de SHA-1 sont
disponibles telles que SHA-256, SHA-384 et SHA-512
|
On pense que MD5 est
cryptographiquement cassé et peut avoir des collisions
|
|
La version optimisée de SHA-1 est plus rapide que MD5
|
MD5 est relativement plus rapide que SHA
|
|
Il n'y a eu aucune attaque sérieuse contre SHA-1
|
D'autres attaques ont été signalées sur
MD5
|
Tableau II- 3: Comparaison entre MD5 et
SHA
II.8 La longueur de la clé
Le nombre de bits utilisés pour le chiffrement ou le
déchiffrement est appelé longueur de clé. Des clés
plus longues augmentent la sécurité, mais présentent
l'inconvénient d'un chiffrement et d'un déchiffrement plus
lents [77].
De plus, la longueur de la clé varie en fonction de la
méthode de cryptage. La longueur de clé utilisée dans la
cryptographie à clé symétrique est
d'environ 40 à 128 bits. Dans la cryptographie à
clé publique, des clés de différentes
longueurs d'environ 100 bits à 2048 bits sont utilisés.
II.9 Limite de la cryptographie [78]
[79]
II.9.1 Limitation de la cryptographie a clé
publique (asymétrique)
Dans le chiffrement asymétrique, l'utilisateur utilise
la même clé pour chiffrer et déchiffrer, La raison
principale que la cryptographie à clé publique a une limitation
réside sur la performance et la lenteur à laquelle se font les
opérations de chiffrement et de déchiffrement. En effet cette
méthode de cryptage nécessite un nombre très important de
calculs c'est-à-dire le temps de calcul devient long parce que la
lenteur d'exécution nécessité de faire beaucoup de
calculs.
27 NIST : National
Institute of Standards and Technology est un laboratoire de sciences physiques
et une agence non réglementaire du Département du commerce des
États-Unis. Sa mission est de promouvoir l'innovation et la
compétitivité industrielle.
Chapitre II Fonctionnement de la blockchain
[51]
De plus, la cryptographie à clé publique
présente un autre problème, à savoir que la taille des
données cryptées est limitée. Par exemple, RSA ne peut pas
crypter des données supérieures à 4096 bits. Cette taille
est liée à la longueur de sa clé c'est-à-dire Cette
méthode du chiffrement ne peut donc pas être utilisée pour
des grands fichiers à transférer.
II.1 Limitation de la cryptographie a clé
secrètes (symétrique)
Dans le chiffrement symétrique, c'est une même
clé secrète qui permet à la fois d'effectuer le
chiffrement et le déchiffrement. Lorsque la personne qui devra
déchiffrer les données n'est pas la même que celle qui les
a chiffrées, plusieurs problèmes se posent : Tout d'abord, il
faut une nouvelle clé secrète pour chaque couple
émetteur/récepteur. De plus, expéditeur et destinataire
doivent se mettre d'accord sur une clé secrète et de
l'échanger de façon confidentielle, c'est-à-dire le grand
problème principal c'est la contribution des clés. En effet, la
clé de chiffrement est identique à la clé de
déchiffrement. Ainsi, c'est la même clé qui va nous
permettre à la fois de crypter le message et aux destinataires de le
décrypter. Donc, le problème majeur est l'échange de
clé entre les deux individus. Or, cela est difficile à
réaliser, puisque, tant que la clé n'est pas transmise, il
n'existe pas de moyen sûr d'échange d'information, à part
une rencontre physique.
| 


