Les algorithmes que nous allons étudier permettent de
rechercher une solution à un CSP (n'importe laquelle,
c'est-à-dire la première que l'on trouve). Suivant les
applications, »résoudre un CSP» peut signifier autre chose que
chercher simplement une solution. En particulier, il peut s'agir de chercher la
»meilleure» solution selon un critère donné. Par
exemple, pour le problème du coloriage d'une carte, on peut chercher la
solution qui utilise le moins de couleurs possibles,... Ces problèmes
d'optimisation sous contraintes, oùl'on cherche à optimiser une
fonction objective donnée tout en satisfaisant toutes les contraintes,
peuvent être résolus en explorant l'ensemble des affectations
possibles selon la stratégie de »Séparation & Evaluation
» (»Branch & Bound») bien connue en recherche
opérationnelle.
2.4.1 L'algorithme »génère et teste»
Principe de l'algorithme »génère et
teste» :
La façon la plus simple ( et très naïve! )
de résoudre un CSP sur les domaines finis consiste à
énumérer toutes les affectations totales possibles
jusqu'àen trouver une qui satisfait toutes les contraintes. Ce principe
est repris dans la fonction récursive
»génèreEtTeste(A,(X,D,C))» décrite ci-dessous.
Dans cette fonction, A contient une affectation partielle et (X,D,C)
décrit le CSP à résoudre (au premier appel de cette
fonction, l'affectation partielle A sera vide). La fonction retourne vrai si on
peut étendre l'affectation partielle A en une affectation totale
consistante (une solution), et faux sinon.
20
Fonction génèreEtTeste( A
: affectation partielle, (X,D,C) : CSP
sur les domaines finis) :
booléen
Si (toutes les variables de X sont
affectées à une valeur dans A ) Alors
[ A est une affectation totale]
Si (A est consistante) Alors [ A
est une solution]
Retourner vrai
Sinon
Retourner faux
Fin Si
Sinon
[ A est une affectation
partielle]
choisir une variable X de X qui n'est pas
encore affectée à une valeur dans A Pour toute valeur
V appartenant à D(X ) faire
Si (génèreEtTeste(A U
(X ,V ), (X,D,C)) = vrai )
Alors
Retourner vrai
Fin Si
Fin Pour
Retourner faux
Fin Si
Fin
Algorithme 1: Génère et teste
Exemple de trace d'exécution de
»génère et teste»
Considérons par exemple le CSP (X,D,C) suivant
:
· X = {a,b,c,d}
· D(a) = D(b) = D(c) = D(d) = {0, 1}
· C = {a =6 b,c =6 d,a + c < b}
L'enchainement des appels successifs à la fonction
genereEtTeste (abrégée par GET) est
représentéci-dessous (voir Figure 2.4) (chaque rectangle
correspond à un appel de la fonction, et précise la valeur de
l'affectation partielle en cours de construction A).
GET
A = {}
retourne vrai Choix de Xi = a

GET
A = {(a,0)}
retourne vrai
Vi = 0
Choix de Xi = b
Vi = 0 Vi = 1
retourne faux retourne faux retourne faux retourne faux
retourne faux retourne vrai
21
FIGURE 2.4 - Exécution de
génère et teste sur un CSP simple
2.4.2 L'algorithme »simple retour-arrière»
Principe de l'algorithme »simple
retour-arrière»
Une première façon d'améliorer l'algorithme
»génère et teste» consiste à tester au fur et
à mesure de la construction de l'affectation partielle sa consistance :
dès lors qu'une affectation partielle est inconsistante, il
est inutile de chercher à la compléter. Dans ce
cas, on »retourne en arrière» (»backtrack» en
anglais) jusqu'àla plus récente instanciation partielle
consistante que l'on peut étendre en affectant une autre valeur à
la dernière variable affectée.
22
Par exemple, sur la trace d'exécution décrite
ci-dessus, on remarque que l'algorithme génère tous les
prolongements de l'affectation partielle A={(a, 0), (b,
0)}, en énumérant toutes les possibilités
d'affectation pour les variables c et d, alors qu'elle viole la contrainte a =6
b. L'algorithme »simple retour-arrière» ne va donc pas
chercher à étendre cette affectation, mais va »retourner en
arrière» à l'affectation partielle précédente
A={(a,0)}, et va l'étendre en affectant 1 à
b , . . .
Ce principe est repris dans la fonction récursive
»simpleRetourArrière(A,(X,D,C))»
décrite ci-dessous. Dans cette fonction, A contient une
affectation partielle et (X,D,C) décrit le
CSP à résoudre (au premier appel de cette fonction, l'affectation
partielle A sera vide). La fonction retourne vrai si on peut
étendre l'affectation partielle A en une affectation totale
consistante (une solution), et faux sinon.
Fonction simpleRetourArrière( A
: affectation partielle,
(X,D,C) : CSP sur les domaines
finis)
: booléen
Si (A n'est pas consistante )
Alors
Retourner faux
Fin Si
Si (toutes les variables de X sont
affectées à une valeur dans A ) Alors
[ A est une affectation totale et consistante = une
solution]
Retourner vrai
Sinon
[ A est une affectation partielle
consistante]
choisir une variable X de X qui n'est pas
encore affectée à une valeur dans A Pour toute valeur
V appartenant à D(X )
faire
Si (simpleRetourArrière(A U
(X ,V ), (X,D,C)) = vrai)
Alors
Retourner vrai
Fin Si
Fin Pour
Retourner faux
Fin Si
Fin
Algorithme 2: simpleRetourArrière
Exemple de »trace d'exécution» de
SimpleRetourArrière
Considérons le problème des 4 reines, Il s'agit
de placer 4 reines sur un échiquier comportant 4 lignes et 4 colonnes,
de manière à ce qu'aucune reine ne soit en prise. On rappelle que
deux reines sont en prise si elles se trouvent sur une même diagonale,
une même ligne ou une même colonne de l'échiquier.
· Variables : X = {X1, X2
X3, X4}
·
Domaines : D(X1) = D(X2) = D(X3) =
D(X4) = {1,2,3,4}
· Contraintes : C = {X =6 Xj | i élément-de
{1, 2,3, 4}, j élément-de {1, 2,3, 4} et i =6 j} U {X + i =6 Xj +
j | i élément-de {1,2,3,4}, j élément-de {1,2,3,4}
et i =6 j} U {X - i =6 Xj -j | i élément-de {1,2,3,4}, j
élément-de {1,2,3,4} et i =6 j} L'enchainement des appels
successifs à la fonction SimpleRetourArrière peut être
représentépar l'arbre suivant (Figure 2.5) (chaque noeud
correspond à un appel de la fonction, l'échiquier
dessinéà chaque noeud décrit l'affectation partielle en
cours)
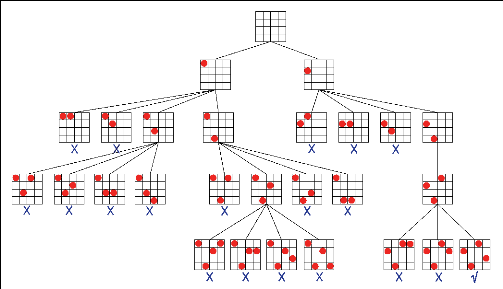
FIGURE 2.5 - Exécution de SimpleRetourArrière
(cette image est empruntée au »Guide to Constraint
Programming» de Roman Bartak)
2.4.3 L'algorithme »anticipation»
Notions de filtrage et de consistance locale
Pour améliorer l'algorithme »simple
retour-arrière», on peut tenter d'anticiper (»look ahead»
en anglais) les conséquences de l'affectation partielle en cours de
construction sur les domaines des variables qui ne
24
sont pas encore affectées : si on se rend compte qu'une
variable non affectée X n'a plus de valeur dans son domaine
D(X ) qui soit »localement consistante» avec l'affectation
partielle en cours de construction, alors il n'est pas nécessaire de
continuer à développer cette branche, et on peut tout de suite
retourner en arrière pour explorer d'autres possibilités.
Pour mettre ce principe en oeuvre, on va, à chaque
étape de la recherche, filtrer les domaines des variables non
affectées en enlevant les valeurs »localement inconsistantes»,
c'est-à-dire celles dont on peut inférer qu'elles
n'appartiendront à aucune solution. On peut effectuer différents
filtrages, correspondant à différents niveaux de consistances
locales, qui vont réduire plus ou moins les domaines des variables, mais
qui prendront aussi plus ou moins de temps à s'exécuter :
considérons un CSP (X,D,C), et une affectation partielle
consistante A.
· le filtrage le plus simple consiste à anticiper
d'une étape l'énumération: pour chaque variable X
non affectée dans A, on enlève de D(X )
toute valeur v telle que l'affectation A U {(X
,v)} soit inconsistante. - Par exemple pour le
problème des 4 reines, après avoir instanciéX1 à 1,
on peut enlever du domaine
de X2 la valeur 1 (qui viole la contrainte X1 =6
X2) et la valeur 2 (qui viole la contrainte 1-X1 =6
2-X2).
Untel filtrage permet d'établir ce qu'on appelle la
consistance de noeud, aussi appelée
1-consistance.
· Un filtrage plus fort, mais aussi plus long à
effectuer, consiste à anticiper de deux étapes
l'énumération: pour chaque variable X non
affectée dans A, on enlève de D(X ) toute
valeur v telle qu'il existe une variable Xj non
affectée pour laquelle, pour toute valeur w de D(Xj),
l'affectation A U {(X ,v),(Xj,w)}
soit inconsistante.
- Par exemple pour le problème des 4 reines,
après avoir instanciéX1 à 1, on peut enlever la valeur 3
du domaine de X2 car si X1=1 et X2=3, alors la variable X3 ne peut plus prendre
de valeurs : si X3=1, on viole la contrainte X3 =6 X1 , si X3=2, on
viole la contrainte X3+3 =6 X2+2 , si X3=3, on viole la contrainte X3
=6 X2 , et si X3=4, on viole la contrainte X3-3 =6
X2-2.
Notons que ce filtrage doit être
répétéjusqu'àce que plus aucun domaine ne puisse
être réduit. Ce filtrage permet d'établir ce qu'on appelle
la consistance d'arc, aussi appelée
2-consistance.
· Un filtrage encore plus fort, mais aussi encore plus
long à effectuer, consiste à anticiper de trois étapes
l'énumération. Ce filtrage permet d'établir ce qu'on
appelle la consistance de chemin, aussi appelée
25
3-consistance.
· . . .et ainsi de suite.. .notons que
s'il reste k variables à affecter, et si l'on anticipe de k
étapes l'énumération pour établir la
k-consistance, l'opération de filtrage revient à résoudre
le CSP, c'est-à-dire que toutes les valeurs restant dans les domaines
des variables après un tel filtrage appartiennent à une
solution.
Principe de l'algorithme
»anticipation»
Le principe général de l'algorithme
»anticipation» reprend celui de l'algorithme »simple
retour-arrière», en ajoutant simplement une étape de
filtrage à chaque fois qu'une valeur est affectée à une
variable. Comme on vient de le voir, on peut effectuer différents
filtrages plus ou moins forts, permettant d'établir différents
niveaux de consistance locale (noeud, arc, chemin, . . .).
Par exemple, la fonction récursive
»anticipation/noeud(A, (X, D, C))» décrite ci-dessous
effectue un filtrage simple qui établit à chaque étape la
consistance de noeud. Dans cette fonction, A contient une affectation
partielle consistante et (X, D, C) décrit le CSP à
résoudre (au premier appel de cette fonction, l'affectation partielle
A sera vide). La fonction retourne vrai si on peut étendre
l'affectation partielle A en une affectation totale consistante (une
solution), et faux sinon.
26
Fonction anticipation( A :
affectation partielle, (X,D,C) :
CSP sur les domaines finis) :
booléen
Si (A n'est pas consistante )
Alors
Retourner faux
Fin Si
Si (toutes les variables de X sont
affectées à une valeur dans A )
Alors
[ A est une affectation totale et consistante = une
solution]
Retourner vrai
Sinon
[ A est une affectation partielle consistante]
choisir une variable Xi de X qui n'est pas
encore affectée à une valeur dans A Pour
toute valeur Vi appartenant à D(Xi)
faire
[ filtrage des domaines par rapport à A U
(Xi,Vi) ]
Pour toute variable Xj de X
qui n'est pas encore affectée faire
Dfiltré(Xj) ?{Vj
élément de D(Xj) / A U
{(Xi,Vi),(Xj,Vj)} est consistante }
Si (Dfiltré(Xj) est
vide ) Alors
Retourner faux
Fin Si
Fin Pour
Si (anticipation(A U
(Xi,Vi),
(X,Dfiltré,C))=vrai )
Alors
Retourner vrai
Fin Si
Fin Pour
Retourner faux
Fin Si
Fin
Algorithme 3: anticipation/noeud
Exemple de »trace d'exécution» de
»anticipation»
Considérons de nouveau le problème du placement
de 4 reines sur un échiquier 4 x 4. L'enchainement des appels successifs
à la fonction »Anticipation/noeud» peut être
représentépar l'arbre suivant(Figure 2.6) (les valeurs
supprimées par le filtrage sont marquées d'une croix) :
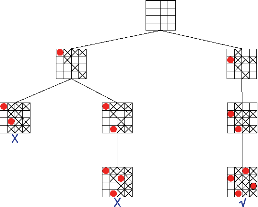
27
FIGURE 2.6 - Exécution d'anticipation (cette image est
empruntée au »Guide to Constraint Programming» de Roman
Bartak)
Si on appliquait un filtrage plus fort, qui
rétablirait à chaque étape la consistance d'arc,
l'enchainement des appels successifs à la fonction
»Anticipation/arc» correspondante serait le suivant (Figure 2.7) (les
valeurs supprimées par le filtrage sont marquées d'une croix)
:
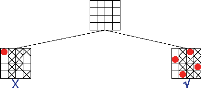
FIGURE 2.7 - Exécution d'anticipation 2 (cette image
est empruntée au »Guide to Constraint Programming» de Roman
Bartak)
Ainsi, on constate sur le problème des 4 reines que le
filtrage des domaines permet de réduire le nombre d'appels
récursifs : on passe de 27 appels pour »simple
retour-arrière» à 8 appels pour l'algorithme d'an-ticipation
avec filtrage simple établissant une consistance de noeud. En utilisant
des filtrages plus forts, comme celui qui établit la consistance d'arc,
on peut encore réduire la combinatoire de 8 à 3 appels
récursifs. Cependant, il faut noter que plus le filtrage
utiliséest fort, plus cela prendra de temps pour l'exécuter...
28
De façon générale, on constate que,
quelque soit le problème considéré, l'algorithme
»anticipation/noeud» est généralement plus rapide que
l'algorithme »simple retour-arrière» car le filtrage
utiliséest vraiment peu coûteux. En revanche, si l'algorithme
»anticipation/arc» envisage toujours moins de combinaisons que
l'algorithme »anticipation/noeud», il peut parfois prendre plus de
temps à l'exécution car le filtrage pour établir une
consistance d'arc est plus long que celui pour établir la consistance de
noeud.



