1. Le norvégien habite la première maison.
· Variables du problème : on associe une variable
par attribut (couleur, animal, boisson, nationalité, cigarette) X =
{blanche, rouge, verte, jaune, bleue, norvégien, anglais, ukrainien,
japonais, espagnol, cheval, renard, zèbre, escargot, chien, thé,
eau, lait, café, vin, kools, Chesterfield, Old-Golds, cravens,
gitanes}.
· Domaines des variables : D(X ) = {1, 2,3,4,
5}, pour toute variable X de X
· Contraintes :
- On pose tout d'abord une contrainte pour chaque assertion de
l'énoncé:
norvégien = 1
bleue = norvégien + 1
lait = 3
16
anglais = rouge
verte = caféjaune = kools
blanche = verte + 1 espagnol = chien
ukrainien = théjaponais = cravens
Old-Golds = escargot
gitanes = vin
(Chesterfield = renard + 1) ou (Chesterfield = renard - 1)
(kools = cheval + 1) ou (kools = cheval - 1)
- De plus, toutes les variables de même »type»
doivent avoir des valeurs différentes (il ne peut pas y
avoir plusieurs maisons qui ont la même couleur, ou un
même animal, ...)
blanche =6 rouge =6 verte =6 jaune =6 bleue
thé=6 eau =6 lait =6 café=6 vin
norvégien =6 anglais =6 ukrainien =6 japonais =6
espagnol
cheval =6 renard =6 zèbre =6 escargot =6 chien
kools =6 Chesterfield =6 Old-Golds =6 cravens =6 gitanes
2.3.2 Problème de Coloriage d'une carte
* Enoncé:
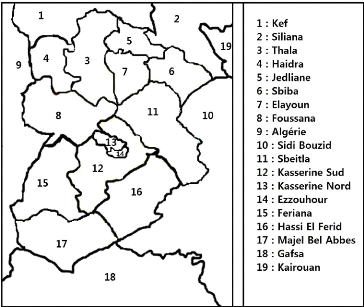
Il s'agit de colorier les 19 régions de la carte
ci-dessous (gouvernorat de Kasserine ( voir Figure 2.2 )), de sorte que deux
régions ayant une frontière en commun soient coloriées
avec des couleurs différentes. On dispose pour cela des 4 couleurs
suivantes : bleu, rouge, jaune et vert.
17
FIGURE 2.2 - gouvernorat de Kasserine
* Modélisation sous forme d'un CSP : On
définit le CSP (X,D,C) tel que:
· X = {X1, X2,...,
X19}
(On associe une variable X différente par région j
à colorier.)
· Pour tout X élément de X, D(X ) = {bleu,
rouge, vert, jaune} (Chaque région peut être coloriée avec
une des 4 couleurs.)
· C = {X =6 Xj / X et Xj sont 2 variables de X
correspondant à des régions voisines}
(2 régions voisines doivent être de couleurs
différentes.)
Pour être plus précis, on peut définir
explicitement les relations de voisinage entre régions, par exemple
à l'aide d'un prédicat voisines/2, tel que voisines(X,Y ) soit
vrai si X et Y sont deux régions voisines. Ce prédicat peut
être défini en extension, en listant l'ensemble des couples de
régions ayant une frontière en commun : voisines(X,Y ) ? (X,Y )
élément-de {(1,2), (1,3), (1,4), (1,5), (1,9), (2,5), (2,6),
(2,19), (3,1), (3,4),
18
(3,5), (3,7), (3,8), (4,1), (4,3), (4,8), (4,9), (5,1), (5,2),
(5,3), (5,6), (5,7), (6,2), (6,5), (6,7), (6,10), (6,11), (7,3), (7,5), (7,6),
(7,11), (8,3), (8,4), (8,9), (8,11), (8,12), (8,13), (8,15), (9,1), (9,4),
(9,8), (9,15), (9,17), (9,18), (10,2), (10,6), (10,11), (10,16), (10,18),
(10,19), (11,6), (11,7), (11,8), (11,10), (11,12), (11,16), (12,8), (12,11),
(12,13), (12,14), (12,15), (12,16), (12,17), (13,8), (13,12), (13,14), (14,12),
(14,13), (15,8), (15,9), (15,12),(15,17), (16,10), (16,11), (16,12), (16,17),
(16,18), (17,9), (17,12), (17,15), (17,16), (17,18), (18,9), (18,10), (18,17),
(19,2), (19,10)}. On peut alors définir l'ensemble des contraintes C de
la façon suivante :
C = {Xi =6 Xj | Xi et Xj sont 2 variables différentes
de X et voisines, (Xi,Xj) = vrai }
Donc, on peut colorier la carte comme suit (Figure 2.3) :
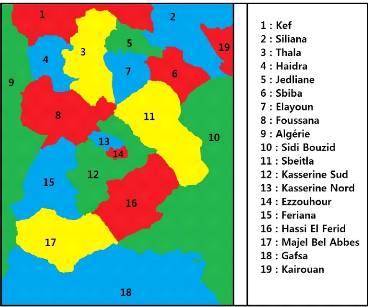
FIGURE 2.3 - Coloriage correcte du gouvernorat de Kasserine
Ce problème de coloriage d'une carte est un cas
particulier du problème du coloriage des sommets d'un graphe (deux
sommets adjacents du graphe doivent toujours être de couleurs
différentes). De nombreux problèmes »réels» se
ramènent à ce problème de coloriage d'un graphe :
problème des examens, d'emploi du temps, de classification,...



