3.7 Outils d'implémentation
· Nous avons utiliséessentiellement comme logiciels
pour l'implémentation et les tests de l'algorithme
précèdent :
DEVC++(4.9.9.2) : Dev-C++ est un environnement
de développement intégré(IDE) permettant de programmer en
C et en C++.
54
Matlab (7.12.0.0) : Matlab est un
environnement de développement . Il est utiliséà des fins
de calcul numérique. Développépar la
sociétéThe MathWorks.
· Et comme langage de programmation nous avons
utilisé:
C++ : C++ est un langage de programmation compilé,
permettant la programmation sous de multiples paradigmes comme la programmation
procédurale, la programmation orientée objet et la programmation
générique.
Matlab : ( matrix laboratory ) est un langage
de programmation de quatrième génération, MATLAB permet de
manipuler des matrices, d'afficher des courbes et des données, de mettre
en oeuvre des algorithmes, de créer des interfaces utilisateurs, et peut
s'interfacer avec d'autres langages comme le C, C++, Java, et Fortran.
3.8 Expérimentation
Dans cette section, nous testerons l'efficacitéde
l'algorithme proposéen termes de temps et de pourcentage de contraintes
satisfaites.
3.8.1 Complexitéde l'algorithme proposé
Notre algorithme va parcourir m contraintes pour
calculer les scores (instruction 1) et pour construire le graphe (instruction
2), puis O(n) matrice de dimension
O(n2) (si on utilise une matrice pour
représenter le graphe) (n qui est égal au nombre de
variables), pour identifier les sources. Donc la complexitéde notre
algorithme est O(max(m,n3)), qui est une
complexitépolynomiale. Le temps nécessaire pour résoudre
des instances du problème de différentes tailles est
représentédans le tableau ci-dessous.
|
Nombre des variables
|
5
|
10
|
20
|
50
|
250
|
1000
|
10000
|
|
Temps de résolution
|
1.25 us
|
10 us
|
80 us
|
1.25 ms
|
156 ms
|
10 s
|
2.7 heures
|
TABLE 3.2 - temps nécessaire à l'exécution
d'un algorithme de complexitécubique (polynomiale) [8]
Comme on peut le constater, notre algorithme s'est
avéréplus performant en termes de temps d'exécution par
rapport aux algorithmes complets que nous avons testéau début du
chapitre.
3.8.2 Satisfaction des contraintes
Après avoir testél'efficacitétemporelle de
l'algorithme, nous proposons à présent, d'évaluer sa
capacitéde satisfaire les contraintes données.
Pour cela, nous avons fixéle nombre de variables, puis
nous avons variéle nombre de contraintes, commençant par 20 et
allant jusqu'à5000 contraintes, en ajoutant à chaque fois 20
contraintes et en calculant le pourcentage des contraintes satisfaites.
Pour faire cette tâche, nous avons implémenter
avec DEVC++ trois programmes, un générateur de contraintes qui
génère des contraintes aléatoires à partir d'un
ensemble de n variables et qui les passe à un autre programme
qui implémente notre algorithme pour la résolution. Ensuite, la
solution trouvée est passée avec les contraintes, comme
donnés, au troisième programme qui calcule le pourcentage des
contraintes satisfaites. Nous avons traitéles résultats obtenus,
avec l'outil MATLAB, »plottool», pour visualiser les
résultats.
- La Figure 3.1 présente les tests pour 100 variables
:
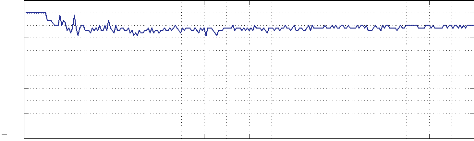
pourcentage des contraintes satisfaites
100
90
80
70
60
50
55
0 500 1000 1500 2000 2500 3000 3500 4000 4500
5000
nombre des contraintes
FIGURE 3.1 - Pourcentage des contraintes
satisfaites par rapport au nombre de contraintes sur problème impliquant
100 variables
- La Figure 3.2 présente les tests pour 300 variables :
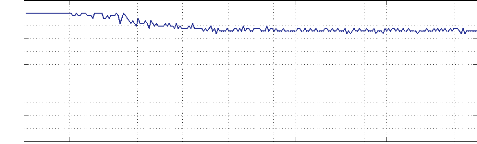
pourcentage des contraintes satisfaites
100
90
80
70
60
50
0 500 1000 1500 2000 2500 3000 3500 4000 4500
5000
nombre de contraintes
FIGURE 3.2 - Pourcentage des contraintes satisfaites par rapport
au nombre de contraintes sur problème impliquant 300 variables
- La Figure 3.3 représente les tests pour 600 variables
:
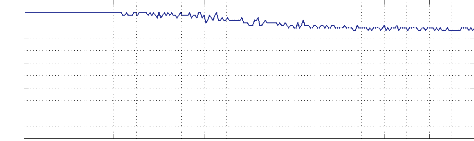
pourcentage des contraintes satisfaites
100
90
80
70
60
50
56
0 500 1000 1500 2000 2500 3000 3500 4000 4500
5000
nombre de contraintes
FIGURE 3.3 - Pourcentage des contraintes satisfaites par rapport
au nombre de contraintes sur problème impliquant 600 variables
57
Nous remarquons que dans les trois figures
précédentes (Figure 3.1, 3.2 et 3.3), le pourcentage des
contraintes satisfaites est stable à 100% au début pour se
déstabiliser ensuite entre les valeurs 93% et 97%.
Nous avons reproduit le même traitement, pour illustrer
les moyennes des pourcentages des contraintes satisfaites en fonction du nombre
des variables (débutant de la valeur 50 et allant jusqu'à700).
Nous avons obtenu le résultat suivant (voir Figure 3.4)
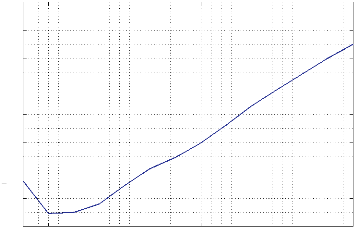
100 200 300 400 500 600 700
pourcentage moyen des contraintes satisfaites
97.5
96.5
95.5
94.5
98
97
96
95
94
nombre de variables
FIGURE 3.4 - contraintes satisfaites par rapport au nombre de
variables
On remarque, que lorsque le nombre de variables augmente, le
pourcentage des contraintes satisfaites tend vers 100% ce qui met en valeur
l'efficacitéde notre algorithme.
| 


