Résolution d'un problème de satisfaction de contraintes sur les intervalles

3.5.4 Résolution proposée

L'avantage des algorithmes que nous venons d'envisager c'est qu'ils arrivent toujours à trouver une solution, car ce sont des algorithmes complets. Mais l'inconvénient est le temps d'exécution.

L'utilisation d'une heuristique peut considérablement accélérer le temps d'exécution car elle nous aide ^àchoisir un bon ordonnancement des variables sans être obligéde retourner en arrière ou même d'anticiper

les conséquences d'une affectation.

Le problème auquel nous nous intéressons (voir Section 3.2) est un problème d'optimisation pour lequel on ne connait pas d'algorithme permettant de trouver une solution exacte en un temps polynomial. Nous essayons, alors, de trouver un algorithme qui satisfait le plus grand nombre de contraintes possible en un temps raisonnable (polynomial).

Notre idée est de transformer toute contrainte quaternaires C E C de la forme C =Min(x ₁,x ₂)<Max(x ₃,x ₄), à des contraintes d'aritébinaire sous la forme x <xj, tel que i E{i1, i2} et j E {i3, i4}. Pour cela on va utiliser une méthode heuristique pour décider du minimum, respectivement, du maximum entre chaque paire de variables apparaissant à la partie gauche, respectivement, droite d'une contrainte.

Heuristique utilisée

Pour transformer les contraintes quaternaires du problème en des contraintes binaires , nous proposons de compter, pour chaque variables x E X, son nombre d'occurrence dans la partie gauche Min ' des contraintes puis nous lui soustrayons son nombre d'occurrence dans la partie droite, Max , des contraintes. Nous obtenons ainsi un score h(x ) pour chaque variable.

- Pour décider du minimum entre deux variables x et xj, on choisit la variable qui a le plus grand score. En cas d'égalitéde score entre deux variables différentes, nous évitons cette égalitéen soustrayant 1 du score de l'une de ces deux variables.

- Pour décider du maximum entre deux variables x et xj, on choisit la variable qui a le plus petit score. En cas d'égalitéde score entre deux variables différentes, nous évitons cette égalitéen soustrayant 1 du score de l'une de ces deux variables.

Il faut, toutefois, signaler que ce choix peut nous mener à des contraintes non valides (cas rares), ces contraintes sont généralement sous la forme x <x (impossible), c'est à cause de l'apparition de la variable

41

xi dans les deux parties de la contrainte, dans ce cas on a deux choix.

1. choix1 :

xi apparait dans les deux parties de la contrainte, elle est sous la forme C=Min (xi1,xi2)<Max(xi3,xi4) tel que _xi1=xi3 , alors on va choisir comme suit :

si (h(xi₁)>h(xi₂))alors _{Min(xi1,xi2)=xi1} , et par conséquent _{Max(xi3,xi4)=xi4,} d'ou la contrainte devient : xi1<xi4.

Sinon , Si (h(xi₁)<h(xi₂)), alors _{Min(xi1,xi2)=xi2,} et on a _xi1=xi3, ^donc _xi2<xi3 est vérifié, d'ou la contrainte devient : xi2<xi3.

Enfin, en cas d'égalitédu score on choisit comme suit :

Si |h(xi₃)-h(xi₄)| > |h(xi2)-h(xi₁)| alors

Min(xi1,xi2) =xi1

Max(xi3,xi4) =xi4

d'ou la contrainte devient : xi1<xi4

Sinon, si |h(xi₃)-h(xi₄)| < |h(xi₂)-h(xi1)| alors

Min(xi1,xi2) =xi2

Max(xi3,xi4)=xi3

d'ou la contrainte devient : xi2<xi3

2. choix2 :

Si on a _{h(xi1)=h(xi2)} et |h(xi₁) - h(xi₂)| = |h(xi₃) - h(xi₄)|, on ne peut pas choisir le «Min» et le «Max» en utilisant le choix 1. Alors, nous décidons de choisir aléatoirement xi et xj telque la contrainte soit valide (xi =6 xj)

Résolution du problème transformé

Après la transformation de la forme des contraintes, on peut parler de contraintes de précédence, on peut considérer xi et xj comme des taches telles que xi précède xj si on a la contrainte xi<xj. Nous allons alors associer à ces contraintes de précédence, un graphe de contraintes sur les tâches et les relations de précédence entre elles. C'est un graphe orientéet nous allons représenter chaque contrainte sous la forme _xi<xj par un

42

arc sortant de x et entrant dans xj, puis nous allons ordonner ces taches comme suit :

1. Associer un ensemble de valeurs possibles aux variables. Cet ensemble sera initialiséà l'ensemble des nombres naturels de 1 à n et sera notéD (Domaine des variables).

2. identifier les sommets sources du graphe.

3. choisir la source qui a le plus d'arcs sortants.

4. associer à cette source la valeur minimale de D et éliminer cette valeur de D puis éliminer ce sommet du graphe, ainsi que les arcs qui en sortent.

5. répéter le traitement de 2 à 4 jusqu'àce qu'on ne trouve plus de source.

6. Affecter les variables qui n'ont pas reçus une valeur par les valeurs restantes dans D en utilisant une méthode que nous décrivons dans ce qui suit.

Et par cette démarche nous obtenons une affectation de valeurs aux variables qui satisfait toutes les contraintes.

Nous affectons les variables qui n'ont pas reçu une valeur par la démarche précédente, comme suit :

1. associer le minimum des valeurs restantes dans l'ensemble D, à la variable qui a le plus grand score et supprimer cette valeur de D.

2. Répéter l'étape 1 jusqu'àce que D=Ø.

43

3.6 Algorithme propo^sé3.6.1 algorithme

Entrées:

(X,D,C) : un CSP [- X : l'ensemble de n variables

- D : domaine des variables 1..n - C : ensemble des contraintes.]

G=(S, A) : Graphe orienté[ - S= l'ensemble des sommets

- A= l'ensemble des arcs]

h : table de score de n éléments entiers

Traitement:

0) Début

1) Pour (tout Ci E C) faire [remplissage de h] h(xi₁)?h(xi₁)+1 h(xi₂)?h(xi₂)+1 h(xi₃)?h(xi₃)-1 h(xi₄)?h(xi₄)-1

Fin Pour

2) Pour (tout Ci E C) faire

(xi,xj)? Transformer (X,Ci, h) [ transformation des contraintes à la forme xi<xj] A?A U (xi, xj) [ Ajout d'arc sortant de xi vers xj au graphe G ]

Fin Pour

3) Répéter

xi?Source(G) [xi reçoit la variable qui représente la source du graphe G qui a le plus d'arcs]

G?G\{xi}

xi?min(D) [affecter la valeur minimale de D à la variable xi]

D?D\{min(D)}

jusqu'àce que (xi=Ø)

4) Compléter (X,D,h)

5) Fin

Algorithme 4: Algorithme proposé

Fonction Transformer(X : variables, C : contrainte, h : table de score) : contrainte binaire Si (h(xi₁)=h(xi₂)) Alors

h(xi₁) --h(xi₁) - 1

Fin Si

Si ((h(xi₃)=h(xi₄)) Alors

h(xi₃) --h(xi₃) - 1

Fin Si

Si (h(xi₁)>h(xi₂)) Alors

xi --xi1

Sinon

xi --xi2

Fin Si

Si (h(xi₃)<h(xi₄)) Alors

xj --xi3

Sinon

xj --xi4

Fin Si

Si (xi=xj) Alors

[Contrainte non valide ] Si (h(xi₁)>h(xi₂)) Alors xi --xi1

xj --xi4

Sinon

Si (h(xi₁)<h(xi₂)) Alors

xi --xi2

xj --xi1

Sinon

Si (|h(xi₂)-h(xi₁)|#|h(xi₄)-h(xi₃)|) Alors

Si (|h(xi₂)-h(xi₁)|>|h(xi₄)-h(xi₃)|) Alors xi --xi2

xj --xi3 Sinon

xi --xi1

xj --xi4

Fin Si

Sinon

Tant que (xi=xj) faire

(xi,xj) --Choix Aléatoire(C)

Fait

Fin Si

Fin Si

Fin Si

Fin Si

Fin

Retourner (xi,xj) [Contrainte transformée]

44

Algorithme 5: fonction transformer

Procédure completer(X : variables , D : domaines , h : table de score)

Tant que (D0Ø) faire

t?Min(D)

xi?Max(h) [la variable qui a h max]

D?D\{t}

Fin

Fait

45

Algorithme 6: procedure completer

3.6.2 Exemple

A titre d'exemple, nous proposons de résoudre le problème posédans la Section 3.3 :

X={x1, x2, ..., x10} D={1..10}

C={C1, C2, ..., C20} |

C1 = Min(x8,x5)<Max(x1,x10) C2 = Min(x6,x2)<Max(x8,x2) C3 = Min(x2,x7)<Max(x9,x6)

C4 = Min(x7,x2)<Max(x9,x10) C5 = Min(x8,x10)<Max(x6,x5) C6 = Min(x4,x2)<Max(x10,x9)

C7 = Min(x1,x6)<Max(x3,x9) C8 = Min(x1,x3)<Max(x5,x9) C9 = Min(x3,x1)<Max(x2,x1)

C10 = Min(x7,x2)<Max(x4,x9) C11 = Min(x4,x5)<Max(x5,x7) C12 = Min(x10,x7)<Max(x4,x8)

C13 = Min(x9,x3)<Max(x10,x2) C14 = Min(x6,x10)<Max(x9,x5) C15 = Min(x8,x7)<Max(x4,x7)

C16 = Min(x6, x5)<Max(x3,x1) C17 = Min(x8,x4)<Max(x8,x3) C18 = Min(x1,x2)<Max(x7,x6)

C19 = Min(x6,x5)<Max(x2,x3) C20 = Min(x1,x2)<Max(x5,x7) }

Nous allons employer l'heuristique déjàdéfinie pour transformer les contraintes quaternaires à des contraintes binaires comme suit :

· Instruction 1) : calcule des scores

X	x1	x2	x3	x4	x5	x6	x7	x8	x9		x10	h(X)
2	3	-1	0	-1	2	1	1	-6	-1

· Instruction 2) : Transformation des contraintes et construction du graphe - C1 = Min(x8,x5)<Max(x1,x10)

h(x8)= 1, h(x5)= -1 Min(x8,x5)= x8

46

h(x1)=2, h(x10)= -1 = Max(x1,x10)= x10 = C1=x8<x10

- C2 = Min(x6,x2)<Max(x8,x2)

Min(x6,x2)=x2 Max(x8,x2)=x8 = C2=x2<x8

- C3 = Min(x2,x7)<Max(x9,x6) = C3=x7<x9

- C4 = Min(x7,x2)<Max(x9,x10) = C4=x7<x9

- C5 = Min(x8,x10)<Max(x6,x5) = C5=x10<x6

- C6 = Min(x4,x2)<Max(x10,x9) = C6=x2<x9

- C7 = Min(x1,x6)<Max(x3,x9)

Ici , h(x6)=h(x1)=2 = h(x1)?h(x1)-1, on change la table des scores comme suit :

X	x1	x2	x3	x4	x5	x6	x7	x8	x9		x10	h(X)
1	3	-1	0	-1	2	1	1	-6	-1

= C7=x6<x9

- C8 = Min(x1,x3)<Max(x5,x9) = C8=x1<x9

- C9 = Min(x3,x1)<Max(x2,x1)

= C9=x1<x1 = contraite non valide!, on a : h(x1)>h(x3) = C9=x1<x2

- C10 = Min(x7,x2)<Max(x4,x9) = C10=x2<x9

- C11 = Min(x4,x5)<Max(x5,x7) = C11=x4<x5

- C12 = Min(x10,x7)<Max(x4,x8) = C12=x7<x4

- C13 = Min(x9,x3)<Max(x10,x2)

C13=x3<x10

- C14 = Min(x6,x10)<Max(x9,x5)

C14=x6<x9

- C15 = Min(x8,x7)<Max(x4,x7)

C15=x7<x4, et la table des scores devient :

X	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10
h(X)	1	3	-1	0	-1	2	1	0	-6	-1

- C16 = Min(x6,x5)<Max(x3,x1)

C16=x6<x3

- C17 = Min(x8,x4)<Max(x8,x3)

C17=x4<x3, et la table des scores devient :

X	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10
h(X)	1	3	-1	0	-1	2	1	-1	-6	-1

- C18 = Min(x1,x2)<Max(x7,x6)

C18=x2<x7

- C19 = Min(x6,x5)<Max(x2,x3)

C19=x6<x3

- C20 = Min(x1,x2)<Max(x5,x7)

C20=x2<x5

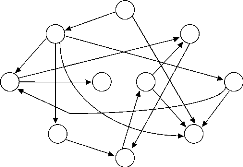
Ensuite, nous construisons un graphe orientéG comme suit : les sommets sont les variables et les arcs sont les contraintes :

47

G :

·

X₄

X₂ X₃

X₅ X₆ X₇

X₈ X₉

X₁

X10

48

Instruction3) : En utilisant ce graphe, nous associons à chaque variable X de X un nombre du domaine

D={1, 2,3,4,5,6,7,8,9, 10}.

- Itération 1 :

I on note S l'ensemble des sources dans le graphe, S={x1}

I la source choisie s=x1

I x1?1

I X={1,x2,x3,x4,x5,x6,x7,x8,x9,x10}

I D={2,3,4,5,6,7,8,9,10}

I G :

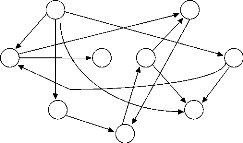
X₄

X₂ X₃

X₅ X₆ X₇

X₈ X₉

X10

I S={x1} nombre de sources =1, on répète: - Itération 2 :

I S={x2}

I S=x2

I x2?2

I X={1, 2, x3, x4, x5, x6, x7, x8, x9, x10}

I D={3, 4,5,6,7,8,9, 10}

I G :

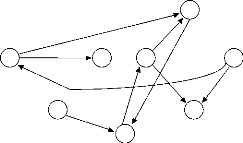
X₄ X₅

X₈

X10

X₆ X₇

X₃

X₉

I S={x2} nombre de sources =1. - Itération 3 :

I S={x7, x8}

I S=x7

I x7?3

I X={1,2,x3,x4,x5,x6,3,x8,x9,x10}

I D={4, 5,6,7,8,9, 10}

I G :

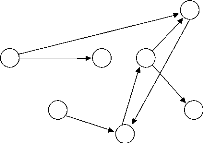
X₄ X₅

X₈

X10

X₆

X₃

X₉

49

50

I S={x7, x8} nombre de sources =2.

- Itération 4 :

I S={x4, x8}

I S=x4

I x4?4

I X={1, 2, x3, 4, x5, x6, 3, x8, x9, x10}

I D={5, 6, 7, 8, 9, 10} I G :

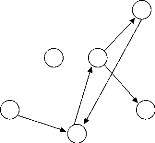
X₈

X₅

X10

X₆

X₃

X₉

I S={x4, x8} nombre de sources =2.

- Itération 5 :

I S={x8, x5}

I S=x8

I x8?5

I X={1, 2, x3, 4, x5, x6, 3,5, x9, x10}

I D={6, 7, 8, 9, 10}

I G :

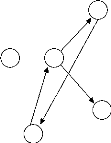
X₅

X10

X₆

X₃

X₉

51

I S={x5, x8} nombre de sources =2.

- Itération 5 :

I S={x5}

I s=x5

I x5?6

I X={1, 2, x3, 4, 6, x6,3, 5, x9,x10}

I D={7,8,9,10}

I G :

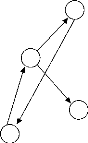
X10

X₆

X₃

X₉

I S={x5} nombre de sources =1.

- Itération 6 :

I S=Ø

I s=Ø, à ce niveau, on n'a plus de sources on termine 4).

· 52

Instruction 4) : Application de la procédure Compléter pour affecter le reste des variables.

I La table des scores :

X	x1	x2	x3	x4	x5	x6	x7	x8	x9		x10	h(X)
1	3	-1	0	-1	2	1	-1	-6	-1

I X={1,2,x3,4,6,x6,3,5,x9,x10} I D={7, 8,9, 10}

- Iteration 1 :

Max(h(x3), h(x6), h(x9), h(x10))=h(x6)

I D'ou x6-7

I X={1, 2,x3,4, 6,7,3,5, x9, x10}

I D={8,9,10}.

- Iteration 2 :

Max(h(x3), h(x9), h(x10))=h(x3)

I D'ou x3-8

I X={1, 2, 8, 4, 6, 7, 3, 5, x9,x10}

I D={9, 10}.

- Iteration 3 :

Max(h(x9), h(x10))=h(x10)

I D'ou x10-9

I X={1, 2, 8, 4, 6, 7, 3, 5, x9,9}

I D={10}.

- Iteration 4 :

Max( h(x9))=h(x9)

I D'ou x9-10

I X={1, 2, 8, 4, 6, 7, 3, 5, 10, 9}

I D=Ø, la procédure s'arrête..

On obtient ainsi X = {1, 2,8,4, 6, 7,3, 5, 10, 9}, qui satisfait toutes les contraintes données. En effet, on a :

53

- C1 = Min(x8,x5)<Max(x1,x10) = 5 < 9 = Vrai.

- = Min(x6,x2)<Max(x8,x2) = 2 < 5 = Vrai.

- C3 = Min(x2,x7)<Max(x9,x6) = 2 < 10 = Vrai.

- C4 = Min(x7,x2)<Max(x9,x10) = 2 < 10 = Vrai.

- C5 = Min(x8,x10)<Max(x6,x5) = 5 < 7 = Vrai.

- C6 = Min(x4,x2)<Max(x10,x9) = 2 < 10 = Vrai.

- C7 = Min(x1,x6)<Max(x3,x9) = 1 < 10 = Vrai.

- C8 = Min(x1,x3)<Max(x5,x9) = 1 < 10 = Vrai.

- C9 = Min(x3,x1)<Max(x2,x1) = 1 < 2 = Vrai.

- C10 = Min(x7,x2)<Max(x4,x9) = 2 < 10 = Vrai.

- C11 = Min(x4,x5)<Max(x5,x7) = 4 < 6 = Vrai..

- C12 = Min(x10,x7)<Max(x4,x8) = 3 < 5 = Vrai.

- C13 = Min(x9,x3)<Max(x10,x2) = 8 < 9 = Vrai.

- C14 = Min(x6,x10)<Max(x9,x5) = 7 < 10 = Vrai.

- C15 = Min(x8,x7)<Max(x4,x7) = 3 < 4 = Vrai.

- C16 = Min(x6,x5)<Max(x3,x1) = 6 < 8 = Vrai.

- C17 = Min(x8,x4)<Max(x8,x3) = 4 < 8 = Vrai.

- C18 = Min(x1,x2)<Max(x7,x6) = 1 < 7 = Vrai.

- C19 = Min(x6,x5)<Max(x2,x3) = 6 < 8 = Vrai.

- 0 = Min(x1,x2)<Max(x5,x7) = 1 < 6 = Vrai.