2.7.2 Le graphe de contraintes temporelles
Le graphe de contraintes temporelles décrit les
contraintes temporelles sur les tâches et les relations de
précédence entre elles. Un graphe de contraintes temporelles est
un graphe simple orientéacyclique G=(T,E). Il
est à noter que les noeuds qui forment l'ensemble T sont
divisés en trois sous-ensembles T=TI?TM?TF de
tàaches tels que TI est l'ensemble de tâches qui n'ont
pas de prédécesseurs (les tàaches initiales), TM
est
36
l'ensemble de tâches qui ont des
prédécesseurs et des successeurs et TF est l'ensemble
des tâches finales qui n'ont pas de successeurs et qui, en
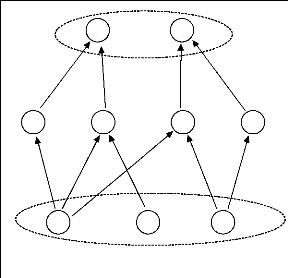
général, appartiennent à l'ensemble des buts. La figure
ci-dessous (Figure 2.12) représente un graphe de contraintes temporelles
tel que TI={t1, t2, t3 }, TF={ t8, t9}
et TM = {t4,. .. ,t7}.
t4 t5 t6
t7
t1 t2 t3
t8 t9
FIGURE 2.12 - Un graphe de contraintes temporelles de
précédence
2.8 Conclusion
Dans ce chapitre, nous avons fourni une présentation
formelle des problèmes de satisfaction des contraintes, leurs solutions,
et leurs représentations graphiques et nous avons illustréces
concepts à travers des exemples.
Nous nous sommes concentrés sur certains algorithmes de
résolution d'un CSP. Nous avons ensuite présentéles
réseaux de contraintes temporelles. Plus précisément,
l'algèbre des intervalles d'Allen (1983) [5] et l'algèbre
de point de Vilain et Kautz (1986) [6] qui ont reçu un
traitement formel de contrainte. Nous avons fini par présenter les
problèmes de planification. La suite de notre travail consiste à
résoudre un problème spécifique de satisfaction des
contraintes en s'appuyant sur ce que nous avons vu dans ce chapitre.
37
| 


