CHAPITRE IV :
APPLICATION DE LA LOGIQUE FLOU DANS LA REGULATION DE
VITESSE D'UN MOTEUR A COURANT CONTINU
Cahier des charges :
Il s'agit d'un moteur LEROY SOMER MS1 classe F801 L06 de
puissance nominale 0,44kw, de vitesse nominale 1500tr/min (soit
157rad /s).
Le constructeur donne les inductions suivante :
La=30mH ; J=0,003kg .m² (moteur seul) Un=170V ; couple nominal 3
N.m ; classe F ; If = 0,38A
Ian=3A ; rendement nominale hors excitation : 0,74 ; R
mesuré est : 5 ?
Le calcul montre que K= (170-5x3) /157= 0,987 wb, La
mesuré est 0,0243H
La constant de temps électrique vaut donc ôe=La
/Ra=4,86 ms
La méthode du ralentissement a donné J=
0,004Kg .m², car le moteur est accouplé à une charge
mécanique .La constant de temps électromécanique est donc
ôem= RJ/K² =20,5ms
On néglige les autres pertes
Le couple nominal résistant est de 3,25 N.m.
Le hacheur se comporte comme un amplificateur de gain A=100.
La constant de dynamo tachymétrique est a =0,01146.
Notre travail dans ce chapitre consiste a faire une étude
comparative entre un régulateur classique PID et un régulateur a
logique flou dans la régulation de la vitesse d'un moteur a courant
continu
Démarche a suivre
· Appliquer un couple résistant Cr= 3.25 au
démarrage dans les 2 système (avec PID, avec RLF)
· Régler le RLF pour le mener a l'état
idéal
· S'assurer que le RLF marche bien quelque soit le couple
appliqué
· Appliquer le même couple résistant
retardé de 0.3s
· Régler le RLF pour le mener a l'état
idéal
· S'assurer que le RLF marche bien quelque soit le couple
appliqué
Partie I : comparaissant entre un PID et RLF avec un
couple résistant au démarrage
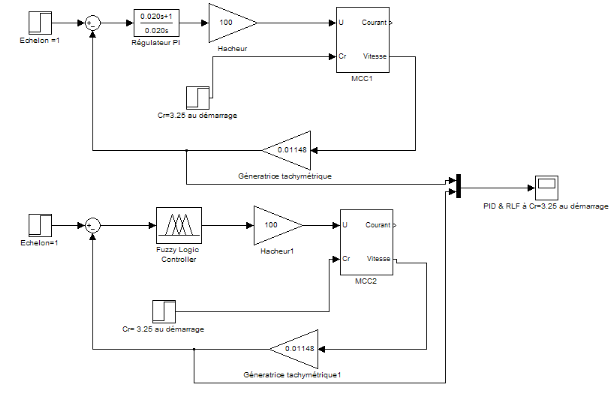
Figure 4.1.1: schéma blocs du système avec un
PID et avec un RLF sans gains
On appliquant un Cr=3.25 au démarrage avec les
échelles suivants :
Entrée erreur [-10 12]
Sortie commande [-10 12]
On obtient les résultats suivants :
· Un régulateur PID performant, la mesure suit la
consigne avec une rapidité remarquable et sans dépassement ainsi
qu'une erreur nulle
· Un RLF qui est ni rapide ni précis mais il est
stable
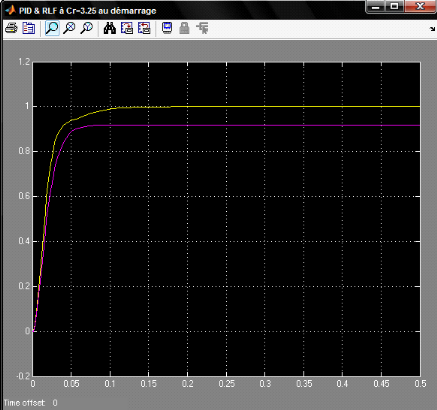
Figure 4.1.2: Réponses des systèmes avec un
PID et avec un RLF
On va introduire un gain à l'entrée du RLF et un
autre gain à la sortie de ce dernier
On remarque qu'à chaque fois on intervient sur le gain
d'entrée de notre RLF on agit sur la rapidité du système
et à chaque fois qu'on intervient sur le gain de la sortie du
système on agit sur la précision.
Après plusieurs réglages effectués, notre
système deviens performant (plus rapide et plus précis) avec les
valeurs suivantes :
Gain à l'entrée (erreur) égal
à 1
Gain à la sortie (commande) égal
à 1.09
Voir la réponse du système dans la figure 1.4
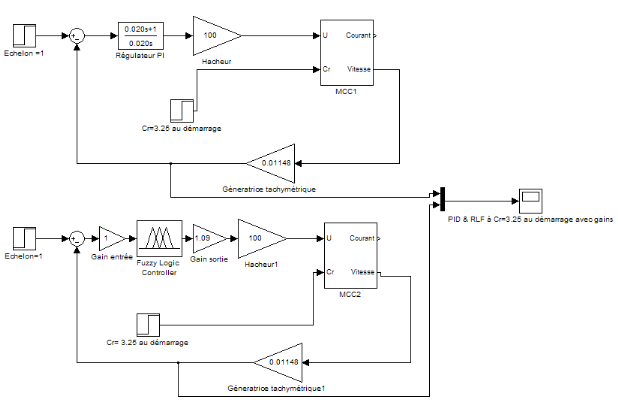
Figure 4.1.3: schéma blocs du système avec un
PID et avec un RLF avec gains
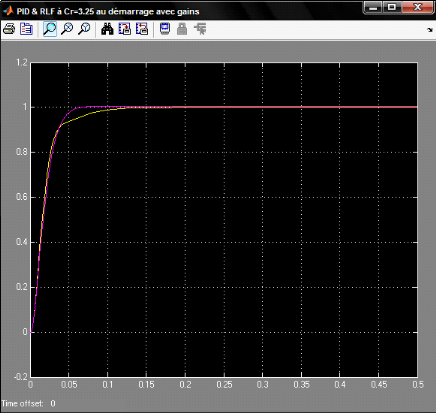
Figure 4.1.4: Réponses des systèmes avec un
PID et avec un RLF
Pour rendre notre RLF autonome (éliminer les gains) on va
introduire nos gain à l'intérieur de notre RLF et plus
précisément en agissant sur les échelles ;
La méthode consiste à deviser l'échelle de
l'entrée (erreur) sur le gain à l'entrée du RLF, et
à multiplier l'échelle de la sortie (commande) par le gain
à la sortie du RLF :
Gain à l'entrée (erreur) égal
à 1
[-10 12] / 1 => [-10 12]
Gain à la sortie (commande) égal
à 1.09
[-10 12] * 1.09 => [10.9 13.08]
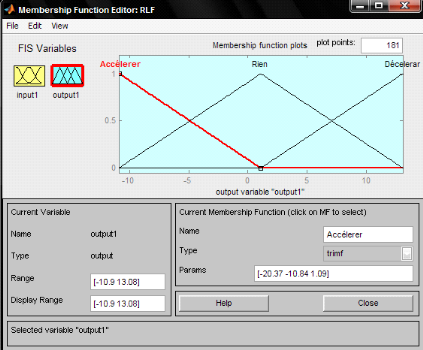
Figure 4.1.5: Introduction de la nouvelle échelle
dans le bloc de sortie du RLF
Partie II : comparaissant entre un PID et RLF avec
un couple résistant en régime permanent
On va appliquer le même couple résistant qui est de
3.25 mais cette fois ci retardé de 0.3s pour pouvoir détecter la
réponse du système au milieu du régime permanant
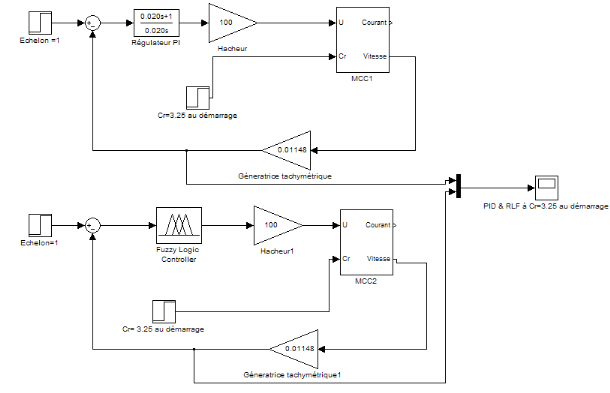
Figure 4.1.6: schéma blocs du système avec un
PID et avec un RLF avec gains
La simulation nous donne le graphe ci-dessous
La courbe jaune représente la réponse du
système avec un PID
La courbe mauve représente la réponse du
système avec un RLF
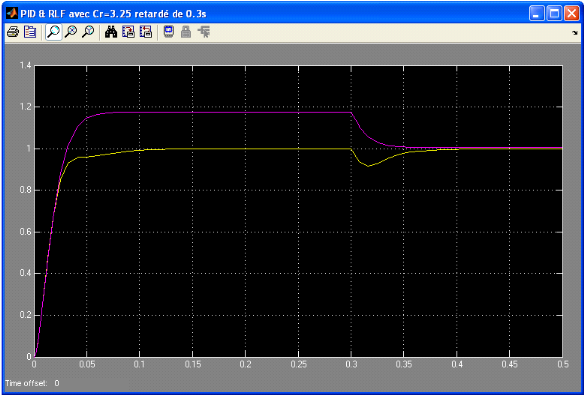
Figure 4.1.7: Réponses des systèmes avec un Cr
à 0.3s
On constate que la réponse du système avec un RLF
perde encor une fois sa précision au démarrage
On v procéder au réglage des échelles on
utilisant la même méthode utilisé au paravent
commençant par introduire un gin a l'entrée de notre fameux RLF
et un autre gain à la sortie de ce dernier, et en agissant sur le
1ère gain le system change de stabilité, et en agissant sur le
2ème le système change de précision.
Apres plusieurs essais on relève les valeurs
idéales qui correspondent à un RLF puissant et performant qui
répond au cahier des charges, ces valeurs sont les suivants.
Gain de l'entrée (erreur) est 400
Gain de sortie (commande) est 1
« prenant en considération qu'un gain de 1.09 est
déjà appliqué»
Pour pourvoir donner a notre RLF son autonomie on procède
par l'élimination de ces gain en les intégrants a
l'intérieur du RLF et plus précisément dans les
échelles d'entrée et sortie
Gain à l'entrée (erreur) égal
à 400
[-10 12] / 400 => [-0.025 0.03]
Gain à la sortie (commande) égal
à 1
[10.9 13.08]* 1 => [10.9 13.08]
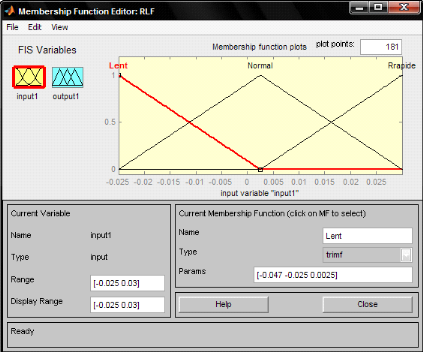
Figure 4.1.8: Introductions de la nouvelle échelle
dans le bloc d'entrée du RLF
En agit sur l'échelle de l'entrée seul comme la
montre cette fenêtre en dessus, en enregistre les modifications et on les
charges dans le bloc Fuzzy sur simulink
Apres avoir éliminer les 2 gains et changer les
échelles en simule et on obtient la réponse ci-dessous
La courbe en jaune représente la réponse avec un
PID
La courbe en mauve représente la réponse avec un
RLF
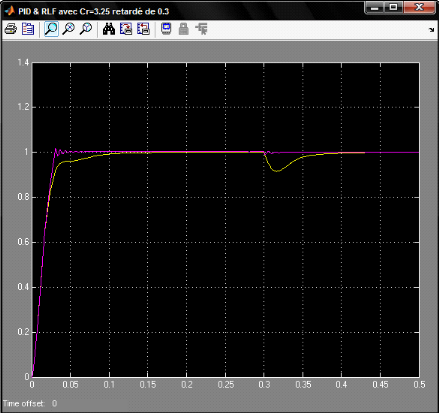
Figure 4.1.9: Réponses des systèmes avec un Cr
à 0.3s
Une réponse très puissante qui répond a
notre cahier des charges, dès le moment de la perturbation le
système réagit rapidement (plus rapide que le PID) pour corriger
l'erreur et remettre la mesure a l'état de consigne.
Pour s'assurer des réglages effectués on a
changé le couple résistant, et le système répond
parfaitement son aucun déréglage, cela implique que notre RLF
correctement paramétré
En propose une vus zoom de la réponse autour de la
perturbation pour pouvoir détecter l'allure de des courbes
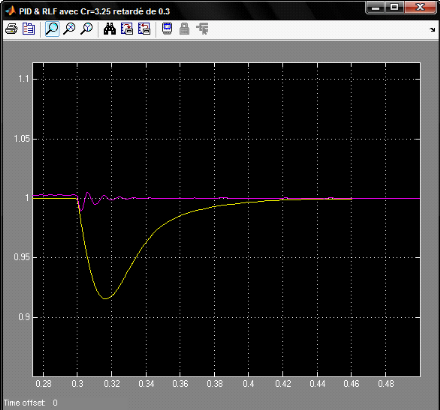
Figure 4.1.10: Vue zoom de la réponse système
autour de la perturbation
Ces graphes illustres des résultats obtenus très
satisfaisants, un régulateur à logique flou musclé et
très performant par rapport au régulateurs classique.
La logique floue (Fuzzy logic) est de grande actualité. Le
but visé dans cette étude été de présenter
d'un part le principe de cette nouvelle méthode de réglage et
établir d'autre part une comparaison entre les méthodes
conventionnelles et cette dernière, ceci pour mieux éclaircir les
différences, de familiariser avec la nouvelle méthode puis
connaître ces avantages dans le réglage automatique.
LES AVANTAGES ET LES DESAVANTAGES DU REGLAGE PAR
LOGIQUE DE FLOUE
Evidemment, le réglage par la logique floue
réunit un certain nombre d'avantages et de désavantages. Les
avantages essentiels sont :
· La non nécessité modélisation
(cependant il peut être utile d'un modèle convenable);
· la possibilité d'implémenter des
connaissances (linguistiques) de l'opérateur du processus;
· la maîtrise des systèmes à
régler avec un comportement complexe (fortement non linéaire et
difficile à modéliser);
· L'obtention fréquente de meilleures
prestations dynastiques (régulateur non linéaire):
· L'emploi possible aussi pour des processus rapides
(grâce à des processeurs dédicacés);
· la disponibilité des systèmes de
développement efficaces, soit pour microprocesseurs ou PC (solution
logicielle). soit pour circuits intégrés (processeurs
dédicacée, Fuzzy processor, solution matérielle).
Par contre, les désavantages sont :
· Le manque de directives précises pour la
conception d'un réglage (choix des grandeurs à mesurer,
détermination de la Fuzzification, des inférences et de
Défuzzification);
· L'approche artisanale et non systématique
(implémentation des connaissances de l'opérateur souvent
difficile);
· L'impossibilité de la démonstration
de la stabilité du circuit de réglage en toute
généralité(en l'absence d'un modèle valable);
· La possibilité d'apparition de cycles
limites à cause du fonctionnement non linéaire;
· la précision du réglage souvent peu
élevée;
· la cohérence des inférences non
garantie a priori (apparition de règles d'inférence
contradictoires possible).
| 


