|
INFINITE DILUTION ACTIVITY COEFFICIENT
MEASUREMENTS
OF ORGANIC SOLUTES IN
FLUORINATED IONIC LIQUIDS BY
GAS-LIQUID
CHROMATOGRAPHY AND THE INERT GAS
STRIPPING METHOD
Submitted in fulfillment of the academic requirements for the
degree of Master of Science,
Faculty of Engineering, School of Chemical
Engineering,
University of KwaZulu-Natal
by
Kaniki Armel Tumba
[BSc. Eng (Chem)]
Supervisor: Prof. Deresh Ramjugernath
Co-Supervisor: Dr. Paramespri Naidoo
i Declaration
DECLARATION
I, Kaniki Armel Tumba, declare that:
(i) The research reported in this thesis, except where otherwise
indicated, is my
original work.
(ii) This thesis has not been submitted for any degree or
examination at any other university.
(iii) This thesis does not contain other persons` data,
pictures, graphs or other information, unless specifically acknowledged as
being sourced from other persons.
(iv) This thesis does not contain other persons` writing,
unless specifically acknowledged as being sourced from other researchers. Where
other written sources have been quoted, then:
a) their words have been re-written but the general information
attributed to them has been referenced;
b) where their exact words have been used, their writing has
been placed inside quotation marks, and referenced.
(v) Where I have reproduced a publication of which I am an
author, co-author or editor, I have indicated in detail which part of the
publication was actually written by myself alone and have fully referenced such
publications.
(vi) This thesis does not contain text, graphics or tables
copied and pasted from the internet, unless specifically acknowledged, and the
source being detailed in the thesis and in the References sections.
Kaniki A. Tumba (Candidate) Date
As the candidate`s Supervisor I agree/do not agree to the
submission of this thesis.
Prof. Deresh Ramjugernath Date
ABSTRACT
Environmental and safety concerns have prompted an active quest
for green? alternatives to
molecular solvents currently used in industrial
chemical processes. In recent years, ionic liquids
have been reported as
potentially good replacements for conventional solvents. Activity
coefficients at infinite dilution, of various organic solutes
have been measured in the
temperature range from 313.15 to 373.15 K by gas-liquid
chromatography and the inert gas
stripping techniques in seven fluorinated
ionic liquids (FILs). Partial molar excess enthalpies at
infinite dilution
of the solutes in the ionic liquids have been derived from the temperature-
dependence of experimental values. Selectivities and capacities
have been calculated for
various separation problems and compared to literature values for
other ionic liquids, as well as conventional solvents. The effect of structure
on the selectivity has been investigated.
The present work, initiated in the context of South Africa`s
Fluorochemical Expansion Initiative is a contribution to the understanding of
how structure influences FILs selectivity and capacity in different separation
problems. FILs are interesting for South Africa as its geology contains large
amounts of fluorine ores.
For the n-hexane/benzene, and n-hexane/hex-1-ene systems which
represent the aliphatics/aromatics and paraffins/olefins separation problems,
higher selectivities at infinite dilution were obtained with FILs consisting of
short-chained cations and small anions. The opposite trend was observed for the
methanol/acetone and the ethanol/butan-2-one systems as representatives of the
alcohols/ketones separation problem as well as the methanol/benzene system
which refers to the alcohols/aliphatics mixtures. FILs with long cation alkyl
chains and large anions tend to be the most selective for the benzene/
butan-2-one system, indicative of the aliphatics/ketones separation problem.
The natural logarithm of has been found to vary linearly with
the carbon number of the alkyl
chain attached to the methylpyrrolidinium or
methylimidazolium group. On this ground, a
simple equation correlating as
well as selectivity with the cation alkyl chain length has been
proposed. It has been successfully tested using experimental data
related to pyrrolidinium and imidazolium-based ionic liquids.
ACKNOWLEDGEMENTS
Glory and Praise to Jehovah, the all mighty God who allowed me to
achieve this research work.
I express my utmost gratitude to Prof. Deresh Ramjugernath for
his dedicated supervision and his priceless assistance throughout this study.
Dr Paramespri Naidoo, the co-supervisor is sincerely acknowledged for her
pertinent suggestions and skillful guidance.
This work is based upon research supported by the South
African Research Chairs Initiative of the Department of Science and Technology
and National Research Foundation (NRF) which is acknowledged for its financial
support.
I would be remiss if I do not extend my appreciations to the
following individuals as well:
· My wife Fanny Tshabu Kaniki who deserves a medal for her
patience and support;
· My parents, brothers and sisters for their
encouragements;
· Messers Lindinkosi Mkinze and Ayanda Khanyile, The
Thermodynamics Research Unit laboratory technicians;
· Messers Ken Jack and Kelly Robertson, Mechanical workshop
staff in the School of Chemical Engineering;
· Glass blower Peter Siegling and UKZN Chemical Engineering
ICT manager P. Nayager;
· Prof. Urszula Domañska and Dr. Andrzej Marciniak
(Warsaw University of Technology, Poland) for insightful discussions on the
behavior of ionic liquids;
· Dr. Fabrice Mutelet (Laboratoire de Thermodynamique
des Milieux Polyphasés, Nancy, France) for his availability to answer
some tricky questions on the GLC experimental procedure;
· Dr. Christophe Coquelet (Laboratoire des Equilibres
Thermodynamiques, ENSM, Fontainebleau, France) who helped in advising on the
construction of the inert gas stripping apparatus;
· All Thermodynamics Research Unit postgraduate students
and friends: J. Chiyen, M. Tshibangu, J. Kapuku, T. P. Benecke, M. Tadie, S.
Iwarere, B. Moller, F. Kabulu, P.N. Thokozani, ...
· E. Olivier and N. Gwala who authorized the use of
their experimental data in this study;
· All UKZN Chemical Engineering lecturers who expressed
interest in this project: Prof. J.D. Raal, Prof. D. Arnold, Mr Baah,...
TABLE OF CONTENTS
DECLARATION i
ABSTRACT ii
ACKNOWLEDGEMENTS iii
TABLE OF CONTENTS iv
LIST OF FIGURES ix
LIST OF PHOTOGRAPHS xxi
LIST OF TABLES xxiiNOMENCLATURE
.......................................................................
xxvi
ABBREVIATIONS xxix
CHAPTER ONE: INTRODUCTION 1
CHAPTER TWO: LITERATURE REVIEW 4
2.1. Ionic liquids 4
2.1.1. Definition and structure 4
2.1.2. History 4
2.1.3. Properties of ionic liquids 6
2.1.4. Potential applications of ionic liquids in the chemical
industry 6
2.1.5. Commercial applications of ionic liquids 7
2.1.6. Use of ionic liquids as solvents in separation processes.
8
2.1.7. Barriers to the commercial use of ionic liquids 10
2.1.8. Fluorinated ionic liquids. (FILs) 11
2.2. Infinite dilution activity coefficients 12
2.2.1. Definition 12
2.2.2. Importance and use of infinite dilution activity
coefficient data 12
2.2.3. Temperature dependence of activity coefficient 15
2.2.4. Predictive activity coefficient models 16
2.2.5. Experimental techniques for IDACs measurements 19
2.3. Advances in the design of IGS equipment 21
2.3.1. Major developments in the use of the IGSM 21
2.3.2. The number of cells required for IDAC measurements 22
2.3.3. Cell design parameters. 22
2.3.4. Review of previous equilibrium cells 24
v
CHAPTER THREE: THEORETICAL CONSIDERATIONS 34
3.1. Gas liquid chromatography 34
3.2. Inert gas stripping method 37
3.2.1. Equations for IDACs computation 37
3.2.2. Mass Transfer considerations in the equilibrium cell.
50
CHAPTER FOUR: EXPERIMENTAL APPARATUS AND PROCEDURE
52
4.1. Limiting activity coefficient measurements by gas liquid
chromatography 52
4.1.1. Chemicals 52
4.1.2. Experimental set up 53
4.1.3. Experimental procedure 54
4.2. The inert gas stripping technique 56
4.2.1. Chemicals 56
4.2.2. Experimental Set-up 56
4.2.3. Experimental procedure 60
CHAPTER FIVE: RESULTS 62
5.1. Results from Gas-Liquid Chromatography 63
5.1.1. Hexadecane 63
5.1.2. Trihexyltetradecylphosphonium bis
(trifluoromethylsulfonyl) imide,
[3C6C14P] [Tf2N] 64
5.1.3. Trihexyltetradecylphosphonium tetrafluoroborate,
[3C6C14P] [BF4] 71
5.1.4. Trihexyltetradecylphosphonium hexafluorophosphate,
[3C6C14P] [PF6] 78
5.1.5. Methyltrioctylammonium bis (trifluoromethylsulfonyl)
imide, [C13C8N] [Tf2N] 85
5.1.6. 1-Butyl-3-methylimidazolium hexafluoroantimonate, [BMIM]
[SbF6]. 92
5.1.7.1-ethyl-3-methylimidazolium trifluoromethanesulfonate,
[EMIM] [TfO] 99
5.1.8. 1-methyl-3-octylimidazolium hexafluorophosphate,
[MOIM][PF6] 106
5.2. Results from the inert gas stripping technique 112
5.2.1. N-methyl-2-pyrrolidone, NMP 112
5.2.2. Trihexyltetradecylphosphonium bis
(trifluoromethylsulfonyl) imide 113
5.3.Separation potential of the investigated ionic liquids.
113
CHAPTER SIX: DISCUSSION 115
6.1. Fluorinated Ionic Liquids investigated in this work 115
6.1.1. Gas-Liquid Chromatography 115
6.1.2. The inert gas stripping technique 118
6.1.3. Error estimation 119
vi
6.2. Limiting activity coefficients of fluorinated ionic liquids
120
6.2.1. Hierarchy of IDACs values. 122
6.2.2. Effect of structure on IDACs of organic solutes in
Fluorinated Ionic Liquids, FILs 125
6.3. Limiting selectivity and capacity of fluorinated ionic
liquids 127
6.3.1. n-Hexane (1)/Benzene (2) separation problem 128
6.3.2. Methanol (1)/benzene (2) separation problem 130
6.3.3. Methanol (1)/acetone (2) separation problem 131
6.3.4. n-hexane (1)/ hex-1-ene (2) separation problem 132
6.3.5. Benzene (1)/ butan-2-one (2) separation problem 134
6.3.6. Ethanol (1)/ butan-2-one (2) separation problem 135
6.4. Correlation of limiting activity coefficient and selectivity
with the FIL alkyl chain 135
CHAPTER SEVEN: CONCLUSION AND RECOMMENDATIONS
137
REFERENCES 141
APPENDIX A: SOURCES OF IDACs LITERATURE DATA
160
APPENDIX B: STRUCTURE OF IONIC LIQUIDS 165
APPENDIX C: ORIGIN AND PURITY OF CHEMICALS
166
APPENDIX D: FUGACITIES, CRITICAL DATA AND IONIZATION
ENERGIES167
APPENDIX E: CALIBRATION DATA 168
APPENDIX F: SELECTIVITIES AND CAPACITIES 169
APPENDIX G: EFFECT OF STRUCTURE ON IDAC VALUES
170
1. Infinite dilution activity coefficients of alkanes in
fluorinated ionic liquids 170
1.1. Infinite dilution activity coefficients
of alkanes in imidazolium-based
fluorinated ionic liquids. 170
1.2. Infinite dilution activity coefficients of alkanes in
phosphonium-based FILs 172
1.3. Infinite dilution activity coefficients of alkanes in
ammonium-based FILs 173
1.4. Infinite dilution activity coefficients of alkanes in
pyridinium-based FILs 173
1.5. Infinite dilution activity coefficients of alkanes in
pyrrolidinium-based FILs 173
1.6. Infinite dilution activity coefficients of alkanes in
sulfonium-based FILs 174
2. Infinite dilution activity coefficients of alk-1-enes
in fluorinated ionic liquids. 174
2.1. Infinite dilution activity coefficients of alk-1-enes in
imidazolium-based FILs 174
2.2. Infinite dilution activity coefficients of alk-1-enes in
phosphonium-based FILs 177
2.3. Infinite dilution activity coefficients of alk-1-enes in
ammonium-based FILs 177
2.4. Infinite dilution activity coefficients of alk-1-enes in
pyridinium-based FILs 178
2.5. Infinite dilution activity coefficients of alk-1-enes in
pyrrolidinium-based FILs 178
3. Infinite dilution activity coefficients of alk-1-ynes
in fluorinated ionic liquids. 179
3.1. Infinite dilution activity coefficients of alk-1-ynes in
imidazolium-based FILs 179
3.2. Infinite dilution activity coefficients of alk-1-ynes in
phosphonium-based FILs 181
3.3. Infinite dilution activity coefficients of alk-1-ynes in
ammonium, pyrrolidinium and sulfonium-based FILs 182
4. Infinite dilution activity coefficients of
cycloalkanes in fluorinated ionic liquids. 182
4.1. Infinite dilution activity coefficients of cycloalkanes in
imidazolium-based FILs 182
4.2. Infinite dilution activity coefficients of cycloalkanes in
phosphonium-based FILs 185
4.3. Infinite dilution activity coefficients of cycloalkanes in
ammonium-based FILs 185
4.4. Infinite dilution activity coefficients of cycloalkanes in
pyridinium-based FILs 185
4.5. Infinite dilution activity coefficients of cycloalkanes in
pyrrolidinium-based FILs 186
4.6. Infinite dilution activity coefficients of cycloalkanes in
sulfonium-based FILs 186
5. Infinite dilution activity coefficients of
alkan-1-ols in fluorinated ionic liquids 186
5.1. Infinite dilution activity coefficients of alkan-1-ols in
imidazolium-based FILs 186
5.2. Infinite dilution activity coefficients of alkan-1-ols in
phosphonium-based FILs 189
5.3. Infinite dilution activity coefficients of alkan-1-ols in
ammonium-based FILs 189
5.4. Infinite dilution activity coefficients of alkan-1-ols in
pyridinium-based FILs 190
5.5. Infinite dilution activity coefficients of alkan-1-ols in
pyrrolidinium-based FILs 190
5.6. Infinite dilution activity coefficients of alkan-1-ols in
sulfonium-based FILs 190
6. Infinite dilution activity coefficients of
alkylbenzenes in fluorinated ionic liquids. 191
6.1. Infinite dilution activity coefficients of alkylbenzenes in
imidazolium-based FILs 191
6.2. Infinite dilution activity coefficients of alkylbenzenes in
phosphonium-based FILs 193
6.3. Infinite dilution activity coefficients of alkylbenzenes in
ammonium-based FILs 193
6.4. Infinite dilution activity coefficients of alkylbenzenes in
pyridinium-based FILs 194
6.5. Infinite dilution activity coefficients of alkylbenzenes in
pyrrolidinium and sulfoniumbased FILs 194
7. Infinite dilution activity coefficients of ket-2-ones
in fluorinated ionic liquids. 195
7.1. Infinite dilution activity coefficients of ket-2-ones in
imidazolium-based FILs 195
7.2. Infinite dilution activity coefficients of ket-2-ones in
phosphonium-based FILs 196
7.3. Infinite dilution activity coefficients of ket-2-ones in
ammonium-based FILs 197
7.4. Infinite dilution activity coefficients of ket-2-ones in
pyridinium-based FILs 197
7.5. Infinite dilution activity coefficients of ket-2-ones in
pyrrolidinium-based FILs 197
APPENDIX H: EFFECT OF STRUCTURE ON LIMITING SELECTIVITY
AND CAPACITY 198
1. Benzene/n-hexane separation problem 198
1.1. Imidazolium-based fluorinated ionic liquids 198
1.2. Phosphonium-based fluorinated ionic liquids 199
1.3. Ammonium-based Fluorinated ionic liquids 199
2. Methanol/benzene separation problem 200
2.1. Imidazolium-based fluorinated ionic liquids 200
2.2. Phosphonium-based fluorinated ionic liquids 200
2.3. Ammonium-based fluorinated ionic liquids 201
3. Methanol/acetone separation problem 201
3.1. Imidazolium-based fluorinated ionic liquids 201
3.2. Phosphonium-based fluorinated ionic liquids 202
3.3. Ammonium-based fluorinated ionic liquids 203
4. n-Hexane/hex-1-ene separation problem 203
4.1. Imidazolium-based fluorinated ionic liquids 203
4.2. Phosphonium-based fluorinated ionic liquids 204
4.3. Ammonium-based fluorinated ionic liquids 204
4.4. Pyrrolidinium-based fluorinated ionic liquids 205
5.Benzene/butan-2-one separation problem 205
5.1 Imidazolium-based fluorinated ionic liquids 205
5.2 Phosphonium-based fluorinated ionic liquids 206
6. Ethanol/butan-2-one separation problem 206
6.1 Imidazolium-based fluorinated ionic liquids 206
6.2 Phosphonium-based fluorinated ionic liquids 206
APPENDIX I: CORRELATION OF INFINITE DILUTION ACTIVITY
COEFFICIENT, SELECTIVITY AND CAPACITY 207
1. Infinite dilution activity coefficient correlation
with the ionic liquid alkyl chain length 207
1.1. Imidazolium-based fluorinated ionic liquids 207
1.2. Pyrrolidinium-based fluorinated ionic liquids 208
2. Infinite dilution selectivity coefficient correlation
with the ionic liquid alkyl chain length 209
2.1. n-hexane/benzene system 209
2-2. n-hexane/hex-1-ene system 209
LIST OF FIGURES
Figure 2-1: Structure of ionic liquids.
Figure 2-2: Dilutor cell constructed by Leroi et
al. (1977).
Figure 2-3: Equilibrium cell constructed by
Richon et al. (1980).
Figure 2-4: Dilutor cell used by Richon and
Renon (1980).
Figure 2-5: Dilutor cell designed by Legret et
al. (1983).
Figure 2-6: Dilutor cell designed by Richon et
al. (1985) for viscous and foaming mixtures. Figure 2-7:
Equilibrium cell designed by Bao et al. (1994).
Figure 2-8: Equilibrium cell designed by Hovorka
et al. (1997).
Figure 2-9: Equilibrium cell designed by Miyano
et al. (2003) for the determination of Henry`s law constants using the dilutor
technique.
Figure 2-10: Dilutor cell designed by Dobryakov
et al. (2008).
Figure 2-11: The dilutor cell designed by
Kutsuna and Hori (2008).
Figure 4-1: Flow diagram of the experimental
set up for the inert gas stripping method.
Figure 4-2:
Cross Section of the cold trap to illustrate its inner working (George
2008).
Figure 4-3: Typical plots of solute GC peak area and
ln (solute peak area) versus time.
Figure 5-1: Plots of versus for alkanes in
[3C6C14P] [Tf2N] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-2: Plots of versus for alk-1-enes in
[3C6C14P] [Tf2N] together with a linear
correlation of the data
using the Gibbs-Helmholtz equation.
Figure 5-3: Plots of versus for cycloalkanes in
[3C6C14P] [Tf2N] together with a
linear correlation of the data
using the Gibbs-Helmholtz equation.
Figure 5-4: Plots of versus for alk-1-ynes in
[3C6C14P] [Tf2N] together with a linear
correlation of the data
using the Gibbs-Helmholtz equation.
Figure 5-5: Plots of versus for alkanols in
[3C6C14P] [Tf2N] together with a linear
correlation of the data
using the Gibbs-Helmholtz equation.
Figure 5-6: Plots of versus for alkylbenzenes in
[3C6C14P] [Tf2N] together with a
linear correlation of the data
using the Gibbs-Helmholtz equation.
Figure 5-7: Plots of versus for ketones in
[3C6C14P] [Tf2N] together with a linear
correlation of the data
using the Gibbs-Helmholtz equation.
Figure 5-8: Plots of versus the number of carbon
atoms for n-alkanes, alk-1-enes,
cycloalkanes, alk-1-ynes, ketones, alkanols
and alkylbenzenes in [3C6C14P] [Tf2N].
Figure 5-9: Plots of versus for n-alkanes in
[3C6C14P] [BF4] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-10: Plots of versus for alk-1-enes in
[3C6C14P] [BF4] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-11: Plots of versus for alk-1-ynes in
[3C6C14P] [BF4] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-12: Plots of versus for cycloalkanes in
[3C6C14P] [BF4] together with a
linear correlation of the data using the Gibbs-Helmholtz
equation.
Figure 5-13: Plots of versus for alkanols in
[3C6C14P] [BF4] together with a linear
correlation of the data
using the Gibbs-Helmholtz equation.
Figure 5-14: Plots of versus for alkylbenzenes
in [3C6C14P] [BF4] together with a
linear correlation of the data
using the Gibbs-Helmholtz equation.
Figure 5-15: Plots of versus for ketones in
[3C6C14P] [BF4] together with a linear
correlation of the data
using the Gibbs-Helmholtz equation.
Figure 5-16: Plots of versus the number of
carbon atoms for n-alkanes, alk-1-enes, alk-1-
ynes, cycloalkanes, alkanols,
alkylbenzenes and ketones in [3C6C14P] [BF4].
Figure 5-17: Plots of versus for alkanes in
[3C6C14P] [PF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-18: Plots of versus for alk-1-enes in
[3C6C14P] [PF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-19: Plots of versus for alk-1-ynes in
[3C6C14P] [PF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-20: Plots of versus for cycloalkanes in
[3C6C14P] [PF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-21: Plots of versus for alkanols in
[3C6C14P] [PF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-22: Plots of versus for alkylbenzenes
in [3C6C14P] [PF6] together with a
linear correlation of the data using the Gibbs-Helmholtz
equation.
Figure 5-23: Plots of versus for ketones in
[3C6C14P] [PF6] together with a linear
correlation of the data
using the Gibbs-Helmholtz equation.
Figure 5-24: Plots of versus the number of
carbon atoms for n-alkanes, alk-1-enes, alk-1-
ynes, cycloalkanes, alkanols,
alkylbenzenes and ketones in [3C6C14P] [PF6].
Figure 5-25: Plots of versus for alkanes in
[C13C8N] [Tf2N] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-26: Plots of versus for alk-1-enes in
[C13C8N] [Tf2N] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-27: Plots of versus for alk-1-ynes in
[C13C8N] [Tf2N] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-28: Plots of versus for cycloalkanes in
[C13C8N] [Tf2N] together with a
linear correlation of the data using the Gibbs-Helmholtz
equation.
Figure 5-29: Plots of versus for alkanols in
[C13C8N] [Tf2N] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-30: Plots of versus for alkylbenzenes
in [C13C8N] [Tf2N] together with a
linear correlation of the data using the Gibbs-Helmholtz
equation.
Figure 5-31: Plots of versus for ketones in
[C13C8N] [Tf2N] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-32: Plots of versus the number of
carbon atoms for n-alkanes, alk-1-enes, and
alk-1-ynes, cycloalkanes, alkanols, alkylbenzenes and ketones in
[C13C8N] [Tf2N]. Figure 5-33: Plots of versus for alkanes in
[BMIM] [SbF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-34: Plots of versus for alk-1-enes in
[BMIM] [SbF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-35: Plots of versus for alk-1-ynes in
[BMIM] [SbF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-36: Plots of versus for cycloalkanes in
[BMIM] [SbF6] together with a
linear correlation of the data using the Gibbs-Helmholtz
equation.
Figure 5-37: Plots of versus for alkanols in
[BMIM] [SbF6] together with a linear
correlation of the data using the
Gibbs-Helmholtz equation.
Figure 5-38: Plots of versus for alkylbenzenes
in [BMIM] [SbF6] together with a
linear correlation of the data using the
Gibbs-Helmholtz equation.
Figure 5-39: Plots of versus for ketones in
[BMIM] [SbF6] together with a linear
correlation of the data using the
Gibbs-Helmholtz equation.
Figure 5-40: Plots of versus the number of
carbon atoms for alk-1-enes, alk-1-ynes,
cycloalkanes, alkanols,
alkylbenzenes and ketones in [BMIM] [SbF6].

List of figures
Figure 5-41: Plots of versus for alkanes in
[EMIM] [TfO] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-42: Plots of versus for alk-1-nes in
[EMIM] [TfO] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-43: Plots of versus for alk-1-ynes in
[EMIM] [TfO] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-44: Plots of versus for cycloalkanes in
[EMIM] [TfO] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-45: Plots of versus for alkanols in
[EMIM] [TfO] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-46: Plots of versus for alkylbenzenes
in [EMIM] [TfO] together with a
linear correlation of the data using the Gibbs-Helmholtz
equation.
Figure 5-47: Plots of versus the number of
carbon atoms for n-alkanes, alk-1-enes, alk-1-
ynes, cycloalkanes, alkanols and alkylbenzenes in [EMIM]
[TfO].
Figure 5-48: Plots of versus for n-alkanes in
[MOIM] [PF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-49: Plots of versus for alk-1-enes in
[MOIM] [PF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-50: Plots of versus for alk-1-ynes in
[MOIM] [PF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-51: Plots of versus for cycloalkanes in
[MOIM] [PF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-52: Plots of versus for alkanols in
[MOIM] [PF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation.
Figure 5-53: Plots of versus for alkylbenzenes
in [MOIM] [PF6] together with a
linear correlation of the data using the Gibbs-Helmholtz
equation.
Figure 5-54: Plots of versus the number of
carbon atoms for n-alkanes, alk-1-enes, alk-1-
ynes, cycloalkanes, alkanols and alkylbenzenes in [MOIM]
[PF6].
Figure 6-1: Experimental infinite dilution
activity coefficients of n-hexane and cyclohexane in
various fluorinated ionic liquids at 313.15 K.
Figure 6-2: Experimental infinite dilution
activity coefficients of hex-1-ene and hex-1-yne in
various fluorinated ionic liquids at 313.15 K.
Figure 6-3: Experimental infinite dilution
activity coefficients of ethanol, benzene and acetone in various fluorinated
ionic liquids at 313.15 K.
Figure B-1: Ions present in the structure of
ionic liquids used in this work. Figure E-1: Temperature
calibration curve for the dilutor cell Pt 100.
Figure E-2: Pressure calibration curve for the
dilutor cell pressure transducer.
Figure G-1: Plots of versus Nc for alkanes in
imidazolium-based FILs comprising
[BF4]- ion.
Figure G-2: Plots of versus Nc for alkanes in
imidazolium-based FILs comprising
[Tf2N] - ion.
Figure G-3: Plots of versus Nc for alkanes in
imidazolium-based FILs comprising [PF6]-
ion.
Figure G4: Plots of versus Nc for alkanes in
imidazolium-based FILs comprising [TfO]-,
[SbF6]- and [TFA]- ions.
Figure G-5: Plots of versus Nc for alkanes in
imidazolium-based FILs comprising
[EMIM]+ ion.
Figure G-6: Plots of versus Nc for alkanes in
imidazolium-based FILs comprising
[BMIM]+ ion.
Figure G-7: Plots of versus Nc for alkanes in
imidazolium-based FILs comprising
[HMIM]+ ion.
Figure G-8: Plots of versus Nc for alkanes in
imidazolium-based FILs comprising
[MOIM]+ ion.
Figure G-9: Plots of versus Nc for alkanes in
phosphonium-based FILs comprising
[3C6C14P]+ ion.
Figure G-10: Plots of versus Nc for alkanes in
ammonium-based FILs comprising
[Tf2N] - ion.
Figure G-11: Plots of versus Nc for alkanes in
pyridinium-based FILs
Figure G-12: Plots of versus Nc for alkanes in
pyrrolidinium-based FILs comprising
[Tf2N] - ion.
Figure G-13: Plots of versus Nc for alkanes in
pyrrolidinium-based FILs comprising
[BMPyrr]+ ion.
Figure G-14: Plots of versus Nc for alkanes in
the sulfonium-based FIL [Et3S] [Tf2N]
List of figures
xiv
Figure G-15: Plots of versus Nc for alk-1-enes
in imidazolium-based FILs comprising
[BF4]- ion.
Figure G-16: Plots of versus Nc for alk-1-enes
in imidazolium-based FILs comprising
[Tf2N] -ion.
Figure G-17: Plots of versus Nc for alk-1-enes
in imidazolium-based FILs comprising
[PF6]- ion.
Figure G-18: Plots of versus Nc for alk-1-enes
in imidazolium-based FILs comprising
[TfO]- ion.
Figure G-19: Plots of versus Nc for alk-1-enes
in imidazolium-based FILs comprising
[EMIM]+ ion.
Figure G-20: Plots of versus Nc for alk-1-enes
in imidazolium-based FILs comprising
[BMIM]+ion.
Figure G-21: Plots of versus Nc for alk-1-enes
in imidazolium-based FILs comprising
[HMIM] +ion.
Figure G-22: Plots of versus Nc for alk-1-enes
in imidazolium-based FILs comprising
[MOIM]+ion.
Figure G-23: Plots of versus Nc for alk-1-enes
in phosphonium-based FILs comprising
[3C6C14P]+ ion.
Figure G-24: Plots of versus Nc for alk-1-enes
in ammonium-based FILs comprising
[Tf2N] - ion.
Figure G-25: Plots of versus Nc for alk-1-enes
in the pyridinium-based FIL [Epy] [Tf2N]
Figure G-26: Plots of versus Nc for alk-1-enes
in pyrrolidinium-based FILs comprising
[Tf2N]- ion.
Figure G-27: Plots of versus Nc for alk-1-enes
in pyrrolidinium-based FILs comprising
[BMPyrr]+ ion.
Figure G-28: Plots of versus Nc for alk-1-enes
in the sulfonium-based FIL [Et3S] [Tf2N]
Figure G-29: Plots of versus Nc for alk-1-ynes
in imidazolium-based FILs comprising
[BF4]- ion.
Figure G-30: Plots of versus Nc for alk-1-ynes
in imidazolium-based FILs comprising
[PF6]- ion.
Figure G-31: Plots of versus Nc for alk-1-ynes
in imidazolium-based FILs comprising
Figure G-32: Plots of versus Nc for alk-1-ynes
in imidazolium-based FILs comprising
[TfO]- ion.
Figure G-33: Plots of versus Nc for alk-1-ynes
in imidazolium-based FILs comprising
[EMIM]+ ion.
Figure G-34: Plots of versus Nc for alk-1-ynes
in imidazolium-based FILs comprising
[BMIM]+ ion.
Figure G-35: Plots of versus Nc for alk-1-ynes
in imidazolium-based FILs comprising
[HMIM]+ ion.
Figure G-36: Plots of versus Nc for alk-1-ynes
in phosphonium-based FILs comprising
[3C6C14P]+ ion.
Figure G-37: Plots of versus Nc for alk-1-ynes
in an ammonium, a pyrrolidinium and a
sulfonium-based FILs.
Figure G-38: Plots of versus Nc for cycloalkanes
in imidazolium-based FILs comprising
[BF4]- .
Figure G-39: Plots of versus Nc for cycloalkanes
in imidazolium-based FILs comprising
[Tf2N] - ion.
Figure G-40: Plots of versus Nc for cycloalkanes
in imidazolium-based FILs comprising
[PF6]- ion.
Figure G-41: Plots of versus Nc for cycloalkanes
in imidazolium-based FILs comprising
[TfO]- ion.
Figure G-42: Plots of versus Nc for cycloalkanes
in imidazolium-based FILs comprising
[EMIM]+ ion.
Figure G-43: Plots of versus Nc for cycloalkanes
in imidazolium-based FILs comprising
[BMIM]+ ion.
Figure G-44: Plots of versus Nc for cycloalkanes
in imidazolium-based FILs comprising
[HMIM]+ ion.
Figure G-45: Plots of versus Nc for cycloalkanes
in imidazolium-based FILs comprising
[MOIM]+ ion.
Figure G-46: Plots of versus Nc for cycloalkanes
in phosphonium-based FILs
comprising [3C6C14P]+ ion.
Figure G-47: Plots of versus Nc for cycloalkanes
in ammonium-based FILs comprising
Figure G-48: Plots of versus Nc for cycloalkanes
in the pyridinium-based FILs [Epy]
[Tf2N] and [BMPy] [BF4].
Figure G-49: Plots of versus Nc for cycloalkanes
in pyrrolidinium-based FILs
comprising [BMPyrr]+ ion.
Figure G-50: Plots of versus Nc for cycloalkanes
in the sulfonium-based FIL [Et3S]
[Tf2N].
Figure G-51: Plots of versus Nc for alkan-1-ols
in imidazolium-based FILs comprising
[BF4]- ion.
Figure G-52: Plots of versus Nc for alkan-1-ols
in imidazolium-based FILs comprising
[Tf2N] -ion.
Figure G-53: Plots of versus Nc for alkan-1-ols
in imidazolium-based FILs comprising
[PF6]- ion.
Figure G-54: Plots of versus Nc for alkan-1-ols
in imidazolium-based FILs comprising
[TfO]- ion.
Figure G-55: Plots of versus Nc for alkan-1-ols
in imidazolium-based FILs comprising
[EMIM]+ ion.
Figure G-56: Plots of versus Nc for alkan-1-ols
in imidazolium-based FILs comprising
[BMIM]+ ion.
Figure G-57: Plots of versus Nc for alkan-1-ols
in imidazolium-based FILs comprising
[HMIM]+ ion.
Figure G-58: Plots of versus Nc for alkan-1-ols
in imidazolium-based FILs comprising
[EMIM]+ ion.
Figure G-59: Plots of versus Nc for alkan-1-ols
in phosphonium-based FILs comprising
[3C6C14P]+ ion.
Figure G-60: Plots of versus Nc for alkan-1-ols
in ammonium-based FILs comprising
[Tf2N]- ion.
Figure G-61: Plots of versus Nc for alkan-1-ols
in the pyridinium-based FILs [BMPy]
[BF4] and [Epy] [Tf2N].
Figure G-62: Plots of versus Nc for alkan-1-ols
in pyrrolidinium-based FILs comprising
[BMPyrr]+ ion.
Figure G-63: Plots of versus Nc for alkan-1-ols
in the sulfonium-based FIL [Et3S][Tf2N].
Figure G-64: Plots of versus Nc for
alkylbenzenes in imidazolium-based FILs
comprising [BF4]- ion.
Figure G-65: Plots of versus Nc for
alkylbenzenes in imidazolium-based FILs
comprising [Tf2N]- ion.
Figure G-66: Plots of versus Nc for
alkylbenzenes in imidazolium-based FILs
comprising [TfO]- ion.
Figure G-67: Plots of versus Nc for
alkylbenzenes in imidazolium-based FILs
comprising [EMIM]+ ion.
Figure G-68: Plots of versus Nc for
alkylbenzenes in imidazolium-based FILs
comprising [BMIM]+ ion.
Figure G-69: Plots of versus Nc for
alkylbenzenes in imidazolium-based FILs
comprising [HMIM]+ ion.
Figure G-70: Plots of versus Nc for
alkylbenzenes in imidazolium-based FILs
comprising [MOIM]+ ion.
Figure G-71: Plots of versus Nc for
alkylbenzenes in phosphonium-based FILs
comprising [3C6C14P]+ ion.
Figure G-72: Plots of versus Nc for
alkylbenzenes in ammonium-based FILs comprising
[Tf2N]- ion.
Figure G-73: Plots of versus Nc for
alkylbenzenes in the pyridinium-based FILs [BMPy]
[BF4] and [Epy] [Tf2N].
Figure G-74: Plots of versus Nc for
alkylbenzenes in [BMPyrr] [Tf2N] and [Et3S] [Tf2N].
Figure G-75: Plots of versus Nc for ket-2-ones
in imidazolium-based FILs comprising
[BF4]- ion.
Figure G-76: Plots of versus Nc for ket-2-ones
in imidazolium-based FILs comprising
[Tf2N] - ion.
Figure G-77: Plots of versus Nc for ket-2-ones
in imidazolium-based FILs comprising
[EMIM]+ ion.
Figure G-78: Plots of versus Nc for ket-2-ones
in imidazolium-based FILs comprising
[BMIM]+ ion.
Figure G-79: Plots of versus Nc for ket-2-ones
in imidazolium-based FILs comprising
[HMIM]+ ion.
Figure G-80: Plots of versus Nc for ket-2-ones
in phosphonium-based FILs comprising
[3C6C14P]+ ion.
Figure G-81: Plots of versus Nc for ket-2-ones
in ammonium-based FILs comprising
[Tf2N]- ion.
Figure G-82: Plots of versus Nc for ket-2-ones
in the imidazolium-based FILs [Epy]
[Tf2N] and [BMPy] [BF4].
Figure G-83: Plots of versus Nc for ket-2-ones
in the pyrrolidinium-based FIL [BMPyrr]
[Tf2N].
Figure H-1: Limiting selectivity at 313.15 K of
imidazolium-based fluorinated ionic liquids for the hexane (1)/benzene (2)
system, representing aliphatics/aromatics separation problems.
Figure H-2: Limiting capacity at 313.15 K of
imidazolium-based fluorinated ionic liquids for the hexane (1)/benzene (2)
system, representing aliphatics/aromatics separation problems.
Figure H-3: Limiting selectivity and capacity at
313.15 K of phosphonium-based fluorinated ionic liquids for the hexane
(1)/benzene (2) system, representing aliphatics/aromatics separation
problems.
Figure H-4: Limiting selectivity and capacity at
313.15 K of ammonium-based fluorinated
ionic liquids for the hexane (1)/benzene (2) system, representing
aliphatics/aromatics separation problems.
Figure H-5: Limiting selectivity at 313.15 K
of ammonium-based fluorinated ionic liquids for the methanol (1)/benzene (2)
system, representing alcohols/aromatics separation problems.
Figure H-6: Limiting selectivity and capacity at
313.15 K of phosphonium-based fluorinated ionic liquids for the methanol
(1)/benzene (2) system, representing alcohols/aromatics separation problems.
Figure H-7: Limiting selectivity and capacity at
313.15 K of ammonium-based fluorinated
ionic liquids for the methanol (1)/benzene (2) system,
representing alcohols/aromatics separation problems.
Figure H-8: Limiting selectivity at 313.15 K of
imidazolium-based fluorinated ionic liquids for the methanol (1)/acetone (2)
system, representing alcohols/ketones separation problems.
Figure H-9: Limiting capacity at 313.15 K of
imidazolium-based fluorinated ionic liquids for the methanol (1)/acetone (2)
system, representing alcohols/ketones separation problems.
Figure H-10: Limiting selectivity and capacity
at 313.15 K of phosphonium-based fluorinated
ionic liquids for the methanol
(1)/acetone (2) system, representing
alcohols/ketones separation problems.
Figure H-11: Limiting selectivity and capacity
at 313.15 K of ammonium-based fluorinated
ionic liquids for the methanol
(1)/acetone (2) system, representing
alcohols/ketones separation problems.
Figure H-12: Limiting selectivity at 313.15 K of
imidazolium-based fluorinated ionic liquids
for the n-hexane (1)/hex-1-ene (2) system, representing
paraffins/olefins
separation problems.
Figure H-13: Limiting capacity at 313.15 K of
imidazolium-based fluorinated ionic liquids for the n-hexane (1)/hex-1-ene (2)
system, representing paraffins/olefins separation problems.
Figure H-14: Limiting selectivity and capacity
at 313.15 K of phosphonium-based fluorinated ionic liquids for the n-hexane
(1)/hex-1-ene (2) system, representing paraffins/olefins separation
problems.
Figure H-15: Limiting selectivity and capacity
at 313.15 K of ammonium-based fluorinated
ionic liquids for the n-hexane (1)/hex-1-ene (2) system,
representing paraffins/olefins separation problems.
Figure H-16: Limiting selectivity and capacity
at 313.15 K of pyrrolidinium-based fluorinated ionic liquids for the n-hexane
(1)/hex-1-ene (2) system, representing paraffins/olefins separation
problems.
Figure H-17: Limiting selectivity at 313.15 K of
imidazolium-based fluorinated ionic liquids
for the benzene (1)/butan-2-one (2) system, representing
ketones/aromatics separation problems.
Figure H-18: Limiting capacity at 313.15 K of
imidazolium-based fluorinated ionic liquids for the benzene (1)/butan-2-one (2)
system, representing ketones/aromatics separation problems.
Figure H-19: Limiting selectivity and capacity
at 313.15 K of phosphonium-based fluorinated
ionic liquids for the benzene (1)/butan-2-one (2) system,
representing
ketones/aromatics separation problems.
Figure H-20: Limiting selectivity at 313.15 K of
imidazolium-based fluorinated ionic liquids
for the ethanol (1)/ butan-2-one (2) system, representing
alcohols/ketones separation problems.
Figure H-21: Limiting selectivity and capacity
at 313.15 K of phosphonium-based fluorinated ionic liquids for the ethanol (1)/
butan-2-one (2) system, representing alcohols/ketones separation problems.
Figure I-1: Variation of limiting activity
coefficients of various solutes depending on Nc, the carbon number of the alkyl
chain attached to the methylimidazolium group with [BF4]- anion.
Figure I-2: Variation of limiting activity
coefficients of various solutes depending on Nc, the carbon number of the alkyl
chain attached to the methylimidazolium group with [Tf2N] - anion.
Figure I-3: Variation of limiting activity
coefficients of various solutes depending on Nc, the carbon number of the alkyl
chain attached to the methylimidazolium group with [TfO]- anion.
Figure I-4: Variation of limiting activity
coefficients of n-hexane and hex-1-ene depending on Nc, the carbon number of
the alkyl chain attached to the methylpyrrolidinium group with
[Tf2N]- anion.
Figure I-5: Variation of limiting selectivities
of n-hexane to benzene depending on Nc, the carbon number of the alkyl chain
attached to the methylimidazolium group with common [BF4]-,
[Tf2N]- and [TfO]- anions.
Figure I-6: Variation of limiting selectivity of
n-hexane to hex-1-ene depending on Nc, the carbon number of the alkyl chain
attached to the methylpyrrolidinium or methylimidazolium group with common
[Tf2N]- anion.
LIST OF PHOTOGRAPHS
Photograph 2-1: The helical plate used in the
dilutor cell designed by Kutsuna and Hori (2008). Photograph 4-1:
Gas-Liquid Chromatography equipment.
Photograph 4-2: Set-up of the inert gas
stripping apparatus.
Photograph 4-3: The dilutor cell.
LIST OF TABLES
Table 2-1: Potential applications of ionic
liquids in the chemical industry (Plechkova and Seddon 2008).
Table 2-2: Ionic liquids versus molecular
solvents (Plechkova and Seddon, 2008).
Table 2-3: Literature selectivity and capacity
data at infinite dilution for selected ionic
liquids, NMP and sulfolane for different separation problems at
T = 313.15 K. Table 2-4: Advantages and disadvantages
of the Gas Liquid Chromatographic method. Table 2-5:
Advantages and disadvantages of the inert gas stripping method.
Table 4-1: GC specification and set-up.
Table 5-1: Infinite dilution activity
coefficients of selected organic solutes in n-hexadecane.
Table 5-2: Activity coefficients at infinite
dilution of organic solutes
intrihexyltetradecylphosphonium bis-(trifluoromethylsulfonyl)
imide with solvent column loading n3 = 1.577 mmol (29.5 %) at T
= (313.15, 333.15, 353.15 and 373.15) K.
Table 5-3: Activity coefficients at infinite
dilution of organic solutes in
trihexyltetradecylphosphonium bis (trifluoromethylsulfonyl) imide
with solvent column loading n3 =2.236 mmol (31.7 %) at T =
(313.15, 333.15, 353.15 and 373.15) K.
Table 5-4: Average activity coefficients at
infinite dilution of organic solutes in
trihexyltetradecylphosphonium bis-(trifluoromethylsulfonyl) imide
at T = (313.15, 333.15, 353.15 and 373.15) K.
Table 5-5: Partial molar excess enthalpies at
infinite dilution for organic solutes in the
ionic liquid trihexyltetradecylphosphonium
bis-(trifluoromethylsulfonyl) imide, calculated from the Gibbs Helmholtz
equation.
Table 5-6: Activity coefficients at infinite
dilution of organic solutes in
trihexyltetradecylphosphonium tetrafluoroborate with solvent
column loading
n3 = 2.395 mmol (25.09 %) at T = (313.15,
333.15, 353.15 and 373.15) K.
Table 5-7: Activity coefficients at infinite
dilution of organic solutes in
trihexyltetradecylphosphonium tetrafluoroborate with solvent
column loading
n3 = 2.236 mmol (30.97 %) at T = (313.15,
333.15, 353.15 and 373.15) K.
Table 5-8: Average activity coefficients at
infinite dilution of organic solutes in
trihexyltetradecylphosphonium tetrafluoroborate at T =
(313.15, 333.15, 353.15 and 373.15) K.
Table 5-9: Partial molar excess enthalpies at
infinite dilution for organic solutes in the
ionic liquid trihexyltetradecylphosphonium tetrafluoroborate,
calculated from the Gibbs-Helmholtz equation.
Table 5-10: Activity coefficients at infinite
dilution of organic solutes in
trihexyltetradecylphosphonium hexafluorophosphate with
n3 = 1.615 mmol (25.1 %) at T = (313.15, 333.15, 353.15 and
363.15) K.
Table 5-11: Activity coefficients at infinite
dilution of organic solutes in
trihexyltetradecylphosphonium hexafluorophosphate with
n3 = 2.659 mmol (29.4 %) at T = (313.15, 333.15, 353.15 and
363.15) K.
Table 5-12: Average activity coefficients at
infinite dilution of organic solutes in
trihexyltetradecylphosphonium hexafluorophosphate at T =
(313.15, 333.15, 353.15 and 363.15) K.
Table 5-13: Partial molar excess enthalpies at
infinite dilution for organic solutes in the
ionic liquid trihexyltetradecylphosphonium hexafluorophosphate
calculated from the Gibbs-equation.
Table 5-14: Activity coefficients at infinite
dilution of organic solutes in
methyltrioctylammonium bis-(trifluoromethylsulfonyl) imide with
n3 = 1.77 mmol (25.33 %) at T = (303.15, 313.15 and 323.15)
K.
Table 5-15: Activity coefficients at infinite
dilution of organic solutes in
methyltrioctylammonium bis-(trifluoromethylsulfonyl) imide with
n3 = 2.044 mmol (29.63 %) at T = (303.15, 313.15 and 323.15)
K.
Table 5-16: Average activity coefficients at
infinite dilution of organic solutes in
methyltrioctylammonium bis-(trifluoromethylsulfonyl) imide at
T = (303.15, 313.15 and 323.15) K.
Table 5-17: Excess molar enthalpies at infinite
dilution of organic solutes in the ionic
liquid methyltrioctylammonium bis-(trifluoromethylsulfonyl)
imide, calculated using the Gibbs-Helmholtz equation.
Table 5-18: Activity coefficients at infinite
dilution of organic solutes in 1-butyl-3-
methylimidazolium hexafluoroantimonate with n3 = 3.312
mmol (26.90 %) at T = (313.15, 323.15 and 333.15) K.
Table 5-19: Activity coefficients at infinite
dilution of organic solutes in 1-butyl-3-
methylimidazolium hexafluoroantimonate with n3 = 4.578
mmol (31.98 %) at T = (313.15, 323.15 and 333.15) K.
Table 5-20: Average activity coefficients at
infinite dilution of organic solutes in 1-butyl-3-
methylimidazolium hexafluoroantimonate at T = (313.15,
323.15 and 333.15) K. Table 5-21: Excess molar enthalpies at
infinite dilution of organic solutes in the ionic
liquid 1-butyl-3-methylimidazolium hexafluoroantimonate
calculated using the Gibbs-Helmholtz equation.
Table 5-22: Activity coefficients at infinite
dilution of organic solutes in 1-ethyl-3
methylimidazolium trifluoromethanesulfonate with n3 =
8.01 mmol (29.3 %) at T = (313.15, 323.15 and 333.15) K.
Table 5-23: Activity coefficients at infinite
dilution of organic solutes in 1-ethyl-3
methylimidazolium trifluoromethanesulfonate with n3 =
6.23 mmol (32.88 %) at T = (313.15, 323.15 and 333.15) K.
Table 5-24: Average activity coefficients at
infinite dilution of organic solutes in 1-ethyl-3
methylimidazolium trifluoromethanesulfonate at T =
(313.15, 323.15 and 333.15) K. Table 5-25: Excess molar
enthalpies at infinite dilution of organic solutes for the ionic
liquid 1-ethyl-3-methylimidazolium trifluoromethanesulfonate,
calculated using the Gibbs-Helmholtz equation.
Table 5-26: Activity coefficients at infinite
dilution of organic solutes in 1-methyl-3
octylimidazolium hexafluorophosphate with n3 = 6.69 mmol
(28.55 %) at T = 313.15, 323.15 and 333.15 K.
Table 5-27: Activity coefficients at infinite
dilution of organic solutes in 1-methyl-3-
octylimidazolium hexafluorophosphate with n3 = 5.135
mmol (33.26 %) at T = 313.15, 323.15 and 333.15 K.
Table 5-28: Average activity coefficients at
infinite dilution of organic solutes in 1-methyl-
3-octylimidazolium hexafluorophosphate at T = (313.15,
323.15 and 333.15) K. Table 5-29: Excess molar enthalpies at
infinite dilution of organic solutes for the ionic
liquid 1-methyl-3-octylimidazolium hexafluorophosphate,
calculated using the Gibbs-Helmholtz equation.
Table 5-30: Experimental infinite dilution
activity coefficients of n-hexane as well as Cyclohexane in NMP obtained by the
dilutor method and comparison with literature data taken from Gruber et al.
(1999).
Table 5-31: Experimental infinite dilution
activity coefficients obtained by the inert gas stripping method (IGST) for six
different organic solutes in the ionic liquid
Trihexyltetradecylphosphonium bis- (trifluoromethylsulfonyl)
imide, and comparison with similar data compiled with the help of the GC
method.
Table 5-32: Selectivity and Capacity at infinite
dilution at 313.15 K of the ionic liquids investigated in this work for
different separation problems and comparison with industrial separation agents
as well as other ionic liquids.
Table 6-1: Comparison of experimental IDACs in
the ionic liquid [3C6C14P] [Tf2N] at 313.15 K
from this work to available literature data.
Table 6-2: Comparison of experimental IDACs in
the ionic liquid [3C6C14P] [BF4] at 313.15 K
from this work to available literature data.
Table 6-3: Uncertainties on experimental
parameters for the GC method.
Table 6-4: Uncertainties on experimental
parameters for the dilutor method.
Table 6-5: Overall uncertainties on experimental
data and derived quantities.
Table 6-6: List of fluorinated ionic liquids
investigated in the literature and assigned numbers.
Table A-1: Literature data for in
imidazolium-based fluorinated ionic liquids. Table A-2:
literature data for in phosphonium-based fluorinated ionic liquids.
Table A-3: Literature data for in pyridinium and
pyrrolidinium-based fluorinated ionic
liquids.
Table A-4: Literature data for in ammonium and
sulfonium-based fluorinated ionic liquids.
Table A-5: Literature data for in
non-fluorinated ionic liquids.
Table C-1: Origin and Stated purity of solutes
and solvents.
Table C-2: Densities of solvents after
purification at different temperatures-Accuracy: #177; 0.4 % Table C-3:
Refractive indices of purified solvents at 293.15 K.
Table D-1: Saturation fugacity coefficients of
selected solutes at different temperatures. Table D-2:
Critical volumes, critical temperatures, and ionization energies,
IC of the
solutes and the carrier gas used in the calculation of the virial
coefficients. Table F-1: Infinite dilution selectivity and
capacity data at 313.15 K for FILs and selected industrial solvents
investigated in the literature as well as in this work.
NOMENCLATURE
Symbols
-- Solute peak area detected by gas chromatography (mV.min) --
Slope (min-1)
B -- Second virial coefficient (cm3
mol-1)
-- Concentration (mol cm-3)
-- Pure carrier gas flow rate (cm3min-1)
-- Total gas flow at still exit
(cm3min-1)
-- Solvent gas flow in the stream entering the still
(cm3min-1) -- Diffusion constant of solute in
solvent(cm2 s-1)
-- Diameter of bubbles (cm)
-- Fugacity for pure species
-- Fugacity for species in solution
-- Gibbs energy
-- Gravitational acceleration (cm2s-1)
-- Henry`s law constant --Enthalpy (J)
-- Path length of bubbles in solution (cm)
-- Poynting correction
-- Partitioning coefficient -- Capacity
-- Correction factors
-- Mass transfer coefficient in the liquid
(mol.s-1.cm2)
-- Molar mass (g.mol-1) -- Mass (g)
-- Amount of solvent in the still
-- Amount of solute in the still
-- Pressure (kPa)
or - vapour pressure (kPa)
-- Partial pressure (kPa)
-- Gas constant (J.mol-1 K-1) -- Radius of
bubbles (cm)
-- Selectivity
-- Absolute temperature (K)
-- Boiling point temperature (K)
-- Volume (cm3)
-- Volume of the vapour space in the still (cm3)
-- Mole fraction in the liquid phase -- Mole fraction in the
vapour phase
-- Compressibility factor
Greek letters
-- Activity coefficient, species in solution
-- Fugacity coefficient -- Density (g.cm-3)
-- Separation factor
-- Calibration detector constant
-- Ratio of mass transfer in the cell to mass transfer to reach
equilibrium taking into account liquid phase resistance only
-- Same as taking into account gas phase diffusion only
-- Limiting speed of bubbles in solution (cm.s-1)
-- Corrected activity coefficient at infinite dilution
-- Kinematic viscosity (cSt) -- Dynamic viscosity (cP)
-- Acentric factor
Subscripts
1-- Solute
2-- Carrier gas
3-- Solvent.
CG-- Carrier gas
-- Properties related to pure component i -- Interaction
properties
-- Critical Properties -- Reduced Properties -- Liquid
phase
o -- Initial value
f -- Final value
--Flowmeter --Gas phase
V --Vapour phase
Superscripts
--Ideal solution --Liquid phase --Vapor phase -- Infinite
dilution
-- Initial value --At saturation
-- Excess properties
-- Property in vapour phase
-- Property in liquid phase
-- Experimentally determined
-- Literature value
ABBREVIATIONS
CG -- Carrier gas
IDAC -- Infinite dilution activity coefficient IGST -- Inert Gas
Stripping Technique GLC -- Gas-Liquid Chromatography
COSMO-RS -- Conductor-like Screening Model for Real Solvents
DCT -- Double Cell Technique
SCT -- Single Cell Technique
GC -- Gas Chromatography
VLE -- Vapour Liquid Equilibrium LLE --Liquid Liquid Equilibrium
RD-- Relative Deviation
GCMs -- Group Contribution Methods FILs - Fluorinated Ionic
Liquids
Cations
[EMIM]+-- 1-ethyl-3-methylimidazolium
[HMIM]+-- 1-hexyl-3-methylimidazolium [MOIM]+--
1-methyl-3-octylimidazolium [BMIM]+-- 1-butyl-3-methylimidazolium
[3C4C1P]+-- Tributylmethylphosphonium [3C6C14P]+--
Trihexyltetradecylphosphonium [Py]-- Pyridinium
[Epy]-- Ethylpyridinium
[BMPy]+-- n-butyl-4-methylpyridinium
[MOPyrr]+-- 1-octyl-1-methyl-pyrrolidinium [BMPyrr]+--
1-butyl-1-methyl-pyrrolidinium [HMPyrr]+--
1-hexyl-1-methyl-pyrrolidinium [Et3S]+-- Triethylsulfonium
[C13C8N]+-- Methyltrioctylammonium
[3C1C4N]+-- Trimethylbutylammonium [C16MIM]+--
1-hexadecyl-3-methylimidazolium [CpMIM]+--
1-butyronitrile-3-methylimidazolium [EDMIM]+--
1-ethyl-3-dimethylimidazolium
[CpMMIM]+-- 1-butyronitrile-2,
3-dimethylimidazolium
[PDMIM]+-- 1-propyl-3-dimethylimidazolium.
[MMIM]+--1-methyl-3-methylimidazolium.
[PBA-MIM]+-- 1-propyl boronic acid-3-methylimidazolium
[PBA-OMIM]+-- 1-propyl boronic acid-3-octylimidazolium
[PBA-C10MIM]+-- 1-propyl boronic acid-3-decylimidazolium
[PBA-C12MIM]+-- 1-propyl boronic
acid-3-dodecylimidazolium [PropOMIM]+--
1-propenyl-3-methyloctylimidazolium
[PropC10MIM]+--1-propenyl-3-decylimidazolium
[PropC12MIM]+-- 1-propenyl-3-dodecylimidazolium
[H-O-MIM]+--1-hexyloxymethyl-3-methylimidazolium
[DH-O-MIM]+--1, 3-dihexyloxymethylimidazolium
Anions
[SCN]--- Thiocyanide
[Tf2N] --- Bis (trifluoromethylsulfonyl) Imide
[BF4]--- Tetrafluoroborate [TOS]---
Tosylate
[MeSO4]--- Methyl sulfate
[(C2F5)3PF3]--- Tris (pentafluoroethyl)
trifluorophosphate
[TFA]--- Trifluoroacetate [TfO]---
Trifluoromethylsulfonate
[SbF6]--- Hexafluoroantimonate [PF6]---
Hexafluorophosphate
[MDEGSO4]--- Diethyleneglycolmonoethylethersulfate
[Me2PO4]--- Dimethylphosphate
[C1OC2SO4]--- Methoxyethylsulfate
[FeCl4]--- Tetrachloridoferrate (III)
[Et-SO4]--- Ethylsulfate [Oc-SO4]---
Octylsulfate [N (CN) 2]- -- Dicyanamide
[(C8 H17)2PO2]--- Dimethylpentylphosphinate
[n-C18H35OO]--- Stearate [n-C16H33OO]---
Palmitate
CHAPTER ONE: INTRODUCTION
Organic molecular solvents are used in different industrial
chemical processes with satisfying technical results. However, most of these
chemicals represent a risk to human health and are ecologically unfriendly due
to their volatility. A good illustration of how destructive modern chemical
products can be is given by this non-exhaustive list of disasters (Moutiers et
al., 2003):
· Toxic cloud over Seveso in Italy, 1976;
· 3500 lives claimed when in 1984, the Bhopal based
pesticide factory released toxic emissions in India;
· The devastating explosion of the AZF chemical plant in
the French city of Toulouse in 2001.
Such accidents contribute to the increased awareness of
environmental and health threats resulting from the large number of industrial
processes. The development of less-polluting solvents and safe processes is
nowadays a high priority on the agenda for green chemistry?. There is a
pressing need to rethink the design of unsafe chemical processes so that
younger generations inherit a healthy and safer environment.
In recent years, ionic liquids, salts that are liquids at low
temperatures (Plechkova and Seddon, 2008) received the most attention as
alternatives to volatile organic solvents in reactive chemistry, as well as,
separation processes due to their negligible vapour pressure and wide liquid
range.
Researchers at the Thermodynamics Research Unit, in the School
of Chemical Engineering,
University of KwaZulu-Natal in South Africa along
with other academic institutions carried out
systematic measurements of infinite dilution activity
coefficients ( ) for a wide range of
organic solutes in various ionic liquids in order to assess
their effectiveness as extracting solvents.
Though encouraging results were achieved, there is still an
obvious appeal for more investigations in order to:
· Assess the solvent potential of the large number of ionic
liquids that have not yet been investigated;
· Correlate the ionic liquid`s structure and its ability to
separate particular mixtures.
The present work has been conducted to increase the
understanding of these two phenomena. Moreover, South Africa has nearly a third
of the world`s fluorspar (CaF2) reserves (Meshri, 2000) and in the context of
the Fluorochemical Expansion Initiative recently launched by its government,
there are no better candidates for investigation than fluorinated ionic
liquids. Thus this work is a focus on the measurement of infinite dilution
activity coefficients in Fluorinated Ionic Liquids (FILs), bearing in mind
their performance in separation processes.
An inert gas stripping apparatus for measurement of infinite
dilution activity coefficients, (IDACs), for systems involving ionic liquids
was constructed. The objective of this work was to answer the following
questions:
· What performance can be expected from FILs as extracting
solvents in extractive distillation and liquid-liquid extraction?
· How is the selectivity towards various systems affected
by the anion-cation combination found in the structure of FILs?
· Can a reliable dilutor technique apparatus be locally
designed, constructed and commissioned for use with small amounts of ionic
liquids as solvent?
To address the above questions the methodological approach in
this work consisted of:
· Generating new experimental activity coefficient data for
organic solutes in selected fluorinated ionic liquids;
· Using experimental IDACs to determine limiting
selectivity and capacity values for all FILs newly investigated, as well as,
data reported in the literature;
· Analyzing the trends of variation of IDACs to gain
insight into the influence of structure on limiting selectivity and
capacity;
· Reviewing advances recorded in the use of the inert gas
stripping technique;
· Constructing an apparatus similar to one developed
previously in the Thermodynamics Research Unit (George, 2008) and reported in
the open literature;
· Assessing its reliability in measuring infinite
dilution activity coefficients by comparison of IDAC results obtained for the
same systems using both Gas-Liquid Chromatography (GLC) and the Inert Gas
Stripping Technique (IGST).
All experimental procedures have been conducted in the
Thermodynamics Research Unit laboratories, in the School of Chemical
Engineering, University of KwaZulu-Natal. All appropriate experimental
equipment and necessary facilities were available to undertake the research
work. Experimentally investigated ionic liquids are:
· Trihexyltetradecylphosphonium tetrafluoroborate,
[3C6C14P] [BF4]
· Trihexyltetradecylphosphonium
bis(trifluoromethylsulfonyl) imide, [3C6C14P] [Tf2N]
· Trihexyltetradecylphosphonium hexafluorophosphate,
[3C6C14P] [PF6]
· Methyltrioctylammonium bis (trifluoromethylsulfonyl)
imide, [C13C8N] [Tf2N]
· 1-ethyl-3-methylimidazolium trifluoromethanesulfonate,
[EMIM] [TfO]
· 1-butyl-3-methylimidazolium hexafluoroantimonate, [BMIM]
[SbF6]
· 1-methyl-3-octylimidazolium hexafluorophosphate.
[MOIM][PF6]
Data have been generated at temperatures ranging from (313.15
to 373.15) K whereas solutes were selected among n-alkanes, alk-1-enes,
alk-1-ynes, cycloalkanes, alkan-1-ols, alkylbenzenes and ket-2-ones. Separation
problems are discussed through the n-hexane /benzene, methanol/benzene,
methanol/acetone, n-hexane/hex-1-ene, ethanol/butan-2-one and
benzene/butan-2-one systems.
During this study, contributions were made to publications by
Olivier et al. (2010a, b and c), as well as, Gwala et al. (2010). This
consisted of producing part of the published data i.e. infinite dilution
activity coefficients in [EMIM] [TfO], [MOIM][PF6], [BMIM] [SbF6] and [C13C8N]
[Tf2N]. Full results obtained by these authors are used in this dissertation
with their authorization.
This thesis is organized as follows. After this brief
introduction (as chapter one), previous scientific work related to ionic
liquids, generalities on activity coefficient at infinite dilution and recent
advances in the design of inert gas stripping equipment are reviewed in chapter
two. The third chapter provides details about the theory behind GLC and the
IGST, as well as, equations used to compute infinite dilution activity
coefficients. Chapter four is a description of the materials, the experimental
set up and the experimental procedure used in this work. Infinite dilution
activity coefficient experimental data are presented in chapter five. Results
are discussed in the sixth chapter. Lastly, chapter seven is devoted to the
conclusion and the recommendations for future investigations.
CHAPTER TWO: LITERATURE REVIEW
Chapter overview
In order to assist in determining the significance of previous
similar works and understand the impact of the present study, this chapter
reviews the following:
· Ionic liquids in the chemical industry;
· Generalities on activity coefficient at infinite
dilution;
· Recent advances in the design of inert gas stripping
equipments.
Experimental and predictive methods for infinite dilution
activity coefficient determination are
outlined. Only the two experimental
techniques used in this work, gas-liquid chromatography
and the inert gas
stripping method are discussed. A closer look is taken at attempts made in
the
open literature to predict in ionic liquids. The most promising
predictive methods for
systems involving ionic liquids are discussed in terms of
accuracy and reliability. Since the objective of this study involves
understanding the effect of fluorinated ionic liquids` structure on their
ability to separate various mixtures and the construction of a dilutor cell,
the results obtained from previous scientific investigation in these regards
are reviewed. A treatment of ionic liquids in general and the fluorinated ones,
in particular, is provided.
2.1. Ionic liquids
2.1.1. Definition and structure
Ionic liquids are materials that are solely composed of
cations and anions, and melt at or below 100 oC (Endres and El
Abedin 2006). The most commonly found structures of ionic liquids are given in
figure 2-1.
2.1.2. History
In 1914, Paul Walden (1914) reported the physical properties
of the first useful ionic liquid, ethylammonium nitrate, which had a melting
point of 12 oC. It was synthesized by the reaction of concentrated
nitric acid with ethylamine. Thereafter, Hurley and Weir (1951) stated the
possibility of preparing room temperature ionic liquids by simply mixing and
warming 1- ethylpyridinium in the presence of aluminum chloride; Chum et al.
(1975), Robinson et al. (1979), Wilkes et al. (1982), Seddon et al. (1983) and
Appleby et al. (1986) directed extensive research works towards new aluminum
chloride-based ionic liquids in 1970s and 1980s. These ionic liquids did not
find many practical applications due to their hydroscopic nature which required
both preparation and handling to take place in an inert gas atmosphere. In
1992, water
and air stable 1-ethyl-3-imidazolium-based ionic liquids were
reported by Cooper and O`Sullivan (1992), as well as Zaworotko and Wilkes
(1992) in separate works. They developed imidazolium-based ionic liquids which
consisted of alternative anions: acetate ([CH3CO2]-), nitrite
([NO2]-), tetrafluoroborate ([BF4]-), trifluoromethane
sulfonate ([CF3SO3]-) and methylsulfate, ([CH3SO4]-).
Since then, new anions were incorporated in the structure of ionic liquids:
hexafluorophosphate ([PF6]-), biscyanamide ([N (CN)2]2-),
trifluoroacetate ([C2F3O2]-), sulfate ([SO4]2-),
hydrogensulfate ([HSO4]-), alkylsulfate ([R-SO4]-) ,
nitrate,([NO3]-). Contrary to chloroaluminates salts, these ionic
liquids can be prepared on the bench. However, they can absorb water from the
atmosphere, and they do not react with water. The development of more
hydrophobic ionic liquids started in the second half of the 1990s through the
work of Bonhôte et al. (1996). They reported the synthesis and
characterization of ionic liquids containing hydrophobic anions such as
trifluoromethane sulfonate ([CF3SO3]-), triflate
([OTf]-), tris (trifluoromethylsulfonyl) methanide {[C
(CF3SO2)3]-} and bis (trifluoromethylsulfonyl) imide. As scientific
research chemicals, ionic liquids were commercially available in 1999 (Letcher
2007). Nowadays, around 1018 ionic liquids have been predicted
(Endres and El Abedin 2006) and could be synthesized by combining different
ions like the ones shown in figure 2-1.
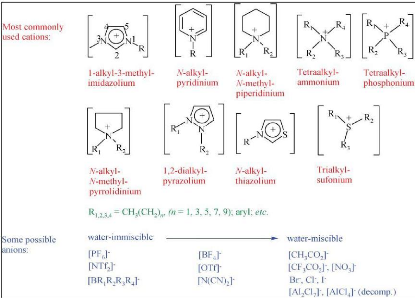
Figure 2-1: Structure of ionic liquids
(Plechkova and Seddon 2008)
2.1.3. Properties of ionic liquids
It is because of their advantageous properties that ionic
liquids attracted much attention from the scientific and industrial spheres.
The most interesting properties of these compounds are listed below:
a) Extremely low vapour pressure: they are eco-friendly. (Welton
1999, and Wasserscheid and Keim 2000);
b) Low or reduced flammability hazards (Fox et al. 2008);
c) Tunable properties (Rogers and Seddon 2003);
d) Excellent solvation properties for a variety of organic and
inorganic compounds (Rogers and Seddon 2003);
e) High electric conductivities (Trulove and Mantz 2003);
f) High thermal stability (Dupont 2004);
g) Wide liquid range (Huddleston et al. 2001);
h) Wide electrochemical window (Shröder et al. 2000).
Though ionic liquids are generally known as safe and benign
compounds, some of them are volatile (Earl et al. 2006) and others are
flammable (Smiglak et al. 2006).
2.1.4. Potential applications of ionic liquids in the
chemical industry
The properties of a given ionic liquid are determined by the
nature of its ions (Rogers and Seddon 2003). Any desired set of properties can
be imparted to an ionic liquid by a proper selection of the anion-cation pair.
This tunability of ionic liquids` properties allows a very wide range of
applications as shown in the table below.
Table 2-1: Potential applications of ionic
liquids in the chemical industry.
(Plechkova and Seddon 2008)
Chemical engineering Electrochemistry
Biochemistry
Mass separating agents Electrolyte batteries Biomass
processing
Catalyst Metal plating Drug delivery
Coatings Solar panels Personal care
Lubricants Fuel cells Biocides
Plasticizers Electro-optics. Embalming
Dispersing agents
2.1.5. Commercial applications of ionic
liquids
Many companies have recently invested considerably in the
development of ionic liquids-based commercial processes. Examples of publicly
reported achievements regarding industrial uses of ionic liquids, as reviewed
by Plechkova and Seddon (2008) are briefly discussed in this section.
2.1.5.1. BASIL Process
The Biphasic Acid Scavenging utilizing Ionic Liquids (BASIL)
process is the most popular industrial application of ILs. It has been used by
the German company BASF in the production of alkophenyl phosphines.
1-methylimidazolium chloride is used to scavenge the acid formed during the
reaction. Results are better than in the original process where triethylamine
was used.
2.1.5.2. Isobutene alkylation
Petro China performs isobutene alkylation with an ionic liquid.
This is the largest commercial use of ionic liquids.
2.1.5.3. DIMERSOL Process
In this process, IFP (Institut Français du Pétrole)
utilizes chloroaluminate (III) ionic liquids for alkenes dimerisation.
2.1.5.4. Other commercial uses
The following success stories have also been reported:
a) Pharmaceutical intermediate production by Central glass Co,
Ltd in Japan;
b) 2, 5-dihydrofuran production by Eastman Chemical Company from
1996 to 2004;
c) Production of lithium ion rechargeable battery by Pionics in
Japan.
2.1.5.5. Advanced projects
Besides the very small number of established industrial
processes, one can list many promising projects, some at pilot plant stage. The
most known ones include:
a) Metathesis and olefin trimerisation by SASOL in South
Africa;
b) Azeotrope-breaking for water -ethanol and water
-tetrahydrofuran with reduced; costs of solvent recovery by BASF;
c) Cellulose dissolution by BASF;
d) Aluminum plating by BASF;
e) Phosgene replacement by an ionic liquid in 1,
4-dichlorobutane production, achieved by BASF.
2.1.6. Use of ionic liquids as solvents in separation
processes 2.1.6.1. Ionic liquids versus molecular solvents
Due to properties stated in section 2.1.3, ionic liquids
attracted much attention in recent years as potential replacements to
conventional molecular organic solvents.
With hundreds of thousands of ion combinations, it is possible
to design an ionic liquid with the desired properties to suit a particular
application by a proper anion and cation selection. One can adjust and tune
ionic liquids to provide a specific property, including density, melting point,
viscosity, hydrophobicity, miscibility and selectivity in separation processes.
The tunability of ionic liquids provides flexibility for both reaction and
combined reaction/separation schemes. And, since thermodynamics and kinetics of
reactions taking place in ionic liquids differ from those in conventional
solvents, it is clear that ionic liquids open new opportunities for both
separation and combined reaction/separation processes. In ionic liquids, ions
are held together by wide range interactions such as high coulombic forces and
in some cases, hydrogen bondings resulting in near-zero vapour pressure and
therefore no emission to the atmosphere. This nonvolatile nature of ionic
liquids allows the design and development of new environmentally-friendly
separation processes. Another benefit is of course the reduced losses of
solvents used in such processes. In addition, ionic liquids being generally non
flammable, they should lead to safety benefits compared to molecular solvents
commonly used in chemical engineering nowadays. Table 2-2 highlights more
advantages of ionic liquids over molecular solvents that have enhanced their
popularity.
Table 2-2: Ionic liquids versus molecular
solvents (Plechkova and Seddon 2008).
Property Organic solvents Ionic
liquids
Number of solvents 1000 1 000 000
Applicability Single function Multifunction
Catalytic ability Rare Common and tuneable
Chirality Rare Common and tuneable
Vapour pressure Obeys the Clausius-Clapeyron Negligible vapour
pressure
equation under normal conditions
Flammability Usually flammable Usually nonflammable
Solvation Weakly solvating Strongly solvating
Polarity Conventional polarity concepts Polarity concept
questionable
Tuneability Limited range of solvents Virtually unlimited range
means
available ==designer solvents«
Cost Normally cheap Typically between 2 and 100
times the cost of organic solvents
Recyclability Green imperative Economic imperative
Viscosity/ Cp 0.2 - 100 22- 40 000
Density/g cm3 0.6- 1.7 0.8- 3.3
Refractive index 1.3- 1.6 1.5- 2.2
2.1.6.2. Recent scientific investigations
Investigations on the suitability of ionic liquids as
separation solvents are reviewed by Heintz (2005). In the last four years, the
list of ionic liquids investigated is in steady progression. A large number of
data have been experimentally generated to deal with various separation
problems (David 2004). Some recent examples are studies on the basis of
experimental VLE (Zhao et al. 2006, and Zhang et al. 2009) and LLE (Deenadayalu
et al. 2006b and Meindersma et al. 2006) data which are available in the
literature. All available experimental infinite dilution activity coefficient
data for organic solutes in fluorinated and non-fluorinated ionic liquids can
be found in publications listed in appendix A. The chemical quantum approach
has also been used in the open literature to deal with problems such as:
a) Olefins-paraffins separation (Lei et al. 2007);
b) Diesel desulphurization (Kumar and Banerjee 2009);
c) Alkanols/ olefins separation (Banerjee 2008).
Patents have been granted for these processes involving ionic
liquids as mass separation agents for organic liquid mixtures:
a) Separation of ionic compounds (Roetteger et al. 2003);
b) Separation of close-boiling or azeotropic mixtures (Arlt et
al. 2002);
c) Separation of dienes from olefins (Boudreau et al. 2002);
d) Removal of polarizable impurities from hydrocarbons and
hydrocarbon mixtures (Wasserscheid et al. 2002);
e) Mercaptans removal from hydrocarbon streams (O` Rear et al.
2001);
f) Extraction of aromatic hydrocarbons from aromatic petroleum
streams (Gmehling and Krummen 2001).
All these research works established that ionic liquids are
potentially good alternatives to currently used organic molecular solvents. As
illustrated by table 2-3, for the separation of aromatic from aliphatic
compounds, represented by the n-hexane/benzene and cyclohexane/ benzene
systems, many ionic liquids can lead to higher limiting selectivities, and
sometimes higher capacities than commonly used molecular solvents such as
sulfolane and NMP. Regarding the influence of structure on extraction capacity,
it is worthy to mention that only imidazolium and ammonium-based ionic liquids
have been widely investigated with respect to aromatic/aliphatic compounds
separation problems. It has been found that selectivity for aromatic
hydrocarbons/aliphatic hydrocarbons increases with decreasing length of the
alkyl chain on the cation (Letcher et al. 2009). Favorable anions are those
with small volume and sterical shielding around the charge centre. An
investigation on olefins/ paraffins separation problem revealed the same trends
(Lei et al. 2006, 2007b). More thermodynamic data is needed
for a better understanding of the effect of structure on the
extracting capacities for other types of ionic liquids and separation
problems.
Table 2-3: Literature selectivity and capacity
data at infinite dilution of selected ionic
liquids, NMP and sulfolane for different separation problems at
T = 313.15 K.
Reference
Laskowska (2009)
Marciniak (2008b)
Foco et al. (2006)
Heintz et al. (2001)
Kato and Gmehling
(2004)
Letcher et al. (2005a)
Krummen et al. (2002)
Kato and Gmehling
(2004)
and
Marciniak (2007)
Sumartschenkowa et al.
(2006)
Marciniak (2009)
Möllmann et al. (1997) Krummen et al. (2004) Kato and
Gmehling (2005b)
Kato and Gmehling (2004)
Krummen et al. (2004) Krummen et al. (2004) Kato and Gmehling
(2004)
Letcher and Reddy
(2007)
Letcher et al. (2009) David et al. (2003)
Deenadayalu et al.
(2006)
Letcher et al. (2005b) Letcher et al. (2008)
Solvent
|
for for
Hexane/Benzene Cyclohex. /Benz.
|
|
[BMIM][SCN]
|
84.55
|
23.90
|
0.46
|
|
[EMIM][SCN]
|
78.41
|
28.37
|
0.29
|
|
[EMIM][BF4]
|
45.87
|
20.06
|
0.41
|
|
[BMPy][BF4]
|
36.88
|
-
|
0.61
|
|
[MMIM][CH3OC2H4SO4]
|
-
|
25.45
|
0.23
|
|
[BMIM][MDEGSO4]
|
33.66
|
15.35
|
0.50
|
|
[MMIM][BTI]
|
27.26
|
-
|
0.74
|
|
[MMIM][(CH3)2PO4]
|
-
|
13.13
|
0.28
|
|
[BMIM][TFA]
|
27.00
|
12.96
|
0.36
|
|
[EMIM][Et-SO4]
|
25.77
|
11.11
|
0.34
|
|
[Et3S][BTI]
|
25.10
|
12.76
|
0.90
|
|
Sulfolane
|
18.20
|
9.84
|
0.43
|
|
NMP+6 %(w/w)H2O
|
16.08
|
9.07
|
0.52
|
|
[BMPyrr][BTI]
|
15.47
|
-
|
1.16
|
|
[MMIM][Me-SO4]
|
14.33
|
17.55
|
0.15
|
|
NMP + 3 %(w/w)H2O
|
13.79
|
10.00
|
0.71
|
|
NMP
|
11.49
|
7.72
|
0.99
|
|
[Py][[C2H5OC2H4SO4]
|
11.18
|
8.47
|
0.26
|
|
[3C4C1P][Me-SO4]
|
9.90
|
5.50
|
1.00
|
|
[BMPyr][TOS]
|
9.65
|
5.54
|
0.25
|
|
[MOIM][Cl]
|
8.71
|
5.40
|
0.56
|
|
[MOIM][MDEGSO4]
|
8.69
|
4.99
|
0.73
|
|
[BMIM][Oc-SO4]
|
5.27
|
3.49
|
0.69
|
|
[3C6C14P][(C8H17)2PO2]
|
1.52
|
1.125
|
2.08
|
2.1.7. Barriers to the commercial use of ionic
liquids
In December 2002, Chemical vision 2020 Technology partnership
(Ford et al. 2004), an american industry-led organization appointed a task
force to reflect on the barriers to the widespread use of ionic liquids and how
to overcome them. Two years later, the vision 2020 ionic liquid task force
(Ford et al. 2004) identified six barriers to the widespread use of ionic
liquids in the chemical industry, including separation processes:
a) Lack of performance data under industrial conditions;
b) Lack of environmental and safety data for many ionic
liquids;
c) Lack of economic benefit analyses;
d) Lack of fundamental understanding of compositional structure
versus performance;
e) Ionic liquid manufacturing cost and scale-up;
f) Institutional issues such intellectual property and
communication between researchers.
Seven years later, these obstacles still stand on the
promising way leading to a wide scale incorporation of ionic liquids in
chemical engineering processes. The present study falls under the fourth
barrier.
2.1.8. Fluorinated ionic liquids (FILs)
For apparently unknown reasons, Fluoroanions and fluorocations
ionic liquids are often respectively referred to as fluorous and fluorinated
ionic liquids (Heitzman et al. 2006). Interesting reviews on fluorinated ionic
liquids discuss specific features of this subset of ionic liquids (Xue et al.
2006 and Hagiwara and Ito 2000). Ionic liquids with fluorine-containing anions
are the most commercially available and the most investigated as potential
separation agents. Commonly found anions include [BF4]-, [PF6] - ,
[CF3SO3]-, [(CF3SO2)2N]-, [CF3CO2] - and
[SbF6]-. Fluorine-containing ionic liquids are of great interest for
South Africa. Its government launched recently the Fluorochemical Expansion
Initiative aimed at researching and developing South Africa`s fluorinated
products. The move is expected to put an end to the paradox pointed out by
Prof. Deresh Ramjugernath1, the South Africa`s Research Chair in
Fluorine process engineering and separation technology in these terms: South
Africa possesses the second to largest supply of Fluorspar; it currently
imports all its fluorinated products.? Synthesizing FILs at reasonable costs is
therefore a possibility in this country. First direct measurements of IDACs in
a fluorinated ionic liquid were reported by Heintz et al. (2001).
1
http://www.caes.ukzn.ac.za/Collegeboastsnewresearchchairs,
accessed 15 February 2009.
2.2. Infinite dilution activity coefficients
2.2.1. Definition
The activity coefficient of species in a solution is defined by
the following ratio:
(2-1)
where, is the fugacity of component in solution, its pure
component fugacity and, its
molar fraction. Activity coefficient is also defined as the
proportionality constant between the activity of a substance and its mole
fraction in a given solution.
(2-2)
In the study of phase equilibria and therefore the design and
optimization of separation processes, the concept of activity coefficient is
used rather than activity.
2.2.2. Importance and use of infinite dilution activity
coefficient data
The infinite dilution activity coefficient , also referred to as
limiting activity coefficient is the
limiting value of the activity coefficient of a solute when
its concentration tends towards zero. Alessi et al. (1991) defined the infinite
dilution region as one where each molecule of the solute is surrounded by
molecules of the solvent only. Only solute-solvent interactions take place.
This can be assumed for mole fractions ranging between 10-7 and
10-4, depending on components under investigation. The infinite
dilution region of solutions attracted much interest for couple of reasons
underlining its great importance (Raal and Mühlbauer 1998):
a) The system behavior in the very dilute regions is
instrumental in obtaining high purity products;
b) The most difficult and costly stage of a separation process
is the removal of the last traces of impurity;
c) The greatest departure from ideality occurs in the very
dilute regions;
d) Environmental concerns are based on the very dilute regions
in the gas phase which is air.
Sandler (1996) discusses theoretical and practical
applications of infinite dilution activity coefficient (IDAC) values in
chemical and environmental engineering. The most important ones that are
related to chemical engineering are listed below:
a) Synthesis, design and optimization of separation
processes;
b) Calculation of Henry`s law constants;
c) Predicting the existence of an azeotrope;
d) Development of predictive methods for
e) Characterization of behavior for liquid mixtures.
2.2.2.1. Synthesis, design and optimization of separation
processes
Separation is a critical stage in most of chemical processes
by virtue of its sensitive impact on the global cost, as well as the quality of
the product. One of the most important applications of IDACs is found in
separation processes. IDAC values are used in the preliminary selection of
solvent in view of extractive distillation, as well as, liquid-liquid
extraction (Tiegs et al. 1986). The potentially best separating agent, called
entrainer, is the one allowing the highest selectivity and capacity values. In
other words, when solvents are investigated to find out the most suitable
separating agent for a mixture containing two components and , their respective
IDAC
values in each solvent are determined. Equation (2-3) is then
used to calculate the selectivity at infinite dilution of each solvent with
respect to the system.
(2-3)
and represent the limiting activity coefficients of and
respectively in the solvent,
. is the limiting selectivity of solvent for the system
consisting of components and
. Thus, selectivity values at infinite dilution are important for
a preliminary selection of an
entrainer. A second quantity to look at is the
solvent capacity at infinite dilution, which is
numerically the maximum amount of species that can be dissolved
in the solvent.
(2-4)
Additionally, capacity reveals how much solvent is used during
the separation process. The greater the solvent capacity, the smaller the
amount of solvent used. In principle, the solvent to use as separating agent is
supposed to have the greatest value of both selectivity and capacity. But in
practice, a compromise is to be found, since these two quantities are in
inverse variation with respect to one another. A criterion that incorporates
both selectivity and capacity together
is called performance index, given by the product of these
properties (Kumar and Banerjee
2009). Thus, at infinite dilution,
(2-5)
The determination of permits one to evaluate the potential use of
solvents. Therefore, it
serves as a preselection criterion. Other criteria (Lydersen
1983) leading to the definitive choice of a solvent include: recoverability,
distribution coefficient, solvent solubility, density, interfacial tension,
viscosity, cost, corrosiveness, non-flammability, low toxicity, etc.
2.2.2.2. Calculation of Henry's law constants
There is a relationship between the Henry`s law constant of a
solute in a solvent and its limiting activity coefficient:
(2-6)
represents the Henry`s law constant for solute i in the
solvent and is the vapour pressure
of solute i at the temperature for which the IDAC is
determined. Equation (2-6) shows that
Henry`s law constants can be found
through IDAC values. In cases where the temperature of the
system is above
the critical temperature of the solute, the Henry`s law constant, rather than
the
ln e
8 i
l l 8
IDAC is useful (Eike et al. 2004). Design calculations for gas
separation applications commonly ln e j
involve the use of Henry`s law constants.
2.2.2.3. Predicting the existence of an
azeotrope
Conditions for the occurrence of an azeotrope in binary
systems can be established using infinite dilution activity coefficient data
(Gmehling and Möllmann 1998). For a system showing positive deviation from
Raoult`s law, an azeotrope with a temperature-minimum (pressure-maximum) takes
place when
(2-7) For a system exhibiting negative deviation from Raoult`s
law, an azeotrope with a temperature- maximum (pressure-minimum) takes place
when:
(2-8)
From equations 2-7 and 2-8, it obviously appears that the
knowledge of the IDAC values can help in predicting conditions leading to an
azeotropic mixture.
2.2.2.4. Development of predictive methods
for
Values of infinite dilution activity coefficient are important
for the development of new thermodynamic models, the adjustment of parameters,
as well as the expansion of the applicability for the existing group
contribution models (Gmehling 2003 and Nebig et al. 2009). With the aid of an
appropriate correlation, one can use infinite dilution activity coefficient
values to come up with VLE data in the intermediate concentration range.
Additionally, it is recommended to fit group interaction parameters
simultaneously to all available VLE, LLE and infinite dilution activity
coefficient experimental data (Weidlich and Gmehling 1987).
2.2.2.5. Characterization of behavior for liquid
mixtures
The infinite dilution activity coefficient value is an
indication of the nature of interactions between solute and solvent molecules
(McMillan and Mayer 1945). A high IDAC value is synonymous of weak
solute-solvent interactions i.e. low solubility (Cheong 2003). The IDAC value
is also a limiting measurement of the nonideality (Bao and Han 1995) of a
solution. For an
E
? ? G RT
E
? ?
/ ? H
ideal system, whereas a departure from ideality corresponds to
IDAC values greater or
RT 2
?? = T ??
smaller than unity.
2.2.3. Temperature dependence of activity
coefficient
The Gibbs-Helmholtz equation (2-9) depicts the effect of
temperature change on activity coefficient.
This leads to the following significant relations:
(2-10)
(2-11)
Using experimental ã8 data, the partial excess
enthalpy at infinite dilution for a given solute i,
can be directly obtained from the slope of a straight line
derived from equation (2-11), where is the gas constant. It only takes an
approximation of experimental values by the linear regression,
(2-12)
This procedure is widely used in the experimental section of this
thesis.
2.2.4. Predictive activity coefficient models
Predictive thermodynamic models are very important in separation
processes (Lei et al. 2008) as they allow:
a) A rapid solvent selection at reduced costs (Novak et al.
1987);
b) Accessing data that are difficult or impossible to obtain
experimentally;
c) The development of process simulators (Gmehling 2003).
It is beyond the scope of this study to review all the
thermodynamic models used to predict infinite dilution activity coefficients.
Only the most promising models used for systems involving ionic liquids are
dealt with in this section. The most successful models used by various
researchers to predict activity coefficients of various solutes in ionic
liquids can be classified into two categories:
a) Group contribution methods;
b) COSMO-based methods.
2.2.4.1 Group Contribution methods. (GCMs)
These methods are based on the group contribution concept
which assumes that the interaction energy of a system is the sum of functional
groups interaction energies, provided that groups are properly defined
(Gmehling 2009). Molecules are therefore split into smaller structures called
groups to which parameters are assigned. These activity coefficient models are
mostly based on the relationship between the latter and the excess free
energy.
The ASOG (Analytical Solution of Group) Model
The ASOG (Analytical Solution of Group) model was developed by
Derr and Deal (1969) who exploited previous works by Wilson and Deal (1962). It
was redefined by Kojima and Tochigi (1979) who modified several parameters in
order to account for the effect of temperature changes. In this method, the
expression of the activity coefficient is composed of two parts: the size
contribution term and the group interaction one. Go et al. (2007) used the ASOG
model to correlate experimental infinite dilution activity coefficient data of
n-octane, n-nonane and ndecane in the ionic liquid
4-methyl-n-butylpyridinium tetrafluoroborate in the temperature range
from 297 to 344 K. Their results were in good agreement with the experimental
measurements. Twelve interaction parameters related to three structural groups,
CH2, pyridinium and BF4 were determined.
The UNIFAC model and its modifications
After its publication by Fredenslund et al. (1975), the UNIFAC
(Uniquac Quasi-Chemical Functional Activity Coefficient) underwent a plethora
of revisions and extensions which are outlined in reviews by Lei et al. (2008)
and Castells et al. (1999).
The original UNIFAC, as stated by Lohmann and Gmehling (2001),
presented the following advantages:
a) Availability through commercial processes simulators;
b) Reliability in predicting VLE results;
c) Applicability over a wide range of mixtures.
The same authors highlight its weaknesses as follows:
a) Incorrect description of the temperature-dependence of the
activity coefficient and other related properties;
b) Unsatisfactory results when predicting properties in the
dilute region, as well as for asymmetric systems.
In an attempt to remedy these limitations, more advanced
versions of the UNIFAC model were developed, the most important ones being
UNIFAC (Dortmund) by Weidlich and Gmehling (1987) and UNIFAC (Lynby) by Larsen
et al. (1987). The modified UNIFAC (Dortmund) differs from the original UNIFAC
model in that it uses a different combinatorial part and it reliably takes into
account the temperature dependence of group interaction parameters. Its
developers introduced new van der Waals quantities as well. No thermodynamic
model can claim as much popularity as UNIFAC (Do). This is attributed to the
amount of research work and publications related to it in the last twenty
years. Moreover, around fifty companies and
institutions work actively in the UNIFAC Consortium to support
directly or indirectly its perfections. The Thermodynamics Research Unit, at
the University of KwaZulu-Natal is part of this organization. Successes
recorded in improving the predictability of properties using UNIFAC (Dortmund)
are presented in publications by Gmehling and Schiller (1993), Hansen et al.
(1991), Gmehling (1995), Gmehling et al.(1998), Gmehling et al.(2002), Gmehling
et al.(2009), Lohmann and Gmehling (2001), Wittig et al.(2001) and Jakob et al.
(2006). Recently, Prof. Gmehling`s group started to assess the predictive
ability of UNIFAC (Do) for systems involving ionic liquids. The parameter
matrix of this model has been expanded, allowing for the prediction of infinite
dilution activity coefficients of:
a) n-alkanes and alk-1-enes in [BMPyr] [BTI], [HMPyr] [BTI] and
[OMPyr] [BTI] (Nebig et al. 2009);
b) Methylcyclohexane and toluene in [HMIM] [BTI] (Liebert et al.
2008);
c) n-alkanes, benzene and toluene in [MMIM] [BTI] [BMIM] [BTI]
[HMIM] [BTI], as well as benzene and toluene in [BMIM] [BTI] (Nebig et al.
2007);
? ? d ?
d) n-alkanes, alk-1-enes, cycloalkanes, cycloalkenes, aromatics,
alcohols, ketones, esters, ethers and water in [HMIM][BTI], [OMIM][BTI],
[BMPyr][BTI];
e) The binary mixture of [BMIM] [BTI] and [EMIM] [BTI] (50:50
weight percent) (Kato and Gmehling 2005b).
It is clear that the parameter matrix remains very limited
when one looks at the number of ions involved in the structure of ionic
liquids. The major weakness of GCMs is their inability to deal with isomers,
proximity effects and systems involving groups for which experimental data have
never been compiled (Putnam et al. 2004).
2.2.4.2. COSMO-based methods
The conductor-like screening model (COSMO) is a predictive
method for thermophysical properties using a quantum chemical approach. Its two
most widely used variants for infinite dilution activity coefficients in ionic
liquids are COSMO-RS (The conductor-like screening model for real solvents),
developed by Klamt (1995) and COSMO-SAC (The conductor-like screening model,
solvation activity coefficients) (Lin and Sandler 2002). These two models
involve statistical thermodynamics, along with quantum chemical calculation
(Eckert and Klamt 2003). They require -profiles of molecules in the same manner
as group contribution methods rely on group interaction parameters. A -profile
is defined by Klamt and Eckert (2000) as a distribution function of the amount
of surface having a screening charge density between and
?. COSMO-based models are parameterized for 9 elements so far:
hydrogen, carbon, nitrogen, oxygen, fluorine, chlorine, bromine, iodine and
sulfur. They rely on a very small
number of parameters (Eckert and Klamt 2003) which are not
specific regarding molecules types or functional groups. This represents a
great advantage as compared to GCMs which involve a large number of functional
groups. Even components that have never been synthesized before can be studied
since no experimental data are needed to carry out predictions as shown by
Klamt et al. (1998). Long computation time and high computation costs are the
major disadvantages of these COSMO-based models. In a paper discussing
comparisons between COSMO-RS and GCMs, Grensemann and Gmehling (2005), taking
into account another article to which Klamt himself contributed (Putnam et al.
2004) reveal the following:
a) COSMO-RS achieves poor results in the applicability limits of
GCM`s, more especially, UNIFAC (Do);
b) COSMO-RS is advisable in cases of unknown GCMs parameters,
isomer and proximity effects.
This paper prompted a strong reaction from the developer of
COSMO-RS (Klamt 2005) who found its conclusions biased in order to clearly
favour the Modified UNIFAC (Do). From a neutral point of view, more time is
required to confirm whether COSMO-RS is inferior or superior to GCMs (Klamt and
Eckert 2008). More importantly, extensions are under way to improve both
models. Infinite dilution activity coefficients of a large spectrum of solutes
in some ionic liquids have been predicted using COSMO-RS. In a study on the
removal of thiophene from diesel oil (Kumar and Banerjee 2009), COSMO-RS
predictions of infinite dilution activity coefficient of alkanes, alk-1-enes
and cycloalkanes in [HMIM] [PF6], [HMIM] [BF4], [MOIM] [Cl] and [EMIM] [Tf2N]
are reported. The average absolute deviation of their predictions was found to
be 12% with respect to experimental data. Larger errors are observed in a
quantum chemical approach work by Sumon (2005) when predicting of toluene
and
heptane in a large number of ionic liquids. Other similar
predictive works (Banerjee and Khanna 2006, and Lei et al. 2007b) were in fair
agreement with experimental measurements, exhibiting the same range of
errors.
2.2.5. Experimental techniques for IDACs
measurements
Various experimental methods exist for determining infinite
dilution activity coefficients:
a) Gas-Liquid Chromatography (Letcher 1980);
b) Inert Gas Stripping Method (Leroi et al. 1977 and Richon et
al. 1980);
c) Headspace Analysis Method (Hussam and Carr 1985);
d) Indirect Headspace Chromatography. (Li and Carr 1993);
e) Dew Point Method (Eckert and Sherman 1996);
f) Differential Static Cell Method (Alessi et al. 1986);
g) Differential Ebulliometry Method (Gautreaux and Coates
1955);
h) Rayleigh Distillation Method (Dohnal and Horakova 1991).
The two methods used in this work, are the most popular ones
for ionic liquids. They are discussed here, with an emphasis on their
suitability for this class of solvents. A useful review paper by Kojima et al.
(1997) gives more details on other experimental techniques used for direct IDAC
measurements.
2.2.5.1. Gas liquid chromatography (GLC)
In this technique, the solvent, used as stationary phase, is
loaded onto the column. The solute, which is the mobile phase, is injected in a
carrier gas through the column. The eluted solute is detected and its retention
time, along with other experimental parameters, is used in an equation to
compute the IDAC. Gas-liquid chromatography can be used for IDACs of volatile
solutes in non-volatile or low volatility solvents. It is not applicable to
systems involving a mixture of solvents. Table 2-4 summarizes the advantages
and disadvantages of Gas-Liquid Chromatography.
Table 2-4: Advantages and disadvantages of the
Gas Liquid Chromatographic method
Advantages Disadvantages
Sample purity is not required The method is suited to low
volatility
or non-volatile solvents only
The method is rapid as many solutes can be injected at once
Reactive systems can be investigated
The IDAC of the solvent in the solute cannot be determined
2.2.5.2. The inert gas stripping technique.
(IGS)
In this method, a highly dilute solute is stripped from a
solution by a constant inert gas flow under isothermal conditions. The vapour
leaving the cell is periodically analyzed by gas chromatography. It is observed
that the peak area depicting the solute concentration in the vapour phase
decreases exponentially with time. Under this particular condition of
exponential dilution, the infinite dilution activity coefficient of the solute
in the solvent is related to the
decreasing rate of its corresponding peak area with time. The IGS
method is used to measure
of volatile solutes in non-volatile or volatile solvents.
Systems with solvent mixtures can be
investigated. The method is
alternatively called the dilutor technique, as well as continuous gas
extraction technique (Vitenberg 2003; Dobryakov and Vitenberg
2006). Table 2-5 presents the advantages and disadvantages of this
technique.
Table 2-5: Advantages and disadvantages of the
inert gas stripping method
Advantages Disadvantages
GC calibration is not required since only peak area ratios are
involved in calculations
A mixture of solvents can be investigated.
Systems with high volatility solvents can be measured
Many solutes can be investigated at once
Solutes must be purified.
Low volatility solutes are difficult to measure.
A good gas-liquid contact is critical to obtain reliable
results.
2.3. Advances in the design of IGS equipment 2.3.1. Major
developments in the use of the IGSM
Since its establishment by Leroi et al. (1977), the IGSM
underwent some improvements in terms of modernization of the analytical tool
(GC), temperature and pressure sensors, achievement of isothermal conditions
during experiments, etc. But the most important advance in this technique lies
in a better understanding of factors affecting the accuracy of measurements
provided by many research works. This resulted in various cell designs in order
to suit different types of systems. Bao and Han (1995) sum up the major
advances in the inert gas stripping technique as follows:
a) Establishment of the IGS technique by Leroi et al. (1977);
b) Correction by Duhem and Vidal (1978) for the liquid
concentration of the solute by taking into account its partition between the
two phases in the dilutor cell;
c) Modification of the dilutor cell structure by Richon and
coworkers (Richon et al. 1980 and Richon and Renon 1980);
d) Use of the two-cell technique in order to investigate low
boiling solvents. (Doleúal et al. 1981, and Doleúal and Holub
1985);
e) Extension of the technique to viscous or foaming systems by
Richon et al. (1985);
f) Further extension to mixtures containing food or oil
(Lebert and Richon 1984a, b). More recent developments involve the liquid
analysis gas stripping method (Hradetzky et al. 1990), the use of the inert gas
stripping technique for systems with ionic liquids ( Krummen et al. 2002) and
its extension to more delicate solvents of environmental interest involving
semi-volatile and surface tension solutes (Kutsuna and Hori 2008).
2.3.2. The number of cells required for IDAC
measurements
Either one or two cells can be used to measure infinite
dilution activity coefficients by the inert gas stripping method. The single
cell technique is suitable for systems with low volatility solvents and
relatively high volatility solutes. The double cell technique is required when
the solvent is a high volatile compound or mixture. In this variant, a
presaturation cell is used to saturate the stripping gas with the solvent
before the solute stripping process. This prevents any transfer of the solvent
from the liquid to the vapour phase which would lead to changes of the amount
of solvent in the dilutor cell. The single cell technique is appropriate to
systems involving ionic liquids since they are generally very high boiling
compounds and non volatile. Krummen et al. (2002) reported infinite dilution
activity coefficient data for n-alkanes and alk1-enes, cyclic hydrocarbons,
aromatic hydrocarbons, ketones, alcohols, and water in the ionic liquids
1-methyl-3-methylimidazolium bis (trifluoromethylsulfonyl) imide, 1-ethyl-3-
methylimidazolium bis (trifluoromethyl sulfonyl) imide,
1-butyl-3-methylimidazolium bis (trifluoromethylsulfonyl) imide, and
1-ethyl-3-methylimidazolium ethylsulfate in the temperature range between
293.15 K and 333.15 K. Activity coefficients at infinite dilution of alkanols
in the ionic liquids 1-butyl-3-methylimidazolium hexafluorophosphate,
1-butyl-3- methylimidazolium methylsulfate, [BMIM][MeSO4], and
1-hexyl-3-methylimidazolium bis(trifluoromethylsulfonyl) imide, [HMIM][Tf2N],
were measured by Dobryakov et al (2008). Using the same method, Nebig et al.
(2009) determined for n-alkanes and alk-1-enes in the
ionic liquids 1-butyl-1-methylpyrrolidinium bis
(trifluoromethylsulfonyl) imide, 1-hexyl-1- methyl pyrrolidinium bis
(trifluoromethylsulfonyl) imide and 1-methyl-1-octylpyrrolidinium bis
(trifluoromethylsulfonyl) imide. Kato and Gmehling (2005a, b) presented
infinite dilution activity coefficient data for seven solutes in the ionic
liquids 1-butyl-3-methylimidazolium bis (trifluoromethylsulfonyl) imide and
1-ethyl-3-methylimidazolium bis (trifluoromethylsulfonyl) imide using the
methods of gas liquid chromatography and the inert gas stripping technique.
Their results show a good agreement between the two methods.
2.3.3. Cell design parameters
Thermodynamic equilibrium between the gas leaving the dilutor
cell and the remaining liquid is instrumental in obtaining accurate infinite
dilution activity coefficient data.To achieve this, three conditions must be
met (Leroi et al. 1977):
a) Large total mass transfer area;
b) Sufficiently long contact time;
c) Good dispersion of bubbles in the liquid.
Studies mentioned in the two previous sections threw light on
these factors which affect the
performance of the IGSM:
a) Dispersion device;
b) Bubble rise height;
c) Stripping gas flow rate;
d) Bubble size;
e) Liquid viscosity;
f) Range of IDACs to be measured.
For accurate measurements of IDAC, it is essential to take
into account these factors when designing dilutor cells. The impact of each of
these parameters is briefly explained in the light of expressions derived by
Richon et al. (1980) which are reviewed in Chapter 3 of this thesis.
2.3.3.1. Dispersion device
In the original version of the method by Leroi et al (1977)
(See Figure 2-2), a fine porosity fritted glass was used as dispersion device.
Recently constructed dilutor cells are generally provided with stainless steel
capillaries with very small inner diameters. Stainless steel is known as a non
corrosive material. To ensure that the total mass transfer area is large, the
inert gas, generally helium or nitrogen, is dispersed into very small bubbles.
Capillaries must be in reasonable number and well spaced to avoid any bubble
coalescence. Dobryakov et al. (2008) designed a very small cell, of volume 5
cm3, with just a single capillary tube used as the dispersion
device.
2.3.3.2. Bubble rise height
The liquid level in the cell must be high enough for
sufficient contact time between the bubbles and the investigated solution. This
is a very important condition in view of attaining the required thermodynamic
equilibrium.
2.3.3.3. Stripping gas flow rate
Efficient solute mass transfer from the liquid phase to the
gaseous phase requires low inert gas flow rates as this results in longer
contact times. The optimum flow rate depends on the system under investigation.
It has been shown that when thermodynamic equilibrium has been attained between
the two phases inside the dilutor cell, measured infinite dilution activity
coefficients do not depend on the flow rate value. Additionally, the size of
bubbles is affected by the flow rate, increasing up when the flow rate is
increased. In previous works, experiments were performed with inert gas flow
rates ranging between some tenths to tens of cm3 (Kutsuna and Hori
2008, and Krummen et al. 2002)
2.3.3.4. Bubble size
The smaller the bubble size, the more efficient is the mass
transfer. In effect, when the inert gas is dispersed into the solution as small
bubbles, the total mass transfer area is increased. If bigger bubbles are used,
the height of the cell must be high enough to ensure a long residence time of
the gaseous phase in the solution.
2.3.3.5. Liquid viscosity
A high viscosity hinders mass transfer. Its other effect
consists of reducing the bubble rise and consequently allowing larger contact
times. The two effects with regards to mass transfer and equilibrium conditions
in the cell compensate each other. However, more sophisticated features need to
be incorporated in the design of the dilutor cell, more especially its stirrer,
for very viscous mixtures (Richon et al. 1985).
2.3.3.6. Range of IDACs to be measured
When very high infinite dilution activity coefficient values
have to be measured, large amounts of solute are stripped out of the solution
in a very short period of time, since there are very weak interactions between
the components involved in the mixture. If care is not taken, this will
compromise the attainment of equilibrium and reduce the mass transfer extent as
the contact time may be insufficient. It is not therefore surprising that the
worst agreement between infinite dilution activity coefficient data obtained
with the GLC method and the dilutor technique were observed for very high
activity coefficients (Leroi et al. 1977). The designer should take into
account the range of IDACs values the cell is supposed to deal with in order to
tune other parameters such as the height and the dispersion device.
2.3.4. Review of previous equilibrium cells
Various cell designs have been reported over the last forty
years as part of the inert gas stripping set up for the determination of
infinite dilution activity coefficient, Henry`s law constant and partition
coefficient. The most efficient ones, taken from the open literature are
reviewed. The various researchers who designed the cells discussed in this
section reported a good agreement with infinite dilution activity coefficient
data obtained by the GC method. And, reproducibilities better than 2% were
obtained. However, the reliability seemed to be compromised when very
high values had to be measured. The other issue of concern is the
determination of in
viscous mixtures.
2.3.4.1. Leroi et al. (1977)
Leroi et al. (1977) used the pyrex glass cell represented in
figure 2-2 to measure infinite dilution activity coefficient for n-hexane and
benzene in ten different nonvolatile solvents, including Nmethyl-2-pyrrolidone
(NMP), dimethylsulfoxide (DMSO), dimethylformamide (DMF), nitrobenzene,
ethylene glycol and hexadecane. A solution of volume 25 cm3
could be accommodated by the still and an experiment lasted one to two hours.
Solutes were introduced into the cell by means of a 10 syringe via the septum.
Inert gas flow rates ranged from 50 to
150 cm3 .min-1. To ensure accurate
measurements, liquid drop entrainment was limited by a dead space above the
solution. This gas phase volume was kept small enough to ensure accurate
measurements. The dispersion device consisted of a fine porosity fritted glass
disk as mentioned previously.
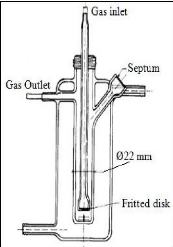
Figure 2-2: Dilutor cell constructed by Leroi et
al. (1977)
2.3.4.2 Richon et al. (1980)
Richon et al. (1980) designed the dilutor cell shown in figure
2-3, similarly to the one constructed by Leroi et al. (1977). Their major
improvements to the first cell include the following features:
a) Equal sized bubbles are introduced from the bottom by means
of fine capillaries;
b) A conical outlet gas collector is adopted to minimize liquid
entrainment.
They investigated infinite dilution activity coefficients of
alkanes from C1 to C9 in hexadecane. Experiments undertaken concluded that the
inert gas stripping method could be easily extended to Henry`s law constant
measurements. For Henry`s law constants greater than 30 atm., their work showed
the necessity to keep a very small and homogeneous vapour phase in the cell.
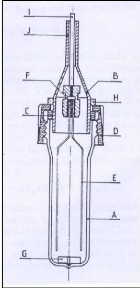
Figure 2-3: Equilibrium cell constructed by
Richon et al. (1980)
A - glass still body, B - conical collector of gas
outlet, C - gasket, D - plug, E - capillaries, F -
Teflon seal, G - magnetic
stirrer, H - metallic ring used to adjust the depth of the conical
collector
B in the still, I - tube for carrier gas inlet, J - gas outlet.
2.3.4.3. Richon and Renon (1980)
In this design, Richon and Renon (1980) abandoned the previous
conical shape in favour of a simpler shape as shown in figure 2-4. A
considerably reduced 1 cm high gas phase is kept above the solution inside the
dilutor cell. Their cell was used to determine infinite dilution activity
coefficients of light hydrocarbons in n-hexadecane, n-octadecane and 2, 2, 4,
4, 6, 8, 8- heptamethylnonane.
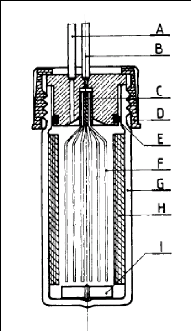
Figure 2-4: Dilutor cell used by Richon and
Renon (1980).
A - vapour phase outlet, B - inert gas inlet, C - Teflon seal,
D - plug, E - O-ring, F -
capillaries, G - glass still body, H - baffles, I
-magnetic stirrer.
2.3.4.4. Legret et al. (1983)
Legret et al. (1983) used the cell below (figure 2-5) to
determine partition coefficients which are related to activity coefficients at
infinite dilution. Their study involved some alkanes as solutes in the
methane/n-decane system. The pre-saturator and the dilutor cell were fitted
with 20 and 50 capillaries respectively. The capillary inner diameter was 0.3
mm for the pre-saturation cell and 0.1 mm for the dilutor cell. Both cells
contained 40 cm3 of solvent.
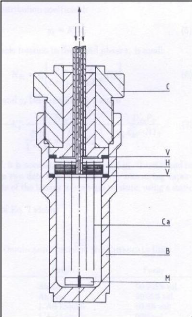
Figure 2-5: Dilutor cell design by Legret et al.
(1983)
B - body, C - cap, Ca - capillaries, H - capillary holder, M -
magnet, V - O?-ring
2.3.4.5. Richon et al. (1985)
Richon et al. (1985) designed the cell presented in figure 2-6
in order to extend the use of the inert gas stripping technique to foaming and
viscous mixtures. Examples of these are aqueous mixtures of glucides, polyols
and proteins whose viscosities can be as high as 1000 cP. Since a magnetic
stirrer would be inefficient due to high viscosity, the mixture is circulated
inside the internal cylinder from top to bottom, by means of an Archimedes
screw that is maintained by two pivots and activated by a permanent magnet. A
special device is used to break foams without disturbing phase equilibrium
inside the cell. The cell is provided with a bladed screw which prevents liquid
rotation in the cell and promotes the coalescence of gas bubbles.
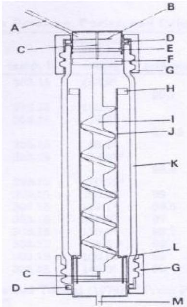
Figure 2-6: Dilutor cell designed by Richon et
al. (1985) for viscous and foaming mixtures.
A - vapour phase outlet, B -
deflector, C - pivot, D - gasket, E - foam-breaking device, F -
permanent
magnet, G - plug, H - bladed screw, I - Archimedes screw, J - internal
cylinder, K -
dilutor cell, L - carrier gas capillary injectors and M -
carrier gas inlet.
2.3.4.6. Bao et al. (1994)
In the design given in figure 2-7 proposed by Bao et al.
(1994), a liquid-conducting tube is placed between the capillaries and the cell
body to create a countercurrent flow of circulating solution to the stripping
bubbles. This is aimed at enhancing mass transfer as well as making the
stripping process more efficient. Bao et al. (1994) used stainless steel
capillary tubes of 0.1 mm inner diameter as dispersion device.
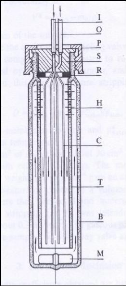
Figure 2-7: Equilibrium cell designed by Bao
et al. (1994).
B - Body, C - capillaries, H - small holes, I - inert gas
inlet, M - magnet, O - vapour phase
outlet, P - plug, R - O-ring, S-seal, T
- liquid-conducting tube.
2.3.4.7. Hovorka and Dohnal (1997)
As shown in figure 2-8, Hovorka and Dohnal (1997) designed an
all-glass jacketed device accommodating both the pre-saturator and the dilutor
cell. The pre-saturation compartment is divided by fritted glass disks into
plates in order to allow efficient saturation of the inert gas with the solvent
vapour, yet maintaining a small pressure drop across it. The saturated inert
gas is dispersed in small bubbles into the diluted solution through a fine
porosity fritted glass tip. Liquid droplet entrainment is prevented by the
vapour space of the cell and a special design of the gas outlet. Their set up
allowed measuring infinite dilution activity coefficients in the range from 230
to 70000.
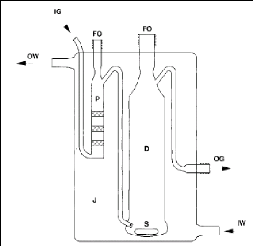
Figure 2-8: Equilibrium cell designed by
Hovorka et al. (1997).
P - Pre-saturator with fritted glass disks, D -
dilutor cell, S - stirrer, J - thermo-statted jacket,
IW - input of
thermo-statted water, OW - output of thermo-statted water, IG - input
of
stripping gas, OG - outlet of saturated stripping gas, FO - filling
openings.
2.3.4.8. Miyano et al (2003)
The cell shown in figure 2-9 was used by Miyano et al (2003)
to determine Henry`s law constants and the infinite dilution activity
coefficients of butane, isobutane, 1-butene and isobutene in methanol from (255
to 320) K. A counter flow of liquid against the rising bubbles is achieved in
the inner tube of the cell to increase the contact time. They used a maximum
inert gas flow rate of 2 cm3. min-1.
Figure 2-9: Equilibrium cell designed by
Miyano et al. (2003) for the determination of Henry`s
law constants using
the dilutor technique.
2.3.4.9. Dobryakov et al. (2008)
Gas outlet
Inert gas inlet
Capillary tube
In order to investigate infinite dilution activity coefficient
of alcohols in three different ionic liquids, Dobryakov et al. (2008)
constructed a 5 cm3 dilutor cell which was filled with 3
cm3 of solvent during experiments. Their still which is shown in
figure 2-10 used a single capillary tube plumbed in at the bottom as a
dispersion device. Measurements were done with inert flow rates between 8 and
20 cm3. min-1.
Figure 2-10: Dilutor cell designed by Dobryakov
et al. (2008). 2.3.4.10. Kutsuna and Hori (2008)
Drawing inspiration from previous work by Lei et al (2007a)
and Shunthirasingham et al. (2007), which established that the IGSM led to
inaccurate Henry`s law constants in case of semi-volatile and surface active
solutes, particularly when small gas bubbles such as those with < 1 mm in
radius were used, Kutsuna and Hori (2008) proposed the design shown in figure
2-11 and photograph 2-1. They determined Henry`s law constants of
perfluorooctanic acid (PFOA) in aqueous sodium chloride and sulfuric acid
mixtures. To deal with semi-volatile and surface active solutes, their design
incorporated a helical plate that increased the residence time. In addition,
the dispersion device allows the formation of larger bubbles. Kutsuna and Hori
performed experiments with 300 cm3 of solvent in the dilutor cell,
achieving a residence time of 15 seconds and using bubbles larger than 3 mm in
radius and an inert gas flow rated as high as 80 cm3.
min-1. Photograph 2-1 shows bubbles rising up along the underside of
the glass helix from the bottom to the top of the solution placed in the
cell.
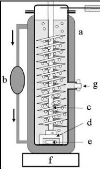
Figure 2-11: The dilutor cell designed by
Kutsuna and Hori (2008).
a- Jacketed Duran glass column; b-
Temperature-controlled water circulator; c- Gas-
introduction tube with a
glass helix; d- Polytetrafluoroethylene support; e- Magnetic bar;
F-
magnetic stirrer; g- Sampling port for injection.

Photograph 2-1: The helical plate used in the
dilutor cell designed by Kutsuna and Hori (2008).
Chapter 3: Theoretical considerations
CHAPTER THREE: THEORETICAL CONSIDERATIONS
Chapter overview
The theory and equations used to compute infinite dilution
activity coefficients by two selected methods are presented. Where necessary,
enough details on derivation procedures are provided. Assumptions leading to
the derivation of these mathematical relationships are highlighted. They
determine the reliability of the experimentally generated data. The modeling of
mass transfer in the dilutor cell, as presented in the literature, is reviewed.
It represents an important basis on which the dilutor cell constructed for this
work was designed.
3.1. Gas liquid chromatography
Gas liquid chromatography is a well established method for
determining infinite dilution activity coefficient of volatile solutes in
nonvolatile solvents (Letcher 1980). It is logically used
C L
in this study of ionic liquids which are generally known as high
boiling solvents. Equations
K C M
involved in IDAC`s computations, discussed by Letcher (1980)
as well as Condor and Young (1979) and used in this work are given below. As
the solute (1) moves through the column, it is assumed that:
· The mobile or gas phase is an ideal mixture composed of
the carrier gas (2) and the solute (1);
· The stationary gas is a real liquid mixture, containing
the solute and the solvent (3);
· The gas phase (mobile phase denoted as M) and the liquid
phase (stationary phase, denoted as L, i.e. ionic liquid) are in thermodynamic
equilibrium, well described by the modified Raoult`s law.
The distribution coefficient, of the solute between the two
phases, according to Condor and
n
Young (1979), is:
(3-1)
Concentration of the solute in the liquid and gas phases are
given by
(3-2)
and, (3-3)
where and are the mole fractions of the solute in the liquid
and gas phases respectively,
is the number of moles of the carrier gas in the mobile phase,
is the number of moles of the
solvent in the stationary phase, is the volume of the gas phase
and
stationary phase. From equations (3-1) through (3-3), it can be
found that:
|
is the volume of the
|
|
(3-4)
|
|
|
(3-5)
|
and using modified Raoult`s law, i.e.
|
|
(3-6)
|
Equation (3-4) can be written in a simplified form as:
|
|
|
(3-7)
|
|
|
At mean column pressure (Laub and Peacsok 1978), the net
retention volume, , is related to the distribution coefficient and the volume
of the stationary phase by:
(3-8)
When this expression is used in equation (3-7), the following
equation determined by Porter et al. (1956) is obtained:
(3-9)
When the solute-solute and solute-carrier gas imperfections,
as well as the pressure drop along the column are considered, a more accurate
equation (Everett 1965, Cruickshank et al. 1966a and 1969) is derived:
(3-10)
where is the infinite dilution activity coefficient of a solute
(1) in a solvent (3), T is the
column temperature, is the column outlet pressure, the same as
the atmospheric pressure,
is the column inlet pressure, is the mean column pressure, , the
saturated pressure
vapour of the solute at temperature T, is the molar
volume of the solute, is the partial
molar volume at infinite dilution, equal to, in this particular
case. is the pressure
correction term given by
(3-11)
is the net retention volume given by
(3-12)
, the column outlet flow-rate, the retention time for the solute
and is the inert gas retention time.
The second virial coefficients of pure solutes were calculated
using the McGlashan and
Potter equation (1962).
(3-13)
The same equation allowed the calculation of mixed virial
coefficients
? ? ? ? ? ? . Other mixed
properties are determined by means of Hudson and McCourbey`s
(1960) mixing rules as follows:
(3-14)
(3-15)
(3-16)
(3-17) In the last four expressions, subscripts =1`, =2` and
=12` refer to the solute, the carrier gas and the mixture of these two
components, n is the number of carbon atoms and is equated to one
for
x f I y P
1 ? 1 = ?
1 1
compounds with no carbon atom. Critical properties and as well
as the ionization
energies, are found in the literature (CRC Handbook 2005).
Modified Rackett equation (Poling et al. 2001) gives the values of molar
volumes as follows:
(3-18) Saturated vapour pressures involved in equation (3-10)
were calculated using the Antoine, modified Antoine or Wagner equations in
compliance with the applicability range of each
x f oq I y P
3 ? 3 3 = ?
3 3 3
correlation. Constants for vapour pressure correlations which
are required in equation (3-10) as well as acentric factors were taken from the
literature (Poling et al. 2001).
3.2. Inert gas stripping method
3.2.1. Equations for IDACs computation
3.2.1.1. Equations proposed by Leroi et al.
(1977)
3.2.1.1(a) General equations proposed by Leroi et al.
(1977)
Leroi et al. (1977) derived basic equations to compute
infinite dilution activity coefficients from the dilutor technique. The
starting point of their formulation is the assumption that the two phases in
the cell are in thermodynamic equilibrium. The equilibrium equations for each
of the components are:
(3-19)
(3-20)
(3-21)
where the subscripts refer to the solute (1), the carrier gas
(2) and the solvent (3), is the mole
fraction in the liquid phase, is the mole fraction in the vapour
phase, is the pressure, is
the fugacity, is the fugacity coefficient, is the reference
fugacity for a liquid at pure state
and zero pressure, is the activity coefficient, is the Henry`s
law constant and is the
Poynting correction given by:
(3-22)
In the above equation, is the molar volume of the component at
temperature. The
L
reference state is the pure component at zero pressure for both
solvent and solute. At low
v
pressure, (conditions at which all the experiments in this
study were carried out), the vapour phase corrections can be derived from
second virial coefficients. Fugacity coefficients, which can be determined at
low pressures from second virial coefficients, are used to account for the
vapour phase imperfections as follows:
(3-23)
(3-24)
is the system temperature, is the virial coefficient related to
bimolecular interactions between and molecules, is the mixed second virial
coefficient at temperature . R is
the gas constant. The equation below can be used to determine
reference fugacity values, that are required in equations (3-19) and (3-20).
(3-25)
where is the reference molar volume of liquid component, is the
vapour pressure of
component and is the fugacity coefficient in the vapour phase at
saturation. If the solute is
considered infinitely dilute in the solvent and
the carrier gas is insoluble or of negligible
solubility in the liquid phase, then the activity coefficient
of the solute, can be equated to its infinite dilution activity coefficient in
the solvent (3), and both the activity coefficient of the solvent, and its mole
fraction, in the liquid phase to 1. Neglecting vapour phase imperfections,
equilibrium equations (3-19) and (3-20) can be written as follows:
(3-27)
Amounts of solute and solvent removed from the equilibrium cell
by the carrier gas flow can be calculated with the aid of these equations:
(3-28)
(3-29)
where and are respectively the number of moles for the solute
and the solvent in the
equilibrium cell at time , and give the change in the amount of
the two components
with time. is the total volumetric rate of the gas phase leaving
the still, converted to pressure
and temperature . A combination of equations (3-26) through
(3-29) leads to:
(3-30)
(3-31)
From overall mass balance calculations around the equilibrium
cell, the total volumetric rate
of the gas phase leaving the still can be related to, the pure
carrier gas flow rate measured at system pressure and system temperature.
(3-32)
Combining equations (3-30) through (3-32) gives:
|
Chapter 3: Theoretical considerations
|
|
(3-33)
(3-34)
(3-35)
|
1 ?
At infinite dilution, it can be deduced that
N P P
|
|
|
The differential equations (3-30) and (3-31) describe the
variations of the number of moles in
the cell with time for both the solute
and the solvent. Substituting in these two equations by
equation (3-33) and replacing by (3-35) result in:
(3-36)
(3-37)
where is the saturated vapour pressure of component . The last
two equations have been
derived using the following three assumptions:
· the vapour phase is ideal;
· The carrier gas solubility in the liquid phase is
negligible;
· The solute is infinitely diluted in the solvent.
In quest of simplification, Leroi et al. (1977) added more
assumptions depending on the volatility of the solvent.
3.2.1.1(b) Equation proposed by Leroi et al. (1977) for
non-volatile solvents.
A non-volatile solvent is one with negligible vapour pressure
equal or less than 1 mmHg (George 2008). Leroi et al. (1977) added the
following assumptions with reference to equations (3-36) and (3-37):
· is constant due to the non-volatile nature of the
solvent;
. The ratio is negligible with respect to 1 since the vapour
pressure of the
solvent is close to zero;
. The term is ignored due to the infinite dilution
assumption.
Thus, equation (3-37) does not exist any longer whereas
equation (3-36) can be written as
(3-39)
where is the initial number of moles for the solute in the cell.
During infinite dilution activity
coefficient measurements, it is advisable to maintain the gas
sampling valve at constant temperature and to ensure that the GC detector
linearity is satisfied. If these requirements are met, the amount of the solute
injected into the column given by the corresponding peak area from the GC, will
be proportional to its partial pressure over the solution.
(3-40)
is the proportionality constant depending on the GC used. From
equations (3-26), (3-35), (3-39) and (3-40), an equation showing an exponential
decrease of the solute peak area with
? = ln
13 DP t
sat ( )
A
time can be obtained.
(3-41)
is the initial solute peak area. Finally, the infinite
dilution activity coefficient of the solute (1) in the solvent (3) is
determined by means of this equation derived from expression (3-41):
(3-42) where N is the number of solvent moles in the dilutor
cell and expresses the initial solute peak area.
3.2.1.1(c) Equation proposed by Leroi et al. (1977) for
volatile solvents
When a volatile solvent is used, its amount in the cell varies
with time. Therefore, the two
equations (3-36) and (3-37) are worked out simultaneously to
give the following solution. n
(3-43)
3.2.1.2. Equation proposed by Duhem and Vidal (1978) for
non volatile solvents
Leroi et al. (1977) derived equation (3-43) on the basis of some
assumptions such as neglecting the term appearing in equations (3-36) and
(3-37). Duhem and Vidal established that
for large infinite dilution activity coefficients, this
particular assumption is no longer valid. Apart from dropping this assumption,
they expressed the mole fraction of the solute in the liquid phase by
(3-44)
This allowed them to come up with the following equation:
(3-45)
?
?
? 1 ?
Assuming a constant inert gas flow rate
N ? 1 ? , after incorporating a vapour
space correction into
? ? ?
? RT N ?
equation (3-45), Duhem and Vidal derived the following equation
which is more accurate for systems with large activity coefficients at infinite
dilution:
? ? (3-46)
? 1
? V 1 V 1
G
?
where is given by:
(3-47)
In the above equation and are the number of moles of the solute
in the still at a certain time and the initial number of moles for the solute
respectively. is the volume of the vapour
phase evaluated from equation
(3-48) (Bao et al. 1993a, b).
(3-48)
3.2.1.3. Equation proposed by Bao and Han (1995) for a
volatile solvent
Following the example of Duhem and Vidal (1978), Bao and Han
(1995) used equation (3-44)
/ ? 1 Psat / P?
to express the solute mole fraction in the liquid phase.
Neglecting the correction term suggested by Bao and Han, they solved the
differential equations (3-36) and (3-37) to obtain the following final result,
applicable to a volatile solvent:
?

(3-49)
3.2.1.4. Equation proposed by Hovorka and Dohnal
(1997)
According to Leroi et al. (1977), under the assumption that
the solvent is non-volatile, the partial pressure of the solute is negligible
as compared to the total pressure in the cell, the vapour phase is ideal and
neglecting the effect of the vapour space, the limiting activity coefficient
can be determined as follows:
(3-50)
For a volatile solvent, a presaturation cell is used as
explained in section 2.3.2. It is Hovorka and
Dohnal`s statement that after
presaturation the flow rate of the stripping gas is increased by a
factor where is the saturation vapour pressure of the solvent.
Thus, for the
double cell technique, the activity coefficient at infinite
dilution is computed as
(3-51)
These last two equations provide the first order approximation
of the infinite dilution activity
coefficient, denoted as , with a
sufficient degree of accuracy in most cases. However, for
improved accuracy, the second order approximation can be
used.
(3-52)
where is given by equation (3-50) or (3-51). Correction factors
are defined as follows:
· , correction factor associated with the change of the
inert stripping gas flow rate due
to the saturation in the cell is given for the single cell
technique (Equation 3-53) and the double cell technique (Equation 3-53)
respectively by:
(3-53)
and
(3-54) where is the mean amount of the solute in the cell
during the measurement and is given by:
(3-55)
is the initial amount of the solute in the cell, and are solute
peak areas at the
? ?
end and the beginning of the experiment, respectively.
k ? is always less than unity and
2 RT
rises with increasing volatility of the solvent and the
solute.
· is the correction factor associated with solvent removal
due to its volatility. When a presaturation cell is not used, this correction
term is written as:
(3-56)
where is the total stripping time, denotes the initial amount
of the solvent in the cell
and D is the stripping gas flow rate. If the stripping gas is
saturated, will become equal
to unity; it is always less than unity and
rises with decreasing cell volume and increasing
3 ? 3 ? 3
solvent volatility.
· is related to the amount of the solute in the vapour
space above the solution in the
cell. It is calculated by
(3-57)
where is the vapour space volume. is greater than unity and
rises with the solute
volatility and with the increasing ratio of the vapour space
volume to the amount of the solvent in the equilibrium cell.
· is the vapour phase nonideality correction factor given
by:
(3-58)
where subscripts =1` and =2` refer to the solute and the
stripping gas, respectively. is
the pure solute molar volume, is the second virial coefficient.
Depending on the
system and experimental conditions, can be either greater or
smaller than unity.
3.2.1.5. Equation proposed by Krummen et al.
(2000)
Krummen et al. (2000) proposed a formulation which takes into
account the saturation fugacity of the components under investigation and the
increase of the stripping gas flow rate caused by its saturation with the
solvent. Assuming that the liquid phase is in equilibrium with the gas phase in
the cell, these equations can be written:
(3-59)
(3-60)
Further assumptions are:
· The solute is highly dilute in the solvent. This implies
that:
(3-61)
(3-62)
(3-63)
· Measurements are carried out at low pressures or pressure
differences . Thus,
(3-64)
· The stripping gas is of negligible solubility in the
liquid phase. Therefore, (3-65) And for the solvent, it is assumed that:
(3-66)
The above simplifications allow writing equations (3-59) and
(3-60) as follows:
(3-67)
(3-68)
The flow rate of the stripping gas stream entering the dilutor
cell is made up of the flow rate
of the stripping gas stream entering the saturation cell,and the
flow rate of the solvent stream, .
(3-69)
The amount of solvent leaving the presaturator is provided by its
saturation vapour pressure and mixes with the pure stripping gas entering the
dilutor cell.
(3-70)
Combining equations (3-68) through (3-70) leads to:
(3-71)
y
According to Krummen et al. (2000), the solvent content in the
stripping gas stream cannot be dt RT
neglected when is greater than 5 mbar. , the flow rate of the
stripping gas stream
leaving the dilutor cell, is given by:
(3-72) where is the flow rate of the solute removed from the
measurement cell, which under the assumption of an ideal gas, can be calculated
as follows:
(3-73)
decreases with time. When the last two equations are combined, it
follows that:
(3-74) In order to determine activity coefficients at infinite
dilution by the inert gas stripping technique, the variation of the amount of
solute in the dilutor cell is measured as a function of time. This variation
can be expressed by the following equation:
(3-75)
Since the stripping gas is saturated with the solvent,
(3-76)
Taking into account equation (3-75), equation (3-74) can be
written as:
(3-77)
Combining equations (3-77) and (3-67) results in:
(3-78)
When equation (3-77) is used in equation (3-75) and combined with
equation (3-67), the result is:
(3-79)
For relatively volatile solutes, high saturation vapour
pressures of the solvent or large infinite dilution activity coefficient
values, Krummen et al. (2000) suggest that only the solute content in the
liquid phase should be taken into account when determining the solute molar
fraction.
n 1
x
(3-80)
Assuming ideal gas behaviour, the content of the solute in the
gas phase can be calculated as follows:
(3-81)
When equations (3-81) and (3-67) are combined and the resulting
expression is inserted into equation (3-80), the result is:
(3-82)
If equation (3-82) is used in equation (3-79), the variation of
the amount of solute with time can
? ?
1 1 1
? ? sat sat
P V ? ? ? ? st sat
P n RT
1
be expressed by:
?
NRT ?
(3-83)
In the above equation, is the corrective term used to take
into
account the variation of the solute gas stream during
measurements. If the change in the solute flow rate is neglected with respect
to the inert gas stream, the corrective term is equated to unity. In this
particular case, the integration of equation (3-83) yields:
(3-84)
If the linearity of the detector is assured and condensation
effects in the sample loop and other k n
tubes are avoided, the solute peak area A, is given
by:
(3-85)
k is the proportionality constant. When equations (3-82), (3-67)
and (3-85) are combined, the result is:
(3-86)
All the quantities on the right--hand side of this equation do
not vary during the measurements
? ?
except the number of moles for the solute,n,
Using from equation (3-86) in equation (3-84)
leads to:
(3-87)
Solving the equation for gives:
(3-88)
where is the slope of the graph of the natural logarithm of the
solute peak area versus time.
(3-89)
Using equation (3-71), expression (3-88) can be written as:
(3-90)
where is the vapour phase volume and
T P is the stripping gas flow rate as it enters the
FM
presaturator at the system temperature .
Equation (3-90) is also applicable to solvent mixtures with the
aid of these formulae:
(3-91)
(3-92)
where and are respectively saturation vapour pressures and
amounts of individual
solvents involved in the solution. Equation (3-90) shows that
activity coefficients at infinite dilution can be determined from the
experimentally measured slope, the saturation vapour pressures of the solute
and the solvent, the saturation fugacity coefficient of the solute, the system
pressure and temperature, the inert gas flow rate and the vapour phase volume.
The inert gas flow rate needs to be converted to the cell conditions using the
following equations, depending on the type of flowmeter used:
(Electronic flowmeter) (3-93)
(Soap bubble flowmeter) (3-94)
where is the inert gas flow rate at the flowmeter, is the
pressure at the flowmeter,
is the saturation vapour pressure for water, is the pressure in
the measurement cell. Equation (3-94) was also useful for determining the
corrected flow of the carrier gas when using GLC.
3.2.2. Mass Transfer considerations in the equilibrium
cell.
Richon et al. (1980) developed a useful model to calculate mass
transfer of the solute from the
solution to the vapour phase in the still. A
condition of validity of their method is that
thermodynamic equilibrium
should be achieved between the saturated gas leaving the still and
the liquid. Assuming that there is a very quick diffusion of
solute into the bubble, the modified Raoult`s law describes the existing
vapour-liquid equilibrium in the still, bubbles are perfectly spherical and the
carrier gas is not soluble in the solvent, they derived equations (3-95) and
(3-96) for the attainment of equilibrium in the liquid phase and in the vapour
phase respectively.
(3-95)
(3-96) where is the ratio of mass transfer in the cell to mass
transfer to reach equilibrium, taking into consideration only the liquid phase
resistance is the same as , taking into consideration gas phase diffusion only.
As the system approaches equilibrium, as well as approach
unity. is the path length of the bubbles in the equilibrium
still. is the density in g .cm-3,
is the temperature in Kelvin, is the diffusion coefficient of
solute, , in solvent,, in the
gas phase, is the bubble radius, is the solvent molar mass in
g/mol., is the solute
vapour pressure at temperature in atm and is the
limiting bubble speed given by
(3-97)
, kinematic viscosity in cP and is the diameter of bubbles. Many
authors have designed
dilutor cells on the basis of mass transfer calculation proposed
by Richon et al. (1980).
Of particular importance is equation (3-95) which allows the
determination of the optimal cell height (Li et al. 1993). It has been used for
this end in this work. Infinite dilution activity coefficients values were
computed using equation (3-90). Saturation fugacity coefficients were
determined from second virial coefficients (See appendix D)
CHAPTER FOUR: EXPERIMENTAL APPARATUS
AND
PROCEDURE
Chapter overview
For each of the two techniques used in this work, the
materials used, the experimental set up and the experimental procedure are
described. Solvents and solutes preparation and purification before
measurements by Gas Liquid Chromatography and the Inert Gas Stripping Technique
are explained. This chapter also presents the main features of the dilutor cell
designed for this study with emphasis on the procedure used to determine its
optimal height. Uncertainties on the experimental parameters and variables are
provided as they allowed determining the errors attached to the experimental
data reported in this work.
4.1. Limiting activity
coefficient measurements by gas liquid chromatography
4.1.1. Chemicals
The reliability and accuracy of an experimental procedure has
to be checked by comparison with data available in the literature. In this
study, systems involving n-hexadecane as the solvent has been used to test the
exactness of the procedure. The following ionic liquids have been used as
solvents:
· Trihexyltetradecylphosphonium tetrafluoroborate,
[3C6C14P] [BF4]
· Trihexyltetradecylphosphonium
bis(trifluoromethylsulfonyl) imide, [3C6C14P] [BTI]
· Trihexyltetradecylphosphonium hexafluorophosphate,
[3C6C14P] [PF6]
· Trioctylmethylammonium bis(trifluoromethylsulfonyl)
imide, [3C8C1N] [BTI]
· 1-ethyl-3-methylimidazolium trifluoromethanesulfonate,
[EMIM] [TfO]
· 1-n-Butyl-3-methylimidazolium hexafluoroantimonate,
[BMIM] [SbF6]
· 1-Octyl-3-methylimidazolium hexafluorophosphate.
[OMIM][PF6]
The above fluorinated ionic liquids, whose structures are
given in appendix B, have been selected because IDAC data for phosphonium-based
FILs were found to be rare. In addition, these ionic liquids were selected
because of their availability. Before use, they were heated at T =
353.15 K for seven hours under vacuum, using a vacuum pump, to remove all
possible traces of impurities, including moisture. For all solvents, stated
purities, densities and refractive indices are provided in tables C-1 through
C-3 in appendix C. Densities of purified samples were measured by the vibrating
tube method using a DMA 5000 Anton Paar densitometer. Refractive index
measurements were carried out using an RX-7000á automatic digital
refractometer. Both properties were measured in the Thermodynamics Research
Unit laboratory. Solutes, including n-alkanes, alk-1-enes, alk-1-ynes,
alkanols, cycloalkanes, alkylbenzenes and
ketones were used without any purification since impurities
were separated by the GC during the measurement process. Diatomaceous earth,
celite (Chromosorb W HP 80/100 mesh) was used as inert solid support onto which
the solvent was coated. It was purified by vacuum heating under the same
conditions as the ionic liquid. Dichloromethane was used as solvent to aid
uniform coating of the ionic liquid onto the inert solid support and removed
afterwards by evaporation. Dry helium was used as carrier gas.
4.1.2. Experimental set up
Experiments were performed using a Shimadzu GC-2014 gas
chromatograph apparatus, equipped with a thermal conductivity detector, an
auto-sampler and auto-injector. Retention times and chromatograms related to
each run were made available on a PC monitor by means of a GC solution
workstation software. The set up, shown in Photograph 4-1, is programmable so
that it can carry out injections of samples from 125 different vials and
acquire data with minimum human supervision.

Photograph 4-1: Gas-Liquid Chromatography
equipment.
1. Vials; 2. Tray; 3. Auto-sampler (arm); 4. Column oven; 5. Soap
bubble flow-meter; 6. Auto-
injector; 7. GC screen; 8. Operation panel; 9.
PC monitor
4.1.3. Experimental procedure
The experimental procedure used in this work has been well
documented by numerous authors (David et al. 2003, Letcher et al. 2003a,b and
Deenadayalu et al. 2005). To check for adsorption problems, two different
stainless steel columns of length 1 m and 4.1 mm inner diameter were used with
two different mass percent packings. To avoid adsorption effects, mass percent
packings of the ionic liquid that are large enough were used. Before packing,
the columns were washed with hot soapy water, rinsed with cold water and
flushed with acetone to minimize the drying time. The original and final masses
of the ionic liquid and chromosorb mixture were in agreement to within 0.0005
g. Measurements were done at different temperatures between (303.15 and 373.15)
K, i.e. (303, 313.15, 323.15, 333.15, 353.15, 363.15 and 373.15) K.
Reproducibility was checked by undertaking three experimental runs. It was
observed that retention times were reproducible within 0.05 minutes. The flow
rate of dry helium, the carrier gas, was determined with the aid of a soap
bubble flow meter placed at the outlet of the detector. The flow rates were
corrected for water vapour pressure and varied from 0.3 to 0.7
um3.s-1 .The carrier gas flow rate was allowed to
stabilize for at least 15 min prior to any series of runs. The pressure drop
through the column varied from (25 to 50) kPa, providing conducive retention
times and sharp peaks. The injected volumes ranged between 0.1 and 0.5 ul and
were considered small enough to comply with the condition of infinite dilution
of the solutes on the column. Both the injector and the detector were at
T = 523.15 K. More details on the experimental parameters and
variables needed to compute infinite dilution activity coefficients by means of
equation (3-10), are discussed below.
4.1.3.1 Temperature control
The equipment, not only controls the temperature using a
thermostat, but also displays its value
5
on the monitor. The column oven temperature was known with an
accuracy of #177; 0.01 K and a stability of 0.05 K. The design of the GC was
such that an electronically controlled thermostat was used to reliably control
the column temperature.
4.1.3.2 Pressure measurement
The outlet pressure which is the same as the atmospheric
pressure was measured with the aid of a digital barometer with an uncertainty
of #177;0.30 %. The pressure drop through the packed column was fixed by the
equipment, depending on the inert gas flow-rate set by the operator. The
uncertainty in the inlet pressure measurement was #177;0.50 %.
4.1.3.3 Flow-rate measurement
A bubble soap flow-meter consisting of a 100 ml calibrated
cylinder was used for the determination of helium flow rate. The uncertainty in
the flow rate measurement was estimated as #177;0.20 %.
4.1.3.4 Infinite dilution range
Injections between 0.1 and 0.5ul were considered small enough
to comply with the infinite dilution requirement. It is however advisable to
check whether the retention time for a solute at the selected injection volume
and flow rate remains the same as when it is part of a mixture.
4.1.3.5 Column packing
This is the most critical step when undertaking measurements
via the Gas-Liquid Chromatography technique. Large error margins are caused by
a careless column packing. The uncertainty in determining the mass of the
solvent loaded into the column was #177;0.03 %.
Column cleaning
The column was washed with soapy water and flashed with acetone
to facilitate drying with air.
Determination of solvent number of moles
The following procedure was employed:
1. The mass of an empty flask was measured using a digital
balance;
2. Chromosorb, the solid support for the solvent was added to the
flask and weighed;
3. The amount of solvent to be added was roughly calculated on
the basis of the desired percent loading of the solvent;
4. The solvent was added and its weight found accurately.
Coating the support with the IL
Dichloromethane was added to the flask content to distribute
the solvent evenly on chromosorb. Thereafter, a rotary evaporator was used to
remove the Dichloromethane. This step ended when the mass of the mixture in the
content was equal to the one measured before adding dichloromethane.
Filling the column
The support loaded with IL was filled in the column with the
aid of a vacuum pump. One had to
make sure that the load was equally
distributed inside the column. The mass of the packed
column had to be known before and after each series of runs to
check for a probable elution of the solvent.
4.2. The inert gas
stripping technique
4.2.1. Chemicals
To validate the method, experiments were performed with NMP as
solvent whereas n-hexane, hex-1-ene, hex-1-yne, methanol, cyclohexane, benzene
and acetone were used as solutes in the ionic liquid
trihexyltetradecylphosphonium bis (trifluoromethylsulfonyl) imide, [3C6C14P]
[BTI]. Appendix C provides additional information about the solvents, including
their source, purity, density and refractive index. No further purification was
undertaken for the solutes as they were of high purity. Solvents were purified
by heat treatment under vacuum.
4.2.2. Experimental Set-up
As part of this study, it was intended to construct an entire
inert gas stripping set up with an equilibrium cell able to accommodate small
volumes of samples, less than 50 g. This was a necessity since ionic liquids
are very expensive chemicals. The second reason why a dilutor cell was needed
is for systems that are not suitable when using the GLC technique. Examples of
these are systems involving solutes that are solid at room temperature, solvent
mixtures and those leading to a very long retention time. Design parameters for
the dilutor cell were discussed in the previous chapter. The greatest part of
the design work was centered on the dilutor cell as it is the most determinant
piece of the set up performance. Figure 4-1 presents the simplified flow
diagram of the set up used in this study, which is similar to the one described
by Krummen et al. (2000) and Coquelet and Richon (2005). Photograph 4-2 gives
the experimental set up of the inert gas stripping apparatus.
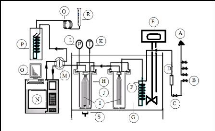
Figure 4-1: Flow diagram of the experimental
set up for the inert gas stripping method.
A-Helium, Nitrogen and air supply
for the GC; B- Nitrogen line; C-Valve; D- flow regulator; E-
Immersion
temperature controller; F-Coil tube (Heat exchanger); G-Transparent acrylic
bath; H- Dilutor
cell; I-Capillaries; J-Presaturation cell; K-Platinum
resistance thermometer; L-Pressure transducer; M-
Sampling valve; N-GC
apparatus; O-PC monitor; P-Cold trap; Q- Coil tube (Heat exchanger);
R-Soap
bubble flow-meter; S-Magnetic stirrer.
4.2.2.1. Gas cylinders
Four gases are used in this work:
· Nitrogen as stripping gas;
· Helium as carrier gas for the GC apparatus;
· Air and Hydrogen to produce the ignition flame for the GC
(FID only).
The four cylinders containing the above gases are fitted with
regulators. Nitrogen flow rate is controlled by a smaller regulator. Its value
is determined by means of a soap bubble flow meter.
4.2.2.2. Water bath
An 18-litre transparent acrylic water bath, with maximum
allowed temperature of 70 oC, was used to accommodate the cells
during experiments. During experiments, leaks could be easily detected by the
observation of gas bubbles, due to the transparency of the bath. A Haake
Difisons temperature controller kept the water in the bath at a constant
temperature set before each run. The nitrogen line (1/4 inch inner diameter and
12 m long) was coiled and immersed in the water bath to allow the gas to
equilibrate to the set-point temperature before entering the cells. In order to
reduce heat loss to the atmosphere, the water surface in the bath was
completely covered with polystyrene chips. The temperature stability of the
bath was #177;0.1 K.
4.2.2.3. Cells
The two glass cells are identical and have a total volume of
50 cm3 each. They were made for the purpose of this work by a Durban
glass blower, Mr. Peter Siegling. Metallic parts were manufactured and fitted
by the School of Chemical Engineering workshop staff members, Mr. Ken Jack and
Mr. Kelly Robertson. The shape is similar to the cells previously used by other
researchers (Coquelet and Richon 2005). Mass transfer considerations discussed
by Richon et al. (1980) were taken into account to determine the cell height
using equation (3-95), assuming
the degree of the equilibrium attainment = 0.99 From the
literature, ranges of different
properties related to FILs (See table 2-2) were used in
equation (3-95) to find out the most suitable height for the cell. The same
procedure was used by Li et al. (1993) to find out the optimum height of the
dilutor cell used in the study of IDAC`s for nonelectrolytes solutes in water.
For systems involving ionic liquids, the presaturator cell was removed. As
shown in Photograph 4-3, the dilutor cell is fitted with ten stainless steel
capillaries (0.1 mm inner diameter) purchased from Anatech, through which the
stripping gas is introduced. During experiments, they should be placed in such
a way that bubbles are not directed to the vortex. This will prevent bubbles
coalescence (George 2008). A class A Pt-100 temperature sensor (length 250 mm,
outer diameter 3 mm and limiting error of 0.25 oC) fitted with
stainless steel pot seal and a Sensotec pressure transducer are inserted in
order to measure the temperature of
the mixture and the pressure in the dilutor cell. To obtain
accurate readings, both sensors had to be calibrated. A CTH 6500 digital
thermometer (accuracy: #177;0.03 %) and a CPH 6000 pressure calibration
standard (accuracy: #177;0.1 %) for temperature and pressor sensor
calibrations, respectively. The bolt (G) along with the Teflon piece (H) seal
the cell to ensure that no portion of nitrogen flows through other channels
than the provided capillaries. Agitation of the solution contained in the cell
is achieved by means of a magnetic stirrer. Other features of the designed cell
are given by Photograph 4-3.
4.2.2.4. Cold trap
The stream leaving the dilutor cell contains not only
nitrogen, but also solute and probably solvent vapours. A cold trap serves as a
separation unit to ensure that the flow rate determined by the soap bubble
flow-meter is actually the one of nitrogen which is required in the infinite
dilution activity coefficient computation equation. Failure to condense solute
and solvent vapours will lead to inaccurate data. The cold trap as shown in
figure 4-2 consists of two chambers. The upper chamber (A) contains an
ice-acetone solution in which a 1/4 inch ID copper coil is completely immersed.
The outlet gas stream from the dilutor cell flows through the coils and ends
its path in the lower chamber (B) where the condensate is trapped. Nitrogen,
the only gaseous component after this process, rises up to exit through the
pipe (C) and makes its way to the soap bubble flow-meter (J). Valve (E) can be
opened to drain out the liquid captured in chamber (B).

Photograph 4-2: Set-up of the inert gas
stripping apparatus. A-flow regulator; B-Coil tube
(Heat exchanger);
C-Presaturation cell; D- Dilutor cell; E-Magnetic stirrer; F-Sampling
valve;
G-Cold trap; H-GC apparatus; I-GC lines; J-Soap bubble flow-meter;
K-Pressure transducer; L-
Pressure and temperatures displays; M-Immersion
temperature controller; N-Polystyrene chips;
O-Transparent acrylic bath.

Photograph 4.3: The dilutor cell. A-Glass
still; B-Capillaries; C-Temperature probe (Pt 100);
D-Gas inlet; E-Gas
outlet; F-Pressure transducer tube; G-Bolt (seal); H-Teflon plug (seal).
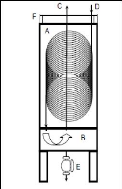
Figure 4-2: Cross Section of the cold trap to
illustrate its inner workings (George 2008)
A - Upper chamber, B - lower
chamber, C - gas inlet, D - non-condensable gas outlet, E -
release valve, F
- lid.
4.2.2.5. Gas Chromatography apparatus
In this work, a SHIMADZU GC 14A gas chromatograph equipped
with a FID detector was used. The FID has the advantage over the TCD to be very
sensitive to small amounts of solutes injected. GC settings and column
conditions during experiments are displayed in table 4-1. To avoid condensation
of the solute as the stream flows from the dilutor cell outlet to the GC
injection port via the six-port sampling valve, these lines had to be heated
and thermostated at a temperature approximately 40 oC higher than
the system temperature (Krummen et al. 2000).
Table 4-1: GC specification and set-up.
Column CRS; 2m x 1/8`; Packed column
GC Program Clarity work station
Detector type FID
Carrier gas Helium
Injection Port Temperature 493.15 K
Column Oven Temperature 393.15 K-453.15 K
Detector Temperature 493.15 K
4.2.3. Experimental procedure
First, the cells were cleaned and thereafter filled with the
required components. The solvent was poured into each cell. The mass of the
solvent in the dilutor cell had to be known accurately. The solute was injected
into the dilutor cell in very small concentration to comply with the infinite
dilution requirement, less than 0.001 mole fraction. The injected volume ranged
between (10 and 25). Density data of the solvent (given in appendix C) were
used to
determine by difference the vapour phase volume. The cells
were then sealed and fitted onto the set up. The equipment was checked for
leaks, the cold trap upper chamber was filled with acetone-ice mixture, the GC
apparatus and all electrical equipments with desired settings were switched on.
Thereafter the procedure below was followed:
1. The water bath, the sampling valve, the mixture in the
dilutor cell and all other tubing were allowed to equilibrate to their
respective set-point temperatures, the magnetic stirrer being switched on;
2. The inert gas was allowed to flow through the cell. A
bubble soap flow-meter was used to measure the flow rate. Li et al. (1993)
suggested that the infinite dilution activity coefficient obtained should be
independent of the flow rate;
3. The gas sampling valve was set to the fill? position,
allowing the inert gas to flow for some minutes;
4. The gas sampling valve was set to the inject? position for
one to two minutes;
5. The sampling valve was set back to the fill? position;
6. Steps 4 and 5 were repeated periodically. The time
interval between two successive injections depended on the system under
investigation. The natural logarithm of the solute peak area was expected to
decrease linearly with time as illustrated by figure 4-3 which was taken from a
publication by Krummen et al. (2000);
7. After a number of runs with sufficient data to compute
infinite dilution activity coefficient values, the experiment was ended.
Equation (3-90) was used to determine experimental IDAC values.
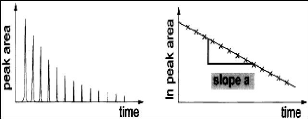
Figure 4-3: Typical plots of solute GC peak area
and ln (solute peak area) versus time.
CHAPTER FIVE: RESULTS
Chapter overview
Results presented in this work consist of the following:
· Infinite dilution activity coefficients data for various
organic solutes in n-hexadecane and seven different FILs, obtained from
Gas-Liquid Chromatography;
· Excess molar enthalpies at infinite dilution of the same
solutes in the fluorinated ionic liquids, calculated from experimental infinite
dilution activity coefficients data;
· Correlation of experimental infinite dilution activity
coefficient data with temperature and the carbon chain length of solutes;
· Infinite dilution activity coefficients data for six
organic solutes in NMP and one fluorinated ionic liquid;
· Limiting selectivities and capacities of the seven
investigated fluorinated ionic liquids for selected separation problems;
· Estimation of experimental errors in determining activity
coefficients, Excess molar enthalpies, selectivities and capacities at infinite
dilution.
Equations (3-10) and (3-90) were used to calculate IDACs from
experimental parameters obtained by the GC method and the IGST respectively.
Excess molar enthalpies at infinite dilution were determined using equation
(2-11). Some experimental data obtained in this study have been published as
part of collaborative work with Prof. Nirmala Deenadayalu ([C13C8] [Tf2N]) and
Mr. Eugene Olivier ([EMIM] [TfO], [BMIM] [SbF6] and [MOIM] [PF6]). These
results are also included in this chapter.
5.1. Results from Gas-Liquid Chromatography
5.1.1. Hexadecane
Table 5-1: Infinite dilution activity
coefficients of selected organic solutes in n-hexadecane.
Solutes
|
T /K
|
|
|
R.D#./ %
|
n-pentane n-pentane n-hexane n-hexane n-hexane n-heptane
n-heptane
|
323.15 333.15 303.15 313.15 323.15 303.15
? )
1
323.15
lit
|
0.839 0.870 0.882 0.892 0.896 0.882 0.890
|
0.814a
0.833
a
0.880-0.904bc
0.870-0.910
b
0.860-0.905 a bd
0.916-0.927 b
0.867-0.921
ad
|
3.1 4.4 1.8 1.4 0.6 4.3 0.4
|
Hex-1-ene
|
323.15
|
0.862
|
0.855 a
|
0.8
|
Hept-1-ene
|
323.15
|
0.866
|
0.902 a
|
4.0
|
Cyclopentane
|
323.15
|
0.695
|
0.686 a
|
1.3
|
Cyclohexane
|
303.15
|
0.775
|
0.795 b
|
2.5
|
Cyclohexane
|
313.15
|
0.776
|
0.778 b
|
0.3
|
Cyclohexane
|
323.15
|
0.736
|
0.739-0.787 ad
|
3.5
|
Benzene
|
303.15
|
1.071
|
1.105-1.110 be
|
3.3
|
Benzene
|
313.15
|
1.010
|
1.006-1.051 b
|
0.4
|
Benzene
|
323.15
|
0.953
|
0.932-0.995 ad
|
2.1
|
Toluene
|
323.15
|
0.953
|
0.941 a
|
1.3
|
Dichloromethane
|
303.15
|
1.428
|
1.440b
|
0.8
|
|
a Schult et al. (2001); bChien et al
(1981) c Cruickshank et al. (1966b); d Castells et al.
(1990);
e Gainey and Young (1968)
# Relative deviation, R.D., given by
5.1.2. Trihexyltetradecylphosphonium bis
(trifluoromethylsulfonyl) imide,
[3C6C14P] [Tf2N]
Table 5-2: Activity coefficients at infinite
dilution of organic solutes in
trihexyltetradecylphosphonium bis (trifluoromethylsulfonyl)
imide with solvent column loading
n3 = 1.577 mmol (29.5 %) at T = (313.15,
333.15,
|
353.15 and 373.15) K.
|
|
Experimental
|
at /K
|
|
|
Solute
|
n3/ mmol
|
T=313.15
|
T=333.15
|
T=353.15
|
T=373.15
|
n-pentane
|
1.577
|
0.970
|
0.976
|
0.988
|
0.990
|
n-hexane
|
1.577
|
1.101
|
1.119
|
1.126
|
1.130
|
n-heptane
|
1.577
|
1.163
|
1.249
|
1.315
|
1.434
|
n-octane
|
1.577
|
1.405
|
1.443
|
1.459
|
1.495
|
n-nonane
|
1.577
|
1.607
|
1.681
|
1.769
|
1.871
|
Pent-1-ene
|
1.577
|
0.810
|
0.833
|
0.841
|
0.862
|
Hex-1-ene
|
1.577
|
0.909
|
0.932
|
0.941
|
0.943
|
Hept-1-ene
|
1.577
|
1.030
|
1.064
|
1.102
|
1.123
|
Oct-1-ene
|
1.577
|
1.163
|
1.384
|
1.610
|
1.905
|
Pent-1-yne
|
1.577
|
0.611
|
0.640
|
0.662
|
0.701
|
Hex-1-yne
|
1.577
|
0.691
|
0.707
|
0.718
|
0.730
|
Hept-1-yne
|
1.577
|
0.730
|
0.747
|
0.764
|
0.780
|
Oct-1-yne
|
1.577
|
0.841
|
0.872
|
0.890
|
0.899
|
Nony-1-ne
|
1.577
|
0.850
|
0.912
|
0.954
|
0.977
|
Cyclopentane
|
1.577
|
0.686
|
0.696
|
0.714
|
0.723
|
Cyclohexane
|
1.577
|
0.797
|
0.800
|
0.802
|
0.805
|
Cycloheptane
|
1.577
|
0.865
|
0.882
|
0.895
|
0.910
|
Cyclooctane
|
1.577
|
0.965
|
1.000
|
1.065
|
1.119
|
Methanol
|
1.577
|
1.077
|
1.025
|
0.921
|
0.865
|
Ethanol
|
1.577
|
1.270
|
1.096
|
0.953
|
0.880
|
Propan-1-ol
|
1.577
|
1.279
|
1.155
|
1.070
|
0.954
|
Butan-1-ol
|
1.577
|
1.425
|
1.194
|
1.090
|
0.949
|
Benzene
|
1.577
|
0.390
|
0.403
|
0.414
|
0.432
|
Toluene
|
1.577
|
0.450
|
0.471
|
0.485
|
0.512
|
Acetone
|
1.577
|
0.299
|
0.318
|
0.328
|
0.332
|
Butan-2-one
|
1.577
|
0.317
|
0.329
|
0.331
|
0.333
|
|
Table 5-3: Activity coefficients at infinite
dilution of organic solutes in
trihexyltetradecylphosphonium bis (trifluoromethylsulfonyl)
imide with solvent column loading
n3 =2.236 mmol (31.7 %) at T = (313.15,
333.15,
|
353.15 and 373.15) K.
|
|
Experimental
|
at /K
|
|
|
Solute
|
n3/ mmol
|
T=313.15
|
T=333.15
|
T=353.15
|
T=373.15
|
n-pentane
|
2.236
|
0.950
|
0.980
|
0.992
|
1.014
|
n-hexane
|
2.236
|
1.091
|
1.103
|
1.122
|
1.130
|
n-heptane
|
2.236
|
1.139
|
1.257
|
1.309
|
1.412
|
n-octane
|
2.236
|
1.403
|
1.439
|
1.463
|
1.491
|
n-nonane
|
2.236
|
1.593
|
1.659
|
1.777
|
1.867
|
Pent-1-ene
|
2.236
|
0.802
|
0.815
|
0.843
|
0.838
|
Hex-1-ene
|
2.236
|
0.905
|
0.910
|
0.919
|
0.941
|
Hept-1-ene
|
2.236
|
1.034
|
1.066
|
1.100
|
1.121
|
Oct-1-ene
|
2.236
|
1.159
|
1.382
|
1.606
|
1.901
|
Pent-1-yne
|
2.236
|
0.615
|
0.632
|
0.664
|
0.697
|
Hex-1-yne
|
2.236
|
0.695
|
0.711
|
0.722
|
0.734
|
Hept-1-yne
|
2.236
|
0.722
|
0.751
|
0.760
|
0.784
|
Oct-1-yne
|
2.236
|
0.831
|
0.858
|
0.882
|
0.899
|
Nony-1-ne
|
2.236
|
0.856
|
0.918
|
0.958
|
0.981
|
Cyclopentane
|
2.236
|
0.688
|
0.700
|
0.712
|
0.719
|
Cyclohexane
|
2.236
|
0.793
|
0.794
|
0.794
|
0.795
|
Cycloheptane
|
2.236
|
0.875
|
0.880
|
0.887
|
0.900
|
Cyclooctane
|
2.236
|
0.961
|
0.996
|
1.073
|
1.121
|
Methanol
|
2.236
|
1.089
|
1.027
|
0.923
|
0.861
|
Ethanol
|
2.236
|
1.268
|
1.094
|
0.949
|
0.884
|
Propan-1-ol
|
2.236
|
1.281
|
1.149
|
1.074
|
0.952
|
Butan-1-ol
|
2.236
|
1.421
|
1.188
|
1.080
|
0.959
|
Benzene
|
2.236
|
0.392
|
0.407
|
0.420
|
0.442
|
Toluene
|
2.236
|
0.454
|
0.473
|
0.487
|
0.508
|
Acetone
|
2.236
|
0.295
|
0.300
|
0.320
|
0.330
|
Butan-2-one
|
2.236
|
0.325
|
0.326
|
0.333
|
0.335
|
|
Table 5-4: Average activity coefficients at
infinite dilution of organic solutes in
trihexyltetradecylphosphonium bis (trifluoromethylsulfonyl)
imide at T = (313.15, 333.15,
353.15 and 373.15) K.
Experimental at /K
Solute
|
T=313.15
|
T=333.15
|
T=353.15
|
T=373.15
|
n-pentane
|
0.960
|
0.978
|
0.990
|
1.002
|
n-hexane
|
1.096
|
1.111
|
1.124
|
1.130
|
n-heptane
|
1.151
|
1.253
|
1.312
|
1.423
|
n-octane
|
1.404
|
1.441
|
1.461
|
1.493
|
n-nonane
|
1.600
|
1.670
|
1.773
|
1.869
|
Pent-1-ene
|
0.806
|
0.824
|
0.842
|
0.850
|
Hex-1-ene
|
0.907
|
0.921
|
0.930
|
0.942
|
Hept-1-ene
|
1.032
|
1.065
|
1.101
|
1.122
|
Oct-1-ene
|
1.161
|
1.383
|
1.608
|
1.903
|
Pent-1-yne
|
0.613
|
0.636
|
0.663
|
0.699
|
Hex-1-yne
|
0.693
|
0.709
|
0.720
|
0.732
|
Hept-1-yne
|
0.726
|
0.749
|
0.762
|
0.782
|
Oct-1-yne
|
0.836
|
0.865
|
0.886
|
0.899
|
Non-1-yne
|
0.853
|
0.915
|
0.956
|
0.979
|
Cyclopentane
|
0.687
|
0.698
|
0.713
|
0.721
|
Cyclohexane
|
0.795
|
0.797
|
0.798
|
0.800
|
Cycloheptane
|
0.870
|
0.881
|
0.891
|
0.905
|
Cyclooctane
|
0.963
|
0.998
|
1.069
|
1.120
|
Methanol
|
1.083
|
1.026
|
0.922
|
0.863
|
Ethanol
|
1.269
|
1.095
|
0.951
|
0.882
|
Propan-1-ol
|
1.280
|
1.152
|
1.072
|
0.953
|
Butan-1-ol
|
1.423
|
1.191
|
1.085
|
0.954
|
Benzene
|
0.391
|
0.405
|
0.417
|
0.437
|
Toluene
|
0.452
|
0.472
|
0.486
|
0.510
|
Acetone
|
0.297
|
0.327
|
0.332
|
0.334
|
Butan-2-one
|
0.321
|
0.328
|
0.324
|
0.331
|
|
Table 5-5: Partial molar excess enthalpies at
infinite dilution for organic solutes in the
ionic liquid trihexyltetradecylphosphonium bis
(trifluoromethylsulfonyl) imide, calculated from
the Gibbs-Helmholtz
equation.
SOLUTE
|
Linear regression using Eq.(2-11)
|
|
|
|
|
n-pentane
|
-0.083
|
0.223
|
0.995
|
-0.69
|
n-hexane
|
-0.061
|
0.286
|
0.982
|
-0.51
|
n-heptane
|
-0.398
|
1.413
|
0.987
|
-3.31
|
n-octane
|
-0.116
|
0.710
|
0.990
|
-0.96
|
n-nonane
|
-0.306
|
1.440
|
0.988
|
-2.54
|
Pent-1-ene
|
-0.107
|
0.126
|
0.985
|
-0.89
|
Hex-1-ene
|
-0.072
|
0.132
|
0.995
|
-0.60
|
Hept-1-ene
|
-0.166
|
0.563
|
0.994
|
-1.38
|
Oct-1-ene
|
-0.953
|
3.186
|
0.997
|
-7.92
|
Pent-1-yne
|
-0.253
|
0.312
|
0.981
|
-2.10
|
Hex-1-yne
|
-0.105
|
-0.029
|
0.997
|
-0.87
|
Hept-1-yne
|
-0.140
|
0.129
|
0.991
|
-1.17
|
Oct-1-yne
|
-0.142
|
0.278
|
0.984
|
-1.18
|
Nony-1-ne
|
-0.270
|
0.710
|
0.970
|
-2.24
|
Cyclopentane
|
-0.097
|
-0.065
|
0.990
|
-0.81
|
Cyclohexane
|
-0.011
|
-0.192
|
0.982
|
-0.10
|
Cycloheptane
|
-0.075
|
0.100
|
0.987
|
-0.63
|
Cyclooctane
|
-0.303
|
0.923
|
0.978
|
-2.52
|
Methanol
|
0.459
|
-1.372
|
0.978
|
3.81
|
Ethanol
|
0.723
|
-2.078
|
0.991
|
6.02
|
Propan-1-ol
|
0.557
|
-1.528
|
0.987
|
4.63
|
Butan-1-ol
|
0.757
|
-2.075
|
0.990
|
6.30
|
Benzene
|
-0.211
|
-0.269
|
0.980
|
-1.75
|
Toluene
|
-0.228
|
-0.067
|
0.986
|
-1.90
|
Acetone
|
-0.079
|
-0.880
|
0.994
|
-0.66
|
Butan-2-one
|
-0.218
|
-0.514
|
0.998
|
-1.81
|
|
0.8
0.6
ln(1113)
0.4
0.2
0
-0.2
2.6 2.7 2.8 2.9 3 3.1 3.2 3.3
1000K/T
Figure 5-1: Plots of versus for alkanes in
[3C6C14P] [Tf2N] together with a
linear correlation of the data using the Gibbs-Helmholtz
equation; () n-pentane,
() n-hexane, (?) n-heptane and (?) n-octane, ()
n-nonane.
2.6 2.7 2.8 2.9 3 3.1 3.2 3.3
1000K/T
ln(1313)
-0.2
-0.4
0.8
0.6
0.4
0.2
0.0
Figure 5-2: Plots of versus for alk-1-enes in
[3C6C14P] [Tf2N] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
pent-1-ene, () hex-1-ene,
(?) hept-1-ene and (?) oct-1-ene.
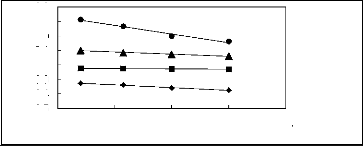
ln(1313)
-0.1
-0.2
-0.3
-0.4
-0.5
0.2
0.1
0
2.6 2.8 3 3.2 3.4
1000K/T
Figure 5-3: Plots of versus for cycloalkanes in
[3C6C14P] [Tf2N] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
cyclopentane, () cyclohexane,
(?) cycloheptane and (?) Cyclooctane.
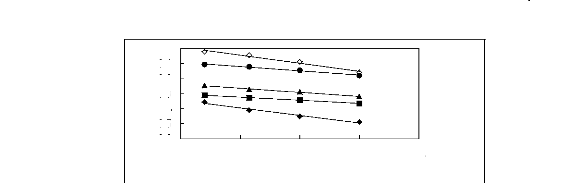
0.0
-0.1
-0.2
ln( LP 13)
-0.3
-0.4
-0.5
-0.6
2.6 2.8 3 3.2 3.4
1000K/T
Figure 5-4: Plots of versus for alk-1-ynes in
[3C6C14P] [Tf2N] together with a linear
correlation of the data using the Gibbs-Helmholtz equation;
()pent-1-yne, () hex-1-yne,
(?) hept-1-yne, (?) oct-1-yne and ()
n-nonyne.
lii( LP 13)
|
0.4 0.3 0.2 0.1
0 -0.1 -0.2
|
|
|
2.6 2.7 2.8 2.9 3 3.1 3.2 3.3
1000K/T
Figure 5-5: Plots of versus for alkanols in
[3C6C14P] [Tf2N] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
methanol, () ethanol,
(?) propan-1-ol and (?) butan-1-ol.
ln( LP13)
|
-0.5 -0.6 -0.7 -0.8 -0.9
-1
|
|
|
2.6 2.8 3 3.2 3.4
1000K/T
Figure 5-6: Plots of versus for alkylbenzenes in
[3C6C14P] [Tf2N] together with a
linear correlation of the data using the Gibbs-Helmholtz
equation; () benzene and () toluene.
1n(L13)
|
-1.08 -1.12 -1.16 -1.20 -1.24
|
|
|
2.6 2.7 2.8 2.9 3 3.1 3.2 3.3
1000K/T
Figure 5-7: Plots of versus for ketones in
[3C6C14P] [Tf2N] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
acetone and () butan-2-one.
0 1 2 3 4 5 6 7 8 9 10
Number of Carbon atoms, Nc
Figure 5-8: Plots of versus the carbon number of
the solute at 313.15 K for () n-alkanes,
() alk-1-enes, (?) cycloalkanes, (?) alk-1-ynes () ketones,
(?) alkanols and (?)
alkylbenzenes in [3C6C14P] [Tf2N].
5.1.3. Trihexyltetradecylphosphonium tetrafluoroborate,
[3C6C14P] [BF4]
Table 5-6: Activity coefficients at infinite
dilution of organic solutes in
trihexyltetradecylphosphonium tetrafluoroborate with solvent
column loading
n3 = 2.395 mmol (25.09 %) at T = (313.15,
333.15,
|
353.15 and 373.15) K.
|
|
|
Experimental
|
at /K
|
|
|
Solute
|
n3/ mmol
|
T=313.15
|
T=333.15
|
T=353.15
|
T=373.15
|
n-pentane.
|
2.395
|
1.231
|
1.211
|
1.208
|
1.199
|
n-hexane
|
2.395
|
1.392
|
1.368
|
1.362
|
1.353
|
n-heptane
|
2.395
|
1.579
|
1.538
|
1.525
|
1.516
|
n-octane
|
2.395
|
1.792
|
1.769
|
1.711
|
1.697
|
n-nonane
|
2.395
|
2.053
|
1.965
|
1.936
|
1.912
|
n-decane
|
2.395
|
2.400
|
2.236
|
2.184
|
2.125
|
Pent-1-ene
|
2.395
|
0.971
|
0.984
|
0.992
|
1.017
|
Hex-1-ene
|
2.395
|
1.117
|
1.120
|
1.125
|
1.131
|
Hept-1-ene
|
2.395
|
1.247
|
1.250
|
1.254
|
1.262
|
Oct-1-ene
|
2.395
|
1.403
|
1.412
|
1.413
|
1.419
|
Non-1-ene
|
2.395
|
1.630
|
1.589
|
1.568
|
1.596
|
Pent-1-yne
|
2.395
|
0.569
|
0.591
|
0.624
|
0.690
|
Hex-1-yne
|
2.395
|
0.610
|
0.646
|
0.682
|
0.705
|
Hept-1-yne
|
2.395
|
0.670
|
0.697
|
0.749
|
0.820
|
Octy-1-ne
|
2.395
|
0.760
|
0.818
|
0.870
|
0.923
|
Non-1-yne
|
2.395
|
0.784
|
0.871
|
0.950
|
1.025
|
Cyclopentane
|
2.395
|
0.841
|
0.816
|
0.813
|
0.802
|
Cyclohexane
|
2.395
|
0.970
|
0.935
|
0.919
|
0.905
|
Cycloheptane
|
2.395
|
1.047
|
1.007
|
0.982
|
0.965
|
Cyclooctane
|
2.395
|
1.112
|
1.088
|
1.073
|
1.063
|
Methanol
|
2.395
|
0.548
|
0.500
|
0.466
|
0.453
|
Ethanol
|
2.395
|
0.611
|
0.553
|
0.507
|
0.479
|
Benzene
|
2.395
|
0.432
|
0.440
|
0.447
|
0.464
|
Toluene
|
2.395
|
0.524
|
0.539
|
0.546
|
0.564
|
Ethylbenzene
|
2.395
|
0.659
|
0.665
|
0.682
|
0.696
|
Acetone
|
2.395
|
0.436
|
0.437
|
0.438
|
0.439
|
Butan-2-one
|
2.395
|
0.450
|
0.452
|
0.455
|
0.457
|
|
Table 5-7: Activity coefficients at infinite
dilution of organic solutes in
trihexyltetradecylphosphonium tetrafluoroborate with solvent
column loading
n3 = 2.236 mmol (30.97 %) at T = (313.15,
333.15,
|
353.15 and 373.15) K.
|
|
|
Experimental
|
at /K
|
|
|
Solute
|
n3/ mmol
|
T=313.15
|
T=333.15
|
T=353.15
|
T=373.15
|
n-pentane
|
2.694
|
1.285
|
1.269
|
1.230
|
1.193
|
n-hexane
|
2.694
|
1.408
|
1.400
|
1.358
|
1.311
|
n-heptane
|
2.694
|
1.577
|
1.590
|
1.527
|
1.458
|
n-octane
|
2.694
|
1.788
|
1.729
|
1.701
|
1.623
|
n-nonane
|
2.694
|
2.069
|
1.991
|
1.912
|
1.812
|
n-decane
|
2.694
|
2.360
|
2.290
|
2.172
|
2.069
|
Pent-1-ene
|
2.694
|
1.017
|
0.990
|
0.958
|
0.929
|
Hex-1-ene
|
2.694
|
1.101
|
1.090
|
1.083
|
1.073
|
Hept-1-ene
|
2.694
|
1.273
|
1.248
|
1.234
|
1.192
|
Oct-1-ene
|
2.694
|
1.449
|
1.402
|
1.393
|
1.345
|
Non-1-ene
|
2.694
|
1.640
|
1.607
|
1.580
|
1.476
|
Pent-1-yne
|
2.694
|
0.599
|
0.611
|
0.638
|
0.594
|
Hex-1-yne
|
2.694
|
0.596
|
0.650
|
0.668
|
0.697
|
Hept-1-yne
|
2.694
|
0.806
|
0.789
|
0.793
|
0.746
|
Oct-1-yne
|
2.694
|
0.738
|
0.820
|
0.838
|
0.839
|
Non-1-yne
|
2.694
|
0.862
|
0.871
|
0.894
|
0.931
|
Cyclopentane
|
2.694
|
0.845
|
0.838
|
0.809
|
0.812
|
Cyclohexane
|
2.694
|
0.980
|
0.947
|
0.887
|
0.883
|
Cycloheptane
|
2.694
|
0.993
|
0.965
|
0.952
|
0.931
|
Cyclooctane
|
2.694
|
1.248
|
1.160
|
1.077
|
1.011
|
Methanol
|
2.694
|
0.526
|
0.482
|
0.446
|
0.381
|
Ethanol
|
2.694
|
0.547
|
0.513
|
0.495
|
0.423
|
Benzene
|
2.694
|
0.388
|
0.410
|
0.437
|
0.432
|
Toluene
|
2.694
|
0.528
|
0.523
|
0.574
|
0.584
|
Ethylbenzene
|
2.694
|
0.661
|
0.677
|
0.686
|
0.734
|
Acetone
|
2.694
|
0.426
|
0.427
|
0.428
|
0.431
|
Butan-2-one
|
2.694
|
0.438
|
0.442
|
0.447
|
0.451
|
|
Table 5-8: Average activity coefficients at
infinite dilution of organic solutes in
trihexyltetradecylphosphonium tetrafluoroborate at T =
(313.15, 333.15, 353.15 and 373.15) K.
|
|
Experimental at
|
/K
|
|
Solute
|
T=313.15
|
T=333.15
|
T=353.15
|
T=373.15
|
n-pentane.
|
1.258
|
1.240
|
1.219
|
1.196
|
n-hexane
|
1.400
|
1.384
|
1.360
|
1.332
|
n-heptane
|
1.578
|
1.564
|
1.526
|
1.487
|
n-octane
|
1.790
|
1.749
|
1.706
|
1.660
|
n-nonane
|
2.061
|
1.978
|
1.924
|
1.862
|
n-decane
|
2.380
|
2.263
|
2.178
|
2.097
|
Pent-1-ene
|
0.994
|
0.987
|
0.975
|
0.973
|
Hex-1-ene
|
1.109
|
1.105
|
1.104
|
1.102
|
Hept-1-ene
|
1.260
|
1.249
|
1.244
|
1.227
|
Oct-1-ene
|
1.426
|
1.407
|
1.403
|
1.382
|
Non-1-ene
|
1.635
|
1.598
|
1.574
|
1.536
|
Pent-1-yne
|
0.584
|
0.601
|
0.631
|
0.642
|
Hex-1-yne
|
0.603
|
0.648
|
0.675
|
0.701
|
Hept-1-yne
|
0.738
|
0.743
|
0.771
|
0.783
|
Oct-1-yne
|
0.749
|
0.819
|
0.854
|
0.881
|
Non-1-yne
|
0.823
|
0.871
|
0.922
|
0.978
|
Cyclopentane
|
0.843
|
0.827
|
0.811
|
0.807
|
Cyclohexane
|
0.975
|
0.941
|
0.903
|
0.894
|
Cycloheptane
|
1.020
|
0.986
|
0.967
|
0.948
|
Cyclooctane
|
1.180
|
1.124
|
1.075
|
1.037
|
Methanol
|
0.537
|
0.491
|
0.456
|
0.417
|
Ethanol
|
0.579
|
0.533
|
0.501
|
0.451
|
Benzene
|
0.410
|
0.425
|
0.442
|
0.448
|
Toluene
|
0.526
|
0.531
|
0.560
|
0.574
|
Ethylbenzene
|
0.660
|
0.671
|
0.684
|
0.715
|
Acetone
|
0.431
|
0.432
|
0.433
|
0.435
|
Butan-2-one
|
0.444
|
0.447
|
0.451
|
0.454
|
|
Table 5-9: Partial molar excess enthalpies at
infinite dilution for organic solutes in the
ionic liquid trihexyltetradecylphosphonium tetrafluoroborate,
calculated from the Gibbs-
Helmholtz equation.
SOLUTE
|
Linear regression using Eq.(2-11)
|
|
|
|
n-pentane.
|
0.096
|
-0.077
|
0.984
|
0.80
|
n-hexane
|
0.095
|
0.035
|
0.964
|
0.79
|
n-heptane
|
0.115
|
0.093
|
0.933
|
0.96
|
n-octane
|
0.144
|
0.123
|
0.989
|
1.20
|
n-nonane
|
0.192
|
0.108
|
0.997
|
1.60
|
n-decane
|
0.241
|
0.093
|
0.999
|
2.00
|
Pent-1-ene
|
0.044
|
-0.149
|
0.952
|
0.37
|
Hex-1-ene
|
0.018
|
0.065
|
0.949
|
0.10
|
Hept-1-ene
|
0.048
|
0.077
|
0.939
|
0.40
|
Oct-1-ene
|
0.056
|
0.174
|
0.940
|
0.47
|
Non-1-ene
|
0.118
|
0.115
|
0.988
|
0.98
|
Pent-1-yne
|
-0.195
|
0.082
|
0.975
|
-1.62
|
Hex-1-yne
|
-0.290
|
0.425
|
0.986
|
-2.40
|
Hept-1-yne
|
-0.124
|
0.087
|
0.925
|
-1.03
|
Oct-1-yne
|
-0.312
|
0.720
|
0.960
|
-2.60
|
Non-1-yne
|
-0.335
|
0.870
|
0.996
|
-2.78
|
Cyclopentane
|
0.088
|
-0.455
|
0.966
|
0.74
|
Cyclohexane
|
0.177
|
-0.594
|
0.967
|
1.48
|
Cycloheptane
|
0.140
|
-0.431
|
0.990
|
1.17
|
Cyclooctane
|
0.253
|
-0.642
|
0.999
|
2.10
|
Methanol
|
0.486
|
-2.169
|
0.996
|
4.04
|
Ethanol
|
0.472
|
-2.046
|
0.981
|
3.92
|
Benzene
|
-0.179
|
-0.316
|
0.978
|
-1.49
|
Toluene
|
-0.183
|
-0.068
|
0.925
|
-1.52
|
Ethylbenzene
|
-0.149
|
0.054
|
0.913
|
-1.24
|
Acetone
|
-0.017
|
-0.786
|
0.946
|
-0.14
|
Butan-2-one
|
-0.044
|
-0.671
|
0.993
|
-0.37
|
|
Chapter 5: Results
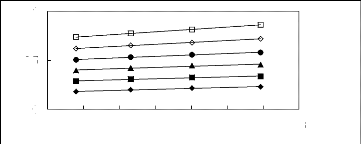
2.6 2.7 2.8 2.9 3 3.1 3.2 3.3
1000K/T
ln( LP 13)
0.5
0
1
Figure 5-9: Plots of versus for n-alkanes in
[3C6C14P] [BF4] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
n-pentane, () n-hexane,
(?) n-heptane, (?) n-octane, () n-nonane and (?)
n-decane.
|
0.6 0.5 0.4 0.3 0.2 0.1
0
-0.1
|
|
ln( LP 13)
|
|
|
|
|
2.6 2.8 3 3.2 3.4
1000K/T
Figure 5-10: Plots of versus for alk-1-enes in
[3C6C14P] [BF4] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
pent-1-ene, () hex-1-ene,
(?) hept-1ene, (?) oct-1-ene and () non-1-ene.
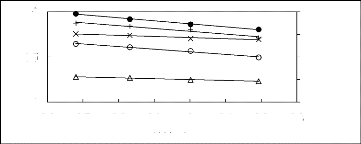
1n1 L13)
-0.5
-1
0
2.6 2.7 2.8 2.9 3 3.1 3.2 3.3
1000K/T
Figure 5-11: Plots of versus for alk-1-ynes in
[3C6C14P] [BF4] together with a linear
correlation of the data using the Gibbs-Helmholtz equation;
(?) pent-1-yne, (?) hex-1-yne,
(x) hept-1-yne, (+) oct-1-yne and (?)
non-1-yne.
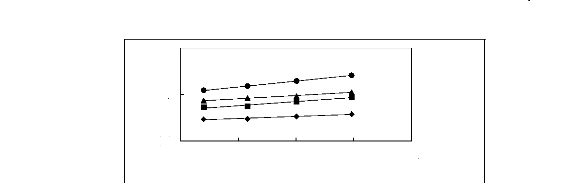
0.4
ln(1113)
0
-0.4
2.6 2.8 3 3.2 3.4
1000K/T
Figure 5-12: Plots of versus for cycloalkanes in
[3C6C14P] [BF4] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
cyclopentane, () cyclohexane,
(?) cycloheptane and (?) cyclooctane.
|
-0.4 -0.5 -0.6 -0.7 -0.8 -0.9
|
|
ln(1313)
|
|
|
|
|
2.6 2.8 3 3.2 3.4
1000K/T
Figure 5-13: Plots of versus for alkanols in
[3C6C14P] [BF4] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; (?)
methanol and (?) ethanol.
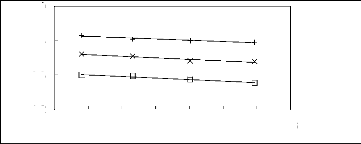
ln(111:13)
-0.4
-0.8
-1.2
0
2.6 2.7 2.8 2.9 3 3.1 3.2 3.3
1000K/T
Figure 5-14: Plots of versus for alkylbenzenes
in [3C6C14P] [BF4] together with a
linear correlation of the data using the Gibbs-Helmholtz
equation; (?) benzene, (x) toluene and
(+) ethylbenzene.
Figure 5-15: Plots of versus for ketones in
[3C6C14P] [BF4] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; (?)
acetone and (?) butan-2-one.
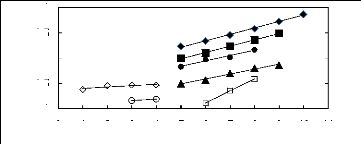
ln(119:13)
-0.5
0.5
-1
0
1
0 1 2 3 4 5 6 7 8 9 10 11
Number of carbon atoms, Nc
Figure 5-16: Plots of versus the number of
carbon atoms at 313.15 K for () n-alkanes,
() alk-1-enes, (?) alk-1-ynes, (?) cycloalkanes, () alkanols,
(?) alkylbenzenes and
(?) ketones in [3C6C14P] [BF4].
5.1.4. Trihexyltetradecylphosphonium
hexafluorophosphate, [3C6C14P] [PF6] Table 5-10: Activity
coefficients at infinite dilution of organic solutes in
trihexyltetradecylphosphonium hexafluorophosphate with
n3 = 1.615 mmol (25.1 %) at T =
(313.15, 333.15, 353.15
and 363.15) K.
|
Experimental
|
at /K
|
|
|
Solute
|
n3/mmol
|
T=313.15
|
T=333.15
|
T=353.15
|
T=363.15
|
n-pentane.
|
1.615
|
1.773
|
1.517
|
1.268
|
1.193
|
n-hexane
|
1.615
|
1.960
|
1.687
|
1.482
|
1.430
|
n-heptane
|
1.615
|
2.246
|
1.806
|
1.648
|
1.555
|
n-octane
|
1.615
|
2.528
|
2.120
|
1.869
|
1.812
|
n-nonane
|
1.615
|
2.774
|
2.426
|
2.088
|
1.984
|
n-decane
|
1.615
|
3.278
|
2.620
|
2.295
|
2.186
|
Pent-1-ene
|
1.615
|
1.421
|
1.236
|
1.066
|
1.049
|
Hex-1-ene
|
1.615
|
1.665
|
1.410
|
1.138
|
1.128
|
Hept-1-ene
|
1.615
|
1.857
|
1.581
|
1.321
|
1.269
|
Oct-1-ene
|
1.615
|
2.023
|
1.752
|
1.514
|
1.437
|
Non-1-ene
|
1.615
|
2.400
|
2.013
|
1.617
|
1.539
|
Dec-1-ene
|
1.615
|
2.788
|
2.276
|
1.827
|
1.750
|
Pent-1-yne
|
1.615
|
1.025
|
0.549
|
0.697
|
0.668
|
Hex-1-yne
|
1.615
|
1.145
|
0.649
|
0.780
|
0.732
|
Hept-1-yne
|
1.615
|
1.216
|
0.630
|
0.833
|
0.798
|
Oct-1-yne
|
1.615
|
1.369
|
0.754
|
0.962
|
0.928
|
Non-1-yne
|
1.615
|
1.476
|
0.827
|
1.063
|
0.978
|
Dec-1-yne
|
1.615
|
1.595
|
0.865
|
1.117
|
1.031
|
Cyclopentane
|
1.615
|
1.348
|
1.079
|
0.901
|
0.883
|
Cyclohexane
|
1.615
|
1.475
|
1.212
|
0.969
|
0.951
|
Cycloheptane
|
1.615
|
1.574
|
1.299
|
1.084
|
1.035
|
Cyclooctane
|
1.615
|
1.643
|
1.402
|
1.171
|
1.115
|
Cyclononane
|
1.615
|
1.883
|
1.567
|
1.319
|
1.234
|
Methanol
|
1.615
|
2.115
|
1.412
|
0.938
|
0.855
|
Ethanol
|
1.615
|
2.215
|
1.515
|
0.989
|
0.893
|
Benzene
|
1.615
|
0.659
|
0.543
|
0.438
|
0.415
|
Toluene
|
1.615
|
0.772
|
0.671
|
0.535
|
0.506
|
Ethylbenzene
|
1.615
|
0.961
|
0.783
|
0.630
|
0.626
|
Propylbenzene
|
1.615
|
1.103
|
0.949
|
0.779
|
0.735
|
Acetone
|
1.615
|
0.648
|
0.517
|
0.388
|
0.371
|
Butan-2-one
|
1.615
|
0.677
|
0.524
|
0.396
|
0.375
|
|
Table 5-11: Activity coefficients at infinite
dilution of organic solutes in
trihexyltetradecylphosphonium hexafluorophosphate with
n3 = 2.659 mmol (29.4 %) at T =
(313.15, 333.15, 353.15
and 363.15) K.
|
Experimental
|
at /K
|
|
|
Solute
|
n3/mmol
|
T=313.15
|
T=333.15
|
T=353.15
|
T=363.15
|
n-pentane.
|
2.659
|
1.921
|
1.553
|
1.288
|
1.251
|
n-hexane
|
2.659
|
2.072
|
1.795
|
1.496
|
1.472
|
n-heptane
|
2.659
|
2.194
|
2.004
|
1.668
|
1.651
|
n-octane
|
2.659
|
2.492
|
2.184
|
1.831
|
1.742
|
n-nonane
|
2.659
|
3.040
|
2.468
|
2.054
|
2.004
|
n-decane
|
2.659
|
3.324
|
2.896
|
2.309
|
2.236
|
Pent-1-ene
|
2.659
|
1.541
|
1.368
|
1.134
|
1.069
|
Hex-1-ene
|
2.659
|
1.701
|
1.436
|
1.264
|
1.174
|
Hept-1-ene
|
2.659
|
1.903
|
1.591
|
1.361
|
1.299
|
Oct-1-ene
|
2.659
|
2.199
|
1.794
|
1.484
|
1.433
|
Non-1-ene
|
2.659
|
2.496
|
1.975
|
1.627
|
1.549
|
Dec-1-ene
|
2.659
|
2.810
|
2.290
|
1.851
|
1.740
|
Pent-1-yne
|
2.659
|
1.061
|
0.861
|
0.713
|
0.654
|
Hex-1-yne
|
2.659
|
1.125
|
0.889
|
0.758
|
0.714
|
Hept-1-yne
|
2.659
|
1.250
|
1.034
|
0.831
|
0.822
|
Oct-1-yne
|
2.659
|
1.333
|
1.160
|
0.952
|
0.942
|
Non-1-yne
|
2.659
|
1.498
|
1.247
|
1.011
|
0.966
|
Dec-1-yne
|
2.659
|
1.615
|
1.315
|
1.063
|
1.009
|
Cyclopentane
|
2.659
|
1.344
|
1.141
|
0.941
|
0.871
|
Cyclohexane
|
2.659
|
1.459
|
1.234
|
1.049
|
0.991
|
Cycloheptane
|
2.659
|
1.602
|
1.335
|
1.100
|
1.049
|
Cyclooctane
|
2.659
|
1.799
|
1.442
|
1.199
|
1.143
|
Cyclononane
|
2.659
|
1.891
|
1.601
|
1.333
|
1.304
|
Methanol
|
2.659
|
2.139
|
1.444
|
0.984
|
0.881
|
Ethanol
|
2.659
|
2.315
|
1.491
|
1.015
|
0.911
|
Benzene
|
2.659
|
0.705
|
0.553
|
0.448
|
0.419
|
Toluene
|
2.659
|
0.814
|
0.639
|
0.541
|
0.516
|
Ethylbenzene
|
2.659
|
1.005
|
0.835
|
0.694
|
0.642
|
Propylbenzene
|
2.659
|
1.139
|
0.939
|
0.799
|
0.777
|
Acetone
|
2.659
|
0.694
|
0.507
|
0.404
|
0.381
|
Butan-2-one
|
2.659
|
0.735
|
0.542
|
0.410
|
0.373
|
|
Table 5-12: Average activity coefficients at
infinite dilution of organic solutes in
trihexyltetradecylphosphonium hexafluorophosphate
at T
= (313.15, 333.15, 353.15 and 363.15) K.
|
Experimental at
|
/K
|
|
Solute
|
T=313.15
|
T=333.15
|
T=353.15
|
T=363.15
|
n-pentane.
|
1.847
|
1.535
|
1.278
|
1.222
|
n-hexane
|
2.016
|
1.741
|
1.489
|
1.451
|
n-heptane
|
2.220
|
1.905
|
1.658
|
1.603
|
n-octane
|
2.510
|
2.152
|
1.850
|
1.777
|
n-nonane
|
2.907
|
2.447
|
2.071
|
1.994
|
n-decane
|
3.301
|
2.758
|
2.302
|
2.211
|
Pent-1-ene
|
1.481
|
1.302
|
1.100
|
1.059
|
Hex-1-ene
|
1.683
|
1.423
|
1.201
|
1.151
|
Hept-1-ene
|
1.880
|
1.586
|
1.341
|
1.284
|
Oct-1-ene
|
2.111
|
1.773
|
1.499
|
1.435
|
Non-1-ene
|
2.448
|
1.994
|
1.622
|
1.544
|
Dec-1-ene
|
2.799
|
2.283
|
1.839
|
1.745
|
Pent-1-yne
|
1.043
|
0.852
|
0.705
|
0.661
|
Hex-1-yne
|
1.135
|
0.898
|
0.769
|
0.723
|
Hept-1-yne
|
1.233
|
1.003
|
0.832
|
0.810
|
Oct-1-yne
|
1.351
|
1.161
|
0.957
|
0.935
|
Non-1-yne
|
1.487
|
1.250
|
1.037
|
0.972
|
Dec-1-yne
|
1.605
|
1.354
|
1.090
|
1.020
|
Cyclopentane
|
1.346
|
1.110
|
0.921
|
0.877
|
Cyclohexane
|
1.467
|
1.223
|
1.009
|
0.971
|
Cycloheptane
|
1.588
|
1.317
|
1.092
|
1.042
|
Cyclooctane
|
1.721
|
1.422
|
1.185
|
1.129
|
Cyclononane
|
1.887
|
1.584
|
1.326
|
1.269
|
Methanol
|
2.127
|
1.428
|
0.961
|
0.868
|
Ethanol
|
2.265
|
1.503
|
1.002
|
0.902
|
Benzene
|
0.682
|
0.548
|
0.443
|
0.417
|
Toluene
|
0.793
|
0.655
|
0.538
|
0.511
|
Ethylbenzene
|
0.983
|
0.809
|
0.662
|
0.634
|
Propylbenzene
|
1.121
|
0.944
|
0.789
|
0.756
|
Acetone
|
0.671
|
0.512
|
0.396
|
0.376
|
Butan-2-one
|
0.706
|
0.533
|
0.403
|
0.374
|
|
Table 5-13: Partial molar excess enthalpies at
infinite dilution for organic solutes in the
ionic liquid trihexyltetradecylphosphonium hexafluorophosphate
calculated from the Gibbs-
equation.
SOLUTE
|
Linear regression using Eq.(2-11)
|
|
|
|
|
n-pentane.
|
0.918
|
-2.325
|
0.999
|
7.63
|
n-hexane
|
0.742
|
-1.673
|
0.999
|
6.17
|
n-heptane
|
0.722
|
-1.516
|
0.999
|
6.00
|
n-octane
|
0.765
|
-1.528
|
0.999
|
6.36
|
n-nonane
|
0.839
|
-1.621
|
0.999
|
6.98
|
n-decane
|
0.894
|
-1.668
|
0.999
|
7.43
|
Pent-1-ene
|
0.754
|
-2.014
|
0.999
|
6.27
|
Hex-1-ene
|
0.844
|
-2.181
|
0.999
|
7.02
|
Hept-1-ene
|
0.845
|
-2.075
|
0.999
|
7.03
|
Oct-1-ene
|
0.855
|
-1.991
|
0.999
|
7.11
|
Non-1-ene
|
1.026
|
-2.388
|
0.999
|
8.53
|
Dec-1-ene
|
1.053
|
-2.338
|
0.999
|
8.76
|
Pent-1-yne
|
0.741
|
-1.979
|
0.999
|
6.16
|
Hex-1-yne
|
0.845
|
-2.183
|
0.999
|
7.03
|
Hept-1-yne
|
0.850
|
-2.087
|
0.999
|
7.07
|
Oct-1-yne
|
0.857
|
-1.998
|
0.999
|
7.13
|
Non-1-yne
|
1.028
|
-2.396
|
0.999
|
8.55
|
Dec-1-yne
|
1.093
|
-2.445
|
0.982
|
9.09
|
Cyclopentane
|
0.949
|
-2.741
|
0.999
|
7.89
|
Cyclohexane
|
0.925
|
-2.578
|
0.999
|
7.69
|
Cycloheptane
|
0.936
|
-2.533
|
0.999
|
7.78
|
Cyclooctane
|
0.933
|
-2.445
|
0.999
|
7.76
|
Cyclononane
|
0.882
|
-2.188
|
0.999
|
7.33
|
Methanol
|
1.989
|
-5.611
|
0.999
|
16.54
|
Ethanol
|
2.042
|
-5.718
|
0.999
|
16.98
|
Benzene
|
1.086
|
-3.860
|
0.999
|
9.03
|
Toluene
|
0.975
|
-3.352
|
0.999
|
8.11
|
Ethylbenzene
|
0.980
|
-3.154
|
0.999
|
8.15
|
Propylbenzene
|
0.878
|
-2.694
|
0.999
|
7.30
|
Acetone
|
1.294
|
-4.545
|
0.999
|
10.76
|
Butan-2-one
|
1.408
|
-4.853
|
0.999
|
11.71
|
|
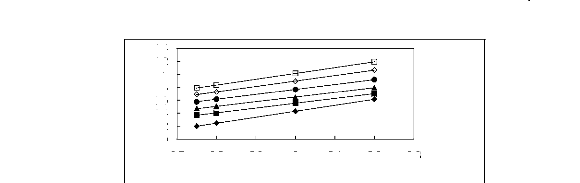
1.4
1.2
1
ln(111:i3)
0.8
0.6
0.4
0.2
0
2.7 2.8 2.9 3 3.1 3.2 3.3
1000K/T
Figure 5-17: Plots of versus for alkanes in
[3C6C14P] [PF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
n-pentane, () n-hexane,
(?) n-heptane, (?) n-octane, () n-nonane and (?)
n-decane.
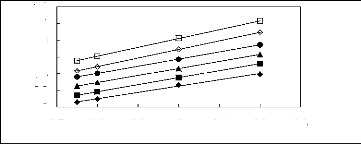
ln( IIP i3)
0.8
0.6
0.4
0.2
1.2
0
1
2.7 2.8 2.9 3 3.1 3.2 3.3
1000K/T
Figure 5-18: Plots of versus for alk-1-enes in
[3C6C14P] [PF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
pent-1-ene, () hex-1-ene,
(?) hept-1-ene, (?) oct-1-ene and () non-1-ene.
ln(111:13)
|
0.6
0.4
0.2
0 -0.2 -0.4 -0.6
|
|
|
2.7 2.8 2.9 3 3.1 3.2 3.3
1000K/T
Figure 5-19: Plots of versus for alk-1-ynes in
[3C6C14P] [PF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
pent-1-yne, () hex-1-yne,
(?) hept-1-yne and (?) oct-1-yne.
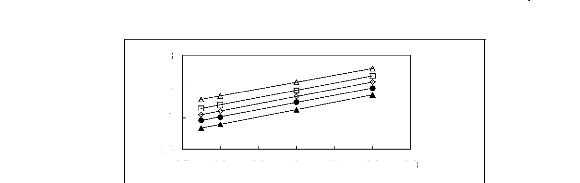
0.8
0.4
ln(I I 113)
0
-0.4
2.7 2.8 2.9 3 3.1 3.2 3.3
1000K/T
Figure 5-20: Plots of versus for cycloalkanes in
[3C6C14P] [PF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation;
(?) cyclopentane, (?) cyclohexane,
() cycloheptane, (?) cyclooctane and (?)
Cyclononane.
2.7 2.8 2.9 3 3.1 3.2 3.3
1000K/T
Figure 5-21: Plots of versus for alkanols in
[3C6C14P] [PF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
methanol and (?) ethanol
2.7 2.8 2.9 3 3.1 3.2 3.3
1000K/T
Figure 5-22: Plots of versus for alkylbenzenes
in [3C6C14P] [PF6] together with a
linear correlation of the data using the Gibbs-Helmholtz
equation; () benzene, () toluene,
(?) ethylbenzene and (?) propylbenzene.
2.7 2.8 2.9 3 3.1 3.2 3.3
1000K/T
Figure 5-23: Plots of versus for ketones in
[3C6C14P] [PF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
acetone and () butan-2-one.
ln(I 1 113)
|
1.2 0.9 0.6 0.3
0 -0.3 -0.6
|
|
|
0 1 2 3 4 5 6 7 8 9 10 11
Nc
Figure 5-24: Plots of versus the number of
carbon atoms at 313.15 K for ()n-alkanes, ()
alk-1-enes, (?) alk-1-ynes, (?) cycloalkanes, () alkanols, (?)
alkylbenzenes and (?)
ketones in [3C6C14P] [PF6].
5.1.5. Methyltrioctylammonium bis
(trifluoromethylsulfonyl) imide, [C13C8N] [Tf2N]. Table 5-14: Activity
coefficients at infinite dilution of organic solutes in
methyltrioctylammonium bis (trifluoromethylsulfonyl) imide
with n3 = 1.77 mmol (25.33 %) at
T = (303.15, 313.15 and
323.15) K.
|
Experimental at
|
/K
|
|
Solute
|
n3/mmol
|
T=303.15
|
T=313.15
|
T=323.15
|
n-pentane
|
1.77
|
1.47
|
1.44
|
1.42
|
n-hexane
|
1.77
|
1.70
|
1.72
|
1.69
|
n-heptane
|
1.77
|
1.85
|
1.83
|
1.83
|
n-octane
|
1.77
|
2.17
|
2.06
|
2.04
|
n-nonane
|
1.77
|
2.57
|
2.39
|
2.21
|
n-decane
|
1.77
|
3.20
|
2.72
|
2.50
|
Pent-1-ene
|
1.77
|
1.16
|
1.17
|
1.14
|
Hex-1-ene
|
1.77
|
1.22
|
1.21
|
1.21
|
Hept-1-ene
|
1.77
|
1.44
|
1.43
|
1.42
|
Oct-1-ene
|
1.77
|
1.69
|
1.67
|
1.66
|
Non-1-ene
|
1.77
|
1.99
|
1.91
|
1.85
|
Dec-1-ene
|
1.77
|
2.22
|
2.11
|
2.05
|
Pent-1-yne
|
1.77
|
0.72
|
0.74
|
0.75
|
Hex-1-yne
|
1.77
|
0.83
|
0.86
|
0.87
|
Hept-1-yne
|
1.77
|
0.89
|
0.91
|
0.92
|
Oct-1-yne
|
1.77
|
1.05
|
1.06
|
1.08
|
Non-1-yne
|
1.77
|
1.15
|
1.17
|
1.18
|
Dec-1-yne
|
1.77
|
1.30
|
1.31
|
1.34
|
Cyclopentane
|
1.77
|
0.90
|
0.98
|
0.97
|
Cyclohexane
|
1.77
|
1.18
|
1.19
|
1.16
|
Cycloheptane
|
1.77
|
1.32
|
1.31
|
1.26
|
Cyclooctane
|
1.77
|
1.54
|
1.47
|
1.43
|
Cyclononane
|
1.77
|
1.74
|
1.68
|
1.61
|
Methanol
|
1.77
|
1.26
|
1.19
|
1.11
|
Ethanol
|
1.77
|
1.32
|
1.24
|
1.13
|
Benzene
|
1.77
|
0.45
|
0.43
|
0.43
|
Toluene
|
1.77
|
0.51
|
0.52
|
0.53
|
Acetone
|
1.77
|
0.35
|
0.38
|
0.44
|
Butan-2-one
|
1.77
|
0.34
|
0.35
|
0.39
|
|
Table 5-15: Activity coefficients at infinite
dilution of organic solutes in
methyltrioctylammonium bis (trifluoromethylsulfonyl) imide
with n3 = 2.044 mmol (29.63 %)
at T = (303.15, 313.15 and
323.15) K.
Experimental at /K
Solute
|
n3/mmol
|
T=303.15
|
T=313.15
|
T=323.15
|
n-pentane
|
2.044
|
1.43
|
1.44
|
1.44
|
n-hexane
|
2.044
|
1.68
|
1.60
|
1.61
|
n-heptane
|
2.044
|
1.83
|
1.81
|
1.79
|
n-octane
|
2.044
|
2.23
|
2.16
|
2.10
|
n-nonane
|
2.044
|
2.59
|
2.39
|
2.21
|
n-decane
|
2.044
|
3.00
|
2.72
|
2.50
|
Pent-1-ene
|
2.044
|
1.14
|
1.11
|
1.12
|
Hex-1-ene
|
2.044
|
1.30
|
1.29
|
1.27
|
Hept-1-ene
|
2.044
|
1.44
|
1.43
|
1.42
|
Oct-1-ene
|
2.044
|
1.69
|
1.67
|
1.66
|
Non-1-ene
|
2.044
|
1.99
|
1.91
|
1.85
|
Dec-1-ene
|
2.044
|
2.22
|
2.11
|
2.05
|
Pent-1-yne
|
2.044
|
0.74
|
0.74
|
0.77
|
Hex-1-yne
|
2.044
|
0.83
|
0.84
|
0.85
|
Hept-1-yne
|
2.044
|
0.89
|
0.91
|
0.92
|
Oct-1-yne
|
2.044
|
1.05
|
1.06
|
1.08
|
Non-1-yne
|
2.044
|
1.15
|
1.17
|
1.18
|
Dec-1-yne
|
2.044
|
1.30
|
1.31
|
1.34
|
Cyclopentane
|
2.044
|
1.10
|
1.00
|
0.99
|
Cyclohexane
|
2.044
|
1.20
|
1.15
|
1.14
|
Cycloheptane
|
2.044
|
1.34
|
1.29
|
1.28
|
Cyclooctane
|
2.044
|
1.52
|
1.47
|
1.43
|
Cyclononane
|
2.044
|
1.74
|
1.68
|
1.61
|
Methanol
|
2.044
|
1.24
|
1.17
|
1.15
|
Ethanol
|
2.044
|
1.34
|
1.24
|
1.17
|
Benzene
|
2.044
|
0.43
|
0.45
|
0.47
|
Toluene
|
2.044
|
0.51
|
0.52
|
0.53
|
Acetone
|
2.044
|
0.35
|
0.38
|
0.44
|
Butan-2-one
|
2.044
|
0.34
|
0.37
|
0.41
|
|
Table 5-16: Average activity coefficients at
infinite dilution of organic solutes in
methyltrioctylammonium bis (trifluoromethylsulfonyl)
imide
at T = (303.15, 313.15 and 323.15) K.
Experimental
|
at /K
|
|
Solute
|
T=303.15
|
T=313.15
|
T=323.15
|
n-pentane
|
1.45
|
1.44
|
1.43
|
n-hexane
|
1.69
|
1.66
|
1.65
|
n-heptane
|
1.84
|
1.82
|
1.81
|
n-octane
|
2.20
|
2.11
|
2.07
|
n-nonane
|
2.58
|
2.39
|
2.21
|
n-decane
|
3.10
|
2.72
|
2.50
|
Pent-1-ene
|
1.15
|
1.14
|
1.13
|
Hex-1-ene
|
1.26
|
1.25
|
1.24
|
Hept-1-ene
|
1.44
|
1.43
|
1.42
|
Oct-1-ene
|
1.69
|
1.67
|
1.66
|
Non-1-ene
|
1.99
|
1.91
|
1.85
|
Dec-1-ene
|
2.22
|
2.11
|
2.05
|
Pent-1-yne
|
0.73
|
0.74
|
0.76
|
Hex-1-yne
|
0.83
|
0.85
|
0.86
|
Hept-1-yne
|
0.89
|
0.91
|
0.92
|
Oct-1-yne
|
1.05
|
1.06
|
1.08
|
Non-1-yne
|
1.15
|
1.17
|
1.18
|
Dec-1-yne
|
1.30
|
1.31
|
1.34
|
Cyclopentane
|
1.00
|
0.99
|
0.98
|
Cyclohexane
|
1.19
|
1.17
|
1.15
|
Cycloheptane
|
1.33
|
1.30
|
1.27
|
Cyclooctane
|
1.53
|
1.47
|
1.43
|
Cyclononane
|
1.74
|
1.68
|
1.61
|
Methanol
|
1.25
|
1.18
|
1.13
|
Ethanol
|
1.33
|
1.24
|
1.15
|
Benzene
|
0.44
|
0.44
|
0.45
|
Toluene
|
0.51
|
0.52
|
0.53
|
Acetone
|
0.35
|
0.38
|
0.44
|
Butan-2-one
|
0.34
|
0.36
|
0.40
|
|
Table 5-17: Excess molar enthalpies at
infinite dilution of organic solutes in the ionic
liquid methyltrioctylammonium bis (trifluoromethylsulfonyl)
imide, calculated using the Gibbs-
Helmholtz equation.
SOLUTE
|
Linear regression using Eq.(2-11)
|
|
|
|
|
n-pentane
|
0.694
|
0.142
|
1.00
|
5.77
|
n-hexane
|
0.120
|
0.128
|
0.92
|
1.00
|
n-heptane
|
0.082
|
0.338
|
0.97
|
0.68
|
n-octane
|
0.305
|
-0.220
|
0.96
|
2.53
|
n-nonane
|
0.774
|
-1.606
|
1.00
|
6.44
|
n-decane
|
1.075
|
-2.425
|
0.99
|
8.93
|
Pent-1-ene
|
0.088
|
-0.150
|
1.00
|
0.73
|
Hex-1-ene
|
0.080
|
-0.033
|
1.00
|
0.67
|
Hept-1-ene
|
0.105
|
0.028
|
0.96
|
0.87
|
Oct-1-ene
|
0.120
|
0.128
|
0.92
|
1.00
|
Non-1-ene
|
0.419
|
-0.698
|
0.98
|
3.48
|
Dec-1-ene
|
0.419
|
-0.580
|
0.97
|
3.48
|
Pent-1-yne
|
-0.201
|
0.348
|
0.97
|
-1.67
|
Hex-1-yne
|
-0.178
|
0.402
|
0.96
|
-1.48
|
Hept-1-yne
|
-0.111
|
0.250
|
1.00
|
-0.92
|
Oct-1-yne
|
-0.140
|
0.517
|
0.97
|
-1.16
|
Non-1-yne
|
-0.129
|
0.563
|
0.97
|
-1.07
|
Dec-1-yne
|
-0.114
|
0.640
|
0.96
|
-0.95
|
Cyclopentane
|
0.101
|
-3.333
|
1.00
|
0.84
|
Cyclohexane
|
0.171
|
-0.390
|
1.00
|
1.42
|
Cycloheptane
|
0.231
|
-0.476
|
1.00
|
1.92
|
Cyclooctane
|
0.338
|
-0.692
|
0.99
|
2.81
|
Cyclononane
|
0.386
|
-0.715
|
1.00
|
3.21
|
Methanol
|
0.505
|
-1.445
|
0.99
|
4.20
|
Ethanol
|
0.727
|
-2.113
|
1.00
|
6.05
|
Benzene
|
-0.112
|
-0.454
|
0.75
|
-0.93
|
Toluene
|
-0.286
|
0.267
|
0.97
|
-2.38
|
Acetone
|
-0.962
|
2.062
|
0.98
|
-8.00
|
Butan-2-one
|
-1.029
|
2.349
|
1.00
|
-8.56
|
|
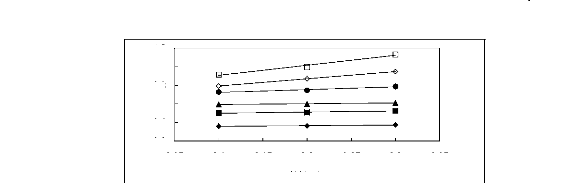
3.05 3.1 3.15 3.2 3.25 3.3 3.35
1000K/T
1.2
1
1n(L13)
0.8
0.6
0.4
0.2
Figure 5-25: Plots of versus for alkanes in
[C13C8N] [Tf2N] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
n-pentane, () n-hexane,
(?) n-heptane, (?) n-octane, () n-nonane and (?)
n-decane.
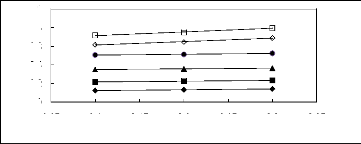
3.05 3.1 3.15 3.2 3.25 3.3 3.35
1000/T/K-1
In(L13)
0.8
0.6
0.4
0.2
0
1
Figure 5-26: Plots of versus for alk-1-enes in
[C13C8N] [Tf2N] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
pent-1-ene, () hex-1-ene,
(?) hept-1-ene, (?) oct-1-ene, () non-1-ene and
(?) dec-1-ene.
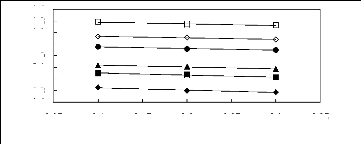
3.05 3.1 3.15 3.2 3.25 3.3 3.35
1000K/T
In(L13)
-0.1
-0.2
-0.3
-0.4
0.4
0.3
0.2
0.1
0
Figure 5-27: Plots of versus for alk-1-ynes in
[C13C8N] [Tf2N] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
pent-1-y-ne, () hex-1-yne,
(?) hept-1-yne, (?) oct-1-yne, () non-1-yne and
(?) dec-1-yne.
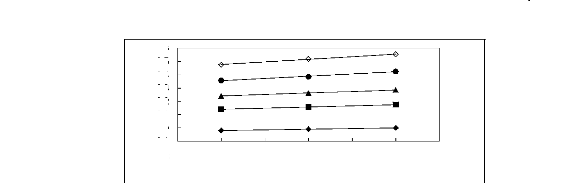
3.05 3.1 3.15 3.2 3.25 3.3 3.35
1000K/T
0.6
0.5
0.4
lii(LP13)
0.3
0.2
0.1
0
-0.1
Figure 5-28: Plots of versus for cycloalkanes in
[C13C8N] [Tf2N] together with a
linear correlation of the data using the Gibbs-Helmholtz
equation; () cyclopentane,
() cyclohexane, (?) cycloheptane, (?) cyclooctane
and () cyclononane.
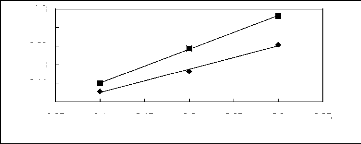
3.05 3.1 3.15 3.2 3.25 3.3 3.35
1000K/T
lii(LP13)
0.26
0.22
0.18
0.14
0.3
0.1
Figure 5-29: Plots of versus for alkanols in
[C13C8N] [Tf2N] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
methanol and () ethanol.
|
-0.6 -0.65 -0.7 -0.75
|
|
|
ln(ffi3)
|
|
|
|
-0.8
-0.85
|
|
|
|
|
|
|
3.05 3.1 3.15 3.2 3.25 3.3 3.35
1000K/T
Figure 5-30: Plots of versus for alkylbenzenes
in [C13C8N] [Tf2N] together with a
linear correlation of the data using the Gibbs-Helmholtz
equation; () benzene and () toluene.
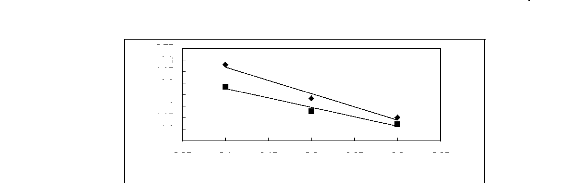
-0.75
-0.8
-0.85
hi( Du 13)
-0.9
-0.95
-1
-1.05
-1.1
-1.15
3.05 3.1 3.15 3.2 3.25 3.3 3.35
1000K/T
Figure 5-31: Plots of versus for ketones in
[C13C8N] [Tf2N] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
acetone and () butan-2-one.
0 1 2 3 4 5 6 7 8 9 10 11
Number of Carbon atoms, Nc
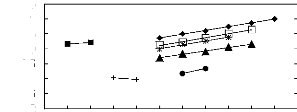
ln( LP13)
-0.5
-1.5
0.5
1.5
-1
-2
0
1
Figure 5-32: Plots of versus the number of
carbon atoms at 313.15 K for () n-alkanes,
(?) alk-1-enes, and (?) alk-1-ynes, (*) cycloalkanes, ()
alkanols, and (?) alkylbenzenes and
(+) ketones in [C13C8N] [Tf2N].
5.1.6. 1-Butyl-3-methylimidazolium hexafluoroantimonate,
[BMIM] [SbF6]
Table 5-18: Activity coefficients at infinite
dilution of organic solutes in
1-butyl-3-methylimidazolium hexafluoroantimonate with
n3 = 3.312 mmol (26.90 %) at T =
(313.15, 323.15 and
333.15) K.
|
Experimental at
|
/K
|
|
Solute
|
n3/mmol
|
T=313.15
|
T=323.15
|
T=333.15
|
n-pentane.
|
3.312
|
19.611
|
17.552
|
16.962
|
n-hexane
|
3.312
|
28.627
|
26.428
|
25.994
|
n-heptane
|
3.312
|
37.066
|
34.182
|
31.424
|
n-octane
|
3.312
|
40.437
|
39.454
|
39.176
|
n-nonane
|
3.312
|
47.704
|
44.947
|
44.137
|
Pent-1-ene
|
3.312
|
9.956
|
10.168
|
9.938
|
Hex-1-ene
|
3.312
|
14.006
|
13.017
|
13.356
|
Hept-1-ene
|
3.312
|
19.291
|
17.762
|
15.857
|
Oct-1-ene
|
3.312
|
25.680
|
24.604
|
24.205
|
Non-1-ene
|
3.312
|
32.427
|
30.780
|
30.800
|
Pent-1-yne
|
3.312
|
2.817
|
2.885
|
2.933
|
Hex-1-yne
|
3.312
|
4.256
|
4.108
|
4.102
|
Hept-1-yne
|
3.312
|
5.741
|
5.816
|
5.739
|
Oct-1-yne
|
3.312
|
8.678
|
8.820
|
8.558
|
Non-1-yne
|
3.312
|
11.426
|
10.934
|
10.894
|
Cyclopentane
|
3.312
|
11.379
|
10.560
|
10.193
|
Cyclohexane
|
3.312
|
16.409
|
11.044
|
14.132
|
Cycloheptane
|
3.312
|
19.954
|
15.745
|
17.295
|
Cyclooctane
|
3.312
|
22.852
|
17.172
|
20.433
|
Methanol
|
3.312
|
1.701
|
1.639
|
1.565
|
Ethanol
|
3.312
|
2.334
|
2.144
|
2.005
|
Propan-1-ol
|
3.312
|
3.128
|
2.819
|
2.513
|
Benzene
|
3.312
|
1.229
|
1.276
|
1.314
|
Toluene
|
3.312
|
1.866
|
1.876
|
1.916
|
Ethylbenzene
|
3.312
|
3.113
|
3.085
|
3.176
|
Acetone
|
3.312
|
0.403
|
0.445
|
0.463
|
Butan-2-one
|
3.312
|
0.648
|
0.681
|
0.702
|
|
Table 5-19: Activity coefficients at infinite
dilution of organic solutes in
1-butyl-3-methylimidazolium hexafluoroantimonate with
n3 = 4.578 mmol (31.98 %) at T =
(313.15, 323.15 and
333.15) K.
Experimental at /K
Solute
|
n3/mmol
|
T=313.15
|
T=323.15
|
T=333.15
|
n-pentane.
|
4.578
|
21.459
|
18.268
|
18.088
|
n-hexane
|
4.578
|
27.893
|
28.232
|
26.626
|
n-heptane
|
4.578
|
38.734
|
35.798
|
34.386
|
n-octane
|
4.578
|
44.603
|
42.656
|
42.714
|
n-nonane
|
4.578
|
48.766
|
49.123
|
47.263
|
Pent-1-ene
|
4.578
|
10.474
|
10.232
|
10.442
|
Hex-1-ene
|
4.578
|
13.134
|
14.103
|
13.754
|
Hept-1-ene
|
4.578
|
21.109
|
19.698
|
16.623
|
Oct-1-ene
|
4.578
|
25.700
|
25.696
|
24.915
|
Non-1-ene
|
4.578
|
32.573
|
33.420
|
32.620
|
Pent-1-yne
|
4.578
|
2.883
|
2.885
|
3.027
|
Hex-1-yne
|
4.578
|
4.054
|
4.232
|
4.318
|
Hept-1-yne
|
4.578
|
6.109
|
6.084
|
6.231
|
Oct-1-yne
|
4.578
|
9.402
|
9.080
|
8.992
|
Non-1-yne
|
4.578
|
11.634
|
11.846
|
11.646
|
Cyclopentane
|
4.578
|
11.881
|
10.860
|
10.657
|
Cyclohexane
|
4.578
|
15.391
|
18.626
|
14.558
|
Cycloheptane
|
4.578
|
18.666
|
21.075
|
18.175
|
Cyclooctane
|
4.578
|
23.418
|
27.128
|
21.467
|
Methanol
|
4.578
|
1.880
|
1.711
|
1.565
|
Ethanol
|
4.578
|
2.456
|
2.296
|
2.065
|
Propan-1-ol
|
4.578
|
3.222
|
2.961
|
2.747
|
Benzene
|
4.578
|
1.311
|
1.374
|
1.370
|
Toluene
|
4.578
|
1.784
|
1.944
|
1.972
|
Ethylbenzene
|
4.578
|
2.917
|
3.225
|
3.450
|
Acetone
|
4.578
|
0.437
|
0.459
|
0.487
|
Butan-2-one
|
4.578
|
0.632
|
0.681
|
0.718
|
|
Table 5-20: Average activity coefficients at
infinite dilution of organic solutes in
1-butyl-3-methylimidazolium hexafluoroantimonate at T
= (313.15, 323.15 and 333.15) K.
|
Experimental
|
at /K
|
|
Solute
|
T=313.15
|
T=323.15
|
T=333.15
|
n-pentane.
|
20.535
|
17.910
|
17.525
|
n-hexane
|
28.260
|
27.330
|
26.310
|
n-heptane
|
37.900
|
34.990
|
32.905
|
n-octane
|
42.520
|
41.055
|
40.945
|
n-nonane
|
48.235
|
47.035
|
45.700
|
Pent-1-ene
|
10.215
|
10.200
|
10.190
|
Hex-1-ene
|
13.570
|
13.560
|
13.555
|
Hept-1-ene
|
20.200
|
18.730
|
16.240
|
Oct-1-ene
|
25.690
|
25.150
|
24.560
|
Non-1-ene
|
32.500
|
32.100
|
31.710
|
Pent-1-yne
|
2.850
|
2.885
|
2.980
|
Hex-1-yne
|
4.155
|
4.170
|
4.210
|
Hept-1-yne
|
5.925
|
5.950
|
5.985
|
Oct-1-yne
|
9.040
|
8.950
|
8.775
|
Non-1-yne
|
11.530
|
11.390
|
11.270
|
Cyclopentane
|
11.630
|
10.710
|
10.425
|
Cyclohexane
|
15.900
|
14.835
|
14.345
|
Cycloheptane
|
19.310
|
18.410
|
17.735
|
Cyclooctane
|
23.135
|
22.150
|
20.950
|
Methanol
|
1.790
|
1.675
|
1.565
|
Ethanol
|
2.395
|
2.220
|
2.035
|
Propan-1-ol
|
3.175
|
2.890
|
2.630
|
Benzene
|
1.270
|
1.325
|
1.342
|
Toluene
|
1.825
|
1.910
|
1.944
|
Ethylbenzene
|
3.015
|
3.155
|
3.313
|
Acetone
|
0.420
|
0.452
|
0.475
|
Butan-2-one
|
0.640
|
0.681
|
0.710
|
|
Table 5-21: Excess molar enthalpies at
infinite dilution of organic solutes in the ionic
liquid 1-butyl-3-methylimidazolium hexafluoroantimonate
calculated using the Gibbs-
Helmholtz equation.
Solute
|
Linear regression using Eq.(2-21)
|
|
|
|
|
n-pentane.
|
0.793
|
0.467
|
0.851
|
6.59
|
n-hexane
|
0.357
|
2.198
|
0.999
|
2.97
|
n-heptane
|
0.707
|
1.371
|
0.994
|
5.88
|
n-octane
|
0.189
|
3.141
|
0.803
|
1.57
|
n-nonane
|
0.270
|
3.013
|
0.999
|
2.25
|
Pent-1-ene
|
0.012
|
2.285
|
0.987
|
0.10
|
Hex-1-ene
|
0.006
|
2.590
|
0.964
|
0.05
|
Hept-1-ene
|
1.091
|
-0.474
|
0.969
|
9.07
|
Oct-1-ene
|
0.225
|
2.527
|
0.999
|
1.87
|
Non-1-ene
|
0.123
|
3.088
|
1.000
|
1.02
|
Pent-1-yne
|
-0.223
|
1.758
|
0.936
|
-1.85
|
Hex-1-yne
|
-0.066
|
1.634
|
0.936
|
-0.55
|
Hept-1-yne
|
-0.050
|
1.940
|
0.991
|
-0.42
|
Oct-1-yne
|
0.149
|
1.727
|
0.966
|
1.24
|
Non-1-yne
|
0.114
|
2.080
|
0.998
|
0.95
|
Cyclopentane
|
0.547
|
0.694
|
0.921
|
4.55
|
Cyclohexane
|
0.515
|
1.114
|
0.961
|
4.28
|
Cycloheptane
|
0.425
|
1.598
|
0.995
|
3.53
|
Cyclooctane
|
0.496
|
1.556
|
0.995
|
4.12
|
Methanol
|
0.672
|
-1.567
|
1.000
|
5.59
|
Ethanol
|
0.814
|
-1.731
|
0.998
|
6.77
|
Propan-1-ol
|
0.942
|
-1.858
|
1.000
|
7.83
|
Benzene
|
-0.276
|
1.126
|
0.912
|
-2.30
|
Toluene
|
-0.316
|
1.617
|
0.939
|
-2.63
|
Ethylbenzene
|
-0.471
|
2.611
|
0.999
|
-3.92
|
Acetone
|
-0.615
|
1.105
|
0.998
|
-5.11
|
Butan-2-one
|
-0.519
|
1.218
|
0.987
|
-4.32
|
|
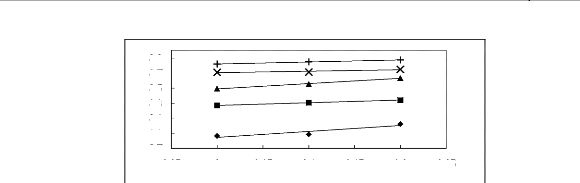
3.9
3.7
In( 0'13)
3.5
3.3
3.1
2.9
2.7
2.95 3 3.05 3.1 3.15 3.2 3.25
1000K/T
Figure 5-33: Plots of versus for alkanes in
[BMIM] [SbF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
n-pentane, () n-hexane,
(?) n-heptane, (x) n-octane, (+) n-nonane.
2.95 3 3.05 3.1 3.15 3.2 3.25
1000K/T
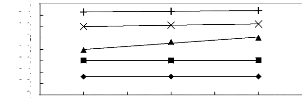
1n( L13)
2.8
2.6
2.4
2.2
3.6
3.4
3.2
2
3
Figure 5-34: Plots of versus for alk-1-enes in
[BMIM] [SbF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
pent-1-ene, () hex-1-ene,
(?) hept-1-ene, (x) oct-1-ene and (+) non-1-ene
2.95 3 3.05 3.1 3.15 3.2 3.25
1000K/T
Figure 5-35: Plots of versus for alk-1-ynes in
[BMIM] [SbF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
pent-1-yne, () hex-1-yne,
(?) hept-1-yne, (x) oct-1-yne and (?)
non-1-yne.
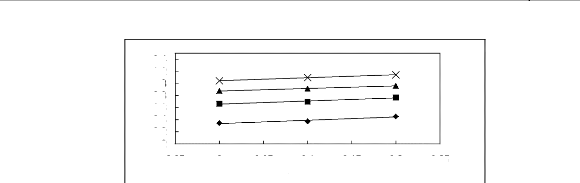
2.95 3 3.05 3.1 3.15 3.2 3.25
1000K/T
3.4
3.2
3
111( EF13)
2.8
2.6
2.4
2.2
2
Figure 5-36: Plots of versus for cycloalkanes in
[BMIM] [SbF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
cyclopentane, () cyclohexane,
(?) cycloheptane and (x) cyclooctane.
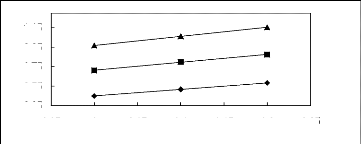
111( EF13)
0.95
0.75
0.55
0.35
1.15
2.95 3 3.05 3.1 3.15 3.2 3.25
1000K/T
Figure 5-37: Plots of versus for alkanols in
[BMIM] [SbF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
methanol, () ethanol and
(?) propan-1-ol.
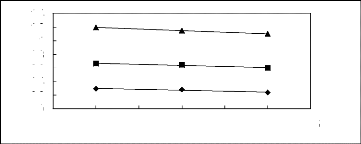
1.4
1.2
1
0.8
0.6
0.4
0.2
0
2.95 3 3.05 3.1 3.15 3.2 3.25
1000K/T
In( 0'13)
Figure 5-38: Plots of versus for alkylbenzenes
in [BMIM] [SbF6] together with a
linear correlation of the data using the Gibbs-Helmholtz
equation; () benzene, () toluene and
(?) ethylbenzene.
2.95 3 3.05 3.1 3.15 3.2 3.25
1000K/T
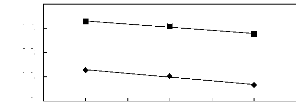
-0.2
-0.4
in( L1:13)
-0.6
-0.8
-1
Figure 5-39: Plots of versus for ketones in
[BMIM] [SbF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
acetone and () butan-2-one.
0 1 2 3 4 5 6 7 8 9 10
Nc
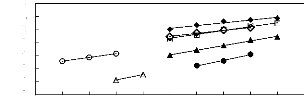
in (L13)
-1
-2
4
2
3
0
5
1
Figure 5-40: Plots of versus the number of
carbon atoms at 313.15 K for () n-alkanes,
(?) alk-1-enes, (?) alk-1-ynes, and () cycloalkanes, (o)
alkanols, (?) alkylbenzenes and (?)
ketones in [BMIM] [SbF6].
5.1.7.1-ethyl-3-methylimidazolium
trifluoromethanesulfonate, [EMIM] [TfO]
Table 5-22: Activity coefficients at infinite
dilution of organic solutes in 1-ethyl-3-
methylimidazolium trifluoromethanesulfonate with n3 =
8.01 mmol (29.3 %)
at T = (313.15, 323.15 and 333.15) K.
Experimental at /K
Solute
|
n3/mmol
|
T=313.15
|
T=323.15
|
T=333.15
|
n-pentane
|
8.01
|
40.74
|
38.62
|
36.57
|
n-hexane
|
8.01
|
66.98
|
63.11
|
60.16
|
n-heptane
|
8.01
|
107.28
|
99.46
|
93.32
|
n-octane
|
8.01
|
170.38
|
154.86
|
143.78
|
Hex-1-ene
|
8.01
|
28.60
|
27.68
|
26.72
|
Hept-1-ene
|
8.01
|
47.01
|
44.82
|
42.87
|
Oct-1-ene
|
8.01
|
75.66
|
70.99
|
67.26
|
Non-1-ene
|
8.01
|
122.18
|
113.25
|
105.70
|
Dec-1-ene
|
8.01
|
171.88
|
162.96
|
154.72
|
Undec-1-ene
|
8.01
|
315.79
|
283.50
|
257.07
|
Pent-1-yne
|
8.01
|
3.95
|
4.02
|
4.08
|
Hex-1-yne
|
8.01
|
6.35
|
6.43
|
6.47
|
Hept-1-yne
|
8.01
|
9.83
|
9.79
|
9.78
|
Oct-1-yne
|
8.01
|
16.32
|
16.24
|
16.07
|
Non-1-yne
|
8.01
|
23.77
|
24.07
|
24.14
|
Cyclopentane
|
8.01
|
20.92
|
20.00
|
18.99
|
Cyclohexane
|
8.01
|
33.30
|
31.24
|
29.29
|
Cycloheptane
|
8.01
|
46.87
|
43.29
|
40.23
|
Cyclooctane
|
8.01
|
67.24
|
61.17
|
56.18
|
Methanol
|
8.01
|
0.73
|
0.70
|
0.67
|
Ethanol
|
8.01
|
1.19
|
1.12
|
1.06
|
Benzene
|
8.01
|
2.23
|
2.25
|
2.26
|
Toluene
|
8.01
|
3.62
|
3.65
|
3.67
|
Ethylbenzene
|
8.01
|
6.37
|
6.32
|
6.28
|
|
Table 5-23: Activity coefficients at infinite
dilution of organic solutes in 1-ethyl-3-
methylimidazolium trifluoromethanesulfonate with n3 =
6.23 mmol (32.88 %)
at T = (313.15, 323.15 and 333.15) K.
|
Experimental at
|
/K
|
|
Solute
|
n3/mmol
|
T=313.15
|
T=323.15
|
T=333.15
|
n-pentane
|
6.23
|
42.50
|
39.52
|
36.94
|
n-hexane
|
6.23
|
67.09
|
65.82
|
61.25
|
n-heptane
|
6.23
|
102.33
|
94.91
|
90.16
|
n-octane
|
6.23
|
162.50
|
159.27
|
145.47
|
Hex-1-ene
|
6.23
|
29.47
|
27.76
|
27.84
|
Hept-1-ene
|
6.23
|
45.57
|
43.07
|
43.57
|
Oct-1-ene
|
6.23
|
74.91
|
68.50
|
64.18
|
Non-1-ene
|
6.23
|
126.58
|
117.25
|
106.34
|
Dec-1-ene
|
6.23
|
179.20
|
166.94
|
160.49
|
Undec-1-ene
|
6.23
|
320.33
|
288.38
|
260.50
|
Pent-1-yne
|
6.23
|
4.01
|
4.00
|
3.98
|
Hex-1-yne
|
6.23
|
6.36
|
6.51
|
6.76
|
Hept-1-yne
|
6.23
|
9.59
|
9.75
|
9.87
|
Oct-1-yne
|
6.23
|
15.56
|
16.56
|
17.03
|
Non-1-yne
|
6.23
|
24.02
|
24.13
|
24.36
|
Cyclopentane
|
6.23
|
21.22
|
20.92
|
19.50
|
Cyclohexane
|
6.23
|
34.13
|
32.13
|
30.31
|
Cycloheptane
|
6.23
|
45.37
|
43.95
|
38.46
|
Cyclooctane
|
6.23
|
69.71
|
62.49
|
55.74
|
Methanol
|
6.23
|
0.72
|
0.69
|
0.68
|
Ethanol
|
6.23
|
1.15
|
1.09
|
1.07
|
Benzene
|
6.23
|
2.21
|
2.23
|
2.28
|
Toluene
|
6.23
|
3.51
|
3.53
|
3.64
|
Ethylbenzene
|
6.23
|
6.03
|
6.22
|
6.46
|
|
Table 5-24: Average activity coefficients at
infinite dilution of organic solutes in 1-ethyl-
3-methylimidazolium trifluoromethanesulfonate at T =
(313.15, 323.15 and 333.15) K.
Experimental
|
at /K
|
|
Solute
|
T=313.15
|
T=323.15
|
T=333.15
|
n-pentane
|
41.62
|
39.07
|
36.76
|
n-hexane
|
67.04
|
64.47
|
60.71
|
n-heptane
|
104.81
|
97.19
|
91.74
|
n-octane
|
166.44
|
157.07
|
144.63
|
Hex-1-ene
|
29.04
|
27.72
|
27.28
|
Hept-1-ene
|
46.29
|
43.95
|
43.22
|
Oct-1-ene
|
75.29
|
69.75
|
65.72
|
Non-1-ene
|
124.38
|
115.25
|
106.02
|
Dec-1-ene
|
175.54
|
164.95
|
157.61
|
Undec-1-ene
|
318.06
|
285.94
|
258.79
|
Pent-1-yne
|
3.98
|
4.01
|
4.03
|
Hex-1-yne
|
6.36
|
6.47
|
6.62
|
Hept-1-yne
|
9.71
|
9.77
|
9.83
|
Oct-1-yne
|
15.94
|
16.40
|
16.55
|
Non-1-yne
|
23.81
|
24.10
|
24.25
|
Cyclopentane
|
21.07
|
20.46
|
19.25
|
Cyclohexane
|
33.72
|
31.69
|
29.80
|
Cycloheptane
|
46.12
|
43.62
|
39.35
|
Cyclooctane
|
68.48
|
61.83
|
55.96
|
Methanol
|
0.73
|
0.70
|
0.68
|
Ethanol
|
1.17
|
1.11
|
1.07
|
Benzene
|
2.22
|
2.24
|
2.27
|
Toluene
|
3.57
|
3.59
|
3.66
|
Ethylbenzene
|
6.20
|
6.27
|
6.37
|
|
Table 5-25: Excess molar enthalpies at
infinite dilution of organic solutes for the ionic
liquid 1-ethyl-3-methylimidazolium trifluoromethanesulfonate,
calculated using the Gibbs-
Helmholtz equation.
SOLUTE
|
Linear regression using Eq.(2-11)
|
|
|
|
|
n-pentane
|
0.648
|
1.659
|
0.999
|
5.39
|
n-hexane
|
0.516
|
2.561
|
0.981
|
4.29
|
n-heptane
|
0.695
|
2.430
|
0.997
|
5.78
|
n-octane
|
0.731
|
2.784
|
0.986
|
6.08
|
Hex-1-ene
|
0.327
|
2.321
|
0.936
|
2.72
|
Hept-1-ene
|
0.360
|
2.681
|
0.928
|
2.99
|
Oct-1-ene
|
0.709
|
2.054
|
0.997
|
5.90
|
Non-1-ene
|
0.832
|
2.167
|
0.998
|
6.92
|
Dec-1-ene
|
0.563
|
3.368
|
0.994
|
4.68
|
Undec-1-ene
|
1.076
|
2.327
|
1.000
|
8.94
|
Pent-1-yne
|
-0.065
|
1.590
|
0.990
|
-0.54
|
Hex-1-yne
|
-0.209
|
2.515
|
0.994
|
-1.74
|
Hept-1-yne
|
-0.061
|
2.469
|
0.999
|
-0.51
|
Oct-1-yne
|
-0.197
|
3.401
|
0.928
|
-1.64
|
Non-1-yne
|
-0.096
|
3.477
|
0.973
|
-0.80
|
Cyclopentane
|
0.471
|
1.550
|
0.953
|
3.91
|
Cyclohexane
|
0.644
|
1.463
|
0.999
|
5.35
|
Cycloheptane
|
0.826
|
1.202
|
0.965
|
6.87
|
Cyclooctane
|
1.053
|
0.866
|
0.999
|
8.75
|
Methanol
|
0.373
|
-1.516
|
0.992
|
3.10
|
Ethanol
|
0.491
|
-1.415
|
0.989
|
4.09
|
Benzene
|
-0.116
|
1.668
|
0.983
|
-0.96
|
Toluene
|
-0.129
|
1.683
|
0.931
|
-1.08
|
Ethylbenzene
|
-0.141
|
2.273
|
0.987
|
-1.17
|
|
Chapter 5: Results
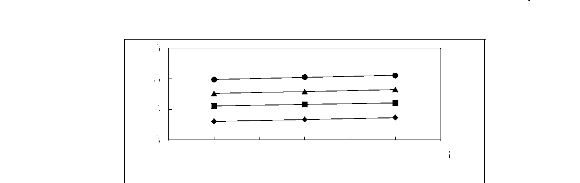
6
5
4
3
2.95 3 3.05 3.1 3.15 3.2 3.25
1000K/T
1n( L13)
Figure 5-41: Plots of versus for alkanes in
[EMIM] [TfO] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
n-pentane, () n-hexane, (?)
n-heptane and (?) n-octane.
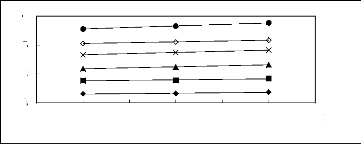
6
5
4
3
2.95 3 3.05 3.1 3.15 3.2 3.25
1000K/T
In( EP13)
Figure 5-42: Plots of versus for alk-1-nes in
[EMIM] [TfO] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
hex-1-ene, () hept-1-ene,
(?) oct-1-ene, (x) non-1-ene, () dec-1-ene and (?)
undec-1-ene.
2.95 3 3.05 3.1 3.15 3.2 3.25
1000K/T
Figure 5-43: Plots of versus for alk-1-ynes in
[EMIM] [TfO] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
pent-1-yne, () hex-1-yne,
(?) hept-1-yne, (?) oct-1-yne and () non-1-yne.
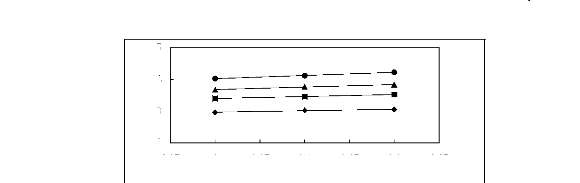
2.95 3 3.05 3.1 3.15 3.2 3.25
1000K/T
In( EF13)
3
2
Figure 5-44: Plots of versus for cycloalkanes in
[EMIM] [TfO] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
cyclopentane, () cyclohexane,
(?) cycloheptane and (?) cyclooctane.
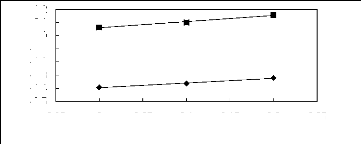
2.95 3 3.05 3.1 3.15 3.2 3.25
1000K/T
In( EF13)
-0.1
-0.2
-0.3
-0.4
-0.5
0.2
0.1
0
Figure 5-45: Plots of versus for alkanols in
[EMIM] [TfO] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
methanol and () ethanol.
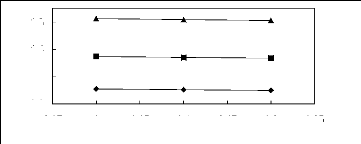
2.95 3 3.05 3.1 3.15 3.2 3.25
1000K/T
ln( L13)
0.6
1.8
1.4
1
Figure 5-46: Plots of versus for alkylbenzenes
in [EMIM] [TfO] together with a
linear correlation of the data using the Gibbs-Helmholtz
equation; () benzene, () toluene and
(?) ethylbenzene.
Chapter 5: Results
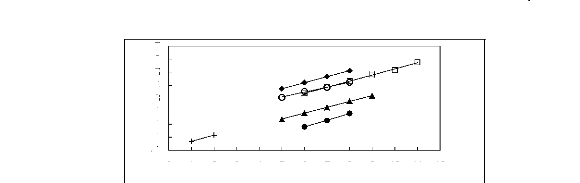
0 1 2 3 4 5 6 7 8 9 10 11 12
Nc
7
6
5
4
in(L13)
3
2
1
0
-1
Figure 5-47: Plots of versus the number of
carbon atoms at 313.15 K for () n-alkanes,
(?) alk-1-enes, (?) alk-1-ynes, and (?) cycloalkanes, (+)
alkanols and (?) alkylbenzenes in
[EMIM] [TfO].
5.1.8. 1-methyl-3-octylimidazolium hexafluorophosphate,
[MOIM][PF6]
Table 5-26: Activity coefficients at infinite
dilution of organic solutes in 1-methyl-3-
octylimidazolium hexafluorophosphate with n3 = 6.69
mmol (28.55 %)
at T = (313.15, 323.15 and 333.15) K.
Experimental at /K
Solute
|
n3/mmol
|
T=313.15
|
T=323.15
|
T=333.15
|
n-pentane
|
6.69
|
8.21
|
8.06
|
7.83
|
n-hexane
|
6.69
|
10.75
|
10.56
|
10.20
|
n-heptane
|
6.69
|
14.07
|
13.78
|
13.24
|
n-octane
|
6.69
|
18.34
|
17.87
|
17.04
|
n-decane
|
6.69
|
31.75
|
30.25
|
28.23
|
n-undecane
|
6.69
|
42.06
|
39.62
|
36.52
|
Hex-1-ene
|
6.69
|
6.17
|
6.15
|
6.06
|
Hept-1-ene
|
6.69
|
8.23
|
8.18
|
8.02
|
Oct-1-ene
|
6.69
|
10.77
|
10.66
|
10.39
|
Non-1-ene
|
6.69
|
14.16
|
13.93
|
13.50
|
Dec-1-ene
|
6.69
|
16.32
|
16.52
|
16.34
|
Undec-1-ene
|
6.69
|
25.10
|
24.01
|
22.75
|
Pent-1-yne
|
6.69
|
1.70
|
1.75
|
1.78
|
Hex-1-yne
|
6.69
|
2.24
|
2.30
|
2.34
|
Hept-1-yne
|
6.69
|
2.81
|
2.87
|
2.93
|
Oct-1-yne
|
6.69
|
3.77
|
3.87
|
3.94
|
Non-1-yne
|
6.69
|
4.38
|
4.65
|
4.83
|
Cyclopentane
|
6.69
|
5.02
|
4.92
|
4.77
|
Cyclohexane
|
6.69
|
6.74
|
6.56
|
6.29
|
Cycloheptane
|
6.69
|
8.24
|
7.97
|
7.63
|
Cyclooctane
|
6.69
|
10.21
|
9.85
|
9.39
|
Methanol
|
6.69
|
1.77
|
1.61
|
1.46
|
Ethanol
|
6.69
|
2.22
|
2.00
|
1.79
|
Benzene
|
6.69
|
0.96
|
0.99
|
1.00
|
Toluene
|
6.69
|
1.31
|
1.35
|
1.37
|
Ethylbenzene
|
6.69
|
1.95
|
1.98
|
1.99
|
|
Table 5-27: Activity coefficients at infinite
dilution of organic solutes in 1-methyl-3-
octylimidazolium hexafluorophosphate with n3 = 5.135
mmol (33.26 %)
at T = (313.15, 323.15 and 333.15) K.
Experimental at /K
Solute
|
n3/mmol
|
T=313.15
|
T=323.15
|
T=333.15
|
n-pentane
|
5.14
|
8.32
|
8.11
|
7.99
|
n-hexane
|
5.14
|
11.01
|
10.68
|
10.41
|
n-heptane
|
5.14
|
14.30
|
13.59
|
13.21
|
n-octane
|
5.14
|
17.64
|
17.09
|
16.93
|
n-decane
|
5.14
|
31.68
|
30.80
|
28.98
|
n-undecane
|
5.14
|
41.33
|
40.13
|
36.99
|
Hex-1-ene
|
5.14
|
6.45
|
6.29
|
6.15
|
Hept-1-ene
|
5.14
|
8.19
|
8.12
|
8.14
|
Oct-1-ene
|
5.14
|
10.30
|
10.23
|
10.34
|
Non-1-ene
|
5.14
|
13.48
|
13.25
|
13.28
|
Dec-1-ene
|
5.14
|
16.66
|
16.30
|
16.36
|
Undec-1-ene
|
5.14
|
25.24
|
24.79
|
22.52
|
Pent-1-yne
|
5.14
|
1.72
|
1.79
|
1.84
|
Hex-1-yne
|
5.14
|
2.33
|
2.38
|
2.43
|
Hept-1-yne
|
5.14
|
2.93
|
2.98
|
3.04
|
Oct-1-yne
|
5.14
|
3.90
|
3.94
|
4.03
|
Non-1-yne
|
5.14
|
4.47
|
4.71
|
4.91
|
Cyclopentane
|
5.14
|
5.06
|
4.95
|
4.79
|
Cyclohexane
|
5.14
|
6.82
|
6.61
|
6.30
|
Cycloheptane
|
5.14
|
8.02
|
7.74
|
7.75
|
Cyclooctane
|
5.14
|
9.92
|
9.51
|
9.37
|
Methanol
|
5.14
|
1.85
|
1.65
|
1.50
|
Ethanol
|
5.14
|
2.32
|
2.05
|
1.82
|
Benzene
|
5.14
|
0.97
|
0.99
|
1.03
|
Toluene
|
5.14
|
1.36
|
1.37
|
1.41
|
Ethylbenzene
|
5.14
|
1.95
|
1.98
|
2.02
|
|
Table 5-28: Average activity coefficients at
infinite dilution of organic solutes in 1-
methyl-3-octylimidazolium hexafluorophosphate at T =
(313.15, 323.15 and 333.15) K.
Experimental
|
at /K
|
|
Solute
|
T=313.15
|
T=323.15
|
T=333.15
|
n-pentane
|
8.27
|
8.09
|
7.91
|
n-hexane
|
10.88
|
10.62
|
10.31
|
n-heptane
|
14.19
|
13.69
|
13.23
|
n-octane
|
17.99
|
17.48
|
16.99
|
n-decane
|
31.72
|
30.53
|
28.61
|
n-undecane
|
41.70
|
39.88
|
36.76
|
Hex-1-ene
|
6.31
|
6.22
|
6.11
|
Hept-1-ene
|
8.21
|
8.15
|
8.08
|
Oct-1-ene
|
10.54
|
10.45
|
10.37
|
Non-1-ene
|
13.82
|
13.59
|
13.39
|
Dec-1-ene
|
16.49
|
16.41
|
16.35
|
Undec-1-ene
|
25.17
|
24.40
|
22.64
|
Pent-1-yne
|
1.71
|
1.77
|
1.81
|
Hex-1-yne
|
2.29
|
2.34
|
2.39
|
Hept-1-yne
|
2.87
|
2.93
|
2.99
|
Oct-1-yne
|
3.84
|
3.91
|
3.99
|
Non-1-yne
|
4.43
|
4.68
|
4.87
|
Cyclopentane
|
5.04
|
4.94
|
4.78
|
Cyclohexane
|
6.78
|
6.59
|
6.30
|
Cycloheptane
|
8.13
|
7.86
|
7.69
|
Cyclooctane
|
10.07
|
9.68
|
9.38
|
Methanol
|
1.81
|
1.63
|
1.48
|
Ethanol
|
2.27
|
2.03
|
1.81
|
Benzene
|
0.97
|
0.99
|
1.02
|
Toluene
|
1.34
|
1.36
|
1.39
|
Ethylbenzene
|
1.95
|
1.98
|
2.01
|
|
Table 5-29: Excess molar enthalpies at
infinite dilution of organic solutes for the ionic
liquid 1-methyl-3-octylimidazolium hexafluorophosphate,
calculated using the Gibbs-
Helmholtz equation.
SOLUTE
|
Linear regression using Eq.(2-11)
|
|
|
|
n-pentane
|
0.229
|
1.381
|
0.999
|
1.90
|
n-hexane
|
0.283
|
1.485
|
0.994
|
2.35
|
n-heptane
|
0.366
|
1.485
|
1.000
|
3.04
|
n-octane
|
0.300
|
1.933
|
0.999
|
2.49
|
n-decane
|
0.537
|
1.748
|
0.973
|
4.46
|
n-undecane
|
0.656
|
1.643
|
0.966
|
5.45
|
Hex-1-ene
|
0.172
|
1.294
|
0.991
|
1.43
|
Hept-1-ene
|
0.083
|
1.840
|
0.996
|
0.69
|
Oct-1-ene
|
0.085
|
2.084
|
0.999
|
0.71
|
Non-1-ene
|
0.165
|
2.099
|
0.999
|
1.37
|
Dec-1-ene
|
0.045
|
2.660
|
0.996
|
0.37
|
Undec-1-ene
|
0.551
|
1.473
|
0.937
|
4.58
|
Pent-1-yne
|
-0.297
|
1.487
|
0.989
|
-2.47
|
Hex-1-yne
|
-0.224
|
1.541
|
0.998
|
-1.86
|
Hept-1-yne
|
-0.205
|
1.708
|
0.999
|
-1.70
|
Oct-1-yne
|
-0.200
|
1.982
|
0.997
|
-1.66
|
Non-1-yne
|
-0.501
|
3.088
|
0.994
|
-4.16
|
Cyclopentane
|
0.276
|
0.739
|
0.982
|
2.29
|
Cyclohexane
|
0.386
|
0.684
|
0.980
|
3.21
|
Cycloheptane
|
0.291
|
1.165
|
0.986
|
2.42
|
Cyclooctane
|
0.368
|
1.133
|
0.998
|
3.06
|
Methanol
|
1.050
|
-2.760
|
1.000
|
8.73
|
Ethanol
|
1.195
|
-2.996
|
0.999
|
9.94
|
Benzene
|
-0.263
|
0.806
|
0.999
|
-2.19
|
Toluene
|
-0.210
|
0.960
|
0.996
|
-1.75
|
Ethylbenzene
|
-0.145
|
1.132
|
0.999
|
-1.21
|
|
2.95 3 3.05 3.1 3.15 3.2 3.25
1000K/T

4
3.5
111( EP13)
3
2.5
2
1.5
Figure 5-48: Plots of versus for n-alkanes in
[MOIM] [PF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
n-pentane, () n-hexane,
(?) n-heptane, (?) n-octane, () n-decane and (?)
n-undecane.
2.95 3 3.05 3.1 3.15 3.2 3.25
1000/T/K-1
Figure 5-49: Plots of versus for alk-1-enes in
[MOIM] [PF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
hex-1-ene, () hept-1-ene,
(?) oct-1-ene, (?) non-1-ene, () dec-1-ene and (?)
undec-1-ene.

2.95 3 3.05 3.1 3.15 3.2 3.25
1000K/T
In(L13)
0.8
0.6
0.4
1.8
1.6
1.4
1.2
1
Figure 5-50: Plots of versus for alk-1-ynes in
[MOIM] [PF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
pent-1-yne, () hex-1-yne,
(?) hept-1-yne, (?) oct-1-yne and () non-1-yne.
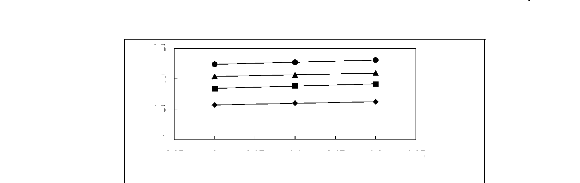
2.95 3 3.05 3.1 3.15 3.2 3.25
1000K/T
2.5
2
ln( L13)
1.5
1
Figure 5-51: Plots of versus for cycloalkanes in
[MOIM] [PF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
cyclopentane, () cyclohexane,
(?) cycloheptane and (?) cyclooctane.
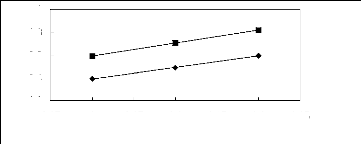
2.95 3 3.05 3.1 3.15 3.2 3.25
1000K/T
In( EF13)
0.8
0.6
0.4
0.2
1
Figure 5-52: Plots of versus for alkanols in
[MOIM] [PF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
methanol and () ethanol.
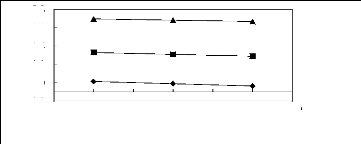
-0.22.95 3 3.05 3.1 3.15 3.2 3.25
1000K/T
In( E1:13)
0.8
0.6
0.4
0.2
0
Figure 5-53: Plots of versus for alkylbenzenes
in [MOIM] [PF6] together with a linear
correlation of the data using the Gibbs-Helmholtz equation; ()
benzene, () toluene and
(?) ethylbenzene.
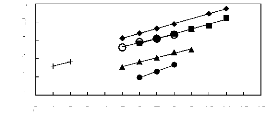
0 1 2 3 4 5 6 7 8 9 10 11 12 13
4
3
In( EF13)
2
1
0
-1
Nc
Figure 5-54: Plots of versus the number of
carbon atoms at 313.15 K for () n-alkanes,
() alk-1-enes, (?) alk-1-ynes, and (?) cycloalkanes, (+)
alkanols and (?) alkylbenzenes in
[MOIM] [PF6]
5.2. Results from the inert gas stripping
technique
5.2.1. N-methyl-2-pyrrolidone, NMP
Table 5-30: Experimental infinite dilution
activity coefficients of n-hexane as well as cyclohexane in NMP obtained by the
dilutor method and comparison with literature data taken from Gruber et al.
(1999). Experimental values were determined using equation (3-90).
T
K
|
Experimental data
|
Literature data
|
Deviation#
%
|
|
|
D/ cm3.min-1
|
|
|
303.15
|
7.550
|
13.278
|
21.4 -35.4
|
13.10
|
1.359
|
303.15
|
14.96
|
13.28
|
21.4 -35.4
|
13.10
|
1.374
|
303.15
|
20.23
|
13.271
|
21.4 -35.4
|
13.10
|
1.305
|
313.15
|
7.480
|
11.561
|
21.4 -35.4
|
11.80
|
-2.025
|
313.15
|
15.21
|
11.568
|
21.4 -35.4
|
11.80
|
-1.966
|
313.15
|
19.94
|
11.549
|
21.4 -35.4
|
11.80
|
-2.127
|
323.15
|
7.620
|
10.992
|
21.4 -35.4
|
10.90
|
0.844
|
323.15
|
15.09
|
11.009
|
21.4 -35.4
|
10.90
|
1.000
|
323.15
|
19.85
|
10.983
|
21.4 -35.4
|
10.90
|
0.761
|
Cyclohexane
|
303.15
|
7.510
|
8.199
|
21.4 -35.4
|
8.06
|
1.725
|
303.15
|
15.07
|
8.213
|
21.4 -35.4
|
8.06
|
1.898
|
303.15
|
21.53
|
8.184
|
21.4 -35.4
|
8.06
|
1.538
|
313.15
|
7.660
|
7.546
|
21.4 -35.4
|
7.40
|
1.973
|
313.15
|
15.14
|
7.539
|
21.4 -35.4
|
7.40
|
1.878
|
313.15
|
20.39
|
7.541
|
21.4 -35.4
|
7.40
|
1.905
|
323.15
|
7.480
|
6.836
|
21.4 -35.4
|
6.80
|
0.529
|
323.15
|
14.98
|
6.841
|
21.4 -35.4
|
6.80
|
0.603
|
323.15
|
21.43
|
6.839
|
21.4 -35.4
|
6.80
|
0.574
|
|
# Relative deviation, R.D., given by
5.2.2. Trihexyltetradecylphosphonium bis
(trifluoromethylsulfonyl) imide
Table 5-31: Experimental infinite dilution
activity coefficients obtained by the inert gas
stripping method (IGSM) for
six different organic solutes in the ionic
liquid
Trihexyltetradecylphosphonium bis (trifluoromethylsulfonyl) imide,
and comparison with
similar data obtained by the GLC method.
Results
Results from the IGST from GLC
T D D D Deviation#
K cm3/min cm3/min cm3/min
(Average) %
n-hexane
303.15 7.55 1.087 15.05 1.084 20.98 1.083 1.085 1.089 -0.367
313.15 7.48 1.101 14.91 1.109 - - 1.105 1.096 0.821
323.15 7.52 1.116 15.65 1.121 - - 1.119 1.103 1.451
Hex-1-ene
303.15 7.51 0.895 15.32 0.899 19.87 0.890 0.895 0.900 -0.556
313.15 7.72 0.911 15.45 0.916 - - 0.914 0.907 0.772
T C
323.15 7.43 0.924 15.50 0.918 - - 0.921 0.913 0.876
? ? ? ?
13 1 ? 1
? Cyclohexane
303.15 7.53 0.801 15.29 0.815 21.52 0.803 0.806 0.794 1.511
3
313.15 7.52 0.813 14.82 0.821 - - 0.817 0.795 2.767
323.15 7.59 0.825 14.93 0.821 - - 0.823 0.796 3.392
Methanol
303.15 7.64 1.140 14.48 1.111 20.06 1.136 1.129 1.151 -1.911
313.15 7.62 1.105 15.08 1.094 - - 1.100 1.083 1.570
323.15 7.57 1.033 15.86 1.058 - - 1.046 1.048 -0.191
Benzene
303.15 7.61 0.391 15.11 0.399 20.15 0.387 0.392 0.381 2.887
313.15 7.55 0.406 15.72 0.400 - - 0.403 0.391 3.069
323.15 7.52 0.409 14.98 0.413 - - 0.411 0.398 3.266
Acetone
303.15 7.54 0.285 15.64 0.287 21.33 0.289 0.287 0.297 -3.367
313.15 7.66 0.303 14.89 0.308 - - 0.306 0.297 3.030
- 0.321 0.311 3.215
323.15 7.46 0.318 15.41 0.323 -
# Relative deviation given by
5.3.Separation potential of the investigated ionic
liquids
From experimental data, equations (2-3) and (2-4) were used to
calculate selectivities, and
capacities, at infinite dilution for seven different separation
problems. Table 5-32 gives an
insight into the effectiveness of the ionic liquids
investigated in this work as a separation solvent, as compared to other ionic
liquids and some industrial molecular solvents such as sulfolane, NMP,
dimethylsulfoxide and chlorobenzene.
Table 5-32: Selectivity and capacity at
infinite dilution at T = 313.15 K of the ionic liquids
investigated
in this work for different separation problems and comparison with
industrial
separation agents as well as other ionic liquids
Benzene
n-hexane/ benzene
Methanol/ benzene
Ethanol/
benzene
Butan-2-one /benzene
Hexane/
hex- 1 - ene
Methanol/ acetone
Ethanol /
butan-2- one
Methanol
Hex- 1 - ene
Butan-2-one
Selectivity at infinite dilution, Limiting Capacity,
[EMIM][BF4]a
|
38.65
|
0.17
|
0.31
|
0.65
|
2.02
|
0.39
|
0.47
|
0.41
|
0.02
|
2.33
|
0.62
|
[C16MIM][BF4]b
|
3.10
|
1.52
|
1.94
|
1.32
|
1.35
|
1.28
|
1.47
|
1.27
|
0.55
|
0.83
|
0.96
|
[3C6C14P][BF4]c
|
3.41
|
1.31
|
1.41
|
1.08
|
1.26
|
1.25
|
1.30
|
2.44
|
0.90
|
1.86
|
2.25
|
[3C6C14P][Tf2N]c
|
2.80
|
2.77
|
3.25
|
0.81
|
1.21
|
3.85
|
4.00
|
2.56
|
1.10
|
0.92
|
3.15
|
[3C6C14P][PF6]c
|
2.96
|
3.12
|
3.32
|
1.04
|
1.20
|
3.13
|
3.21
|
1.47
|
0.59
|
0.32
|
1.42
|
[3C6C14P][(C2F5)3PF3]d
|
3.25
|
5.83
|
5.87
|
-
|
1.23
|
|
-
|
5.00
|
1.89
|
0.86
|
-
|
[3C1C4N][Tf2N]e
|
13.94
|
1.07
|
1.38
|
-
|
1.89
|
3.33
|
-
|
0.75
|
0.10
|
0.70
|
-
|
[BMPyrr][Tf2N]f
|
15.47
|
-
|
2.01
|
0.62
|
1.92
|
|
3.26
|
1.16
|
0.14
|
-
|
1.89
|
[C13C8N] [Tf2N]c
|
3.77
|
2.68
|
2.82
|
0.82
|
1.33
|
3.13
|
3.44
|
2.27
|
0.80
|
0.85
|
2.78
|
[EMIM][TfO]c,j
|
30.20
|
0.33
|
0.53
|
-
|
2.31
|
|
-
|
0.45
|
0.03
|
1.38
|
-
|
[MOIM][PF6]c
|
11.27
|
1.88
|
2.35
|
-
|
1.72
|
|
-
|
1.04
|
0.16
|
0.55
|
-
|
[BMIM][SbF6]c
|
22.25
|
1.41
|
1.89
|
0.50
|
2.08
|
4.35
|
3.74
|
0.79
|
0.07
|
0.56
|
1.56
|
Sulfolaneg
|
18.17
|
0.91
|
1.26
|
0.83
|
-
|
1.37
|
1.52
|
0.43
|
-
|
0.47
|
0.51
|
NMPh
|
11.24
|
-
|
-
|
-
|
0.53
|
|
-
|
0.95
|
0.16
|
-
|
-
|
Chlorobenzenei,k
|
-
|
-
|
-
|
-
|
-
|
0.17*
|
8.29
|
-
|
-
|
-
|
0.47
|
Dimethylsulfoxidek
|
-
|
-
|
-
|
-
|
-
|
0.35*
|
0.20*
|
-
|
-
|
2.00*
|
0.35*
|
|
aFoco et al. (2006),
bMutelet and Jaubert (2007), cThis work, d
Letcher et al. (2008, e Heintz et al
(2006b), f Kato
and Gmehling (2005), gMöllmann and Gmehling
(1997),hKrummen et al. (2000),
iKossack et al.(2008),
jOlivier et al.(2010a); kDortmund Data Bank, DDB, * Data
obtained at
298.15 K.
CHAPTER SIX: DISCUSSION
6.1. Fluorinated Ionic Liquids investigated in this work
6.1.1. Gas-Liquid Chromatography
6.1.1.1. Phosphonium-based Ionic Liquids
Infinite dilution activity coefficients of various organic
solutes in the ionic liquids [3C6C14P] [Tf2N], [3C6C14P]
[BF4], [3C6C14P] [PF6] are listed in tables 5-2 through 5-4,
5-6 through 5-8 and 5-10 through 5-12. For two different solvent loadings IDAC
values obtained with the same solutes generally remained close to each other.
It is an indication that no adsorption took place onto the column packing, even
for polar solutes such as ketones and alcohols. For all the three
phosphonium-based ionic liquids, infinite dilution activity coefficients
decrease in the order: nalkanes alk-1-enes alcohols > cycloalkanes >
alk-1-ynes > alkylbenzenes > ketones. IDAC values for ketones were the
smallest for all the investigated solutes, an indication of strong
solute-solvent interactions. This can be attributed to the interaction between
the two pairs of electrons on the oxygen atom of the ketone with the cation of
the IL, as well as between the positive pole of the ketone and the ionic
liquid`s anion. Banerjee and Khanna (2006), Letcher et al. (2008) and Revelli
et al. (2009) reported infinite dilution activity coefficients of various
organic solutes in [3C6C14P] [Tf2N] and/or [3C6C14P]
[BF4]. In this work, a larger number of solutes have been considered.
Additionally, IDAC data of organics in the ionic liquid [3C6C14P][Tf2N]
obtained from the inert gas stripping technique are presented. Tables 6-1 and
6-2 allow a quick comparison of experimental infinite dilution activity
coefficient data obtained in this work to literature data. Results from this
study are in good agreement with those published by Letcher et al. (2008) and
Revelli et al. (2009). However, there are large discrepancies between data
reported in this work and those obtained by Banerjee and Khanna (2006). This
may be due to different purities as far as ionic liquids samples are concerned.
Moreover, the methodological approach used by Banerjee and coworkers is
different from the one used in this study.
During experiments, it was observed that alcohols led to very
long retention times. Resulting peaks were so broad that a very accurate
determination of the retention time was not possible. This is the reason why
the linear regression of experimental data shown in Figures 5-5 and 5-13 was
not convincingly successful.
Table 6-1: Comparison of experimental IDACs
in the ionic liquid [3C6C14P] [Tf2N] at 313.15 K
from this work
to literature data;*Interpolated data.
Solute
|
*Banerjee and Khanna
(2006)
|
Letcher et al.
(2008)
|
*Revelli et al.
(2009)
|
This
work
|
n-Hexane
|
0.759
|
1.130
|
1.064
|
1.096
|
Hex-1-ene
|
0.498
|
0.920
|
0.889
|
0.907
|
Cyclohexane
|
0.611
|
0.830
|
0.802
|
0.795
|
Methanol
|
0.951
|
1.230
|
1.128
|
1.083
|
Benzene
|
0.405
|
0.400
|
0.392
|
0.391
|
Butan-2-one
|
-
|
-
|
0.270
|
0.321
|
|
Table 6-2: Comparison of experimental IDACs
in the ionic liquid [3C6C14P] [BF4] at 313.15 K
from this work to
literature data; * Interpolated data.
Solute
|
*Banerjee and
Khanna (2006) This work
|
n-Hexane
|
0.956
|
1.400
|
Hex-1-ene
|
0.565
|
1.109
|
Cyclohexane
|
0.725
|
0.975
|
Methanol
|
6.524
|
0.537
|
Benzene
|
0.369
|
0.410
|
|
Partial molar excess enthalpies at infinite dilution were
calculated from the plots of
as a function of provided in Figures 5-1 through 5-7, 5-9
through 5-15 and 5-17
through 5-23, using the Gibbs-Helmholtz equation:
(2-11)
Tables 5-5, 5-9 and 5-13 show that partial molar excess
enthalpies at infinite dilution are
generally small. Thus, limiting activity
coefficients values vary little with temperature. (The
greatest variation was 0.023 K-1). Positive values of
partial molar excess enthalpies imply
that infinite dilution activity coefficients decrease with
increasing temperature. In addition, positive infinite dilution partial molar
excess enthalpies indicate that dissociation effects outweigh association
effects in very dilute mixtures involving the ionic liquid and the solute under
consideration. Negative infinite dilution partial molar excess enthalpies
indicate that association effects outweigh dissociation effects. Figures 5-8,
5-16 and 5-24 show that
extending the solute alkyl chain weakens its interaction with
the ionic liquid as values
increase when the number of carbon atoms is increased.
Table 5-32 shows selectivities and capacities at infinite
dilution for selected ionic liquids and some industrial solvents in relation
with n-hexane/benzene, n-hexane/hex-1-ene and methanol/acetone separation
problems. It appears that the studied phosphonium-based fluorinated ionic
liquids are poor solvents for separating aromatics from aliphatics. However,
they are fairly more selective when it comes to the methanol/benzene and
methanol/acetone separation problems. For example, the limiting selectivity
value of the ionic liquid [3C6C14P] [Tf2N] for the methanol/ acetone mixture
was calculated as 3.85 at 313.15 K, with the limiting capacity found to be 2.3.
These values lead to one of the best selectivity-capacity combinations at
infinite dilution for ionic liquids reported in the open literature.
6.1.1.2. Ammonium-based Ionic Liquid.
Experimental limiting activity coefficients of the
investigated solutes in the ionic liquid [C13C8N] [Tf2N] are listed in Tables
5-14 through 5-16. They decrease in the following order: n-alkanes >
alk-1-enes > alcohols > cycloalkanes > alk-1-ynes > alkylbenzenes
> ketones. Alk1-ynes, alkylbenzenes and ketones have low IDAC values in the
ionic liquid. This is due to the interaction between the electrons of these
unsaturated inorganics and the cation of the ionic liquid [C13C8N] [Tf2N].
From Figure 5-32, it can be seen that for all classes of
solutes, except ketones, IDAC values increase with the increasing number of
carbon atoms in the structure of the solutes. The magnitude of solute-solvent
interactions which is related to the infinite dilution activity coefficient is
determined by the solute polarity. The more polar the solute, the stronger the
interaction and the smaller the limiting activity of the solute in the ionic
liquid.
Temperature-dependence of IDAC values is depicted by Table
5-17 obtained from Figures 5-25 through 5-31. IDACs of unsaturated organic
solutes, except alk-1-enes increase with increasing temperature. Thus, they
exhibit negative partial molar excess enthalpies. Limiting selectivities and
capacities displayed in Table 5-32 reveal that similar to the three phosphonium
ionic liquids discussed in the previous section, [C13C8N] [Tf2N] exhibits poor
separation performance for the n-hexane/benzene system. It is likely to
represent a fair separation agent for ketones/alcohols and aromatic
compounds/alcohols mixtures.
6.1.1.3. Imidazolium-based Ionic Liquids.
Infinite dilution activity coefficients and partial molar
excess enthalpies of different organic
solutes are provided in tables 5-18
through 5-21 for [BMIM] [SbF6], 5-22 through 5-25 for
[EMIM] [TfO], 5-26
through 5-29 for [MOIM] [PF6]. Polar solutes have strong interaction with
the investigated imidazolium-based ionic liquids. The following
hierarchies in the variation of IDAC values have been observed:
· [BMIM] [SbF6]: n-alkanes > cycloalkanes alk-1-enes
> alcohols > alk-1-ynes >
alkylbenzenes > ketones;
· [EMIM] [TfO]: n-alkanes > cycloalkanes alk-1-enes >
alk-1-ynes > alkylbenzenes > alcohols;
· [MOIM] [PF6]: n-alkanes > alk-1-enes cycloalkanes >
alcohols alk-1-ynes >
alkylbenzenes.
For all three imidazolium-based ionic liquids, infinite dilution
activity coefficients increase with increasing number of carbon atoms as shown
in Figures 5-40, 5-47 and 5-54.
From the plots presented in Figures 5-33 through 5-39 for
[BMIM] [SbF6], 5-41 through 5-46 for [EMIM] [TfO] and 5-48 through 5-53 for
[MOIM] [PF6], the partial molar excess enthalpy at infinite dilution of all
investigated unsaturated solutes, except alk-1-enes was found to be
negative.
These three ionic liquids are potentially effective
separation agents for aromatic/aliphatic compounds mixtures (Table 5-32). Their
limiting selectivity and capacity data are high compared to NMP and
sulfolane.
6.1.2. The inert gas stripping technique
Mixtures of n-hexane and cyclohexane as solutes in NMP were
used as test systems. Measurements were carried out in the temperature range
from 303.15 K and 323.15 K at three different stripping gas flow rates.
Experimental results presented in table 5-30 were within 2 % of published
literature data. Good agreement was also observed between data obtained from
the gas-liquid chromatography and the dilutor method. Table 5-31 lists infinite
dilution activity coefficients of six solutes, each one representing a
functional group, in the ionic liquid [3C6C14P] [Tf2N]. A comparison, in term
of relative deviations was made to assess the extent of the agreement between
the two experimental techniques used in this work with exactly the same
systems. It was found that experimental results agreed within approximately 3.4
%. This is significant as not only the reliability of the newly constructed gas
stripping set up was confirmed but also doubts on the validity of the GG
experimental procedure were dispelled. In effect, the open literature (Mutelet
and Jaubert 2006) warns of large experimental errors in the GC method when
polar solutes are investigated due to adsorption of the latter onto the column
packing and probably onto the inner walls of the GC column. To minimize
adsorption effects, large mass fractions of the ionic liquids were used during
the column packing stage. This
strategy was effective since even for methanol and acetone
results from the GC and the dilutor techniques are not very different, and are
within experimental errors.
Table 6-4 suggests that the uncertainty in determining the
flow rate was the largest contributor to the overall error of infinite dilution
activity coefficient data. Apart from the inability of the flow regulator to
stabilize the inert gas flow rate over a long period of time, no major
difficulties were encountered. All minor problems were sorted out as soon as
they had arisen. Using the dilutor technique, a typical run with flow rates
around 15 cm3. min.-1 could last three and eight hours
for results displayed in tables 5-30 and 5-31 respectively. An experiment was
terminated when, according to Krummen et al. (2000), around 15 % of the solute
was stripped out of the system. It took a month and half to generate these data
when, for the same systems and number of runs, the GLC equipment used in this
study would require only a single day. The inert gas stripping technique is
known as a more time consuming technique than GLC. These durations are not
particularly longer than those reported by other authors. In order to decrease
the experimental time, the first attempt consisted of increasing the inert gas
flow rate. The best compromise between thermodynamics and kinetics of the
stripping process was observed in the neighborhoods of flow rates about 23
cm3.min-1. Beyond this value, infinite dilution activity
coefficient values tended to depend on the stripping gas flow rate, an
indication that thermodynamic equilibrium was not achieved in the cell. For
similar systems involving NMP, Krummen et al. (2000) took only 90 minutes to
achieve a run. They used a dilutor cell with larger volume and probably higher
height than the one constructed for this study, and flow rates as high as 20 to
40 cm3.min-1.
6.1.3. Error estimation
Uncertainties in determining the various quantities required
to calculate activity coefficients at infinite dilution are provided in tables
6-3 and 6-4. The presented values were obtained by taking into account the
accuracy of sensors as stated by suppliers, the stability of experimental
parameters and deviations of parameters under different experimental
conditions. The procedures described by George (2008) were used in this work to
assign errors to mass, gas flow rate, as well as temperature measurements. As
suggested by Harris (2000), the relative standard deviation of experimental
variables were calculated according to the method presented by Skoog et al.
(1996). Table 6-5 gives the overall relative errors calculated using the law of
error propagation applied to equations (2-3), (2-4), (2-11), (3-9) and (3-88).
Additional details are provided by the experimental procedures given in Chapter
four.
Table 6-3: Uncertainties on experimental
parameters for the GLC method.
Number of moles for the solvent,
|
#177;0.03
|
%
|
Oven temperature,
|
#177;0.35
|
%
|
Inlet pressure
|
#177;0.50
|
%
|
Outlet pressure
|
#177;0.30
|
%
|
Carrier gas flow rate
|
#177;0.20
|
%
|
Saturation vapour pressures
|
#177;0.30
|
%
|
Net retention volume
|
#177;3.00%
|
Difference of retention times (Solute - inert gas)
|
#177;0.20 %
|
|
Table 6-4: Uncertainties on experimental
parameters for the dilutor method.
Number of moles for the solvent,
|
#177;0.03
|
%
|
System temperature,
|
#177;0.10
|
%
|
Dilutor cell pressure
|
#177;0.03
|
%
|
Stripping gas flow rate
|
#177;3.33
|
%
|
Saturation vapour pressures
|
#177;0.30
|
%
|
Saturation fugacity coefficients
|
#177;0.50
|
%
|
Flow-meter pressure
|
#177;0.03
|
%
|
|
Table 6-5: Overall uncertainties on
experimental data and derived quantities.
Infinite dilution activity coefficient (GLG method)
|
#177;3.68
|
%
|
Infinite dilution activity coefficient (Dilutor method)
|
#177;4.26
|
%
|
Molar excess enthalpy at infinite dilution
|
#177;7.66
|
%
|
Selectivity at infinite dilution
|
#177;7.36
|
%
|
Capacity at infinite dilution
|
#177;3.68
|
%
|
|
6.2. Limiting activity coefficients of fluorinated ionic
liquids
It was found, after an extensive literature survey, up to
October 2009, experimental infinite dilution activity coefficients of 37
fluorinated ionic liquids, including the ones studied in this thesis, were
available (See Table 6-6). In this section, experimental data, others than
those generated in this work, were taken from various research papers published
in the following journals:
· The Journal of Chemical Thermodynamics
· The Journal of Chemical and Engineering Data
· Fluid Phase Equilibria
· The Journal of Physical Chemistry B
· The Journal of Chromatography A
Numbers which are assigned to ionic liquids in table 6-6 are
used as x-coordinates in the plots presented in Figures 6-1 through
6-3. The fluorinated ionic liquids 1-butyronitrile-3- methylimidazolium bis
(trifluoromethylsulfonyl) imide ([CpMIM] [Tf2N]), 1-butyronitrile-2, 3-
dimethylimidazolium bis(trifluoromethylsulfonyl) imide ([CpMMIM][Tf2N]),
1-hexyloxymethyl-3-methylimidazolium bis
(trifluoromethylsulfonyl) imide ([H-O-MIM]
[Tf2N] , 2009b) and 1,3-dihexyloxymethyl-imidazolium
bis(trifluoromethylsulfonyl)-imide ([DH-O-MIM] [Tf2 , 2009b)
are not discussed in this dissertation due to insufficient
database for comparison.
Table 6-6: List of fluorinated ionic liquids
investigated in the literature and assigned numbers.
No. Ionic Liquid No. Ionic Liquid No. Ionic Liquid
1
|
[EMIM][BF4]
|
14
|
[C16MIM][BF4]
|
27
|
[BMIM][SbF6]
|
2
|
[EMIM] [Tf2N]
|
15
|
[3C6C14P][BF4]
|
28
|
[BMIM][PF6]
|
3
|
[MMIM][Tf2N]
|
16
|
[3C6C14P][Tf2N]
|
29
|
[EMIM][TFA]
|
4
|
[BMIM][BF4]
|
17
|
[3C6C14P][(C2F5)3PF3]
|
30
|
[HMIM][TfO]
|
5
|
[BMIM][Tf2N]
|
18
|
[3C1C4N][Tf2N]
|
31
|
[BMPyrr][TfO]
|
6
|
[BMIM][TfO]
|
19
|
[BMPy][BF4]
|
32
|
[HMPyrr][Tf2N]
|
7
|
[MMPIM][BF4]
|
20
|
[BMPyrr][Tf2N]
|
33
|
[OMPyrr][Tf2N]
|
8
|
[EMMIM][Tf2N]
|
21
|
[Et3S][Tf2N]
|
34
|
[CpMIM][Tf2N]
|
9
|
[HMIM][BF4]
|
22
|
[Epy][Tf2N]
|
35
|
[CpMMIM][Tf2N]
|
10
|
[HMIM][PF6]
|
23
|
[3C6C14P][PF6]
|
36
|
[H-O-MIM][Tf2N]
|
11
|
[HMIM][Tf2N]
|
25
|
[EMIM][TfO]
|
37
|
[DH-O-MIM][Tf2N]
|
13
|
[MOIM][Tf2N]
|
26
|
[MOIM][PF6]
|
|
|
12
|
[MOIM][BF4]
|
24
|
[3C8C1N][Tf2N]
|
|
|
|
Chapter 6: Discussion
6.2.1. Hierarchy of IDACs values
Figures 6-1 to 6-3 shows a comparison of limiting activity
coefficients of six solutes, each one representing a homologous series, in
fluorinated ionic liquids.

Infinite dilution activity
coefficient
250
200
300
150
100
50
0
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
Ionic liquids
Figure 6-1: Experimental infinite dilution
activity coefficients of (?) n-hexane and (?)
cyclohexane in various
fluorinated ionic liquids at 313.15 K.;1, [EMIM][BF4][1][2]; 2,
[EMIM]
[Tf2N] [3][5]; 3, [MMIM] [Tf2N] [4] ; 4, [BMIM][BF4] [6] ;
5, [BMIM] [Tf2N] [4] ; 6,
[BMIM][TfO] [9] ; 7, [MMPIM][BF4] [10] ; 8,
[EMMIM] [Tf2N] [3] ; 9, [HMIM][BF4] [12] ; 10,
[HMIM][PF6] [13] ; 11, [HMIM]
[Tf2N] [14][15] ; 12, [MOIM][BF4] [17] ; 13, [MOIM] [Tf2N] [16] ;
14,
[C16MIM][BF4] [18] ; 15, [3C6C14P][BF4] [19] ; 16, [3C6C14P] [Tf2N]
[19] ; 17,
[3C6C14P][(C2F5)3PF3] [20] ; 18, [3C1C4N] [Tf2N] [21] ; 19,
[BMPy][BF4] [22] ; 20, [BMPyrr]
[Tf2N] [16] ; 21, [Et3S] [Tf2N] [24] ; 22,
[Epy] [Tf2N] [25] ; 23, [3C6C14P][PF6] [19] ; 24, [3C8C1N]
[Tf2N]
[27]; 25, [EMIM][TfO] [28]; 26, [MOIM][PF6]
[29]; 27, [BMIM][SbF6] [30] ; 28,
[BMIM][PF6] [31] ; 29,
[EMIM][TFA] [32] ; 30, [HMIM][TfO] [33] ; 31, [BMPyrr][TfO] [34] ;
32,
[HMPyrr] [Tf2N] [35] ; 33 , [OMPyrr] [Tf2N] [35]
Superscripts on ionic liquids` abbreviations in this section,
as well as, in appendices F, G, H and I correspond to the following
publications used as references: [1] Ge et al. (2008a); [2] Foco et al. (2006);
[3] Heintz et al. (2002); [4] Krummen et al. (2002); [5] Deenadayalu et al.
(2005); [6] Zhou and Wang (2006); [7] Zhou et al. (2007) ; [8]Heintz et al.
(2005) ; [9]Domañska, U. and Marciniak, A., (2008a) ; [10]Wang et al.
(2008) ; [11] Ge et al. (2008b); [12]Letcher et al. (2003b) [13]Letcher et al.
(2003a) [14]Heintz et al. (2006a); [15]Letcher et al. (2005); [16]Kato et al.
(2005) [17]Heintz et al. (2005b) [18]Mutelet et al. (2007); [19]Domañska
et al. (2009); [20]Letcher and Reddy (2005); [21]Heintz et al. (2006b);
[22]Heintz et al. (2001); [23]Heintz et al. (2002); [24]Domañska and
Marciniak (2009); [25] Kato and Gmehling (2004); [26]Kato and Gmehling (2005);
[27]Gwala et al. (2010), [28]Olivier et al (2010a); [29]Olivier et al (2010b);
[30]Olivier et al. (2009c) ; [31]Shimoyama et al. (2008); [32]Domañska,
U. and Marciniak, A., (2007) [33]Yang et al. (2008) [35]Nebig et al. (2009);
[36] Möllmann and
Gmehling (1997); [37] Krummen et al. (2000); [38]Kossack et
al.(2008); [39]Dortmund Data Bank, DDB.
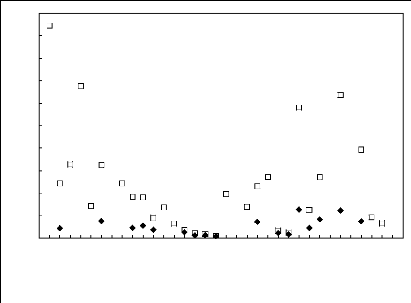
Infinite dilution activity coefficient
50
45
40
35
30
25
20
15
10
5
0
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
Ionic liquids
Figure 6-2: Experimental infinite dilution
activity coefficients of (?) hex-1-ene and () hex-1-
yne in various
fluorinated ionic liquids at 313.15 K; 1, [EMIM][BF4] [2]; 2,
[EMIM][Tf2N] [4][5];
3, [MMIM][Tf2N] [4] ; 4, [BMIM][BF4] [2][6] ; 5,
[BMIM][Tf2N] [4] ; 6, [BMIM][TfO] [9]; 8,
[EMMIM][Tf2N] [3] ; 9,
[HMIM][BF4] [12] ; 10, [HMIM][PF6] [13] ; 11, [HMIM][Tf2N] [14][15] ;
12,
[MOIM][BF4] [17] ; 13, [MOIM][Tf2N] [16] ; 14, [C16MIM][BF4] [18] ; 15,
[3C6C14P][BF4] [19] ;
16, [3C6C14P][Tf2N] [19] ; 17, [3C6C14P][(C2F5)3PF3]
[20] ; 18, [3C1C4N][Tf2N] [21] ; 20, [BMPyrr]
[Tf2N] [16] ; 21,
[Et3S][Tf2N] [24] ; 22, [Epy][Tf2N] [25] ; 23, [3C6C14P][PF6] [19] ; 24,
[3C8C1N]
[Tf2N] [27]; 25, [EMIM][TfO] [28]; 26,
[MOIM][PF6] [29]; 27, [BMIM][SbF6] [30] ;
29,
[EMIM][TFA] [32] ; 31, [BMPyrr][TfO] [34] ; 32,
[HMPyrr][Tf2N] [35] ; 33 , [OMPyrr][Tf2N] [35]
Chapter 6: Discussion
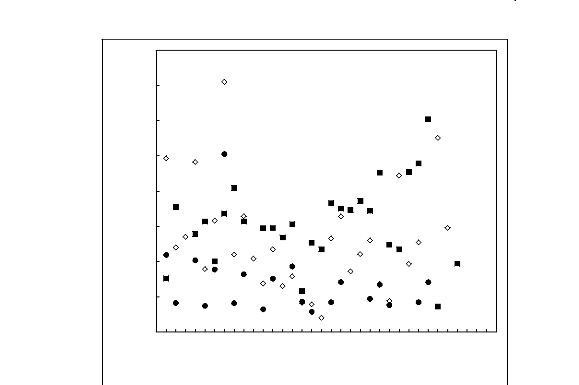
4
3.5
Infinite dilution activity coefficient
3
2.5
2
1.5
1
0.5
0
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
Ionic liquids
Figure 6-3: Experimental infinite dilution
activity coefficients of () ethanol, () benzene and
(?) acetone in various
fluorinated ionic liquids at 313.15 K.; 1, [EMIM][BF4] [2];
2,
[EMIM][Tf2N] [4]; 3, [MMIM][Tf2N] [4] ; 4, [BMIM][BF4] [6][7]
; 5, [BMIM][Tf2N] [8] ; 6,
[BMIM][TfO] [9] ; 7, [MMPIM][BF4]
[10][11] ; 8, [EMMIM][Tf2N] [3] ; 9, [HMIM][BF4] [2] ; 10,
[HMIM][PF6] [13]
; 11, [HMIM][Tf2N] [16] ; 12, [MOIM][BF4] [17] ; 13, [MOIM][Tf2N] [16] ;
14,
[C16MIM][BF4] [18] ; 15, [3C6C14P][BF4] [19] ; 16, [3C6C14P][Tf2N] [19]
; 17,
[3C6C14P][(C2F5)3PF3] [20] ; 18, [3C1C4N][Tf2N] [21] ; 19,
[BMPy][BF4] [22][23] ; 20, [BMPyrr]
[Tf2N] [16] ; 21, [Et3S][Tf2N] [24] ;
22, [Epy][Tf2N] [25][26] ; 23, [3C6C14P][PF6] [19] ; 24,
[3C8C1N][Tf2N]
[27]; 25, [EMIM][TfO] [28]; 26, [MOIM][PF6]
[29]; 27, [BMIM][SbF6] [30] ; 28,
[BMIM][PF6] [31] ; 29, [EMIM][TFA]
[32] ; 30, [HMIM][TfO] [33] ; 31, [BMPyrr][TfO] [34] ; 32,
[HMPyrr][Tf2N]
[35] ; 33 , [OMPyrr] [Tf2N] [35]
According to the above plots, activity coefficient values for
organic solutes in FILs follow the following patterns:
· Imidazolium, pyridinium, pyrrolidinium and
sulfonium-based fluorinated ionic liquids: n-alkanes > cycloalkanes >
alk-1-enes > alk-1-ynes > alcohols > alkylbenzenes > ketones
· Phosphonium-based fluorinated ionic liquids:
n-alkanes alk-1-enes alcohols > cycloalkanes > alk-1-ynes
> alkylbenzenes >
ketones
· Ammonium-based fluorinated ionic liquids:
No clear hierarchy is observable.
6.2.2. Effect of structure on IDACs of organic solutes
in Fluorinated Ionic Liquids, FILs
It would be misleading to conclude that the stated
hierarchies fully translate the behavior of all mixtures of fluorinated ionic
liquids and the solutes under consideration. These are merely general trends.
However, the only constant for all systems is that alkanes and ketones lead to
the largest and the smallest experimental infinite dilution activity
coefficient values respectively.
Linear alkanes are non-polar organic compounds. They interact
with ILs mostly through small range van der Waals forces which are weaker than
induced dipole-dipole interactions appearing in systems involving corresponding
alk-1-enes, alk-1-ynes and aromatic compounds. These compounds have delocalized
electrons that enhance polarisability. Increasing polarisability leads
naturally to smaller limiting activity coefficients. Infinite dilution activity
coefficient values of alcohols are even smaller due to their polar nature and
the presence of an electronegative oxygen atom which is likely to interact more
strongly with the positive charge of the ionic liquid cation. Infinite dilution
activity coefficients values for ketones are the smallest, an indication of
strong solute-solvent interactions. This can be attributed to the interaction
between the two pairs of electrons on the oxygen atom of the ketone with the
cation of the IL, as well as, between its positive pole and the ionic liquid
anion.
There are strong cation-anion coulombic interactions in
imidazolium and pyridinium-based ionic liquids due to the polarisability of
their molecules. Conversely, no delocalized electrons exist in phosphonium,
ammonium and sulfonium-based fluorinated ionic liquids. Association with
organic solutes is likely to be stronger with these solvents in comparison with
imidazolium and pyridinium-based ionic liquids as accommodating a solute will
not require overcoming the strong coulombic interactions and probably hydrogen
bonds. It follows that for the same solute, the limiting activity coefficient
value increases with the introduction of a polarisable ring in the cation of
the ionic liquid. Extending the alkyl chain of the solute generally weakens the
interactions between organic solutes and ionic liquids as infinite dilution
activity coefficients increase with increasing solute carbon number. This is
visible in Figures G-1 through G-83 of Appendix G which relate the infinite
dilution activity coefficient at 313.15 K to the carbon number of various
solutes in all investigated fluorinated ionic liquids. In the presence of
hydrogen bonds and coulombic forces that are common in ionic liquids,
long-chained ionic
liquids are probably too large and closely packed to
accommodate solutes. Exceptions include
the following systems: alkan-1-ols +
[BMIM] [Tf2N], alkan-1-ols + [3C6C14P] [(C2F5)3PF3] and
ket-2-ones + [C13C8N][Tf2N] . Their corresponding plots of the
natural logarithm of versus
carbon number are found in Figures G-56, G-59 and G-81
respectively. It is possible that lengthening the alkyl chain of an alcohol or
a ketone to a certain extent in these particular cases favours additional
attractive forces between the alkyl chain of the solute and the one of the
solvent through van der Waals interactions.
As far as the effect of the ionic liquid anion is concerned,
shape, polarity and size have to be taken into account to interpret infinite
dilution activity coefficient experimental results. Most polar ionic liquids
i.e. those containing [BF4] - and [TFA] - do not generally interact strongly
with the solutes due probably to strong intrinsic anion-cation coulombic
forces, as well as hydrogen bonds.
6.2.2.1. Infinite dilution activity coefficients in
imidazolium-based FILs
An examination of figures in Appendix G gives an insight into
how IDACs values are affected by the presence of a particular cation in the
structure of the imidazolium-based FILs . It appears that for the same anion,
limiting activity coefficients of n-alkanes (Figures G-1 to G-4), alk-1- enes
(Figures G-15 to G-18), alk-1-ynes (Figures G-29 to G-32), cycloalkanes
(Figures G-38 to G-41), alkan-1-ols (Figures G-51 to G-54), alkylbenzenes
(Figures G-64 to G-66) and ket-2- ones (Figures G-75 to G-76) decrease with
increasing alkyl chain length of the IL cation.
It is observed that for n-alkanes (Figures G-5 to G-8),
alk-1-enes (Figures G-19 to G-22), cycloalkanes (Figures G-42 to G-45) and
ket-2-ones (Figures G-77 to G-79), infinite dilution activity coefficients
decrease when the anion is changed in the following order: [BF4]-
> [TFA]- > [TfO]- > [SbF6]- ;
[PF6]- > [Tf2N] - . This is the general trend as in some cases
this is not true (Figures G-44 and G-78)
No such clear hierarchy is displayed by mixtures involving
alk-1-ynes (Figures G-33 to G-35) and alkan-1-ols (Figures G-55 to G-58).
However, for all investigated FILs, the smallest activity coefficient values
are obtained with [Tf2N] - anion.
6.2.2.2. Infinite dilution activity coefficients in
phosphonium-based FILs
The available experimental data allow examination of the
effects of the anion only, since all the phosphonium-based fluorinated ionic
liquids studied so far have in common the [3C6C14P] + cation.
According to the plots represented in Figures G-9, G-23 and G-46, G-71
and G-80, the infinite dilution activity coefficients of all classes of
solutes, except alcohols and alk-1-ynes,
decrease when anions are changed in the following order:
[PF6]- > [BF4] - > [Tf2N]- >
[(C2F5)3PF3]-. The following hierarchy is observed for alcohols:
[PF6]- > [Tf2N]-; [(C2F5)3PF3] - >
[BF4]- (See Figure G-59). And for alk-1-ynes: [PF6]- >
[Tf2N] - > [BF4]- > [(C2F5)3PF3]- . (Figure
G-36)
6.2.2.3. Infinite dilution activity coefficients in
ammonium-based FILs
There are no data for a reliable description of the effect of
the anion as only two ammonium-based fluorinated ionic liquids have been
investigated in the literature. They have in common the [Tf2N]-
anion. For n-alkanes (Figure G-10), alkan-1-ols (Figure G-60), alkylbenzenes
(Figure G-72) and ket-2-ones (Figure G-81), limiting activity coefficients
decrease with increasing alkyl chain length of the ammonium-based FILs. The
opposite trend is observed only for cycloalkanes (Figure G-47).
6.2.2.4. Infinite dilution activity coefficients in
pyrrolidinium-based FILs
Under the same anion, the limiting activity coefficients of
n-alkanes (Figure G-12) and alk-1- enes (Figure G-26) decrease with the
increasing alkyl chain length of pyrrolidinium-based fluorinated ionic liquids.
There are no literature data related to alk-1-ynes, cycloalkanes, alkan1-ols
and alkylbenzenes. Limiting activity coefficients of n-alkanes (Figure G-13),
alk-1-enes (Figure G-27) and cycloalkanes (Figure G-49) decrease when the anion
is changed from [TfO]- to [Tf2N] - . The reverse is observed for
alkan-1-ols. (Figure G-62). Data for other classes of solutes are not
available.
6.3. Limiting selectivity and capacity of fluorinated
ionic liquids
The theory of Prausnitz and Anderson (1961) explains the
separation mechanism of a mixture of hydrocarbons using a polar separation
agent. It is also true for ionic liquids. To act as an effective entrainer or
extractant, an ionic liquid has to interact differently with the mixed
components. This occurs when one of the components is saturated whereas the
other is not. The ionic liquid solvent polarises the non-saturated component.
The former interacts more strongly with the solvent and is carried along as the
bottom product. Selectivity values depend on the relative polarisability of the
two components to be separated. This explains in part the trends of selectivity
and capacity values described in this section and depicted by Figures
H-1through H21 in Appendix H. Solvent capacity is, the numerical amount of
solute removed from the mixture by the extracting solvent. Selectivity normally
decreases with temperature and often follows a different trend from solvent
capacity. The compromise between selectivity and capacity is quantified as the
Performance Index, P.I., which is the arithmetic product of these two
properties. For each separation problem discussed in this work, the effect of
structure on the
separation ability of ionic liquids is reflected by the
hierarchies given in each of the following sections. When analyzing the trends
of selectivity and capacity, it is essential to incorporate in addition to
polarisability, the shape and the size of species, as well as hydrogen bonding
potential within ionic liquids.
6.3.1. n-Hexane (1)/Benzene (2) separation problem
Limiting selectivities of the experimentally investigated
fluorinated ionic liquids follow this
pattern:
|
|
|
|
|
|
|
|
|
[EMIM][BF4]
|
>
|
[BMPy][BF4]
|
>
|
[EMIM][TfO]
|
> [MMIM][Tf2N]
|
|
> [EMIM][TFA]
|
>
|
[BMIM][BF4]
|
>
|
[BMIM][TfO]
|
>
|
[Et3S][Tf2N]
|
> [BMIM][SbF6]
|
>
|
[EMIM][Tf2N]
|
>
|
[HMIM][BF4]
|
>
|
[HMIM][PF6]
|
>
|
Sulfolane >
|
[BMPyrr][Tf2N]
|
>
|
[BMIM][Tf2N]
|
>
|
|
[HMIM][TfO] > [3C1C4N] [Tf2N] > [MOIM][PF6] > NMP
> [HMIM] [Tf2N] > [MOIM][BF4] > [MOIM][Tf2N] > [3C8C1N][Tf2N] >
[3C6C14P][BF4] > [3C6C14P][(C2F5)3PF3] > [C16MIM][BF4] >
[3C6C14P][PF6] >[3C6C14P] [Tf2N]
In terms of good compromise between selectivity and capacity,
FILs are arranged in decreasing order of limiting performance index values, as
follows:
[BMPy][BF4] > [Et3S][Tf2N] > [MMIM][Tf2N] >
[Epy][Tf2N] > [BMPyrr][Tf2N] > [HMIM][PF6] > [EMIM][Tf2N] >
[BMIM][SbF6] > [BMIM][Tf2N] > [HMIM][Tf2N] > [3C6C14P][(C2F5)3PF3]
> [EMIM][BF4] > [BMIM][TfO] > [EMIM][TfO] > [MOIM][Tf2N] >
[HMIM][BF4] > [MOIM][PF6] > NMP > [3C1C4N][Tf2N] > [BMIM][BF4] >
[EMIM][TFA] > [HMIM][TfO] > [3C8C1N] [Tf2N] > [MOIM][BF4] >
[3C6C14P][BF4] > Sulfolane > [3C6C14P][Tf2N] > [3C6C14P][PF6] >
[C16MIM][BF4]
The best selectivity is obtained with [EMIM] [BF4]. The ionic
liquid [BMPy] [BF4] presents the best compromise between selectivity and
capacity at infinite dilution. It is a remarkable fact that a great deal of
FILs would potentially perform better than industrial molecular solvents NMP
and Sulfolane, as separation agents. At 313.15 K [EMIM] [BF4] is twice as
selective as Sulfolane. The infinite dilution performance index of [BMPy] [BF4]
is three times higher than the one obtained with the same industrial molecular
solvent.
6.3.1.1. Imidazolium-based fluorinated ionic
liquids
According to Figures H-1 and H-2 in Appendix H, favorable
structures of FILs for separating aromatic/aliphatic compounds mixtures are
that the alkyl chain of the cation is short and the anion is small with
sterical shielding around its charge centre. For the same anion, selectivity at
infinite dilution decreases with alkyl chain extension. For the same cation,
the smaller the anion,
the higher the limiting selectivity. In all cases, limiting
capacity and limiting selectivity for the n-hexane (1)/benzene (2) system vary
in inverse orders.
Extending the alkyl chain of the IL cation accentuates the
steric hindrance on the imidazolium ring. This results in poorer ability to
polarize the benzene molecule and thus, lower selectivity whereas interactions
with n-hexane do not vary notably. Capacity increases with increasing alkyl
chain length because greater van der Waals volume weakens the intrinsic
hydrogen bond within the IL.
Under the same anion, it is observed that selectivities of
pyrrolidinium and pyridinium-based FILs which have six-membered rings exhibit
higher selectivities of n-hexane to benzene in comparison with the
corresponding imidazolium-based ones. The similarity of their rings to benzene
explains this. It is one of the reasons why investigated phosphonium and
ammonium-based FILs manifest poor potential for separating aliphatic/aromatic
compounds mixtures. Kumar and Banerjee (2009) came up with a similar
interpretation when studying thiophene separation from diesel. They pointed out
that thiophene with its five-membered ring preferentially attaches more to an
imidazolium-based cation provided with a five-membered ring, in comparison with
a pyridinium or quinolinium (six-membered) cation.
In the absence of sterical shielding effect, the anion tends
to approach the positive center of the cation leading to a closed shape for the
molecule. Interactions between the positive charge centers of the IL cation and
the delocalized electrons of benzene are hindered since the polarity of the IL
is reduced. This is why anions with sterical shielding effect around the charge
center lead to higher selectivities. Moreover, the increase in the volume of
the cation results in a greater solvent ability to remove benzene.
These explanations are consistent with the recent publication
by Kumar and Banerjee (2009), as well as, the findings related to
olefin/aliphatic separation reported by Lei et al. (2006, 2007b) and hold for
non-polar systems discussed in the following sections as well. Concerning polar
systems, the overall effect of structure on selectivity and capacity is a
result of the relative magnitude of polarity and molecular volume of entities
composing the ionic liquid.
To understand the trends described hereafter, one should bear
in mind that, depending on anions comprising FILs , polarity together with
intrinsic strength of hydrogen bonding varies in the order:
[TFA]- [TfO]- > [BF4]- >
[PF6]- > [Tf2N] - . Volume increases as follows: [BF4] - <
[TFA] -
< [PF6] - < [TfO] - < [Tf2N] - .
6.3.1.2. Phosphonium-based fluorinated ionic liquids
As indicated by Figure H-3 in Appendix H, for the n-hexane
(1)/benzene (2) system
decreases with the increasing anion volume. Selectivity values
remain very small as compared
to Sulfolane, a commonly used industrial
solvent for aliphatic/aromatic compounds mixtures.
Smaller anions lead to higher selectivities. The value for
[3C6C14P] [(C2F5)3PF3] is an
outlier, probably due to differences in experimental
conditions. Limiting capacity tends to increase with increasing anion volume.
In the absence of data related to the ionic liquid [3C6C14P] [PF6] which were
provided by this thesis, it would be difficult to reliably derive these
hierarchies of limiting capacity and selectivity values with only the
previously published experimental results. This emphasizes the contribution of
the present study to the expansion of knowledge in relation of FILs.
6.3.1.3. Ammonium-based fluorinated ionic
liquids
Only the effect of the cation can be discussed in the light
of available data. Extending the alkyl chain of the ionic liquid leads to lower
selectivities and higher capacities. This is observed in Figure H-4 in Appendix
H.
6.3.2. Methanol (1)/benzene (2) separation
problem
Infinite dilution selectivities of the experimentally
investigated fluorinated ionic liquids for the Methanol (1)/benzene (2) system
decrease in this order:
[3C6C14P][(C2F5)3PF3] > [3C6C14P][PF6] > [3C6C14P] [Tf2N]
> [3C8C1N] [Tf2N] >
[MOIM][PF6] > [MOIM] [Tf2N] > [HMIM] [Tf2N] >
[HMIM][PF6] > [C16MIM][BF4] > [BMIM][SbF6] > [3C6C14P][BF4] >
[Et3S] [Tf2N] > [BMIM] [Tf2N] > [EMIM] [Tf2N] > [3C1C4N] [Tf2N] >
[Epy] [Tf2N] > [MOIM][BF4] > [BMPy][BF4] > [BMIM][BF4] >
[BMIM][TfO] > [HMIM][BF4] > [EMIM][TfO] > [DMPIM][BF4] >
[EMIM][BF4] > [EMIM][TFA]
Performance indices follow the sequence below:
[3C6C14P][(C2F5)3PF3] > [3C6C14P] [Tf2N] > [3C8C1N] [Tf2N]
> [3C6C14P][PF6] >
[3C6C14P][BF4] > [MOIM] [Tf2N] > [HMIM] [Tf2N] >
[MOIM][PF6] > [C16MIM][BF4] > [HMIM][PF6] > [BMIM] [Tf2N] > [EDMIM]
[Tf2N] > [Et3S] [Tf2N] > [BMIM][SbF6] > [EMIM] [Tf2N] > [3C1C4N]
[Tf2N] > [Epy] [Tf2N] > [MOIM][BF4] > [BMPy][BF4] > [BMIM][TfO]
> [HMIM][BF4] > [BMIM][BF4] > [EMIM][TfO] > [EMIM][BF4] >
[EMIM][TFA]
Depending on whether methanol is collected as part of the
bottom or overhead stream, [EMIM] [TFA] and [3C6C14P] [(C2F5)3PF3] are found to
be the best solvents for this separation problem. Due to the absence of the
required data, no comparison with industrial molecular solvent is attempted.
6.3.2.1. Imidazolium-based fluorinated ionic
liquids
For the same anion, it is observed in Figures H-2 and H-5
that infinite dilution selectivity and capacity for the methanol (1)/benzene
(2) decrease when the alkyl chain is shortened. Figure H-2 is applicable to
both methanol/benzene and hexane/benzene capacity values. Experimental data do
not totally agree on a common pattern as far as the effect of the anion is
concerned. However, according to Figure H-5, it seems that imidazolium-based
fluorinated ionic liquids with low selectivity are the ones containing anions
such as [BF4]-, [TFA] - and [TfO]-, characterized by
small volume and a sterical shielding effect around the anion charge centre. As
far as limiting capacity is concerned, it is found to increase with increasing
anion volume.
6.3.2.2. Phosphonium-based fluorinated ionic
liquids
Limiting selectivity values of phosphonium-based FILs containing
the common cation
[3C6C14P] + are observed to decrease when the anion is changed
in this order (Figure H-6): [(C2F5)3PF3]- > [PF6] - > [Tf2N] -
> [BF4]-
The general trend is that limiting selectivity and limiting
capacity increase with increasing anion volume and decreasing polarity of the
ionic liquid, [3C6C14P] [PF6] being an outlier.
6.3.2.3. Ammonium-based fluorinated ionic
liquids
Figure H-7 in Appendix H suggests that lengthening the ionic
liquid alkyl chain leads to higher
values of infinite dilution selectivity and capacity for the
methanol (1)/benzene (2) system.
6.3.3. Methanol (1)/acetone (2) separation
problem
For the methanol (1)/acetone (2) system, the hierarchy of
selectivity values is:
[BMIM][SbF6] > [3C6C14P][Tf2N] > [HMIM][Tf2N] >
[3C1C4N][Tf2N] > [EMIM][Tf2N] > [3C6C14P][PF6] > [3C8C1N][Tf2N] >
[BMIM][PF6] > [BMIM][Tf2N] > [Epy][Tf2N] > [BMPy][BF4] >
[C16MIM][BF4] > [MOIM][BF4] > [3C6C14P][BF4] > [BMIM][BF4] >
[HMIM][BF4] > [BMIM][TfO] > [EMIM][BF4] > Dimethylsulfoxide
Infinite dilution performance indices for the methanol
(1)/acetone (2) system can be arranged in this order:
Dimethylsulfoxide > [3C6C14P] [Tf2N] > [HMIM] [Tf2N]
> [BMIM] [Tf2N] > [3C8C1N] [Tf2N] > [EMIM] [Tf2N] > [BMIM][SbF6]
> [3C1C4N] [Tf2N] > [3C6C14P][BF4] > [Epy] [Tf2N] > [3C6C14P][PF6]
> [BMPy][BF4] > [BMIM][PF6] > [MOIM][BF4] > [HMIM][BF4] >
[BMIM][TfO] > [C16MIM][BF4] > [BMIM][BF4] > [EMIM][BF4].
[BMIM][SbF6] and [3C6C14P] [Tf2N] lead to the
highest selectivity and performance index respectively. No FIL is potentially
better than dimethylsulfoxide, one of the most suitable molecular solvents for
this separation problem. The limiting selectivity of [BMIM][SbF6] is 19 %
smaller than the one given by dimethylsulfoxide. Compared with
[3C6C14P] [Tf2N] , the infinite dilution performance index of DMSO
is three times higher.
6.3.3.1. Imidazolium-based fluorinated ionic
liquids
Data represented in Figure H-8 show that under the same
anion, selectivity and capacity tend to increase with increasing alkyl chain
length of the FIL cation. Both properties increase with increasing anion
volume. It can be noted that [BMIM] +-containing ionic liquids do
not rigorously comply with trends possibly due to experimental uncertainties.
More data are required for a more accurate description of the influence of
structure on the separation performance of imidazolium-based FILs for the
methanol (1)/acetone (2) system.
6.3.3.2. Phosphonium-based fluorinated ionic
liquids
An examination of Figure H-10 in Appendix H reveals that
infinite dilution selectivity for the methanol (1)/acetone (2) system increases
with increasing anion volume. No regular variation trend regarding capacity
emerges.
6.3.3.3. Ammonium-based fluorinated ionic
liquids
Infinite dilution selectivity of ammonium-based FILs for the
methanol (1)/acetone (2) system reduces when the alkyl chain is extended as
shown by Figure H-11. The reverse is true for limiting capacity.
6.3.4. n-hexane (1)/ hex-1-ene (2) separation
problem
Selectivity of n-Hexane to Hex-1-ene decreases according to this
order:
[BMPyrr][TfO] > [EMIM][TFA] > [Epy] [Tf2N] >
[EMIM][TfO] > [MMIM][Tf2N]> [BMIM][TfO] > [Et3S] [Tf2N] >
[HMIM][PF6] > [BMIM][SbF6] > [EMIM] [Tf2N] > [EDMIM] [Tf2N] >
[EMIM][BF4] > [HMIM][BF4] > [BMPyrr] [Tf2N] > [BMIM] [Tf2N] >
[3C1C4N] [Tf2N] > [MOIM][PF6] > [MOIM][BF4] > [BMIM][BF4] >
[HMPyrr] [Tf2N] >
[HMIM] [Tf2N] > [MOIM] [Tf2N] > [OMPyrr] [Tf2N] >
[C16MIM][BF4] > [3C8C1N] [Tf2N]
> [3C6C14P][BF4] > [3C6C14P][(C2F5)3PF3] > [3C6C14P]
[Tf2N] > [3C6C14P][PF6] > NMP.
Performance indices follow this trend:
[3C6C14P][(C2F5)3PF3] > [3C6C14P] [Tf2N] > [3C6C14P][BF4]
> [3C8C1N] [Tf2N] >
[C16MIM][BF4] > [3C6C14P][PF6] > [MOIM] [Tf2N] >
[OMPyrr] [Tf2N] > [HMIM] [Tf2N] > [HMPyrr] [Tf2N] > [BMPyrr] [Tf2N]
> [MOIM][PF6] > [BMIM] [Tf2N] > [MOIM][BF4] > [HMIM][PF6] >
[HMIM][BF4] > [3C1C4N] [Tf2N] > [Et3S] [Tf2N] > [Epy] [Tf2N] >
[EMIM] [Tf2N] > [EDMIM] [Tf2N] > [BMIM][SbF6] > [BMIM][TfO] >
[MMIM] [Tf2N] > [BMPyrr][TfO] > NMP > [EMIM][TfO] > [EMIM][TFA]
> [BMIM][BF4] > EMIM][BF4].
On the basis of experimental data, the best selectivity is
obtained with the ionic liquid [BMPyrr] [TfO]. It amounts to an increase of 30
% when compared to NMP. It can be seen that the ionic liquid [3C6C14P]
[(C2F5)3PF3] leads to the best compromise between selectivity and capacity. The
calculated value of its limiting performance index is 29 times higher than NMP.
Where comparison is possible, the above hierarchies are consistent with the
findings of Lei and coworkers (Lei et al. 2006, 2007) in their study related to
n-hexane (1)! hex-1-ene (2) separation using the quantum approach. In relation
to the effect of the anion, their finding is that higher selectivities are
obtained with smaller anions with sterical shielding effect around the anion
charge centre. Additionally, they predicted that the best ionic liquid for this
separation problem is 1-octylquinolinium bis (trifluoromethylsulfonyl) imide.
However, the present study could not confirm this result due to the lack of
experimental infinite dilution activity coefficient data in the ionic liquid
1-octylquinolinium bis (trifluoromethylsulfonyl) imide.
6.3.4.1. Imidazolium-based Fluorinated ionic
liquids
For the same anion, selectivity at infinite dilution
decreases with increasing alkyl chain length (Figure H-12). A look at Figure
H-12, as well as the hierarchy of selectivities provided in the previous
section reveals that small anions with sterical shielding effect around the
charge center are essential to achieve high selectivities. Capacity increases
with increasing alkyl chain length, as well as, increasing anion volume, as
illustrated by Figure H-13.
6.3.4.2. Phosphonium-based fluorinated ionic
liquids
For phosphonium-based FILs containing the [3C6C14P] + cation,
selectivity at infinite dilution for the n-hexane (1)! hex-1-ene (2) system
decreases slightly with increasing anion size (Figure H-14) whereas capacity at
infinite dilution for this system and this class of FILs seems to be
constant.
6.3.4.3. Ammonium-based Fluorinated ionic
liquids
With increasing alkyl chain length the limiting selectivity of
ammonium-based FILs decreases and limiting capacity increases, as can be seen
in Figure H-15.
6.3.4.4. Pyrrolidinium-based Fluorinated ionic
liquids
The available experimental data used in Figure H-16, Appendix
H, suggest that for the same cation, limiting selectivity of
pyrrolidinium-based FILs reduces when the anion size increases, whereas
limiting capacity follows the opposite trend.; and for the same anion, the
longer the alkyl chain of the ionic liquid cation, the smaller the selectivity
and the higher the capacity (Figure H-16).
6.3.5. Benzene (1)/ butan-2-one (2) separation
problem
Limiting selectivities of the experimentally investigated
fluorinated ionic liquids follow this pattern:
[EMIM] [Tf2N] > [Epy][Tf2N] > [BMIM][SbF6] >
[BMPy][BF4] > [HMIM][Tf2N] > [BMPyrr][Tf2N]> [EMIM][BF4] >
[BMIM][BF4] > [HMIM][BF4] > [3C6C14P][Tf2N] > [3C8C1N][Tf2N] >
[MOIM][BF4] > [3C6C14P][PF6] > [3C6C14P][BF4] > [C16MIM][BF4]
In terms of good compromise between selectivity and capacity,
FILs are arranged in decreasing order of limiting performance index values as
follows:
[EMIM][Tf2N] > [HMIM][Tf2N] > [3C6C14P][Tf2N] >
[3C8C1N][Tf2N] > [BMIM][SbF6] > [Epy][Tf2N] > [BMPyrr][Tf2N]>
[3C6C14P][BF4] > [BMPy][BF4] > [3C6C14P][PF6] > [HMIM][BF4] >
[MOIM][BF4] > [EMIM][BF4] > [BMIM][BF4] > [C16MIM][BF4].
The best selectivity and the best performance index are obtained
with [EMIM] [Tf2N]. No
comparison with industrial solvents is possible due to lack of
required experimental data.
6.3.5.1. Imidazolium-based fluorinated ionic
liquids
Figures H-17 and H-18 show that with increasing anion volume,
the limiting selectivity and the limiting capacity of imidazolium-based FILs
for the benzene (1)/butan-2-one (2) system increase. And the longer the alkyl
chain of the FIL cation, the smaller the selectivity and the higher the
capacity at infinite dilution.
6.3.5.2. Phosphonium-based fluorinated ionic
liquids
Due to a very limited database, it is not possible to reliably
derive the effect of structure on
selectivity or capacity in this case using
Figure H-19. Only three ionic liquids having a common
cation are considered and the obtained selectivity and capacity
plots do not allow any derivation of the effect of the anion on these two
properties.
6.3.6. Ethanol (1)/ butan-2-one (2) separation problem
Infinite dilution selectivities of the experimentally
investigated fluorinated ionic liquids for the ethanol (1)/butan-2-one (2)
system decrease in this order:
Chlorobenzene > [3C6C14P] [Tf2N] > [BMIM][SbF6] >
[EMIM] [Tf2N] > [HMIM] [Tf2N] > [3C8C1N] [Tf2N] > [BMPyrr] [Tf2N] >
[3C6C14P][PF6] > [BMIM][PF6] > [Epy] [Tf2N] > [BMPy][BF4] >
[MOIM][BF4] > [C16MIM][BF4] > [HMIM][BF4] > [3C6C14P][BF4] >
[BMIM][BF4] > [EMIM][BF4].
Performance indices follow the sequence below:
[3C6C14P] [Tf2N] > [3C8C1N] [Tf2N] > [HMIM] [Tf2N] >
[EMIM] [Tf2N] > [BMPyrr] [Tf2N] > [BMIM][SbF6] > [3C6C14P][PF6] >
[Epy] [Tf2N] > Chlorobenzene > [BMIM][PF6] > [3C6C14P][BF4] >
[BMPy][BF4] > [MOIM][BF4] > [C16MIM][BF4] > [HMIM][BF4] >
[BMIM][BF4] > [EMIM][BF4].
On the basis of selectivity and performance index at infinite
dilution, the best potential solvent for this separation problem is
[3C6C14P] [Tf2N]. Chlorobenzene, a commonly used industrial
molecular solvent is twice as selective as [3C6C14P] [Tf2N]. However
its limiting performance index is 3.25 times smaller than the one achieved with
the same ionic liquid.
6.3.6.1. Imidazolium-based fluorinated ionic
liquids
According to Figure H-20 and H-18 (Since the capacity value
at a given temperature for the ethanol/ butan-2-one is the same as for the
benzene/butan-2-one system), high limiting selectivity and capacity are
achieved with imidazolium-based fluorinated ionic liquids consisting of
long-chained cations and big-sized anions.
6.3.6.2. Phosphonium-based fluorinated ionic
liquids
It can be seen in Figure H-21 that the limiting selectivity
of phosphonium-based fluorinated ionic liquids for the ethanol (1)/ butan-2-one
(2) system increases with increasing anion volume. It is impossible to derive a
reliable trend for capacity variation.
6.4. Correlation of limiting activity coefficient and
selectivity with the FIL alkyl chain
It is the outcome of this study that a simple model can
correlate with the alkyl chain length
of the pyrrolidinium and
imidazolium-based FILs at constant temperature. As shown in the plots
presented in Figures I-1 through I-4 in Appendix I, obtained
from experimental data published
by different groups under different
conditions, the natural logarithm of of n-hexane, hex-1-
ene, cyclohexane, ethanol, benzene and acetone is a linear
function of the carbon number of the alkyl chain attached to the imidazolium or
pyrrolidinium moiety. The quality of correlation is good except for ketones and
alkan-1-ols in [BF4]--containing FILs. Available data allowed to
examine imidazolium-based FILs containing [BF4]- (Figure I-1),
[Tf2N]- .
(Figure I-2) and [TfO]- (Figure I-3) anions as well
as a few systems involving pyrrolidinium- based fluorinated ionic liquids
(Figure I-4) The correlating equation is:
(6.1)
where a and b are parameters related to the
nature of the anion, as well as, the solute under consideration. is obviously
always greater than zero. Consequently, it can be stated that the
natural logarithm of both limiting selectivity and capacity of
imidazolium-based FILs for different systems are also linear functions of the
carbon number of the alkyl chain attached to the methylimidazolium as well as
the methylpyrrolidinium. A similar equation to (6-1) can be used to relate
selectivity to the alkyl chain length as follows:
(6.2)
Figures I-5 and I-6 in Appendix D show a good quality of the
linear regression used to approximate experimental selectivity data. Systems
referred to include n-hexane/benzene (Figure I-5) and n-hexane/hex-1-ene
(Figure I-6).
CHAPTER SEVEN: CONCLUSION AND RECOMMENDATIONS
The objective of this study was to investigate the effect of
structure on fluorinated ionic liquids ability to separate organic mixtures. To
assess the effectiveness of FILs as separation agents, limiting experimental
selectivities and capacities were calculated from experimental infinite
dilution activity coefficient data.
Infinite dilution activity coefficients of various organic
solutes have been measured by gas-liquid chromatography over a wide temperature
range in seven fluorinated ionic liquids:
· Trihexyltetradecylphosphonium tetrafluoroborate,
[3C6C14P] [BF4];
· Trihexyltetradecylphosphonium
bis(trifluoromethylsulfonyl) imide, [3C6C14P] [Tf2N];
· Trihexyltetradecylphosphonium hexafluorophosphate,
[3C6C14P] [PF6];
· Methyltrioctylammonium bis (trifluoromethylsulfonyl)
imide, [C13C8N] [Tf2N];
· 1-ethyl-3-methylimidazolium trifluoromethanesulfonate,
[EMIM] [TfO];
· 1-butyl-3-methylimidazolium hexafluoroantimonate, [BMIM]
[SbF6];
· 1-methyl-3-octylimidazoliumhexafluorophosphate.
[MOIM][PF6].
Two of these FILs ([3C6C14P] [BF4] and [3C6C14P]
[Tf2N]) have been investigated previously with a smaller number of solutes and
a narrower temperature range than in this study. Most of the reported
measurements are new. For each solvent, the Gibbs-Helmholtz equation was used
to derive molar excess enthalpies of solutes at infinite dilution. This was
important as the property provides information on the tendency of the solvent
to associate with a solute of interest. The large number of newly generated
infinite dilution activity coefficient values expanded the database used for
examining the effect of structure on the separation ability of FILs. If these
additional data were not produced, some of the useful evidences exploited
herein would not have emerged.
A simple empirical correlation was also proposed for limiting
activity coefficient as a function of the alkyl chain length. This is
significant since in previous work, the description of change with the alkyl
chain length has been merely qualitative. As a matter of fact, the natural
logarithm of was found to vary linearly with the carbon number of the alkyl
chain attached to the methylpyrrolidinium or methylimidazolium group. The same
applied to limiting selectivity. The model correlated well and limiting
selectivity with the cation alkyl chain length for
systems involving non-polar components as solutes. Poor
correlation coefficients were however observed for polar solutes. This outcome
can be exploited when developing a priori predictive thermodynamic models.
A detailed analysis of infinite dilution activity
coefficient, selectivity and capacity data obtained from this work and the
literature, allowed to derive the following trends, in relation to six
separation problems selected among the most interesting ones for the chemical
industry:
· n-hexane (1)/benzene (2) system:
Pyridinium and imidazolium-based FILs were potentially the best
suitable solvents for this separation problem. The best selectivity was
obtained with [EMIM] [BF4]. The ionic liquid [BMPy] [BF4] presented the best
compromise between selectivity and capacity at infinite dilution. Higher
selectivities were obtained with short-chained cations and small anion
volumes.
· Methanol (1)/benzene (2): [EMIM]
[TFA] and [3C6C14P] [(C2F5)3PF3] were found to be the best solvents for this
separation problem, depending on the stream in which methanol was to be
collected i.e. overhead or bottom stream. Phosphonium-based fluorinated ionic
liquids with large anion volume and an appropriate cation would be more
selective. FILs with short alkyl chain length for the cation and a small anion
volume were generally the least favorable ones.
· Methanol (1)/acetone (2): Limiting
capacity and selectivity varied in the same manner as for the previous system
except in case of ammonium-based FILs. [BMIM][SbF6] and [3C6C14P]
[Tf2N] lead to the highest selectivity and performance index respectively.
· n-Hexane (1)/ hex-1-ene (2):
Regardless of the class of the ionic liquid, higher selectivities were
obtained with longer alkyl chains attached to the cation and smaller anions
with sterical shielding effect around the anion charge centre. The best
selectivity was displayed by the ionic liquid [BMPyrr] [TfO]. It was seen that
the ionic liquid [3C6C14P] [(C2F5)3PF3] lead to the best compromise between
selectivity and capacity.
· Benzene (1)/ butan-2-one (2): The
best selectivity as well as the best performance index was obtained with [EMIM]
[Tf2N]. With increasing anion volume, the limiting selectivity was found to
increase. And the longer the alkyl chain of the cation, the smaller the
selectivity. Due to insufficient database, no reliable conclusion could be
reached for phosphonium-based FILs.
· Ethanol (1)/ butan-2-one (2):
[3C6C14P] [Tf2N] was found to be the best potential solvent
for this separation problem on the basis of both selectivity and performance
index. It was found that fluorinated ionic liquids consisting of long-chained
cations and big-sized anions were potentially the best separation agents for
this system.
Judging from performance index values it was observed that
the ionic liquid [3C6C14P] [Tf2N] would be a reasonable separation
solvent for all the investigated mixtures, except the n-Hexane/ Benzene system.
In some cases, no comprehensive conclusion could be made due to insufficient or
incoherent data. Nevertheless, where comparison was possible, the findings were
consistent with previously published results derived from COSMO-RS (Kumar and
Banerjee, 2009 and Lei et al. 2006, 2007). It is an indication that the
approach consisting of using experimental data was at once economic, less time
consuming and qualitatively effective.
These results emphasize the important role played by the
nature of ions comprising the ionic liquid in determining the magnitude of
activity coefficient values and consequently its effectiveness as separation
solvent. Chances to have a FIL which would act as a universal separation agent?
are very slim. For a given separation problem, there is a specific profile for
appropriate ionic liquid solvents.
The importance of this study lies in its contribution to the
understanding of how structure influences ionic liquids selectivity and
capacity in different separation problems. It expands the knowledge about FILs
which are potentially green separation agents. Additionally, the reported
infinite dilution activity coefficient data can be used to extend the
applicability range of predictive thermodynamic models. Such are UNIFAC, and
modified UNIFAC models which are already incorporated in some chemical
engineering process simulators.
Due to the limited nature of the data set used in this work, the
following was not addressed:
· The effect of the cation for phosphonium-based FILs on
limiting activity coefficient, selectivity and capacity;
· The effect of the anion for ammonium -based FILs;
· The effect of both cation and anion in other types of
ILs such as quinolinium, guadinium, sulfonium, piperidinium and
thiazolium-based FILs (though they are less popular in separation-related
studies);
· The effect of introducing functional groups other than
n-alkyl in the cation of different FILs.
These topics are worthy of interest for future work. They will
require more experimental data or the use of the quantum approach.
The calculated relative error on data obtained by the IGST was
larger than most values
reported in the literature, due to high uncertainties in
determining the flow-rate. Its stability left much to desire. Replacing the
flow-regulator is to be considered for more accurate measurements.
REFERENCES
Alessi, P., Fermeglia, M. and Kikic, I., (1986), A Differential
Static Apparatus for the
Investigation of the Infinitely Dilute Region?, Fluid Phase
Equilibr., 29, 249-256.
Alessi, P., Fermeglia, M. and Kikic, I., (1991), Significance of
Dilute Regions?, Fluid Phase Equilibr., 70, 239-250.
Appleby, D., Hussey, C. L., Seddon, K. R. and Turp, J. E.,
(1986), Room-temperature ionic liquids as solvents for electronic absorption
spectroscopy of halide complexes?, Nature, 323, 614-615.
Arlt, W., Seiler, M., Jork, C. and Schneider, T., (2002),
"Ionic liquids as selective additives for the separation of close-boiling or
azeotropic mixtures", Patent; Basf Aktiengesellschaft, Germany.
2002-EP2824 (2002074718), 29, 3-14-2002, WO.
Banerjee, T. and Khanna, A., (2006), Infinite Dilution
Activity Coefficients for Trihexyltetradecylphosphonium Ionic Liquids:
Measurements and COSMO-RS Prediction?, Journ. Chem. Thermodyn., 51,
2170-2177.
Banerjee, T., (2008), Liquid-Liquid Equilibrium for Ionic Liquid
Systems Using COSMO-RS: Effect of Cation and Anion Dissociation?, AIChE
J., 54, 1874-1885.
Bao J. B., Hang L. L., Ling Y-P., Chen, G-H. and Han S-J.,
(1993a), "Studies on the determination of infinite dilution activity
coefficients of acetone-cycloalkanes systems by gas stripping method",
Chem. J. Chin. Univ., 14, 1280-1283.
Bao, J. B., Huang, Q., Chen, G-H and Han, S-J, (1993b),
Determination of large value activity coefficients at infinite dilution?,
Acta Phys. Chem., 9, 724-727.
Bao, J. B., Hang L. L. and Han S-J., (1994), Infinite Dilution
Activity Coefficients of
(propanone + an n-alkanes) by Gas Stripping?,
Journ. Chem. Thermodyn., 26, 673-680.
Bao, J-B and Han, S-J, (1995), Infinite Dilution Activity
Coefficients for Various Types of Systems?, Fluid Phase Equilibr.,
112, 307-316.
Bonhôte, P., Dias, A. P., Papageorgiou, N.,
Kalyanasundaram, K. and Grätzel, M., (1996), Hydrophobic, Highly
Conductive Ambient-Temperature Molten Salts?, Inorg. Chem., 35,
1168-1178.
Boudreau, L. C., Driver, M.S., Munson, C.L. and Schinski, W.
L., (2001), "Separation of dienes from olefins using ionic liquids and metal
salt complexing agents", Patent; USA. 2001- 37044(2003125599), 15
12-31-2001, US.
Castells R. C., Arancibia, E. L., Nardillo A. M. and Castells
C., (1990), Thermodynamics of Hydrocarbon solutions using GLC, n-Hexane,
n-Heptane, Benzene and Toluene as solute, each at infinite dilution, in
n-Hexadecane, n-Octadecane and n-Eicosane?, Journ. Chem. Thermodyn.,
22, 969-977.
Castells, C. B. and Carr P. W., (1999), A Comparative Study of
Semi-theoretical models for Predicting Infinite Dilution Activity Coefficients
of Alkanes in Organic Solvents?, Ind. Eng. Chem. Res., 38,
4104-4109.
Cheong W. J., (2003), A critical examination of the limiting
activity coefficients of normal alkanes in common organic liquids?, Bull.
Kor. Chem. Soc., 24, 1708-1710.
Chien, C. F., Kopecni, M. M., Laub R. J. and Smith C. A.,
(1981), Solute Liquid-Gas Activity and Partition Coefficients with Mixtures of
n-Octadecane with N, N-Dibutyl-2- EthylHexylamine Solvents?, Journ. Phys.
Chem., 85, 1864-1871.
Chum, H. L., Koch, V. R., Miller, L. L. and Osteryoung, R. A.,
(1975), Electrochemical scrutiny of organometallic iron complexes and
hexamethylbenzene in a room temperature molten salt?, J. Am. Chem.
Soc., 97, 3264-3265.
Condor, J. R. and Young, C. L., (1979), Physico-chemical
Measurement by Gas Chromatography?, John Willey and Sons, U.S.A.
Cooper, E. I. and O`Sullivan, E. J. M., (1992), "Proceedings
of the Eighth International Symposium of Molten Salts, Physical and High
Temperature Materials Division Proceedings ", 92-16.
Coquelet, C. and Richon, D., (2005), Measurement of Henry`s
Law Constants and Infinite Dilution Activity Coefficients of Propyl Mercaptan,
Butyl Mercaptan, and Dimethyl Sulfide in Methyldiethanolamine (1) + Water (2)
with w1=0.5 Using a Gas Stripping Technique?, J. Chem. Eng. Data, 50,
2053-2057.
CRC Handbook of Chemistry and Physics, (2005), 86th
ed., Taylor & Francis, London.
Cruickshank, A. J. B., Windsor M. L., and Young C. L.,
(1966a), Prediction of Second Virial Coefficients of Mixtures from the
principles of Corresponding states?, Trans. Faraday Soc., 62,
2341-2355.
Cruickshank, A. J. B., Windsor, M. L., and Young, C. L.,
(1966b), The Use of Gas-Liquid Chromatography to Determine Activity
Coefficients and Second Virial Coefficients of Mixtures; II Experimental
studies on hydrocarbon solutes«, Proc. R. Soc. London, Ser.
A, 295-271.
Cruickshank, A. J. B., Gainey, B. W., Hicks, C. P., Letcher,
T.M., Moody, R. W. and Young, C. L., (1969), Gas-Liquid Chromatographic
Determination of Cross-Term Second Virial Coefficients Using Glycerol?,
Trans. Faraday Soc., 65,1014-1031.
David W., Letcher, T.M. and Ramjugernath, D., (2003), Activity
Coefficients of Hydrocarbon Solutes at Infinite Dilution in the Ionic Liquid
1-methyl-3-octylimidazolium chloride from Gas-liquid chromatography?,
Journ. Chem. Thermodyn., 35, 1335-1341.
David, W., (2004), Ionic liquids as solvents in separation
processes? MSc Thesis, University of KwaZulu-Natal, South Africa.
Deenadayalu, N., Letcher, T. M. and Reddy, P., (2005),
Determination of Activity Coefficients at Infinite Dilution of Polar and
Nonpolar Solutes in the Ionic Liquid 1-Ethyl-3- methylimidazolium
Bis(trifluoromethylsulfonyl) Imide Using Gas-Liquid Chromatography at the
Temperature 303.15 K or 318.15 K.?, J. Chem. Eng. Data, 50,
105-108.
Deenadayalu, N., Thango, S. H., Letcher, T. M. and
Ramjugernath, D., (2006a), Measurement of activity coefficients at infinite
dilution using polar and non-polar solutes in the ionic liquid
1-methyl-3-octyl-imidazolium diethyleneglycolmonomethylethersulfate at T =
(288.15, 298.15, and 313.15) K?, Journ. Chem. Thermodyn., 38,
542-546.
Deenadayalu, N., Ngcongo C. N., Letcher, T. M. and
Ramjugernath, D., (2006b), Liquid-liquid equilibria for ternary mixtures (an
ionic liquid + benzene + heptane or hexadecane at T= 298.15 K and atmospheric
pressure?, J. Chem. Eng. Data, 51, 988-991.
Derr E. L. and Deal C. H., (1969), Analytical Solutions of
Groups: correlation of activity coefficients through structural group
parameters?, Inst. Chemical. Eng, Sympos. Ser. London., 32,
3:44-3:51.
Dobryakov, Y. G. and Vitenberg, A. G., (2006), Determination
of distribution coefficients of volatile sulfur-containing compounds among
aqueous solutions and gas phase by continuous gas extraction?, Russ. J.
Appl. Chem., 79, 1244-1250.
Dobryakov, Y. G., Tuma, D. and Maurer, G., (2008), Activity
Coefficients at Infinite Dilution of Alkanols in the Ionic Liquids
1-Butyl-3-methylimidazolium Hexafluorophosphate, 1-
Butyl-3-methylimidazoliumMethyl Sulfate, and 1-Hexyl-3-methylimidazolium
Bis(trifluoromethylsulfonyl) Amide Using the Dilutor Technique.», J.
Chem. Eng. Data, 53, 2154-2162.
Dohnal V. and Horakova I., (1991), A New Variant of the Rayleigh
Distillation Method for the Determination of Limiting Activity Coefficients?,
Fluid Phase Equilibr., 68, 173-185.
Doleúal, B., Popl, M. and Holub, R., (1981), Determination
of activity coefficients at very low concentrations by the inert gas stripping
method?, J. Chromatogr., 207: 193-201.
Doleúal, B. and Holub, R., (1985), Approximate
relations for determining the activity coefficients at very low concentration
by the method of variation of solute concentration?, Coil. Czech. Chem.
Commun., 50, 704-711.
Domañska, U. and Marciniak, A., (2007), Activity
Coefficients at Infinite Dilution Measurements for Organic Solutes and Water in
the Ionic Liquid 1-Ethyl-3- methylimidazolium Trifluoroacetate?, J. Phys.
Chem. B, 111, 11984-11988.
Domañska, U. and Marciniak, A., (2008a), Activity
Coefficients at Infinite Dilution Measurements for Organic Solutes and Water in
the Ionic Liquid 1-Butyl-3- methylimidazolium Trifluoromethanesulfonate?,
J. Phys. Chem. B, 2008, 112 (35), 11100- 11105.
Domañska, U. and Marciniak, A., (2008b), Measurements
of activity coefficients at infinite dilution of aromatic and aliphatic
hydrocarbons, alcohols and water in the new ionic liquid [EMIM] [SCN] using
GLC?, Journ. Chem. Thermodyn., 40, 860-866.
Domañska, U. and Laskowska, M., (2009), Measurements of
activity coefficients at infinite dilution of aliphatic and aromatic
hydrocarbons, alcohols, thiophene, tetrahydrofurane, MTBE and water in ionic
liquid [BMIM] [SCN] Using GLC?, J. Chem. Thermodyn., 41, 645-650.
Domañska, U. and Marciniak, A., (2009a), Activity
coefficients at infinite dilution measurements for organic solutes and water in
the ionic liquid triethylsulphonium bis (trifluoromethylsulfonyl) imide?,
Journ. Chem. Thermodyn., 41, 754-758.
Domañska, U. and Marciniak, A., (2009b), Activity
coefficients at infinite dilution measurements for organic solutes and water in
the 1-hexyloxymethyl-3-methyl-imidazolium and 1,3-dihexyloxymethyl-imidazolium
bis(trifluoromethylsulfonyl)-imide ionic liquids-- The cation influence?,
Fluid Phase Equilibr., 286, 154-161.
Domañska, U., Redhi, G.G. and Marciniak, A., (2009),
Activity coefficients at infinite dilution measurements for organic solutes and
water in the ionic liquid 1-butyl-1- methylpyrrolidinium
trifluoromethanesulfonate using GLC?, Fluid Phase Equilibr., 278,
97-102.
Dortmund Data Bank, DDB,
www.ddbst.com. Accessed 15
October 2009.
Duhem, P. and Vidal, J., (1978), Extension of the Dilutor Method
to Measurement of High Activity Coefficients at Infinite Dilution?, Fluid
Phase Equilibr. 2, 231-235.
Dupont, J., (2004), On the Solid, Liquid and Solution Structural
Organization of Imidazolium Ionic Liquids?, J. Braz. Chem. Soc., 15,
341-350.
Earle, M. J., Esperança, J. M. S. S., Gilea, M. A.,
Lopes, J. N. C., Rebelo, L. P. N., Magee, J. W., Seddon, K. R. and Widegren, J.
A., (2006), The distillation and volatility of ionic liquids?, Nature,
439, 831-834.
Eckert, C. A. and Sherman, S. R., (1996), Measurement and
Predictions of Limiting Activity Coefficients?, Fluid Phase Equilibr.,
116, 333-342.
Eckert F, and Klamt A., (2003), Prediction of halocarbon
thermodynamics with COSMO-RS?, Fluid Phase Equilibr., 210, 117-141.
Eike D.M., Brennecke, J.F., and Maginn, E.J., (2004) Predicting
Infinite-Dilution Activity Coefficients of organic solutes in ionic liquids?
Ind. Eng. Chem. Res., 43, 1039-1048.
Ellis, S.R.M. and Jonah, D.A., (1962) Prediction of Activity
Coefficients at Infinite Dilution.? Chem. Eng. Sci., 17, 971-976.
Endres, F. and El Abedin, S.Z., (2006), Air and water stable
ionic liquids in physical chemistry? Phys. Chem. Chem. Phys., 8,
2101-2116.
Everett, D. H., (1965), Effect of Gas Imperfection on
Gas-Liquid Chromatography Measurements: a Refined Method for Determining
Activity Coefficients and Second Virial Coefficients?, Trans. Faraday Soc.
61, 1637-1645.
Foco, G. M., Bottini, S. B., Quezada, N., De la Fuente, J.C.
and Peters, C.J., (2006), Activity Coefficients at Infinite Dilution in
1-Alkyl-3-methylimidazolium Tetrafluoroborate Ionic Liquids?, J. Chem. Eng.
Data, 51, 1088-1091.
Ford, E., DePaoli, D., Miller, J., Kanel, J. and Tiley, R.,
(2004), Accelerating Ionic Liquid Commercialization; Research Needs to Advance
New Technology?, Workshop Results, BCS, Incorporated.
Fox, D. M., Gilman, J. W., Morgan, A. B., Shields, J. R.,
Maupin, P. H., Lyon, R. E., De Long, H. C. and Trulove, P. C., (2008),
Flammability and Thermal Analysis Characterization of Imidazolium-Based Ionic
Liquids?, Ind. Eng. Chem. Res., 47, 6327-6332.
Fredenslund, A., Jones, R. L. and Prausnitz, J. M., (1975), Group
Contribution Estimation of Activity Coefficients in Nonideal Liquid Mixtures?,
AIChE J., 21, 1086-1099.
Gainey B. W., and Young C. L., (1968), Activity coefficients
of benzene in solution of nalkanes and the second virial coefficients of
benzene + nitrogen mixtures; Gas-chromatographic investigation?, J. Chem.
Soc., Faraday Trans. 64, 349-358.
Gautreaux, M. F., Jr. and Coates, J., (1955), Activity
Coefficients at Infinite Dilution?, AIChE J., 1, 406-500.
Ge, M-L., Wang, L-S. Li, M-Y. and Wu, J-S., (2007), Activity
Coefficients at Infinite Dilution of Alkanes, Alkenes, and Alkyl Benzenes in
1-Butyl-3-methylimidazolium Trifluoromethanesulfonate Using Gas-Liquid
Chromatography?, J. Chem. Eng. Data, 52, 2257-2260.
Ge, M-L. and Wang, L-S., (2008), Activity Coefficients at
Infinite Dilution of Polar Solutes in 1-Butyl-3-methylimidazolium
Trifluoromethanesulfonate Using Gas-Liquid Chromatography?, J. Chem. Eng.
Data, 53, 846-849.
Ge, M-L., Wang, L-S., Wu, J-S., and Zhou, Q., (2008a),
Activity Coefficients at Infinite Dilution of Organic Solutes in
1-Ethyl-3-methylimidazolium Tetrafluoroborate Using Gas-Liquid Chromatography?,
J. Chem. Eng. Data, 53, 1970-1974.
Ge, M-L., Wu, J-S., Wang, M-H. and Wang, L-S., (2008b),
Activity Coefficients at Infinite Dilution of Polar Solutes in 1-Propyl-2,
3-dimethylimidazolium Tetrafluoroborate Using Gas-Liquid Chromatography? J.
Chem. Eng. Data, 53, 871-873.
George, S., (2008), Determination of activity coefficients at
infinite dilution using the inert gas stripping technique?, MSc Thesis,
University of KwaZulu-Natal, South Africa.
Gmehling, J., Li, J. and Schiller, M., (1993), A Modified
UNIFAC Model 2. Present parameters Matrix and Results for Different
Thermodynamic Properties?, Ind. Eng. Chem. Res., 32, 178-193.
Gmehling, J., (1995), From UNIFAC to Modified UNIFAC to PSRK with
the help of DDB?, Fluid Phase Equilibr.., 107, 1-29.
Gmehling J., and Möllmann, C., (1998), Synthesis of
Distillation processes using thermodynamic models and the Dortmund Data Bank?,
Ind. Eng. Chem. Res., 37, 3112- 3123.
Gmehling J., Lohmann J., Jakob A., Li, J. and Joh, R., (1998), A
Modified UNIFAC Model 3: Revision and Extension», Ind. Eng.
Chem. Res., 37, 4876-4882.
Gmehling, J., Krummen, M. and Carl, V., (2001), "Use of ionic
liquids as entraining agents and selective solvents for separation of aromatic
hydrocarbons in aromatic petroleum streams", Patent; Ossietzky
Universitaet Oldenburg, 2001-10154052(10154052), 14, 11-2-2001, DE.
Gmehling, J., Wittig, R., Lohmann, J. and Joh, R., (2002), A
Modified UNIFAC (Dortmund) Model 4: Revision and Extension?, Ind. Eng.
Chem. Res., 41, 1678-1688.
Gmehling, J., (2003), Potential of thermodynamic tools (group
contribution methods, factual data banks) for the development of chemical
processes?, Fluid Phase Equilibr., 210, 161- 173.
Gmehling, J., (2009), Present status and potential of group
contribution methods for process development?, Journ. Chem. Thermodyn.,
41, 731-747.
Go, I, Yoshio, I., Munehiro, Y., Katsumi, H. and Yasuhiko, A.,
(2007), Measurement of infinite dilution activity coefficients of n-alkanes in
4-methyl-n-butylpyridinium tetrafluoroborate using gas-liquid chromatography ?,
Fluid Phase Equilibr., 251, 17-23.
Grensemann, H. and Gmehling, J., (2005), Performance of A
Conductor-Like Screening Model for Real Solvents Model in Comparison to
Classical Group Contribution Methods?, Ind. Eng. Chem. Res., 44,
1610-1624.
Gruber, D., Krummen, M. and Gmehling, J., (1999), The
Determination of Activity Coefficients at Infinite Dilution with the Help of
the Dilutor Technique (Inert Gas Stripping)?, Chem. Eng. Technol.,
22, 827-831.
Gwala, N.V., Deenandayalu, N., Tumba, K. and Ramjugernath, D.,
(2010), Activity Coefficients at Infinite Dilution for Different Solutes in an
Ammonium Ionic Liquid Using Gas Liquid Chromatography at T = (303 or
313 or 323) K?, J. Chem. Thermodyn., 42, 256- 261.
Hagiwara, R. and Ito, Y., (2000), Room temperature ionic liquids
of alkylimidazolium cations and fluoroanions?, Journ.Fluor. Chem.,
105, 221-227.
Hansen H.K., Schiller, M., Fredenslund A., Gmehling J. and
Rasmussen P., (1991), VapourLiquid Equilibria by UNIFAC Group Contribution
Method: Revision and Extension 5? Ind. Eng. Chem. Res., 30,
2352-2355.
Harris, R. A., (2000), Monoethanolamine: suitability as an
extractive solvent?, MSc Thesis, University of KwaZulu-Natal, South Africa.
Heintz, A., Kulikov, D.V. and Verevkin, S.P., (2001),
Thermodynamic Properties of Mixtures Containing Ionic Liquids. 1. Activity
Coefficients at Infinite Dilution of Alkanes, Alkenes, and Alkylbenzenes in
4-Methyl-n-butylpyridinium Tetrafluoroborate Using Gas-Liquid Chromatography?
J. Chem. Eng. Data, 46, 1526-1529.
Heintz, A., Kulikov, D. V. and Verevkin, S. P., (2002a),
Thermodynamic properties of mixtures containing ionic liquids. Activity
coefficients at infinite dilution of polar solutes in
4-methyl-N-butyl-pyridinium tetrafluoroborate using gas-liquid
chromatography?, Journ. Chem. Thermodyn., 34, 1341-1347.
Heintz, A., Kulikov, D. V. and Verevkin, S. P., (2002b),
Thermodynamic Properties of Mixtures Containing Ionic Liquids. 2. Activity
Coefficients at Infinite Dilution of Hydrocarbons and Polar Solutes in
1-Methyl-3-ethyl-imidazolium Bis(trifluoromethylsulfonyl) Amide and in
1,2-Dimethyl-3-ethyl-imidazolium Bis(trifluoromethyl-sulfonyl) Amide Using
Gas-Liquid Chromatography?, J. Chem. Eng. Data , 47, 894-899.
Heintz, A., (2005), Recent developments in Thermodynamics and
Thermo physics of non-aqueous mixtures containing ionic liquids?, Journ.
Chem. Thermodyn., 37, 525-535.
Heintz, A., and Verevkin, S. P., (2005), Thermodynamic
Properties of Mixtures Containing Ionic Liquids. 6. Activity Coefficients at
Infinite Dilution of Hydrocarbons, Alcohols, Esters, and Aldehydes in
1-Methyl-3-octyl-imidazolium Tetrafluoroborate Using Gas-Liquid
Chromatography?, J. Chem. Eng. Data, 50, 1515-1519.
Heintz, A., Casa's, L. M., Nesterov, I. A., Emel`yanenko, V.
N. and Verevkin, S. P., (2005), Thermodynamic Properties of Mixtures Containing
Ionic Liquids 5.Activity Coefficients at Infinite Dilution of Hydrocarbons,
Alcohols, Esters, and Aldehydes in 1-Methyl-3-butylimidazolium
Bis(trifluoromethyl-sulfonyl) Imide Using Gas-Liquid Chromatography?, J.
Chem. Eng. Data, 50, 1510-1514.
Heintz, A., Verevkin, S.P. and Ondo, D., (2006a),
Thermodynamic Properties of Mixtures Containing Ionic Liquids. 8. Activity
Coefficients at Infinite Dilution of Hydrocarbons, Alcohols, Esters, and
Aldehydes in 1-Hexyl-3-methylimidazolium Bis(trifluoromethylsulfonyl) Imide
Using Gas-Liquid Chromatography?, J. Chem. Eng. Data, 51,
434-437.
Heintz, A., Vasiltsova, T. V., Safarov, J., Bich, E. and
Verevkin, S. P., (2006b), Thermodynamic properties of mixtures
containing ionic liquids; 9. Activity coefficients at infinite dilution of
hydrocarbons, alcohols, esters, and aldehydes in trimethylbutylammonium bis
(trifluoromethylsulfonyl) imide using gas-liquid chromatography and static
method?, J. Chem. Eng. Data, 51, 648-655.
Heintz, A., Verevkin, S. P., Lehmann, J. K., Vasiltsova, T. V.
and Ondo, D., (2007), Activity coefficients at infinite dilution and enthalpies
of solution of methanol, 1-butanol, and 1- hexanol in
1-hexyl-3-methyl-imidazolium bis (trifluoromethyl-sulfonyl) imide?, Journ.
Chem. Thermodyn., 39, 268-274.
Heitzman, H., Young, B. A., Rausch, D. J., Rickert, P.,
Stepinski, D. C. and Dietz, M. L., (2006), Fluorous ionic liquids as solvents
for the liquid-liquid extraction of metal ions by macrocyclic polyethers?,
Talanta, 69, 527-531.
Hovorka S. H. and Dohnal V., (1997), Determination of
Air-Water Partitioning of Volatile Halogenated Hydrocarbons by Inert Gas
Stripping Method?, J. Chem. Eng. Data, 42, 924- 933.
Hradetzky, G., Wobst, M., Vopel, H. and Bittrich H. J., (1990),
Measurement of activity
coefficients in highly dilute solutions part I?, Fluid Phase
Equilibr., 54, 133-145.
Huddleston, J. G, Visser, A. E., Reichert, W. M., Willauer, H.
D., Broker, G. A. and Rogers, R.D., (2001), Characterization and comparison of
hydrophilic and hydrophobic room temperature ionic liquids incorporating the
imidazolium cation?, Green Chem., 3, 156-164.
Hudson, G. H. and McCoubrey, J. C., (1960), Intermolecular
Forces Between Unlike Molecules; A More Complete Form of the Combining Rules?,
Trans. Faraday Soc. 56, 761- 766.
Hurley, F. H. and Weir, T. P., (1951), The Electrodeposition of
Aluminum from Nonaqueous Solutions at Room Temperature? J. Electrochem
Soc., 98, 207-212.
Hussam, A. and Carr, P. W., (1985) A Study of Rapid and
Precise Methodology for the Measurement of Vapor/Liquid Equilibria by Headspace
Gas Chromatography?, Anal. Chem., 57, 793-801.
Jakob A, Grensemann H., Lohmann J. and Gmehling J., (2006),
Further Development of Modified UNIFAC (Do): Revision and Extension 5?,
Ind. Eng. Chem. Res., 45, 7924-7933.
Jork, C., Kristen, C., Pieraccini, D., Stark, A., Chiappe, C.,
Beste, Y.A. and Arlt, W., (2005), Tailor-made ionic liquids?, Journ. Chem.
Thermodyn., 37, 537-558.
Kato, R. and Gmehling, J., (2004), Activity coefficients at
infinite dilution of various solutes in the ionic Liquids
[MMIM]+[CH3SO4]-,
[MMIM]+[CH3OC2H4SO4]-,
[MMIM]+[(CH3)2PO4]-, [C5H5NC2H5]+[(CF3SO2)2N]-
and [C5H5NH]+[C2H5OC2H4OSO3]-?, Fluid Phase
Equilibr., 226, 37-44.
Kato, R. and Gmehling, J., (2005a), Systems with ionic liquids:
Measurement of VLE and
data and prediction of their thermodynamic behaviour using
original UNIFAC, mod. UNIFAC (Do) and COSMO-RS (Ol)?, Journ. Chem.
Thermodyn., 37, 603-619.
Kato, R. and Gmehling, J., (2005b), Measurement and
correlation of vapor-liquid equilibria of binary systems containing the ionic
liquids [EMIM] [(CF3SO2)2N], [BMIM] [(CF3SO2)2N], [MMIM] [(CH3)2PO4] and
oxygenated organic compounds respectively water?, Fluid Phase
Equilibr., 231, 38-43.
Kato, R. and Gmehling, J., (2005c), Erratum to Activity
coefficients at infinite dilution of various solutes in the ionic liquids
[MMIM]+[CH3SO4]-, [MMIM]+[CH3OC2H4SO4]-, [MMIM]+[(CH3)2PO4]-,
[C5H5NC2H5]+[(CF3SO2)2N]- and [C5H5NH]+[C2H5OC2H4OSO3]-?[Fluid Phase Equilib.
226 (2004) 37-44]?, Fluid Phase Equilibr., 235, 124.
Khasanshin, T. S., Samuilov, V. S. and Shchemelev, A. P.,
(2009), Determination of the thermodynamic properties of liquid
n-hexadecane from the measurements of the velocity of sound?,
Journ. Eng. Phys. Thermophys., 82,149-156.
Klamt A., (1995), Conductor-Like Screening Model for
Real-Solvents (COSMO-RS): A New Approach the Quantitative Calculation of
Solvation Phenomena?, Journ. Phys. Chem., 99, 2224-2235.
Klamt A. (2005), Comments on Performance of a Conductor-Like
Screening Model for Real Solvents Model in Comparison to Classical Group
Contribution Methods?, Ind. Eng. Chem. Res., 44, 7042
Klamt A. and Eckert F., (2008), Comments on Refining of COSMO-SAC
and the Applications?, Ind. Eng. Chem. Res.. 47, 1351-1352.
Klamt A., Jones, V., Burger, T. and Lohrenz, J. C. W., (1998),
Refinement and Parameterization of COSMO-RS?, Journ. Phys. Chem. A.,
102, 5074-5085.
Klamt, A. and Eckert F., (2000), COSMO-RS: A Novel and Efficient
Method for the A Priori
Prediction of Thermophysical Data of Liquids? Fluid Phase
Equilibr., 172, 43-72.
Kneisl, P. and Zondlo, J. W., (1987), Vapor Pressure, Liquid
Density, and the Latent Heat of Vaporization as Functions of Temperature for
Four Dipolar Aprotic Solvents?, J. Chem. Eng. Data, 32, 11-13.
Kojima K and Tochigi K., (1979), Prediction of Vapor-Liquid
Equilibria by the ASOG Method; Elsevier :Tokyo.
Kojima, K., Zhang, S. and Hiaki, T., (1997), Measuring methods
of infinite dilution activity coefficients and a database for systems including
water? Fluid Phase Equilibr., 131, 145- 179.
Kossack, S., Kraemer, K., Gani, R. and Marquardt, W. (2008), A
systematic synthesis
framework for extractive distillation processes?,
Chem. Eng. Res. and Des., 86, 781-792.
Kozlova, S.A., Verevkin, S.P., Heintz, A., Peppel, T. and
Köckerling, M., (2009), Activity coefficients at infinite dilution of
hydrocarbons, alkylbenzenes, and alcohols in the paramagnetic ionic liquid
1-butyl-3-methyl-imidazolium tetrachloridoferrate (III) using gas-liquid
chromatography?, Journ. Chem. Thermodyn., 41, 330-333.
Krummen M., Gruber D. and Gmehling J., (2000), Measurement of
Activity Coefficients at Infinite Dilution in Solvent Mixtures using the
Dilutor Technique?, Ind. Eng. Chem. Res., 39, 2114-2123.
Krummen, M. and Gmehling, J., (2004), Measurement of activity
coefficients at infinite dilution in N-methyl-2-pyrrolidone and
N-formylmorpholine and their mixtures with water using the dilutor technique?,
Fluid Phase Equilibr., 215, 283-294.
Krummen, M., Wasserscheid, P. and Gmehling, J., (2002),
Measurement of Activity Coefficients at Infinite Dilution in Ionic Liquids
Using the Dilutor Technique?, J. Chem. Eng. Data, 47, 1411-1417.
Kumar, A.A.P. and Banerjee, T., (2009), Thiophene separation with
ionic liquids for Desulphurization: A Quantum Chemical Approach?, Fluid
Phase Equilibr., 278, 1-8.
Kutsuna, S. and Hori, H., (2008), Experimental determination
of Henry`s law constant of perfluorooctanoic acid (PFOA) at 298 K by means of
an inert-gas stripping method with a helical plate?, Atm. Environ.,
42, 8883-88920.
Larsen B.L, Rasmussen P and A. Fredenslund., (1987), A
Modified UNIFAC Group Contribution Method for Prediction of Phase Equilibria
and Heats of Mixing?, Ind. Eng. Chem. Res., 26, 2274-2286.
Laub, R. J. and Peacsok, R. L., (1978), Physico-chemical
Applications of Gas Chromatography?, John Willey and Sons, U.S.A.
Lebert, A. and Richon, D., (1984a), Infinite dilution activity
coefficients of n-alcohols as a function of dextrin concentration in
water-dextrin systems?, J. Agric. Food Chem., 32: 1156-1161.
Lebert, A. and Richon, D., (1984b), Study of the influence of
solute (n-alcohols and n-alkanes)
chain length on their retention by purified olive oil?, J.
Food Sci., 49, 1301-1304.
Legret, D., Desteve, J., Richon D. and Renon H., (1983),
"Vapor-liquid equilibrium constants at infinite dilution determined by a gas
stripping method: Ethane, propane, n-butane, n-pentane in the methane-n-decane
system", AIChE J., 29, 137-144.
Lei, Z., Arlt, W. and Wasserscheid, P., (2006), Separation of
1-hexene and n-hexane with ionic liquids?, Fluid Phase
Equilibr., 241 290-299.
Lei, Y.D., Shunthirasingham, C. and Wania, F., (2007a),
Comparison of headspace and gas-stripping techniques for measuring the
air-water partitioning of normal alkanols (C4 to C10): effect of temperature,
chain length, and adsorption to the water surface?, J. Chem. Eng. Data,
52, 168-179.
Lei, Z., Arlt, W. and Wasserscheid, P., (2007b), Selection of
entrainers in the 1-hexene/nhexane system with a limited solubility?, Fluid
Phase Equilibr. 260, 29-35.
Lei, Z., Chen, B., Li, C., and Liu, H., (2008), Predictive
Molecular Thermodynamic Models for
Liquid Solvents, Solid Salts, Polymers,
and Ionic Liquids?, Chem. Rev., 108, 1419-1455.
Leroi, J. C., Masson, J. C., Renon, H., Fabries, J. F. and
Sannier H., (1977), Accurate Measurement of Activity Coefficients at Infinite
Dilution by Inert Gas Stripping and Gas Chromatography?, Ind. Eng. Chem.
Process Des. Dev, 16, 139-144.
Letcher, T. M., (1980), Activity Coefficients at Infinite
Dilution from Gas-Liquid Chromatography?, Faraday symposium, 15,
103-111.
Letcher, T. M., Soko, B., Ramjugernath, D., Deenadayalu, N.,
Nevines, A. and Naicker, P. K., (2003a), Activity Coefficients at Infinite
Dilution of Organic Solutes in 1-Hexyl-3- methylimidazolium Hexafluorophosphate
from Gas-Liquid Chromatography?, J. Chem. Eng. Data, 48, 708-711.
Letcher, T. M., Soko, B., Reddy, P. and Deenadayalu, N.,
(2003b), Determination of Activity Coefficients at Infinite Dilution of Solutes
in the Ionic Liquid 1-Hexyl-3- methylimidazolium Tetrafluoroborate Using
Gas-Liquid Chromatography at the Temperatures 298.15 K and 323.15 K?, J.
Chem. Eng. Data, 48, 1587-1590.
Letcher, T. M., Domañska, U., Marciniak, M., and
Marciniak, A., (2005a), Activity coefficients at infinite dilution measurements
for organic solutes in the ionic liquid
1-butyl3-methyl-imidazolium2-(2-methoxyethoxy) ethylsulfate using g.l.c. at T =
(298.15, 303.15, and 308.15) K?, Journ. Chem. Thermodyn., 37,
587-593.
Letcher, T. M., Marciniak, A. and Marciniak, M., (2005b),
Determination of Activity Coefficients at Infinite Dilution of Solutes in the
Ionic Liquid 1-Butyl-3-methylimidazolium Octyl Sulfate Using Gas-Liquid
Chromatography at a Temperature of 298.15 K, 313.15K, or 328.15 K?, J.
Chem. Eng. Data, 50, 1294-1298.
Letcher, T. M., Marciniak, A., Marciniak, M. and
Domañska, U., (2005c), Activity coefficients at infinite dilution
measurements for organic solutes in the ionic liquid
1-hexyl-3-methylimidazolium bis (trifluoromethylsulfonyl)-imide using g.l.c. at
T = (298.15, 313.15, and 333.15) K?, J. Chem. Thermodyn. 37,
1327-1331.
Letcher, T. M. and Reddy, P., (2005), Determination of
activity coefficients at infinite dilution of organic solutes in the ionic
liquid, Trihexyltetradecylphosphonium tris (pentafluoroethyl)
trifluorophosphate, by gas-liquid chromatography?, Fluid Phase
Equilibr., 235, 11-17.
Letcher, T. M. and Reddy, P., (2007), Determination of
activity coefficients at infinite dilution of organic solutes in the ionic
liquid, tributylmethylphosphonium methylsulphate by gas- liquid
chromatography?, Fluid Phase Equilibr., 260, 23-28.
Letcher T. M., (2007), in Thermodynamics, Solubility and
environmental issues?, T.M. Letcher (Ed.) Elsevier B.V., Amsterdam, First
edition.
Letcher, T. M., Ramjugernath, D., Laskowska, M.,
Królikowski, M., Naidoo, P. and Do ,
U., (2008a), Determination of activity coefficients at
infinite dilution of solutes in the ionic liquid, trihexyltetradecylphosphonium
bis (trifluoromethylsulfonyl) imide, using gas-liquid chromatography at T
(303.15, 308.15, 313.15 and 318.15) K?, J. Chem. Eng. Data,
53, 2044-2049.
Letcher, T.M., Ramjugernath, D., Laskowska, M.,
Królikowski, M., Naidoo, P. and Domañska, U., (2008b), Activity
coefficients at infinite dilution measurements for organic solutes in the ionic
liquid trihexyltetradecylphosphonium-bis-(2, 4, 4-trimethylpentyl) -
phosphinate using g.l.c. at T = (303.15, 308.15, 313.15, and 318.15) K?,
Journ. Chem. Thermodyn., 40, 1243-1247.
Letcher, T. M., Ramjugernath, D., Królikowski, M.,
Laskowska, M., Naidoo, P. and Domañska, U., (2009), Activity
coefficients at infinite dilution measurements for organic solutes in the ionic
liquid N-butyl-4-methylpyridinium tosylate using GLC at T = (328.15, 333.15,
338.15, and 343.15) K?, Fluid Phase Equilibr., 276, 31-36.
Li, J. and Carr, P.W., (1993), Measurement of water-hexadecane
partition coefficients by headspace gas chromatography and calculation of
limiting activity coefficients in water?, Anal. Chem., 65,
1443-1450.
Li, J., Dallas, A. J., Eikens, D. I. and Carr, P. W., (1993),
Measurement of Large Infinite Dilution Activity Coefficients of Nonelectrolytes
in Water by Inert Gas Stripping and Gas Chromatography?, Anal. Chem.,
65, 3212-3218.
Liebert, V., Nebig, S. and Gmehling, J., (2008), Experimental
and predicted phase equilibria
and excess properties for systems with ionic
liquids?, Fluid Phase Equilibr., 268, 14-20.
Lin, S. and Sandler, I., (2002), A Priori Phase Equilibrium
Prediction from a Segment Contribution Solvation Model?, Ind. Eng. Chem.
Res. 41, 899-913.
Lohmann J. and Gmehling J., (2001), Modified UNIFAC (Dortmund):
reliable model for the
development of Thermal Separation processes?, J. Chem. Eng.
Japan, 24, 43-54.
Lydersen A.L. Mass transfer in Engineering Practice. (1983) John
Willey& sons.
McGlashan, M. L. and Potter, D. J. B., (1962), The Second Virial
Coefficients? Proc. Roy. Soc., 267, 487-500.
McMillan, W.G. and Mayer, J.E., (1945), The Statistical
Thermodynamics of Multicomponent Systems?, J. Chem. Phys., 13,
276-305.
Mehra, R, (2003), Application of refractive index mixing rules
in binary systems of hexadecane and heptadecane with n-alkanols at
different temperatures?, Proc. Indian Acad. Sci. (Chem.
Sci.), 115, 147-154.
Meindersma, G.W., Podt, A. and Haan, A.B. (2006) Ternary
liquid-liquid Equilibria for mixtures of an aromatic + an aliphatic hydrocarbon
+ 4-methyl-N-butylpyridinium tetrafluoroborate? J. Chem. Eng Data, 51,
1814-1819.
Meshri, D.T., (2000), in advanced inorganic fluorides: Synthesis,
Characterization and applications?, Elsevier, 661-682.
Miyano Y., Nakanishi K. and Kukuchi K., (2003), Henry`s constants
of butane, isobutene, 1- butene and isobutene in methanol at 255-320K?,
Fluid Phase Equilibr., 208, 223-238.
Möllmann, C. and Gmehling, J., (1997), Measurement of
Activity Coefficients at Infinite Dilution Using Gas-Liquid Chromatography 5.
Results for N-Methylacetamide, N, NDimethylacetamide, N, N-Dibutylformamide,
and Sulfolane as Stationary Phases?, J. Chem. Eng. Data, 42, 35-40.
Moutiers G. and Isabelle Billard, (2003), Des solvents plus
propres?, Nature, 311, 45-49.
Mutelet, F. and Jaubert, J-N., (2006), Accurate measurements
of thermodynamic properties of solutes in ionic liquids using inverse gas
chromatography?, Journ. Chromatograph. A, 1102, 256-267.
Mutelet, F., Jaubert, J-N., Rogalski, M., Boukherissa, M. and
Dicko, A., (2006), Thermodynamic Properties of Mixtures Containing Ionic
Liquids: Activity Coefficients at Infinite Dilution of Organic Compounds in
1-Propyl Boronic Acid-3-Alkylimidazolium Bromide and
1-Propenyl-3-alkylimidazolium Bromide Using Inverse Gas Chromatography?, J.
Chem. Eng. Data, 51, 1274-1279.
Mutelet, F. and Jaubert, J-N, (2007), Measurement of activity
coefficients at infinite dilution in 1-hexadecyl-3 methylimidazolium
tetrafluoroborate ionic liquid?, Journ. Chem. Thermodyn., 39,
1144-1150.
Nebig, S., Bölts, R. and Gmehling, J., (2007),
Measurement of vapor-liquid equilibria (VLE) and excess enthalpies
(HE) of binary systems with 1-alkyl-3-methylimidazolium Bis
(trifluoromethylsulfonyl)imide and prediction of these properties and
ã8 using modified UNIFAC (Dortmund)?, Fluid Phase
Equilibr., 258, 168-178.
Nebig, S., Liebert, V. and Gmehling, J., (2009), Measurement
and prediction of activity coefficients at infinite dilution ( ), vapor-liquid
equilibria (VLE) and excess enthalpies (
) of binary systems with 1, 1-dialkyl-pyrrolidinium bis
(trifluoromethylsulfonyl) imide using mod UNIFAC (Dortmund)?, Fluid Phase
Equilibr., 277, 61-67.
Novak, J. P. and Matous, J.; Pick, J., (1987), Liquid-Liquid
Equilibria?, Elsevier: Amsterdam,
Olivier, E., Letcher, T.M., Naidoo, P. and Ramjugernath, D.,
(2010a), Activity coefficients at infinite dilution of organic solutes in the
ionic liquid 1-ethyl-3-methylimidazolium trifluoromethanesulfonate using
gas-liquid chromatography at T = (313.15, 323.15, and 333.15) K?, Journ.
Chem. Thermodyn., 42, 78-83.
Olivier, E., Letcher, T.M., Naidoo, P. and Ramjugernath, D.,
(2010b), Activity coefficients at infinite dilution of organic solutes in the
ionic liquid1-Octyl-3-methylimidazolium hexafluorophosphate using gas-liquid
chromatography at T = (313.15, 323.15, and 333.15) K?, Journ. Chem.
Thermodyn., doi:10.1016/j.jct.2009.12.004.
Olivier, E., Letcher, T.M., Naidoo, P. and Ramjugernath, D.,
(2010c), Activity coefficients at infinite dilution of organic solutes in the
ionic liquid 1-Butyl-3-methylimidazolium hexafluoroantimonate using gas-liquid
chromatography at T = (313.15, 323.15, and 333.15) K?, Unpublished
manuscript.
O'Rear, D. J., Boudreau, L. C., Driver, M. S., and Munson, C.
L., (2001), "Removal of mercaptans from hydrocarbon streams using ionic
liquids", Patent; Chevron U.S. 2001- US32211 (2002034863), 19,
10-16-2001.
Pereiro, A. B., Legido, J. L. and Rodriguez, A., (2007),
Physical properties of ionic liquids based on 1-alkyl-3-methylimidazolium
cation and hexafluorophosphate as anion and temperature dependence?, J.
Chem. Thermodyn. 39 , 1168-1175.
Plechkova, N. V. and Seddon, K. R., (2008), Applications of ionic
liquids in the chemical industry?, Chem. Soc. Rev., 37, 123-150.
Poling, B.E, Prausnitz, J.M. and O`Connell, J.P., (2001), The
Properties of Liquids and Gases?, Fifth ed., McGraw-Hill, New York.
Porter, P. E., Deal, C. H. and Stross, F. H., (1956), The
Determination of Partition Coefficients
from Gas-Liquid Partition Chromatography?, J. Am. Chem.
Soc., 78, 2999-3006.
Prausnitz, J. M. and Anderson, R., (1961), Thermodynamics of
Solvent Selectivity in Extractive Distillation of Hydrocarbons?, AIChE
J., 7, 96-101.
Putnam R.; Taylor R.; Klamt A.; Eckert F. and Schiller M.,
(2004), Prediction of Infinite
Dilution Activity Coefficients using
COSMO-R?, Ind. Eng. Chem. Res. 42, 3635-3641.
Raal, JD and Mühlbauer, A.L, (1998), Phase Equilibria:
Measurement and Computation?, Taylor and Francis, Bristol P.A.
Revelli, A-L., Sprunger, L.M., Gibbs, J., Acree Jr., W.E.,
Baker, G.A. and Mutelet, F., (2009) Activity Coefficients at Infinite Dilution
of Organic Compounds in Trihexyl(tetradecyl)phosphonium
Bis(trifluoromethylsulfonyl)imide Using Inverse Gas Chromatography?, J.
Chem. Eng. Data, 54, 977-985.
Richon D., Antoine P. and Renon H., (1980), Infinite Dilution
Activity Coefficients of Linear and Branched Alkanes from C1 to C9 in
n-Hexadecane by Inert Gas Stripping?, Ind. Eng. Chem. Process Des.
Dev., 19, 144-147.
Richon, D. and Renon, H., (1980), Infinite dilution Henry's
constants of light hydrocarbons in n-hexadecane, n-octadecane, and 2, 2, 4, 4,
6, 8, 8-heptamethylnonane by inert gas stripping?, J. Chem. Eng. Data,
25, 59-60.
Richon, D., Antoine, P. and Renon, H., (1980), Infinite
dilution activity coefficients of linear and branched alkanes from C 1 and C 9
in n-hexadecane by inert gas stripping.? Ind. Eng. Chem. Process Des.
Dev., 19, 144-147.
Richon D., Sorrentino F. and Voilley A., (1985), Infinite
Dilution Activity Coefficients by Inert Gas Stripping Method: Extension to the
Study of Viscous and Foaming Mixtures?, Ind. Eng. Chem. Process Des.
Dev., 24, 1160-1165.
Robinson, J. and Osteryoung, R.A., (1979), An electrochemical
and spectroscopic study of some aromatic hydrocarbons in the room temperature
molten salt system Aluminum Chloride-n-Butylpyridinium Chloride?, J. Am.
Chem. Soc., 101,323-327.
Rodriguez, A. and Brennecke, J. F., (2006), Temperature and
Composition Dependence of the Density and Viscosity of Binary Mixtures of Water
+ Ionic Liquid?, J.Chem. Eng. Data, 51, 2145-2155.
Roettger, D., Nierlich, F., Krissmann, J., Wasserscheid, P.
and Keim, W., (2003), "Method for separating organic compounds by extracting or
washing them with ionic liquids", Patent; Oxeno, Olefinchemie G.
2003-EP430 (2003070667), 16. 1-17-2003. WO.
Rogers, R. D. and Seddon, K. R., (2003), Ionic Liquids-Solvents
of the Future??, Science, 302, 792-793.
Sandler, S.I., (1996), Infinite Dilution Activity Coefficients in
Chemical, Environmental and Biological engineering?, Fluid Phase Equilibr.
116, 343-353.
Schult C. J., Neely B. J., Robinson Jr R. L., Gasema, K. A. M.
and Todd, B. A., (2001), Infinite Dilution Activity Coefficients for several
solutes in Hexadecane and in n-Methyl2-Pyrrolidone (NMP): Experimental
Measurements and UNIFAC Predictions?, Fluid Phase Equilibr., 179,
117-129.
Seddon, K. R., Scheffler, T. B., Hussey, C. L., Kear, C. M.
and Armitage, P. D., (1983) Molybdenum Chloro Complexes in Room-Temperature
Chloroaluminate Ionic Liquids: Stabilization of [MoCl6]2- and
[MoCl6]3-?, Inorg. Chem., 22, 2099-2100.
Shimoyama, Y., Hirayama, T. and Iwai, Y., (2008), Measurement
of Infinite Dilution Activity Coefficients of Alcohols, Ketones, and Aromatic
Hydrocarbons in 4-Methyl-Nbutylpyridinium Tetrafluoroborate and
1-Butyl-3-methylimidazolium Hexafluorophosphate by Gas- Liquid Chromatography?,
J. Chem. Eng. Data, 53 , 2106-2111.
Shröder, U., Wadhawan, J. D., Compton, R. G., Marken, F.,
Suarez, P. A. Z., Consorti, C. S., De Souza, R. F. and Dupont, J., (2000),
Water-induced accelerated ion diffusion : voltammetric studies in 1-methyl-3-
I 2,6-(S)-dimethylocten-2-yl
]imidazolium tetrafluoroborate, 1-butyl-3 methylimidazolium
tetrafluoroborate and hexafluorophosphate ionic liquids?, New J.
Chem., 24, 1009-1015.
Shunthirasingham, C., Lei, Y.D., Wania, F., (2007), Evidence
of bias in air water Henry`s law constants for semivolatile organic compounds
measured by inert gas stripping?, Environ. Sci. Technol. 41,
3807-3814.
Skoog, D. A., West D. M. and Holler, F. J., (1996), Fundamentals
of Analytical Chemistry?, 7th Edition, Saunders College Publishing,
Philadelphia.
Smiglak, M., Reichert, W.M., Holbrey, J.D., Wilkes, J.S., Sun,
L., Thrasher, J.S., Kirichenko, K., Singh, S., Katritzkyc, A.R. and Rogers,
R.D., (2006), Combustible ionic liquids by design: is laboratory safety another
ionic liquid myth??, Chem. Commun., 2554-2556.
Smith, J.M., Van Ness, H.C. and Abbott, M.M., (2005),
Introduction to Chemical Engineering Thermodynamics?, McGraw Hill,
7th Ed.
Sumartschenkowa, I. A., Verevkin, S. P., Vasiltsova, T. V.,
Bich, E., Heintz, A., Shevelyova, M. P. and Kabo, G. J., (2006), Experimental
Study of Thermodynamic Properties of Mixtures Containing Ionic Liquid
1-Ethyl-3-methylimidazolium Ethyl Sulfate Using Gas-Liquid Chromatography and
Transpiration Method?, J. Chem. Eng. Data, 51, 2138-2144.
Sumon, K.Z., (2005), Extraction of aromatics using green
solvents based on ionic liquids?,
MSc thesis, King Fahd University of
Petroleum and minerals, Dhahran, Saudi, Arabia.
Tiegs, D.G., Medina, A., Soares, M., Bastos, J., Alessi, P.,
Kikic, I., (1986), Activity Coefficients at Infinite Dilution?, Vol. 9, Part 1,
Dechema Chemistry Data Series, Dechema, Frankfurt.
Trulove, P.C. and Mantz, R.A., (2003), in Ionic Liquids in
Synthesis?, ed. P. Wasserscheid and T.Welton, Wiley-VCH, Weinheim, 103-126.
Vitenberg, A. G., (2003), Equilibrium model in the description of
gas extraction and headspace analysis?, J. Anal, Chem., 58, 2-15.
Walden, P., (1914), Ueber die Moleculargrösse und
elektrisehe Leitfähigkeit einiger gesehmolzenen salze?,
Bull. Acad. Imper. Sci. (St. Petersburg), 1800-1801.
Wang, M-H., Wu, J-S., Wang, L-S. and Li, M-Y., (2007),
Activity Coefficients at Infinite Dilution of Alkanes, Alkenes, and Alkyl
Benzenes in 1-Propyl-2,3-dimethylimidazolium Tetrafluoroborate Using Gas-Liquid
Chromatography?, J. Chem. Eng. Data, 52, 1488-1491.
Wasserscheid, P. and Keim, W., (2000), Ionic liquids-New
Solutions? For Transition Metal Catalysis?, Angew., Chem. Int. Ed., 39,
3772-3789.
Wasserscheid, P., Boesmann, A., Jess, A., Datsevitch, L.,
Schmitz, C., and Lauter, A., (2002) "Extractive method for eliminating
polarizable impurities from hydrocarbons and hydrocarbon mixtures using ionic
liquids as the extractants", Patent ; Solvent, Innovation G.
2002-EP12239(2003037835), 18. 11-2-2002. WO.
Weidlich, U. and Gmehling, J., (1987), A modified UNIFAC model,
1: Prediction of VLE, HE, and gamma infinity?, Ind.
Eng. Chem. Res., 26, 1372-1381.
Welton T., (1999), Room temperature ionic liquids. Solvents for
synthesis and catalysis?, Chem. Rev., 99, 2071-2083.
Wilkes, J. S., Levisky, J. A., Wilson, R. A. and Hussey, C.
L., (1982), Dialkylimidazolium chloroaluminate melts: a new
class of room-temperature ionic liquids for electrochemistry, spectroscopy and
synthesis?, Inorg. Chem., 21, 1263-1264.
Wilson G.M. and Deal C.H, (1962), Activity Coefficient and
Molecular Structure. Activity coefficients in changing environments-solutions
of groups?, Industrial Engineering Chemistry Fundamentals, 1,
20-23.
Wittig R.; Lohmann J.; Joh R; Horstmann S, Gmehling J.,
(2001), Vapour-Liquid Equilibria and Enthalpies of Mixing in a Temperature
Range from 298.15 to 413.15 K for the Further Development of Modified UNIFAC
(Dortmund)?, Ind. Eng. Chem. Res., 40, 5831-5838.
Xue, H., Verma, R. and Shreeve, J.M., (2006), Review of the IL`s
with fluorine-containing anions?, Journ. Fluor. Chem., 127,
159-176.
Yang, X-J., Wu, J-S., Ge, M-L., Wang, L-S. and Li, M-Y,
(2008), Activity Coefficients at Infinite Dilution of Alkanes, Alkenes, and
Alkyl Benzenes in 1-Hexyl-3-methylimidazolium Trifluoromethanesulfonate Using
Gas-Liquid Chromatography?, J. Chem. Eng. Data, 53, 1220-1222.
Zaworotko, M. J. and Wilkes, J. S., (1992), Air and Water Stable
1-Ethyl-3- methylimidazolium Based Ionic Liquids?, J. Chem. Soc., Chem.
Comm., 13, 965-967.
Zhang, J., Zhang, Q., Qiao, B. and Deng, Y., (2007),
Solubilities of the Gaseous and Liquid Solutes and Their Thermodynamics of
Solubilization in the Novel Room-Temperature Ionic Liquids at Infinite Dilution
by Gas Chromatography?, J. Chem. Eng. Data, 52, 2277-2283.
Zhang, L., Qiao, B., Ge, Y., Deng, D. and Ji, J., (2009),
Effect of ionic liquids on (vapor + liquid) equilibrium behavior of (water +
2-methyl-2-propanol)?, Journ. Chem. Thermodyn., 41, 138-143.
Zhao, J., Cong-Cong, D., Chun-Xi, L., Meng, H. and Zi-Hao, W.,
(2006), Isobaric vapor-liquid equilibria for ethanol-water system containing
different ionic liquids at atmospheric pressure?, Fluid Phase Equilibr.,
242, 147-153.
Zhou, Q. and Wang, L-S., (2006), Activity Coefficients at
Infinite Dilution of Alkanes, Alkenes, and Alkyl Benzenes in
1-Butyl-3-methylimidazolium Tetrafluoroborate Using Gas-Liquid Chromatography?,
J. Chem. Eng. Data, 51, 1698-1701.
Zhou, Q., Wang, L-S, Wu, J-S. and Li, M-Y., (2007), Activity
Coefficients at Infinite Dilution of Polar Solutes in
1-Butyl-3-methylimidazolium Tetrafluoroborate Using Gas-Liquid Chromatography?,
J. Chem. Eng. Data, 52, 131-134.
APPENDIX A: SOURCES OF IDACs LITERATURE DATA
Table A-1: Literature data for in
imidazolium-based fluorinated ionic liquids.
|
Ionic liquids
|
References
|
No. of Solutes
|
Data
Points
|
Temp. Range
(K)
|
Method
|
|
[EMIM][Tf2N]
|
Deenadayalu et al. (2005)
|
15
|
30
|
303.15-318.15
|
GLC
|
|
Heintz et al. (2002b)
|
19
|
76
|
313.15-343.15
|
GC
|
|
Kato and Gmehling (2005a,b)
|
4
|
4
|
353.15
|
VLE
|
|
Krummen et al. (2002)
|
20
|
80
|
293.15-323.15
|
GST
|
|
[BMIM][PF6]
|
Dobryakov et al. (2008)
|
8
|
32
|
293.15-353.15
|
GST
|
|
Shimoyama et al. (2008)
|
18
|
54
|
315.9-334.8
|
GLC
|
|
[HMIM][Tf2N]
|
Dobryakov et al. (2008)
|
8
|
32
|
293.15-353.15
|
GST
|
|
Heintz et al. (2007)
|
3
|
18
|
301-396
|
GLC
|
|
Kato and Gmehling (2005a)
|
26
|
148
|
303.15-333.15
|
GLC/GST
|
|
Letcher et al. (2005c)
|
15
|
45
|
298.15-333.15
|
GC
|
|
Heintz et al. (2006a)
|
52
|
52
|
301-396
|
GLC
|
|
[MOIM][BF4]
|
Jork et al. (2005)
|
4
|
4
|
363.15
|
GLC
|
|
Foco et al. (2006)
|
20
|
46
|
303-343
|
GLC
|
|
Heintz and Verevkin (2005)
|
51
|
51
|
302-396
|
GLC
|
|
Zhang et al. (2007)
|
14
|
28
|
298-323
|
GLC
|
|
[EMIM] [TFA]
|
(2007)
|
29
|
185
|
298.15-368.15
|
GLC
|
|
[BMIM][TfO]
|
(2008a)
|
32
|
242
|
298.15-368.15
|
GLC
|
|
Ge et al. (2007)
|
17
|
119
|
303.15-363.15
|
GLC
|
|
Ge and Wang (2008)
|
17
|
115
|
303.15-363.15
|
GLC
|
|
[EMIM][BF4]
|
Foco et al. (2006)
|
18
|
41
|
303-343
|
GLC
|
|
Ge et al. (2008a)
|
25
|
175
|
303.15-363.15
|
GLC
|
|
Jork et al. (2005)
|
4
|
4
|
363.15
|
GLC
|
|
[BMIM][BF4]
|
Foco et al. (2006)
|
20
|
46
|
303-343
|
GLC
|
|
Jork et al. (2005)
|
4
|
4
|
363.15
|
GLC
|
|
Zhang et al. (2007)
|
14
|
28
|
298-323
|
GLC
|
|
Zhou and Wang (2006)
|
17
|
85
|
303.15-343.15
|
GLC
|
|
Zhou et al. (2007)
|
17
|
85
|
303.15-343.15
|
GLC
|
|
[BMIM][Tf2N]
|
Heintz et al. (2005)
|
53
|
53
|
302-385
|
GLC
|
|
Kato and Gmehling (2005b)
|
3
|
3
|
353.15
|
VLE
|
|
Krummen et al. (2002)
|
13
|
52
|
293.15-323.15
|
IGST
|
|
Zhang et al. (2007)
|
15
|
15
|
323
|
GLC
|
|
[PDMIM][BF4]
|
Ge et al. (2008b)
|
17
|
119
|
303.15-363.15
|
GLC
|
|
Wang et al. (2007)
|
17
|
119
|
303.15-363.15
|
GC
|
Table A-1: Literature data for in
imidazolium-based fluorinated ionic liquids (Continued).
|
Ionic liquids
|
References
|
No. of
Solutes
|
Data
Points
|
Temp.
Range(K)
|
Method
|
|
[HMIM][BF4]
|
Foco et al. (2006)
|
20
|
42
|
303-343
|
GLC
|
|
Letcher et al. (2003b)
|
15
|
26
|
298.15-323.15
|
GLC
|
|
[MOIM][Tf2N]
|
Kato and Gmehling (2005a)
|
21
|
119
|
303.15-333.15
|
GLC/GST
|
|
EMIM][Tf2N]+ [BMIM][Tf2N]
|
Kato and Gmehling (2005b)
|
7
|
28
|
293.15-353.15
|
IGST
|
|
[MMIM][Tf2N]
|
Krummen et al. (2002)
|
13
|
54
|
293.15-333.15
|
IGST
|
|
[HMIM][PF6]
|
Letcher et al. (2003a)
|
16
|
43
|
298.15-
323.15
|
GLC
|
|
[C16MIM][BF4]
|
Mutelet and Jaubert (2007)
|
31
|
93
|
323.15-
343.15
|
GLC
|
|
[HMIM][TfO]
|
Yang et al. (2008)
|
17
|
119
|
303.15-
363.15
|
GLC
|
|
[CpMIM][Tf2N]
|
Zhang et al. (2007)
|
15
|
29
|
303-323
|
GLC
|
|
[CpMMIM][Tf2N]
|
Zhang et al. (2007)
|
15
|
29
|
303-323
|
GLC
|
|
[EDMIM][Tf2N]
|
Heintz et al (2002b)
|
19
|
76
|
313.15-
343.15
|
GLC
|
|
[H-O-MIM] [Tf2N]
|
Do Marciniak (2009b)
|
35
|
280
|
298.15-
368.15
|
GLC
|
|
[DH-O- MIM][Tf2N]
|
Marciniak (2009b)
|
35
|
280
|
298.15-
368.15
|
GLC
|
Table A-2: literature data for in
phosphonium-based fluorinated ionic liquids.
|
Ionic liquids
|
References
|
No. of
Solutes
|
Data
Points
|
Temp.
Range
(K)
|
Method
|
|
[3C6C14P][BF4]
|
Banerjee and Khanna
|
16
|
48
|
308.15-
|
GLC
|
|
(2006)
|
|
|
328.15
|
|
|
Banerjee and Khanna
|
16
|
48
|
308.15-
|
GLC
|
|
(2006)
|
|
|
328.15
|
|
|
Letcher et al. (2008a)
|
18
|
72
|
303.15-
|
GLC
|
|
[3C6C14P][Tf2N]
|
|
|
|
318.15
|
|
|
Revelli et al. (2009)
|
39
|
117
|
302.15-
|
GLC
|
|
|
|
|
322.35
|
|
|
[3C6C14P][(C2F5)3PF3]
|
Letcher and Reddy
|
17
|
51
|
308.15-
|
GLC
|
|
(2005)
|
|
|
328.15
|
|
Table A-3: Literature data for in pyridinium
and pyrrolidinium-based fluorinated ionic
liquids
|
Ionic liquids
|
References
|
No. of
Solutes
|
Data
Points
|
Temp.
Range
(K)
|
Method
|
|
Heintz et al. (2002a)
|
19
|
76
|
313.15-
|
GLC
|
|
|
|
|
343.15
|
|
|
Heintz et al. (2001)
|
19
|
76
|
313.1-363.1
|
GLC
|
|
[BMPy][BF4]
|
Go et al. (2007)
|
3
|
18
|
297-344
|
GLC
|
|
Shimoyama et al.
|
4
|
12
|
306.6-325.3
|
GLC
|
|
(2008)
|
|
|
|
|
|
[EPy][Tf2N]
|
Kato and Gmehling (2004)
|
31
|
122
|
303.15-
333.15
|
GLC/GST
|
|
[BMPyrr][TfO]
|
. (2009)
|
32
|
245
|
298.15-
|
GLC
|
|
|
|
|
368.15
|
|
|
[BMPyrr][Tf2N]
|
Kato and Gmehling
|
15
|
60
|
303.15-
|
IGST
|
|
(2005a)
|
|
|
333.15
|
|
|
[HMPyrr][Tf2N]
|
Nebig et al. (2009)
|
11
|
44
|
303.15-
|
IGST
|
|
|
|
|
333.15
|
|
|
[OMPyrr][Tf2N]
|
Nebig et al. (2009)
|
7
|
28
|
303.15-
|
IGST
|
|
|
|
|
343.15
|
|
Table A-4: Literature data for in ammonium and
sulfonium-based fluorinated ionic liquids.
|
Ionic liquids
|
References
|
No. of
Solutes
|
Data
Points
|
Temp.
Range
(K)
|
Method
|
|
[Et3S][Tf2N]
|
(2009a)
|
32
|
250
|
298.15-
368.15
|
GLC
|
|
[3C1C4N][Tf2N]
|
Heintz et al. (2006b)
|
54
|
54
|
302-393
|
GLC/SM
|
Table A-5: Literature data for in
non-fluorinated ionic liquids
|
Ionic liquids
|
References
|
No. of
Solutes
|
Data
Points
|
Temp.
Range(K)
|
Method
|
|
[MOIM][Cl]
|
David et al. (2003)
|
15
|
45
|
298.15-
318.15
|
GLC
|
|
[MOIM][MDEGSO4]
|
Deenadayalu et al. (2006a)
|
23
|
45
|
288.15-
313.15
|
GLC
|
|
[BMIM][MeSO4]
|
Dobryakov et al. (2008)
|
8
|
32
|
293.15-
353.15
|
IGST
|
|
[EMIM][SCN]
|
(2008b)
|
29
|
203
|
298.15-
368.15
|
GLC
|
|
[BMIM][SCN]
|
(2009)
|
32
|
231
|
298.15-
368.15
|
GLC
|
|
[BMIM][Cl]
|
Jork et al. (2005)
|
4
|
4
|
363.15
|
GLC
|
|
Kato and Gmehling (2005c)
|
5
|
5
|
353.15
|
VLE
|
|
[MMIM][Me2PO4]
|
|
|
|
303.15-
|
|
|
Kato and Gmehling (2004)
|
15
|
59
|
383.15
|
IGST
|
|
[MMIM][C1OC2SO4]
|
Kato and Gmehling (2004)
|
15
|
60
|
303.15-
343.15
|
IGST
|
|
Kato and Gmehling (2004)
|
14
|
56
|
303.15-
333.15
|
GLC
IGST
|
|
[MMIM][MeSO4]
|
Kato and Gmehling
|
|
|
303.15-
|
|
|
(2005c)
|
2
|
8
|
333.15
|
IGST
|
|
[BMIM][FeCl4]
|
Kozlova et al. (2009)
|
19
|
19
|
303-403
|
GLC
|
|
Krummen et al. (2002)
|
10
|
42
|
293.15-
333.15
|
IGST
|
|
[EMIM][Et-SO4]
|
Summartschenkowa et al.(2006)
|
46
|
46
|
301-427.15
|
GLC
TM
|
|
[BMIM][MDEGSO4]
|
Letcher et al (2005a)
|
16
|
48
|
298.15-
328.15
|
GLC
|
|
Letcher et al (2005b)
|
16
|
47
|
298.15-
328.15
|
GLC
|
|
[BMIM][Oc-SO4]
|
|
|
|
323.15-
|
|
|
Mutelet and Jaubert (2006)
|
29
|
87
|
343.15
|
GLC
|
Appendix A: Sources of infinite dilution activity
coefficients literature data
Table A-5: Literature data for in
non-fluorinated ionic liquids (Continued)
|
Ionic liquids
|
References
|
No. of
Solutes
|
Data
Points
|
Temp.
Range(K)
|
Method
|
|
[EMIM][TOS]
|
Mutelet and Jaubert (2006)
|
29
|
29
|
323.15
|
GLC
|
|
[PropMIM][Br]
|
Mutelet et al. (2006)
|
28
|
28
|
323.15
|
GLC
|
|
[PropOMIM][Br]
|
Mutelet et al. (2006)
|
28
|
28
|
323.15
|
GLC
|
|
[PropC10MIM][Br]
|
Mutelet et al. (2006)
|
28
|
28
|
323.15
|
GLC
|
|
[PropC12MIM][Br]
|
Mutelet et al. (2006)
|
28
|
28
|
323.15
|
GLC
|
|
[PBA-MIM][Br]
|
Mutelet et al. (2006)
|
21
|
21
|
323.15
|
GLC
|
|
[PBA-OMIM][Br]
|
Mutelet et al. (2006)
|
23
|
23
|
323.15
|
GLC
|
|
[PBA-C10MIM][Br]
|
Mutelet et al. (2006)
|
23
|
23
|
323.15
|
GLC
|
|
[PBA-C12MIM][Br]
|
Mutelet et al. (2006)
|
23
|
23
|
323.15
|
GLC
|
|
[BMIM][n-
C16H31OO]
|
Zhang et al. (2007)
|
14
|
14
|
333
|
GLC
|
|
[BMIM][n-
C18H35OO]
|
Zhang et al. (2007)
|
14
|
28
|
323-333
|
GLC
|
|
[CpMIM][N(CN)2]
|
Zhang et al. (2007)
|
14
|
28
|
323-333
|
GLC
|
|
[CpMMIM][N(CN)2]
|
Zhang et al. (2007)
|
14
|
28
|
323-333
|
GLC
|
|
[3C6C14P][Cl]
|
Banerjee and Khanna (2006)
|
16
|
48
|
308.15-328.15
|
GLC
|
|
[3C6C14P]
[(C8 H17)2PO2]
|
Letcher et al. (2008b)
|
14
|
70
|
298.15-318.15
|
GLC
|
|
[3C4C1P][MeSO4]
|
Letcher and Reddy (2007)
|
12
|
36
|
308.15-318.15
|
GLC
|
|
[Py][C1OC2SO4]
|
Kato and Gmehling (2004)
|
14
|
56
|
303-333.15
|
IGST
|
|
[BMPy][TOS]
|
Letcher et al. (2009)
|
19
|
76
|
328.15-343.15
|
GLC
|
Appendix B: Structure of ionic liquids
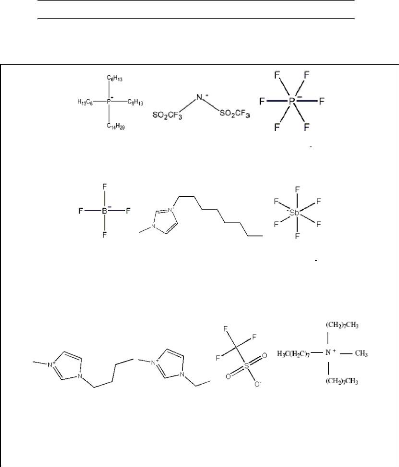
APPENDIX B: STRUCTURE OF IONIC LIQUIDS
[3C6C14P]+ [Tf2N] - [PF6]
[BF4]- [OMIM] + [SbF6]
[BMIM]+ [EMIM] + [TfO] - [C83C1N] +
Figure B-1: Ions present in the structure of
ionic liquids used in this work.
Appendix C: Origin and purity of chemicals
APPENDIX C: ORIGIN AND PURITY OF CHEMICALS
Table C-1: Origin and Stated purity of solutes
and solvents.
|
Compound
|
Origin
|
Stated purity (Mass %)
|
|
[3C6C14P] [Tf2N]
|
Cytec
|
= 0.98
|
|
[3C6C14P] [BF4]
|
Cytec
|
= 0.98
|
|
[3C6C14P] [PF6]
|
Cytec
|
= 0.98
|
|
[3C8C1N] [Tf2N]
|
Solvent innovation
|
0.98
|
|
[BMIM] [SbF6]
|
Capital Lab
|
= 0.98
|
|
[EMIM] TfO]
|
Capital Lab
|
= 0.98
|
|
[MOIM] [PF6]
|
Capital Lab
|
= 0.95
|
|
NMP
|
Merck
|
= 0.98
|
|
n-hexadecane
|
Acros
|
0.99
|
|
n-alkanes (C5 to C12)
|
Capital Lab
|
= 0.98
|
|
Alk-1-enes (C5 to C12)
|
Capital Lab
|
= 0.98
|
|
Alk-1-ynes (C5 to C12)
|
Capital Lab
|
= 0.98
|
|
Cycloalkanes (C5 to C10)
|
Capital Lab
|
= 0.98
|
|
n-alkanols (C1 to C4)
|
Capital Lab
|
= 0.98
|
|
Alkylbenzenes (C6 to C9)
|
Capital Lab
|
= 0.98
|
|
Ket-2-ones (C3 to C4)
|
Capital Lab
|
= 0.98
|
Table C-2: Densities of solvents after
purification at different temperatures-Accuracy: #177; 0.4
%.;*Interpolated
value;# Extrapolated data aFrom Rodriguez and Brennecke
(2006); b From
Pereiro et al. (2007); c From Kneisl
and Zondlo, (1987); d From Khasanshin et al (2009).
|
Solvents
|
293.15 K
|
303.15 K
|
313.15 K
|
323.15 K
|
333.15 K
|
Literature Data at
293.15 K
|
|
[3C6C14P] [Tf2N]
|
1.068870
|
1.062387
|
1.056497
|
1.051422
|
1.047132
|
|
|
[3C6C14P] [BF4]
|
-
|
-
|
-
|
0.925100
|
-
|
|
|
[3C6C14P] [PF6]
|
-
|
-
|
-
|
0.987150
|
-
|
|
|
[3C8C1N] [Tf2N]
|
1.112700
|
-
|
-
|
-
|
-
|
|
|
[BMIM] [SbF6]
|
1.694300
|
-
|
-
|
-
|
-
|
|
|
[EMIM] TfO]
|
1.387070
|
1.375511
|
1.369032
|
1.363705
|
1.359564
|
1.387392a*
|
|
[MOIM] [PF6]
|
1.238510
|
-
|
-
|
-
|
-
|
1.23957b
|
|
NMP
|
-
|
1.025173
|
1.017633
|
1.010888
|
1.004919
|
1.032313c#
|
|
n-hexadecane
|
0.770522
|
-
|
-
|
-
|
-
|
0.77418d#
|
Table C-3: Refractive indices of solvents
after purification at 293.15 K. #Extrapolated
data;
aMehra, (2003); bFrom
www.haochem.com?; cFrom
Pereiro et al. (2007).
|
Solvents
|
Refractive index
|
Literature Data
|
|
[3C6C14P] [Tf2N]
|
1.45069
|
|
|
[3C8C1N] [Tf2N]
|
-
|
|
|
[BMIM] [SbF6]
|
1.41568
|
|
|
[EMIM] TfO]
|
1.43434
|
|
|
[MOIM] [PF6]
|
1.42430
|
1.42440c
|
|
NMP
|
1.47047
|
1.465-1.470b
|
|
n-Hexadecane
|
1.43463
|
1.4356a#
|
Appendix D: Fugacities, critical data and ionization
energies
APPENDIX D: FUGACITIES, CRITICAL DATA AND
IONIZATION
ENERGIES
Table D-1: Saturation fugacity coefficients of
selected solutes at different temperatures
determined from second virial
coefficients (Smith et al (2005).
|
Solutes
|
303.15 K
|
313.15 K
|
323.15 K
|
|
n-hexane
|
0.982
|
0.977
|
0.970
|
|
Hex-1-ene
|
0.981
|
0.974
|
0.967
|
|
Cyclohexane
|
0.988
|
0.983
|
0.978
|
|
Methanol
|
0.997
|
0.995
|
0.993
|
|
Benzene
|
0.989
|
0.986
|
0.981
|
|
Acetone
|
0.988
|
0.984
|
0.980
|
Table D-2: Critical volumes, critical
temperatures,and ionization energies, IC of the
solutes and the carrier gas used in the calculation of the
virial coefficients. (Reference: CRC
Handbook of Chemistry and Physics).
|
Solute
|
TC /K
|
VC/
cm3.mol-1
|
IC/ kJ.mol-1
|
|
n-pentane
|
469.7
|
304
|
998.62
|
|
n-hexane
|
507.4
|
370
|
977.39
|
|
n-heptane
|
540.3
|
432
|
957.13
|
|
n-octane
|
568.8
|
492
|
947.48
|
|
n-nonane
|
594.7
|
555.2
|
937.83
|
|
Pent-1-ene
|
464.7
|
300
|
917.57
|
|
Hex-1-ene
|
504
|
350
|
910.82
|
|
Hept-1-ene
|
537.2
|
405
|
910.82
|
|
Oct-1-ene
|
566.6
|
464
|
909.85
|
|
Pent-1-yne
|
493.4
|
278
|
969.67
|
|
Hex-1-yne
|
539.29
|
331
|
960.02
|
|
Hept-1-yne
|
551.621
|
376.53
|
960.02
|
|
Oct-1-yne
|
598.46
|
441
|
960.02
|
|
Nony-1-ne
|
611
|
513.3
|
955.20
|
|
Cyclopentane
|
511.7
|
259
|
1014.05
|
|
Cyclohexane
|
553.8
|
308
|
951.34
|
|
Cycloheptane
|
604.2
|
353
|
961.95
|
|
Cyclooctane
|
647.2
|
410
|
941.69
|
|
Methanol
|
512.6
|
118
|
1046.86
|
|
Ethanol
|
516.2
|
167
|
1010.20
|
|
Propan-1-ol
|
536.7
|
218.5
|
986.07
|
|
Butan-1-ol
|
562.9
|
274
|
970.64
|
|
Benzene
|
562.1
|
259
|
892.10
|
|
Toluene
|
591.7
|
316
|
851.00
|
|
Acetone
|
508.1
|
209
|
935.90
|
|
Butan-2-one
|
535.6
|
267
|
918.54
|
|
Helium
|
5.2
|
57.5
|
2372.56
|
Appendix E: Calibration data
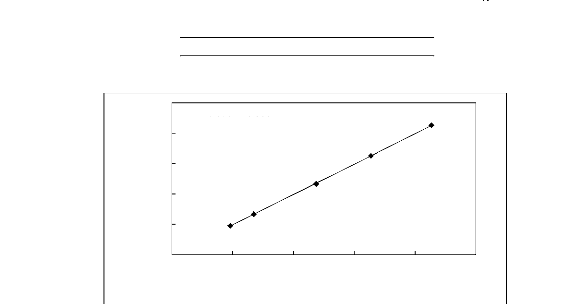
APPENDIX E: CALIBRATION DATA
y = 1.001x - 0.229
R2 = 0.999
20 30 40 50 60 70
Display Temperature, (oC)
70
Actual Temperature, (°C)
60
50
40
30
20
Figure E-1: Temperature calibration curve for
the dilutor cell Pt 100.
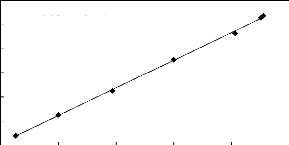
y = 1.149x + 3.572
R2 = 0.999
84 86 88 90 92 94
Display Pressure (kPa)
112
Actual Temperature (kPa)
110
108
106
104
102
100
Figure E-2: Pressure calibration curve for the
dilutor cell pressure transducer.
Appendix F: Selectivities and capacities
APPENDIX F: SELECTIVITIES AND CAPACITIES
Table F-1: Infinite dilution selectivity and
capacity data at 313.15 K for FIL`s and selected industrial solvents
investigated in the literature (Subscripts are references given in Chapter 6)
as well as in this work*; #Data obtained at 298.15
K.
Butan-2-one (2)
Benzene (2)
Hex-1-ene (2)
Acetone (2)
Hexane (1)
/benzene (2)
Cyclohexale
(1 )/benzene (2)
Methanol (1) /benzene (2)
Benzene (1)
/butan-2-one (2)
Hexane (1)
/he(-1-ene (2)
Methanol (1) /acetone (2)
Ethanol (1)
/butan-2-one (2)
Limiting Selectivity Limiting Capacity
|
[EMIM][BF4][1][2]
|
38.65
|
20.06
|
0.17
|
1.54
|
2.02
|
0.39
|
0.47
|
0.41
|
0.02
|
0.91
|
0.62
|
|
[EMIM] [Tf2N] [3][4][5]
|
21.12
|
9.75
|
1.08
|
2.40
|
2.08
|
3.17
|
3.54
|
0.83
|
0.08
|
2.44
|
2.00
|
|
[MMIM] [Tf2N] [4]
|
27.26
|
15.48
|
-
|
-
|
2.24
|
-
|
-
|
0.74
|
0.06
|
-
|
-
|
|
[BMIM][BF4][2][6][7]
|
23.84
|
12.53
|
0.52
|
1.51
|
1.70
|
1.23
|
0.87
|
0.41
|
0.03
|
0.98
|
0.63
|
|
[BMIM] [Tf2N] [4][8]
|
15.13
|
9.16
|
1.23
|
-
|
1.89
|
2.97
|
-
|
1.12
|
0.14
|
2.70
|
-
|
|
[BMIM][TfO][9]
|
23.04
|
10.66
|
0.44
|
-
|
2.23
|
0.79
|
-
|
0.63
|
0.06
|
1.13
|
-
|
|
[DMPIM][BF4][10][11]
|
70.40
|
31.77
|
0.24
|
-
|
-
|
0.34
|
-
|
0.28
|
-
|
0.40
|
-
|
|
[EDMIM] [Tf2N] [3]
|
23.03
|
13.22
|
1.33
|
1.92
|
2.07
|
3.56
|
3.58
|
0.91
|
0.08
|
2.44
|
1.75
|
|
[HMIM][BF4][2][12]
|
19.53
|
5.61
|
0.41
|
1.49
|
2.00
|
0.82
|
1.42
|
0.61
|
0.11
|
1.22
|
0.91
|
|
[HMIM][PF6][13]
|
18.46
|
10.19
|
1.54
|
-
|
2.11
|
-
|
-
|
0.96
|
0.11
|
-
|
-
|
|
[HMIM] [Tf2N] [14][15][16]
|
11.22
|
6.70
|
1.65
|
1.64
|
1.69
|
3.54
|
3.50
|
1.46
|
0.22
|
3.13
|
2.38
|
|
[MOIM][BF4][17]
|
10.01
|
7.04
|
0.83
|
1.17
|
1.71
|
1.29
|
1.48
|
0.85
|
0.15
|
1.33
|
1.00
|
|
[MOIM] [Tf2N] [16]
|
7.89
|
5.52
|
1.75
|
-
|
1.57
|
-
|
-
|
1.54
|
0.31
|
-
|
-
|
|
[C16MIM][BF4][18]
|
3.10
|
2.13
|
1.52
|
0.76
|
1.35
|
1.29
|
1.47
|
1.27
|
0.55
|
1.08
|
0.96
|
|
[3C6C14P][BF4]*
|
3.41
|
2.38
|
1.31
|
0.92
|
1.26
|
1.25
|
1.30
|
2.44
|
0.90
|
2.32
|
2.25
|
|
[3C6C14P] [Tf2N]*
|
2.80
|
2.03
|
2.77
|
1.23
|
1.21
|
3.80
|
4.00
|
2.56
|
1.10
|
3.51
|
3.15
|
|
[3C6C14P][(C2F5)3PF3][20]
|
3.25
|
2.40
|
5.83
|
-
|
1.23
|
-
|
-
|
5.00
|
1.89
|
-
|
-
|
|
[3C1C4N] [Tf2N] [21]
|
13.94
|
0.58
|
1.07
|
-
|
1.89
|
3.38
|
-
|
0.75
|
0.10
|
2.38
|
-
|
|
[BMPy][BF4][22][23]
|
36.88
|
17.71
|
0.66
|
1.66
|
-
|
1.52
|
1.78
|
0.61
|
-
|
1.41
|
1.01
|
|
[BMPyrr] [Tf2N] [16]
|
15.47
|
-
|
-
|
1.62
|
1.92
|
-
|
3.26
|
1.16
|
0.14
|
-
|
1.89
|
|
[Et3S] [Tf2N] [24]
|
22.71
|
12.76
|
1.28
|
-
|
2.17
|
-
|
-
|
0.90
|
0.09
|
-
|
-
|
|
[Epy] [Tf2N] [25][26]
|
24.38
|
14.31
|
0.95
|
2.00
|
2.33
|
2.62
|
2.65
|
0.77
|
0.07
|
2.13
|
1.54
|
|
[3C6C14P][PF6]*
|
2.96
|
2.15
|
3.12
|
0.97
|
1.20
|
3.17
|
3.21
|
1.47
|
0.59
|
1.49
|
1.42
|
|
[C13C8N] [Tf2N] [27]*
|
3.77
|
2.70
|
2.68
|
1.22
|
1.33
|
3.11
|
3.44
|
2.27
|
0.80
|
2.63
|
2.78
|
|
[EMIM][TfO][28]*
|
30.20
|
15.19
|
0.33
|
-
|
2.31
|
-
|
-
|
0.45
|
0.03
|
-
|
-
|
|
[MOIM][PF6][29]*
|
11.27
|
7.03
|
1.88
|
-
|
1.72
|
-
|
-
|
1.04
|
0.16
|
-
|
-
|
|
[BMIM][SbF6][30]*
|
22.25
|
12.52
|
1.41
|
1.98
|
2.08
|
4.26
|
3.74
|
0.79
|
0.07
|
2.38
|
1.56
|
|
[BMIM][PF6][31]
|
-
|
-
|
-
|
-
|
3.06
|
3.06
|
-
|
-
|
-
|
1.41
|
1.01
|
|
[EMIM][TFA][32]
|
27.03
|
12.97
|
0.08
|
-
|
2.34
|
-
|
-
|
0.36
|
0.03
|
-
|
-
|
|
[HMIM][TfO][33]
|
14.37
|
7.37
|
-
|
-
|
-
|
-
|
-
|
0.68
|
-
|
-
|
-
|
|
[BMPyrr][TfO][34]
|
-
|
-
|
-
|
2.45
|
-
|
-
|
-
|
-
|
0.05
|
-
|
-
|
|
[HMPyrr] [Tf2N] [35]
|
-
|
-
|
-
|
1.70
|
-
|
-
|
-
|
-
|
0.22
|
-
|
-
|
|
[OMPyrr] [Tf2N] [35]
|
-
|
-
|
-
|
1.53
|
-
|
-
|
-
|
-
|
0.30
|
-
|
-
|
|
Sulfolane[36]
|
18.17
|
9.81
|
0.91
|
1.20
|
-
|
1.38
|
1.52
|
0.43
|
-
|
0.64
|
0.51
|
|
NMP[37]
|
11.24
|
7.05
|
-
|
-
|
0.53
|
-
|
-
|
0.95
|
0.16
|
-
|
-
|
|
Chlorobenzene[38][39]
|
-
|
-
|
-
|
-
|
-
|
0.17*
|
8.29
|
-
|
-
|
-
|
0.47
|
|
Dimethylsulfoxide[38][39]
|
-
|
-
|
-
|
-
|
-
|
0.35*
|
0.20*
|
-
|
-
|
0.38*
|
0.35*
|
Appendix G: Effect of structure on infinite dilution activity
coefficient values
APPENDIX G: EFFECT OF STRUCTURE ON IDAC VALUES
1. Infinite dilution activity coefficients of alkanes in
fluorinated ionic liquids.
1.1. Infinite dilution activity coefficients of alkanes
in imidazolium-based fluorinated ionic liquids.
1.1.1. Effect of the cation
|
1n(L413)
|
7 6 5 4
3 2 1 0
|
|
[EMIM] [BF4] [1] ? [BMIM] [BF4] [6]
[MMPIM] [BF4] [10]
[HMIM] [BF4] [12] ? [MOIM] [BF4] [17] O
[C16MIM] [BF4] [18]
|
4 5 6 7 8 9
Nc
Figure G-1: Plots of versus Nc for alkanes in
imidazolium-based FILs comprising [BF4] -
ion.
|
lii(LP13)
|
4.5
4
3.5
3
2.5
2
1.5
1
|
|
[EMIM] [Tf2N] [3]
[MMIM] [Tf2N] [4] ? [BMIM] [Tf2N] [4]
O [EMMIM] [Tf2N] [3] ? [HMIM] [Tf2N] [14]
[OMIM] [Tf2N] [16]
|
|
4 5 6 7 8 9
|
|
Nc
Figure G-2: Plots of versus Nc for alkanes in
imidazolium-based FILs comprising [Tf2N]-
ion.
1n(L13)
|
3.5
3
2.5
2
|
|
[HMIM] [PF6] [13] ? [OMIM] [PF6] [29]
|
|
4 5 6 7 8 9
Nc
Figure G-3: Plots of versus Nc for alkanes in
imidazolium-based FILs comprising [PF6] -
ion.
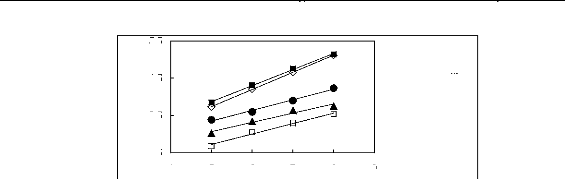
5.5
4.5
3.5
2.5
1n(L413)
? [BMIM] [TfO] [9] [EMIM] [TfO] [28] ?
[BMIM] [SbF6] [30] [EMIM] [TFA] [32]
4 5 6 7 8 9
Nc
Figure G4: Plots of versus Nc for alkanes in
imidazolium-based FILs comprising [TfO]-,
[SbF6] - and [TFA]- ions.
1.1.2. Effect of the anion
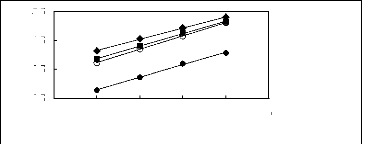
[EMIM] [BF4] [1] ? [EMIM] [Tf2N][3] O
[EMIM] [TfO] [28] [EMIM] [TFA] [32]
1n(L13)
4.5
3.5
2.5
5.5
4 5 6 7 8 9
Nc
Figure G-5: Plots of versus Nc for alkanes in
imidazolium-based FILs comprising
[EMIM] + ion.
|
1n(L13)
|
5 4 3 2
|
|
[BMIM] [BF4] [6] ? [BMIM] [Tf2N][4]
[BMIM] [TfO] [9] ? [BMIM] [SbF6] [30]
|
|
4 5 6 7 8 9
|
|
Nc
Figure G-6: Plots of versus Nc for alkanes in
imidazolium-based FILs comprising
[BMIM] + ion.
Appendix G: Effect of structure on infinite dilution activity
coefficient values
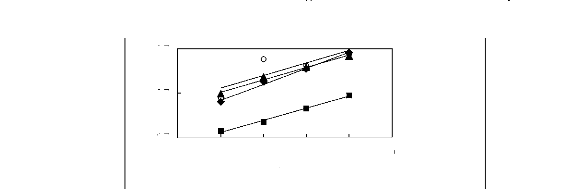
3.7
2.7
1.7
Nc
1n(L113)
4 5 6 7 8 9
O [HMIM] [BF4] [12]
· [HMIM] [PF6] [13]
· [HMIM] [Tf2N][14] ? [HMIM] [TfO]
[33]
Figure G-7: Plots of versus Nc for alkanes in
imidazolium-based FILs comprising
[HMIM] + ion.
1n(L13)
|
3.2
2.2
1.2
|
|
? [OMIM] [BF4] [17]
· [OMIM] [Tf2N][16] n [OMIM] [PF6]
[29]
|
|
|
|
|
Nc
Figure G-8: Plots of versus Nc for alkanes in
imidazolium-based FILs comprising
[MOIM] + ion.
[20]
1.2. Infinite dilution activity coefficients of alkanes
in phosphonium-based FILs
· [3C6C14P] [BF4] [19] ? [3C6C14P] [Tf2N]
[19]
· [3C6C14P] [(C2F5)3PF3]
· [3C6C14P] [PF6] [19]
|
1n(L413)
|
1.2
0.8
0.4
0 -0.4 -0.8
|
|
4 5 6 Nc 7 8 9
Figure G-9: Plots of versus Nc for alkanes in
phosphonium-based FILs comprising
[3C6C14P] + ion.
Appendix G: Effect of structure on infinite dilution activity
coefficient values
1.3. Infinite dilution activity coefficients of alkanes
in ammonium-based FILs
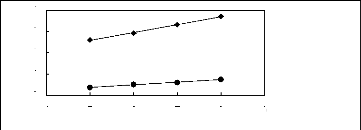
4
3
2
1n(L413)
[3C1C4N] [Tf2N] [21] ? [3C8C1N] [Tf2N]
[27]
1
0
4 5 6 7 8 9
Nc
Figure G-10: Plots of versus Nc for alkanes in
ammonium-based FILs comprising
[Tf2N] - ion.
1.4. Infinite dilution activity coefficients of alkanes
in pyridinium-based FILs
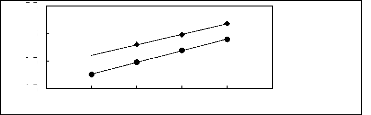
[BMPy] [BF4] [22] ? [EPy] [BTI] [25]
lii(LP13)
4.5
2.5
5.5
3.5
4 5 6 7 8 9
Nc
Figure G-11: Plots of versus Nc for alkanes in
pyridinium-based FILs.
1.5. Infinite dilution activity coefficients of alkanes
in pyrrolidinium-based FILs 1.5.1. Effect of the cation
1n(L413)
|
3.2 2.7 2.2 1.7 1.2
|
|
[BMPyrr] [Tf2N] [16]
[HMPyrr] [Tf2N] [35] O [MOPyrr] [Tf2N]
[35]
|
|
|
|
|
Nc
Figure G-12: Plots of versus Nc for alkanes in
pyrrolidinium-based FILs comprising
[Tf2N] - ion.
1.5.2. Effect of the anion
1n(L13)
|
4.2 3.2 2.2 1.2
|
|
[BMPyrr] [Tf2N] [16] ? [BMPyrr] [TfO]
[34]
|
|
4 5 6 7 8 9
Nc
Figure G-13: Plots of versus Nc for alkanes in
pyrrolidinium-based FILs comprising
[BMPyrr] + ion.
1.6. Infinite dilution activity coefficients of alkanes
in sulfonium-based FILs
4 5 6 7 8 9
Nc
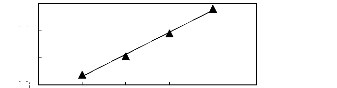
? [Et3S] [Tf2N] [24]
1n(L13)
3.6
3.2
2.8
4
Figure G-14: Plot of versus Nc for alkanes in
the sulfonium-based FIL [Et3S] [Tf2N].
2. Infinite dilution activity coefficients of alk-1-enes
in fluorinated ionic liquids. 2.1. Infinite dilution activity coefficients of
alk-1-enes in imidazolium-based FILs 2.1.1. Effect of the cation
1n(L13)
|
4
3.5
3
2.5
2
1.5
|
|
[EMIM] [BF4] [2] ? [BMIM] [BF4] [2] ?
[HMIM] [BF4] [12] [MOIM] [BF4] [17]
|
|
|
|
|
Nc
Figure G-15: Plots of versus Nc for alk-1-enes
in imidazolium-based FILs comprising
[BF4]- ion.
Appendix G: Effect of structure on infinite dilution
activity coefficient values
1n(L413)
|
4.5 3.5 2.5 1.5 0.5
|
|
O [EMIM] [Tf2N] [4] ? [MMIM] [Tf2N] [4]
[BMIM] [Tf2N] [4] + [EMMIM] [Tf2N]
[3] [HMIM] [Tf2N] [14] ? [MOIM] [Tf2N]
[16]
|
|
|
|
|
Nc
Figure C-16: Plots of versus Nc for alk-1-enes
in imidazolium-based FILs comprising
[Tf2N]- ion.
4 5 6 7 8 9
Nc
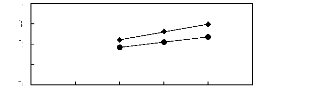
[HMIM] [PF6] [13] ? [MOIM] [PF6] [29]
lii(LP13)
4
2
3
0
1
Figure C-17: Plots of versus Nc for alk-1-enes
in imidazolium-based FILs comprising
[PF6]- ion.
4 5 6 7 8 9
Nc
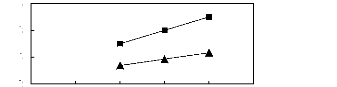
[EMIM] [TfO] [28] ? [BMIM] [TfO] [9]
1n(L13)
4
2
6
8
Figure C-18: Plots of versus Nc for alk-1-enes
in imidazolium-based FILs comprising
[TfO]- ion.
2.1.2. Effect of the anion
1n(L13)
|
4.5
3
1.5
|
|
· [EMIM] [BF4] [2] n [EMIM] [Tf2N]
[4] O [EMIM] [TfO] [28] A [EMIM] [TFA] [32]
|
|
|
|
|
Nc
Figure G-19: Plots of versus Nc for alk-1-enes
in imidazolium-based FILs comprising
[EMIM] + ion.
|
5
4 3 2 1 0
|
|
|
1n(L113)
|
|
· [BMIM] [BF4] [2] A [BMIM] [Tf2N]
[4]
· [BMIM] [TfO] [9] O [BMIM] [SbF6]
[30]
|
|
|
|
|
4 5 6 7 8 9
Nc
Figure G-20: Plots of versus Nc for alk-1-enes
in imidazolium-based FILs comprising
[BMIM] + ion.
ln(L413)
|
2.8 2.3 1.8 1.3 0.8
|
|
A [HMIM] [BF4] [12]
O [HMIM] [PF6]
[13]
· [HMIM] [Tf2N] [14]
|
|
4 5 6 7 8 9
Nc
Figure G-21: Plots of versus Nc for alk-1-enes
in imidazolium-based FILs comprising
[HMIM] + ion.
Appendix G: Effect of structure on infinite dilution
activity coefficient values
1n(L413)
|
2.8 2.3 1.8 1.3 0.8
|
|
· [MOIM] [BF4] [17] ? [MOIM] [Tf2N]
[16]
· [MOIM] [PF6] [29]
|
|
|
|
|
Nc
Figure G-22: Plots of versus Nc for alk-1-enes
in imidazolium-based FILs comprising
[MOIM] + ion.
2.2. Infinite dilution activity coefficients of
alk-1-enes in phosphonium-based FILs
Ini3)
|
1.2 0.7 0.2 -0.3 -0.8
|
|
· [3C6C14P] [BF4] [19]
· [3C6C14P] [Tf2N] [19]
· [3C6C14P] [(C2F5)3PF3] [20] ? [3C6C14P] [PF6]
[19]
|
|
|
|
|
Nc
Figure G-23: Plots of versus Nc for alk-1-enes
in phosphonium-based FILs comprising
[3C6C14P] + ion.
2.3. Infinite dilution activity coefficients of
alk-1-enes in ammonium-based FILs
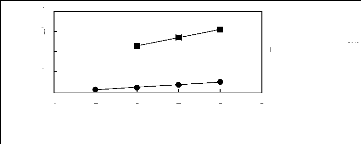
1n(L13)
4
2
3
0
1
4 5 6 7 8 9
Nc
· [3C1C4N] [Tf2N] [21]
· [3C8C1N] [Tf2N] [27]
Figure G-24: Plots of versus Nc for alk-1-enes
in ammonium-based FILs comprising
[Tf2N] ion.
2.4. Infinite dilution activity coefficients of
alk-1-enes in pyridinium-based FILs
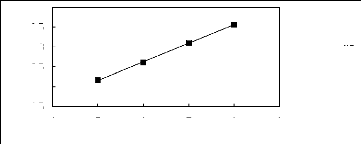
4 5 6 7 8 9
Nc
. [EPy] [Tf2N] [25]
1n(L113)
2.5
3.5
1.5
4
2
3
Figure G-25: Plot of versus Nc for alk-1-enes in
the pyridinium-based Fl L [Epy] [Tf2N].
2.5. Infinite dilution activity coefficients of
alk-1-enes in pyrrolidinium-based FILs 2.5.1. Effect of the cation
1n(L113)
|
3
2.5
2
1.5
1
0.5
0
|
|
· [BMPyrr] [Tf2N] [16] ? [HMPyrr] [Tf2N]
[35]
· [MOPyrr] [Tf2N] [35]
|
|
4 5 6 7 8 9
Nc
Figure G-26: Plots of versus Nc for alk-1-enes
in pyrrolidinium-based Fl Ls comprising
[Tf2N] - ion.
2.5.2. Effect of the anion
|
1n(L113)
|
4
3
2
1
|
|
· [BMPyrr] [Tf2N] [16]
· [BMPyrr] [TfO] [34]
|
4 5 6 7 8 9
Nc
Figure G-27: Plots of versus Nc for alk-1-enes
in pyrrolidinium-based Fl Ls comprising
[BMPyrr] + ion.
1.2.7. Infinite dilution activity coefficients of
alk-1-enes in sulfonium-based FILs
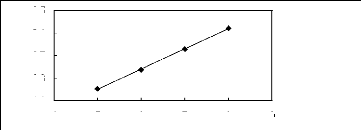
4 5 6 7 8 9
Nc
[Et3S] [Tf2N] [24]
Ini3)
3.5
3.1
2.7
2.3
1.9
Figure G-28: Plot of versus Nc for alk-1-enes in
the sulfonium-based FIL [Et3S] [Tf2N].
3. Infinite dilution activity coefficients of alk-1-ynes
in fluorinated ionic liquids. 3.1. Infinite dilution activity coefficients of
alk-1-ynes in imidazolium-based FILs 3.1.1. Effect of the cation
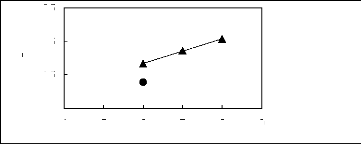
4 5 6 7 8 9
Nc
? [HMIM] [BF4] [12] ? [C16MIM] [BF4]
[18]
ln(L13)
-0.5
2.5
0.5
1.5
Figure G-29: Plots of versus Nc for alk-1-ynes
in imidazolium-based FILs comprising
[BF4] - ion.
|
2
1.5
1
0.5
0
|
|
|
|
in(Li3)
|
|
[HMIM] [PF6] [13]
? [MOIM] [PF6]
[29]
|
|
|
|
4 5 6 7 8 9
Nc
Figure G-30: Plots of versus Nc for alk-1-ynes
in imidazolium-based FILs comprising
[PF6] - ion.
|
1.8
1.4
1 0.6 0.2
|
|
|
|
1n(L113)
|
|
[EMIM] [Tf2N] [5] ? [HMIM] [Tf2N] [15]
|
|
|
|
4 5 6 7 8 9
Nc
Figure G-31: Plots of versus Nc for alk-1-ynes
in imidazolium-based FILs comprising
[Tf2N] - ion.
|
1n(L413)
|
2.5
1.5
0.5
|
|
? [BMIM] [TfO] [9] O [EMIM] [TfO] [28]
|
|
|
|
4 5 6 7 8 9
Nc
Figure G-32: Plots of versus Nc for alk-1-ynes
in imidazolium-based FILs comprising
[TfO] - ion.
3.1.2. Effect of the anion
|
1n(L413)
|
3 2 1 0
|
|
[EMIM] [Tf2N] [5] ? [EMIM] [TfO] [28] O
[EMIM] [TFA] [32]
|
4 5 6 7 8 9
Nc
Figure G-33: Plots of versus Nc for alk-1-ynes
in imidazolium-based FILs comprising
[EMIM] + ion.
Appendix G: Effect of structure on infinite dilution activity
coefficient values
|
2.5
2
1.5
1
0.5
|
|
|
|
1n(L13)
|
|
? [BMIM] [TfO] [9] ? [BMIM] [SbF6] [30]
|
|
|
|
4 5 6 7 8 9
Nc
Figure G-34: Plots of versus Nc for alk-1-ynes
in imidazolium-based FILs comprising
[BMIM] + ion.
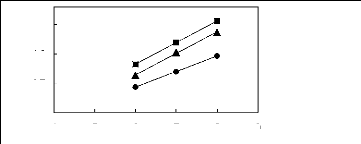
4 5 6 7 8 9
Nc
? [HMIM] [BF4] [12] [HMIM] [PF6] [13] ?
[HMIM] [Tf2N] [15]
in(L13)
0.7
0.2
1.7
1.2
Figure G-35: Plots of versus Nc for alk-1-ynes
in imidazolium-based FILs comprising
[HMIM] + ion.
3.2. Infinite dilution activity coefficients of
alk-1-ynes in phosphonium-based FILs
|
1n( L13)
|
0.4
0
-0.4
-0.8
-1.2
|
|
[3C6C14P] [BF4] [19] ? [3C6C14P] [Tf2N]
[19]
? [3C6C14P] [(C2F5)3PF3] [20] [3C6C14P] [PF6]
[19]
|
4 5 6 7 8 9
Nc
Figure G-36: Plots of versus Nc for alk-1-ynes
in phosphonium-based FILs comprising
[3C6C14P] + ion.
Appendix G: Effect of structure on infinite dilution activity
coefficient values
3.3. Infinite dilution activity coefficients of
alk-1-ynes in ammonium, pyrrolidinium and sulfonium-based FILs
1n(L113)
|
3 2 1 0 -1
|
|
[Et3S] [Tf2N] [24]
? [C13C8N] [Tf2N] [27] ? [BMPyrr] [TfO]
[34]
|
|
4 5 6 7 8 9
Nc
Figure G-37: Plots of versus Nc for alk-1-ynes
in an ammonium, a pyrrolidinium and a
sulfonium-based FILs.
4. Infinite dilution activity coefficients of
cycloalkanes in fluorinated ionic liquids. 4.1. Infinite dilution activity
coefficients of cycloalkanes in imidazolium-based FILs
4.1.1. Effect of the cation
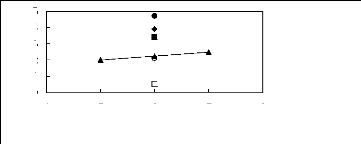
[EMIM] [BF4] [2] [BMIM] [BF4] [6] ?
[MMPIM] [BF4] [10] ? [HMIM] [BF4] [12] O [MOIM] [BF4]
[17] ? [C16MIM] [BF4] [18]
4 5 6 7 8
Nc
1n(L13)
4
2
5
3
0
1
Figure G-38: Plots of versus Nc for cycloalkanes
in imidazolium-based FILs comprising
[BF4]- ion.
|
4.5 3.5 2.5 1.5 0.5
|
|
|
|
1n(L413)
|
|
[EMIM] [Tf2N] [5] ? [MMIM] [Tf2N] [4] ?
[BMIM] [Tf2N] [4]
[EMMIM] [Tf2N] [3] ? [HMIM] [Tf2N]
[15] O [MOIM] [Tf2N] [16]
|
|
|
|
4 5 6 7 8 9
Nc
Figure G-39: Plots of versus Nc for cycloalkanes
in imidazolium-based FILs comprising
[Tf2N] - ion.
Appendix G: Effect of structure on infinite dilution activity
coefficient values
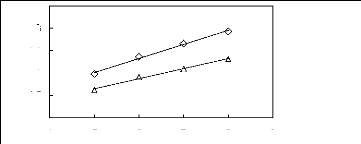
4 5 6 7 8 9
Nc
O [HMIM] [PF6] [13]
A [MOIM] [PF6]
[29]
ln(LI13)
2.5
3.5
1.5
2
3
1
Figure G-40: Plots of versus Nc for cycloalkanes
in imidazolium-based FILs comprising
[PF6] - ion.
1n(L13)
|
4.5
4
3.5
3
2.5
2
|
|
· [BMIM] [TfO] [9] O [BMIM] [TfO]
[28]
· [HMIM] [TfO] [33]
|
|
4 5 6 7 8 9
Nc
Figure G-41: Plots of versus Nc for cycloalkanes
in imidazolium-based FILs comprising
[TfO] - ion.
4.1.2. Effect of the anion
|
ln(LI13)
|
4.5
4
3.5
3
2.5
2
|
|
· [EMIM] [BF4] [2] n [EMIM] [Tf2N]
[5] O [EMMIM] [Tf2N]] [3]
· [EMIM] [TfO] [28] A [EMIM] [TFA]
[32]
|
4 5 6 7 8 9
Nc
Figure G-42: Plots of versus Nc for cycloalkanes
in imidazolium-based FILs comprising
[EMIM] + ion.
Appendix G: Effect of structure on infinite dilution activity
coefficient values
ã 1 3
|
3.7 3.2 2.7 2.2 1.7 1.2
|
|
|
1n(L13)
|
|
[BMIM] [BF4] [6] [BMIM] [Tf2N] [4] O
[BMIM] [TfO] [9] ? [BMIM] [SbF6] [30]
|
|
|
|
|
4 5 6 7 8 9
Nc
Figure G-43: Plots of versus Nc for cycloalkanes
in imidazolium-based FILs comprising
[BMIM] + ion.
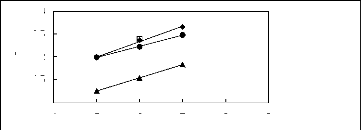
3
2.5
2
1.5
1
in(L13)
? [HMIM] [BF4] [12]
[HMIM] [PF6] [13] ?
[HMIM] [Tf2N] [15] ? [HMIM] [TfO] [33]
4 5 6 7 8 9
Nc
Figure G-44: Plots of versus Nc for cycloalkanes
in imidazolium-based FILs comprising
[HMIM] + ion.
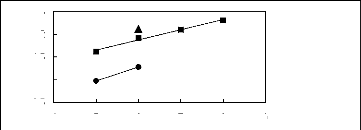
4 5 6 7 8 9
Nc
? [MOIM] [BF4] [17] ? [MOIM] [Tf2N]
[16]
in(L413)
2.5
0.5
1.5
2
1
Figure G-45: Plots of versus Nc for cycloalkanes
in imidazolium-based FILs comprising
[MOIM] + ion.
Appendix G: Effect of structure on infinite dilution
activity coefficient values
4.2. Infinite dilution activity coefficients of
cycloalkanes in phosphonium-based FILs
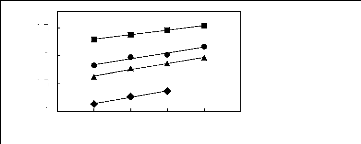
0.5
0
-0.5
-1
1n(L413)
? [3C6C14P] [BF4] [19]
? [3C6C14P] [Tf2N] [19]
[3C6C14P] [(C2F5)3PF3] [20] [3C6C14P] [PF6]
[19]
4 5 6 7 8 9
Nc
Figure G-46: Plots of versus Nc for cycloalkanes
in phosphonium-based FILs
comprising [3C6C14P] + ion.
4.3. Infinite dilution activity coefficients of
cycloalkanes in ammonium-based FILs
|
0.6 0.4 0.2 E-15 -0.2 -0.4 -0.6
|
|
|
-1
ln(i3)
|
|
[3C1C4N] [Tf2N] [21] ? [C13C8N] [Tf2N]
[27]
|
|
|
|
|
4 5 6 7 8 9
Nc
Figure G-47: Plots of versus Nc for cycloalkanes
in ammonium-based FILs comprising
[Tf2N] - ion.
4.4. Infinite dilution activity coefficients of
cycloalkanes in pyridinium-based FILs
|
4
3.5
3
2.5
2
|
|
|
1n(L13)
|
|
[BMPy] [BF4] [22] ? [EPy] [Tf2N] [25]
|
|
|
|
|
4 5 6 7
Nc
Figure G-48: Plots of versus Nc for cycloalkanes
in the pyridinium-based FILs
[Epy] [Tf2N] and [BMPy] [BF4].
Appendix G: Effect of structure on infinite dilution
activity coefficient values
4.5. Infinite dilution activity coefficients of
cycloalkanes in pyrrolidinium-based FILs
|
4
3.5
3
2.5 2 1.5
|
|
|
1n(L13)
|
|
[BMPyrr] [Tf2N] [6] ? [BMPyrr] [TfO]
[34]
|
|
|
|
|
4 5 6 7 8 9
Nc
Figure C-49: Plots of versus Nc for cycloalkanes
in ammonium-based FILs comprising
[BMPyrr] + ion.
4.6. Infinite dilution activity coefficients of
cycloalkanes in sulfonium-based FILs
in(1113)
|
3.2
2.8
2.4
2
|
|
? [Et3S] [Tf2N] [24]
|
|
|
|
|
4 5 6 7 8 9
Nc
Figure C-50: Plots of versus Nc for cycloalkanes
in the sulfonium-based FIL [Et3S]
[Tf2N].
5. Infinite dilution activity coefficients of
alkan-1-ols in fluorinated ionic liquids. 5.1. Infinite dilution activity
coefficients of alkan-1-ols in imidazolium-based FILs 5.1.1. Effect of the
cation
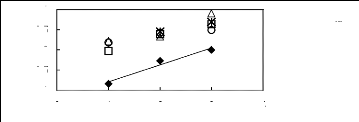
0 1 2 3 4
Nc
[EMIM] [BF4] [2] ? [BMIM] [BF4] [7] *
[HMIM] [BF4] [2] ? [MOIM] [BF4] [17] O [C16MIM] [BF4]
[18]
In(L13)
-0.5
0.5
-1
0
1
Figure C-51: Plots of versus Nc for alkan-1-ols
in imidazolium-based FILs comprising
[BF4]-ion.
Appendix G: Effect of structure on infinite dilution activity
coefficient values
1n(L413)
|
1.2
1 0.8 0.6 0.4 0.2
0
|
|
· [EMIM] [Tf2N] [4] O [BMIM] [Tf2N]
[8]
· [EMMIM] [Tf2N] [3] O [HMIM] [Tf2N]
[16] A [MOIM] [Tf2N] [16]
|
|
|
|
|
Nc
Figure C-52: Plots of versus Nc for alkan-1-ols
in imidazolium-based FILs comprising
[Tf2N]- ion.
1n(L413)
|
1.6
1.4
1.2
1 0.8 0.6 0.4 0.2
0
|
|
· [HMIM] [PF6] [13]
· [MOIM] [PF6] [29]
· [BMIM] [PF6] [31]
|
|
0 1 2 3 4
Nc
Figure C-53: Plots of versus Nc for alkan-1-ols
in imidazolium-based FILs comprising
[PF6]- ion.
0 1 2 3 4
Nc
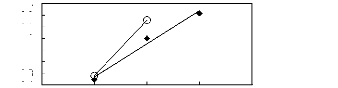
· [BMIM] [TfO] [9] O [EMIM] [TfO]
[28]
1n(L413)
-0.1
-0.2
-0.3
-0.4
0.3
0.2
0.1
0
Figure C-54: Plots of versus Nc for alkan-1-ols
in imidazolium-based FILs comprising
[TfO]- ion.
5.1.2. Effect of the anion
in(L413)
|
1
0.5
0
-0.5
-1
-1.5
-2
|
|
· [EMIM] [BF4] [4] n [EMIM] [Tf2N]
[28]
· [EMIM] [TfO] [32] * [EMIM] [TFA]
[2]
|
|
|
|
|
Nc
Figure C-55: Plots of versus Nc for alkan-1-ols
in imidazolium-based FILs comprising
[EMIM] + ion.
1n(L13)
|
1.5
1
0.5
0
-0.5
|
|
A [BMIM] [BF4] [7] O [BMIM] [Tf2N] [8]
· [BMIM] [TfO] [9]
· [BMIM] [SbF6] [30]
· [BMIM] [PF6] [31]
|
|
|
|
|
Nc
Figure C-56: Plots of versus Nc for alkan-1-ols
in imidazolium-based FILs comprising
[BMIM] + ion
0 1 2 3 4
Nc
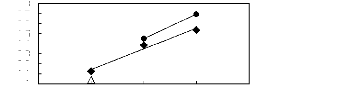
· [HMIM] [BF4] [2] A [HMIM] [PF6]
[13]
· [HMIM] [Tf2N] [16]
in(L413)
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
Figure C-57: Plots of versus Nc for alkan-1-ols
in imidazolium-based FILs comprising
[HMIM] + ion.
Appendix G: Effect of structure on infinite dilution activity
coefficient values
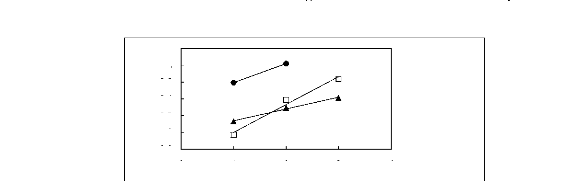
0 1 2 3 4
Nc
n [MOIM] [BF4] [17] ? [MOIM] [Tf2N] [16] .
[MOIM] [PF6] [21]
1
0.8
0.6
1n(L13)
0.4
0.2
0
-0.2
Figure G-58: Plots of versus Nc for alkan-1-ols
in imidazolium-based FILs comprising
[EMIM] + ion.
5.2. Infinite dilution activity coefficients of
alkan-1-ols in phosphonium-based FILs
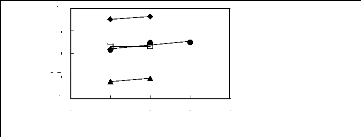
1
0.5
0
-0.5
-1
lii(LP13)
? [3C6C14P] [BF4] [19]
· [3C6C14P] [Tf2N] [19]
n [3C6C14P] [(C2F5)3PF3] [20]
· [3C6C14P] [PF6] [19]
Nc
0 1 2 3 4
Figure G-59: Plots of versus Nc for alkan-1-ols
in phosphonium-based FILs comprising
[3C6C14P] + ion.
5.3. Infinite dilution activity coefficients of
alkan-1-ols in ammonium-based FILs
0 1 2 3 4
Nc
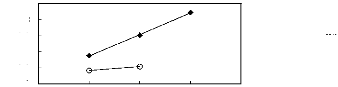
· [3C1C4N] [Tf2N] [21] O [C13C8N] [Tf2N]
[27]
1n(L13)
0.8
0.6
0.4
0.2
0
1
Figure G-60: Plots of versus Nc for alkan-1-ols
in ammonium-based FILs comprising
[Tf2N]- ion.
Appendix G: Effect of structure on infinite dilution activity
coefficient values
5.4. Infinite dilution activity coefficients of
alkan-1-ols in pyridinium-based FILs
0 1 2 3 4
Nc
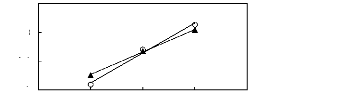
O [BMPy] [BF4] [23] ? [EPy] [Tf2N] [25] [26]
1n(L413)
0.8
0.4
1.2
0
Figure G-61: Plots of versus Nc for alkan-1-ols
in the pyridinium-based FILs
[BMPy] [BF4] and [Epy] [Tf2N].
5.5. Infinite dilution activity coefficients of
alkan-1-ols in pyrrolidinium-based FILs
|
0.6
0.4
|
|
|
|
|
|
|
1n(L113)
|
0.2
0
-0.2
-0.4
-0.6
|
|
[BMPyrr] [Tf2N] [16] ? [BMPyrr] [TfO]
[34]
|
|
|
|
0 1 2 3 4
Nc
Figure G-62: Plots of versus Nc for alkan-1-ols
in pyrrolidinium-based FILs comprising
[BMPyrr] + ion.
5.6. Infinite dilution activity coefficients of
alkan-1-ols in sulfonium-based FILs
|
1
0.5
0
|
|
|
|
1n(L13)
|
|
[Et3S] [Tf2N] [24]
|
|
|
|
0 1 2 3 4
Nc
Figure G-63: Plots of versus Nc for alkan-1-ols
in the sulfonium-based FILs
[Et3S] [Tf2N].
6. Infinite dilution activity coefficients of
alkylbenzenes in fluorinated ionic liquids
6.1. Infinite dilution activity coefficients of
alkylbenzenes in imidazolium-based FILs 6.1.1. Effect of the cation
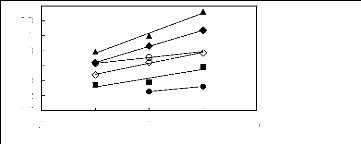
2.8
2.3
1.8
1.3
0.8
0.3
-0.2
-0.7
lii(LP13)
· [EMIM] [BF4] [2] O [BMIM] [BF4] [2]
A [MMPIM] [BF4] [10] O [HMIM] [BF4] [2]
· [MOIM] [BF4] [17]
· [C16MIM] [BF4] [18]
5 6 7 8 9
Nc
Figure G-64: Plots of versus Nc for
alkylbenzenes in imidazolium-based FILs
comprising [BF4]- ion.
ln(L13)
|
1.3 0.8 0.3 -0.2 -0.7
|
|
· [EMIM] [Tf2N] [4] A [MMIM] [Tf2N]
[4] A [BMIM] [Tf2N] [8] O [EMMIM] [Tf2N]
[3]
· [HMIM] [Tf2N] [16]
· [MOIM] [Tf2N] [16]
|
|
|
|
|
Nc
Figure G-65: Plots of versus Nc for
alkylbenzenes in imidazolium-based FILs
comprising [Tf2N]- ion.
5 6 7 8 9
Nc
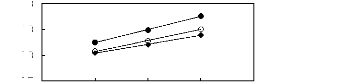
O [BMIM] [TfO] [9]
· [EMIM] [TfO] [28]
· [HMIM] [TfO] [33]
ln(L413)
-0.7
2.3
0.3
1.3
Figure G-66: Plots of versus Nc for
alkylbenzenes in imidazolium-based FILs
comprising [TfO]- ion.
6.1.2. Effect of the anion
5 6 7 8 9
Nc
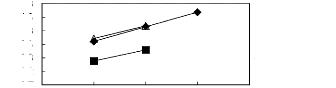
· [EMIM] [BF4] [2]
· [EMIM] [Tf2N] [4] A [EMIM] [TFA]
[32]
1n(L13)
-0.2
-0.7
2.3
0.8
0.3
1.8
1.3
Figure C-67: Plots of versus Nc for
alkylbenzenes in imidazolium-based FILs
comprising [EMIM] + ion.
|
1.8 1.3 0.8 0.3 -0.2 -0.7
|
|
|
|
ln(L13)
|
|
n [BMIM] [BF4] [2] * [BMIM] [Tf2N] [8] O
[BMIM] [TfO] [9] A [BMIM] [SbF6] [30]
|
|
|
|
5 6 7 8 9
Nc
Figure C-68: Plots of versus Nc for
alkylbenzenes in imidazolium-based FILs
comprising [BMIM] + ion.
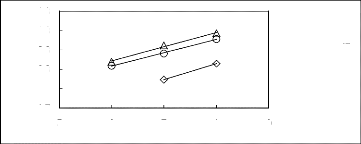
5 6 7 8 9
Nc
A [HMIM] [BF4] [2] O [HMIM] [Tf2N] [16]
O[HMIM] [TfO] [33]
ln(L113)
-0.2
-0.7
0.8
0.3
1.8
1.3
Figure C-69: Plots of versus Nc for
alkylbenzenes in imidazolium-based FILs
comprising [HMIM] + ion.
5 6 7 8 9
Nc
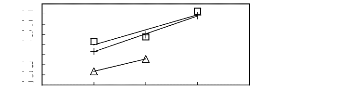
? [MOIM] [BF4] [17] ? [MOIM] [Tf2N] [16]
+ [MOIM] [PF6] [29]
0.9
0.7
0.5
1n(L413)
0.3
0.1
-0.1
-0.3
-0.5
-0.7
Figure G-70: Plots of versus Nc for
alkylbenzenes in imidazolium-based FILs
comprising [MOIM] + ion.
6.2. Infinite dilution activity coefficients of
alkylbenzenes in phosphonium-based FILs
[3C6C14P] [BF4] [19] O [3C6C14P] [Tf2N]
[19] ? [3C6C14P] [(C2F5)3PF3] [20] [3C6C14P] [PF6]
[19]
5 6 7 8 9
Nc
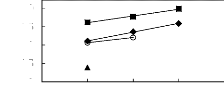
1n(L13)
-0.5
-1.5
-1
-2
0
Figure G-71: Plots of versus Nc for
alkylbenzenes in phosphonium-based FILs
comprising [3C6C14P]+ ion.
6.3. Infinite dilution activity coefficients of
alkylbenzenes in ammonium-based FILs
5 6 7 8 9
Nc
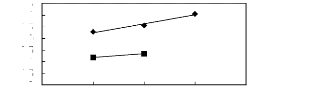
[3C1C4N] [BTI] [21] [C13C8N] [BTI]
[27]
1n(L13)
-0.5
-1.5
0.5
1.5
-1
-2
0
1
Figure G-72: Plots of versus Nc for
alkylbenzenes in ammonium-based FILs comprising
[Tf2N]- ion.
6.4. Infinite dilution activity coefficients of
alkylbenzenes in pyridinium-based FILs
|
1.1 0.9 0.7 0.5 0.3 0.1 -0.1 -0.3 -0.5
|
|
|
|
In(L13)
|
|
? [BMPy] [BF4] [22] ? [EPy] [Tf2N] [25]
|
|
|
|
5 6 7 8
Nc
Figure G-73: Plots of versus Nc for
alkylbenzenes in the pyridinium-based FILs
[BMPy] [BF4] and [Epy] [Tf2N].
6.5. Infinite dilution activity coefficients of
alkylbenzenes in pyrrolidinium and sulfoniumbased FILs
|
2
1
0
-1
-2
|
|
|
|
lii(L113)
|
|
[BMPyrr] [Tf2N] [16] [Et3S] [Tf2N]
[24]
|
|
|
|
5 6 7 8 9
Nc
Figure G-74: Plots of versus Nc for
alkylbenzenes in [BMPyrr] [Tf2N] and [Et3S] [Tf2N].
7. Infinite dilution activity coefficients of ket-2-ones
in fluorinated ionic liquids 7.1. Infinite dilution activity coefficients of
ket-2-ones in imidazolium-based FILs 7.1.1. Effect of the cation
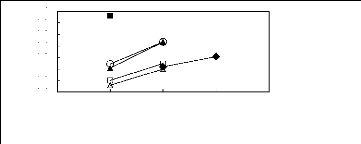
O [EMIM] [BF4] [2]
A [BMIM] [BF4]
[2]
· [MMPIM] [BF4] [11] n [HMIM] [BF4]
[2] A [MOIM] [BF4] [17]
· [C16MIM] [BF4] [18]
2 3 4 5 6
Nc
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
1n(L13)
Figure C-75: Plots of versus Nc for ket-2-ones
in imidazolium-based FILs comprising
[BF4] - ion.
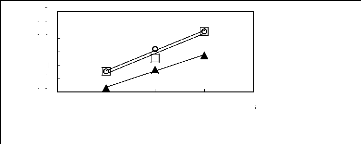
1n( L13)
-0.2
-0.4
-0.6
-0.8
-1.2
-1
0
2 3 4 5 6
Nc
n [EMIM] [[Tf2N]] [4] O [EMMIM] [Tf2N]
[3] A [HMIM] [Tf2N] [16]
Figure C-76: Plots of versus Nc for ket-2-ones
in imidazolium-based FILs comprising
[Tf2N] - ion.
7.1.2. Effect of the anion
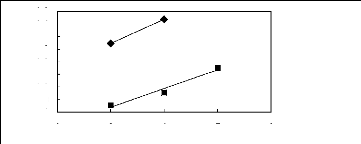
2 3 4 5 6
Nc
· [EMIM] [BF4] [2]
· [EMIM] [Tf2N] [4]
1n( L13)
-0.2
-0.4
-0.6
-0.8
0.6
0.4
0.2
-1
0
Figure C-77: Plots of versus Nc for ket-2-ones
in imidazolium-based FILs comprising
[EMIM] + ion.
Appendix G: Effect of structure on infinite dilution activity
coefficient values
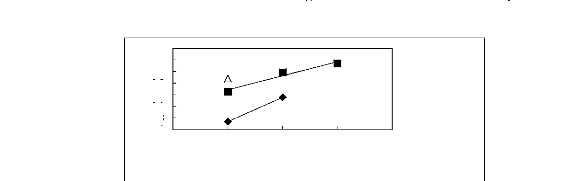
0.4
0.2
0
ln(LI13)
-0.2
-0.4
-0.6
-0.8
-1
A [BMIM] [TfO] [9] O [BMIM] [SbF6] [30]
· [BMIM] [PF6] [31]
2 3 4 5 6
Nc
Figure G-78: Plots of versus Nc for ket-2-ones
in imidazolium-based FILs comprising
[BMIM] + ion.
2 3 4 5 6
Nc
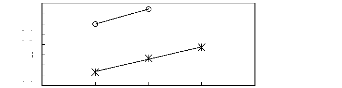
O [HMIM] [BF4] [17] * [HMIM] [Tf2N] [16]
1n(L13)
-0.2
-0.4
-0.6
-0.8
-1.2
-1.4
0.2
-1
0
Figure G-79: Plots of versus Nc for ket-2-ones
in imidazolium-based FILs comprising
[HMIM] + ion.
7.2. Infinite dilution activity coefficients of
ket-2-ones in phosphonium-based FILs
1n(L413)
|
0 -0.2 -0.4 -0.6 -0.8
-1 -1.2 -1.4
|
|
· [3C6C14P] [BF4] [19] A [3C6C14P]
[Tf2N] [19]
· [3C6C14P] [PF6] [19]
|
|
2 3 4 5
Nc
Figure G-80: Plots of versus Nc for ket-2-ones
in phosphonium-based FILs comprising
[3C6C14P] + ion.
7.3. Infinite dilution activity coefficients of
ket-2-ones in ammonium-based FILs
|
-0.8
-0.85
-0.9
-0.95
-1
-1.05
|
|
|
1n(L413)
|
|
· [3C1C4N] [Tf2N] [21]
· [C13C8N] [Tf2N] [27]
|
|
|
|
|
2 3 4 5
Nc
Figure G-81: Plots of versus Nc for ket-2-ones
in ammonium-based FILs comprising
[Tf2N] - ion.
7.4. Infinite dilution activity coefficients of
ket-2-ones in pyridinium-based FILs
|
0.3 0.1 -0.1 -0.3 -0.5 -0.7 -0.9
|
|
|
1n(L113)
|
|
? [BMPy] [BF4] [22] n [EPy] [Tf2N] [25]
|
|
|
|
|
2 3 4 5 6
Nc
Figure G-82: Plots of versus Nc for ket-2-ones
in the imidazolium-based FILs
[Epy] [Tf2N] and [BMPy] [BF4].
7.5. Infinite dilution activity coefficients of
ket-2-ones in pyrrolidinium-based FILs
|
-0.2 -0.3 -0.4 -0.5 -0.6 -0.7
|
|
|
|
1n(L413)
|
|
· [BMPyrr] [Tf2N] [16]
|
|
|
|
3 4 5 6
Nc
Figure G-83: Plot of versus Nc for ket-2-ones in
the pyrrolidinium-based FIL [BMPyrr]
[Tf2N].
APPENDIX H: EFFECT OF STRUCTURE ON
LIMITING
SELECTIVITY AND CAPACITY
1. Benzene/n-hexane separation problem
1.1. Imidazolium-based fluorinated ionic
liquids
Limiting Selectivity
|
50 40 30 20 10 0
|
|
[EMIM] + [BMIM] + ? [HMIM] + ? [MOIM] + O [C16MIM] +
|
|
|
|
|
Anions
Figure H-1: Limiting selectivity at 313.15 K
of imidazolium-based fluorinated ionic liquids for
the hexane (1)/benzene
(2) system, representing aliphatics/aromatics separation
problems.
[EMIM][BF4][1][2];[EMIM] [Tf2N] [3][4];
[BMIM][BF4][2][6] ; [BMIM] [Tf2N] [4][8] ;
[BMIM][TfO] [9] ;
[HMIM][BF4] [12][2] ; [HMIM][PF6] [13] ; [HMIM] [Tf2N] [14][16]
;
[MOIM][BF4] [17] ; [MOIM] [Tf2N] [16] ; [C16MIM][BF4] [18] ; [EMIM][TfO]
[28]; [MOIM][PF6]
[29]; [BMIM][SbF6] [30] ; [BMIM][PF6] [31] ;
[EMIM][TFA] [32] ; [HMIM][TfO] [33].
|
2
1.5
1
0.5
0
|
|
|
|
Limiting Capacity
|
|
[EMIM] + ? [BMIM] + [HMIM] + ? [MOIM] + O [C16MIM] +
|
|
[BF4]- [PF6] - [TfO] - [SbF6] - [TFA] - [Tf2N]-
|
|
Anions
Figure H-2: Limiting capacity at 313.15 K of
imidazolium-based fluorinated ionic liquids for
the hexane (1)/benzene (2)
system, representing aliphatics/aromatics separation
problems.
[EMIM][BF4][2];[EMIM] [Tf2N] [4];
[BMIM][BF4][6] ; [BMIM] [Tf2N] [8] ; [BMIM][TfO] [9]
;
[HMIM][BF4] [2] ; [HMIM][PF6] [13] ; [HMIM] [Tf2N] [16] ; [MOIM][BF4] [17]
; [MOIM]
[Tf2N] [16] ; [C16MIM][BF4] [18] ; [EMIM][TfO] [28];
[MOIM][PF6] [29]; [BMIM][SbF6] [30] ;
[BMIM][PF6] [31] ;
[EMIM][TFA] [32] ; [HMIM][TfO] [33].
1.2. Phosphonium-based fluorinated ionic
liquids
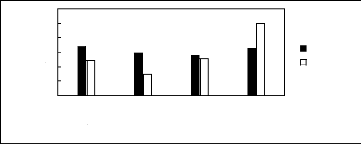
Limiting Selectivity
and Capacity
4
2
6
3
0
5
1
[3C6C14P][BF4] [3C6C14P][PF6] [3C6C14P]
[Tf2N] [3C6C14P][(C2F5)2PF3]
Ionic liquids with a common cation
Selectivity Capacity
Figure H-3: Limiting selectivity and capacity
at 313.15 K of phosphonium-based fluorinated
ionic liquids for the hexane
(1)/benzene (2) system, representing aliphatics/aromatics
separation
problems. References: [3C6C14P] [BF4] [19]; [3C6C14P]
[Tf2N] [19]; [3C6C14P] [(C2F5)3PF3] [20];
[3C6C14P] [PF6]
[19].
1.3. Ammonium-based Fluorinated ionic liquids
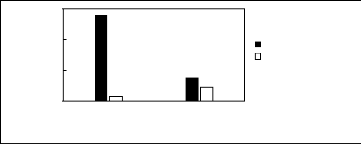
Limiting Selectivity
and Capacity
15
10
5
0
Ionic liquids with a common anion
[3C1C4N][Tf2N] [C13C8N][Tf2N]
Limiting Selectivity Limiting Capacity
Figure H-4: Limiting selectivity and capacity
at 313.15 K of ammonium-based fluorinated
ionic liquids for the hexane
(1)/benzene (2) system, representing aliphatics/aromatics
separation
problems. References: [3C1C4N] [Tf2N] [21]; [C13C8N]
[Tf2N] [27].
Appendix H: Effect of structure on limiting selectivity and
capacity
2. Methanol/benzene separation problem
2.1. Imidazolium-based fluorinated ionic
liquids
|
Selectivity at infinite
dilution
|
2 1.6 1.2 0.8 0.4
0
|
|
[EMIM] + [BMIM] + ? [HMIM] + ? [MOIM] + *[C16MIM] +
|
[BF4]- [PF6] - [TfO] [SbF6] - [TFA] - [Tf2N]-
Anions
Figure H-5: Limiting selectivity at 313.15 K of
imidazolium-based fluorinated ionic liquids for the methanol (1)/benzene (2)
system, representing alcohols/aromatics separation problems.
References: [EMIM][BF4][2];[EMIM] [Tf2N]
[4]; [BMIM][BF4][6][7]; [BMIM] [Tf2N] [8]
;
[BMIM][TfO] [9] ; [HMIM][BF4] [12] ; [HMIM][PF6] [13] ; [HMIM] [Tf2N]
[16]; [MOIM][BF4] [17]
; [MOIM] [Tf2N] [16] ; [C16MIM][BF4] [18];
[EMIM][TfO] [28]; [MOIM][PF6] [29];
[BMIM][SbF6][30] ;[EMIM][TFA] [32].
2.2. Phosphonium-based fluorinated ionic
liquids
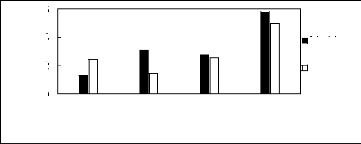
Limiting Selectivity
and Capacity
4
2
6
0
[3C6C14P][BF4] [3C6C14P][PF6] [3C6C14P][Tf2N]
[3C6C14P][(C2F5)2PF3]
Ionic liquids with a common cation
Limiting Selectivity Limiting Capacity
Figure H-6: Limiting selectivity and capacity
at 313.15 K of phosphonium-based fluorinated
ionic liquids for methanol
(1)/benzene (2) system, representing alcohols/aromatics separation
problems.
References: 3C6C14P] [BF4] [19]; [3C6C14P] [Tf2N] [19]; [3C6C14P]
[(C2F5)3PF3] [20];
[3C6C14P] [PF6] [19].
2.3. Ammonium-based fluorinated ionic liquids
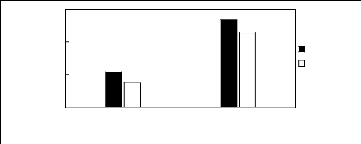
Limiting Selectivity
and Capacity
3
2
0
1
[3C1C4N][Tf2N] [C13C8N][Tf2N]
Ionic liquids with a common anion
Selectivity Capacity
Figure H-7: Limiting selectivity and capacity
at 313.15 K of ammonium-based fluorinated
ionic liquids for methanol
(1)/benzene (2) system, representing alcohols/aromatics separation
problems.
References: [3C1C4N] [Tf2N] [21]; [C13C8N] [Tf2N]
[27].
3. Methanol/acetone separation problem
3.1. Imidazolium-based fluorinated ionic
liquids
|
5 4 3 2 1 0
|
|
|
|
Limiting Selectivity
|
|
[EMIM] + ? [BMIM] + ? [HMIM] + [MOIM] + * [C16MIM] +
|
|
[BF4]- [PF6] - [TfO] - [SbF6] - [TFA] - [Tf2N]-
|
|
Anions
Figure H-8: Limiting selectivity at 313.15 K
of imidazolium-based fluorinated ionic liquids for
methanol (1)/acetone (2)
system, representing alcohols/ketones separation problems.
References:
[EMIM][BF4][2];[EMIM] [Tf2N] [4]; [BMIM][BF4] [7]
[2] ; [BMIM] [Tf2N] [8] ;
[BMIM][TfO] [9] ;
[HMIM][BF4][2] ; [HMIM] [Tf2N] [16];
[MOIM][BF4][17] ; [C16MIM][BF4] [18]
; [BMIM][SbF6]
[30] ; [BMIM][PF6] [31] .
Appendix H: Effect of structure on limiting selectivity and
capacity
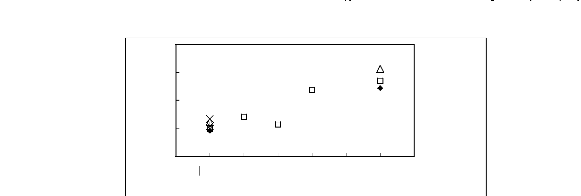
4
Limiting Capacity
3
2
1
0
[EMIM] + ? [BMIM] + ? [HMIM] + X [MOIM] + * [C16MIM] +
[BF4]- [PF6] - [TfO] - [SbF6] - [TFA] -
[Tf2N]-
Anions
Figure H-9: Limiting capacity at 313.15 K of
imidazolium-based fluorinated ionic liquids for
methanol (1)/acetone (2)
system, representing alcohols/ketones separation problems.
References:
[EMIM][BF4][2];[EMIM] [Tf2N] [4];
[BMIM][BF4][2] ; [BMIM] [Tf2N] [8] ;
[BMIM][TfO]
[9] ; [HMIM][BF4][2] ; [HMIM] [Tf2N] [16];
[MOIM][BF4][17] ; [C16MIM][BF4] [18]
; [BMIM][SbF6]
[30] ; [BMIM][PF6] [31].
3.2. Phosphonium-based fluorinated ionic
liquids
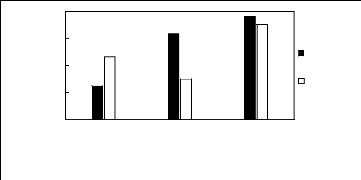
Limiting Selectivity and
Capacity
4
3
2
0
1
[3C6C14P][BF4] [3C6C14P][PF6] [3C6C14P][Tf2N]
]
Ionic liquids with a common cation
Limiting Selectivity
Limiting
Capacity
Figure H-10: Limiting selectivity and capacity
at 313.15 K of phosphonium-based fluorinated
ionic liquids for methanol
(1)/acetone (2) system, representing alcohols/ketones separation
problems.
References: 3C6C14P] [BF4] [19]; [3C6C14P] [Tf2N] [19]; [3C6C14P]
[(C2F5)3PF3] [20];
[3C6C14P] [PF6] [19].
3.3. Ammonium-based fluorinated ionic liquids
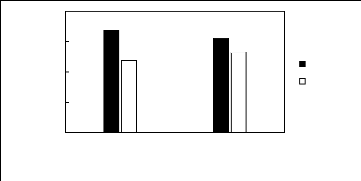
Limiting Selectivity and
Capacity
4
3
2
0
1
Ionic liquids with a common anion
[3C1C4N][Tf2N] [C13C8N][Tf2N]
Selectivity Capacity
Figure H-11: Limiting selectivity and capacity
at 313.15 K of ammonium-based fluorinated
ionic liquids for methanol
(1)/acetone (2) system, representing alcohols/ketones separation
problems.
References: [3C1C4N] [Tf2N] [21]; [C13C8N] [Tf2N]
[27].
4. n-hexane/hex-1-ene separation problem
4.1. Imidazolium-based fluorinated ionic
liquids
Anions
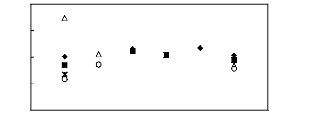
[EMIM] + [BMIM] + ? [HMIM] + ? [MOIM] + * [C16MIM] +
4
3
2
1
0
Selectivity at infinite dilution
[BF4]- [PF6] - [TfO] - [SbF6] - [TFA] -
[Tf2N]-
Figure H-12: Limiting selectivity at 313.15 K
of imidazolium-based fluorinated ionic liquids
for the n-hexane
(1)/hex-1-ene (2) system, representing paraffins/olefins separation
problems.
References: [EMIM][BF4][1][2];[EMIM] [Tf2N]
[3][5]; [BMIM][BF4] [6] [2] ; [BMIM] [Tf2N]
[4];
[BMIM][TfO] [9] ; [HMIMI[BF4] [12] ; [HMIM][PF6] [13] ; [HMIM]
[Tf2N] [14] ; [MOIM][BF4]
[17] ; [MOIM] [Tf2N] 16] ; [C16MIM][BF4]
[18] ; [EMIM][TfO] [28]; [MOIM][PF6] [29];
[BMIM][SbF6]
[30] ; [EMIM][TFA] [32].
Appendix H: Effect of structure on limiting selectivity and
capacity
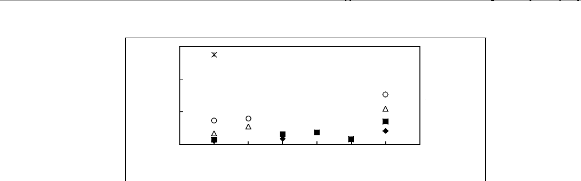
[BF4]- [PF6] - [TfO] - [SbF6] - [TFA] - [Tf2N]-
[EMIM] + [BMIM] + ? [HMIM] + ? [MOIM] + * [C16MIM]
0.6
Limiting Capacity
0.4
0.2
0
Figure H-13: Limiting capacity at 313.15 K of
imidazolium-based fluorinated ionic liquids for
the n-hexane (1)/hex-1-ene
(2) system, representing paraffins/olefins separation problems.
References:
[EMIM][BF4][2];[EMIM] [Tf2N] [5];
[BMIM][BF4][2] ; [BMIM] [Tf2N] [4] ;
[BMIM][TfO] [9] ;
[HMIM][BF4] [12] ; [HMIM][PF6] [13] ; [HMIM] [Tf2N] [14] ; [MOIM][BF4]
[17]
; [MOIM] [Tf2N] [16] ; [C16MIM][BF4] [18] ; [EMIM][TfO] [28];
[MOIM][PF6] [29];
[BMIM][SbF6] [30] ; [EMIM][TFA] [32].
4.2. Phosphonium-based fluorinated ionic
liquids
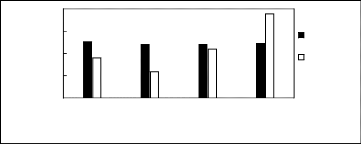
Limiting Selectivity
and Capacity
0.5
1.5
2
0
1
[3C6C14P][BF4] [3C6C14P][PF6] [3C6C14P][Tf2N]
[3C6C14P][(C2F5)2PF3]
Ionic liquids with a common cation
Limiting
Selectivity Limiting
Capacity
Figure H-14: Limiting selectivity and capacity
at 313.15 K of phosphonium-based fluorinated
ionic liquids for the n-hexane
(1)/hex-1-ene (2) system, representing paraffins/olefins
separation
problems. References: 3C6C14P] [BF4] [19]; [3C6C14P]
[Tf2N] [19]; [3C6C14P] [(C2F5)3PF3] [20];
[3C6C14P] [PF6]
[19].
4.3. Ammonium-based fluorinated ionic liquids
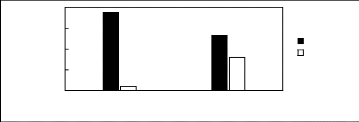
Limiting
Selectivity and
Capacity
0.5
1.5
2
0
1
[3C1C4N][Tf2N] [C13C8N][Tf2N]
Ionic liquids with a common anion
Selectivity Capacity
Figure H-15: Limiting selectivity and capacity
at 313.15 K of ammonium-based fluorinated
ionic liquids for the n-hexane
(1)/hex-1-ene (2) system, representing paraffins/olefins
separation
problems. References: [3C1C4N] [Tf2N] [21]; [C13C8N] [Tf2N]
[27].
4.4. Pyrrolidinium-based fluorinated ionic
liquids
Limiting Selectivity
and Capacity
3
2
0
1
[TfO]- [Tf2N]-
Anions
S8 for [BMPyrr] +
n S8 for [HMPyrr] + ?Safer [MOPyrr] +
k8 for [BMPyrr]+
? k8 for [HMPyrr]+ ? k8 for
[MOPyrr]+
Figure H-16: Limiting selectivity and capacity
at 313.15 K of imidazolium-based fluorinated
ionic liquids for the n-hexane
(1)/hex-1-ene (2) system, representing paraffins/olefins
separation
problems. References: [BMPyrr] [TfO] [34]; [HMPyrr]
[Tf2N] [35]; [MOPyrr] [Tf2N] [35].
5. Benzene/butan-2-one separation problem
5.1 Imidazolium-based fluorinated ionic
liquids
|
2.5
2
1.5
1
0.5
0
|
|
|
|
Limiting Selectivity
|
|
[EMIM] +
? [BMIM] +
? [HMIM] + X [MOIM] +
* [C16MIM] +
|
|
[BF4]- [SbF6] - [Tf2N]-
|
|
Anions
Figure H-17: Limiting selectivity at 313.15 K
of imidazolium-based fluorinated ionic liquids
for the benzene
(1)/butan-2-one (2) system, representing ketones/aromatics separation
problems.
References: [EMIM][BF4][2];[EMIM] [Tf2N]
[4]; [BMIM][BF4] [2]; [HMIM][BF4][2] ;
[HMIM]
[Tf2N] [16] ; [MOIM][BF4] [17] ; [C16MIM][BF4] [18] ;
[BMIM][SbF6] [30].
|
2.5
2
1.5
1
0.5
0
|
|
|
|
Limiting Capacity
|
|
[EMIM] +
? [BMIM] + ? [HMIM] +
* [MOIM] +
? [C16MIM] +
|
|
[BF4]- [PF6] - [SbF6] - [Tf2N]-
|
|
Anions
Figure H-18: Limiting capacity at 313.15 K of
imidazolium-based fluorinated ionic liquids for
the benzene (1)/butan-2-one
(2) system, representing ketones/aromatics separation problems.
References:
[EMIM][BF4][2];[EMIM] [Tf2N] [4]; [BMIM][BF4]
[2]; [HMIM][BF4][2] ; [HMIM]
[Tf2N] [16] ; [MOIM][BF4] [17]
; [C16MIM][BF4] [18] ; [BMIM][SbF6] [30].
5.2 Phosphonium-based fluorinated ionic
liquids
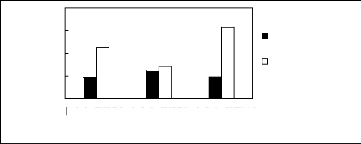
Limiting Selectivity
and
Capacity
4
3
2
0
1
[3C6C14P][BF4] [3C6C14P][PF6] [3C6C14P][Tf2N]
Ionic liquids with a common cation
Limiting Selectivity Limiting Capacity
Figure H-19: Limiting selectivity and capacity
at 313.15 K of phosphonium-based fluorinated
ionic liquids for the benzene
(1)/butan-2-one (2) system, representing ketones/aromatics
separation
problems. References: 3C6C14P] [BF4] [19]; [3C6C14P] [Tf2N] [19];
[3C6C14P]
[(C2F5)3PF3] [20]; [3C6C14P] [PF6] [19].
6. Ethanol/butan-2-one separation problem
6.1 Imidazolium-based fluorinated ionic
liquids
|
Limiting
Selectivity
|
4 3 2 1 0
|
|
[EMIM] +
n [BMIM] + ? [HMIM] + *[MOIM] +
? [C16MIM] +
|
|
[BF4]- [PF6] - [SbF6] - [Tf2N]-
Anions
|
|
Figure H-20: Limiting selectivity at 313.15 K
of imidazolium-based fluorinated ionic liquids
for the ethanol (1)/
butan-2-one (2) system, representing alcohols/ketones separation
problems.
References: [EMIM][BF4][2];[EMIM] [Tf2N]
[4]; [BMIM][BF4][7][2]; [HMIM][BF4][2] ;
[HMIM]
[Tf2N] [16] ; [MOIM][BF4] [17] ;
[C16MIM][BF4] [18] ; [BMIM][SbF6] [30] ; [BMIM][PF6] [31].
6.2 Phosphonium-based fluorinated ionic
liquids
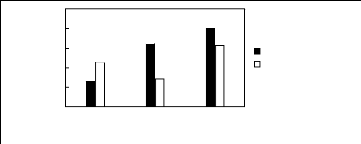
Limiting Selectivity
and Capacity
5
4
3
2
0
1
[3C6C14P][BF4] [3C6C14P][PF6] [3C6C14P][Tf2N]
Ionic liquids with a common cation
Limiting Selectivity Limiting Capacity
Figure H-21: Limiting selectivity and capacity
at 313.15 K of phosphonium-based fluorinated
ionic liquids for the ethanol
(1)/ butan-2-one (2) system, representing alcohols/ketones
separation
problems. References: 3C6C14P] [BF4] [19]; [3C6C14P] [Tf2N]
[19];
[3C6C14P] [(F5)3PF3] [20]; [3C6C14P] [PF6]
[19].
APPENDIX I: CORRELATION OF INFINITE
DILUTION
ACTIVITY COEFFICIENT, SELECTIVITY AND CAPACITY
1. Infinite dilution activity coefficient correlation
with the ionic liquid alkyl chain length 1.1. Imidazolium-based fluorinated
ionic liquids
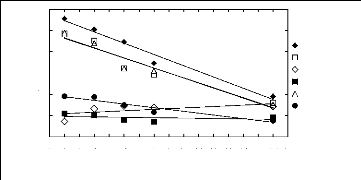
In (1113)
-1
4
2
5
3
0
1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
Nc
n-Hexane Hex-1-ene Ethanol Acetone Cyclohexane Benzene
Figure I-1: Variation of limiting activity
coefficients of various solutes depending on Nc, the
carbon number of the
alkyl chain attached to the methylimidazolium group with [BF4]-
anion.
Nc values corresponding to data points are: 2 for [EMIM]
[BF4][1][2], 4 for [BMIM] [BF4][2][6][7],
6 for [HMIM] [BF4][2][12], 8 for [MOIM]
[BF4][17] and 16 for [C16MIM] [BF4][18].
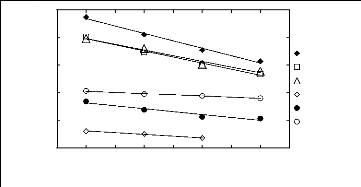
WS 13)
-0.5
-1.5
2.5
3.5
0.5
1.5
1 2 3 4 5 6 7 8 9
Nc
n-Hexane Hex-1-ene Cyclohexane Acetone Benzene Ethanol
Figure I-2: Variation of limiting activity
coefficients of various solutes depending on Nc, the
carbon number of the
alkyl chain attached to the methylimidazolium group with [Tf2N]-
anion.
Nc values corresponding to data points are: 2 for [EMIM] [Tf2N]
[3][4][5], 4 for [BMIM] [Tf2N]
[4][8], 6 for [HMIM] [Tf2N]
[14][15][16] and 8 for [MOIM] [Tf2N] [16].
1 2 3 4 5 6 7
Nc
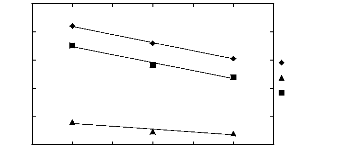
n-Hexane Benzene Cyclohexane
5
4
3
In(11113)
2
1
0
Figure I-3: Variation of limiting activity
coefficients of various solutes depending on Nc, the
carbon number of the
alkyl chain attached to the methylimidazolium group with [TfO]-
anion.
Nc values corresponding to data points are: 2 for [EMIM] [TfO]
[28], 4 for [BMIM] [TfO] [9] and
6 for [HMIM] [TfO]
[33].
1.2. Pyrrolidinium-based fluorinated ionic
liquids
|
3
2
1
|
|
|
|
|
lii(LPi3 )
|
|
|
Hex-1-ene n-Hexane
|
|
|
|
|
3 4 5 6 7 8 9
Nc
Figure I-4: Variation of limiting activity
coefficients of n-hexane and hex-1-ene depending on
Nc, the carbon number of
the alkyl chain attached to the methylpyrrolidinium group
with
[Tf2N]- anion. Nc values corresponding to data points are: 4
for [BMPyrr] [Tf2N] [16],
6 for [HMPyrr] [35] and 8
for [OMPyrr] [Tf2N] [35].
2. Infinite dilution selectivity coefficient correlation
with the ionic liquid alkyl chain length 2.1. n-hexane/benzene
system
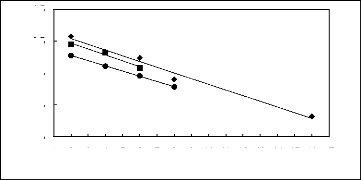
4.5
3.5
in (51:12)
2.5
1.5
0.5
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
Nc
FILs containing [BF4]- FILs containing
[TfO]- ? FILs containing [Tf2N]-
Figure I-5: Variation of limiting
selectivities of n-hexane to benzene depending on Nc, the
carbon number of
the alkyl chain attached to the methylimidazolium group with common
[BF4]-
, [Tf2N]- and [TfO]- anions. Nc
values corresponding to data points are: 2 for [EMIM]
[BF4][1][2],
[EMIM] [TfO][28] and for [EMIM] [Tf2N]
[3][4]; 4 for [BMIM] [BF4][6][2], [BMIM]
[TfO][9] and
[BMIM] [Tf2N] [4][8]; 6 for [HMIM]
[BF4][12][2], [HMIM] [TfO][33] and [HMIM] [Tf2N]
[14][16];8
for [MOIM] [BF4][17] and [MOIM] [Tf2N] [16]
and 16 for [C16MIM] [BF4][18].
2-2. n-hexane/hex-1-ene system
FILs containing [MIM] O FILs containing [MPyrr]

1 2 3 4 5 6 7 8 9
Nc
|
In (S°12)
|
0.8 0.7 0.6 0.5 0.4
|
Figure I-6: Variation of limiting selectivity
of n-hexane to hex-1-ene depending on Nc, the
carbon number of the alkyl
chain attached to the methylpyrrolidinium or methylimidazolium
group with
common [Tf2N]- anion. Nc values corresponding to data points are: 2
for [EMIM]
[Tf2N] [3][4]; 4 for [BMIM] [Tf2N] [4] and
[BMPyrr] [Tf2N] [16] ; 6 for [HMIM] [Tf2N] [14] and
[HMPyrr]
[Tf2N] [35] and 8 for [MOIM] [Tf2N] [16] and [OMPyrr]
[Tf2N] [35].
| 


