Conception et calcul des structures en verre

3.2 Composition

Comme cela a été dit au point précédent, il n'y a pas de formule chimique du verre, et donc pas de composition unique. Cependant, dans les normes européennes, des fourchettes de quantité ont été déterminé. Voici un tableau récapitulatif des différents types de verre et de leur composition. Lors de ce travail, l'intérêt sera porté sur le verre silicio-sodo-calcique qui constitue la majeure partie des vitrages. La composition de deux autres types de verre

est indiquée en guise d'information. Ce sont les pourcentages massiques qui sont utilisés dans le tableau.

		Verre silicio- sodo-calcique EN 572-1	Verres borosilicates EN 1748-1	Vitrocéramiques EN 1748-2
Dioxyde de silicium	SiO2	69 à 74%	70 à 87%	50 à 80%
Oxyde de calcium	CaO	5 à 12%	-	0 à 8%
Oxyde borique	B2O3	-	7 à 15%	-
Oxyde de sodium blanc	Na2O	12 à 16%	0 à 8%	0 à 2%
Oxyde de magnésium	MgO	0 à 6%	0 à 8%	0 à 8%
Oxydes d'aluminium	Al2O3	0 à 3%	0 à 8%	15 à 27%
Oxydes de lithium	Li2O	-	-	0 à 5%
Oxydes de zinc	ZnO	-	-	1 à 5%
Dioxyde de titane	TiO2	-	-	0 à 5%
Dioxyde de zirconium	ZrO2	-	-	0 à 5%
Oxyde de baryum	BaO	-	-	0 à 8%
Oxyde de potassium	K2O	-	-	0 à 2%
Autres		0 à 5%	0 à 8%	0 à 5%

Tableau 3.2.1 : Composition, pourcentages massiques des différents types de verre selon l'Eurocode

Certains adjuvants peuvent encore être ajoutés pour modifier la couleur par exemple, mais leurs concentrations sont tellement faibles qu'ils n'altèrent en rien les propriétés mécaniques du verre.

3.3 Caractéristiques mécaniques

Malgré l'existence de fourchettes dans la composition du verre, les propriétés mécaniques de celui-ci varient peu. Le tableau 3.3.1 met en avant les principales valeurs du verre. On fera particulièrement attention à la valeur du module de Young qui est une donnée importante dans le cas du dimensionnement des éléments et qui interviendra tout au long de ce travail. Pour une masse volumique identique à celle du béton, le verre possède un module de Young bien supérieur, qui est identique à celui de l'aluminium. Cependant, vu ces qualités indéniables, le verre doit faire face un défaut important qui jusque ici, l'a rendu très peu populaire auprès des ingénieurs : il possède une rupture fragile.

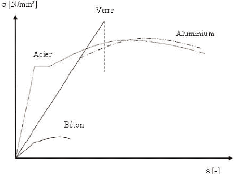
Figure 3.1.1 Graphique contrainte- déplacement pour le verre, l'acier, le béton, l'aluminium [25]

Quand on le compare à l'acier, on peut remarquer le palier plastique de l'acier et toute la réserve de déformation qu'il possède encore avant la rupture. Le verre ne possède pas cette réserve et sa rupture est donc brutale. Les déformations importantes en acier permettent d'anticiper la rupture. C'est pour cette raison qu'il faut prendre des valeurs plus importantes pour les coefficients de sécurité des éléments fragiles.

	Verre silicio- sodo-calcique EN 572-1	Verres borosilicates EN 1748-1
ñ kg/m^3	2500	2200-2500
HK0,1/20Gpa	6	4,5-6
E Mpa	70000	60000-7000
í -	0,2	0,2
		class 1: 3,1-4,0
		class 2:4,1-5,0
á 10^-6 K-1	9	class 3: 5,1-6,0
c J/(kg*K)	750	800
ë W/(m*K)	1	1
å -	0,837	0,837

masse volumique à 18°C Dureté

module de Young

coefficient de Poisson

Coefficient de dilatation

linéique moyen entre 20°C et 300°C

capacité thermique spécifique Conductibilité thermique Emissivité

Tableau 3.3.1 : Propriétés physiques et caractéristiques mécaniques du verre selon l'Eurocode

3.3.1 Résistance théorique

Orowan, en 1949, a établi une formule [16] pour déterminer la valeur théorique de la résistance des matériaux fragile. Cette valeur dépend directement du module de Young (E), de la distance inter-atomique ( a₀ ) et l'énergie de création d'une unité de surface (ã) :

Eã

ó = (3.1)

th

a₀

Si on prend comme valeur pour a₀ = 0.2 nm et pour ã = 3.5 J/m². On obtient comme valeur
théorique 35GPa. Cette valeur n'est en réalité jamais atteinte mais permet de voir le grand
potentiel qu'il y a dans le domaine du verre. Les prochaines parties du chapitre essaieront
d'expliquer pourquoi cette résistance théorique n'est jamais atteinte.