Conception et calcul des structures en verre

9.2 Esquisses et plans

L'idée générale du projet était de créer un véritable puit de lumière afin d'apporter de la lumière naturelle au sein de ce premier niveau de sous-sol de la station Schuman. Le volume souterrain de la station se trouve au milieu de la place entre le rond point et le début de la sortie du tunnel rue de la Loi. Cependant, actuellement les principaux accès à cette station se trouvent éloignés de cet espace central.

En créant un nouvel élément au dessus de cet espace central, on répond à deux objectifs. Tout d'abord, on offre un volume supplémentaire qui permet d'apporter la lumière au niveau du sous-sol. Ensuite, ce nouveau bâtiment offre une nouvelle visibilité à la station. Cependant, ce nouveau volume oblige à le munir de circulations verticales supplémentaires.

Les façades du projet seront également en verre. Celles-ci seront tenues à l'aide de feuilles de verre mise perpendiculairement qui agiront comme une poutre face à l'effet du vent sur les façades.

Sur le plan de structure (Figure 9.2.1), il y a trois éléments plus foncés, ce sont ces éléments-là qui feront l'objet du dimensionnement.

Figure 9.2. 1 Structure du projet en 3d

9.3 Dimensionnement de colonnes et poutres en verre

Les calculs de résistance se porteront exclusivement sur les éléments porteurs en verre (colonne et poutre). Le calcul d'assemblage aborde d'autres aspects et ceux-ci ne seront donc pas abordés dans ce travail de pré dimensionnement. Les éléments porteurs en verre sont tous des verres trempés thermiquement et feuilletés, si l'épaisseur l'exige.

Dans le chapitre 4, sur la résistance du verre, il a été expliqué que la résistance du verre variait en fonction du temps, il est donc important de savoir pour quelle durée de vie la bâtiment est prédestinée. Il s'agit d'un bâtiment de classe 3 selon l'Eurocode 1 [29]

« Structures de bâtiments et autres structures courantes ». Sa durée de vie est donc de 50 ans.

Les calculs relatifs aux colonnes et aux poutres seront précédés du numéro de l'équation auxquels ils se réfèrent.

9.3.1 Dalle de toiture

La toiture est composée d'éléments de vitrage de 3m x 2m qui sont portés par des poutres secondaires qui elles-mêmes rejoignent les poutres principales

.

Le dimensionnement des éléments en verre chargé hors de leur plan n'est pas le travail de ce mémoire. Afin d'obtenir une épaisseur de vitrage indicative pour pouvoir effectuer la descente de charge, les calculs seront faits de manière analogue à celui d'un calcul de dalle. Les calculs ne tiendront compte que du moment et de la flèche de la dalle.

9.3.1.1 Les actions

La toiture du projet est classée d'après l'Eurocode 1 en catégorie H :

« Toitures inaccessibles sauf pour l'entretien normal, les réparations, la peinture et les réparations mineures » [29]

La neige

D'après l'eurocode 1, la charge de neige dépend de l'altitude. A Schuman, on se trouve en dessous de 100m d'altitude. La norme prévoit de prendre une surcharge :

s_k = 0.5 kN/m²

Le vent

Pour le vent, j'ai choisi une valeur de : w_k =0.7 kN/m² Le poids propre de dalle de verre

L'épaisseur de la dalle de verre est de 0.03 m. Il s'agit d'un verre feuilleté et trempé de 3 couches de 1 cm. Sachant que le verre a une masse volumique de 2500 kg/m³ = 25 kN/m³

gdalle = 0.03 25 = 0.75 kN/m² Les surcharges d'exploitation

La toiture doit pouvoir est classée en catégorie H, elle doit donc pouvoir soutenir des surcharges d'exploitation

q_k = 0.75 kN/m² charges réparties Q_k = 1.5 kN charge ponctuelle 9.3.1.2 Le système statique

Les dalles reposent sur des deux poutres secondaires espacées de 2m. Il s'agit d'un système isostatique pour chaque dalle.

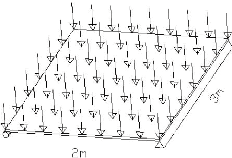
Figure 9.3 1 Schéma statique et chargement de la dalle de toiture

9.3.1.3 Dimensionnement Etat Limite Ultime :

- Sollicitations

Les actions réparties variables		Coefficient partiel	Larg. de bande (m)	Valeur par mètre courrant kN/m
Neige	sk = 0,5 kN/m^2	1,5	1	0,75
vent	wk = 0,7 kN/m^2	1,5	1	1,05
Charges d'exploitation	qk = 0,75kN/m^2	1,5	1	1,125
Les charges réparties permanente
Poids propre	gdalle = 0,75kN/m^2	1,35	1	1,0125
Total				3,93

Les actions ponctuelles variables Coefficient partiel Valeur kN

Charges d'exploitation

variables Q_k = 1,5 kN 1,5 2,25

Total 2 ,25

Le moment sollicitant vaut donc : M_sd = 3,93 2²/8 + 2,25 2/4 = 3,09 kNm - Résistance de calcul du verre (voir chapitre 4)

kmod, combi

1,35 0,75 1,5

× +

( 0,75 0,7 0,5

+ + )

La présence des plusieurs actions avec des durées de chargement différentes oblige calculer un k mod,combi expliqué à la formule (4.6).

= =0,325

0,75 0,75 0,7 0,5

1,35 + 1,5 + 1,5 + 1,5

0,29 0,74 0,74 0,43

La formule (4.8) donne la valeur de la résistance de calcul à long terme en traction du verre.

fg t d = ; ;

0,325 1 45 1 120 45 70,625 / × × × ( ) - + = kN 1,8 1,2

mm

2

- Résistance de la section :

Mrd = fg ; t ; d . W = 70,625.0,03².1/6 = 10,59 kNm

Msd = 3,09 kNm < M_rd = 10,59 kNm ok !

Etat limite de Service : - Sollicitations

Les actions réparties variables		Coefficient partiel	Larg. de bande (m)	Valeur par mètre courrant kN/m
Neige	sk = 0,5 kN/m^2	1	1	0,5
vent	wk = 0,7 kN/m^2	1	1	0,7
Charges d'exploitation	qk = 0,75kN/m^2	1	1	0,75
Les charges réparties permanente
Poids propre	gdalle = 0,75kN/m^2	1	1	0,75
Total				2,7

Les actions ponctuelles variables Coefficient partiel Valeur kN

Charges d'exploitation

variables Q_k = 1,5 kN 1 1,5

Total 1,5

- Flèche

4 3 4 3

f =

mm

5 pl 1 2,7 2

Pl 5 × 1 1,5 2

×

+ = + = 5,15

3 3

384 EI 48 EI 384 1 0,03 48

× 1 0,03

×

70000 × 70000×

12 12

- Flèche admissible

L

f =
max

= 2000 6,66

= mm

300 300

- Vérification

f = 5,15 mm = f max = 6,66mm ok !

9.3.2 Poutre de toiture P.Sec.1

Lors du dimensionnement des poutres, celles-ci sont supposées être tenues latéralement. Cette condition permet de s'affranchir de la vérification au déversement. La poutre secondaire de toiture est de classe 2 d'après le MCC (chapitre 5.2).

9.3.2.1 Les actions Actions de dalle :

Charges réparties variables (voir détails dalle) : 0,5 + 0,7 + 0,75 kN/m² Charges réparties permanentes (voir détails dalle) : 0.75 kN/m²

Charge ponctuelle variable (voir détails dalle) : 1.5 kN/m²

Poids propre de la poutre et section La poutre secondaire a une section efficace de 6cm de large pour une hauteur de 25cm. La poutre est composée de 6 feuilles de verre trempé de 1cm et de 5 intercalaires plastiques de 0,38 mm. Entres les feuilles, un intercalaire d'une épaisseur de 0,38 mm sera placé. gpou ,sec = 0,06 m.0,25m.25 kN/m^3 = 0,375 kN/m

Figure 9.3. 2 Section de la poutre
secondaire

9.3.2.2 Le système statique

Les poutres secondaires entre distantes de 2m relient les poutres principales entre distantes de 6m. C'est un système isostatique. La charge ponctuelle est une charge d'entretient, elle doit donc se trouver à l'endroit le plus défavorable de la poutre, dans ce cas-ci, il s'agit du milieu de la poutre.

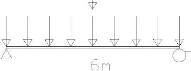
Figure 9.3 3 Schéma statique de la poutre secondaire

9.3.2.3 Dimensionnement Etat Limite Ultime :

- Sollicitations

Les actions réparties variables		Coefficient partiel	Larg. de bande (m)	Valeur par mètre courrant kN/m
Neige	sk = 0,5 kN/m^2	1,5	2	1,5
vent	wk = 0,7 kN/m^2	1,5	2	2,1
Charges d'exploitation	qk = 0,75kN/m^2	1,5	2	2,25
Les actions réparties permanente
Poids propre	gdalle = 0,75kN/m^2	1,35	2	2,025
Poids propre poutre secondaire	gpou ,sec = 0,375 kN/m	1,35		0,506
Total				8,38

Les actions ponctuelles variables Coefficient de sécurité Valeur kN

Charges d'exploitation

variables Q_k = 1,5 kN 1,5 2,25

Total 2 ,25

Le moment sollicitant vaut donc : M_sd = 8,38 6²/8 + 2,25 6/4 = 41,09 kNm - Résistance de calcul du verre

La détermination du k_mod,combi est la même que pour le cas de la dalle : k_mod,combi = 0.325

La formule (4.8) donne la valeur de la résistance de calcul à long terme en traction du verre.

0,325 × 1 × 45 1 ×

= 70, 625 kN /

1,8 1,2

f=
g ; t ;d

(

120 -45

)

2

mm

- Résistance de la section (d'après la formule (5.22)):

Mrd = fg ; t ; d . W = 70,625.0,06.0,25².1/6 = 44,14 kNm
Msd = 41,09 kNm < M_rd = 44,14 kNm ok !

La poutre a une portée de plus de 4m. Il faut donc vérifier s'il est possible d'avoir des feuilles de verre trempé de plus de 4m ou bien, il faut vérifier les sections critiques. La juxtaposition de deux feuilles est une section critique car on ne peut pas considérer que l'ensemble de la section travaille en flexion à cet endroit.

- Résistance à l'effort tranchant (d'après la formule (5.27)) :

V_Rd = Anette ( fg ; t ; d / 3 ) = 0,06.0,25.70625/ 3 = 611, 63kN
V_sd = 26,26kN

Vérification : sd 26,26

V = kN < V_rd = 611,63kN ok !

Etat limite de Service :

- Sollicitations

Les actions réparties variables Coefficient Larg. de Valeur par mètre

partiel bande (m) courrant kN/m

Neige s_k = 0,5 kN/m² 1 2 1,0

vent w_k = 0,7 kN/m² 1 2 1,4

Charges

q_k = 0,75kN/m² 1 2 1,5

d'exploitation

Les actions réparties permanente

Poids propre gdalle = 0,75kN/m² 1 2 1,5

poutre secondaire gpou ,sec = 0,375 kN/m

Poids propre 1 0,375

Total 5,775

Les actions ponctuelles variables Coefficient partiel Valeur kN

Charges d'exploitation

variables Q_k = 1,5 kN 1 1,5

Total 1,5

- Flèche

f =

4 3 4 3 5 pl 1 5,775 2 Pl 5 × 1 1,5 2 × + = + = 19,05 3 3 384 EI 48 EI 384 0,06 0,25 48 × 0,06 0,25 × 70000 × 70000 × 12 12

mm

- Flèche admissible (d'après la formule (5.28))

L = 6000 20

f = = mm

max ^{300 300}

- Vérification

f = 19,05 mm = f max = 20mm ok !

La vérification de la résistance aux chocs est validée par différents essais. Comme la poutre est de classe 3, elle devra être au moins classée P5 A selon la EN 356.

9.3.3 Poutre de toiture P.princ.1

Les poutres principales sont soutenues par deux colonnes. L'ensemble des surcharges de toitures est ramené sur la poutre principale par l'intermédiaire des poutres de secondaire. Les forces à prendre à considération sont donc le poids propre et l'ensemble des charges dû aux poutres secondaire. La poutre principale de toiture est de classe 3 d'après le MCC (chapitre 5.2).

9.3.3.1 Les actions

Effort des poutres secondaires :

- Surcharge permanente (p.p dalle + poutre secondaire) : 1,5 + 0,375= 1,875 kN/m - Surcharge variable (neige + vent + exploitation): 1 + 1,4 +1,5 = 3,9 kN/m

Poids propre de la poutre La poutre a une section efficace de 10 cm de large et une hauteur de 65 cm pour une portée de 12m.La section est composée de 4 feuilles de 25 mm chacune. g pou , princ = 0,1 m.0,65 m.25 kN/m^3 = 1,625 kN/m
	Figure 9.3.4 section de la poutre principale

9.3.3.2 Le système statique

La poutre principale mesure 16m de long. La distance entre appuis est de 12m, il y a un porte-à-faux de 2m de chaque coté. C'est un système isostatique. Les poutres principales sont entre distantes de 6m. Le cas de charge le plus défavorable est celui où il n'y a que les charges permanentes en bout de porte-à-faux et l'ensemble des surcharges entre les appuis dues aux poutres secondaires. Il y a 7 poutres secondaires centrales dont deux qui arrivent directement sur les appuis et deux poutres secondaires de rives, sur le schéma, il n'est pas représenté la charge répartie due au poids propre. (Figure 9.3.3).

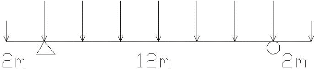
Figure 9.3 4 Schéma statique de la poutre principale

9.3.3.3 Dimensionnement

Etat Limite Ultime :

- Sollicitation

Poutre secondaire de rive seulement chargée avec les charges permanentes :

0,75 kN/m (2 fois une demie dalle) + 0,375 kN/m (p.p. de la poutre sec) = 1,125 kN/m La force ponctuelle agissant en bout de porte-à-faux = 1,125 kN/m.6m.1,35 = 9,11 kN Poutres secondaires centrales chargées avec l'ensemble des surcharges :

[1,5 kN/m (dalle) + 0,375 kN/m].1,35.6 + [1 + 1,4 +1,5].1,5.6= 50,29 kN Poids propre:

g pou , princ = 1,625 kN/m . 1,35 = 2,19 kN/m

Le moment sollicitant vaut donc :

Le moment sollicitant est décomposé en deux parties :

Premièrement, le moment dû au poids propre : M sd , G pou , princ = 2,19 (12²-4.2²)/8 = 35,04 kNm Deuxièmement le moment dû aux autres charges :

Msd = 8. 9,11 + 2. 50,29 + 4. 50,29 - 6. 134.835 = 434,39 kNm

= 469,43 kNm

Msd , tot

- Résistance de calcul du verre (d'après la formule (4.8)):

La détermination du _kmod,combi est la même que pour le cas de la dalle : k_mod,combi = 0.325

f = g ,t,d

0,325 × 1 × 45 + 1 × ( 120 -45 ) = 70,625 kN/ 1,8 1,2

mm

2

- Résistance de la section (d'après la formule (5.22)):

Mrd = fg ; t ; d . W = 70625.0,1.0,65².1/6 = 497,31 kNm

Msd = 469,43 kNm < M_rd = 497,31 ok ! - Résistance à l'effort tranchant (d'après la formule (5.27)):

VRd = Anette ( f g; t ; d / 3 ) = 0,1.0,65.70625/ 3 = 2650,39kN
Vsd = 93,375kN

Vérification : sd 93,375

V = kN < V_rd = 2650,39kN ok !

Etat Limite de Service :

- Sollicitation

Poutre secondaire de rive seulement chargée avec les charges permanentes :

0,75 kN/m (2 fois une demie dalle) + 0,375 kN/m (p.p. de la poutre sec) = 1,125 kN/m La force ponctuelle agissant en bout de porte-à-faux = 1,125 kN/m.6m. = 6,75 kN

Poutres secondaires centrales chargées avec l'ensemble des surcharges : [1,5 kN/m (dalle) + 0,375 kN/m].6 + [1 + 1,4 +1,5].6= 34.65 kN

Poids propre :

g_pou , _princ = 1,625 kN/m

- Flèche :

Le calcul des flèches est séparé en deux. Premièrement, le calcul sera effectué pour l'ensemble des charges ponctuelles. Deuxièmement, le calcul sera effectué pour le poids propre. Les deux flèches seront additionnées et comparées à la valeur admissible.

Pour l'ensemble des charges ponctuelles (effectué par intégrale de Mohr voir Annexe C pour le détail du calcul):

4349,92

Flèche des charges ponctuelles : fponct = = 27,15 mm

0,1 0,65 ³

×

70000 ×

12

qL L

² ( 5 24

2 - c 2 2 2 2

) 1,625.12 5.12 24.2

( - )

=

Flèche charge répartie : f =

rep

= 2,37mm

3

384 EI 0,1.0,65

384.70000.

12

- Flèche admissible (d'après la formule (5.28)) :

L

f =
max

12000 40

= = mm

300 300

- Vérification

f = 29,52 mm = f_max = 40mm ok !

La vérification de la résistance aux chocs est validée par différents essais. Comme la poutre est de classe 3, elle devra être au moins classée P5 A selon la EN 356.

9.3.4 Colonne C 2.1

La colonne a une hauteur de 2,5 m. La colonne principale est de classe 4 d'après le MCC (chapitre 5.2).

9.3.4.1 Les surcharges

Le poids propre et section de la colonne

Comme tout élément structurel le poids propre de la structure est à prendre en compte en considération lors du dimensionnement. Il s'agit d'une colonne en croix composée de 6 feuilles de 25mm Gcol = (0, 4.0,15 (0, 4 0,15).0,15).2,5.25 =6,09kN

Figure 9.3.4 Section de la colonne

Les surcharges verticales

Surcharges variables : [0,5+0,7+0,75].6.2 + [(1 + 1,4 +1,5).6 .7]= 187,2 kN

Surcharges permanentes :

[1,125 kN/m.6m.2 (nombre de poutre de rive) ] + [(1,5 kN/m + 0,375 kN/m).6.7(nombre de poutres centrales)] = 92,25 kN

9.3.4.2 Le système statique

Il s'agit d'un élément en compression, encastré en pied et en tête. Ceci afin de limiter la longueur caractéristique de flambement. La colonne a une hauteur de 2,5m

9.3.4.3 Dimensionnement Etat Limite Ultime

- Sollicitation :

Nsd = 280,8 +24,54 + 8,22 = 214,8kN 2	Gcol =6,09.1,35= 8,22 kN Qvar = 187,2.1,5= 280,8kN Qperm = 92,25.1,35=124,54kN

- Résistance de calcul du verre (d'après la formule (4.8)) :

fgt d = ; ;

0,29 × 1 × 45 + 1 × ( 120 - 45 ) = 69820 kN/ 1,8 1,2

mm

2

- Résistance au flambement (voir chapitre 5.3)

Il faut déterminer la largeur de verre équivalente grâce à la formule (5.16). Avant cela, il faut déterminer les 3 paramètres présents dans cette formules (5.13) ;(5.14) et (5.15)

I_s =5.0,4.0,025.0,02538² = 3,220722 .10^-5 m4 á = 6.0,35.0,025³/12.1/ I_s =0,097

2

i

=

t PVB EI s

0,00038 70000.0,0000322 = 0, 000016

â=

² 29160.0,35.5.0,02538² 1,25 ²

12 I_s ( 1 + á + ð²áâ)

b( 1 + ð²â)

=0,102m

i =n

L_k

G PVBb

( ? z_i)²

3

=

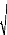
teff

On peut donc considérer une section monolithique en verre dont l'épaisseur est de 0,102m Valeurs caractéristiques pour la section efficace (d'après les formules (5.6) et (5.7)):

Aeff =(0, 4.0,102 (0, 4 0,102).0,102)= 0,0712 m²

Ieff = (0,4.0,102³/12 + 0,102.0,4³/12) = 5,79 10^-4 m⁴ N euler , eff =3,14².70000.(5,79.10^4) /(2,5/2)²= 255,75 kN

ó euler,eff = 255,75/(0, 4.0,102+(0, 4-0,102).0,102)= 3,6 MPa

- Par la méthode du coefficient de réduction (d'après les formules (5.10)):

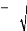
K=

N cr K =
,

1 ( )

GK

² = 880,6 kN

i₀

1

3

69,820 4,4

ë = =

3,6

La valeur du coefficient de réduction doit être déterminée sur la Figure 5.3.4 d'après l'élancement réduit. La valeur de l'effort normal résistant réduit est calculé d'après la formule (5.9).

Nrd = 0,075.0,0712.69850 = 372,99 kN - Par l'effet du second ordre (d'après la formule (5.8)) :

La flèche initiale est de 0,003mm/mm, il s'agit d'une colonne de hauteur 2,5m, la flèche initiale vaut donc 7,5mm.

Concernant l'excentricité, comme cela a été expliqué dans le travail, cette valeur est choisie par l'ingénieur. Pour cet exercice, l'excentricité vaudra 1/10 de la plus grande des dimensions de la section.

214,8 214,8 ? 0,04 0,0075 ?

ó = #177; ? + ?

4

0,0712 5,79.10 - cos(2,5/ 2 214,8/ 70000.5,79.10 ) 1 214,8/ 255,75

- 4

? -

? ? ?

0,2

ó = 9,46MPa = 69,85MPa

- Parois minces (d'après les formules (5.17) et (5.18)) :

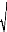
5,79.10

-4

i = = 0,09

⁰ 0,0712

G = 29160MPa

3 -

( 0,4.0,102 2. 0,149.0,102 ³ 2,46.10 ⁴

+ ( ) ) =

Vérification :

214,8 kN < min{372,99 kN ;880,6kN }

La vérification de la résistance aux chocs est validée par différents essais. Comme la colonne est de classe 4, elle devra être au moins classée P6 B selon la EN 356.