5.5 Elément comprimé et
fléchis
Dans le cas d'un élément soumis à une
flexion et à un effort axial, le principe est de s'assurer que la
contrainte maximale dans la fibre la plus sollicitée soit
inférieure à la résistance de calcul du verre. Deux
vérifications s'impose la première pour les zones en traction et
la deuxième pour les zones en compression car la résistance de
calcul n'est pas la même dans les deux cas. Ces inégalités
peuvent être modifiées afin de contenir les influences de la
compression et des moments.
Pour les zones en traction :
ómax = fg ; t ; d
(5.30)
Pour les zones en compression :
ómax = fg ; c ; d
(5.31)
Pour les zones en traction :
N N ? e w ? M M
0 ,
+ ? + ? + + = 1 (5.32)
sd y sd z
,
A f W f
. . cos / 2 / 1 /
; ; ; ; , ? . .
g t d g t d ? ? L N EI - N N W f W
f
k cr e ? y g t d
; ; z g t d
; ;
Pour les zones en compression :
N N ? e w ? M M
0 sd y
, sd z
,
+ ? + ? + + =1 (5.33)
A f W f
. . cos / 2 / 1 /
; ; ; ; , ? . .
g c d g c d ? ? L N EI - N N W f W
f
k cr e ? y g c d
; ; z g c d
; ;
Les deux premiers termes prennent en compte l'effort normal
ainsi que le moment secondaire dû à l'excentricité des
charges, les deux suivants prennent en compte la flexion dans les deux
directions principales.
5.6 Actions accidentelles
Les actions énumérées et
développées au-dessus sont les sollicitations principales des
structures. Ils existent d'autres actions qui doivent être
vérifiées dans le cas d'un calcul de structure complet.
Aujourd'hui, vu le caractère novateur des structures en verre, ces
sollicitations exceptionnelles sont encore très peu
étudiées. Les éléments principaux qu'on peut en
retirer sont développés dans ce paragraphe.
5.6.1 Résistance aux chocs
Encore plus que les autres structures, les
éléments en verre peuvent subir des chocs. De part son image
fragile et cassant, le verre est souvent soumis à des actes de
vandalisme (voir chapitre 7.15). Il faut donc s'assurer que la structure puisse
résister suffisamment aux chocs.
Il existe deux types d'essais afin de vérifier la
résistance aux chocs d'un élément en verre. Il s'agit de
l'essai de chocs de corps mous et de l'essai de chocs de corps durs.
L'essai aux chocs de corps mous permet de mettre en
évidence le type de rupture du verre. Il existe trois types
différents de modes de cassures en fonction du type de verre.
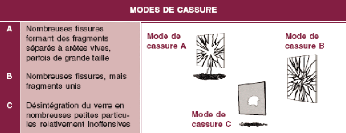
Figure 5.6 1Modes de cassures du verre selon la norme NBN EN
12600 [52]
Dans le cas d'une application structurel du verre, il est
important que le verre possède un mode de rupture au moins de type de B
(caractéristique du verre feuilleté) ou de type C
(caractéristique du verre trempé thermiquement). Afin
d'empêcher des morceaux de verre de se détacher de la structure,
il est bon de prévoir un film plastique sur la face extérieur de
la feuille de verre.
Deux niveaux de classements existent pour la
détermination de la résistance aux chocs de corps durs. Le
premier niveau correspond à l'aptitude des vitrages à
résister aux jets d'objets. L'essai à la chute de bille de 4,1 kg
est satisfait si 3 éprouvettes résistent à la
pénétration (3 impacts en triangle). Le deuxième niveau
correspond aux tentatives d'effraction à l'aide d'une masse ou d'une
hache pour réaliser une ouverture de 40 cm x 40 cm, appelée
"passage d'homme". Le nombre d'impacts nécessaires à sa
réalisation détermine la classe du vitrage.
Dans le tableau suivant (Tableau 5.6.1), une relation a
été établie entre les classes de la norme EN 356 et le
classement MCC. Lors d'une utilisation structurelle du verre, le choix
de la classe du verre est importante, mais celui-ci est déterminé
par deux critères (les mêmes que pour le classement MCC,
voir paragraphe 5.2), l'accessibilité de la structure et le rôle
de l'élément au sein de la structure. Dans le cas de
bâtiments publics, il est possible d'obtenir des verres résistants
à l'onde de choc d'une explosion.
Le classement de la structure, selon le MCC permet
d'avoir une information sur la résistance aux chocs nécessaire
pour ce type d'élément.
Classe MCC
EN356
Niveau 1 :
hauteur de chute (m) de 3
billes
P1 A 1,5 m
P2 A 3 m
P3 A 6 m
P4 A 9 m 1
P5 A 9 m (chute de 9 billes) 2-3
Niveau 2 :
Masse + hache (coups min.)
P6 B 30 coups 4
P7 B 51 coups 5
P8 B 71 coups 6
Tableau 5.6 1 Classement des éléments en verre aux
chocs de corps durs d'après la EN 356
5.6.2 Résistance au feu et gradient thermique
De par sa nature, le verre est un matériau
incombustible. Cependant, des bris par choc thermique peuvent apparaître
s'il existe entre deux zones d'une feuille de verre une différence
importante de température. Si l'élément vitré est
chauffé de matière constante, il y a une dilatation
générale de la pièce. Cependant, si une seule partie de la
pièce est soumise à un changement de température et que
l'autre reste froide alors celle-ci empêchera la libre dilatation et il
se crée alors des contraintes de traction qui peuvent être plus
important que la résistance du verre. Dans ce cas-là, il y a donc
un bris par choc thermique. L'existence et l'apparition de ces gradients
thermiques sont multiples. La résistance à ces bris varie en
fonction du type de verre et logiquement, celui possédant la
résistance la plus grande est le verre trempé car il
possède une meilleure résistance en traction. Voici les valeurs
des gradients thermiques maximales pour les différents types de
verre.
- Le verre trempé : 200°K (EN 12150-1) - Le verre
durci : 100°K (EN 1863-1)
- Le verre recuit : 40°K (EN 572-1)
Il existe des feuilles de verre pouvant résister
à la chaleur comme les verres borosilicatés ou bien les
vitrocéramiques. Ceux-ci ont des coefficients de dilatation proche de
zéro ce qui leur permet de résister au feu pendant près de
4 heures.
A l'heure actuelle, ceci est la seule information sur la
résistance du verre sous l'effet de la température. Aucune
information sur l'évolution du module de Young ou de l'inertie en
fonction de la température n'existe comme c'est le cas dans l'acier ou
bien encore le béton. Il est donc impossible aujourd'hui de dimensionner
un ouvrage, un bâtiment aux normes incendies. Ceci est donc un champ
d'investigation possible pour de futures recherches dans le domaine verrier.
| 


