Etude de la stabilité aux petites perturbations dans les grands réseaux électriques: Optimisation de la régulation par une méthode metaheuristique

ANNEXES

Annexe A. Transformation de Park.

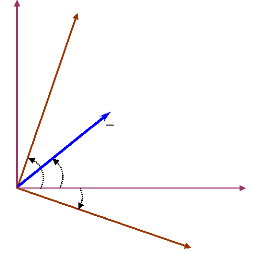
Afin d'établir les équations décrivant le comportement du système globale, il est nécessaire de ramener les grandeurs (décrits dans un repère local d-q) de chaque générateur à un seul repère commun pour tous les générateurs, il s'agit du repère D-Q, comme le montre la figure (1A).

L'axe réel (D) du repère commun est habituellement employé comme une référence pour mesurer l'angle de rotor de machine. Pour une machine représentée en détail comprenant la dynamique d'un ou plusieurs circuits de rotor, l'angle ä de rotor est défini par l'angle entre l'axe (q) de la machine et l'axe réel (D), comme il est montré par la figure suivante.

Pour une machine représentée par un modèle classique, l'angle de rotor ä est l'angle entre la tension E^' et l'axe réel (D), (Chatelain, 1983). En régime dynamique, l'angle ä se varie avec la vitesse de rotor.

Q

q

V

ä

á

D

ä

d

Figure 1A. Changement de référentiel du repère local (d-q) au repère commun (D-Q).

De la figure (1A), soit V un vecteur dans l'espace. Dans le repère (D-Q), il s'écrit :

V ( DQ) = Ve (1A)

já

Alors que dans le repère (d-q), il s'écrit :

V dq Ve (2A)

j ( )

á - ã

=

( )

Sachant que ã =ä- 90°, l'équation (2A) devient :

V dq Ve e (3A)

j á j ä

- - °

( 90 )

=

( )

Ainsi, le passage d'un repère à l'autre s'effectue par une simple rotation comme l'exprime l'équation suivante :

V dq V _DQ e (4A)

j ( 90 )

° -ä

( ) ( )

=

En décomposant en parties réelle et imaginaire et en regroupant sous forme matricielle, on obtient les équations décrivant le passage d'un repère à l'autre:

? -

sin cos

ä ä ?

? ?

?cos sin ä ä ?

? V ?
D

? ?

? VQ ?

? V ?

d

? ?

? V q ?

? V ?

Q

? ?

? V D ?

?sin cos
ä ä ?
? ?
? - cos sin

ä ä ?

? V ?

d

? ?

? V q ?

( ( ) )

C E S X X I

' + - ' Ä

ij qj ij qj dj qj ä j (10A)

Ä = ?

I Y

di ij

- Ä ? + ? ? Ä

Y S E Y C X X I

ij qj dj qj

( )

ij ij

qj ij

(5A)

Annexe B.

Modèle linéaire.

Appliquons la méthode de la linéarisation sur l'ensemble des équations différentielles non-linéaires, (31), (32), (33) et (34). Nous obtenons alors l'ensemble des équations suivantes :

1

Ä & = Ä ? Ä ? Ä

ù i T T D

( )

mi ei i ù i (6A)

2 H i

Ä ä i = ù ₀ Ä ù i

1

& (7A)

Ä & ' =

E ( ( ) )

T '

qi

doi

Ä ? Ä ? ? ? ? Ä

E E X X I (8A)

fdi qi di di di

1

Ä & = ? Ä ? Ä ? Ä

E ( ( ) )

K V U E (9A)

fdi ai ti Si fdi

T ai

Pour obtenir le modèle d'état, nous devons exprimer ces équations linéaires uniquement en fonction des variables d'état. Pour ce faire, nous commençons par appliquer la méthode de la linéarisation sur les deux composants du courant Ii, décrits par les équations (39) :

Ainsi pour Idi :

Ä = Ä ä + Ä + Ä

[ ] [ ][ ] [ ][ ] [ ][ ]

I P Q E M I

' (11A)

d d d q d q

Où :

P Y C E S X X I j i (12A)

dij ij ij qj ij qj dj qj

= - + - ?

[ ' ( ' ) ]

P dii P dij (13A)

= - ?

j i

?

Qdij = -Y _ij S ij (14A)

Mdij = Y _ij C _ij X qj - X dj (1 5A)

( ' )

De même, en ce qui concerne le courant Iqi, nous obtenons : (1 ( )) ( ( ) ) - ? ? Ä = ? ' - - ' Ä Y S X X I Y S E C X X I ii ii qi di qi ij ij qj ij qj dj qj ä j + Ä ? + ? ? Ä Y C E Y S X X I ij ij qj ij ij qj dj qj ( )

(16A)

Ä = Ä ä + Ä (17A)

[ ][ ] [ ][ ] [ ][ ]

L I P Q E '

q q q q q

Où :

PY S E C X X I j i (18A)

qij ij ij qj ij qj dj qj

= - - - ?

[ ' ( ' ) ]

P qii P qij (19A)

= - ?

j i

?

Q qij = Y _ij C ij (20A)

Lqii Y _ii S _ii X _qi X di j i

= 1 - ( - ' ) = (21A)

Lqij Y _ij S _ij X _qj X dj j i

= - ( - ' ) ? (22A)

Pour le calcul de tous les coefficients P, Q, L et M, les valeurs initiales de E^'qj, Iqj, äj doivent être utilisées.

En remplaçant successivement les matrices [ÄId], [ÄI_q], des équations (11A) et (1 7A), nous obtenons tous calculs faits les solutions suivantes :

[ÄId]=[Yd][ÄE ' q ]+[F_d][Ää] (23A)

[ÄI_q]=[Y_q][ÄE^'_q]+[F_q][Ää] (24A)

Où :

[Y_d]=[Q_d]+[M_d][Y_q] (25A)

[F_d]=[P_d]+[M_d][F_q] (26A)

[ ] [ ] ¹ [ ]

Y q L q - Q q

= (27A)

[ ] [ ] ¹ [ ]

F q L q - P q

= (28A)

Le Calcul des constantes K1ij...K6ij : de la linéarisation est réalisé de la façon suivante :

1. En Linéarisant l'équation du couple électrique de la i^ème machine, donnée par l'équation (35), nous obtenons :

Ä = + ? + ? Ä

T E X X I F X X I F

[( ( ) ) (( ) ) ]

' ' '

ei qi qi di di qij qi di qi dij ä _j

+ + - + - [( ( ) ) (( E X X I Y X ' ' qi qi di di qij qi	X ' di	I Y E ' ) ) ] qi dij qj Ä			(29A)
++ - + - [( ( ) ) (( ) E X X I Y X X I ' ' ' qi qi di di qii qi di qi				Y I E ' ) ] dii qi qi + Ä

Ä = Ä ä + Ä + Ä (30A)

T K K E K E

' '

ei ij j ij qj ii qi

1 2 2

Où :

K1 ij =DtFdij +Q _t F qij (31A)

K ij D _t Y _dij Q _t Y qij j i

2 = + ? (32A)

K ii D _t Y _dii Q _t Y _qii I qi j i

2 = + + = (33A)

Dt(

X qi X ' di ) I qi = - (34A)
Q t = E ' qi + (X_qi - X ' di )I di (3 5A)

En remplaçant _ÄTei tirée de l'équation (30A) dans l'équation (6A), nous obtenons: 1

Ä = ? Ä ? Ä ? Ä ? Ä + Ä

ù& ä ù

( )

K K E K E D T

' ' (36A)

i 1 2

ij j ij qj ii qi i i mi

2

²H

i

2. La tension interne linéairisée de la i^ème machine, donnée par l'équation (8A), peut être réécrite comme suit :

(1 ) ( )

+ Ä = Ä ? ? Ä

ST E E X X I

' ' ' (37A)

do i qi fdi di di di

En remplaçant _ÄIdi tirée de l'équation (23A) dans cette dernière équation et en arrangent le résultat, nous obtenons de même:

1

) (38A)

(1 ) (

' '

+ Ä = Ä ? Ä ? Ä

ST K E K E K

' ä E

doi ii qi ii fdi ij j

3 3 4 qj

K3 ij

Ä & = ? Ä ä ? Ä ? Ä + Ä

1 1 1

' '

( E E

'

E E

K ) (39A)

^qi T ' 4 ij j qj qi fdi

j

K K

doi 3 i3ii

Où :

K ij X _di X _di Y dij j i

3 [( ) ]

' -1 ?

= - (40A)

K ii X _di X _di Y dii j i

3 [1 ( ) ]

' -1

= + - = (41A)

K ij ( X _di X ' di ) F dij

4 = - (42A)

3. La linéarisation de l'équation (38) représentant la tension terminale de la i^ème machine et les équations (36), (37) constituant les composantes de cette tension nous donne :

V _ti ÄV ti = V_di Ä V_di + V _qi ÄV qi (43A)

ÄV di = XqiÄIqi (44A)

ÄV qi = ÄE qi - XdiÄIdi (45A)

En utilisant les équations (23A), (24A), pour exprimer ÄIdi, ÄIqi dans l'équation (43A), nous obtenons :

1 1 '

V X F V V X F ) ä

di qi qij ti qi di dij

? Ä

-

( )

V V X Y V V X Y V V E

- - -

1 1 ' 1 '

ti di qi qij ti qi di dij ti qi qi

? + Ä

ÄVti

(V -

ti

(46A)

ÄV ti = K _ij Ä ä _j + K _ij Ä E qj (47A)

'

5 6

Où :

K ij D v X qi F qij Q v X ' di F dij 5 = -

(48A)

K D X Y Q X Y Q (49A)

ij v qi qij v di dij v

= - ' +

6

D_v V ti - 1 V di

= (50A)

Q

v V ti - 1 V qi = (51A)
En remplaçant _ÄVti tirée de l'équation (47A) dans l'équation (9A), nous obtenons :

Ä & = - Ä ä - Ä + Ä ? Ä

1 ( )

K K K K E K U E

'

E (52A)

fdi Ai ij j ai ij qj ai Si fdi

5 6

T ai