UNIVERSITE MONTESQIEU BORDEAUX IV
Une description de différentes options
exotiques à partir du modèle de Cox
Ross et Rubinstein sur quelques
périodes.
MÉMOIRE
soutenu le 20 mai 2008
pour l'obtention du
Master 1 Mention Ingénierie Mathématique,
Statistique et
Economique
(Ingénierie Economique)
par
Richard Jean-Charles
Composition du jury
Mme. Christine Marois
Melle. Benoite de Saporta
Remerciements
Je tiens à remercier Mme. Christine Marois, responsable de
loption, pour mavoir conseillé et encadré tout au long de ce
travail
TABLE DES MATIÈRES
INTRODUCTION 1
Partie I Introduction du modèle 4
CHAPITRE 1:
LE MODÈLE DE COX ROSS RUBINSTEIN
1 Les hypothèses du modèle . . . . . . . . . . . .
. . 5
2 Le modèle sur une période . . . . . . . . . . . .
. . . . . . . . . . . . . 6
3 Le modèle sur T périodes . . . . . . . . . . . .
. . . . . . . . . . . . . . . . 8
4 Les options dans le modèle CRR . . . . . . 12
5 Un choix de u, d . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . 14
Partie II Quelques options "path independent" 17
CHAPITRE 1:
LES OPTIONS BINAIRES
|
1
|
L'option cash or nothing . . . . . . . . . . . . . . . . . . . .
. . . . . .
|
18
|
|
1.1
|
Exemple . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . .
|
18
|
|
1.2
|
Expression mathématique. . . . . . . . .
|
20
|
|
1.3
|
Convergence du modèle de Cox Ross Rubinstein
|
21
|
|
2
|
L'option asset or nothing . . . . . . . . . . . . . . . . . . . .
.
|
25
|
|
2.1
|
Exemple ....... . .. . . .. . . . . . . . . . . . . . . . . . . .
.
|
26
|
|
2.2
|
Expression mathématique. . . . . . . . .
|
26
|
|
2.3
|
Convergence du modèle de Cox Ross et Rubinstein
|
28
|
|
3
|
La formule de Black et Scholes. . . . . . . . . . . . . .
|
30
|
CHAPITRE 2:
LES OPTIONS SUR OPTIONS 34
Partie III Quelques options path dependent 41
CHAPITRE 1:
LES OPTIONS LOOKBACK
|
1 Le call lookback fixe européen . . . . . . . . . . .
2 Le call lookback flottant européen . . . . . . . . .
.
3 Evaluation du call lookback flottant pour r = ó 2 . . .
. . .
|
. . . . . . . . .
|
44
45
47
|
|
CHAPITRE 2:
LES OPTIONS BARRIÈRES
|
52
|
|
|
1 Evaluation par l'arbre binomial . . . . . . . . . . . . . .
.
|
. .
|
54
|
|
CONCLUSION
|
60
|
|
|
|
|
|
BIBLIOGRAPHIE
|
61
|
|
|
|
iv
|
Table des figures
|
1
|
Arbre binomial à une période . . . . . . . . . . .
. . . . . . . . . . .
|
6
|
|
2
|
Arbre binomial à trois périodes . . . . . . . . . .
. . .
|
8
|
|
1
|
Exemple du payoff cash or nothing K=100, Q=10, T=1 an
|
18
|
|
2
|
Evaluation du call cash or nothing dans l'arbre binomial
|
19
|
|
3
|
Exemple du payoff asset or nothing K=100T=1 an
|
25
|
|
4
|
Evaluation du call asset or nothing dans l'arbre binomial
|
26
|
|
5
|
Exemple de payoff de l'option vanille K=80, T=1 an
|
30
|
|
6
|
Evaluation d'un call vanille . . . . . . . . . . . . . . . . .
.
|
32
|
|
7
|
Convergence vers Black et Scholes . . .
|
33
|
|
1
|
Evaluation d'un call sur call . . . . . . . . . . . . . . . . .
.
|
36
|
|
2
|
Evaluation d'un put sur put . . . . . . . . . . . . . . . . .
.
|
37
|
|
3
|
Evaluation d'un call sur put . . . . . . . . . . . . . . . . . .
. .
|
38
|
|
4
|
Evaluation d'un put sur call . . . . . . . . . . . . . . . . . .
. .
|
39
|
|
1
|
payoff du call lookback fixe . . . . . . . . .
|
43
|
|
2
|
payoff du call lookback flottant . . . . . . .
|
43
|
|
3
|
arbre d'évaluation d'un call lookback à prix
d'exercice fixe
|
45
|
|
4
|
arbre d'évaluation d'un call lookback à prix
d'exercice flottant
|
46
|
|
5
|
Encadrement de la trajectoire de St . . . . . . . . . . . . . . .
. . . . . . . .
|
48
|
6 Le principe de réflexion du brownien . . . . . . . . . .
. 49
7 Call lookback flottant pour r = ó 2 . . . . . . . . . .
. . . . . . . . . . . . . 51
1 exemple de barrière up-in . . . . . . . . . . . . . . .
. . . . . . . . . . . 53
2 Le problème de la barrière . . . . . . . . . . .
. . . . . . . . . . . . . . . 55
3 encadrement de la barrière . . . . . . . . . . . . . . .
. . . . . . . . . . . . 56
4 encadrement de la barrière sur un noeud . . . . . . . .
. 57
5 Option up and out avant interpolation . . . . . . . . . . 58
6 Option up and out après interpolation . . . . . . . . .
. . 59
INTRODUCTION
Dans les années 1980, suite aux variations des taux
dintérêtréels sur les marchés, les produits
dérivés tels que les options se sont développés. En
effet la formule d'évaluation des options sur actions découverte
par Black et Scholes en 1973 a permis une meilleure compréhension de ces
outils financiers , et un nouvel horizon de choix tant au niveaudes
stratégies d'investissements que des couvertures de portefeuilless
L'option est alors devenue un instrument majeur et
incontournable en finance comme le montrent les nombreuses pertes subies
récemment par certaines banques et entreprisess Les sommes mises en jeu
étant de plus en plus colossales, les entreprises et lesbanques ont fait
apparaitre sur les marchés les options dites de « seconde
génération »ou «exotiques qui permettent de
répondre à des besoins de couvertures ou encore
despéculationde plus en plus précis.
Ces options sont conditionnées par différentes
contraintes qui permettent de construire des stratégies en fonctions du
marchéOn peut classer les options exotiques endeux catégories :
les !path dependent", c'est à dire dont le prix dépend detoutes
les valeurs que le sous jacent peut prendre, et les path independent" dont le
prix ne dépend que de la valeur finale du sous jacent pour les options
européennes.
Le modèle développé par Cox Ross et
Rubinstein en 1979 est lanalogue en temps discret de celui du modèle de
Black et Scholes. Ce modèle est couramment appelé le
modèle binomial car on y représente l'évolution du
sous-jacent sous formedun arbrebinaire où à chaque période
le sous-jacent ne peut prendre que deux valeurs.
Nous allons tenter d'exposer ici dans un premier temps
ladéfinitiondu modèlebinomial, pour s'intéresser ensuite
aux différents types doptions exotiques ainsi que leurs
évaluations
en temps discret et une approche en temps continu
Première partie

Introduction du modèle
CHAPITRE 1
LE MODÈLE DE COX ROSS RUBINSTEIN
1 Les hypothèses du modèle
Le modèle développé par CRR est
basé sur plusieurs hypothèses.Le prixdes différents actifs
reflète à tout moment toute l'information disponible. Tout le
monde possède la même information tout le monde doit pouvoir
accéder au marché et il nexiste pas de coûts de transaction
(commissions, frais de courtage.) De plus tous les actifs sont supposés
parfaitement divisibles et liquidesLe taux de placement est le même que
le tauxdemprunt, on l'appelle le taux sans risque r. Enfin la vente à
découvert est autorisée.
On admettra aussi la proposition suivanteLa diffusion suivie par
le soussjacent correspond à un mouvement brownien
géométrique sous la probabilité historique
dSt =uStdt+óStdWt
où les variables sont au temps t :
|
St
u
ó
|
prix du sous jacent
la moyenne du taux de rendement de l'actif Volatilité du
sous jacent
|
|
Wt
|
un mouvement brownien
|
Où W t est un mouvement brownien standard.
Cette idée futintroduite par LouisBachelier en 1900 puis reprise par
Black et Scholes dans leur célèbre modèle
dévaluationdes options européennes.
2 Le modèle sur une période
Nous définissons un marché financier composé
de deux actifs dont le prix à la date t est noté :
avec 0 < t < T l'actif risqué l'actif non
risqué
St Rt
L'actif risqué peut prendre deux valeurs S à la
fin de la période soit il est multiplié par u soit par d tel que
S0 <uS0 et S0 > dS0. On a une première propriété
implicite : u> 1 et d < 1. On représente ce modèle sous
forme d'arbre binaire, du fait des deux valeurs prises par l'accroissement de
l'actif. On note Q la probabilité historique telle que l'actif a un prix
qui augmente avec la probabilité q et un prix qui diminue avec la
probabilité (1 - q). On notera S0 = S. Sous forme d'arbre on a donc :

FIG. 1 - Arbre binomial à une période
Nous allons tout d'abord définir une condition
fondamentale que le modèledoit respecc ter : l'absence
d'opportunité d'arbitrage, c'est à dire que
u>1+r>d
Définition 1. On appelle univers risque neutre, une
économie oùles agents sont en moyenne indi~érents entre
gagnerdel'argent ssirement (placement enanque auauu sans risque r) ou le jouer
avec du risque (acheter des actions risquéesetc..).
Proposition 1. la probabilité de hausse dansl'univers
risque au neutreest
r+ 1--d
preuve : Si un actif vaut S à la date initiale, à
la date t = 1 sa valeur espérée est pour une probabilité p
:
E[S1] =p.uS+(1 --p)dS
Dans l'univers que l'on veut créer cette espérance
doit avoir la même valeur que si l'on avait placé la valeur de
l'actif au taux sans risque r. Soit :
E[S1] = (1+r)S
p.uS+(1--p)dS= (1+r)S
r+1--d
|
p=
|
|
|
|
|
|
|
|
u--d
|
|
|
|
|
1--p= 1
|
|
r+1--d
|
u--(1+r)
|
|
u--d
|
|
u--d
|
etdonc0<p< 1'~d< 1+r<u
La condition u > 1 + r > d est donc equivalente à
l'existence d'une probabilité risque neutre. Sous cette
probabilité les agents sont neutres au risque, nous allons doncdans la
suite calculer toutes les espérances sous cette probabilité P.
7
3 Le modèle sur T périodes
On généralise le modèle à une
période en considérant que le marché financier peut se
dupliquer aux instants t = [0, 1, ..., T]. L'actif non risqué
évolue toujours au taux constant r entre deux périodes de temps
[t,t + 1]. On le note au temps t
Rt=(1+r)t
L'actif risqué prend deux valeurs à chaque
période detempstelles que
|
?
?????
?????
|
Su t+1 = u.St
Sd t+1 = d.St
|
Sur l'arbre suivant nous pouvons observer lensemble des
probabilités en rouge et des valeurs du sous jacent en noir sur trois
périodesChaque probabilité est celle datteindre la valeur du sous
jacent.
uuuS
ppp
uuS pp
uS
uudS
p
3pp(1 -p)
dS
1-p
uddS
3p(1-p)(1-p)
On peut généraliser et dire que sur T
périodes la valeur SuhdT -h atteinte par ST cor-

(1-p)(1 -p)
FIG. 2 Arbre binomial à trois périodes
|
St+1 - St
St+1 = Stît+1 ? = ît+1- 1 ?
St
|
?
?????
?????
|
u-1 >0
d-1 <0
|
respond à une trajectoire dont la probabilité est
ph(1 - p)T_h. Si l'on fait l'hypothèse que
(T )
ces mouvements, à la hausse ou à la baisse sont
indépendants, il y a exactement h trajectoires qui atteignent cette
valeurLes T + 1 valeurs SuhdT _h, h = 0, ..., T que peut prendre ST
sont les T + 1 valeurs possibles d'une variable aléatoire deloi
binomiale donnée par :
( (T )
ST = SuhdT _h)
i = (ph)(1 - p)T_h
h
Soit ît E Q = {u,d} tel que :
St+1 = S0î1î2...ît+1
la loi de probabilité de ît est :
i (ît =u)= 1-i (ît =d)=p
La filtration naturelle associée représente
l'information accumulée sur les prix de lactif risqué
jusqu'à t , on la note :
(Ft)t<T = a{S0, S1, S2, S3, ...St}
Une hausse ou baisse est en fait celle du taux de rendement de
lactif qui par hypothèse est de variance historique a2 et de
moyenne u par unité de temps. Ces variations sont telles que ?t E {0,
.., T} et ?ît E {d, u}
autrement dit sil'on ne peut pas gagnerde l'argent àpartir
de rien.
En effet, par exemple, si r + 1 > u, alors le taux sans
risque rapporte plus quun actif risqué : à t = 0 on vend le
sous-jacent S et on place la somme acquise au taux sans risque. On
rachète à t = T le même sous jacent. La somme sans risque
ayant évolué plus vite que l'actif risqué, à terme
la différence entre ce que lon a vendu et rachetésera positive,
on aura gagné de l'argent sans en investir.
Proposition 2. Un marché financier est viable si et
seulement s'il eeiste une probabilité P* équivalente à Q ,
la probabilité historique, pourlaquelle le cours actualisé des
actiis ((St) 0 t T) est une martingale, c'est à dire St
(1+r)t est une martingale
Démonstration : Rappelons que Mt est une martingale sous
P* si
Ejp*[Mt+1 | Ft] = Mt
Par hypothèse l'information acquise sur les prix du sous
jacent jusque t n'influe pas sur ce qui se passe en t + 1 et
ît+1 est indépendant de Ft.
Alors Mt = St
(1+r)t est une martingale sous P* si Ejp*[Mt+1 | Ft] =
Mt.
[ St+1 1 = Ejp*[Stît+1 | Ft]
Or : Ejp* (1 + r)t+1 | Ft(1 + r)t+1
St
(1+r)t+1 Ejp*[ît+1 | Ft]
(1 + r)t+1 [p*u + (1 - p*) d]
St
= Mt [p*u + (1 -p*)d]
(1+ r)
et donc la condition à remplir est :
up*+(1--p*)d= 1+r
u.p* + d.(1 -- p*) =1 1+r
On en déduit que la probabilité risque neutre P
est la seule probabilité pour laquelle le prix du sous jacent
actualisé est une martingale et doncla seule probabilité pour
laquelle il n'existe pas d'opportunité d'arbitrageP* est une
probabilité si et seulement si :
0<
1+r--d
=p*<1
u--d
?
?????
?????
Les inégalités sont strictes puisque que lon veut
quily ait durisque.Or
p* > 0 1+ r > d
p* <1 1+ r < u
On en déduit que si l'action prend deux valeurs distinctes
à chaque noeud
0<d<1+r<u
Une condition pour que le marché soit viable est donc r
?]d -- 1; u -- 1[, la probabilité risque neutre P est donc la seule
probabilité pour laquelle le prix du sous jacent actualisé au
taux sans risque est une martingaleDansla suite les espérances seront
calculées sous cette probabilité risque neutre.
4 Les options dans le modèle CRR
Une option, ou plus généralement un actif
dérivé, est un actifdont la valeurdépenddes prix d'autres
actifs (ou sous jacent)actionsobligations, tauxdintérês.... Une
option est un contrat qui donne le droit et non l'obligation au souscripteur de
vendre/dacheter un sous-jacent à un prix donné (le strike),
à un moment donné (option européenne) ou jusquà un
moment donné (option américaine). Nous nous intéresserons
seulement aux options européennes. On introduit alors quelques
notations
~ T : la durée de vie de l'option
- K : le prix d exercice de l'option
- St : cours de l'actif sous jacent au temps t
Si on reprend les notations de hausse u et de baisse d, pour h
hausses l'actif risqué vaut au temps t St = uhdt_h avec h E
{0,1,...,t}.
Nous avons deux types d'option, les achats (call) et les ventes
(put)
Définition 3. Un call/put européen est un
contrat entre deux parties par eeuel'une ac corde à l'autre le droit
(mais nonl'obligation) de lui acheter/vendre auprixK un actif au terme T.
Nous étudierons seulement les calls dans un premier temps,
puis les puts quinous le verrons sont liés par une relation aux calls
Définition 4. Le payoff d'un call européen (resp
put) àl'échéance est fonction dea diff férence (ST
- K) (resp (K - ST)) . Si elle est positive on la note (ST - K)+ et
alors
St = uhdt--h > K (resp (K --
ST)+ et alors St = uhdt--h > K), l'option
est exercée et la valeur du payoff prend différentes formes selon
le type d'option, sinon e payoff vaut 0 et l'option n'est pas exercée La
valeur dun call à la date t = 0 est donc l'espérance
actualisée sous la probabilité risque neutre du payoff du
call.
On note xt la somme investie en sous-jacent durant la
période [t, t + 1] et yt la somme placée au taux sans risque
durant la même période.
On cherche à évaluer un call au temps t. Pour cela
on constitue un portefeuille au temps t en achetant xt unités de
sous-jacent et en plaçant un montant yt au taux sans risque r. La valeur
du call en t est équivalente à la valeur du portefeuille en t
:
Ct = xtSt + yt
En t + 1 le sous-jacent peut prendre deux valeurs, donc le
portefeuille Ct+1 s'écrit :
|
{
|
Cut+1 = xtuSt + yt (r +1)
Cdt+1 =
xtdSt + yt (r + 1)
|
{
xt =
yt =
On a un système à deux équations et deux
inconnues xt et yt. La résolution donne :
Cu --Cd
t+1 t+1
St(u--d)
uCd --dCu
t+1 t+1
(1+r)(u--d))
En remplaçant dans l'équation initiale on trouve la
valeur du call à la date t :
Cu t+ 1 -- Cdt+ 1
Ct =
( u -- d) +
uCdt+1 -- dCut+1
(1+ r) (u -- d))
que l'on peut réécrire
~ ~
1 1 + r - d u - (1 + r)
Ct = Cu t+1 u - d + Cd t+1
(1 + r) u - d
On reconnait alors la probabilité risque neutre que lon
a déja définie et donc Ct =
[ 1 ]
E1 (1+r) Ct+1 | Ct . On en déduit que le call
actualisé au taux sans risque sous la probabilité risque neutre P
possède la propriété de martingale :
|
Ct
|
~ Ct+1 ~
= E1 (1 + r)t+1 | St
|
|
(1 + r)t
|
Proposition 3. Le prix d'un call européen à la date
t = 0 dans le marché CRR est donné par la formule :
C0= (1+r)T .
XT ~T ~
(ph)(1 - p)T -h(SuhdT -h -
K)+
h
h=0
1
5 Un choix de u, d
Pour que le modèle soit conforme aux hypothèses
de Black et Scholes il faut que la variance du sous jacent de notre
modèle sous la probabilité risque neutre soit la plus proche de
celle de l'univers réel, c'est à dire de l'univers sous la
probabilitéditehistorique Q. Puisque la probabilité risque
neutre, nousl'avons vu, ne dépend que de u et d il nous faut donc bien
estimer ces paramètres en fonction du nombre de périodes du
modèle.
On divise la durée T de vie de l'option en n
périodes de durée de A = T et les coefficients à chercher
sont notés u et d pour ce partage en n périodes. On se place sur
une période I = [0, Ä ].On admet que Ä est très proche
de 0. On a vu en première partie que c'était le taux de rendement
de l'actif qui augmentait ou diminuait
On a Sn = Suhn-h, en
passant au log on obtient le taux de rendement log-normal suivant
(ST
ln in ( ST ST-1
S1)
S ) 1 \
\ST-1 ST-2 . . S
= ln
(ST ) ( ST-1) \ST-1 j \ST-2
+...+ln (S2) +ln(S1) S1 S
?t E {0, ..,T}et ?ît E {d, u}
De plus le changement de la probabilité historique
à la probabilité risque neutre ninfluant pas sur la variance,
l'hypothèse :: de: = udt+ówt, t E [O ,T] implique que
sous la probabilité historique ln (ST) suit une loi normale de variance
ó2T et donc il en est de même pour la variance de ln
(Sj) sous la probabilité risque neutre. En notant Sk =
SkAn pour tout k E [1, .., n] on a sous la probabilité
historique Q, par indépendance sur les périodes :
VQ [ln ( Sn )1 =VQ [ln G,Sn )1 + VQ [ln
( SSn-1 )1 +...+ V [ln (S1S2 )1 + VQ [ln (S1)
) 21
=n [qn (ln (un))2 + (1 -
qn) (ln (un))2 - (qn (ln
(un))2 + (1 - qn) (ln
(dn)))21 =n [qn (1 - qn) ln un
dn
On doit donc choisir un et dn tels que :
|
lim
n?+8
|
n[qn (1 - qn) (ln
(udni
|
21 = ó2T
|
Par ailleurs sur la probabilité historique on a la
contrainte sur lespérance
|
lim
n?+8
|
n [qn ln (un) + (1 - qn) ln
(dn)] = uT
|
On peut faire le choix un = dn 1 ce qui donne :
limn-4+00 (1 - qn) 4nqn (ln
(un))2 = ó2T lim
(2qn-1)nln(un)=uT
n-4+00
qT
Si on choisit ln (un) =ó n il faut
s'assurer de la compatibilité entre
|
?
?????
?????
|
lim
qn(1-qn)4n(ln(un))2 =1
n-4+00
sv/
lim (2qn - 1) n ln (un) = u T
n-4+00
|
v v
ce qui est le cas pour (2qn - 1) = u óvn
et donc qn = 1
T 2 + u 2óvn La probabilité risque
T
neutre est alors :
1 + rn - e-óvÄn er4n+óvn - 1
|
pn =
|
==
eóvÄn - e-óvÄn
|
|
|
e2óvn - 1
|
Pour n suffisamment grand, An proche de O on peut
utiliser le développement limité
ex 1 + x pour x proche de zero
D'où
|
lim pn =
n-4+00
|
1
2
|
|
lim
n-4+00
|
4pn(1 - pn) = 1
|
( (ST ))
et donc sous la probabilité risque neutre on a aussi VP ln
= ó2T
S
Deuxième partie

Quelques options "path independent"
CHAPITRE 1
LES OPTIONS BINAIRES
1 L'option cash or nothing
Définition 5. L'option cash or nothing permet
àl'acheteur de recevoirune prime Q déterminée dans le
contrat, lorsque loptionest eexercée, c'est à dire sie cours
duous-jacent dépasse K dans le cas d'un call ( et sile cours est en
dessous danse cas d'un putt. Le graphique suivant montre le payoff dun tel
call, enabscisse S est la valeur du sous jacent à
l'échéance.
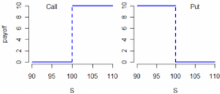
FIG. 1 - Exemple du payoff cash or nothing K=100, Q=10, T=1 an
1.1 Exemple
On veut acheter un call cash or nothing. A t = 0 le cours du
sous jacent vaut S = 50 euros. On donne le taux d'intérêt annuel r
= 5% ,la date d'échéance T = 6 mois et le nombre de
périodes où l'on observe le cours du sous jacent n = 6 . On
estime de plus la volatilité annuelle du sous jacent à a = 0, 4.
Le vendeur de l'option donne le prix d'exercice à K = 50 et offre une
prime de Q = 50. Autrement dit si à la date d'échéance de
l'option le sous jacent est supérieur à 50 l'option est
exerçable et nous rapportera 50. Dans le cas contraire la somme que l'on
aura dépensée pour acheterloption sera perdue.
Nous allons utiliser la méthode de l'arbre binomialOn
commence par estimer nos para-
mètres.
0,5 1+ rn = er1n = 1.0042, un =
eó'4n = 1,1224, dn = e-ó'1n = 0.8909
T
An = n
6,
d'ou :
|
p
|
er1n - e-ó'1n
|
= 0, 4892 = 1-p = 0, 5108
|
|
eó'1n - e-ó'1n
|
Nous passons ensuite à l'arbre des valeurs du sous
jacent.
Tree Display
At each node:
Upper value = Underlying Asset Price Lower value = Option
Price
Values in red are a result of early exercise.
25,008
0
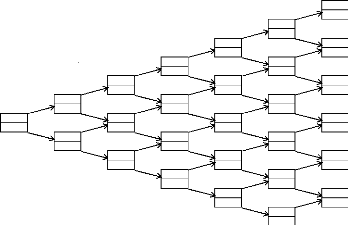
Time step, dt = 0, 0833 years, 30,42 days
Strike price = 50 1,0042
Growth factor per step, a = 1,0042
Discount factor per step = 0,9958
Probability of up move, p = 0,4892
Up step size, u = 1,1224
Down step size, d = 0,8909
15,788
50
23,494
44,547
8,5353
56,12
62,989
2,8164
33,003
39,689
14,579
50
42,799
44,547
70,699
5,7811
35,361
23,89
56,12
0
49,586
79,353
62,989
36,648
39,689
31,505
11,867
50
0
0
49,793
49,793
24,359
44,547
28,069
89,066
70,699
35,361
56,12
0
0
0
62,989
99,967
79,353
39,689
31,505
50
50
50
50
0
0
0
Node Time:
0,0000 0,0833 0,1667 0,2500 0,3333 0,4167 0,5000
FIG. 2 - Evaluation du call cash or nothing dans l'arbre
binomial
Lecture de l'arbre On observe les valeurs de St à
chaque étape. En noir sont données les valeurs du cours et du
call (en dessous) et en rouge les valeurs du payof. On déduit les
valeurs des options à chaque période par le principe de
rétroduction : la valeur de loption en t = 6 se déduit de (ST --
K)+ . On déduit les valeurs précédentes en
calculant l'espérance sous probabilité risque neutre que l'on
actualise au taux sans risque. On remonte ensuite de la même
manière jusqu'en t = 0. On a par exemple la valeur du call après
deux montées
1
Cuu = 1+ r[pCuuu + (1 -- p) Coud]
n
1.2 Expression mathématique
De façon mathématique on peut exprimer le call d'un
option cash or nothing comme
|
?
????????? ?
??????????
|
Q si ST > K
0 sinon
Ou encore QlST>K
|
Pour exercer ce call il faut que le sous jacent dépasse le
seuil K à la date T. Nous allons donc définir le nombre minimal
de hausses qu'il faut pour remplir cette condition.
Proposition 4. Le nombre minimal de hausses pour que la valeur du
ours du sous acent dépasse K est h0 tel que :
SuhdT-h > K
K
SdT
uh
<#> >
dh
ln( ) ln( T)
Soit l'entier naturel h0 = 1+ S(d)1 qui est la partie
entiére deSdaugmentée de
ln(7/) ) 1.
Proposition 5. Le prix d'un call binaire cash or nothing dans le
modèle CRR adate
d'aujourd'hui est
C0 = e-rTQ.P(ST > K)
preuve : Le prix d'un call à la date t = 0 est
l'espérance actualisée au taux sans risque du payoff de l'option.
Soit
C 0 = e -rT E 4 [Q1ST =K]
Nous allons donc nous attacher à trouver la
probabilité P pour que ST soit supérieur à K.
1.3 Convergence du modèle de Cox Ross Rubinstein
Nous avons calculé le call uniquement en prenant en
compte que le sous-jacent pouvait varier chaque mois. Or en
réalité il varie tout le tempsLe problème est que pour un
nombre de périodes n très grand, le nombre de calculs à
faire est considérablepuisque dans un arbre à n périodes
il y a 2n trajectoires du sous-jacent. Nous allons donc faire
converger la loi binomiale qui on le sait pour n très grand converge
vers une loi normale beaucoup plus facile à estimer. On divisera la
période de vie de l'option T en n petits intervalles
'h = [hzn, (h + 1)zn]
pour h = 0,....n - 1 et on note zn = T n .On se
retrouve comme si on regardait l'actif au bout de chaque intervalle 'h.
Le taux d'intérêt discret sans risque rn
sur 'h sera choisi tel que :
lim (1 + rn)n = lim
n?+00 enr4n
n?+00
On choisit 1 + rn = erAn
Le pas des subdivisions que nous avons construites sur [0,n]
tend vers O quand n ? +oc . Il parait naturel de penser que notre suite de
processus discrets va converger vers un marché financier à temps
continu.
?n,?h = {1,...,n - 1} le cours de l'actif risqué pendant
une période de temps Ih peut monter de un ou baisser de
dn tel que :
S(h+1)Än = h+1,nShAn
Pour n fixé les h,n E {un,
dn} sont définies sur l'espace de probabilité
(Qn, Fn, Pn) et sont toutes identiques et
indépendantes telles que
1n ( h,n = un) = p = 1 - 1n (
h,n = dn)
où pn la même probabilité risque
neutre définie dans le modèle une période puisquon ne fait
que répéter ce modèle n fois. Dans la suite nous prendrons
comme paramètres
un = eóvÄn, dn =
e-óvÄn, pn = ertn - dn
un - dn
Proposition 6. La probabilité d'exercer un call binaire
cash or nothingest
1(ST = K) =N(a2)
où N est la fonction de répartition de la loi
normale centrée réduite.
preuve : Sur n périodes un call binaire cash or nothing
s'écrit
|
Ccash n=0 = e-rT Q.P(Sn = K) =
e-rTQ
|
Xn (n )
(ph n)(1 - pn)n-h
h
h=h0
|
où
n
X (n )
(ph n)(1 - pn)n-h
h
h=h0
est la probabilité qu'une loi binomiale de
paramètres (n,pn) prenne des valeurs supérieures
à h0. Soit Xn la loi binomiale de paramètre n et
pn. On cherche la limite quand n tend vers l'infini de
P(Xn = h0). Comme Xn est la somme de n variables de
Bernoulli de même loi, indépendantes, on commence par centrer et
réduire" pour une éventuelle application du
théorème central limite :
|
Xn-npn
/ n (pn(1 - pn)) =
|
h0 - npn
|
|
/
n(pn(1 - pn))
|
On cherche donc la limite quand n tend vers l'infini de
h0 - npn
/
n (pn(1 - pn))
or [x] <x < [x] + 1 donc
|
ln(K ) +na/Än
S 2a/Än < h0 <
|
ln(K ) +na/Än
S +1
2a/Än
|
ln(K S )+na/Än
La limite si elle existe de h0-npn2a/ Än -npn
/n(pn(1-pn))
est celle de vnpn(1-pn)
puisque lim pn = 1 2 et lim 1 /npn(1-pn) =
0
n?+8 n?+8
|
lim
n--+oo
|
|
h0 - npn
|
= lim
n--+oo
|
|
|
|
N/
n (pn(1 - pn))
|
= lim
n--+oo
Donc :
N/n (pn(1 - pn))
ln (K ) + no-vÄn (1 -
2pn)
S
2o- N/Änn (pn(1 - pn))
on a déjà vu :
1
lim pn =
2
n--+oo
Donc
|
lim
n--+oo
|
2o-N/Änn (pn(1 - pn)) =
lim
n--+oo
|
2o- N/AnN/n (pn(1 - pn)) =
o-vT
|
Calculons la limite de no- (1 - 2pn)
vAn. Pour cela on améliore l'approximation de pn.
En utilisant le developpement limité ex 1 + x +
x22 pour x proche de zero et le fait que nÄn = T on
a :
|
pn =
|
1 + rn - e--óN/Än
'
eóN/Än - e--óN/Än
|
rÄn + o-vÄn -
ó2Än
2
2o-vÄn
|
On en déduit d'une part que ::
(
2 2o- 2

r -N/An
o-2 )
pn
1 1
1 o-2
1 - 2pn- (r - 2 N/An
o-
|
lim
n--+oo
|
no- (1 - 2pn) N/An =T (2 - r)
|
|
d'où
|
lim
n--+oo
|
!- npn ln n,)+T (21 o-2 -
r)
N/n (pn(1 - pn)) =a2 avec a2= o-vT
|
D'après le théorème de Lindberg qui
généralise le théorème central limite on peut
affirmer que :
|
lim
u?+00
|
) +00f f a2
Xu -- npu = 1 -y2 1 -y2
P pe2 dy = e
n (pu(1 -- pu)) = -- a2
v2ð v2ð 2dy = N (a2)
-a2 -00
|
où N est la fonction de répartition de la loi
normale centrée réduite.
Application à l'exemple On reprend les données de
l'exemple. On calcule alors a2 = --0,05303. Le calcul donne : N (a2) = 0,47885
et donc le prix du call estCcash
u=0 =
e-rTQ.0, 47885 = e-0,05.0,5.50.0,47885 =
23,351. On remarque que l'écart par rapport
à la méthode de l'arbre est fort, il faudrait un
nombre de périodes plus élevé pourêtre plus
précis.
2 L'option asset or nothing
Définition 6. L'option asset or nothing permet de toucher
la valeur dusous acent ST à la date T , lorsque l'option est
exercée.
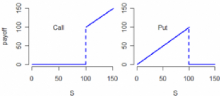
FIG. 3 - Exemple du payoff asset or nothing K=100T=1 an
2.1 Exemple
On reprend toujours les mêmes données mais cette
fois le payoff vaut le sous jacentt
On a sous forme d'arbre Casset
0 = 21, 754
At each node:
Upper value = Underlying Asset Price Lower value = Option
Price
Values in red are a result of early exercise.
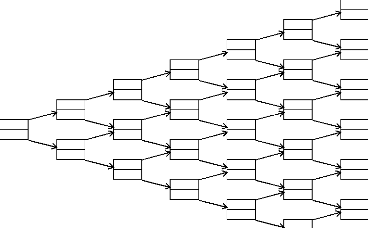
|
Strike price = 50
|
1,0042
|
|
|
Discount factor per step = 0,9958
|
|
|
|
Time step, dt = 0,0833 years, 30,42 days
|
|
|
|
Growth factor per step, a = 1,0042
|
|
79,353
|
|
Probability of up move, p = 0,4892
|
|
79,354
|
|
Up step size, u = 1,1224
|
70,699
|
|
|
Down step size, d = 0,8909
|
64,12
|
|
|
62,989
|
|
62,989
|
0
31,505
0
50
21,754
44,547
32,957
11,202
56,12
47,509
39,689
3,5481
19,289
50
44,547
31,989
35,361
56,12
7,283
50,053
39,689
14,95
50
0
99,967
99,967
89,066
89,066
79,353
79,353
70,699
70,7
62,989
62,989
56,12
30,687
50
0
44,547
0
39,689
0
35,361
0
31,505
0
28,069
0
25,008
0
Node Time:
0,0000 0,0833 0,1667 0,2500 0,3333 0,41 67 0,5000
FIG. 4 - Evaluation du call asset or nothing dans l'arbre
binomial
2.2 Expression mathématique
De façon mathématique on peut exprimer le call
d'une option asset or nothing à ladate T comme :
|
?
????????? ?
??????????
|
ST si ST > K
0 sinon
Ou encore ST1ST=K
|
Pour exercer ce call il faut que le sous jacent dépasse
le seuil K à la date T. De la même manière que pour le call
cash or nothing le nombre minimal de hausses pour que la valeur du cours du
sous jacent dépasse K est égal à
h0 = 1+ rn(S(dKn)l
ln(Unn:)
On peut donc donner le prix du call asset or nothing à la
date initiale.
Proposition 7. Le prix d'un call binaire asset or nothing dans
lele modèle CRR à a date d'aujourd'hui
est
C0 = S.P0(ST > K)
où P0 est une nouvelle probabilité
preuve : Le prix d'un call à la date t = 0 est
l'espérance actualisée au taux sans risque
du payoff de l'option. Soit
[ST1ST=K}]
(1 + rn)n
On partage la durée de vie de l'option en n
périodes on peut alors écrire que
|
donc
|
[ST1ST=K}]
|
= S
|
Xn
h=h0
|
~npnun h (0- pn) dn)n h
h) 1+rn 1+ rn
27
|
|
(1 + rn)n
|
P (ST > K) =
X (nh)pnh(1
n
h=h0
On pose alors
p' n = pnunet 1 - p' n =(1 - pn) dn
1 + rn1 + rn
Et on obtient
|
EP [ST1ST=K] = S
|
Xn(n )
((pn)'h(1 - p' n)
n-h= SP' (ST > K)
h
h=h0
|
2.3 Convergence du modèle de Cox Ross et
Rubinstein
Tout comme dans l'option cash or nothing, on va chercherla
valeur de P' (ST > K) en divisant la période de vie de
l'option en très petites périodes de longueur An de
sorte à faire converger la loi binomiale vers une loi normaleLes
calculssont les mêmes mais la probabilité diffère. Sous les
mêmes conditions queloption cash or nothing nous allons devoir calculer
P' (ST = K)
Proposition 8. La probabilité d'exercer un call binaire
asset or nothing estP' (ST = K) = N (a1) où N est la fonction
de répartition de la loi normale centrée reduite.
preuve : De la mème manière que pour le call cash
or nothing nous allons avoir besoin de calculer :
|
lim
n?+8
|
h0 - np' n
|
=lim
n?+8
|
ln(K ) +nóvÄn(1 - 2p'
n)
S
|
|
/
n (p'n(1 - p'n))
|
/
2ó Änn (p'n(1 -
p'n))
|
en utilisant les developpements limités ex 1 +
x +x2 2 pour x proche de zero et le fait que
nÄn = T on montre :
'
puisque pn = erÄn
n
1 1
' ( ó2 )

+ r + 'VAn
pn R-''' 2 2ó 2
|
1 -- 2pn R-''' --
|
ó) 2
1
r + An
ó ( 2
|
On en déduit d'une part que ::
|
lim
n,+cc
|
2ó'VÄnn (p'n(1
--p'n)) = lim 2ó \lÄnn (1) =
óN/T
n,+cc
4
|
|
d'autre part :
|
lim
n,+cc
|
n (1 -- 2p'n) 'V An = --T
(ó2 + ór )
|
ce qui nous donne :
|
lim
n,+cc
|
|
h 0 -- np'n
|
|
ln (P -- T (52 + ró;)
|
lnGsj+T(`;+
ró;)
ó N/T
|
= --a1
|
|
|
|
|
|
'Vn (p'n(1 -- p'n))
|
|
óN/T
|
On peut alors réécrire la probabilité
suivante en notant X'n la loi binomiale de
paramètre
'
n , pn :
( Xn -- np' h0 --
np'n )
P(X:., > h0) = P n >
'Vn (p'n(1 -- p'n)) -- 'Vn
(1n(1 -- p'n))
et donc
1
P(X'n > h0) = P (AT (0,1) > --a1)
= N/2ð
lim
x,+cc
-y2 1
e 2 dy =
2
y , , r
e 2 ay = JV (a1)
+cc
f
-a1
a1
f
-cc
N/2ð
où AT est la fonction de répartition de la loi
normale centrée réduite
Application à l'exemple On reprend les données
de l'exemple. On calcule alors a1 = 0, 2298 Le calcul donne : V (a1) = 0, 5908.
On multiplie alors par la valeur du sous jacent à l'origine et on
obtient :
C
asset 0 = 50.0, 5908 = 29, 544
Le problème du nombre de
périodes insuffisant est toujours le même.
3 La formule de Black et Scholes
On retrouve la formule de Black et Scholes pour
l'évaluationdun calleuropéen classique (call vanille) avec les
calls cash or nothing et asset or nothing où la prime du callcash or
nothing est le prix d'exercice K.
Cvanille = Casset - Ccash = SV(a1) - Ke_rTV(a2)
puisque le payoff de cette option est donné par
CT = max(ST -K,0)

FIG. 5 - Exemple de payoff de l'option vanille K=80, T=1 an
Sous l'absence d'oportunité d'arbitrage on peut donnerla
formule de parité call/put.
Définition 7. La formule de parité Call/put
s'écrit :
C-P=S-Ke_rt
On en déduit le prix d'un put vanille avec les
propriétés delaloi normale
C = S.V(a1) - Ke_rT.V(a2)
P = Ke_rT.V(-a2) - S.V(-a1) avec
|
a1 =
|
ln(S/K) + (r + 1 2ó2)T
|
|
/
ó T
|
/
a2 = a1 - ó T
Exemple On reprend les mêmes données pour
évaluer le call vanille aveclarbrebinomial ce qui donne :
Tree Display
At each node:
Upper value = Underlying Asset Price Lower value = Option
Price
Values in red are a result of early exercise.

|
|
|
99,96732
|
|
Strike price = 50
|
|
|
49,96732
|
|
Discount factor per step = 0,9958
|
89,06561
|
|
|
|
31,50489
|
|
31,50489
|
|
0
|
|
0
|
28,0692
0
25,00817
0

Time step, dt = 0,0833 years, 30,42 days
Growth factor per step, a = 1,0042
Probability of up move, p = 0,4892
Up step size, u = 1,1224
Down step size, d = 0,8909
5,966018
50
44,54736
56,12005
9,462262
2,66633
4,709153
62,98919
39,68935
0,731652
14,50592
50
21,32023
44,54736
70,69912
56, 12005
8,098216
35,36112
1,501841
0
29,76769
62,98919
3,082786
39,68935
79,35276
13,40412
50
0
44,54736
39,27351
70,69912
20,90702
56, 12005
6,327945
35,36112
0
0
29,35276
62,98919
12,98919
50
0
0
79,35276
39,68935
Node Time:
0,0000 0,0833 0,1667 0,2500 0,3333 0,4167 0,5000
FIG. 6 - Evaluation d'un call vanille
On a bien la formule qui s'applique à l'arbre en
utilisantles calls précédents
Cvanille = Casset-Ccash = 21,754-15, 788 = 5,966 avec les valeurs
trouvées par les arbres
On remarque que le prix d'un call vanille est nettement
inférieur à celui dun call binaire, le payoff étant moins
élevé. En utilisant la formule de Black et Scholes on trouve que
le call vanille vaut
Cvanille = Casset-Ccash = 29, 544-23,351 = 6.193 avec les
valeurs trouvées parl'application numérique
Encore une fois le nombre de périodes ne suffit donc
pasLe graphiquesuivant montre la convergence graphique du modèle
binomial de notre exemple vers la valeur de Black et Scholes suivant le nombre
de périodes :

FIG. 7 Convergence vers Black et Scholes
Pour un résultat correct le nombre de périodes
minimal est de lordre de 80 périodes.
CHAPITRE 2
LES OPTIONS SUR OPTIONS
Les options sur options donnent droit à l'acheteur de
loption de prix dexercice K1 et de maturité T1 (dite!option
mère!) d'acheter ou de vendre une autre option de prix d'exercice K2
> K1 et de maturité T2 > T1 (dite!option fille!) à des
caractéristiques prédéfinies et pendant une période
de référenceLe sous jacent est ici une option. ly a quatre types
d'options composéesle call sur call le call sur put le put sur put et le
put sur call. Pour un call sur call par exemple il faut dabord évaluer
le call fille à la date T1. On peut alors connaitre la valeur du payoff
de l'option mère et en déduire la valeurdu call mère
à la date initiale. Les payoffs respectifs des options
mèressont
Ccall = max(CT1 (S,T2,K2) - K1,0) Cput =
max(PT1 (S,T2,K2) - K1,0) Pcall = max(K1 - CT1 (S, T2,
K2) , 0) Pput = max(K1 - PT1 (S, T2, K2) , 0)
exemple On reprend notre exemple principal. On veut
évaluer un call sur call et un put sur put par la méthode
binomiale. L'option fille a comme support Sde prix dexercice K2 = 50 et de
maturité T2 = 6 mois. L'option mère a comme support l'option
fille, de prix d'exercice K1 = 5 et de maturité T1 = 3 mois. Le premier
arbre donne les valeurs de l'option fille à chaque mois. On regarde
alors la valeurs de cette option à ladate t = 3 mois pour connaitre le
payoff de l'option mère à cette dateOn remonte ensuite
jusquà ladate d'aujourd'hui pour connaitre la valeur à la
dateinitiale.
Tree Display

Time step, dt = 0,0833 years, 30,42 days
strike=5
Strike price = 50
Growth factor per step, a = 1,0042
Discount factor per step = 0,9958
Probability of up move, p = 0,4892
Up step size, u = 1,1224
Down step size, d = 0,8909
5,966018
OPTION MERE
50
44,54736
56, 12005
9,462262
2,66633
4,709153
62,98919
39,68935
0,731652
14,50592
50
44,54736
70,69912
21,32023
56, 12005
8,098216
35,36112
1,501841
0
29,76769
79,35276
62,98919
3,082786
39,68935
31,50489
13,40412
50
0
0
20,90702
44,54736
89,06561
39,27351
70,69912
56,12005
6,327945
35,36112
28,0692
0
0
0
49,96732
99,96732
29,35276
62,98919
39,68935
31,50489
25,00817
79,35276
12,98919
50
0
0
0
0
OPTION FILLE
|
0,1667
|
0,2500
|
0,3333
|
0,4167
|
0,5000
|
|
21,32023
|
|
16,32023
|
|
14,50592
|
|
|
9,526705
|
|
8,098216
|
|
3,098216
|
|
4,709153
|
|
|
1,509358
|
|
1,501841
|
|
0
|
|
0,731652
|
|
|
0
|
|
0
|
|
0
|
Node Time:
0,0000 0,0833
Up step size, u = 1,1224 Down step size, d = 0,8909

9,462262
5,408894
5,966018
3,009085
2,66633
0,735314



Page 1
FIG. 1 - Evaluation d'un call sur call
Tree Display
OPTION FILLE

Strike price = 50
Time step, dt = 0,0833 years, 30,42 days
Discount factor per step = 0,9958
Growth factor per step, a = 1,0042
Probability of up move, p = 0,4892
Up step size, u = 1,1224
Down step size, d = 0,8909
4,731 514
50
44,54736
56,12005
2,311326
7,088076
62,98919
0,690298
3,882726
39,68935
10,21 587
50
44,54736
70,69912
56,12005
6,333369
35,36112
14,01 777
1,35706
0
79,35276
62,98919
39,68935
9,895714
31,50489
18,08017
2,66785
50
0
0
44,54736
89,06561
56,12005
5,244737
35,36112
70,69912
14,43098
28,0692
0
0
0
99,96732
62,98919
39,68935
31,50489
79,35276
10,31 065
18,49511
50
0
0
0
0
21,7229

3,882726
4,731 514
0
0,864596
OPTION MERE
Node Time:
0,0000 0,0833 0,1667
Up step size, u = 1,1224
Down step size, d = 0,8909
0,690298
4,288912
2,311326
2,992185
1,897499 1,774731
7,088076
|
0,2500
|
0,3333
|
0,4167
|
25,00817
|
|
24,99183
|
|
0,5000
|
|
0
|
|
5
|
|
|
1,35706
|
|
3,64294
|
|
6,333369
|
10,21 587
0
14,01 777
0
Page 1
FIG. 2 - Evaluation d'un put sur put
On regarde également l'évaluation d'un call sur put
et d'un put sur call
Tree Display
OPTION FILLE

Strike price = 50
Time step, dt = 0,0833 years, 30,42 days
Discount factor per step = 0,9958
Growth factor per step, a = 1,0042
Probability of up move, p = 0,4892
Up step size, u = 1,1224
Down step size, d = 0,8909
4,731 514
50
44,54736
56,12005
2,311326
7,088076
62,98919
0,690298
3,882726
39,68935
10,21 587
50
44,54736
70,69912
56,12005
6,333369
35,36112
14,01 777
1,35706
0
79,35276
62,98919
39,68935
9,895714
31,50489
18,08017
2,66785
50
0
0
44,54736
89,06561
56,12005
5,244737
35,36112
70,69912
14,43098
28,0692
0
0
0
99,96732
62,98919
39,68935
31,50489
79,35276
10,31 065
18,49511
50
0
0
0
0
21,7229
|
0,2500
|
0,3333
|
0,4167
|
25,00817
|
|
24,99183
|
|
0,5000
|
|
0
|
|
0
|
|
|
1,35706
|
|
0
|
|
6,333369
|
|
1,333369
|
|
14,01 777
|
|
9,01 7772
|
OPTION MERE
strike=5
Node Time:
0,0000 0,0833 0,1667
Up step size, u = 1,1224
Down step size, d = 0,8909
0,690298
0
2,311326
0,345005
4,731 514
1,691124 0,678247
7,088076
2,994166
10,21 587
5,236665


3,882726
Page 1
FIG. 3 - Evaluation d'un call sur put
Tree Display

Time step, dt = 0,0833 years, 30,42 days
strike=5
Strike price = 50
Growth factor per step, a = 1,0042
Discount factor per step = 0,9958
Probability of up move, p = 0,4892
Up step size, u = 1,1224
Down step size, d = 0,8909
5,966018
OPTION MERE
50
44,54736
56, 12005
9,462262
2,66633
4,709153
62,98919
39,68935
0,731652
14,50592
50
44,54736
70,69912
21,32023
56, 12005
8,098216
35,36112
1,501841
0
29,76769
79,35276
62,98919
3,082786
39,68935
31,50489
13,40412
50
0
0
20,90702
44,54736
89,06561
39,27351
70,69912
56,12005
6,327945
35,36112
28,0692
0
0
0
49,96732
99,96732
29,35276
62,98919
39,68935
31,50489
25,00817
79,35276
12,98919
50
0
0
0
0
OPTION FILLE
3,4981 59
Node Time:
0,0000 0,0833 0,1667
|
0,2500
|
0,3333
|
0,4167
|
0,5000
|
|
21,32023
|
|
0
|
|
|
8,098216
|
|
0
|
|
|
1,501841
|
Up step size, u = 1,1224
Down step size, d = 0,8909
14,50592
0
9,462262
0,905138
5,966018
1,980956
2,66633
3,027491
4,709153
4,247558
0,731652
1,779415
0
5
Page 1
FIG. 4 - Evaluation d'un put sur call
Ces options sont souvent utilisées par un agent de
couverture qui nest par certain
d'avoir besoin de se couvrir, leur prix est donc moins
élevé que celui dune optionclassique. De plus on remarque que ces
options qu' une infinité de combinaisons est possible entre la prime de
l'option mère et celle de l'option fille on peut donc répartirles
coûts de couverture en fonction des besoins de l'entreprise. De plus la
volatilité est figée durant la période de vie de l'option
sur option cela évite les risques liés au fluctuation du
marché quand onest proche de l'échéance.
Troisième partie

Quelques options path dependent
CHAPITRE 1
LES OPTIONS LOOKBACK
Définition 8. Les options lookback donnent à leur
détenteurle droitde cchoisir comme prix d'exercice, le cours de l'actif
le plusfavorable sur la période considérée.
Il existe deux types d'options lookback
L'option lookback avec un prix d'exercice fixe qui pourun call a
unpayoff ééal à a différence positive entre le
maximum du cours et du prix d'exercice~xé

FIG. 1 - payoff du call lookback fixe
L'option lookback avec un prix d'exercice flottant qui pour un
call a un payoff ééal à a différence positive entre
le prix du sous jacent à ladated'exercice eteminimum duours. Le prix
d'exercice pour le call est alors min0<t<T St. Pour un put le
prix d'exercice est max0<t<TSt

1. Le call lookback fixe européen
Ces types d'options ont un intérêt pourl'acheteur
qui pense qu'il existera une forte variation des cours surla période,
mais enen iignorant complltementa date, ainsi quee parfait moment
d'investissement.Elles sont donc parfaitement adaptées aux optionsuroo
péennes puisque on ne peut pas connaitrele maxou emindu cours avanta
date d'exercice. Il faut noter que ces options sont toujours exercées
cequi rend eur prix beaucoup plus élevé qu'une option classique
européenne comme nous allons evoir
1 Le call lookback fixe européen
Le payoff de l'option lookback fixe est
CT= max (St)-KpourK<S0
0<t<T
|
PT=K- min
0<t<T
|
(St) pour K ~ S0
|
Exemple On veut connaitre le prix d'un call lookback
européen fixe. Pour calculer le payoff à la date T on choisira
toujours le cours maximun atteint parle sous jacent sur tous les chemins menant
à cette date moins le prix dexercice K. Par exemple si l'actif vaut
à la date T, ST = 79, 353 on prendra comme cours maximum Smax = 89,066.
Le payoff vaut alors : Smax - K = 89,066 - 50 = 39, 066. Une fois les payoffs
calculés on appliquela rétroduction. Nous obtenons l'arbre
suivant

FIG. 3 - arbre d'évaluation d'un call lookback à
prix d'exercice fixe
2 Le call lookback flottant européen
Le payoff de l'option lookback flottant qui est toujours
exercée est
CT = ST -- min (St)
0<t<T
PT= max (St)--ST 0<t<T
Exemple On veut connaitre le prix d'un call lookback
européen flottant àla date daujourd'hui. On utilise l'arbre
binomial, dans un premier temps commetoujours on calcule l'évolution du
sous jacent. Pour calculer le payoff àla date T on choisira toujours le
cours minimum atteint par le sous jacent sur tous les chemins menant à
cette date. Par exemple si l'actif vaut à la date T, ST = 79,353 on
prendra comme cours minimum Smin = 44, 547. Le payoff vaut alors ST - Smin =
79,353 - 44, 547 = 34,806 Une fois les payoffs calculés on applique la
rétroduction. Nous obtenons l'arbre suivant

FIG. 4 - arbre d'évaluation d'un call lookback à
prix d'exercice flottant
Conclusion On remarque que le prix du call loockback est
beaucoup plus élevé que pour un call européen classique
(de l'ordre de trois à quatrefoissupérieurdans nos cas) Mais un
problème reste, en effet à moins de pouvoir regarder à
tout instant le prix dusous jacent, on peut rater une valeur du cours et donc
il estimpossible de connaitre le maximum oule minimum du cours réel en
utilisant l'arbre binomial
3 Evaluation du call lookback flottant pourr = ó
2
Sous la probabilité risque neutre P l'évolution du
cours du sous jacent est donnée par
|
l'équation :
|
dSt
St
|
= rdt + ódWt
|
où Wt est un P mouvement brownien standard, r le taux
continu sans risque , et ó2 la
variance par unité
de temps. La formule d'Ito admise permet dobtenir pour tout t de [0; T]
|
(St J
ln
S
|
(= r -
|
ó2 J2
|
t + óWt
|
Pour simplifier on se place dans un cas particulier r = ó
2 donc ln (St ) = óWt. Pour évaluer
S
le call loockback de prix d'exercice minSt pour t E 0 = t = T il
nous faut connaître la loi de
|
min
0<t<T
|
St = S min
0<t<T
|
eóWt
|
Pour cela , on va commencer par determiner la loi de minSt pour t
E 0 = t = T. On obtient la relation pour b = a et b = 0
Propriété 1.
J
2b
/
ó T
( J ( -a J ( -a +
P óWT = a et min
0<t<T óWtb = N / - N
ó T
On peut expliquer ce résultat par la
propriété de reflexion du mouvement brownien sur le graphique
suivant où t = 0, W0 = 0 :
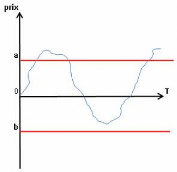
FIG. 5 Encadrement de la trajectoire de St
Démonstration : En effet par le principe de
réflexion du mouvement brownien autour de la droite de "niveau b" on
peut écrire
( ) f-a + 2b
P óWT > a et min
0<t<T óWt b = P (óWT 2b - a) = f './
ó T
Chaque trajectoire (óWt)0 t T, où
óWt a même loi que ó'./t f (0, 1) qui atteint b sur [0, T]
et dépasse a en T, est réfléchie par rapport à cet
axe en une trajectoire qui en T prend une valeur inférieure à 2b
- a. Ce principe est représenté par la figure suivante
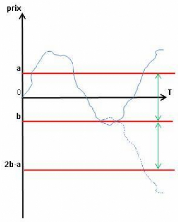
FIG. 6 - Le principe de réflexion du brownien
Si óWT est la trajectoire initiale, alors 2b -- óWT
est la trajectoire réfléchie par rapport à la constante de
niveau b et
óWT = a?2b--óWT < 2b--a <b
Donc
)
2b
v
ó T
( ) (--a +
P óWT = a et min
0<t<T óWt < b = N
D'où puisque
( ) ( )
P óWT = a et min
0<t<T óWt = b + P óWT = a et min
0<t<T óWt < b
=P(óWT = a)
( )
N (0; 1) = a
= P v
ó T
=N
( --a )
v
ó T
On en déduit que pour tout a= b et b = 0:
( J ( --a J
P óWT = a et min
0<t<T óWt = b = N v -- N
ó T
( --a + 2b J
v
ó T
En particulier pour a = b
( J ( J
P óWT = b et min
0<t<T óWt = b = P 0<t<T óWt
= b
min
D'où pour tout b = 0
( J ( --b J ( b
J
P 0<t<T óWt = b
min = N v -- N v
ó T ó T
Le payoff du call lookback est égal à
|
ST -- min
0<t<T
|
St = Seó' T -- S min
0<t<T
|
eó't
|
et la valeur de ce call en 0 est donnée par
( J v
Clookback
0 = e_rT E P ST -- S min
0<t<T eó't T puisque r = ó2
= SN (d1)--SN (--d1) où d1 = ó2
car E (eó'T ) = e ó2 2 Tpuisque W
t est un mouvement brownien et eó'T + ó2 2
t est une martingale.
Exemple Dans notre exemple en maintenant ó = 0,4 il
faudrait avoir r* = 0,16
2= 8%. Ceci permet de garder le même arbre
pour le sous jacentseule la probabilitérisque neutre change:
1, 1224 -- 0,8909
= 0,4989
(1,08)
p=
1 12 --0,8909
Le taux d'actualisation période est r6 = (1,08) 1 12
1,0064. On obtient l'arbre suivant :
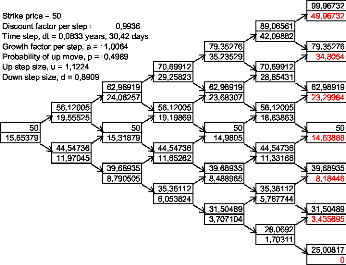
FIG. 7 Call lookback flottant pour r = ó2 2
La formule que nous avons trouvé nous
donneClookback
0 = SN (d1) - SN (-d1), avec
v T = 0, 4v0, 5 = 0, 28284 d'où Clookback
d1 = ó 0 = 50.0, 6113-50.0, 3886 = 11, 13503. Avec
l'arbre on trouve une valeur relativement proche donc un nombre
de périodes un peu plus élevé pourrait nous donner une
bonne approximation
CHAPITRE 2
LES OPTIONS BARRIÈRES
Définition 9. Les options à barrière
peuvent être désactivantes (out) ou activantes (in)) L'option se
comporte comme une option de type européenne saufqu'elles sont
dotées d'une barrière c'est à dire d'un prix du sous
jacent à partir duquel 'option meurt (out) ou prend vie (in). L'option
disparaît ou apparaît dès que le cours du sous-jacent
atteint, pendant la période de référence, la
barrière fixée préalablement il y a donc deux principaux
types d'options barrière :
~ Option down : l'option est désactivée ou
activée lorsque e cours du sous jacent franchit la barrière
à la baisse
~ Option up : l'option est désactivée ou
activée lorsque e cours du souss-acent franchit la barrière
à la hausse.
Quelques options versent parfois une compensation si la
barrière n'est pas touchéee One place dans le cas où
aucune prime n'est versée

FIG. 1 - exemple de barrière up-in
Il existe huit types d'options barrières dont es
payo~ss'écrivent
|
Down ?4 in Cati Down ?4 in Put Down ?4 out Caii Down ?4 out
Put Up ?4 in Cati
Up ?4 in Put
Up ?4 out Cati
|
= max(ST - K, 0) si min0<t<T(St) <B =
max(K - ST, 0) si min0<t<T(St) < B = max(ST - K, 0) si
min0<t<T(St) > B = max(K - ST, 0) si min0<t<T(St) > B =max(ST
- K, 0) si max0<t<T(St) > B = max(K - ST, 0) si max0<t<T(St)
> B = max(ST - K, 0) si max0<t<T(St) < B
|
|
Up ?4 outPut
|
= max(K - ST, 0) si max0<t<T(St) <B
|
Remarque On a une relation de parité entre in et out. Si
par exemple on additionne le
payoff d'un call up&in et d'un call
up&out on obtient le payoff d'un call européen classique
1 Evaluation par l'arbre binomial
L'arbre va nous permettre de bien voir ce qui se passe autour
de la barrière. On a vu que pour évaluer un call dans l'arbre
binomial on utilisait un principe de rétroduction. ci nous allons avoir
un problème pour appliquer cette méthode puisque l'on a
très peu de chance que la barrière se situe sur les noeuds et
pour évaluer le call on a besoin de cette valeur. La figure suivante
nous montre le problème

barrière
FIG. 2 Le problème de la barrière
Pour évaluer le call aujourd'hui il nous faut donc
connaître la valeur exacte du call à chaque noeud avant que le
sous jacent ne franchisse la barrière. Nous allons utiliser une
méthode d'interpolation pour approximer la valeur du call sur la
barrière. Pour cela on determine d'abord deux autres barrières,
supérieure et inférieure, qui encadrent la vraie barrière
comme le montre la figure suivante

barrière supérieure
vraie barrière
barrière inférieure
FIG. 3 encadrement de la barrière
Plaçons sur un noeud coupé par la
barrière de valeur B. On note Cu la valeur du call quand le
sous jacent monte et Cd quand il baisse. Pour connaitre la valeur du call sur
la barrière on donne un poids à chacun des deux calls que l'on
additionne ensuite.

FIG. 4 - encadrement de la barrière sur un noeud
En notant Cb la valeur du call sur la barrière on a :
B--dS uS--B
Cb = uS -- dS Cd +uS--dS Cu
Une fois ces valeurs calculées il ne nous reste plus
quà appliquer le principe de rétroduction en prenant soint de ne
pas modifier les valeurs des calls calculés par linterpolation sur la
barrière.
Exemple On reprend notre exemple avec une barrière
à 58 euros et un prix dexercice de 35 euros. On veut évaluer un
call up and out. Le premier arbre donneles valeurs du call avant
l'interpolation, le deuxième après.
Tree Display
At each node:
Upper value = Underlying Asset Price Lower value = Option
Price
Values in red are a result of early exercise.
|
|
|
99,96732
|
|
Strike price = 35
|
|
|
0
|
|
89,06561
|
|
|
|
Discount factor per step = 0,9958
|
|
|

Time step, dt = 0,0833 years, 30,42 days
Growth factor per step, a = 1,0042
Probability of up move, p = 0,4892
Up step size, u = 1,1224
Down step size, d = 0,8909
4,238316
50
44,54736
56,12005
2,954266
5,502917
62,98919
5,807897
39,68935
50
0
4,398537
44,54736
70,69912
56,12005
7,205414
0
79,35276
62,98919
8,647241
39,68935
50
0
0
44,54736
70,69912
56,12005
7,629954
9,692611
0
0
5,256081 5,883803 4,68935
35,36112
3,432395
31,50489
1,112872
35,36112
2,284436

31,50489
0
28,0692
0
25,00817
0
79,35276
0
62,98919
0
50
15
39,68935
Node Time:
0,0000 0,0833 0,1667 0,2500 0,3333 0,4167 0,5000
FIG. 5 - Option up and out avant interpolation
Tree Display
|
At each node:
Upper value = Underlying Asset Price Lower value = Option
Price
Values in red are a result of early exercise.
|
|
|
99,96732
|
|
|
Strike price = 35
|
0
|

0
70,69912
0
62,98919
0
89,06561
0
70,69912
0
79,35276
0
62,98919
0
Discount factor per step = 0,9958
Time step, dt = 0,0833 years, 30,42 days
79,35276
0
Growth factor per step, a = 1,0042
Probability of up move, p = 0,4892
Up step size, u = 1,1224
Down step size, d = 0,8909
62,98919

3,481573
50
44,54736
56,12005
2,954266
4,01521
4,467842
3,577065
39,68935
50
44,54736
56,12005
0,567186
5,587365
35,36112
3,432395
5,325808
39,68935
5,883803
31,50489
1,112872
50
44,54736
2,284436
56,12005
0,983874
9,692611
35,36112
28,0692
39,68935
31,50489
4,68935
50
15
0
0
25,00817
0
Node Time:
0,0000 0,0833 0,1667 0,2500 0,3333 0,4167 0,5000
FIG. 6 - Option up and out après interpolation
La valeur théorique calculée avec un pricer
d'option donne la valeur du call à 2,7054. Avec six périodes on
est loin d'avoir une valeur approchée correcte en utilisant llarbre
binomial. Néanmoins, comme le montre les deux arbres l'interpolation
permet de se rapprocher plus rapidement vers la valeur théorique pour un
nombre de périodes inchangé
CONCLUSION
Le développement des options a d'abord
été une réponse aux demandes des investisseurs en
matière de gestion du risque et de protection face aux fluctuations du
marché La grande souplesse d'utilisation des options et leurs
diversités permettent de répondre parfaitement aux besoins des
investisseurs, tant sur le choix des couvertures que des
spéculations.
De plus, l'une des spécificités majeure des
options de première génération et des options exotiques de
seconde génération est la possibilité de réaliser
des profits important en engageant des capitaux limités. Dans ce
mémoire, nous avons présenté quelques exemples d'options
exotiques, réparties en deux grandes parties (non path dependent et path
de- pendent) dont on évaluait le prix suivant le modèle binomial
de Cox Ross et Rubinstein.
Comme nous l'avons vu, le principal but de ce modèle est
de fournir une bonne compréhension des méthodes
d'évaluations des options et de comprendre leursdi~érences de
prix.
Néanmoins un nombre trop faible de périodes ne
permet pas une évaluation correcte de ce prix, mais il faut rappeler que
l'informatique ne sest développée que depuis une vingtaine
d'années, et que ce modèle construit en 1979 permettait de se
faire rapidement une idée des prix de l'option durant sa période
de vie
Aujourd'hui les options sont des outils indispensables pour tous
les professionnels des marchés financiers de plus en plus importants.
Ce mémoire m'a beaucoup apporté, tant sur le
plan intellectuel que sur le plan de lintérêt personnel. A travers
mes recherches et lectures jai pu découvrir l'univers des options, de la
finance de marché et des ses principaux acteurs. Notamment j'ai appris
comment étaient évaluées les options en fonction du
marché, dont un des intérêts dans la couverture n'est pas
de faire du profit mais de ne pas subir de perte
BIBLIOGRAPHIE
[11 E. Derman, I Kani, D Ergener and I Bardhan, "Enhanced
Numerical Methods or Options with Barriers" ,Financial Analysts Journal,
Nov-Dec 1995, pp65-74
[2] J. Hull, "Options futures et autres
actifsdérivés, 6e d.~ ,Pearson Education, Avril 2007.
[31 J.Boissonnade, "Les options exotiques" ,Eska, mai 1997.
[4] http ://www.mathfsu.edu/ whu/OptGUI1.html, "Pricer
ddoptions~
[5] http ://eriskgroupcom/,"Pricer doptions~



