Etude, développement et mise en oeuvre de deux observateurs de position pour la commande sans capteurs de la Machine Synchrone à Aimants Permanents (MSAP)

ANNEXES

Annexe A : Implantation de l'encodeur

Pour se familiariser avec l'environnement de travail (commande numérique par ordinateur et carte DSP), nous avons commencé par l'implantation de l'encodeur. Ce petit travail que nous présentons dans cette section des Annexes nous a permis de comprendre la configuration et l'usage du logiciel control desk. Nous avons jugé utile de bien comprendre le capteur de position car c'est l'élément qui nous gène et que l'on veut remplacer par nos observateurs de position.

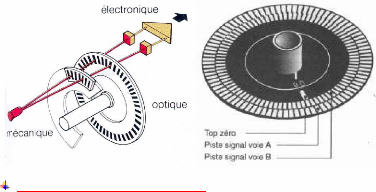
Principe de l'encodeur incrémental

Le rôle des pistes A et B c'est de déterminer le sens de rotation de l'arbre de la machine avec lequel est lié l'encodeur de telle sorte que si A est en avance de phase par rapport a B, la machine tourne dans le sens 1 et dans le cas contraire c'est le sens 2. L'encodeur se compose aussi d'un compteur qui compte dans chaque tour 1024 impulsions

Et il se reintialise à l'aide de l'indicateur (piste Z) qui doit aussi figurer et être initialisé dans le programme Simulink.

Implantation de l'encodeur via DS1104

Dans la fenêtre MATLAB, on exécute la commande rti (Real time Interface). On choisit la librairie master PPC puis l'encodeur DS1 104ENC_POS_C1, DS1 104ENC_SETUP et le bloc DS 11 04ENC_INDEX_C 1. Avant de commencer la simulation il faut régler les paramètres de ces blocs de l'encodeur.

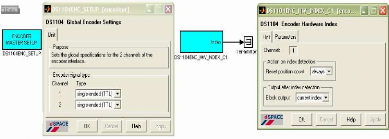
Configuration de DS1104ENC SETUP

Pour ce qui est de la configuration, nous devons spécifier quel type d'entrée nous utilisons car on a aussi bien des entrées digitales TTL que des entrées analogiques RS232 et RS442/485. Dans notre cas on utilise une des entrées digitales. (canal1)

Reglage de DS1104ENCEPOSC1

On doit spécifier le numéro de l'entrée car comme nous l'avons dit il en existe deux. Sur l'option Unit specification, on choisit donc channel number 1. Il faut aussi régler les paramètres d'initialisation. On a initialisé à O.

Configuration de DS1104enc INDEX C1

Dans ce bloc on doit indiquer le numéro de l'entrée (channel number). Pour ce qui est des paramètres, remettre la position à zéro à chaque tour et non une seule fois (Always). Ensuite pour le paramètre output after index detection on met l'option current index.

Simulation

On sait que le bloc de l'encodeur nous donne comme information sur l'angle un nombre N proportionnel à ce dernier (1024 par tour). Pour avoir l'angle en degré nous devons multiplier ce nombre par un gain à savoir 360/1024.

Quant à la détermination de la vitesse, puisque le bloc DS 1 04ENC_POS_C 1 nous donne le delta position, il nous suffit de la diviser par la le delta temps qui n `est rien d'autre que la période d'échantillonnage Te, puis de la multiplier par un gain (60/1024) pour avoir la vitesse en tour par minute.

Paramètre d'Affichage :

· Affichage numérique : Aller dans Virtuel instrument puis sélectionner display puis le mettre dans la layout et glisser la variable que vous voulez le voir en « affichage numérique ».

Résultats de la simulation :

On voit bien (figure B. 1) que la vitesse avant filtrage est trop bruitée, c'est pour cela qu'on insère un filtre pass-bas avec une pulsation de coupure (wcf=60). On pourrait envisager un bande passante beaucoup plus étroite que ça mais on est limité par le temps de réponse car si on prend par exemple wcf=10, le temps de réponse de notre filtre serait de 3*0.1s, c'est trop lent comme filtre !!!

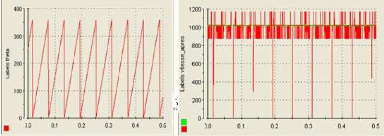
Figure A. 1 angle thêta en degré figure A.2 vitesse non filtrée et

vitesse filtrée en tr/min

On a envisagé un autre type de filtrage discret. L'idée est de prendre à chaque instant la mesure en cours et plusieurs mesures précédentes puis calculer la moyenne arithmétique. Dans notre cas on prend la mesure à l'instant n et les 9 mesures précédentes. On remarque sous les mêmes conditions que ce deuxième filtre est moins efficace que le premier car la vitesse est un peu plus bruitée.
On fait la simulation avec un filtre qui a une bande passante plus étroite wcf=10 (figure A.3). On voit que la vitesse et tèrs bien filtrée mais toutefois le temps de réponse de ce filtre est relativement trop grand.
	Figure A.3. Vitesse filtrée en tr/min

NOTATIONS

Modélisation de la MSAP

MSAP Machine Synchrone à Aimants Permanents

(d, q) Indice du référentiel de Park

(á,â) Indice du référentiel (á,â)

R Résistance statorique

Ld Inductance statorique directe

L_q Inductance statorique quadratique

L_c=L Inductance statorique cyclique

Ms Inductance mutuelle

Ö m Flux d'excitation de l'aimant permanent

Ö Flux statorique

( Ö _má , Ö mâ) Composantes du flux rotorique

( Ö _á , Ö _â ) Composantes du flux statorique

Cem Couple électromagnétique

C_r Couple résistant

p Nombre de paires de pôles de la machine

J Moment d'inertie totale de la machine

f Coefficient de frottement visqueux

ù_e Pulsation électrique rotorique

ù_m , Ù Vitesse de rotation mécanique du rotor

è_e Angle électrique du rotor

i Courants statoriques

v Tensions simples

ø Déphasage entre le courant et la tension

P_e Puissance électromagnétique

KT Constante de couple

Ke Constante de fem

ô_ù Constante de temps du modèle convertisseur - machine

Autres notations

ô R/L inverse de la constante électrique

A Matrice d'état du modèle d'état de la machine dans (á,â)

B Matrice du modèle d'état de la machine dans (á,â)

C Matrice de sortie du modèle d'état de la machine

G Gain de l'observateur

x Vecteur d'état

y Sortie de l'observateur

xà Vecteur d'état reconstitué (estimé)

yà Sortie reconstituée

F matrice d'état de l'observateur de Luenberger

ë_i Valeurs propres de l'observateur

s Opérateur de Laplace

O Matrice d'observabilité

Aii Composante de la matrice A pour l'observateur réduit

Bii Composante de la matrice B pour l'observateur réduit

v Nouveau vecteur d'état de l'observateur réduit

G_r Gain de l'observateur réduit