PARTIE 2
ANALYSE ET MISE EN OEUVRE DES
OBSERVATEURS DE POSITION POUR LA
COMMANDE DE LA MACHINE SYNCHRONE
A AIMANTS PERMANENTS
CHAPITRE 2
DIMENSIONNEMENT DES OBSERVATEURS ET SIMULATION
I. INTRODUCTION
Nombreuses sont les techniques d'estimation de position et de
vitesse du rotor de l'arbre des machines électrique. Dans notre
étude nous nous intéressons aux méthodes basées sur
les observateurs, plus particulièrement à un observateur
d'état des flux rotoriques d'ordre minimal à savoir l'ordre deux.
Durant notre période de stage nous avons étudié en premier
lieu un observateur réduit qui donne une estimation de la vitesse et
suite à une intégration la position du rotor. Nous avons
laissé tombé cet observateur qui, dans son modèle
d'état, fait intervenir les équations mécaniques qui
demeurent non maîtrisables à cause de la variation des
paramètres mécaniques. Cet observateur sera
présenté à la fin de ce chapitre avec les résultats
de simulation.
Dans un premier lieu, nous étudierons un observateur de
Luenberger d'ordre quatre basé sur
la reconstruction des flux
rotoriques. La position électriqueèe , est
déterminé en calculant
Ö
l'arc tangente de m â . Cet observateur
proposé dans [BATZ-LEE_1 ,2,3] présente
Ö m á
d'énormes avantages mais nous jugeons qu'il
nécessite un temps de calcul important vu l'ordre qui est assez grand
(ordre quatre). C'est ainsi que nous avons eu l'idée de proposer de
réduire l'ordre de cet estimateur puisque une partie du vecteur
d'état peut être reconstituée par une combinaison des
entrées, des mesures et des états reconstitués.
C'est cet observateur d'ordre deux qui fera l'objet de notre
étude dans la deuxième section de ce chapitre. Nous
présenterons le dimensionnement, le schéma de principe ainsi que
la simulation de notre estimateur et nous comparerons les résultats avec
les deux autres observateurs étudiés.
En dernière position nous présenterons le premier
observateur étudié qui est basé sur la reconstruction de
la vitesse avant de faire conclusion de ce chapitre.
27
II. OBSERVATEUR DE POSITION DU ROTOR BASE SUR LA
RECONSTRUCTION DES FLUX STATORIQUES
1. Introduction
Nous étudierons dans cette section un observateur
d'état pour reconstituer le vecteur d'état constitué des
deux composantes du flux statoriques et des deux composantes du flux rotorique
dans le référentiel biphasé (á,â). Nous
devons avoir tout d'abord un modèle de la machine dans ce même
référentiel pour ensuite se baser sur pour synthétiser
notre observateur. Dans cette section nous rappelons le modèle de notre
MSAP avec les équations aux flux, ensuite nous allons valider ce
modèle puis nous passons au dimensionnement de l'observateur puis
à sa simulation.
2. Modèle de la machine dans le
référentiel
(á,â)
Ici nous allons nous intéresser au modèle de la
machine dans (á,â) suivant :
di
v R i L e
á = á + + á
á
. c .
dt
di
v R i L e
â = â + + â
â
. c .
dt
Ö á,â =
Liá,â +Ö m
(è)
m á â,
dÖáâ =
á â
di d Ö
, ,
+
L .
dt dt dt
3. Equations d'état
A partir des équations ci-dessus, nous établissons
les équations d'état de la machine de manière à
avoir :
T
Entrées : u=vá
vâ
T
Vecteur d'état :
x=Öá Ö
â Ö má Ö
mâ
T
Sorties : y=iá
iâ
x Ax Bu
& = +
y Cx
=
0 0
- ô
000
0 00
ù e
01
B= et
1 0 1 0
L L
-
0 1 0 1
L L
-
A
C =

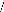
ô
-ùe
00
00
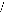
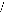
d Ö á
dt
Nous détaillerons par la suite les calculs qui nous ont
permis de déterminer ce modèle d'état.
28
Nous remarquons bien ici que la matrice d'état A
dépend de la vitesse du rotor donc nous avons un modèle non
linéaire car la vitesse est étroitement liée à la
position que nous voulons en fin de compte estimer.
4. Validation du modèle de la machine
L'observateur d'état se base sur le modèle
d'état de la machine que nous venons d'établir, pour s'assurer
que ce modèle (qui a pour vecteur d'état le vecteur (les flux))
converge vers le premier modèle étudié, nous avons
jugé nécessaire de simuler ce modèle et comparer le
vecteur d'état avec les flux déterminés par calcul simple
à partir du modèle que nous avons auparavant établit dans
le référentiel de Park d-q. Afin de ne pas compliquer la
simulation nous supposons que la vitesse est constante et que la pulsation
rotorique ùe l'ai trivialement aussi.
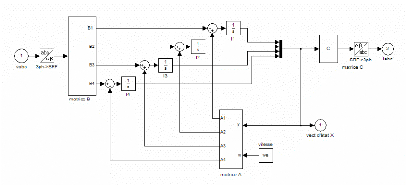
Figure II. 17 : Schéma de simulation du
modèle d'état de la MSAP
4.1. Résultats de simulation de la Validation du
modèle de la machine
Ce modèle a pour entrées les tensions et pour
sorties les courants statoriques. Dans notre simulation nous nous
intéressons par contre à la visualisation des composantes du
vecteur d'état afin de s'assurer que ce modèle nous donne des
flux qui convergent vers les flux déterminés par calcul à
partir du modèle dans d-q que nous avons déjà
validé.
Nous remarquons ici dans la Figure II.18 que le flux converge
très rapidement, ce qui nous permet d'affirmer que le modèle
présenté est correcte et que nous pouvons faire la
synthèse de l'observateur basé sur ce modèle.
29
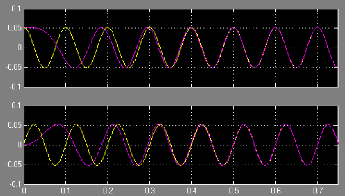
Figure II.18 : Flux rotoriques Ö m
á , Ö m â
5. Estimation de la position du rotor
5.1. Synthèse de l'Observateur de Luenberger
d'ordre complet 5.1.1. Equations d'état et principe
En considérant le modèle présenté ci
haut on a :
v = Ö Ö +
R
á á á
( )
- m
L
R
d Ö
â
+
vâ =
dt
Ö Ö
â â
- m
L ( )
Représentation d'état :
On modélise le système de façon à
considérer :
T
Entrées : u=vá
vâ
Vecteur d'état : x
=Öá Ö â
Ö má Ö mâ T
Sorties : y =iá i â
T
D'après les équations précédentes on
a :
|
d R
Ö á = -
v
dt L
á
d R
Ö â = -
v
dt L
â
|
( )
Ö - Ö
á m á
( )
Ö - Ö
â â
m
|
en posant ô =
|
R
|
|
|
L
|
30
|
On sait que
|
Ö = Ö =
m m
( ) ( )
è ù t
|
Ö = Ö
m m
á
Ö = Ö
m m
â
|
cos( )
ù e t
sin( )
ù e t
|
d
dt
d

dt
Ö = - Ö = Ö
m m e m
á ù ù ù
sin( )
t â
e e
Ö = Ö = Ö
m m e m
â ù ù ù
cos( )
t á
e e
On a :
Ö - ô ô
0 0 1 0
Ö
á á
d v
Ö 0 0 0 1
- Ö
ô ô
â â á
= +
dtvÖ 0 0 0 0 0
- ù Ö m á
e m á â
Ö 0 0 0 0 0
ù Ö
m â e m â
1 ( )
Ö - Ö
iá =
i â=
L
1
L
á á
m
( )
Ö - Ö
â â
m
1 0 1 0
L L
-
i L L
0 1 0 1
-
â
i á
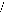
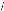
Ö á
Ö â
Ömá
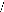

Ö má
|
On a le système
|
x Ax Bu
& = +
y Cx
=
|
avec
|
|
-ô
|
0 0
ô
|
1 0
|
0 0
- ô
000
0 0 0
ù e
0 1
B= et
1 0 1 0
L L
-
0 1 0 1
L L
-
A
C =
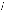
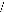
ô
- ùe
00
00
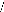
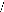
Ici on constate bien que la matrice d'état A dépend
de la pulsation ou vitesse électrique
ùe.
Nous avons un modèle non
linéaire. Pour considérer ce système comme un
système linéaire pendant une période
d'échantillonnage, nous devons poser l'hypothèse suivante.

y' Nous considérons très lente la variation de la
vitesse par rapport à la fréquence d'échantillonnage.
31
5.1.2. Estimation de la position du rotor
La position du rotor èe est
donnée par : à m
Ö
èe = Arctg â
Ö m á
à
xà 4
è = Arctg On a besoin de reconstruire x3
et x4
e à
x3
Observateur de Luenberger (ordre n=4)
x Ax Bu
&= +
On a
y Cx
=
x Ax Bu
& à à
= +
y Cx
à à
=
Ce qui donne un observateur d'ordre 4 (même ordre que le
système) à
x & =
Fx Ju Gy Fx Ju GCx
à à
+ + = + +
x x Ax Bu Fx Ju Gy
& &
- = + - - -
à à
x ~ & = Fx ~
+ - - + -
( A F GC ) x ( B J)u
x ~ &= Fx ~ = ( A - GC
)x ~
G est le gain d'observateur x~ l'erreur d'estimation
Remarque
Pour avoir une bonne estimation, il faut que x~ tend
vers 0 pour t tend vers l'infini. x ~ &= Fx ~ implique
que les valeurs propres de F doivent impérativement être
stables.
Sous cette condition, on détermine la matrice G (gain
par placement de pôle). Il existe plusieurs méthodes pour
déterminer le gain G, soit par placement de pôle directement avec
la forme canonique d'observabilité soit en utilisant l'algorithme
général d'Ackermann basé sur un model quelconque du
système.

La dynamique de l'observateur dépend donc de la
dynamique du polynôme
caractéristique sI - (A
- GC) = 0 . On se propose un polynôme
caractéristique suivant :
|
ë ë
=
1 2
|
*
|
(conjugué)
|
|
f(s)=(s-ë1)(s-ë2)(s-ë3)(s-ë4)
avec
|
et
ë ë
=
1 3
|
ë ë
=
2 4
donc 2 * 2
f ( s ) = ( s - ë
1 ) ( s - ë 1 )
32
5.1.3. Observabilité
La condition d'observabilité du système est
donnée par le rang de la matrice d'observabilité
'
O C CA CA CA
2 3
=
Il faut que cette matrice soit de rang complet. Cette matrice
n'est pas carrée on détermine l'observabilité du
système par la méthode suivante :
- on calcule T
O puis T
Qs = O · O
- on détermine le rang de Qs
Dans notre cas O est une matrice (8*4) et Q (4*4) :
matrice carrée.
On montre que, quelle que soit ùe
vitesse angulaire électrique du rotor supérieure à
zéro le système est observable [BATZ-LEE_1 ,2].
5.1.4. Détermination de la matrice gain de
l'observateur G :
|
1 0
On pose : I=et
0 1
|
J=
|
0 1
-
10
|
Nous choisissons une forme de la matrice gain G comme la suivante
:
g g
11 12
g g
G
21 22
g g
31 32
g g
41 42
= avec
g g g
= =
11 22 1
g I g J
1 2 2 2 2 2
× ×
+
g I g J
+
3 2 2 4 2 2
× ×
g g g
= =
on a G =
31 42 2
g g g
= - =
21 12 3
g g g
= - =
41 32 4
g R
= -
1
ù e ô
On montre que ( )
R ë ë
+
1 2
g =
3
ô
g4 =
R ( )
ë ë ù 2
- - + +
1 2 e
ùeô
Ce qui nous donne la matrice gain de l'observateur :
33
|
-R
|
-
|
R ë ë
1 2
|
|
|
|
w t
e
R R
ë ë
1 2 -
|
ë ë *
=
1 2
|
|
G=
|
ù e ô
( ) ( )
ë ë ë ë ù 2
R R
1 2 1 2
+ - + e
|
Avec
|
et
ë ë
=
1 3
|
ë ë
=
2 4
ô ù e ô
-R
( ) ( )
- + + +
ë ë ù ë ë
2 R
1 2 e 1 2
ùô ô
e
ë i valeurs propres de (A- GC)
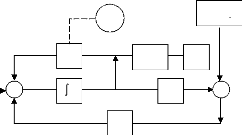
Le schéma de principe de l'observateur est donné
par la figure suivante, avec comme entrées de l'observateur les tensions
et les courants statoriques dans le référentiel biphasé
(a,f3). L'observateur de Luenberger utilise les matrices A, B et C du
modèle de la machine sur lequel on se base pour le
synthétisé.
váâ
+
àx&
A
xà
ùà e
G
atan
C
èàe
yà
abc/af3
+
iáâ
abc/af3
B


ùe
=
ùà e
( )
( ) ( )
v á Ri á v â Ri
â
- + -
2 2
Ö
m
MSAP
vabc

iabc

Figure II.19 : Schéma de principe de l'Observateur
d'état de notre modèle de la MSAP
5.2. Estimation de la vitesse
Nous remarquons bien ici que la matrice d'état A
dépend de la pulsation rotorique, donc nous avons un modèle non
linéaire car non seulement cette pulsation varie en fonction du temps
mais elle est étroitement liée à la position que nous
voulons en fin de compte estimer. Nous devons à chaque instant avoir une
estimation de la vitesse afin de l'insérer dans la matrice A que nous
noterons par la suite Aoe. Considérant l'inertie de la MSAP, nous
34
pouvons assimiler la pulsation rotorique égale à
une constante durant une période d'échantillonnage, ainsi le
modèle devient linéaire.
On sait qu'en régime permanent, = 0
di donc on a :
dt
dÖ má
v Ri Ri Ri t
= + = ? Ö = ? Ö cos( )
á á á á
ù ù ù
e e e
m m
á
dt
v Ri Ri t
â â
= + Ö = + Ö
m m sin( )
â â
ù ù ù
e e e
ù e Ö m =
- Ö
ù e m
= -
v Ri
á á
cos( )
ù t
e
ùÖ
e
m wet v Ri
sin( ) = -
â â
( ) 2 ( )2
v Ri v Ri
á á â â
- - -
( )
( ) ( )
v á Ri á v â Ri
â
- + -
ùe
2 2
=
Ö
m
Cette estimation est valable en régime permanent et
même à très basses vitesses 5.3. Justification du
choix des valeurs propres
Nous choisissons les valeurs propres de l'observateur par un
placement de pôle adéquat. En effet pour avoir une bonne dynamique
de notre observateur, nous choisirons des valeurs propres très rapides
que les pôles du système (processus) et aussi plus rapides que la
pulsation rotorique. Toutefois il faut noter que le fait de prendre des valeurs
propres plus rapides, l'erreur de l'observateur converge plus rapidement vers
zéro mais l'on risque d'augmenter la bande passante et cela peut
amplifier les bruits. Dans un premier temps, nous choisissons des valeurs
propres assez grandes qui assurent la convergence rapide de l'erreur
d'estimation.
Après modélisation de l'ensemble convertisseur
machine, nous nous rendons compte que
1
l'ensemble se comporte comme un premier ordre dont on le
modélise comme suit :
1 +ôùs
avec ôù déterminé
par des essais de la machine à vide.
Pour choisir les pôles du gain de l'observateur, il faut
tenir compte du fait que l'observateur
doit avoir une dynamique beaucoup
plus rapide que l'ensemble moteur convertisseur. Pour
cela, nous avons pris en premier lieu les pôles

ë ë
=
0 1
== 1 10
ô w
Nous choisissons ë1 = -90 puis dans un
deuxième temps des valeurs propresë 1 = -200. 5.4.
Choix de valeurs propres dynamiques
Le fait de choisir des valeurs propres qui ont une dynamique
rapide par rapport à la pulsation électrique rotorique
ùe réduit l'erreur de l'estimation de
position.
35
Nous proposons donc une stratégie qui permet de choisir
des valeurs propres adaptées à la vitesse de l'arbre du rotor
pour essayer de gérer la bande passante et de ne pas amplifier
gratuitement les bruits.
|
ë 0 = ù e
|
( - k reel + jkim),
cette méthode est très pratique elle marche très bien en
simulation
|
comme nous allons le voir dans la section qui suit.
5.5. Utilisation de l'observateur pour la commande de la
machine
Notre objectif final est de réaliser la commande sans
capteur de la machine synchrone à aimants permanents. C'est ainsi que
nous envisageons faire la synthèse de notre observateur d'état
afin de boucler le système non avec les grandeurs mesurées mais
avec les grandeurs estimées à l'instar de la position et de la
vitesse.
6. Simulation sous MATLAB SIMULINK
6.1. Résultats de simulation et
interprétations
Nous utilisons l'observateur en boucle fermée pour la
commande vectorielle de la machine. Dans la simulation, nous démarrons
la commande avec les grandeurs mesurées et après quelques
secondes nous basculons vers les grandeurs estimées grâce à
un switch que nous avons judicieusement placé. Dans un premier temps
nous réalisons la simulation en ne tenant pas compte du couple de
charge. Nous appliquons une charge Cr de 0,14Nm à t=4s. Cette charge
correspond au couple de charge de la machine à courant continu à
vide qui est accouplée à notre machine synchrone.
Nous remarquons ici dans la Figure II.20, que le couple
présente un pique lorsque nous appliquons l'échelon et il
converge bien vers la valeur du couple résistant à vide qui est
de 0,14Nm. La vitesse de référence étant fixée
à 1000tr/min, nous remarquons bien que aussi bien la vitesse
mesurée que celle estimée convergent vers la
référence, l'observateur répond avec une dynamique
très rapide, comme nous voyons dans la Figure II.21, les deux courbes
sont pratiquement collées. Il en est de même pour les positions
électriques mesuré et estimé de la Figure II.22, ceci en
boucle fermée ; c'est-à-dire que nous réalisons la
commande ici, non pas à l'aide des grandeurs mesurées mais avec
les position et vitesse estimées.

temps (s)
temps (s)
Figure II.20 : Couple Cem (Nm) Figure II.21 : Vitesses
mesurée et estimée tr/min
36

temps (s)
Figure II.22 : Angles mesurée et estimée en
rad
6.2. Simulation en tenant compte des bruits et de
l'OFFSET
Dans cette section, nous ajoutons intentionnellement des
bruits sur les grandeurs mesurées (tensions et courants) et un OFFSET
pour essayer de s'approcher un peu de la réalité. Dans le cas des
valeurs propres statiques judicieusement choisies, nous avons les
résultats suivants de simulation.
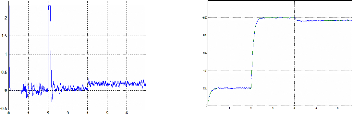
temps (s) temps (s)
Figure II.23 : Couple électromagnétique
Figure II.24 : vitesses mesurée et estimée
Nous remarquons aussi comme pour le cas idéal sans
bruits ni OFFSET que l'allure des courbes est pratiquement la même sauf
que les grandeurs estimées présentes quelques ondulations
négligeables de l'ordre de 0.5%.
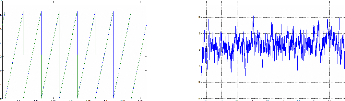
temps (s) temps (s)
Figure II.25 : Angles mesurée et estimée
Figure II.26 : erreur de vitesse (tr/min)
37
L'erreur de vitesse ne dépasse pas 10tr/min pour un
double échelon de vitesse de 200 vers 1000tr/min (Figure II.26), ceci
avec un bruit de 5% sur les mesure et un OFFSET de 0.08V pour les tensions et
0.02A pour les courants.
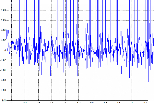
temps (s)
Figure II.27 : erreur de position
électrique
L'erreur de position électrique dans ces mêmes
conditions ne dépasse pas 2,3°, même en tenant compte de tous
ces bruits. Ces résultats nous permettent d'affirmer que l'observateur
converge avec efficacité et arrive à s'en passer des bruits de
mesures.
Nous choisissons maintenant des valeurs propres de la matrice
d'état de l'observateur proportionnelles à la valeur absolue de
la vitesse. P0 = ù ( - k
reel + jkim), cette stratégie permet
un bon rejet des bruits de mesure.
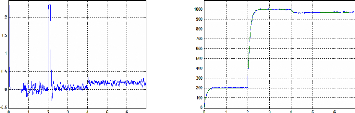
temps (s) temps (s)
Figure II.28 : Couple électromagnétique
(Nm) Figure II.29 : vitesses mesurée et estimée
38
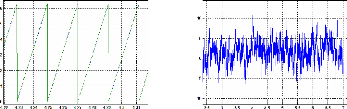
temps (s) temps (s)
Figure II.30 : Angles élec mesurée et
estimée Figure II.31 : erreur de vitesses (tr/min)
Nous constatons dans ce cas que l'allure du tracé du
couple ainsi que de la vitesse est presque la même. Le fait de prendre
des valeurs propres dynamiques adaptées à la vitesse n'affecte
pas l'allure de la vitesse elle-même par contre nous constatons un bon
rejet des perturbation au niveau de la positon électrique
estimée. Nous avons maintenant une erreur d'environs 0.01rad soit
1,1° (Figure II.32) pour la position électrique. C'est une valeur
très négligeable.
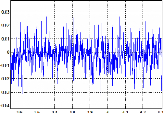
temps (s)
Figure II.32 : erreur angle électrique
(rad)
6.3. Simulation en pleine charge (la charge nominale de
notre machine est de 0.8Nm)
La charge nominale de notre machine étant de 0.8Nm, nous
simulons la commande vectorielle avec cette charge et nous obtenons les courbes
suivantes.
L'erreur de position est dans ce cas décalée de
-0.02 par rapport au premier cas où nous considérons seulement
une charge de 0. 14Nm.
39
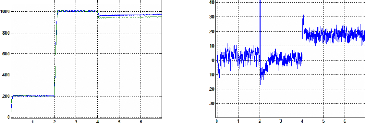
temps (s) temps (s)
Figure II.33 : Vitesses mesurée et estimée
tr/min Figure II.34 : erreur de vitesse pleine charge
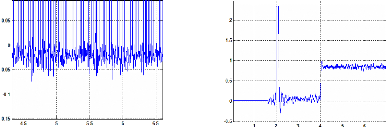
temps (s) temps (s)
Figure II.35 : erreur de position pleine charge (rad)
Couple Electromagnétique pleine charge (Nm)
7. Conclusion
Nous avons présenté dans cette section la
synthèse d'un observateur de position d'ordre complet de type Luenberger
destiné à la commande vectorielle de la MSAP. Après avoir
présenté le modèle de la machine sur lequel notre
observateur d'état se base pour reconstruire la position et la vitesse,
nous avons essayé d'éclaircir le dimensionnement et le principe
de calcul des différentes matrices de l'observateur. Ensuite nous sommes
passés à la simulation de la commande vectorielle en utilisant
notre estimateur dans le cas idéal sans bruit ni OFFSET et dans un autre
cas où nous considérons les mesures avec des bruits et des
offset. Nous avons remarqués après analyse des résultats
de simulation que non seulement l'observateur répond et converge
très rapidement mais elle marche très bien et il réalise
bien la commande sans avoir recours au capteur.
40
III. OBSERVATEUR REDUIT DE POSITION BASE SUR
LA
RECONSTRUCTION DES FLUX STATORIQUES
1. Introduction
Pour minimiser le temps de calcul et alléger le
programme, nous avons pensé à améliorer notre observateur
en minimisant l'ordre à l'ordre deux. Cela est possible car une partie
du vecteur d'état peut être reconstituée facilement. Nous
proposons donc dans cette section un observateur réduit basé sur
le modèle de la machine et sur les mêmes équations
d'état.
2. Equations d'état On considère
les mêmes équations d'état que précédemment
avec comme :
T
Entrées : u=vá
vâ
Vecteur d'état : x= Ö
á Ö â Ö
má Ö mâ T
Sorties : y=iá
iâ T
Ö - ô ô
0 0 1 0
Ö
á á
d v
Ö 0 0 0 1
? Ö
ô ô
â â á
= +
dt v
Ö 0 0 0 0 0
- ù Ö
m á e m á â
Ö 0 0 0 0 0
ù Ö
m â e m â
i á
1/ 0 1/ 0
L L
-
x
i L L
0 1/ 0 1/
-
â
3. Estimation de la position du rotor 3.1.
Synthèse de l'Observateur réduit
On veut faire un observateur d'ordre réduit car nous
constatons ici que les états Öá et
Öâ peuvent être obtenus par une
combinaison des mesures, donc il nous restera seulement Ö
má et Ö mâ d'autant plus que ces
deux derniers états sont largement suffisants pour reconstituer la
position électriqueèe . Nous
réarrangeons l'équation d'état comme suit :
Ö 0 0 0 0 0
- ù Ö
m á e m á
dvÖ ù 0 0 0 0 0
m â e m
â á
= +
Ö
Ö ô ô
? Ö v
0 0 1 0
dt á á â
Ö 0 0 0 1
ô - ô Ö
â â
41
On pose :
On pose donc les nouvelles matrices réduites :
A11 = Jù e ; A12 =
[0] ; A21 = ôI ; A22 =
-ôI ; B 1 = [0] ; B2 =
I
Et
Ö Ö
m á
Ö â
v = ; y á
Ömâ
On a donc :
v &=
A11v+A12y+B 1
u
y&- A22y-B2u =
A21v
3.1.1. Principe de l'observateur d'ordre réduit
Nouvelle entrée : A12y +
B1u
T
Nouveau vecteur d'état : v=Ö m á
Ömâ
Nouvelle sortie : y&- A22y
- B2u
On pose z=v à -Gy
z A G A z A G A G A G A y B GrB u
& = - + - + - + -
( 11 21 ) [( 11 21 ) 12 22 ] ( 1 2 )
r r r r
v z G y
à = + r
On se donne le polynôme caractéristique suivant :
f(s) = (s - ë
0 ) = s - 2 ë 0 s +
ë 0 avec ë0 pôle stable
plus rapide que le système de
2 2 2
commande et plus rapide que le procédé.
3.1.2. Observabilité
L'observateur d'ordre réduit que nous utilisons dans
cette section se base sur le même modèle de la machine que
précédemment que nous avons déjà fait
l'étude de l'observabilité. Si la paire (A,C) est
observable (A11,A22) l'est aussi [OSTER].
42
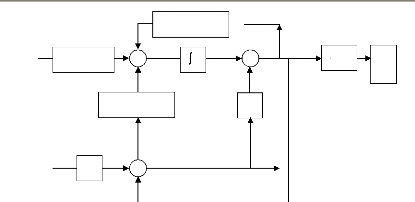
A1 1-GrA21
B1-GrB2
atan
èàe
váâ
+
+
A12-GrA22
Gr
y
iáâ
L
+
và
Figure II.36 : schéma de principe de
l'observateur réduit
3.1.3. Calcul du gain de l'observateur réduit
Gr
avec
g g
On se propose un gain Gr de la forme : 11 12
G =
rg g
21 22
g11 = g22 = g1
et g21 = -g12 =
g2
|
g g
- 1 0 0 1
-
Donc on a : 1 2
G g g g I g
= = + = +
r 1 2 1 2
g g 0 1 1 0
2 1
|
J
|
On pose aussi F = A11 - G r
A21
F =ù e J-G r
ôI=ù e J-ô
[g1I+g2J]
0 1 0 0
- g g
1 2
F = ù - ô -
e 1 0 0 0
g g
1 2
- - +
ô ù ô ô ù ô
g g s g g
+ -
1 2
e 1 2
e
F = ( )
sI F
- =
ù ô ô ù ô ô
- -
g g - - +
( 2 ) 1
g s g
e 2 1 e
det( ) ( 1 ) ( e 2 ) 2 1 ( 1 ) ( 2 )
sI - F = s + ô g +
ù - ô g = s + ô g s +
ô g + ù e - ô g
2 2 2 2 2
Puisque nous avons cité plus haut que nous voulons une
dynamique de
f ( s ) = ( s - ë
0 ) = s - 2 ë 0 s +
ë 0
2 2 2
Donc on identifie membre à membre l'équation
det(sI - F) = f(s) et on obtient :
- ë
0
- =
2 0 2 g 1 g 1
ë ô =
ô
43
De même
ù
ë ô ù ô
0 ( 1 ) ( 2 ) 2 e
2 2 2
= + -

g e g g =
ô
On obtient enfin la matrice gain :
ëù
- -

0 e
ë ù
0 e
ù ë
e 0
ëù
0 e
- ù ë
e 0
on pose Gr 0 =
-
g g
Gr
-
1 2 ô ô 1
= = = -
g g ù ë ô
2 1 e 0

-
ô ô
1
Donc 0
G r G r
= -
ô
F = A 11 - G r A 21
3.1.4. Calcul de la matrice d'état réduit
:
Ce sont les valeurs propres de cette matrice qui imposent la
dynamique de l'observateur.
Nous avons vu que F = ù e J -
G r ô I = ù e J -
ô [ g 1 I + g
2 J ] d'où :
- - +
ô ù ô ë
g e g 0
0
F = = = ë I
ù ô ô ë
2 1 0
1 2
- -
e g g 0
0
avec I matrice identité d'ordre 2
3.1.5. Calcul du gain K0 =
A12 - G r A22
Nous savons bien que A22 est une matrice
nulle, il vient que :
K G r A 1 G
r ( ô I ) G r
= - = - = -
0 21 0 0
ô
3.1.6. Calcul du gain B0 =
(B1 - GrB2)
1
B ( B G r B ) G r B
G r I B G r
= - = - = = -
0 1 2 2 0 0
ô
Récapitulons :
Nous avons les matrices suivantes pour l'observateur
réduit :
0
ë 0
F=
-
Gr
0
Gr
0
ë 0
K 0
=
= -
B 0
ô
-
1 e
ë ù
0
ô ù ë
-e 0
1 e
ë ù
0
ù ë
e 0
ë ù
0 e
=
- ù ë
e 0
ë ù
0 e
- ù ë
e 0
44
3.2. Estimation de la vitesse
avec ôù =0.1s.
Nous utilisons le même estimateur de vitesse que
précédemment :
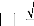
( )
( ) ( )
v á Ri á v â Ri
â
- + -
ùe
2 2
=
Ö
m
4. Justification du choix des valeurs propres
Nous avons vu que le modèle répond avec une dynamique
assimilable à un premier ordre
1
de la forme :
1+ôùs
Pour choisir les pôles du gain de l'observateur, il faut
tenir compte du fait que l'observateur doit avoir une dynamique beaucoup plus
rapide que l'ensemble moteur convertisseur.
Comme précédemment, nous choisissons
ë1 = -90 un pôle double pour notre
observateur.
Nous remarquons que cette valeur est nettement
supérieure à 10, nous avons une dynamique neuf fois plus
rapide.
5. Choix de valeurs propres dynamiques
Le fait de choisir des valeurs propres qui ont une dynamique
rapide par rapport à la pulsation électrique rotorique
ùe réduit l'erreur de l'estimation de
position.
6. Simulation sous MATLAB SIMULINK 6.1. Résultats
de simulation et interprétations
temps (s)
temps (bis)
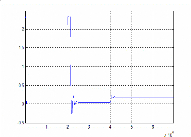
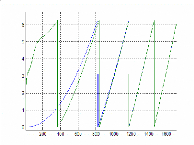
Figure II.37 : Couple électromagnétique
(Nm) Figure II.38 : Réponse de l'angle électrique
Les courbes des Figure II.37, Figure II.38 et Figure II.39,
nous montrent bien que la dynamique de cet observateur réduit est la
même que celle à ordre complet. Ce qui est logique car nous nous
basons sur le même modèle et que nous choisissons des valeurs
propres qui sont les mêmes pour les deux cas de figures.
45
Nous avons réalisé la simulation dans le cas
idéal sans tenir compte des perturbations dans un premier temps. Nous
remarquons que l'erreur de position est nulle ainsi que l'erreur de vitesse.
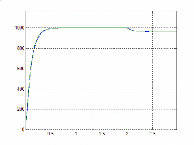
temps (s)
temps (as)
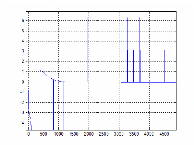
Figure II.39 : Vitesses estimée et mesurée
tr/min Figure II.40 : Erreur de position (rad)
temps (s)
Figure II.41 : erreur de vitesse
6.2. Simulation en tenant compte des bruits et de
l'OFFSET (plus proche de la réalité)
Comme précédemment dans le cas de l'observateur de
Luenberger d'ordre complet on applique les mêmes conditions de
perturbation afin de s'approcher un petit peu de la réalité.
Même en tenant comptes des bruits et de l'OFFSET au
niveau des mesures des courants et des tensions qui sont les entrées de
notre observateur, nous remarquons que les deux courbes de la vitesse
mesurée et celle estimée sont pratiquement collées (Figure
II.43). L'erreur de vitesse dans ce cas ne dépasse pas 5tr/min pour un
échelon de référence de 1000t/min (Figure II.42).
46
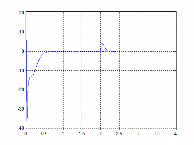
temps (s)
temps (s)
Figure II.42 : Erreur de vitesse en tr/min Figure II.43 :
vitesses mesurée et estimée (tr/min)
temps (ris)
temps (us)
Figure II.44 : erreur de position (rad) Figure II.45 :
Angles élec mesuré et estimé (rad)
6.3. Simulation en tenant compte de la charge nominale
0.8Nm
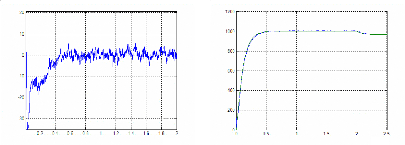
temps (s) temps (s)
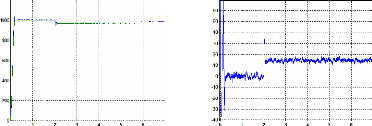
Figure II.46 : Vitesses mesurée et estimée
tr/min Figure II.47 : erreur de vitesse en tr/min
47
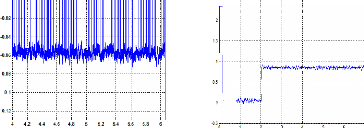
temps (s) temps (s)
Figure II.48 : erreur de position (rad) Couple
électromagnétique en (Nm)
7. Conclusion
L'observateur présente les mêmes performances que
l'observateur étudié en premier lieu, avec les avantages suivants
:
y" Ordre réduit donc programme moins lourd y" Temps de
calcul minimisé
y" Bon rejet des perturbations
IV. OBSERVATEUR REDUIT BASE SUR LA RECONSTRUCTION DE LA
VITESSE
1. Introduction
Concernant l'observateur que nous avons étudié
au tout début de notre stage, il se base sur
le modèle de la
machine dans le référentiel de Park. Ce modèle
proposé initialement dans
T
[TAT] a pour vecteur d'état x=iq
ùm , et comme iq peut être
reconstitué à partir
des mesures, il vient l'idée de faire un observateur
réduit pour ne reconstruire que la vitesse puis la position par la
technique d'intégration.
2. Equations d'état
On considère un autre modèle de la PMSM dans le
référentiel (d-q). On a :
v d = R 0 i d + 10
v q 0
R i q 01
+ e d
eq
did
dt
diq
dt
48
di
v Ri L p Li
d
d d m q
= + - ù
dt
di
v Ri L p Li p
q
q q m d m m
= + + + Ö
ù ù
dt
T C K i
= =
e em T q
d C C
ù -
m em r
On s'intéresse au modèle découplé :
on définit donc :
dt J
u v p Li
= + ù
d d m q
u v p Li
= - ù
q q m d
On a donc les équations d'état suivantes :
d k
ù m T
0
dt J ù m
= +
di K R i
q e q
-
-
dt L L


0
1 uq
L
[ ]
0 1
ù m
y=
i q
| 


