Etude, développement et mise en oeuvre de deux observateurs de position pour la commande sans capteurs de la Machine Synchrone à Aimants Permanents (MSAP)

UNIVERSITE CADI AYYAD MARRAKECH
FACULTE DES SCIENCES SEMLALIA

Mémoire

Présenté pour l'obtention du

Diplôme des Etudes Supérieures Approfondies (DESA)
UFR : Génie Electrique
Electrotechnique, Electronique de Puissance et Commande Industrielle

Par

DARKAWI Abdallah Mohamed

Maîtrise ès Sciences et Techniques - Informatique Electronique Electrotechnique
Automatique (IEEA)

Etude, développement et mise en oeuvre de

deux observateurs de position pour la

commande sans capteurs de la Machine

Synchrone à Aimants Permanents (MSAP)

Mémoire soutenu le 19 juillet 2007 devant le jury composé de :

M. Moulay Tahar LAMCHICH	P.E.S	FSSM	Président de jury
M. Driss YOUSFI	P.A	ENSAM	Encadrant
M. Abdelhaq MOUTTAKI	P.A	FSSM	Examinateur
M. Mustapha RAOUFI	P.A	FSSM	Examinateur

A ma très chère mère
A mon père, et à tous mes frères et soeurs
A tous ceux qui m'aiment bien

Résumé

RESUME

Notre étude se base sur la commande numérique sans capteur de la Machine synchrone à aimants permanent pour des applications industrielles de moyennes puissances.

Nous proposons des méthodes basées sur des observateurs afin d'estimer la position du rotor. L'idée est de reconstituer le vecteur d'état contenant les flux afin d'extraire la position du rotor, en se basant sur un model d'état de la machine qui ne fait pas intervenir les équations mécaniques.

Les avantages de cette méthode sont dus au fait que l'observateur proposé n'est sensible ni aux variations du couple, ni aux frottements ni à l'inertie, qui sont des grandeurs non maîtrisables, ce qui est très intéressant pour des applications telles que la propulsion électrique, ainsi que sa capacité à fonctionner même à de très faibles vitesses aussi bien en régime permanent qu'en régime transitoire. L'observateur proposé est insensible au problème de valeur initiale de la position du rotor.

Les résultats expérimentaux confirment les performances citées ci haut des méthodes proposées. L'implantation est faite à partir d'une carte DSP de la gamme DS 1104 dédiée à ce genre d'application.

Mots clefs

Machine synchrone à aimants permanents - Observateur - Commande sans Capteur - Commande des moteurs - Estimation de position et de vitesse - Contrôle Automatique.

Abstract

ABSTRACT

Title : «Study and implementation of two position observer methods for PMSM
sensorless control»

Our researches are based to the Sensorless Control of the Permanent Magnet Synchronous Motor Drive, for industry applications.

We proposed in our study two methods based to observer flux linkage for the estimation of the rotor position for the sensorless control of the PMSM. The observer produces accurate rotor angle estimates in steady-state and transient, and is attractive for electric propulsion in industry applications due to its independence from mechanical parameters such as load torque, inertia, and friction. The proposed observer does not need the initial condition of the rotor angle.

These sensorless PMSM techniques are implemented in a real time motor control system to from a sensorless electric drive prototype. Experiment results are included in order to confirm the effectiveness, and the advantageous of the proposed approach. A DS 1104 digital signal processor is used to execute these rotor position estimating techniques.

Key words

Permanent Magnet Synchronous Motor - Observer - Sensorless control - Motor drives - position and speed Estimators - Automatic control.

AVANT-PROPOS

Au terme de mon stage de fin d'étude passé au « Laboratoire des Systèmes Embarqués et de Commande Numérique » de l'ENSA, je suis très heureux de pouvoir exprimer mes remerciements à tous ceux qui ont contribué à l'aboutissement de ce travail d'initiation à la recherche.

D'abord les membres du jury :

y' Monsieur MOULAY TAHAR LAMCHICH Professeur (PES) à la faculté des Sciences Semlalia Marrakech responsable de la formation doctorale DESA Electrotechnique, Electronique de Puissance et Commande industrielle, pour m'avoir fait l'honneur de présider mon jury et de m'avoir encadré durant les années de formation pour la préparation du Diplôme des Etudes Supérieures Approfondies.

y' Monsieur D. YOUSFI : Professeur Assistant à l'Ecole Nationale des Sciences Appliquées, pour m'avoir accueilli et encadré durant ma période de stage au sein de leur Laboratoire, pour avoir dirigé ce travail, pour les nombreuses discussions que nous avons eues, malgré un emploi du temps chargé, pour sa sensibilité, son égard, le respect et la sympathie dont je fus témoin et pour m'avoir montré l'importance de notre étude et de la recherche en générale vis-à-vis du monde industriel.

y' Monsieur A. MOUTTAKI, Professeur à la Faculté des Sciences Semlalia Marrakech, pour avoir accepté de faire partie des membres du jury ainsi que pour sa disponibilité, ses conseils pertinents et les efforts qu'il n'a cessé de déployer à me trouver les documents que je ne pouvais me procurer à cause de mes moyens très modestes.

y' Monsieur Mustapha RAOUFI, Professeur à la Faculté des Sciences Semlalia Marrakech, pour avoir accepté de faire partie des membres du jury et de m'avoir donner son temps pour des discussions sur tout ce qui concerne l'électronique de puissance plus particulièrement sur « les convertisseurs statiques »

Mes sincères remerciements à tout le corps enseignant de la formation doctorale Electronique de Puissance, Electrotechnique et Commande industrielle.

Mes profondes gratitudes à Monsieur le Docteur Fidèle CODJIA Abdelghani tant bien pour son soutient moral, que pour ses conseils pertinents et son encadrement en tant que spécialiste dans le domaine de la psychologie et la psychopédagogie durant mes six années passées à Marrakech, ville de mes études.

Je ne peux terminer sans remercier tous mes collègues de classe ainsi que les collègues du laboratoire avec qui j 'ai passé des moments forts et inoubliables.

J'ai également une pensée pour tous mes amis et pour toutes mes chéries qui m'ont soutenu durant toutes les années que j 'ai passé au Maroc et particulièrement à Marrakech.

Je finis ces remerciements par mes parents, mes frères et soeurs. Ils m'ont toujours soutenu tout au long de mes études. Je leur dois beaucoup. Qu'ils trouvent dans ce manuscrit toute ma reconnaissance et le signe que je suis enfin arrivé au bout.

Enfin je ne saurais exprimer en quelques mots tout ce que je dois à ma très chère MAMAN, pour le soutien et les encouragements constants qu'elle m'a apporté depuis mon enfance jusqu'aujourd'hui.

Par DARKA WI. A, Marrakech, le 5 juillet 2007

TABLE DES MATIERES

RESUME i

ABSTRACT ii

AVANT-PROPOS iii

TABLE DES MATIERES v

LISTE DES FIGURES ix

INTRODUCTION GENERALE 1

PARTIE 1
ETUDE BIBLIOGRRAPHIQUE

CHAPITRE 1

MODELISATION DE LA MACHINE SYNCHRONE A AIMANTS PERMANENTS (MSAP) ET ETAT DE L'ART DE LA COMMANDE SANS CAPTEUR 4

I. INTRODUCTION 4

II. MODELISATION ET COMMANDE DE LA MSAP 5

1. Introduction 5

2. Généralité sur les machines synchrones 5

2.1. Machines Synchrones à rotors bobinés 5

2.1.1. Machines Synchrones à rotors bobinés à pôles lisses 6

2.1.2. Machines Synchrones à rotors bobinés à pôles saillants 6

2.2. Machines Synchrones à Aimants 6

2.3. Machines Synchrones à f.e.m sinusoïdale 7

3. Modélisation de la MASP pour la commande vectorielle 7

3.1. Expression des flux 7

3.1.1. Expression des flux induits sur les enroulements statoriques. 8

3.2. Expression des tensions 8

3.3. Expression du couple 9

3.4. Equation mécanique 10

3.5. Modèle de la machine dans le repère triphasé abc 10

4. Commande vectorielle de la MSAP 10

4.1. Hypothèses simplificatrices 11

4.2. Stratégies de Commande 11

4.3. Modélisation de la machine dans les référentiels diphasés 12

4.3.1. Modélisation de la machine dans le référentiel de PARK 12

Table des matières
	4.3.2. Modélisation de la machine dans le référentiel(á,â) 4.3.2.1. Transformation de Concordia 4.3.2.2. Equation aux tensions de la machine :		12 12 12
	4.4.	Principe de la commande vectorielle	13
	4.4.1.	Compensation et découplage	13
	4.4.2.	Schémas de principe de la commande vectorielle	14
	4.4.3.	Synthèse des régulateurs	14
	4.4.3.1.	Boucle de courant (boucle interne)	15
	4.4.3.2.	Boucle de tension (boucle de vitesse)	16
5.	Commande avec capteurs mécaniques (encodeur, resolver)		18
	5.1.	Principe	18
	5.2.	Limites de la commande avec capteurs mécaniques	18
	5.3.	Perspectives envisagées	18
6.	Conclusion		19

III. ETAT DE L'ART DES TECHNIQUES D'ESTIMATION DE LA POSITION ET DE LA VITESSE DESTINEE A LA COMMANDE SANS CAPTEURS 19

1. Introduction 19

2. Techniques utilisant les mesures algébriques 20

2.1. Méthodes utilisant les tensions et les courants pour calculer le flux

principal 20

2.2. Méthode utilisant la différence entre des prédictions modèle de la tension

du courant et leurs valeurs réelles 20

2.3. Méthode utilisant les équations, les paramètres connus de la machine et

les manipulations algébriques 21

3. Autres techniques d'estimation 21

	3.1.	Techniques utilisant l'acquisition de la f.e.m aux bornes de la machine ..21
	3.2.	Intégration de la f.e.m	21
	3.3.	Technique basée sur les réseaux de neurones	22
	3.4.	Technique basée sur la logique floue	22
4.	Techniques basées sur les observateurs		22
	4.1.	Observateur déterministe de Luenberger	23
	4.2.	Observateur à ordre réduit	23
	4.3.	Observateur à mode glissant	24
	4.4.	Estimateur Standard de Kalman	24
5.	Conclusion		24
IV.	CONCLUSION		25

PARTIE 2
ANALYSE ET MISE EN OEUVRE DES OBSERVATEURS DE POSITION POUR
LA COMMANDE DE LA MACHINE SYNCHRONE A AIMANTS PERMANENTS

CHAPITRE 2

DIMENSIONNEMENT DES OBSERVATEURS ET SIMULATION 27

I. INTRODUCTION 27

II. OBSERVATEUR DE POSITION DU ROTOR BASE SUR LA RECONSTRUCTION DES FLUX STATORIQUES 28

1. Introduction 28

2. Modèle de la machine dans le référentiel (á,â) 28

3. Equations d'état 28

4. Validation du modèle de la machine 29

4.1. Résultats de simulation de la Validation du modèle de la machine 29

5. Estimation de la position du rotor 30

5.1. Synthèse de l'Observateur de Luenberger d'ordre complet 30

5.1.1. Equations d'état et principe 30

5.1.2. Estimation de la position du rotor 32

5.1.3. Observabilité 33

5.1.4. Détermination de la matrice gain de l'observateur G 33

5.2. Estimation de la vitesse 34

5.3. Justification du choix des valeurs propres 35

5.4. Choix de valeurs propres dynamiques 35

5.5. Utilisation de l'observateur pour la commande de la machine 36

6. Simulation sous MATLAB SIMULINK 36

6.1. Résultats de simulation et interprétations 36

6.2. Simulation en tenant compte des bruits et de l'OFFSET 37

6.3. Simulation en pleine charge (charge nominale 0.8Nm) 39

7. Conclusion 40

III. OBSERVATEUR REDUIT DE POSITION BASE SUR LA RECONSTRUCTION DES FLUX STATORIQUES 41

1. Introduction 41

2. Equations d'état 41

3. Estimation de la position du rotor 41

3.1. Synthèse de l'Observateur réduit 41

3.1.1. Principe de l'observateur d'ordre réduit 42

3.1.2. Observabilité 42

3.1.3. Calcul du gain de l'observateur réduit Gr 43

3.1.4. Calcul de la matrice d'état réduit F = A₁₁ - G r A21 44

3.1.5. Calcul du gain K₀ = A₁₂ - G r A22 44

3.1.6. Calcul du gain B₀ =(B₁ -G _r B2) 44

3.2. Estimation de la vitesse 45

4. Justification du choix des valeurs propres 45

5. Choix de valeurs propres dynamiques 45

6. Simulation sous MATLAB SIMULINK 45

6.1. Résultats de simulation et interprétations 45

6.2. Simulation en tenant compte des bruits et de l'OFFSET 46

6.3. Simulation en tenant compte de la charge nominale 0.8Nm 47

7. Conclusion 48

IV. OBSERVATEUR REDUIT BASE SUR LA RECONSTRUCTION DE LA VITESSE 48

1. Introduction 48

2. Equations d'état 48

3. Estimation de la position du rotor 49

3.1. Synthèse de l'Observateur réduit 49

3.1.1. Principe de l'observateur réduit 50

3.1.2. Détermination des matrices de l'observateur 50

3.2. Estimation de la position du rotor 51

3.3. Choix des valeurs propres 51

4. Simulation sous MATLAB SIMULINK 52

4.1. Résultats de simulation et interprétations 52

5. Conclusion 53

V. CONCLUSION 53

CHAPITRE 3

VALIDATION EXPERIMENTALE - IMPLANTATION SUR DS1104 55

I. INTRODUCTION 55

II. IMPLANTATION DES DIFFERENTS OBSERVATEURS 56

1. Observateur d'ordre complet de la position du rotor, basé sur la reconstruction des flux statoriques 56

1.1. Considérations pratiques 56

1.2. Résultats et mesures expérimentaux de la commande 57

1.2.1. Faibles vitesses 57

1.2.2. Echelon de vitesse 57

1.2.3. Echelon de vitesse croissant 58

2. Observateur réduit de position du rotor basé sur la reconstruction des flux

statoriques 59

2.1. Résultats et mesures expérimentaux de la commande 59

2.1.1. Faibles vitesses 59

2.1.2. Echelon de vitesse 60

2.1.3. Echelon de vitesse croissant 60

3. Essais en charge cas des deux observateurs 61

4. Conclusion 62

III. CONCLUSION 63

CONCLUSION GENERALE 64

ANNEXES 67

NOTATIONS 71

BIBLIOGRAPHIE 73

Articles 77

LISTE DES FIGURES

CHAPITRE 1 : MODELISATION ET ETAT DE L'ART DE LA COMMANDE SANS CAPTEUR DE LA MSAP

Figure I.1 : Machine à pôles saillants 6

Figure I.2 : Machine à pôles lisses 6

Figure I.3 Machine a fem sinusoïdale 7

Figure I.4 : Machine a fem trapézoïdale 7

Figure I.5 : Schéma monophasé équivalent 9

Figure I.6 : Diagramme vectoriel 9

Figure I.7 : Schéma synoptique de la commande avec onduleur contrôlé en courant 11
Figure I.8 : Diagramme vectoriel pour la stratégie 1 (Couple maximal 'P=0) 12

Figure I.9 : Schéma synoptique de la structure autopilotée avec capteur 14

Figure I.10 : Schéma bloc de principe de la commande vectorielle à flux orienté 14

Figure I.11 : Boucle de courant Id 15

Figure I.12 : Boucle de courant Iq 15

Figure I.13 : Boucle de tension (boucle de vitesse) 16

Figure I.14 : simplification de la boucle de tension 17

Figure I.15 : Boucle de vitesse en tenant compte de .ref(tr/ min) 17

Figure I.16 : Schéma synoptique de la commande avec observateur 22

CHAPITRE 2 : ETUDE ET SIMULATION

Figure II. 17 : Schéma de simulation du modèle d'état de la MSAP 29

Figure II.18 : Flux rotoriques Im _á , I_mp 30

Figure II.19 : Schéma de principe de l'Observateur d'état du modèle de la MSAP 34

Schémas de simulation : Observateur de Luenberger d'ordre complet

Figure II.20 : Couple Cem 36

Figure II.2 1 : Vitesses mesurée et estimée 36

Figure II.22 : Angles mesurée et estimée 37

Simulation en tenant compte des bruits et de l'OFFSET (plus proche de la réalité)

Figure II.23 : Couple électromagnétique 37

Figure II.24 : vitesses mesurée et estimée 37

Figure II.25 : Angles mesurée et estimée 37

ix

Figure II.26 : erreur de vitesse (tr/min) 37

Figure II.27 : erreur de position électrique 38

Valeurs propres dynamiques

Figure II.28 : Couple électromagnétique Cem 38

Figure II.29 : vitesses mesurée et estimée 38

Figure II.30 : Angles élec mesurée et estimée 39

Figure II.31 : erreur de vitesses (tr/min) 39

Figure II.32 : erreur angle électrique (rad) 39

Simulation en pleine charge (la charge nominale de notre machine est de 0. 8Nm)

Figure II.33 : Vitesses mesurée et estimée 40

Figure II.34 : erreur de vitesse pleine charge 40

Figure II.3 5 : erreur de position pleine charge 40

Schémas de simulation : Observateur réduit de position

Figure II.36 : schéma de principe de l'observateur réduit 43

Figure II.37 : Couple électromagnétique 45

Figure II.3 8 : Réponse de l'angle électrique 45

Figure II.39 : Vitesses estimée et mesurée 46

Figure II.40 : Erreur de position (rad) 46

Figure II.4 1 : erreur de vitesse 46

Simulation en tenant compte des bruits et de l'OFFSET (plus proche de la réalité)

Figure II.42 : Erreur de vitesse 47

Figure II.43 : vitesses mesurée et estimée 47

Figure II.44 : erreur de position 47

Figure II.45 : Angles élec mesuré et estimé 47

Simulation en pleine charge (la charge nominale de notre machine est de 0. 8Nm)

Figure II.46 : Couple électromagnétique 47

Figure II.47 : Angles élec mesuré et estimé 47

Figure II.48 : erreur de position 48

Schémas de simulation : Observateur de réduit de vitesse

Figure II. 49 : Schéma de principe de l'observateur réduit de vitesse 51

Figure II.50 : Couple électromagnétique 52

Figure II.5 1 : Vitesses estimée et mesurée 52

Figure II.5 2 : positions estimé et mesuré 52

Figure II.53 : erreur de vitesse (tr/min) 52

Figure II.54 : erreur de position elec (rad) 53

CHAPITRE 3 : VALIDATION EXPERIMENTALE

Figure III.55 : photographie du banc d'essai 56

Résultats expérimentaux : Observateur de Luenberger d'ordre complet Faibles vitesses

Figure III.56 : positions estimé et mesuré 57

Figure III.57 : erreur de position 57

Figure III.58 : vitesses mesurée et estimée 57

Echelon de vitesses

Figure III.59 : positions estimé et mesuré 58

Figure III.60 : erreur de position en degré 58

Figure III.6 1 : vitesses estimée et mesurée 58

Figure III.62 : courants id et iq 58

Echelon croissant

Figure III.63 : positions estimé et mesuré 59

Figure III.64 : erreur de vitesse (tr/min) 59

Figure III.65 : vitesses estimée et mesurée 59

Résultats expérimentaux : Observateur de Luenberger d'ordre complet Faibles vitesses

Figure III.66 : positions estimé et mesuré 59

Figure III.67 : erreur de position en degré 59

Figure III.68 : vitesse estimée et mesurée tr/min 60

Echelon de vitesses

Figure III.69 : positions estimé et mesuré 60

Figure III.70 : erreur de position en degré 60

Figure III.7 1 : vitesse estimée et mesurée tr/min 60

Figure III.72 : courants id et iq 60

Echelon croissant

Figure III.73 : positions estimé et mesuré 61

Figure III.74 : erreur de position en degré 61

Figure III.75 : Vitesse estimée et mesurée 61

Essais encharge pour les deux observateurs

xi

Figure III.76 : Vitesses estimée et mesurée 61

Figure III.77 : Vitesses estimée et mesurée 61

Figure III.78 : positions estimé et mesuré 62

Figure III.79 : positions estimé et mesuré 62

Figure III.80 : Erreur de position 62

Figure III.81 : Erreur de position 62

xii

INTRODUCTION GENERALE

De nos jours, l'utilisation des machines électriques aussi bien dans le milieu industriel que dans les applications domestiques se veut indispensable. Suivant le type d'application et suivant le cahier de charge, un choix s'impose entre les différentes machines qui existent. Les machines synchrones à aimants sont de plus en plus utilisées, vu l'efficacité et les nombreux avantages de ce type d'actionneur. La MSAP présente une puissance massique importante et a la possibilité de fonctionner à très haute vitesse. C'est ainsi qu'elle peut être très utile dans de nombreuses applications.

Comme toutes les autres variantes de moteurs électriques, la commande de ce type de machine ne cesse d'évoluer car nombreuses sont les recherches axées dans ce sens. Dans certaines applications voire même la majorité, l'encombrement causé par les capteurs mécaniques pose problème. Toutefois la commande sans capteurs mécaniques de la MSAP fait l'objet de plusieurs sujets de recherche depuis le début des années 1990.

Les techniques sont nombreuses et chaque méthode présente aussi bien des avantages que des inconvénients. Le choix d'une approche ou d'une autre dépend du cahier de charge imposé, du type d'application et de la particularité de la machine utilisée.

Dans ce mémoire, nous proposons deux techniques semblables d'estimation de position et de vitesse destinées à la commande vectorielle à flux orienté de la Machine Synchrone à Aimants Permanents sans saillance. Nous nous intéressons à l'étude d'observateurs d'état basés sur un modèle de la machine dans le référentiel stationnaire biphasé (á,â). L'idée de base est de reconstituer un vecteur d'état comportant les deux composantes du flux rotorique pour en déduire l'angle électrique et donc la position du rotor.

Le mémoire s'articule en trois chapitres repartis en deux principales parties :

La première partie comprend un chapitre consacré à une étude bibliographique sur la commande sans capteur de la MSAP. Dans ce chapitre introductif, après avoir rappelé les généralités des machines synchrones, nous passons à la modélisation de la MSAP, dans le repère triphasé (abc), puis dans les référentiels biphasés (référentiel de Park et référentiel (á,â) en vu de la commande vectorielle. Nous présentons ensuite l'état de l'art de la commande sans capteurs mécaniques de la MSAP afin de situer notre étude.

La deuxième partie comprend deux chapitres : le deuxième axé sur le dimensionnement des observateurs et la Simulation sous MATLAB - Simulink et un troisième intitulé Validation Expérimentale - Implantation sur DS1 104.

Dans le deuxième chapitre, nous développons la méthode de calcul et de dimensionnement des différents observateurs étudiés, ensuite nous simulerons les méthodes étudiées sur l'environnement MATLAB - Simulink. Pour se rapprocher un peu du cas réel de la pratique, nous ajouterons un bruit et un OFFSET dans les mesures pour tester la robustesse des observateurs. Nous simulerons aussi la commande avec une charge équivalente à la charge nominale de notre machine.

Le troisième chapitre présente les résultats de la validation expérimentale en implantant la commande dans une carte DSP de type DS1 104. Avant d'implanter la commande sans capteur, nous passerons en revues quelques considérations pratiques. Nous présenterons dans ce même chapitre les résultats expérimentaux de la commande sans capteurs en utilisant dans un premier lieu, l'observateur d'ordre plein (ordre4) et ensuite le nouvel observateur d'ordre minimal (ordre2) que nous avons proposé, analysé et mis en oeuvre.

Nous terminerons notre mémoire par une conclusion générale dans laquelle nous passerons en revue les commentaires des techniques étudiées et nous citerons les perspectives envisagées pour une étude ultérieure dans le but d'affiner la recherche.

PARTIE 1

ETUDE BIBLIOGRAPHIQUE

CHAPITRE 1

MODELISATION DE LA MACHINE SYNCHRONE A AIMANTS PERMANENTS (MSAP) ET ETAT DE L'ART DE LA COMMANDE SANS CAPTEUR

I. INTRODUCTION

Comme nous le savons, la machine synchrone ne peut fonctionner en boucle ouverte, car pour injecter des courants de forme appropriée il faut connaître la position du rotor : la machine doit être autopiotée.

Pour cet autopilotage et la commande de la MSAP, la méthode la plus classique pour réaliser cette tache est d'utiliser des capteurs, soient optiques, c'est le cas de l'encodeur incrémental par exemple, ou électromagnétiques à l'instar du resolver. Ces deux familles de capteurs donnent des résultats très satisfaisants mais néanmoins elles présentent nombreux inconvénients qui suscitent la recherche et le développement de nouvelles techniques de commande sans capteur.

Dans certaines applications l'utilisation des capteurs ne pose pas de problème bien qu'elle présente quelques inconvénients. Par contre pour des applications telles que la propulsion des véhicules électriques ou la propulsion des sous marins par exemple, suite à des problèmes d'encombrement la méthode de commande sans capteur s'avère plus efficace.

Dans ce chapitre nous présenterons deux grandes sections dont la première est consacrée à la modélisation de MSAP, et la deuxième sur l'état de l'art de la commande sans capteur de la MSAP.

II. MODELISATION ET COMMANDE DE LA MSAP

1. Introduction

Les principes généraux des commandes vectorielles des machines synchrones restent identiques à ceux introduits par les moteurs asynchrones mais avec des spécificités suivants les technologies utilisées (machines à rotors bobinés, à pôles lisses ou saillants, à réluctance variable directe ou inverse, à aimants).

Ces contrôles permettent une amélioration du temps de réponse et de la qualité du couple mais conduisent à des commandes relativement complexes comme le cas de la commande vectorielle des machines alimentées en tension et régulées en courant sur le référentiel de Park d-q, que nous utiliserons par la suite.

Après avoir rappeler les généralités sur les machines synchrones, nous allons aborder les deux types de modélisations de la MSAP que nous utiliserons dans les chapitres qui suivent. Le modèle de la machine dans le référentiel de Park nous sera utile dans la commande vectorielle à flux orienté. Quant au modèle dans le référentiel (á,â) il sera utilisé dans la synthèse des observateurs. C'est sur ce modèle que seront basées la modélisation et le dimensionnement des observateurs étudiés.

2. Généralité sur les machines synchrones

Le terme de machine synchrone regroupe toutes les machines dont la vitesse de rotation de l'arbre de sortie est égale à la vitesse de rotation du champ tournant. Pour obtenir un tel fonctionnement, le champ magnétique rotorique est généré soit par des aimants, soit par un circuit d'excitation. La position du champ magnétique rotorique est alors fixe par rapport au rotor, ce qui impose en fonctionnement normal une vitesse de rotation identique entre le rotor et le champ tournant statorique.

Cette famille de machine regroupe en fait plusieurs sous familles, qui vont de l'alternateur de plusieurs centaines de mégawatts au moteur de quelques watts, en passant par les moteurs pas à pas. Néanmoins, la structure de toutes ces machines est relativement proche. Le stator est généralement constitué de trois enroulements triphasés répartis, tel que les forces électromotrices générées par la rotation du champ rotorique soient sinusoïdales où trapézoïdales. Les stators, notamment en forte puissance, sont identiques à ceux d'une machine asynchrone.

Il existe trois grandes familles de rotor, ayant pour rôle de générer le champ d'induction rotorique. Les rotors bobinés à pôles lisses, les rotors bobinés à pôles saillants ainsi que les rotors à aimants :

2.1. Machines Synchrones à rotors bobinés

Dans le cas des moteurs à rotors bobinés, le rotor supporte un bobinage monophasé alimenté par un courant continu tandis que le stator est équipé d'un bobinage polyphasé à courant alternatifs. L'obtention d'une valeur de couple moyen non nulle passe alors par la vérification de la condition de synchronisme qui impose une égalité stricte entre vitesse du champ tournant stator et vitesse du champ tournant rotor.

Afin de s'en parer des contacts glissants (bague balais) comme pour les machines à courant continu, les machines synchrones à rotor bobiné font appel, le plus souvent, à une excitatrice (ou alternateur d'excitation) associée à un redresseur tournant, pour éliminer tout contact glissant. Cet alternateur auxiliaire dont l'induit est accouplé à l'arbre de la machine débite dans l'inducteur, par l'intermédiaire du pont redresseur à diodes tournant aussi avec l'arbre de la machine.

Le rotor peut être lisses ou saillant, et est généralement équipé de circuits amortisseurs.



Figure I.1 : Machine à pôles saillants Figure I.2 : Machine à pôles lisses

2.1.1. Machines Synchrones à rotors bobinés à pôles lisses

Plutôt adaptées pour des applications à forte puissance et grande vitesse ; le bobinage est dans ce cas logé dans des encoches pratiquées dans la masse du rotor et fermées par des clavettes en acier amagnétique (Figure I.1). Les têtes de bobines inductrices sont maintenues en place par des frettes en acier amagnétique. L'entrefer étant d'épaisseur constante, seule la répartition des encoches et /ou leur remplissage constitue un paramètre structurel jouant sur la forme d'onde des f.e.m attendues. Une disposition appropriée permet d'obtenir des f.e.m sinusoïdales à très faible taux d'harmoniques.

2.1.2. Machines Synchrones à rotors bobinés à pôles saillants

Pour les machines à rotors à pôles saillants (Figure I.2), les bobines inductrices sont montées autour de noyaux polaires massifs ou feuilletés.

Pour ces machines, le rotor est un électroaimant dont les pôles sont alternativement nord et sud. Les enroulements sont alimentés en courant continu, ils sont placés autour des noyaux polaires. Le nombre de pôles est toujours pair, il varie suivant la machine. Elles sont utilisées pour des applications qui nécessitent une simplicité de constitution. Ce type de machine possède un facteur de puissance relativement faible qui impose un surdimensionnement des convertisseurs statiques ; ceci est un inconvénient pour la l'alimentation à fréquence variable. Pour des application de faible puissance aux environ de quelques kilowatts on peut s'affranchir de cette faiblesse de ce genre des machines.

2.2. Machines Synchrones à Aimants

Les Machines Synchrones à Aimants présentent d'énormes avantages et sont de plus en
plus utilisées dans les applications industrielles. Concernant ces machines à aimant, il existe

deux grandes familles selon la forme géométrique des aimants (radiale ou tangentielle) et la distribution des bobinages au stator (sinusoïdale ou trapézoïdale).



Figure I.3 Machine a fem sinusoïdale Figure I.4 : Machine a fem trapézoïdale

2.3. Machines Synchrones à f.e.m sinusoïdale

Elles utilisent des aimants d'arc polaire de 120° (Figure I.3), pour obtenir une induction quasi sinusoïdale, et sont alimentées en ondes sinusoïdales pures de courant ou de tension afin d'obtenir un couple uniforme. Les actionneurs correspondant présentent les propriétés des machines synchrones classiques à flux sinusoïdal et sont dites sans balais synchrones (PMSM : Permanent Magnet Synchronous Motors).

2.4. Machines Synchrones à f.e.m trapézoïdale

Elles utilisent des aimants d'arc polaire de 180° (Figure I.4) et sont alimentées en étoile par des créneaux de courant à 120°. Elles présentes les propriétés des machines à courant continu. Une variante consiste à utiliser des aimants d'arc polaire de 120° et une alimentation en triangle par des créneaux de courant de 180°. Les actionneurs correspondants sont appelés actionneurs à courant continu sans balais (Brushless Direct Current (BLDC) Motors).

3. Modélisation de la MASP pour la commande vectorielle

Afin de réaliser la commande vectorielle et ou la simulation, il est évident de modéliser la machine. La machine considérée est à p paires de pôles lisses à aimant. Nous recherchons un modèle simple et adapté à un traitement numérique.

3.1. Expression des flux

Dans le cas général:

Les flux induits par l'inducteur dans les trois phases statoriques a, b et c s'écriront:

2.ð 2.ð

Ö fa = Ö _m. f(è_e) Ö = Ö è -

fb f e

. ( ) Ö = Ö è +

fc f e

. ( )

m m

3 3

Dans le cas particulier d'une répartition spatiale sinusoïdale du champ Bf.

2.ð 2.ð

Ö fa = Ö_m.cos(è_e) m

Ö = Ö è - m

.cos( ) Ö = Ö è +

.cos( )

fb e fc e

3 3

3.1.1. Expression des flux induits sur les enroulements statoriques.

Pour la phase aa', le flux totalisé Ö_a représente la somme de quatre termes:

Flux propre de a sur a : Öaa = Ls.ia .

Flux mutuel de b sur a : Öba = Ms.ib .

Flux mutuel de c sur a : Öca = M_s.i_c.

Flux mutuel de l'inducteur sur a : Öfa

Ö Ö Ö Ö Ö

a = aa +ba +ca +fa = L_s. i _a +M_s(ib +i_c)+ Ö fa

En supposant le neutre non relié. (ib +i c = - i_a), cette dernière relation s'écrit:

fa

Ö = - + Ö = + Ö

a s s a fa c a

( ). .

L M i L i

L_c Inductance cyclique d'un enroulement statorique. L c = L s - M _s .

Remarque: Le terme _Lc.ia représente le flux induit dans la phase a par le champ tournant créé par les trois courants i_a, ib et i_c.

3.2. Expression des tensions

En convention récepteur la tension sur la phase a s'écrit:

dÖ di didi

a c fa

d

a b Ö

+ = . + . + . +

L M M

s s s

dt dt dt dt

v R i

a a

= .



dt

En supposant que le neutre soit non relié. L'équation précédente devient:

v R i L di a

a a c

= . + .

d

+ Ö

d fa

dt

t

avec

e v i d Ö fa fa

d Ö d è e fa

d Ö

= . = . Ù .

p

a a a

= ( = 0 ) =

dt d è dt d è

e e

La tension sur la phase a s'écrit:

v R i L di

= . + . +

a p a a c dt

d Ö fa R i L di

. Ù . = . + . +

e_a

a

a c

d è dt

e

Sur les deux autres phases

v R i L di = . + . + b p b b c dt	d Ö fb = . + . + b R i L di . Ù . e d è b b c dt e
v R i L di = . + . + c p c c c dt	d Ö fc = . + . + c R i L di . Ù . e d è c c c dt e

Le schéma électrique d'une phase est représenté à la figure suivante :



Figure I.5 : Schéma monophasé équivalent



Figure I.6 : Diagramme vectoriel

Nota : Ce schéma n'est valable que pour des Machine à pôles lisses en Absence de saturation et pour un Neutre non relié.

3.3. Expression du couple

Si nous raisonnons sur les énergies relatives à la phase a on a :

di

v i dt R i L i dt e i dt

. . . . . . . .

= + +

2 a

a a a c a a a

dt

Avec :

v_a . i _a .dt : Energie électrique fournie à la phase.

R . i a : Energie dissipée sous forme de pertes joules dans la phase.

2

di L i dt . . . a c a dt

: Energie électromagnétique stockée dans la phase.

e_a .i _a .dt : Energie électromagnétique restituée sous forme d'énergie mécanique. Conversion Electromécanique : Cemdèm = P_edt

La puissance électromagnétique instantanée s'écrit:

P e =ea.ia+eb.ib+ec.ic

d'où le couple électromagnétique

_C+ +

p e i e i e i

= =

e a . a b . b c . c

emÙ Ù

En remplaçant les f.e.m par leurs expressions en fonction des flux, on obtient:

d d d

Ö Ö Ö

C p i i i

. . .

fa fb fc

=

em a b c

+ +

d è d è d è

e e e

3.4. Equation mécanique

L'équation fondamentale de la dynamique s'écrit:

d d

Ù = ? = è = è

2 2

J d e

dt dt p dt

em r 2 2

m

J C C J

3.5. Modèle de la machine dans le repère triphasé abc

On établi le modèle de la machine à partir des équations suivantes.

v R i L di

= . + . +

a p a a c dt

d Ö fa R i L di

. Ù . = . + . +

e_a

a

a c

d è dt

e

v R i L di = . + . + b p b b c dt

d Ö fb = . + . + R i L di b . Ù . e b c d è dt e

b



v R i L di

= . + . +

c p c c c d t

d Ö fc = . + . +

e c

R i L di c

. Ù .

dt

c c

dè_e

d d

Ù = ? = è = è

2 2

J d e

m

J C C J

dt dt p dt

em r 2 2

d d d

Ö Ö Ö

C p i i i

. . .

fa fb fc

= + +

em a b c

d è d è d è

e e e

4. Commande vectorielle de la MSAP

Notre objectif étant d'établir les conditions pour que le couple développer par la machine soit à valeur moyenne non nulle et, autant que possible, exempt d'ondulations, la solution adaptée est d'injecter dans les trois enroulements des courants dont la forme dépendra de l'expression des f. e.m induites dans les trois phases. Nous pouvons constater que le fait d'injecter des courants fonction de la position angulaire èe revient à autopiloter la position angulaire du champ tournant statorique au champ tournant rotorique.



Figure I.7 : Schéma synoptique de la commande avec onduleur contrôlé en courant

4.1. Hypothèses simplificatrices

On considère que :

V' les circuits magnétiques ne sont pas saturés, l'hystérésis et les courants de Foucault sont négligeables : les inductances ne dépendent pas des intensités des courants et les pertes fer sont nulles.

V' les résistances des enroulements ne varient pas en fonction de la température. V' les inductances sont indépendantes de la position du rotor. Ld=Lq=Lc

4.2. Stratégies de Commande

On dispose trois stratégies qui permettent d'optimiser certains critères. On peut envisager en régime permanent:

V' d'obtenir un couple maximum pour un échauffement donné, V' de minimiser le dimensionnement du variateur,

V' de fonctionner au-delà de la vitesse nominale.

On envisage dans notre cas la première stratégie : avoir un couple maximum pour un échauffement donné. Le couple sera maximum pour un échauffement donné donc pour un courant donné, si l'on maintient Ø à zéro et le flux inducteur à sa valeur maximale (Figure I.8).

Avec cette condition : (En négligeant la chute de tension dans la résistance R)

11



Figure I.8 : Diagramme vectoriel pour la stratégie 1 (Couple maximal Ø=0)

4.3. Modélisation de la machine dans les référentiels diphasés 4.3.1. Modélisation de la machine dans le référentiel de PARK

di

v R i L p L i

d

= +

. . - ù

di

v R i L e

= + +

a

. .

a a c a

dt

di

v R i L e

= + +

b

. .

b b c b

dt

di

v R i L e

= + +

c

. .

c c c c

dt

d d c m c q

dt

di

v R i L p L i p

q

= +

. . + ù + ù Ö

q q c m c d m m

dt

3

Cem = p Ö m = K _T i q

2

d ù

J C C f C

m = - - ù -

em r m s

dt

Ce modèle sera utilisé pour la commande vectorielle à flux rotorique orienté. 4.3.2. Modélisation de la machine dans le référentiel(á,â)

4.3.2.1. Transformation de Concordia

1 1

- -

2 2 2

3 3 3

0

x_á
x_â

1





2 2

x_a
x_b
x_c

4.3.2.2.Equation aux tensions de la machine :

di

v R i L e

= + +

a

. .

a a c a

dt

di

v R i L e

= + +

b

. .

b b c b

dt

di

v R i L e

= + +

c

. .

c c c c

dt

di

v R i L e

á = á + + á

á

. c .

dt

di

v R i L e

â = â + + â

â

. c .

dt

12



má

e_á

d Ö

dt

Avec :

d Ö

=

mâ

e_â

dt

On sait que :

Ö _á,â =Liá , â +Ö _m (è)

^m á â,

d Ö áâ = á â

di d Ö

, ,

+

L .

dt dt dt

C'est sur ce modèle que nous allons nous baser pour faire notre observateur (chapitre2). 4.4. Principe de la commande vectorielle

Stratégie de commande vectorielle considérée : Elle consiste à maintenir le courant i_d nul et réguler la vitesse via la tensionu_q. Lorsque id est nul, le modèle de la PMSM se réduit à celui d'un MCC à excitation indépendante. La relation couple - courant est linéaire:

3

Cem = p Ö _m =K_T i q

2

4.4.1. Compensation et découplage

Le modèle de l'équation de la machine est couplé, il faut donc réaliser un découplage et une compensation afin d'avoir un modèle complètement découplé et compensé.

+

pùmLciq

di

découplage

v R i L p L i

d

= +

. . - ù

d d c m c q

dt

di

v R i L p L i p

q

= +

. . + ù + ù Ö -

q q c m c d m m

dt

p ù _m L _c i _d - _pùmÖm découplage et compensation



On obtient ainsi le modèle découplé et compensé suivant :

u R i L = + . . d d c		did dt
u R i L = + . . q q c	di q dt

Et les mêmes équations mécaniques en ne tenant pas compte du couple de frottement sec : 3

Cem = p Ö m = K _T i q

2

d ù

J C C f

m = - - ù

em r m



Chapitre 1 : Modélisation de la MSAP et Etat de l'art de la commande sans capteur

La synthèse des régulateurs sera basée sur ce modèle avec ces équations complètement indépendantes.

4.4.2. Schémas de principe de la commande vectorielle

Nous rappelons ici le schéma de principe de la commande de notre machine. Le convertisseur statique est alimenté par une source de tension _VDC, les signaux de commande proviennent de la modulation à largeur d'impulsion venant du dispositif de commande qui a pour entrées les tensions et les courants statoriques, la position et la vitesse mesurées ou estimées.

Réseau

Figure I.9 : Schéma synoptique de la structure autopiotée avec capteur

VDC

i_d

+

+

-

PIi

dq

abc

MS

MLI

ùref

+

+

-

PIi

+

PI_ù

+

-

iabc

dq

abc

Capteur

è_e

ù_m

Figure I.10 : Schéma bloc de principe de la commande vectorielle à flux orienté

4.4.3. Synthèse des régulateurs

On se base sur le modèle compensé et découpé de la MSAP suivant:

14

u_d = R.i_d (s) + Lsid(s) u_q = R.i_q (s) + Lsiq(s) 3

Cem = p Ö m = KTiq

2

d ù

J C f

m = - ù on néglige pour un premier lieu le couple résistant.

t

em m

d

4.4.3.1.Boucle de courant (boucle interne)

I s R H s

d ( ) 1 1 ( )

= = = 1

L

+ s

R

de même 2

H s

s

R



u s R Ls

( ) 1

+

d

I s

( ) 1

( ) = =

R

q

u s L

q ( ) 1 +

On a : 1 ( ) 2 ( ) ( )

H s H s H s

= = =

1

1 L

k = et e

ô = constante de temps électrique R R

k

avec

+ ô s

e

On a le schéma synoptique suivant :



U_d I_d

*

H₁(s)

+

-

+

PI

I_d^*

Figure I.11 : Boucle de courant Id

&



* Uq *

Iq + PI

-

+

H₂(s)

I_q

Figure I.12 : Boucle de courant Iq

On veut corriger ce système avec un PI de la forme
k k k

ii ii pi

PI ( ) (1 )

s k s

= + = +

^pi s s k ii

Premier indice pour proportionnel (p) ou intégral (i)

Deuxième indice pour le courant (i) ou la vitesse (ù)

k k

PI s s

( ) (1 )

= s + ô la fonction de transfert en boucle ouverte est (1 ) (1 )

kii H s

ii

i BO = + +

s s

ô ô

e

k

On pose pi

ô == ô_e

k ii

k k

pour compenser le pôle. On obtient ii

H = iBO s

et

H iBO

H iBF

1+

H iBO

HiBF

1 1

1+

11 + ô s s i

kk ii

avec 1

ô = Normalement on doit choisir ô i << ô _e pour imposer

ⁱ kkii

une dynamique un peu plus rapide.

Calcul des paramètres k_ii et k_pi : D'une manière générale pour ô_i choisie :

k pi 1 = ô k k = · avec k R e pi ii ii

1 1 1 1 LL k k k = · = · · = ii pi k ôRkôô pi i i i

R

Et 1 1

k k

= ·

ii ii

kô ô

i i

k

On a ^pi

k ii



= ô, on prend ô_i = ô e

e

k 11

pi = k R

= =

k k k k

pi

.

ii ii

1 1 1 L

= ô k R L

= · = · =

k k k R

e ii

· ô

ii e

Les deux chaîne de calcul des courants id et iq sont totalement indépendantes :

Id^*				Id
		HiBF
Iq^*					Iq
	HiBF

4.4.3.2.Boucle de tension (boucle de vitesse)

La boucle de courant de iq est à l'intérieur de la boucle de tension. Au fait le courant de référence iq et déterminé par la boucle de vitesse.



ùref

(rad)

+

-

+

PI_ù (s)

I_q^*

HiBF(s)

I_q

KfT r

1+

ô s
m

ù

Figure I.13 : Boucle de tension (boucle de vitesse)

Hypothèses :

v On néglige le couple de charge en le considérant comme une perturbation.

v On considère que la boucle de courant est assez rapide qu'on puisse le modéliser par un gain unitaire, on a donc :



PI_ù (s)

+

+

HiBF (s)

I_q^*

ù

(rad)

ùref

-

Figure I.14 : simplification de la boucle de tension

K

= et ' T

k =

f_r

Avec m

ô

J
f_r

De même on veut un PI pour la boucle de tension de la forme

PIù	k k k ( ) (1 ) s k s = + = + i i p ù ù ù p ù s s kiù		on fait un placement de pôle (1 + ôms) = (1 + ôs)
PI s s ù = + ô ( ) (1 ) ki ù s		k avec p ô = = ô ù m k iù		idem que la boucle de courant.

La fonction de transfert en boucle ouverte de processus est :

k k k k k k k

' ' ' '

· ·

( ) (1 ) ( )

i ù i ù i ù

H PI s

= · = + · =

ù ô H s =

^BO 1 1

m BO

s s s

+ +

ô ô

s s

mm

Enfin la fonction de transfert en boucle fermée est donnée par :

1 1

H H

==

BF

^BF 1 1

s

1+

+ ô_ù 0 s

1

avec 0

ô =
ù

k' k i

· ù

k k

'· i ù

En considérant la vitesses du rotor en tr/min on a :

ùref

(tr/ min)



+

-

+

PI_ù(s)

I_q^*

HiBF(s)

g

ù

Figure I.15 : Boucle de vitesse en tenant compte de ùref ( tr / min)

Avec 60

g=

gain permettant de passer de rad/s vers tr/min

2ð

HBF

1 1 1

= = ô =

1 '

0 s s g k k

ù

1+

ô ô

ù ù

+ · · i ù

g

Calcul des paramètres k i ù et kp ù :

k p ù



= ô_m

f_r

=

k 1

i ù

On a k =

g k g k

· · ·

ô m

1 '

· ô

T m

i ù

	=	ôm
g k k · '· i ù

k p /

J f J

^ù ô ô ô ô

k k f

r

= m p m i

ù ù

= · = · =

· · · ·

r

k g k g k

i ù T m T m

On trouve enfin les paramètres du correcteur PI de la boucle de tension :

kiù

k p ù

f r

g k

·

· ô

T m

J

g k

· · ô

T m

5. Commande avec capteurs mécaniques (encodeur, resolver)

5.1. Principe

Dans un premier temps nous allons implanter la commande vectorielle de la machine en utilisant le capteur pour s'assurer de l'étude faite sur la modélisation de la machine et la synthèse des différents régulateurs. La position et la vitesse de l'arbre du rotor de la machine sont données par l'encodeur.

5.2. Limites de la commande avec capteurs mécaniques

Nous avons vu plus haut que les capteurs mécaniques, non seulement ils coûtent trop cher mais ils peuvent dans certains cas poser un grand problème d'encombrement pour des applications particulières.

5.3. Perspectives envisagées

Nous envisageons donc de faire la synthèse d'un observateur de position robuste d'ordre minimal (ordre2) en se basant sur un observateur de Luenberger (d'ordre complet) proposé par T.D BATZEL dans [BATZ-LEE_1]. Notre observateur a les avantages suivants :

y' Dynamique très bonne

y' Fonctionne bien en régime permanent qu'en régime transitoire

y' Il ne dépend pas de la valeur initiale de la position du rotor

y' Il est bien adapté à la propulsion électrique, car il ne dépend pas des paramètres

mécaniques tels que, l'inertie, le couple de charge ainsi que les frottements.

y' Fonctionne aussi bien même à très faibles vitesses et à des vitesses plus proches de

zéro

6. Conclusion

Dans cette section nous avons présenté les généralités sur les machines synchrones ensuite nous avons établit les deux types de modèles que nous allons utiliser ultérieurement pour la commande vectorielle à flux rotorique orienté de la MSAP sans capteur de position. Le principe de la commande est rappelé ainsi que la stratégie de commande adoptée. Toutefois certaines hypothèses simplificatrices ont été énumérées afin de ne pas alourdir les calculs.

III. ETAT DE L'ART DES TECHNIQUES D'ESTIMATION DE LA POSITION
ET DE LA VITESSE DESTINEE A LA COMMANDE SANS CAPTEURS

1. Introduction

Les capteurs mécaniques, qui font partie intégrante de l'ensemble alimentation - convertisseur - machine, possèdent de nombreux inconvénients. En effet, leur emploi génère une augmentation non négligeable du coût et parfois du volume du moteur. Pour des moteurs de petite taille, la présence d'un tel capteur au niveau de l'arbre peut rendre ce dernier quasi-inaccessible. De même, pour des moteurs à arbre creux, le couplage du capteur avec le rotor peut s'avérer délicat. L'installation de ces dispositifs de mesure nécessite un calage relatif au rotor. Cette opération s'avère laborieuse à reproduire en série, même si elle peut être réalisée par la commande numérique. Pour pallier les inconvénients mentionnés ci-dessus une méthode consiste à mettre en oeuvre une détection indirecte de la position.

La commande sans capteur de position pose deux problèmes majeurs. Le premier concerne la localisation de la position initiale du rotor. La connaissance de la position initiale est nécessaire à la fois pour démarrer le moteur avec le couple maximum et pour éviter une rotation du moteur dans le sens inverse. Le second problème consiste à assurer l'autopilotage malgré les variations paramétriques et des différentes perturbations agissant sur l'axe du moteur.

Dans le cadre de nos travaux d'initiation à la recherche, nous avons étudié une structure de commande permettant de supprimer le capteur de position. De plus, cette structure doit être robuste aux variations paramétriques et aux différentes perturbations. Avant d'introduire la structure étudiée, nous allons effectuer un bref rappel bibliographique sur les stratégies de reconstruction de la position rotorique [VAS] [JOHN99] [ERTU] [JABB] [BAG99], en décrivant les principales méthodes, avec leurs avantages et leurs inconvénients.

De nos jours, la commande vectorielle de la MSAP se voit remplacée par la commande vectorielle sans capteurs mécaniques pour des raisons aussi bien d'ordre économique que technique.

Vu la diversité des nouvelles méthodes, il n'est pas évident de trouver la seule et meilleure
façon de classer les techniques d'estimation de position et de vitesse de la commande sans

capteur mécanique des moteurs électriques. Plusieurs techniques ont été publiées auparavant et nombreux sont les nouvelles méthodes développées au troisième millénaire ; c'est sur cette base que nous allons classifier ces techniques en quatre principaux groupes :

v Les techniques utilisant les mesures algébriques

v Techniques utilisant la f.e.m

v Techniques basée sur la logique floue et réseau de neurones

v Les techniques utilisant les observateurs

2. Techniques utilisant les mesures algébriques

Nous allons nous limiter pour ce sous ensemble à trois techniques.

2.1. Méthodes utilisant les tensions et les courants pour calculer le flux principal

Les méthodes similaires sont présentées dans [WU9 1] [SENJ]. On considère l'équation électrique :

v R i = .	+	d Ö
		dt

Cette équation est intégrée pour avoir le flux :

t

Ö = ( . )

v - R i dt

0

La connaissance de la position initiale, des paramètres de la machine et de la relation liant le flux principal à la position du rotor permet l'estimation de cette dernière grandeur. La vitesse est estimée en déterminant le taux de variation du flux principal résultant de cette intégration. Une variante de cette méthode procède par une extraction polynomiale basée sur les valeurs précédentes de la position pour prédire la position suivante. Les méthodes basées sur le calcul du flux principal ont permis de s'affranchir de besoin du neutre en utilisant les tensions composées au lieu des tensions simples ; cet avantage est le côté attirant principal de ces méthodes. D'autres techniques ont combiné, pour réguler la boucle de vitesse, les méthodes de calcul du flux avec des stratégies de commande perfectionnées telles que les observateurs d'état, la commande adaptive.

2.2. Méthode utilisant la différence entre des prédictions modèle de la tension du courant et leurs valeurs réelles

Cette méthode a été publiée par N. MATSUI, dans [MATS-1] [MATS-2] [MATS-3]. Cet auteur a fondé la théorie de sa méthode sur le modèle de la machine représentée dans un référentiel de Park d-q lié au rotor. Les tensions et les courants mesurés sont projetés dans ce référentiel puis comparés à leurs images obtenues par reconstruction dans un référentiel

semblable mais hypothétique. Les différences obtenues informent sur la variation de la position qui s'est produite depuis la position précédente [WAT].

2.3. Méthode utilisant les équations, les paramètres connus de la machine et les manipulations algébriques

En ce qui concerne l'estimation de la position et de la vitesse, ce type d'estimateur utilise la théorie des référentiels et des transformations géométriques en plus des équations et des paramètres de la machine. Initialement les tensions et les courants mesurés sont transformés dans des référentiels de Park liés au rotor et au stator. Le passage du référentiel statorique à celui rotorique est donné par la transformation matricielle standard suivante :

x x

cos sin

û û

--

dr ds

=

x x

sin cos

û û

qr qs

Cette transformation permet de substituer les variables liées au référentiel statorique dans les équations de la machine représentée dans le référentiel rotorique. Un fois que ces équations sont totalement en terme de variables statorique, les manipulations convenables conduisent à une expression de la position [WAT]. Ensuite, étant donné le flux rotorique ct_m, l'expression de la vitesse est déduite pour une machine isotrope. On trouve

des variantes de cette méthode dans d'autres publications.

3. Autres techniques d'estimation

3.1. Techniques utilisant l'acquisition de la f.e.m aux bornes de la machine

Dans un fonctionnement à flux orienté de la machine synchrone, la f.e.m et le courant dans une phase sont alignés. Les instants de commutation du convertisseur peuvent être obtenus en connaissant juste le passage par zéro de la f. e.m et l'angle de la commande [LIZU85]. On détecte le passage par zéro de la f. e.m lorsque le courant est nul. Une fois les instants sont détectés et décodés on produit les signaux de commande du convertisseur. Cette méthode n'est pas praticable pour des faibles vitesses puisque la f.e.m est nulle à l'arrêt et proportionnelle à la vitesse en marche. Toutefois, à très haute vitesse, le procédé d'orientation du flux est bouleversé d'où une limitation de la vitesse autour de 1000- 6000tr/min.

3.2. Intégration de la f.e.m

La position du rotor est déduite d'une intégration programmée de la f. e.m de la phase ouverte du moteur [KONG02] [PET]. L'intégration au moment où cette f. e.m passe par zéro. L'opération d'intégration est arrêtée lorsque la f. e.m dépasse un certain seuil correspondant à l'instant de commutation. Du moment que la f. e.m peut être supposée linéaire et à pente indépendante de la vitesse au voisinage du passage par zéro pour les machines synchrones à f.e.m trapézoïdale, la tension de seuil peut être prise constante dans toute la plage des vitesses. Des circuits spéciaux basés sur cette méthode ont été conçus et commercialisés. Cette technique est insensible aux bruits de commutation et s'adapte

21

automatiquement à toute variation de vitesse jusqu'une limite de 3600tr/min. Toutefois elle reste moins efficace concernant les faibles vitesses.

3.3. Technique basée sur les réseaux de neurones

De nouvelles techniques basées sur l'intelligence artificielle sont proposées. Dans [BATZ] les auteurs proposent un réseau de neurones à propagation inversée établi sous forme de filet non linéaire liant les grandeurs électriques mesurées à la position du rotor. La position générée par ce réseau est utilisée ensuite pour estimer le flux principal que l'on compare au flux réel calculé par intégration de la f. e.m mesurée. La différence obtenue est propagée dans le réseau pour permettre la modification des paramètres et l'estimation de la position du rotor. Une valeur initiale du flux ou carrément de la position est exigée.

3.4. Technique basée sur la logique floue

Dans [HAMD], un schéma de commande sans capteur basée sur la logique floue est proposé. Dans cet article le système de logique floue estime, d'un côté la position du rotor à partir des mesures des courants et des tensions ; et de l'autre, il gère les références de courant nécessaires pour réaliser un mode de fonctionnement à couple maximal ou à facteur de puissance unitaire. Dans [BIL], un observateur flou est utilisé pour estimer la position et la vitesse du rotor. Cet observateur flou prend comme entrée les courants statoriques estimés et la différence entre les mesures et les estimations de ces derniers.

4. Techniques basées sur les observateurs

De nombreuses méthodes de commande des processus utilisent le principe du retour d'état (commande optimale, découplage, placement de pôles,...). Comme dans la plupart des cas, les seules grandeurs accessibles du système sont les variables d'entrée et de sortie, il est nécessaire, à partir de ces informations, de reconstruire l'état du modèle choisi pour élaborer la commande.



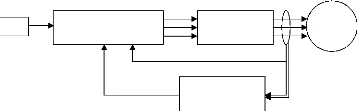
Réf

Régulation de
courant et tension

Position

Vitesse

Courants

Observateur ou
Reconstructeur

Etage de
puissance

Courants & tensions

MSAP

Figure I.16 : Schéma synoptique de la commande avec observateur

Un reconstructeur d'état ou estimateur est un système (Figure I.16) ayant comme entrées les entrées et les sorties du processus réel et dont la sortie est une estimation de l'état de ce processus.

22

Sous l'hypothèse de linéarité du modèle du processus, la structure de base de l'estimateur est toujours la même, mais sa réalisation dépendra du contexte choisi : continu ou discret, déterministe ou stochastique.

Dans le cas où ce modèle est un modèle déterministe, le reconstructeur d'état sera appelé observateur. Dans le cas de systèmes bruités, où interviennent des phénomènes aléatoires, on parle de filtre ou filtre de Kalman.

La théorie des observateurs a été développée initialement par D. Luenberger aux années 1964 [LUEN] [GREL]. Un observateur standard est un système qui a comme entrées les signaux d'entrée et de sortie d'un processus et produit à sa sortie le vecteur d'état du système. On élimine l'erreur d'estimation grâce à une loi de commande bien appropriée [GREL] [MINZ] [OREIL] [OSTER]. En ce qui concerne les actionneurs électriques, le vecteur d'état est généralement constitué des courants et du couple électromagnétique, en plus de la position et de la vitesse du rotor. Vu la non linéarité de l'équation d'état, l'observateur résultant est non linéaire. Il existe deux approches concernant la théorie des observateurs :

v Les observateurs déterministes

v Les observateurs Optimisant un critère stochastique

Pour les observateurs déterministes on cite :

4.1. Observateur déterministe de Luenberger

L'observateur de Luenberger est le plus connu dans la classe de type déterministe [LUEN] [GREL] [OREIL]. A partir des mesures des entrées et sorties, nous pouvons reconstruire l'état du système linéaire observable. Il est utilisé dans la commande par retour d'état lorsque tout ou une partie du vecteur d'état ne peut être mesuré. Dans sa version étendue, il permet d'estimer les paramètres variables ou inconnus d'un système. Dans [BATZ-LEE_1], un observateur déterministe de flux de type Luenberger est utilisé pour reconstruire la position du rotor. L'estimateur proposé présente beaucoup d'avantages notamment le fait qu'il ne dépend pas du tout de la position initiale du rotor et en plus il fonctionne aussi bien à vitesse avoisinant le zéro qu'à très haute vitesse. L'implantation de cette technique est présentée dans [BATZ-LEE_2] où les résultats expérimentaux ont été présentés et commentés.

4.2. Observateur à ordre réduit

Dans le cas où seulement quelques unes des variables d'états seraient intéressantes, on pratique un couplage par transformation linéaire, des sorties de l'observateur avec le vecteur d'état du système. L'observateur résultant est d'ordre inférieur au premier, il a l'avantage d'alléger le temps de calcul [SOLS] [TAT]. Dans [TAT] [J.KIM] les observateurs à ordre réduit présentés estiment la f. e.m de la machine pour déduire la position et la vitesse du rotor.

Une variante de cette technique est l'observateur à perturbation [MATS-3]. Il est basé sur
l'hypothèse d'un vecteur d'état quasi statique ; hypothèse justifiable chaque fois qu'on a

une fréquence d'échantillonnage et un temps de calcul rapides. Les variations légères des variables d'états sont dites des perturbations et elles se manifestent par des petites fluctuations de la position du rotor.

De nouvelles techniques basées sur les observateurs de flux rotorique à ordre réduit sont présentés dans [BATZ-LEE_1,2,3] [SHIN]. Ces observateurs publiés dans [BATZLEE_1,2,3] [SHIN] sont insensibles aux variations des paramètres mécaniques et sont aussi robustes dans la mesure où la position initiale inconnue du rotor ne pose pas problème contrairement à nombreuses méthodes antérieurement proposées.

4.3. Observateur à mode glissant

L'idée de l'observateur par mode de glissement consiste à utiliser des fonctions de commutation variables de manière à ce que l'erreur d'estimation converge vers zéro dans une surface plane glissante de l'espace d'état [FUR] [PEIX]. Le principe de l'observateur en mode glissant consiste à contraindre les dynamiques d'un système d'ordre n à converger vers une variété de dimension (n-p) dite surface de glissement (p étant la dimension du vecteur de mesure). L'attractivité de cette surface est assurée par des conditions appelées "conditions de glissement". Si ces conditions sont vérifiées, le système converge vers la surface de glissement et y évolue suivant une dynamique d'ordre (n-p).

En conclusion, l'observateur en mode glissant consiste à attirer la trajectoire des erreurs d'observation vers une surface correspondant à une erreur d'estimation de sortie nulle. Sur cette surface, les dynamiques sont stabilisées de manière à annuler l'erreur d'estimation.

En ce qui concerne les observateurs optimisant un contexte stochastique, l'estimation est optimale lorsque les propriétés stochastiques des bruits sont suffisamment connues. On cite l'estimateur standard de Kalman et le filtre de Kalman étendu [BOL] [GREL] [OREIL].

4.4. Estimateur Standard de Kalman

Ce type d'observateur donne une estimation optimale (au sens d'un critère statistique) de l'état du système perturbé par des bruits dont les propriétés stochastiques sont connues. Il est souvent mis en oeuvre pour donner une estimation du flux, de la vitesse ou des paramètres rotoriques utilisés pour la synthèse des commandes vectorielles. Dans [BOL], ce type de reconstructeur est utilisé pour la commande sans capteur des machines synchrones à aimants permanents.

5. Conclusion

Cet état de l'art a permis de lister quelques différentes techniques permettant d'estimer la position et la vitesse du rotor pour la commande vectorielle de la machine synchrone à aimants permanents. Globalement, nous avons classifié les méthodes en quatre grandes familles. Compte tenu de l'exigence du cahier des charges, les observateurs de flux s'avèrent être des structures intéressantes pour la commandes sans capteurs des machines électriques notamment la MSAP.

24

IV. CONCLUSION

Nous avons présenté dans ce chapitre les différentes modélisations de la machine qui seront utilisées ultérieurement pour la commande vectorielle sans capteur de la MSAP. Et après avoir rappeler le principe de la commande vectorielle, et rappelée la stratégie de commande adoptée nous avons fait l'étude de dimensionnement des régulateurs de la boucle de courant et de la boucle de tension. Toutefois certaines hypothèses simplificatrices ont été énumérées afin de ne pas alourdir les calculs.

Il nous a été nécessaire de passer en revue les méthodes nouvelles proposées durant les dernières années concernant la commande sans capteurs des machines électriques plus particulièrement la machine synchrone à aimants. Le développement des estimateurs ne cesse de prendre de l'ampleur, ce qui pousse les laboratoires universitaires d'approfondir leurs études de recherche.

Nous avons vu, concernant les estimateurs de position et de vitesse de la MSAP, que les méthodes sont nombreuses et que même la classification en sous ensemble n'est pas une chose aisée. Toutefois nous avons classé les techniques en quatre sous groupes :

y' Les techniques utilisant les mesures algébriques

y' Techniques utilisant la f.e.m

y' Techniques basée sur la logique floue et réseau de neurones

y' Les techniques utilisant les observateurs

Nous nous intéresserons par la suite aux techniques utilisant les observateurs car c'est dans cet axe que sera basée notre étude de développement, d'analyse, de simulation et d'implantation de la commande vectorielle à flux orienté de la MSAP en utilisant les observateurs.

Nous nous baserons bien sur cette bibliographie pour faire l'étude de l'observateur que nous allons proposé par la suite.

PARTIE 2

ANALYSE ET MISE EN OEUVRE DES

OBSERVATEURS DE POSITION POUR LA

COMMANDE DE LA MACHINE SYNCHRONE

A AIMANTS PERMANENTS

CHAPITRE 2

DIMENSIONNEMENT DES OBSERVATEURS ET SIMULATION

I. INTRODUCTION

Nombreuses sont les techniques d'estimation de position et de vitesse du rotor de l'arbre des machines électrique. Dans notre étude nous nous intéressons aux méthodes basées sur les observateurs, plus particulièrement à un observateur d'état des flux rotoriques d'ordre minimal à savoir l'ordre deux. Durant notre période de stage nous avons étudié en premier lieu un observateur réduit qui donne une estimation de la vitesse et suite à une intégration la position du rotor. Nous avons laissé tombé cet observateur qui, dans son modèle d'état, fait intervenir les équations mécaniques qui demeurent non maîtrisables à cause de la variation des paramètres mécaniques. Cet observateur sera présenté à la fin de ce chapitre avec les résultats de simulation.

Dans un premier lieu, nous étudierons un observateur de Luenberger d'ordre quatre basé sur
la reconstruction des flux rotoriques. La position électriqueè_e , est déterminé en calculant

Ö

l'arc tangente de m â . Cet observateur proposé dans [BATZ-LEE_1 ,2,3] présente

Ö m á

d'énormes avantages mais nous jugeons qu'il nécessite un temps de calcul important vu l'ordre qui est assez grand (ordre quatre). C'est ainsi que nous avons eu l'idée de proposer de réduire l'ordre de cet estimateur puisque une partie du vecteur d'état peut être reconstituée par une combinaison des entrées, des mesures et des états reconstitués.

C'est cet observateur d'ordre deux qui fera l'objet de notre étude dans la deuxième section de ce chapitre. Nous présenterons le dimensionnement, le schéma de principe ainsi que la simulation de notre estimateur et nous comparerons les résultats avec les deux autres observateurs étudiés.

En dernière position nous présenterons le premier observateur étudié qui est basé sur la reconstruction de la vitesse avant de faire conclusion de ce chapitre.

27

II. OBSERVATEUR DE POSITION DU ROTOR BASE SUR LA RECONSTRUCTION DES FLUX STATORIQUES

1. Introduction

Nous étudierons dans cette section un observateur d'état pour reconstituer le vecteur d'état constitué des deux composantes du flux statoriques et des deux composantes du flux rotorique dans le référentiel biphasé (á,â). Nous devons avoir tout d'abord un modèle de la machine dans ce même référentiel pour ensuite se baser sur pour synthétiser notre observateur. Dans cette section nous rappelons le modèle de notre MSAP avec les équations aux flux, ensuite nous allons valider ce modèle puis nous passons au dimensionnement de l'observateur puis à sa simulation.

2. Modèle de la machine dans le référentiel (á,â)

Ici nous allons nous intéresser au modèle de la machine dans (á,â) suivant :

di

v R i L e

á = á + + á

á

. c .

dt

di

v R i L e

â = â + + â

â

. c .

dt

Ö á,â = Liá,â +Ö _m (è)

^m á â,

dÖáâ = á â

di d Ö

, ,

+

L .

dt dt dt

3. Equations d'état

A partir des équations ci-dessus, nous établissons les équations d'état de la machine de manière à avoir :

T

Entrées : u=v_á v_â

T

Vecteur d'état : x=Ö_á Ö _â Ö _má Ö mâ

T

Sorties : y=i_á i_â

-ô

0 0 ô

1 0

x Ax Bu

& = +

y Cx

=

0 0

- ô

000

0 00

ù e

01

B= et

1 0 1 0

L L

-

0 1 0 1

L L

-

A

C =





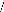
ô
-ù_e

00

00





d Ö á

dt

Nous détaillerons par la suite les calculs qui nous ont permis de déterminer ce modèle d'état.

28

Nous remarquons bien ici que la matrice d'état A dépend de la vitesse du rotor donc nous avons un modèle non linéaire car la vitesse est étroitement liée à la position que nous voulons en fin de compte estimer.

4. Validation du modèle de la machine

L'observateur d'état se base sur le modèle d'état de la machine que nous venons d'établir, pour s'assurer que ce modèle (qui a pour vecteur d'état le vecteur (les flux)) converge vers le premier modèle étudié, nous avons jugé nécessaire de simuler ce modèle et comparer le vecteur d'état avec les flux déterminés par calcul simple à partir du modèle que nous avons auparavant établit dans le référentiel de Park d-q. Afin de ne pas compliquer la simulation nous supposons que la vitesse est constante et que la pulsation rotorique ù_e l'ai trivialement aussi.



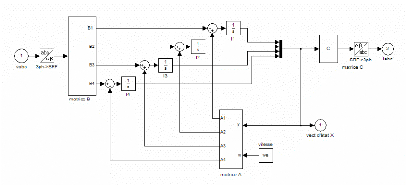
Figure II. 17 : Schéma de simulation du modèle d'état de la MSAP

4.1. Résultats de simulation de la Validation du modèle de la machine

Ce modèle a pour entrées les tensions et pour sorties les courants statoriques. Dans notre simulation nous nous intéressons par contre à la visualisation des composantes du vecteur d'état afin de s'assurer que ce modèle nous donne des flux qui convergent vers les flux déterminés par calcul à partir du modèle dans d-q que nous avons déjà validé.

Nous remarquons ici dans la Figure II.18 que le flux converge très rapidement, ce qui nous permet d'affirmer que le modèle présenté est correcte et que nous pouvons faire la synthèse de l'observateur basé sur ce modèle.

29



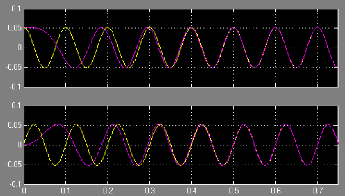
Figure II.18 : Flux rotoriques Ö m á , Ö m â

5. Estimation de la position du rotor

5.1. Synthèse de l'Observateur de Luenberger d'ordre complet 5.1.1. Equations d'état et principe

En considérant le modèle présenté ci haut on a :

v = Ö Ö +

R

á á á

( )

- m

L

R

d Ö

â

+

vâ =

dt

Ö Ö

â â

- m

L ( )

Représentation d'état :

On modélise le système de façon à considérer :

T

Entrées : u=v_á v_â

Vecteur d'état : x =Ö_á Ö _â Ö _má Ö mâ T

Sorties : y =i_á i â T

D'après les équations précédentes on a :

d R Ö á = - v dt L á d R Ö â = - v dt L â	( ) Ö - Ö á m á ( ) Ö - Ö â â m	en posant ô =	R
			L

30

On sait que

Ö = Ö = m m ( ) ( ) è ù t

Ö = Ö m m á Ö = Ö m m â

cos( ) ù e t sin( ) ù e t

d
dt
d



dt

Ö = - Ö = Ö

m m e m

á ù ù ù

sin( )

t â

e e

Ö = Ö = Ö

m m e m

â ù ù ù

cos( )

t á

e e

On a :

Ö - ô ô

0 0 1 0

Ö

á á

d v

Ö 0 0 0 1

- Ö

ô ô

â â á

= +

dtvÖ 0 0 0 0 0
- ù Ö m á e m á â
Ö 0 0 0 0 0

ù Ö

m â e m â

1 ( )

Ö - Ö

iá =
i â=

L
1
L

á á

m

( )

Ö - Ö

â â

m

1 0 1 0

L L

-

i L L

0 1 0 1

-

â

i á





Ö á
Ö â

Ömá





Ö má

On a le système		x Ax Bu & = + y Cx =		avec
-ô	0 0 ô		1 0

0 0

- ô

000

0 0 0

ù e

0 1

B= et

1 0 1 0

L L

-

0 1 0 1

L L

-

A

C =





ô
- ù_e

00

00





Ici on constate bien que la matrice d'état A dépend de la pulsation ou vitesse électrique ù_e.
Nous avons un modèle non linéaire. Pour considérer ce système comme un système linéaire pendant une période d'échantillonnage, nous devons poser l'hypothèse suivante.



y' Nous considérons très lente la variation de la vitesse par rapport à la fréquence d'échantillonnage.

31

5.1.2. Estimation de la position du rotor

La position du rotor è_e est donnée par : à m

Ö

è_e = Arctg â

Ö m á

à

xà 4

è = Arctg On a besoin de reconstruire x3 et x4

e à

x₃

Observateur de Luenberger (ordre n=4)

x Ax Bu

&= +

On a

y Cx

=

x Ax Bu

& à à

= +

y Cx
à à

=

Ce qui donne un observateur d'ordre 4 (même ordre que le système) à

x & =

Fx Ju Gy Fx Ju GCx

à à

+ + = + +

x x Ax Bu Fx Ju Gy

& &

- = + - - -

à à

x ~ & = Fx ~

+ - - + -

( A F GC ) x ( B J)u

x ~ &= Fx ~ = ( A - GC )x ~

G est le gain d'observateur x~ l'erreur d'estimation

Remarque

Pour avoir une bonne estimation, il faut que x~ tend vers 0 pour t tend vers l'infini. x ~ &= Fx ~ implique que les valeurs propres de F doivent impérativement être stables.

Sous cette condition, on détermine la matrice G (gain par placement de pôle). Il existe plusieurs méthodes pour déterminer le gain G, soit par placement de pôle directement avec la forme canonique d'observabilité soit en utilisant l'algorithme général d'Ackermann basé sur un model quelconque du système.



La dynamique de l'observateur dépend donc de la dynamique du polynôme
caractéristique sI - (A - GC) = 0 . On se propose un polynôme caractéristique suivant :

ë ë = 1 2		*	(conjugué)
f(s)=(s-ë1)(s-ë2)(s-ë3)(s-ë4) avec	et ë ë = 1 3

ë ë
=

2 4

donc 2 * 2

f ( s ) = ( s - ë ₁ ) ( s - ë ₁ )

32

5.1.3. Observabilité

La condition d'observabilité du système est donnée par le rang de la matrice d'observabilité

'

O C CA CA CA

2 3

=

Il faut que cette matrice soit de rang complet. Cette matrice n'est pas carrée on détermine l'observabilité du système par la méthode suivante :

- on calcule ^T

O puis T

Q_s = O · O

- on détermine le rang de Q_s

Dans notre cas O est une matrice (8*4) et Q (4*4) : matrice carrée.

On montre que, quelle que soit ù_e vitesse angulaire électrique du rotor supérieure à zéro le système est observable [BATZ-LEE_1 ,2].

5.1.4. Détermination de la matrice gain de l'observateur G :

1 0 On pose : I=et 0 1

J=

0 1 - 10

Nous choisissons une forme de la matrice gain G comme la suivante :

g g

11 12

g g

G

21 22

g g

31 32

g g

41 42

= avec

g g g

= =

11 22 1

g I g J

1 2 2 2 2 2

× ×

+

g I g J

+

3 2 2 4 2 2

× ×

g g g

= =

on a G =

31 42 2

g g g

= - =

21 12 3

g g g

= - =

41 32 4

g R

= -

1

g2	=	Rëë 1 2

ù _e ô

On montre que ( )

R ë ë

+

1 2

g =

3

ô

g₄ =

R ( )

ë ë ù ²

- - + +

1 2 e

ù_eô

Ce qui nous donne la matrice gain de l'observateur :

33

-R		-	R ë ë 1 2
w t e R R ë ë 1 2 -						ë ë * = 1 2
G=	ù e ô ( ) ( ) ë ë ë ë ù ^2 R R 1 2 1 2 + - + e				Avec		et ë ë = 1 3

ë ë
=

2 4

ô ù _e ô

-R

( ) ( )

- + + +

ë ë ù ë ë

² R

1 2 e 1 2

ùô ô

e

ë _i valeurs propres de (A- GC)

Le schéma de principe de l'observateur est donné par la figure suivante, avec comme entrées de l'observateur les tensions et les courants statoriques dans le référentiel biphasé (a,f3). L'observateur de Luenberger utilise les matrices A, B et C du modèle de la machine sur lequel on se base pour le synthétisé.

váâ



+

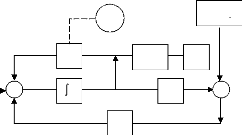
^àx&

A

xà

ùà _e

G

atan

C

è^à_e

yà

abc/af3

+

iáâ

abc/af3

B





ù_e

=

ùà _e

( )

( ) ( )

v _á Ri á v _â Ri â

- + -

2 2

Ö

m

MSAP

vabc



iabc



Figure II.19 : Schéma de principe de l'Observateur d'état de notre modèle de la MSAP

5.2. Estimation de la vitesse

Nous remarquons bien ici que la matrice d'état A dépend de la pulsation rotorique, donc nous avons un modèle non linéaire car non seulement cette pulsation varie en fonction du temps mais elle est étroitement liée à la position que nous voulons en fin de compte estimer. Nous devons à chaque instant avoir une estimation de la vitesse afin de l'insérer dans la matrice A que nous noterons par la suite Aoe. Considérant l'inertie de la MSAP, nous

34

pouvons assimiler la pulsation rotorique égale à une constante durant une période d'échantillonnage, ainsi le modèle devient linéaire.

On sait qu'en régime permanent, = 0

di donc on a :

dt

dÖ má

v Ri Ri Ri t

= + = ? Ö = ? Ö cos( )

á á á á

ù ù ù

e e e

m m

á

dt

v Ri Ri t

â â

= + Ö = + Ö

m m sin( )

â â

ù ù ù

e e e



ù e Ö m =

- Ö

ù e m

= -

v Ri

á á

cos( )

ù t

e

ùÖ

e

m wet v Ri

sin( ) = -

â â

( ) 2 ( )2

v Ri v Ri

á á â â

- - -



( )

( ) ( )

v _á Ri á v _â Ri â

- + -

ù_e

2 2

=

Ö

m

Cette estimation est valable en régime permanent et même à très basses vitesses 5.3. Justification du choix des valeurs propres

Nous choisissons les valeurs propres de l'observateur par un placement de pôle adéquat. En effet pour avoir une bonne dynamique de notre observateur, nous choisirons des valeurs propres très rapides que les pôles du système (processus) et aussi plus rapides que la pulsation rotorique. Toutefois il faut noter que le fait de prendre des valeurs propres plus rapides, l'erreur de l'observateur converge plus rapidement vers zéro mais l'on risque d'augmenter la bande passante et cela peut amplifier les bruits. Dans un premier temps, nous choisissons des valeurs propres assez grandes qui assurent la convergence rapide de l'erreur d'estimation.

Après modélisation de l'ensemble convertisseur machine, nous nous rendons compte que

1

l'ensemble se comporte comme un premier ordre dont on le modélise comme suit :

1 +ô_ùs

avec ô_ù déterminé par des essais de la machine à vide.

Pour choisir les pôles du gain de l'observateur, il faut tenir compte du fait que l'observateur
doit avoir une dynamique beaucoup plus rapide que l'ensemble moteur convertisseur. Pour

cela, nous avons pris en premier lieu les pôles



ë ë
=

0 1

== 1 10
ô w

Nous choisissons ë₁ = -90 puis dans un deuxième temps des valeurs propresë 1 = -200. 5.4. Choix de valeurs propres dynamiques

Le fait de choisir des valeurs propres qui ont une dynamique rapide par rapport à la pulsation électrique rotorique ù_e réduit l'erreur de l'estimation de position.

35

Nous proposons donc une stratégie qui permet de choisir des valeurs propres adaptées à la vitesse de l'arbre du rotor pour essayer de gérer la bande passante et de ne pas amplifier gratuitement les bruits.

ë 0 = ù e

( - k reel + jkim), cette méthode est très pratique elle marche très bien en simulation

comme nous allons le voir dans la section qui suit.

5.5. Utilisation de l'observateur pour la commande de la machine

Notre objectif final est de réaliser la commande sans capteur de la machine synchrone à aimants permanents. C'est ainsi que nous envisageons faire la synthèse de notre observateur d'état afin de boucler le système non avec les grandeurs mesurées mais avec les grandeurs estimées à l'instar de la position et de la vitesse.

6. Simulation sous MATLAB SIMULINK

6.1. Résultats de simulation et interprétations

Nous utilisons l'observateur en boucle fermée pour la commande vectorielle de la machine. Dans la simulation, nous démarrons la commande avec les grandeurs mesurées et après quelques secondes nous basculons vers les grandeurs estimées grâce à un switch que nous avons judicieusement placé. Dans un premier temps nous réalisons la simulation en ne tenant pas compte du couple de charge. Nous appliquons une charge Cr de 0,14Nm à t=4s. Cette charge correspond au couple de charge de la machine à courant continu à vide qui est accouplée à notre machine synchrone.

Nous remarquons ici dans la Figure II.20, que le couple présente un pique lorsque nous appliquons l'échelon et il converge bien vers la valeur du couple résistant à vide qui est de 0,14Nm. La vitesse de référence étant fixée à 1000tr/min, nous remarquons bien que aussi bien la vitesse mesurée que celle estimée convergent vers la référence, l'observateur répond avec une dynamique très rapide, comme nous voyons dans la Figure II.21, les deux courbes sont pratiquement collées. Il en est de même pour les positions électriques mesuré et estimé de la Figure II.22, ceci en boucle fermée ; c'est-à-dire que nous réalisons la commande ici, non pas à l'aide des grandeurs mesurées mais avec les position et vitesse estimées.



temps (s)

temps (s)

Figure II.20 : Couple Cem (Nm) Figure II.21 : Vitesses mesurée et estimée tr/min

36



temps (s)

Figure II.22 : Angles mesurée et estimée en rad

6.2. Simulation en tenant compte des bruits et de l'OFFSET

Dans cette section, nous ajoutons intentionnellement des bruits sur les grandeurs mesurées (tensions et courants) et un OFFSET pour essayer de s'approcher un peu de la réalité. Dans le cas des valeurs propres statiques judicieusement choisies, nous avons les résultats suivants de simulation.



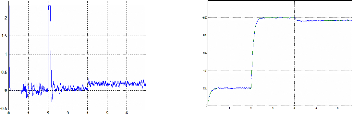
temps (s) temps (s)

Figure II.23 : Couple électromagnétique Figure II.24 : vitesses mesurée et estimée

Nous remarquons aussi comme pour le cas idéal sans bruits ni OFFSET que l'allure des courbes est pratiquement la même sauf que les grandeurs estimées présentes quelques ondulations négligeables de l'ordre de 0.5%.



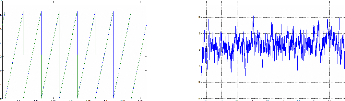
temps (s) temps (s)

Figure II.25 : Angles mesurée et estimée Figure II.26 : erreur de vitesse (tr/min)

37

L'erreur de vitesse ne dépasse pas 10tr/min pour un double échelon de vitesse de 200 vers 1000tr/min (Figure II.26), ceci avec un bruit de 5% sur les mesure et un OFFSET de 0.08V pour les tensions et 0.02A pour les courants.



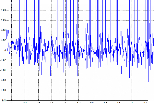
temps (s)

Figure II.27 : erreur de position électrique

L'erreur de position électrique dans ces mêmes conditions ne dépasse pas 2,3°, même en tenant compte de tous ces bruits. Ces résultats nous permettent d'affirmer que l'observateur converge avec efficacité et arrive à s'en passer des bruits de mesures.

Nous choisissons maintenant des valeurs propres de la matrice d'état de l'observateur proportionnelles à la valeur absolue de la vitesse. P₀ = ù ( - k _reel + jki_m), cette stratégie permet un bon rejet des bruits de mesure.



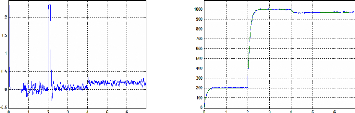
temps (s) temps (s)

Figure II.28 : Couple électromagnétique (Nm) Figure II.29 : vitesses mesurée et estimée

38



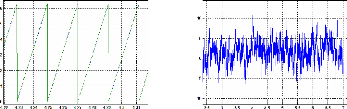
temps (s) temps (s)

Figure II.30 : Angles élec mesurée et estimée Figure II.31 : erreur de vitesses (tr/min)

Nous constatons dans ce cas que l'allure du tracé du couple ainsi que de la vitesse est presque la même. Le fait de prendre des valeurs propres dynamiques adaptées à la vitesse n'affecte pas l'allure de la vitesse elle-même par contre nous constatons un bon rejet des perturbation au niveau de la positon électrique estimée. Nous avons maintenant une erreur d'environs 0.01rad soit 1,1° (Figure II.32) pour la position électrique. C'est une valeur très négligeable.



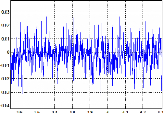
temps (s)

Figure II.32 : erreur angle électrique (rad)

6.3. Simulation en pleine charge (la charge nominale de notre machine est de 0.8Nm)

La charge nominale de notre machine étant de 0.8Nm, nous simulons la commande vectorielle avec cette charge et nous obtenons les courbes suivantes.

L'erreur de position est dans ce cas décalée de -0.02 par rapport au premier cas où nous considérons seulement une charge de 0. 14Nm.

39



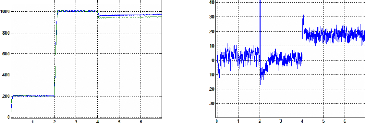
temps (s) temps (s)

Figure II.33 : Vitesses mesurée et estimée tr/min Figure II.34 : erreur de vitesse pleine charge



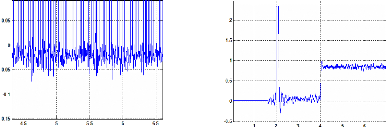
temps (s) temps (s)

Figure II.35 : erreur de position pleine charge (rad) Couple Electromagnétique pleine charge (Nm)

7. Conclusion

Nous avons présenté dans cette section la synthèse d'un observateur de position d'ordre complet de type Luenberger destiné à la commande vectorielle de la MSAP. Après avoir présenté le modèle de la machine sur lequel notre observateur d'état se base pour reconstruire la position et la vitesse, nous avons essayé d'éclaircir le dimensionnement et le principe de calcul des différentes matrices de l'observateur. Ensuite nous sommes passés à la simulation de la commande vectorielle en utilisant notre estimateur dans le cas idéal sans bruit ni OFFSET et dans un autre cas où nous considérons les mesures avec des bruits et des offset. Nous avons remarqués après analyse des résultats de simulation que non seulement l'observateur répond et converge très rapidement mais elle marche très bien et il réalise bien la commande sans avoir recours au capteur.

40

III. OBSERVATEUR REDUIT DE POSITION BASE SUR LA

RECONSTRUCTION DES FLUX STATORIQUES

1. Introduction

Pour minimiser le temps de calcul et alléger le programme, nous avons pensé à améliorer notre observateur en minimisant l'ordre à l'ordre deux. Cela est possible car une partie du vecteur d'état peut être reconstituée facilement. Nous proposons donc dans cette section un observateur réduit basé sur le modèle de la machine et sur les mêmes équations d'état.

2. Equations d'état On considère les mêmes équations d'état que précédemment avec comme :

T

Entrées : u=v_á v_â

Vecteur d'état : x= Ö _á Ö _â Ö _má Ö mâ T

Sorties : y=i_á i_â T

Ö - ô ô

0 0 1 0

Ö

á á

d v

Ö 0 0 0 1

? Ö

ô ô

â â á

= +

dt v

Ö 0 0 0 0 0

- ù Ö

m á e m á â

Ö 0 0 0 0 0

ù Ö

m â e m â

i á

1/ 0 1/ 0

L L

-

x

i L L

0 1/ 0 1/

-

â

3. Estimation de la position du rotor 3.1. Synthèse de l'Observateur réduit

On veut faire un observateur d'ordre réduit car nous constatons ici que les états Ö_á et Ö_â peuvent être obtenus par une combinaison des mesures, donc il nous restera seulement Ö má et Ö _mâ d'autant plus que ces deux derniers états sont largement suffisants pour reconstituer la position électriqueè_e . Nous réarrangeons l'équation d'état comme suit :

Ö 0 0 0 0 0

- ù Ö

m á e m á

dvÖ ù 0 0 0 0 0
m â e m â á
= +
Ö
Ö ô ô

? Ö v

0 0 1 0

dt á á â

Ö 0 0 0 1

ô - ô Ö

â â

41

On pose :

1 0 I=et 0 1

J=

0 1 - 10

On pose donc les nouvelles matrices réduites :

A11 = Jù e ; A₁₂ = [0] ; A₂₁ = ôI ; A₂₂ = -ôI ; B 1 = [0] ; B₂ = I

Et

Ö Ö

m á

Ö â

v = ; y á

Ömâ

On a donc :

v &= A11v+A12y+B 1 u
y&- A22y-B2u = A21v

3.1.1. Principe de l'observateur d'ordre réduit Nouvelle entrée : A₁₂y + B₁u

T

Nouveau vecteur d'état : v=Ö m á Ömâ

Nouvelle sortie : y&- A₂₂y - B₂u

On pose z=v à -Gy

z A G A z A G A G A G A y B GrB u

& = - + - + - + -

( 11 21 ) [( 11 21 ) 12 22 ] ( 1 2 )

r r r r

v z G y

à = + r

On se donne le polynôme caractéristique suivant :

f(s) = (s - ë ₀ ) = s - 2 ë ₀ s + ë ₀ avec ë₀ pôle stable plus rapide que le système de

2 2 2

commande et plus rapide que le procédé. 3.1.2. Observabilité

L'observateur d'ordre réduit que nous utilisons dans cette section se base sur le même modèle de la machine que précédemment que nous avons déjà fait l'étude de l'observabilité. Si la paire (A,C) est observable _(A11,A22) l'est aussi [OSTER].

42



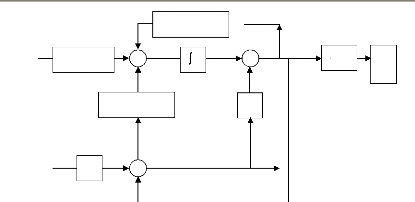
A1 1-GrA21

B1-GrB2

atan

è^à_e

váâ

+

+

A12-GrA22

G_r

y

iáâ

L

+

và

Figure II.36 : schéma de principe de l'observateur réduit

3.1.3. Calcul du gain de l'observateur réduit Gr

avec

g g

On se propose un gain Gr de la forme : 11 12

G =

^rg g

21 22

g11 = g₂₂ = g₁ et g₂₁ = -g₁₂ = g₂

g g - 1 0 0 1 - Donc on a : 1 2 G g g g I g = = + = + r 1 2 1 2 g g 0 1 1 0 2 1

J

On pose aussi F = A₁₁ - G r A21

F =ù _e J-G _r ôI=ù _e J-ô [g₁I+g₂J]

0 1 0 0

- g g

1 2

F = ù - ô -

^e 1 0 0 0

g g

1 2

- - +

ô ù ô ô ù ô

g g s g g

+ -

1 2

e 1 2

e

F = ( )

sI F

- =

ù ô ô ù ô ô

- -

g g - - +

( 2 ) 1

g s g

e 2 1 e

det( ) ( 1 ) ( e 2 ) 2 1 ( ₁ ) ( 2 )

sI - F = s + ô g + ù - ô g = s + ô g s + ô g + ù e - ô g

2 2 2 2 2

Puisque nous avons cité plus haut que nous voulons une dynamique de

f ( s ) = ( s - ë ₀ ) = s - 2 ë ₀ s + ë 0

2 2 2

Donc on identifie membre à membre l'équation det(sI - F) = f(s) et on obtient :

- ë

0

- =

2 ₀ 2 g 1 g 1

ë ô =

ô

43

De même

ù

ë ô ù ô

0 ( ₁ ) ( 2 ) 2 e

2 2 2

= + -



g e g g =

ô

On obtient enfin la matrice gain :

ëù

- -



0 e

ë ù

0 e

ù ë

e 0

ëù

0 e

- ù ë

e 0

on pose G_r 0 =

-

g g

G_r

-

1 2 ô ô 1

= = = -

g g ù ë ô

2 1 e 0



-

ô ô

1

Donc 0

G r G r

= -

ô

F = A 11 - G _r A 21

3.1.4. Calcul de la matrice d'état réduit :

Ce sont les valeurs propres de cette matrice qui imposent la dynamique de l'observateur.

Nous avons vu que F = ù _e J - G _r ô I = ù _e J - ô [ g ₁ I + g ₂ J ] d'où :

- - +

ô ù ô ë

g e g 0

0

F = = = ë I

ù ô ô ë

2 1 0

1 2

- -

e g g 0

0

avec I matrice identité d'ordre 2

3.1.5. Calcul du gain K₀ = A₁₂ - G r A22

Nous savons bien que _A22 est une matrice nulle, il vient que :
K G _r A ¹ G _r ( ô I ) G r

= - = - = -

0 21 0 0

ô

3.1.6. Calcul du gain B₀ = (B₁ - GrB2)

1

B ( B G _r B ) G _r B G _r I B G r

= - = - = = -

0 1 2 2 0 0

ô

Récapitulons :

Nous avons les matrices suivantes pour l'observateur réduit :



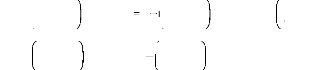
0

ë 0

F=

-

G_r

0

G_r

0

ë 0

K 0

=

= -

B 0

ô

-

1 e

ë ù

0

ô ù ë

-e 0

1 e

ë ù

0

ù ë

e 0

ë ù

0 e

=

- ù ë

e 0

ë ù

0 e

- ù ë

e 0

44

3.2. Estimation de la vitesse

avec ô_ù =0.1s.

Nous utilisons le même estimateur de vitesse que précédemment :



( )

( ) ( )

v _á Ri á v _â Ri â

- + -

ù_e

2 2

=

Ö

m

4. Justification du choix des valeurs propres Nous avons vu que le modèle répond avec une dynamique assimilable à un premier ordre

1

de la forme :

1+ô_ùs

Pour choisir les pôles du gain de l'observateur, il faut tenir compte du fait que l'observateur doit avoir une dynamique beaucoup plus rapide que l'ensemble moteur convertisseur.

Comme précédemment, nous choisissons ë₁ = -90 un pôle double pour notre observateur.
Nous remarquons que cette valeur est nettement supérieure à 10, nous avons une dynamique neuf fois plus rapide.

5. Choix de valeurs propres dynamiques

Le fait de choisir des valeurs propres qui ont une dynamique rapide par rapport à la pulsation électrique rotorique ù_e réduit l'erreur de l'estimation de position.

6. Simulation sous MATLAB SIMULINK 6.1. Résultats de simulation et interprétations

temps (s)





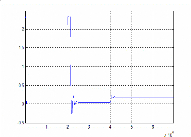
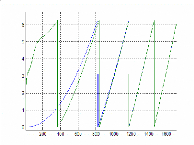
temps (bis)

Figure II.37 : Couple électromagnétique (Nm) Figure II.38 : Réponse de l'angle électrique

Les courbes des Figure II.37, Figure II.38 et Figure II.39, nous montrent bien que la dynamique de cet observateur réduit est la même que celle à ordre complet. Ce qui est logique car nous nous basons sur le même modèle et que nous choisissons des valeurs propres qui sont les mêmes pour les deux cas de figures.

45

Nous avons réalisé la simulation dans le cas idéal sans tenir compte des perturbations dans un premier temps. Nous remarquons que l'erreur de position est nulle ainsi que l'erreur de vitesse.



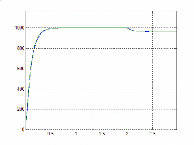
temps (s)

temps (as)



Figure II.39 : Vitesses estimée et mesurée tr/min Figure II.40 : Erreur de position (rad)



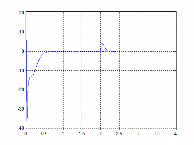
temps (s)

Figure II.41 : erreur de vitesse

6.2. Simulation en tenant compte des bruits et de l'OFFSET (plus proche de la réalité)

Comme précédemment dans le cas de l'observateur de Luenberger d'ordre complet on applique les mêmes conditions de perturbation afin de s'approcher un petit peu de la réalité.

Même en tenant comptes des bruits et de l'OFFSET au niveau des mesures des courants et des tensions qui sont les entrées de notre observateur, nous remarquons que les deux courbes de la vitesse mesurée et celle estimée sont pratiquement collées (Figure II.43). L'erreur de vitesse dans ce cas ne dépasse pas 5tr/min pour un échelon de référence de 1000t/min (Figure II.42).

46



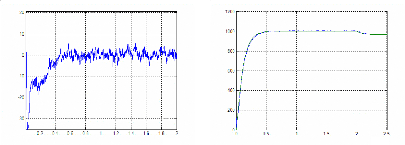
temps (s)

temps (s)

Figure II.42 : Erreur de vitesse en tr/min Figure II.43 : vitesses mesurée et estimée (tr/min)



temps (ris)



temps (us)

Figure II.44 : erreur de position (rad) Figure II.45 : Angles élec mesuré et estimé (rad)

6.3. Simulation en tenant compte de la charge nominale 0.8Nm



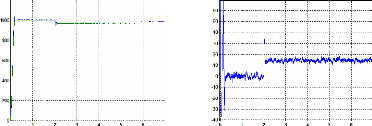
temps (s) temps (s)

Figure II.46 : Vitesses mesurée et estimée tr/min Figure II.47 : erreur de vitesse en tr/min

47



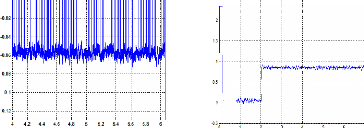
temps (s) temps (s)

Figure II.48 : erreur de position (rad) Couple électromagnétique en (Nm)

7. Conclusion

L'observateur présente les mêmes performances que l'observateur étudié en premier lieu, avec les avantages suivants :

y" Ordre réduit donc programme moins lourd y" Temps de calcul minimisé

y" Bon rejet des perturbations

IV. OBSERVATEUR REDUIT BASE SUR LA RECONSTRUCTION DE LA VITESSE

1. Introduction

Concernant l'observateur que nous avons étudié au tout début de notre stage, il se base sur
le modèle de la machine dans le référentiel de Park. Ce modèle proposé initialement dans

T

[TAT] a pour vecteur d'état x=i_q ù_m , et comme i_q peut être reconstitué à partir

des mesures, il vient l'idée de faire un observateur réduit pour ne reconstruire que la vitesse puis la position par la technique d'intégration.

2. Equations d'état

On considère un autre modèle de la PMSM dans le référentiel (d-q). On a :

v d = R 0 i d + 10
v q 0 R i q 01

+ e d

e_q

di_d

dt

di_q

dt

48

di

v Ri L p Li

d

d d m q

= + - ù

dt

di

v Ri L p Li p

q

q q m d m m

= + + + Ö

ù ù

dt

T C K i

= =

e em T q

d C C

ù -

m em r

On s'intéresse au modèle découplé : on définit donc :

dt J

u v p Li

= + ù

d d m q

u v p Li

= - ù

q q m d

On a donc les équations d'état suivantes :

d k

ù m T

0

dt J ù m

= +

di K R i

q e q

-

-

dt L L





0

1 u_q

L

[ ]

0 1

ù m

y=

i q

3. Estimation de la position du rotor

3.1. Synthèse de l'Observateur réduit

Ici le vecteur d'état est : x ( ù _m i q ) '

= On veut simplement reconstruire la vitesse

mécanique ù_m car déjà i_q peut être obtenue par mesure. On définit donc un observateur d'ordre très réduit (ordre 1). On reconstitue une seule valeur du vecteur d'état.

1

v a a v b

& 11 12

u

₂q

= +

y a a y b

& 2 1 22

y i

= q

On considère

ù m = v : Nouveau vecteur d'état

y=i_q : sortie

u = u_q : entrée

z =v à - g_r · y : telle que g_r : Gain de l'observateur réduit.

Entrée : a₁₁y + b₁u Nouvelle entrée de l'observateur réduit Sortie : y&- a₂₂y - b₂u

49

v a v a

& = +

y

+ b u

1

11 12

y & =

a 22

y b - 2

u a v = 21

3.1.1. Principe de l'observateur réduit

( ) [ ( ) ] ( )

a gra z a gra gr a gra y b grb u

à

11 21 11 21 12 22 1 2

z & =

- + - + - + -

v z gry

= +

Avec (a₁₁ -gra₂₁)=F

F a g a

= -

11 21

r

- k k

F gr g

L

e e

= -

0 = r

L

Ici :

a 11 0

a k J

=

12 T

a k J

= -

21 e





a 22 = - ô



b 1 0

b L

2

= 1

3.1.2. Détermination des matrices de l'observateur

On se donne le polynôme caractéristique f ( s ) = ( s - ë₀ )
f s s sI F

( ) ( ) ( )

= - = -

ë det

0

k

det e

( )

sI F s g s

- = - = - ë

r 0

L

k L

ë ·

e 0

ë = g g =

0 r r

L k e

On note

z A z B u K i

& = + +

0 0 0

à

q q

ù = +

Dz g y

m r

avec :

A a g a F

= - =

0 11 21

r

A 0 ë 0

ë ë

L 1

0 0

B b g b B

= - = - ·

0 1 2



( ) 0 = -

^r keL ke

0

50

K A g a g a

= + -

0 0 12 22

r r

ë ë ë ë

K L

= ë . .

0 ⁰ k

k L L R

2

- R k

.

0 0 0 0

T T



+ - = + +

J k L k k J

e e e e

k_T

² . L R k

+

K K R L

ë ë ë ë

0 0 T 0

= + = + +

( )

⁰ k J k J

0 0

e e

D 0 1

On retrouve en fin de compte :



ë · L ë ë k

= A 0 = ë 0 0

0

g =

r B0 _ke K R L

= - ( )

+ ë +

0 T

0 0

k k J

e e

On représente l'observateur dans le schéma de principe de la figure suivante avec toutes les matrices utilisées.



u_q

B0

A0

^àx& xà

g_r

K0

y

i_q

+

và

+

à

è_e

Figure II. 49 : Schéma de principe de l'observateur réduit de vitesse

3.2. Estimation de la position du rotor

Ici nous utilisons une intégration de la vitesse pour estimer la position du rotor. Cette méthode pose d'énormes problèmes notamment dans la simulation que dans le cas réel de la pratique à cause des bruits que peut engendrer l'intégration et le fait de ne pas maîtriser la contrainte de la valeur initiale de l'arbre du rotor.

3.3. Choix des valeurs propres

Par la même philosophie que précédemment, le choix des valeurs propres de l'observateur dépend de la dynamique du procédé. Nous choisissons des valeurs propres qui ne varient pas en fonction de la vitesse.

Nous utilisons cet observateur pour réaliser la boucle fermée dans la commande vectorielle. Les résultats de simulation sont présentés dans la section qui suit.

51

4. Simulation sous MATLAB SIMULINK

4.1. Résultats de simulation et interprétations

Nous simulons la commande vectorielle de notre machine avec cet observateur dans le cas idéal sans bruit. Nous remarquons que l'erreur de vitesse converge vers zéro sans problème (Figure II.53), tandis que concernant l'erreur de position, elle dépend de la charge contrairement aux deux observateurs antérieurement présentés. Ceci est du au fait que la position est déterminée par intégration de la vitesse qui elle-même est estimée par cet observateur qui prend en compte l'équation mécanique où on a négligé le couple de charge dans les calculs. Dès que l'on applique le couple de charge à vide qui est 0, 14Nm, l'erreur de position augmente. Elle augmente aussi avec l'échelon de vitesse. Nous avons dans la Figure II.54 une erreur de 0,2rad pour la position électrique soit 11.42° contre 1° pour le cas des deux observateurs étudiés plus haut.



temps (s)

temps (s)

Figure II.50 : Couple électromagnétique (Nm) Figure II.51 : Vitesses estimée et mesurée tr/min

temps (s)

temps (s)



Figure II.52 : positions estimé et mesuré (rad) Figure II.53 : erreur de vitesse (tr/min)

52



temps (s)

Figure II.54 : erreur de position elec (rad)

5. Conclusion

Dans cette section nous avons présenté l'étude d'un observateur réduit de vitesse basé sur le modèle de la machine dans le référentiel de Park. Cet estimateur, contrairement aux deux autres étudiés dans ce même chapitre, est moins performant et moins robuste. Les résultas de simulation confirment cette affirmation, car nous remarquons que même dans les conditions idéales sans bruits ni OFFSET, l'erreur de position de converge pas. D'autant plus que lorsque nous appliquons le couple ne charge à vide, nous remarquons, contrairement aux deux autres modelés proposés précédemment, que l'erreur de position augmente. C'est-à-dire qu'elle augmente avec la charge donc ceci est un point faible par rapport aux deux premiers. En ce qui concerne la partie expérimentale, nous n'allons pas mettre en oeuvre ce dernier observateur, nous nous contentons de la comparaison des deux premiers.

V. CONCLUSION

L'étude faite dans ce chapitre est basée sur la synthèse des observateurs de position destinés à la commande sans capteur de la MSAP. Nous avons étudié en premier lieu un Observateur d'état qui reconstitue le vecteur d'état composé des composantes des flux statoriques et rotoriques dans le référentiel biphasé (a,p). Ensuite nous utilisons la relation

liant l'angle électrique O_e aux deux composantes du flux rotoriques(cb m a ,cb _{m p}). Dans le

modèle d'état que nous nous basons pour faire la synthèse de cet observateur, la matrice d'état A dépend de la pulsation rotorique alors que cette dernière est étroitement liée à la position électrique. Mais nous avons considéré le fait que la variation de la vitesse rotorique est très lente par rapport à la fréquence d'échantillonnage donc nous considérons le modèle comme linéaire. Nous avons utilisé une méthode basée sur un calcul direct pour estimer la valeur de la pulsation rotorique w_e . Avant de passer à la simulation de la commande sans

capteur en utilisant notre observateur, nous avons pris le soin de détailler le principe ainsi que le calcul des paramètres de l'observateur. Les résultats de simulation prouvent bien la robustesse de l'observateur et le choix des valeurs propres.

53

Vu que l'on s'intéresse seulement à deux grandeurs du vecteur d'état, nous avons pensé à réduire l'ordre de notre observateur dans le but de diminuer un peu le temps de calcul et d'alléger le programme. C'est ainsi que nous avons proposé un observateur d'ordre deux basé sur le même modèle. L'idée est la même et nous avons utilisé la même méthode d'estimation de la vitesse qui marche aussi bien en régime permanent qu'en régime transitoire. Après avoir rappelé le principe d'un observateur d'ordre réduit, nous avons présenté le calcul des différentes matrices de l'observateur en se basant sur le polynôme caractéristique que nous nous imposons au début.

Les résultats de simulation de la commande vectorielle en utilisant cet observateur réduit confirment l'efficacité de notre reconstructeur, car après avoir testé la commande sans capteur avec la charge au couple de charge à vide nous avons fait la simulation avec un couple résistant égal à la charge nominale qui est 0.8Nm et nous avons remarqué que l'erreur reste toujours très négligeable environ 2,6° électrique soit 0.8° d'erreur pour la position mécanique. Concernant les simulations en pleine charge nous avons toujours considéré les perturbations au niveau des entrées de nos observateurs.

En troisième position, nous avons étudié un observateur réduit qui est largement moins performent que les deux premiers. Néanmoins, nous avons pris le soin de présenter dans chapitre les calculs des paramètres ainsi que les résultats de simulation de ce dernier.

54

CHAPITRE 3

VALIDATION EXPERIMENTALE - IMPLANTATION SUR DS1104

I. INTRODUCTION

L'objectif de toute notre étude est de réaliser enfin la commande vectorielle à flux orientée de la machine synchrone à aimants permanents sans utiliser de capteur mécanique. Dans le chapitre précédant nous avons fait l'étude des observateurs et nous avons fait la simulation de la commande sans capteur.

Dans ce chapitre, nous présenterons les résultats expérimentaux de l'implantation de la commande sans capteur à l'aide d'une carte DSP dédiée à ce genre d'application.

Nous commandons la machine numériquement à partir du PC via la carte DS1 104. Dans un premier lieu, nous allons présenter les résultats de la commande sans capteur en utilisant l'observateur d'ordre complet à vide et en charge, puis nous présenterons les résultats obtenus avec l'observateur réduit. Nous avons étudié et proposé dans le chapitre deux des valeurs propres dynamiques qui varient en fonction de la vitesse de rotation de la machine et nous avons simulé la commande pour les deux observateurs avec cette considération et nous avons obtenu des résultats très satisfaisants. Par contre en pratique, pour des raisons de limitation de vitesse nous n'avons pas testé cette nouvelle stratégie.

II. IMPLANTATION DES DIFFERENTS OBSERVATEURS

1. Observateur d'ordre complet de la position du rotor, basé sur la reconstruction des flux statoriques

1.1. Considérations pratiques

Dans la pratique, nous remarquons que, en tenant compte de tous les problèmes qui existent réellement avec surtout les appareils de mesure, il nous a fallu modifier un tout petit peu le programme en insérant par exemple des filtres ou des corrections dans le schéma de commande.

Les essais pratiques ont été réalisés au sein du laboratoire des systèmes embarqués et de commande numérique de l'ENSA Marrakech dont nous présentons dans la figure ci- dessous la photographie du banc d'essais.



Figure III.55 : photographie du banc d'essai

1.2. Résultats et mesures expérimentaux de la commande 1.2.1. Faibles vitesses

Dans un premier temps après avoir fait plusieurs essais pour la commande sans capteurs, nous avons déterminé la vitesse minimale avec laquelle notre observateur marche très bien pour la commande de la machine.

Nous remarquons à très faible vitesse plus précisément à partir de 35tr/min notre observateur peut remplacer le capteur mécanique. Nous avons relevé les courbes de vitesse de position et de l'erreur de position pour une vitesse relativement faible (50tr/min). Nous constatons bien ici que l'erreur de position électrique est très faible, la plage de variation de l'erreur ne dépasse pas 5° au maximum. C'est-à-dire que l'erreur de position mécanique est pratiquement nulle 1.666° (Figure III.57).

Concernant la vitesse nous voyons les deux courbes rouge (pour la vitesse mesurée) et bleue pour la vitesse estimée sont pratiquement collée. L'erreur de vitesse ne dépasse pas 5tr/min.



Figure III.56 : positions estimé et mesuré en rad

Figure III.57 : erreur de position en degré



Figure III.58 : vitesses mesurée et estimée (tr/min

1.2.2. Echelon de vitesse

Nous appliquons un échelon de vitesse de 200tr/min à partir d'une vitesse de 100tr/min pour voir la dynamique en régime transitoire. On ne peut qu'apprécier l'exactitude des grandeurs estimées des courbes de la Figure III.59 pour la position et de la Figure III.61 pour ce qui est de la vitesse. L'erreur de position électrique ne dépasse pas 3° en valeur absolue. C'est-à-dire que l'erreur de position mécanique ne dépasse pas 1° tout comme la

simulation. Nous pouvons nous réjouir de ce résultat très satisfaisant qui confirme la robustesse de notre observateur.



Figure III.59 : positions estimé et mesuré (rad) Figure III.60 : erreur de position en degré

Figure III.61 : vitesses estimée et mesurée (tr/min) Figure III.62 : courants id et iq en A

La Figure III.62, nous montre l'évolution des courants id et iq suite à un échelon de vitesse. Nous remarquons un pic qui dépasse légèrement 3A au niveau de iq au moment où on applique l'échelon, ce qui est très évident. Ensuite le courant iq converge rapidement vers 0.6A qui correspond exactement à la valeur de iq pour la charge du couple résistant à vide de la MCC accouplée à notre MS qui est de 0. 14Nm.

1.2.3. Echelon de vitesse croissant

Pour vérifier la poursuite et la variation de la vitesse de référence, nous avons pensé à appliquer une succession d'échelons de 50 à 700tr/min. Nous remarquons que la vitesse estimée tout comme celle mesurée suit parfaitement la consigne (Figure III.65). Les deux courbes de position estimé et mesuré sont parfaitement collées aussi (Figure II.63). Nous remarquons au niveau de l'erreur de position électrique de légères variations dues aux changements brusques de vitesses. Toutefois l'erreur de position ne dépasse pas 5° en valeur absolue.



Figure II.63 : positions estimé et mesuré en rad Figure II.64 : erreur de position en degré



Figure III.65 : vitesses estimée et mesurée en tr/min

2. Observateur réduit de position du rotor basé sur la reconstruction des flux statoriques

2.1. Résultats et mesures expérimentaux de la commande 2.1.1. Faibles vitesses

De même pour l'observateur à ordre réduit, nous déterminons la vitesse minimale pour laquelle la commande sans capteur marche sans problème. Nous présentons dans les Figure III.66, Figure III.67 et Figure III.68 les mesures en régime établi des positions estimée et mesurée, de l'erreur de position et des vitesses estimée et mesurée. Une des avantages de nos deux observateurs est la capacité à fonctionner même à de très faible vitesse avoisinant le zéro, une exigence que plusieurs techniques présentées auparavant dans la littérature n'arrivent pas à satisfaire.



Figure III.66 : positions estimé et mesuré en rad Figure III.67 : erreur de position en degré



Figure III.68 : vitesse estimée et mesurée tr/min



2.1.2. Echelon de vitesse

Figure III.69 : positions estimé et mesuré (rad) Figure III.70 : erreur de position en degré

Figure III.71 : vitesse estimée et mesurée tr/min Figure III.72 : courants id et iq (A)

Nous obtenons presque les mêmes réponses que l'observateur à ordre complet. Sauf que pour cette fois nous remarquons que les bruits sur l'erreur de position électrique sont minimisés, bien que dans les deux cas cette erreur est pratiquement nulle.

2.1.3. Echelon de vitesse croissant

Nous appliquons à présent un échelon croissant de vitesse à partir de 50tr/min jusqu'à 700 tr/min, en passant par 200 et 400tr/min, comme nous l'avons fait pour le premier observateur.



Figure III.73 : positions estimé et mesuré (rad) Figure III.74 : erreur de position en degré



Figure III.75 : Vitesse estimée et mesurée (tr/min)

La poursuite est parfaite et l'erreur de position est toujours très faible sauf qu'elle présente des petits pics aux instants d'accélération ce qui est très normal. Toutefois la plage de variation de l'erreur dans ces conditions est de 5° comme nous le constatons dans la Figure III.74 en valeur absolue. Concernant l'erreur de position mécanique elle ne dépassera pas le tiers de 5 (1.666°) puisque nous avons une machine à trois paires de pôle.

3. Essais en charge cas des deux observateurs

Nous allons faire des essais en charge pour les deux observateurs et nous allons faire une comparaison sur la vitesse, la position et l'erreur de position plus particulièrement.



Figure III.76 : Vitesses estimée et mesurée
(Observateur à ordre 4)

Figure III.77 : Vitesses estimée et mesurée
(Observateur à ordre réduit)



Figure III.78 : positions estimé et mesuré
(Observateur à ordre 4)

Figure III.79 : positions estimé et mesuré
(Observateur à ordre réduit)



Figure III.80 : Erreur de position en degré
(Observateur à ordre 4)

Figure III.81 : Erreur de position en degré
(Observateur à ordre réduit)

4. Conclusion

Dans cette section, nous avons présenté les résultats de simulations réalisées sous les mêmes conditions, de l'observateur de Luenberger (ordre complet) et de l'observateur à ordre réduit que nous avons proposé. Nous ne pouvons qu'affirmer l'efficacité des deux observateurs car comme nous avons constaté dans l'analyse des résultats expérimentaux de la commande sans capteur, l'erreur de position dans les deux cas est quasi nulle pour ce qui de l'essai à vide. Nous avons vu que l'erreur de position mécanique ne dépasse pas 1.667° en valeur absolue et ce, en régime transitoire. En régime permanent elle ne dépasse pas un degré pour les deux cas de figure.

Concernant l'essai en charge, nous allons toujours nous limiter en terme de vitesse. La vitesse mesurée est de 670tr/min en pleine charge, tandis que la vitesse estimée la dépasse légèrement. Ceci est dû à notre méthode d'estimation de la vitesse qui ne prend pas en compte un terme contenant le courant. Alors que le courant est étroitement lié à la charge. Nous voyons dans les Figure III.80 et Figure III.81 que l'erreur de position pour les deux observateurs est très faible bien que nous avons chargé la machine avec un couple résistant presque quasi égal au couple nominale en charge. Dans la conclusion générale nous allons présenter pour les perspectives envisagées, l'idée de proposer une technique mieux adaptée à l'estimation de la vitesse aussi bien à vide qu'en charge. L'observateur est insensible à la charge.

III. CONCLUSION

Nous avons consacré ce chapitre à la présentation des résultats de l'implantation de la commande vectorielle sans capteur de la machine synchrone à aimants permanents dans un environnement pratique réel.

Comme nous l'avons constaté, nos deux observateurs nous donnent une excellente estimation de la position et de la vitesse, aussi bien en régime transitoire qu'en régime permanent, à vide et en charge.

CONCLUSION GENERALE

Dans ce mémoire, une étude bibliographique, théorique et expérimentale portant sur la commande vectorielle sans capteur, à flux orienté de la machine synchrone à aimants permanents (MSAP) autopilotée a été présentée.

Dans le premier chapitre après avoir fait la modélisation de la machine en vue de la commande vectorielle, et après avoir rappelé le principe de la commande vectorielle et dimensionné les régulateurs, nous avons présenté l'état de l'art de la commande sans capteur dans le but d'étudier la littérature concernant notre sujet de recherche.

Nous avons vu, concernant les estimateurs de position et de vitesse de la MSAP, que les méthodes sont nombreuses et que même la classification en sous ensembles n'est pas une chose aisée. Toutefois nous avons classé les techniques en trois sous groupes, mais nous nous sommes intéressés par la suite aux techniques utilisant les observateurs car c'est dans cet axe qu'a été basée notre étude.

Cette étude bibliographique nous a permis de bien aborder la deuxième partie de notre travail qui est basé sur l'étude et la mise en oeuvre des observateurs de position destinés à la commande vectorielle sans capteur de la MSAP.

Dans le deuxième chapitre, nous avons présenté l'étude et le développement de deux observateurs de positions basés sur la reconstitution du flux rotorique, et un observateur de vitesse basé directement sur l'équation mécanique, que nous avons par la suite simulé leur fonctionnement dans la commande vectorielle en ne tenant compte que du couple résistant à vide dans un premier temps, puis du couple équivalent à la charge nominale de notre machine dans un second. Les résultats de simulation sont très satisfaisants. Surtout pour les deux premiers observateurs de position basés sur un modèle qui ne fait pas intervenir les équations mécaniques de la machine. L'étude du premier observateur d'ordre complet a été déjà faite et présentée par T.D BATZEL et al dans [BATZ-LEE_1 ,2].

Nous avons pensé au modèle réduit de ce même observateur pour diminuer l'ordre de ce dernier afin de réduire le temps de calcul et l'erreur de convergence.

Nous avons vu avec un choix judicieux des valeurs propres, notre observateur présente les mêmes performances que l'observateur étudié en premier lieu, avec les avantages suivants :

y" Ordre réduit donc programme moins lourd y" Temps de calcul minimisé

y" Bon rejet des perturbations

Dans ce même chapitre, nous avons étudié en troisième lieu un observateur de vitesse
proposé par TATEMTSUI dans [TAT], nous l'avons simulé sous les mêmes conditions que
les deux premiers mais nous avons constaté que ces performances sont loin d'être

comparables. Cet observateur reconstruit la vitesse, et par une méthode d'intégration on estime la position du rotor. Puisqu'elle tient compte de l'équation mécanique, cet observateur nous donne, dans la simulation de la commande sans capteur, une erreur de position qui varie linéairement avec le couple de charge. Nous ne l'avons pas jugé intéressant et c'est ainsi que nous ne l'avons pas impliqué dans l'implantation.

Pour valider notre étude, il a été impératif de passer dans la pratique pour pouvoir enfin réaliser notre commande dans le banc d'essais. Nous avons consacré tout le dernier chapitre pour la validation expérimentale.

Dans ce chapitre, après avoir introduit et défini les considérations pratiques, nous avons présenté les résultats expérimentaux qui ont été aussi très satisfaisants que ceux de la simulation.

Tout d'abord nous avons testé la vitesse minimale pour laquelle nos observateurs fonctionnent correctement en boucle fermée et nous avons remarqué que, à 3 5tr/min, nous pouvons compter sur nos observateurs pour remplacer le capteur mécanique. Ensuite nous avons appliqué des échelons tout comme dans la simulation pour voir la dynamique et avons analysé les résultats, surtout l'erreur de position. Nous avons vu que dans les deux cas, cette erreur de position électrique ne dépasse pas 5° en valeur absolue en régime transitoire et nous ne pouvons que nous réjouir de cette aubaine. En régime établi, l'erreur électrique ne dépasse pas 3°, c'est-à-dire que concernant l'erreur de position mécanique quant à elle, elle ne dépasse pas 1° en valeur absolue en rémige permanent et ceux pour les deux observateurs (ordre complet et ordre réduit). Par contre pour l'observateur réduit, nous constatons qu'il y a légèrement moins de bruits au niveau de cette erreur. Pour tester la poursuite de la vitesse de consigne nous avons appliqués des échelons croissants et nous remarquons que les performances de nos observateurs restent inchangées.

Même lorsque nous avons chargé la machine les performances de nos observateurs ne sont pas dégradées du tout, nous obtenons toujours les mêmes résultats, une erreur de position électrique qui ne dépasse pas 3° en régime établit. Ce qui confirme encore une fois la robustesse de nos deux observateurs et leur insensibilité face aux variations des paramètres mécaniques comme nous l'avons démontré dans l'étude théorique et confirmé dans la simulation.

Dans la continuité des travaux que nous avons effectué, plusieurs point peuvent être développés. Nous proposons donc les points suivants à développer pour une étude ultérieure :

y' Etudier la faisabilité du démarrage sans capteur en utilisant notre observateur réduit. y' Résoudre le problème de l'estimation de la vitesse qui varie en fonction de la

charge. Donc mettre en oeuvre une technique couplée d'estimation de la vitesse,

pour basculer d'une méthode à une autre quand la charge devient importante et

qu'elle impose une erreur considérable de vitesse.

y' Prendre en compte la variation des paramètres de la machine notamment la résistance et l'inductance. Nous pouvons utiliser des estimateurs des paramètres lorsque ces derniers varient beaucoup et que leur effet est flagrant sur les mesures ou sur les grandeurs estimées.

V Prendre en compte les caractéristiques stochastiques des bruits et élaborer un Filtre de KALMAN correspondant à cet observateur.

ANNEXES

Annexe A : Implantation de l'encodeur

Pour se familiariser avec l'environnement de travail (commande numérique par ordinateur et carte DSP), nous avons commencé par l'implantation de l'encodeur. Ce petit travail que nous présentons dans cette section des Annexes nous a permis de comprendre la configuration et l'usage du logiciel control desk. Nous avons jugé utile de bien comprendre le capteur de position car c'est l'élément qui nous gène et que l'on veut remplacer par nos observateurs de position.



Principe de l'encodeur incrémental

Le rôle des pistes A et B c'est de déterminer le sens de rotation de l'arbre de la machine avec lequel est lié l'encodeur de telle sorte que si A est en avance de phase par rapport a B, la machine tourne dans le sens 1 et dans le cas contraire c'est le sens 2. L'encodeur se compose aussi d'un compteur qui compte dans chaque tour 1024 impulsions

Et il se reintialise à l'aide de l'indicateur (piste Z) qui doit aussi figurer et être initialisé dans le programme Simulink.



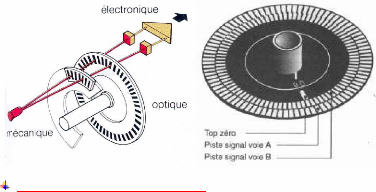
Implantation de l'encodeur via DS1104

Dans la fenêtre MATLAB, on exécute la commande rti (Real time Interface). On choisit la librairie master PPC puis l'encodeur DS1 104ENC_POS_C1, DS1 104ENC_SETUP et le bloc DS 11 04ENC_INDEX_C 1. Avant de commencer la simulation il faut régler les paramètres de ces blocs de l'encodeur.

Configuration de DS1104ENC SETUP

Pour ce qui est de la configuration, nous devons spécifier quel type d'entrée nous utilisons car on a aussi bien des entrées digitales TTL que des entrées analogiques RS232 et RS442/485. Dans notre cas on utilise une des entrées digitales. (canal1)



Reglage de DS1104ENCEPOSC1

On doit spécifier le numéro de l'entrée car comme nous l'avons dit il en existe deux. Sur l'option Unit specification, on choisit donc channel number 1. Il faut aussi régler les paramètres d'initialisation. On a initialisé à O.



Configuration de DS1104enc INDEX C1

Dans ce bloc on doit indiquer le numéro de l'entrée (channel number). Pour ce qui est des paramètres, remettre la position à zéro à chaque tour et non une seule fois (Always). Ensuite pour le paramètre output after index detection on met l'option current index.





Simulation

On sait que le bloc de l'encodeur nous donne comme information sur l'angle un nombre N proportionnel à ce dernier (1024 par tour). Pour avoir l'angle en degré nous devons multiplier ce nombre par un gain à savoir 360/1024.

Quant à la détermination de la vitesse, puisque le bloc DS 1 04ENC_POS_C 1 nous donne le delta position, il nous suffit de la diviser par la le delta temps qui n `est rien d'autre que la période d'échantillonnage Te, puis de la multiplier par un gain (60/1024) pour avoir la vitesse en tour par minute.

Paramètre d'Affichage :


· Affichage numérique : Aller dans Virtuel instrument puis sélectionner display puis le mettre dans la layout et glisser la variable que vous voulez le voir en « affichage numérique ».

Résultats de la simulation :

On voit bien (figure B. 1) que la vitesse avant filtrage est trop bruitée, c'est pour cela qu'on insère un filtre pass-bas avec une pulsation de coupure (wcf=60). On pourrait envisager un bande passante beaucoup plus étroite que ça mais on est limité par le temps de réponse car si on prend par exemple wcf=10, le temps de réponse de notre filtre serait de 3*0.1s, c'est trop lent comme filtre !!!



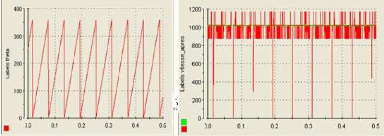
Figure A. 1 angle thêta en degré figure A.2 vitesse non filtrée et

vitesse filtrée en tr/min

On a envisagé un autre type de filtrage discret. L'idée est de prendre à chaque instant la mesure en cours et plusieurs mesures précédentes puis calculer la moyenne arithmétique. Dans notre cas on prend la mesure à l'instant n et les 9 mesures précédentes. On remarque sous les mêmes conditions que ce deuxième filtre est moins efficace que le premier car la vitesse est un peu plus bruitée.
On fait la simulation avec un filtre qui a une bande passante plus étroite wcf=10 (figure A.3). On voit que la vitesse et tèrs bien filtrée mais toutefois le temps de réponse de ce filtre est relativement trop grand.
	Figure A.3. Vitesse filtrée en tr/min

NOTATIONS

Modélisation de la MSAP

MSAP Machine Synchrone à Aimants Permanents

(d, q) Indice du référentiel de Park

(á,â) Indice du référentiel (á,â)

R Résistance statorique

Ld Inductance statorique directe

L_q Inductance statorique quadratique

L_c=L Inductance statorique cyclique

Ms Inductance mutuelle

Ö m Flux d'excitation de l'aimant permanent

Ö Flux statorique

( Ö _má , Ö mâ) Composantes du flux rotorique

( Ö _á , Ö _â ) Composantes du flux statorique

Cem Couple électromagnétique

C_r Couple résistant

p Nombre de paires de pôles de la machine

J Moment d'inertie totale de la machine

f Coefficient de frottement visqueux

ù_e Pulsation électrique rotorique

ù_m , Ù Vitesse de rotation mécanique du rotor

è_e Angle électrique du rotor

i Courants statoriques

v Tensions simples

ø Déphasage entre le courant et la tension

P_e Puissance électromagnétique

KT Constante de couple

Ke Constante de fem

ô_ù Constante de temps du modèle convertisseur - machine

Autres notations

ô R/L inverse de la constante électrique

A Matrice d'état du modèle d'état de la machine dans (á,â)

B Matrice du modèle d'état de la machine dans (á,â)

C Matrice de sortie du modèle d'état de la machine

G Gain de l'observateur

x Vecteur d'état

y Sortie de l'observateur

xà Vecteur d'état reconstitué (estimé)

yà Sortie reconstituée

F matrice d'état de l'observateur de Luenberger

ë_i Valeurs propres de l'observateur

s Opérateur de Laplace

O Matrice d'observabilité

Aii Composante de la matrice A pour l'observateur réduit

Bii Composante de la matrice B pour l'observateur réduit

v Nouveau vecteur d'état de l'observateur réduit

G_r Gain de l'observateur réduit

BIBLIOGRAPHIE

[ALHAS05] Yasser ALHASSOUN, «Etude et mise en oeuvre de machines à aimantation induite fonctionnant à haute vitesse» Thèse de doctorat ENSEEIHT, Toulouse mai 2005.

[BAGH99] Lotfi BAGHLI, «Contribution à la commande de la machine asynchrone, utilisation de la logique floue, des réseaux de neurones et des algorithmes génétiques»

[BATZ] TODD D. BATZEL, «Electric propulsion using the Permanent Magnet Synchronous Motor without rotor position transducers» Ph.D. thesis, Dept. Elect. Eng., Pennsylvania State Univ., University Park, PA, 2000.

[BATZ-LEE_1] TODD D. BATZEL & KWANG Y. LEE, «Electric Propulsion With the sensorless Permanent Magnet Synchronous Motor: Model and Approach» IEEE TRANSACTIONS ON ENERGY CONVERSION, vol. 20, no. 4, december 2005

[BATZ-LEE_2] TODD D. BATZEL & KWANG Y. LEE, «Electric Propulsion With Sensorless Permanent Magnet Synchronous Motor : Implementation and Performance» IEEE TRANSACTIONS ON ENERGY CONVERSION, vol. 20, no. 3, september 2005.

[BATZ-LEE_3] TODD D. BATZEL & KWANG Y. LEE, «Application of sensorless electric drive to unmanned undersea vehicle propulsion» 15^th Trennizl World Congre ss, Barcelona, Spain, 2002.

[BAY06] BAYRAM TOUNSI, «Etude comparative des groupes électrogènes embarqués à large gamme de vitesse variable associant machines à aimants et conversion statique», Thèse de doctorat, ENSEEIHT, Toulouse, janvier 2006.

[B IL] BILAL GUMU and MEHMET OZEDEMIR, «New control of PMSM using a fuzzy logic observer» june 2005.

[BOL] BOLOGNANI S, TUBIANA L, ZIGLIOTTO M, «Extended Kalman Filter tuning in sensorless PMSM drives» Industry Applications IEEE, nov-dec 2003, vol 39 issue 6 page 1741-1747.

[ERTU] N. ERTUGURL, P.P ACARNLEY, «Indirect rotor position sensing in real time for Brushless PMSM drives» IEEE trans. On Power Electronics Vol 13, No 4, july 1999, pp 608-616.

[FAB] FABIO GIULII CAPONI, GIULIO DE DONATO, LUCA DEL FERRARO, O
HONORATI, M C HARKE, ROBERT D. LORENZ «AC brushless Drive with Low

73

resolution hall-Effect Sensors for surface-Mounted PM machines» IEEE transactions on Industry applications. Vol 42, No 2 mars-april 2006.

[FAD06] FADLI OUAHIBA, «Modélisation et commande non linéaire de l'association : Machine Synchrone à Aimants Permanents - Onduleur de Tension à Trois Niveaux», Thèse de doctorat, ENSEEIHT Toulouse, juin 2006.

[FILP] FILIPESCU, DUGARD, «Application of Sliding of Permanent Magnet Motors», Decision and Control, 2003. Proceedings. 42nd IEEE Conference on Volume 4, Issue , 9-12 Dec. 2003 Page(s): 3537 - 3542 vol.4.

[FUR] T. FURUHASHI, S. SANGWONGWANICH, and S. OKUMA, «A Position and Velocity Sensorless control for Brushless DC motors using an Adaptive Sliding Mode Observer», IEEE Trans on industrial Electronics, Vol 39 pp 89-9 5, april 1992

[GASC04] Laurent GASC, «Conception d'un actionneur à aimants permanents à faibles ondulation de couple pour assistance de direction automobile, Approche par la structure et par la commande» Thèse de doctorat ENSEEIHT, Toulouse novembre 2004.

[GREL] G. GRELLET, G. CLERC, «Actionneurs Electriques», Edition Eyrolles, novembre 1999.

[HAMD] M. HAMDI and M. GHRIBI, «A sensorless Control Scheme Based on Fuzzy Logic for A C Servo Drives Using a Permanent magnet Synchronous Motor», IEEE Control Conf. on electrical and Computing Engineering pp. 306-309. 1995.

[J.KIM] J. KIM and S Sul, «High performance PMSM Drives without Rotational Position Sensors using Reduced Order Observer», Record of the 1995 IEEE Industry Applications Conf. vol 1 pp 75-82, 1995.

[JABB] M.A JABBAR, M. A. HOQUE, M.A. RHLAN, «Sensorless PMSM drives». IEEE Canadian Conference on Electrical and Computer Engineering, 1997 Engineering Innovation. Voyage of Discovery Vol 2, pp 878-883.

[JI-Li] JI-LIANG SHI, TIAN-HUA LIU, YUNG-CHI CHANG, «Optimal controller design of a sensorless PMSM control system» Industry Electronics Society, 2005, IECON, 31^st Annual Conference IEEE nov 2005.

[JOHN99] J. P JOHNSON, M. AHSANI and Y. GUZCLGUNLER, «Review of sensorless methods for BLDC». 34^th IEEE Annual Meeting, 1999, Proc Vol 1pp 143-150.

[KIM] Y.H. KIM, Y.S KOOK, «High performance IPMSM drives without rotational position sensors using reduced EKF», IEEE Trans. On Energy Conversion, Vol 14, No4, dec 1999

[KONG02] KONGHIRUN, M.; LONGYA XU; FIGOLI, «D. Implementation of generic
sensorless direct field Oriented Control of AC motors on a low-cost, fixed-point digital

74

signal processor» Applied Power Electronics Conference and Exposition, 2002. APEC 2002. Seventeenth Annual IEEE Volume 1, Issue, 2002 Page(s):304 - 309 vol.1.

[KYE] KYE-LYONG KANG, JANG-MOKKIM, KEUN-BAE HWANG, KYUNG-HOON KIM, «Sensorless control of PMSM in high speed range with iterative sliding mode observer» Nineteenth Annual IEEE Applied Power electronics conference and Exposition, 2004. APEC Vol 2, Issue, 2004 page(s) : 1111-1116.

[LIU] LIU, TIAN-HUA, HUNG, CHEKAI, CHEN, DER FA, «A matrix Converter-Fed sensorless PMSM Drive system» Electric Power Components and systems, Vol 33, No 8, August 2005, page(s) : 877-893. Edition Taylor and Francis Ltd

[LIZU85] K. LIZUKA et al, «Microcomputer Control for Sensorless Brushless Motor», IEEE Trans. On Industry Applications, vol IA-27, pp. 595-601, june 1985.

[LUEN] D. LUENBERGER, «A sensorless Control Scheme Based on Fuzzy Logic for AC Servo Drives Using a Permanent magnet Synchronous Motor», IEEE Control Conf. on electrical and Computing Engineering pp. 306-309. 1995.

[MATS-1] N. MATSUI, «Sensorless for Permanent Magnet Brushless DC Motors», IEEE Trans. On Industrial Electronics, vol 43, pp 300-308, april 1996.

[MATS-2] N. MATSUI and TAKESHITA, «A novel stating Method of Sensorless SalientPole Brushless Motor», IEEE IAS Annual Meeting, October 1994, Proc. Vol 1 pp. 386-392.

[MATS-3] N. MATSUI and M. SHIGYO, «Brushless DC Motor Control Without Position and Speed Sensors», IEEE Trans. On Industrial Applications, vol 28, No 1, jan/feb. 1992, pp 120-127.

[MING] MINGHUA FU, LONGYA XU, «A Novel Sensorless Control Technique for Permanent magnet Synchronous Motor, Using Digital Signal Processor».

[MINZ] VIOREL MINZU and BERNAR LANG, « Commande automatique des systèmes linéaires continus » Edition Ellipses. Janvier 2001.

[OREIL] J. OREILLY, « Observer for Linear Systems », Edition ACADEMIC PRESS 1983, inc (LONDON) LTD.

[OSTER] E. OSTERTAG, «Commande et estimation multivariables - Méthodes linéaires et optimisation quadratique»Edition Ellipse. Février 2006.

[PAUL] PAUL P. ACARNLEY AND JOHN F. WATSON, «Review of Position-Sensorless Operation of Brushless Permanent-Magnet Machines» IEEE Transactions On Industrial Electronics, vol. 53, no. 2, arpil 2006.

[PEIX] Z. PEIXTO and P. SEIXAS, «Application of Sliding of Permanent Magnet Motors», IEEE Conf. pro. of IECON, pp 599-6 19, 1995.

75

[PET] D. PETERS and J. HARTH, «I. C.s Provide Control for Sensorless DC Motors», END, pp 85-94 april 1993.

[SENJ] T. SENJYU and K. VEZATO, «Adjustable Speed Control of Brushless DC motors Without Position ans Speed sensors», International IEEE/IAS Conference Proc. On Industrial Automation and Control. Energing Technologies pp1 60-164 1995.

[SHIN] SHINJI. SHINNAKA, "New sensorless Vector Control Using Minimum-Order Flux State Observer in a stationary reference frame for permanent magnet Synchronous Motors" IEEE Transactions on Industry Applications Vol 53. No 2 Ap. 2006.

[SOLS] J. SOLSANA, M.I. VALLA, and C. MURAVCHIK, «A Nonlinear Reduced order Observer for PMSM», IEEE Trans. On Industrial Electronics, vol 43, pp 38-43, aug 1996.

[TAT] TATEMASTU, HAMADA, UCHIDA, WAKAO & ONUKI, «New Approaches with Sensorless Drives» IEEE Industry Application Magazine July/August 2000.

[VAS] P. VAS, M. RASHED, A. SRTONACH, A.K.M. JOUKHADAR, «Sensorless Drives, State of the art», Poceeding on CD of PCIM'2001, Nurenberg.

[WAT] H. WATANABE, H. KATSUSHIMA and T. FUJI, «An improved Measuring System of Rotor Position Angles of the sensorless Direct Drive Servomotor», IEEE proc. of the 1PPP int'1, on Industrial Electronics, Control and Instrumentation, pp 165-170 1991.

[WU91] WU. R, SELMON G.R,«A permanent Magnet Motor Drive Without a shaft sensor», IEEE Trans. Industry Application, Vol 27, No 5 sept/oct 1991, pp 1005-1011

[YOUS0 1] D. YOUSFI, "Estimateur de position et de vitesse destinée à la commande sans capteur mécanique des machines synchrones autopilotées", Thèse de doctorat EST, Oujda mai 2001

Thèse de doctorat Université HENRI Poincaré NANCY 1, janvier 1999.

76

Articles

Articles

YOUSFI DRISS; DARKAWI ABDALLAH , «Comparison of two position and speed estimation techniques used in PMSM sensorless vector control» - Page(s): 626-630, The 4th International Conference on Power Electronics, Machines and Drives 2008 (PEMD 2008) 2 - 4 April 2008, York St John University College, York, UK

77