
 |
Programmation des robots industriel et application sur le robot manipulateur Algérie machines outil 1( Télécharger le fichier original )par Abdelkader BENMISRA Université de Saad Dahleb de Blida (Algérie) - Magistère en Génie Mécanique 2007 |
1.5 Les porteurs (bras) : F9, 14, 140] :Cette configuration permet de classifier les robots par type de porteurs :
1-5 Caractéristiques générales des robots : [21] :
CHAPITRE 2MODELISATIONS GEOMETRIQUE, CINEMATIQUE ET
DYNAMIQUE
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
T 0 6 |
r11 |
r12 |
r 13 |
dx d y dz |
0001
( ) ( ) ( ) ( ) ( ) ( 6 )
è è è è è è
(2.8)
5
= T T T T T T
0 . . . . .
2
1 3 4
1 1 2 2 3 3 4 4 5 5 6
Par exemple la première étape sera comme suit : On
multiplie de part et d'autre
la matrice ( 1 )
T 1 è , le résultat sera : [ ] 1
1
0 T 1 . T = T
0 - (2.9)
0
1 6
On s'intéresse toujours à la dernière colonne de la matrice, qui contient à chaque étape les équations découplées qui permettent de résoudre le problème du modèle géométrique inverse, toutefois le modèle géométrique comporte aussi des inconvénients :
La non unicité du modèle géométrique inverse implique qu'il existe plusieurs "chemins" pour se rendre d'un point à un autre. Le traitement par incrément peut amener à des imprécisions. Des singularités mécaniques et / ou mathématiques apparaissent.. Une haute précision de solutions obtenues n'est pas nécessaire puisqu'il suffit de fournir à l'utilisateur une vision globale, le calcul des accroissements est à chaque fois effectué à partir d'une nouvelle configuration exacte du robot. Quant au problème des singularités, il existe plusieurs méthodes mathématiques pour les traiter et les éviter.
2.5.1 Absence de solution :
2.5.1.1 Origine mécanique :
les mouvements du mécanisme tiennent compte des limites des rotations et translations. Des butées empêchent le robot d'atteindre les points en dehors de volume du travail malgré l'existence de solutions mathématiques.
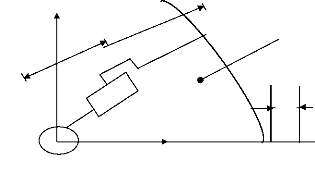
Surface de travail
Y
12
T
R0
a
Q0
X
Figure. 2.4 : Le robot R.P. [38]
Q
2-5-1-2 Origine mathématique :
un système dont le nombre de variables est inférieur au nombre d'équations ne donne pas de solutions mathématiques. Cela revient, en robotique, à imposer plus de contraintes qu'il n'existe de degrés de liberté.
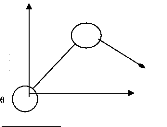
Y
O2
1 Q X
Figure 2.5 : La structure R.P. [38]
1
R
0
2-5-2 Infinité de solution :
& f &
? j
×= j q
?? q j j
j
(2.10)
31
lorsque le nombre de contraintes est inférieur au nombre de d.d.l .du robot, on se trouve en face de surabondance de potentialités en fonction de la tâche demandée. La solution consiste à réduire le nombre de variables articulaires en leur imposant une valeur. Dans le second cas, le robot se trouve en position de singularité.
Cette configuration particulière est créée par exemple lors de la mise en parallèle de deux axes.
è6
è4
è5
Q
Figure 2.6 : Représentation d'un poignet. [38]
2-5-3 Nombre fini de solutions:
Si le nombre de contraintes est égal au nombre de d.d.l .du mécanisme et si le robot ne se trouve pas dans un des cas décrits plus haut, alors il existe une ou plusieurs solutions au problème.
2-6 Calcul du modèle inverse :
Pour la résolution des problèmes inverse c'est-à-dire résoudre le système d'équations non linéaires, on utilisera les méthodes de Newton- Raphson,Range kutta,loi de Bang-Bang et le formalisme de Newton-Euler (voir appendices).
*
Le modèle cinématique direct permet d'obtenir la vitesse de l'organe terminal dans l'espace opérationnel en fonction des vitesses articulaires.
En différenciant l'équation * on obtient:
La position de l'organe terminal dans l'espace opérationnel peut être écrite en termes de variables articulaires comme suit :
x = f(q)
[ & ×]=[J][ & q] (2.11)
?fj
[ ]
J
?q j
La Jacobinne du système est définie par :
(2.12)
Les accélérations sont données par :
|
& & |
? ? ? ? ? ? ? f & & & & i q q 2 f i + + q j j j j ? q q q j k j k |
(2.13) k |
Ou bien sous forme matricielle par :
|
& & x |
= [ J ] & q & + [A] & q2 |
(2.14) |
|
|
ou : [ ]t q q , q 2, .... = 1 |
(2.15) |
||
q & 2 = q & 1 q & 1 , q & 1 q & 2 . .(2.16)
[ ]t
j (q) est la matrice Jacobienne donnée par :
? q
j q
( ) =
?fj
.(2.17)
f
Et : [ ] ??
A 2 .(2.18)
? ? ?
j = ??q q
? ? ?
j k ?
A partir du modèle cinématique (2.18) on peut écrire le modèle différentielle (2.19). Supposons que les variables qi soient maintenant non les variables articulaires de DenavitHartenberg, mais les variables associées aux déplacements des moteurs rotatifs ou linéaires et que le robot présente une chaîne cinématique directe passant par ces moteurs. Il existe alors un modèle différentiel du type (2.24). Chaque actionneur peut associer en statique la force ou le couple ä i qu'il exerce et forme le vecteur :
= [ä1 ä i ä n ] T (2.19)
Des forces articulaires sous l'effet de ces forces combinées, l'organe terminal exerce sur l'environnement des forces qui peuvent être réduites à leur torseur résultant (force et mouvement) noté F , qui a donc six composantes. En utilisant alors la relation :
|
?P ? ? ? = 0 ( ) J q ? ù N? |
q (2.20) |
Ou: ( PN) : La vitesse du point de référence par rapport au repère Fixe.
(ù N ) : La vitesse de rotation instantanée et le principe des travaux virtuels pour des déplacements infinitésimaux de type (2.24) ou à alors :
= 0 . (2.21)
J T f
Qui permet de calculer les forces matrices nécessaires pour exercer sur l'environnement des forces données. L'équation (2.22) constitue donc plutôt un modèle inverse au sens habituel du terme. Le modèle direct ne peut s'obtenir que si la matrice J est régulière.
Dans le cas d'un robot non redondant (n=6) et en dehors des singularités, on a alors le modèle direct :
F J (2.22)
= ( ) -1
T
0
Tableau 2.1 : Les paramètres géométriques du robot type.[140,141]
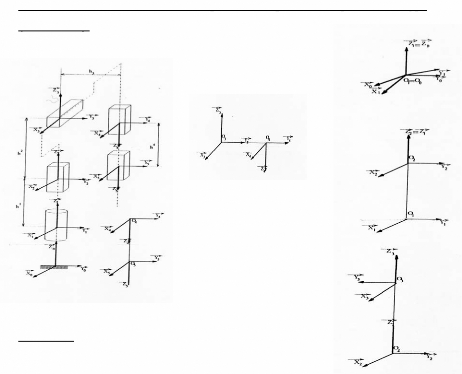
2-8 Détermination des matrices de changements de repères <i-1/i> pour le robot type
(ALG-M.O. 1).
Figure 2.7 : Les différents repères liés au corps du robot.
Indice
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
di |
0 |
h1 |
h2 |
h3 |
h4 |
|
|
ái |
0 |
ð/2 |
ð/2 |
0 |
||
|
ó |
0 |
1 |
1 |
1 |
1 |
|
|
ri |
0 |
Z 2 |
Z 3 |
Z 4 |
Z5 |
|
|
è i |
ã |
0 |
0 |
0 |
0 |
2-8-1 Espace de travail :
L'espace de travail est l'ensemble des positions et/ou orientations accessible par l'organe terminal du robot.
Le volume ou l'espace de travail d'un robot dépend généralement de trois facteurs : - De la géométrie du robot,
- De la longueur des segments,
- Du débattement des articulations (limité par des butées)
2-8-2 Analyse de l'espace de travail du robot type (ALGERIE-MACHINES OUTILS-1) : L'analyse de l'espace de travail des robots trouve de nombreuses applications. Notamment dans le domaine de la C.A.O.- Robotique pour la conception optimale des robots, des sites robotisés, et pour la programmation hors ligne.
Soit q = [q1 qn] un élément de IRn représentant une configuration articulaire donnée et
soit x = [x1 xn] l'élément de l'espace opérationnel IRn correspondant, tel que :
X = f(q) (2.23)
On note Q l'ensemble des configurations accessibles compte tenu des butées articulaires. Par conséquent, Q sera appelé domaine articulaire :
L'image de Q par le modèle géométrique direct f définit l'espace de travail W du robot :
W = f(Q) (2.24)
2-8-3 Calcul de l'espace de travail du robot choisi :
Comme on l'a définie précédemment, la position de l'organe terminal dans le repère atelier est donnée par le vecteur position dans la matrice de transformation qui exprime le repère R5 dans R0 noté :

ã1
()
z z c
3 4
-
ã1
()
z z s
3 4
-
?
; avec ??
??
+ + + +
h h h z
2 3 4
ph= z 1
px
?
?
??
?
??
py
P
pz
?1
?
? ?
??
?
??
-
z5
2
px
py
(2.25)
En développant un programme qui a comme paramètres entrées les limites articulaires de chaque articulation et sortie toutes les configuration possibles de l'organe terminal.
2-8-4 Algorithme simplifié du programme :
Algorithme 2.1: Algorithme simplifié du programme :
Début programme
Entrer h min et h max pour chaque articulation ;
Début Do
Incrémentation de h1 et entre h1min et h1max
Incrémentation de h2 et entre h2min et h2max Incrémentation de h3 et entre h3min et h3max
(
-
z3
)cã1
px
z4
ã1
() z z s
3 4
-
py
?
??
??
2 - z5
|
p h = z 1 |
+ + + + h h h z 2 3 4 |
Fin Do
Sortie (Px,Py,Pz)
Les modèles dynamiques des bras manipulateurs sont décrits par un ensemble d'équations mathématiques qui portent la dynamique de ceux-ci et peuvent être simulées sur ordinateur dans le but de synthétiser une commande conditionnée par des performances désirées, les équations différentielles qui décrivent le comportement d'un mécanisme à plusieurs corps articulés peuvent être déterminer par des lois mécaniques classiques Newtoniennes (théorèmes généraux de la mécanique classiques) et Lagrangiennes.
Les approches d' Euler- Lagrange et Newton- Euler permettent d'aboutir aux équations du mouvement des robots.
Les principales méthodes actuelles d'obtention du modèle dynamique sont basées sur l'un des quatre formalismes suivants :
- La notion d'énergie d'accélération ou fonction de Gibbs.
- Les équations de Newton et d' Euler.
- Le principe du travail virtuel de D'Alembert.
- Les équations de Lagrange.
Ces dernières semblent les plus utilisées et peuvent être les plus faciles à manipuler. 2-10-1 Obtention du modèle dynamique : [42, 43]
L'énergie cinétique du système est une forme
quadratique des vitesses articulaires :
Eq t A q
c = 1 / 2 [ ] & ..(2.26)
Tel que :
[A] : matrice (n x n) symétrique définie positive d'éléments génériques : Aij (q) dépendant du variable articulaires q.
q & = (q&1,q&2, q &3, & qn ) Matrice uni colonne des vitesses généralisées.
t
L'énergie potentielle est due aux champs de pesanteur, alors l'effort généralisé par le champ de pesanteur sur l'articulation i s'écrit :
|
G p ä E i ä = - q |
(2.27) |
|
Ep : Représente l'énergie potentielle externe du système.
Le Principe des puissances virtuelles donne les équations suivantes : Ai = Fi .. .(2.28)
Ai : Désigne la quantité d'accélération généralisée.
Fi : Désigne les forces généralisées.
Tel que : Ai=äi (Ec) (2.29)

d
?
?
??
-
? q
? q
?
??
i
i
d t
?
??
?
??
?
(2.30)
?i
|
? E ? E F + D P = - i i ? q ? q i i |
(2.31) |
ED : Energie de dissipation par effet du frottement visqueux.
i: Forces généralisées non conservatives.
Les équations scalaires de Lagrange peuvent se mettre sous la forme suivante :
n ? n ? ? A ? A ? A ? ? ? A ? A
ij ik jk ij ij 2
= ? + ? + - ?? q q + - - ?? q G
i ij j
A q & & & & 1 &
? ? ?
?? ?? -
j k j ? (2.32)
i
q ? q ? q q q
j = 1 = + 1
? ? 2 ?
k j k j i ? ?
? ? ? j j ? ? ?
Avec :
?A ?A ij ik
+
-
ijk ? q ? q ? q
k j
j
B
=
?Ajk
(2.33)
C ij 2 q
?
? ? q j j ?
(2.34)
? ? A 1 ? A ?
ij ij
?? - - ??

|
G i |
? E p |
(2.35) |
||
|
? q i |
[A] : Matrice carrée de dimension (n x n) symétrique définie positive. C'est la matrice de masse du système, elle intervient dans le calcul du couple / force d'inertie exprimé par le
..
produit [A]. q .
[B] : Matrice de dimension (n x (n-1) n/2), appelée matrice des termes de Coriolis.
[C] : Matrice de dimension (n x n), appelée matrice des termes centrifuges. G : Matrice colonne de dimension (n x 1), représentant les forces généralisées aux champs de pesanteur.
q & = (q&1,q&2, q &3, & qn ) Matrice uni colonne des accélérations généralisées.
t
|
qq q q q q q q q q q q & & & & & & & & & & & & v n n n = - ( , , , , ) 1 2 1 3 1 2 3 1 |
t |
q & 2 = ( q & 1 2, q & 2 2, q & 3 2, & qn 2) t
Les équations peuvent être regroupées sous la forme matricielle suivante:
= [ A ] & q & + [ B ] & qq & + [ C ] q&2-G (2.36)
Les éléments des A, B, C et G s'appellent les coefficients dynamiques du système Ils sont
des paramètres géométriques d'inertie du mécanisme.
Le modèle dynamique générale d'un robot manipulateur rigide à n degrés de liberté peut être représenté par un système d'équation différentielle non linéaire de second ordre à n entrée formant le vecteur de forces ou couples généralisées T, et n sorties qui forment le vecteur position q, les équations de ce système à n liaisons, décrites dans l'espace des coordonnées articulaires, sont données sous forme matricielle comme suit :
M(q) q + B(q, q ) q +K(q, q )q+ G(q) +H( q )= Tp(t) +T(t) ..(2.37)
. ..
Avec Avec q ? Rn ; q ? Rn ; q ? Rn représente respectivement les positions, les
vitesses et les accélérations articulaires et : M(q) ? Rnxn : Matrice d'inerte ;
. .
B(q, q )+K(q, q )q ? Rn : Englobe les couples dus aux forces de Coriolis et centrifuges ;
G(q) ? Rn : Vecteur de forces ou couples dus aux forces de gravitation ;
Tp ? Rn : Le vecteur de forces ou couples de perturbation externe ;
T(t) ? Rn : Vecteur de forces ou couples moteurs .
Les éléments de M, B, K, G et H sont généralement des fonctions très compliqués et non linéaires par rapport aux coordonnées généralisées de manipulateur.
Le modèle précédant du robot est complexe mais vérifie certaines propriétés fondamentales qui peuvent être exploitées pour l'analyse du comportement du système et le calcul de commande.
Propriété 1 : La matrice M(q) est symétrique
définie positive ( S. D. P.) , par conséquent tous les
éléments diagonaux de cette matrice sont positifs { Mij (q) 0 i
= 1, ,n }
Propriété 2 : Les matrices M, B, K et les vecteurs
G,H sont uniformément bornés. Propriété 3 :
L'entrée de commande est indépendante pour chaque articulation du
manipulateur.
.
Propriété 4 : Le vecteur des frottements visqueux et secs H( q) est caractérisé par les n éléments.
. . . .
{ Hi(qi)0 i = 1, ,n }, tel que : Hi(qi) Évi qI + Ési sgn (qI ) (2.38)
Avec Évi et Ési sont respectivement les coefficients des frottements visqueux et secs de la ième articulation.
Les propriétés 1-4 découlent de la nature physique du robot manipulateur. La propriété 3 est du au fait que les flexibilités des articulations et des structures n'ont pas été prises en compte.
Dans ce cas de figure chaque degré de liberté (D.D.L.) est piloté par un actionneur (moteur à courant continu.
2-10- 4 Modèle dynamique directe : Ce modèle consiste à déterminer les variables articulaires en fonction des forces (ou / et couples ) généralisés.
Le calcul de ces variables se fait en résolvant le système d'équations différentielles non linéaires suivant :
|
.. = [A] q+ [B] |
. . . q.q +[C] q2-G (2.39) |
À t =t0 q(t0) =q0 , q(t0) = 0
La résolution peut se faire par plusieurs méthodes numériques dans notre cas nous utilisons la méthode de Runge-Kutta à 4 approximations.
2-11 L'utilisation de la méthode de Runge -Kutta [21, 45, 46] : dt [y] = É (t,y) avec [y] = [y0] pour t= t0
[y]t+dt = [y]t + 1/6 [[k1] +2[k2] +2[k3]+[k4]] (2.40)
[K1] = É (t , [y] ) dt ...(2.41)
[K2]= É ( t + dt/2 , [y] +k1/2 ) dt (2.42)
[K3]= É ( t + dt/2 , [y] +k2/2 ) dt (2.43)
[k4] = É ( t + dt , [y] +[k3] ) dt . (2.44)
Le système d'équation peut se mettre sous la forme suivante :
.. . . .
q= - [A]-1 [[B](q q) + [c] q2-g-] .. (2.45)
T= t0 , q(t0) = q0 , (t0) =0


. . .
- [A]-1 [B] (q q) + [c] q2-G-
... (2.46)
q =
q&&



q
[y] = É (t , y ) = d[y] /dt =
.
q
Pour modélisé un système, c'est-à-dire gouverner ses sorties, il faut prévoir le comportement du système, en réponse aux différentes excitations d'entrer qui pourront lui être appliquées; la démarche est de représenter le comportement du système sous la forme d'un modèle, une telle démarche s'appelle la modélisation; d'une manière générale, on recherche toujours le modèle le plus simple qui permet d'expliquer, de manière satisfaisante, le comportement du processus dans son domaine d'application; les modèles de transformation entre l'espace opérationnel (dans lequel est définie la situation de l'organe terminal) et l'espace articulaire. (Dans lequel est définie la configuration du robot), On distingue :
· Les modèles géométriques qui expriment la situation de l'organe terminal en fonction de la configuration du mécanisme.
· Les modèles cinématiques permettent de contrôler la vitesse de déplacement du robot afin de connaître la durée d'exécution d'une tâche.
· Les modèles dynamiques définissent les " équations du mouvement du robot qui permettent d'établir les relations entre les couples ou forces exercés par les actionneurs et positions, vitesses et accélérations.
Nous supposons que la déformation du joint est supposée localisée à la sortie réductrice. Pour chaque articulation nous prendrons deux variables articulaires q2i-1 et q2i ou :
Q2i-1 : Variable articulaire délivrée par l'actionneur;
Q2i : Variable articulaire prise par le segment ;
3.1.2 Hypothèses du travail:
- Les segments sont supposés parfaitement rigides;
- Les liaisons sont prismatiques ou rotoides élastiques linéaires;
- La dissipation d'énergie dans les liaisons est du type visqueux.
3.1.3 Mise en équation : [49, 50, 51, 52, 53, 54] :
Pour la mise en équation du modèle dynamique nous avons utilisées le formalisme de Lagrange associé à la méthode Uiker (même démarche que dans le chapitre 2), ce qui conduit au calcul de:
L'énergie de dissipation par frottement visqueux dans le joints EP=Ep (q2i-1 ,q2i). 3.1.4 Energie cinétique, potentiel et de dissipation du système :
Pour un système mécanique articulé à joints flexibles, l'énergie cinétique est calculée en considérant ; la structure comme une chaîne ouverte simple à 2n éléments les n segments et les n actionneurs qu'on peut mettre sous la forme quadratique suivante :
1 2 [ ] 2 2 2 1 [ ] 2 1
1
E q A q q I q
c i
= + - -
& & & &
t t ... (3.1)
i i a i
2
[A] : Représente la matrice de masse relative aux coordonnées généralisées q2i.dimension (n*n) symétrique définie positive.
41 [Ia] : Matrice des inerties des actionneurs de dimension (n*n) diagonal, construite par les éléments de type 2
Ni Ia tel que:
Ni: Rapport de transmission du iéme actionneur Ni = 1
Ia : Inertie du rotor et du premier étage du réducteur du iéme actionneur.
Q2i : Vitesse généralisée relative au iéme segment .
Q2i-1: Vitesse généralisée relative au iéme segment.
L'énergie potentielle est calculée de la même façon que dans le cas rigide, mais tout considérons la structure comme une chaîne cinétique simple à 2n éléments, les n segments et les n actionneurs :
Ep =Ep (ext)+Ep (int) (3.2)
Avec Ep(ext)=Ep (pesanteur).
Ep(int)= Ep (élastique).
L'énergie potentielle s'écrit sous la forme :
|
n Epint = ? i 1 = |
Epi ( q2i-1-q2i) . (3.3) |
n
Epint = ?=
i 1
1 Ki ( q2i-1-q2i)2 . (3.4)
2
En posant:
EPint = ?i = q2i-1-q2i .(3.5)
n
EPint = ?=
i 1
1 Ki (?i)2 . (3.6)
2
|
ED=?= i 1 |
ED ( |
. q2i-1 , |
. q2i-1 ) (3.9) |
Ki: Représente la constante de rigidité du ieme joint élastique.
?i: Représente le déplacement angulaire relatif au niveau du iéme joint :
EPint = 1 {? }T [ T] {? } ....(3.7)
2
{? } : Matrice uni colonne des déplacements angulaires.
[K] : Matrice de rigidité des joints de dimension (n*n).diagonale :
n
|
EPext = Epg =? i 1 = |
Epg ( q2i) .(3.8) |
C'est une forme quadratique des vitesses angulaires relatives aux joints, on aura:
n
n
ED=?=
i 1
. .
1 bi ( q2i-1 , q2i ) 2 (3.10)
2
n
ED = ?=
i 1
1 .
bi (?)2 (3.11)
2
. .
ED = 1 { ? }T [D] {? } (3.12)
2
{? }: Matrice uni colonne constituée des vitesses angulaires.
[D]: Matrice des coefficients d'amortissement dimension (n*n) diagonale.
Si nous appliquons le principe des puissances virtuelles et le formalisme de Lagrange conduisent aux 2n équations suivantes:
+j j = 1,2 .n (3.13)
Ki( q2i-q2i-1)-bi( q2i-q2i-1) = i si i = 2i-1
+Ki( q2i-q2i-1)-bi( 2qi-q2i-1) = 0 si j = 2i (3.14)
? E p
? q j
? E c =
?ED
?
?
?
??
d
.
? q
j
?Epg
+
? q i
?Epg
+
?qi
? E c
?
?
?
??
? q j
? q j
dt
d ? ? E ?
c
dt ?? q ??
? i
d ??E?
c
dt ?? q ??
? i
-
-
?E c
?qi
?q i
?E c
On posant la variable articulaire [q]= telle que : [qi]=[q2i-1] et [q2]=[q2i] i=1,n.
On aura le système d'équation suivant :
.. .
[A] q1+[B] q1
..
. . .
q1+[C] 2
q& 1 - G + [K] ( q1-q2) +[D] (q1-q 2) = 0
(3.15)
. .
[Ia] q2 - [K] (q1-q2) -[D] (q1 - q2) =
[A] : Matrice de masse.
[B] : Matrice de Coriolis.
G : Matrice uni colonne des termes de gravité.
Si le système mécanique est à joints parfaitement rigides. Le coefficient de rigidité K -) 8
B -) 0 , q1-) q2 et q1-q2-) 0.
Le système d'équation devient alors :
|
.. [As] q1+[B] |
. q1 |
. q1+[C] 2 q& i - G = 0 |
||
|
[Ia] |
.. q1 = |
(3.16) |
||
Tel que [As] est la matrice d'inertie de la partie segments et [Ia] est la matrice d'inertie de la partie actionneurs.
Si on additionne membre à membre les équations (1) et (2) on retrouve les équations du système poly articulés indéformables données sous la forme matricielle suivante :
.. . . .
=[A] q+[B] q.q +[C] q2 - G Sachant que [A]=[AS]+[Ia].
3.1.5 Résolution des équations: [4 , 49, 68, 69] :
Pour la résolution du système d'équations on utilise la méthode de Runge - Kutta à quatre approximations pour cela on arrange le système comme suit :
.. . . . .
q1 = - [Aï1 [B] q1q1+[C] 2
0
0
q& i - G + [K] ( q1-q2) +[D] (q1 - q2)
..
. .
q2 = [Iaï1 [ + [K] ( q1-q2) +[D] (q1 - q 2)]
(3.17)
Les conditions initiales sont :
|
q1 |
( ) 0 ( ) 0 t = q q & t = q & 0 1 1 0 1 |
q t = q q & t = q &
2 0 2 2 0 2
( ) 0 ( ) 0
on pose
|
[Y] = |
q1 q2 |
? ? ? ? ? ? |
Et donc nous avons : |
d= dt |
q1 . q1 q2 . q2 |
? ? ? ? ? ? ?? |

? ? ? ? ? ?
&
2
G+
-
1
&
q1
[ ] [ ] , [ ]
A q B q q C q
- 1 & & & &
1 1 2
+ +
[ ] ( ) [ ] ( )
K q q D q q
- + -
& &
1 2 1 2
)]
?
?
?
?
?
??
.(3.18)
d Y
[ ]
=
dt
&
q2
K q q D q q
& &
1 2 1 2
I a
[ ] [ [] ( ) [ ] (
- 1 + - + -
q1
&
q1
q2
q2
d
dt
Qu'on peut poser sous la forme suivante :
d [Y] = É (t , [Y] ) dt

Sachant que [Y(t0)] = [Y0] on obtient le système d'équation différentielle suivant :
d [Y] = É (t , [Y] ) dt
[Y] = [Y0] pour t = t0
Qu'on peut résoudre par la méthode de Runge -Kutta .
3.2.1 Les erreurs de positionnement d'un manipulateur [55, 65] :
Le positionnement réel d'un manipulateur, que ce soit en statique ou en dynamique (poursuit des trajectoires) s'écarte inévitablement et pour différentes causes, de sa position désirée. De même, un manipulateur ne se positionne jamais au même endroit lorsque la même trajectoire est répétée plusieurs fois ».
Ces erreurs de positionnement sont d'origines diverses, peuvent être classées en quatre catégories principales :
- Erreurs de quantification et de calcul.
- Erreurs cinématique de type aléatoire dominant.
- Erreurs d'étalonnage et d'identification.
- Erreurs cinématique de type systématique dominant.
Les erreurs de quantification et de calcul :
sont liées à :
- L'arrondi dans les calculs effectués par le calculateur.
- La quantification des codeurs incrémentaux ou absolus utilisés pour la détermination des coordonnées articulaires.
- La performance du calcul numérique et des algorithmes employés.
- La troncature des valeurs numériques dans les calculs trigonométriques
Les erreurs cinématique de type aléatoire dominant:
Chacune des articulations d'un manipulateur à motorisation électrique peut être déplacée à l'intérieur d'une petite zone, sans entraîner de signale d'erreur à l'intérieur du système d'asservissement. Cette zone morte est due aux défauts géométriques non systématiques des organes mécaniques (les jeux mécaniques) à la résolution des capteurs et aux performances des asservissements (non linéarités dues aux frottements mécaniques par exemple) [10, 65].
Les erreurs cinématiques de types systématique dominante sont liées à :
- La déformation des segments sous l'effet des charges statiques et dynamiques.
- La déformation des articulations sous l'effet des charges statiques et dynamique. - La dilatation des pièces mécaniques de la structure sous l'effet de la température.
L'identification consiste à déterminer, suite à une série de mesures et à l'aide des méthodes de masse du manipulateur [55,66].
Les erreurs de positionnement statique d'un manipulateur sont de deux natures : Géométrique et non géométrique.
Les erreurs géométriques : Elles regroupent les imprécisions de fabrication dons les corps et les liaisons et les erreurs d'initialisations des offsets codeurs (les valeurs des offsets codeurs correspondants à la configuration initiale géométrique dans laquelle les variables articulaires sont nulles).
Les erreurs non géométriques : Elles regroupent les déformations, les jeux dans les chaînes cinématiques, les erreurs liées à la résolution des capteurs et aux performances des asservissements. Elles ne sont pas accessibles à la calibration géométrique.
La procédure d'identification géométrique distingue trois niveaux de complexité :
Niveaux 1 : Ou « calibration des articulations », l'objectif est d'établir la relation la plus exacte entre le signal produit par les capteurs de position et les déplacements articulaires. Ceci, implique généralement la calibration de la cinématique des organes d'entraînement (réducteurs, courroies, .etc.), les mécanismes des valeurs des offsets codeurs.
Niveaux 2 : Ou « calibration géométrique globale » dans ce niveau on doit identifier tous les paramètres géométriques de description du manipulateur. L'objectif de ce niveau est de déterminer le modèle géométrique de base, qui lie les coordonnées opérationnelles aux coordonnées articulaires (ou valeurs de commande des actionneurs).
Niveaux 3 : Ou « calibration non géométrique », il porte sur les possibilités de compenser les erreurs d'ordre non géométriques à savoir les déformations des articulations et des segments et des frottements.
Pour utiliser le modèle dynamique, il faut connaître les valeurs numériques des paramètres de masse (masse, centre de masse, et matrice d'inertie) relatifs aux différents corps et qui interviennent dans le modèle dynamique. Plusieurs techniques peuvent être envisagées pour estimer ces paramètres : Soit par calcul au moment de la conception, surtout si on utilise un logiciel de C.A.O. performant, soit par mesure corps par corps avant le montage ou par identification.
La technique d'identification des paramètres, consiste à exploiter le caractère linéaire des actions dynamiques relativement à ces paramètres pour les identifier, en utilisant la méthode d'optimisation des moindres carrée[56] .
La précision d'un manipulateur est généralement définie en terme de précision statique (les caractéristiques de pose) et de précision dynamique (les caractéristiques de trajectoire), ces deux caractéristiques, quantifient la différence entre la situation désirée et celle réellement atteinte [10, 65, 67].
Pour les manipulateurs utilisés dans les tâches d'assemblages, d'insertion de composants, de soudage par point..., les caractéristiques de composantes sont les caractéristiques de pose. Ces caractéristiques sont définies par trois termes:
- Exactitude statique.
- Répétitivité statique.
- Temps de stabilité et dépassement statique.
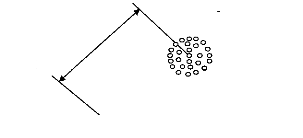
Selon la définition ISO, l'exactitude statique est représentée par l'écart entre une pose commandée (Pc) et la moyenne des poses réellement atteintes (figures 3.1) , lorsqu'on demande au manipulateur de se positionner plusieurs fois en Pc en suivant toujours la même trajectoire (exactitude statique unidirectionnelle) soit Pc le point de la position commandée de coordonnées Xc , Yc , Zc dans le référentiel de bas {Ro}; Pi une des positions réellement atteintes (i= 1, k) , Pc = [ Xc , Yc , Zj
et Pi = [Xi , Yi , Zi]T
Pi
Les positions atteintes
Pc
La position programmées
Figure 3.1: L'exactitude de positionnement statique d'un manipulateur [55].
L'exactitude locale de position Es est la distance entre le point Pc et le point Pg barycentre de tous les points atteints Pi donc:
E s ( x
=
g xc)2 ( y g y c ) 2 ( z g z c )2
- + - + -

(3.19)
? yi
=1 ; i = = 1
i =
Y g = 1 ; k
Z g
k k
avec: Xg i
? xi
? zi
i k
|
= |
i k =i k = |
Pour les rotations, on peut définir de la même manière la variation entre la moyenne des positions angulaires atteintes et la valeur commandée.
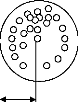
Par définition la répétitivité statique unidirectionnelle est la distance maximale entre le point moyen Pg et les points réellement atteints Pi , i= 1 .k (Figure 3.2)
Pg
Pi
Les positions atteintes. Rs
Figure 3.2: La répétitivité de positionnent statique d'un manipulateur [55].
R Max 1 x x y y z z
= = - + - + -
( ) 2 ( ) 2 ( )2 .. (3.20)
s i k k i k i k i
La norme (NF-E 61-103) définit également une répétitivité statique à partir de la moyenne de distances entre Pg et les points atteints Pi.
Si les trajectoires pour atteindre la position désirée Pc sont différentes (on partira de différentes positions vers la même destination). L'exactitude et la répétitivité vont avoir des valeurs différentes appelées exactitudes et répétitivité multidirectionnelles.
Dans le cas où la position commandée serait définie par apprentissage, la répétitivité est la même, par contre l'exactitude est très différente, pour les manipulateurs très précis la répétitivité peut être de l'ordre du centième de mm, alors que l'exactitude de position programmée peut être de plusieurs mm.
Remarque: Au terme répétitivité on associe souvent la notion de réversibilité qui caractérise la précision statique quant le point est atteint selon plusieurs directions ; elle est plus mauvaise que la répétitivité.
Il est bien intéressant de connaître le comportement du robot lorsqu'il approche une pose commandée. Suivant le réglage des asservissements des actionneurs et le niveau de déformations des segments, le manipulateur peut osciller, dépasser la situation commandée ou au contraire s'en approcher sans oscillation, ce comportement se traduit par deux caractéristiques : Dépassement et temps de stabilisation ces caractéristiques peuvent être utiles pour régler une temporisation du manipulateur avant d'effectuer une tâche ; la
connaissance du dépassement permet de s'assurer que l'espace dégagé autour du point d'arrêt est suffisant pour éviter les collisions de l'outil avec l'environnement [65].
En robotique, de nombreuses tâches sont réalisées en utilisant un mode de commande de type interpolation linéaire ou circulaire afin de quantifier les défauts et les écarts entre la trajectoire réellement parcourue et la trajectoire commandée, les caractéristiques essentielles pour ces applications sont définies par les notions d'exactitudes et de répétitivité de trajectoire.
Elle caractérise l'aptitude d'un manipulateur à faire suivre à l'interface mécanique (l'effecteur) une trajectoire désirée le fois dans la même direction et le fois dans la direction opposée [10].
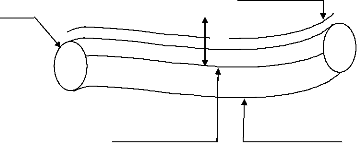
L'exactitude de trajectoire est définie par la distance maximale entre la ligne moyenne des trajectoires réellement atteintes et la ligne programmée (Figure 3.3), mesurée dans un plan orthogonal à la trajectoire.
Et
R+
La ligne moyenne des trajectoires effectuées
Enveloppe des trajectoires effectuées
Trajectoire programmée
Figure 3.3: Exactitude de trajectoire [55]
L'exactitude pour des positions ou des trajectoires programmées dépend surtout ds erreurs d'étalonnage et des erreurs dues aux déformations de la structures mécanique du manipulateur [10, 65, 70].
La répétitivité de trajectoire (ou dynamique) est la distance moyenne (ligne des barycentres des trajectoires effectuées) et une trajectoire effectuée; sera donc le rayon du tore qui contiendrait toutes les trajectoires effectuées (Figure 3.3).
Les erreurs de répétitivité sont dues aux défauts géométriques non systématiques des organes mécaniques, à la résolution des codeurs de positions et aux performances des asservissements (non linéarités dues aux frottements mécaniques par exemple)
[10, 65] avec le développement de l'électronique, de l'informatique et des moyens de fabrication (machine à commande numérique, CFAO) la précision géométrique en terme de répétitivité tend à devenir largement suffisant pour la majorité des applications industrielles.
Les applications industrielles de la robotique font appel à des modes d'emploi principaux des manipulateurs:
De point d'arrêt acquis par apprentissage d'une suite discrète de configuration articulaires.
- De trajectoires acquises par l'enregistrement échantillonné d'une suite continue de configurations articulaires correspondants aux mouvements que doit reproduire le manipulateur.
Les points d'arrêt sont seuls fonctionnels (travail en cours mouvement).
Dans ces quatre types d'emploi, le problème de précision prend des dimensions tout à fait différentes:
- Il peut dépendre de la répétitivité de la réversibilité, de l'exactitude statique ou dynamique (§ 3.3) ou de l'un de ces critères seulement.
Les déformations de la structure mécanique peuvent être tout à fait transparentes à l'utilisateur comme elles peuvent s'imposer comme un aspect du comportement dont la modélisation et la prise en charge est vital pour l'application.
La simulation de l'effecteur dans l'espace opérationnel est donnée par le vecteur x. Si on désigne par:
XD : la situation instantanée de l'effecteur correspond à la configuration déformée du manipulateur.
XR : La situation de l'effecteur correspond à la configuration non déformée du manipulateur.
L'erreur de positionnement ou de poursuite de trajectoire instantané sera donnée par:
ä X = XD - XR .(3.21)
La situation XR de l'effecteur est donnée par le modèle géométrique direct, dans l'hypothèse rigide obtenu par le produit des matrices de transformations homogènes
Ces matrices sont calculées sur la base des paramètres de descriptions géométrique de la topologie du manipulateur.
Les déformations d'un segment (segment Cj-1)
engendre un torseur des déplacements au
point de l'articulation en
aval (point Oi) du segment et se traduisent par une variation de la

O 'j 1
Trans (xj 1,Lj 1)
C)j
X2j 1
Y'j 1
T~ flex
Yj Zj
o
Xj
Y2j-1
Rot (xj-1, áj-1)
Y3j-1
Z3 j-1
X3 j-1
Rot (Zj-1, èj)
Zj-1
oj-1
X'j 1
Xj-1
Yj 1
j-1
T f ~
transformation relative entre deux repères consécutifs (le repère {Rj-1 } et le repère {Rj } ) le modèle d'évaluation de la situation XD de l'effecteur peut être donc obtenu par un modèle géométrique modifié basé sur des matrices de transformations homogènes corrigées pour prendre en compte l'effet des déformations sur la situation de l'effecteur .
3-2-4 Le modèle géométrique direct corrige [55]
La figure 3.4 représente le corps Cj-1 du manipulateur dans la configuration rigide puis en position déformée et les deux référentiels {Rj-1 } et {Rj} associés aux articulateurs Ai-1 et Ai respectivement.

Y
o
o
Z
Z X
Figure : 3.4 Flexibilité d'un segment du manipulateur [55]
Le passage de {Rj-1} à {Rj} s'exprime en
fonction des composants du vecteur des
déplacements dus aux
déformations du corps Cj-1 et des trois paramètres de
descriptions áj,
Lj , et èj . Z2j-1
Z'j-1 oj
La manière de transformation définissant le repère {Rj } dans le repère {Rj-1 } Figure 3.5 est donnée par:
|
T f Trans X L T flex Rot x Rot ( Z j) ~ ~ j j j j j j j j 1 1 1 4 1 á 1 , è = * * * ( , ) - - - - - - ( , ) |
.(3.22) |
Où:
Rot (xj-1) =

Trans (xj-1, Lj-1) =

Rot (zj , èj) =
(3.23)
(3.24)
(3.25)






1 0 0 0
0 0
C S
á á
j j
- - -
1 1
0 0
S C
á á
j j
- -
1 1
0 0 0 1

1

C
è
j
|
S - è j 0100 001 0 00 |
0 0 Lj-1 01 0 |
0 |
S C
è è
j j 00
|
0 0 10 |
|||
|
0 0 01 |

~
La matrice de transformation homogène associée aux déplacements 1
T flexj-
(Translations et rotations) dus aux déformations du corps Cj-1 . Cette matrice peut être décomposée en deux matrices:
Une matrice de transformation pure qui représente les translations dus aux déformations
dx j - 1 , dy j - 1 , dz j - 1 donnée par :
|
100 |
dx |
j-1 |
~
Tflex i = 010 dy j -1 (3.26)
|
001 |
dz |
j |
-1 |
000 1
~
Représente les rotations dues aux déformations Tflexr et une matrice de rotation pure
r x j - 1 , ry j - 1 , r z j - 1 de la section droite d'abscisse bi-1 au corps Ci-1 point Oi-1 par rapport à l'extrémité (point Oj-1) , autour des trois axes xj-1 , yj-1 , zj-1 respectivement les matrices de transformation homogène associées à ces rotations , sont donnée par:
10 00
|
Rot (r xj-1 , xj-1) = |
0 0 C S x x - 0 0 S C x x 00 01 |
(3.27) |
|
|
Cy |
0 0 S y |
||
0100
|
Rot (r yj-1 , yj-1) = |
- |
Sy |
0 0 C y |
(3.28) |
0001
|
C - z |
Sz |
00 |
Rot (rzj-1 , zj-1) =
S C
z z
0 0 10
00
(3.29)
0 0 01
avec: Cx = cos(r xj-1) , Cy = cos(r yj-1) , Cz = cos(r zj-1) Sx = sin(r xj-1) , Sy = sin(r yj-1) , Sz = sin(r zj-1)
Les rotations rxj-1 , ryj-1 , et rzj-1 sont des rotations infinitésimales , on peut écrire:
Cx ? 1 Sy ? ryj -1 S x ? rxj - 1 Cz ?1 Cy ? 1
, ,
Sz ? rz j -1
|
Rot (r xj-1 , xj-1) = |
10 0 0 0 10 - rx j - 1 01 0 rx j - 1 00 0 |
(3.30) |
1
0 0
ry j - 1
0 1 00
Rot (ryj-1 , yj-1) =
- ry j - 1 01 0 (3.31)
0 001
1 - rz j - 1 00
Rot (rzj-1 , zj-1) =
rz j- 1 1 00
0 0 10
(3.32)
0 0 01
~
La matrice homogène est obtenue par le produit des matrices de transformation 1
T flexri -
Rot (rxj-1 , xj-1) , Rot
(ryj-1 , yj-1) ,et Rot (rzj-1 ,
zj-1), on peut effectuer ce produit dans
n'importe quel ordre ,
En faisant abstraction des valeurs infinitésimales de deuxième
ordre
de type r x j - 1 × ry j - 1 , et ryj - 1 × r z j - 1 on obtient :
1 0
r r
z y
j j
- -
1 1
r r
z x
1 0
-
j j
- -
1 1
-r r
y x
j j
- -
1 1
~
Tflexr =
1 0
(3.33)
0 0 0 1
La matrice de transformation homogène associée aux déplacements dus aux déformations du corps Cj-1 ( la matrice de flexibilité) est donnée donc par:
~ ~
T flexr j- * 1
T flext j-
1
~
= 1
T flexj-
1 r z j - 1
r d
y x
j j
- -
1 1
~
Tflexj- 1
r r
z x
= ? 1 -
j j
- 1
?
.(3.34)
d
1 1
y j -
d
z
j j
- 1
1
- r r
y x
j - 1
1
0 0 0 1
Soit RE (oE , xE , yE , zE ) un repère lié à l'effecteur , la position et l'orientation de l'effecteur (l'outil) correspondant à la configuration déformée du manipulateur , sont définies dans le repère {Ro} par la matrice de transformation :
|
~ |
n-1 T~f n |
1~fT 1 o = E T~f o T~f 2 |
..(3.35) |
Le modèle géométrique direct corrigé du manipulateur est l'ensemble des relations qui permettent d'exprimer la situation de l'effecteur qui correspond à la configuration déformée du manipulateur Xd en fonction des coordonnées articulaires q et des vecteurs des déplacements dus aux déformations des différents segments: [63]
Xd = Fd (q , u) (3.36 a)
Les trois premières composantes de Xj fixent la position du point OE de l'effecteur par rapport au repère ({RE}/{Ro}) .
3-2-4-1 Procédure et modèle de compensation :

La configuration rigide La configuration déformée La configuration corrigée
La configuration déformée
après deformation
XC
XE
äX
äX
XC
La situation désirée
Supposons que le manipulateur est dans une configuration q bien déterminée, les erreurs dues aux déformations des segments correspondant à cette configuration sont représentées par le vecteur äX , la correction ou la compensation de ces erreurs port de l'idée schématisée ci-après:
On commande le déplacement du manipulateur sur une situation XC = XR - äX
(La situation de l'effecteur qui correspond à la configuration corrigée et non déformée du manipulateur) dans l'espace de travail de telle sorte que:
Xed XC + äX = XE - äX + äX = XE ..(3.36 b)
La situation que doit atteindre le manipulateur rigide permet de calculer; si elles existent les solutions articulaires possibles.
Parmi ces solutions, il existe une solution définie dans l'espace articulaire par le vecteur des coordonnées généralisées (q + äq) qui est la plus indiquée pour réaliser la tâche car elle se traduit par de légères corrections sur les variables de commande relativement à l'hypothèse rigide.
Ainsi au lieu de traiter le problème par la résolution du modèle géométrique inverse, il est plus pratique d'utiliser le modèle différentiel:
~
X J q q q J q X
~ - 1
- = = = -
ä ä ä ä
( ) ( ) (3.37)
qC =q+äq (3.38)
äq : Représente le mouvement correctif à effectuer au niveau des variables articulaires, à partir de la configuration rigide.
qc : Les coordonnées articulaires corrigées permettant la compensation des erreurs dues aux déformations élastiques des segments.
L'organigramme figure 3.7 présente, de manière chronologique les étapes de calcul nécessaire à l'évaluation et à la compensation des erreurs de positionnement ou de poursuite dues aux déformations quasi-statiques des segments d'un manipulateur en fonction des paramètres cinématiques (coordonnées, vitesses, et accélérations généralisées) et de charge.
REMARQUES:
Pour un manipulateur à moins de six degrés de liberté, plan par exemple, il est bien évident que les mouvements correctifs - äq ne pourront jamais compenser une erreur qui se produirait hors plan. Donc dans la relation (3.37), on ne tiendra pas compte les composantes de - äX qui ne peuvent pas être engendrées par -äq.
Si l'écart - äX est important, on ne peut pas compenser l'erreur de positionnement d'un seul coup, mais il faut faire la compensation par plusieurs itérations.
|
Les données du problème: - Les paramètres géométriques et mécaniques du manipulateur . (q , q & , & & q)- Les paramètres cinématiques |

|
Modèle géométrique direct: Situation de l'effecteur dans l'hypothèse du manipultateur rigide XE = F(q) |

|
Modèle des déformations : Evaluation des torseurs des déplacements élémentaires par segments: Uj = [ d x j , d y j , d z j , 1 r x j , r y j , r z ]T j = 1 .n. |

|
Modèle géométrique direct corrigé: Situation de l'effecteur correspond à la configuration déformée du manipulateur: Xd = Fd (q , u) |
|
|
Modèle d'évaluation des erreurs : Erreurs de positionnement ou de poursuite: äX = Xd - XE |

Début

Fin
Modèle de compensation :
0J~(q) Calcul de la matrice jacobienne du manipulateur: Algorithme de Greville :
0J~(q) la pseudo-inverse de J~ - 1(q) Calcul de la matrice * äX J ~-1( q)Compensation : äq = -qc = q + äq
3-2-4-2 Calibration et déformation des manipulateurs :[56,66] :
L'étalonnage ou l'identification géométrique consiste à déterminer, suite à une série de mesures et à l'aide d'un modèle mathématique basée sur un modèle géométrique de description du manipulateur et des offsets codeurs.
Les valeurs des paramètres géométriques et des offsets codeurs identifiés au cours de l'étalonnage sont des valeurs optimisées, l'optimisation est itérative est basé sur la méthode des moindre carrés. Les paramètres géométriques identifiés, selon les procédures classiques de calibration, intégrant moyennement les effets des déformations.
Manipulateur non calibré, l'écart de positionnement entre la situation mesurée et la situation désirée pour une configuration q donné, dépend surtout des erreurs dues aux déformations :
~
Xmes(q)- Xthé(q) = H (q) * (Pg réel - Pg nom ) + ? Xdef (q) (3.39)
Avec : Xmes(q) = la situation mesurée.
Xthé(q) = la situation théorique
~
H (q) = la matrice d'identification
Pg réel = les paramètres géométriques réels du manipulateur
Pg nom= les paramètres géométriques nominaux du manipulateur
Il est suffisant d'intégrer les erreurs deus aux déformations dans les valeurs identifiées des paramètres géométriques de description, la procédure d'identification est celle qui est classiquement utilisée:
~
Xmes(q)- Xthé(q) = ð(q) x (Pg thé - Pg nom ) ....(3.40)
Avec : Pg thé : les valeurs des paramètres géométriques et offsets codeurs identifiés.
Dans les cas, des manipulateurs flexibles ou applications exigeantes en précision. La calibration géométrique préalable n'est pas en mesure de rendre compte, à elle seule du problème des déformations. La compensation est incontournable et un modèle des déformations est donc nécessaire.
4.1 Introduction [2]:
Java est un langage de programmation, fortement inspiré des langages C et C++, et fait partie des langages orientés objets.
Dans ce chapitre je vais présenter des modélisations développés en java simulent la géométrie, cinématique et la dynamique directe et inverse d'un manipulateur [Algérie- Machines Outils -1].
Le programme est un système développé en créant le projet robot avec les interfaces (figure 4.6), (figure 4.7), (figure 4.8), (figure 4.9) et (figure 4.10) montrent un exécutable dans sa forme la plus simple ; c'est un modélisateur pour robots mécaniques, la modélisation présente une interface graphique qui permet avec les paramètres géométriques de manipuler chaque lien du robot. Le but principal de ce modélisateur est la simulation des robots industriels employés sur le marché. Il a été développé à l'université de Saad Dahleb de Blida faculté des sciences de l'ingénieur département de génie mécanique, il est basé sur le projet de recherche nationale: ROBOT, on peut obtenir une visualisation qui exprimait le circuit travail du robot type [ALG.- M. O.-1] dans une station d'usinage dans un environnement deux dimensions.
Lors du développement de ce système je suis passé par plusieurs étapes, chacune d'elles m'a donné un résultat que je l'ai évalué selon mes besoins. Le système spatial du robot mis en application possède cinq articulations, une rotode et quatre prismatique dont le schéma cinématique est définit dans le corps du mémoire , les paramètres géométrique et inertiels sont résumés dans les appendices, j'ai déterminé les matrices de passage associées à chaque repère. J'ai considéré les éléments du système comme étant rigides que le mouvement s'effectue sans frottements.
Dans cette section je vais exposer un ensemble de résultats obtenus pendant le développement de ce système. Dans la première position, le but (besoin) était la localisation des chaînons en deux dimensions (2D) sur l'écran, pour cela la première position conçue était l'état initial. La figure 4.1 montre la position du robot au repos.

x =
p1
y=
p 1
200, 200, 250, 250
x x x
= = =
p p p
2 3 4
250, 150, 150, 200
y y y
p p p
= = =
2 3 4

=250
x x x x
= = =
200, 200, 250,
p p p p
1 2 3 4
y y y y
p p p p
= = = =
300, 200, 200, 250
1 2 3 4
Figure 4.2 : Phase de fraisage
Figure 4.1 : Position 1, (l'état initial)(Dimension en centimètre).
Dans la deuxième position, le but (besoin) était la localisation des chaînons en deux dimensions (2D) sur l'écran, pour cela la deuxième position conçue était la phase de fraisage (faiseuse verticale),La figure 4.2 montre la position du robot sur la faiseuse verticale.
Dans la troisième position, le but (besoin) était la localisation des chaînons en deux dimensions (2D) sur l'écran, pour cela la troisième position conçue était la phase de fraisage (faiseuse universel), La figure 4.3 montre la position du robot sur la faiseuse universel.

x x x x
p p p p
= = = =
200, 200, 250, 300
1 2 3 4
|
y= p 1 |
300, 200, 200, 200 y y y = = = p p p 2 3 4 |
200, 200, 150, 100
x x x
= = =
p p p
2 3 4
y y y y
= = = =
270, 170, 170, 170
p p p p
1 2 3 4

x =
p 1
Figure 4.3 : Phase de fraisage (fraiseuse universelle) (Dimensions en centimètre).
Dans la quatrième position, le but (besoin) était la localisation des chaînons en deux dimensions (2D) sur l'écran, pour cela la quatrième position conçue était la phase de perçage La figure 4.4 montre la position du robot sur la perceuse.
Dans la cinquième position, le but (besoin) était la localisation des chaînons en deux dimensions (2D) sur l'écran, pour cela la cinquième position conçue était la phase d'alésage La figure 4.5 montre la position du robot sur l'aléseuse.
2 00 , 2 00 , 150, 1 00
x x x x
p p p p
= = =
1 2 3 4
y y y y
p p p p
= = = =
300, 200, 200, 230
1 2 3 4

=
Figure 4.5 : Phase d'alésage (Dimensions en centimètre).
Ayant exposé les différents logiciels et bibliothèques utilisés pour le développement de l'interface, je passe maintenant, à la description de cette dernière. Dans mon interface, je propose un espace graphique, c'est-à-dire que j'offre à l'utilisateur un espace bidimensionnel, où il peut projeter cinq états du robot mais aussi,faire animer ces derniers et obtenir les différentes possibilités des modèles géométriques cinématique et dynamique directes et inverses de ce robot .Les figures (4.6),(4.7),(4.8),(4.9)et(4.10),permettent de connaître les valeurs des coordonnées généralisées de chaque chaînon pour une position donnée,ainsi que la position de l'effecteur dans l'espace.
On précise que l'utilisateur dispose dans l'interface une palette, cette dernière comporte les différents types de curseurs, alors l'utilisateur peut déplacer, faire tourner, pivoter le robot dans tous les sens.

Figure 4.6 : Interface de l'utilisateur pour l'état initial

Figure 4.7 : Interface de l'utilisateur pour la fraiseuse verticale

Figure 4.8 : Interface de l'utilisateur pour la fraiseuse universelle

63
Figure 4.9 : Interface de l'utilisateur pour la perceuse
Figure 4.10 : Interface de l'utilisateur pour l'aléseuse
Afin de mieux apprécier les caractéristique géométrique cinématique et dynamique de robot type, j'ai déterminé ces derniers pour un seul temps de mouvement T nécessaire
Les énergies cinétiques potentielles et de dissipation sont données, les équations de Lagrange sont établies. Pour effectuer un cycle de travail. J'obtiendrait sur les graphe ci dessous des figures (4.11),(4.12),(4.13) et (4.14) l'évolution en fonction du temps des position, des vitesses. Des accélérations ainsi que des couples et forces pour un temps T égal à 5, secondes.
Dans ce mémoire j'ai présenté un interface en exposant les différentes palettes qu'elle comporte, et en expliquant les différentes possibilités qu'elle offre à l'utilisateur.
Le logiciel fortran consiste en un langage interprété qui s'exécute dans une fenêtre dite d'exécution. L'intérêt de fortran tient, d'une part, à sa simplicité d'utilisation, et à sa richesse fonctionnelle arithmétique matricielle et nombreuses fonctions, analyse numérique, graphique.
En ce qui me concerne, j'ai utilisé la version Fortran 6.1, pour deux raisons la première sa puissance en calcul matriciel,la deuxième raison ,est l'utilisation des boucles pour l'obtention des exécutables.
En considérant les systèmes d'équations différentielle de la géométrie cinématique et dynamique et après récupération des variables et appel aux fonctions et affectation de coordonnées et rotations on aboutit à l'affichage des résultats sous forme de bloques de matrices, on peut illustré ces résultats numérique en utilisant l'outil Microsoft Excel.
Dans le cas où les causes structurelles seraient considérées les paramètres pris en considération seront l'inertie du rotor, les inerties de l'arbre entrée réducteur, rapport de réduction et coefficients du frottement visqueux, en ce qui concerne les termes de Coriolis sont représenté sou forme matricielle de dimension (n x (n-1) n/2).
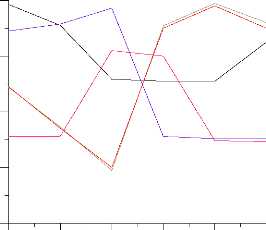
Les graphes:
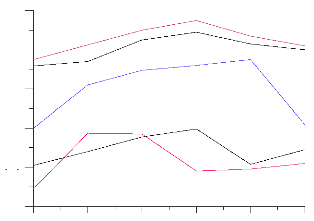
-0.20
q2
position (rad .m)
0.60
q5
q4
0.40
0.20
0.00
q3
q1
-0.40
0.00 1.00 2.00 3.00 4.00 5.00
temps (sec)
Figure 4.11: Positions
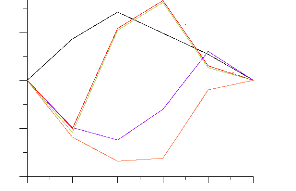
Vitesse(rad .m/s) 1.00
V4
V1
0.50
V5
V3
0.00
V2
-0.50
-1.00
Temps(sec)
0.00 1.00 2.00 3.00 4.00 5.00
Figure 4.12: Vitesses
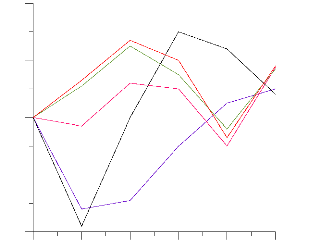
Accélération(rad .m/s2)
40.00
a5
a1
20.00
a4
a2
0.00
a3
-20.00
-40.00
0.00 1.00 2.00 3.00 4.00 5.00
Temps(sec)
Figure 4.13: Accélérations
Force (N) Couple (N.m)
c3
c2
c4
c1
c5
400.00
200.00
0.00
-200 .00
-400.00
Temps(sec)
0.00 1.00 2.00 3.00 4.00 5.00
Figure 4.14: Forces, couples
Un programme de simulation a été finalisé qui englobe les différentes étapes de l'étude, dont La partie géométrique illustrée par les différentes courbes de position de ce robot manipulateur (Figure 4.11). Un régime adéquat de fonctionnement du robot a été indiqué, dont la partie cinématique (Figure 4.12) et (Figure 4.13). Et à la fin les courbes dynamiques (Figure 4.14). Dans mon système, l'utilisateur peut choisir le type d'actionneur -moteur asynchrones- autre que les actionneur de type hydraulique, et ainsi faire rentrer les caractéristiques spécifiques, ceci va faire intervenir la dynamique des moteurs asynchrones dans la dynamique des différentes articulations. En peut voire une série de simulations appliquée au robot en passant par un interface de code source du microcontrôleur du servomoteur PIC, et une série de capteurs cartes de ENTRE SORTIE connectées par l'intermédiaire d'un automate et armoire de commandes,avec les actionneurs du robot situées dans le circuit hydraulique du robot.
Ce programme nous permet d'étudier n'importe quels robots industriels pour les différentes stations d'usinage, dont le but d'augmenter la productivité de n'importe quel atelier d'usinage flexible.
Si les vitesses augmentent, il est évident que les modèles calculés sont très loin de la réalité, parce que d'une part des forces inertielles, centrifuges et de couplage apparaissent et d'autre part les jeux dus aux frottements et élasticités de toutes origines ne sont plus négligés. Il est donc nécessaire de revoir la modélisation en tenant compte des ces phénomènes dynamiques. Le calcul effectué détermine les variables articulaires en fonction des forces (ou / et couples) généralisés. Pour le calcul j'ai utilisé la méthode de rung-kutta d'ordre 4 à pas variable pour la résolution des systèmes différentiels. Un modèle des déformations est nécessaire, quant à la validation et comparaison, mes résultats présente une co-ressemblance avec les résultats [21], [55] et [71], malgré les différences de performances entre nos robots.
Des paramètres comme la vitesse, la température ou le temps vont influer et certaines formes d'usure sont relativement irrégulières, d'autres au contraire provoque des sauts très brutaux, dont des rapports pouvant aller parfois de 1 à 100 000 ou plus, lorsque certaines valeurs critiques sont franchies.
Tout pays rêve d'évoluer à chaque instant par l'amélioration de sa production, ces produits,son service pour arriver à la plate- forme d'un atelier, ce dernier est un rêve dans notre pays cette majeur automation (atelier flexible de fabrication), nécessite une large présence des robots industriels.
On abordait la modélisation en appliquant la convention de Denavit-Hartenberg, le calcul du modèle géométrique inverse nous a permis la localisation de l'effecteur à n'importe quel point de l'espace de travail, les inconvénients sont évités ou contournés de la manière suivante : Le problème de multiples solutions du modèle inverse n'intervient pas. En effet, le robot possède une configuration initiale connue, et se rend à une autre solution à partir de celle-ci, il ne sert à rien de calculer des configurations du robot qui seraient impossibles à atteindre depuis sa position ; Une haute précision de solutions obtenues n'est pas nécessaire puisqu'il suffit de fournir à l'utilisateur une vision globale, le calcul des accroissements est à chaque fois effectué à partir d'une nouvelle configuration exacte du robot. Quant au problème des singularités, il existe plusieurs méthodes mathématiques pour les traiter et les éviter.
La géométrie de la mécanique rend impossible la détermination d'une solution car les contraintes imposées ne sont pas atteintes.La modélisation cinématique directe ou inverse ma permet de déterminer la vitesse de l'organe terminal. Par contre des butées empêchent le robot d'atteindre les points en dehors de volume du travail malgré l'existence de solutions mathématiques. Pour la mise en équation du modèle dynamique j'ai utilisé le formalisme de Lagrange, ce qui conduit au calcule de l'énergie de dissipation par frottement visqueux dans les joints .La modélisation dynamique m'a permis de mettre en évidence un énorme calcul. J'ai constaté que les erreurs sont dues aux défauts géométriques des organes mécaniques, (non linéarités dues aux frottements mécaniques par exemple). Et avec le développement de l'électronique, de l'informatique et des moyens de fabrication (machine à commande numérique, CFAO) la précision tend à devenir largement suffisante pour la majorité des applications industrielles, j'ai conçu un programme à partir de la géométrie, afin de mieux
apprécier les caractéristiques cinématique et dynamique de mon robot type, pour effectuer un cycle de travail, en exploitant les modèles géométriques cinématiques et dynamiques et en tenant compte des lois de mouvements utilisées en robotique dans le but d'évaluer les couples articulaires pour mon manipulateur qui n'est alors qu' une composante de la cellule robotisée . J'obtient sur les graphe de l'évolution en fonction du temps des position, des vitesses, des accélérations ainsi que des couples et forces. Le travail effectué me permet d'étudier n'importe quels robots industriels pour les différentes stations d'usinage dont le but d'augmenter la productivité de n'importe quel atelier d'usinage flexible.
J'ai constaté que dans tous les cas il est nécessaire de bien comprendre les mécanismes du frottement de manière à adapter au mieux les résultats .On peut augmenter l'espace de travail, ainsi que l'autorisation d'une charge utile plus importante, on peut donc parler d'une famille de robots (ALG.-M.O. -1). (ALG.-M .O. -2).
Pour une valorisation de mon travail, j'ai élaboré comme première application, une simulation, sous diverses configurations, permettant de visualiser le fonctionnement du robot dans son environnement de travail.
Un brevet d'invention a été déposé à l' I.N.A.P.I. et également une conception d'un modèle- type a été proposée, une banque des données sur les paramètres de la mécanique articulée et des articulateurs types sera proposée. Et en fin mon travail de recherche aura pour perspective une communication sur le modèle mathématique des systèmes mécanique poly articulé. Ce travail, est sujet à des améliorations. En ce qui concerne ses améliorations ultérieures pour un même travail, il est recommandé aux personnes devant pour suivre ce travail de : Faire une étude bien détaillée sur la modélisation dynamique en tenant compte les caractéristiques dynamiques et les erreurs statiques et dynamiques ainsi que la précision.
Je souhaite que les promotions à venir complèteront mon travail pour réaliser le manipulateur après calcul et acquisition des organes constitutifs.
Il est à noter que le rapprochement entre l'université et l'industrie est seul et unique moyen pour le développement industriel et avec le soutien de DIEU on peut résoudre les problèmes existants dans cet univers ou dans la vie.
Appendice A [138] :
Titre de l'invention :
Robot manipulateur des machines - outils (Algérie- M.O.-1)
Domaine technique auquel se rapporte l'invention :
La présente invention concerne les robots industriels utilisés dans les ateliers flexibles de fabrication mécanique, qui forment une nouvelle série de fabrication (Brevets d'invention: WO 9507799623622 AL 1996088, 9622856 AL 19960801, 9620818 AL 19960711. . .).
But de l'invention :
La nouvelle structure très simple du robot industriel type (ALG. -M.O. -l) est une nouveauté en Algérie et a été adaptée aux données d'une station d'usinage composée de quatre phases d'usinage différentes, et en vue de transformer cette unité de fabrication mécanique en une cellule flexible.
Etat de la technique antérieure :
L'opération après amélioration des caractéristiques techniques y compris le centre de fraisage alésage, pour la fabrication d'une grande variété des pièces constructives des véhicules industriels se caractérise par une trajectoire fermée d'une suite de déplacement et d'arrêt avec une livraison évacuation des pièces à l'aide de la main et cela après un choix optimal de toutes les caractéristiques.
Les différentes opérations qui comportent la descente, la fermeture et la montée de la main ainsi que le déchargement à l'aide des circuits et des modules judicieux réalisés. Les phases intermédiaires sont celles du déclenchement de l'usinage dans les différentes phases et de l'évacuation vers les transporteurs à palettes, après fabrication.
Les modules utilisés pour la conception, le fonctionnement et suivant le cahier des charges de ce robot industriel sont composés de cylindres, de vérins hydrauliques, des éléments auxiliaires qui constituent les composantes du circuit hydraulique, des
éléments d'assemblage, la main de chargement et déchargement et de moteurs électriques.
Les blocs ci-dessus sont liés entre eux et équipés par des capteurs qui permettent de produire les positionnements et l'ordre d'orientation des objets à traiter à l'entrée des installations automatiques lors de l'exécution des opérations et le déchargement de la dernière phase, ainsi que la synchronisation pendant les rotations d'angles (90°, 17°, 56° et 90°) pour effectuer les différentes phases. La chaîne de production existante sur la figure 1 pour quatre postes de travail, deux palettes (ao et bo) et deux chariots de transport de pièce (a et b), le chariot (a) livre les pièces, tandis que le chariot (b) les évacue.
Le robot est situé au centre des quatre postes, le centre est bien la position repère. Le cycle des mouvements est :
La rotation initiale du robot industriel vers le chariot (a) (angle = 1 35°),la descente de la main dépend des caractéristiques des machines-outils utilisées synchronisées par les capteurs.
La fermeture de la main sur la pièce répond aux poids des pièces usinées et qui ne doivent pas dépasser deux tonnes. Le régime de fonctionnement proposé, ainsi que la montée et la rotation vers (a0) (angle= 90°) et le déchargement dans la deuxième phase de fabrication d'un repère (angle = 45°).
Il en est de même pour la troisième phase (b0) après avoir exécuté la
quatrième phase (b).
Un déchargement correct de la pièce est effectué à l'aide d'un mouvement de rotation d'un angle (ã = 270°), le robot est positionné devant le chariot (a) pour exécuter une nouvelle gamme d'usinage.
Enoncé des figures :
De toutes façons , l'invention sera bien comprise à l'aide de la description qui suit, en références au dessins annexés , représentant , à titre d'exemple non limitatifs , plusieurs formes d'exécution de ce robot manipulateur :
-figure A-1 est une vue de la station de fraisage -alésage ;
-figure A-2 représente le schéma cinématique du robot industriel, avec la convention du cycle des mouvements.
-figure A-3 est une vue en élévation et partiellement en coupe d'un robot manipulateur, avec ses modules et la partie du circuit hydraulique.
-figure A-4 est une vue en coupe du module de levage à un cylindre à double effet. -figure A-5 a présenté un module de rotation à deux cylindres.
-figure A-6 est une vue du module de déplacement longitudinal vers le bas de l'organe terminal.
-figure A-7 a présenté le module de la main sous forme de mâchoire pour garantir une bonne adhérence.
Présentation de l'essence de l'invention et son mode de réalisation :
Le robot industriel (fig. 3) est solidaire d'une base (1), maintenue à sa partie inférieure par un corps (2), qui sert aussi de support à la colonne du module de déplacement vertical (fig. 4) et à son intérieur sont encoché les éléments du circuit hydraulique. Au dessus du cylindre (côté frontale), on a monté le module de rotation (fig. 5) et au dessus (cylindre) les modules de déplacement transversal (fig. 6) de la fermeture , d'ouverture et de la main.
Le bâti du robot est composé d'une base (1) et le corps (2), ce dernier est lié à la base par quatre supports (3) (fig. 3). Les boulons (4) servent pour la fixation au sol.
Dans la direction verticale, on a placé une colonne (5) fixée au-dessus du bras par soudage à la plate-forme (6), celle-ci est fixée par des boulons (7) avec
le module de déplacement transversal. Et ce bâti est limité par des couvercles - avant, latéraux et arrières.
Le module de rotation (fig. 5) est constitué de deux cylindres (1) et (2) installé dans le corps (3) à l'aide des éléments de fixation (4) et (5).
La transmission par crémaillère et la roue dentée (6) et (7) transforme le mouvement rectiligne des vérins plongeurs ( à double effet) en un mouvement de rotation de la colonne.
C'est un système réversible ayant les avantages d'une réalisation simple pouvant supporter des grandes charges.
La pièce (8) sert en même temps pour le guidage de la crémaillère et à la fixation du vérin avec le corps.
La partie saillante du couvercle (9) permet l'amortissement du mouvement du piston (10) en formant un lit de l'huile une fois engagée dans le creux aménagé dans le piston. Le module de levage fonctionne à l'aide d'un cylindre à double effet (fig. 4).
Dans le cylindre (6) ou se trouve le piston (7) qui est garni par deux joints, la tige (8) du piston est connectée avec la plate forme de dessus (9), la partie inférieure du carré, qui fixe la superficie extérieure du cylindre par un jeu, où sont encochés des billes (10).
Le déplacement rectiligne de l'ensemble (7, 8 et 9) s'effectue grâce à un
système de guidage protégé par un cache en caoutchouc (14) le long du cylindre (1), écrou (2) et une tige (3).
Le déplacement vers le haut s'effectue par une transmission de l'huile dans
la conduite (13) et en bas à l'aide de la fente (12) au dessus sur le méplat (4) sont placés des capteurs de positions, qui confirment le passage des chaînons mobiles dans les points des différentes positions à l'aide des aimants (5).
La transmission de l'huile dans la conduite inférieure (13) pousse le piston (7) vers le haut et par la suite fait monter le bras horizontal.
Pour un bon guidage lors de la montée ( ou de la descente) on utilise des billes.
Le mécanisme sert comme plate-forme pour le module de déplacement
transversal et repose ( en bas) sur le module de rotation.
Le module de déplacement longitudinal vers le bas de l'organe terminal (fig. 6) sert à rapprocher la main de la zone du travail, c'est un vérin à double effet, constitué d'un cylindre (1) à l'intérieur duquel se déplace le piston creux (2) muni d'une garniture d'étanchéité aux deux extrémités (3).
Les tiges creuses (4) et (5) assurent le guidage parfait du piston. Aux
extrémités du cylindre (1) sont installées des douilles, à gauche douille (6) avec les joints d'étanchéité qui sont fixés par des vis, à droite la douille (7) avec un filetage contre-écrou (9), et la douille (8) qui est liée par un filetage à la tige (4). A droite, le piston est connecté à la bride (10) avec la douille (11) auquel
est fixée l'installation de l'organe terminal.
Le cylindre est muni des conduites (12) et (13) pour la circulation de l'huile assurant le déplacement en va et vient des pistons.
Le module de la main (fig. 7) est composé par une structure dont le bout est constitué de leviers articulés (1, 2, 3 et 4) et de doigts, qui sont au nombre
de deux sous forme de mâchoire, inclinés, changeables pour garantir une bonne adhérence. Le robot industriel peut adapter plusieurs variétés de mains en cas de nécessité.
La main possède un système vis écrou (5) pour le réglage de la hauteur en cas de besoin.
Le bout supérieur du cylindre (10) hydraulique d'attrape est lié par goujon
au bout inférieur du piston (12) qui sert à déplacer la main vers le bas pour une opération de chargement ou vers le haut pour véhiculer la pièce.
Le piston active dans un cylindre hydraulique (13) lié au module de déplacement transversal par deux équerres fixées par quatre boulons pour chacun, ce dispositif permet la fixation des diverses mains sur le robot.
Les deux cylindres sont munis des conduites (6) pour celui de dessus afin d'assurer la descente et la montée du piston (7). Et celui du bas pour attraper la pièce (8) et la décharger.
Le développement de l'effort nécessaire est pris en considération en cas de contact.
La main peut avoir un mouvement de rotation actionné par le circuit hydraulique ainsi que le positionnement de l'organe terminal sur la pièce à soulever est réalisé par un contact de fin de course.
Revendications :
1. Le principe de montage, de déchargement sur le dispositif d'usinage des différentes stations de fabrication mécanique s'effectue par un procédé d'une cellule flexible, en améliorant quelques caractéristiques techniques, en augmentant la cadence, la précision et la simplicité des phases d'usinage selon les données de l'unité de production.
2. Robot selon la revendication 1, ces structures des installations proposées pour Le robot industriel manipulateur est construit suivant le principe d'approvisionnement des éléments de base par blocs pour les différents schémas technologiques proposés et déchargement.
3. Robot selon la revendication 1, la construction et le principe d'action des modules et des installations complémentaires doivent permettre d'accomplir la manipulation et l'évacuation de produits usinés, les opérations de base sont réalisées grâce aux passages inventés et leur simplicité d'utilisation.
4. Robot selon la revendication 1, la production en série, ou en grande série augmente par ce procédé de robotisation. Le remplacement du processus manuel par un autre plus précis et robuste permet l'optimisation des indices technico-économiques.
5. Robot selon la revendication 1 ,le choix des nuances répondant aux constructions des éléments, l'utilisation des pièces universelles dans la construction du manipulateur, la simplicité des commandes directes ou indirectes, l'amélioration de la fiabilité de l'ensemble permettent d'avoir un produit de qualité et moins coûteux.
Abrége descriptif :
Titre de l'invention :
Robot manipulateur des machines - outils (Algérie -M.O.-1).
Le robot industriel (ALG. -M.O. -l) proposé pour les différentes stations d'usinage est adapté aux différentes données de fabrication mécanique. Il est composé de modules utilisés pour la conception et cela suivant le cahier des charges proposé à l'étude.
Le robot est solidaire à une base maintenue par un corps, qui sert aussi de support à la colonne du module de déplacement vertical.
A l'intérieur de ce corps se trouvent les éléments du circuit hydraulique, juste à la partie inférieure du cylindre est fixé le module de rotation, au dessus à l'aide de supports est maintenu le module de déplacement longitudinal, à l'extrémité de ce dernier est monté
le module de la main avec ses deux cylindres hydrauliques qui servent pour la montée et la descente, ainsi que le serrage et le déchargement de la pièce dans les différentes phases d'usinage.

R1 450
4 rails
56o




R y
+
X2
+
T2
T1
+
D
T3
T4
Figure A-2 : Schéma cinématique du robot industriel, avec la convention du cycle des mouvements.

5
2
3
4
1
7
Figure A-3 : Vue en élévation et partiellement en coupe d'un robot manipulateur, avec ses modules et la partie du circuit hydraulique.
8 9 14
|
5 4 3 2 1 |
12 10 3
6 7 1
Figure A-4 : Vue en coupe du module de levage à un cylindre à double effet.

7
3
2
5
1 4
10
6
9
Figure A-5 : Module de rotation à deux cylindres.

9
2
1
4
8
12
7
3
5
6
13

6
10
10
13
9
2
1
3
4
5
5
Piéce
13
12
7
8
Figure A-6 : Module de déplacement longitudinal vers le bas de l'organe terminal.

060205
X
24 AVR 2006
14H00
ALGERIENNE
ALLALI ABDERRAZAK Beni-Mered Blida
BRAHIMI ABDELHALIM El-Affroun Blida
BENMISRA ABDELKADER Zabana Blida
HALAIMIA MUS TAPHA KAMEL Ouled Yaich Blida
Yasminallali@Yahoo.fr
ROBOT MANIPULATEUR DES MACHINES
OUTILS
(ALGERIE.-M.O.-1)
BLIDA 24 AVR 2006
ALLALI .A BRAHIMI .A BENMISRA .A HALAIMIA .MK
Program CALCUL DES ROBOTS INDUSTRIELES MODELISATION GEOMETRIQUE CINEMATIQUE ET DYNAMIQUE ELABORE PAR A. ALLALI , M.M.HATTALI, A.BENMISRA, M.MEGHERBI, N.BEDHIAF, R.MAZARI, K.AIMEUR, N.MOHAMMEDI, K.TOUMADJ, A.BRAHIMI, M.K.HALAIMIA.
En collaboration : Départements d\u8217Informatique, Mathématique, Electronique, Aéronautique et Génie mécanique de l\u8217Université de Saad Dahleb de Blida.
· Bibliothèque de l\u8217Ecole Nationale Polytechnique d\u8217El-Harrache, Alger.
· Département de Génie Mécanique, Laboratoire de Vibroacoustique et Bibliothèque centrale de l\u8217Université de M\u8217hamed Bouguarra de Boumerdès.
· Centre de Développement des Technologies Avancé, C.D.T.A., de Baba Hssene, Alger.
· Le Centre de Recherche sur l\u8217Informatique Scientifique et Technique, C.R.I.S.T., Ben Aknoun, Alger.
Université de Saad Dahleb de Blida
19 Mai 2006 22
:54
Nbre. d\u8217articulations, coord. Point initial, coord. Point final, temps T, \u916ÄT, paramètres de D.H. ; Positions, Vitesses, Accélérations, Forces et Couples, Variable articulaire.
Programme d'un espace de travail.
c PROGRAM: ESPACE DE TRAVAIl.
c PURPOSE: Entry point for the console application.
c program ESPACEDETRAVAIL
c Déclaration des variables
c Variables
integer n,i,j,k
real a,b,c,e,f,d,r,u,q,p,z2,z3,z4,z5,h1 ,h2,h3,h4
real ydmax, ydmin,ymin, ymax,ydmaxi,ydmini, ymini,ymaxi, pi real y1,y2,y6, y3,y4,px,py,pz ,hmin,hmax
real d3,d4
dimension T(3),ymin( 1 ),ymax( 1) ,hmin( 1) ,hmax( 1)
C
c introduction de la dimension des matrices de passages
pi=3. 1415926535897932384626433832795
c déclaration de PI pour la transformation des degrés en radiants
n=5
d3=0.6 d4=0.6 z2=600 z3=635 z4=700 z5=500
c Entrer des paramétres de Dénavit-Hertenberg
c write(*,*)'chargement des limites artiulaires '
! do k=1,n
c incrémentation chaque matrice de passage
write(*,*)'donner les limites angulaires des butées mécaniques
+ de 1 articulation k'
write(*,*)'theta min'
read(*,*) theta min
ymini=(theta min*pi)/1 80
write(*,*)'ymini'
write(*, *)'theta max'
read(*, *)theta max
ymaxi=(theta max*pi)/1 80 write(*,*)'ymaxi'
write(*, *)'theta min','=', ymini, 'theta max','=',ymaxi
c ymin(k)=ymini
ymax(k)=ymaxi
write(*,*)'(ymax(i)* 1 80/pi,i=1 ,5)'
write(*,*)'(ymin(i)* 1 80/pi,i1 ,5)'
do k=1,n
write(*,*)'donner les limites de la distance des butées mécaniques + de K articulation k'
write(*,*)'zmin'
read(*,*) zmin
write(*,*)'zmax'
read(*,*) zmax
write(*, *)'zmin',k,'=', zmin ,'zmax',k,'=',zmax
write(*,*)'hmin' read(*,*) hmin
write(*,*)'hmax' read(*,*) hmax
write(*, *)'hmin',k,'=', hmin , 'hmax',k,'=',hmax
c Entrer des paramétre de Dénavit-Hertenberg
c write(*,*)'chargement des limites artiulaires '
c incrimentation pour chaque matrice de passage
write(*,*)'donner les limites angulaires des butés mécanique
+ de 1 articuiation k'
write(*, *)'theta min'
read(*,*) ydmin
ymini=(ydmin*pi)/1 80
write(*, *)'theta max'
read(*,*) ydmax ymaxi=(ydmax*pi)/1 80
write(* ,*)'theta min',k,'=', ydmin, 'theta max',k,'=',ydmax
c ymin(k)=ymini
ymax(k)=ymaxi end do
write(*, *)'(ymax(i)* 1 80/pi,i= 1,5)'
write(*,*)'(ymin(i)* 1 80/pi,i1 ,5)'
c calcul des matrice de transformation
a=ymin(1)
b=ymax(1)
c=ymin(2)
e=ymax(2)
f=ymin(3)
p=ymax(3)
write(*,*)'calcul du vecteur P(Px,Py,Pz)Position des
+ coordonnées articulaires'
do 11 yl=a,b,0.05
do l1 y2=c,e,1
do 11 y3=f,p,0.1
c calcul des élément de T(m,m) et son remplissage
write(*,*)' calcul des élément de T(m,m) et son remplissage ' T(1 )=(z3-z4)*cos(y1)
T(2)=(z3-z4)*sin(y1)
T(3)= (h1)+(h2)+(h3)+(h4)+z2-z5
px=T(1)
py=T(2)
pz=T(3)
!write(*, *) (T(i),i=1,3) !write(*,*) (T(i),i=1,3),';' write(*,*) T(1),T(2),T(3)
10 format (3f)
11 write(*,*)
c Body of Espace de travail
end .
Appendice C : Programme principale
c PROGRAM implicit none
real,dimension( 100):: qi,qf,kv,ka,q,a,c,v,st,tf
real alpha1 ,alpha2,alpha3 ,alpha4,alpha5,teta1 ,teta2,teta3, +teta4,teta1 5
integer i,j ,ii,jj ,t,dt,tfm,w
WRITE(*, *) write(*, *)
write(*,*)'nombre articulation w'
read(*,*)w
write(*,*)'les parametres de Denavit Hartenberg'
write(*, *)'alpha1 ,alpha2,alpha3 ,alpha4,alpha5'
read(*, *)alpha1 ,alpha2,alpha3 ,alpha4,alpha5
write(*, *)'teta1 ,teta2,teta3 ,teta4,teta1 5'
read(*, *)teta1 ,teta2,teta3 ,teta4,teta1 5
write(*,*)'LES PARAMETRES DU CHAINON'
do 122 j=1,5
write(*, *)'coordone de point initial=qi(j)'
read(*,*) qi(j)
write(*,*)'coordone de point final=qf'
read(*,*) qf(j) write(*,*)'kv(j)' read(*,*)kv(j) write(*,*)'ka(j)' read(*,*)ka(j) read(*,*) qi(j),qf(j) ,kv(j) ,ka(j)
122 continue
st (1)=a cos (-1.) /180
st (2) =1
st (3)=1
st (4) =1
st (5) =1
dt=30
tfm=5
t=0
40 continue
call synch(qi,qf,kv,ka,tfm,st,tf)
print*,'tfm=',tfm
do 41 i=1,5
call para (qi(i),qf(i),kv(i),ka(i) ,q(i),v(i) ,a(i) ,st(i),tfm,t)
41 continue
print*, '(q(i) ,i=1,5) ,t,q'
print*,' (v(i) ,i=1,5), v'
write(*,*)'t q(2) q(3) q(4) q(5)'
write(*,*)t,q(2),q(3),q(4),q(5)
write(*,*)'t v(2) v(3) v(4) v(5)'
write(*, *)t,v(2),v(3),v(4),v(5)
write(*,*)'t a(2) a(3) a(4) a(5)'
write(*,*)t,a(1 ),a(2),a(3) ,a(4),a(5)
call dynami (q,v, a, c)
write(*,*)'t c(2) c(3) c(4) c(5)'
write(*,*)t,c(1 ),c(8),c(1 5),c(24)
write(*,*)'le vecteur <c(ii)> '
write(*,*)'calcul des forces et les momoment articulaires' write(*,*)t,(c(ii),ii=1 ,5)
write(*,*)t,(c(jj),jj=6, 11)
write(*,*)t,(c(jj),jj=1 2,17)
write(*,*)t,(c(jj),jj=1 8,24)
t=t+1
if(t.le.6)goto 40
end .
Appendice D :
Programme Synchronisation
C**************************************************************** C Synchronisation
C***************************************************************** subroutine synch(qi,qf,kv,ka,tfm,st,tf)
real qi(5),qf(5),kv(5),ka(5),tf(5),tfm,st(5),lamda(5),nu(5),s(5),
+sl, s2,p(5)
integer i,J
do 4 j=l,5
sl=abs(qf(j) - qi (j) )
s2=kv(j) **2/ka (j)
if ( sl.gt.s2) go to 4
print*,'La condition du palier vitesse pour 1 articulation'
4 continue
tfm =0
print*,'qi=' , (qi(i),i=l,5)
print*,'qf=',(qf(i),i=l,5)
print*,'kv= ',(kv(i),i=1,5)
print*,'ka=',(ka(i),i=1 ,5)
print*,'st=',(st(i),i=1 ,5)
pause
do 15 j=l,5
tf(j)=kv(j) /ka(j) +abs ( (qf(j)-qi(j) ) *st(j) ) /kv(j)
print*,'tf(j)',tf(j)
pause
if (tf(j).ge.tfm) go to 15
tfm=tf(j)
15 continue
print*,'tfm-synhcronisation ,tfm '
pause
do 2 j=1,5
s1 =tfm-kv(j)/ka(j)
lamda(j)=abs(qf(j) -qi (j)) *st(j) / (kv(j) *sl)
kv(j ) =lamda(j) *kv(j)
ka(j)=lamda(j)*ka(j)
print*,kv(j),ka(j),kv,ka, tps mini pause 'kv ,ka'
2 continUe
return end.
Appendice E :
Programme E.1 : Programme de calcul des coordonnées; vitesses et accélérations articulaires
C ******************************************************************
c calcul des coordonnees; vitesses et accélérations
C articulaires
c******************************************************************
subroutine para (qi,qf,kv,ka,q,v,a,st,tfm,t)
real qi, qf, kv, ka, q, v,a, t, t0, si, tfm
c******************** Loi de Bang-Bang avec palier de vitesse ************
t0=kv/ ka
if (t.le.t0) then
q=qi+ ( (ka*t*t/2)/st) *abs (qf-qi) / (qf-qi)
v=ka*t*abs (qf-qi) / (qf-qi)
a=ka*abs (qf-qi) / (qf-qi)
return
else
if (t.le.tfrn-t0) then
q=qi+( (t-t0/2)*Kv/st) *abs(qf-qi) / (qf-qi)
v=kv*abs (qf-qi) / (qf-qi)
a=0 return
else
if (t.gt.t0) then
q=qf- ((tfm-t) **2/2*ka) /st*abs (qf-qi) / (qf-qi)
v=(tfm-t)*ka*abs (qf-qi) / (qf-qi)
a=-ka
endif
endif endif return end
Programme E.2 : Programme de calcul des forces et les moment articulaires
C ****************************************************************** c calcul des forces et les moment articulaires
c ******************************************************************* subroutine dynami (q,v, a,c)
real v(4),a(4),q(4),c(24),m(4),x(3),z1 ,z2,z3 ,z4,z5,z6,z7,z8,z9,zl0,
+z1 1,j(4)
j(1)=.0319
j(2)=0.0508
j(3)=129. 14
j (4)=6.283
m(1)=25.549
m(2)=40.70
m(3)=241 .779
m(4)=39.049 X(2)=0.02 x(3)=0.02 l2=0.6
z1=a(4)+v(1 )**2*q(4)
z2=a( 1 )*q(4)+2*v( 1 )*v(4)
z3=m(4)*9.81+m(4)* (a(2)+a (3))
z4=a( 1)*q(3)+2*v(1)*v(3)
z5=m(4)+m(3) z6=x(2)+x(3)+1 2
z7=a(3)-v(1 )**2*q(3)
z8=m(2)+m(3)+m(4)
z9=l2/2
z10=q (2) +12/2
z 11 =m( 1 )+m(2)+m( 3)+m(4)
C(1)=m(4)*z1
C(2)=m(4)*z2
C(3)=z3
C(4)=q(3)*z3
C(5)=-q(4)*z3
C(6)=q(4)*m(4)*z2-q(3)*m(4)*zl+J(1 )*a(1)
C(7)=-m(3)*z4+z4*zl C(8)=m(4)*z2+m(3)*z7
C(9)=z5 *9 .81 +z5 *a(2)+m(4)*a(3)
C(1 0)=z5*9.8 1+z5*a(2)+m(4)*a(3)-z6*(m(4)*z2+m(3)*z7)
C( 11 )=q(4)*z2+z6+(-m(3)*z4+m(4)*z 1) C(12)=m(4)*q(4)*z2-3*q(3)*m(4)*z1+m(3)*q(3)*z4+(j(3)+j (4)) *a(1)
C(13)=-m(3) *z4+m(4) *z1 C( 1 4)=m(4)*z2+m(3)*z7 C(1 5)=rn8*((9. 81 )+a(2))
C( 1 6)=q(3)*z5 *(9. 81 )+z5 *a(2)+m(4)*a(3)-(z6+z9+zl0)*(m(4)*z2+m(3) +*z7)
C( 1 7)=q(4)*z3+(-z9-zl0+z6)*(m(4)*z1-m(3)*z4)
C(1 8)=-3 *m(4)*q(3)*zl+m(4)*q(4)*z2+m(3)*q(3)*z4
C(1 9)=-m(3)*z4+m(4)*z1 C(20)=m(4)*z2+m(3)*z7 C(21)=z1 1*9.81+z8*a(2)
C(22)=q(3)*(z5 *(9. 81 +a(2))+m(4)*a(3))-(z6+z9+zlO)*(m(4)*z2+m(3) +*z7) C(23)=q(4)*z3+(-m(3)*z4+m(4)*z1 )*(-z9+z6+z1 0) C(24)=m(4)*q(4)*z2-m(3)*q(3)*z4+m(4)*q(3)*z1
return
end
Appendice F :
Programme de calcul des forces actives
c* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * c CALCUL DES FORCES ACTIVES
c* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * subroutine dynami (q,v,a,c 1 ,c2,c3, c4)
real v(5),a(5),q(5),c 1 ,c2,c3 ,c4,m(5),x(5),b,
+s1, s2, s3, s4, s5, s6, s7, s8, s9, s10, s11, s12, s13, s14, s15,
+ s16, s17, s18, s19 , s20, s21, s22, s23, s24, s25, s26, s27, s28, +s29, s30, r (5)
m(1)=25.549
m (2 ) =40.70
m (3 ) =241.779
m(4)=39.049
x(1)=0.6 x (2) =0.6 x(3)=0
x(4)=0.4 r(1)=0.05 r(2)=0.05 r(3)=0
r(4)=0.06 b=0.7
a1 =0.2
s10=m(3) +m(4)
s1 1=m(3)*(b*cos(2*q(1))+2*q(3))
s1 2=m(4)*q(3)*(sin(q(1 )))**2
s1 3=m(2)+m(3)
s14=m(2) +m(3) +m(4)
s15=m(4)
s1 6=1+(sin(q(1)))**2
s17=m(1)*x(1)**2
s18=m(2) * (3*r(2) **2+4*x (2) **2) /12
s1 9=m(3)*((a1 **2+1 3 *b**2)/1 2+b*q(3)*cos(2*q(1 ))+q(3)*2) s20=(3 *r(4)**2+4*r(4)**2)/1 2
s21=x(4) *q(4) +2*q(3) **2
s22=2* (q (4) **2+q (3) **2)
s23=b*cos(2*q(1 ))+2*q(3)
s24=2*b*q(3)*v(1 )*sin(2*q(1))
s25=x(4)*v( 4) +4*q ( 3) *v ( 3)
s26 =q(4) *v (4) +q (3)*v(3)
s27=q(4) **2+q(3)**2
s28=v(1 )*sin(q(1 ))*cos(q(1)) s29=m(3)*b*q(3)*sin(2*q(1)) s30=(q(4)**2+q(3)**2)*cos(q(1))*sin(q(1))
c 1=((s 17/1 2)+s 1 8+s 1 9+s1 5*(s20s2 1+s22+s1 6))*a(1 )+(m(3)*(s23 *v(3).. +s24)+s15*(4*s26*s16..s25+4*s27*s28))*v(1)+(s29..2*s15*s30)*v(1).. +q(2) *1000
c2=s13*q(2) +9.81*s14..1000 c3=a(3)*s10.. (s1 1+4*s12) * (v(1) **2)
c4=s1 5*(a(4)+(x(4)..4*s1 6*q(4))*v(1)**2)
return
end
Appendice G : Programme de simulation
/*
* JFrame.java *
* Created on 19 mai 2006, 22:54
*/
/* *
*
* @author Redha
*/
import java.awt. *;
public class JFrame extends javax.swing.JFrame {
/** Creates new form JFrame */ public JFrame() {
initComponents();
ann= new Annimation(this); setBounds(1 00,100,750,480); j Slider1 .setEnabled(false);
setVisible(true);
}
/** This method is called from within the constructor to * initialize the form.
* WARNING: Do NOT modify this code. The content of this method is
* always regenerated by the Form Editor.
*/
private void initComponents() {
buttonGroup 1 = new javax. swing.ButtonGroup(); jPanel1 = new javax.swing.JPanel();
jSlider1 = new javax.swing.JSlider();
jComboBox1 = new javax. swing.JComboBox(); jRadioButton1 = new javax. swing.JRadioButton(); jRadioButton2 = new javax. swing.JRadioButton(); j Label 1 = new javax. swing.JLabel();
jPanel2 = new javax.swing.JPanel();
canvas1 = new java.awt.Canvas();
jMenuBar2 = new javax. swing.JMenuBar(); jMenu2 = new javax.swing.JMenu();
jMenuItem2 = new javax.swing.JMenuItem(); j Table 1 = new javax. swing.JTable();
getContentPane(). setLayout(new javax.swing.BoxLayout(getContentPane(), javax.swing.BoxLayout.X_AXIS));
addWindowListener(new java.awt.event.WindowAdapter() {
public void windowClosing(java.awt.event.WindowEvent evt) { exitForm(evt);
}
});
jPanel1 . setLayout(null);
j Panel 1 .setBorder(new javax. swing.border.TitledBorder(""));
j Slider1 .setMinimum(1);
j Slider1 .setValue(20);
j Slider1 .addChangeListener(new javax.swing.event.ChangeListener() {
public void stateChanged(javax.swing.event.ChangeEvent evt)
{
j Slider1 StateChanged(evt);
}
});
jPanel1 .add(j Slider1);
j Slider1 .setBounds(1 00, 200, 140, 50);
jComboBox1 .setModel(new javax. swing.DefaultComboBoxModel(new String[] { "Position 1", "Position 2", "Position 3", "Position 4",
"Position 5" }));
jComboBox1 .addActionListener(new
java.awt.event.ActionListener() {
public void actionPerformed(java.awt.event.ActionEvent evt)
{
jComboBox1 ActionPerformed(evt);
}
});
jPanel1 .add(jComboBox1);
jComboBox1 . setBounds( 100, 100, 130, 25);
jRadioButton1 .setSelected(true);
jRadioButton1 . setText("Choisir La Position");
buttonGroup 1 .add(jRadioButton1);
jRadioButton1 .addActionListener(new
java.awt.event.ActionListener() {
public void actionPerformed(java.awt.event.ActionEvent evt)
{
jRadioButton1 ActionPerformed(evt);
}
});
jPanel1 .add(jRadioButton1); jRadioButton1 .setBounds(1 0, 50, 131, 24);
jRadioButton2. setText("Annimer Le Bras");
buttonGroup 1 .add(jRadioButton2); jRadioButton2.addActionListener(new
java.awt.event.ActionListener() {
public void actionPerformed(java.awt.event.ActionEvent evt)
{
jRadioButton2ActionPerformed(evt);
}
});
j Table 1 .setModel(new javax. swing.table.DefaultTableModel( new Object [][] {
{null, "X", "Y"},
{"P1", null, null},
{"P2", null, null},
{"P3", null, null},
{"P4", null, null} },
new String [] {
"Title 1", "Title 2", "Title 3"
}
));
jPanel1 .add(jTable1);
jTable1 .setBounds(80, 270, 200, 80);
jPanel1 .add(jRadioButton2);
jRadioButton2.setBounds(1 0, 150, 130, 24);
jLabel 1. setText("La Vit\u00e8se "); jPanel1 .add(jLabel1);
jLabel1.setBounds(40, 210, 60, 20);
getContentPane().add(j Panel 1);
jPanel2.setLayout(new java.awt.GridLayout());
jPanel2. setBackground(new java.awt.Color(255, 255, 255));
jPanel2.setDebugGraphicsOptions(javax. swing.DebugGraphics.NONE_OPTION); jPanel2.add(canvas 1);
getContentPane().add(jPanel2);
jMenu2. setText("Fichier");
jMenuItem2. setText("Quiter");
jMenuItem2.addActionListener(new
java.awt.event.ActionListener() {
public void actionPerformed(java.awt.event.ActionEvent evt)
{
jMenuItem2ActionPerformed(evt);
}
});
jMenu2.add(jMenuItem2); jMenuBar2.add(jMenu2); setJMenuBar(jMenuBar2); pack();
private void jRadioButton2ActionPerformed(java.awt.event.ActionEvent evt) {
// Add your handling code here: ann= new Annimation(this); if(jRadioButton2.isSelected()) {
ann. stop();
j Slider1 .setEnabled(true); jComboBox1 .setEnabled(false); ann.start();
}
}
private void
jRadioButton1 ActionPerformed(java.awt.event.ActionEvent evt) {
// Add your handling code here: if(jRadioButton1 .isSelected()) { ann. stop();
j Slider1 .setEnabled(false); jComboBox1 .setEnabled(true);
}
}
private void jMenuItem2ActionPerformed(java.awt.event.ActionEvent evt) {
// Add your handling code here:
ann.stop();
System.exit(0);
}
private void jComboBox1 ActionPerformed(java.awt.event.ActionEvent evt) {
// Add your handling code here:
ann= new Annimation(this);
switch(jComboBox1 .getSelectedIndex()) {
case(0):Exemple 1();
position="Position 1 "; break;
case(1 ):Exemple3();
position="Position 2"; break;
case(2):Exemple4();
position="Position 3"; break;
case(3):Exemple2();
position="Position 4"; break;
case(4):Exemple5();
position="Position 5"; break;
}
ann.start();
}
void j Slider1 StateChanged(javax.swing.event.ChangeEvent evt) { // Add your handling code here:
}
/** Exit the Application */
private void exitForm(java.awt.event.WindowEvent evt) { ann. stop();
System.exit(0);
}
public Graphics Mypaint(Graphics g) {
for(int jcas=1; jcas<=NbrCas; j cas++) {
XA[jcas] [Nbr+1 ]=(cas*30)+XA[jcas] [Nbr];
YA[j cas] [Nbr+1 ]=30+YA[jcas] [Nbr];
int x1=150, y1=380, x2=250, y2=350;
int x3=(x1+x2)/2-2;
int y3=y1-y2;
int Xh=0,Yh=0,px=0,py=0; // Longueur du bras vertical
g.
setColor(Color.black);
g.fillRect(x1 ,y1 ,100,10);// Base horizontale imposée g.fillRect(x3,y2,5,y3); // Bras vertical imposé
int j1 j2;
g. setColor(Color.red);
Font f = new Font("Comic Sans MS",14,20);
g. setFont(f);
g.drawString(" Simulation d'un robot manipulateur",40,50); g.drawString(" ( ALG.MO- 1 )", 150,80);
f = new Font("Comic Sans MS",14,24);
g. setFont(f);
g.drawString(" "+position,Xpos,Ypos);
f = new Font("Comic Sans MS",25,16);
g. setFont(f);
// Trace Bras
for(j1=2; j1<=Nbr+1; j1++){
g.setColor(Color.black); if(j 1<=Nbr) {
if(j 1<4){ px=10;py=0;}
if(j1>=4){ py =10;px=0;}
if((pos == 1||pos==3) && j1==Nbr){ py=-10;px =10;} Xh=XA[jcas] [j 1] + ((XA[jcas] [j 1-1]- XA[jcas] [j 1 ])/2)+px; Yh=YA[jcas] [j 1] + ((YA[jcas] [j 1-1]- YA[jcas] [j 1])/2)-py;
g.drawString("h"+String.valueOf(j 1-1 ),Xh,Yh);
}
g.drawLine(XA[jcas][j1-1], YA[jcas][j1-1], XA[jcas][j1],
YA[jcas][j1]);
System.out.println("J= "+j1+" XA= "+XA[jcas][j1]+" YA= "+YA[jcas][j 1]);
for(j2=1; j2<=Nbr; j2++){
if(Type[j2]==1) /* Articulation Rotoide */ {
g. setColor(Color.blue);
g.fillOval(XA[jcas] [j2]-R/2, YA[jcas] [j2]-R/2, R, R);
g. setColor(Color.red);
Font Dialog=new Font("Dialog", Font.BOLD, 13);
g. setFont(Dialog);
g.drawString("R", XA[jcas] [j2] -R/4, YA[jcas] [j2]+R/4); }
else if(Type[j2]==2)/* Articulation Prismatique */ {
g. setColor(Color.red);
g.fillRect(XA[jcas] [j2]-R/2, YA[jcas] [j2]-R/2, R, R);
g. setColor(Color.blue);
Font Dialog=new Font("Dialog", Font.BOLD, 13);
g. setFont(Dialog);
g.drawString("P", XA[jcas] [j2] -R/4, YA[jcas] [j2]+R/4); }
}
}
j Table 1. setValueAt(new Integer(XA[ 1] [2]), 1,1); jTable 1. setValueAt(new Integer(XA[ 1] [3]), 2,1); j Table 1. setValueAt(new Integer(XA[ 1] [4]), 3,1); jTable 1. setValueAt(new Integer(XA[ 1] [5]), 4,1); j Table 1. setValueAt(new Integer(YA[ 1] [2]), 1,2); jTable 1. setValueAt(new Integer(YA[ 1] [3]), 2,2); j Table 1. setValueAt(new Integer(YA[ 1] [4]), 3,2); jTable 1. setValueAt(new Integer(YA[ 1] [5]), 4,2); return g;
//========================== Exemple n°1==================
public static void Exemple 1() { // Cas de 1 bras de 5 articulations
NbrCas=1; // Nombre de cas
Nbr=5; // Nombre d'articulation
cas =1;
pos = 1;
//Sinq articulations de type RPRP
Type[1]=1; // Articulation Rotoide
Type[2]=2; // Articulation Prismatique
Type[3]=2; // Articulation Prismatique
Type[4]=2; // Articulation Prismatique
Type[5]=2; //Articulation Prismatique
// Premier cas (premier bras):
XA[1][1 ]=200; // X du premier cas, première
articulation
YA[ 1] [1 ]=350; // Y du premier cas, Première
articulation
XA[1][2]=200; //X du premier cas, 2end
articulation
YA[1][2]=250; //Y du premier cas, 2end articulation
XA[1] [3]=200; //X du premier cas, 3ème
articulation
YA[1][3]=150; //Y du premier cas, 3ème articulation
XA[1][4]=250; //X du premier cas, 4ème
articulation
YA[1][4]=150; //Y du premier cas, 4ème articulation
XA[1][5]=250; //X du premier cas, 5ème articulation YA[1][5]=200; //Y du premier cas, 5ème articulation Xpos=30+XA[ 1][5];
Ypos=30+YA[ 1][5];
public static void Exemple5(){
// Cas de 1 bras de 5 articulations NbrCas=1; // Nombre de
cas
Nbr=5;
cas=-1; // Nombre d'articulation
pos =5;
//Sinq articulations de type RPRP
Type[1]=1; // Articulation Rotoide
Type[2]=2; // Articulation Prismatique
Type[3]=2; // Articulation Prismatique
Type[4]=2; // Articulation Prismatique
Type[5]=2; //Articulation Prismatique
// Premier cas (premier bras):
XA[1][1 ]=200; // X du premier cas, première
articulation
YA[ 1] [1 ]=350; // Y du premier cas, Première
articulation
XA[1][2]=200; //X du premier cas, 2end
articulation
YA[1][2]=300; //Y du premier cas, 2end articulation
XA[1] [3]=200; //X du premier cas, 3ème
articulation
YA[1][3]=200; //Y du premier cas, 3ème articulation
XA[ 1] [4]=1 50; //X du premier cas, 4ème
articulation
YA[1][4]=200; //Y du premier cas, 4ème articulation
XA[1][5]=60; //X du premier cas, 5ème articulation YA[1][5]=280; //Y du premier cas, 5ème articulation Xpos=-50+XA[ 1][5];
Ypos=50+YA[ 1][5]; // Second cas (2 bras):
XA[2][1]=200; // X du 2end cas, première articulation
YA[2][1]=300; // Y du 2end cas, Première articulation
XA[2][2]=210; //X du 2end cas, 2end
articulation
YA[2][2]=300; //Y du 2end cas, 2end articulation
XA[2][3]=250; //X du 2end cas, 3ème
articulation
YA[2][3]=200; //Y du 2end cas, 3ème articulation
XA[2][4]=300; //X du 2end cas, 4ème
articulation
YA[2][4]=100; //Y du 2end cas, 4ème articulation
XA[2] [5]=200; //X du second cas, 5ème articulation YA[2][5]=100; //Y du second cas, 5ème articulation
// Troisième cas (3ème bras):
XA[3] [1 ]=200; // X du 3ème cas, première articulation YA[3][1]=350; // Y du 3ème cas, Première articulation
XA[3][2]=250; //X du 3ème cas, 2end
articulation
YA[3][2]=300; //Y du 3ème cas, 2end articulation
XA[3][3]=300; //X du 3ème cas, 3ème
articulation
YA[3][3]=200; //Y du 3ème cas, 3ème
articulation
XA[3][4]=-10; //X du 3ème cas, 4ème articulation YA[3][4]=100; //Y du 3ème cas, 4ème articulation
XA[3][5]=-50; //X du troisième cas, 5ème articulation YA[3][5]=100; //Y du troisième cas, 5ème articulation
}
//===================== Exemple n°3====== ============
public static void Exemple3(){
// Cas de 1 bras de 5 articulations
NbrCas=1; // Nombre de cas
Nbr=5;
cas =1; // Nombre d'articulation
pos=3;
//Sinq articulations de type RPRP
Type[1]=1; // Articulation Rotoide
Type[2]=2; // Articulation Prismatique
Type[3]=2; // Articulation Prismatique
Type[4]=2; // Articulation Prismatique
Type[5]=2; //Articulation Prismatique
// Premier cas (premier bras):
XA[1][1 ]=200; // X du premier cas, première
articulation
YA[ 1] [1 ]=350; // Y du premier cas, Première
articulation
XA[1][2]=200; //X du premier cas, 2end
articulation
YA[1][2]=300; //Y du premier cas, 2end articulation
XA[1] [3]=200; //X du premier cas, 3ème
articulation
YA[1][3]=200; //Y du premier cas, 3ème articulation
XA[1][4]=250; //X du premier cas, 4ème
articulation
YA[1][4]=200; //Y du premier cas, 4ème articulation
XA[1][5]=250; //X du premier cas, 5ème articulation YA[1][5]=250; //Y du premier cas, 5ème articulation Xpos=30+XA[ 1][5];
Ypos=30+YA[ 1][5];
// Second cas (2 bras):
XA[2][1]=200; // X du 2end cas, première
articulation
YA[2][1]=350; // Y du 2end cas, Première articulation
XA[2][2]=150; //X du 2end cas, 2end
articulation
YA[2][2]=300; //Y du 2end cas, 2end articulation
XA[2][3]=250; //X du 2end cas, 3ème
articulation
YA[2][3]=200; //Y du 2end cas, 3ème articulation
XA[2][4]=300; //X du 2end cas, 4ème
articulation
YA[2][4]=100; //Y du 2end cas, 4ème articulation
XA[2] [5]=200; //X du second cas, 5ème articulation YA[2][5]=100; //Y du second cas, 5ème articulation
// Troisième cas (3ème bras):
XA[3] [1 ]=200; // X du 3ème cas, première articulation YA[3][1]=350; // Y du 3ème cas, Première articulation
XA[3][2]=250; //X du 3ème cas, 2end
articulation
YA[3][2]=300; //Y du 3ème cas, 2end articulation
XA[3][3]=300; //X du 3ème cas, 3ème
articulation
YA[3][3]=200; //Y du 3ème cas, 3ème
articulation
XA[3][4]=-10; //X du 3ème cas, 4ème articulation YA[3][4]=100; //Y du 3ème cas, 4ème articulation
XA[3][5]=-50; //X du troisième cas, 5ème articulation YA[3][5]=100; //Y du troisième cas, 5ème articulation
}
//====================== Exemple n°4 ========== ==
public static void Exemple4(){ // Cas de 1 bras de 5 articulations
NbrCas=1; // Nombre de cas
Nbr=5;
cas=1; // Nombre d'articulation
pos =4;
//Sinq articulations de type RPRP
Type[1]=1; // Articulation Rotoide
Type[2]=2; // Articulation Prismatique
Type[3]=2; // Articulation Prismatique
Type[4]=2; // Articulation Prismatique
Type[5]=2; //Articulation Prismatique
// Premier cas (premier bras):
XA[1][1 ]=200; // X du premier cas, première
articulation
YA[ 1] [1 ]=350; // Y du premier cas, Première
articulation
XA[1][2]=200; //X du premier cas, 2end
articulation
YA[1][2]=300; //Y du premier cas, 2end articulation
XA[1] [3]=200; //X du premier cas, 3ème
articulation
YA[1][3]=200; //Y du premier cas, 3ème articulation
XA[1][4]=250; //X du premier cas, 4ème
articulation
YA[1][4]=200; //Y du premier cas, 4ème articulation
XA[1][5]=300; //X du premier cas, 5ème articulation YA[1][5]=200; //Y du premier cas, 5ème articulation Xpos=-30+XA[ 1][5];
Ypos=60+YA[ 1][5];
// Second cas (2 bras):
XA[2][1]=200; // X du 2end cas, première
articulation
YA[2][1]=350; // Y du 2end cas, Première articulation
XA[2][2]=150; //X du 2end cas, 2end
articulation
YA[2][2]=300; //Y du 2end cas, 2end articulation
YA[2][3]=200; //Y du 2end cas, 3ème articulation
XA[2][4]=300; //X du 2end cas, 4ème
articulation
YA[2][4]=100; //Y du 2end cas, 4ème articulation
XA[2][5]=200; //X du second cas, 5ème
articulation
YA[2][5]=100; //Y du second cas, 5ème articulation
// Troisième cas (3ème bras):
XA[3][1]=200; // X du 3ème cas, première
articulation
YA[3][1]=350; // Y du 3ème cas, Première
articulation
XA[3][2]=250; //X du 3ème cas, 2end
articulation
YA[3][2]=300; //Y du 3ème cas, 2end articulation
XA[3][3]=300; //X du 3ème cas, 3ème
articulation
YA[3][3]=200; //Y du 3ème cas, 3ème
articulation
XA[3][4]=-10; //X du 3ème cas, 4ème articulation YA[3][4]=100; //Y du 3ème cas, 4ème articulation
XA[3][5]=-50; //X du troisième cas, 5ème articulation
YA[3][5]=100; //Y du troisième cas, 5ème articulation
}
//========================= Exemple n°2=========================
public static void Exemple2(){ // Cas de 1 bras de 2 articulations
NbrCas=1; // Nombre de cas
Nbr=5;
cas=-1; // Nombre d'articulation
pos= 2;
//Sinq articulations de type RPRP Type[1]=1; // Articulation Rotoide
Type[2]=2; // Articulation Prismatique
Type[3]=2; // Articulation Prismatique
Type[4]=2; // Articulation Prismatique
Type[5]=2; //Articulation Prismatique
// Premier cas (premier bras):
XA[1][1 ]=200; // X du premier cas, première
articulation
YA[ 1] [1 ]=350; // Y du premier cas, Première
articulation
XA[1][2]=200; //X du premier cas, 2end
articulation
YA[1][2]=300; //Y du premier cas, 2end articulation
XA[1] [3]=200; //X du premier cas, 3ème
articulation
YA[1][3]=200; //Y du premier cas, 3ème articulation
XA[ 1] [4]=1 50; //X du premier cas, 4ème
articulation
YA[1][4]=200; //Y du premier cas, 4ème articulation
XA[1][5]=120; //X du premier cas, 5ème articulation YA[1][5]=200; //Y du premier cas, 5ème articulation Xpos=- 100+XA[ 1][5];
Ypos=50+YA[ 1][5];
// Second cas (2 bras):
XA[2][1]=200; // X du 2end cas, première
articulation
YA[2][1]=350; // Y du 2end cas, Première articulation
XA[2][2]=150; //X du 2end cas, 2end
articulation
YA[2][2]=300; //Y du 2end cas, 2end articulation
XA[2][3]=250; //X du 2end cas, 3ème
articulation
YA[2][3]=200; //Y du 2end cas, 3ème articulation
XA[2][4]=300; //X du 2end cas, 4ème
articulation
YA[2][4]=100; //Y du 2end cas, 4ème articulation
XA[2] [5]=200; //X du second cas, 5ème articulation YA[2][5]=100; //Y du second cas, 5ème articulation
// Troisième cas (3ème bras):
XA[3] [1 ]=200; // X du 3ème cas, première articulation YA[3][1]=350; // Y du 3ème cas, Première articulation
XA[3][2]=250; //X du 3ème cas, 2end
articulation
YA[3][2]=300; //Y du 3ème cas, 2end articulation
XA[3][3]=300; //X du 3ème cas, 3ème
articulation
YA[3][3]=200; //Y du 3ème cas, 3ème
articulation
XA[3][4]=-10; //X du 3ème cas, 4ème articulation YA[3][4]=100; //Y du 3ème cas, 4ème articulation
XA[3][5]=-50; //X du troisième cas, 5ème articulation YA[3][5]=100; //Y du troisième cas, 5ème articulation
}
/* *
* @param args the command line arguments */
public static void main(String args[]) { new JFrame().show();
}
// Variables declaration - do not modify
private javax.swing.ButtonGroup buttonGroup1; public java.awt.Canvas canvas1;
private javax. swing.JComboBox jComboBox1; private javax.swing.JLabel jLabel1;
private javax. swing.JMenu jMenu2;
private javax. swing.JMenuBar jMenuBar2;
private javax. swing.JMenuItem jMenuItem2;
private javax.swing.JPanel jPanel1;
private javax.swing.JPanel jPanel2;
public javax.swing.JRadioButton jRadioButton1;
private javax. swing.JRadioButton jRadioButton2;
public javax.swing.JSlider j Slider1;
private javax.swing.JTable jTable1;
public Annimation ann;
public String position;
// End of variables declaration
static int R=20;
static int Nbr; //Nombre d'articulation
static int cas;
static int pos =0,Xpos,Ypos;
static int NbrCas;//=Nombre de bras
static int Type[]=new int[50]; //Type d'articulation
static int XA[][]=new int[50][50]; //Coordonnées suivant X static int YA[][]=new int[50][50]; //Coordonnées suivant Y
// La Calss Annimation Pour géré l'annimation du Bras class Annimation extends Thread {
JFrame MyForm;
Annimation(JFrame MyForm) {
this.MyForm = MyForm;
}
public void run() {
if(MyForm.jRadioButton1 .isSelected()) {
MyForm.canvas 1 .getGraphics().clearRect(0,0,500,500); MyForm.Mypaint(MyForm.canvas 1 .getGraphics());
while(true) {
try{
MyForm.Exemple 1();
position="Position 1";
MyForm.canvas 1 .getGraphics().clearRect(0,0,500,500); MyForm.Mypaint(MyForm.canvas 1 .getGraphics()); this.sleep((int)20000/MyForm.j Slider1 .getValue()); MyForm.Exemple3 ();
position="Position 2";
MyForm.canvas 1 .getGraphics().clearRect(0,0,500,500); MyForm.Mypaint(MyForm.canvas 1 .getGraphics()); this.sleep((int)20000/MyForm.j Slider1 .getValue()); MyForm.Exemple4();
position="Position 3";
MyForm.canvas 1 .getGraphics().clearRect(0,0,500,500); MyForm.Mypaint(MyForm.canvas 1 .getGraphics()); this.sleep((int)20000/MyForm.j Slider1 .getValue()); MyForm.Exemple2();
position="Position 4";
MyForm.canvas 1 .getGraphics().clearRect(0,0,500,500); MyForm.Mypaint(MyForm.canvas 1 .getGraphics()); this.sleep((int)20000/MyForm.j Slider1 .getValue()); MyForm.Exemple5();
position="Position 5";
MyForm.canvas 1 .getGraphics().clearRect(0,0,500,500); MyForm.Mypaint(MyForm.canvas 1 .getGraphics()); this.sleep((int)20000/MyForm.j Slider1 .getValue());
}
catch(Exception e) { }
}
}
}
}
///////////////////* * * *Fin du programme* * **///////////////////////////////////////
Appendice H :
Programme de model géométrique direct
******************************************************************** C PROGRAM: MGD
c PURPOSE: Entry point for the console application.
c program MGD
c Variables
c******************************************************************* implicit none
integer ij
real theta1 ,h1,h2,h3,h4,z2,z5,z3,z4
real c1,s1
real d3,d4,Pi
real T(4,4)
d4=0.6
C selon le cahier de charge
d3=d4
Pi=3. 1415926535897932384626433832795
write(*,*) 'donner la valeur de theta1'
read(*,*) theta1
theta1=(theta1 *Pi)/1 80.
write(*, *) 'theta1r=',theta1
write(*,*) 'donner la valeur de h1 =,h2=,h3=,h4=,z2=,z5=,z3=,z4='
read(*,*) h1,h2,h3,h4,z2,z5,z3,z4
c
write (*,*)'calcul des éléments de la matrice de transformation
+ homogène T<0,5>'
c
c1 =cos(theta1)
s1 =sin(theta1)
write(*,*) 'c1 =cos(theta1 )=',c1 ,'s 1 =sin(theta1 )=', s1
write (*,*)'la matrice t(i,j)'
T(1,1)=c1-s1
T(1 ,2)=0 T(1 ,3)=0 T( 1 ,4)=(z3-z4)*c 1
T(2,1)=c1+s1
T(2,2)=0 T(2,3)=0 T(2,4)=(z3-z4)*s 1
T(3, 1)=0 T(3 ,2)=0 T(3,3)=1 T(3 ,4)=h1 +h2+h3+h4+z2-z5
T(4, 1)=0 T(4,2)=0 T(4,3)=0 T(4,4)=1 write(*,*)' ((T(i,j)j=1,4),i=1,4)'
5 format (4F)
do 2 i=1,4
write( *,*)(T(i,j),j=1,4)
2 continue
write(*,*) 'CE PROGRAMME MARCHE TRES BIEN ' c Body ofMGD
end.
APPENDICE I :
Organigramme général : (Proposé comme une banque des données) :



lel,Modèle d'évaluation des erreurs: associé à un balyage systémathique des coordonnées articulaires et un critère de classement
lerModèle d'évaluation des erreurs : Erreurs de positionnement ou de poursuite
Modèle des déformations :
Evaluation des torseurs des déplacements élémentaires par segments
Fa
·
e




|
Lr 5'p |




n

Organigramme I.1 : Organigramme général
Appendice J : F21]
Le système d'équation non linéaire est du type

f1(q1,q2,q3... .qm) + x1 = 0
? T
f2(q1,q2,q3... .qm) + x2 = 0 . fm(q1,q2,q3... .qm) + x1 = 0
Ou q1,q2,q3....qm sont des inconnues réelles indépendantes et f1, f2 fm sont des
fonctions réelles données des m variables qi , un tel système de m équation à m inconnues est dit d'ordre m.
Principe de la méthode :
Soit Q(0) = (q01 q0m) un point initial de Rm . Q(0) est considéré comme une
approximation de la solution Q* =(q*1 q*m) du système son linéaire ci-dessus. En supposant que Q(0) soit suffisamment voisin de Q* que la fonction f1(q1,q2,q3....qm), i=1, m soit suffisamment dérivables. Le développement en série de Taylor de ces fonctions s'écrit sous la forme :
j m
=j m
= k m
= 2
? f 1 ? f
f Q f Q q q
( ) ( ) ( ) ( )
* 0 * 0 1 0 ( )( ) ( )
* ( 0) ( 0 ) 1 ( 0)
= + - Q q q q q
= - -
* +
1 1 j j j
? = ?? Q
j k k
? q 2! ? ?
q q
j 1 j j = 1 1
k = j k
Pour i=1, .....m. si on néglige les termes d'ordre supérieur à 1, on définit une nouvelle approximation :
Q(1) = (qi1 .....qm1) de Q* par les égalités :
|
j m = ? f f Q q q 1 Q ( ) ( ) 1 ( 0 0 * 0 + ? - j j ? q j = 1 j |
) |
0 pour i=1 .....m ainsi le vecteur |
Q(1) = (qi(1) ..... qm(1)) est défini comme étant la deuxième approximation de la solution qui s'exprime par Q(1) = Q(0) + ?Q(0), les composantes ?q1(0), ?q2(0), ?q3(0) ..... ?qm(0) étant la solution du système linéaire mis sous forme
0 = 0

f ( 0 )
?f ( 0 ) ? f ( 0 )
1 ( 0 ) 1
?
? q1
? +
q f
( 0)

( )
j ( )
j
? f ? f
1 1
=
? q j
f 1 j = f ( Q j
( ) ( )
? q j
1
)
( ( )
Q j
? + +
q 2 m 1
? q ? q
2 m
( 0 )
(0)
u
? f
? f
? f
(0)
0
m m m
( 0 ) ( 0) 0
? +
q q
( 0 ) ? + + ? + =
q f
?
1 2 m m
q1
? q ? q
2 m

Le processus est ensuite itéré à partir de la nouvelle approximation Q(1) de la solution
|
Q* ainsi on passera de l'itération n à l'itération n+1 par la relation |
Q n = Q n + ? Q n ( 1 ) ( ) ( ) + |
les composantes ?q1n . ?q2n . .....?qmn. étant la solution du système linéaire mis sous forme développée :
( 0 ) n ( )
n
? f ? f ( )
n ( ) 1
? f
1 ( ) 1 n ( )
q q ? + =
( ) 0
? + ? + + q f
n n
1 2 m 1
? q ? q ? q
1 2 m
f ( )
n ( )
n m
? f ( )
n
? ? f n
m ( ) ( ) ( ) ( ) 0
? +
q ? + +
q n m ? + =
q f
n n
1 2 m m
? q ? q ? q
1 2 m
Sous la forme matricielle, ce système d'équation est noté
? ? f
( ) = ( Q )
i
J Q ?
? ? ? q j
?
?
? ?
Pour i=1, ....., m et j=1, ...., m, la matrice J est appelée matrice Jacobinne des fonctions
fi i= 1, ....., m évoluée au point Q.
A l'aide de ces notations, le système linéaire permettant d'obtenir l'approximation (n+ 1) peut se mettre sous la forme matricielle et par suite l'approximation Q(n+1) est donnée par :
|
Q Q J Q n n n + = - - ( 1 1 |
) ( ) - [ n { n } ] F Q XLe processus itératif est arrêté lorsqu'il y a |
convergence, c'est-à-dire lorsque - ( - 1 ) = å
sup q 1 n q n
( )
1
Dérivation de la matrice de transformation homogène :
Soit Tij la matrice de transformation du repère Ri au repère rj qu'on peut mettre sous forme :
T T i T i T T
ij i i i i j j
= + + + + -
( 1) . ( 1) . ( 1 )( 2 ) ( 1 )elle dépend des variables qi+1, .qj
Pour calculer la dérivée partielle de Tij par rapport à la variable q1. On distingue les deux cas suivants :
1 ièr cas : i = 1 >j Les éléments de la matrice Tij ne dépend pas de q1 alors :
|
? Tij |
[ 0] |
2èmecas :i<1=j
? T ij = ?
?q1 ? q 1
? ? T ( 1 1 ) 1 ?
-
[ ]
T T T T T T
i i i i j j i i i i j j
= T T
( 1 ) ( 1 )( 2 ) ( 1 ) ( 1 ) ( 1 )( 2 ) ( 1 2 ) ( 1 1 )
. . ... ...
+ + + - + + + - - ( 1 1 ) 1 ( 1 )
- -
?? q ??
? 1
Sachant que :
?
??
?T (
i i T
i . i
?
i 1 ) 1
?
- 1 )
(
? q i
?? =
? i 1
=
|
0 (1 - ó 1 ) 0 |
- |
(1 |
- ó 1 ) 0 |
0 0 0 0 |
0 ? 0 ? ? ó 1 ? ? 0 ? |
ój = 0 pour une liaison rotoïde ój=1 pour une liaison prismatique.
?T ij= ? = ?
T T T T T
? q 1
i i ij i j
( 1 ) ( 1 1 ) 1 11 1 11 1
- -
?
T ij T T

= ?
i j
? q 1
1 11 1
On pose ? j 1 =T j 1.?11.T ij et on peut écrire :
?
T ij= ? = ? = ?
T T T T T T
i j ij ( j . j ) ij j
? q 1
1 11 1 1 11 1 1
Notons ici que : ? i 1 T ij = ( T i 1 ? 11 T 1 i ) T ij = T ij ? j 1
= T i ( T j 1 ? 11 T 1 j ) = T ij ? j 1
Donc on a : ? ij . T ij = T ij ? j 1
Finalement on peut écrire :
? [0
?
?
T ij
.?j 1
?Tij
? q 1
] si
si i
, i > 1> j
< 1= j
,

0 1
= > n
,
n
. ? n
0 1
< = n
,
? [ 0
?
?
T0
]si
n=
? T 0
?q1
1
si
Matrice d'un système constitué de n corps :
Soit T0n la matrice de transformation homogène du repère R0 au repère Rn alors :
Appendice L
L-1 La trajectoire : [12, 3, 4, 21, 27, 71, 90, 91] ; Selon la tâche que doit accomplir le robot, on peut classer les différents mouvements selon deux catégories de trajectoires l'une libre l'autre imposée, [90, 91], (voir figure L.7, L.8, L.9).
La génération de trajectoire est une étape très importante dans la commande des robots manipulateurs. Elle consiste à calculer les consignes de référence en position, en vitesse, et en accélération, qui décrivent leurs mouvements désirés
Cependant, la trajectoire est l'évolution de la position, et ses dérivées temporelles en fonction du temps pour chacune des articulations; le mouvement le plus simple est d'aller d'un point initial à un point final, ainsi le robot est commandé pour changer sa configuration initiale vers une configuration finale, ce type de mouvement convient aux tâches de transfert d'objets quand l'espace de travail ne comporte aucun obstacle ; le chemin à suivre par l'élément terminal peut être contraint par l'addition de points intermédiaires aux configurations initiales et finales.
Pour assurer le fonctionnement normal du mécanisme, on choisira des mouvements continus, pour cela on définit une fonction lisse, (dérivées première et secondaire continues), afin d'éviter les risques d'usure (voir chapitre des causes structurales) et de vibrations pouvant exciter les modes propres du manipulateur.
En résumé, le parcours peut être planifié de différentes manières dont on distingue : Le mouvement entre les deux points avec une trajectoire libre entre les points.
Le mouvement entre deux points via des points intermédiaires avec une trajectoire libre entre les points intermédiaires.
Le mouvement entre deux points avec une trajectoire contrainte entre les points (trajectoire rectiligne).
Le mouvement entre deux points via des points intermédiaires avec une trajectoire contrainte entre les points intermédiaires.
Dans les deux premiers cas, la génération de la trajectoire peut se faire directement dans l'espace articulaire. Quant aux deux derniers, la trajectoire étant décrite dans l'espace opérationnelle, il est préférable de raisonner dans cet espace.
L-1-1 Génération de la trajectoire dans l'espace articulaire : [12, 3, 4, 21, 27] : La génération de trajectoire dans l'espace articulaire donne au résultat un ensemble de données : Positions, vitesses et
accélérations articulaires ( è d ,è & d ,è & & d ) qui sont utilisées comme un signal de référence, pour une position initiale et finale données dans l'espace de travail, on utilise la géométrie inverse pour
déterminer les angles articulaires correspondant à cette position et même pour l'orientation. La position initiale du manipulateur devient un ensemble d'angles articulaires d'arrivée, ce qui est demandé pour la planification de la trajectoire est de trouver une fonction lisse pour chaque articulation dont la valeur à l'instant t0 est la position initiale de l'articulation et dont la valeur à l'instant tf est la position désirée de cette même articulation. Il y a beaucoup de fonctions lisses O (t), qui pourraient être utilisées pour interpoler les valeurs d'angles articulaires. On cite :
L-1-1-1 La fonction polynomiale cubique F26, 27] : Il s'agit d'une interpolation simple en effectuant un simple mouvement continu, au moins quatre contraintes sur O (t) sont évidentes pour avoir une fonction polynomiale cubique de la forme :
è(t) =a 0 + a1t + a 2 t + a t
2 3 (L.1)
3
Ainsi on obtient la vitesse articulaire :
è& t = a1 + 2a2t + 3 a 3 t (L.2)
( ) 2
et aussi l'accélération articulaire :
è&& (t)=2a2+6a3t (L.3)
Sachant qu'un polynôme du 3 ème degré, admet quatre coefficients, il peut être donc construit à partir de quatre contraintes, deux sont obtenues à partir du choix des valeurs initiales et finales de la
|
position : O (0) = O 0 , Od (tf) = Of quant aux deux autres contraintes, elles proviennent du fait que l'articulation démarre et arrive avec une vitesse nulle O (0) = O 0 , Od (tf) = 0 et en combinant les deux fonctions : è(t) et è&(t) avec les quatre contraintes, on obtient quatre équations à quatre inconnues : O0 = a0 ....(L.4) 2 3 (L.5) èf = a + a t f + a t f + a t f 0 1 2 3 0 = a 1 ..(L.6) 2 0 = a 1 + 2a2t f + 6a3t f .... .(L.7) |
En relevant ce système d'équations on obtient :
a 0 = è 0 .
(L.8)
a1=0 (L.9)
3
a (L.10)
2 = 2 è f - è 0
( ).
tf
|
2 a 3 = - 3 è f - è 0 ( ). t f |
(L.11) |
30 30 14 16 3 2
è è è è è è
- + & + & - & & - & &
( ) ( ) 2
0 0 0
f f f f f
t t
4
2t f
a 4 =
(L.22)
12 12 6 6
- - & + & - & & - & &
( ) ( ) 2
è è è è
è è
f f f f f
0 0 0
t t
(L.23)
a =
5 2
5
t
f
Avec ces quatre coefficients, on peut calculer le polynôme cubique qui connecte n'importe quelle position désirée.
Exemple de génération d'une trajectoire articulaire (voir figure L.7, L.8, L.9).
L-1-1-2 Polynôme de degré cinq : [12, 26] : On peut avoir des polynômes d'ordre supérieur pour la planification de la trajectoire, ils sont quelquefois utilisés dans le cas où on voudrait indiquer la position, la vitesse, et l'accélération au début et à la fin de la trajectoire. Ils sont aussi utilisés quand les robots manipulateurs fonctionnent à une grande vitesse. Il est nécessaire d'assurer la continuité des accélérations afin d'éviter l'excitation du mécanisme. Il faut avoir un polynôme d'ordre cinq de la forme :
2 3 4 5
è = + + + + +
( ) 0 1 2
t a a t a t a t a t a t (L.12)
3 4 5
Pour déterminer les coefficients de ce polynôme, il faut avoir au moins six contraintes, deux sur la vitesse et deux autres sur l'accélération :
è 0 = a 0 (L.13)
è&0=a1 (L.14)
è& & 0=2a2 (L.15)
f a a t a t a t a t a t
2 4 5
è = + + + + +
3 (L.16)
0 1 2 3 4 5
è& & = a + a t + a t + a t
2 6 1 2 20
2 3
f f f f (L. 17)
2 3 4 5
En résolvant le système d'équation, on trouve :
a 0 = è 0 (L.18)
a 1 = è& 0 (L.19)
a2 =è& & 0 (L.20)
|
a |
= |
20 20 8 12 3 - - & + & + & & - & & ( ) ( ) 2 f f f f f 0 0 t t |
(L.21) |
|
|
3 |
2t3 f |
L-1-1-3 Loi Bang-Bang avec palier de vitesse (loi trapèze) : [12, 26] : Une autre voie pour générer les consignes est ce qu'on appelle segment linéaire avec portions paraboliques ou bien loi Bang-Bang avec palier de vitesse. Cette trajectoire est telle que la vitesse est rampée en haut à sa valeur spécifique initialement et puis rampée en bas au début (position désirée). Pour accomplir tout. Cela on spécifie la position désirée en trois phases.
La première phase de l'instant t0 à l'instant tb est polynomiale quadratique.
A l'instant tb la position change de forme et devient linéaire cela correspond à une vitesse constante. Finalement à l'instant tf- tb la trajectoire de position redevient polynomiale quadratique de sorte que la vitesse soit linéaire.
On choisit l'instant tb de façon à ce que la courbure de position soit symétrique, par convention, on suppose que t0 =0 et q ( tf ) = q ( 0 )= 0 puis entre les instants 0 et tb on a :
qd(t) =a 1 +a 1 t + a t 2 (L.24)
2
de façon que la vitesse soit :
qd(t) =a 1 + a2 (L.25)
t
Les contraintes q ( 0)= 0 et q ( 0)= 0 impliquent que :
a 0 = q0 (L.26)
a1 =0 (L.27) Puisque à l'instant tb on veut que la vitesse soit égale à une constante donnée on aura : qd(t b ) = 2a2tb = V (L.28)
ce qui implique que : a2 = V! 2t6 .. .(L.29)
Par conséquent, la trajectoire requise entre les instants 0 et tb est donnée par :
q d (t) = q0 +V!2tb.t2 = q0 +a!2.t2 ... (L.30)
q d (t)=q0+V!t
b .t=at . (L.31)
q d = V!t
b . = a .. (L.32)
Où a est l'accélération.
Maintenant et ente les instants tf et tf- tb , la trajectoire est un segment linéaire qui correspond à une vitesse constante V :
qd(t)=á0+á 1 t=á0+Vt .... . (L.33)
+
Par symétrie : qd t
( ) q 0 q 1
= . (L.34)
2

2
+ a
.
t
q 0
. 0
2
< =
t t
d f
V tf
+Vt
-
2
2
q q
+
f 0
2
- at at t
2 -
f f
+
t t t t
d f b
< = -
(L.42)
2 2
t
q f
t t t t
f b f
- < =
?
?
( )
t
q d
?
On aura : q 0 q 1 = + Vtf
+ á (L.35)
2 02
Ce qui implique que :
q + q - Vtf
á = (L.36)
0 1
0 2
Comme les deux segments coïncident à l'instant tb on obtient :
q + +
Vtb q q V t V tb
+ = .(L.37)
0 1 2
0 2 2
Ce qui donne l'expression :
|
tb = |
q0 ql 1 V + - |
(L.38) |
||
|
2 |
Il est à noter qu'on a la contrainte : 0 f
t
< t < (L.39)
b 2
Ceci mène à l'inéquation :
q q f
f 0 2( - 0 )
- q q
< =
t (L.40)
f
V V
q q 0 2( - 0 )
+ q q
f f
Autrement dit : < =
V (L.41)
t t
f f
Par conséquent, la vitesse spécifiée doit être entre ces deux limites ou bien le mouvement ne sera pas possible, la portion de la trajectoire entre tf- tb et tf est maintenant déterminée par des considérations de symétrie. La trajectoire complète est donnée par :
L-1-2 Génération de la trajectoire dans l'espace cartésien : Les trajectoires dans l'espace articulaire sont plus faciles à calculer et elles sont plus simples, cependant elles deviennent complexes si elles sont décrites dans l'espace cartésien puisque dans le premier cas on ne fait aucune correspondance continue entre l'espace articulaire et l'espace cartésien; il n' y a aucun problème avec les singularités du mécanisme.
La trajectoire dans l'espace cartésien donne comme résultat la position, la vitesse et l'accélération cartésienne (x, x & , &x&). Pour certaines structures de commande spécifique, ces données doivent être
converties en grandeurs équivalentes dans l'espace articulaire. Une analyse complète devrait être utilisée comme un signal de référence pour le régulateur synthétisé dans l'espace articulaire. Dans l'espace de travail, la forme du parcours prise par l'élément terminal n'est pas simple, mais
plutôt une forme compliquée qui dépend de la géométrie du manipulateur. Les formes du parcours sont décrites en terme des fonctions du temps qui déterminent la position et l'orientation cartésiennes, la forme spatiale du parcours entre ces points peut être : Une ligne droite, circulaire, sinusoïdale,
ellicoïdale ou d'autres formes.
Pour la planification de trajectoire basée sur l'espace cartésien, les fonctions qui forment une trajectoire sont des fonctions du temps qui représentent les variables cartésiennes. Ces parcours peuvent être planifiés directement à partir de la définition, par l'utilisation des points de parcours qui sont les spécifications sur le parcours désiré.
L-1-3 Problème géométrique dans un parcours cartésien : [27] : Plusieurs problèmes sont posés dans la génération des trajectoires cartésiennes à cause de la correspondance continue qui se trouve entre la forme de la trajectoire décrite dans l'espace cartésien et celle décrite dans l'espace articulaire. On en cite trois problèmes majeurs :
Problème du type 1 : C'est le problème des points intermédiaires inaccessibles, comme il est présenté dans la figure L. 1, si on veut que le robot démarre du point A pour arriver au point B en passant par une trajectoire désirée qui est une ligne droite par exemple, bien que les points initials et finals du parcours soient compris dans l'espace de travail du robot, il y a certains points qui appartiennent à cette trajectoire et qui n'appartiennent pas à l'espace de travail du manipulateur. Ces points deviennent inaccessibles, ce qui rend impossible d'effectuer cette tâche dans l'espace opérationnel. Néanmoins il n'y aurait pas ce type de problème dans l'espace articulaire.

B
A
Figure L.1 : Problème de type 2
Problème de type 2 : C'est le problème de vitesse articulaire qui est trop élevée en passant près de la singularité. Certains parcours dans l'espace cartésien sont impossibles à exécuter par le robot manipulateur surtout dans le cas où il devrait suivre une trajectoire en s'approchant d'une singulière du mécanisme, (par exemple une ligne).
Une ou plusieurs vitesses articulaires peuvent augmenter vers l'infini. Puisque les vitesses des articulations sont bornées supérieurement, cette situation a pour conséquence la déviation du robot manipulateur de son parcours désiré. La figure L.1 montre un robot à deux articulations, ayant la même longueur, se déplaçant le long du parcours du point A au point B , la trajectoire désirée correspond au mouvement de l'élément terminal du manipulateur à vitesse linéaire constante le long d'un parcours rectiligne. Sur la figure, on montre plusieurs positions intermédiaires du manipulateur qui ont été dessinées pour mieux voir le mouvement, et tous les points de la trajectoire sont accessibles, mais dès que la vitesse de l'articulation 01 devient très élevée, plus le parcours s'approche étroitement de l'axe articulaire 01, plus la vitesse sera grande.

B
La vitesse est infinie (Jacobien singulier)
A
Figure L.2 : Problème de type 3.
Problème de type 3 : Le troisième problème se produit quand il y à plusieurs solutions pour atteindre un point donné dans la trajectoire, la figure L.2 montre un robot manipulateur à deux liaisons de même longueur, ayant des butées au niveau des articulations qui diminue le nombre de solutions avec lesquelles il peut atteindre un point donné dans l'espace. En particulier, un problème surviendrait si le point final ne peut pas être atteint dans la même solution physique quand le robot est au point de départ.
Comme il se voit dans la figure L. 1, le manipulateur peut atteindre tous les points du parcours pour une certaine solution, mais pas pour n'importe quelle solution. Dans cette situation le système ne peut pas se déplacer à cause des butées mécaniques.
L-1-4 Étude comparative et discussion du choix d'une trajectoire : [12, 27] : Les deux approches étudiées précédemment présentent plusieurs avantages et inconvénients. La génération du mouvement dans l'espace articulaire présente les avantages suivants :
Elle nécessite moins de calculs en ligne puisqu'il n'y a pas d'appel au modèle géométrique ou cinématique inverse. Le mouvement n'est pas affecté par le message, par les configurations singulières. Les contraintes de vitesse et de couples maximaux sont directement déduites des limites physiques des actionneurs. .En contre partie, la géométrie de la trajectoire de l'organe terminal dans l'espace opérationnel est imprévisible bien qu'elle soit répétitive : Il y a donc un risque de collision, lorsque le robot évolue dans un environnement encombré. Ce type du mouvement est par conséquent approprié pour réaliser des déplacements rapides dans un espace libre. La génération des mouvements dans l'espace opérationnel permet de contrôler la géométrie de la trajectoire. En revanche:
Elle exige la transformation en coordonnées articulaires de chaque point de la trajectoire. Elle peut être mise en échec lorsque la trajectoire calculée passe par une position singulière.
Elle est mise en échec chaque fois que les points de la trajectoire engendrée ne sont pas dans l'espace accessible par le robot ou chaque fois que la trajectoire impose une reconfiguration du mécanisme (changement d'aspect en cours de trajectoire); les limites en vitesse et en couple dans l'espace opérationnel varient selon la configuration du robot. On exprime alors ces limites par des valeurs traduisant des performances moyennes, satisfaisantes quelle que soit la configuration du robot. On impose donc au robot de travailler au-delà de ses capacités réelles.
Le choix d'une méthode de génération de mouvement dépend de l'application considérée. Chaque approche a ses propres limites, inhérente au fait que les contraintes sont exprimées soit dans l'espace articulaire (vitesse, couples, butées) soit dans l'espace opérationnel (précision, obstacles).
L-1-5 Génération de trajectoire dans l'espace cartésien :
L-1-5-1 Description d'une trajectoire planaire : On veut générer une trajectoire dans l'espace cartésien, pour imposer une position et une orientation au manipulateur à suivre, on veut que l'élément terminal du bras manipulateur suive un demi cercle qui se situe dans le plan OXZ, le centre du cercle est repéré par les coordonnées suivantes (x', z' ) et dont le rayon est R. on impose une orientation à l'outil terminal de façon à ce qu'il soit radial au sens rentrant et en arrivant à l'extrémité de l'arc il conserve son orientation perpendiculairement au tronçon rectiligne.

O' Z
O' Z
Z' O
XT
X'O
ZT
p
+
p0
XT
O'
a
Point initial
Z0
0
Y0
X0
O'X
O'X
d2 +d3
Figure L.3 : Schéma représentatif d'une trajectoire dans le plan.
On désire que l'outil parcoure le demi cercle dans le sens de la flèche. L'orientation de l'outil terminal est représentée par l'angle p(t) pour lequel le point concerné sur le demi cercle est repéré par l'angle a(t).
Ainsi nous obtenons les équations suivantes :
)
' r
sin( á
= +
x ox
t
Z t á
= z oz R
t
d2 d 3 oy
+ =
(L.43)
?
??
??
'
'
= + cos(
)
yt
On impose à l'angle p une variation linéaire en fonction de a :

p
|
p 0 + it p 0 |
p ? [p 0, p 0 + it /2 ] ; a ? [p 0 + it, p 0 + 2 it] |
||
(L.46).

? á
/ 2
( ) ( )
t t
= á
x R
& = cos( á
t
?
??
)
- R sin( á
)
z t
0
y t
Figure L.4 : Variation de l'angle p en fonction du a. + p + 2 a
D'où ?(t)=1/2á(t)+1/2á0-ð/2 (L.44)
L-1-5-1-1 Génération de trajectoire sur le 1er tronçon: L'évolution de l'angle a (t) est imposée telle qu'il suive une loi Bang -Bang avec palier de vitesse.
En résumé : Position :
? x ox r
= +
' sin( )
á
t
? oz R
' cos( )
+ á
?
Z t
= ? y d d oy
= + = (L.45)
t 2 3
? á á
= ( )
t
1 / 2 / 2
á ð
0 -
?
? ( ) 1 / 2 ( )
? ? á
t t
= +
Vitesse :
Accélération :
) á 2 + R sin(á ) á
z R
& & = cos( á t
& &
0
yt
? á á
( ) ( )
t t
=
(L.47).
?
??
/ 2
R R
sin( ) 2 cos(
á á á
-
) á
& &
xt
L-1-5-1-2 Génération de trajectoire sur le 2ème tronçon: L'outil se déplace le long du diamètre AO'B tel qu'il reste perpendiculaire à AB. Donc l'orientation de l'outil est maintenue constante de sorte que l'angle p vérifie toujours l'équation : p = p0 + ir/2 .
Cependant le point figuratif est sur l'axe Q'Z' Ô ;
Les équations horaires donnant les coordonnées du Wrist sont les suivantes :
La position :
x o x z
= +
'
t
y d d
= +
a z
z o z z
= +
' " cos( 0)
?
t
? ?
?
??
(L.48).
"
sin( 0)
?
+
0 ð
/2
?
( )
t

Z'
Z69
p0
XT X'O
O'
ZT
+
Figure L.5 : Génération du deuxième tronçon.
La vitesse :
? V =0
TY
TX Z V Y
??
V V
= " sin( 0) "
? TZ Z ?
= cos( 0) (L.49).
?? ? = 0
L'accélération :
?
a = 0 TY TX Z a a
??
a a
= " sin( 0) '
? TZ Z ?
= cos( 0)(L.50).
?? ? = 0
L-1-5-2 Description d'une trajectoire spatiale : On veut que l'outil terminal suit la trajectoire décrite ci-dessus (glissement sur la face d'un huitième de sphère de rayon R et de centre O' ( x'0 , y'0 , z'0 ) donné. L'orientation est calculée pour assurer la direction radiale entrante de l'outil afin qu'il puisse réaliser la tâche demandée (polissage par exemple) sachant que nous avons adopté la représentation d'Euler concernant les orientations.
Les angles ö etø sont des paramètres auxiliaires qui servent à déterminer la position et l'orientation
de l'outil terminal dans les repères lié à la sphère, et par une simple translation du vecteur [x'0, y'0 , z'0] on retrouvera les coordonnées cartésiennes de l'outil dans le repère de la base.
En fonction des paramètre ö etø on peut exprimer le vecteur des positions et orientations comme
suit :

'
0
+
y
? ø
sin
y R
= sin
z R z
= +
' cos '
?
(L.51)
?
?
0
á
ø
-
ð
â ?
=
ø
?ä
x R x
= +
sin cos
? ø
'
0
[ / 2,0]
(L.52)
Avec
??
? ø
? [0, / 2]
ð
Ou : x , y et z représentent la position de l'outil et á, â et ä sont les angles d'Euler
Correspondants à l'orientation de l'outil terminal exprimées dans le repère de base .
Les angles ö etø obéissent à une loi d'évaluation dans le temps du type Bang Bang avec palier de
vitesse comme il est schématisé ci-dessous. Les vitesses :

)
x R
& = +
(cos cos sin sin
?? ø ? ??
á
ø
ø
?ä
Figure L.6 : Génération d'une trajectoire tridimensionnelle.
y
(L.53)
Les accélérations :
sin( )
? ?
x R
& & = -
(
- -
cos( ) sin( )
? ? ø ø
2 cos cos( ) cos
ø ? ? ø
+ +
)ø
-
? ø
cos(
sin
? ø
sin(
sin
(
& &
R
y
2 sin ø
- sin( )
? ?
+ + +
cos( ) sin cos( ) cos( )
? ? ø ? ? ø ø
cos( ) sin(
? ? ø
)ø
2 sin
+
? ø
sin(
)ø
) ø
2 -
?
?
?
?ä
á
â ?
=
cos( ) sin(
? ? ø
z R
& & = -
ø
ø
(cos(?
)?
)ø
2
+ sin
+
sin( ?
? ø
cos(
) ?
) ø
(L.54)
Z'
y
x
y
x
+
y
z
x Y'
X
O
ø
z
z
X
O
x
(cos sin sin cos
?? ø ? ?? +
z R
& = -sin
â ?
=
?
?
)
y Rb
& =
??
70
Exemple de trajectoires de la position articulaires, vitesse angulaire et accélération articulaire.
On veut générer la trajectoire articulaire pour passer d'un angle initial de 5° à un angle final de 65° dans 4 secondes [27,28].


25
20
15
10
5
1 2 3 4
0
60
50
40
30
20
10
0
1 2 3 4
temps (sec)
temps (sec)
Figure L.7 : Position articulaire Figure L.8 : Vitesse Angulaire

30
20
10
0
-10
-20
-30
0 1 2 3 4
temps (sec)
Figure L.9 : accélération articulaire
Planification des mouvements
Introduction sur la planification :
L'utilisation courante manipulateurs dans l'exécution des taches répétitives fait que les recherches se sont naturellement orientées vers la planification de mouvements minimisant un coût relatif essentiellement le rendement du robot et son fonctionnement. Cette idée générale a conduit à la formulation du problème de planification dans lesquels des grandeurs physiques telles que la durée de parcours, les efforts actionneurs ou la puissance consommée soient optimisés individuellement ou globalement.
Définition :
Trajectoire libre : appelée aussi mouvement point à point ou mouvement de transfert. Seules les configurations initiale et finale doivent être respectées en plus des obstacles à éviter. La trajectoire quoi relie ces deux configurations est alors libre. Ceci peut être le cas de la manutention d'objets ou de soudure point à point.
Trajectoire imposée : de tel mouvement sont rencontrés lorsque l'outil en fin de chaîne sur son environnement sans interruption et selon un parcours déterminé.
Il est nécessaire de spécifier la trajectoire de l'effecteur. On citera par exemple les travaux de découpage ou de soudure en continu. Dans ces deux cas, il existe généralement plusieurs trajectoires possibles. Il faut profiter de cette multiplicité de choix pour adapter la meilleure solution afin d'accomplir la tache. Pour les mouvements libres, l'optimisation a pour but de rechercher le trajectoire à suivre de ainsi que les modalités pour la parcourir tandis que pour les mouvements imposés, l'optimisation ne porte que sur les modalités de la parcourir.
Fonction objectif :
Le choix du critère de performance est déterminant quant la à la qualification du mouvement et conditionne l'efficacité des méthodes de résolution du problème. Le critère à minimiser peut se présenter sous 3 formes distinctes : une fonctionnelle de type intégrale, de type terminal ou de type ou de type mixte. Bien que formulés différemment, ces 3 problèmes sont équivalents, la fonctionnelle intégrales est le milieux adaptée pour les mouvements de transfert. Les critères à optimiser dans ce cas se mettent sous la forme générale suivante [71, 90,91 ] :

.
L(q(t), q (t),
q .. (t), ) = u + 1- u ? n 2
i t
( )
2 i
avec u ? ] 0,1[ (L.60)
max
i 1
=
F (u,t) = ?T 0 L (x(t) ,u) dt (L.56)
Ou :
L : représente le lagrangien qui prend la forme selon l'objectif visé.
X(t) : vecteur de variables d'état à l'instant t ?[0,T]
U : vecteur qui représente la commande à optimiser, considère comme une inconnue du problème. T : temps de transfert total entre les configurations initiale et finale.
Pour le cas d'une planification de mouvements libres, u représente les couples moteurs, x(t) les
. ..
variables articulaires de position q(t), de vitesse q (t) et d'accélération q (t) Dans ce cas, le critère s'écrit de la manière suivante :
. ..
F( ,T ) ?T 0 L(q(t), q(t), q (t), ) dt (L.57)
Pour générer des mouvements de qualité, on peut citer parmi les critères les plus significatifs la durée de parcours, mixte temps - efforts quadratiques et mixte avec puissance quadrique .
Critère durée de parcours :
Il suscite l'intérêt d'un bon nombre de chercheurs roboticiens [92] car pour les robots qui travaillent d'une manière cyclique, la rapidité d'exécution (rentabilité ) est un critère très significatif. La dynamique du robot n'est pas représenté directement ans cette formulation. Ceci conduit à des commandes optimales discontinues.
Les couples articulaires ne sont pas représentés dans le lagrangien d'où une forme simple comparée aux autres.
. ..
L(q(t), q (t), q (t), ) = 1 (L.58)
Alors : F(T, ) = F(T) = ?T 0 dt = T (L.59)
Critère mixte temps efforts quadratiques :
Comparativement au critère précédant implique des discontinuités lors des transferts de charges, donc, nuisible au bon fonctionnement du manipulateur, ce critère est un moyen efficace pour régularisé les vitesses et les couples, en introduisant un facteur de pondération u , on peut favoriser
soit le temps, soit les efforts ( couples) [93], le lagrangien prend la forme suivante :
l'optimisation du temps. Le choix DE u d2temine alors le compromis entre ces deux quantités. Ceci conduit à une certaine souplesse d'exécution en tenant compte de la durée de la tache. Néanmoins, on rencontre des difficultés dans la formation de ce critère vu l'existence des efforts dans le lagrangien. Les contraintes :
Pour que la planification du mouvement soit possible, on tient compte des capacités technologiques du robot et des spécificités de la tache à effecteur. Ceci indique une restriction des solutions. Pour planifier un mouvement, on s'intéresse aux contraintes suivantes :
Contraintes sur les débattements :
Du fait de la conception de la liaison et que les mouvements sont limités entre des butées mécaniques, les mouvements ne doivent pas dépasser les capacités de la structure. Tout ceci se traduit par la formule suivante :
? t ? [0, T] , qi(t) = qimax i =1, .,n (L.61)
T : représente le temps
qi(t) : représente les coordonnées généralisées de la iéme articulation.
qimax : représente la valeur maximale de la iéme articulation ( valeur intrinsèque du robot) Contraintes cinématiques :
La conception des articulations et la technologie des actionneurs impliquent une limitation des caractéristiques cinématiques notamment pour les objets manipulés sensibles aux survitesse, accélération et freinages ( par exemple des liquides qui peuvent se déverser ).
Les formulations se traduisent par :
Vitesse :
|
? t ? [0,T] , Accélérations ? t ? [0,T] , |
. i t q ( ) : .. q i t ) ( |
. = qimax i =1, .. = qimax i =1, |
.,n .,n |
|
. ..
q imax et q imax sont imposées par les caractéristiques techniques et la nature de la tache à effectuer .
Contraintes sur les couples moteurs:
Les capacités maximales des actionneurs impliquent la formule suivante [94]
? t ? [0,T] , i(t) = imax i =1, .,n (L.64)
Contraintes dues aux obstacles dans l'espace opérationnel :
L'encombrement du à la présence robots fait que la planification tient compte de ces obstacles.
Ces contraintes rendent le problème très complexe. Pour éviter les collisions et si g traduit le distance entre le robot et l'obstacle, la formulation mathématique est la suivante [95,96,97] :
En plus des disfonctionnements déjà cités, la génération des mouvements peut aussi entraîner les phénomènes de survitesses au niveau des articulations [98]. La puissance instantané est telle que :
.
P(t) = (t) . q (t) (L.65)
Le lagrangien s'écrit dans ce cas :


2 n pi t
( ) 2

. .. n ( )
L (q(t), q (t), q (t), ) = u + 1 - u á ?= + (1-á) ?= (L.66)
2 i max pi max
i 1 i 1
.
Ou : pimax = imax. q imax
q . imax représente la vitesse articulaire maximale tolérée de la iéme articulation.
Quand à á, il joue le même rôle que u mais sur le terme des puissances quadratiques si veut
accorder plus ou moins d'importance à la minimisation de ces dernières . G(q(t)] = 0.
l ?
T y ik q k
? . ?
= ? ?+= ?
? k i 1 ?
dTy
? ?
?
l
? ?
dt
k i
= + 1
?
ik q k ? T
. y
?
Donc
Appendice M :
Dérivée de la matrice de transformation homogène par rapport au temps :
l
?
T y
k
dT ?+= ?
y dq
k i k
1
q
dT k
l ? T dq
y y

dt
k i k
+= ? q
1
.
dt
?
Il existe deux formes pour la dérivée de Ty par rapport au temps :
dT l
l
y
y = = ? + ? = ? = ? + ?
. .
y k ik k
?

ik T q q
? k i
dt k i 1 1
dT
l l ?
y T q T q

. . ?
= = ? + ? = ? = ? + ?
dt
y ik k y ik k
?
k i 1 1
? k i ?
Appendice N :
Expression de l'énergie cinétique
Expression de la matrice d'inertie A :
Soit Mk un point appartenant au solide Sk tel que :
O0Mk = T0k(OkMk) OkMk = cte cas des rigides
0
0 = =
( k ) ( k ) ( k )[ k k ]
d 0 d
V M O M T O M
0 0
dt dt
n
?=1 a i b = Trace a b

( [ ][ ] t )
i
Soit deux vecteurs a .et .b alors a .et .b = i
[ ( ) ] ( [ ( ) ] [ ( ) ] T )
0 =
2
V M Trace V M V M
0 0
k k k
t
k k
[ ( ) ] [ ] [ ] ?
T ?
T k
? T ? ? ? T 0 k
V M O M
0 0
?
? . q O M
? = ?
k = ? = = ?
k k i k k
? ? q ? ? i i
? q
i 1 i 1 ?
L'énergie cinétique du solide Sk est donnée par :
E k = ? [ V ( M k ) ] dm
1 2
0
0 2
|
E= |
1 2 |
? k k ? ? ? [ ][ ] ? ? ? T ? ? T ? ? 0 0 ? k ? . . T k Trace ?? q ?? q dm ?? ?? q O M O M i k k k k i ? q ? ? i = 1 i i = 1 i ? |
k k
1 ? k ? ? T ? ? ? ?
[ ][ ] i l
T k
?
E Trace
0 ?? ? ?
0 T 0
k
= ? O M O M dm
. .
q q
k k k k k
2 ?? ?? ?
? q ?? ?? q
i = = =
1 1 1
l ? ? ?
i i i ? ?
[ J ] = ? [ O M ][ O M ] T dm K k k k k .
[Jk] c'est la pseudo matrice d'inertie de dimension (4) relative au corps Sk de la chaîne dans le repère Rk.
Elle est constitué a partir :
Du moment d'ordre zéro dv Sk : mk masse de Sk.
Des moments d'ordre un de Sk : Gk centre de masse de Sk.
Des moments d'ordre deux Sk qui représente la matrice d'inertie [Ik] en Ok dans le repère Rk.
[ ]
I k
[ )
J k
? ? ?
??
Ixx
I xz
-
- -
I xy
-
Ixy
I yx
Iyy
?
?
?
? ?
I I I
xz yz zz
-
( )
- + +
I I I
xx yy zz
- I xy
/ 2 - I xy
( )
I I I
xx yy zz
- +
?
mx ?
m y
mz
m
- I xz
( ) / 2
/ 2 - I yz
yy zz
k ? - - + -
I I I I I
x xx
z
yz
?
mx m y mz
k k
1 ? ?
?? [ ]
? T ? ? T
? ? ?
0 0
k
E Trace k
= ? ? ? J ? . .
q q
& &
0 k k j i
2 ?? ??
= = ? ? ? q ? ?
? ? q
1 1
j i j ? i ? ?
L'énergie cinétique total du système est donnée par :
n
E c E k
= 0
?=
i 1
|
E c |
n k k 1 ? ? ? T ? ? ? T ? ? k ??? [ ] k Trace ? 0 0 . . ? ? J ? q q & & k j l 2 ?? ?? = = = ? ? ? ? ? ? ? q q i 1 1 1 j l j ? l ? ? |
En tenant compte de l'annexe 3 on a :
? T 0 k = ? q l
T 0 k . ? 0 j
? [ ]
0
?
?
si j>k si j=k
tenant compte de l'annexe 3 on a :
? T 0
k =
k l
. ? 0
? q
T 0
l
? T 0
k =
k l
. ? 0
? q
T 0
l
? [ ]
0
?
?
? [ ]
0
?
?
si l>k
si j=k
si l>k
si j=k
|
Puisque |
? T 0 k = ? q j |
[ 0] |
si j>k et |
? T k 0 ? q 1 |
[ 0] |
si l>k alors on peut écrire : |
1
E = ??? c 2 i = = =
n n n
1 1 1
j k
? ? ? T ? ? ?
0 0
k [ ] j l
? T ?
k
Trace ?
? ? J ? . & . &
q q
k
? ? ? q ?? q ??
?
? ? j ? ? l ? ?
1
E = ??? c 2 j = = =
n n n
1 1 1
i k
? ? ? T ? ? ?
0 0
k [ ] j l
? T ?
k
Trace ?
? ? J ? . & . &
q q
k
? ? ? q ?? q ??
?
? ? j ? ? l ? ?
Pour cela :

? T 0
? T 0
Si k < max (l, j) Si k = max (l,j)
? T 0
? T 0
?q
?q
?
?
??
j
l
?
??
??
?q
?q
l
?
?
??
j
[ ]
0
? ?
? [ ]
J k ??
? ?
k
?
??
k
? ?
? [ ]
J k ??
? ?
k
?
??
k
n n
1 ? n ? ? T ? ? ? T ? ?
0 0
k k
E Trace
= ?? ?
? ? ? [ ]
J ? q q
& &
c k j l
2 ?? ??
= = =
? ( ) ?
? ? ? ? q
j 1 1 max ,
l k l j j ? q
? l ? ?
|
n ? k On pose [ ] ? T ? ? A Trace = 0 0 ? T k ? ? ? J ij k ?? = ( ) ? ? max , ? ? ? q q k l j j ? l |
? |
|
|
1 E c = ?? A jl . q & j q & l 2 |
E c [ q & ][ . A ][ . & q] 1 = 2 |
|
Les éléments de la matrice d'inertie [A] sont donnés par la relation suivante :
|
n A Trace = ? ij k i j = max , ( ) |
? |
? T ? ? 0 0 ? T ? k k [ ] J ? ? k ?? ? q???q i j ?? |
Approche d'Euler - Lagrange :[12, 30, 31, 30, 88, 89] : L'approche d'Euler- Lagrange sert à modéliser et présenter la dynamique des robots à travers les équations du mouvement. Elle s'adapte lors des calculs manuels ainsi que pour des calculs par ordinateur. Le formalisme d'Euler- Lagrange et la, transformation homogène de Denavit - Hartenberg amène à un algorithme compact pour présenter les équations dynamiques du mouvements.
L'équation d'Euler- Lagrange est :

?
??
?L
?L
d
-
+
?Ed =
i=
?
??
a, ,n.
Ti
d t
?qi
?qi
?qi
Ou : L est le Lagrangien qui s'exprime par :
L = Ec - Ep
Ec = Energie cinétique totale de toutes les liaisons.
Ep = Energie potentielle totale de toutes les liaisons.
Ed = Energie de dissipation en cas de présence de frottement visqueux. n : Nombre de degré de liberté.
qi : Coordonnée généralisée d'ordre i.
.
q i : Dérivée de la coordonnée généralisée.
Energie cinétique :
L'énergie cinétique est calculée par l'expression de la vitesse :

i
V0
dr i
0
dt
i
?
??
??
r i
r T
i
0 0
=
Ou :ri i est la coordonnée homogène du point (i) exprimée dans le repère Ri comme la
dri
liaison n'est pas flexible, on a i = 0 donc :
dt
i
dq
j
r i
dt
|
V0i = |
i ? Ti 0 = ?= ? q j i j |
Avec Ti i -1 est la matrice de transformation homogène sous une forme plus compacte, nous pouvons écrire :
i
i
V0 iU q r
= ?= [ ]
ij i i
j i
Et
T Q
j - 1
0 j
? ??
U ij 0
=
??
T j i
i =
j - 1
j = i
Pour une liaison rotative on a :
|
Qj |
0 1 0 0 - ? 1 0 0 0 ? ? 0 0 0 0 ? ? 0 0 0 0 ? |
Et pour une liaison de translation :
? 0 0 0 0 ?
? 0 0 0 0 ?
Qj )
= ? ?
? 0 0 0 1 ?
? ?
? 0 0 0 0 ?
L'énergie cinétique de l'élément i dans la liaison i est : dEci = 1/2 trace ( Vi VT i ) dm
En développant l'expression précédente, on obtient :
i i
|
dEci = Y2 trace [? j 1 = |
?= k 1 |
Uij (ri i ri i Tdm ) UT ik qj qk ] |
L'énergie cinétique de la liaison i est :
|
i dEci = Y2 trace [? j 1 = Avec : |
i ?= k 1 |
Uij Ji UT ik qj qk ] |
x dm
i
yi
dm
z dm
i
?
?
?
?
?
?
dm ?
2
? ? ? ?
x dm x y dm x z dm
i i i i i
Ji =
x i
y i
? ? ? ?
dm y dm y z dm
2 i
i i
z dm
i
z dm
i
? ? ? ?
2
x i
y i
z dm
i
x dm
i
y i
dm
? ? ? ?
z dm
i
L'énergie cinétique des actionneurs est définie par :
n
dEca = Y2 ? Ii qi
i 1
=
Où Ii caractérise le moment d'inertie dans le cas d'une rotation d'une masse, pour une translation de l'actionneur i.
L'énergie cinétique totale sera :
n
|
Ec = ?= i 1 |
Eci + Eca |
Energie potentielle :
L'énergie potentielle est décrite par :
n n
|
Ep = ?= i 1 |
- mi gT ri 0 = - ?= i 1 |
- mi gT Ti 0 ri i |
gT = [ 0 0 - g 1 ]
Ou : g est l'accélération gravitationnelle. Enfin, l'énergie de dissipation est donnée par :
n
|
ED = Y2 ?= i 1 |
2 Évi qi |
n i i n
|
L = 1/2 ?= i 1 |
?= j 1 |
?= k 1 |
trace (Uij Ji UT ik ) qj qk + ? i |
mi gT TT ' 0 ri i |
En appliquons la formule d'Euler - Lagrange à la fonction Lagrangienne donnée ci- dessous, on trouve la force ou le couple généralisé.
n
i =?=
j 1
n
..
tr(Ujk Ji UT ji)qk +?=
j 1
n
(Ujkl Ji UT ji ) q k. q l -?
. .
j 1
=
mi gT Uji ri i+ Éviqi
j
?=
k 1
j
j
?= k 1
?
l = 1
(2.55) Avec :
|
Uijk = |
- 1
T k 1
- Qk T j - Qj Ti j - 1 k = j = i
0 k 1
- 1
T j 1
- Qj Tk- Qk Ti k - 1 ' j = k = i
0 j 1
0 j i k

i =1, .,n
j =1, .,n
Méthode directe 1 :
Cette méthode est basée essentiellement sur l'équation d'Euler - Lagrange, sa forme est :
n i n
|
i = ?= j 1 |
Mij (q) |
. qj + ?= k 1 |
?= k 1 |
.. . .. Nijk (q) q j q k+ Gi (q) +Hi ( q j ) , i =1, n |
Avec :
n
Mij (q) = ?
k max( i , j )
=
n
trace (Uki Jk UTki )
Nijk (q) = ?
l max( i , j , k )
=
i =1, .,n
j =1, .,n
k =1, .,n
trace (Uljk Jl UT li )

|
Gi (q) = ?= j 1 |
mj gT Uji |
n
. .
Hi( q i ) = Éviq i
On écrit l'équation dynamique sous forme matricielle qui sera :
T(t) = M(q) q+ N(q, q)+ G(q) +H(q)
. ..
Avec q E Rn ; q ERn ; q E Rn représentent respectivement les positions, les
vitesses et les accélérations articulaires est :
M(q) E Rnxn : Matrice symétrique définie positivement les accélérations inertielles dans l'élément Mij, cette matrice est l'inertie de la ième articulation sur la ième articulation ;
.
N(q, q) E Rn : Vecteur de forces et/ou couples aux accélérations de Coriolis et
centrifuge ;
G(q) E Rn : Vecteur de force et/ou couples dus aux forces de gravitation ;
.
H( q )E Rn : Représente les frottements visqueux ;
T(t) E Rn : Vecteur de force et/ou couples moteurs.
Méthode directe 2 : La méthode directe citée auparavant est efficace, en déterminant le vecteur due aux accélérations de Coriolis et centrifuge.
Pour cela, le modèle dynamique est calculé en 3 étapes :
Calcul des éléments de la matrice d'inertie par méthode directe 1.
Calcul de deux matrices centrifuges de Coriolis qui sont multipliées par leurs vecteurs, la somme des vecteurs obtenue nous donne le vecteur voulu N.
L'extrait de ces dernières matrices se fait par la dérivation de la matrice d'inertie le principe de la conservation d'énergie.
Enfin, le calcul des vecteurs des gravités et des visqueux, s'effectue par la méthode directe, en se basant sur les équations (2.61) et (2.6 3) respectivement. La forme appropriée du modèle final sera :
T(t) = M(q) q+ D(q)[ q q]+ C(q) [q2]+G(q) +H(q)
|
. Avec q ERn ; qERn ; |
q .. E Rn représentent respectivement les positions, les |
vitesses et les accélérations articulaires et :
M(q) E Rnxn : Matrice symétrique définie positive des accélérations inertielles dont l'élément Mij de cette matrice est l'inertie de la ième articulation sur la ième articulation et vive versa ;
C(q) E Rnxn : Matrice des couples centrifuges ;
(n-1)
D(q) ERnx n 2 : Matrice des couples de Coriolis ;
.
H( q )E Rn : Représente les frottement visqueux ; T(t) E Rn : Vecteur de force ou couples généralisés;
. . ( n - 1 )
[ q q ] ?R n 2 : Vecteur de produit des vitesses généralisées;
.
[ q 2 ] ? Rn : Vecteur de carrée des vitesses généralisées; Ou :
|
. . [ q q] = [ q 1 |
. . .
q 1 q n q 2
]T....(2.64)
.
q 2
.

.
q 2
.
q
.
q
.
q
.
q
.
q
n-2
n-1
n
n.....
n
q 3
[2 q ] = [ q 1 q 2 qn ]
2 2 2T
Le calcul de la matrice D de Coriolis se base essentiellement sur la formule suivante :
Dij = 2âiJk
Ou le symbole de Christoffel définit par :

1
? M
i j,
?Mik
? Mij
B
,k =
+
k
ik
?
?
??
j i
? q
? q
? q
?
?
??
2
? M
? M
Puisque la matrice d'inerte est positive on aura les propriétés suivantes :
k
ji ? ; ;
ij
= i j
?
qk
? q j
? M ij
? q k
0pour i = k , j= k
Les éléments de l amatrice centrifuge sont définis par l'équation suivante :
Cij = â iJj
Appendice O :
Expression des coefficients dynamiques
? A
=
Expression des éléments de la matrice des termes de Coriolis
Bi , jl
? A ? A ij il jl
+ +
? q l
? q ? q
j i
? [ ]
? ? ? 2 T ? ?
0 0
n
? T ? ?
Bi , jl 2
Trace
k k
? ? ? J ?? ?
k ??
k i j l
= max( , , )
? ? ? q q ? ?
? ? ? q
j l ? l ? ?
B Trace
, 2
= ?
i jl
n
[ [ ][ ] [ ] ]
l
? ? ?
0 . 0 0 0 0
j l k k k j k
T J T
|
k i = max( , |
j l , |
) |
Expression des éléments de la matrice des forces centrifuges :
C ij ? q 2 ? q
i
i
1
? A ij
? A n
-

C i ,
|
n ? ? 2 ? ? [ ] ? T ? ? ? T ? k = k 2 Trace ? ? ? J ?? ? j k ?? = ? ? ? ? max( , ) ? ? ? ? q q q k i j j l ? i ? ? |
||||
|
n C Trac , 2 = ? i j |
[ [ ][ ] [ ] ] l e T J T ? ? ? 0 . 0 0 0 0 j l k k k j k |
|||
|
k i = max( , |
j l , |
) |
||
Expression des éléments du vecteur force de gravité :
? E p
? q i
n
E p m i g T i u i
= -
? ( )
. . . donc G i
i = 1
G i
n ? ? T ?
?= ?
. .
0 i
- m g
i q
?
i i
? ?
1 ?
n
? . . 0 . 0
G = - ?
i m i g T i i
i = 1
Appendice P F71] :
Propriété des coefficients dynamiques: Termes de Coriolis :
? Aij ? Aik Ajk
B
jk ?
i = + +
?qk ?qi
?qi Avec : Bjl
i = - Bij l si j = i et j = 1
B
Bjj i = - Bij j si j = 1 jk i = 0 si j
= 1
Termes centrifuges :
? Ajj
?qi
|
Cij |
? - 1/2 Aij ?qk |
Avec : Cij = 1/2 Bij j si j >i Cii = 0
|
. co0 = 0 |
, co0 = 0 , |
. V0 = 0 |
Appendice Q [71] :
Formalisme de NEWTON - EULER
Il est adapté à la construction du modèle dynamique inverse. Il permet le dimensionnement de la structure te des actionneurs. Le caractère itératif de ce formalisme réduit le temps de calcul par rapport au formalisme de LAGRANGE [12,31,88,89], il est basé sur une double récurrence : une récurrence avant de la base du robot vers l'effecteur en utilisant al formule de composition pour calculer les vitesses et accélérations donc, le torseur dynamique est une récurrence arrière de l'effecteur vers la base pour calculer les couples des actionneurs en exprimant le bilan des efforts pour chaque corps. La composition des vitesses donne :
.
co j = co j-1 + aj qj aj .( Q . 1 )
|
Vj = Vj-1 1Lj +aj |
. q. (Q.2) j ai |
On dérive ces 2 expressions par rapport au temps pour obtenir la composition des accélérations :
. .
coj = coj-1 + aj ( qjaj + coj-1 A q j aj ) . ( Q . 3)
. ..
..
V J = VJ-1 + coj-1A Lj +coj-1 A(coj-1 A Lj+ a j qj aj ) +aj ( qj aj + co j-1 A qj aj ) ( Q .4)
On arrange l'expression ( Q . 4 ) comme suit :
|
.. V J = V J-1 + |
. coj-1A Lj +coj-1 A (coj-1 A Lj) +aj ( |
.. q j |
q j aj ) ..( Q . 5) |
On peut utiliser cette dernière expression pour déterminer la vitesse du centre de gravité, à savoir :
|
. V GJ = |
1.7 J +coj A(coj A Sj) .( Q . 6) |
Ce qui permet d'obtenir le torseur dynamique :
Fj = mj V GJ .( Q . 7)
.
Nj = Cj coj +coj A( Cj A coj) .( Q . 8)
Fj et Nj représente respectivement la somme totale des forces extérieures et le somme totale des moments extérieurs. On initialise la récurrence par :
Convention de Denavt-Hartenberg: [8, 10, 12,35, 83, 85].
Denavit-Hartenberg ont établi une convention pour définir un repère Ri+1 par rapport à un autre repère Ri en utilisant quatre paramètres a i, ai ,ei,ri selon la figure ci-dessous:

v
yi
e
xi
Zi+1
ai a i
Vi+1
Oi+1
Oi Xi+1
z
r
Figure Q.1 : Représentation des paramètres de Denavit-Hartenberg
[12, 8, 10, 35, 38, 85]
La matrice de transformation homogène ainsi obtenue définit la ième transformation du repère Ri par rapport au repère Ri+1 par la matrice Ti (i+1) :
|
cos sin è è i i - |
cos sin sin cos á è á è i i i i i a |

(
1)
T i
i+
sin cos
è è
i i
-
cos cos sin sin
á è á è
i i i i i
a
ri
0 sin cos
á á
i i
(Q.9)

?
?
? ? ? ?
(Q.11)
cosè -
i
sin 0 0
è i
. ( , ) i i
zi i è è
sin cos0 0
?
è = ? 0 0 1 0
?
Rot
? 0 0 01
0 0 0 1
Cette matrice est une fonction ( i )
T i +1 q de la ième coordonnée généralisée qi notée :
i
q i = óè i +ó i r i avec ói = 1 quand la liaison est prismatique et ói = 0 quand la liaison est rotoïde.
Cette matrice a été obtenue par composition des matrices suivantes :
Rot.(zi,ei).Trans. (zi,ri) Rot.(xi, ai). Trans. (xi+1 ,ai) (Q.1 0)
? ?
?
Trans z r
. ( , ) =
i i ?
?
?
1000 ?
?
0100
001 r i
00 0 1
(Q.12)

?
?
? ? ? ?
(Q.13)
Rot xi
. (
? ?
?
, )
á =
i ?
?
?
0 0 0
1
á á
i i
- sin0
á á
i i
cos0
0 0 0 1
0 cos
0 sin
? ?
?
Trans x a
. ( 1 , )
i i
+ = ?
?
?
?
?
?
0010 ?
?
?
100 ai
0100
0001
(Q.14)
Le modèle géométrique est élaboré à partir du produit des matrices Ti associées à chaque repère
TT T T
n 1 2 1
n +
0 0
= (Q.15)
1 n
Appendice R : [41]
Rappel des notions de théorie des matrices la matrice est un tableau rectangulaire de nombres disposés par ligne et par colonnes. Le tableau ci-dessous
a11 a12
A
a1n
a21 a22
qui contient m lignes et n colonnes est une matrice d'ordre m x
n. Les matrice sont généralement désignées par des
lettres majuscules ( A,B ), les élément des
matrices, par des
lettres minuscules ( aik , bik.....), chacun des
éléments de la matrice est effectué d'un double indice. Le
premier indice i désigne le numéro de la colonne.
Si la matrice contient autant de lignes que de colonnes (m=n), on l'appel la matrice carrée.
Par exemple la matrice de rotation (3x3) est une matrice carrée.
Il y a des cas particulier ou la, matrice ne contient qu'une seule colonne ou une seule ligne, par exemple :
b1
b2
.
.
.
bn
A = ÐÐ a1, a2, an ÐÐ ; b =
La matrice colonne et la matrice ligne sont
désignées par une lettre minuscule (a1b1 ) les
éléments de telles matrice unidimensionnelles sont
désignées par la
même lettre affectée d'un indice
qui indique le numéro de l'élément.
les opérations fondamentales effectuées sur la matrice sont les suivantes : Transposition : la transposée A' de la matrice A s'obtient en substituant à chaque ligne de la matrice A une colonne de même numéro.
Par exemple étant donnée une matrice carrée (3 x 3 ) A .
|
A = |
a11 a12 a13 a21 a22 a23 a31 a32 a33 |
|||||||
|
Sa transposé sera |
A' = |
a11 a12 a13 |
a21 a22 a23 |
a31 a32 a33 |
||||
Multiplication par un scalaire le produit de multiplication de la matrice A par le scolaire X est la matrice
X a11 X a12 X a13
X a21 X a22 X a23
X A =
X a31 X a32 X a33
Obtenu par multiplication de chaque élément de la matrice A par la quantité X Les produits XA et A X définissent une seule et même matrice XA = A X.
Addition : deux matrice A et B sont additionnables si elles ont un même nombre de ligne et même nombres de colonnes.
Par addition des matrices A et B on obtient une matrice C,
C = A + B
Dont les éléments
Cik = aik + bik ( pour tout i,k )
Sont les sommes correspondants des matrice A et B
L'addition des matrices est commutative et associative.
A + B = B + A
A + (B + C) = (A + B) + C = A + B + C
Il en est de même pour la soustraction de deux matrices, car A -B = A +(-1) B . En cinématique des mécanismes, les opérations d'addition des matrices et de leur multiplication par un scolaire s'effectuent sur des matrices colonnes.
Multiplication matricielle. O, ne peut multiplier deux matrices A et B si la première a autant de colonnes que la deuxième a de lignes.
Si A est une matrice d'ordre (m x n ) et b est une matrice d'ordre (m x r ) . Illustrons la règle de multiplication de ces matrices par un schéma :
|
c11 . c1r ci1 .... cir ò k am1 cmr |
a11 . . a1n |
||||||||||||||||
|
ai1 ain am1 amn |
|||||||||||||||||
|
b11 |
b1k |
.. b1r |
|||||||||||||||
|
bn1 |
Bnk |
bnr |
|||||||||||||||
On considère les lignes de la matrice A et les colonnes de
la matrice B comme des vecteurs dimensionnels qui ont pour projections les
éléments des lignes et des colonnes correspondantes. C'est ainsi
que dans la matrice A les éléments de l'i-ème
ligne a11, a12 ,
. a1n sont considérés comme les
projections du vecteur ai de même, la k-ième
colonne
de la matrice B est considérée comme un vecteur bk qui a comme
projection
b1k, b2k , bnk ( remarquons que k est le second indice
) conformément à la règle
de multiplication
matricielle, l'élément cik de la matrice C se trouve
à l'intersection de l'ième ligne et de la
k-ième colonne est produit scalaire cik=ai bk de
l'ième ligne de la matrice A par la k-ième
colonne de la matrice B,
|
n cik=ai1 b1k + ai2 b2k + .+ ain bnk = ? s 1 = |
ais bsk |
(i = 1,2 .m ; k= 1,2 .r) (a)
Au cas ou m=n = r = 3 c'est -à-dire lorsque A,B et C sont des matrices carrées ( 3 x 3 ) (tel est le cas des matrices de rotation), la formule (a) devient
3
|
cik= ?= s 1 |
ais bsk ( i,k = 1,2,3) |
Citons un exemple de multiplication de deux matrices :
|
C = = |
3 . 1 5 12 |
0 1 2 21 15 51 |
= |
4 |
7 8 |
3.4+0.6 |
3.7+0.8 |
Considérons encore un cas particulier: C=Ab
On multiplie ici la matrice ( m x n ) A par la matrice colonne ( n x 1 ) b ; le produit en est la matrice colonne (m x 1 ) c.
En vertu de la règle de multiplication des matrices
b1
x
bm
c1
ci
cm
=
a11 . . a1n
ai1 ain
am1 amn
n
|
ci=ai1 b1 + ai2 b2 + .+ ain bn = ? s 1 = |
ais bs ( i= 1,2,.....,m) |
pour m= n = 3 cette formule traduit l'opération de multiplication de la matrice ( 3x 3) A par une colonne b à trois éléments. Ce cas a lieu pendant la transformation matricielle des projections d'un vecteur.
De façon générale, la multiplication matricielle est non commutative.
AB ? BA
Mais par contre, elle est associative et distributive : (AB)C = A (BC) = ABC (associativité)
A (B+C)=AB+AC (Distributivité)
Techniques stochastiques d'optimisation
Résoudre un problème d'optimisation, c'est trouver parmi un ensemble? de solutions possible S, la solution S* minimisant (ou maximisant) une fonction objectif F(S) donnée. Les techniques déterministes sont efficaces à condition que F(S) soit continue et comporte très peu d'extremums (minimums locaux) sinon les développements mathématiques deviennent très lourds et difficiles à établir. De plus, elles se basent sur
la construction d'une direction de recherche privilégiée dans? donc, le risque de manque l'optimum global S* est d'autant plus quand F(S) comporte plusieurs optimums locaux. Dans ce cas, les techniques stochastiques qui se basent sur une
recherche aléatoire de S* uniformément distribuée dans l'espace? Sont préférées. Seules des informations sur les valeur de F(S) sont nécessaires. Les techniques stochastiques les plus répandues sont :
La technique de Monté-Carlo. Méthode de Hill-Climbing
- Méthode de Monté-Carlo.avec réduction d'intervalle. Le recuit simulé.
Les algorithmes génétiques.
La recherche taboue.
Technique de Monte-Carlo :
Elle consiste à générer
aléatoirement plusieurs solutions S, de les comparer en
retenant
à chaque fois la meilleure solution[5 1]. L'algorithme du
cycle de base présente comme
suit :
Algorithme R. 1 Algorithme de la technique de Monte-Carlo Générer aléatoirement une solution initiale S0 dans ? Prendre S* = S0
Générer aléatoirement une solution S dans ?
Evaluer F (S)
Si F(S) < F(S0 ) alors S* = S

F(S)
F(S*)
I
Figure R. 1 : Convergence d'une technique de Monte-Carlo

Fin Répéter
processus de base est arrête après un nombre d'itérations 1 suffisant pour que la solution recherchée soit acceptable. Pour réduire l'effort de calcul et accélérer la convergence, on introduit la notion de voisinage V(Si) défini par son étendue Li de la meilleure solution Si obtenue à l'étape i. cette idée est exploitée dans les techniques de HillClimbing, Monte-Carlo, recuit simulé et recherche Tabou.
Méthode de Hill-Climbing :
Elle propose d'effectuer une recherche dans un voisinage V(S) d'étendue fixe L
centrée autour de la meilleure solution retenue [52]
S
S

F(S)
F(S)
L
L
|
Centre actuel |
Nouveau centre |
|||
Figure R.2 : Meilleur solution trouvée.
Changement du centre dans la technique de Hill-Climbing
La seul difficulté réside dans le choix de la taille de L. un mauvais choix induit à : Piégeage de la technique dans un minimum local (L trop petit).
Augmentation du temps de calcul (L trop grands)
L'algorithme correspondant est comme suit :
Algorithme R.2 Algorithme de la technique de Hill-Climbing Générer aléatoirement une solution initiale S0
S* = S0
Centre de voisinage = S*
Générer aléatoirement S dans le voisinage V(S*)
Evaluer F(S)
Si F(S) < F(S*) alors S=S*
Centre du voisinage S*
Jusqu'à convergence
Méthode de Monté-Carlo avec réduction d'intervalle :
C'est une version améliorée de la méthode précédente. Elle introduit un facteur de réduction de l'intervalle L. lors du tirage initial, L est choisi large. Au fur et à mesure que le nombre d'itérations i augmente, la taille de L est réduite afin d'affiner la solution. Soit E le nombre d'échecs successifs comptabilisés depuis la dernière amélioration (on considère un échec quand le choix de S fait augmenter F(S)). Quand E prend des valeurs significatives et pour rentabiliser le calcul, on réduit l'intervalle L. pour cela, on se fixe un seuil Emax pour une prise de décision.
L'algorithme correspondant sera alors :
Algorithme R.3 Algorithme de la technique de Monte-Carlo réduction d'intervalle Générer initiale S0 aléatoirement
S* = S0
Générer une solution S dans V(S*) , évaluer F(S*)
Si F(S) < F(S*), alors S*=S
Sinon compter E
Si E = Emax
Réduire V(S)
Jusqu'à convergence
L'efficacité de cette méthde dépend du choix du facteur de réduction de L et de Emax Recuit simulé :
Le fait, à tout prix, de diminuer la fonction objectif F(S) peut conduire à une situation de piégeage de la recherche autour d'un optimum local. L'idée de cette méthode est de
faire échapper F(S) de cette situation (permettre l'augmentation de F(S) pour pouvoir se déplacer vers l'optimum global) [53, 54] .
En métallurgie, le recuit est un traitement thermique qui consiste à chauffer un métal à un niveau tel qu'il permet l'équilibre physico-chimique et structurel d'un matériau et de le refroidir par palier afin que les atomes s'organisent de manière à le faire passer (le matériau) d'une configuration de haute énergie à celle d'énergie minimale. Ce passage obéit à la loi de Boltzman :
P = exp [dE/KT]
Ou :
K : constante de Boltzman
dE : différence d'énergie entre les niveaux initial et final.
F : température.
P : probabilité de passage d'un groupe d'atomes d'un niveau d'énergie E1 à un niveau d'énergie supérieure E2
Par analogie, les configurations stables correspondent aux solutions qui font diminuer la fonction objectif, les configurations instables font augmenter la fonction objectif. La loi de Boltzman adaptée s'écrit alors :
P = exp[?F/T]
e) Recherche Tabou :
Cette technique consiste à se déplacer d'une solution à une autre en s'interdisant de revenir à une solution déjà rencontrée. On définit un voisinage V(S) pour chaque solution S en supposant qu'on dispose d'une liste Tab de toutes les solutions rencontrées depuis le début de l'exécution de la méthode. A partir de la solution courante Si on passe à une solution Si+1 ....V(S) minimisant la fonction objectif et en ajoutant Si à la liste Tab. En pratique, ce processus utilise trop de place mémoire ainsi que le temps de calcul (on doit comparer chaque solution choisie avec tous les éléments de la liste Tab). Pour éviter cet inconvénient, la méthode Tabou préconise de conserver en mémoire la transformation élémentaire qui permet de passe de la solution courante à la suivante en s'interdisant d'appliquer son inverse (la solution courante n'est pas
ajoutée à la liste Tab). La recherche tabou se prête bien au problème d'optimisation discret (optimisation dans les réseaux) [13, 14, 15, 55]
Algorithme R.4 Algorithme de la recherche Tabou
L'algorithme correspondant sera :
Générer aléatoirement une solution initiale S0
S* = S0
Tab = Ø
Répéter
Générer une solution aléatoire S dans V(S*)
Si S Tab alors évaluer F(S)
Si F (S)<F(S*) alors S*=S
Centre du voisinage S*
Sinon ajouter S à la liste Tab
Jusqu'à convergence
Algorithme génétique :
Ils sont basés sur des mécanismes de sélection naturelle et sur la génétique. A partir d'une population de solutions potentielles (chromosomes) initiale arbitrairement choisie, on évalue leurs performances en utilisant des opérateurs simples : la sélection, le croisement et la mutation et on recommence le cycle 16 17 56 .Ces algorithmes différent des méthodes précédentes par les deux points suivants :
On utilise un codage des paramètres (solutions).
On travaille sur une population de points au lieu d'un point unique.
Algorithme R.5 Algorithme génétique
L'algorithme sera le suivant :
Générer une population initiale.
Répéter
Evaluer les performances de chaque individu
Les sélectionner et les regroupe par paires selon leurs
Performances
Générer une nouvelle population (appliquer les opérations de croisements et de mutations)
Jusqu'à convergence
Organigramme R.1: Organigramme d'un processus d'optimisation [71]
Lecture des données géométriques et inertielles des robots

Performances des robots (limites sur les vitesses, les
accélérations et les couples)
Caractéristiques de la
tache (configuration initiale et finale, vitesses initiales et finales)

Initialisation du processus d'optimisation Np=1
Fobj (meilleure)=+8

Générer aléatoirement une courbe q1(spline)
Non
Vérifier les débattements de
q1(spline)
Oui
Calculer q2(spline) à partir de q1(spline)
Non
Vérifier les débattements de
q2(spline)
1 2
3
4
Intervalle de recherche = débattements
Echecmax,
intervalle de recherche minimum

4
1
5
2
Oui
3
Calculer S1 , S2, S3
Calculer T*Q=min Fobj (S1 , S2, S3)
Non
Fobj (T*Q, S1, S2, S3) = Fobj (meilleure)
Calculer T1 , T2
Calculer Ta
Calculer Tv
Calculer T1, Tr
Oui
Calculer T* = intersection (T1, T2, Ta, Tv, T1, Tr)
Fobj (T*) = Fobj (meilleure)
Non
Oui
Echec = Echec + 1
Non
6
7 8
Oui
9
7

|
Fobj (meilleure) = Fobj(T*) |


CONV
Non
Oui
Echec = 0
Arrêter
Oui Non
Affiner la solution
Echec = 0


Echec = Echec max
Tableau R.2 : Liste des systèmes de CAO ayant des application,s dédiées à la robotiques [64] .
|
Fournisseur |
Produit |
Caractéristiques |
Matériel |
|
COMPUTERVISION Tout Gallieni 2 36 av. Gallieni 175 BAGIVOLET Tel 43 60 01 51 |
ROBOGRAPHIX |
Modules spécifiques ROBOT KINEMATIC MODEL et AOUTPUT PROCESSOR représentation Filaire. |
Stations CDS 400 Et Designer v-x |
|
DASSAULTSYSTEMES 40 bd. H. Sellies 92150 SURENES Tel 47 28 00 44 |
CATIA ROBOTICS |
Jusqu'à 20 ddl efforts statiques description minimal des taches. visualisation de la trace. |
IBM 30 XX |
|
GENERAL ELECTRIC /CALM 31 Bd. Bouvets 92000 NANTERRE Tel 47 76 44 31 |
ROBT-SIM |
Représentation filaire. Langage CRL. Modèles dynamiques. |
Famille Appollo Et vax |
|
INTEGRAPH 101 Rue des Slets SILIC 578 94653 Rungis cedex Tel 46 87 15 62 |
INTEGRAPH ROBOT PROGRAMMINNG |
Bibliothèque de trois robots. Pas de chronométrage sur l'image |
Vax et micro- vax integraph |
|
IRISA Compus de Beaulien 35042 RENNES CEDEX Tel 99 36 20 00 |
SIEL (diponible ss certaines conditions) |
Simulation de capteurs locaux et des lois de commande associées. |
Vax et Tektronix |
|
Fournisseur |
Produit |
Caractéristiques |
Matériel |
|
Mc DONNEL DOUGLAS 106 Breaux de la Colline 22213 St Cloud Tel 46 02 31 01 |
ROBOTICS : BUILD PLACE COMMAND ADJUST |
Représentations filaire. Boucles Complexes. Parallélisme. Coopérations de robots. ADJUST pour calibrations. |
Gamme Dec station de travail Evans et Sutherland |
|
SILMA 2111 Grand Road Los ALTOS CA 94029, USA Tel 415 967 5878 |
CIMSTATION (ex ROBOCAM ) |
Représentation filaire. Plusieurs lois de comande parallélisme langage SIL. Aide à l'implantation de sites . |
Famille Appollo |
|
TECNOMATIX Herntalesebeai 55 B.2100 ANTWEPEN ( DEURNE), Belgique Tel .3 332 38 90 |
ROBCAD |
Recherche automatique de trajectoires optimales en temps langage TDL . Collision parallélisme. |
Stations ROBCAD 50 Et ROBCAD 100 |
Tableau R.3 : Avantages comparés des programmations par CAO et par langages textuels [64].
|
CAO |
LANGAGES |
|
|
Raisonnement dans un univers 3D (trajectoire sans collision, apprentissage de pointes étude des contacts...) |
Naturel |
Difficile |
|
Utilisation des structures logiques |
Peu naturelle |
Naturelle |
|
Intégration des informations sensorielles |
Nécessite des modèles de capteurs |
Possible |
|
Evaluation du temps de cycle |
Fonctions Intégrées |
Difficile |
|
Vérification des programmes, apprentissage. |
Hors -ligne (disponibilité totale du matériel) |
Impossible |
|
Optimisation des taches. |
Selon différents Critères |
Sur le site (immobilisation du matériel) |
|
Indépendances robot / programme |
Total |
Partielle |
|
Mise en oeuvre |
Transparence par rapport au robot: ergonomie élevée. |
Apprendre autant de langage que de robots. |
|
Ecart entre trajectoire programmé et trajectoire réelle |
Erreur de modélisation + même sources d'erreurs que les langages |
Due au changeur de coordonnées et à la précision de répétition |
|
Coût |
Elevé |
Raisonnable |
Développement d'un système de CAO sur micro-ordinateur:
Le système est organisé autour d'une base de donnée géométrique tridimensionnelle de type réseau. Un logiciel de modélisation permet de définir des objets par assemblage de primitives élémentaires. Une interface de dialogue opérateur assure une manipulation simple des modèles, essentiellement grâce à une tablette à digitaliser. Enfin, un logiciel graphique soumet les informations vectorielles 3D et les informations de type texte à un contrôler spécialisé.
Base e données : afin de répondre au exigences ce temps de réponse et de place mémoire d'un micro- ordinateur. La base a été spécifiée autour des concepts suivants : Les entités sont stockées sur deux supports différents ; les modèles actifs, c'est-à-dire sollicités par l'application, restant en mémoire vive; les entités activables sont stockées en mémoire de masse et sont accessibles grâce à un répertoire. On minimise ainsi le nombre d'accès disque.
Les modèles activés plusieurs fois dans une même scène ne sont pas dupliqués, ceci pour éviter toute redondance de l'information, la mémoire est gérée dynamiquement. Les trois types d'entités fondamentales représentées en base de données sont les objets, les robots
(Chaînes cinématiques simples) et les outils. A ces entités de base, collectionnées par type dans des bibliothèques, il convient d'ajouter scène, qui rassemblent plusieurs entités ainsi qu'un certain nombre d'élément géométriques de conception (point, droite, plan, repère...) logiciel de modélisation tridimensionnelle :
Les primitives polyédriques sont de type simple (prismatique ou de révolution), ou de type complexe (bielle, chape, équerre). A chaque primitive, est associée une description volumique paramétrée de type quadrique (suspensoïde) , qui constitue une enveloppe convexe englobante de al description. A partir de cette description, les calculs d'interférence entre solides peuvent être rapides.
La modélisation des robots se fait au moyen d'un éditeur graphique interactif permettant de définir, de modifier ou de supprimer, des articulations de type primastique ou rotoide non couplées. Pour chaque liaison, on peut spécifier les limites articulaires, ainsi que les performances en vitesse et en accélération.
Interface de dialogue :
Il met à la disposition de l'opérateur plusieurs fonctionnalités :
La trace d'une évolution d'une session de modélisation dans l'arbre hiérarchique des menus est toujours présente à l'opérateur;
Un ensemble de fonction d'analyse permet d'accéder à la description des entités à tous les niveaux de conception,
La gestion de la tablette à digitaliser permet de décrire et de manipuler les modèles en limitant au strict minimum les saisies au clavier,
Les fonctions graphiques classiques (point observé, distance et direction d'observation, changement d'échelle, zoom) peuvent ter utilisées mode incrémental, procurant ainsi une pression des déplacement continu. Ces fonctions sont accessibles en permanence. Logiciel graphique : il réalise le prétraitement des données géométriques destinées au contrôleur graphique 3D qui assure les transformations, les projections 2D/3D et le clipping. Le logiciel effectue aussi une élimination des lignes cachées, partielle en ce sens que seules les lignes non visibles de chaque solide pris indépendamment des autres solides de la scène ne sont pas visualisées. On arrive ainsi à un compromis réalisme de la scène/temps de traitement satisfaisant.
L'édition d'un fichier graphique intermédiaire 3D permet en outre d'envisager un couplage avec les systèmes de DAO en vue de constituer des dossiers techniques (cotations, sortie graphiques...).
Nous avons développé autour de ce système une application interactive pour la programmation de robots de type SCARA, à partir d'une tablette à digitaliser. Celle-ci offre un moyen simple et efficace de définition de trajectoires 2D, l'altitude et l'orientation de l'outil sont gérées dans des zones spécifiques de la tablette. La trajectoire cartésienne peut être programmée soit en pointant, sur un schéma de la cellule posé sur la tablette, les points de passage désirés, soit en faisant référence à des entités géométriques de la scène représentant la cellule en base de données le choix d'une configuration de départ (coude à droite ou coude à gauche) est spécifié par l'utilisateur [64,101,102,130].
Programmation et contrôle d'exécution d'une cellule flexible d'assemblage : Introduction :
Une cellule flexible d'assemblage (C.F.A) est le lieu, dans un atelier flexible, ou les taches d'assemblage et les opérations associées sont effectivement réalisées. Elle comprend un ensemble d'éléments fortement liés tels que manipulateurs, capteurs et dispositifs de péri- robotique. Ces éléments coopèrent étroitement pour réaliser une tache (ou un ensemble de taches) d'assemblage.
A l'inverse de la problématique des robots dits " d'intervention" (robots mobiles autonomes par exemple) dans laquelle le système évolue dans un environnement peut ou pas structuré (et changeant), et acquiert par lui-même l'essentiel des information nécessaires, la problématique de la CFA est celle de la robotique dite " à poste fixe ". Elle s'intéresse à l'exécution, par un système robotisé, d'une tache pré-établie dans un environnement bien structuré et connu à priori, les aspects essentiels sont, dans ce cas, la programmation, ou plus généralement la " préparation des travaux " ainsi que l'ensemble des moyens permettant une exécution efficace et "robuste" de la tache, d'où la mise en avant des notions de flexibilité et d'autonomie.
La flexibilité : une CFA doit être conçu de manière à permettre la réalisation non pas d'une seule tache mais d'un ensemble de taches appartenant à une même application. Il doit être possible de la programmer (et de la reprogrammer) facilement, de changer ou d'ajouter un composant, d'en modifier la configuration spatiale, de construire de nouveaux programmes traitant de nouvelles variantes de pièces. Bien qu'un certain niveau de flexibilité existe désormais au niveau des composants (manipulateurs généraux programmables dans l'espace cartésien, système de vision programmables ...), ceci ne suffit pas pour obtenir une flexibilité raisonnable au niveau de l'ensemble.
Des méthodes et outils doivent être développés de manière à aider l'utilisateur à réaliser des taches d'assemblage. En effet, une telle programmation nécessite l'intégration et l'utilisation d'un grand nombre d'information et de connaissances provenant de sources très diverses et il n'est pas simple de les combiner dans le cadre d'une approche structurée bien définie.
L'autonomie : a l'exécution, une CFA doit se comporter comme un système autonome qui délivre des pièces assembler selon un processus préalablement défini. Elle doit être capable de gérer ses propres ressources, d'adapter son fonctionnement conformément aux informations les plus récentes, de traiter les événements qui interviennent au niveau de la cellule de manière " Transparente". On ne fera appel au système de gestion de plus
haut niveau (atelier, opérateur) que si les taches sui sont allouées à la cellule ne peuvent être réalisées conformément aux spécifications [64,104].
le système NNS :
Le système NNS comporte un environnement de programmation (environnement hors- ligne) et un système de conduite (système en ligne) (figure R-3)
L'environnement de programmation inclut essentiellement des Modules Décisionnels Spécialisés à aider le programmeur à spécifier et à raffiner progressivement une tache d'assemblage pour une cellule donnée.
A partir de cette description, le compilateur de tache d'assemblage produit un ensemble structuré d'informations appelé modèle d'exécution.
ENVIRONNEMENT DE PROGRAMMATION
Module Décisionnels
Spécialises
Compilateur de tache d'assemblage

Modèle d'Exécution

SYSTÈME DE CONDUITE

Système de commande des composants de la cellule
Figure R-3 : Architecture du système
Le système de conduite est un système basé sur la connaissance (Knowledge - Based system); il assure l'exécution de la tache. Il utilise le modèle d'exécution pour générer, au fur et à mesure, les consignes nécessaires à la réalisation de la tache, à partir des informations provenant de l'environnement (arrivée d'une pièce, fin d'une action, détection d'une anomalie...)
Cette architecture est fondée sur les idées suivantes.
Des capacités décisionnelles doivent être mises en oeuvre à la fois hors - ligne et en- ligne afin de répondre aux objectifs de flexibilité et d'autonomie visés.
Toutefois, il est important de pouvoir distinguer clairement les informations provenant de la phase de conception de la cellule et de définition de la tache, les problèmes qui
peuvent être résolus à la programmation ainsi que les décisions qui doivent être prises au cours de l'exécution. Il est également important de noter que la plupart des problèmes nécessitant des processus décisionnels " lourds" peuvent être traités hors- ligne.
Les aspects modélisation et représentation de la connaissance sont ici de première importance. En effet, tant à la programmation qu'à l'exécution, le système doit être capable de raisonner sur la tache, sur la cellule et sur ses interactions avec (environnement à différents niveaux d'abstraction.
La modélisation :
L'ensemble du système est basé sur une modélisation se la tache à différents niveaux d'abstraction:
Le niveau PROCESSUS D'ASSEMBLAGE spécifié les différents opérations qui doivent être réalisées sur les pièces: alimentation, montage, inspection,etc..
Le niveau TACHE conserve l'évolution des pièces dans la cellule, il définit les différentes actions qui permettent à la cellule considérée de réaliser un processus d'assemblage donné.
Le niveau ACTION explicite la manière de faire évoluer les pièces dans la cellule : grands mouvements d'approche, prise d'objets.
Stratégies d'inscription...ce niveau établit notamment une modélisation fonctionnelle des éléments de la cellule à partir des fonctions qui leurs sont allouées dans le cadre des taches d'assemblage (effecteurs, support, capteur, machine spécialisée, opérateur atelier) ainsi q'une structuration de l'espace de la cellule (en vue de sa gestion pour l'exécution des différentes opérations).
Le niveau FONCTION " encapsule" les primitives fournies parlent systèmes de commande des différents composants de la cellule dans des fonctions génériques manipulées par les niveaux supérieurs.
Un processus d'assemblage consiste en un ensemble d'opérations partiellement ordonnées. Les composants primaires sont introduits dans la cellule et les produits fins repartent sur des convoyeurs.
Une pièce représente l'état d'avancement (pièce primaire, sous - assemblage ...). Chaque pièce est caractérisée par son identité.
Exemple :
L'identité " pièce A " indique que la pièce
correspondante est du type " pièce A " ; l'identité "?(
pièce A1 pièceA2 .pièce An ) " indique que la
pièce
correspondante est du type " pièce A", ou " pièce
A2" ... c'est le cas typique de pièces
fournisseurs à la cellule dans un ordre quelque ou après une opération d'indentification qui ne discrimine pas complément l'identité d'une pièce;
L'identité "INCONNU" ou "!" est associée à toute pièce qui ne correspond à aucune étape du processus d'assemblage.
Les opérations d'un processus d'assemblage font apparaître, disparaître ou modifient l'identité des pièces dans la cellule. Nous définissons les opérations
Opération d'assemblage
Pièce X& pièce Y pièce X Y
Opération de démontage

Pièce X pièce X1 & pièce X2
Opération technologique
Pièce X pièce X*
Opération d'inscription :

pièce X pièce X+ / pièce X-
Opération d'identification

? ( pièce X1 pièce Xn ) pièce X1 pièces Xn
Opération de déchargement
... opération d'alimentation
Pièce X
pièce x

Un processus d'assemblage est spécifié par la donnée de l'ensemble des pièces concernées ainsi que les différents opérations à réaliser sur ces pièces.
Le processus peut comporter plusieurs ordonnancements possibles des opérations.
Exemple :
" Trois pièces A,B et C sont assemblées puis
inspectées avant d'être déchargées. Il existe N
variantes de la pièce A : ( A1 .An); elles sont
alimentées sur un convoyeur
et doivent être identifiées.
Les pièces B et C sont fournies par un autre convoyeur. La pièce
B peut être présenté dans deux positions d'équilibre
différentes (à l'endroit ou l'univers). C doit subir une
opération de vissage avant d'être assemblée. Les
pièces ABC. Peuvent être obtenus soit par l'assemblage de A; et de
B puis de C, soit par l'assemblage de B et de C puis Ai"
L'ensemble du processus peut être représenté par la liste des opérations suivantes :
Algorithme [Processus] R-6 :

? ( A1 .An) alimentation

? ( A1 .An) A1 An |! Identification
B | C alimentation
! déchargement
C C* Op er . technologique
Ai& B ABi assemblage
ABi& C* ABCi assemblage
B& C* BC assemblage
Ai& BC ABCi assemblage
ABCi + ABCi |- ABCi inspection
+ ABCi déchargement

- ABCi déchargement
L'état d'un processus d'assemblage peut être représenté, à chaque instant par l'identité de toutes les pièces présentes dans la cellule :
< état. Processus > :: ( <pièce> * )
Cette représentation est indépendante de toute cellule particulière remarquons qu'elle peut être utilisée en- ligne au niveau de la gestion de l'atelier pour connaître l'état d'avancement d'un processus dans une cellule ainsi que les capacités fonctionnelles d'une cellule après une panne ou un incident (opérations qui ne peuvent plus être réalisées).
L'environnement de programmation :
L'objectif du système d programmation est de préparer et de structurer l'ensemble des connaissances qui sont nécessaire pour gérer et contrôler l'exécution.
Outils pour la programmation avancée des taches de manipulation:
Le but de ce paragraphe est montré, sans aucune prétention à l'exhaustivité, la grande variété des problèmes soulevés par la programmation et la conduite de taches d'assemblage robotisées.
Au cours des dix dernières années des efforts importantes ont été consacrés à la programmation avancée des robots [107,108] de nombreux aspects ont été abordés.
la programmation automatique essentiellement fondée sur les techniques de raisonnement géométrique.
Des résultats significatifs ont été obtenus concernant notamment l'évitement d'obstacles
[ 64,109,110,111,112] la détermination des positions de prise des objets [113], la génération des mouvements fins [114,115,116], l'analyse des incertitudes de positionnement [117,118]. Ces différentes techniques constituent incontestablement les "briques de base" des systèmes de programmation à venir. Cependant deux difficultés demeurent. D'une part, la plupart de ces systèmes sont encore en cours de développement et ne peuvent traiter de manière complètement automatique que des cas relativement simples. D'autre part, l'intégration de ces modules décisionnels pose de problèmes difficiles.
En effets, dans le cas général, une opération d'assemblage ne peut se décomposer aisément en sous- problèmes résolus séparément (grands mouvement; mouvement d'approche, détermination des positions de prise; synthèse des stratégies d'insertion...) Des travaux récents dans ce domaine sont en cours notamment dans le cadre des projets ATALAS- HANDEY [119,120,121]
le développement d'outils d'aide à la programmation au moyen de logiciels de type CAO [123,124] ce sont généralement des outils interactifs. Les principales fonctions fournies concernant l'aide à la configuration des cellules robotisés (choix de manipulateurs, emplacements ...), l'aide à la construction de trajectoires, simulation et la vérification des choix opérés par l'utilisateur.
Le développement de logiciels pour la programmation de taches de montage complexe nécessitant notamment une interprétation des efforts et l'adoption de stratégies locales exprimées directement dans l'espace de la tache [123,125,126,127,128] .
La modélisation des processus d'assemblage pour la génération automatique de séquences opératoires [129] ou la mise en oeuvre d'un ordonnancement opportuniste des actions [105,106] .
Le contrôle d'exécution: ces recherches visent à doter le robot de moyens lui permettant de contrôler l'exécution d'un plan ou d'un programme [130,13 1,132,] l' système doit être capable de vérifier en permanence de conformité de l'état réel de la tache avec l'état planifié.
Au plus bas niveau, la surveillance est effectuée principalement au moyen de capteurs. Le système de conduite doit être capable de déterminer, en fonction de contexte, quelle
sont les surveillance qu'il doit activer. Par ailleurs, il doit être capable de réagir, avec un temps de réponse compatible avec la dynamique de l'environnement, à une grande variété d'évènements généralement asynchrone (échec d'une opération, détection d'une situation non prévue dans le plan courant, ordre en provenance de l'opérateur ou de l'atelier...). Les réactions du système peuvent entraîner des conséquences plus ou moins importantes sur l'exécution en cours: correction locale d'une anomalie de
fonctionnement, amendement, planification totale, arrêt partiel.
Tableau R-4 : Principales formes d'usure [138].
|
Usure abrasive |
à trois corps (low stress) à deux corps (high stress) coupe sous l'effet de chocs (gouging) meulage (grinding) polissage (polishing) |
|
Usure adhésive (scufflng) |
douce (oxidative wear) sévère avec grippage (seizure) galling |
|
Corrosion induite par petits débattements (UIP- usure PEDEBA) |
corrosion de contact ou corrosion de frottement (fretting wear, fretting corrosion) fatigue induite par la corrosion de contact (fretting fatigue) faux effet Brinell (fa/se brinelling) |
|
Usure par fatigue superficielle |
piqûration (pitting), écaillage (spalling) formation de taches grises (frosting) |
|
Usure par fatigue thermique |
|
|
Usure par érosion et cavitation |
érosion par un fluide (impingement érosion) érosion par un fluide chargé (slurry érosion) érosion par gouttelettes liquides cavitation (cavitation érosion) |
|
Corrosion sous frottement |
dépassivation |
RÉFÉRENCES
1. B.MADANI ; « Dynamique de système multi corps ; application à la conception mécanique des robots », Mémoire de Magistère, I.N.G.M. Boumerdès, 07 Juin 1998.
2. E. AURELIEN ; « Cours de JAVA 2 », ENSERB Informatique.
3. C.BARTHLEY. D WILLIS ; « Conception mécanique cinématique et dynamique des robots », Revue Française de Mécanique N° 1995-4, Paris, Automne 1989.
4. M.VUKOBRATOVIK, M. KIRCANSKI ; « Kinematics and trajectory synthesis of manipulation robots », Springer Verlag, Berlin, 1986.
5. P.CHEDMAIL, E. DOMBRE, P. WANGER ; « CAO en robotique outils et méthodologies » Hermès, Paris, 1998.
6. N. SEGUY ; « Système de commande d'un manipulateur S7732 Traité Informatique Industrielle », (c) Technique de l'Ingénieur, France, Décembre 2005.
7. Y. KOREN ; « La robotique pour ingénieurs », Mc Graw Hill, Paris, 1986.
8. P. COIFFET ; « Les robots, Tome 1 : Modélisation et commande » Hermès, Paris, 1981.
9. L. PERROTTE ; « Modélisation et commande », Hermès, Paris, 1994.
10. M. GIORDANO, J.LOTTIN ; « Cours de robotique description et fonctionnement des robots industriels », Armand Colin, Paris, 1990.
11. J.GRANT, F.BARA ; « Introduction à la robotique » Dalloz, 1994.
12. W. KHALIL, E.DOMBRE ; « Modélisation identification et commande des rebots », Hermès Sciences Publications, Paris, 1999.
13. J.DENAVIT, R. S.HARTENBERG ; « Kinématic rotation for lower-pair mechanisms based on matrices », Jour Appl Mech ASME 22.215-221, 1955.
14. P. COIFFET ; « Robots : définitions et classifications R7700 traité Mesures et Contrôle », (c) Technique de l'Ingénieur, France, Décembre 2005.
15. L. KHEMICI ; « Génération de trajectoires optimales coordonnées et sans collision en vue de la supervision multi-robots », Mémoire de Magister, Département d'Electronique, Université de Saad Dahlab de Blida, 2003.
16. P.COIFFET ; « La robotique : principes et applications », Hermès, Paris, 1986.
17. M. PARENT, C.LAURGEAU ; « Les robots : langages et méthodes de
programmation », Hermès, Paris, 1983.
18. V.DUPOURQUE ; « Les contrôleurs de robots », collection Novotique INRIA/AFRI/ADI, 1986.
19. UNIMATION ® : « Unimate Puma Mark II Robot, User's Guide de Val version
560.18.T.A », Unimation Inc® .,1983.
20. C. MELIN, H. HAMDI ; « Automatique Robotique R8 langages de programmation des robots R7720 », (c) Techniques de l'Ingénieur, France, Octobre 1991.
21. M.M. HATTALI ; « Logiciel de calcul de robots industriels application au robot de soudage ALG.SOUD. 1 », Mémoire de Magister, Département de Mécanique, Université de Saad Dahlab de Blida, 2001.
22. E.DOMBRE ; « Environnement de programmation par CAO que faut-il entendre ? », 16p. 36 ref Actes séminaire SYSCOROB Collection A.F.R.I/A.D.I, 1986
23. R. POPPESTONE.P.AMBLER, I.BELLOS ; « An interpreter for a language for describing assemblies robot motion : planning and control », 585 p.317 réf, MIT Press, Cambridge Massachusetts, 1983.
24. M.AIT AHMED ; « Contribution à la modélisation géométrique et dynamique des robots parallèle », thèse de Doctorat, Toulouse, 1993.
25. K.JABELLA B.LASSAMI ; « Développement d'un logiciel d'animation et de commande pour Bras Manipulateurs », Projet de Fin d'études, Département Génie Electrique, Ecole National Poly Technique, El Harrach, Alger, 2002.
26. MARK W. SPDNG AND M.VIDYASAGAR ; « Robot Dynamics and control », Quinnwoodbine, USA, 1981.
27. JOHN J.CRAIG ; « Introduction to robotics : Mechanics and Control », 2nd ed, Addison Wesley Publishing Company, Canada, 1989.
28. R.J. SCHILING.; « Fundamentals of robotics: analysis and control», Prentice Hall, 1990.
29. B. ARMSTRONG, O. KHATIB AND J. BURDICK ; « The explixit Dynamique Model and Inertial parameters of the Puma 560 Arm », In ProcIEEE Int. Conf. On Robotics and Automation, San Francisco, C.A. ,1986.
30. T.MADANI ; « Différentes Approches de Commande Décentralisée à Structure Variables Appliquées en Robotique », Mémoire de Magister, Ecole National Polytechnique, Alger, 2000.
31. J.P LALLEMAND, S.ZEGHLOUL ; « Robotique ; Aspects Fondamentaux, Modélisation Mécanique C.A.O. Robotique Commande », Masson, Paris, Milan, Barcelone, 1994.
32. S.CHARENTUS ; « Modélisation et commande d'un manipulateur redondant composé de plusieurs plate formes de Stewart », Thèse de Doctorat, Université Paul Sabatier, Toulouse, France, Avril 1990.
33. B. GORLA, M.RENAUD ; « Modèles des robots manipulateurs : application à leur commande », Cepadues Edition, 1984.
34. P. BORREL; « Contribution à la modélisation géométrique des robots manipulateurs : application à la conception assistée par ordinateur », Thèse d'État, U.S.T.L. Montpellier, Juillet 1986.
35. ANGELES; « Fundamentals of Robotic Mechanical Systems : Theory methods and algorithms Mechanical Engineering Series», Springer, Verlag, 1997.
36. M .MINOUX ; « Programmation mathématique : Théorie et algorithmes, tome 1 », Éditions Dunod, Bordas et C.E.N.T E.N.S.T., Paris, 1983.
37. Z. MICHALEWICZ ; « Genetic algorithms +data structures = evolution programs », Springer, Verlag, 1992.
38. A. PRUSKI ; « Robotique générale », Ellipses, Paris, 1988.
39. R.J HOOKER; J-PEREIRA ; « An integrated robot analysis procedure vol , N° 10 , PP1069 », IEEE, 1997.
40. A. LIÉGEOIS ; « Modélisation et commande des robots manipulateurs R7730, automatique robotique R8 (c) Techniques de l'ingénieur », France, Octobre 1991.
41. M. RENAUD ; « Contribution à la modélisation et à la commande dynamique des robots manipulateurs », Thèse Doctorat d'Etat Université Paul Sabatier de Toulouse, Septembre 1980.
42. H. ASADA J.J. SLOTINE ; « Robot analysis and control », John Willey & sons, New York, 1990.
43. M.J. ALDON ; « Elaboration automatique des méthodes dynamiques des robots en vue de leur commande », Thèse de Doctorat d'Eétat, Université de Langue de Doc. Montpellier, 1982.
44. A.ALAPETITE, P.COHADE, J.PETTRE ; « B E de vision en robotique sur robot COGNEX-SANKYO », http://alexandre.alapetite.net/dess-irr/robotique/sankyo/index.html. Alexandre Alapetite, Pierre Cohade, Julien Pettre 16-01-2003.
45. A. CASSANO, A, CARDANO ; « A comparison between three variable step algorithms for the integration of motion in structural dynamics », Latin American Research, 1991.
46. COMPUTER SIMULATION OF MANIPULATOR DYNAMICS USING DIFFERENT CONTROL LAWS : «Third International Conference on Advanced Robotics», Versailles, 1987.
47. DYNAMIQUE BEHAVIOUR OF DEFORMABLE AND RIGID ARTICULATED SYSTEMS : «Structural Mechanics in Reactor Technology 10th Conf.», Los Angels, August 1989.
48. SHYING HER LIN , SABRI TOSUNOGLI et DELBERT TESAR ; « Control of a six degree-of- freedom flexible industrial manipulator », I.E.E.E. Journal of Robotics Research, 1995.
49. P.ANDER , J.N KAUFMAN ; LHOTE ; JP TAIL LARD ; « Le robots, tome 4 : Les constituants technologiques », Hermès, Paris, 1983.
50. K.A TABOUB ; P.C MULLER ; « A new control method applied to robot with joint elasticity », PP 565-570, I.E.E.E., 1994.
51. K.P JAUKOWSKY ; H.A EL MAGHY ; « Dynamic decoupling for hydride control of rigid/flexible joint robots interacting with the environment vol 22 » , N°4 , PP 736-747 I.E.E.E., 1992.
52. KHOSMAN ; « Adaptive control of flexible joint robots vol 8 », N° PP 250-267 I.E.E.E., 1992.
53. M.C READMAN ; P.R BELANGER ; « Analysis and control of flexible joint robot », I.E.E.E., 1990.
54. P.RUSSEL ; « Procedure of control for flexible joint robots », I.E.E.E., 1997.
55. M. HADDAD; « Modélisation des Déformations des Bras Manipulateurs par les Concepts de Base de la Théorie des Poutres Evaluation et Compensation des Erreurs » Mémoire de Magister, (c) E. M. P. Bordj El Bahri, Alger, Septembre 1999.
56. A. YOUSNADJI; « La robotique et son environnement rétrospective et aperçu général sur les bras manipulateurs actes des journées d'études sur la robotique et son environnement », (c) E.N.I.T.A.ROB'95, du 16 au 18 Septembre 1995.
57. K.TOUMADJ « Etude et conception d'un robot type utilisé pour le soudage par résistance a Alger SOUD 1, partie cinématique », Projet fin d'étude, Université Saad Dahlab de BLIDA, Département d'Aéronautique , 1988.
58. A.BENSAFIA ; « Etude du comportement dynamique des système polyarticulé plans flexibles », Mémoire de Magistère, I.N.G.M. Boumerdès, 14 Juin 1996.
59. M. BENZAOUI; « Les techniques de commande sous contraintes d'un robot manipulateur redondant », Mémoire de Magister, Automatique, systèmes intelligents de commande et robotique Ecole National Polytechnique, El Harrache, Alger, 2006.
60. GERARD ROORYCK ; « Aspects généraux de la robotique », R 7700, (c) Techniques de l'Ingénieur, France, Octobre 1991.
61. SAIDOUNI TARIK ; « Etude critique et classification des méthodes de description des robots manipulateurs », Thèse de D.E.A. F.N.S.A.M., Paris, 19 Septembre 1990.
62. G.GOYU ; P. COIFFET ; A.BARRACO ; « Mathématique pour la robotique : Représentation des déplacements des robots », Hermès, Paris 1997.
63. J.P LALLEMAND ; S.ZEGHLOUL ; « Robotique aspects fondamentaux : Modélisation mécanique, C.A.O. Robotique, Commande », Masson, Paris, Barcelone, 1994.
64. J.D. BOISSONNAT B. FAVERJON J.P. MERLET ; « Techniques de la robotique tome 2 perception et planification » Hermès, Paris, 1988.
65. P. PRIEL ; « Les robots industriels : Caractéristiques performances et choix » A.F.NOR.
66. Z.ROTH. BENJAMIN ; W. MOORING. ; B. RAVANI; « An overlew of robot calibration », I.E.E.E., Journal of Robotics and Automation vol.R.A3 N° 5, October 1987.
67. A. LIEGOIS ; « Les robots : Analyse des performances et C.A.O. Tome7 » Hermès, Paris, 1984.
68. M.C. READMAN ; P.R. BELANGER ; « Analysis and control of flexible joint robot », I.E.E.E., 1990.
69. B.RUSSEL ; « Procedure of control for flexible joint robots », I.E.E.E., 1997.
70. A. BELAID ; A. KHOUKIH ; « Compensation des erreurs systématiques de positionnement des robots industriels », C.N.P. 1er Colloque National sur la Productique, Tizi ouzou, Algérie, 1998.
71. A . BOUGUERRA ; « Contribution à la planification optimale des robots cooperants », Mémoire de Magister, Département de Mécanique, Université de Saad Dahlab de Blida, Janvier 2005.
72. P . ATHANASIOS ; « Probability random variables and stochastic processes », W.C.B., 1991.
73. S . KRIK PATRIK, C.D. GELATT and P.M .VECCHI ; «Optimization by simulated annealing science » 220 p 671.681, 1983 .
74. J . LAM and J. M . DELOSME ; « Logic minimization using simulated annealing Proc.», International Conference on Computer Aided Design I.C.C.A.D.86, Santa Clara C.A., p.348-351, Novembre 1986.
75. J.LAM and J.M. DELOSME « Simulated annealing : A fast heversitic for some generatic layout problems »
76 . R. BATTITI, G TECCHIOLI ; « The reactive tabu search », O.R.S.A. Journal on Compuling, p.126-140, 1994.
77. F . GLOVER ; « Tabu search » port 2 ORSA J. on computing 1(3) p. 190-206. 1989.
78. F. GLOVER ; « Tabu search » port 2 ORSA J. on computing 2(1) p. 04.32. 1990.
79. T . CRAINIC M. GENDERAU P. SORIANO and M. TOULOUSE ; « A tabu search procedure for multicommodity location all ocation with balancing requirement », Annals of Operations Research, 42 ( 1- 4) p.359-383, 1993.
80. D. DAVIS Cd ; « Genetic algorithms and simulated annealing », Morgan Kaufmann.
81. R. DORSEY and W.MAYER ; « Genetic algorithm for estimation problems with multiple optimal: Nondiffe rentability and other irregular features », Journal of Business and Economic Static's, 13 (1) p. 53-60, 1995.
82. K. KRISHNAKUMAR and D.GOLDBERG ; « Control system optimization using genetic algorithm », Journal of Guidance, Control and Dynamics, 15(3) p.735.740, 1992.
83. M. KIRKANSKI ;O. TIMENKO ; « A geometric approach to manipulator path planning in 3d space in the presence of obstacles avoidance », Robotica, vol, 10p. 32 1-328, 1992.
84. P. BORNE ; G.D. TANGUY ; J.P. RICHARD ; F. ROTELLA ;I.ZAMBETTAKIS ; «Commande et optimisation des processus », Editions Techni, 1990.
85. J.J. GRAIG ; « Introduction to robotics, mechanics and control », Addison Wesley.
86. W KHALIL, J.F. KLEIN FINGER ; « A new geometric notation for open and close loop robots », Proceeding of the I.E.E.E. Int. Conf. on Robotics and Automation, p 1174.1180, San Francisco , 1986.
87. R.P.PAUL ; « Robot manipulators, mathematics, programming and control » ; The M.I.T. Press., Cambridge, 1981.
88. A.A. KOBRINSKI ; A.E. KOBRINSKI ; « Bras manipulateurs des robots : Architecture et théorie » ; Edition Mir, Moscou, 1989.
89. V .ARNOLD ; « Les méthodes mathématiques de la mécanique classique », Edition Mir, Moscou, 1976.
90. L. LANDAU , E.LIFCHITZ ; « Mécanique » ; Edition Mir, Moscou, 1988.
91. R.L. FOX « Optimization methods for engineering design » ; Addison-Wesley, 1971.
92. T. LALIBERTE , C.M. GOSSELIN « Efficient algorithm for the trajectory planning of redundant manipulators with obstacles avoidance » ; I.E.E.E., International Conference on Robotics and Automatics, vol.3, p. 2044,2049, May 1994.
93. Z. SHILLER « Time optimal control of articulated systems with geometric path constraints », I.E.E.E. int. Conf. on Rob and Aut., vol 4p, 2680.2685, May 1994.
94. T. CHETTIBI , H. E. LEHTIHET ; « A new approach for point to point optimal motion planning probles of robotic manipulators » E.S.D.A.2002 A.P.M.-10 A.S.M.E. conf. 2002.
95. K. GLASS, R.COLBAUGH, D. LIM, H. SERADJ ; « Real time collision avoidance for redundant manipulators », I.E.E.E. Transaction on Rob and Aut. N° 1 1,vol 3p. 448-457, 1995.
96. S. MITSI ; K. D. BOUZAKIS ; G. MANSOUR ; « Optimization of robot links motion in inverse kinematics solution considering collision avoidance and joints limits », Mach.and Mec. Theory, N°30 vol 5.p 653.663, 1995.
97. R.V. MA YORGA ; « A frame work for the path planning of robot manipulator », Lasted Thirol Int. Conf. on Rob. and Manufacturing, p61.66, June 1995.
98. F.DANES ; « Critères et contraintes pour la synthèse optimale de robots
manipulateurs : Applications à l'évitement d'obstacles » Thèse de Doctorat d'Etat, Université de Poitiers, 1998.
99. ARTOBOLEVSKI « Théorie des mécanismes et des machines », (c) Editions Mir, Moscou, 1977.
100. D. PAYANNET ; « Modélisation et correction des erreurs statiques des robots manipulateurs », Thèse de Docteur Ingénieur, Montpellier, U. S.T.L., Octobre 1985.
101. M. ABDELHADI ; « Etude et réalisation d'un système de C.A.O. pour la robotique; application à la modélisation l'évolution et la simulation des robots manipulateurs », Thèse de Docteur Ingénieur, U.ST.L., Montpellier, Juillet 1988.
102. C.QUARO ; « Etude et réalisation d'un système graphique interactif pour la robotique », Thèse de Docteur Ingénieur, U.S.T.L., Montpellier, Octobre 1985.
103. E. SCRIVE ; « Etude et réalisation d'un système de C.A.O. pour la robotique, application à la programmation graphique des robots de type SCARA », Thèse de 3ème Cycle, U.S.T.L., Montpellier, Juillet 1988.
104. G. GIRALT ; « Research trends in decisional and multisensory aspects of third generation robots », 2nd I.S.R.R., Kyoto, Japan, Août 1984.
105. B.R. FOX ;K.G. KEMPE; « Opportunistic scheduling for robotic assembly », I.E.E.E., International Conférence en Robotics and Automation, Saint-Louis, Avril 1985.
106. L. S. HOMEM DE MELLO ; A. C. SANDERSON ; « AND./OR. graph. : Représentation of assembly plans », C.M.U.-R.I.-T.R. -86-8, Carnegie- Mellon University, 1986.
107. J.C. LATOMBE ; « Une analyse structure d'outils de programmation pour la robotique industrielle », Séminaire International Sur Les Méthodes de Langages de Programmation de Robots Industriels I.R.I.A., Juin 1979.
108. T. LOZANO-PEREZ ; « Robot programming », Al. Memo Artificial Intelligence Lab. M.I.T, 1982.
109. T. LOZANO-PEREZ ; « Automatic planning of manipulator transfer movements » , I.E.E.E., Transaction on System, Man and Cybernetics, S.M.C. 11.10, 1981.
110. L. GOUZENES ; « Strategies for solving collision-free trajectories problems for mobile or manipulator robot international », Journal of Robotics Research, vol.3, N°4, Winter 1984.
111. B. FAVERJON ; « Obstacle avoidance using an octree in the configuration space of a manipulator », I.E.E.E. International Conference on Robotics and Automation, Atlanta, Mars 1984.
112. B. FAVERJON ; P. TOURNASOUD ; « Planification de trajectoire et systèmes multi-robots : Technique de la robotique », tome 1, Hermès, 1988.
113. J. TROCCAZ ; « Modélisation du raisonnement géométrique pour la programmation de robots », Thèse I.N.P.G., France, Juillet 1986.
114. M. T .MASON; « Manipulator grasping and pushing operations », P.H.D. Thesis MIT. Al. Lab., 1982.
115. J. M .VALADE ; « Geometric reasoning and synthesis of assembly trajectory 85», I.C.A.R, Japon, Septembre 1985.
116. C. LAUGIER ; PUGET ; P. THEVENEAU ; « Traitement des incertitudes en programmation automatique des robots : Techniques de la robotique », Hermès, tome 1, Paris, 1986.
117. R.A. BROOKS ; « Symbolic error analysis and robot planning », The International Journal of Robotics Research, vol 1 N°4, Winter 1983.
118. TROCCAZ. P PUGET ; « Dealing with uncertainties using program proving method », U.T. I.S.R.R. Santa Cruz, USA, Aout 1987.
119. T. LOZANO-PEREZ, R A BROOKS ; « A approach to automatic robot programming » , Al. Memo 842, Al. lab. MIT., 1984.
120. T. LOZANO-PEREZ ; J.L. JONES; E. MAZER et AL. HANDY; « A robot system that recognizes : Plans and manipulates » I.E.E.E., International Conference on robotics and automation, Raleigh, USA, Avril 1987.
121. E. MAZER , T. LAZANO-PEREZ ; « The structure of an interpreter for task-level robot programs » I.C.A.R. 87, Versailles, Octobre 1987.
122. C. LAUGIER. J. TROCCAZ; « A system for automatic programming of manipulation robots » 3rd International Symposium of Robotics Research, Gouvieux, France, Octobre 1985.
123. JOURNÉES ANNUELLES DU PROGRAMME A.R.A. ; Toulouse, Septembre 1984.
124. E. DOMBRE, P BOREL, A LIÉGEOIS ; « A CAD. system for industrial automation », vol 2, 1984.
125. A. GIRAUD ; « Generalized active compliance for part mating with ensemble robots », Isrt. I.S.R.R., Britton Woods, Septembre 1983.
126. C. REBOULET ; A ROBERT ; « Hybrid control of a manipulator equipped with an active compliant wrist : Robotics research 3», Mit press., USA, 1986.
127. O. KHATIB ; I .BURDICK ; « Motion and force control of robot manipulators », I.E.E.E. International Conference on Robotics and Automation, San Francisco, USA, Avril 1986.
128. J. IRIGOYEN ; « Commande en position et en force d'un robot manipulateur d'assemblage », Doctorat de l'Université Paul Sabatier, Toulouse, Octobre 1986.
129. A. BOURJAULT ; « Contribution a une approche méthodologique de l'assemblage robotisé; l'élaboration automatique des séquences opératoires », Thèse d'Etat, Université de Franche-Comté, Besançon, Novembre 1984.
130. M. GHALLAB ; « Task execution monitoring by compiled production rules in an advanced multi- sensor robot », 2nd Intentional Symposium or Robotics Research, Kyoto, Japon, Août 1984.
131. DONNEES TECHNIQUES ; « Machines outils, perceuses radiales, TGL 42 995 », République Démocratique Allemande, Aout 1985.
132. DONNEES TECHNIQUES ; « Appareil de fraisage vertical Ap. FS. 250/2 » Caractéristiques techniques « DZFG 200 x 500 » ; Atelier de fabrication mécanique, Département de Génie Mécanique, Université Saad-Dahleb de Blida.
133. R. MAZARI ; N. MOHAMMEDI ; « Etude dynamique et avant projet de conception d'un Robot de soudage [ALG.SOUD.1] », Projet de fin d'étude, Département de Génie Mécanique, Université Saad-Dahleb de Blida, 1998.
134. N. MEGHERBI ; N. BEDIAF ; « Programmation d'un robot manipulateur des machines-outils (ALGERIE-M.O.-1) », Projet de Fin d'Etude Département d'Aéronautique Université de Saad-Dahleb, 2005.
135. A. TIAIBA ; « Etude et conception d'un Robot manipulateur type (ALGERIEM.O.1) », Mémoire de fin d'étude, Département de Génie Mécanique, Centre Universitaire de M'sila, 1995.
136. A. ALLALI ; A. BRAHIMI, M. M. HATTALI ; «Model mathématique d'un robot de soudage par résistance par points [type : ALG.Soud.-1] » Communication aux JMA 2000.
137. A. ALLALI ; A. BRAHIMI ; A. BENMISRA ; M. K. HALAIMIA ; «Model mathématique d'un système mécanique articulé» Communication aux NCMES'07, May 26-27,2007.
138. A. ALLALI ; A. BRAHIMI ; A. BENMISRA ; M. K. HALAIMIA ; «Robot manipulateur des machines outils», Brevet d'invention, I.N.A.P.I. , Alger, Mai 2007.
139. A. ALLALI ; D. TOUMI ; A. BRAHIMI ; M. M. HATTALI ; «Robot de soudage par résistance», Brevet d'invention, I.N.A.P.I. , Alger, Octobre 1999.
140. R. CHATILA ; « Mobile robot navigation space modeling and decisional processes », Robotics Research 3 ,MIT. Press., USA, 1986.
141. E. LOPEZ MELLADO ; « Le control d'exécution dans les cellules flexibles d'assemlages », Thèse de Docteur- Ingénieur U.P.S. L.A.A.S., Toulouse, Décembre 1986.
142. R. S. SMITH ; M. GINI ; « Robot tracking and control issues in an intelligent error recovery system », I.E.E.E. International Conference on Robotics and Automation, San Francisco, USA, Avril 1986.
143. V. DUPOURQUE ; « Architecture matérielles des contrôleurs de robots : Techniques de la robotique», tome 1, Hermès, 1988.
145. D. A. BOURNE ; M. S. FOX ; « Autonomous manufacturing automating the job- shop » I.E.E.E. Computer vol. N° 4, Winter 1983.
146. A. R. SANDERSON ; G. PERRY ; « Sensor- based robotic assembly systems : Research and application in electronic manufacturing », proceedings of the I.E.E.E., Vol. 71, N° 7, Juillet 1983.
147. R. CASSINIS ; « Resource allocation in industrial multirobot systems », I.E.E.E. International Conference on Robotics and Automation, San Francisco, USA, Avril 1986.
148. A. CORNET ; J.-P. DEVILLE ; « Physique et ingénierie des surfaces », (c)EDP Sciences, Paris, 1998.
149. D. DRIBINE ; « Modélisation cinématique et dynamique de bras manipulateur », Thèse de Fin d'Etude Electronique, Ecole Nationale Polytechnique, El Harrache, Alger ,1996.

