Programmation des robots industriel et application sur le robot manipulateur Algérie machines outil 1

CHAPITRE 2

MODELISATIONS GEOMETRIQUE, CINEMATIQUE ET DYNAMIQUE
DIRECT ET INVERS DES SYSTEMES MECANIQUES POLY ARTICULE AUX
ELEMENTS RIGIDES

2.1 Modèle géométrique [9, 27] :

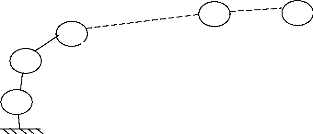
Le modèle géométrique d'un robot constitue une représentation mathématique, en le considérant comme une chaîne simple, ouverte, de (n) solides (corps), rigides, sans boucles ni branchement, sans masses, articulés entre eux; chaque corps est réduit à sa plus simple expression, c'est-à-dire à son orientation et à sa position par rapport au corps précédent.

Ci = (Pi, Oi) = (position i, orientation i).

Ci Cn

C2

P2O2 PiOi PnOn

C1

R

P1O1

Figure 2.1 : Structure arborescente. [21,38]

Chaque configuration géométrique possible est définie par un ensemble de variables articulaires qui traduisent les déplacements relatifs d'un corps par rapport au précédent. Les variables articulaires (ou coordonnées articulaires ou coordonnées généralisées) font le lien entre la position et l'orientation de l'organe terminal et les consignes définies dans un repère de base.

Nous l'exprimons par : X _i /R i = F(q₁,q₂, q n (2.1)

Variables Variables

opérationnelles articulaires

2.2 Les variables articulaires :

Les variables articulaires expriment l'ensemble des possibilités de mouvement entre deux articulations, le modèle géométrique est composé tel que sur les six possibilités de mouvements élémentaires d'un corps par rapport à un autre (3 rotations et 3 translations) une seule est retenue[8, 10, 11,12] . Ainsi les possibilités de mouvements multiples aux niveaux technologiques sont décomposées en mouvements élémentaires, au niveau du modèle, l'orientation entre deux repères peut être traitée selon plusieurs techniques classiques ;Les matrices de rotation, les cosinus directeurs, les angles de Bryant, les angles d'Euler [12, 10, 11]...

.

2.3 Le système de paramètres de Denavit-Hartenberg : [11, 12, 13, 24, 25, 26, 27, 28] :

La méthode est la plus couramment utilisée en robotique pour la définition de l'orientation et de la position des différents éléments d'un système mécanique articulé.

Dans le domaine de la robotique, l'élaboration du modèle nécessite une étude détaillée et approfondie de la structure du robot. Dans la littérature il existe plusieurs méthodes pour la modélisation des mécanismes à structures de chaînes simples ou complexes, ouvertes ou fermées [24].

Les plus utilisées sont les méthodes de Denavit-Hartenberg et Sheth-Uiker, La première est très bien adaptée pour les mécanismes à structures de chaînes simples où toutes les liaisons sont élémentaires, mais, elle présente des difficultés lorsqu'il s'agit de mécanismes à structures de chaînes complexes; en effet les corps possédant plusieurs liaisons élémentaires (rotoïdes et / ou prismatiques) en aval, doivent être dotés d'autant de repères, ce qui entraîne des lourdeurs. La deuxième méthode vient palier les inconvénients cités précédemment, mais elle présente des redondances pour les mécanismes à structures de chaînes simples.

L'utilisation de la transformée de Denavit-Hartenberg (D.-H.), facilite la description géométrique du manipulateur ; cette dernière nous permet d'aboutir au modèle cinématique et géométrique direct et inverse du robot.

La même transformation offre une souplesse dans le calcul du modèle dynamique direct en utilisant le formalisme d'Euler Lagrange [25, 26, 27, 28].

Denavit et Hartenberg ont proposé une méthode qui repose sur l'assignation d'un repère
unique pour chaque lieu, cette convention est une méthode systématique, elle permet le

passage entre articulations adjacentes d'un système robotique, elle concerne les chaînes cinématiques ouvertes ou l'articulation possède uniquement un degré de liberté, les surfaces adjacentes restent en contact. 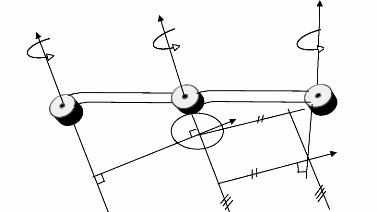Le choix adéquat des repères dans les liaisons, facilite le calcul des matrices homogènes de Denavit-Hartenberg et permet d'arriver rapidement aux informations de l'élément terminal dans la base et vice versa; la figure 2.2 représente l'utilisation de cette notation pour deux liens successifs l'axe Zi du repère est concourant avec l'axe de l'articulation i, quand à l'axe Xi, il est sur la droite perpendiculaire aux axes Z i -1 et _Zi. .

Zi-2

è i

è i+1

Joint i+1

Joint i-1

zi

Zi-1

Segment i-1 Joint i Segment i

è i-1

Xi-¹

xi

d i

li

Figure 2.2 : Système de Coordonnées et Paramètres de Denavit-Hartenberg

[12, 21, 27, 29, 30,31, 38,71].

Quatre paramètres sont alors utilisés pour décrire la forme géométrique d'un lien et sa position par rapport au lien précédent, la notation de Denavit-Hartenberg ne fonctionne que pour des chaînes cinématiques sérielles, (pour des chaînes arborescentes des ambiguïtés apparaissent),

Cette notation, apparue très tôt dans le domaine de la robotique est encore largement utilisée par la communauté scientifique pour décrire les robots en vue de leur analyse et/ ou modélisation; quelques variantes relativement proches sont aussi courantes, comme par exemple la notation Paul, cette notation se différencie, essentiellement, de celle de Denavit-Hartenberg, par l'assignation des paramètres, relativement aux liens, (décalage des indices).

Les étapes à suivre pour cette technique sont les suivantes :

1^ére. Numérotation des segments constitutifs du bras manipulateur de la base vers l'élément terminal, on associe le référentiel "zéro" à la base de celui-ci, et l'ordre "n" à l'élément terminal (effecteur).

2^éme.Définition des axes principaux de chaque segment :

· Si zi et z _i-1 ne se coupent pas, on choisit xi de manière à être en parallèle avec l'axe perpendiculaire à z _i et z i-1.

· Si zi et _zi-1 sont colinéaires, on choisit xi dans le plan perpendiculaire à zi-1. 3éme . Fixer les quatre paramètres géométriques : di, Oi, ai et ai, (voir la figure 2.2) pour chaque articulation tels que :

· di. est une coordonnée de l'origine oi sur l'axe z _i-1 pour une glissière di est une variable et pour une charnière di est une constante.

· Oi. est l'angle que l'on obtient par vissage de x _i-1 vers xi autour de l'axe z _i-1 pour une glissière Oi c'est une constante et pour une charnière Oi c'est une variable.

· li. est la distance entre les axes z _i et z _i-1 mesuré sur l'axe xi négatif à partir de son origine jusqu'à l'intersection avec l'axe z i-1.

· a _i. est l'angle entre l'axe zi et z _i-1 obtenu en vissant z _i-1 vers zi autour de xi . 4éme . On forme enfin, la matrice homogène de Denavit-Hartenberg de déplacement qui lie la rotation et la translation, la partie supérieure gauche définit la matrice de rotation _Ri-1 et le vecteur de translation à droite ⁱ

di -1.

Par la suite on aboutit à la matrice de transformation de Denavit-Hartenberg suivante :

a i - 1

cos è è

- sin0

i i

d i

1 =

- -

sin sin

á á

- -

1 1

i i

sin è á è á

cos cos cos

i i i i

- 1

T -

i ? sin sin cos sin cos cos

è á è á á á

i i i

-

- -

1 1 d

?

i

(2.2)

i

i i i

- -

1 1

0 0 0 1

Finalement on peut écrire le modèle géométrique direct sous la forme :

X= f (q) (2.3)

Avec X ? 6

Rles coordonnées cartésiennes, et q? 6

R , les coordonnées articulaires, on va admettre quelques hypothèses [12 , 27, 29, 30, 31] dans le but de simplifier la modélisation des robots, ces hypothèses sont les suivantes :

Les liaisons du manipulateur sont rigides.

Les jeux dans les articulations sont négligeables.

Les capteurs ont un gain unitaire et de dynamique négligeable

L'orientation d'un repère est donnée par une matrice 3x3, représentant les 3 vecteurs unitaires. On a cependant indiqué que dans ces 9 valeurs, plusieurs sont redondantes et qu'en fait, il est possible de donner l'orientation en donnant simplement 3 valeurs. Supposons, par exemple, qu'on désire avoir un robot qui suit une certaine trajectoire dans l'espace en lui donnant un certain nombre de points intermédiaires à passer. Si chacun des points est donné par 3 positions et une matrice d'orientation 3x3, cela risque de prendre assez de mémoire, il est préférable de ne prendre que 3 chiffres pour l'orientation, en fait il y a une infinité de choix possibles pour définir une orientation d'un repère par rapport à un autre, l'idée est de trouver 3 transformations qui vont faire passer le premier dans le deuxième, on peut adopter la paramétrisation d'Euler ZYZ, chaque liaison d'un manipulateur fait des rotations ou des translations par rapport au référentiel d'inertie fixe, par exemple, un repère fixé à la base du robot.

Le calcul des coordonnées des liaisons du manipulateur exprimées dans le référentiel d'inertie de la base est relativement difficile, cette difficulté augmente suivant l'ordre de la liaison jusqu'à l'élément terminal; pour ne pas alourdir les calculs et ramener toutes les informations géométriques au repère d'inertie de la base, il est judicieux de localiser les articulations correspondantes et situer chaque liaison à son propre référentiel.

Le passage d'un référentiel à un autre est garanti par les transformations homogènes. Lorsqu'on a uniquement des rotations, on se satisfait d'une matrice de transformation R de troisième ordre, et lorsqu'il existe une translation autour d'un point, on est obligé de passer à une matrice de quatrième ordre pour permettre au référentiel de transformer, dans ce cas le vecteur de position ^ap sera augmenté par une quatrième composante pour avoir un vecteur de position ^ap' exprimé par ses coordonnées homogènes [27, 30] :

? P ?

x

? ?

(2.4)

p= ? P_y ?

? ?

? Pz ?

Le vecteur homogène correspondant est :

? P ?

x

? ?

? P_y ?

P_z

? ?

(2.5)

? 1 ?

p ' = ? ?

La matrice augmentée de transformation aura la forme suivante [27, 30] :

?

(2.6)

r r r d ? 11 12 13 x

?

? ?
r r r d
21 22 23 y ?
T = ? ?
r r r d

31 32 33 z

? ?

? 0001 ?

Avec _rij les composantes de la matrice de rotation R1 et d_x, d_y et d_z sont les composantes du vecteur de translation qui comportent les coordonnées du repère de destination dans le repère source. Si on appelle T la matrice de transformation du référentiel (x1,y1,z1) vers le référentiel (x2,y2,z2) alors P' x2 y2 z2 = T P' x1 y1 z1 . (2.7)