Applications des intégrales stochastiques en macroéconométrie

1

UNIVERSITE DE KINSHASA

FACULTE DES SCIENCES Département des Mathématiques et Informatique

Directeur : Professeur Ordinaire Mbuyi Mukendi Eugène Co - Directeur : Professeur Mabela Matendo Rossin

Applications des intégrales Stochastiques en

macroéconométrie

Mambo Ntanu Bin Kikuni Lewis
[e-mail]

4 octobre 2019

1

"In almost all circumstances, and at all times, we find ourselves in a state of uncertainty. Uncertainty in every sense. Uncertainty about actual situations, past and present... Uncertainty in foresight this would not be eliminated or diminished even if we accepted, in its most absolute form, the principle of determinism; in any case, this is no longer in fashion. Uncertainty in the face of decisions more than ever in this case... Even in the field of tautology (i.e of what is true or false by mere definition, independently of any contingent circumstances) we always find ourselves in a state of uncertainty ... (for instance, of what is the seventh, or billionth, decimal place of n ...)..." Bruno de Finetti ([? ],p.3)

» The advancement and perfection of mathematics are intimately connected with the prosperity of the State» Napoleon¹

1. cited [? ]

2

Notation et Abréviations

1ç(x) fonction indicatrice

lim infx_n limite inférieure

lim sup limite supérieure

fl intersection

U union

~ distribuée

oc infini

® produit tensoriel

a A b minimum de a et b

ìeb maximum de a et b

= identiquement égal

a_n = o(bn) an

bn ? 0

a_n = O(bn) an

bn est bornée

(Ù, 3, P) : espace de probabilité

N ensemble des nombres entiers

R ensemble des nombres réels

C ensemble des nombres complexes

c`adl`ag continue à droite, limite à gauche

p.s. presque sûrement

v.a. variable aléatoire

L_s opérateur elliptique

max maximum

min minimum

exp exponentiel

h.it variation quadratique

. :valeur absolue

k.k_p norme d'ordre p

Ck dérivable d'ordre k

P somme

f intégrale

X+ partie positive de X

X partie négative de X

E(x) espérance mathématique

E(x P) espérance conditionnelle

P(A B) probabilité conditionnelle

var(x) variance de x

? dérivée partielle

?xi

Ati = ti - ti-1

3

f odWt intégrale de Stratonovich

Wt processus de Wiener standard au temps t Bt mouvement brownien au temps t

Résumé

Motivation

Problem Statement

Approach

Results

Conclusion

Les incertitudes dominent le monde réel et rendent les décisions issues de la mathématique inefficace. Pour prendre en compte ces incertitudes observées ou non dans les variables et/ou paramètres,les mathématiciens désenveloppent la théorie des processus stochastiques.Beaucoup de phénomènes sont formulés sous forme des équations différentielles stochastiques et aussi non observables Xiong[177], [166],[167], [67] [177], Stokey[166],[67]. La question que ce travail va répondre est comment peut - on estimer les coefficients stochastiques du modèle macroéconomique?

La modélisation du monde réel n'a pas de sens lorsque le modélisateur ne tient pas en compte l'incertitude qui induit les décideurs en erreur.

Cette étude a trois objectifs :(i) présenter les outils et

1

Introduction

Problématique

Les équations différentielles stochastiques constituent un choix naturel pour modéliser les systèmes dynamiques qui subissent les influences aléatoires [31]. Par exemples, Beaucoup de phénomènes tant naturels qu'économiques sont formulés sous forme des équations différentielles stochastiques [177], [166][167], [67].

Considérons un modèle économétrique qui se présente sous forme d'équation différentielle stochastique d'Itô paramétrique suivant

dXt = u(e, t, Xt)dt + u(19, t, Xt)dWt, t = 0, X0 = (,

où {Wt, t = 0} est le processus de Wiener standard, u : O × [0,T] × R ? R, appelé le drift coefficient et u : E × [0, T] × R ? R⁺, appelé le coefficient de diffusion. Ces coefficients sont des fonctions continues et les paramètres à estimer e et 19, O ? R, E ? R et E(0) < 8, sont des inconnus du modèle économétrique à estimer.

Le drift coefficient est appelé le coefficient de tendance ou damping coefficient ou translation. Le coefficient de diffusion est aussi appelé volatilité. Les coefficients de tendance et de volatilité sont respectivement la moyenne instantanée et la déviation instantanée du processus.

Sous les conditions lipschitzienne et de croissance linéaire sur les les coefficients u et u, il existe une solution forte unique de l'équation différentielle stochastique.

(1) condition lipschitzienne ku(t,x) - u(t,y)k = K|x - y| |á(t,x) - á(t, y)| = K|x - y|

et

(2) condition de croissance linéaire ku(t, x) - u(t, y)k² = K(1 + |x|²) |á(t, x) - á(t, y)|² = K(1 + |x|²)

Cette solution est appelée le processus de diffusion ou simplement diffusion, est une semimartingale markovienne forte continue.

En économie, les incertitudes dominent et rendent les décisions issues de la modélisation économétrique inefficaces. Pour prendre en compte ces incer-

2

titudes observées ou non dans les variables et/ou paramètres les mathématiciens développent la théorie de processus stochastiques. La modélisation de l'économie dans son ensemble, macroéconomie, n'a pas de sens lorsque l'économiste ne tient pas en compte les incertitudes qui induisent les décideurs en erreur.

Cette étude se focalise à répondre aux questions suivantes : (i) Comment peut - on estimer les paramètres de modèles économétriques présentés sous forme des équations différentielles stochastiques? (ii) Comment peut-on estimer les paramètres stochastiques de modèles économétriques présentés sous forme des équations différentielles stochastiques suivant un processus stochastique?

Objectifs du travail

Cette recherche a trois objectifs : (i) présenter les outils et techniques de la modélisation stochastique en général et ceux des intégrales stochastiques en particulier; (ii) passer en revue l'aspect théorique existante des applications des intégrales stochastiques à la théorie d'estimations de paramètres des modèles mathématiques stochastiques [37],[170], [171], [172], [122], [124], [22], [116], [21], [116], [117], [110], [31], [177], [17], [98], [141]; et (iii) présenter les applications de calcul stochastique à la modélisation économétrique de l'économie congolaise en vue d'orienter les décideurs congolais.

Revue de la littérature

La littérature sur le calcul stochastique est abondante et dynamique date depuis les travaux pionniers de Wiener, Itô, Stratonovich, Fisk, et Skorohod[87], [45], [97], [155], [111], [135].Cette évolution rapide est due au développement technologie des outils informatiques. [149] ,[61], [95], [106],[145] [82], [31], [49], [146] , Les livres références sont ceux de [92], [58], [88], [25], [105], [87], [136], [162], [50], [149], [147], [150]. Le domaine de l'estimation statistique a subi des avancés de cette théorie [37], [172], [173], [170], [1], [171], [122]. Les propriétés asymptotiques telles que la consistance forte ou faible, la normalité asymptotique, l'efficience asymptotique, etc. pour certains estimateurs de paramètres drift des équations différentielles de Itô observés à travers l'intervalle de temps, ont été étudiés durant les quatre dernières décennies.

3

La méthode de maximum de vraisemblance a été utilisée pour les équations différentielles stochastiques linéaires homogènes [154], [153] et les équations différentielles stochastiques non linéaires homogènes [115], [153]. Les méthodes d'estimation Bayésienne, de probabilité maximale, de contraste minimale, de M - estimation, et de distance minimale sont employées pour estimer les paramètres des équations différentielles stochastiques [115], [179]. Pour les équations différentielles stochastiques non linéaires et non homogènes, les méthodes de maximum de vraisemblance et Bayésienne [115], [154], [5]. Les études empiriques pour l'estimation des paramètres de processus de diffusion sont abondantes [153] , [5], [3],[4],[2], [116],[117].

La deuxième application des intégrales stochastiques de cette recherche est sur la théorie de filtre stochastique. L'objectif de filtre stochastique est d'utiliser les outils de probabilité pour estimer les processus stochastiques non observables qui apparaissent dans plusieurs domaines tels que la com-munication,target tracking, et la mathématique de finance [177]. Ces cinq dernières décennies les recherchent ne cessent de croitre abondamment dans l'estimation de paramètres des équations différentielles stochastiques et la théorie de filtre stochastique [22] , [173],[10], [23],[161], [110], [116], [21] , [31], [177], [16], [17], [98] , [141].

L'application de calcul stochastique en économétrie est très importante car les incertitudes gouvernent le monde économique. On peut dire qu'en économie, l'incertitude est par tout et pour tout. La modélisation économétrie classique suppose que les variables et les paramètres sont non stochastiques (déterministes) et que le terme d'erreur est aléatoire [46],[168][129], [131], [130], [72],[128], [127], [80], [130]. Cette modélisation suppose l'absence d'incertitudes dans les variables et les paramètres ce qui ne reflète pas la réalité.

En macroéconomie, par exemple, les politiques économiques prises sur base de cette modélisation sont erronées et inefficaces. Le calcul stochastique vient corriger en supposant que les incertitudes sont dans les variables et les paramètres. En économétrie des séries temporelles, par exemple, le concept stochastic a progressivement documenté la théorie économétrique pour mesurer l'incertitude observée. Avec les modèles GARCH ont utilité les concepts stochastic volatility Model pour mesurer la volatilité stochastique [57], [60],[36].

4

Contribution scientifique originale

Cette recherche a comme contribution principale de tracer la nouvelle direction de la théorie économétrique basée sur les calculs stochastiques en comblant l'écart qui existe entre la théorie et la pratique.

En effet, cette étude a confronté la théorie de l'économétrie de processus de diffusion aux données congolaise théorie d'estimation optimale. Cette étude donne deux résultats : (i) pour la première application, le résultat de l'estimation montre que l'inflation observée à Kinshasa est un processus de diffusion généré par l'équation différentielle stochastique dont le coefficient de persistance est 54 pour cent(ii) pour la seconde, les contributions de différents facteurs explicatifs, les investissements et la main d'oeuvre, du bien - être économique congolais sont des processus stochastiques.

Hypothèses

Dans ce travail deux hypothèses ont été retenues à savoir : (i) cette recherche suppose que les variables et les paramètres sont des processus stochastiques, i.e., les incertitudes peuvent être observées ou non dans les variables et les paramètres du modèle économétrique. Pour bien appliquer les techniques aux données congolaises, deux modèles séparés ont été faits avec des données différentes. Dans le premier modèle suppose que la variable est un processus de diffusion et le second suppose que les paramètres des sont des processus stochastiques non observables.

Méthodologies utilisées

Pour des raisons de clarté,simplicité et synthèse, les démonstrations de théorèmes et propositions ne sont pas présentées ici mais le lecteur intéressé peut consulter les références mentionnées. Nous avons passer en revue la théorie des processus stochastiques en bien maitriser

Limitation du travail

Cette étude présente deux limites principales : (i) cette recherche fait appel aux théories mathématiques et statistiques complexes, (ii) les applications

5

sont faites sur les données macroéconomiques congolaises.

Canevas du travail

Hormis l'introduction et la conclusion, ce travail est subdivisé en quatre chapitres. Le premier aborde les préliminaires mathématiques sur les processus stochastiques. Le deuxième chapitre introduit la théorie des équations différentielles stochastiques et les intégrales stochastiques. Le troisième présente les applications des intégrales stochastiques à la théorie de l'estimation statistique. Et le dernier chapitre présente deux applications de la théorie à l'économie congolaise.

6

Chapitre 1

Préliminaires mathématiques

Nous donnons un court résumé des théorèmes et définitions que nous allons utiliser dans les autres chapitres. Ce chapitre présente les fondements mathématiques élémentaires sur les théories de la mesure et intégration, probabilité, et des processus stochastiques.

1.1 Eléments de la théorie de la mesure et intégration

Définition 1.1.1. Soit X un ensemble abstrait (par exemple R). Une tribu (également appelée u - algèbre),e sur l'ensemble X est une famille de sous - ensembles de X telle que :

(i) X E e ;

(ii) VA E e,A^c E e ;

(iii) Si A_n E e, Vn E N alors _UnENAn E e.

e est donc une classe non - vide de parties de X. e est appelé la tribu des ensembles mesurables de X.

Nous considérons une fonction particulière qui permet entre autre de définir les fonctions en escalier : la fonction indicatrice notée 1A (également appelée fonction caractérique),application de X dans R.

Définition 1.1.2. [94] La fonction indicatrice de A est la fonction 1ç(x) valant 1 si x E A et 0 sinon .

lim infAn =

oo n=0

\oo k=n

X Ak = {w E S2, n>0

1Ac

< oo}

7

On a les propriétés suivantes :

1Ù(x) = 1,

1_A,(x) = 1 - 1A(x),

1AnB(x) = 1A(x)1B(x).

Pour une réunion de deux ensembles, on a

1AUB(x) = 1A(x) + 1B(x) - 1AnB(x).

Définition 1.1.3. Soit (S2, T) un espace mesurable. Une subdivision de S2 est un ensemble finie D d'ensembles mesurables (D = {A1, ..., A_n} C T) qui sont mutuellement disjoint et dont la réunion est S2.

Définition 1.1.4. Soit (S2, T) un espace mesurable. Une fonction u : T ? R+ est appelée une mesure (sur l'espace mesurable (S2, T) ou sur la tribu T) si elle vérifie les conditions suivantes :

(i) u(0) = 0 ;

(ii) u est u - additive : si, pour tout n E N, on a A_n E T et si les A_n sont deux à deux disjoints (n =6 m A_n f1 A_m = 0), alors on a u(UA_n) = Ioon=0 u(An).

Définition 1.1.5. Un espace mesuré est un triplet (S2, T,u), où S2 est un ensemble, T est une tribu sur S2 et u est une mesure sur T.

La proposition suivante donne les propriétés d'un espace mesuré.

Proposition 1.1.0.1. Soit (S2, T, u) un espace mesuré. Alors u a les propriétés suivantes

(i) (additivité). Si A1, ..., A_n E T sont deux à deux disjoints, alors u(UAi) = Ini=1 u(Ai)

(ii) (Croissance). Si A, B E T avec A C B, alors u(A) < u(B),

(iii) (Continuité pour des suites croissantes). Si _(An)nEN est une suite croissante d'ensembles mesurables (Vn E N)

1.1.1 Limite inférieure et supérieure

Soit (S2, A) un espace probabilisable et A_n une suite d'événements de A.

Définition 1.1.6. La limite inférieure de la suite A_n est l'ensemble des w qui appartiennent à tous les A_n sauf peut - être un nombre fini

Définition 1.1.7. La limite supérieure de la suite A_n est l'ensemble des w qui appartiennent à une infinité de A_n

lim supAn =

n n=0

oo U k=n

X Ak = {w ? S2, n>0

1A~ = 8}

8

1.1.2 Espaces vectoriels normés

Définition 1.1.8. Un espace préhilbertien (réel)(S2, h.i) est un espace vectoriel (réel) S2 sur lequel est défini un produit scalaire hi : S2 × S2 ? 18 vérifiant les propriétés suivantes :

(i) (Positivité)hx, xi > 0 si x =6 0, ?x ? S2

(ii) (Symmétrie)hx, yi = hy, xi,?x, y ? S2

(iii) _hc1x1 + _c2x2, yi = c1hx, yi + c2hx, yi pour tous c1, c2 ? 18,?x, y ? S2.

Ces propriétés ont pour conséquence immédiate l'inégalité de Cauchy -

Schwarz : |hx, yi| = hx, xi² hy, yi² et le produit scalaire induit une norme sur

X :

k x k= hx, xi².

Un espace de Hilbert est un espace pré-hilbertien complet.

Soient (S2, 3 , u) un espace mesuré. Si f ? ,C¹_p(S2, 3 ), alors

k f k1=k f k= ^fn |f|du.

Théorème 1.1.1. (Théorème de Hölder) Soit 1 = p = +8. Si f ? I[p(X, 3 , u) et g ? I[q(X, 3 , u), alors fg ? I[¹(X, 3 , u) et

k fg k1=k f k_pk g k_q

avec égalité lorsque 1 = p = +8 si et seulement si u - presque partout sur X, on a

k g kq_q |f(x)|p =k f kp_p |g(x)|q.

Théorème 1.1.2. (Théorème de Minkowski) Soit 1 = p = +8. Si f, g ? I[p(X, 3 , u), alors f + g ? I[p(X, 3 , u) et

k f + g k_p=k f k_pk g k_p

avec égalité lorsque 1 = p = +8 si et seulement si u - presque partout sur X, on a

k g k_p f(x) =k f k_p g(x).

Théorème 1.1.3. (Théorème de Riesz - Fisher) Soit 1 = p = +8. Si f, g ? I[p(X, 3 , u).L'espace (,Cp_u(X, 3 , kk_p) est un espace de Banach et la convergence en moyenne entraîne la convergence en mesure.

9

Définition 1.1.9. Soit f = P^Mj=1 ÀjXA3 une fonction étagée positive sur un ensemble S2 muni d'une tribu r et u : r -+ [0, +oo] une mesure positive. L'intégrale de la fonction f relativement à la mesure positive u est, par définition, la quantité

ZÙ f(ù)du(ù) = Àju(Aj) E [0, +oo].

j=1
_XM

Soit S2 un ensemble, r une tribu sur S2,u : r -+ [0, oo] une mesure positive. On dit alors que la fonction étagée f est une fonction étagée intégrable sur (S2, r) relativement à la mesure positive u. Soient f et g deux fonctions étagées sur S2(muni de la tribu r) telles que f < g partout, on a

_{Z Z}

_Ù f(ù)du(ù) < Ù g(ù)du(ù)

1.1.3 Propriétés de l'intégrale des fonctions étagées positives

Les propriétés auxquelles se plie l'intégrale des fonctions étagées positives (additivité,positivité homogénéité,monotonie) pourront évidemment s'étendre à l'intégrale des fonctions mesurables positives. De fait, le résultat crucial ici est le théorème de Beppo Levi qui donne le résultat intéressant pour la convergence croissante des fonctions mesurables positives.

Théorème 1.1.4. (Théorème de Beppo Levi)[178] Soient _(fn)n>1 une suite croissante de fonctions (S2, r) - ([0, oo], B) mesurables sur un ensemble S2 muni d'une tribu r et f la limite de la suite f_n lorsque n tend vers +oo. Alors f est aussi (S2, r) - ([0, oo], B) mesurable et si u : r -+ [0, oo] est une mesure positive, on a ^RÙ fdu = limn-00(RÙ f_ndu) E [0, +oo] et que si À > 0, on a

R_Ù(Àf)du = ÀR_Ù fdu.

Théorème 1.1.5. (Lemme de Fatou) Soit S2 un ensemble,r une tribu sur S2, et u : r -+ [0, oo] une mesure positive. Soit (fn)n>1 une suite de fonctions

(S2, B mesurable, on a alors ^RÙ (lim inf_n f_n) du < lim infn I R fndu ^I .

10

1.1.4 Produit des espaces mesurés

Définition 1.1.10. Soit (Ù, ô, u) un espace mesuré. La mesure u est dite ó - finie s'il existe une suite (A_n)n E N d'éléments de ô (que l'on peut supposer croissante) telle que u(A_n) < oo pour tout k et que

Ù = _U A_n.

n

Proposition 1.1.5.1. Soient (Ù1, ô1, u1) et (Ù2,ô2, u2) deux espaces mesu-rés,les mesures u1 et u2 étant toutes les deux ó - finies. Il existe alors une unique mesure u1 ®u2 : ô1 ® ô2 -+ [0, oo] telle que,pour tout A E ô1,pour tout B E ô2, on ait ô1 ® ô2(A x B) = ô1(A) x ô2(B)(toujours avec la convention 0 x oo = 0).

L'unique mesure positive sur la tribu produit est appelé ainsi mesure produit de u1 et u2. Plus généralement, si E désigne un élément quelconque de ô1 x ô2, les fonctions x E ó1 -+ u2(E_x), E_x := y E ó2; (x, y) E E, y E ó2 -+ u1(E_x), E_x := y E ó1; (x, y) E E sont respectivement (Ù1, ô1) - ([0, oo], B) et (Ù2,ô2) - ([0, oo], B) mesurables et on a

(u1 ® u2)₍E) = f1 u2(Ex)du1(x)

= f~2 u1(Ey)du2(y).

Théorème 1.1.6. (Théorème de Fubini - Tonelli)[178] Soient (Ùj, ôj, uj), j = 1, 2, deux espaces mesurés, les mesures u1 et u2 étant ó - finies ô1 ® ô2 la tribu produit et u1 ® u2 : ô1 ® ô2 -+ [0, oo] la mesure produit définie à la proposition précédente. Pour toute fonction f(Ù1xÙ2, B mesurable, les fonctions

Zx E Ù1 -+ _Ù2 f(x, y)du2(y),

Zy E Ù2 -+ _Ù1 f(x, y)du1(x)

sont respectivement (Ù1, B) et (Ù2, B) mesurables et on a :

f(x, y)d[ui ®u2](x, y) = fel [ f~2 f(x, y)du2(y)] du1(x)

fe1xÙ2

fg.22 [ fs~1 f(x, y)du1(y)] du2(y)

Théorème 1.1.7. (Théorème de Fubini)[178] Soit f une fonction

(Ù1 xÙ2, B) mesurable et intégrable relativement à la mesure produit u1 ®u2.

11

Pour u1 presque partout dans SZ1, la fonction f_x : y E S22 -+ f(x, y) est intégrable ₍relativement à la meure u2 ;de plus, la fonction x -+ _fÙ2 f(x, y)du2(y)

se prolonge en une fonction (SZ1, B) mesurable, intégrable relativement à la mesure u1 et l'on a la formule :

fÙ1xÙ2 f(x, y)d[u1 ® u2](x, y) = fÙ1 [ fÙ2 f(x, y)du2(y)] du1(x).

1.1.5 Conditionnement et indépendance de probabilité

[56] Si A est un événement de probabilité P(A) > 0, la mesure de probabilité conditionnelle, A étant donné, associe à tout événement B la probabilité

P(B | A) := P(BnA)

P (A) .

La formule du conditionnement en chaine s'exprime en disant que si n > 2 et A1, A2, ..., A_n est une suite den événement tels que P(A1, A2, ..., A_n) > 0, on a l'identité :

P(A1, A2, ..., A_n) = P(A_n | A1, ..., An_1)P(An_1 | A1, ..., A2)...P(A2 | A1)P(A1).

On dit qu'une suite (A_n) d'événement est un système complet si

(i) i =6 j = AZ n Aj = Ø (les événements sont deux à deux incompatibles)

(ii) P(E_n A_n) = En P(A_n) = 1 (presque sûrement l'un des événements A_n se réalise).

Deux événements A et B sont indépendants si l'on a P(AnB) = P(A)P(B). Soit (X_n) une suite de variables (mutuellement) indépendantes si pour toute suite finie (i1 < ... < i_r) d'entiers telle que r > 2 et toute suite (B1, ..., B_r) d'ensembles boréliens, on a l'identité

P{XZ1 ^E _B1...XZr E B_r} = P{XZ1 E B1}....P{XZ_r E B_r}.

1.2 Espérance conditionnelle

Dans ce point un rappel sur les règles de calcul des espérances conditionnelles, auquel nous nous sommes constamment reportés pour le traitement de la théorie des martingales.

Soient X et Y deux variables aléatoires avec Y réelle et X prenant ses valeurs dans un ensemble fini ou dénombrable.

12

Définition 1.2.1. Soit X une variable aléatoire à valeurs dans un ensemble E fini ou dénombrable dont les points sont notés {x1, x2, ..., x_n, ...}. Soit Y une autre variable aléatoire réelle, définie sur le même espace de probabilité (Ù, F,P). Si P(X = xj) > 0, l'espérance conditionnelle de Y sachant {X = xj} est le nombre E(Y |X = xj) = EQ₃(Y ),espérance de Y pour Qj, où Qj est la probabilité sur (Q, F) donnée par Q(A) = P(A|X = xj), pourvu que EQ₃(|Y |) < oo (i.e.,Y est Qj - intégrable).

Lorsque Y est elle-même une variable aléatoire discrète prenant ses valeurs dans {y1, y2, ...} pour Y,on obtient le résultat suivant.

Théorème 1.2.1. Dans la situation précédente, pour tout j tel que

P(X = xj) > 0 on a E(Y |X = xj) = Ek1 ykP(Y = yk|X = xj) pourvu que la série ci - dessus soit absolument convergente.

Définition 1.2.2. Soit X une variable aléatoire à valeurs dans un espace E fini ou dénombrable, et Y une variable aléatoire réelle définie sur le même espace de probabilité. L'espérance conditionnelle deY sachant X est

E(Y |X) = f(X) où f est donnée par la définition précédente ()et pourvu que cette fonction f soit bien définie.

Si par exemple X est une application de S2 dans Rⁿ, la tribu engendrée par X est

o-(X) = X^-1(Bⁿ) = {F E SZ : X^-1(93) = F pour un 93 E Bⁿ}.

Définition 1.2.3. Soit Y E L²(S), F, P). L'espérance conditionnelle de Y sachant X est l'unique élément Y de L²(SZ, cr(X), P) qui vérifie

E(Y^àZ) = E(Y Z) pour tout Z E L²(SZ, u(X), P). On note cette espérance conditionnelle par E(Y |X).

Définition 1.2.4. Soit Y E L²(SZ, F, P) et G une sous-tribu de F. L'espérance conditionnelle deY sachant G est l'unique élément E(Y |G) de L²(SZ, G, P) qui vérifie E(Y Z) = E(E(Y |G)Z) pour tout Z E L²(SZ, F, P).

Théorème 1.2.2. [90] Soit Y E L²(Q, F, P) et G une sous-tribu de F.

(i) Si Y > 0 alors E(Y |G) > 0,

(ii) Si G = u(X) pour une variable aléatoire X à valeurs dans Rⁿ,il existe une fonction borélienne f sur R telle que E(Y |G) = f(X),

(iii) E(E(Y |G)) = E(Y ),

(iv) L'application Y -+ E(Y |G) est une application linéaire.

Théorème 1.2.3. Soit Y une variable aléatoire positive ou intégrable sur (S), F, P) et G une sous - tribu. Alors E(Y |G) = Y si et seulement si Y est G-mesurable.

13

Théorème 1.2.4. Soit Y E L¹(Ù, F, P) et si X est une variable aléatoire indépendante de Y , on a E(Y |X) = E{Y }.

Théorème 1.2.5. Soit X, Y des variables aléatoires réelles sur (Ù, F, P) et G une sous - tribu de F par rapport à laquelle X est mesurable. On a alors E(XY |G) = XE(Y |G, dans chacun de deux cas suivants:

(a) les v.a. X, Y et XY sont intégrables,

(b) les v.a. X et Y sont positives.

Théorème 1.2.6. [90] Soit _(Yn)n=1 une suite de variables aléatoires réelles sur (Ù, F, P) et G une sous - tribu.

(i) (Convergence monotone.)Si les Y_n sont positives et croissent p.s. vers une limite Y ,alors

limn?8 E(Y_njG) = E(Y |G) p.s. ;

(ii) (Lemme de Fatou.)Si les Y_n sont positives, on a E(lim _infn?8 Y_n|G) < lim inf E(Y_n|G) p.s.;

(iii) (Théorème de convergence dominée de Lebesgue.) Si les Y_n convergent p.s. vers une limite Y , et si on a Y_n| = Z pour tout n et pour une certaine v.a. Z E L¹(Ù,F,P),alors

lim n?8

E(Yn|G) = E(Y |G) p.s..

1.2.1 Variables aléatoires

Un processus stochastique est un ensemble des variables aléatoires (Xi, t E Ø) dans un espace de probabilité (Ù, t9, P). Dans le sens général, les processus stochastiques sont des fonctions X(t, w) dépendant du temps. Pour une éventualité w fixé,X(t, w) sont des variables aléatoires sur (Ù, t9, P) [135]

Le processus stochastique X est dit être adapté si Xt E Øi pour tout t,où Øt représente

Interprétation du paramètre t comme index de temps introduit un aspect dynamique : pour modéliser le fait que l'incertitude des événements de Ù devient de moins en moins incertaine lorsque le temps s'écoule, i.e. on possède de plus en plus d'information, on introduit la notion de filtration.

1.2.2 Modes de convergence

On rappelle succinctement les définitions des différents modes de convergence des variables aléatoires. Ces éléments sont tirés de [94]. Pour une ana-

14

lyse plus approfondie le lecteur intéressé peut consulté [29],[30], [14]. La suite de variables aléatoires X_n converge presque surement (p.s.) vers la variable aléatoire X, si la convergence a lieu sauf peut - être pour un ensemble de mesure négligeable.

La suite de variables aléatoires X_n converge dans Lp vers la variable aléatoire X si

Proposition 1.2.6.1. La suite de variables aléatoires réelles X_n converge en probabilité si et seulement si pour tout r > 0,

supE(|X_n+k - X_n|^p) ^P-? 0 quand n ? 8.

La suite de variables aléatoires réelles X_n converge en probabilité si et seulement si pour tout r > 0,

^P-?

IE(sup|X_n+k - X_n| > r) 0 quand n ? 8.

Définition 1.2.5. Une suite de variables aléatoires réelles X_n est uniformément intégrable si

sup \ ( Ixn

|Xn /~ I dIE ? 0 quand n ? 8

|>0

autrement dit si pour tout e > 0, il existe a tel que pour tout n,

f

|X_n|dIE |Xn|>a < e.
1

e JC1<0 |y - x| < c2|yi - xi|Pt,x(t + e, dy) = c2e f Pt,x(t + e, dy)

y-x|>c

flimkX_n - Xk_p = lim( |X_n - X|^pdIE)¹/^p = 0.

La suite de mesure positives bornées u_n converge faiblement vers u, si pour toute fonction continue sur R qui tend vers zéro à l'infini, on a

_{f f}

lim fdu_n = du.

La suite de mesures positives bornées u_n converge étroitement vers u, si pour toute fonction continue bornée de R

_{f f}

lim fdu_n = du.

15

La suite de mesures positives bornées u_n converge étroitement vers u si et seulement si u_n converge faiblement vers u et si

limu_n(R) = u(R).

La suite de variables aléatoires X_n converge en probabilité vers la variable aléatoire X si

P(|X_n - X| = 6) ? 0,?E > .0

La suite de variables aléatoires X_n converge en loi vers la variable aléatoire X si les mesures P_x convergent étroitement vers la mesure P_x.

Les modes de convergences sont liés entre eux : Certains en impliquent d'autres.

Proposition 1.2.6.2. La convergence dans Lp entraîne la convergence en probabilité si la suite X_n converge vers X dans Lp, alors X_n converge vers X en probabilité

X_n -? X X_n -? X

Proposition 1.2.6.3. La convergence presque sûrement entraîne la convergence en probabilité

p.s.

X_n --? X X_n-? X

P

Proposition 1.2.6.4. La convergence en probabilité entraîne la convergence en loi

X_n -? X X_n -? X

Soit X_n une suite de variables aléatoires réelles.

Proposition 1.2.6.5. La suite de variables aléatoires réelles X_n converge en probabilité si et seulement si pour tout r > 0,

supP(|X_n+k - X_n| > r) ? 0 quand n ? 8.

Proposition 1.2.6.6. La suite de variables aléatoires réelles X_n converge en probabilité si et seulement si pour tout r > 0,

supE(|X_n+k - X_n|^p) ? 0 quand n ? 8.

La suite de variables aléatoires réelles X_n converge en probabilité si et seulement si pour tout r > 0,

P(sup|X_n+k - X_n| > r) ^P-? 0 quand n ? 8.

16

1.3 Processus stochastiques

Dans cette section nous donnons une brève présentation sur la notion des processus stochastiques tels que les chaines de Markov, Martingales, les mouvements browniens.

1.3.1 Processus de Markov

Soit (S2, T, P) un espace de probabilité et (E, B) l'espace des états, B désigne la tribu des boréliens de E. Un processus Xt est un processus de Markov si pour tout u et t > 0 et pour tout T E B, on a

P(Xt+u E T|X_s, s < t) = P(Xt+u E T|Xt)

Ce qui signifie que le processus ne dépend que du dernier instant et non de tout son histoire.

La probabilité de transition pour passer de l'état x au temps s à un étant appartenant à T à l'instant t est notée par s < t

Ps,t(X, T = p(s, x; t, T) = P(Xt E T|Xt = x).

La fonction T -+ T) = P(Xt E T est une probabilité sur T . La probabilité de transition vérifie l'équation de Chapman - Kolmogorov qui s'écrit sous les formées suivantes. Soit s < u < t tel que X_u = y, on a

ZPs,t(X, T) = Ps,u(x, dy)P_u,t(y, T).

et dans le cas d'un espace E dénombrable

XPs,t(X, z) = Ps,u(x, y)Pu,t(y, z).

yEE

Le processus Xt est un processus de Markov homogène si pour tout sett de T, la transition

p(s, x;t, B) = p(x; ô, B)

ne dépend que de ô = t - s.

17

Processus de diffusion

Définition 1.3.1. [111] Un processus de Markov Xt de réels dans Rⁿ, a < t < b, est appelé un processus de diffusion si ses probabilités de transition {Ps,x(t, .)} satisfait les trois conditions suivantes pour tout t E [a, b], x E Rⁿ, et c > 0 ;

(1) limå?0 1 å fy-x|=c Pt,x(t + e, dy) = 0

(2) limå?0 E fy-x|<c(yi - xi)Pt,x(t + e, dy) = pi(t, x) existe.

(3) limå?0 E fy-x|<c(yi - xi)(yj - xj)Pt,x(t + e, dy) = Qi j(t x) existe .

La condition (1) implique que le processus stochastique Xt ne peut pas avoir des sauts instantanés ; De plus on observe que pour tout c2 > c1 > 0 qui tend à 0 quand e -+ 0 dans l'équation (1). Il s'en suit que la limite dans l'équation (2) est indépendante de la constante c. De même, la limite dans l'équation (3) est aussi indépendante de la constante c. Ainsi pi(t, x) et Qi,j sont respectivement donnés₍ par pi(t, x) = limå?0 É fRn(yi - xi)Pt,x(t + e, dy) Qi,j(t, x) = limå?0 E fy-x|<c(yi - xi)(yj - xj)Pt,x(t + e,dy)

Définition 1.3.2. [111] Le vecteur p(t, x) = (p1(t, x), p2(t, x), ..., p_n(t, x)) et le paramètre Q(t, x) = [Qi,j(t, x)]i,j sont respectivement appelés les coefficients dérive (drift) et volatilité (diffusion) du processus de diffusion Xt.

Il est important de note qu'une classe spéciale de processus de diffusion donnée par la solution des équations différentielles stochastiques.

Processus de Lévy

Définition 1.3.3. [94] Un processus Xt adapté à la filtration _Tt est un processus de Lévy si X0 = 0, si les trajectoires de Xt sont continues à droite et avec des limites à gauche (càdlàg) et tel que pour tout s, t > 0 la variable Xt+s - Xt est indépendante de la tribu _Tt et de même loi que X_s.

Théorème 1.3.1. [94] Soit Xt un processus de Lévy adapté à la filtration Tt et de la loi ut.

(1) Les lois ut forment un sous - groupe de convolution

ut * u_s = ut+s

(2) Les processus Xt satisfait la propriété de Markov pour le noyau ZPt(x, A) = 1A(x + y)ut(dy)

18

Théorème 1.3.2. [94](Lévy - Khintchine) La fonction caractéristique d'un processus de Lévy Xt est de la forme

E(e^ièXt) = e-tø(è)

où ø(è) est l'exposant caractéristique de la loi indéfiniment divisible de Xt qui s'écrit

(è) = iaè +1

2u²è² + f(1 - e^ièx + ièx1(|x|<1))F(dx)

La quantité a est réelle, a E 1[8,ó > 0, et F est une mesure concentrée sur ]0, +oo[ telle que

A (1 x^2)F(dx) < oo.

Le triplet (a, ó, F) est appelé triplet de Lévy - Khintchine associé au processus Xt.

Processus du second ordre [94],

Définition 1.3.4. Un processus Xt est un processus du second ordre si E|Xt|² < oo. Une série chronologique est un processus du second ordre à temps discret.

Matrice stochastique

Une matrice carrée M dont ses composantes sont toutes strictement positives est appelée matrice positive. Aussi une matrice M des éléments réels est dite non négative (notée M > 0) quand toutes ses éléments sont non négatifs : (aij) > 0, Vi = 1, 2, ..., N j = 1, 2, ..., L. Une matrice M de N x N est une matrice stochastique si ses éléments sont des nombres réels satisfaisant les conditions suivantes [9] :

1 0 < (mij) < 1, Vi, j = 1, 2, ..., N

2 chaque colonne de M est une distribution de probabilité,c'est - à - dire, I^Ni=1(mij) = 1 V

Les éléments de la matrice stochastique sont des probabilités, des nombres réels dans l'intervalle fermé [0, 1]. Conséquemment, les matrices stochastiques sont des matrices non négatives. La première conséquence de ces conditions est que toutes les puissances successives de Mp sont aussi des matrices stochastiques :

N i=1

(mij)^p=

XN i=1

(mij)^p-1=

N i=1

(mij)^2= ... =

N i=1

N i=1

(mik)(mkj) = 1

19

La seconde conséquence, lorsque on manipule une distribution de probabilité d'une matrice stochastique, cette dernière produit une autre une distribution de probabilité.

1.3.2 Chaînes de Markov

La théorie de chaines de Markov est couramment utilisée dans plusieurs domaines à cause de sa rigueur scientifique et sa simplicité dans la modélisation du monde réel. Dans cette étude nous allons parler, de façon brève, de chaines de Markov car ces dernières sont des processus stochastiques particuliers.

Chaines de Markov à temps discret. Supposons _Pij est une probabilité fixée indépendante du temps telle que

P(Xⁿ⁺¹ = i | Xⁿ = j, X^n-1 = in-1, ··· , X⁰ = i0) = Pij, n = 0

oïi,¹₂ i, j, i0, i1, · · · , in-1 ? espace d'état .

Théorème 1.3.3. (Propriétés de Markov forte)[Loustau,p.] Soit (Xn)n>0 une chaine de Markov (ii, P). Alors, quelque soit x ? E, conditionnellement à {XT = x} (l{T < 8},(XT+p)p>0 est une chaine de Markov (S_x, P) indépendante de (X0, ..., XT). On peut s'écrire, quelque soit A ? TT :

P(A

n XT+1 = x1, ..., XT+p = xp|XT = x, T < 8) = P(A|XT = x,T < 8)P_x(X1 = x1, ..., X_p = x Classification des états. Les états d'une chaîne de Markov se repar-

tissent en classes que l'on définit à partir de la matrice de transition

Définition 1.3.5. On dit que l'état j est accessible à partir de l'état i, on est conséquent de l'état i, s'il existe un entier n > 0 tel que p(n)

i,j > 0. On

écrit : i j.

Proposition 1.3.3.1. (i) La relation d'accessibilité entre états est réflexive et transitive.

20

(ii) Soient i, j deux états ; les deux propriétés suivantes sont équivalentes.

(a) l'état j est accessible à partir de l'état i, soit i j.

(b) le processus, portant de i, passe par j avec une probabilité strictement positive.

Définition 1.3.6. On dit deux états i et j communiquent et on l'écrit i ,

si on a à la fois i j etj

i.

Proposition 1.3.3.2. La relation de communication entre états est une relations d'équivalence. Pour tout i, on a p(0)

i,i = 1, tout état communique avec

lui - même.

Un état est appelé état de retour, s'il existe n > 1 tel que p(n)

i,i = 0. Il existe des états i tel que pour tout n > 1 (donc 0 exclu ) on dit p(n)

i,i = 0. De tels états sont p(n)

i,i = 0appelés états de non - retour. Pour la relation de communication l'ensemble E des états se partitionne en classes d'équivalence, disjointes et non vides, dites classes indécomposables. Certaines classes peuvent ne comporter qu'un seul élément ; ce sont les singleton comme exemples, mentionnons :

* un état de non - retour i :p⁽⁰⁾i,i = 1, p(n)

i,i = 0 pour n > 1;

* un état absorbant i :p⁽⁰⁾i,i = 1, p(n)

i,i = 1 pour n > 1.

Définition 1.3.7. S'il n'y a qu'une seule classe pour la relation de communication, autrement dit, si tous les états communiquent entre eux, la chaîne est dite irréductible.

Définition 1.3.8. On dit que l'état récurrent ou transient si pi,i < 1. Théorème 1.3.4. (Critère de récurrence) Un état j est récurrent ou transient selon que

_X

n>0

_X

n>0

pi,i = +8 (n)

ou que

pi,i < +8 (n)

Proposition 1.3.4.1. On a les identités

1

Pj,j(s) = 1 - Fj,j(s), Pi,j(s) = Fi,j(s) (i =6 j),

que l'on peut réunir en une seule formule

Pj,j(s) = äi,j + Fi,j(s)Fj,j(s)

21

Proposition 1.3.4.2.

X X P(n) j,j (s) = Si,j + fi,j n0 n0

(s)f^(n) j,j (s)

_X

n>0

1

pi,i =
(n)

1 - fj,j

ou que

_X

n~0

(Z = ) J,7 (Z ~ j

p )

1 - fj,j

1.3.3 Temps d'arrêt

Une variable aléatoire T : (S2, 3 , P) -+ N^* un temps pour la filtration 3_n si pour tout entier n, l'événement (T = n) E 3_n.

Proposition 1.3.4.3. Si S et T sont deux temps d'arrêt alors sup(S, T) = S ^V T et inf(S, T) = S ^A T sont des temps d'arrêt. Si (S_n) est une suite de temps d'arrêt alors sup(S_n) est un temps d'arrêt.

Proposition 1.3.4.4. [94] Si (X_n) est une sous-martingale(respectivement martingale, surmartingale), T un temps d'arrêt alors, la suite (X_TA_n) est une sou - martingale(respectivement martingales, surmartingale).

On dit que le processus X = (X(t) : t > 0) est adapté au processus Z = (y(t) : t > 0) si pour tout t > 0 il est existe une fonction gt = (.) telle que X(t) = gt(Z(t) : 0 < S < t). On dit que M_n : n > 0) est une martingale adaptée à (Z(t) : t > 0) si

(i) E | M_n |< oo pour n > 0,

(ii) (M_n : n > 0) est adaptée à Z_n : n > 0),

(iii) E[Mn+1 | Z0, ..., Z_n] = M_n presque surement pour n > 0.

On dit que M_n : n > 0) est une sous-martingale (surmartingale) adaptée à (Z(t) : t > 0) si

(i) E | M_n |< oo pour n > 0,

(ii) (M_n : n > 0) est adaptée à Z_n : n > 0),

(iii) E[Mn+1 | Z0, ..., Z_n] > M_n (E[Mn+1 | Z0, ..., Z_n] < M_n) presque surement pour n > 0.

Proposition 1.3.4.5. Soit M = M_n : n > 0) une martingale adaptée à Z_n : n > 0) et O_n : n > 0) est une suite de variables aléatoires bornées qui est adaptée à Z_n : n > 0). Alors M_n - I Oj-1 A Mj est une martingale adaptée

22

à Z_n : n > 0) où OMj = Mj - Mj-1 pour j > 1 et E[(Mj - M0)²] = PE[0²_j-1(OMj)²].

Définition 1.3.9. Un processus stochastique X(t) : a < t < b est appelé continu ï6¹₂ droite si toutes les trajectoires d'échantillon sont des fonctions continues à droite sur [a, b].

Définition 1.3.10. Une martingale M = (Mt, IFt), t E R⁺ est dite carrée - intégrable

si

sup E(M²_t ) < oo. |_{z}

t

Nous donnons le théorème de d'inégalité de Doob d'une sous - martingale donne les valeurs maximales attentes par une sous-martingale.

Théorème 1.3.5. (Inégalité de Doob) Soit X(t), a < t < b une sous - mar-

tingale continue à droite. Alors VA > 0, P[ sup |{z} a<t<b

X(t) > A] < ^1ë[X(b)^+] où

X(b)⁺ est la partie positive de X(b),c'est- à-dire,X(b)⁺ = max(X(b), 0). En particulier, si X(t) est une martingale continue à droite, alors pour tout

P[ sup |{z} a<t<b

X(t) > A] = ^1ë[X(b)^+]

Le théorème d'arrêt de Doob montre que l'inégalité des sous - martingales est conservée par passage à un temps d'arrêt borné.

Théorème 1.3.6. [94](Théorème d'arrêt de Doob) Soi X_n une surmartingale (resp. martingale,sous - martingale), S et T deux temps d'arrêt bornés (S < T < k). Les variables XS et XT sont dans L¹ et on a

E(XT FS) = XS, (respectivement =, <)

1.3.4 Martingales à état indépendant

Nous considérons la classe des processus à état dépendant S de la forme Mt = f(Xt) où Xt : t > 0) est une chaine de Markov.

Proposition 1.3.6.1. Supposons que f est une fonction telle que

EX f(Xt) < oo pour t > 0 et x E S.

(i) Si f = P f, alors (f(Xt : t > 0)) est une martingale adapté à (Xt : t > 0),

(ii)

23

Si f = Pf, alors (f(Xt : t = 0)) est une surmartingale adapté à (Xt : t = 0),

(iii) Si f = Pf, alors (f(Xt : t = 0)) est une sous-martingale adapté à (Xt : t = 0),

Théorème 1.3.7. Soit (Mt : t = 0) une sous-martingale adapté à (Zt : t = 0). Alors pour X > 0,

P[max s.. {z } 0<k<t

Mk > X] = EM+ X . t

La propriété de sous-martingale est préservée sous applications convexes.

Proposition 1.3.7.1. Soit ç : R ? R convexe. Si Mt : t = 0) est une martingale adaptée à (Z_n : n = 0) pour laquelle E|ç(Mt)| < 8 pour n = 0, alors (ç(M_n) : n = 0) est une sous-martingale adaptée à (Z_n : n = 0). Si ç est à la fois convexe et croissante et Mt : t = 0) est une sous-martingale pour laquelle |ç(Mt)|8 pour n = 0, alors (Mt : t = 0) est une sous-martingale adaptée à (Mt : t = 0).

Théorème 1.3.8. (Théorème de convergence des martingales)

(i) Soit Mt : t = 0) est une sous-martingale adaptée à (Zt : t = 0). Si E|Mt| < 8, alors il existe une variable aléatoire à valeur finie M₈ telle que Mt ? M₈ presque surement quand t tend vers 8.

(ii) Soit Mt : t = 0) est une sous-martingale non négative adaptée à (Zt : t = 0), alors il existe une variable aléatoire à valeur finie M₈ telle que Mt ? M₈ presque surement quand t tend vers 8.

Quand (Mt : t = 0) est une martingale,(ii) est appelée le théorème de convergence de martinga

1.3.5 Mouvement brownien

Le botaniste Robert Brown en 1827 pour décrire le mouvement irrégulier de particules de pollen dans un fluide. Le cadre d'application du mouvement brownien a largement dépassé l'étude des particules microscopiques pour être utilise en finance dans la modélisation des prix d'actions, historiquement depuis Bachelier en 1900.

Définition 1.3.11. [150](Mouvement brownien standard) Un mouvement brow-

nien standard vectoriel (d-dimensionnel) sur T = [0, T] ou R+ est un proces-

( ~

sus continu à valeurs dans R^d, (Wt)tET = W t 1 , ..., W t d tET tel que

(i)

24

W0 = 0

(ii) Pour tous 0 =< t dans T, l'accroissement Wt - W_s est indépendant de u(W_u, u = s) et suit une gaussienne centrée de matrice de variance - covariance (t - s)I - d où Id est la matrice d'identité d × d.

Définition 1.3.12. (Mouvement brownien standard,[Pham,p.6]) Un mouvement brownien standard vectoriel (d-dimensionnel) sur T = [0, T] ou R+ par

rapport à une filtration F = (ft)tET est un processus continu F-adapté à va-

( )

leurs dans R^d, (Wt)tET = W t 1 , ..., W t d tET tel que

(i) W0 = 0

(ii) Pour tous 0 =< t dans T, à l'accroissement Wt -W_s est indépendant de u(W_u, u = s) et suit une gaussienne centrée de matrice de variance - covariance (t - s)I - d où Id est la matrice d'identité d × d.

Définition 1.3.13. [94](Mouvement brownien fractionnaire) Soit Xt un processus. On dit que la loi de Xt est autosimilaire de facteur H si ?a > 0>, la loi de _Xat est la même que la loi de a^HXt. On suppose que Xt est un processus gaussien à accroissement stationnaires (Xt - X_s a même loi que Xt-s).Si H ? ]0, 1[, on dit que Xt est un mouvement brownien fractionnaire d'exposant H(appelé paramètre de Hurst). Dans le cas où H = 1/2, Xt est appelé le mouvement brownien fractionnaire standard.

1.3.6 Quelques modification du mouvement brownien

Les éléments développés ici peuvent être trouvés dans[94]. Les modification introduites sont toutes des processus de Markov dont les trajectoires sont presque sûrement continues.

Définition 1.3.14. (Mouvement brownien réfléchi) Soit {X(t) : t 0} un mouvement brownien. Le processus {Y (t) : t 0} où {Y (t) :=| X(t) |, t 0} est appelé mouvement brownien réfléchi( à l'origine).

q2t

Proposition 1.3.8.1. On a : E[Y(t)] = ð et VarY (t) = (1 - 2 ðt).

Définition 1.3.15. (Le mouvement brownien absorbé) Dans la définition du mouvement brownien donnée c -dessus, on remplace la condition (1) X(0) par (1^' X(0) = x > 0. On obtient le mouvement brownien commerce en x. Désignons par T le premier instant où ce mouvement brownien atteint la valeur 0 et introduisons le processus {Z(t) : t 0} défini par

Z(t) := {X(t), sit 6 T; 0, sit> T. (1.1)

25

Ce processus est appelé mouvement brownien absorbé ( à l'origine).

Définition 1.3.16. (Le mouvement brownien à dérive) Soient {X(t) : t 0} un mouvement brownien et , un nombre réel. Le processus {Y (t) : t 0}, où Y (t) := X(t) + ,it, est appelé mouvement brownien à dérive; la constante ,t est le paramètre de dérivé.

Si ,u = 0, le processus n'est plus symétrique et le principe de réflexion ne s'applique plus pour le calcul de la loi du maximum.

Proposition 1.3.8.2. Le mouvement brownien avec dérive a les propriétés suivantes :

(a) Y (t) = 0;

(b) le processus est à accroissement indépendants et stationnaire;

(c) pour toutt > 0, la variable aléatoire Y (t) suit la loi normale de paramètre (sit, /t).

Définition 1.3.17. (Le mouvement brownien géométrique) Soit {X(t) : t 0} un mouvement brownien. Le processus {Y (t) : t 0}, où Y (t) := exp(X(t)), est appelé mouvement brownien géométrique.

Lorsque le mouvement brownien sous - adjacent est à dériver, à même s'il est de la forme X(t) = t9î(t) + ,it où (t) : t 0} est le mouvement brownien standard.

Proposition 1.3.8.3. Soient {î(t) : t 0} le mouvement brownien standard et {Y (t) : t 0} le processus géométrique défini par:

Y (t) = e(uî(t)+ut). Alors

E[Y (t)] = et(u+ u2 2 )

V arY (t) = e2t(u+u2 ₂ )(etu2 - 1)

Définition 1.3.18. (Processus d'Ornstein - Uhlenbeck) Soient {X(t) : t 0} un mouvement brownien et a un nombre strictement positif. Le processus

{Y (t) : t 0}, ou Y (t) := e- át 2 (e^át), est appelé processus d'Ornstein -
Uhlrnbeck.

Proposition 1.3.8.4. Pour tout t 0, on a E[Y (t)] = 0 et pour 0 < s < t < +00, on a :

á(t-s)

Cov(Y (s), Y (t)) = e- 2 .

Théorème 1.3.9. Le mouvement brownien standard {X(t) : t 0} est une

martingale par rapport à la famille {F; t 0} où {F; t 0} est la tribu
engendrée par les variables X_s (0 s t).

26

1.3.7 Martingales et Semimartingales

La notion fondamentale dans l'analyse des processus markoviens est celle de martingale. Les martingales forment aussi la base de la théorie moderne d'intégration stochastique. Elles jouent un rôle important dans l'analyse des chaines markoviennes et des processus markoviens.

Définition 1.3.19. (Martingale) Un processus (Xt)t E T adapté est appelé surmartingale si E[Xt] < oo pour tout t E T et E[Xt | 3_s] < X_s,p.s. pour tout 0 < s < t,s, t E T. X est une sous-martingale si -X est une surmartingale. On dit que X est une martingale si elle est à la fois une surmartingale et une sous - martingale.

Un exemple important de martingale est le mouvement brownien. Théorème 1.3.10. (Convergence des martingales)

(1) Soit X = (Xt)t>0 est une surmartingale cád-lág bornée dans £1 ( en particulier si elle est positive). Alors Xt converge p.s. quand t -+ +oo.

(2) Soit X = (Xt)t>0 est une martingale cád-lág dans £¹ (en particulier si elle est positive). Alors Xt est uniformément intégrable si et seulement si Xt converge p.s. et dans £¹ quand t -+ +oo vers une variable aléatoire X+oo. Dans ce cas,X+oo ferme X à droite, i.e. Xt = E[X+oo | 3t] pour tout t > 0.

Théorème 1.3.11. (Théorème d'arrêt des martingales) Soit M =(Mt)tET une martingale càd-làg et u, r deux temps d'arrêt bornés à valeurs dans T tel que u < r. Alors

E[M_ô | 3_ó] = M_ó,p.s.

Corollaire 1.3.11.1. Soit X = (Xt)tET un processus càd-làg adapté.

(1) X est une martingale si et seulement si pour tout temps d'arrêt r borné à valeurs dans T, on a X_ô E £¹ et

(2) Si X est une martingale et r est un temps d'arrêt alors le processus arrêt X^ô est une martingale.

Théorème 1.3.12. [150](Inégalité de Doob) Soit X = (Xt)tET une sous-martingale positive ou une martingale càd-làg. Alors pour tout temps d'arrêt

r à valeur dans T,on a : ~ P sup |{z} 0=t=ô		~= E | Xô | | Xt | = ë ë ,?ë > 0
~ E sup |{z} 0=t=ô	~ Xt | =(pp )p E[ | Xô |^pi,?A> 0 - 1

Définition 1.3.20. (Martingale locale) Soit X un processus càd-làg adapté. On dit que X est une martingale locale s'il existe une suite de temps d'arrêt

(rn)n=1 telle que lim |{z} n?+8

rn = +8 p.s. et le processus arrête X^ônest une

martingale pour tout n.

Proposition 1.3.12.1. Soit M = (Mt)t?T une martingale locale. Supposons

~que E sup |{z} 0=t=ô

~| Ms | < +8, ?t ? T. Alors M est une martingale.

Proposition 1.3.12.2. Soit M une martingale locale positive telle que M0 ? £¹. Alors M est une surmartingale.

Proposition 1.3.12.3. Soit M = (Mt)t?T une martingale locale continue M0 = 0. Alors si M est à variation finie,M est une indistinguable de 0.

Théorème 1.3.13. (Variation quadratique)

(1) Soient M = (Mt)t?T et N = (Nt)t?T deux martingales locales dont l'une des deux est localement bornée (par exemple continue). Alors il existe un unique processus prévisible à variation finie, noté hM, Ni, nul en 0, tel que MN - hM, Ni soit une martingale locale.Cette martingale locale est continue si M et N le sont. De plus, pour tout t ? T,si 0 = tⁿ₀ = tⁿ₁ = ... = tⁿk_n = t est subdivision de [0, t] de pas tendant vers 0, on a :

hM, Nit = lim n?+8

Xkn i=k

(Mt^ni - Mtni-1)(Ntni - Ntni-1),

27

au sens de la convergence en probabilité. Le processus hM, Ni est appelé Crochet (Oblique) de M et N On dira de plus que M et N sont orthogonales si hM, Nh= 0 ce qui signifie que le produit MN est une martingale locale.

(2) Lorsque M = N, le processus hM, Ni, noté parfois hMi et appelé la variation quadratique de M ou le processus croissant de M, est croissant. De plus, on a la relation de polarisation

hM, Ni = ¹₂(hM + N, M + Ni - hM, Mi - hN, Ni).

L'inégalité suivante est utile pour définir l'intégrale stochastique.

Proposition 1.3.13.1. (Inégalité de Kunita - Watanabe) Soient M et N deux martingales locales continues et á, 3 deux processus mesurables sur T×I muni de la tribu produit /3(T) ? F. Alors, on a pour tout t ? T :

f t ( f t ) 0hásih/3sid | hM, Nis = 0 á2 sdhM, Nis ment.

2 ( f t 1 ) 0 /3^2sdhM, Nis

1 2

, presque sûre-

L'inégalité fondamentale suivante pour les martingales (locales) sera très utile lorsqu'on s'intéressera aux martingales locales définies par des intégrales stochastiques pour lesquelles on arrive souvent en pratique à calculer la variation quadratique.

Théorème 1.3.14. [150](Inégalité de Burkholder - Davis - Gundy) Pour tout p > 0, il existe des constantes positives c_p et C_p telles que pour toute martingale locale continue M = (Mt)tET et tout temps d'arrêt r à valeurs dans T,on a

[ ]

p

c_pE hMi ô 2 =E[sup

|_{z}

0<t<ô

[ ]

p

| Mt |]p = C_pE hMi ô 2

28

Proposition 1.3.14.1. (Martingale de carré intégrable) Soit M = (Mt)t?T une martingale locale continue. Alors M est une martingale de carré intégrable si et seulement si E[hMit] < +8 pour tout t ? T. Dans ce cas,

M2 - hMi est une martingale continue et si M0 = 0, on a :

E[hMi_T].

E[M2 _t ] = E[hMit], ?t ? T. De plus, M est bornée dans £² si et seulement si E[hMit] < +8 et dans ce cas : E[M2 _T] =

L'espace H2 c muni du produit scalaire (M, N)H2 c = E[hMi_T] est un espace de Hilbert.

Le théorème suivant est connu sous le nom de théorème de décomposition de Doob-Meyer des surmartingales.

Théorème 1.3.15. (Décomposition de Doob - Meyer) Soit X une surmar-tingale càd - làg. Alors X admet une décomposition unique de la forme

X = X0 + M - A (1.2)

où M est une martingale locale càd-làg nulle en 0 et A est un processus prévisible croissant et nul en 0. Si X est positif, alors A est intégrable,i.e. E[A_T] < +8, où AT = limt~T At p.s.

29

Définition 1.3.21. Une semimartingale est un processus càd - làg adapté X admettant une décomposition de la forme

X = X0 + M - A (1.3)

où M est une martingale locale càd - làg nulle en 0 et A est un processus prévisible croissant et nul en 0. Si X est positif, alors A est intégrable,i.e.

Théorème 1.3.16. (Théorème de Girsanov)[Pham [150],p.22] Soit Q « p et Z son processus de densité martingale. On suppose que Z est continu. Soit M une martingale locale continue. Alors le processus

Z 1

MQ = M - Z d(M, Z(

est une Q-martingalelocalecontinue De plus, si N est une martingale locale continue, on a

(M^Q, Z^Q(= (M, Z(

Si on a de plus Q ti P, i.e.,Z est strictement positif presque sûrement, alors il existe une unique martingale locale continue L nulle en t = 0, telle que :

1

Zt = exp(Lt - ₂(L, L)t) =: Et(L), t E 7r, p.s. et L est donné par

t1

Lt = f Z3 dZ₃, t E r, p.s.

La Q - martingale locale MQ s'écrit alors aussi

MQ = M - (M,L(.

Dans le cas d'un mouvement brownien, on a le résultat important suivant.

Théorème 1.3.17. (Cameron - Martin)[150] Soit W un mouvement brownien. Soit Q ti P de processus de densité martingale

dQ

dP |Ft = Et(L),

où L est une martingale locale continue. Alors le processus

WQ = W - (W,L(.

est un Q - mouvement brownien.

30

Il est important d'avoir des conditions assurant que (L) soit une martingale.

Proposition 1.3.17.1. (Condition de Novikov)[150] Soit L une martingale locale continue avec L0 = 0 telle que

E[exp(¹ ₂hW,Lh T )] < +8.

Alors L est une martingale uniformément intégrable avec E[exp(L T 2

)] < +8

et (L). est une martingale uniformément intégrable.

Définition 1.3.22. (Le pont brownien) Soit {X(t) : t 0} un mouvement brownien standard. Le processus {Y (t) : 0 6 t 6 1brownien.}, où Y (t) := X(t)tX(t) est appelé pont brownien.

Presque toute trajectoire de ce pont est une courbe continue sur [0, 1] passant par les points (0, 0) et (1, 0)

Propriété 1.3.1. Les fonctions d'espérance et des variances - covariances du pont brownien sont données par:

(a) E[Y (t)] = 0 0 6 t 6 1 ;

(b) cov(Y (s),Y (t)) = s(1 - t)(0 6 s 6 t 6 1)

Proposition 1.3.17.2. Soient {X(t) : t 0} un mouvement brownien

standard et 0 < t1 < ... < t_n < 1 une suite de nombres. Alors la loi de (X(t1),...., X(t_n)), conditionnelle à {X(1) = 0} suit la loi normale N(0, F^')

En particulier, pour 0 < s < 1, la loi de X(s) conditionnelle à {X(1) = 0} \/est la loi normale N(0, s(1 - s).

31

Chapitre 2

Equations Différentielles et

Intégrales Stochastiques

Ce chapitre a comme objectif de donner la formulation des équations différentielles stochastiques en clarifiant la différence entre équations différentielles stochastiques ordinaires et partielles. Certes, beaucoup de phénomènes aléatoires tant naturels qu'économiques apparaissent dans un environnement incertain et peuvent être modélisés sous forme d'équations différentielles. Le développement plus détaillé, avancé et récent des équations différentielles et intégrales stochastiques peut être trouvé dans les ouvrages [88],[89][12],[54], [92].

2.1 Calculs stochastique

Définition 2.1.1. [87] Pour X et Y E Q, on dit que X et Y sont équi-valent,i.e.,

X Y si X(t) - X(s) = Y (t) - Y (s) p.s. pour tout 0 s t.

clairement cette relation est une relation d'équivalence. La classe d'équivalence contenant X est représentée par dX et appelée différentielle stochastique de X. Par définition, js t dX(u) est le processus X(t) - X(s).

Soit dQ = {dX;X E Q}, di = {dM;M E i} et d = {dA;A E }. On introduit les opérations algébriques suivantes :

(i) Addition : dX + dY = d(X + Y ), pour X, Y E Q.

(ii) Multiplication : dX.dY = (MX, MY ), pour X, Y E Q. où MX et MY sont les parties martingales respectivement de X et Y .

(iii) â - multiplication : si ö E â et X E Q alors

Z t Z t

(ö.X) = X(0) + ₀ ö(s, w)dMX(s) + ₀

ö(s, w)dAX(s), t > 0

est définie comme un élément dans Q.

Comme d(ö.X) est uniquement définie a partir de ö et dX. Maintenant on définit un élément ö.dX de dQ par

ö.dX = d(ö.X)

.

Théorème 2.1.1. [87] L'espace de dQ avec les opérations (i) - (iii) est une algèbre commutative satisfaisant aux relations suivantes :

1. ö.(dX + dY ) = ö.dX + ö.dY

2. ö.(dX.dY ) = (ö.dX).dY

3. (ö + ø)dX = ö.dX + ø.dX

4. (ö.ø).dX = ö.(ø.dX)

pour ö, ø E â et dX, dY E dQ.

Si X¹, X², ..., X^d E Q et f est une fonction continue de classe C² alors Y = f(X¹, X², ..., X^d) E Q et la différentiation totale de la fonction f est

dY =

d i=1

^d (?if).dX^i+ E (?i?jf).dX^i.dX^j, ^2i,j=1

32

où ?if et _?i?jf sont les éléments de â définis respectivement par ?xi (X¹, X², ..., X^d) et ?2f

?f ?xi?xj (X¹, X², ..., X^d).

Si dX¹, dX²,...., dX^d E du et dXⁱdXj = äijdt, i, j = 1, 2, ...., d, alors (X¹(t), X²(t), ..., X^d(t)) est une martingale de Wiener de d dimensions.

33

2.2 Equations différentielles stochastiques

Cette section donne quelques notions importantes sur les équations différentielles stochastiques. L'objectif poursuivi ici est de faire la différence entre les équations différentielles stochastiques ordinaires et les équations aux dérivées partielles stochastiques. Ces formulations mathématiques ont une importance capitale car beaucoup de phénomènes stochastiques, par exemple économiques, sont produits en suivant ces types de modèles statistiques ([7],[8], [34],[26], [151],[58],[62],[87],[95],[101],[107],[68],[114], [113],[138],[145],[149],[62], [156],[88], [89],[162]).

2.2.1 Equations différentielles stochastiques ordinaires

Soit W(t) un processus stochastique satisfaisant le système suivant :

dW(t)^' = á(W(t), t) + u(W(t), t)dW(t), W(0)^' = W0

avec á(x,t) = (á1(x,t),· · · ,á_n(x,t)) et cr(x,t) = uij(x,t), 1 = i,j = n. On suppose que á(x, t) et u(x, t) sont mesurables dans Rⁿ ×[0, T], et satisfaisant les conditions suivantes :

(1) condition lipschitzienne ku(t, x) - u(t, y)k = K|x - y| |á(t,x) - á(t,y)| = K|x - y|

(2) condition de croissance linéaire ku(t, x) - u(t, y)k² = K(1 + |x|²) |á(t, x) - á(t, y)|² = K(1 + |x|²)

et W0 est indépendant du mouvement brownien W(t),

E | W0 |²< 8.

Théorème 2.2.1 (Théorème de l'existence et unicité de solutions). Soient les équations ?? et Alors,il existe une solution unique W de kkkkkkkkkkk et dans M² _w[0, T]. L'unicité signifie que si W est une autre solution dans M2 _w[0,T], alors

P[W(t) =6 W(x)] = 0,

34

Démonstration. On va démontrer l'existence et l'unicité de la solution de l'équation différentielle stochastique. Pour l'existence, on définit

Z t Z t

Øm+1(x) = Ø0 + ₀ á(Ø_m(s), s)ds + ₀

u(Ø_m(s), s)dcw(s), m > 0

et on fait par induction que Ø_m ? M²_w[0, T] et

E | Øk+1(t) - Øk(t) |² = (Mt)k+1

(k + 1)! pour 1 = k = m - 1,

où M est une constante positive dépendante de k et T. Il est facile de démontré que existe pour k = m et Øm+1 ? M²_w[0, T]. Ensuite, on trouve que

E sup |{z} 0<t<T	| Øm+1(t) - Øm(t) |2= C(MT )m m! .
Par conséquent P( sup |{z} 0<t<T		| Øm+1(t) - Øm(t) |>^1 2m) =2mC(MT )m m! .

Le Lemme de Borel - Cantelli implique que

P( sup |{z} 0<t<T

| Øm+1(t) - Øm(t) |> 1 2m i.o) = 0.

Ainsi pour tout w, il existe m0 = m0(t) tel que

(sup | Øm+1(t) - Ø_m(t) |> 1

2m) = 0. si m0 = m0(w).

Il s'en suit que la suite Ø0 + Pô (Øm+1(t) - Ø_m(t)) converge uniformément

dans t ? [0,T].

En notant la limite par 0(t) nous avons en suite

2.2.2 Equations aux dérivées partielles stochastiques

Dans cette section, nous allons étudier les problèmes de certaines classes des équations aux dérivées partielles stochastiques du premier et deuxième ordre.

Soit l'équation aux dérivées partielles stochastiques du premier ordre

Z t

u(x, t) - f(x) = 0 F(x, u, u_x, ?ds)

où ?ds représente l'intégrale stochastique de Stratonovich. Le théorème suivant prouve l'existe et l'unicité des solutions de l'équation aux dérivées partielles linéaires du premier ordre.

Théorème 2.2.2. (Théorème de l'existence ) On suppose que la fonction F de l'équation ( ? ? ?) est une C^k,ä - semimartingale continue avec la caractéristique locale appartenant à la classe (B^k+1,ä, B^k,ä) pour quelque k = 4 et

35

S = 0 et f est une fonction de C^k,ä.

Soit (çot, 17t, Xt) la courbe caractéristique stochastique de l'équation. La fonction u(x, t) est définie par

~ ) [ ]

u(x, t) = ç ?_¹(x) , t ? 0, u(x) ,

est une solution locale de l' équation (2.7). De plus, elle est une Ck-1,å - semimartingale continue locale pour tout > 0.

Avant la démonstration du théorème, nous donnons le lemme suivant qui va aider à démontrer ce théorème de l'existence et de l'unicité de solutions de l'équation aux dérivées partielles linéaires du premier ordre.

Lemme 2.2.2.1. Soit ?i = ?^-1

d . Les relations suivantes sont alors vérifiées :

Le théorème suivant donne la condition de l'unicité de solution de l'équation aux dérivées partielles stochastiques du premier ordre annoncée ci - dessus.

Théorème 2.2.3 (Unicité de solution). Nous supposons que les mêmes condi-

tions pour F et f .[ ]

Soit u(x, t), t ? 0, cr(x)une solution locale arbitraire de l'équation 5 tel

qu'elle est une Ck-1,å - semimartingale pour > 0. Alors elle peut s'écrire comme suit :

[ ]

u(x, t) = çt ? øt(x) pour t ? 0, T (x) ? u(x)

Définition 2.2.1. ([87]) Soit Xt une semi - martingale continue, c'est - à - dire, un processus représenté sous la forme suivante :

Xt = X0 + Mt + At

où X0 est une variable aléatoire .T - mesurable, Mt est une martingale et At est la partie variationnelle fermée.

On présente le problème à valeurs initiales des équations aux dérivées partielles stochastiques du second ordre à coefficients aléatoires suivant :

Z t d Z t

₀ F ⁱ(x, ?ds) ?u

u(x, t) = f(x) + ₀ L_su(x, t)ds + ?xi (x, s)

i=0

Z t

+ ₀ F^d+1(x, ?ds)(x, s),

où L_s est un opérateur elliptique de la forme ,

1 XL_su =

^ij

?

2

2 ^a

^{(x, s)}

^aaxj+ bi(x's)ax Ou + d(x, s)u i i

36

et le domaine aléatoire (F¹, F², ..., F^d+1) sont des fonctions C^k,d - semimar-tiangale satisfaisant la condition _(D1)k,ä pour tout k > 3 et ä > 0 tous deux pour avant et arrière direction. Les différentielles Fⁱ(x, ods) sont les différentielles de Stratonovich. Dans le séquentiel, nous supposons que les coefficients de l'opérateur L_s satisfont la condition suivante _(D2)k,ä pour tout k > 3 et ä > 0. La condition _(D2)k,ä, il existe une fonction non négative et symétrique continue aⁱj(x, y, s) appartenant à la classe Ck+1,ä

ub telle que

aⁱj(x, s) = aⁱj(x, x, s). La fonction d(x, s) est continue en (x, s) et de classe C^k,b. De plus aⁱj et d

(1+|x|) sont des fonctions bornées

Ldu = 2 E Ëij(x,

y, t) ?xiaxj E [Ë^i,d+1(x,y,t) + Cⁱ(x,t)_J?xi t=1

1

+ 2

D(x, t) + Ë^d+1,d+1(x, y, t)u

où Cⁱ(x,l) = Ed ?azyz ¹(x, y, l) . En faisant recours à l'intégrale d'Itào,

y=x

l'équation (1) peut être écrite comme suit

Z t

u(x, l) = f(x) + ₀ (L_s + L_s)u(x, l)ds

d r ?u r

+ E f Fⁱ(x, ds) _?xi (x, s) + ^f Fⁱ(x, ds)u(x, s)

r=1

En effet, les intégrales de Stratonovich sont représentées par

Z0

r au r ôu 1 au

Fⁱ(x, ods) = Fⁱ(x, ds) + (F(x, t), )

?xi o axⁱ 2 axⁱ

fr au 1 r d ?2u
Fi (x, ds) + Ë^j (x, x, s) ds

o ?xⁱ 2 ( fo 0 i axi?xj

r d ?Ëⁱj ?u i,d+1 ?u

+ + Ë (x, x, s) ds

Jo ?yⁱ y=x ?xj

?xⁱ

j=1

+f

^r?Ëz?(x,y,s) udsl

o ?y y=x /

37

De façon similaire, nous avons

_lot

F^d+1(x,ods)u = J t F^d+1(x, ds)u + 2 { f t [Ëd+1(x,x,s)?xjids

f

t d+1 d+1 1

o J

d t

En substituant ces relations dans l'équation (1), nous obtenons l'équation (4). Inversement, soit u(x, t) un C²- processus continu satisfaisant l'équation représentée par les intégrales d^'Itào suivantes

u(., t) = f + ^f Ë_su(s)ds + E f Fⁱ(., ds)_?x + f t F^d+1(., ds)u(s).

i=1

Si la fonction u(x, t) est une C² - semimartingale, elle est représentée par

l'équation (1), en remplaçant L_s par Ë_s - L_s où L_s est définie par l'équation 3.

2.3 Intégrales stochastiques

Dans cette section, nous présentons de façon brève, sans démonstration, certains théorèmes et définitions sur les intégrales stochastiques d'Itô et Stratonovich.Les intégrales stochastiques jouent un rôle important dans l'évaluation des équations différentielles stochastiques. Pour constituer cette partie nous avons consulté certains ouvrages( voir [87], [111],[146], [155], [90], [164], [43], [23], [24]).

2.3.1 Intégrale Stochastique d'Itô

Avant de définir l'intégrale d'Itô , on va définir l'intégrale de Wiener pour le mouvement Brownien. Soit f une fonction déterministe et f E L²[a, b].

Définition 2.3.1. ([111],p.11) L'intégrale de Wiener de f est notée par

Za

b f(t)dB(t) ou f b f(t)dB(t, w)

a

Théorème 2.3.1. Pour chaque f E L²[a, b],l'intégrale de Wiener ^fab f(t)dB(t) est une variable aléatoire Gaussien de moyenne nulle et de variance

II f II2= fa b f(t)2dt.

Ainsi,l'intégrale de Wiener I : L²[a, b] ? L²(Ù) est une isométrie Car elle préserve le produit scalaire comme montre le corolaire suivant.

Corollaire 2.3.1.1. Si f, g E L²[a, b], alors

Z b

E(I(f)I(g)) = a f(t)g(t)dt.

En particulier,si f et g sont orthogonales alors les variables aléatoires Gaussiennes I(f) et I(g) sont indépendantes.

Théorème 2.3.2. ([111],p.12) Soit f une fonction continue de variations bornées. Alors pour presque tout w E Ù,

fab f(t)dB(t)) (w) = fb f(t)dB(t, w),

a

où à gauche comme à droite de l'équation ci-haut, il s'agit respectivement de l'intégrale de Wiener et Riemann -Stieltjes.

Le théorème suivant donne la formule générale d'Itô.

Théorème 2.3.3. ([111],p.103) Soit Xt un processus d'Itô donné par

Xt = X_a + f t f(s)dB(s) + f t g(s)ds, a < t < b.

a a

Supposons que Z(t, x) est une fonction continue avec les dérivées partielles

continues ?Z ?t,?Z

_?x,^?2Z

?x2 . Alors Z(t, Xt) est aussi un processus d'Itô et

Z(t, Xt) = Z(a, X_a) + ft Ox

(s, X_s)f(s)dB(s)

ds.

t 2

ât (s, X_s) + _Ox

+ f(s, X_s)f(s)²1

_s

(s, X

)g(s) + 2 âx²

38

Avant de présenter la formule d'Itô de dimension n,nous donnons d'abord la définition d'une matrice stochastique.

Définition 2.3.2. ([28],p.7) Soit N un entier strictement positif. Une matrice P de taille N xN est une matrice stochastique si ses éléments de matrice pij = (p)ij satisfont

0 < pij < 1, Vi, j,

et

_XN pij = 1, Vi. j=1

Soient B1(t), B2(t), ..., B_n(t), n mouvements browniens indépendants.

On considère n processus d'Itô x(1)

t , x(2)

t , ..., x(n)

t , données par

xt = x^(0) + (i)

m t X f fij(s)dBj(s) + ^f gid(s), 1 < i < n, j=1 a a

ou _fij E L_ad(Ù, L²[a, b]) etgi E L_ad(Ù, L¹[a, b]), V 1 < t < n et 1 < t < m. Sous forme matricielle,

? ? B(t) = ?

B1(t) ... Bm(t)

? ? ? ? ? (1) xt g1(t) ? , Xt =?...?, g(t) =? ?... ? x(t) gn(t) m

,

?

?

f(t) = ?

?

f11(t) ... f1_m(t)

?... ... ... ?
f_n1(t) ... f_nm(t)

39

L'équation (1) peut être écrite comme suit :

Xt = X_a + f t f(s)dB(s) + f t g(s)ds, a < t < b.

a a

~ ~

On suppose que ø t, x(1)

t , x(2)

t , ..., x⁽ⁿ⁾ est fonction continue sur

t

[a, b] x Rⁿ et a des dérivées partielles continues _?Ø?t , ?xi ?Ø_, ?²Ø

i,j < n.

?xi?x; , pour , 1 <

La différence totale stochastique de Ø(t, x(t)⁽¹⁾, x(t)⁽²⁾, ..., x(t)⁽ⁿ⁾) est donnée par

dØ(t, x1(t), x^(t)2 , ..., x_n(t)) = ?Ø?t (t, x(t)⁽¹⁾, x(t)⁽²⁾, ..., x(t)⁽ⁿ⁾)dt

_X ?Ø

+ _?t (t, x1(t), x2(t), ..., x_n(t))dxi(t)

1 _X ?²Ø

+?x(t)i?x(t)j (t, x(t)(1), x(2)

t , ..., x(t)⁽ⁿ⁾)dx(t)⁽ⁱ⁾dx(t)^(j)

2

où le produit dx⁽ⁱ⁾

t dx(j)

t doit être calculé en utilisant la table d'Itïô suivante

x dBj(t) dt
dBj(t) _äijdt 0

dt 0 0

Le produit dBi(t)Bj(t) = 0 pour i =6 j est l'expression symbolique du fait suivant. Soient B1(t) et B2(t) deux mouvements browniens indépendants et soit

40

O_n = {t0, t1, ..., t_n} une partition de [a, b]. Alors >(B1(ti) - B1(ti1)(B2(ti) - B2(ti1) -+ 0 dans L²(Ù) quand O_n = max(ti - ti_1) -+ 0.

Soit M(t) une martingale continue à droite avec des limites à gauche finies tel que E(M(t)²) < oo pour chaque t E [a, b].

Théorème 2.3.4. Soient M(t) une martingale continue de carrée intégrable et F une fonction continue de classe C². Alors,

F(t, Mt) = F(a, M_a) + fat ?t (s, Ms)ds x

+ fa dM_s + 2 fa a²_x2 (s, M_s)d(M)_s

2.3.2 Intégrale Stochastique de Stratonovich

L'intégrale stochastique de Stratonovich est une application du calcul d'Itô. Elle constitue un outil puissant dans la résolution des équations aux dérivées partielles stochastiques. Cette étude réfère aux livres [111],[145]. On considère une intégrale simple dans le calcul de Leibniz - Newton :

f

b f(x)dx = F(b) - F(a). L'égalité correspondante dans le calcul d'Itô est donné par

Z b

a f(B(t))dB(t) = F(B(b)) - F(B(a)) - 2 f b f(B(t))dt.

La différence entre les deux formules susmentionnés est le terme additionnel dans l'intégrale d'Itô. Ce terme est une conséquence de la variation quadratique non nulle du mouvement Brownien B(t). Mais aussi il est une conséquence de la définition de l'intégrale d'Itô.

Définition 2.3.3. ([111],p.120) Soient Xt et Yt deux processus d'Itô. L'intégrale stochastique de Stratonovich de Xt sachant Yt est définie par :

f

b b 1 b
Xt o dYt = XtdYt + 2 L (Xt)(dYt), a a

ou par sa forme différentielle équivalente :

1

Xt o dYt = XtdYt + ₂(Xt)(dYt).

Proposition 2.3.4.1. Soient x et y deux semimartingales. La différentielle et l'intégrale sont données par y o dx = y.dx + ¹₂dy.dx et ^f0t odx = f^t₀(y, x)t oï3/4¹₂ o est le produit de Stratonovich.

(1) Soient x et y dans S_c,alors l'intégrale se Stratonovich - Fisk s'écrit :

f0t y o dx = E yTi+yTi+1

2 (xTi+1 - xTi) en probabilité.

(2) Si ni x ni y est dans A_c, alors ^f0t y o dx = f0t ydx.

Les propriétés importantes de l'intégrale stochastique de Stratonovich sont énoncées dans le théorème suivant.

Théorème 2.3.5. Les propriétés de l'intégrale stochastique de Stratonovich sont les suivantes :

(1) x o (dy + dz) = x o dy + x o dz,

(2) (x+y)odz=xodz+yodz,

(3) x o ( dy.dz) = (x o dy).dz,

(4) x o ( dy.dz) = x o ( dy.dz) ou x o ( dy.dz) = (x.y) o dz.

Théorème 2.3.6. Supposons que x1, x2, ..., xd sont des semimartingales continues. De plus,on suppose que U est un sous- ensemble ouvert de R^d et que (x1, x2, ..., xd) E U pour tout t , avec une probabilité égale à 1. Soit f : U -+ R de classe C³. Alors,

f(x1, x2, ..., xd) = Edi=1 aif(x1, x2, ..., xd) o dxⁱ.

Nous pouvons poser la question suivante : est-que l'intégrale de Stra-tonovich ^fab f(t) o dB(t) peut - elle être définie comme la limite de somme de Riemann ? La réponse à cette question pour une fonction f(t, B(t)) est donnée par le théorème suivant.

Théorème 2.3.7. [111] Soit f(t, xt) une fonction de classe C². Alors,

Za

b f(t, B(t)) o dB(t) = lim |{z} IIonII-+0

Xn i=1

1 f(t* i , 2(B(ti_1) + B(ti)))(B(ti) + B(ti_1),

41

en probabilité, où ti_1 < tz < ti, O_n = {t0, t1, ..., _{tn_1,} t_n} est une partition de

l'intervalle fini [a, b] et II On II= max | {z } 1<i<n

(ti - ti_1).

2.4 Schémas numériques

On décrit dans cette section des méthodes numériques pour la résolution d'équations différentielles stochastiques développées dans les ouvrages

42

de Kloeden et Platen [106], [105], Jentzen et Kloeden[95], [94].

Pour approcher numériquement l'équation différentielle stochastique

dXt = t9(t, Xt)dt + u(t, Xt)dBt,

on utilise des schémas aux différences classiques et le fait que pour un pas h donné les variables _{(B(n+1)h-Bnh)} suivent des lois gaussiennes indépendantes de variance h. On note xt le processus approché et on considère la subdivision 0 = t0 < t1 < .... < tN_1 < TN = T de pas régulier h = At = tn+1 - t_n. Dans le cas multidimensionnel t9 = (t91, ..., t9_n) et Xt = X1(t), ..., X_n(t)) sont des vecteurs de Rⁿ.

Le mouvement brownien a p composantes Bt = (B1(t), ..., B_p(t)) et crj(cr1 _j , ..., crn _j ) pour j = 1, ..., n.

L'équation s'écrit comme suit

dXt = t9(t, Xt)dt + _Xp uj(t, Xt)dBj(t),

i=1

et se traite de la même manière.

La vitesse de convergence forte du schéma est le plus grand coefficient á tel que

EMXT - xNhM = O(h^á)

et la vitesse de convergence faible est le plus grand coefficient 3 tel que E|Ef(XT) - Ef(xNh)| = O(h^â)

pour tout polynôme f.

2.4.1 Schéma d'Euler

On utilise l'approximation suivante

dXt dt '

Xt+h - Xt

h

valable lorsque le pas h = At est suffisamment petit. Sur un intervalle élémentaire [t, t + h], l'équation générique devient

Z t+h Z t+h

Xt+h ' Xt t t9(t, Xt)ds + t ó(t, Xt)dB_s,

43

Le processus approché xt consiste à considérer les intégrands constants

xt+h = xt + h19(t, xt) + u(t, xt)(B(n+1)h - Bnh).

Le schéma d'Euler converge en moyenne quadratique vers Xt quand h tend vers 0. La mauvaise convergence de ce schéma est due à la présence de l'intégrale stochastique dont la majoration est trop grossière. Pour remédier à cela on introduit le développement de Taylor.

2.4.2 Schéma de Milstein

Les ouvrages qui traitent dans l'application de la méthode de Runge - Kutta aux equations différentielles stochastiques ( [139],[157][112], [95]).

On remplace le processus Xt par une approximation _Xtn. On a

1

Xt = Xt_n + 19(t_n, Xt_n)h - ₂u(t_n, Xt_n)axu(tn, Xt_n)h

+ u(t_n, _Xtn) A B_n + u

₂(tn, Xt_n)axu(tn, Xt_n)(AB_n)².

1

dans le cas multidimensionnel avec les notations précédentes et sous la condition que

?xój.ók = ?xók.ój

Xtn+1 = Xt_n + 19(t_n, _Xtn)h + E crj(t_n, Xt_n) An+1 Bj

uk(t_n, Xt_n)cj(tn, Xt_n) An+1 ^Bj _An+1 Bk

_E

k<j

E p

+

j=2

1

2

+

_Ep i=1

cj(t_n, _Xtn)cj(tn, Xt_n)((ABj)² - h).

avec

ABj = Bj(tn+1) - Bj(t_n)

. La convergence forte du schéma de Milstein vaut 1. Ce schéma est donc meilleur que le schéma d'Euler, mais plus compliqué à programmer. En utilisant des développements d'ordre supérieur, on peut espérer améliorer la convergence.

44

2.4.3 Schéma de Heun

Soit l'équation différentielle stochastique de Stratonovitch suivante [94]

dXt = ?(t, Xt)dt + ó(t, Xt) o dBt

équivaut à équation différentielle stochastique d'Itô suivante

1

dXt = (?(t, Xt) + ₂ó(t, Xt)?_xó(t, Xt))dt + ó(t, Xt)dBt

qui discrétisée selon le schéma de Heun s'écrit

1 1

Xtn+1 = Xt_n + ₂h(?(t_n, _Xtn) + ?(t_n, _Ytn)) + ₂(ó(t_n, _Xtn) + ó(t_n, _Ytn) 4 B_n.

avec

Ytn+1 = Xt_n + ?(t_n, _Xtn)h + ó(t_n, _Xtn) 4 B_n.

Le schéma de Heun converge en moyenne quadratique et est d'ordre O(h²).

2.4.4 Méthodes de Runge - Kutta

Il y a plusieurs ouvrages qui traitent de l'application de méthode de Runge - Kutta aux equations différentielles stochastiques ( [157],[112], [95],[139]).

Dans le cas des équations différentielles stochastiques, les méthodes de Rung - Kutta utilisent deux vecteurs á et â et deux matrices A et B. Le schéma est de la forme

Xtn+1 = Xt_n + hö(t_n, _Xtn, h) + ø(t_n, _Xtn, h) 4 B_n.

où les fonctions ö et ø sont définies par

ö(t_n, _Xtn, h) = á2k2, á1k1, ..., árkr. ø(t_n, _Xtn, h) = â2l2,â1l1, ..., ârlr.

avec

k1 = ?(t_n, _Xtn), ..., kj = ?(t_n + cjh, Yj), l1 = ó(t_n, _Xtn), ..., lj = ó(t_n + cjh, Yj)

45

et

Ytn+1 = Xt_n + h j-1 X aiuku + j-1 X bjuku A B_n.

u=1 u=1

Les vecteurs á et â vérifient

á1 + á2 + ... + á_r = 1,â1 + â2 + ... + â_p = 1,

Les éléments supérieurs de la matrice A sont nuls,aij = 0 si j > i et les coefficients cj sont les sommes des éléments d'une ligne de la matrice A

cj =

j-1 X k=1

ajk.

Si ?,â et toutes leurs dérivées sont bornées alors le schéma de Runge - Kutta converge en moyenne quadratique vers la solution Xt de l'équation d^'Itô suivante

dXt = (?(t, Xt) + ëó(t, Xt)?_xó(t, Xt))dt + ó(t, Xt)dBt avec ë = 0 si r = 1, et si r > 1

ë =

r j=1

bj

j-1 X u=1

bju.

2.4.5 Schéma de Platen

Dans le schéma de Platen, on utilise l'approximation des incréments du brownien et de leur intégrale. On pose

n+1

AU_n =

f(B_s - Bt_n)ds

n

Le schéma est de la forme

Xtn+1 = Xt_n + h?_n + ó_n A B_n + ₂ón?xón((ABn)² - h)

1

+ _ón?x?n A U_n + _(?n?x?n + ₂(ó²

¹_n?xxón)(h A B_n - AU_n) + ¹₂?xxón

avec

?_n = ?(t_n, _Xtn), ó_n = ó(t_n, Xt_n),

La converge de ce schéma est en O(h³).

46

Chapitre 3

Applications des intégrales

stochastiques à l'estimation

statistique

Ce présent chapitre présente les applications des intégrales stochastiques à la théorie de l'inférence statistique. Le domaine de l'estimation statistique est vaste ([37], [170], [172],[63], [122], [118],[184],[120],[171],[117],[116],[91]).

Ces cinq dernières décennies, les recherches ne cessent de croire abondamment dans l'estimation de paramètres des équations différentielles stochastiques et la théorie de filtre stochastique Arato,Kolmogorov et Sinai (1962) et Liptser et Shiryayer (1978)( [124], [22],[91] [86],[110], [116],[21]).

Dans cette recherche l'estimation de paramètres des équations différentielles stochastiques et la théorie de filtre stochastique sont considérées. Car ces deux techniques sont des outils puissants dans le domaine de la modélisation macroéconométrique ([131] [130],[128],[127][11]).

3.1 Estimation de paramètres des équations différentielles stochastiques

L'estimation de paramètres des équations différentielles stochastiques consti-

tue l'un des problèmes majeurs de la théorie de l'inférence statistique moderne([6],[152], [126]).

47

3.1.1 Estimation des paramètres pour les équations différentielles stochastiques linéaires

Le Breton(1998) a étudié l'estimation de paramètres et l'estimation de filtre dans un modèle linéaire simple conduit par les mouvements browniens de diffusion. Aussi et Le Breton (2002) ont étudié les problèmes d'estimation des paramètres pour le processus de type Ornstein - Uhlenbeck fractionnel ([154] ).

L'un des outils de base dans l'étude de la théorie de l'asymptotique de l'inférence statistique est le concept de la normalité. Plusieurs propriétés importances des estimateurs exigées dans tels processus apparaissent comme une conséquence de la normalité asymptotique locale de la famille de mesures de probabilité générée par les processus.

On considère l'équation différentielle stochastique linéaire

dXt = ä(è, t, Xt)dt + ødW_t^H, (3.1)

X0 = x0, 0 < t < T,

où X0 E R, ö E (0,1), ä(è, t, Xt) : R^d x R -- R est une fonction déterministe avec le paramètre, è E O E R^d est un paramètre inconnu et WH = {W_t^H, 0 < t < T} est un processus brownien fractionnel avec l'indice de Hurt H E (¹₂, 1). L'équation 3.1.1 modélise un système dynamique avec un petit bruit qui est un processus Brownien fractionnel.

On suppose que le processus {Xt, 0 < t < T} est observé sur un intervalle [0,T]. Le problème d'intérêt est l'estimation de paramètre è basée sur les observations ou les données {Xt, 0 < t < T}.

Nous définissons le concept de la normalité asymptotique locale pour une famille de mesures de probabilité.

Nous discutons généralement sur les classes de processus stochastiques satisfaisant l'équation différentielle stochastique linéaire conduit par un mouvement brownien fractionnaire et l'étude des estimateurs de maximum de vraisemblance et de Bayes de ces processus.

On considère l'équation différentielle stochastique suivante :

dXt = ä(è,t, Xt)dt + ødW_t^H, X0= x0, 0 < t < T,

où X0 E R, ö E (0, 1), ä(è, t, Xt) : R^d x R -- R est une fonction déterministe avec le paramètre, è E O E R^d est un paramètre inconnu et

WH = {W_t^H, 0 < t < T} est un mouvement brownien fractionnaire avec l'indice de Hurst H E (¹₂,1). L'équation 4.1 modélise un système dynamique

avec un petit bruit qui est un processus Brownien fractionnaire. On suppose que le processus {Xt, 0 < t < T} est observé sur un intervalle [0,T]. Le problème est l'estimation du paramètre è basée sur les observations ou les données {Xt, 0 < t < T}.

On définit le concept de la normalité asymptotique locale pour une famille de mesures de probabilité. On analyse les classes de processus stochastiques satisfaisant l'équation différentielle stochastique linéaire conduit par un mouvement brownien fractionnaire et l'étudions les estimateurs de maximum de vraisemblance et de Bayes de ces processus.

On considère l'équation différentielle stochastique un processus brownien fractionnaire suivante :

dXt = [á(t, X(t)) + èâ(t, X(t))]dt + ó(t)dW^H, X(0) = 0, t > 0,

où è E O C 1R, W = {W_t^H, t > 0} est un processus brownien fractionnaire avec un paramètre de Hurst et ó(t) est une fonction positive non nulle dans[0, +oo). En d'autres termes,X = {Xt, t > 0} est un processus stochastique satisfaisant l'équation intégrale stochastique

Z t Z t

X(t) = 0 [á(s, X(s)) + èâ(s, X(s))]ds + ₀ ó(s)dw^H, t > 0

avec ?(è, t) = á(t, X(t)) + èâ(t, X(t)).

On suppose que les trajectoires de l'échantillon du processus

[?(è,t) ó(t) ,t > 0] sont tels que le processus

QH,è(t) =dWtH ft kH(è, s) _ó((,) , t > 0.

On suppose que les trajectoires de l'échantillon du processus _{QH,è(t), 0 < t < T} appartiennent presque sûrement à L²([0, 1], dW^H(t)). On définit

Z(t) =

lo ó(è) , t > 0.

t kH(è, s)

48

Alors, le processus Z(t) = {Z(t), 0 < t < T} est une Fø - semimartingale qui admet le processus de décomposition suivante :

t

Z₍t) = Jo QH_,è(s)dW^H(t) + M^H(t)

49

où M^H est une martingale fondamentale et le processus X admet la représentation suivante:

Z t

X(t) = 0 Kó _H(t, s)dZ_s

où la fonction Kó H est définie par :

Z t

Kf _H(t, s) = -2H d s f(r)rH- 2 1 (r - s)H- 2 1 dr, 0 s t. ds

Comme en déterministe, pour estimer les paramètres des équations différentielles stochastiques, il important de donner les conditions de l'existence et de l'unicité. de solutions. Pour l'équation ??,on donne le théorème suivante.

Théorème 3.1.1.

Soit Pè ^T la mesure induite par le processus X(t) = {X(t), 0 t T}

où est le vrai paramètre. Kleptsyna et al.(2000) ont dérivé le théorème de Girsanov - type qui permet de trouver la dérivée de Radon - Nikodym de P_è^T relativement à P ₀ ^Tde la manière suivante [154] :

P è T P 0 T

Z T Z T = exp{ 0 QH,è(s)dZs - 1 0 Q2 H,è(s)dW s H }. 2

Cette quantité est indispensable pour l'utilisation de la méthode du maximum de vraisemblance dans l'estimation des paramètres de modèles statistiques.

Cette quantité est indispensable à l'utilisation de méthode du maximum de vraisemblance dans l'estimation des paramètres de modèles statistiques.

3.1.2 Méthodes d'estimation des paramètres

La littérature est vaste mais cette étude a retenu seulement deux méthodes parmi les utilisées, méthode de maximum de vraisemblance et méthode bayésienne, à cause de leur fondement mathématique solide et leur robustesse dans les études empiriques.

3.1.3 Méthode de maximum de vraisemblance

Cette méthode est couramment utilisée en analyse statistique empirique

([51],[19],[42], [16], [142],[121], [159],[96],[48],[69],[148], [137],[70])

50

On considère le problème de paramètre è basé sur l'observation du processus X = {Xt, 0 < t < T} et étudions ses propriétés asymptotiques

T

quand T -+ oo. On note par LT(è) la dérivée de Radon - Nikodym ^dpô .

L'estimateur de maximum de vraisemblance ^àèT est défini par la relation

LT(

^àèT) = sup \J èEÈ

LT(è).

On suppose qu'il existe un estimateur mesurable du maximum de vraisemblance. Les conditions suffisantes peuvent être données pour l'existence d'un tel estimateur.

On sait que

QH,è(t) =

dJo ^t dWtH kH(è, ^s^)a(s) ds.

= dWH d Lt kH(è,s)^á((_s)⁾ds + è_dW_H f^tkH(è,s)^â((s)⁾ds.

t t

= ë1 + èë2.

Alors

logLT(è) = f ^T(ë1 + èë2)dZt - 2 JoT (ë1 + èë2)²dW_s^H

et l'équation de vraisemblance est donnée par

Z0	T ë2dZt - fT (ë1 + èë2)ë2dWs^H = 0.

Par conséquent, l'estimateur du maximum de vraisemblance est donné par

.

f0 T ë2(t)dZt - f0 T ë1(t)ë2(t)dW H

^àèT = t

f0 T ë22(t)dWtH

Soit è0 le vrai paramètre. En utilisant le fait que

Z T

dZ(t) = 0 (ë1(t) + è0ë2(t))ë2(t)dW^H(t) + dM^H(t).

On montre que

dP_è^T

dP^T

è0

Z T Z T

= exp{(è - è0) ₀ ë2(t)dM^H(t) - 1 ₂(è - è0)2 0 ë2 2(t)dWH(t)}.

51

En suivant la représentation de la dérivée de Randon - Nikodym, on obtient

__ f0 ë2(t)dMH(t)

(^àèT - è0) f0T ë22(t)dWH(t)

Le théorème suivant établit la consistance forte de l'estimateur du maximum de vraisemblance.

'

Théorème 3.1.2. L

estimateur du maximum de vraisemblance

èN,E est fortement consistant,c'est- à -d ire, èN,E ? è0 presque surement _[P90] quand T ? 8 en considérant ^f0T ë2(t)dW^H(t) ? 8 presque surement _[P90] quand T ? 8.

3.1.4 Méthode d'estimation Bayésienne

Cette méthode s'impose de plus tant dans les analyses théoriques qu'empi-

riques ([39],[134],[65],[64],[102],[182],[183],[7],[123],[143],[144],[79],[27],[37],[40],

[156],[52],[125],[59],[158],[163],[160],[108].

On suppose que l'espace du paramètre O est un ouvert et A une mesure de probabilité a priori sur l'espace paramétré O. En plus,on suppose que A a la densité ê() en accord avec la mesure de Lebesgue. La fonction de densité

est continue et positive dans un ouvert au voisinage de è0,le vrai paramètre. f T

Soit öT = IT RT = IT ₀ ë2(t)dM^H(t), t = 0 et

çT = IThRiT = I2 f0 T ë2²(t)dM^H(t), t = 0.

T

L'estimateur du maximum de vraisemblance satisfait la relation suivante

öT = (

^àèT - è0)I^-^1 T çT.

La densité de probabilité a posteriori de è basée sur l'observation X^T = X_s, 0 = t = T est

dPe dPï

p(è|X^T) = dPe ë(è)/ fo dPe ë(è)dè.

0 0

Soit t = I-1

T (è0 - BT) et nous définissons

p^*(è|X^T) = ITp(^àè + tIT|X^T).

Alors, la fonction p^*(è|X^T) est la densité de probabilité a posteriori de la

variable transformée t = I-1

T (è0 - ^àèT).

52

3.2 Estimation des équations aux dérivées partielles stochastiques avec dérive linéaire

Soient U un espace de Hilbert séparable réel et Q un opérateur auto-adjoint positif. Supposons que l'opérateur Q est nucléaire [154]. Alors, Q admet une séquence des valeurs propres {ã_n, n > 0}, 0 < ã_n décroissant à zéro quand n -+ oo et ^I000 ã_n < oo. En plus,les vecteurs propres correspondants {í_n, n > 1} forment une matrice orthonormée dans U. On définit un mouvement brownien fractionnel à dimension infinie sur U avec une matrice de covariance Q comme

00

ù^H_ã (t) = _Nh_nø_nW_ã^H(t)

n=0

où W_ã^H(t), n > 0, sont des mouvements browniens fractionnaires avec l'indice de Hurst(cf.Tindel et al.2003). Soient U = L2[0, 1] et W_ã^H(t) un mBf à dimension infinie sur U avec comme indice de Hurst H et l'opérateur de covariance nucléaire Q. Considérons le processus

du_å(t, x) = (Au_å(t, x) + èdu_å(t, x))dt + ?dW_ã^H(t)

où A = ?2

?x2 .

Supposons que å -+ oo et è E O c R.Aussi nous supposons que les conditions initiales et aux limites bornées sont données par

u_å(0, x) = f(x), f E L2[0,1]

u_å(t,0) = u_å(t,1) = 0, 0 < t < T

Tindel et al.(2003) ont donné les conditions suffisantes pour l'existence et l'intégrité carrée d'une solution u_å(t, x) pour l'équation différentielle stochastique conduite par un mouvement brownien fractionnel à dimension infinie [154].

Nous supposons que les conditions suffisantes soient remplies, alors il existe une solution carrée intégrable unique u_å(t, x) de [? ] sous les conditions (3) et (4). Nous considérons cette solution unique comme une somme suivante

00

u_å(t, x) = ui_å(t)íi(x).

i=1

Alors le coefficient de Fourrier ui_å(t) satisfait l'équation différentielle stochastique

dui_å(t) = (è - ëi)ui_å(t)dt + ø

v1 + ëidwHi (t), 0 < t < T,

avec la condition initiale ui_å(0) = õi, uiå = f01 f(x)ãi(x)dx. Soit P⁽_èå) la mesure probabilisée générée par u_å quand le vrai paramètre. On suppose que è0 est le vrai paramètre et {ui_å(t), 0 < t < T} est un processus de type Urnstein - Uhlenberg fractionnaire [104], [153]. On définit

MHi(t)= ^ft kH(t, s)dW_iH(s), 0 < t < T,

0

Qi_å(t) = 1 + ëi d ft kH(t, s)ui_å(s)ds, t E [0, 1] ø dW_t^H

1

Zi_å(t) = (è - ëi) ^f Qi_å(s)ds + M^H_i (t),

0

alors il s'en suit que

Z t

ui_å(t) = 0 Kfiå

H (t, s)dZi_å(t),

fi_å(t) -- ø

et

ü 1 + ëi

alors M^H_i (t) est une martingale gaussienne de moyenne nulle. D'après le théorème de Girsanov - type tiré du livre [154]

dP T,å iè log T = dPièô	1 + ëi	1(è - è0) Jo Qiå(t)dZi (t)
	ø2

?

1

₂[(è - ëi)² - (è0 - ëi)2] ^ft Q2iå(s)dWtH ?

Soit u^N_å (t, x) la projection de la solution u_å(t, x) dans le sous - espace engendré par des vecteurs propres {ãi,1 < i < N}. Alors u^N_å (t, x) s'écrit

N

u^N_å (t, x) = ui_å(t)ãi(x).

i=1

De l'indépendance des processus {W_t^H, 1 < i < N} et les séquences des processus {ui_å,1 < i < N},

dP T,å iè log T = dPièo	N i=1	1 + ëi	? ?Z^t (è - è0) 0 Qiå(t)dZiå(t) ?
		ø2

53

?

[(è - ëi)² - (è0 - ëi)2] ^ft Q2iå(s)dWtH ?

54

En plus l'information de Fisher est donnée par

alog(k) IiE(B) = E9[^alog(k)]^2 = N 1 + Xi Eo(ff^t Q^2å(s)dWt^H) ae aez-i2 Jo où On peut vérifier que l'estimateur de maximum de vraisemblance

^àeN,å du

paramètre e basé sur la projection u^N_å de u_å est donné par

_PN v1 + Ai R0 t Qiå(t)dMH _i (t) i=1

^àeN,å =

PNi=1(1 + Ai)2 R0 t Q2iå(t)dWtH

On suppose que e0 est le vrai paramètre. On peut vérifier que e e = N

v1 + Ai ^R0t Qiå(t)dMHi(t)

-1

(^àN_,E- 0) PNi=1(1 +Ai)2R0 t Q2 iå(t)dW t H

On observe que Mi,1 = i = N, sont des martingales gaussiennes indépen-

^àeN,å est for-

dantes des moyennes nulles avec hMii = W^H, 1 = i = N. Théorème 3.2.1. L'estimateur de maximum de vraisemblance

tement consistent, c'est - à - dire,

^àeN,å ? e0 p.s. [Pè0] quand e ? 0. sous

condition que

N

f

^t(Ai + 1)QÉ(s)dW_t^H = X f ^T(Ai + 1)Q²_iå(s)dW_t^H ? 0p.s.[Pè₀] quand e ? 0. o i=0
3.3 Estimation des paramètres stochastiques

par le filtre stochastique

L'objectif de la théorie de filtre stochastique est d'estimer les processus stochastiques non observables qui apparaissent dans plusieurs domaines tels que l'économie, la communication, la finance, etc.( [98],[141], [18] [181],[? ],[? ] [111], Bertein et Ceschi (2007), [71] ,[177](2008), [17],[1],[23], [20],[85],[84],[109],[119],[133],[83],[176],[175],[169],[168],[165], [180], Bain et Cri-san (2009).

3.3.1 Formulation du modèle d'état - espace stochastique

Le problème de filtre consiste à estimer la variable stochastique non observable à partir de deux processus :le signal est celui l'on veut estimer et

55

le processus observation qui fournit les informations sur base desquelles les estimations sont faites.

Pour le processus observation Y(t),nous supposons qu'il est gouverné par l'équation différentielle stochastique suivante

dXt = ( bt + btXt)dt + _ctdWt + ótdBt, dYt = ( ht + htXt)dt + dWt,

où X0 est un vecteur aléatoire normale avec comme moyenne ^X0 E R^d et la matrice de covariance P0 E R^dxd, (Wt, Bt) est un mouvement Brownien de dimension (m x n) et les coefficients sont des matrices déterministes de dimensions respectivement de

3.3.2 Filtre stochastique de Kalman - Bucy

Les ouvrages suivants nous ont permis d'élaborer cette sous - section et peuvent être exploité par les lecteurs intéressés ([44],[66],[18],[55]). On dérive

les équations pour les processus

-kt et ãt en utilisant l'équation de filtrage

de Kalman - Bucy [100]. Ces processus sont supposés être Gaussiens, qui ont les moments de n'importe quel ordre. Pour tout t > 0 et pour ù E SZ étant fixé,ðt(ù) est une mesure de probabilité normale multivariée sur IR^d. La matrice ãt est non aléatoire. En effet,pour 1 < i, j < d, nous avons ã_t = E(Xⁱ

ij tXj _t )-E(

i_t

j_t )

X

X

-kt =

Z t Z t ^àX0 + 0 (bs + bs ^àXs)ds + 0 (bs + ãshs)dvs.

L'existence et l'unicité du système d'équations différentielles stochastiques sont données respectivement dans les théorèmes suivants.

Théorème 3.3.1. ([177], Le processus ( Xt, ít) est la solution unique au système d'équations différentielles stochastiques (3.20)-(3.21), avec vt étant un processus brownien de dimension d donné par

t

vt = Yt - f (h_s + h_s X_s)ds.

où Xt et ãt représentent respectivement la moyenne conditionnelle et la ma-

trice covariance conditionnelle de la distribution normale multivariée corres-

pondant à la mesure aléatoire ðt. En utilisant le calcul d'Itô

Théorème 3.3.2. ([177],p.163) Le processus ( ^àXt,ãt) est une solution unique

du système des équations stochastiques.

56

Le processus ( Xt,ãt) est appelé le filtre de Kalman - Bucy pour le modèle d'état - espace stochastique.

3.3.3 Filtre stochastique optimal

Le Lemme suivant concerne l'estimation de la valeur d'une variable aléatoire basée sur les informations disponibles représentées par

Lemme 3.3.2.1. [177.1 Soit ? une variable aléatoire à carré intégrable dans un espace de probabilité (S2, F, P). Soit G une sous - tribu de F , alors

E((? - E(E(?|G)²)) = min{E((? - ç)²) : ç E L²(S2, F, P)}.

Très souvent,on sera intéressé par quelques quantités qui sont des fonctions du signal en lieu et place du signal lui - même.

Malgré que E(Xt | Tt) est le meilleur estimateur de Xt, f(E(Xt|Tt)) n'est pas le meilleur estimateur de f(Xt) basé sur le critère des moindres carrés ordinaires si f n'est pas une fonction linéaire.

Soit ðt(·) - P(Xt E · | Tt) la distribution de probabilité conditionnelle régulière de Xt étant donné Tt ;

à [0, 1] tel que (i)Vù E S2ðt(·, S2) est une mesure de probabilité sur une variable aléatoire

l'espérance conditionnelle est donnée par l'intégrale de f avec la distribution de probabilité conditionnelle régulière ðt.

Rappelons que Cb(R^d) est l'ensemble des fonctions bornées et continues sur Rd et (ðt, f) est l'intégrale de la fonction f conditionnellement à la mesure u. Le théorème de Kallianpur - Stiebel est une formule de Bayes utilisée en théorie de filtre pour calculer l'espérance conditionnelle en considérant la mesure de probabilité P^à.

Théorème 3.3.3. (Théorème de Kallianpur - Stiebel) Le filtre optimal peut être représenté comme suit

(ðt, f) = (ðt, 1),V)

(ðt,

f E Cb(R^d),

rd = E(Mtf(Xt)|Tt).

Théorème 3.3.4. [177.1 (Equation de Zakai) Le filtre non normalisé Vt satisfait l'équation différentielle stochastique suivante :

Z t Z t

(Vt, f) = (V0, f) + ₀ (V_s, Lf)ds + ₀ (V_s, V^*f_c + fh^*)dY_s

57

où ,Cf = 1 Pd i,j=0 aij?2 _ijf + Pd i=0 bi?i, fest le générateur du processus signal 2

et la matrice A = (aij) est donnée par Ad x d = CC^* + óó^*.

3.3.4 Approximation discrète - temporelle du filtre de Kalman - Bucy

La revue de littérature sur l'approximation des équations différentielles stochastiques est abondante [95], [139],[140],[68],[105]. Les méthodes d'approximation les plus couramment utilisées sont celles de type Taylor telles que les méthodes d'Euler-Maruyama,de Milstein , de Runge - Kuta, et Crank - Nicolson.

Pour obtenir la solution numérique du filtre de Kalman - Bucy, nous utilisons la méthode d'Euler au temps t = kä, k = 0,1, 2, · · · , dont les formules récursives suivantes

àXä(k+1)ä = àXäkä + _(6kä + _{bkäàXkä)ä} + _(ckä + ãäkähkä)(íä(k+1)ä - í^ä_kä), í^ä(k+1)ä = í^äkä + Y(k+1)ä - Ykä + _(hkä + _hkä 50_cä), et

ã^ä(k+1)ä = ã^äkä + _(ãäkäbkä + _bkäãkä + akä - (ckä + _{ãäkähkä)(ckä} + ã^äkähkä).

Théorème 3.3.5 ([177],p.165). Supposons que les coefficients b,b, c et h sont des fonctions lipschitziennes et continues dans t. Alors, il existe une constante K1 tel que

E max | {z } kä<T

|ä ä 2 X(k+1)ä - Xkä| + max | {z } kä<T

|í^ä(k+1)ä - í^äkä| -- K1ä.

3.3.5 Equations de Filtre de Kalman pour les processus discrets

Plusieurs auteurs ont présenté le filtre de Kalman [46], [44], [55],[66], [108], [77]. Cependant, le présent résumé est tiré de (Leondes,p.241). Le modèle dynamique se présente comme suit

Xk = ök-1Xk-1 + ùk-1, ùk-1 ^' N(0, Qk-1) et l'équation de l'état se présente

Zt = HkXk + õk, õk ^' N(0, Rk)

58

les conditions initiales sont

E(X0) =

^àX0|0,

E(X0 -

^àX0|0)(X0 - ^àX0|0) = P0|0, E(wkv⁰_j) = 0 pour tous k et j.

^àXk|k-1 = Ok-1^àXk-1|k-1

error covariance propagation

Pk|k-1 = Ok-1Pk-1|k-1(1)⁰k-1 + Qk-1

state estimate update

[ ]

^àXk|k = ^àXk|k-1 + Kk Zk - H ^àXk|k-1

error covariance update

[ ]

Pk|k-1 = I - KkHk Pk|k-1

La matrice de gain de Kalman gain est donnée par

Kk = Pk|k-1Hk [HkPk|k-1H⁰k + Rk] -1

59

Chapitre 4

Applications aux processus

stochastiques temporels

Dans ce chapitre il sera question d'appliquer les théoriques des équations et intégrales stochastiques à la macroéconométrie. Les travaux relatifs aux applications du calcul stochastique en économie en général et en économétrie en particulier sont abondants et récents. Nous pouvons citer à titre illustratif le modèle Black - Scholes [33] qui a permis à ses auteurs Robert C.Merton et Myron S. Scholes de remporter le prix Nobel en économie en 1997.

L'objectif de ce chapitre est d'appliquer ces techniques et méthodes de modélisation macroéconométrique aux données congolaises.

4.1 Revue empirique sur la modélisation stochastique

Dans cette section nous présentons en résumé quelques modèles empiriques développés par certains auteurs mentionnés dans .

60

4.1.1 Modèle de Bachelier

Bachelier [15] a modélisé le prix des options européennes qui se présente sous forme d'équation différentielle stochastique suivante :

dXt = /3dt + udWt

où Wt est un processus gaussien avec une moyenne nulle et une variance t, c'est - à - dire une martingale.La faiblesse de cette formulation est que le prix peut être négatif [93].

4.1.2 Modèle de Black - Scholes

dXt = /3Xtdt + uXtdWt

4.1.3 Modèle de Cox - Intgersoll - Ross

Le modèle Cox - Ingersoll - Ross [47] est utilisé en mathématique financière pour modéliser l'évolution des taux d'intérêt de court terme. Il s'agit

de la solution de l'équation différentielle stochastique

/

dr(t) = k( - r(t))dt + u (r(t))dW (t), r(0) = r0,

où k, , u sont des constantes et W(t) est un mouvement brownien standard au temps t [41].

4.1.4 Modèle de Heath - Jarrow - Morton

Heart, Jarrow et Morton (1992) ont supposé pour une maturité fixe T le taux instantané f(t, T) sous une mesure donnée, suit un processus de diffusion

df(t, T) = á(t, T)dt + u(t, T)dW(t),

f(t,T) = f^M(0,T),

avec T -~ f^M(0, T) est fonction instantanée au temps t = 0, et où W = (W1, ..., WN) est un mouvement brownien de N dimension, u(t, T) = (u1(t, T), ..., uN(t, T)) est un vecteur des processus adaptés et á(t, T) est aussi un processus adapté.

4.1.5 Modèle de Vasicek

Le modèle de Vasicek est un modèle mathématique qui tire son nom Vasicek (1977) suppose que le taux de spot instantané suivait un processus d'Ornstein - Uhlenberg avec coefficients constants [38]. Ce modèle se présente comme suit :

dr(t) = k[3 - r(t)]dt + udW(t), r(0) = r0,

où r0, k,3 et u sont des constantes positives .

4.1.6 Modèle de Black - Karasinski

Le modèle de Black - Karasinski [32] est un modèle mathématique appliqué en mathématiques de finance. Black et Karasinski (1991) ont modélisé le comportement du taux d'intérêt d'un titre conduit par le processus suivant :

d[Logr(t)] = (á(t) - 3(t)Logr(t)]dt + u(t)dW(t), r(0) = r0, (4.1)

où r(0) est une constante positive et á(t), 3(t) et u(t) sont des fonctions déterministes du temps. Aussi dW(t) est un mouvement brownien standard.

4.1.7 Modèle de Hull - While

Hull et White (1990) suppose que le processus du taux de cout terme instantané sous le mesure de risque neutre se présente comme suit :

dr(t) = [e(t) + 3(t)r(t)]dt + u(t)X^0.5

t dWt (4.2)

où , 3 et u sont des fonctions déterministes du temps [38].

4.1.8 Modèle de Aït - Sahalia

dXt = (á + 3Xt + 'yX-1 _t + 8X2 _t )dt + uXã _t dWt

61

62

4.2 Estimation des paramètres de l'équation différentielle stochastique de l'inflation

Avant tout, estimer un paramètre c'est donner une valeur approchée de ce paramètre à partir des résultats obtenus sur un échantillon aléatoire extrait de la population (Veysseyre,p.210).

4.2.1 Présentation théorique de l'inflation

Par définition, l'inflation est l'augmentation du niveau général des prix [35]. Algébriquement, on a

ðt = /-(log(Pt)) = log(Pt+1) - log(Pt)

où log est le logarithme naturel et Pt est l'indice général des prix. Le taux d'inflation mesure la vitesse avec laquelle les prix augmentent[132].La mesure de l'inflation elle - même n'est pas exempte de difficultés. On adopte en général le point de vue du consommateur : l'indice de prix à la consommation (IPC) mesure le prix d'un panier de biens représentatif de la consommation des ménages [35]. L'un des avantages de l'indice des prix à la consommation prend en compte l'effet du taux de change sur le prix intérieur des importations [35]. Pourquoi l'inflation suscite - t elle un problème social? Les différents coûts de l'inflation sont perdus selon qu'il s'agit de l'inflation anticipée ou non ou encore s'il s'agit de la situation plus grave de l'hyperinflation.

Les coûts de l'inflation anticipée sont (i) la taxe d'inflation perçue sur la quantité de monnaie détenue par les agents,(ii) le coût de menu qui s'explique par l'obligation dans laquelle se trouvent les entreprises de modifier plus souvent leurs listes de prix. Changer les prix implique des couts d'impression et de distribution d'une nouvelle liste de prix ou d'un nouveau catalogue,(iii) le coût dû à la variabilité des prix relatifs, (iv) le cout de l'inflation est suscité par les législations fiscales. De nombreux articles du code fiscal ignorent les impacts de l'inflation.(v) le coût de l'inflation provient du fait qu'il est plus inconfortable de vivre dans un monde où les prix fluctuent que dans un monde où les prix sont stables. L'inflation rend plus difficile la planification financière individuelle.

L'impact de l'inflation non anticipée est plus pernicieux qu'aucun des couts de l'inflation anticipée stable : (i) elle redistribue de manière arbitraire la richesse entre les gens,(ii) elle pénalise les personnes vivant de revenus

63

fixes, tels que les pensions de retraite.Plus le taux d'inflation est variable, plus grande est l'incertitude à laquelle sont confrontés tant les préteurs que les emprunteurs.

Les coûts de l'inflation augmentent considérablement en période d'hyperin-flation. Certes, l'hyperinflation accélérée le processus de dollarisation (circulation de devises étrangères) de l' économie nationale.

Empiriquement, Bruno et Easterly (1996) ont trouvé que la croissance était affectée par une inflation supérieure à un chiffre de 20 % à 40 % par an. Barro (1997) chiffre entre 0,3 % à 0,4 % point la perte de croissance induite par un supplément d'inflation de 10 points, tout en admettant que ce résultat est surtout vrai pour les inflations élevées ([35],p.221).

Quelle est la source de l'inflation? En se basant sur la théorie quantitative de la monnaie, relation mathématique entre la quantité de monnaie et les prix, les économistes disent que l'inflation est toujours d'origine monétaire ([174], [132] ). En conséquence, la théorie quantitative de la monnaie établit que la banque centrale, qui contrôle l'offre de monnaie, contrôle du même fait , en dernier ressort, le taux d'inflation. Si la banque centrale préserve la stabilité de l'offre de monnaie, le niveau des prix sera également stable. Si la banque centrale accroit rapidement le stock de monnaie, le niveau des prix augmentera lui aussi rapidement ([132],p.195).

4.2.2 Présentation du modèle économétrique

Nous supposons que l'inflation kinoise,calculée à partir de l'indice de prix à la consommation observé dans la Ville Province de Kinshasa,peut être modélisée comme suit

Z t Z t

irt = ir0 + e ₀ ir_sds + u ₀ dB_s (4.3)

où et u sont des paramètres à estimer appelés respectivementdrift et diffusion et B est un processus brownien. u peut être interprété comme la volatilité stochastique du phénomène sous analyse.

Cette équation intégrale stochastique peut se présenter en équation différentielle stochastique suivante

dirt = eirtdt + udBt. (4.4)

64

Après quelques manipulations algébriques, cette équation se présente comme un processus auto - régressif d'ordre 1 ci-après :

ðt - ðt_1 = èðt_1 + ó(Bt - Bt_1), ðt = (1 + _{è)ðt_1} + ó(Bt - Bt_1), ðt = ?ðt_1 + åt, å ~ iid(0, ó² _å),

où ? = (1 + è), åt = ó(Bt - Bt_1).

L'abréviation iid signifie la variable aléatoire est indépendante et identiquement distribuée. Pour assurer la stabilité du processus markovien, on suppose que |?| < 1. Le paramètre ? mesure la persistance de l'inflation kinoise. L'hypothèse å ~ iid(0, ó² _å) signifie que la variable aléatoire, terme d'erreurs, suit une distribution normale de moyenne nulle et de variance constante (ó²_å).

Cependant, cette hypothèse d'homoscédasticité (la constance de la variance des erreurs) peut ne pas être vraie dans la réalité dans ce cas on parle dans la littérature économétrique de la présence d'hétéroscédasticité ([72], [70],[80],[57],[78]).

Dans le cas de cette étude, pour de raison de simplicité et de limite observée du développement théorique, on se limite à l'hypothèse d'homoscédasticité.

4.2.3 Estimation du processus stochastique autorégres-sif d'ordre 1

En économétrie,les méthodes de maximum de vraisemblance et des moindres carrés ordinaires sont couramment utilisées pour estimer le paramètre è du modèle AR(1) susmentionné [70].

Pour estimer ce paramètre nous supposons que l'inflation est un processus faiblement stationnaire,c'est- à -dire,ses moments d'ordre 1 et 2 ne varient pas avec le temps,i.e., E(åt|ðt) = 0. Dans cette étude, la méthode des moindres carrés ordinaire a été utilisée pour estimer les deux coefficients. Ce choix est fait à cause de la simplicité de son langage mathématique et sa mise en pratique. La formulation mathématique du principe de la méthode de moindres carrés ordinaires est la minimisation de la somme des carrés des er-reurs.Par conséquent, l'estimateur des moindres carrés ordinaires. Nous supposons aussi que l'estimateur des moindres carrés ordinaires est le meilleur estimateur linéaire non biaisé (Best Linear Estimator Unbiased).

65

4.2.4 Résultats des estimations

Nous avons utilisé l'indice des prix à la consommation (IPC) calculé par la Banque Centrale du Congo observé à Kinshasa pour la période allant de janvier 2004 à avril 2016. Pour obtenir l'inflation,nous avons transformé cette variable en log-différentiel,i.e,

tt =A (log(IPC)t) = logYt - logYt_1. Pour le modèle AR(1), les résultats se présentent comme suit

àðt = 0, 54irt_1, T = 146,

t - Student = 7,71, DW = 2, 19,

où T représente la taille de l'échantillon, t - Student est la statistique de Student pour tester la significativité des paramètres estimés et DW représente la statistique de Durbin et Watson pour tester l'absence d'auto-corrélation des erreurs du modèle estimé.

t t

Après l'estimation de notre modèle AR(1), l'équation intégrale stochastique de l'inflation de Kinshasa se présente comme suit

_{Z Z}

àðt = ir0 + 0, 46 ₀ ir_sds + 0, 02 ₀ dBs.

Comme la statistique de t-student du coefficient estimé est supérieure à 2, en valeur absolue ,selon la règle de pouce,nous pouvons conclure que ce paramètre estimé t9 à est significatif,c'est- à -dire,ce paramètre est statistiquement différent de zéro. Aussi comme la valeur estimée de la statistique de Durbin - Watson est au tour de 2, nous concluons qu'il y a absence d'autocorré-lation des erreurs dans le modèle AR(1) estimé. La valeur de la volatilité stochastique est de 0,02 qui montre sous la période sous analyse une faible présence d'incertitude. La persistance à la hausse de l'inflation de Kinshasa est de 54%,c'est-à -dire,l'inflation du mois passé contribue de 54% à l'inflation présente .

4.3 Estimation de la contribution stochastique de la main d'oeuvre congolais sur son bien - être économique

Connaitre les contributions de différentes variables explicatives du développement économique de sa population est une préoccupation majeure de tout décideur ou le planificateur du développement économique. Le filtre de Kalman - Bucy est reconnu comme l'une des techniques couramment utilisées dans les domaines de navigation, contrôle, de lancement de missiles et navettes spatiales, analyse de processus de signaux médicaux, etc. ([77],[53],[46],[103],[81],[? ],[161],[13],[129],[131]). La portée de cette technique ne s'est pas limitée uniquement dans ces domaines mais aussi elle est utilisée en macroéconométrie pour estimer les composantes non observables stochastiques des agrégats macroéconomiques ([73], [75], [76],[74] ).

4.3.1 Modèle théorique du bien - être économique

L'analyse théorique des effets des facteurs de production (travail, capital et la technologique) est plus ancienne et constitue la préoccupation des économistes théoriciens et des décideurs politiques en charge de la bonne conduite de la politique économique du pays.

Nous supposons que la fonction de production de bien

4.3.2 Spécification économétrique du modèle état - espace du développement économique

Nous supposons que le modèle d'état - espace du bien - être congolais se présente comme suit :

le processus d'observation

gt = ^à131,txt +

^à132,tyt +

^ài3,tZt + [var = exp(

^àe1)]

avec les processus stochastiques non observés d'états suivants

^àâ1,t =	^à/1,t-1 + [var = exp(	^àe2)],
^àâ2,t =	^àe4 + à/32,t-1 + [var = exp(^àe3)],

66

^à/33,t = ^àe5 + ^à/33,t-1,

à

où _/3j,t mesurent les effets de ces trois différents facteurs de bien - être congolaise au temps t et ^àBi sont les paramètres constants du modèle état - espace stochastique.

Les hypothèses du modèle sont (i) les séquences vt et _Ek,t sont des bruits Gaussiens,(ii) les coefficients sont des processus stochastiques et variants avec le temps.

4.3.3 Estimation du modèle de bien - être congolais

Il y a deux avantages de présenter un système dynamique dans le modèle d'état - espace : (i) le modèle d'état espace permet aux variables non observables (variables d'état) d'être incorporées et estimées dans le modèle observé, (ii) les modèles d'état espace peuvent être analysés en utilisant l'algorithme récursif puissant comme le filtre de Kalman et Bucy [99] et [100], (iii) E[vtEk,t] = 0, .

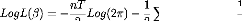
Pour implémenter le filtre de Kalman, nous appliquons la fonction de maximum de vraisemblance suivante

2 Log(2r) - 2 Log

Ft(B)

1

|

|-

2 ~-1

t (è)~t(è).

t t

Cette fonction peut être évaluée en utilisant le filtre de Kalman. En utilisant les dérivées numériques, les techniques itératives standards peuvent être employées pour maximiser la fonction de maximum de vraisemblance des paramètres inconnus. Dans cette étude la technique itérative utilisée est celle de Berndt, Hall,Hall et Hausman [? ].

L'algorithme de BHHH [? ] est une méthode numérique similaire à celle de Gauss - Newton. Elle se présente comme suit. Supposons que la fonction à optimiser est Q(/3). Alors les algorithmes sont itératifs définissant une suite d'approximation, /3k, donnée par

?Q

/3k+1 = /3k - ëkAk a/3 (/3k)

où /3k est le paramètre à estimer à l'étape k, et Ak est une paramètre appelé la taille de l'étape qui partiellement détermine l'algorithme particulier. Pour l'algorithme BHHH de Ak par les calculs avec une étape donnée est déterminé L 'Algorithme de Kalman que nous avons utilisé peut être résumé comme suit

LogL(/3) = -

nT

67

68

(Leondes,p.241). Le modèle dynamique se présente comme suit

Xk = Ok-1Xk-1 + Wk-1, Wk-1 ^' N(0, Qk-1)

et l'équation de l'état se présente

Zt = HkXk + vk, vk ^' N(0, Rk)

les conditions initiales sont

E(X0) =

^àX0|0,

E(X0 -

^àX0|0)(X0 - ^àX0|0) = P0|0, E(Wkv⁰_j) = 0 pour tous k et j.

^àXk|k-1 = Ok-1^àXk-1|k-1

La matrice de covariance des erreurs de propagation est donnée par

Pk|k-1 = Ok-1Pk-1|k-1(P⁰k-1 + Qk-1

Le vecteur état

[ ]

^àXk|k = ^àXk|k-1 + Kk Zk - H ^àXk|k-1

Matrice de covariance des erreurs est donnée [ ] Pk|k-1 = I - KkHk Pk|k-1 La matrice de gain de Kalman est donnée par Kk = Pk|k-114 [HkPk|k-1H ^0k + Rk]

-1

4.3.4 Présentation et Interprétation des résultats

Les résultats de cette étude sont présentés dans le tableau suivant :

69

Paramètres du modèle valeurs estimées

^àè1 -3,3867^*

^àè2 -16, 2692

^àè3 -6, 4230

^àè4 1,2807

^àè5 -0, 0081^**

Etats du modèle valeurs estimées

^àâ1 -0,3634^**

^àâ2 49, 6594^*

^àâ3 0, 2352

(*) et (**) sont respectivement significatifs au seuil de 5% et 10%.

Comme indiqué dans le tableau ci - dessus, la significativité des paramètres de ce modèle est déterminée par la valeur de Z - statistique associée à chaque paramètre. La lecture de ce tableau montre que les coefficients de variables investissements et populations sont significatifs.

Eu égard à ces estimations, la population active congolaise ont des effets positifs sur la croissance économique. Par contre, les investissements ont des

effets négatifs sur la croissance économique.

Conclusion

La modélisation d'une économie gouvernée par les phénomènes aléatoires conduit aux mauvaises prévisions rendant certainement les politiques économiques inefficaces.

70

Bibliographie

[1] N. U. Ahmed. Linear and Nonlinear Filtering for Scientists and Engineers. World Scientific, Singapore, 1998.

[2] Y. Ait Sahalia. Testing continuous - time models of the spot interst rate. Review of Financial Studies, 9 :385 - 426, 1996.

[3] Y. Ait Sahalia. Transition densities for interest rates and other nonlinear diffusions. Journal of Finance, 54 :499 - 547, 1999.

[4] Y. Ait Sahalia. Maximum likelihood estimation of discretely sampled diffusions : A closed - form approximation approach. Econometrica, 70 :223 - 262, 2002.

[5] Y. Ait-Sahalia, Lars P. Hansen, and Jose A. Scheinkman. Operator Methods for Continuous-Time Markov Processes, volume Handbook of Financial Econometrics : Tools and Techniques. Elsevier, North Holland, 2010.

[6] Y. Ait Sahalia and Robert Kimmel. Maximum likelihood estimation of stochastic volatility models. Journal of Financial Economics, 83 :413 - 452, 2007.

[7] J. Albert. Bayesian Computation with R. John Wiley and Sons, New York, 2 edition, 2009.

[8] S. Albeverio, R. Fan, and F. Herzberg. Hyperfinite Dirichlet Forms and Stochastic Processes. Verlag. Springer, Berlin and Heidenlberg, 2011.

[9] R. Aldrovandi. Special Matrices of Mathematical Physics Sochas-tic,Circulant and Bell Matrices. World Scientific, Danvers, 2001.

[10] E. Allen. Modeling with Ito Stochastic Differential Equation. Springer, 2007.

[11]

71

T. Amemiya. Advanced Econometrics. Harvard University Press, Cambridge, 1985.

[12] D. Applebaum. Lévy Processes and Stochastic Calculus. Cambridge University Press, Cambridge, 2 edition, 2009.

[13] D. Ardia. Financial Risk Management with Bayesian Estimation of GARCH Models Theory and Applications. Verlag. Springer, Berlin, 2008.

[14] G. Aubert and P. Kornprobst. Mathematical Problems in Image Processing Partial Differential Equations and the Calculus of Variations. Springer Science + Business Media, New York, 2 edition, 2006.

[15] L. Bachelier. Théorie de la spéculation. PhD thesis, Ecole Normale Supérieure de Paris, Paris, mars 1900.

[16] J. Bai. Testing for parameter constancy in linear regressions : An empirical distribution function approach. Econometrica, 64(3) :597 - 622, May 996.

[17] Z. Bai, Y. Chen, and Y. C. Lian. Random Matrix Theory and Its Applications. World Scientific, Danvers, 2009.

[18] A. V. Balakrishnan. Kalman Filtering Theory. Optimization Software, New York, 1984.

[19] Y. Bard. Nonlinear Parameter Estimation. Academic Press, New York, 1974.

[20] H. Bart, I. Gohberg, M.A. Kaashoek, and A.C.M. Ran. A State Space Approach to Canonical Factorization with Applications. Birkhauser, Basel, 2007.

[21] I. V. Basawa, C.C. Heyde, and R.L. Taylor, editors. Seleted Proceedings of the symposium on Inference for Stochastic Processes, volume 37. Institute of Mathematical Statistics, 2001.

[22] Ishwar V. Basawa and B.L.S. Prakasa Rao. Statistical Inference for Stochastic Processes. Acedemic Press, London, 1980.

[23] M. Basin. New Trends in Optimal Filtering and Control for Polynomial and Time - Delay Systems. Number 380. Springer - Verlag, Berlin and Heidelberg, 2008.

[24]

72

H. Bauer and Robert B.Burkel. Measure and Integral. Wlter de Gruy-ter, Berlin, 2001.

[25] Peter H. Baxendale and Sergey V. Lototsky. Stochastic Differential Equations: Theory and Applications, volume 2 of Interdisciplinary Mathematical Sciences. Danvers, 2007.

[26] F. E. Benth, G. Di Nunno, and T.Zhang T. Lindstrom, B. Oksental, editors. Stochastic Analysis and Applications, Berlin and Heidelberg, 2007. The Abel Symposia and The Norwegian Mthematical Society, Springer - Verla.

[27] James O. Berger. Statistical Decision Theory and Bayesian Analysis. Springer-Verlag, New York, 2 edition, 1985.

[28] N. Berglund. Martingales et calcul stochastique. Master 2,Université d'Orléans, 2014.

[29] P. Billingsley. Weak Convergence of Measures : Applications in Probability. SIAM, Philadelphia, 1971.

[30] P. Billingsley. Convergence of Probability Measures. John Wiley and Sons, Danvers, 2 edition, 1999.

[31] Jaya P.N. Bishwal. Parameter Estimation in Stochastic Differential Equations. Springer - Verlag, New York, 2008.

[32] F. Black and P. Karasinski. Bond and option pricing when short rates are lognormal. Financial Analysts Journal, pages 52 - 59, 1991.

[33] F. Black and M. Scholes. The pricing of options and corporate liabilities. The Journal of Political Economy, 81(3) :637 - 654, 1973.

[34] P. Blanchard, P. Combe, and W. Zheng. Mathematical and Physical Aspects of Stochastic Mechanics. Springer Verlag, Berlin and Heidelberg, 1987.

[35] A. Bénassy Quéré, B. Coeuré, P. Jacquet, and J.Pisani Ferry. Politique économique. De Boeck and Larcier, Bruxelles, 2004.

[36] T. Bollerslev. A conditional heteroskedastic time series model for speculative prices and rates of return. The Review of Economics and Statistics, 69(3) :542 - 547, 1987.

[37]

73

Larry G. Bretthorst. Bayesian Spectrum Analysis and Parameter Estimation. Springer - Verlag, Heidelberg, 1988.

[38] D. Brigo and F. Mercurio. Interest Rate Models Theory and Practice with Smile, Inflation and Credit. Springer - Verlag, Berlin and Heidelberg, 2006.

[39] James V. Candy. Bayesian Signal Processing Classical,Modern and Particle Filtering Methods. John Wiley and Sons, Hoboken, 2009.

[40] Bradley P. Carlin and Thomas A. Louis. Bayesian Methods for Data Analysis. Taylor and Francis Group,LLC, Boca Raton, 3 edition, 2009.

[41] René A. Carmona and Michael R. Tehranchi. Interest Rate Models an Infinite Dimensional Stochastic Analysis Perspective. Springer, Berlin and Heidelberg, 2006.

[42] M. Carrasco, Liang Hu, and Werner Ploberger. Optimal test for markov switching parameters. Econometrica, 82(2) :765 - 784, March 2014.

[43] J.A. Chao and W.A. Woyczynski. Martingales Theory in Harmonic Analysis and Banach Spaces. Springer Verlag, Berlin, 1982.

[44] C.K. Chui and G. Chen. Kalman Filtering with Real - Time Applications. Springer, Berlin Heidelberg, 4 edition, 2009.

[45] K. L. Chung and John B. Walsh. Markov Processes, Brownian Motion, and Time Symmetry. Springer, Berlin, 2005.

[46] Jacques J.F. Commandeur and S. Jan Koopman. An introduction to State Space Time Series Analysis Practical Econometrics. Oxford University Press, Oxford, 2007.

[47] J.C. Cox, J.E. Ingersoll, and S..A. Ross. Atheory of the term structure of interest rates. Econometrica, 53 :385 - 405, 1985.

[48] Jan S. Cramer. Econometric Application of Maximum Likelihood Methods. Cambridge University Press, New York, 1986.

[49] S. Cyganowski, P. Kloeden, and J. Ombach. From Elementary Probability to Stochastic Differential Equations with MAPLE. Springer - Verlag, Berlin and Heidelberg, 2002.

[50] G. Da Prato and L. Tubaro. Stochastic Differential Equations and Applications - VII, volume 245 of Lecture Note in Pure and Applied Mathematics. Chapman and Hall/CRC, Boca Raton, 2006.

[51]

74

A. P. Dempster, N.M. Lair, and D.B. Rubin. Maximum likelihood from incomplete data via the em algorithm. Journal of the Royal Statistical Society, 39(1) :1 - 39, 1977.

[52] Dipak K. Dey and C.R.Rao. Bayesian Thinking Modeling, volume 25 of Handbook of Statistics. Elsevier B.V., 2005.

[53] J. Durbin and S.J. Koopman. Time Series Analysis by State Space Methods. Oxford University Press, Oxford, 2004.

[54] D. Durrett. Probability Theory and Examples. Cambridge University Press, New York, 4 edition, 2010.

[55] G. Evensen. Data Assimilation the ensemble Kalman Filter. Springer, Berlin and Heidelberg, 2 edition, 2009.

[56] A. Foata and A. Fuchs. Processus Stochastique Processus de Poisson, chaine de Markov et martingales. Dunod, Paris, 2004.

[57] C. Francq and J. M. Zakoian. GARCH Models Structure,Statistical inference and Financial Application. John Wiley and Sons, West Sussex, 1 edition, 2010.

[58] A. Friedman. Stochastic Differential Equations and Applications. Academic Press, 1975.

[59] D. Gamerman and H.F. Lopes. Markov Chains Monte Carlo Stochastic Simulation for Bayesian inference. Taylor and Francis Group, Boca Raton,FL, 2 edition, 2006.

[60] J. Gatheral. The Volatility Surface A practtioner's Guide. Wiley Finance, Hoboken, 2006.

[61] L. Gawarecki and V. Mandrekar. Stochastic Differential Equations in Infinite Dimensions with Applications to Stochastic Partial Differential Equations. Springer Verlag, Berlin and Heidelberg, 2011.

[62] L. Gawarecki and V.Mandrekar. Stochastic Differential Equations in Infinite Dimensions. Springer, Berlin, 2011.

[63] S. Geisser and W. Johnson. Modes of Parametric Statistical Inference. John Wiley and Sons, Hoboken, New Jersey, 2006.

[64] A. Gelman, John B. Carlin, Hal S. Stein, and Dolnald B.Rubin. Baye-sian Data Analysis. Chapman and Hall/CRC, Boca Raton, 2 edition, 2004.

[65]

75

A. Gelman and Xiao Li Meng. Applied Bayesian Modeling and Causal Inference from Incomplete - Data Perspectives. John Wiley and Sons, Hoboken, 2004.

[66] Bruce P. Gibbs. Advanced Kalman Filtering Least - Squares and Modeling a Practical Handbook. John Wiley and Sons, Hoboken, 2011.

[67] G. Gong and W. Semmler. Stochastic Dynamic Macroeconomics : Theory, Numerics and Empirical Evidence. Oxford University Press, New York, 2006.

[68] C. Graham and D. Talay. Stochastic Simulation and Monte Carlo Methods. Springer - Verlag, Berlin and Heidelberg, 2013.

[69] W. Greene and R. Carter Hill. Maximum Simulated Likelihood Methods and Applications, volume 26 of Advances in Econometrics. Emerald Group, Howard House, 2010.

[70] William H. Greene. Econometric Analysis. Pearson Education, Upper Saddle River, 5 edition, 2003.

[71] Mohinders S. Grewal and Agnus P. Andrews. Kalman Filtering : Theory and Practice using MATLAB. John Wiley and Sons, New York, 2 edition, 2001.

[72] Damodar N. Gujarati. Basic Econometrics. The McGraw - Hill, 4 edition, 2005.

[73] James D. Hamilton. A new approach to the economic analysis of nons-tationary time series and business cycle. Econometrica, 57(2) :357 - 384, March 1989.

[74] James D. Hamilton. Handbook of Econometrics, volume IV, chapter State Space Models, pages 3041 - 3068. Elvier Science B.V., 1994.

[75] James D. Hamilton. Time Series Analysis. Princeton University Press, Princeton, 1994.

[76] James D. Hamilton and Baldev Raj, editors. Advances in Markov Switching Models. Springer, Berlin and Heidelberg, 2002.

[77] A. Harvey, S. J. Koopman, and N.Shephard. State Space and Unobserved component models : Theory and Applications. Cambridge University Press, Cambridge, 2004.

[78]

76

Andrew C. Harvey. Dynamic Models for Volatility and Heavy Tails with Applications to Financial and Economic Time Series. Econometric Society Monographs. Cambridge University Press, New York, 2013.

[79] Anton J. Haug. Bayesian Estimation and Tracking : A Practical Guide. John Wiley and Sons, Hoboken, 2012.

[80] F. Hayashi. Econometrics. Princeton University Press, Princeton, 2000.

[81] James J. Heckman and Edward E. Leamer, editors. Handbook of Econometrics, volume 6A. North - Holland Elsevier, Amsterdam, 2007.

[82] D. Henderson and P. Plaschko. Stochastic Differential Equations in Science and Engineering. World Scientific Publishing Co.Pte.Ltd, New Jersey, 2006.

[83] D. Hinrichsen and Pritchard A.J. Mathematical Systems Theory I : Modelling, State Space Analysis Stability and Robustness. Springer-Verlag, Berlin and Heidelberg, 2005.

[84] S. L. Hobbs and S.S. Sritharan. Nonlinear filtering theory for stochastic reactiond - iffusion equations. In N. Gretsky, J.Goldstein, and J. J. Uhl, editors, Probability and Modern Analysis, pages 219 - 234. Marcel Dekker, 1997.

[85] Rob J. Hyndman, Anne B. Koetler, J.Keith Ord, and Ralph D. Snyder. Forecasting with Exponential Smoothing: The State Space Control Systems. Springer- Verlag, Berlin, 2008.

[86] I. A. Ibragimov and R.Z. Hasminskii. Statistical Estimation Asymptotic Theory. Springer Science + Business Media, New York, 1981.

[87] N. Ikeda and S. Watanabe. Stochastic Differential Equations and Diffusion Processes. North - Holland Publishing Company. Kodansha Scientific Books, New York, 2 edition.

[88] K. Itô. Foundations of stochastic differential equations in infinity dimensional space. volume 47, Philadelphia, 1984. Conference Board of the Mathematical Sciences and National Science Foundation, Society for Industrial and Applied Mathematics.

[89] K. Itô and Henry P. McKean Jr. Diffusion Processus and their Sample Paths. Springer - Verlag, Berlin and Heidelberg, 1996.

[90]

77

J. Jacob and Philip E. Protter. Discretization of Processes. Springer - Verlag, Berlin and Heidelberg, 2012.

[91] P. N. Jaya and N.Bishwal. Parameter Estimation in Stochastic Differential Equations. Springer - Verlag, Berlin and Heidelberg, 2008.

[92] Andrew H. Jazwinski. Stochastic Processses and Filtering Theory. Academic Press, New York, 1970.

[93] M. JeanBlanc. Lectures on mathematical finance. City University, Hong Kong, June 2001.

[94] F. Jedrzejewski. Modèles aléatoires et physique probabiliste. Springer - Verlag France, 2009.

[95] A. Jentzen and Peter E. Kloeden. Taylor Approximations for Stochastic Partial Differential Equations. The Society for Industrial and Applied Mathematics, Philadelphia, 2011.

[96] Nicholas P. Jewell and John d. Kalbfleisch. Maximum likelihood estimation of ordered multinomial parameters. Biostatistics, 5(2) :291 - 306, 2004.

[97] P. Kall and J. Mayer. Stochastic linear Programming. Kluwer Academic Publishers, New York, 2005.

[98] G. Kallianpur and D. Kolzow. Measure Theory Applications to Stochastic Analysis. Springer Verlag, Berlin and Heidelberg, 1978.

[99] R. E. Kalman. A new approach to linear filtering and prediction problems. Journal of Basic Engineering, 82 :35 - 45, 1960.

[100] R. E. Kalman and R.S.Bucy. New results in linear filtering and prediction theory. Journal of Basic Engineering, pages 95 - 108, 1961.

[101] I. Karatzas and Steven E.Shreve. Brownian Motion and Stochastic Calculus. Springer - Verlag, Berlin and Heidelberg, 1988.

[102] D. Kelly and Curtis Smith. Bayesian Inference for Probabilistic Risk Assessment : A Practitioner's Guidebook. Springer Verlag London, London, 2011.

[103] Lawrence R. Klein, A. Welfe, and W. Welfe. Principles of Macroeco-nometric Modeling. Elsevier Science B.V., Amsterdam, 1999.

[104]

78

M. Kleptsyna and A. LeBreton. Statistical analysis of the ornstein - uhlenbeck type process. Statistical Inference for Stochastic Processes, 5(3) :229 - 248, 2002.

[105] Peter E. Kloeden and E. Platen. Numerical Solution of Stochastic Differential Equations. Springer, Berlin, 1995.

[106] Peter E. Kloeden and E. Platen. Numerical Solution of Stochastic Differential Equations, volume 23 of Application of Mathematics. Springer - Verlag, Berlin and Heidelberg, corrected third printing edition, 1999.

[107] Vassili N. Kolokoltsov. Nonlinear Markov processes and Kinetic Equations. Cambridge University Press, New York, 2010.

[108] G. Koop, Dale J. Poitier, and Justin L. Tobias. Bayesian Econometric Methods. Cambridge University Press, Cambridge, 2007.

[109] V. Krishnan. Nonlinear Filtering and Smoothing : an Introduction to martingales, stochastic integrals and Estimation. Dover Publications Inc., Mineola, 1984.

[110] U. Kuckler and Michael Sorensen. Exponential Families of Stochastic Processes. Springer Verlag, New York, 1997.

[111] H. H. Kuo. Introduction to Stochastic Integrals. Universitext. Springer Science Business, New York, 2006.

[112] Harold J. Kushner. Approximaion and weak convergence Methods for Random Processes with Applications to Stochastic Systems Theory. The MIT Press, Cambridge, 1984.

[113] Harold J. Kushner and P.Dupuis. Numerical Methods for Stochastic Control Problems in Continuous Time. Springer-Verlag, 2001.

[114] Harold J. Kushner and G.George Yin. Stochastic Approximation and Recursive Algorithms and Applications. Springer - Verlag, New York, 2003.

[115] Yu.A. Kutoyants. Estimation of the trend parameter of a diffusion process. Theory Probability and its Applications, 22 :399 - 405, 1977.

[116] Yury A. Kutoyants. Statistical Inference for Spatial Poisson Processes. Springer Science+Busmess Media, New York, 1998.

[117]

79

Yury A. Kutoyants. Statistical Inference for ergodic Diffusion Processes. Springer - Verlag, London, 2004.

[118] L. Le Cam. Asymptotic Methods in Statistical Decision Theory. Springer - Verlag, New York, 1986.

[119] K. A. Lee, W.-S. Gan, and Sen M. Kuo. Subband Adaptive Filtering Theory and Implentation. John Wiley and Sons, West Sussex, 2009.

[120] W. Lembe. Term Structure Modeling and Estimation in a state space Framework. Springer Verlag, Berlin and Heidelberg, 2006.

[121] Bernard C. Levy. Principles of signal Detection and Parameter Estimation. Springer Science + Business Media, New York, 2008.

[122] Frank L. Lewis, L. Xie, and D. Popa. Optimal and Robust Estimation with an Introduction to Stochastic Control Theory. Taylor and Francis Group, Boca Raton, 2008.

[123] William A. Link and Richard J. Barker. Bayesian Inference with Ecological Applications. Elsevier, Oxford, 2010.

[124] R. S. Liptser and A.N. Shiryaev. Statistics of Random Processes :II Applications. Springer - Verlag, New York, 2001.

[125] D. V. Lndley. Introduction to probability and Statistics :From a Baye-sian Viewpoint. Cambridge University Press, New York, 1970.

[126] A.W. Lo. Maximum likelihood estiamation of generalized itô processes with discretely sampled data. Econometric Theory, 4 :231 - 247, 1988.

[127] H. Lutkepohl. New Introduction to Multiple Time Series Analysis. Springer - Verlag, Berlin and Heidelberg, 2005.

[128] H. Lutkepohl and Markus Kratzig. Applied Time Series Econometrics. Cambridge University Press, Cambridge, 2004.

[129] G. S. Maddala. Introduction to Econometrics. MACMILLAN Publishing Company, New York, 2 edition, 1992.

[130] G. S. Maddala, C.R.Rao, and H.D.Vinod, editors. Handbook of Statistics, volume 11. Elsevier Science Publishers B.V., Amsterdam, 1993.

[131] G. S. Maddala and In Moo Kim. Unit Roots,Cointegration, and Structural Change. Cambridge University Press, Cambridge, 1998.

[132]

80

Greory N. Mankiw. Macroéconomie. De Boeck University, Bruxelles, 2 edition, 2001.

[133] R. Mansuy and M. Yor. Aspects of Brownian Motion. Springer - Verlag, Berlin and Heidelbert, 2008.

[134] J. M. Marin and Christian P. Robert. Bayesian Core : A Practical Approach to Computational Bayesian Statistics. Springer Science + Business Media, LLC, New York, 2007.

[135] P. Medvegyev. Stochastic Integration Theory. Oxford University Press, New York, 2007.

[136] M. Meyer. Contunuous Stochastic Calculus with Applications to Finance. Chapman and Hall/CRC, Boca Raton, 2001.

[137] Russell B. Millar. Maximum Likelihood Estimation and Inference. John Wiley and Sons, West Susssex, 2011.

[138] G. N. Milstein. Numerical Integration of Stochastic Differential Equations. Springer Science + Business Media, Dordrecht, 1995.

[139] G. N. Milstein. Numerical Integration of Stochastic Differential Equations. Springer Science + Business Media, Dordrecht, 1998.

[140] Yuliya S. Mishura. Stochastic Calculus for Fractional Brownian Motion and Related Processes. Springer - Verlag, Berlin and Heidelberg, 2008.

[141] S. K. Mitter and A. Moro, editors. Nonlinear Filtering and Stochastic Control, Berlin and Heidelberg, July 1983. the Centro Internationale Matematico Estivo, Springer - Verlag.

[142] John C. Nash and M. Walker Smith. Nonlinear Parameter Estimation: An Integrated System in BASIC. Nash Information Service, Ottawa, 1995.

[143] A. O'Hagan. Bayesian Inference, volume 2B of Kendall's Advanced Theory of Statistics. Oxford University Press, New Yok, 2000.

[144] A. O'Hagan and Mike West. The Oxford Handbokk of Applied Bayesian Analysis. Oxford University Press, Oxford, 2010.

[145] B. Oksendal. Stochastic Differential Equations. Springer-Verlag, Berlin, 5 edition, 2000.

[146]

81

McKean Jr. H. P. Stochastic integrals. Academic Press, New York, 1969.

[147] E. Pardoux. Markov Processes and Applications Algorithms, Networks, Genome and Finance. Dunod and John Wiley and Sons, Paris, 2008.

[148] G.A. Pavliotis and A.M. Stuart. Parameter estimation for multiscale diffusion. Journal of Statistical Physics, 127(4) :741 - 781, May 2007.

[149] S. Perzat and J. Zabczyh. Stochastic Partial Differential Equations with Lévy Noise. Cambridge University Press, New York, 2007.

[150] H. Pham. Optimisation et controle stochastique appliqués à la finance. Springer - Verlag, Berlin, 2007.

[151] E. Platen and N.Bruti Liberti. Numerical Solution of Stochastic Differential Equations with jumps in Finance. Springer - Verlag, Berlin and Heidelberg, 2010.

[152] Y. Pokern, Andrew M. Stuart, and Petter Wiberg. Parameter estimation for partially observed hypoelliptic diffusions. Journal of the Statistical Society, 71(1) :49 - 73, 2009. B.

[153] B. L. S. Prakasa Rao. Parameter estimation for linear stochastic differential equations driven by fractional brownian motion. Random Operations and Stochastic Equations, 11 :229 - 242, 2003.

[154] B. L. S. Prakasa Rao. Statistical Inference for Fractional Diffusion Processes. John Wiley and Sons, West Sussex, 2010.

[155] Philip E. Protter. Stochastic Integration and Differential Equations. Springer - Verlag, Berlin and Heidelberg, 2004.

[156] Christian P. Robert. The Bayesian Choice From Decision - Theoretic Foundations to Computational Implementation. Springer Science + Business Media, New York, 2 edition, 2007.

[157] A. Robler. Runge - Kutta Methods for the Numerical Solution for Stochastic Differential Equations. Springer, Berlin, 2003.

[158] Daniel B. Rowe. Multivariate Bayesian Statistics Models for Source Separation and Signal Unimixing. Chapman and Hall/CRC, Boca Raton, 2003.

[159]

82

Thomas H. Scheike and Anders Juul. Maximum likelihood estimation for cox's regression model under rested case - control sampling. Bio-statistics, 5(2) :193 - 206, 2004.

[160] David W. Scott. Multivariate Density Estimation,Theory, Practice and Visualization. John Wiley and Sons, Hoboken, 1992.

[161] Pavel V. Shevchenko. Modelling Operational Risk using Bayesian Inference. Springer - Verlag, Berlin and Heidelberg, 2011.

[162] R. Situ. Theory of Stochastic Differential Equations with Jumps and Applications. Springer Science + Business Media, New York, 2005.

[163] D. Sorensen and Daniel Gianola. Likelihood Bayesian and MCMC Methods in Quantitative Genetics. Springer - Verlag, New York, 2002.

[164] P.J.C. Spreij. Stochastic Integration. Springer Science, New York, 2004.

[165] S. S. Sritharan. Nonlinear filtering of stochastic navier - stokes equations. In T. Funaki and W.A. Woyczynski, editors, Nonlinear Stochastic PDEs : Burgers Turbulence and Hydrodynamic Limit (PDF), pages 247 - 260. Springer-Verlag, 1994.

[166] Nancy L. Stokey. The Economics of Inaction : Stochastic Control Models with Fixed Costs. Princeton University Press, Princeton, 2009.

[167] Nancy L. Stokey, Robert E. Lucas Jr., and Edward C. Prescott. Recursive Methods in Economic Dynamics. Harvard University Press, Cambridge, 1989.

[168] H. Tanizaki and R.S. Mariano. Prediction, filtering and smoothig in nonlinear and non normal cases using monte carlo integration. Journal of Applied Econometrics, 9(2) :163 - 179, 1994.

[169] C. C. Tsui. Robust Control System Design : Advanced State Space Technique. Marcel Dekker, New York, 2 edition, 2004.

[170] A. van den Bos. Parameter Estimation for Scientists and Engineers. John Wiley and Sons, Hoboken, 2007.

[171] F. van der Heijder, R.P.W.Duin, D.de Ridder, and D.M.J.Tax. Classification, Parameter Estimation and State Estimation :An Engineering Aproach using MATLAB. John Wiley and Sons, West Sussex, 2004.

[172]

83

C. van Eeden. Restricted Parameter Space Estimation Problems Admissibility and Minimaxity Properties. Springer Science Business LLC, New York, 2006.

[173] R. van Handel. The stability of conditional markov processes and markov chains in random environment. The Annals of Probability, 37(5) :1876 - 1925, 2009.

[174] Carl E. Walsh. Monetary Theory and Policy. The MIT Press, Cambridge, 3 edition, 2010.

[175] Donald M. Wiberg. State Space and Linear Systems. Schaums Outline series. McGraw - Hill, New York, 1997.

[176] Robert L. Williams and Douglas A. Lawrence. Linear State - Space Control Systems. John Willey and Sons, Hoboken, 2007.

[177] J. Xiong. An Introduction to Stochastic Filtering Theory. Oxford University Press, Oxford, 2008.

[178] A. Yger and J. A. Weil. Mathématiques Appliquées L3. Pearson Education, Paris, 2009.

[179] N. Yoshida. Estimation for diffusion processes from discrete observation. Journal of Multivariate Analysis, 41 :220 - 242, 1992.

[180] A. Zaknick. Principles of Adaptive Filters and Self-learning Systems. Springer - Verlag, London, 2005.

[181] J. Zarzycki. Nonlinear Prediction Ladder - Filters for Higher - Order Stochastic Sequences. Springer - Verlag, Berlin and Heidelberg, 1985.

[182] A. Zellner. An Introduction to Bayesian Inference in Econometrics. JohnWiley and Sons, New York, 1971.

[183] A. Zellner and Joseph B. Kadane. Robustness of Bayesian Analyses, volume 4 of Studies in Bayesian Econometrics. Elsevier Science Publishers B.V., 1984.

[184] W. Zou and M. Schechter. Critical Point Theory and Its Applications. Springer Science + Business Media, New York, 2006.

84

Table des matières

1 Préliminaires mathématiques 1.1 Eléments de la théorie de la mesure et intégration				6 6
	1.1.1	Limite inférieure et supérieure		7
	1.1.2	Espaces vectoriels normés		8
	1.1.3	Propriétés de l'intégrale des fonctions étagées positives		9
	1.1.4	Produit des espaces mesurés		10
	1.1.5	Conditionnement et indépendance de probabilité. . . .		11
1.2	Espérance conditionnelle			11
	1.2.1	Variables aléatoires		13
	1.2.2	Modes de convergence		13
1.3	Processus stochastiques			16
	1.3.1	Processus de Markov		16
	1.3.2	Chaînes de Markov		19
	1.3.3	Temps d'arrêt		21
	1.3.4	Martingales à état indépendant		22
	1.3.5	Mouvement brownien		23
	1.3.6	Quelques modification du mouvement brownien . . . .		24

85

1.3.7 Martingales et Semimartingales

2 Equations Différentielles et Intégrales Stochastiques			26 31
2.1	Calculs stochastique		31
2.2	Equations différentielles stochastiques		33
	2.2.1	Equations différentielles stochastiques ordinaires . .	. . 33
	2.2.2	Equations aux dérivées partielles stochastiques	34
2.3	Intégrales stochastiques		37
	2.3.1	Intégrale Stochastique d'Itô	37
	2.3.2	Intégrale Stochastique de Stratonovich	40
2.4	Schémas numériques		41
	2.4.1	Schéma d'Euler	42
	2.4.2	Schéma de Milstein	43
	2.4.3	Schéma de Heun	44
	2.4.4	Méthodes de Runge - Kutta	44
	2.4.5	Schéma de Platen	45

3 Applications des intégrales stochastiques à l'estimation sta-

tistique 46

3.1 Estimation de paramètres des équations différentielles stochas-

tiques 46

3.1.1 Estimation des paramètres pour les équations différen-

tielles stochastiques linéaires 47

3.1.2 Méthodes d'estimation des paramètres 49

3.1.3 Méthode de maximum de vraisemblance 49

3.1.4 Méthode d'estimation Bayésienne 51

86

3.2 Estimation des équations aux dérivées partielles stochastiques

avec dérive linéaire 52

3.3 Estimation des paramètres stochastiques par le filtre stochas-

tique 54

3.3.1 Formulation du modèle d'état - espace stochastique . . 54

3.3.2 Filtre stochastique de Kalman - Bucy 55

3.3.3 Filtre stochastique optimal 56

3.3.4 Approximation discrète - temporelle du filtre de Kal-

man - Bucy 57

4

3.3.5 Equations de Filtre de Kalman pour les processus discrets 57

Applications aux processus stochastiques temporels 4.1 Revue empirique sur la modélisation stochastique			59 59
	4.1.1	Modèle de Bachelier	60
	4.1.2	Modèle de Black - Scholes	60
	4.1.3	Modèle de Cox - Intgersoll - Ross	60
	4.1.4	Modèle de Heath - Jarrow - Morton	60
	4.1.5	Modèle de Vasicek	61
	4.1.6	Modèle de Black - Karasinski	61
	4.1.7	Modèle de Hull - While	61
	4.1.8	Modèle de Aït - Sahalia	61
4.2	Estimation des paramètres de l'équation différentielle stochas-
	tique de l'inflation		62
	4.2.1	Présentation théorique de l'inflation	62
	4.2.2	Présentation du modèle économétrique	63

87

4.2.3 Estimation du processus stochastique autorégressif d'ordre

1 64

4.2.4 Résultats des estimations 65

4.3 Estimation de la contribution stochastique de la main d'oeuvre

congolais sur son bien - être économique 66

4.3.1 Modèle théorique du bien - être économique 66

4.3.2 Spécification économétrique du modèle état - espace

du développement économique 66

4.3.3 Estimation du modèle de bien - être congolais 67

4.3.4 Présentation et Interprétation des résultats 68