Calcul de la productivité d'un engin de transport dans la mine souterraine: Cas de la benne Sandvik TH551i de Kamoto

III.1. INTRODUCTION

Dans ce chapitre nous procéderons à la présentation des différentes données récoltées sur terrain, lesquelles nous permettrons de calculer grâce à une analyse statistique, les différents paramètres qui entre en jeu dans la détermination des différents rendements ainsi que de la productivité d'une unité de transport comme expliquée dans le chapitre précèdent. Après nous allons évaluer les différents rendements, puis nous allons procéder à une analyse critique et sur base de cette analyse, nous pourront arriver à la fin à donner une suggestion afin de permettre à l'entreprise KCC SA. A améliorer le rendement de ses unités de transport.

III.2. NOTIONS DE LA STATISTIQUE

Nous avons besoin, pour établir les temps moyens cités ci-haut ; de déterminer les valeurs moyennes à l'aide d'une analyse statistique.

III.2.1. Rappel sur les grandeurs statistiques

a)Le nombre de classes (K)

Une classe est l'ensemble d'éléments de la série d'observation définie par la loi de distribution statistique pour couvrir toute la série d'observation. La loi de distribution statistique répartit tous les éléments observés en un nombre de classe (K) défini par l'expression ci-dessous:

(III.1)

Avec :

? n : Nombre total d'observations.

b) L'étendue (d)

L'étendue est la différence entre la plus grande valeur observée de la série et la plus petite valeur observée de la même série. Elle est donnée par la relation suivante :

d=Kmczx- Km/n (III.2)

Avec :

? Xmax : Valeur maximale ;

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

~ 32 ~

? Xmin : Valeur minimale.

c) L'amplitude (a)

Elle représente la longueur d'une classe, elle est exprimée par l'expression mathématique suivante :

a=

d (III.3) K-1

d) Limite supérieure (Ls)

Elle représente la limite supérieure de la dernière classe de la distribution statistique. Elle est évaluée mathématiquement par la formule suivante :

Ls=Xmax+^?? (III.4)

2

e) Limite inférieure (Li)

Elle représente la limite inférieure de la première classe de la distribution statistique. Elle s'exprime mathématiquement par la formule suivante :

??

Li=Xmin-(III.5)

2

f) La fréquence (f??)

Par définition, la fréquence est le nombre d'observation statistique correspondant à un événement donné, une classe donnée.

Soit x la valeur de la variable observée et soit une suite d'intervalle adjacents égaux des dimensions h (h = le pas de la classe).

Soit Xi avec (i=1, 2,3,...) la valeur centrale de chaque intervalle au milieu de chaque classe.

Avec ces conditions la valeur de X ne peut être pas effectuée à l'un des intervalles que si la relation suivante est vérifiée.

(III.6)

La fréquence est définie par l'expression suivante :

???? = N?? (III.7)

N

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

~ 33 ~

g) La moyenne arithmétique (??)

C'est une valeur moyenne de toutes les valeurs observées de la série, cette moyenne peut être une moyenne arithmétique lorsque la distribution est discrète ou une moyenne pondérée lorsque la distribution est continue.

La moyenne arithmétique d'une série classée est donnée par l'expression suivante :

??=????? × ???? (III.8)

Avec :

? ???? : Le centre de classe.

? La variance et l'écart type : la dispersion fournit des renseignements des opérations et leurs moyennes. Le paramètre de dispersion est la variable qui est donné par la formule suivante :

ä=? ???? × (???? - ??) ² (III.9)

? L'écart-type : est la racine carrée de la variance. Il s'exprime dans la même unité que la moyenne est donnée par la formule suivante :

ä = v?? (III.10)

Avec :

? ä : la variance.

La moyenne arithmétique ?? sera comprise dans l'intervalle ci-dessous :

??-v?? = ?? = ?? + v?? (III.11)

Nous appellerons le temps de cycle étant la durée de la réalisation séquentielle d'un certain nombre par exemple l'évacuation des produits abattus sur le point de chargement vers le point de déchargement. C'est ainsi l'espace de temps entre deux chargements exécutifs.

Pour élaborer le présent travail, nous nous sommes basés sur la méthode de chronométrage sur terrain.

Voici une vue en plan du trajet (routes) GRIZZLY vers la zone ETANG sur la figure ci-dessous.

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

~ 34 ~

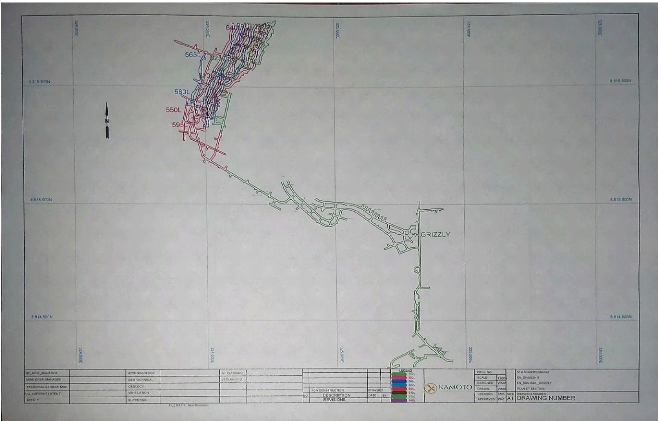
Figure III. 1 : Vue en plan de la mine du trajet GRIZZLI?ETANG

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

~ 35 ~

III.3. PRESENTATION DES DONNEES

Tableau III. 1 : présentation des tonnages transportés du trajet GRIZZLY?ETANG

N°	Tonnage Minerais (T)
1	46,93
2	43,89
3	48,35
4	40,55
5	40,66
6	44,51
7	45,03
8	40,52
9	38,79
10	46,85
11	43,95
12	49,78
13	40,90
14	39,13
15	42,34
16	47,08
17	41,37
18	39,87
19	45,02
20	40,96
21	40,01
22	46,56
23	44,09
24	38,98
25	42,66
26	43,07
27	40,23
28	39,87
29	41,73
30	45,19

III.3.1. Détermination du coefficient de remplissage dans les minerais (Kr) Considérons que X, représente le tonnage et N, l'effectif d'échantillons.

? Xmax : est la plus grande valeur de X ; ? Xmin : est la plus petite valeur de X.

Calculons le coefficient de remplissage moyen en suivant les étapes de la méthode de LIORZOU.

" 36 "

Xmax = 49,78 tonnes et Xmin = 38,79 tonnes

> Détermination du nombre de classes (K)

K = 1+^10 3	log?? Avec : N=30
K = 1+^10 3	log 30 = 5,92 -Þ 6 classes

> Etendue de la population (d)

d = Xmax - Xmin

d = 49,78 - 38,79 = 10,99 > Amplitude (a)

d

a =

K-1

a = 10,99

6-1

= 2,198

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

> Limite inférieure (Li) et limite supérieure (Ls)

Li = Xmin - a 2	= 38,79 - 2,198 2 = 37,691
Ls = Xmax + a 2		= 49,78 + 2.198 2 = 50,879

Tableau III. 2 : calcul statistique du coefficient de remplissage

N°	Classes	X??	????	f??	X
1	37,691 - 39,889	38,790	5	6,59	0,17
2	39,889 - 42,087	40,988	9	12,30	0,30
3	42,087 - 44,285	43,186	6	8,64	0,20
4	44,285 - 46,483	45,384	4	5,90	0,13
5	46,483 - 48,681	47,582	5	8,09	0,17
6	48,681 - 50,879	49,780	1	1,49	0,03
TOTAL			30	43,01	1

Le tonnage moyen dans les minerais est de 43,01 tonnes.

Kr = ????é???? (III.12)

????h

Avec :

+ Kr : Coefficient de remplissage de la benne ; + ????é???? : Tonnage chargé réellement ;

+ ?????? : Tonnage théorique bac benne. ????h = 51 tonnes

Kr = 43,01 51

= 0,84

Le coefficient de remplissage de la benne dans les minerais est de : Kr = 0,84

~ 37 ~

III.4. DETERMINATION DES COEFFICCIENTS DE GESTION D'UN ENGIN

Les heures de travail dans la mine souterraine de kamoto (KCC) sont reparties de la manière suivante :

+ Un poste : 12 heures (de 7h00' à 19h00') ;

+ Visité de la division de maintenance : 30 minutes ;

+ Changement de poste : arrêt des activités 2h00' avant et après poste.

Tableau III. 3 : Catégories d'heure de travail de la mine de kamoto

Heures Possible (HP)	Heures D'inactivité (????????????)	Heures d'activité (????????)	Heures de Mise à Disposition (HMD)	Heures de Maintenance (HM)	Heures d' Utilisation Effective (HUE)	Heures Improductive (HI)
24Heures	4Heures	20Heures	19Heures	1Heure	16Heures	3Heures

> Coefficient de mise à disposition (CMD) : c'est le rapport entre les heures de mise à disposition et les heures possibles :

?????? ^CMD=??P

= 19 24

= 0,792

> Le taux de mise à disposition (TMD) : c'est le produit du coefficient de mise à disposition multiplication par 100.

TMD=CMDx1OO = 0,792 x100 = 79,2 %

> Le coefficient d'utilisation effective (CUE) : c'est le rapport entre les heures d'utilisations effectives et les heures de mise à disposition:

??UE ^CUE=??????

= 16 19

= 0,842

> Le taux d'utilisation effective (TUE) : c'est le produit du coefficient d'utilisation effective multiplié par 100.

TUE=CUEx100 = 0,842 x100 = 84,2 %

> Le coefficient d'utilisation absolue (CUA) : c'est le produit du coefficient de mise à disposition et le coefficient d'utilisation effective.

CUA=CMDxCUE = 0,792 x 0,842 = 0,667

> Le taux d'utilisation absolue (TUA) : c'est le produit entre le coefficient d'utilisation absolue multiplié par 100.

TUA=CUAx100 = 0,667 x 100 = 66,7 %

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

" 38 "

Figure III. 2 : Catégorie des heures prestées des engins de transport dans la mine de kamoto

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

~ 39 ~

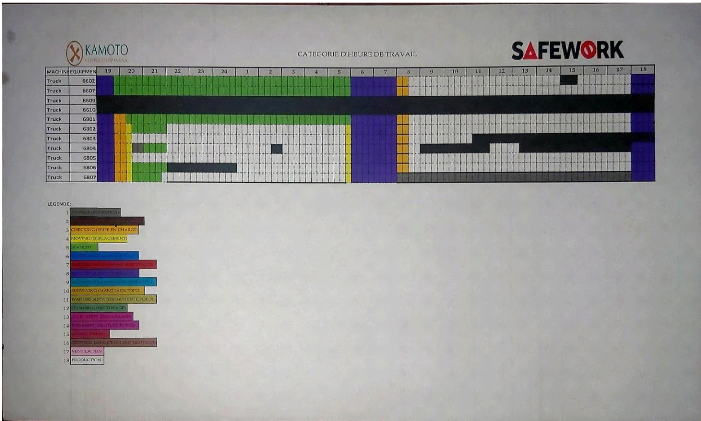
Figure III. 3 : Catégorie des heures de travail des unités de transport dans la mine de kamoto

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

~ 40 ~

III.5. CHRONOMETRAGE DU TEMPS DE CYCLE DE LA BENNE SANDVIK

III.5.1. Chronométrage

Etant une méthode pratique, le chronométrage consiste à effectuer plusieurs mesurages des temps de différentes opérations effectuées par le camion-benne au cours de leur cycle de travail habituel. Pour ce présent travail, l'application HYBRID STOPWATCH and TIMER du système d'exploitation d'Android a été utilisée pour le chronométrage des temps qui est donné en seconde.

Ainsi, les résultats des chronométrages des temps de cycle du camion-benne SANDVIK TH551i effectués à la mine souterraine de kamoto sont repris dans les tableaux suivants.

Après un certain nombre de chronométrage réalisé dans le trajet GRIZZLY?ETANG, nous avons obtenu les résultats qui sont répertoriés dans le tableau ci-dessous, nous notons les différents temps qui entrent dans la formule du temps de cycle de la benne SANDVIK TH551i affectée sur le trajet GRIZZLY?ETANG.

Tableau III. 4 : Temps de cycle de la benne SANDVIK TH551i affectée sur le trajet
GRIZZLY?ETANG

N°	Tmc (sec)	Tc (sec)	Ta (sec)	Tmd (sec)	Td (sec)	Tr (sec)	Tac (sec)
1	66	374	894	27	46	723	104
2	84	336	896	32	60	774	145
3	72	410	915	38	34	751	216
4	88	312	899	33	30	720	90
5	67	367	1009	43	32	809	230
6	71	382	844	28	43	686	273
7	78	296	829	47	30	662	259
8	63	367	845	33	48	701	193
9	102	431	912	37	42	733	110
10	92	328	924	51	39	697	212
11	72	301	891	40	38	725	196
12	98	294	914	28	35	801	68
13	106	381	840	45	29	678	142
14	111	400	953	41	33	737	199
15	91	362	857	38	37	709	233

" 41 "

16	88	370	869	48	37	665	191
17	77	402	888	32	40	819	189
18	121	411	921	43	34	796	172
19	83	374	1061	39	30	753	220
20	90	360	1112	50	31	687	258
21	115	389	906	46	36	691	306
22	100	358	899	37	41	744	145
23	106	415	861	39	29	760	196
24	109	390	809	32	35	823	159
25	79	320	871	29	43	672	222
26	86	412	879	33	38	759	287
27	93	325	797	41	32	723	325
28	96	300	925	37	46	685	253
29	69	326	961	52	37	869	126
30	84	428	824	39	39	702	180

III.6. DETERMINATION DU TEMPS MOYEN DE CYCLE

III.6.1. Calcul du temps moyen de manoeuvre à la chargeuse (??????) ? Détermination du nombre de classes (K)

K = 1+^10 3	log?? Avec : N=30
K = 1+^10 3	log 30 = 5,92 -Þ 6 classes

? Etendue de la population (d)

d = Xmax - Xmin

d = 121 - 63 = 58 ? Amplitude (a)

d

a =

K-1

a = 58

6-1

= 11,6

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

? Limite inférieure (Li) et limite supérieure (Ls)

Li = Xmin - a 2	= 63 - 11,6 2		= 57,2
Ls = Xmax + a 2		= 121 + 11,6 2		= 126,8

~ 42 ~

Tableau III. 5 : Calcul statistique du temps moyen de manoeuvre à la chargeuse

N°	Classes	????	????	f??	??	(????-??)	(????-??)^2	f?? × (????-??)^2
1	57,2-68,8	63	3	0,1	6,3	- 25,52	651,27	65,13
2	68,8-80,4	74,6	7	0,23	17,16	-13,92	193,77	44,57
3	80,4-92	86,2	8	0,27	23,27	-2,34	5,48	1,48
4	92-103,6	97,8	6	0,2	19,56	9,28	86,12	17,22
5	103,6-115,2	109,4	5	0,17	18,60	20,88	435,97	74,11
6	115,2-126,8	121	1	0,03	3,63	32,48	1045,95	31,65
TOTAL			30	1	88,52			234,16

Le temps moyen de manoeuvre à la chargeuse (??????) est de 88,52 secondes. La variance ô=? Fi × (Xi - X) ²= #177; v234,16 = #177; 15,30

+ 88,52+15,30 = 103,82

+ 88,52-15,30 = 73,22

L'intervalle de confiance : I ?? = [73,22 - 103,82]

III.6.2. Calcul du temps moyen de chargement de la benne (??_e) > Détermination du nombre de classes (K)

K = 1+^10 3	log?? Avec : N=30
K = 1+^10 3	log 30 = 5,92 -Þ 6 classes

> Etendue de la population (d)

d = Xmax - Xmin

d = 431 - 294 = 137 > Amplitude (a)

d

a =

K-1

a = 137

6-1

= 27,4

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

> Limite inférieure (Li) et limite supérieure (Ls)

Li = Xmin - a 2	= 294 - 27,4 2		= 280,3
Ls = Xmax + a 2		= 431 + 27,4 2		= 444,7

Tableau III. 6 : Calcul statistique du temps moyen de chargement de la benne

N°	Classes	????	????	f??	??	(????-??)	(????-??)^2	f?? × (????-??)^2
1	280,3-307,7	290,0	4	0,13	38,22	- 68,76	4727,94	614,63
2	307,7-335,1	321,4	5	0,17	54,64	-41,37	1711,48	290,95
3	335,1-362,5	348,8	4	0,13	45,34	-13,97	195,16	25,37
4	362,5-389,9	376,2	8	0,27	101,57	13,43	180,36	48,70
5	389,9-417,3	403,6	7	0,23	92,83	40,83	1667,09	383,43

~ 43 ~

6	417,3-444,7	431	2	0,07	30,17	68,23	4655,33	325,87
TOTAL			30	1	362,77			1688,95

Le temps moyen de chargement de la benne (??_e) est de 362,77 secondes. La variance ô=? Fi × (Xi - X) ²= #177; v1688,95 = #177; 41,10

+ 362,77+41,10 = 403,87

+ 362,77-41,10 = 321,67

L'intervalle de confiance : I e = [321,67 - 403,87]

III.6.3. Calcul du temps moyen d'aller en charge de la benne (????) > Détermination du nombre de classes (K)

K = 1+^10 3	log?? Avec : N=30
K = 1+^10 3	log 30 = 5,92 -Þ 6 classes

> Etendue de la population (d)

d = Xmax - Xmin

d = 1112 - 797 = 315 > Amplitude (a)

d

a =

K-1

6-1

315

a =

= 63

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

> Limite inférieure (Li) et limite supérieure (Ls)

Li = Xmin - ?? 2	= 797 - 63 2		= 765,5
Ls = Xmax + ?? 2		= 1112 + 63 2		= 1143,5

Tableau III. 7 : Calcul statistique du temps moyen d'aller en charge de la benne

N°	Classes	????	????	f??	??	(????-??)	(????-??)^2	f?? × (????-??)^2
1	765,5-828,5	797	3	0,1	79,7	- 103,95	10805,6	1080,56
2	828,5-891,5	860	11	0,37	318,2	-40,95	1676,9	620,45
3	891,5-954,5	923	12	0,4	369,2	22,05	486,2	194,48
4	954,5-1017,5	986	2	0,07	69,02	85,05	7233,5	506,35
5	1017,5-1080,5	1049	1	0,03	31,47	148,05	21918,8	659,36
6	1080,5-1143,5	1112	1	0,03	33,36	211,05	44542,1	1336,26
TOTAL			30	1	900,95			4397,46

Le temps moyen d'aller en charge de la benne (????) est de 900,95 secondes.

La variance ô=? Fi × (Xi - X) ²= #177; v4397,46 = #177; 66,31

~ 44 ~

+ 900,95+66,31 = 967,26

+ 900,95-66,31 = 834,64

L'intervalle de confiance : I ?? = [834,64 - 967,26]

III.6.4. Calcul du temps moyen de manoeuvre au déchargement de la benne (??????) > Détermination du nombre de classes (K)

K = 1+^10 3	log?? Avec : N=30
K = 1+^10 3	log 30 = 5,92 -Þ 6 classes

> Etendue de la population (d)

d = Xmax - Xmin

d = 52 - 27 = 25

> Amplitude (a)

??

a =

K-1

a = 25

6-1

= 5

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

> Limite inférieure (Li) et limite supérieure (Ls)

Li = Xmin - a 2	= 27 - 5 2		= 24,5
Ls = Xmax + a 2		= 52 + 5 2		= 54,5

Tableau III. 8 : Calcul statistique du temps moyen de manoeuvre au déchargement

N°	Classes	????	????	f??	??	(????-??)	(????-??)^2	f?? × (????-??)^2
1	57,2-68,8	27	4	0,13	3,51	- 11,35	128,82	16,75
2	68,8-80,4	32	6	0,2	6,4	-6,35	40,32	8,06
3	80,4-92	37	8	0,27	9,99	-1,35	1,82	0,49
4	92-103,6	42	5	0,17	7,14	3,65	13,32	2,26
5	103,6-115,2	47	4	0,13	6,11	8,47	71,74	9,33
6	115,2-126,8	52	3	0,1	5,2	13,65	186,32	18,63
TOTAL			30	1	38,35			55,52

Le temps moyen de manoeuvre au déchargement (??????) est de 38,35 secondes. La variance ä=? Fi × (Xi - X) ²= #177; v55,52 = #177; 7,45

+ 38,35+7,45 = 45,8

+ 38,35-7,45 = 30,9

L'intervalle de confiance : I ?? = [30,9 - 45,8]

~ 45 ~

III.6.5. Calcul du temps moyen de déchargement de la benne (????) > Détermination du nombre de classes (K)

K = 1+^10 3	log?? Avec : N=30
K = 1+^10 3	log 30 = 5,92 -Þ 6 classes

> Etendue de la population (d)

d = Xmax - Xmin

d = 60 - 29 = 31

> Amplitude (a)

??

a =

K-1

a = 31

6-1

= 6,2

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

> Limite inférieure (Li) et limite supérieure (Ls)

Li = Xmin - a 2	= 29 - 6,2 2		= 25,9
Ls = Xmax + a 2		=60 + 6,2 2		= 63,1

Tableau III. 9 : Calcul statistique du temps moyen de déchargement

N°	Classes	????	????	f??	??	(????-??)	(????-??)^2	f?? × (????-??)^2
1	25,9-32,1	29	8	0,27	7,83	- 7,93	62,88	16,98
2	32,1-38,3	35,2	11	0,37	13,02	-1,73	2,99	1,11
3	38,3-44,5	41,4	7	0,23	9,52	-4,47	19,98	4,60
4	44,5-50,7	47,6	3	0,1	4,76	10,67	113,85	11,39
5	50,7-56,9	53,8	0	0	0	16,87	284,60	0
6	56,9-63,1	60	1	0,03	1,8	23,07	532,22	15,97
TOTAL			30	1	36,93			50,05

Le temps moyen de déchargement (????) est de 36,93 secondes. La variance ô=? Fi × (Xi - X) ²= #177; v50,05 = #177; 7,07

+ 36,93+7,07 = 44

+ 39,93-7,07 = 29,86

L'intervalle de confiance : I ?? = [29,86 - 44]

III.6.6. Calcul du temps moyen retour de la benne (??_r) > Détermination du nombre de classes (K)

K = 1+^10 3	log?? Avec : N=30
K = 1+^10 3	log 30 = 5,92 -Þ 6 classes

~ 46 ~

> Etendue de la population (d)

d = Xmax - Xmin

d = 869 - 662 = 207 > Amplitude (a)

d

a =

K-1

6-1

207

a =

= 41,4

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

> Limite inférieure (Li) et limite supérieure (Ls)

Li = Xmin - ?? 2	= 662 - 41,4 2		= 641,3
Ls = Xmax + ?? 2		=869 + 41,4 2		= 889,7

Tableau III. 10 : Calcul statistique du temps moyen retour à la chargeuse

N°	Classes	????	????	f??	??	(????-??)	(????-??)^2	f?? × (????-??)^2
1	641,3-682,7	662	4	0,13	86,06	- 66,66	4443,56	577,66
2	682,7-724,1	703,4	11	0,37	260,26	-25,26	638,07	236,09
3	724,1-765,5	744,8	7	0,23	171,30	16,14	260,50	59,92
4	765,5-806,9	786,2	4	0,13	102,21	57,54	3310,85	430,41
5	806,9-848,3	827,6	3	0,1	82,76	98,94	9789,12	978,91
6	848,3-889,7	869	1	0,03	26,07	140,34	19695,3	590,86
TOTAL			30	1	728,66			2873,85

Le temps moyen retour à la chargeuse (??_r) est de 728,66 secondes. La variance ä=? Fi × (Xi - X) ²= #177; v2873,85 = #177; 53,61

+ 728,66+53,61 = 782,27

+ 728,66-53,61 = 675,05

L'intervalle de confiance : I ?? = [675,05 - 782,27]

III.6.7. Calcul du temps moyen d'attente à la chargeuse (????c) > Détermination du nombre de classes (K)

K = 1+^10 3	log?? Avec : N=30
K = 1+^10 3	log 30 = 5,92 -Þ 6 classes

> Etendue de la population (d)

d = Xmax - Xmin

d = 325 - 68 = 257 > Amplitude (a)

d

a =

K-1

~ 47 ~

6-1

257

a =

= 51,4

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

? Limite inférieure (Li) et limite supérieure (Ls)

Li = Xmin - ?? 2	= 68 - 51,4 2		= 42,3
Ls = Xmax + ?? 2		=325 + 51,4 2		= 350,7

Tableau III. 11 : Calcul statistique du temps moyen d'attente à la chargeuse

N°	Classes	????	N??	f??	??	(????-??)	(????-??)^2	f?? × (????-??)^2
1	42,3-93,7	68	2	0,07	4,76	- 121,38	14733,10	10313,17
2	93,7-145,1	119,4	6	0,2	23,88	-69,98	4897,20	979,64
3	145,1-196,5	170,8	9	0,3	51,24	-18,58	345,22	103,57
4	196,5-247,9	222,2	7	0,23	51,11	32,82	1077,15	247,74
5	247,9-299,3	273,6	4	0,13	35,57	84,22	7093,01	922,09
6	299,3-350,7	325	2	0,07	22,82	135,62	18392,78	1287,49
TOTAL			30	1	189,3			13853,7

Le temps moyen d'attente à la chargeuse (??????) est de 189,38 secondes. La variance ô=? Fi × (Xi - X) ²= #177; v13853,7 = #177; 117,70

? 189,38+117,70 = 307,08

? 189,38-117,70 = 71,68

L'intervalle de confiance : ???? = [71,68 - 307,08]

Dans le tableau ci-dessous nous présentons le résultat de tous les calculs statistiques des différents temps moyens qui comportent le temps de cycle du camion-benne SANDVIT( TH551i sur le trajet GRIZZLY?ETANG.

Tableau III. 12 : Résultat de tous les calculs statistiques de différents temps moyens qui
composent le temps de cycle de la benne

	T????	T??	T??	T??d	Td	Tr	T????
		(sec)	(sec)	(sec)	(sec)	(sec)	(sec)
	(sec)
Benne	88,52	362,77	900,95	38,35	36,93	728,66	189,38
SANDVIK TH551i

Le temps de cycle de la benne SANDVIK TH551i est donné par l'expression suivante :

T????= T??+ ^Tr+ T????+ T??+ T??d+ ^Td+ T????

T???? = 88,52+362,77+900,95+38,35+36,93+728,66+189,38= 2345,56 sec

Le temps de cycle de la benne SANDVIT( TH551i est de : T???? = 39,09 minutes

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

~ 48 ~

III .7. DETERMINATION DES RENDEMENTS DE LA BENNE SANDVIK TH551i

III.7 .1. Calcul du rendement théorique

Le rendement théorique de l'engin de transport est donné par l'expression suivante :

Avec :

? ????= 28 ??³

60×28×0,84	= 36,10 ??^3/h
39,09

Le rendement théorique du camion-benne SANDVIK TH551i est de :

= 36,10 ????/??

III.7.2. Calcul du rendement pratique ou réel

Ici nous allons tenir compte du coefficient d'utilisation absolue (CUA) trouvé après

calcul.

Alors le rendement pratique du camion-benne vaut :

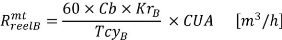
????é??????

???? = × CUA [??³/h]

Connaissant le rendement théorique et le coefficient d'utilisation absolue, nous pouvons calculer le rendement pratique ou réel.

????é??????

???? =36,10 × 0,667 = 24,08 ??³/h

Le rendement pratique ou réel du camion-benne SANDVIK TH551i est de :

????é??????

???? = 24,08 ????/??

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

~ 49 ~

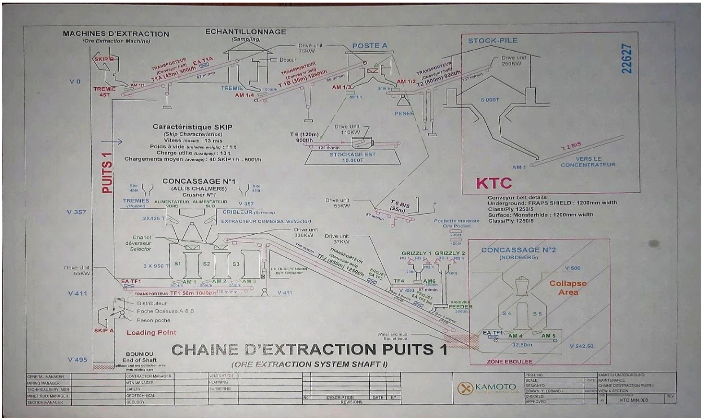
Figure III. 4 : Chaine d'extraction puits 1

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

" 50 "

III.8. CALCUL DE LA DISTANCE STANDARD

Les camions bennes SANDVIK TH 551i de 51 tonnes travaillent généralement sur le trajet GRIZZLI-ETANG et ne transportant que le minerai provenant de la zone ETANG qui est au niveau 640 vers le point de déchargement GRIZZLY qui est au niveau 465.

Pour calculer la distance standard nous allons utiliser la formule (II.16) suivante :

Dst=Dh+10Dv+K

III.8.1 Détermination de la dénivellation (D_r)

La dénivellation est la différence de niveau (altitude) entre deux points de la surface terrestre.

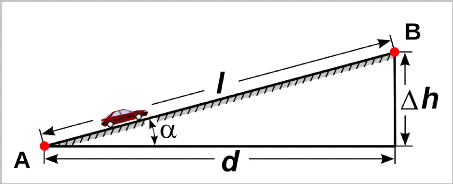
Figure III. 5 : Vue plan de la dénivellation

Avec :

> d : La distance horizontale entre A et B ;

> l : La longueur de la pente AB ;

> á : L'angle de la pente ;

> Äh : La dénivellation entre A et B ;

> AA : L'altitude du point A ;

> Bfi : L'altitude du point B.

La différence de niveau entre deux points est donnée par l'expression suivante :

Äh = AA - Bfi (III.13)
Äh = 640m - 465m = 175m

La dénivellation entre GRIZZLY-ETANG est de : Äh = 175 mètres

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

" 51 "

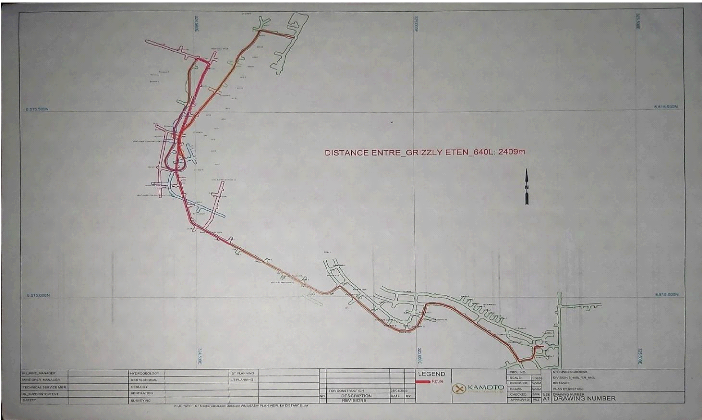
Figure III. 6 : Vue en plan de la route et la distance GRIZZLY-ETANG

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

~ 52 ~

Connaissant la dénivellation entre le point de chargement (GRIZZLY) et de déchargement

(ETANG) et la distance entre ces deux points, nous pouvons calculer la distance standard de la

manière suivante :

?????t= (2409 + 10.175 + 500)10^-3 = 4,659 -Þ 4,7kmst

La distance standard GRIZZLY-ETANG est de : ??????= 4,7 kmst

III.9. CALCUL DE LA PRODUCTIVITE DE LA BENNE

La productivité de la benne SANDVIK TH551i est donnée par l'expression suivante :

Pro=????é??????

???? xDst = 24,08 x4,7 = 113,18 ??³kmst/h

La productivité de la benne SANDVIK est de : Pro = 113,18 ??^??kmst/h

III.10. PRESENTATION DES RESULTATS

Tableau III. 13 : Présentation des résultats trouvés

Différents paramètres	Valeurs	Unités
Coefficient de remplissage de la benne	0,84	-
Coefficient de mise à disposition	79,2	%
Coefficient d'utilisation effective	84,2	%
Coefficient d'utilisation absolue	66,7	%
Temps moyen de cycle	39,09	Minutes
Rendement théorique	36,10	m3
Rendement pratique ou réel	24,08	m3
Distance standard	4,7	Kmst
Productivité	113,18	??^3????????/h

III.11. CONCLUSION PARTIELLE

En ce qui concerne ce chapitre sur le calcul de productivité d'un engin de transport dans la mine souterraine, nous avons commencé par la présentation des différentes données récoltées sur terrain, nous avons aussi déterminé le coefficient de remplissage de la benne, le coefficient de mise à disposition, le coefficient d'utilisation effective, le coefficient d'utilisation absolue, le temps moyen de cycle, le rendement théorique, le rendement pratique, la distance standard ainsi que la productivité de la benne SANDVIK.

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

~ 53 ~

CONCLUSION GENERALE

Nous voici arrivés au terme de notre travail de fin de cycle dont le but primordial était celui de déterminer la productivité d'un engin de transport (cas de la benne SANDVIK TH551i) travaillant dans la mine souterraine de Kamoto.

L'organisation de transport est un problème très important, à ne jamais négliger, qui conditionne en partie les possibilités de production de l'entreprise. Nous avons utilisé un seul engin de transport, camion-benne SANDVIK TH551i ayant une capacité nominale de 51tonnes.

Pour parvenir à faire le calcul de la productivité de cette dernière, nous avons fait une récolte des données par chronométrage pour la détermination par analyse statistique les moyennes pour le temps de cycle de l'engin. Ensuite prélever au service de la planification les données relatives des classes d'heures de travail et la distance entre le point de chargement et le point de déchargement (GRIZZLY-ETANG).

C'est ainsi qu'après traitement des données récoltés sur terrain et usage de quelques formules nous avons trouvé les résultats suivants :

> Coefficient de mise à disposition (CMD) est de 79,2 % ; > Coefficient d'utilisation effective (CUE) est de 84,2 % ; > Coefficient d'utilisation absolue (CUA) est de 66,7 % ; > Temps de cycle moyen benne _(T????) est de 39,09 minutes ;

> Rendement théorique ( ) est de 36,10 ??³/h ;
> Rendement réel (????é??????

???? ) est de 24,08 ??³/h ;

> Distance standard _(D????) est de 4,7 Kmst ;

> Productivité _(P????) est de 113,18 ??^??Kmst/h.

D'après ces résultats obtenus, nous remarquons que la benne SANDVIK TH551i nous offre une mauvaise productivité, pour pouvoir améliorer la productivité de la benne et satisfaire à la demande de l'entreprise à faible coût, l'exploitant doit minimiser les heures improductives qui ont un impact sur le taux d'utilisation absolue, de mettre un apport considérable sur la maintenance et de faire un suivi de près des opérateurs pour leurs habilités.

~ 54 ~

SUGGESTIONS

Pour une bonne productivité de la benne nous demandons à l'entreprise Kamoto copper company (KCC SA) d'améliorer le rendement pratique qui est faible en jouant sur certains paramètres.

De ce fait nous suggérons à l'exploitant de :

> Réduire sensiblement les heures dues à l'attente ;

> Réduire le temps de cycle en assurant régulièrement de piste et chantiers ;

> Réduire les heures de chômage dues aux pannes répétitives des chargeuses qui

conduisent aux attentes chargeuses en réparation ;

> Introduire un système de communication dans les engins de chargement et transport ;

> Installer des capteurs dans les camions bennes pour éviter les accidents ;

> Creusement de retour cat pour faciliter la translation (manoeuvre) de bennes ;

> Insérer un système de communication fiable ;

> Insérer un système de surveillance audiovisuelle assisté à distance ;

> Il faut donner une importance à la sécurité dans la mine pour travailler dans les bonnes

conditions ;

> Mettre en disponibilité les engins de terrassement ;

> L'achat des nouveaux camions améliore le système de transport et nous prépare pour

entamer d'autre projet.

Loin de nous l'idée d'avoir épuisé le sujet si complexe, nous pensons que d'autres

chercheurs pourront entreprendre les efforts similaires dans ce domaine afin d'améliorer nos

résultats.

Comme toute oeuvre humaine n'est jamais parfaite, nous restons ouverts aux critiques

et suggestions éventuelles des lecteurs et collègues visant à l'amélioration de ce travail.

BANZA KATONGOTONGO Jean-Luc [TFC/UNILI]

~ 55 ~