Conclusion partielle
Le chapitre avait pour objectif de présenter les
évolutions du capital humain et de la croissance économique, en
utilisant des données en séries temporelles. Ainsi, il en
découle de notre analyse qu'au regarde de l'indice de capital humain et
du produit intérieur brut par habitant de manière globale que la
RDC aconnu des décennies de conflits, d'instabilité et de
fragilité qui sont expliquées par plusieurs facteurs notamment,
la guerre, la corruption généralisée, la mauvaise gestion
publique, l'insécurité etc. Le pays a toutefois réussi
à améliorer son capital humain et son niveau d'investissement, ce
qui lui a permis de préserver un certain potentiel de
développement.
A présent nous avons vu la description des
différentes évolutions du capital humain et de la croissance
économique qui nous ont permis de voir certains faits marquants qui ont
eu de l'influence sur le capital humain et la croissance
économiquependant la période de l'étude, le prochain
chapitre porte sur le modèle économétrique utilisé
afin d'estimer l'effet du capital sur la croissance économique en
RDC.
CHAPITRE 3 :
MODELISATION ECONOMETRIQUE UTILISEE
Le présent chapitre a pour objectif deprésenter
l'approche économétrique à laquelle le travail a recouru
pour atteindre l'objectif principal. Il comporte deux sections : la
première présente le modèle ARDL, tandis que la
deuxième décrit les variables utilisées dans ces
modèles.
Section 1 :
Présentation du modèle ARDL et spécification des
modèles
A ce niveau, nous construisons un modèle ARDL
(AutoregressiveDistributedLag) pour vérifier empiriquement la relation
entre le capital humain et la croissance économique. Nous
spécifions donc un modèle qui permet de saisir l'impact du
capital humainsur la croissance économique. Ceci dans le but d'atteindre
les objectifs spécifiques exposés dans l'introduction
générale.
M'Amanja et Morrissey (2005), Akpan (2011), ainsi que
Govindaraju et al. (2011) ont également recouru à cette approche
économétrique moderne, respectivement pour les cas du Kenya, du
Nigéria et de la Malaisie. La forme générale du
modèle qui est appliqué dans cette étude est la
suivante :
Yt = 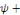
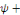 a1 a1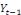
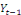 +...+ +...+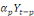
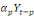 + +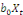
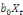 +...+ +...+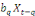
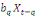 +et +et
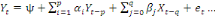
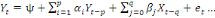 (1) (1)
Dans ce modèle nous avons une partie où la
variable dépendante est expliquée par ses propres valeurs
décalées. Un tel modèle est appelé modèle
autorégressif (AR) dont voici la forme générale :
Yt =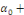
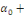 a1 a1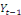
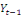 +...+ +...+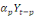
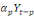 + +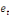
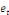
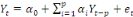
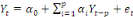 ... (2) ... (2)
Et une autre partie où la variable endogène est
expliquée par la variable (Xt) et leurs valeurs
décalées dans le temps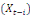
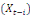 . Il s'agit ici des modèles à retards
échelonnés (DL) et qui peuvent s'écrire : . Il s'agit ici des modèles à retards
échelonnés (DL) et qui peuvent s'écrire :
Yt =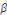
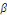 + + 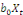
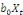 +...+ +...+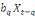
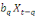 +zt +zt
Yt = 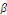
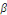 + +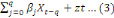
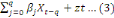
Où « 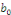
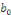 » traduit l'effet à court terme de Xt sur
Yt. Ce faisant ; l'effet à long terme de Xt
sur Yt « soit ?» sera obtenu en partant de la
relation de long terme suivant : » traduit l'effet à court terme de Xt sur
Yt. Ce faisant ; l'effet à long terme de Xt
sur Yt « soit ?» sera obtenu en partant de la
relation de long terme suivant :
Yt = k+ 
 Xt+u Xt+u
Ainsi, nous écrirons :

 =?????/ (1 - ?????) =?????/ (1 - ?????)
Il sied de préciser, comme l'a montré Kibala
(2018) que ces genres de modèles dynamiques sont souvent butés
à des problèmes d'autocorrélation des erreurs dû
à la présence de la variable endogène
décalée comme variable explicative à cause de la partie AR
du modèle et de multi-colinéarité dû au choix des
variables exogènes contenues la partie DL du modèle.
Le modèle de la forme fonctionnelle que nous allons
estimer, va nous permettre de saisir l'effet du capital humain sur la dynamique
de la croissance.
Dans le cadre de ce modèle, il est estimé la
fonction suivante :
lpibhab= f (lich, lfbcf, lapd)(4)
La représentation ARDL de cette fonction qui va nous
permettre de saisir les effets de court et ceux de long terme des variables
explicatives ci-dessus sera :
??Lpibhabt = ??0+
Ó??1ipi= 1 ??Lpibhabt-i +
Ó??2iqi = 0??Licht-i +
Ó??3i??i = 0??Lfbcft-i +
Ó??4i??i = 0??Lapdt-i +
b1Lpibhabt-1 + b2Licht-1 +
b3Lfbcft-1 + b4Lapdt-1 +
et(5)
?? est l'opérateur de différence première ;
??0 est la constante ; ??1...??4 sont des
effets à court terme ; b1......b4la
dynamique de long terme du modèle ; et~ iid (0,
??) terme d'erreur (bruit blanc).
Les modèles dynamiques posent un problème sur le
niveau de décalages. Ce faisant, pour palier à ce
problème, nous allons nous servir des critères d'information
(Akaike-AIC, Shwarz-SIC et Hannan-Quin) pour déterminer les
décalages optimaux (p,q) du modèle ARDL.
L'application d'un modèle ARDL écrit ci-dessus
suppose que les variables soient Co- intégrées, cette relation de
cointégration conditionne l'estimation des coefficients de long terme de
ces variables. La littérature économétrique fournit
plusieurs tests de cointégration dont celui de Engel et Granger (1987),
celui de Johansen (1988,1991), Johansen et Juselius (1990), celui de Pesaran et
al. (1996), Pesaran et Shin (1995) et pesaran et al. (2001). Le test de
cointégration de Engel et Granger (1991) fondé sur la
modélisation à correction d'erreur, n'est applicable que pour
deux variables intégrées de même ordre (soit ordre
d'integration =1), il est donc moins efficace pour le cas multivarié.
Bien que le test de Johansen pallie à ce souci, il est utilisé
pour le cas mutivariés pour les variables intégrées de
même ordre, soit d'ordre d'intégration égale à
l'unité (1) ; il est fondé sur la modélisation
vectorielle à correction d'erreur (VECM), il est ainsi moins efficace
pour les variables intégrées d'ordre différent.
Dans le cadre de cette étude, nous allons recourir au
test de cointégrationPesaran et al. (2001) appelé
« test de cointégration aux bornes » ou
« bounds test to coingration », ce test est applicable pour
le cas multivarié, et pour les variables intégrées d'ordre
différent (soit ordre d'intégration =0 et 1). (Kibala, 2018).
Avant d'en arriver là, nous avons testé l'ordre
d'intégration de nos variables pour pouvoir valider l'estimation du
modèle ARDL. Dans le cadre de ce travail, nous recourons aux tests de la
racine unitaire développés par Dickey et Fuller ainsi que Andrews
et Zivot (AZ) en vue de déterminer l'ordre d'intégration de nos
séries temporelles.
Pour déterminer si une série chronologique
comporte une racine unitaire, Dickey et Fuller (1981) proposent l'estimation
par les MCO des modèles suivants :
Où ? désigne l'opérateur de
différence, Xt la série dont on teste la
stationnarité, åt le terme d'erreur et
è ainsi que ?j les paramètres
à estimer. La valeur de p est déterminée en
minimisant l'un des critères d'information, notamment le critère
bayésien de Schwarz (1978), en vertu du principe de parcimonie.
Tout d'abord, on mène le test classique de Student sur
le coefficient b dans le modèle
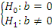
En cas de rejet de l'hypothèse nulle, on conclut que le
processus est non-stationnaire car la tendance linéaire dans le
modèle est déterministe. Le processus {Xt}
est donc un processus TS (Trend Stationnary). La méthode
appropriée de stationnarisation dans ce cas est l'écart à
la tendance. Il sera question pour ce faire de régresser
Xt sur le temps, i.e. 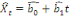
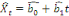 , puis récupérer la série des résidus de
cette régression, i.e. , puis récupérer la série des résidus de
cette régression, i.e. 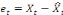
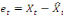 , laquelle sera stationnaire. , laquelle sera stationnaire.
Par contre, si l'hypothèse nulle n'est pas
rejetée, alors la tendance n'est pas significative. Il y a donc lieu de
la retirer du modèle, ce qui nous permet de basculer au modèle.
Dès lors, on mène encore le test classique de Student mais sur le
coefficient c cette fois-ci :
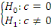
Si l'on rejette l'hypothèse nulle, alors le processus
admet une dérive (drift, en anglais) car la constante dans le
modèle est significative. Alternativement, le non-rejet de
l'hypothèse nulle signifie que le processus est sans drift, le terme
constant étant statistiquement non significatif. Ainsi, le retrait de la
constante nous permettra de passer au modèle.
Il s'agira maintenant de comparer la statistique empirique du
test (ADF, AugmentedDickey-Fuller) à la statistique théorique de
MacKinnon (VCM, Valeur Critique de MacKinnon). Si ADF < VCM, alors on ne
rejette pas l'hypothèse nulle : le processus
{Xt} contient donc une racine unitaire, i.e. le processus
est non-stationnaire.
Alternativement, si ADF > VCM, alors on rejette
l'hypothèse nulle : le processus {Xt} ne
contient pas donc une racine unitaire, i.e. le processus est stationnaire.
Le test d'Andrews et Zivot (AZ), quant à lui, poursuit
le même objectif que le test Dickey-Fuller présenté
ci-dessus, à savoir la détermination de l'ordre
d'intégration d'une série temporelle ainsi que la bonne
méthode de stationnarisation pour une série qui accuse une
rupture de structure ou un changement de régime identifié de
façon endogène.
Cependant, à l'issue de ces différents tests de
stationnarité, rien ne garantit que les variables du modèle
seront toutes à la fois stationnaires en niveau ou
intégrées du même ordre, étant donné leur
nombre élevé. Face à cela, il sied de les
différencier autant de fois jusqu'à ce qu'elles deviennent
stationnaires. Or, l'application du filtre aux différences à une
série temporelle fait perdre d'importantes informations en niveau
pourtant indispensables dans l'explication de la dynamique de cette
série (Gebhard - Wolters, 2007). En d'autres termes, la
stationnarisation par la différenciation retranche à la
série de départ ses propriétés de long terme, la
nouvelle série ne captant désormais que la dynamique de court
terme. Pour pallier à ce sérieux obstacle, il sera utile
d'estimer un modèle à correction d'erreurs (MCE) pour pouvoir
prendre en compte la dynamique de long terme. Avec cette procédure de
Pesaran et al. (2001), un modèle à correction d'erreur peut aider
à confirmer l'existence ou non de la cointégration entre
variables. Dans le cadre de notre étude ces modèles auront les
formes suivantes :
??LPibhabt = á0 +
Ó??1ipi =1 ??LPibhabt-i +
Ó??2iqi = 0??Licht-i +
Ó??3iqi = 0??Lfbcft-i +
Ó??4iqi = 0??Lapdt-i + ?ut-1
+ et (9)
Cette relation fera l'objet d'estimations. Cependant, nous allons
avant tout :
v déterminer le degré d'intégration des
valeurs (test de stationnarité) : le test d'Andrews et Zivot
(AZ)
v tester l'éventuelle existence d'une relation de
coïntégration entre les variables : test de Pesaran et al.
(2001) ou le test de cointegration aux bornes.
Il y a deux étapes pour appliquer le test de test de
coïntégration aux bornes dans un modèle ARDL
« approach to cointegrating »
v Premièrement, il faut déterminer le
décalage optimal (AIC, SIC HQ) ;
v Deuxièmement, implémenter le test de Fisher
pour vérifier les hypothèses suivantes :
(i) 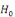
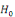 : : 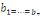
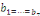 = Existence de la relation de cointégration = Existence de la relation de cointégration
(ii) 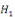
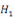 : : 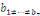
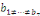 = Absence d'une relation de cointégration = Absence d'une relation de cointégration
La procédure du test est telle que l'on devra comparer
les valeurs de Fisher obtenues aux valeurs critiques (bornes) simulées
pour plusieurs cas et différents seuils par Pesaran et al. L'on notera
des valeurs critiques que la borne supérieure (2ème
ensemble) reprend les valeurs pour lesquelles les variables sont
intégrées d'ordre 1 I(1) et la borne inférieure
(1er ensemble) concernent les variables I(0).
Si Fisher > borne supérieure :
Cointégration existe
Si Fisher < borne inférieure :
Cointégration n'existe pas
Si borne < Fisher < borne supérieure : pas
de conclusion
Nous venons de présenter le modèle
économétrique utilisé dans le cadre de ce travail. Dans la
section suivante, nous décrirons les variables qui ont été
retenues pour la vérification empirique dans le cas spécifique de
l'économie congolaise.
| 


