Modélisation et optimisation de mouvement des conteneurs au niveau du terminal à conteneurs BMT

Promotion : 2022/2023

République Algérienne Démocratique et Populaire

Ministère de l'Enseignement Supérieur et de la Recherche Scientifique

Université Abderrahmane Mira de Béjaia
Faculté des Sciences Exactes

Département de Recherche Opérationnelle

Projet de fin d'étude

En vue de l'obtention du diplôme de Master en Mathématiques Appliquées
Option : Modélisation mathématique et évaluation des performances des réseaux

????????????????????????????????????????????
Modélisation et Optimisation de Mouvement des Conteneurs au

niveau du Terminal à Conteneurs BMT ?

?????????????????????????????????????????????

Réalisé par : M^r. YAICHE Hichem

Soutenu le 03 / 07 / 2023, devant le jury composé de :
Président:	M^r. ASLI Larbi	MCA	Université de Béjaia
Promoteur:	M^r. KABYL Kamal	MCB	Université de Béjaia
Examinatrice:	M^lle. AOUDIA Zohra	MAA	Université de Béjaia
Remerciements

I

Avant tout, je remercie le bon dieu de m'avoir donné la santé, la volonté,le courage et la patience nécessaire pour la réalisation de ce travail.

Je tiens à exprimer mes sincères remerciements à mon promoteur Dr. KABYL Kamal pour son encadrement, son soutien et ses conseils précieux tout au long de ce projet. Son expertise et sa disponibilité ont grandement contribué à la réussite de ce travail. Je tiens à exprimer ma reconnaissance envers les membres de mon jury de mémoire, et les remercier pour leur temps et leur engagement à évaluer mon travail et à me donner des commentaires constructifs. Leurs contributions ont aidé à améliorer la qualité de ce mémoire.

Je remercie également Mr. BOUMERZOUG Moussa chef du service informatique au sein de BMT, pour son accueil chaleureux, son écoute et ses conseils pertinents et le personnel de la Direction des Opérations, ils ont veillé à me fournir un bon environnement de travail, qui m'a permis d'atteindre ces résultats.

Enfin, je suis très reconnaissant envers ma famille pour leur soutien indéfectible et leur encouragement tout au long de mes études. Leurs encouragements m'ont aidé à persévérer et à atteindre mes objectifs académiques.

Encore une fois, je tiens à remercier toutes les personnes qui ont contribué à ce projet de mémoire et qui ont rendu cette réalisation possible.

Dédicaces

Je dédie ce travail avec une profonde gratitude et une immense affection à ma famille, qui m'a soutenu tout au long de ce parcours, en particulier à mes parents pour leur amour inconditionnel, leur soutien financier et leur encouragement constant. Je leur suis reconnaissant de m'avoir donné les ailes pour atteindre mes rêves.

Je dédie également ce mémoire à mon promoteur Dr. KABYL Kamal qui m'a guidé avec sagesse, expertise et bienveillance, et à tous mes enseignants qui m'ont accompagné tout au long de mon cursus académique.

Enfin, je tiens à exprimer ma gratitude à tous mes camarades, qui ont été présents à mes côtés, m'ont encouragé, soutenu et inspiré. Ce mémoire est également dédié à vous tous.

II

YAICHE Hichem

Table des matières

III

Liste des figures V

Liste des tableaux VI

Introduction générale 1

1 Présentation de l'organisme d'accueil 4

Introduction 4

1.1 Définition de Bejaia Mediterranean Terminal (BMT) 4

1.2 Situation géographique 5

1.3 Structure organisationnelle de BMT 5

1.4 Le terminal à conteneurs 6

1.4.1 La zone de quai 7

1.4.2 La zone terrestre 7

1.5 Les outils de gestion du terminal 9

1.5.1 Système de gestion de terminal à conteneurs (CTMS) 9

1.6 Les Équipements de manutention de BMT 9

1.7 Les opérations de BMT 10

1.7.1 Les planifications 10

1.7.2 La manutention 10

1.7.3 L'acconage 11

1.8 Les procédures import / export de BMT 11

1.8.1 À l'import 11

-Page IV-

Table des matières

			IV
	1.8.2 À l'export 1.9 Les objectifs de BMT 1.10 Les atouts de l'entreprise 1.11 Position du problème Conclusion		12 13 13 14 14
2	Revue de littérature		15
	Introduction		15
	2.1	Historique du conteneur	15
	2.2	Travaux de recherche liés au problème traité	16
	2.3	tableau récapitulatif des travaux de recherche liés au problème traité . . .	21
	Conclusion		22
3	Optimisation combinatoire : Concepts de base		23
	Introduction		23
	3.1	Qu'est ce que l'optimisation combinatoire?	23
	3.2	Problème d'optimisation combinatoire (POC)	24
	3.3	Outils de modélisation	24
		3.3.1 La théorie des graphes	25
		3.3.2 La programmation linéaire (PL)	25
		3.3.3 La programmation linéaire mixte (PLM)	26
		3.3.4 La programmation linéaire en nombres entiers (PLNE)	26
	3.4	Théorie de la complexité	27
		3.4.1 Classes des problèmes d'optimisation combinatoire	27
	3.5	Quelques problèmes classiques d'optimisation combinatoire	28
		3.5.1 Problème de transport	28
		3.5.2 Problème d'affectation	29
		3.5.3 Problème d'ordonnancement	30
		3.5.4 Problème du voyageur de commerce	32
	3.6	Méthodes de résolution	34
		3.6.1 Méthodes exactes	34
		3.6.2 Méthodes approchées	37
	Conclusion		38

Table des matières V

4 Modélisation et résolution du problème 39

Introduction 39

4.1 Les hypothèses du modèle 39

4.2 Les paramètres du modèle 40

4.2.1 Les ensembles 40

4.2.2 Les indices et les paramètres utilisés dans le modèle : 40

4.3 Les variables de décision du modèle 42

4.4 Formulation mathématique 43

4.4.1 L'objectif 43

4.4.2 Les contraintes 43

4.5 Le modèle mathématique 46

4.6 Complexité du problème 47

4.7 Exemple numérique 47

4.8 Implémentation et résolution du problème 49

4.8.1 Description de l'outil informatique 50

4.8.2 Rapport de la solution 50

4.8.3 Interprétation des résultats 52

Conclusion 52

Conclusion générale 53

Annexe 55

Bibliographie 61

-Page V-

Table des figures

VI

1.1

	Jointe venture création de BMT.	5
1.2	Situation géographique de BMT	5
1.3	Structure organisationnelle de BMT	6
1.4	Plan du terminal à conteneurs	7
1.5	Les équipements de manutention de BMT	11
3.1	Graphe simple -G-	25
5	Schéma de modèle	60
6	Nouvel assistant de fichier	60
Liste des tableaux

VII

1.1

	Les caractéristiques du quai.	7
1.2	Les caractéristiques des équipements de manutention de BMT	10
2.1	tableau résumant des travaux de recherche liés au problème traité.	21
2.2	tableau résumant des travaux de recherche liés au problème traité (suite). . .	22
4.1	Données d'ordre général.	47
4.2	Le temps de manutention des RTGs	48
4.3	Le temps de transport ti vers la destination sur le quai des conteneurs. . . .	48
4.4	Le temps de transport à vide tvqa des camions du quai vers différentes baies	48
4.5	Les localisations des conteneurs dans la zone de stockage	49
6	Tableau des faits saillants d'AMPL	55
Introduction générale

1

Après la Seconde Guerre mondiale, le transport maritime est devenu un secteur primordial de l'économie mondiale. Il joue un rôle crucial dans la chaîne logistique globale car il représente aujourd'hui l'un des principaux modes de transport pour les échanges internationaux de marchandises. En effet, d'après La Conférence des Nations Unies sur le Commerce et le Développement (UNCTAD), 11 milliards de tonnes est le volume total de marchandises qui ont été transportés par voie maritime en 2021 [23], ce qui est équivalant à Plus de 90% du commerce mondial s'effectue par mer.

L'apparition et le développement de la conteneurisation a joué un rôle majeur dans l'es-sor du transport maritime. La conteneurisation est un concept révolutionnaire qui consiste à utiliser des conteneurs standardisés pour emballer, transporter et stocker les marchandises de manière efficace et sécurisée. Ce concept n'est apparu qu'au 19^ème (années 50), mais depuis lors il est devenu un élément indispensable dans le domaine du transport. le système du conteneur se répand à travers le monde car il permet, en plus de l'optimisation de l'espace à bord des navires, un gain de temps incroyable aux opérations de manutentions. Se met alors en place une normalisation internationale des conteneurs; 20 pieds (6m) et 40 pieds (12m) comme dimensions standard des conteneurs.

Les terminaux maritimes à conteneurs jouent un rôle essentiel dans le système de transport maritime conteneurisé, Ce sont des infrastructures portuaires spécialement conçus pour le traitement efficace des conteneurs lors de leur chargement, déchargement, stockage et transfert entre les différents modes de transport (maritime, terrestre et ferroviaire). Un terminal maritime à conteneurs se décompose en deux grandes zones, chacune étant

Introduction générale 2

-Page 2-

caractérisée par ses propres opérations de manutention et ses équipements. En effet, dans la partie quai, les navires sont chargés/déchargés par des portiques de quai. Tandis que dans la partie terrestre, appelée encore la zone d'entreposage, cette zone possède comme équipements les portiques de cour. Un autre équipement, qui est le véhicule de transport (ce sont généralement des camions portuaires), ils assurent le transport des conteneurs du quai vers la zone d'entreposage et vice-versa.

En pratique, afin d'améliorer l'efficacité des opérations portuaires de manutention à cause des flux plus importants de conteneurs, il est primordial d'identifier et de résoudre une série de problèmes d'optimisation comme : le problème de stockage des conteneurs (PSC), le problème d'allocation des postes à quai, la planification des opérations des portiques de quai, la planification des opérations des portiques de cour, le problème des mouvements improductifs (Rehandle), etc.

Le processus général d'un terminal à conteneurs peut être décrit comme une séquence d'opérations à partir de l'arrivée des porte-conteneurs jusqu'au départ des conteneurs du port ou vice-versa. Les conteneurs destinés à l'exportation arrivent au port par camion, sont répartis entre les blocs et stockés dans une aire de stockage. Après une certaine période de temps, les conteneurs sont retirés des blocs avec les portiques de cour et sont transportés par les véhicules vers les quais où ils sont prélevés par des portiques de quai et chargés sur les navires. Dans la situation d'importation, quand un navire arrive au terminal, les conteneurs importés doivent être déchargés par les portiques de quai. Ensuite, ils sont placés sur des véhicules qui vont les amener jusqu'aux aires de stockage. Après un certain temps, les conteneurs quittent les aires de stockage et ils seront transportés par véhicules.

En termes de gestion, les terminaux à conteneurs font l'objet de l'attention de la communauté scientifique et des professionnels du domaine portuaire, qui ont essayé de proposer des actions d'amélioration des opérations du manutention et d'exploitation des espaces de stockage afin d'améliorer la performance des terminaux portuaires et de faire face à l'aug-mentation du trafic de conteneurs dans les terminaux.

Notre problématique est axée sur la planification des opérations de manutention des conteneurs effectuées par les portiques de cour et les camions. En outre, nous nous focali-

Introduction générale 3

-Page 3-

sons sur la synchronisation des opérations simultanées de manutention entre les portiques de cour et les camions, en tenant compte des éventuelles mouvements non productifs. Ce problème est formulé en programme linéaire mixte puis il est résolu à l'aide de langage AMPL en utilisant le solveur d'optimisation CPLEX dans le but de minimiser le temps de complétion des opérations de manutention des conteneurs destinés à l'exportation.

Organisation du rapport

Pour mener à bien ce travail, nous avons jugé utile de diviser ce mémoire en quatre chapitres :

· Le premier chapitre est consacré à la présentation de l'entreprise BMT, ses structures,ses moyens et ses services, et à la position du problème traité dans ce mémoire.

· Dans le deuxième chapitre, nous citons brièvement quelques travaux de recherche théoriques et expérimentaux sur les problèmes de planification des équipements de manutention dans un terminal maritime

· Dans le troisième chapitre, nous donnons des aspects théoriques de l'optimisation combinatoire tels que : des outils de modélisation, des problèmes classiques d'optimisation, des méthodes de résolution existantes dans la littérature et la complexité algorithmique.

· Le quatrième chapitre quant à lui présente une modélisation de notre problème et en proposant un modèle mathématique d'aide de décision, puis nous donnons un exemple numérique pour comprendre le fonctionnement de notre modèle, ensuite nous allons implémenter le modèle sous le logiciel AMPL et résoudre l'exemple en utilisant le sol-veur d'optimisation CPLEX.

La conclusion de ce travail mettra l'accent sur les recommandations et explorera les perspectives qui en découlent.

4

1

Présentation de l'organisme d'accueil

Introduction

Le transport maritime devient de nos jours, de plus en plus important et représente une alternative crédible et intéressante au transport terrestre et aérien, notamment avec l'évolu-tion du phénomène de conteneurisation.

Dans ce chapitre nous nous intéressons à la présentation du terminal à conteneurs de Bé-jaia (BMT).

1.1 Définition de Bejaia Mediterranean Terminal (BMT)

BMT-SPA (Société Par Actions) est une jointe venture entre l'Entreprise Portuaire de Béjaia (EPB) et Portek Systems and Equipment.EPB est l'autorité portuaire qui gère le port de Béjaia. PORTEK Systems and Equipment,une filiale du Groupe PORTEK qui est un opérateur de Terminaux à conteneurs (Société Singapourienne).

Sa mission principale est de traiter dans les meilleures conditions de délais,de coûts et de sécurité,l'ensemble des opérations qui ont un rapport avec le conteneur. Pour ce faire, elle s'est dotée d'équipements performants et de systèmes informatiques pour le support de la logistique du conteneur afin d'offrir des services de qualité, efficaces et fiables pour assurer une satisfaction totale des clients [3].

BMT veille au développement et à la gestion de son terminal à conteneurs où l'intégrité, la productivité, l'innovation, la courtoisie, et la sécurité sont de rigueur.

La figure (1.1) représente la jointe venture de cet entreprise :

1.3 Structure organisationnelle de BMT 5

-Page 5-

FIGURE 1.1 - Jointe venture création de BMT.

1.2 Situation géographique

L'entreprise BMT est implanté au centre du pays, au coeur de la méditerranée dans le nord du continent africain, le Port de Béjaia occupe une situation géographique stratégique.Il dessert un hinterland important et très vaste. La ville, le port et le terminal à conteneurs de Béjaia disposent de ce fait de voies de communication reliant l'ensemble des routes du pays, des voies ferroviaires et à proximité d'un aéroport international. La figure ci-dessous représente la situation géographique de BMT.

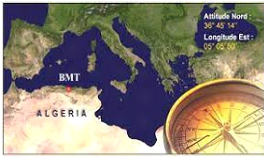
FIGURE 1.2 - Situation géographique de BMT

1.3 Structure organisationnelle de BMT

Dans la structure organisationnelle de BMT,on distingue six directions principales : Direction Générale (DG), Direction de Ressources Humaines et Moyennes (DRHM), Direction des Opérations (DO), Direction Marketing (DM), Direction des Finances et de Comptabilités

1.4 Le terminal à conteneurs 6

-Page 6-

(DFC), Direction Technique (DT). Elle est représentée dans la figure ci-dessous:

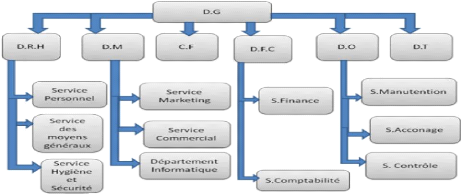
FIGURE 1.3 - Structure organisationnelle de BMT

La direction vers laquelle nous avons été dirigés lors de notre stage dans cette entreprise est la direction des opérations.Cette dernière assure la planification des escales, du parc à conteneurs et la planification des ressources (équipes et équipements). Elle comprend quatre services:

· Service acconage : Assure la gestion des opérations au niveau du terminal.

· Service manutention: Assure la gestion des opérations au niveau des navires.

· Service ressource: Assure une meilleure affectation des équipements et ressources.

· Service logistique: Assure le suivi des moyens logistiques ainsi que la prestation logistique globale.

1.4 Le terminal à conteneurs

Le terminal à conteneurs se décompose en deux grandes zones:

· La zone de quai.

· La zone terrestre.

La figure (1.4) montre ces deux zones:

1.4 Le terminal à conteneurs 7

-Page 7-

FIGURE 1.4 - Plan du terminal à conteneurs

1.4.1 La zone de quai

Le rôle de cette zone est de servir de point de transfert des conteneurs entre le terminal et les navires(chargement/déchargement).

Les caractéristiques de cette zone sont résumées dans le tableau suivant:

Longueur		500mL	Profondeur (tirant d'eau)
12 mL		Superficie du bassin
60ha		Nombre de postes
02 postes à quai

TABLE 1.1 - Les caractéristiques du quai.

1.4.2 La zone terrestre

Cette partie est subdivisée en quatre (04) zones

· Parc à conteneurs pleins,

· Zone visite,

·

1.5 Le terminal à conteneurs 8

-Page 8-

Zone de dépotage/empotage,

· Parc à conteneurs vides et empotés. 1.4.2.1 Le parc à conteneurs pleins

Dans cette cour sont entreposés temporairement les conteneurs déchargés des navires et destinés à être livrés aux clients par voie ferroviaire ou routière et les conteneurs destinés à l'exportation. Cette zone est répartie en cinq (05) blocs (A, B, C, D, E) disposés parallèlement au quai,chaque bloc est constitué de six (06) tronçons adjacents horizontaux formant les rangées et de 52 tronçons adjacents verticaux formant les baies (aussi appelés slots ou piles), une partie de bloc E est réservée pour les Conteneurs frigorifiques (reefers) qui a 500 prises,de plus les conteneurs sont stockés en pile de six (06) niveau. Ainsi, la position d'un conteneur dans la cour est caractérisée par une adresse formée du bloc, numéro de pile(slot), rangée et niveau. Ce parc a une capacité de 8300 EVP et une superficie de 78500m² [3].

1.4.2.2 Le zone visite:

Dans cette zone s'effectue le contrôle des marchandises portées dans les conteneurs (service vétérinaire, phytosanitaire, DCP, Douane), les conteneurs ayant fait la visite seront soit transférés à la zone du stockage ou livrés à leur propriétaire.

1.4.2.3 La zone dépotage/empotage

Dans cette zone s'effectue les opérations de dépotage et d'empotage tels que:

· Empotage : C'est l'opération de chargement des marchandises à l'intérieur d'un conteneur, il peut être effectué soit dans les locaux du client soit à l'intérieur du terminal.

· Dépotage: C'est l'opération de déchargement d'un conteneur de son contenu. Les marchandises dépotées sont livrées à leur propriétaire et les conteneurs vides sont transférés vers la Zone Extra-portuaire (ZEP) là où ils sont stockés temporairement avant d'être réclamés.

Cette zone a une capacité de 600 evp (Équivalent Vingt Pieds) et une Superficie de 3500 m².

1.6 Les Équipements de manutention de BMT 9

-Page 9-

1.5 Les outils de gestion du terminal

Afin d'améliorer les opérations de manutention des conteneurs BMT s'est dotée des système informatiques de gestion du terminal pour assurer une meilleure traçabilité du conteneur et de sa sécurité. Le système le plus important est le CTMS (Container Terminal Management System).

1.5.1 Système de gestion de terminal à conteneurs (CTMS)

BMT dispose de système logistique de gestion du terminal à conteneurs (CTMS) qui a pour objectif d'effectuer des activités, d'assurer une bonne planification du terminal, d'of-frir un niveau élevé de l'efficacité opérationnelle pour ses clients, d'améliorer le service et s'adapter aux besoins des clients. Le CTMS assure plusieurs tâches telles que:

· le suivi du processus d'import et d'export;

· la gestion de retour des conteneurs vides au terminal;

· la gestion des restitutions des conteneurs (vides ou pleins);

· le suivi de dépotage des conteneurs;

· la planification des activités sur les navires (chargement / déchargement);

· le suivi des opérations de chargement et de déchargement;

· la réception des conteneurs à l'exportation;

· le suivi des opérations de shifting au niveau du parc à conteneurs;

· la facturation des clients.

1.6 Les Équipements de manutention de BMT

BMT est le seul Terminal à Conteneur en Algérie à être suffisamment équipé en moyens et matériels spécialisés,de manutention et de levage qui réduisent les temps d'escale permettant de répondre aux attentes et aux exigences des opérateurs. Le tableau ci-dessous montre ces équipements et ses caractéristiques :

La figure (1.5) montre bien ces équipements:

1.7 Les opérations de BMT 10

-Page 10-

Les équipements	Nombre		Tonnage	Grue de quai (QC)
02	40 Tonnes		portiques gerbeurs sur pneus (RTG)
10	40 Tonnes		Camion remorque routière
42	36 Tonnes		Camion remorque portuaire
16	40 Tonnes		Chariots Elevateurs Tonnes
11	2.5,3,5,10 tonnes		Steacker
10	40 tonnes		Spreader
11	10 Tonnes		MHC (Grue)
02	100 Tonnes

TABLE 1.2 - Les caractéristiques des équipements de manutention de BMT.

1.7 Les opérations de BMT

La performance d'un terminal à conteneurs se mesure par le temps d'escale, la rapidité des opérations, la qualité des services et le coût du transit du conteneur. BMT reçoit annuellement un grand nombre de navires pour lesquels elle assure avec un suivi et une traçabilité les opérations de planification, de manutention et d'acconage telles que:

1.7.1 Les planifications

· Planification des escales : programmation des accostages et des postes à quai;

· Planification déchargement/chargement;

· Planification du parc à conteneurs (visite, dépotage, enlèvement et restitution des conteneurs vides au parc);

· Planification des ressources : équipes et moyens matériels. 1.7.2 La manutention

Après accostage du navire, des équipes spécialisées s'occupent de toutes les opérations de manutention au navire:

· Débarquement des conteneurs;

· Shifting des conteneurs;

· Embarquement des conteneurs.

1.8 Les procédures import / export de BMT 11

-Page 11-

FIGURE 1.5 - Les équipements de manutention de BMT

1.7.3 L'acconage

Une fois le conteneur est disposé dans le parc, les opérations suivantes peuvent prendre place:

· Suivi des visites du conteneur par les services concernés;

· Changement de position des conteneurs;

· Suivi des livraisons et des dépotages;

· Suivi des restitutions et des mises à quai;

· Mise à disposition des conteneurs vides pour empotage.

1.8 Les procédures import / export de BMT

1.8.1 À l'import

1. La visite: le transitaire doit remettre au service des opérations certains documents pour la procédure administrative. Par la suite, l'agent de BMT établira une liste complète des conteneurs à préparer pour la visite du lendemain qui sera remise au chef de la section exploitation. Il doit à son tour confirmer la mise à disposition des conteneurs en zone de visite pour le lendemain.

2.

1.8 Les procédures import / export de BMT 12

-Page 12-

La pesée: Le client est appelé à présenter au service des Opérations les documents nécessaires. A ce moment-là, l'agent BMT fait charger le conteneur sur un camion remorque pour effectuer la pesée.

3. La livraison: Pour permettre un suivi rigoureux des livraisons, le transitaire doit remettre un dossier complet. Par conséquent, l'agent chargé des opérations commerciales devrait confirmer la conformité du dossier pour établir le CDO (Container Delivery Order) et l'enregistrer sur fichier électronique consacré au suivi des livraisons.

4. Le dépotage: Le transitaire doit remettre à l'agent de BMT chargé des dépotages un dossier spécifique à l'opération. Par la suite, l'agent de BMT prépare le CMR (Container Movement Request) ;c'est le document nécessaire pour le dépotage à remettre au pointeur affecté à la zone de dépotage,mais au préalable l'agent chargé des opérations commerciales remettra au chef de section exploitation une liste contenant tous les conteneurs à préparer pour le lendemain. Après chaque confirmation de fin dépo-tage,l'agent doit s'assurer que la lettre de dépotage soit signée par le responsable de section pour clôturer le dossier [3].

1.8.2 À l'export

1. La restitution: Pour permettre un suivi rigoureux des restitutions, l'agent responsable de BMT doit exiger du pointeur une liste quotidienne des conteneurs restitués avec leurs positions au terminal et s'assurer de comparer les bons reçus avec le nombre total de conteneurs figurants sur la liste.

2. Suivi des mises à quai: Cette opération est assurée par l'agent responsable des restitutions, qui doit s'en assurer du bon suivi grâce à la tenue d'un fichier électronique mis à jours avec la saisie des restitutions journalières, et ce avec le concours du pointeur désigné et chargé pour le suivi des restitutions conjointement avec l'agent responsable des restitutions à la fin de la journée. La signature des mises à quai est assurée par le chef de section.

3. Mise à disposition: Le suivi des mises à disposition devrait être assuré par l'agent chargé des opérations commerciales responsable des mises à disposition, qui doit par conséquent tenir un fichier électronique spécialement consacré aux conteneurs mis à disposition.

4.

1.10 Les atouts de l'entreprise 13

-Page 13-

Empotage : Le client est libre d'effectuer cette opération soit à l'intérieur du terminal à conteneurs (empotage à quai), soit à l'extérieur (empotage externe) dans ses propres locaux.

5. Visite/Pesée: Le transitaire ou le client final doit remettre au service des opérations les documents nécessaires. A ce moment-là, l'agent de BMT établira une liste complète des conteneurs préparés pour la visite,la pesée et la mise à disposition de ces conteneurs dans la zone de visite [3].

1.9 Les objectifs de BMT

Les objectifs se résument en :

· Faire du terminal à conteneurs de BMT une infrastructure moderne à même de répondre aux exigences les plus sévères en matière de qualité dans le traitement du conteneur;

· La mise à disposition d'une nouvelle technologie dans le traitement de conteneurs pour:

1. Un gain de productivité;

2. Une réduction des coûts d'escale;

3. Une fiabilité de l'information;

4. Un meilleur service clientèle.

· Sauvegarder la marchandise des clients;

· Faire face à la concurrence nationale et internationale;

· Gagner des parts importantes du marché.

1.10 Les atouts de l'entreprise

Pour réaliser ses objectifs BMT mis à la disposition de ses clients une technologie et un savoir-faire dans le traitement du conteneur pour leur assurer:

· une rade où les navires attendent avant de se mettre dans le quai et un port non congestionné.

· Un tirant d'eau d'au moins 12m

· Des quais spécialisés pour le conteneur.

·

1.11 Position du problème 14

-Page 14-

Un temps d'escale réduit.

· Une capacité de stockage importante.

· Des installations spécialisées pour les reefers et les produits dangereux.

1.11 Position du problème

Vu l'augmentation de flux des conteneurs entrant à BMT ces dernières années, une croissance vertigineuse du nombre de conteneurs qui séjournent simultanément au terminal. En outre les conteneurs déchargés des navires et ceux qui sont destinés à l'exportation sont arrangés aléatoirement dans les blocs de la zone de stockage ce qui rend certains d'entre eux inaccessible au moment de leur récupération ainsi des remaniements (ré-arrangements) des conteneurs sont nécessaires pour accéder à ceux désirés, ces remaniements sont considérés comme des mouvements improductifs, car ils monopolisent le matériel et ralentissent les autres opérations portuaires.

Notre objectif est de modéliser les mouvements des conteneurs destinés à l'exportation afin de minimiser le temps de départ des camions qui les transportent et ce qui va entraîner la minimisation du temps de séjour des navires au niveau des quais, par conséquent minimiser le temps d'attente des navires qui sont dans la rade.

Conclusion

Dans ce chapitre, nous avons donné un aperçu général sur l'entreprise d'accueil afin de comprendre le contexte de notre problème, et nous avons expliqué ce dernier.

Dans le chapitre suivant, nous passerons en revue des travaux de recherche pertinents à notre travail.

15

2

Revue de littérature

Introduction

La revue bibliographique constitue une étape fondamentale de toute recherche scientifique. Elle permet d'explorer et d'analyser les travaux antérieurs réalisés dans un domaine spécifique, fournissant ainsi une base solide pour la compréhension de l'état actuel des connaissances, l'identification des lacunes et la formulation des objectifs de recherche.

De nombreuses recherches ont montré la grande importance de la planification et d'opti-misation dans les terminaux à conteneurs. Dans ce chapitre, nous présentons une revue détaillée de la littérature existante sur la planification simultanée des mouvements des portiques de cour et les déplacements des véhicules surtout lorsqu'il s'agit d'une opération d'exportation (outbound).

2.1 Historique du conteneur

Le conteneur a été créé en 1956 par l'Américain Malcolm MacLean, transporteur né en Caroline du Nord en 1913 dans une famille de classe moyenne. En 1953, cet entrepreneur se rend compte que les autoroutes reliant les différents les ports de la côte ouest sont complètement saturés et l'idée d'embarquer les camions remorques directement sur les bateaux. Puis il vend son entreprise de camionnage et investit dans une petite compagnie maritime pour transporter les remorques. Il s'aperçoit rapidement que l'espace utilisé est trop élevé. De là, l'idée lui vint d'enlever le cadre et d'embarquer seulement le haut de la remorque ou la "boîte" elle-même. Le conteneur est né.

Après la naissance du conteneur, il y a une date où les conteneurs sont développés présentés sous forme de flux:

·

2.2 Travaux de recherche liés au problème traité 16

-Page 16-

1958-1961 : Standardisation des tailles de contenants : la « box » commence à conquérir le monde.

· En 1961 apparaissent ISO, 20 pieds (6m) et 40 pieds (12m) comme dimensions standard des conteneurs.

· 2014 : Au 1er janvier, la flotte mondiale comptait 4 976 porte-conteneurs capables de transporter 17,3 millions Boîtes d'EVP simultanément (équivalent 20 pieds).

2.2 Travaux de recherche liés au problème traité

D'après le travail de K. H. KIM (1997) Les travaux de manutention influencent considérablement les performances des grues de transfert dans un terminal à conteneurs. La hauteur et la largeur d'une baie dans la pile de conteneurs sont des variables de décision importantes dans la conception de la configuration de stockage. Et ce sont des facteurs clés qui déterminent le nombre moyen de remaniements pour ramasser un conteneur. Dans cet article, il propose une méthodologie pour estimer le nombre prévu des mouvements non productifs pour ramasser un conteneur arbitraire et le nombre total de portiques de cour pour ramasser tous les conteneurs dans une baie pour une configuration d'empilage initiale donnée. Des tableaux et des équations simples sont fournis pour aider à estimer le nombre de remaniement.

La méthode proposée dans ce travail est un algorithme de routage optimal appelé "Optimal Routing algorithm" basé sur la programmation linéaire pour minimiser le temps total de manutention des conteneurs par les portiques de cour. [15].

Z. WEIYING, L. YAN et J. ZHUOSHANG (2006) voient que le temps d'accostage des navires au port dépend de l'efficacité du chargement et du déchargement des conteneurs, le ré-arrimage est le principal facteur qui influence l'arrimage. Un modèle d'optimisation qui réduit au maximum le nombre de mouvements inutiles est mis en avant lorsque le portique de cour charge les conteneurs aux terminaux portuaires. Chaque étape de l'opération de chargement des conteneurs est considérée comme un noeud de graphiques, les coûts de ramassage des conteneurs sont pris comme coefficients de pondération, puis le moindre arbre couvrant et la méthode heuristique sont utilisés pour obtenir une solution optimale. L'exemple montre que le modèle peut aider le planificateur à obtenir une séquence de chargement optimale, ce qui peut favoriser l'efficacité du chargement. Il fournit une base scienti-

2.2 Travaux de recherche liés au problème traité 17

-Page 17-

fique pour l'opération de chargement dans le terminal à conteneurs d'exportation [22].

A. IMAI, K. SASAKI, E. NISHIMURA et S. PAPADIMITRIOU (2006) considèrent que l'ef-ficacité d'un terminal maritime de conteneurs dépend principalement du bon déroulement et de l'organisation du processus de manipulation des conteneurs, en particulier lors du chargement du navire. Les plans de stockage des conteneurs sur un navire et de chargement sont principalement déterminés par deux critères : la stabilité du navire et le nombre minimal de mouvements improductifs des conteneurs requis. Ce dernier critère est basé sur le fait que la plupart des navires porte-conteneurs ont une structure cellulaire et que les conteneurs d'exportation sont empilés dans une aire de stockage. Ces deux critères de base sont souvent en conflit.

Cet article traite des plans de stockage des conteneurs sur un navire et de chargement des conteneurs qui satisfont ces deux critères. Le problème est formulé comme un programme en nombres entiers multi-objectif. Afin d'obtenir un ensemble de solutions non dominées pour le problème, ils ont utilisé la méthode de pondération. Pour résoudre le problème de chargement des conteneurs sur le navire ainsi celui du problème de remanutention, ils ont utilisé l'algorithme génétique. Une grande variété d'expériences numériques a démontré que les solutions obtenues par cette formulation sont utiles et applicables en pratique [12].

Y. LEE et N-Y. HSU (2007) déclarent que dans la plupart des parcs à conteneurs du monde, les conteneurs sont empilés en hauteur pour utiliser l'espace de stockage plus efficacement. Dans ces parcs, l'un des principaux facteurs affectant leur efficacité opérationnelle est la nécessité de remanier les conteneurs lors de l'accès à un conteneur enterré sous d'autres conteneurs. Une façon d'obtenir une efficacité de chargement plus élevée consiste à pré-organiser les conteneurs de manière à ce qu'ils correspondent à la séquence de chargement. Dans cette recherche, Ils présentent un modèle mathématique pour le problème de pré-marshalling (pré-triage ou bien pré-rassemblement) des conteneurs. En ce qui concerne un agencement d'une zone de stockage donné et une séquence donnée de chargement des conteneurs sur un navire, le modèle fournit un plan pour repositionner les conteneurs d'exportation dans la zone, de sorte qu'aucune re-manipulation supplémentaire ne sera nécessaire pendant l'opération de chargement. L'objectif d'optimisation est de minimiser le nombre de mouvements de conteneurs lors du pré-triage. Le modèle résultant est un modèle de programmation en nombres entiers composé d'un problème de flux multi-

2.2 Travaux de recherche liés au problème traité 18

-Page 18-

marchandises et d'un ensemble de contraintes secondaires. Plusieurs variantes possibles du modèle ainsi qu'une solution heuristique sont également discutées. Des résultats de calcul sont fournis [17].

Y. LEE et Y-J. LEE (2010) étudient le problème de récupération des conteneurs d'un terminal maritime dans une séquence donnée, qui est une partie importante du processus de chargement des navires. Ils disent que les mouvements supplémentaires qui font perdre du temps et de l'argent se produisent lorsqu'un conteneur qui doit être récupéré de la cour est enterré sous d'autres. Une façon de réduire les remaniements consiste à stocker les conteneurs dans des emplacements soigneusement planifiés. Cependant, dans la pratique, les conteneurs d'exportation arrivent au terminal de manière très incertaine. Même lorsque les emplacements de stockage des conteneurs sont soigneusement planifiés, ils peuvent toujours être empilés dans le mauvais ordre en raison d'un manque d'informations précises ou pour d'autres raisons.

Les chercheurs présentent une heuristique basée sur une méthode de recherche locale en trois phases à résoudre pour un plan de travail optimisé pour un portique de cour pour récupérer tous les conteneurs d'une zone de stockage donné selon une commande donnée. L'objectif d'optimisation est de minimiser le nombre de mouvements de conteneurs, ainsi que le temps de travail de portique de cour. Après avoir généré une séquence de mouvements faisable initiale, la deuxième phase réduit la longueur de la séquence en formulant et en générant à plusieurs reprises un programme d'entiers binaires. Avec un autre programme mixte à nombres entiers, la troisième phase réduit le temps de travail de portique de cour en ajustant la séquence de mouvement par itérations. Les résultats des tests numériques montrent que l'heuristique est capable de résoudre des instances avec plus de 700 conteneurs [18].

Selon le travail de J. X. CAO, D.-H. LEE, J. H. CHEN et Q. SHI (2010), la synchronisation des équipements de manutention (notamment portiques de cour et véhicules de transport) permet l'amélioration de la productivité des terminaux à conteneurs. Ils ont proposé un nouveau modèle intégré pour les problèmes de planification des camions et des portiques de cour pour les opérations de chargement dans les terminaux à conteneurs. Le problème est formulé comme un modèle de programmation linéaire mixte pour minimiser le temps de complétion de l'opération de chargement des conteneurs dans la cour destinés à

2.2 Travaux de recherche liés au problème traité 19

-Page 19-

l'exportation en se basant sur les hypothèses suivantes :

1. Seules les opérations de chargement des conteneurs d'exportation sont prises en considération.

2. L'emplacement de chaque conteneur est donné.

3. La localisation des portiques de cour est donnée.

4. Chaque conteneur a un temps de ramassage spécifique et ce temps est le même quelque soit le portique de cour.

5. Après avoir terminé la tâche actuelle, les portiques de cour et les camions peuvent se déplacer vers le point d'origine de la tâche qui suit.

6. La vitesse de déplacement du portique de cour est différente de la vitesse de déplacement du camion.

7. La capacité d'un camion est égale à 1, c'est à dire effectuer une seule tâche.

8. Pas d'interférence entre les camions.

9. Les conteneurs peuvent être manutentionnés dans n'importe quel ordre.

10. Les conteneurs sont disponibles à partir de la cour dans n'importe quel ordre.

11. Pas d'interférence entre les portiques de cour.

Deux méthodes de solution efficaces, basées sur la décomposition de Benders, sont développées pour la résolution du problème; à savoir, la méthode générale et la méthode combinatoire qui sont basées sur la coupe de Benders. Selon les auteurs, la résolution du problème d'ordonnancement des opérations des portiques de cour et des camions est une nouvelle idée permettant l'amélioration de l'efficacité des opérations portuaires.[4].

L'auteur K. Chebli (2011) s'intéresse au problème de mouvements des conteneurs dans le cas d'exportation. Les séquences de fonctionnement des portiques de cour et des camions sont prises en considération en même temps. Elle prend en compte les interférences qui peuvent exister entre les portiques de cour. Le problème de planification des opérations de chargement des conteneurs est d'abord formulé en programme linéaire mixte. La fonction objectif minimise le temps de complétion des opérations de manutention par les portiques de cour. Le modèle mathématique est basé sur plusieurs hypothèses, tenant compte des deux phénomènes d'interférence et des mouvements non productifs. Pour résoudre le problème, une approche heuristique de type Recherche Adaptative à Large Voisinage (ALNS)

2.3 Travaux de recherche liés au problème traité 20

-Page 20-

est développée. Cette méthode a la capacité de résoudre les problèmes d'optimisation dans un terminal à conteneurs. En effet, la méthode ALNS est jugée efficace quelque soit la taille du problème: 10, 20 et 100 conteneurs.

T. ÜNLÜYURT et C. AYDIN (2012) proposent des stratégies de remanutention améliorées à mettre en oeuvre dans la récupération des conteneurs, une partie essentielle des opérations des terminaux à conteneurs. Les auteurs introduisent le problème en notant que la quantité de marchandises chargés dans des conteneurs et transportées à l'étranger a récemment augmenté en raison de l'évolution des barrières commerciales entre les pays ainsi que de la flexibilité et de la fiabilité de ce type de transport.

Les auteurs élaborent des stratégies pour minimiser le temps total requis pour récupérer les conteneurs d'une baie dans une séquence prédéterminée. Par exemple, il peut y avoir d'autres conteneurs au-dessus du conteneur à récupérer, et il peut y avoir d'autres endroits pour que ces conteneurs soient déplacés. Les auteurs utilisent un algorithme basé sur Branch and Bound, et proposent des heuristiques alternatives qui donnent des solutions presque optimales. Ils ont testé les algorithmes sur des configurations de 8000 baies générées aléatoirement avec 200 combinaisons différentes de paramètres [21].

Le sujet d'étude faite par Consuelo PARRENO-TORRES, Ramon ALVAREZ-VALDES et Rubén RUIZ (2019) est le problème de pré-marshalling . Étant donné une configuration de baie initiale, le problème de pré-rassemblement recherche une séquence de travail qui minimise le nombre de mouvements nécessaires pour obtenir une configuration finale dans laquelle les conteneurs seront situés dans la baie n'ayant pas de conteneurs bloquants. Cela peut entraîner des réductions drastiques du temps de chargement car il n'est plus nécessaire d'effectuer des mouvements improductifs dans les baies une fois que les navires sont accostés, ce qui se traduit par des temps d'accostage plus courts, ils trouvent que c'est un moyen efficace d'accélérer les opérations de chargement/déchargement des navires au terminal à conteneurs.

En utilisant des modèles de programmation linéaire entière, les auteurs proposent une approche prometteuse pour résoudre le problème de pré-triage, ils ont développé deux familles de modèles alternatives, ce qui permet d'explorer différentes méthodes de résolution. De plus,ils ont mis au point une procédure de solution itérative qui ne dépend pas d'une borne supérieure difficile à obtenir [20].

2.3 tableau récapitulatif des travaux de recherche liés au problème traité 21

-Page 21-

2.3 tableau récapitulatif des travaux de recherche liés au problème traité

Auteurs	Problème traité	Méthode(s) de réso- lution	Contribution(s)
K. H. KIM(1997)	Estimation du nombre des mouve- ments improductifs pour récupérer un conteneur	Techniques d'optimi- sation	Détermination du nombre moyen de remaniements pour récupérer un conte-neur
Z. WEIYING, L. YAN et J. ZHUO- SHANG(2006)	Réduction au maxi- mum le nombre des mouvements inutiles des conteneurs	-Le moindre arbre couvrant -Méthode heuristique	Améliorer l'efficacité du chargement des conteneurs dans un navire
A. IMAI, K. SASAKI, E. NISHIMURA et S. PAPADIMI- TRIOU(2006)	-Problème de sto- ckage des conte- neurs sur un navire -Minimiser les mou- vements improductifs dans les blocs	-Méthode de pondé- ration -Algorithme géné- tique	Améliorer l'efficacité et la productivité d'un terminal maritime
Y. LEE et N-Y. HSU(2007)	le problème de pré-marshalling des conteneurs	Approche heuristique	Minimiser le nombre de mouvements de conteneurs lors de pré-triage
Y. LEE et Y-J. LEE(2010)	Problème de récupé- ration des conteneurs dans une séquence donnée	Heuristique basée sur une méthode de recherche locale	-Minimiser le nombre de mouvements des conteneurs et le temps de travail des portiques de cour
J. X. CAO et D. -H. LEE (2010)	Problème de planifi- cation des camions et des portiques de cour	Décomposition de Benders : Méthode générale et méthode combinatoire	-Améliorer la produc-tivité d'un terminal à conteneurs

TABLE 2.1 - tableau résumant des travaux de recherche liés au problème traité.

2.3 tableau récapitulatif des travaux de recherche liés au problème traité 22

Auteurs	Problème traité	Méthode(s) de réso- lution	Contribution(s)
K. CHEBLI(2011)	Problème de mou- vements des conte- neurs dans le cas d'exportation	Recherche Adapta- tive à Large Voisi- nage (ALNS)	Minimiser le temps de complétion de ma-nutention par les por-tiques de cour
T. ÜNLÜYURT et C. AYDIN(2012)	Problème de récupé- ration des conteneurs	algorithme basé sur Branch and Bound	stratégies de rema- nutention améliorées à mettre en oeuvre dans la récupération des conteneurs
C. P-TORRES, R. A-VALDES et R. RUIZ(2019)	problème de pré- marshalling des conteneurs	Approche de résolu- tion prometteuse	Configuration opti- male des baies

TABLE 2.2 - tableau résumant des travaux de recherche liés au problème traité (suite).

Conclusion

Dans ce chapitre nous avons cité quelques travaux pertinents liés au problème traité dans ce mémoire. Les études faites dans ces travaux sont diversifiées à cause de diversification des opérations effectuées dans les terminaux maritimes et les équipements de manutention utilisées, on trouve dans certains travaux des sous-problèmes qui sont traités dans un même travail, dans ce cas, l'analyse se complique vu que les opérations des différents équipements se font simultanément.

Des concepts de base, des outils de la Recherche Opérationnelle nécessaires pour la modélisation et la résolution du problème posé seront donnés dans le chapitre suivant, a savoir: quelques notions de base sur l'optimisation combinatoire.

-Page 22-

23

3

Optimisation combinatoire : Concepts de base

Introduction

La recherche opérationnelle est un domaine pluridisciplinaire permettant de produire de meilleures décisions. Elle fournit des outils pour rationaliser, simuler et optimiser l'archi-tecture et le fonctionnement des systèmes industriels et économiques. Elle propose des modèles pour analyser des situations complexes et permet aux décideurs de faire des choix efficaces et robustes.

L'optimisation combinatoire est une méthode clé de la recherche opérationnelle pour résoudre les problèmes d'optimisation, elle étudie comment décrire et atteindre ce qui est meilleur, une fois que l'on connaît comment mesurer et modifier ce qui est bon et ce qui est mauvais. La théorie de l'optimisation comprend l'étude quantitative des optimums et les méthodes pour les trouver,elle cherche à améliorer une performance en se rapprochant d'un point optimum.

3.1 Qu'est ce que l'optimisation combinatoire?

L'optimisation combinatoire est une branche de la recherche opérationnelle.C'est un ensemble d'outils destiné à modéliser et à résoudre une catégorie de problèmes. Cette catégorie est définie par un ensemble fini (d'où le mot combinatoire) de solutions admissibles (réalisables) [2].

3.3 Outils de modélisation 24

-Page 24-

3.2 Problème d'optimisation combinatoire (POC)

Étant donné un ensemble fini d'éléments E = {1, 2,. . . , m}, soit 2^E l'ensemble des parties de E.Soit P un problème où l'on considère comme solutions réalisables des sous ensembles de E vérifiant une certaine propriété. Autrement dit, on considère l'ensemble E ainsi qu'un sous ensemble F c 2^E, considérons f une fonction définie de E dans R. On étend la définition de la fonction f aux parties de E (ie. 2^E), que nous notons F.(eg. F(A) = >e?A f(e)) [2].

Un problème d'optimisation combinatoire (POC) est donc caractérisé par la définition de ces trois éléments:

· l'ensemble élémentaire (ou fondamental);

· l'ensemble F (de sous-ensembles de E );

· la fonction f et son extension (sa définition) sur F. Ce qui correspond respectivement à :

· identification des variables;

· identification des contraintes;

· identification de la fonction objectif [2].

3.3 Outils de modélisation

Définition 3.3.1. La modélisation mathématique consiste à utiliser des outils mathématiques tels que des équations, des fonctions, des graphes, des systèmes dynamiques ou des algorithmes pour représenter et étudier des situations réelles ou abstraites. La modélisation permet de simplifier et de formaliser un système complexe en le décrivant de manière précise et quantitative, ce qui permet d'en comprendre les propriétés et de prédire son comportement dans différentes conditions.

la résolution de problèmes de l'optimisation combinatoire est souvent difficile et nécessite des outils de modélisation mathématique pour formaliser les problèmes et les transformer en modèles mathématiques.Les outils les plus souvent requis pour l'optimisation combinatoire sont:

3.3 Outils de modélisation 25

3.3.1 La théorie des graphes

La théorie des graphes fournit des outils pour résoudre les problèmes d'optimisation combinatoire. Elle offre des algorithmes pour trouver des chemins optimaux, des couplages ou des flots maximaux. Les résultats obtenus peuvent permettre de prendre des décisions plus éclairées et d'optimiser les ressources disponibles pour atteindre des objectifs spécifiques. La théorie des graphes est donc une approche importante pour résoudre les problèmes d'optimisation combinatoire.

Un exemple d'un graphe simple est représenté ci-dessous:

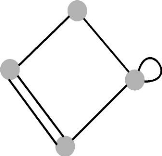
e₅

e₃

2

e₁ e

2

e 6

1 3

e₄

4

G = (V, E) où :

V = {1, 2,3, 4} est l'ensemble des sommets de graphe G

E = {e1, e2, e3, e4, e5, e6} est l'ensemble des arêtes de graphe G

-Page 25-

FIGURE 3.1 - Graphe simple -G-

3.3.2 La programmation linéaire (PL)

Le principe de la programmation linéaire est de modéliser le problème sous forme de contraintes mathématiques linéaires, c'est-à-dire sous forme d'équations ou d'inéquations linéaires reliant les variables du problème. La fonction objectif, qui est à maximiser ou à minimiser, est également une fonction linéaire.

?

?????

?????

(PL)

La forme générale d'un programme linéaire est la suivante:

maximiser z = cx

sous contraintes: Ax = b

x = 0

Avec A E ^m×n est une matrice (m x n),où rang(A) = m < n, b E ^m un vecteur de

3.3 Outils de modélisation 26

-Page 26-

dimension m, c E Rⁿ un vecteur de dimension n et x E Rⁿ est un vecteur inconnu.

Remarque 3.3.1. Tout programme linéaire peut s'exprimer sous forme standard en ajoutant certaines variables appelées variables d'écart, (par exemple, une inéquation a.x1 < b devient l'équation a.x1 + x2 = b, x2 > 0).

3.3.3 La programmation linéaire mixte (PLM)

Un programme linéaire mixte est un type de problème d'optimisation linéaire où les variables de décision peuvent être à la fois des variables continues et des variables binaires (ou entières). Il peut être formulé sous la forme suivante :

(PLM)

{

maximiser z = c1x + c2y sous contraintes : a1x + a2y < b x > 0 y E {0,1}(ou y E N)

3.3.4 La programmation linéaire en nombres entiers (PLNE)

De nombreux problèmes d'optimisation, issus de domaines d'applications très divers, peuvent être modélisés comme des programmes.

Les programmes linéaires ainsi obtenus sont appelés programmes linéaires en nombres entiers.Ils sont souvent difficiles à résoudre, du fait notamment que l'espace de recherche est discret. Toutefois, la programmation linéaire en nombres entiers est un outil utile de modélisation des problèmes et de nombreuses approches de résolution ont été développées. La formulation générale d'un PLNE est la suivante :

(PLNE)

{

maximiser z = f(x1, x2, ... , xn) sous contraintes : gá(x) < bá; á E C x E Nn

Avec g_á(x) et b_á sont généralement composés uniquement de valeurs entières.

Remarque 3.3.2. Dans le cas où les composantes du vecteur x E Nⁿ sont remplacées par x E {0,1}ⁿ, on dit qu'on a un programme linéaire en variables booléennes (PL en 0 - 1) qui

3.5 Théorie de la complexité 27

-Page 27-

s'écrit comme suit:

(PLB)

? ????? ?????

maximiser z = cx sous contraintes: Ax = b x E {0, 1}^n

3.4 Théorie de la complexité

La théorie de la complexité s'attache à classifier les problèmes selon leur difficulté relative à l'algorithme de résolution, on distingue deux grandes classes de problème (en terme de complexité), à savoir: Les problèmes faciles et Les problèmes difficiles.

Les deux paramètres les plus importants pour mesurer la qualité d'un algorithme sont : le temps de l'exécution de l'algorithme et l'espace mémoire qu'il prendra pour résoudre un problème d'une taille donnée.

Définition 3.4.1. Un algorithme déterministe est un algorithme qui suit une séquence d'ins-tructions préétablie et n'utilise pas de source de hasard ou de choix aléatoire pour prendre des décisions.

3.4.1 Classes des problèmes d'optimisation combinatoire

Les classes des problèmes d'optimisation combinatoire sont des catégories qui permettent de classifier les problèmes selon leur complexité et leur difficulté à être résolus par des algorithmes efficaces.Parmi elles,on trouve:

· La classe "P" : Problèmes pouvant être résolus en temps polynomial par un algorithme déterministe.On dit que les problèmes de cette classe sont faciles.

· La classe "NP" : Problèmes pour lesquels une solution peut être vérifiée en temps polynomial, mais pour lesquels il n'est pas clair qu'il existe un algorithme déterministe qui puisse trouver une solution en temps polynomial.

· La classe "NP-complet": Problèmes qui sont dans la classe NP et une solution de celui-ci peut être vérifiée en un temps polynomial.

· La classe "NP-difficile": Un problème de NP est dit NP-difficile, si et seulement si il existe un problème NP-Complet qu'est réductible à lui en temps polynomial.

3.5 Quelques problèmes classiques d'optimisation combinatoire 28

-Page 28-

3.5 Quelques problèmes classiques d'optimisation combinatoire

3.5.1 Problème de transport

Le problème de transport est un problème facile de l'optimisation,il consiste à déterminer la façon la plus efficace de transporter des quantités de marchandises depuis un ensemble de sources vers un ensemble de destinations.

Le problème de transport peut être formulé de la manière suivante : supposons que nous ayons m sources et n destinations. Chaque source i dispose d'une quantité d'offre ai à transporter,et chaque destination j a une quantité de demande bj à satisfaire. Le coût de transporter une unité de marchandise de la source i à la destination j est _cij. Nous devons déterminer le plan de transport qui minimise le coût total tout en satisfaisant les contraintes d'offre et de demande.

3.5.1.1 Formulation mathématique du problème

· Les variables de décision: _xij est la quantité à transportée de la source i ; i = {1, . . . , m} à la destination j ; j = {1,...,n}

· Les contraintes:

1. La disponibilité: la quantité de marchandise provenant de la source i doit être égale à la quantité d'offre ai disponible à cette source.

2. La demande: la quantité de marchandise livrée à la destination j doit être égale à la quantité de demande bj à satisfaire à cette destination.

· La fonction objectif: Minimiser le coût total de transport, représenté par la somme des coûts de transport unitaires _cij multiplié par la quantité de marchandise transportée xij pour chaque paire source-destination.

· Le modèle mathématique: Le problème de transport est donné par le programme linéaire (PL) (3.1) :

3.5 Quelques problèmes classiques d'optimisation combinatoire 29

?

????????????????? ?

??????????????????

m i=1

cijxij

_Xn j=1

xij = ai,

Minimiser Z =

sous contraintes :

_Xn

j=1 m

i=1

?i = {1,...,m}

(3.1)

xij = bj, ?j = {1, ... , n}

xij = 0, ?i = {1, ... , m} et ?j = {1, ... , n}

xij ? N, ?i = {1, ... , m} et ?j = {1, ... , n}

à la destination j, ai est la quantité d'offre disponible à la source i et bj est la quantité de demande à satisfaire à la destination j.

3.5.2 Problème d'affectation

Le problème d'affectation est un cas particulier du problème de transport dans lequel chaque source est affectée à une seule destination, il consiste à établir des liens entre les éléments de deux ensembles distincts, de telle sorte à minimiser le coût total de l'affectation en respectant des contraintes d'unicité de lien pour chaque élément.

Étant donnée n tâches et n agents.Une affectation consiste à affecter la tâche i; i = {1, ... , n} à l'agent j ; j = {1, ... , n} de sorte que :

· chaque agent j ait une et une seule tâche à effectuer à la fois.

· chaque tâche i est attribuée à un seul agent au même temps.

Le coût d'affectation d'une tâche i un agent j est : Cij.

Le problème d'affectation consiste à trouver une affectation de coût minimum.

3.5.2.1 Formulation mathématique du problème

· Les variables de décision :

xij =

{

1 si l'agent j est affecté à la tâche i , 0 sinon

· -Page 29-

Les contraintes :

3.5 Quelques problèmes classiques d'optimisation combinatoire 30

1. chaque agent j ne sera affecté qu'à une et une seule tâche (parmi toutes les tâches

i = {1,...,n}) :

_Xn xij = 1,?i = {1,...,n} i=1

2. chaque tâche i ne sera effectuée que par un seul agent (parmi touts les agents

j = {1,...,n}) :

_Xn xij = 1,?j = {1,...,n} j=1

· La fonction objectif: Elle est triviale car le coût d'avoir affecté i à j est : cijxij , pour tout i,j={1,. . .,n}.Le coût total de l'affectation globale est:

MinimiserZ =

Xn i=1

Xn j=1

cijxij

· Le modèle mathématique: Le problème d'affectation est donné par le programme linéaire en 0 - 1 (PL en 0 - 1) suivant:

_Xn xij = 1,?j = {1,...,n} j=1

xij ? {0,1},?i = {1,...,n} et ?j = {1,...,n}

?

????????????? ?

??????????????

Minimiser Z =

Xn i=1

Xn j=1

cijxij

sous contraintes :

Xn i=1

xij = 1,?i = {1,...,n}

(3.2)

-Page 30-

3.5.3 Problème d'ordonnancement:

Le problème d'ordonnancement est un problème difficile de l'optimisation,il consiste à organiser dans le temps la réalisation d'un ensemble de tâches d'un projet donné, compte tenu des contraintes temporelles (délais, contraintes d'enchaînements,...) et de contraintes portant sur l'utilisation et la disponibilité des ressources requises pour les tâches [16], et visant à minimiser (respectivement maximiser) un certain critère,financiers ou technologiques d'optimalité.De manière plus précise, on parle d'ordonnancement lorsqu'on parvient à fixer les dates de début et de fin de chacune des activités du projet [19].

3.5 Quelques problèmes classiques d'optimisation combinatoire 31

-Page 31-

3.5.3.1 Formulation mathématique du problème

· Les variables de décision:

ti : la date de début d'exécution de la tâche i; td : la date de début du projet; tf : la date de fin de projet.

· La fonction objectif: L'objectif principale en gestion est de minimiser la durée du réalisation du projet qui représente l'écart entre la date de fin du projet et sa date de début:

MinimiserZ = tf - td = tf

Avec td est fixé généralement à td = 0

· Les contraintes:

1. Les contraintes de localisation temporelle: Aucune tâche ne peut commencer avant la date de début de projet:

ti = 0, i = 1,...,n

2. Les contraintes de succession temporelle: Exprimer que tout tâche i ne peut pas débuter avant que toutes ses tâches antérieures j ? ^-(i) soient complètement achevées:

tj + dj = ti, ?j ? ^-(i)

3. Les contraintes de fin de projet: Toutes les tâches du projet doivent terminées avant la date de fin du projet tf :

ti + di = tf, i = 1,...,n

· Le modèle mathématique: Le modèle mathématique formulant le problème courant d'or-donnancement est le programme linéaire (PL) (3.3) :

3.5 Quelques problèmes classiques d'optimisation combinatoire 32

-Page 32-

????????

?

???????? sous contraintes : tj + dj = ti, ?j E ^-(i), i = {1, . . . , n}

Minimiser Z = tf

ti + di = tf, i = {1,...,n}

ti = 0, i = {1,...,n} (3.3)

3.5.4 Problème du voyageur de commerce:

Le problème du voyageur de commerce (TSP, pour "Traveling Salesman Problem" en anglais) est un problème difficile de l'optimisation dans le domaine de la théorie des graphes. Le TSP cherche à déterminer le trajet le plus court pour qu'un voyageur de commerce puisse visiter un ensemble donné de villes une fois chacune et retourner à sa ville de départ. Le défi réside dans le fait que le nombre de trajets possibles augmente rapidement avec le nombre de villes à visiter, rendant la recherche de la solution optimale très difficile.

Le problème du voyageur de commerce peut être formulé de la manière suivante : Soit G = (V, E) un graphe complet (tous les sommets sont adjacents deux à deux) non orienté, où V = {v1,v2, ...,v_n} est un ensemble den sommets (villes) et E est l'ensemble de toutes les arêtes reliant ces sommets. Soit _dij la distance entre les sommets vi et vj pour tout i,j E {1,2,...,n}.

Le problème du voyageur de commerce consiste à trouver un cycle hamiltonien de longueur minimale dans G, c'est-à-dire un cycle qui visite chaque sommet une fois et seulement une fois, et qui revient au sommet de départ.Le coût (ou la longueur) du cycle est défini comme la somme des distances entre les sommets visités dans l'ordre du cycle. Le problème est donc de minimiser:

n-1_X dpi,pi+1 + dp_n,p1 i=1

où pi représente le sommet visité en i-ème position dans le cycle.

3.5 Quelques problèmes classiques d'optimisation combinatoire 33

3.5.4.1 Formulation mathématique du problème

· Les variables de décision:

xij =

? ?? ??

1 si l'arête (i,j) appartienne au cycle hamiltonien , 0 sinon

·

-Page 33-

Les contraintes:

1. Pour chaque sommet i, il y a exactement deux arêtes qui en sortent et deux arêtes qui y entrent:

Xn j=1,j?=i

xij = 2, ?i E {1,2,...,n}

2. Pour chaque arête (i,j), elle ne peut être incluse que si les deux sommets i et j sont tous les deux visités :

xij =

Xn k=1,k?=i

xkj, ?i E {1,2,...,n},j E {1,2,...,n},i =? j

xij =

Xn k=1,k?=j

xik, ?i E {1,2,...,n},j E {1,2,...,n},i =? j

3. Il doit y avoir un unique cycle hamiltonien qui visite tous les sommets:

Xn i=1

Xn j=1,j?=i

xij = n

· Le modèle mathématique: Le modèle mathématique formulant le problème du voyageur de commerce est le programme linéaire en 0 - 1 (PL en 0 - 1) suivant:

Minimiser Z = _Xn- 1 dpi,pi+1 + dp_n,p1

i=1

sous contraintes :

Xn j=1,j?=i

xij = 2, ?i E {1,2,...,n}

xij = _Xn xkj, ?i E {1,2,...,n},j E {1,2,...,n},i =? j (3.4)

k=1,k?=i

3.6 Méthodes de résolution 34

?

??????????????????? ?

????????????????????

-Page 34-

_Xn _Xn xij = n i=1 j=1,j?=i

xij E {0,1}, ?i E {1,2,...,n} et ?j E {1,2,...,n}

3.6 Méthodes de résolution

La résolution des problèmes d'optimisation combinatoire consiste à trouver la meilleure solution, définie comme la solution globalement optimale ou un optimum global.La résolution des problèmes combinatoires est assez délicate puisque le nombre fini de solutions réalisables croît généralement avec la taille du problème, ainsi que sa complexité. Cela a poussé les chercheurs à développer de nombreuses méthodes de résolution en recherche opérationnelle. Ces méthodes sont classifiées en deux grandes classes : Méthodes exactes et Méthodes approchées.

3.6.1 Méthodes exactes:

Elles garantissent la complétude de la résolution,mais elles sont souvent limitées au cas des problèmes de petite taille.Parmi ces méthodes on trouve [14] :

3.6.1.1 Méthode de séparation et évaluation (Branch and Bound)

L'algorithme par séparation et évaluation, également appelé selon le terme anglo-saxon "Branch and Bound", est une méthode générique de résolution de problèmes d'optimisa-tion, et plus particulièrement d'optimisation combinatoire ou discrète.

C'est une méthode d'énumération implicite à l'aide d'une arborescence : toutes les solutions possibles du problème peuvent être énumérées, mais l'analyse des propriétés du problème permet d'éviter l'énumération de larges classes de mauvaises solutions (des branches sont

3.6 Méthodes de résolution 35

-Page 35-

coupées). Dans un algorithme par séparation et évaluation, seules les solutions potentiellement bonnes sont donc énumérées [8].

L'algorithme de branch and bound est basé sur trois axes principaux : séparation,évaluation,et stratégie de parcours.

· Séparation : La séparation consiste à diviser le problème en sous-problèmes. Ainsi, en résolvant tous les sous-problèmes et en gardant la meilleure solution trouvée, on est assuré d'avoir résolu le problème initial. Cela revient à construire un arbre permettant d'énumérer toutes les solutions.

L'ensemble de noeuds de l'arbre qu'il reste encore à parcourir comme étant susceptibles de contenir une solution optimale, c'est-à-dire encore à diviser, est appelée ensemble des noeuds actifs.

Son principe : Soient X_r la solution optimale du programme relaxé (PR) et Xi une variable de base non entière de X_r telles que : [xi] < xi < [xi] + 1.

(P1)

{ (P); et xi = [xi]

(P2)

{ (P); et xi = [xi] + 1

La séparation de (P),selon la variable Xi,consiste à diviser (P) en deux programmes (P1) et (P2). Désignons par :

R0 : la région ne contenant pas de solutions entières ;

R1 : la région des solutions réalisables de (P1) ;

R2 : la région des solutions réalisables de (P2). La séparation consiste à éliminer R0 et à chercher des solutions entières dans les régions R1 et R2 .

· Évaluation : L'évaluation permet de réduire l'espace de recherche en éliminant quelques sous ensembles qui ne contiennent pas la solution optimale. L'objectif est d'essayer d'évaluer l'intérêt de l'exploration d'un sous-ensemble de l'arborescence.

Le branch and bound utilise une élimination de branches dans l'arborescence de recherche de la manière suivante : La recherche d'une solution de coût minimal, consiste à mémoriser la solution de plus bas coût rencontré pendant l'exploration, et à compa-

3.6 Méthodes de résolution 36

-Page 36-

rer le coût de chaque noeud parcouru à celui de la meilleure solution. Si le coût du noeud considéré est supérieur au meilleur coût, on arrête l'exploration de la branche et toutes les solutions de cette branche seront nécessairement de coût plus élevé que la meilleure solution déjà trouvée.

Son principe : On utilise en général des fonctions d'évaluation et des bornes.À l'étape k,on résout le problème relaxé (PRk ) associé à (Pk). Pour se faire, deux cas se présentent:

1. Cas où la solution optimale Xk r est entière, Z(Xk _r ) constitue une borne inférieure à tous les problème prédécesseurs au problème (P_r), et en même temps un majorant à tous les problèmes successeurs au problème (Pk).

2. Cas où la solution optimale obtenue Xk r n'est pas entière, on sépare de nouveau le problème (Pk).

· Stratégie de parcours:

1. Parcours en largeur d'abord: cette stratégie favorise les sommets les plus proches de la racine en faisant moins de séparations du problème initial. Elle est moins efficace que les deux autres stratégies présentées.

2. Parcours en profondeur d'abord: cette stratégie avantage les sommets les plus éloignés de la racine (de profondeur la plus élevée) en appliquant plus de séparations au problème initial. Cette voie mène rapidement à une solution optimale en économisant la mémoire.

3. Meilleur parcours d'abord: cette stratégie consiste à explorer des sous-problèmes possédant la meilleure borne. Elle permet aussi d'éviter l'exploration de tous les sous-problèmes qui possèdent une mauvaise évaluation par rapport à la valeur optimale.

3.6.1.2 Méthode de coupes planes (Cutting-Plane)

La méthode de coupes planes a été développée par (Schrijver 1986), elle est destinée à résoudre des problèmes d'optimisation combinatoire (POC) qui se formulent sous la forme d'un programme linéaire.

3.6 Méthodes de résolution 37

-Page 37-

3.6 Méthodes de résolution 38

Dans le cas où le POC est de grande taille pour le représenter explicitement en mémoire ou pour qu'il tient dans un solveur de programmation linéaire, on utilise une technique qui consiste à enlever une partie de ces contraintes et de résoudre le problème relaxé (PR). La solution optimale de (PL) est contenue dans l'ensemble de solutions réalisables de cette relaxation. Pour un problème de maximisation la solution optimale du problème (PR) est supérieure ou égale à la solution optimale donnée par (POC).

Cette méthode consiste à résoudre un problème relaxé, et à ajouter itérativement des contraintes du problème initial. On définit une contrainte pour le problème de maximisation par le couple (s, s ) où s E Rⁿ et s E R, cette contrainte est dite violée par la solution

courante x si pour tout y E {x : Ax b} on a sx < s et sy ~ s , on appelle alors ces
contraintes des coupes planes. On arrête l'algorithme lorsqu'il n'y a plus de contraintes violées par la solution courante, on obtient ainsi une solution optimale pour le problème initial [10].

Remarque 3.6.1. La méthode des coupes planes est peu performante mais sa performance est améliorée lorsqu'elle est combinée avec la méthode "Branch and Bound".

3.6.1.3 Méthode de Branch and Cut

La méthode des coupes planes n'est pas toujours efficace face aux problèmes difficiles. De même, bien que l'algorithme du "Branch and Bound" puisse être très performant pour une certaine classe de problèmes, pour cela on utilise la méthode "Branch and Cut" qui combine entre l'algorithme du "Branch and Bound" et de la méthode des coupes planes. Pour une résolution d'un programme linéaire en nombres entiers (PLNE), la méthode "Branch and Cut" commence d'abord par relaxer le problème puis appliquer la méthode des coupes planes sur la solution trouvée. Si on n'obtient pas une solution entière alors le problème sera divisé en plusieurs sous-problèmes qui seront résolus de la même manière [10].

3.6.2 Méthodes approchées:

Le but de ces méthodes est de trouver une solution de bonne qualité pour un problème d'optimisation de grande taille en un temps de calcul raisonnable sans garantir l'optimalité de la solution obtenue [14]. Les méthodes approchées sont réparties en deux catégories principales : les heuristiques et les méta-heuristiques.

-Page 38-

3.6.2.1 Les heuristiques

Définition 3.6.1. Une heuristique est un algorithme approché qui permet d'identifier en temps polynomial au moins une solution réalisable rapide, pas obligatoirement optimale.

L'usage d'une heuristique est efficace pour calculer une solution approchée d'un problème et ainsi accélérer le processus de résolution exacte. Généralement une heuristique est conçue pour un problème particulier, en s'appuyant sur sa structure propre sans offrir aucune garantit quant à la qualité de la solution calculée. Parmi elles, on cite : méthode de recherche locale,méthodes gloutonnes,...

3.6.2.2 Les méta-heuristiques

Face aux difficultés rencontrées par les heuristiques pour avoir une solution réalisable de bonne qualité pour des problèmes d'optimisation difficiles, les méta-heuristiques ont fait leur apparition [10].

Définition 3.6.2. Les méta-heuristiques sont plus complets et complexes qu'une simple heuristique,elles permettent généralement d'obtenir une solution de très bonne qualité des problèmes dont on ne connait pas de méthodes exactes pour les traiter ou bien quand la résolution du problème nécessite un temps élevé ou une grande mémoire de stockage.

Plusieurs d'entre elles sont souvent inspirées par des systèmes naturels dans de nombreux domaines tels que : la biologie (algorithmes évolutionnaires et génétiques) la physique (recuit simulé), et aussi l'éthologie (algorithmes de colonies de fourmis).

Conclusion

Dans ce chapitre nous avons passé en revue quelques aspects théoriques sur la Recherche opérationnelle (RO), plus précisément sur l'optimisation combinatoire, ses outils de modélisation ainsi que ses méthodes de résolution

Dans le prochain chapitre, nous allons élaborer un modèle mathématique décrivant le problème qu'on a trouvé à BMT y compris les paramètres, les variables de décision, la fonction objectif et les contraintes utilisées dans notre travail.

39

4

Modélisation et résolution du problème

Introduction

Au cours des dernières années, il y a eu une attention considérable portée à la modélisation et à l'évaluation des performances des mouvements des conteneurs dans le but d'atteindre une fonctionnalité optimale. Cette attention accrue découle de la volonté de maximiser l'efficacité et l'efficience des opérations de transport et de logistique liées aux conteneurs.

Dans ce chapitre, nous décrivons le mouvement des conteneurs destinés à l'exportation à l'aide d'un modèle mathématique conçu pour aider à la prise de décision.

4.1 Les hypothèses du modèle

Lors de l'élaboration d'un modèle mathématique, il faut prendre en compte certaines d'hypothèses. Ces dernières vont être intégrées d'une façon ou d'une autre dans la modélisation. Les hypothèses qu'on a considéré sont les suivantes :

1. On s'intéresse aux opérations de chargement des conteneurs qui sont destinés à l'ex-portation (outbound),

2. Tous les conteneurs sont similaires et ont la même largeur et la même hauteur,

3. On s'intéresse aux conteneurs de 40 pieds.

4. La localisation des conteneurs est donnée,

5. Une zone d'entreposage est formée de plusieurs blocs adjacents,

6. Chaque bloc contient un seul portiques gerbeurs sur pneus (RTG),

7.

4.2 Les paramètres du modèle 40

-Page 40-

Il n'y a pas de déplacement des RTGs entre les blocs de la zone

8. On considère les mouvements simultanés des portiques de cour et des camions,

9. Les mouvements non productifs (inutiles) des conteneurs (Rehandle) sont pris en compte,

10. les baies de chaque bloc ne sont pas totalement pleins,

11. Pour chaque conteneur, on connait sa destination sur le quai (numéro de quai)

12. La vitesse des portiques de cour est de 5km/h,

13. La vitesse des camions portuaires est de 20 km/h,

14. Les conteneurs peuvent être manutentionnés dans n'importe quel ordre.

4.2 Les paramètres du modèle

4.2.1 Les ensembles

· C : Ensemble des conteneurs à récupérer pour l'exportation dans la zone d'entrepo-sage tel que C = {1,... , M} ;

· R : Ensemble des conteneurs qui se trouvent en dessus des conteneurs à récupérer tel que R = {M + 1,...,M^'};

· P : Ensemble des portiques gerbeurs sur pneus (RTG) disponibles dans la zone tel que P = {1, . . . ,N} ;

· V : Ensemble des camions portuaires (CP) disponibles dans la zone tel que V = {1,...,T};

· B : Ensemble des blocs dans la cour;

· L : Ensemble des localisations pour le stockage des conteneurs d'exportation et de livraison au client final (localisation = une adresse formée du numéro du bloc, baie, rangée et étage).

· Q; Ensemble des quais disponibles pour l'embarquement des navires porte-conteneurs. 4.2.2 Les indices et les paramètres utilisés dans le modèle:

· i, j : Indices relatifs aux conteneurs; i, j E C ;

·

4.3 Les paramètres du modèle 41

o : Indice relatif aux conteneurs; o E R;

· i = 0 : Conteneur fictif;

· p : Indice des RTGs p E P ;

· v : Indice des camions v E V ;

· q : Indice des quais; q E Q;

· b :Indice du bloc; b E B ;

· Eb : Nombre des RTGs dans un bloc b;

· li : Localisation d'un conteneur i dans la zone;

· bi : Numéro du bloc dans la zone pour un conteneur i dans une localisation li ;

· ai : Numéro de la baie dans un bloc pour un conteneur i dans une localisation li ;

· ri : Numéro de la rangée pour un conteneur i dans une localisation li ;

· ei : Numéro d'étage pour un conteneur i dans une localisation li ;

· b_o : Numéro du bloc dans la zone pour un conteneur o;

· a_o : Numéro de la baie dans un bloc pour un conteneur o;

· r_o : Numéro de la rangée pour un conteneur o;

· e_o : Numéro d'étage pour un conteneur o;

· S : Grande valeur.

· h1 : Temps de traitement d'un conteneur, c'est à dire le temps pour enlever un conteneur et le mettre dans un emplacement vide s'il s'agit d'un conteneur non désiré ou-bien le charger dans le camion s'il s'agit d'un conteneur concerné par l'exportation;

· h2 : Temps pour enlever un conteneur, le mettre dans un emplacement vide et le remettre à sa place (mouvement non productif); on suppose que h2 = 2h1 ;

· ôi : Temps pour décharger le conteneur i du camion sur le quai.

· kij : Temps de parcours d'un RTG de la zone du conteneur i vers le conteneur j avec i, j sont dans le même bloc et ai =? aj ;

· ti : Temps de transport du conteneur i par un camion, connu a priori, de sa localisation li à sa destination sur le quai;

· tvqiaj : Le temps de retour à vide du camion du quai où il a déchargé le conteneur i vers la baie où il se trouve le prochain conteneur j à transporter à son tour.

-Page 41-

4.4 Les variables de décision du modèle 42

4.3 Les variables de décision du modèle

dRTG _i: Instant de début de prélèvement du conteneur i par un RTG ;

dCP _i: Instant de départ d'un camion transportant le conteneur i ;

xijp =

{

1 si le RTG p traite le conteneur j juste après le conteneur i , 0 sinon;

yijv =

{

1 si le camion v charge le conteneur j juste après le chargement du conteneur i , 0 sinon;

wbb'p =

{

1 si le RTG p se déplace du bloc b vers le bloc b^' , 0 sinon;

mi : Temps de traitement du conteneur i par un RTG qui comprend le temps de prélèvement du conteneur (h1) et le temps pour enlever et remettre les conteneurs au-dessus (ayant le même ai et ri ; de plus ei < e_o) (h2), sachant qu'on a supposé que h2 = 2h1.

· h2

Le temps mi est calculé comme suit;

Xmi = h1 +

oER ai=ao ri=ro ei<eo

où P oER ai=ao ri=ro ei<eo

h2 est le temps non productif des portiques de cour (rehandle).

· La variable mi peut être divisée en deux parties m¹_i et m²_i qui sont respectivement le temps de manutention du conteneur i et de son chargement sur le camion, et le temps de remettre le(s) conteneur(s) qu'on a enlevé à sa (leur) place(s).

D'où mi = m¹_i + m2 i avec; m¹_i = h1 + E

oER ai=ao ri=ro ei<eo

h1 et m²_i = E h2

oER ai=ao ri=ro ei<eo

-Page 42-

4.4 Formulation mathématique 43

4.4 Formulation mathématique

4.4.1 L'objectif

Dans la fonction objectif, on cherche à minimiser le temps de départ du camion CP transportant le conteneur i. En d'autres termes, le but est de minimiser le temps de complétion des opérations de chargement des conteneurs destinés à l'exportation :

Minimiser {max i?C

dCP i },

4.4.2 Les contraintes

1. Chaque conteneur est affecté à un seul portique de cour (le RTG p) :

_XM i=0

_XN p=1

xijp = 1; Vj E C

_M' N

_X xiop = 1; Vo E R
o=0 p=1

2. _XM T i=0 v=1

-Page 43-

Chaque conteneur est affecté à un seul camion portuaire (le CP v) :

yijv = 1; Vj E C, i =? j

3. Chaque RTG p traite un seul conteneur à la fois :

M' X jo=1

x0op = 1; Vp E P

M' X o=1

x0op = 1; Vp E P

4. Chaque camion portuaire v transporte un seul conteneur à la fois :

_XM y0jv = 1; Vv E V

j=1

4.4 Formulation mathématique 44

5. Contrainte de conservation des flux de conteneurs pour les RTGs

XM j=0

xijp =

XM j=0

xjip; i E C,p E P,i =? j

6. Contrainte de conservation des flux de conteneurs pour les camions

XM j=0

xijv =

XM j=0

xjiv; i E C, v E V, i =? j

7. -Page 44-

Contrainte de définir le temps de manutention du conteneur i et de son chargement sur le camion :

Xm1 i = h1 + o?R ai=ao ri=ro ei<eo

h1; i E C

8. Contrainte de définir le temps de remise en place des conteneurs déjà enlevés :

Xm2 i = o?R ai=ao ri=ro ei<eo

h1; i E C

9. Assurer l'ordre de traitement des conteneurs par chaque RTG. Si un RTG p traite le conteneur j juste après le conteneur i avec bi = bj et ai =? aj alors le RTG p va prendre un temps de déplacement _kij pour charger le conteneur j suivant :

_dRTG

j > dRTG

i + (m¹_i + m²_i) + kij + S(xijp - 1); i E C, j E C,bi = bj,p E P

10. Garantir l'ordre d'enchaînement des conteneurs par camion. En d'autres termes, si un camion transporte les conteneurs i et j, cette contrainte garantit que le conteneur i sera transporté avant le conteneur j :

_dCP

j > dCP

i + ti + ôi + tvqiaj + S(yijv - 1); i E C, j E C, v E V

11. Déterminer la séquence de traitement des conteneurs par camion et par RTG :

dCP _i> dRTG i +m¹_i ; i E C

4.5 Formulation mathématique 45

12. Garantir qu'il n'y ait qu'un seul RTG dans un même bloc:

Eb + > _>N wbb^'p = 1; b E B,p E P

b^'?B p=1

13. Pas de déplacement d'un RTG du bloc b vers le bloc b^' :

>

b?B

>

b^'?B

wbb^'p = 0; p E P

14. Les domaines de définition des variables de décision sont donnés comme suit:

_dRT G

i , dCP

i , m1 i , m2 i ~ 0

xijm, yijp, wij E {0, 1}

-Page 45-

4.5 Le modèle mathématique 46

4.5 Le modèle mathématique

Minimiser {max iEC

dCP i }, (4.1)

sous contraintes :

_XN p=1

_XM i=0

xijp = 1; Vj E C,i =? j (4.2)

xiop = 1; Vo E R (4.3)

_M'

_XN p=1

_X

o=0

_XT v=1

_XM i=0

yijv = 1; Vj E C,i =? j (4.4)

_XM j=1

_M'

_X

o=1

x0jp = 1; Vp E P (4.5)

x0op = 1; VpEP (4.6)

_XM y0jv = 1; Vv E V (4.7)

j=1

XM j=0	xijp =	XM j=0		xjip; i E C, p E P, i =? j (4.8)
XM j=0	xijv =		XM j=0		xjiv; i E C, v E V, i =? j (4.9)

Eb + _X N wbb^'p = 1; b E B, p E P (4.15)

b^'EB p=1

Xm1i = h1 + oER ai=ao ri=ro ei<eo		h1; i E C (4.10)
Xm2 i =	h1; i E C (4.11)

oER ai=ao ri=ro ei<eo

dRTG _j> d^RTG _i+ (m¹_i + m²_i) + kij + S(xijp - 1); i E C, j E C, bi = bj, p E P (4.12)

_dCP

j > dCP

i + ti + ôi + tvqiaj + S(yijv - 1); i E C,j E C,v E V (4.13)

dCP _i> d^RTG _i+ m¹_i ; i E C (4.14)

-Page 46-

4.7 Exemple numérique 47

_>2

b?B

_>2

b^'?B

-Page 47-

4.7 Exemple numérique 48

4.8 Implémentation et résolution du problème 49

wbb^'p = 0; p E P (4.16)

_dRT G i , dCP

i , m1 i , m2 i = 0 (4.17)

xijp, yijv, wbb'p E {0, 1} (4.18)

4.6 Complexité du problème

Puisque notre modèle mathématique est un programme linéaire mixte (PLM) qui combine à la fois des variables continues et des variables binaires, La présence de ces dernières rend généralement le problème plus complexe à résoudre que les problèmes linéaires purement continus.

4.7 Exemple numérique

Pour illustrer notre modèle, nous proposons un exemple à résoudre manuellement. On suppose qu'il s'agit de :

· 2 blocs, tels que chaque bloc contient 3 baies, 2 rangées, et 2 étages;

· 2 portiques de cour: RTG1 pour le bloc 1 et RTG2 pour le bloc 2,

· 3 camions portuaire disponibles dans la zone de stockage : CP1, CP2, et CP3,

· 6 conteneurs concernés par l'exportation, sont distribués dans les deux blocs avec la couleur bleu. Les conteneurs en couleur rouge ne sont pas concernés par la récupération,

· 1 quai pour l'embarquement du navire. On résume ces données dans le tableau suivant:

Paramètres		Valeurs	Nombre total de conteneurs concernés par l'exportation
6		Nombre total des RTGs
2		Nombre total des camions
3		nombre de baies par bloc
3		Nombre de rangées par bloc
2		Nombre d'étages
2		Nombre de quais
1

TABLE 4.1 - Données d'ordre général.

-Page 48-

Le temps de manutention des RTGs est représenté dans le tableau suivant:

Paramètres		Valeurs (en sec)	Temps de prélèvement d'un conteneur (h1)
180		Temps pour enlever un conteneur et le remettre à sa place (h2)
360

TABLE 4.2 - Le temps de manutention des RTGs.

Matrice de temps de parcours d'un RTG du conteneur i vers le conteneur j :

kij =

?1 2 3 4 5 ?6

1	2	3	4	5		6	0
30	60	0	0	0 ? ?		30
0	30	0	0	0 ? ?		60
30	0	0	0	? ? ? 0		0
0	0	0	30	? ? ? 60		0
0	0	30	0	? ? ? 30		0
0	0	60	30	0 ?

Le temps de transport ti vers la destination sur le quai des conteneurs est représenté dans le tableau ci-dessous:

Conteneur Ci	C1		C3	C4	C5		C6	Temps de transport (en sec)
120	130	140	200	210	220

TABLE 4.3 - Le temps de transport ti vers la destination sur le quai des conteneurs.

Le temps de déchargement d'un conteneur : ôi = 3min

Le temps de retour à vide des camions (tv_qa) du quai q vers différentes baies est représenté dans le tableau ci-dessous :

Quai q	Baie a		tvqa (en sec)	1
a	120		1
a2	130		1
a3	140		1
a4	200		1
a5	210		1
a6	220

TABLE 4.4 - Le temps de transport à vide _tvqa des camions du quai vers différentes baies

-Page 49-

La localisation de chaque conteneur est comme suit:

C1 :{bloc 1, baie 1, rangée 1, étage 1}

:{bloc 1, baie 2, rangée 2, étage 1}

C3 :{bloc 1, baie3, rangée 1, étage 1}

C4 :{bloc 2, baie 1, rangée 2, étage 1}

C5 :{bloc 2, baie 2, rangée 1, étage 1}

C6 :{bloc 2, baie 3, rangée 2, étage 1}

Les localisations des conteneurs sont représentées dans la table (4.5), il s'agit ici de la partie de stockage des conteneurs : la zone d'entreposage.

Baie ???????????? Rangée	a1	a2		a3	Rangée 2
				Rangée 1
C1		C3

bloc 1

Baie ???????????? Rangée	a4	a5		a6	Rangée 2
C4		C6
	C5

bloc 2

TABLE 4.5 - Les localisations des conteneurs dans la zone de stockage.

Les RTGs se positionnent dans l'un des baies de chaque bloc car il n'y a pas d'ordre de priorité entre les conteneurs.

La valeur maximale atteinte est : dCP3

6 = 1500s = 25min. D'où la valeur optimale est :

Z* = 1500s = 25min

4.8 Implémentation et résolution du problème

Dans cette section, nous allons implémenter notre modèle sous le logiciel AMPL afin de résoudre l'exemple précédent sur machine.

4.8 Implémentation et résolution du problème 50

-Page 50-

Conteneur (i)	dRT G i		dCP i	1
dRTG1 1= 0s	d^CP1 1= dRTG1 1+p11 = 0 + 360 = 360s		2
dRTG1 = dRT G1 2 1 + p1 1 + p2 1 + k12 = 0 + 360 + 180 + 30 = 570s	dCP3 2 = dRTG1 2 + p1 2 = 570 + 360 = 930s		3
d3TG1 = dF^G1 + p^12 + p^22 + k23 = 570 + 360 + 180 + 30 = 1140s	d°^P2 = 4'P2 +t4+ô4+tvq4a3 = 360+ 180 + 180 + 140 = 860s dCP2 3= dRTG1 3+ p^1 3= 1140 + 360 = 1500s		4
dRT G2 4 = 0s	dCP2 4 = dRTG2 4 + p^14 = 0 + 360 = 360s		5
d5 TG2 = dRTG2 + p^14 + p^24 + k45 = 0 + 360 + 180 + 30 = 570s	d5 P1 = dCP1 +t1+ô1+tvq1a5 = 360+ 120 + 180 + 190 = 850s dCP1 5 = dRTG2 5 + p^12 = 570 + 360 = 930s		6
d6TG2 = dp^G2 + p^15 + p^25 + k56 = 570 + 360 + 180 + 30 = 1140s	dg P3 = 4P3 +t2+ô2+tvq2a6 = 930+ 130 + 180 + 240 = 1480s dCP3 6 = dRT G2 6 + p^16 = 1140 + 360 = 1500s

4.8.1 Description de l'outil informatique

L'implémentation et la résolution du problème ont été effectuées sur un PC doté d'un processeur Intel(R) Core(TM) i3-4030U CPU 1.90 GHz et de 4 GB de RAM, en utilisant le langage de programmation mathématique AMPL avec le solveur d'optimisation CPLEX.

4.8.2 Rapport de la solution

4.8 Implémentation et résolution du problème 51

dRT3 [f] := d P [:K]

1 114e 1 : see

2 570 2 93e

3 a 3 360

4 114e 4 1508

5 578 5 930

6 6 908

ni	[x] :=	ml	[: ]	·		J m2	1
54e	1	360		1		2
54e	2	360		2		3
540	3	360		3		4
540	4	360		4		5
540	5	360		5		6
540	6	360		6

[^*1

180

180 180 180 180 180

·

·

._

-Page 51-

	[*,:,1]											[^*,^*,^21
	0	1	2	3	4	5	6					0	1	2	3	4	5	6
	0.	0	0	0	0	0	1		0				0	0	1	0	0	0
1	0.		0	0	0	0	0		1			1		0	0	0	0	0
									2			0	1		0	0	0	0
2	0	0.		0	0	0	0		3			0	0	1		0	0	0
3	0	0	0.		0	0	0		4			0	0	0	0		00
4	1	0	0	0.		0	0		5			0	0	0	0	0.		0
5	0	0	0	0	1.		0		6			0	0	0	0	0	0
6	0	0	0	0	0	1
								:		=
1								1		1
1								1		2
1								^2			1
								122
2								1		1	O
2								1		2	0
--								2		1	et
								222

4.8 Implémentation et résolution du problème 52

4.8.3 Interprétation des résultats

L'application du modèle montre que dans un premier temps les mouvements improductifs des conteneurs influencent considérablement sur le temps de manutention des conteneurs à récupérer. Dans un deuxième temps, le nombre des camions disponibles joue un rôle important dans les opérations de manutention. Enfin, l'ordre de traitement des conteneurs à récupérer n'a pas d'impact sur le temps total de complétion.

Conclusion

Dans ce chapitre, nous avons développé en premier lieu un modèle mathématique du problème qu'on a étudié où on a intégré les hypothèses du problème ainsi que les objectifs à atteindre. En deuxième lieu, nous avons résolu un exemple numérique manuellement pour bien comprendre le fonctionnement de notre modèle, ensuite nous l'avons résolu avec le logiciel AMPL après avoir implémenté le modèle élaboré.

-Page 52-

Conclusion générale

53

Depuis l'introduction des premiers conteneurs au début des années 1960, les techniques et stratégies de manutention des conteneurs ont toujours été des facteurs clés pour mesurer l'efficacité des grands ports. Cependant, en raison de la croissance des porte conteneurs ces dernières années, chaque fois que l'un de ces navires accoste dans un port, un certain nombre de conteneurs qui auraient été impensables il y a quelque temps doivent être manutentionnés en quelques heures seulement. Cela pose un sérieux défi aux opérateurs de terminaux à conteneurs, car le volume de trafic a augmenté de façon exponentielle alors que la surface disponible pour gérer ce trafic est restée pratiquement inchangée. Par conséquent, les techniques d'optimisation de la manutention et de la remanipulation des conteneurs acquièrent un rôle de premier plan dans la promotion de l'efficacité de l'exploitation des terminaux à conteneurs [5].

Notre projet de fin d'étude se concentre sur les problèmes d'optimisation liés à la gestion de mouvement des conteneurs chez le terminal maritime BMT. On a présenté dans le premier chapitre une description de ce dernier, le second chapitre fût consacré à une récapitulation des travaux dans la littérature portant sur le problème d'optimisation dans le cadre des terminaux à conteneurs. Dans le troisième chapitre, nous avons donné quelques notions d'optimisation combinatoire. Après avoir effectué un diagnostic détaillé du fonctionnement de l'entreprise tant au niveau administratif qu'opérationnel pendant notre stage, nous avons modélisé mathématiquement le problème de mouvement des conteneurs destinés à l'expor-tation, ensuite nous avons illustré ce modèle avec deux exemples numériques, puis nous avons implémenté le modèle et les deux exemples à l'aide du langage AMPL en utilisant le solveur d'optimisation CPLEX afin de les résoudre, c'est l'objet de quatrième et dernier chapitre.

Conclusion générale 54

Perspectives

Cependant, ce modeste travail constitue les bases d'un travail à poursuivre et à améliorer pour une étude beaucoup plus approfondie qui pourra faire l'objet de plusieurs projets de master et de thèses de doctorat.

En s'inspirant de ce sujet, plusieurs travaux futurs peuvent être développés et plusieurs problématiques peuvent se poser:

· À partir du modèle mathématique élaboré, une nouvelle modélisation est possible pour combiner les différentes opérations de manutention des autres équipements simultanément afin de minimiser le temps de complétion pour le traitement des conteneurs destinés à l'exportation.

· L'analyse des données historiques et l'utilisation de techniques d'apprentissage automatique peuvent contribuer à une meilleure compréhension des schémas de mouvement des conteneurs, permettant ainsi une planification plus précise et une prise de décision éclairée.

· Il est également primordial d'étudier l'effet de la conception de la zone de stockage (nombre de blocs, nombre des baies, etc.) sur le temps de complétion. Il s'agit de garder le même objectif de notre travail, en variant à chaque fois le nombre de blocs, le nombre de baies, le nombre de portiques de cour et de camions afin de trouver la conception optimale de la zone de stockage.

-Page 54-

Annexe

55

1. Présentation de AMPL

AMPL signifie «A Mathematical Programming Language», est un langage de modélisation algébrique pour modéliser et résoudre des problèmes d'optimisation. Il fournit un ensemble de syntaxes et de commandes spécifiques qui permettent de décrire efficacement les modèles mathématiques et de les résoudre à l'aide de solveurs d'optimisation. Il a été développé par Robert Fourer, David Gay et Brian Kernighan des laboratoires Bell.

1.1 Historique

Année	Étape
1985	Conception et mise en oeuvre d'AMPL
1991	AMPL prend en charge la programmation non linéaire
1995	Extensions pour représenter des structures linéaires et des réseaux
1995	Construction de scripts
1997	Amélioration de la prise en charge des solveurs non linéaires
2002	Soutien à la programmation par contraintes
2003	Création de la société AMPL Optimization LLC
2012	Les développeurs ont reçu le prix INFORMS Impact en tant qu'initiateurs d'un des langages de modélisation algébrique les plus importants
2013	Un nouvel environnement de développement intégré multiplateforme pour AMPL

TABLE 6 - Tableau des faits saillants d'AMPL.

Annexe 56

-Page 56-

1.2 Caractéristiques

1. Syntaxe intuitive: AMPL utilise une syntaxe claire et intuitive, basée sur des expressions mathématiques et des déclarations logiques, ce qui facilite la formulation des modèles d'optimisation. Le code AMPL ressemble souvent à une représentation naturelle du problème réel.

2. Déclaration des ensembles: AMPL permet de déclarer des ensembles pour représenter les données du problème. Par exemple, vous pouvez définir des ensembles pour les produits, les clients, les emplacements, etc. Ces ensembles peuvent être indexés et utilisés pour définir les variables et les contraintes du modèle.

3. Variables et paramètres: AMPL permet de déclarer des variables, qui représentent les quantités à optimiser, ainsi que des paramètres, qui représentent les données constantes du modèle. Les variables peuvent être continues ou discrètes, et les paramètres peuvent être scalaires ou tableaux.

4. Contraintes: AMPL permet de définir facilement des contraintes qui régissent les relations entre les variables. Vous pouvez exprimer des contraintes linéaires et non linéaires à l'aide d'opérateurs mathématiques standard.

5. Objectifs: Vous pouvez définir un objectif à optimiser, qu'il s'agisse de maximiser ou de minimiser une certaine fonction. L'objectif peut être une combinaison linéaire des variables du modèle ou une fonction non linéaire.

6. Solveurs d'optimisation: AMPL est compatible avec différents solveurs d'optimisation, tels que CPLEX, Gurobi, IPOPT, etc. Vous pouvez spécifier le solveur souhaité dans votre modèle AMPL et exécuter la résolution pour obtenir une solution optimale.

7. Interface utilisateur: AMPL fournit une interface utilisateur interactive en ligne de commande, où vous pouvez charger, résoudre et analyser vos modèles. Il existe également des interfaces graphiques et des intégrations avec d'autres langages de programmation, tels que Python, pour faciliter l'utilisation d'AMPL dans des flux de travail plus complexes.

8. Analyse des résultats: Une fois le modèle résolu, AMPL permet d'accéder facilement aux résultats, tels que les valeurs des variables, les valeurs des contraintes, les coûts réduits, etc. Vous pouvez utiliser ces informations pour analyser la solution et prendre des décisions éclairées.

Annexe 57

-Page 57-

1.3 Éléments de base

1. Le langage de programmation AMPL est capable de gérer différents types de variables tels que les variables entières (integer), les variables binaires (binary), les variables continues,

2. Les variables de décision sont déclarées à l'aide du mot clé "var" suivi de leur nom et leur type,

3. Pour définir les ensembles il faut utiliser le mot clé "set",

4. Pour déclarer les paramètres il faut utiliser le mot clé "param",

5. La fonction objectif est précédée du mot clé "minimize" ou "maximize" selon l'objectif d'optimisation suivi de son nom,

6. Chaque contrainte est précédée du mot clé "subject to", suivi de son nom et son indice entre deux accolades,

7. Les principaux opérateurs numériques et logiques tels que l'addition (+), la soustraction (-), la multiplication (*), la division (/), la division entière (div) et le modulo (mod) sont pris en charge, de même que les comparaisons (<=, >= et =),

8. Les commentaires peuvent être encadrés de /* ... */ ou précédés de # sur une seule ligne.

9. Toutes les commandes AMPL se terminent par ";" ,

10. Pour réinitialiser ampl (lorsque vous rencontrez des erreurs) il faut utiliser la commande

"reset",

11. Pour résoudre le modèle il faut d'abord spécifier le solveur d'optimisation avec le mot clé "option" suivi de mot "solver" et le nom de solveur, par exemple : option solver cplex; ensuite il faut utiliser la commande "solve".

12. Pour afficher les résultats du modèle ainsi que les valeurs des variables et les valeurs des contraintes il faut utiliser la commande "display".

1.4 Structure d'un projet AMPL

Un projet AMPL est généralement constitué de 3 types de fichiers:

· Un ou plusieurs fichiers de modèles (.mod),

·

Annexe 58

-Page 58-

Un ou plusieurs fichiers de données (.dat),

· Un ou plusieurs fichiers facultatifs de l'exécution (.run),

Les sections suivantes présentent ces différents fichiers dans l'ordre ci-dessus: 1.4.1 Les fichiers modèle

Les fichiers modèle (.mod) sont le coeur d'AMPL. C'est dans un fichier modèle qu'on indique les constantes, les variables de décision, les contraintes, la fonction objectif d'un problème d'optimisation, et le solveur choisi. Ils sont composés des commandes suivantes: "set","param","var","minimize", et "subject to".

1.4.2 Les fichiers de données

Les fichiers de données (.dat) sont les fichiers dans lesquels on définit les valeurs numériques ou les données du cas d'étude. Ils sont composés des commandes suivantes : "set", et "param" suivis de " :=".

1.4.3 Les fichiers d'exécution

Les fichiers d'exécution (.run) sont les fichiers dans lesquels on définit le problème à résoudre (en faisant notamment appel à un fichier .mod avec la commande "model" et un fichier .dat avec la commande "data"), et qui est exécuté par AMPL en faisant un clic droit, et en choisissant l'option "Send To AMPL". On peut également afficher les valeurs de variables et de contraintes avec la commande "display"

1.5 Solveur CPLEX

CPLEX est l'un des solveurs d'optimisation les plus puissants et largement utilisés qui est pris en charge par AMPL. Il est développé par IBM (International Business Machines Corporation) et est réputé pour sa capacité à résoudre des problèmes d'optimisation linéaire, quadratique, mixte entier et non linéaire.

Voici quelques points clés sur le solveur CPLEX dans AMPL :

1. Performances élevées: CPLEX est reconnu pour sa performance et son efficacité dans la résolution de problèmes d'optimisation complexes. Il utilise des algorithmes avancés, tels que le simplex primal-dual, l'algorithme du point intérieur et la recherche locale, pour trouver des solutions optimales ou de très bonne qualité.

2.

Annexe 59

-Page 59-

Modélisation étendue: CPLEX dans AMPL prend en charge une large gamme de problèmes d'optimisation, y compris les problèmes linéaires, quadratiques, non linéaires, mixtes entiers et continus. Vous pouvez formuler vos modèles dans AMPL et les résoudre avec CPLEX sans avoir à effectuer des modifications substantielles du code.

3. Options de résolution personnalisées: CPLEX offre une gamme d'options de résolution personnalisables pour répondre aux besoins spécifiques des problèmes. Vous pouvez ajuster les paramètres du solveur pour influencer le comportement de la résolution, tels que la limite de temps, la précision de la solution, les stratégies de coupes, etc.

4. Heuristiques et coupes: CPLEX utilise des heuristiques et des coupes pour améliorer l'efficacité de la résolution. Les heuristiques sont des méthodes de recherche intelligente qui permettent de trouver rapidement des solutions de bonne qualité, tandis que les coupes sont des inégalités valides qui réduisent l'espace de recherche et accélèrent la convergence.

5. Capacité de gestion des contraintes et des variables: CPLEX peut gérer des modèles avec un grand nombre de contraintes et de variables. Il est capable de détecter les contraintes redondantes, les variables non utilisées et d'exploiter la structure spécifique du modèle pour améliorer les performances de résolution.

6. Rapports et diagnostics: Une fois la résolution terminée, CPLEX fournit des rapports détaillés sur le processus de résolution, tels que le nombre d'itérations, les temps d'exécution, les coupes appliquées, etc. Ces informations peuvent être utilisées pour analyser la performance du modèle et identifier des opportunités d'amélioration.

7. Intégration avec AMPL : CPLEX est intégré à l'environnement AMPL, ce qui facilite l'utilisation conjointe de ces deux outils. Vous pouvez charger votre modèle AMPL dans CPLEX, spécifier les options de résolution et obtenir les résultats de la résolution dans AMPL pour une analyse et une utilisation ultérieures.

1.5 Étapes de création du projet

1. Tout d'abord il faut créer un projet AMPL dans lequel on pourra définir notre mo-dèle.Pour cela dans AMPL IDE il faut cliquer sur File ? New ? File. La figure (5) montre cette étape:

Annexe 60

FIGURE 5 - Schéma de modèle

2. Une fenêtre s'ouvre : entrez un nom de fichier, choisissez son emplacement (dossier parent) et le type de fichier (.mod pour la rédaction du modèle, ensuite vous répétez les mêmes étapes pour le fichier .dat et le fichier .run). La figure ci-dessus illustre cette étape:

-Page 60-

FIGURE 6 - Nouvel assistant de fichier

Bibliographie

[1]

61

J. AH-PINE, «Introduction à AMPL,» Support de cours en Master 1 Informatique, Université Lumière-Lyon 2, 2016.

[2] Z. AOUDIA, «Optimisation Combinatoire,» Support de cours en Licence 3 RO, Université Abderrahmane Mira - Béjaia, 2020.

[3] «BMT Support Web.» (Avril 2023), adresse : https://bejaiamed.cm/.

[4] J. X. CAO, D.-H. LEE, J. H. CHEN et Q. SHI, «The integrated yard truck and yard crane scheduling problem : Benders decomposition-based methods,» Transportation Research Part E : Logistics and Transportation Review, t. 46, n^o 3, p. 344-353, 2010.

[5] M. CASERTA, S. SCHWARZE et S. VOSS, «Container rehandling at maritime container terminals,» Handbook of terminal planning, p. 247-269, 2011.

[6] K. CHEBLI, «Optimisation des Mouvements des Conteneurs dans un Terminal Maritime,» Thèse de Doctorat, Ecole Polytechnique, Montréal (Canada), 2011.

[7] Y. CHIROUAL et R. HADDOUCHE, «Optimisation Des Temps De Manutention Au Niveau De BMT.,» Mémoire de Master, Université Abderrahmane Mira - Bejaia, 2022.

[8] P. CHRÉTIENNE, «Algorithmes Branch and Bound,» Support de cours en Master 1 Informatique, Université Pierre et Marie-Curie - Paris 6, 2009.

[9] D. DAI et R. FERTAS, «Modélisation Et Optimisation Du Temps De Manutention Au Niveau De Bmt.,» Mémoire de Master, Université Abderrahmane Mira - Bejaia, 2017.

[10] S. M. DOUIRI, S. ELBERNOUSSI et H. LAKHBAB, «Méthodes de Résolution Exactes Heuristiques et Métaheuristiques,» Support de cours en Master Codes, Cryptographie et Sécurité de l'information, Universite mohammed 5, rabat., 2008.

[11]

BIBLIOGRAPHIE 62

-Page 62-

K. HALIMI, H. DKHIL, R. MCHICH et A. YASSINE, «Modélisation en aide à la décision pour une gestion optimale de stockage dans les terminaux à conteneurs,» Revue Marocaine de Management, Logistique et Transport, n^o 3, 2018.

[12] A. IMAI, K. SASAKI, E. NISHIMURA et S. PAPADIMITRIOU, «Multi-objective simultaneous stowage and load planning for a container ship with container rehandle in yard stacks,» European Journal of Operational Research, t. 171, n^o 2, p. 373-389, 2006.

[13] M. L. KHAIROUNE, «Problème De Stockage Des Conteneurs,» Mémoire de Master, Université Abderrahmane Mira - Bejaia, 2019.

[14] L. KHERBOUCHE et Z. OUBAHRI, «Quelques Méthodes De Résolution En Optimisation Combinatoire,» Mémoire de Master, Université Mouloud Mammeri - Tizi Ouzou, 2017.

[15] K. H. KIM, «Evaluation of the number of rehandles in container yards,» Computers and Industrial Engineering, t. 32, n^o 4, p. 701-711, 1997.

[16] O. KONÉ, «Nouvelles Approches pour la Résolution du Problème d'Ordonnancement de Projet à Moyens Limités,» Thèse de Doctorat, Université Paul Sabatier-Toulouse III, 2009.

[17] Y. LEE et N.-Y. HSU, «An optimization model for the container pre-marshalling problem,» Computers and Operations Research, t. 34, n^o 11, p. 3295-3313, 2007.

[18] Y. LEE et Y.-J. LEE, «A heuristic for retrieving containers from a yard,» Computers and Operations Research, t. 37, n^o 6, p. 1139-1147, 2010.

[19] N. MAHFOUF et B. RAMDANI, «Planification Et Ordonnancement D'un Projet A Moyens Limités Au Sein De L'engtp,» Mémoire de Master, Université M'hamed Bougara - Bou-merdes, 2017.

[20] C. PARREÑO-TORRES, R. ALVAREZ-VALDES et R. RUIZ, «Integer programming models for the pre-marshalling problem,» European Journal of Operational Research, t. 274, no 1, p. 142-154, 2019.

[21] T. ÜNLÜYURT et C. AYDIN, «Improved Rehandling Strategies for the Container Retrieval Process,» Journal of Advanced Transportation, t. 46, p. 378-393, 2012.

[22] Z. WEIYING, L. YAN et J. ZHUOSHANG, «Optimization model of containers loading operation in export containers terminal,» WUHAN LIGONG DAXUE XUEBAO JIAOTONG KEXUE YU GIONGCHENG BAN, t. 30, n^o 2, p. 314, 2006.

BIBLIOGRAPHIE 63

[23] «ÉTUDE SUR LES TRANSPORTS MARITIMES,» CONFÉRENCE DES NATIONS UNIES SUR LE COMMERCE ET LE DÉVELOPPEMENT, t. 33, p. 3, 2022.

-Page 63-

Key words : Maritime terminal, Unproductive movements, Container handling, AMPL language, CPLEX optimization solver

Résumé

L'objet du présent mémoire consiste à modéliser et optimiser les mouvements des conteneurs dans un terminal maritime. La gestion des conteneurs dans ces terminaux peut être complexe en raison du grand nombre de mouvements impliqués notamment les mouvements improductifs.

Dans ce mémoire, nous proposons une approche de modélisation qui permet de représenter une sorte de planification et de synchronisation des opérations de manutention des conteneurs par deux équipements importants dans la partie terrestre du terminal; à savoir les portiques de cour (RTGs) et les véhicules internes de transport (Camions Portuaires), tout en tenant compte des mouvements de remanutention des conteneurs par les RTGs (Rehandle).

En outre, nous nous intéressons à la résolution de ce problème à l'aide du langage AMPL en utilisant le solveur d'optimisation CPLEX, dans le but de minimiser le temps de complétion des opérations de manutention des conteneurs destinés à l'exportation.

Mots clés : Terminal maritime, Mouvements improductifs, Manutention des conteneurs, Langage AMPL, Solveur d'optimisation CPLEX

Abstract

The aim of this dissertation is to model and optimize container movements in a maritime terminal. Container management in these terminals can be complex due to the large number of movements involved, particularly unproductive movements.

In this dissertation, we propose a modeling approach that allows for a kind of planning and synchronization of container handling operations by two important equipment in the land-side of the terminal : Rubber-Tired Gantry Cranes (RTGs) and Internal Transport Vehicles (Port Trucks), while considering the rehandling movements of containers by RTGs.

Furthermore, we focus on solving this problem using the AMPL language and the CPLEX optimization solver, with the objective of minimizing the completion time of container handling operations for export.