|
INSTITUT DE FINANCEMENT DU DÉVELOPPEMENT DU MAGHREB
ARABE

Institut de Financement
du Développement du Maghreb Arabe
41 PROMOTION BANQUE
ème -
Décembre 2023
Mémoire de fin d'Etudes
|
Intuition des décideurs : Stress test
inversé sur
le risque du crédit de la BFPME
|
Présenté et soutenu par :
Encadré par :

Thème :
GHADHAB Wassim Mr. NAOUI Kamel
Etudiant(e) parrainé(e) par :
Banque de Financement des Petites et Moyennes
Entreprises

REMERCIEMENTS
Je tiens à exprimer mes sincères
remerciements à tous ceux qui ont contribué à
la
réalisation de notre mémoire, en particulier à mon
encadrant, M. NAOUI
Kamel, pour sa disponibilité et ses
précieux conseils. Je souhaite également
exprimer ma gratitude
envers l'ensemble du personnel de la BFPME,
notamment M. HASSINE Wajih et M.
KSIAA Hamdi, pour leur précieuse
assistance et leur sérieux.
Nous souhaitons adresser nos chaleureux
remerciements à toutes les
personnes qui, de près ou de loin, ont contribué
à
l'élaboration de ce travail.
II
DEDICACES
Je dédie ce travail à :
Mes chers parents, que nulle dédicace ne puisse
exprimer mes sincères sentiments.
Leur patience illimitée,
leur encouragement constant, leur inestimable aide,
témoignent de mon
profond amour et respect pour leurs grands sacrifices.
Mes chers frères, qui ont toujours été
présents avec leur soutien infaillible et leurs
encouragements constants.
Mes aimables amis et collègues
d'étude.
III
RESUME
L'objectif de notre travail est d'appliquer le stress test
inversé sur le risque de crédit afin d'évaluer l'impact
des décisions prises par les responsables sur le niveau des prêts
non performants. Pour ce faire, nous avons suivi une approche en deux
étapes : tout d'abord, une approche descriptive pour présenter
les bases théoriques du risque de crédit et du stress test, puis
une approche empirique. Dans cette approche empirique, nous avons
critiqué le modèle VECM et construit un modèle BSVAR de
risque de crédit plus complet. Enfin, nous avons adopté une
démarche analytique pour évaluer la capacité de la banque
après l'application des scénarios construits.
Les résultats de notre étude empirique indiquent
une précision significative du modèle BSVAR par rapport au
modèle VECM en termes de prévisions. Cela démontre
l'importance de l'intégration de la matrice des effets
instantanés et de la distribution à priori, qui enrichit le
modèle en termes d'informations. La conception de la distribution
à priori nous a conduit à la construction des scénarios
qui décrivent la réaction des décideurs de la BFPME face
à l'arrivée de nouvelles informations. L'analyse des
résultats du stress test inversé dans le cas du choc
extrême nous indique que vers la fin de l'année 2025, tous les
prêts accordés seront non performants. Cependant, sur la base de
l'analyse des niveaux des hyperparamètres, nous avons pu décrire
cette intuition et formuler des recommandations.
Les mots clés : stress test
inversé, modèle VECM, modèle BSVAR, distribution à
priori, Statistique bayésienne, Matrice d'identification,
scénarios.
ABSTRACT
The objective of our work is to apply the reverse stress test
on credit risk to evaluate the impact of decisions made by the managers on the
level of non-performing loans. To achieve this, we followed a two-step
approach: firstly, a descriptive approach to present the theoretical
foundations of credit risk and stress testing, and then an empirical approach.
In this empirical approach, we criticized the VECM model and built a more
comprehensive BSVAR model of credit risk. Finally, we adopted an analytical
approach to assess the bank's capacity after the application of the constructed
scenarios.
The results of our empirical study indicate a significant
accuracy of the BSVAR model compared to the VECM model in terms of forecasts.
This demonstrates the importance of integrating the matrix of instantaneous
effects and à priori distribution, which enriches the model in terms of
information. The design of the à priori distribution led us to construct
scenarios that describe the reaction of BFPME decision-makers to the arrival of
new information. The analysis of the results of the reverse stress test in the
case of an extreme shock indicates that by the end of 2025, all granted loans
will be non-performing. However, based on the analysis of hyperparameter
levels, we were able to describe this intuition and formulate
recommendations.
Keywords : reverse stress test, VECM model, BSVAR model,
à priori distribution, Bayesian statistics, identification matrix,
scenarios.
iv
SOMMAIRE
INTRODUCTION GENERALE ..1
CHAPITRE 1 : GENERALITE SUR LE RISQUE DU CREDIT 3
Introduction 4
Section 1 : Catégorisation des risques dans le secteur
bancaire et analyse du risque de crédit 5
Section 2 : Les déterminants du risque de crédit
11
Section 3 : La réglementation du risque de
crédit 16
Conclusion 24
CHAPITRE 2 : LE STRESS TEST ET GESTION DES RISQUES ..25
Introduction 26
Section 1 : Introduction aux Stress Tests 27
Section 2 : Classification, méthodologies et
modèles de stress tests 32
Section 3 : Mise en place des stress tests : procédures
et démarches 38
Conclusion 43
CHAPITRE 3 : APPLICATION DU STRESS TEST DE RISQUE DE CREDIT
.44
Introduction 45
Section 1 : Présentation et organisation de la BFPME
46
Section 2 : Modélisation du risque de crédit
48
Section 3 : Application du stress test sur le risque de
crédit 67
Conclusion 75
CONCLUSION GENERALE 76
V
LISTE DES ABREVIATIONS
BCT Banque Centrale Tunisienne
BFPME Banque de Financement des Petites et
Moyennes Entreprises
BRI Banque des règlements
internationaux
BSIF Bureau du surintendant des institutions
financières
BSVAR Vectorielle Autorégressive
Structurelle Bayésienne
BU Bottom-up
CEBS Comité européen des
contrôleurs bancaires
DM Test de Diebold-Mariano
EQMP Erreur Quadratique Moyenne de
Prévision
FMI Fonds monétaire international
FSAP Financial Sector Assessment Program
HLN Test de la dominance de
prévision
IPC Indice des Prix à la
Consommation
IPI Indice des Prix Industrielle
LGD Perte en cas de défaut
LogMDD Logarithme de la densité
marginale
MAE Erreur absolue moyenne
NPL Prêts non performants
OCDE Organisation de coopération et de
développement économiques
PCC Provisions sur créances
classées
PD Probabilité de défaut
PIB Produit intérieure brute
RMSE Racine carrée de l'erreur
quadratique moyenne
ROA Ratio de rentabilité des actifs
(Return on assets)
ROE Ratio de rentabilité des capitaux
propres (Return on equity)
SCAP Supervisory Capital Assessment
Program
SVAR Structurelle Vectorielle
Autorégressive
TD Top-down
TMM Taux du Marché Monétaire
UE Union européenne
USD Taux de change USD/TND
VaR Value at Risk
VAR Vectorielle Autorégressive
VECM Vector Error Correction Model
vi
LISTE DES TABLEAUX
Tableau 1 : La réglementation Bâle II 20
Tableau 2 : Types des modèles de stress test 36
Tableau 3 : Les variables micros et macros économiques
50
Tableau 4 : Test de la racine unitaire 51
Tableau 5 : Détermination du nombre des retards 52
Tableau 6 : Les résultats du Test de
cointégration 52
Tableau 7 : Les résultats du Test de Causalité
de Granger 55
Tableau 8 : Les résultats des simulations pour le choix
de la distribution à priori 60
Tableau 9 : Les moyennes et les écarts-type des
distributions à posteriori 61
Tableau 10 : Les résultats de l'indice EQMP 62
Tableau 11 : Les résultats du test de Diebold-Mariano
64
Tableau 12 : Les résultats du test de la dominance des
prévisions 65
Tableau 13 : Décomposition de la variance pour les NPL
66
Tableau 14: Les résultats des simulations pour
l'intuition des décideurs 70
VII
LISTE DES FIGURES
Figure 1 : Intégration du stress test dans la VaR 31
Figure 2 : L'évolution des prêts non performants
49
Figure 3 : Différences entre les approches
fréquentiste et bayésienne 54
Figure 5 : EQMP des NPL 63
Figure 6 : Les fonctions d'impulsion 66
Figure 7 : Prévision des scénarios sur les NPL
fin 2025 71
Figure 8 : Prévision cas extrême sur les NPL
72
1
INTRODUCTION GENERALE
Parmi les rôles cruciaux des banques, l'octroi de
crédit se distingue comme leur activité principale. Avant
d'accorder un prêt, il est impératif d'évaluer le risque
d'insolvabilité de l'emprunteur, également connu sous le nom de
risque de crédit. Ce risque peut être défini comme la
possibilité qu'un emprunteur ne puisse pas rembourser la totalité
ou une partie de son crédit conformément aux
échéances convenues dans le contrat signé entre lui et
l'institution prêteuse. Il convient de noter que ce type de risque a
été à l'origine de plusieurs crises financières,
dont la crise des subprimes aux États-Unis, qui était liée
à des problèmes de non-remboursement des prêts
immobiliers.
Les crises financières récentes ont clairement
démontré que les méthodes de mesure des risques
traditionnelles étaient insuffisantes pour faire face aux chocs
extrêmes auxquels les banques peuvent être exposées. En
accord avec les recommandations de certaines autorités de
régulation, les institutions financières sont tenues d'effectuer
régulièrement des simulations de crise afin d'estimer les pertes
potentielles en cas de fluctuations dangereuses et significatives des facteurs
de risque. Ces simulations de crise, également désignées
sous l'appellation "scénarios de stress test", sont des outils
essentiels pour évaluer les risques. Ils permettent d'établir un
lien entre les décisions des responsables de la banque en réponse
à l'arrivée de nouvelles informations. Cette approche facilite la
mise en place de mesures correctives en cas de constatation d'impacts durables
ou excessivement importants d'un scénario plausible sur le niveau des
prêts non performants de la banque.
Conformément aux recommandations du Comité Bale
et des autorités réglementaires en Tunisie, il est essentiel que
les institutions financières et les banques effectuent
régulièrement des stress tests. Cette démarche vise
à prévenir les pertes potentielles et à garantir la
solvabilité du secteur bancaire, surtout en période de
difficultés économiques.
La Banque de Financement des Petites et Moyennes Entreprises
(BFPME) a mis en place un éventail de prêts destinés au
financement des secteurs stratégiques pour le développement
économique et social du pays à travers l'entreprenariat.
Toutefois, compte tenu de la situation économique du pays depuis la
révolution, il est devenu essentiel d'utiliser le stress test de risque
de crédit. Cette démarche vise à prévenir les
perturbations potentielles susceptibles d'affecter la qualité du
portefeuille de crédit et à anticiper leur impact sur la BFPME.
Cette situation nous
2
amène à poser la question suivante :
Comment pouvons-nous utiliser l'application du stress test
inversé de risque de crédit pour évaluer la
capacité de résilience de la BFPME suite au choc sur la mauvaise
intuition des preneurs des décisions ?
À partir de cette problématique, nous formulons les
questions secondaires suivantes :
- Quels facteurs contribuent à expliquer le risque de
crédit ?
- Quels sont les limites du modèle VECM et qu'elle est
la modélisation convenable au contexte du stress test et qui prend en
considérations ses limites ?
- Dans qu'elle mesure l'intégration du modèle
BSVAR permet d'améliorer la précision des prévisions ?
- Quelles sont les procédures pour mettre en place des
stress tests inversé de risque de crédit provenant de l'intuition
des preneurs des décisions ?
- Quel est l'impact des scénarios défavorables
appliqués sur le risque de crédit de la BFPME ?
Pour aborder cette problématique, nous chercherons
à développer un modèle de risque de crédit
spécifique à la BFPME en tant qu'une banque de
développement. Ce modèle nous permettra de sélectionner
les distributions à priori pour la création de scénarios
de stress tests, ainsi que d'anticiper leur impact sur le risque de
crédit, afin d'évaluer la capacité de résilience de
la banque. Notre démarche de recherche se compose des étapes
suivantes :
- Dans le premier chapitre, nous explorerons les
différents types de risques bancaires en général, en
mettant l'accent sur le risque de crédit, tout en examinant les
réglementations internationales et nationales qui le
régissent.
- Le deuxième chapitre sera dédié
à l'analyse du stress test, comprenant sa typologie, son modèle,
et son approche. Nous nous pencherons ensuite sur les procédures pour
l'application des stress tests en matière de risque de crédit.
- Le troisième et dernier chapitre se concentrera sur
notre étude empirique. Nous y détaillerons les méthodes
que nous avons utilisées, présenterons les résultats issus
de notre modèle, et les interpréterons. De plus, nous analyserons
l'impact des scénarios que nous avons élaborés sur le
risque de crédit afin de déterminer les recommandations
nécessaires à prendre en compte par la BFPME.
3
CHAPITRE 1 : GENERALITE SUR LE RISQUE DU CREDIT
4
CHAPITRE 1 : GENERALITE SUR LE RISQUE DU CREDIT
Introduction
L'environnement bancaire est confronté à une
instabilité croissante et à une vulnérabilité
accrue en raison des fluctuations monétaires. Face à ces
perturbations, les banques sont de plus en plus exposées à une
diversité de risques qui peuvent nuire à leur activité et
à leur position sur le marché financier. Le risque est une
situation ou une activité exposée à un danger
potentiel.
Les banques sont confrontées à divers risques,
parmi lesquels le risque de crédit. Une gestion inadéquate des
risques liés au portefeuille de crédit ou une négligence
des fluctuations économiques ou d'autres circonstances susceptibles
d'affecter la qualité du portefeuille de crédit peuvent
entraîner une détérioration de la solvabilité de la
banque. Il est essentiel de prêter une attention particulière
à ces risques pour maintenir la stabilité financière et
assurer une gestion prudente des actifs et des engagements de crédit.
Dans ce chapitre, nous mettrons l'accent sur le risque de
crédit et ses facteurs déterminants. Tout d'abord, nous
présenterons différents types de risques en identifiant
spécifiquement le risque de crédit. Ensuite, nous nous
concentrerons sur les éléments qui influencent le risque de
crédit. Enfin, nous examinerons l'environnement réglementaire du
risque de crédit, à la fois au niveau international et national.
L'objectif global est de comprendre en détail le risque de
crédit, ses déterminants et le cadre réglementaire qui
entoure ce risque, tant sur le plan national qu'international.
5
Section 1 : Catégorisation des risques dans le
secteur bancaire et
analyse du risque de crédit
Les institutions financières, en particulier les
banques, sont exposées à des risques à la fois internes et
externes. Les risques internes découlent de la nature spécifique
de l'activité bancaire, tandis que les risques externes sont liés
à l'instabilité de l'environnement économique et
monétaire. Dans cette section, nous allons définir la notion de
risque et présenter les risques associés à
l'activité bancaire, en mettant l'accent particulièrement sur le
risque de crédit.
1. Compréhension du concept de risque
Selon (Adamowicz, 2018), le risque est
généralement compris comme la possibilité
d'événements imprévisibles entraînant des effets
indésirables. Dans le contexte bancaire, le risque est défini
comme l'incertitude concernant les résultats et les pertes potentielles
qui peuvent survenir lorsque l'environnement évolue de manière
défavorable. Une conséquence importante de cela est que toute
mesure du risque repose sur l'évaluation de ces
détériorations potentielles et de leur impact sur les
résultats voir (BESSIS, 1995).
Selon J. Tomaszewski, cité par (Adamowicz, 2018), le
risque est défini comme une probabilité mesurable d'un
événement avec des caractéristiques différentes de
l'événement attendu, ayant un impact direct ou indirect sur
l'écart de valeur par rapport au niveau supposé. Cette
définition met l'accent sur la dimension probabiliste et statistique du
risque, où l'incertitude est quantifiée en termes de
probabilité d'occurrence d'événements indésirables
ayant des conséquences financières.
Le risque peut être défini comme un danger
potentiel associé à un événement ou à
plusieurs événements. Il est caractérisé par une
incertitude quant à leur survenance, mais il existe une
probabilité certaine qu'ils se produisent dans une situation
donnée. En d'autres termes, nous ne pouvons pas prédire avec
certitude si ces événements se produiront ou non, mais il y a une
possibilité réelle qu'ils se produisent, avec une certaine
probabilité.
2. Typologie des risques dans le domaine
bancaire
Il existe divers types de risques auxquels les banques
accordent une grande attention, notamment le risque de contrepartie (ou de
crédit), le risque de marché, le risque opérationnel
6
et le risque de liquidité. Ces risques sont
considérés comme des éléments clés dans
l'évaluation globale de la gestion des risques bancaires.
2.1. Le risque de marché
Le risque de marché désigne la
possibilité de subir des pertes dues à des variations
défavorables des taux d'intérêt, des taux de change et des
prix de marché des instruments financiers, tant primaires que
dérivés, détenus par la banque. Ce risque provient de
l'incertitude entourant l'évolution des conditions économiques et
des marchés financiers, ce qui peut entraîner une diminution de la
valeur des actifs détenus par la banque et donc des pertes
financières.
D'après la définition précédente, on
peut conclure que le risque de marché englobe :
- Le risque de taux d'intérêt
est l'une des principales formes de risque auxquelles les banques sont
confrontées en tant qu'intermédiaires financiers. Il peut
être défini comme le risque selon lequel les revenus et/ou la
valeur marchande d'une banque seront affectés par les fluctuations des
taux d'intérêt voir (Ballester , Ferrer, & Gonzàlez,
2009).
- Le risque de change se caractérise
par la possibilité de subir des pertes en raison d'une évolution
inattendue des taux de change. Il se traduit par des conséquences
financières potentielles résultant des variations de valeur entre
différentes devises. Ce risque peut se manifester lorsque la valeur
d'une devise évolue de manière imprévisible par rapport
à une autre. Il peut avoir un impact sur les actifs, les passifs et les
transactions d'une banque, notamment dans le cadre d'opérations
commerciales internationales, d'investissements à l'étranger ou
d'activités de change.
- Le risque sur les titres se traduit par une
variation défavorable des prix de certains actifs spécifiques
tels que les actions et les matières premières. Il
représente la possibilité de subir des pertes en raison de ces
fluctuations de prix sur le marché. Les banques qui détiennent
ces actifs ou sont exposées à ces produits sont exposées
à un risque financier en cas de mouvements défavorables des
prix.
2.2. Le risque opérationnel
Le risque opérationnel, tel que défini par le
Comité de Bâle, se caractérise par des défaillances
ou des lacunes au niveau des procédures, du personnel, des
systèmes internes, ou suite à des événements
externes. Les pertes opérationnelles, engendrées par ce risque,
résultent d'un large éventail de causes, parmi lesquelles :
7
- Perturbations ou interruptions des activités
- Menaces et attaques terroristes
- Catastrophes naturelles
- Fraude, piratage informatique et transactions non
autorisées
- Défaillances des systèmes ou des processus.
2.3. Risque de liquidité
Le risque de liquidité se réfère à
la situation où une banque est incapable de répondre à ses
obligations financières et de mobiliser ses actifs lorsque cela est
nécessaire. Ce risque peut être provoqué par diverses
situations telles que des retraits exceptionnels ou imprévus de
liquidités, ainsi que le défaut de paiement d'une contrepartie.
En d'autres termes, le risque de liquidité pour une banque réside
dans sa capacité à disposer des liquidités
nécessaires pour faire face à ses engagements et obligations
financières à tout moment.
2.4. Risque pays
Le risque souverain concerne les pays en développement
(risque économique) ou en transition avec une dette extérieure
élevée (risque politique). Il se réfère à la
possibilité de non-remboursement de la créance sur un
débiteur privé ou public en raison de la situation
économique et/ou politique du pays dans lequel le débiteur exerce
ses activités. Il peut également être défini comme
le risque de survenance d'un sinistre résultant du contexte
économique et politique d'un État étranger où une
entreprise ou une banque opère une partie de ses activités.
Le risque pays peut être composé de deux
éléments distincts :
- Le risque politique (pays) : découle
soit des actions ou mesures prises par les autorités publiques locales
ou du pays d'origine (gouvernements, législation), soit
d'événements internes tels que des émeutes, ou externes
tels que des conflits ou des guerres. Cette composante est liée aux
facteurs politiques qui peuvent avoir un impact sur la stabilité et la
sécurité du pays, ainsi que sur les activités des
entreprises et des institutions financières qui y opèrent.
- Le risque économique et financier :
qui englobe à la fois la dépréciation de la
monnaie nationale et le manque de devises étrangères, ce qui peut
entraîner des conséquences telles qu'un défaut de paiement.
Cette composante est liée aux facteurs économiques et financiers
qui peuvent affecter la capacité d'un pays à honorer ses
obligations
8
financières, notamment en raison de difficultés
économiques, de fluctuations monétaires ou d'une pénurie
de réserves de devises étrangères. Ces facteurs peuvent
entraîner des retards de paiement, une instabilité
financière et des difficultés pour les entreprises et les
institutions financières opérant dans le pays.
2.5. Le risque d'insolvabilité
Lorsque les fonds propres d'une banque sont insuffisants pour
absorber d'éventuelles pertes, cela crée un risque
d'insolvabilité. La banque est également exposée à
d'autres risques tels que le risque de crédit, le risque de
marché et le risque de taux de change. L'exposition à ces
différents risques peut mettre en péril les activités de
la banque. Afin de faire face à ces engagements, les institutions
financières s'efforcent constamment d'ajuster leurs fonds propres en
fonction des risques encourus voir (Godlewski, 2003).
2.6. Risque systémique
Le risque systémique se réfère à
la probabilité de défaillances généralisées
dans un système dans son ensemble, plutôt que de pannes
individuelles au niveau des composants ou des pièces. Il se manifeste
par des co-mouvements (corrélation) entre la plupart ou la
totalité des parties du système. Dans le domaine bancaire, le
risque systémique se caractérise par une forte corrélation
et une concentration des défaillances bancaires au sein d'un pays, d'un
groupe de pays ou à l'échelle mondiale. Il peut également
se manifester dans d'autres secteurs du secteur financier, tels que les
marchés boursiers, où une baisse simultanée des prix d'un
grand nombre de titres se produit sur un ou plusieurs marchés, à
l'intérieur d'un seul pays ou entre pays. Le risque systémique
peut être de nature domestique ou transnationale voir (Kaufman &
Kenneth, 2003).
3. Évaluation et gestion du risque de
crédit
Le risque de crédit, également connu sous le nom
de risque de défaut de remboursement des prêts, est
considéré comme le plus ancien et le principal risque auquel les
banques et les institutions financières sont confrontées, et il
peut causer les dommages les plus importants. En effet, le défaut de
remboursement de quelques clients importants peut suffire à mettre en
péril la santé financière d'une institution de
crédit. C'est pourquoi les banques accordent une importance
particulière à la gestion du risque de crédit afin
d'éviter ses conséquences préjudiciables.
Dans cette section, nous nous concentrerons sur le risque de
crédit, ses différentes composantes et les conséquences
qu'il peut avoir sur une banque. Nous explorerons les mesures et les
9
stratégies mises en place par les institutions
financières pour gérer ce risque de manière efficace et
réduire les pertes potentielles associées.
3.1. Définition du risque de crédit
Selon (Audu, 2014), le risque de crédit peut être
simplement défini comme la probabilité qu'un emprunteur ou une
contrepartie bancaire ne respecte pas ses obligations conformément aux
conditions convenues. En d'autres termes, il représente le risque de
non-remboursement des prêts ou le défaut de paiement des dettes
contractées. Les banques et les institutions financières doivent
évaluer et gérer ce risque de manière proactive afin de
minimiser les pertes financières potentielles résultant de
l'incapacité des emprunteurs à honorer leurs engagements
financiers.
Selon les recherches de (Spuch¾áková,
Valaková, & Adamko, 2015), le risque de crédit peut
être défini comme la réticence ou l'incapacité d'une
contrepartie à respecter ses engagements en matière de
prêt, de négociation et de règlement des transactions
financières. Traditionnellement, le risque de crédit est
associé à la probabilité que le débiteur d'une
banque ne puisse pas rembourser le montant dû, incluant le capital et les
intérêts, à ladite banque. La gestion efficace du risque de
crédit est essentielle pour les institutions financières afin de
minimiser les pertes et de maintenir la solidité de leur portefeuille de
prêts.
3.2. Les Types du risque de crédit
Les risques de crédit peuvent être classés
selon la typologie suivante : 3.2.1. Le risque de
défaut
Le risque de crédit se réfère à la
situation où le débiteur est incapable ou refuse d'honorer ses
engagements envers le créancier, que ce soit en ce qui concerne le
remboursement du principal de la dette ou le paiement des
intérêts. Il est considéré comme un risque
inhérent à l'activité de l'intermédiation
financière traditionnelle, car il représente la
défaillance potentielle de la contrepartie envers laquelle une
créance ou un engagement est détenu voir (Sylvie, 2005).
Le risque de défaut est associé à la
probabilité de défaillance d'un emprunteur, où celui-ci se
trouve dans l'incapacité de respecter ses engagements de remboursement.
Le Comité de Bâle fournit des critères et des
événements qui définissent une situation de défaut
pour un débiteur.
Un défaut est considéré comme
étant réalisé pour un débiteur spécifique
lorsqu'un ou plusieurs des événements suivants sont
constatés :
10
- Il est probable que le débiteur ne remboursera pas
intégralement ses dettes.
- Le débiteur a initié une procédure de
faillite ou une procédure similaire pour se protéger de ses
créanciers.
3.2.2. Le risque de dégradation du spread
Le terme "spread" désigne la différence entre le
taux d'intérêt de référence,
généralement celui de l'Etat considéré sans risque,
et le taux d'intérêt appliqué à l'emprunteur. Il
représente la prime de risque demandée par le marché pour
compenser le risque associé à la contrepartie. Ainsi, le spread
permet d'évaluer la qualité de l'emprunteur en mesurant la prime
de risque exigée par les investisseurs.
Le risque de spread fait référence à la
possibilité de détérioration de la qualité de
l'emprunteur, ce qui peut avoir un impact sur les flux attendus tels que les
remboursements du principal et les intérêts. L'évolution
aléatoire des spreads constitue en elle-même un risque de
crédit, car elle influe sur la valeur de marché du crédit.
Ainsi, il n'est pas nécessaire que le défaut se concrétise
pour affecter négativement la valeur d'un actif ou d'un portefeuille.
Les fluctuations du spread peuvent entraîner des variations de prix sur
les actifs liés au crédit, ce qui peut avoir des
conséquences sur la valeur globale d'un portefeuille ou d'un actif
spécifique.
3.2.3. Le risque de recouvrement
Le risque de récupération, également
appelé risque de recouvrement, se réfère à
l'incertitude associée au montant que la banque pourra
récupérer sur une créance après le constat d'un
défaut de paiement. Après qu'un débiteur ait fait
défaut, la banque n'est jamais certaine du montant exact qu'elle pourra
recouvrer. Ce risque découle des difficultés potentielles
rencontrées lors de la récupération des fonds, telles que
la liquidation d'actifs, les procédures de faillite, les
négociations avec le débiteur ou les éventuelles pertes
liées à la vente des actifs récupérés.
11
Section 2 : Les déterminants du risque de
crédit
L'incidence des prêts non performants dans les banques
commerciales ne se limite pas seulement à la gestion interne de la
banque, mais est également liée au risque de crédit.
Les prêts non performants (NPL) sont un indicateur de la
qualité du crédit d'une banque et sont considérés
comme un reflet de sa gestion du risque de crédit. Le ratio des
prêts non performants permet de mesurer le pourcentage des pertes de
crédit par rapport au montant total des prêts accordés. Il
offre ainsi une indication sur la manière dont les banques gèrent
leur risque de crédit, en identifiant les prêts qui
présentent un niveau élevé de risque de défaut ou
de non-remboursement.
La littérature a identifié deux tendances
majeures qui mettent en évidence les principaux facteurs susceptibles
d'influencer le risque de crédit bancaire. La première tendance
souligne l'importance des variables internes en tant que déterminants
potentiels du risque de crédit. Cela englobe des éléments
tels que la qualité des politiques de gestion des risques de
crédit au sein des banques, les pratiques de souscription des
prêts, la diversification des portefeuilles de prêts, ainsi que la
qualité des processus de suivi et de recouvrement des
créances.
La deuxième tendance met en évidence
l'évolution des variables externes, notamment les réglementations
prudentielles et les conditions économiques, qui peuvent influencer le
risque de crédit bancaire. Les réglementations prudentielles
peuvent imposer des exigences en matière de capital et de provisions
pour couvrir les pertes potentielles, ce qui peut avoir une incidence sur la
gestion du risque de crédit. Par ailleurs, les conditions
économiques, telles que le cycle économique, le niveau
d'endettement des emprunteurs, les taux d'intérêt et la
stabilité financière, peuvent également exercer une
influence significative sur le risque de crédit bancaire.
En résumé, ces deux tendances soulignent
l'importance de prendre en compte à la fois les facteurs internes et
externes lors de l'évaluation et de la gestion du risque de
crédit bancaire.
1. Facteur externe du risque de crédit
Les facteurs externes du risque de crédit sont des
éléments provenant de l'environnement économique et
financier dans lequel opère la banque. Ces facteurs peuvent influencer
la capacité des emprunteurs à rembourser leurs dettes et
augmenter le niveau de risque de crédit.
12
1.1. La croissance économique
La croissance économique, mesurée par le PIB, a
un effet positif sur la réduction des prêts non performants (NPL).
Lorsque l'économie se développe, les entreprises sont
généralement en meilleure santé financière, ce qui
améliore leur capacité à rembourser leurs dettes et
réduit les risques de NPL. De plus, les agrégats
monétaires tels que M1, M2 et M3 peuvent également jouer un
rôle dans la gestion des NPL, car une augmentation de la masse
monétaire peut stimuler l'activité économique et
contribuer à la réduction des NPL.
1.2. Le chômage
Le chômage a un effet négatif et significatif, ce
qui se traduit par une détérioration de la capacité des
individus à rembourser leurs dettes, ainsi que par des entreprises ayant
des flux de trésorerie faibles en raison d'une baisse de la demande pour
leurs produits selon (Chaibi & Ftiti, 2015). Cette situation entraîne
une diminution de la capacité de remboursement tant des emprunteurs
individuels que des entreprises, ce qui peut accroître le risque de
crédit.
1.3. Le taux d'intérêt
Lorsque les taux d'intérêt sont
élevés, cela entraîne un fardeau de la dette plus
important. Cette situation peut avoir un effet direct sur l'augmentation des
créances non productives voir (Nkusu, 2011). En effet, des taux
d'intérêt élevés peuvent rendre plus difficile pour
les emprunteurs de rembourser leurs dettes, ce qui augmente le risque de
défaut de paiement et entraîne une augmentation des
créances improductives.
1.4. Le taux d'inflation
L'effet du taux d'inflation sur le risque de crédit est
ambigu. Dans certains cas, des taux d'inflation plus élevés
peuvent faciliter le remboursement de la dette en réduisant la valeur
réelle des prêts en cours, voir (Castro, 2013). Cependant, dans
les pays où les taux d'intérêt sont variables, les
prêteurs ajustent les taux pour maintenir leurs rendements réels.
Cela peut rendre le remboursement de la dette plus difficile, notamment pour
les emprunteurs à revenu limité qui doivent faire face à
des taux d'intérêt plus élevés. Par
conséquent, la relation entre l'inflation et le risque de crédit
peut être positive ou négative.
13
1.5. Le taux de change
D'après (Fofack, 2005), une appréciation de la
monnaie peut avoir un impact direct sur la capacité de remboursement de
la dette des particuliers en rendant les produits locaux plus chers. Cela peut
rendre plus difficile pour les emprunteurs honorer leurs engagements de
crédit, notamment dans les industries orientées vers
l'exportation où les marges bénéficiaires peuvent
être réduites. Cependant, les prêts en devises
étrangères peuvent être favorisés par
l'appréciation de la monnaie locale, ce qui les rend moins coûteux
pour les emprunteurs voir (Nkusu, 2011). L'effet des taux de change sur les
prêts non performants (NPL) peut donc être positif ou
négatif en fonction de la devise de la dette, et cet effet est plus
prononcé dans les pays où le pourcentage de prêts en
devises étrangères est élevé.
1.6. La concentration bancaire
(Kjosevski, Petkovski, & Naumovska, 2019) ont
examiné la concentration bancaire comme un facteur explicatif du risque
de crédit. Selon (Jiménez, Lopez, & Saurina, 2013), les
banques dans un environnement concurrentiel cherchent à améliorer
leur gestion des risques par rapport à leurs concurrents. Par
conséquent, les pays disposant d'un secteur bancaire plus
compétitif devraient avoir moins de prêts non performants.
Cependant, selon (Manove, Padilla, & Pagano, 2001) et (Bolt & Tieman,
2004), une concurrence excessive peut pousser les banques à prendre des
risques, tels que la réduction des critères de sélection
des prêts et l'utilisation de critères de prêt moins
stricts, ce qui augmente la probabilité de prêts non performants
plus élevés.
2. Facteurs internes du risque de crédit
Malgré l'importance des développements
macroéconomiques dans l'explication du risque de crédit, des
études récentes accordent également une attention
particulière à des variables spécifiques à la
banque. Parmi ces variables, nous pouvons signaler :
2.1. Taille de la banque
La taille de la banque, mesurée par le total des
actifs, est un facteur important utilisé pour évaluer son
importance sur le marché. Cependant, les études sur la relation
entre la taille des banques et les créances douteuses sont nombreuses et
contradictoires. Certaines études suggèrent un impact
négatif de la taille de la banque sur les prêts non performants,
ce qui signifie que les grandes banques ont généralement de
meilleures stratégies de gestion du risque de crédit par rapport
aux banques de taille plus réduite. Cela peut s'expliquer par leur
expérience
14
accrue et leur capacité à diversifier leur
portefeuille de crédit grâce à leur part de marché
plus importante.
2.2. La croissance du crédit
La croissance du crédit est souvent associée
à une augmentation simultanée des prêts douteux. Les
banques ayant un faible niveau de capital ont tendance à être plus
risquées, car elles accordent souvent des prêts excessifs, ce qui
les expose à des pertes plus élevées sur les prêts.
Cependant, des études ont également montré que la relation
entre le capital et le risque de crédit peut être ambiguë.
Même les banques disposant de ratios de fonds propres adéquats
peuvent créer des portefeuilles de prêts à haut risque, ce
qui peut entraîner un niveau élevé de prêts douteux.
Il existe donc une variabilité dans la relation entre le capital et le
risque de crédit, qui dépend des politiques de prêt
spécifiques mises en place par les banques.
2.3. La rentabilité des actifs et des capitaux
propres
Le ratio de rentabilité des actifs (ROA) et le ratio de
rentabilité des capitaux propres (ROE) sont des mesures
financières qui évaluent la rentabilité des banques. Le
ROA mesure l'efficacité avec laquelle les actifs de la banque sont
utilisés et indique le revenu généré par
l'investissement dans ces actifs. En ce qui concerne la relation entre le ROA
et les prêts non performants, différentes études ont abouti
à des résultats contradictoires. Certains chercheurs, tels (Ahmad
& Bashir, 2013), (Alexandri & Santoso, 2015) ont trouvé une
corrélation positive entre le ROA et les prêts non performants,
suggérant que les banques plus rentables sont également plus
exposées à ce risque. D'autres chercheurs, comme (Messai &
Jouini, Micro and Macro Determinants of Non-performing Loans, 2013) ont
observé une corrélation négative, indiquant que les
banques les plus rentables ont tendance à avoir un niveau
inférieur de prêts non performants. Cette relation peut
s'expliquer par le comportement de prise de risque des banques : les banques
rentables ont moins besoin d'accorder des crédits jugés
risqués.
2.4. Les provisions pour pertes
Selon les recherches de (Hasan & Wall, 2004), il existe un
effet positif des provisions pour pertes sur prêts sur le niveau des
prêts non performants. Lorsque les banques anticipent des pertes
élevées, elles tendent à accroître leurs provisions.
Cette pratique de surfinancement vise à réduire la
volatilité des résultats et à renforcer la
solvabilité de la banque. En anticipant les pertes potentielles, les
banques prennent des mesures pour se protéger contre les
conséquences néfastes des prêts non performants.
15
2.5. Le ratio dépôts sur crédit
Le ratio dépôts sur crédit est
fréquemment utilisé dans la littérature comme un
indicateur de liquidité, représentant les fonds que la banque
utilise pour accorder des prêts à partir des dépôts
collectés. Des études telles que celles de (Dimitrios, Angelos,
& Vouldis, 2012) et (Makri, Tsagkanos, & Bellas, 2014) ont
démontré une relation positive entre ce ratio et le niveau des
prêts non performants. Cela suggère que les banques qui ont un
ratio dépôts sur crédit plus élevé ont
tendance à présenter des niveaux plus élevés de
prêts non performants.
16
Section 3 : La réglementation du risque de
crédit
La fonction d'intermédiation des banques est une
activité distinctive et spécifique qui est soumise à une
réglementation rigoureuse englobant tous les aspects de
l'activité bancaire.
Par conséquent, afin de garantir la stabilité du
système bancaire, les autorités de supervision ont mis en place
des mesures visant à renforcer la gestion et le contrôle des
risques, ainsi qu'à établir des normes réglementaires. Ces
réformes ont pour objectif d'améliorer les procédures de
gestion des risques et de répondre aux exigences de conformité
réglementaire.
1. La réglementation internationale du risque de
crédit
La réglementation internationale du risque de
crédit joue un rôle crucial dans la stabilité du
système financier mondial. Ces réglementations visent à
renforcer la résilience des banques, à promouvoir des pratiques
de gestion des risques plus rigoureuses et à améliorer la
transparence des informations financières.
1.1 La règlementation Bâle I
En Juillet 1988, le Comité de Bâle sur le
Contrôle Bancaire a publié un rapport visant à promouvoir
une harmonisation internationale de la réglementation bancaire, en
particulier en ce qui concerne les fonds propres des banques internationales.
Cet accord, connu sous le nom de Ratio Cooke en référence au
Président du Comité de Bâle à l'époque, a
introduit un ratio de solvabilité comme mesure de la stabilité
financière des banques. Il a été élaboré en
collaboration avec les représentants du groupe des 10 pays les plus
industrialisés.
Dans un contexte marqué par l'instabilité
financière, la fragilité du système bancaire, la
diversification des activités bancaires et l'intensification de la
concurrence, il est devenu essentiel de mettre en place un accord international
établissant un niveau minimum de fonds propres. Cet accord vise à
renforcer la résilience des banques en leur imposant des exigences en
termes de capital, afin de prévenir les risques systémiques et de
garantir la stabilité financière à l'échelle
mondiale.
L'objectif principal de cet accord est d'améliorer la
stabilité du système financier international en introduisant des
exigences de fonds propres applicables à toutes les banques. Son
objectif ultime est de réduire de manière significative le risque
d'insolvabilité et de minimiser les coûts que les investisseurs et
les contribuables devraient assumer en cas de défaillance bancaire.
Des
17
nombreux pays ont intégré les principes de
l'Accord de Bâle I dans leur législation, en les adaptant selon
leurs besoins spécifiques, ce qui est considéré comme une
réussite.
- Le ratio Cooke : en 1988, le premier ratio,
connu sous le nom de Ratio de Bâle I ou Ratio Cooke, a été
introduit. Ce ratio était calculé en comparant les engagements
d'une banque (crédits et autres placements) avec le montant de ses fonds
propres (capital apporté par les actionnaires et les
bénéfices de la banque). Il était fixé à 8%.
Par conséquent, la formule du Ratio Cooke était la suivante :
Total des Fonds Propres
Ratio Cooke = > 8%
Risque du Crédit
- Les pondérations des éléments
du bilan : varient en fonction du type de créance et du
débiteur, ainsi les pondérations des engagements risqués
sont les suivants :
0% pour les créances sur les états membres de
l'OCDE
20% pour les créances sur les banques ou
collectivités locales d'état membres de l'OCDE
50% pour les créances à garanties
hypothécaires
100% pour toutes les autres créances.
- Pour les engagements d'hors bilan : on peut
distinguer deux types de pondérations :
Pour les engagements classiques non liés au cours de
change et au taux d'intérêt, la pondération se fait en
convertissant l'engagement en équivalent crédit à l'aide
d'un coefficient de conversion variant de 0 à 100 % en fonction de leur
nature, puis en les pondérant selon le statut de la contrepartie.
Pour les engagements liés au cours de change et/ou au
taux d'intérêt, l'équivalent risque est calculé
comme la somme du coût de remplacement total des contrats
représentant un gain, ainsi que du risque de crédit potentiel qui
est obtenu en multipliant le nominal par un coefficient de majoration
dépendant de la durée résiduelle et de la nature du
contrat.
Face à l'évolution complexe des techniques
bancaires et à la nécessité de prendre en compte des
approches plus qualitatives, la norme Cooke a été
critiquée pour son manque de considération envers d'autres types
de risques tels que le risque de marché, le risque opérationnel,
le risque de liquidité, etc. De plus, la norme se concentrait
principalement sur les valeurs comptables des actifs plutôt que sur les
valeurs de marché, ce qui a révélé ses limites.
18
1.2 La règlementation Bâle II
L'objectif de la réforme Bâle II est de prendre
en compte la complexité croissante de l'activité bancaire tout en
permettant aux établissements financiers de choisir parmi
différentes options pour déterminer le niveau minimal de fonds
propres requis pour couvrir les pertes potentielles. Cette réforme vise
à apporter davantage de flexibilité et d'autonomie aux banques
dans la gestion de leurs risques, tout en renforçant la stabilité
du système financier voir (Nouy, 2003).
L'approche Bâle II marque un changement significatif en
passant d'une approche purement quantitative à une approche plus
probabiliste et qualitative, où les banques sont tenues d'identifier et
de gérer plus efficacement leurs risques. Ce nouveau dispositif permet
aux établissements financiers de choisir parmi plusieurs méthodes
de calcul des exigences en fonds propres, encourageant ainsi l'utilisation des
modèles internes des banques pour une meilleure évaluation des
risques. Les banques qui démontrent une capacité solide à
gérer leurs risques à l'aide de leurs propres modèles
internes bénéficieront de niveaux d'exigences
réglementaires en capital plus faibles en récompense.
Le nouvel accord prudentiel, connu sous le nom de Bâle
II, vise à améliorer l'évaluation des risques bancaires et
à mettre en place un dispositif de surveillance prudentielle et de
transparence. Il est entré en vigueur à la fin de l'année
2007 et repose sur trois piliers complémentaires et
interdépendants : les exigences minimales de fonds propres, la
surveillance exercée par les Autorités prudentielles pour
s'assurer de l'adéquation des fonds propres, ainsi que la transparence
et la discipline du marché. Ce nouvel accord vise à renforcer la
stabilité du système bancaire en encourageant les banques
à adopter des pratiques de gestion des risques plus rigoureuses et
à améliorer la communication d'informations claires et fiables
aux investisseurs et au public.
1.2.1 Pilier I : exigences minimales en fonds propres
Le nouveau ratio de solvabilité, appelé "ratio
Mac Donough" dans le cadre des accords de Bâle II, prend en
considération les différents risques auxquels une banque est
exposée, notamment risque de crédit, risque de marché et
risque opérationnel. Contrairement au ratio de Cooke, qui ne prend en
compte que le risque de crédit, ce nouveau ratio vise à mieux
évaluer la solvabilité d'une banque en prenant en compte
l'ensemble de ses risques. La formule exacte de ce ratio peut varier en
fonction des méthodes de calcul spécifiques utilisées par
les établissements financiers pour mesurer et gérer ces
risques.
19
Fond Propre Réglementaire
Ratio Mc Donough = > 8%
Risque de
crédit + Risque de marché + Risque
opérationnel
Bâle II, se distingue de Bâle I par sa prise en
compte d'une gamme plus large de risques et par la flexibilité offerte
aux banques dans le calcul des exigences en fonds propres. Concrètement,
les banques ont la possibilité d'utiliser différentes approches
de pondération des risques pour le risque opérationnel et le
risque de crédit. Cela peut inclure des pondérations forfaitaires
basées sur la qualité de la contrepartie ou l'utilisation de
notations internes. Cette approche permet une meilleure adaptation aux
spécificités des banques et favorise une évaluation plus
précise de leurs risques.
1.2.2 Le pilier II : processus de surveillance
prudentielle
Le pilier II de Bâle II complète et renforce le
pilier I en incluant l'analyse des risques globaux de la banque, y compris ceux
déjà couverts par le pilier I. Il implique que la banque calcule
ses besoins en fonds propres en fonction du capital économique et que le
superviseur bancaire compare son évaluation du profil de risque de la
banque à celle de la banque elle-même. Cette confrontation permet
au superviseur d'adapter ses mesures de surveillance prudentielle, telles que
l'exigence de fonds propres supérieurs aux exigences minimales.
1.2.3 Le pilier III : discipline de marché
Le troisième pilier de Bâle II a pour objectif de
promouvoir la transparence et la communication financière des banques en
les obligeant à fournir des informations fiables et
régulières sur leur situation et leurs opérations. Cela
permet au marché d'évaluer correctement l'exposition aux risques
des banques ainsi que leurs capacités en termes de fonds propres pour y
faire face. Ce pilier vise également à permettre aux
investisseurs de mieux comprendre les profils de risque des banques, ainsi que
la gestion et la couverture de ces risques.
En effet, la crise des subprimes qui a éclaté
dès l'été 2007 aux États-Unis a pris une ampleur
mondiale et a eu des répercussions majeures sur le secteur bancaire.
Cela a remis en question la pertinence et l'efficacité du dispositif
Bâle II, qui était sur le point d'être mis en oeuvre. Dans
ce contexte, le Comité de Bâle a rapidement réagi et a
commencé à travailler sur un nouveau dispositif, connu sous le
nom de Bâle III, afin de prendre en compte les leçons de la crise
et de renforcer davantage la réglementation et la supervision
bancaire.
20
Tableau 1 : La réglementation Bâle II
|
Pilier 1 :
Exigence de fonds propres
|
Pilier 2 :
Processus de surveillance
|
Pilier 3 :
Discipline de marché
|
|
Risques de marché Risques de crédit Risques
opérationnels
|
Contrôle des procédures et des méthodes
internes d'allocation des FP
|
Règles de publication
financière sur la structure des FP et des risques
|
Source : Nouy 2003, réforme de Bâle II
1.3 La règlementation Bâle III
En effet, les lignes directrices de Bâle III ont
été publiées en décembre 2010 dans le but
d'améliorer la capacité des banques à faire face aux
conditions économiques et financières, et de renforcer le cadre
réglementaire déjà établi par Bâle I et
Bâle II. Bâle III poursuit les efforts du Comité de
Bâle sur le contrôle bancaire en visant à renforcer la
gestion des risques, à améliorer la résilience du secteur
bancaire face aux chocs économiques et à promouvoir la
transparence des banques. Le dispositif Bâle III conserve la structure
à trois piliers, qui se complètent mutuellement.
Selon (Comité de Bâle sur le contrôle
bancaire, 2010) ce nouvel accord, basé sur plusieurs objectifs, comprend
les éléments suivants :
- Améliorer la qualité des fonds propres des
banques pour renforcer leur capacité à faire face aux pertes et
à maintenir leurs activités.
- Accroître la couverture des risques liés aux
activités de négociation, aux opérations de titrisation,
aux expositions hors bilan et aux instruments dérivés.
- Relever les exigences minimales en matière de fonds
propres, en particulier pour la composante solide des fonds propres de base, et
introduire un volant de conservation pour renforcer les exigences globales.
- Établir un ratio de levier harmonisé au niveau
international pour limiter l'accumulation excessive d'endettement dans le
secteur bancaire.
- Renforcer les normes de surveillance prudentielle, de
communication financière,
d'évaluation, de tests de résilience, de gestion
des risques de liquidité et de gouvernance. - Établir des normes
internationales minimales de liquidité, y compris un ratio de
couverture de liquidité à court terme et un
ratio de financement stable net à long terme.
21
- Encourager les banques à constituer des
réserves de fonds propres pendant les périodes favorables afin de
les mobiliser en cas de détérioration de la situation
économique, y compris un volant de conservation et un volant
contracyclique pour atténuer les fluctuations excessives du
crédit.
2. La règlementation prudentielle en Tunisie
La Banque Centrale de Tunisie (BCT) est responsable de
l'élaboration de la réglementation prudentielle nationale pour la
gestion des risques de crédit. Elle a établi une circulaire
principale, la n° 91-24 du 17 décembre 1991, qui a
été modifiée le 29 juin 2012 par la circulaire n°
2012-09.
Cette circulaire contient des directives et des normes que
tous les établissements de crédit en Tunisie doivent suivre
concernant la division et la couverture des risques, la classification des
actifs bancaires et la constitution des provisions.
En plus de la circulaire n° 91-24 modifiée par la
circulaire n° 2012-09, la Banque Centrale de Tunisie (BCT) a
également émis la circulaire n° 16-06 le 11 octobre 2016,
qui concerne le système de notation des contreparties, ainsi que la
circulaire n° 2020-01 du 29 janvier 2020, qui porte sur les mesures
préliminaires à la mise en place des normes internationales
d'information financière (IFRS) pour les banques et institutions
financières.
2.1 Division des risques
La circulaire n° 91-24 mise en place par la banque
centrale vise à atténuer les pertes potentielles en cas de
défaut et à répartir l'exposition des
établissements de crédit au risque de contrepartie. Selon le
premier article de cette circulaire, le montant total des risques encourus ne
doit pas dépasser les seuils suivants :
- Pour les bénéficiaires dont le risque encouru
est supérieur ou égal à 5% des fonds propres nets (FP
nets) de la banque, le montant total des risques ne doit pas dépasser 3
fois les FP nets bancaires.
- Pour les bénéficiaires dont le risque encouru
est supérieur à 15% des fonds propres nets, le montant total des
risques ne doit pas dépasser 1,5 fois les FP nets bancaires.
De plus, selon le deuxième article de la même
circulaire, la banque centrale limite la valeur maximale des risques encourus
sur un même bénéficiaire à 25% des fonds propres
nets de la banque.
22
Conformément à l'article 23 de la loi
n°2001-65 sur les établissements de crédit, le montant total
des risques encourus sur les personnes liées à la banque ne doit
pas dépasser 25% des fonds propres nets. Ces personnes doivent
être identifiées par le système de mesure de risque de la
banque.
2.2 Couverture des risques
Selon l'article 6 de la circulaire n°91-24, le ratio de
solvabilité bancaire doit être d'au moins 8%. Cela signifie que
les fonds propres nets de chaque établissement de crédit ne
doivent pas représenter moins de 8% de leur total d'actifs, du bilan et
de l'hors-bilan, pondérés en fonction des risques.
2.3 Classification des actifs
Depuis 1991, tous les établissements de crédit
sont tenus de procéder régulièrement à la
classification de leurs actifs afin de déterminer le montant des
provisions nécessaires pour couvrir les risques encourus. Cette
procédure s'applique à tous les types d'actifs, qu'ils soient
inscrits au bilan ou hors-bilan, et qu'ils soient libellés en dinars ou
en devises. Cependant, il convient de noter que les actifs détenus
directement par l'établissement de crédit envers l'Etat ou la
Banque Centrale de Tunisie (BCT) ne sont pas soumis à cette
classification, car ils représentent un risque souverain.
Selon la circulaire n° 91-24 du 17 décembre 1991,
il existe cinq grandes catégories d'actifs, voici une
présentation de ces catégories :
- Classe 0 : il s'agit des actifs sains,
cette catégorie englobe les actifs détenus sur des entreprises
dont la situation financière est solide ou ne suscite pas de
préoccupations majeures.
- Classe 1 : il s'agit des actifs
nécessitant un suivi particulier, cette classe regroupe les actifs
détenus sur des entreprises qui respectent leurs engagements financiers
à leur échéance, mais qui connaissent une
détérioration de leur situation financière ou qui
opèrent dans un secteur d'activité en difficulté.
- Classe 2 : concerne les actifs incertains,
cette classe englobe les actifs détenus sur des entreprises qui
présentent un retard de paiement des intérêts ou du
principal compris entre 90 jours et 180 jours, ainsi que sur des entreprises
présentant des éléments préoccupants.
23
- Classe 3 : il s'agit des actifs
préoccupants, cette classe concerne les actifs détenus sur des
entreprises qui ont un retard de paiement des intérêts ou du
principal dans la plage de 180 jours à 360 jours, ainsi que sur des
entreprises en difficulté sérieuse.
- Classe 4 : pour les actifs compromis, cette
classe englobe les actifs détenus sur des entreprises dont le retard de
paiement des intérêts ou du principal dépasse 360 jours,
ainsi que les actifs restés en suspens pendant plus de 360 jours. Elle
inclut également les autres actifs qui doivent être
considérés comme des pertes après que la banque ait
épuisé toutes les procédures légales visant
à récupérer ces actifs.
24
Conclusion
Parmi les différents risques liés à
l'activité bancaire, tels que le risque de marché, le risque
opérationnel, le risque de liquidité, le risque pays, le risque
d'insolvabilité, le risque systémique et le risque de
crédit, ce dernier est considéré comme le risque principal
auquel une institution bancaire est exposée. Une mauvaise gestion du
risque de crédit peut avoir des conséquences désastreuses
pour la banque.
Effectivement, compte tenu des conséquences
potentiellement néfastes du risque de crédit, les banques doivent
veiller à bien maîtriser les risques qu'elles prennent
vis-à-vis de leurs contreparties. Pour ce faire, une première
étape essentielle consiste à évaluer ce risque de
manière approfondie afin de pouvoir le gérer de manière
optimale. Dans le prochain chapitre, nous explorerons en détail les
différentes méthodes et pratiques de gestion du risque de
crédit.
Dans ce chapitre, nous avons abordé les
différents types de risques bancaires, en mettant en évidence le
risque de crédit. Nous avons également souligné
l'importance pour les banques de maîtriser ce risque en l'évaluant
de manière approfondie et en le gérant efficacement. De plus,
nous avons examiné l'évolution de la réglementation
prudentielle de Bâle, qui a influencé les réglementations
actuelles en Tunisie. Cette réglementation incite les banques à
évaluer et gérer le risque de crédit afin d'assurer une
activité bancaire saine et stable.
25
CHAPITRE 2 : LE STRESS TEST ET GESTION DES RISQUES
26
CHAPITRE 2 : LE STRESS TEST ET GESTION DES RISQUES
Introduction
Après la crise financière de 2007-2008, les
superviseurs et les institutions financières ont de plus en plus
utilisé les stress tests pour évaluer les risques bancaires et
renforcer les exigences de solvabilité et de liquidité. Ces tests
mesurent l'impact des différents risques auxquels les banques sont
exposées et évaluent leur capacité à
résister à des conditions économiques et
financières extrêmes mais plausibles. Les stress tests,
également connus sous le nom de tests de résilience bancaire,
peuvent être réalisés par les banques centrales ou par les
banques individuellement.
Ce chapitre est divisé en trois sections. Dans la
première section, nous aborderons l'historique du stress test, sa
définition et son objectif. La deuxième section portera sur les
différents types, méthodes et approches utilisés pour
effectuer les stress tests. Enfin, dans la dernière section, nous nous
concentrerons sur les procédures à mettre en place pour
réaliser des stress tests, en mettant l'accent sur le stress test du
risque de crédit.
27
Section 1 : Introduction aux Stress Tests
Les stress tests sont fréquemment utilisés par
les établissements financiers pour évaluer quantitativement les
pertes ou les risques potentiels dans des circonstances souvent extrêmes.
Dans cette section, nous débuterons par un bref historique de
l'évolution des stress tests, puis nous présenterons leur
définition et leurs objectifs.
1. L'évolution des Stress Tests
Les premières utilisations des stress tests remontent
au début des années 90, principalement pour la gestion interne
des risques par les banques individuelles. Au fil du temps, la conception et
les fonctions de ces tests ont connu une évolution significative. Avant
la crise financière mondiale, la plupart des exercices étaient de
petite envergure et servaient à compléter d'autres outils
statistiques déjà disponibles au niveau de la direction bancaire
pour évaluer les activités commerciales d'une banque voir
(Blaschke, Jones, Majnoni, & Peria, 2001). Cependant, l'importance des
stress tests s'est accrue, avec des améliorations plus
détaillées introduites par l'amendement de 1996 et l'extension
aux risques de marché dans l'accord sur les fonds propres (Basel
Committee on Banking Supervision, 2009).
De plus, en 2004, dans le cadre de Bâle II, les banques
ont été encouragées à mettre en place des exercices
de stress tests internes rigoureux, tant pour le pilier I que pour le pilier
II. Cependant, Bâle II n'a pas été universellement mis en
oeuvre, et la plupart des modèles de stress tests internes
étaient encore en phase de développement.
Pendant la crise financière mondiale, une attention
croissante a été portée sur les tests de
résilience, et notamment aux États-Unis et dans l'Union
européenne, les autorités ont utilisé des tests de
résilience dans leur réponse à la crise. Cette crise
financière a mis en évidence les conséquences graves sur
l'économie lorsque les banques rencontrent des difficultés et
restreignent les prêts, révélant ainsi les lacunes dans la
gestion des risques à l'échelle du système financier.
Aux États-Unis, le Supervisory Capital Assessment
Program (SCAP) de la Réserve fédérale américaine a
été mis en place en 2009 pour évaluer si les principales
banques nationales disposaient de suffisamment de capital pour absorber les
pertes et continuer à fonctionner. Les résultats ont
été rendus publics, et le Département du Trésor
américain a fourni une garantie de
28
soutien. Cet exercice a été évalué
comme ayant contribué à restaurer la confiance des marchés
et à stabiliser le système financier dans son ensemble voir
(Schuermann, 2014).
Dans l'Union européenne, le Comité
européen des contrôleurs bancaires (CEBS) a effectué des
tests de résilience à partir de 2009. En particulier, en 2010, le
CEBS a mené un exercice à l'échelle de l'UE avec une
divulgation complète de l'impact estimé sur le capital de chaque
banque et de leur exposition au risque, permettant ainsi une comparaison entre
ces deux exercices de crise.
Ces tests de résilience ont joué un rôle
essentiel pour évaluer la solidité des banques et contribuer
à rétablir la confiance des marchés pendant une
période critique de la crise financière mondiale.
Dans le domaine réglementaire, le Comité de
Bâle sur le contrôle bancaire (CEBS) a étudié les
pratiques et publié des principes pour des tests de résilience
solides dès 2009, en les mettant à jour en 2018 voir (Basel
Committee on Banking Supervision, 2018). La communauté officielle a
également encouragé l'intégration d'une dimension
macroprudentielle dans les tests de résilience, et il existe
désormais une littérature en plein essor qui documente les
progrès dans cette direction tel que (Dimitri, 2015). Les
autorités nationales ou régionales chargées des tests de
résilience microprudentiels et macroprudentiels ont également
documenté leurs approches et leur évolution au fil du temps.
2. Définition de stress test
Les tests de résilience sont un outil de gestion des
risques largement utilisé pour évaluer l'impact potentiel
d'événements spécifiques ou de mouvements dans un ensemble
de variables financières sur les établissements financiers. Selon
(Paul, Matthew, & Graham, 2004) ces tests évaluent la
sensibilité d'un portefeuille à un choc donné en mesurant
les variations de sa valeur sous l'effet des changements dans les facteurs de
risques sous-jacents. Les hypothèses formulées pour ces tests
sont généralement suffisamment importantes pour soumettre le
portefeuille à des tensions exceptionnelles, mais elles restent
réalistes et plausibles.
Selon (Comité de Bâle sur le contrôle
bancaire, 2010), les tests de résilience sont des instruments
utilisés par les banques pour la gestion des risques en interne. Ils
permettent également aux autorités de mesurer les effets
potentiels que des chocs négatifs graves mais plausibles pourraient
avoir sur le niveau de fonds propres des établissements bancaires.
Ces
29
tests jouent un rôle essentiel dans l'évaluation
de la capacité des banques à faire face à des situations
de stress financiers et à s'assurer de leur solidité face aux
risques importants.
Le stress test bancaire, ou Stress Testing, sert à
évaluer la résilience d'un établissement financier,
c'est-à-dire sa capacité à faire face aux situations
difficiles. Il permet également de déterminer les pertes
potentielles en cas de chocs macroéconomiques inhabituels mais
plausibles.
3. Les objectifs des stress tests bancaires
Les cadres de simulation de crise doivent être
élaborés afin d'atteindre des objectifs bien définis, qui
sont documentés et approuvés au niveau du conseil
d'administration de l'organisation ou d'une instance de gouvernance
appropriée de niveau supérieur. Ces objectifs doivent être
en harmonie avec le cadre de gestion des risques de la banque ou de
l'autorité de surveillance, ainsi qu'avec ses structures de
gouvernance.
L'utilisation des stress tests internes dans les banques
permet d'évaluer la résilience du portefeuille face à des
pertes sévères, d'identifier des stratégies
appropriées pour réduire les expositions, optimiser les revenus
et protéger le capital.
Les objectifs des stress tests pour les autorités de
supervision bancaire sont les suivants : évaluer l'adéquation du
niveau de capital ou de liquidité des banques sous surveillance,
promouvoir les tests de résilience et évaluer la capacité
de gestion des risques propres aux banques, soutenir d'autres activités
de surveillance telles que les inspections sur place, fournir une
évaluation quantitative des profils de risque des banques, tant au
niveau individuel que pour l'ensemble du système bancaire.
3.1. Structure de gouvernance et Stress tests
Les cadres de stress tests devraient inclure une structure de
gouvernance efficace, claire, complète et documentée. Cette
structure doit définir les rôles et les responsabilités de
la haute direction, des organes de surveillance et des personnes
chargées de superviser le fonctionnement continu du cadre de simulation
de crise. La gouvernance doit également identifier toutes les parties
prenantes clés et garantir une surveillance et un suivi exhaustifs et
cohérents des mesures prises à chaque étape du processus
de simulation de crise d'après (Basel Committee on Banking Supervision,
2018).
30
3.2. Gestion des Risques et Stress Tests
Les stress tests sont considérés comme un outil
efficace pour améliorer la gestion des risques en raison de leur
flexibilité et de la manière dont ils relient explicitement les
impacts potentiels à des événements spécifiques.
Ils permettent de déterminer comment un portefeuille se comportera
pendant une période de crise financière, ce qui en fait l'une des
parties importantes du processus de gestion intégrée des
risques.
L'émergence des stress tests est en grande partie
liée à l'introduction de l'application de modèles dans la
gestion des risques bancaires. Ces modèles représentent une
simplification de la réalité et permettent de mesurer les risques
sous certaines hypothèses spécifiques. Cependant, les conditions
réelles du marché peuvent inclure des scénarios
extrêmes et exceptionnels que ces modèles et leurs
hypothèses ne peuvent pas prendre en compte. Ainsi, l'objectif principal
des tests de résilience est d'analyser de telles lacunes dans la gestion
des risques bancaires voir (Lièák, 2016).
4. Value at Risk et Stress test
Parmi les méthodes les plus utilisées pour
quantifier les risques bancaires se trouvent la VaR (Value at Risk) et le
Stress Testing, qui sont couramment employées. La VaR est un outil de
gestion des risques apprécié pour sa simplicité et sa
flexibilité, adopté progressivement par les institutions
financières depuis les années 90. Cependant, des erreurs
fréquentes de gestion, notamment en période de crise, ont
été constatées lors de son utilisation. Pour faire face
aux risques extrêmes, les premiers stress tests ont été
développés. Plusieurs critiques sont adressées à
l'utilisation de la VaR dans la gestion des risques, notamment le
caractère subjectif du choix des paramètres tels que le niveau de
confiance et l'horizon de détention. De plus, la VaR manque de
précision pour les pertes extrêmes au-delà du niveau de
confiance considéré, ne fournissant pas d'informations sur leur
taille ni leur nature.
Cependant, les stress tests ont apporté deux
innovations majeures voir (Committee on the Global Financial System, 2005) :
- Ils explorent plus en profondeur les queues de la fonction de
distribution de la valeur du
portefeuille au-delà des niveaux de confiance couramment
utilisés dans la VaR.
- Ils établissent un lien flexible et explicite entre
les pertes extrêmes potentielles de la valeur du portefeuille et les
événements sous-jacents, c'est-à-dire les scénarios
de stress.
31
Cela permet d'identifier profondément et explicitement
les sources de risque, contrairement à l'approche purement statistique
de la VaR. Grâce à cette technique, il est possible de mesurer la
contribution de chaque facteur de risque, dans chaque scénario, à
l'évolution potentielle de la valeur du portefeuille.
Les stress tests fournissent des informations sur les risques
qui ne font pas partie de ceux généralement pris en compte par le
cadre de la VaR. En conséquence, ils permettent de mettre en
évidence des risques associés à des mouvements de prix
extrêmes et à des scénarios prospectifs qui ne sont pas
reflétés dans l'historique récent des séries de
prix utilisées pour calculer la VaR.
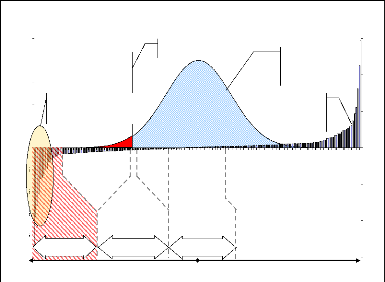
Figure 1 : Intégration du stress test dans la
VaR
2,50%
2,00%
0,50%
0,00%
1,50%
1,00%
Positionnement des scénarii catastrophes
parmi les différents outils de mesure du risque
(zone hachurée rouge)
-5,00 -3,75 -2,50 -1,25 0,00 1,25 2,50 3,75 5,00
%
Univers des scénarios
catastrophes
Chocs extrêmes avec
très
fortes pertes et très
faibles
probabilités d'occurence
Risque 1% mesuré par la
VaR
1%
Amplitudes de chocs
appliqués
Scénarios explorés
par
la VaR (1%)
Faibles chocs mesurés
par les sensibilités
Gain/Perte associé
à chaque scénario de
choc (Echelle de droite)
Probabilité
d'occurrence des différents chocs
(Echelle de gauche)
600
400
200
0
-200
-400
-600
Source : Committee on the Global Financial System.
(2005).
32
Section 2 : Classification, méthodologies et
modèles de stress tests
Dans cette section, nous examinerons en détail les
diverses catégories de stress tests, les approches utilisées pour
les réaliser, ainsi que les modèles et méthodologies
employés dans le processus de stress testing.
1. Les types des stress tests
Les tests de résilience sont généralement
classés en deux catégories distinctes : les tests de
sensibilité et les tests de scénario.
1.1. Test de sensibilité
Les tests de sensibilité consistent
généralement à apporter des changements progressifs
à un ou à quelques facteurs de risque afin de fournir des
réponses aux questions de simulation. Ils sont
généralement réalisés sur une période plus
courte, comme un choc instantané. Comparés aux tests de
scénario, les tests de sensibilité requièrent moins de
ressources et peuvent être utilisés comme une approche plus simple
pour évaluer l'impact des changements de risque lorsque des
résultats rapides ou des évaluations fréquentes sont
nécessaires voir BSIF (2009).
1.2. Tests de scénarios
Exactement, les tests de résilience de scénarios
évaluent l'effet des changements simultanés d'un ensemble de
variables constituant un scénario exceptionnel mais plausible. Ces
scénarios de stress tests doivent prendre en considération
plusieurs événements avec différents degrés de
gravité. Cette approche présente l'avantage de prendre en compte
les effets et les interactions entre plusieurs variables qui influencent le
modèle, ce qui n'est pas possible lorsque seulement un facteur de risque
est soumis à un choc. Les tests de résilience de scénarios
permettent ainsi d'avoir une vision plus réaliste des risques potentiels
et de mieux comprendre comment une combinaison d'événements
extrêmes pourrait affecter la solidité et la résilience
d'une institution financière.
1.2.1. Les types de scénarios stress tests
En général, il existe deux types de
scénarios générés dans un stress test selon
(Moussaoui, 2015):
33
- Scénario de base : C'est un
scénario sans stress qui suppose que la situation de
l'établissement en question suivra la même évolution dans
le futur et qu'il n'y aura pas de chocs prévus à l'avenir. Ce
scénario sert de référence pour évaluer la
performance de l'établissement dans des conditions normales.
- Scénario adverse : C'est un
scénario, également appelé scénario extrême,
dans lequel il est supposé que l'établissement en question soit
confronté à un choc extrême dans l'avenir, mettant ainsi sa
stabilité financière en péril. Ce scénario permet
d'évaluer la résilience de l'établissement face à
des conditions économiques et financières difficiles.
1.2.2. La conception des scénarios stress tests
La conception d'un scénario de stress implique de
définir quantitativement :
- La taille du choc initial : C'est l'ampleur
du changement qui sera appliqué par simulation aux facteurs de
risque.
- La manière dont les changements sont
appliqués et évoluent au fil du temps : Ce sont les
variations des facteurs de risque qui persistent et interagissent tout au long
de l'horizon du test, ce que l'on appelle "le post choc".
- Les probabilités d'occurrence correspondantes
: Il s'agit des probabilités associées à la
réalisation du scénario, c'est-à-dire la
probabilité que les événements stressants se
produisent.
Ces trois composantes, à savoir la taille du choc
initial, les variations post-choc des facteurs de risque et les
probabilités d'occurrence, sont essentielles pour la création et
l'évaluation d'un scénario de stress test.
1.3. Approche du stress test inversé
Les établissements utilisent l'approche du stress test
inversé qui consiste à commencer par l'identification du
résultat souhaité, puis à explorer les scénarios et
les circonstances susceptibles de mener à cette situation. Cette
approche est utilisée comme un outil de gestion des risques pour
améliorer la prise de conscience des vulnérabilités
actuelles et potentielles. Les établissements utilisent ces tests pour
évaluer la viabilité et la durabilité de leurs
modèles.
Ainsi les étapes du stress test se déroule comme
suit :
- Le choix du périmètre du stress test et la
détermination de l'hypothèse de crise permettent de
définir les paramètres spécifiques du test, tels que le
coefficient de
34
solvabilité en dessous de la limite
règlementaire, afin d'évaluer la résilience de
l'établissement face à des situations de crise potentielles de
manière réaliste et pertinente.
- Pour déterminer le couple (PD, LGD) responsable d'un
choc spécifique dans un stress test, il faut identifier le choc,
définir l'hypothèse de crise, collecter les données
historiques sur les défauts et les pertes, puis réaliser une
analyse quantitative pour évaluer son impact.
- Une analyse quantitative avec des modèles
établit les liens entre les variables macroéconomiques, la
probabilité de défaut (PD) et la perte en cas de défaut
(LGD), aidant ainsi à comprendre l'influence des conditions
économiques sur les risques de défaut et les pertes.
- Une analyse d'experts (économistes) évalue les
résultats du modèle pour choisir les variables économiques
responsables du choc dans les stress tests.
2. Les approches de Stress Test
Les modèles de stress test se basent sur deux approches
principales pour définir les événements à tester :
les scénarios historiques et les scénarios
hypothétiques.
- Scénarios historiques (méthodes
objectives) : Ces approches utilisent des événements
réels qui se sont produits dans le passé, tels que des crises
financières ou des périodes de turbulence économique. En
se basant sur ces événements passés, les stress tests
peuvent évaluer la résilience du portefeuille en simulant des
situations de marché réelles et tendues, avec moins de jugements
subjectifs.
- Scénarios hypothétiques
(méthodes subjectives) : Ces approches se concentrent sur des
événements potentiels ou des situations extrêmes qui n'ont
pas encore eu lieu, mais qui pourraient survenir à l'avenir. Les
scénarios hypothétiques permettent d'explorer des risques
spécifiques qui pourraient ne pas être reflétés dans
les événements passés, offrant ainsi une évaluation
plus complète des vulnérabilités du portefeuille.
En pratique, les stress tests peuvent combiner ces deux
approches pour créer des scénarios hybrides, utilisant à
la fois des événements historiques pour calibrer certains aspects
du test, et des éléments hypothétiques pour évaluer
des risques émergents ou inédits. Cette approche mixte permet de
mieux évaluer la robustesse du portefeuille face à un large
éventail de risques potentiels.
35
3. Les modèles de stress test
Les stress tests sont des outils d'évaluation de la
résilience des banques face à des chocs potentiels d'ordre
microéconomique ou macroéconomique. Ils peuvent être
appliqués à l'échelle des institutions financières
individuelles, appelée stress test micro prudentiel, ou à celle
du système financier dans son ensemble, connu sous le nom de stress test
macro prudentiel voir (Mathieu, 2014).
3.1. Les modèles Micro prudentiel
Les tests de résilience microprudentiels, qui sont
effectués à l'échelle de chaque banque individuelle, se
concentrent étroitement sur les risques spécifiques aux banques.
Ils évaluent les expositions au risque à des fins internes pour
déterminer si les fonds propres sont adéquats et pour allouer ces
fonds de manière appropriée. Ces tests sont également
utilisés par les autorités de contrôle pour évaluer
la santé des banques et la résilience du secteur bancaire dans
son ensemble voir (Taskinsoy, 2013).
Les tests de résilience étaient relativement
obscurs au 20éme siècle, mais ils sont devenus
familiers au 21éme siècle. La Banque des
règlements internationaux (BRI) les définit comme «Diverses
techniques utilisées par les institutions financières pour
évaluer leur vulnérabilité potentielle face à des
situations d'événements exceptionnels mais plausibles».
3.2. Les modèles Macro prudentiel
Les macros stress tests ne fonctionnent pas en tant qu'outil
autonome, mais plutôt comme une boîte à outils
utilisée par les banques centrales. Ils fournissent des scénarios
de crise communs aux différentes institutions, permettant ainsi de
tester la solidité financière des banques et des
établissements financiers de manière cohérente et
comparative.
Dans l'ensemble, les tests de résilience (micro et
macro) ont apporté des avantages financiers et sociétaux, car ils
ont permis de rassembler divers points de vue pour atteindre un objectif commun
: la construction et le maintien d'un système financier mondial
résilient, capable de faire face aux chocs, y compris les pires
récessions ou dépressions, comme l'induit un stress test.
Il existe deux principales méthodes d'agrégation
pour mener les tests de résilience : l'approche ascendante "bottom up"
(BU) et l'approche descendante "top down" (TD).
36
- Les tests de résilience microprudentiels (BU)
sont réalisés par les grandes banques individuelles pour
leur gestion interne des risques et par les superviseurs pour évaluer
leur solvabilité selon le pilier II de Bâle II et III, en
utilisant des analyses de sensibilité et des scénarios.
- Les tests de résilience macroprudentiels (TD,
ou une combinaison de BU et TD) sont menés par les banques
centrales et les autorités de contrôle pour évaluer la
stabilité de l'ensemble du système financier, ainsi que pour la
surveillance au niveau national et international.
Ces approches permettent d'évaluer la résilience
du système financier dans son ensemble et de prendre des mesures pour
améliorer sa capacité à faire face à des situations
de stress et de crise.
L'approche "Bottom-up" permet aux autorités
réglementaires d'appliquer un modèle commun à
différentes banques, ce qui leur permet de comparer les résultats
entre les banques afin d'identifier les vulnérabilités
liées à des chocs similaires. Cette méthode permet
d'évaluer la résilience des banques individuelles et de
comprendre comment elles réagiraient face à des scénarios
de stress communs, ce qui contribue à renforcer la stabilité du
système financier dans son ensemble.
L'approche "Top-down" dans les tests de résilience
permet aux banques individuelles d'utiliser leurs modèles internes. Le
principal avantage de cette approche est que les modèles internes des
banques capturent les spécificités de chaque
établissement, ce qui permet de mieux comprendre les facteurs
spécifiques qui influencent les résultats pour chaque banque.
Cette méthode offre une meilleure prise en compte des
caractéristiques propres à chaque institution, ce qui peut
améliorer la pertinence et la précision des résultats du
test de résilience voir (Anand, Guillaume, & Virginie, 2014).
Tableau 2 : Types des modèles de stress test
|
Typologie
|
Utilisation
|
Avantages
|
Inconvénients
|
|
Les banques utilisent leurs
|
Les modèles internes
|
Les banques utilisent des
|
|
propres tests de résilience,
|
évaluent l'adéquation des
|
méthodes de mesure des
|
|
Micro prudentiel
|
|
|
|
|
tels que des analyses de
|
fonds propres et la
|
risques variées, se
|
|
Banque individuelle
|
sensibilité et de scénarios,
pour évaluer leurs
|
résilience des banques.
|
concentrant soit sur des
portefeuilles ciblés, soit
|
|
Bottom up
|
expositions aux risques.
|
|
sur des facteurs de risque uniques.
|
37
|
Les tests de résilience
prudentiels recueillent des
données auprès des
banques
|
L'amélioration de la
gouvernance et de la
transparence est un aspect
|
L'amélioration de la
gouvernance et de la
transparence dans la
|
|
Micro prudentiel
|
pour évaluer leur solidité
|
essentiel de la
|
surveillance bancaire
|
|
financière et s'assurer
|
surveillance bancaire
|
exige des banques des
|
|
Superviseurs
|
qu'elles respectent les
|
pour assurer la stabilité et
|
ajustements coûteux et
|
|
Top down
|
exigences minimales en
|
la confiance dans le
|
complexes en matière de
|
|
termes de fonds propres et de liquidités.
|
secteur financier.
|
prêt et de planification du capital.
|
|
La planification
|
La répartition planifiée
|
La répartition planifiée
|
|
prévisionnelle des fonds
|
du capital consiste à
|
du capital est un
|
|
propres vise à assurer que les
|
appliquer de manière
|
processus prévisible mais
|
|
Macro prudentielle
|
banques disposent de
suffisamment de capitaux
|
cohérente plusieurs
scénarios à l'échelle du
|
coûteux, et complexe.
|
|
Banque centrale Top down
|
propres et de liquidités dans des conditions de
marché hautement improbables.
|
système pour garantir une allocation adéquate des
fonds propres.
|
|
|
L'aide fournie aux pays pour
|
Le coût de l'aide pour
|
Les résultats volontaires
|
|
renforcer leur résilience aux
|
renforcer la résilience aux
|
et trompeurs de l'aide
|
|
Macro prudentielle
|
|
|
|
|
chocs vise à favoriser la
|
chocs est partagé entre le
|
peuvent entraîner une
|
|
FMI, FSAP
|
stabilité financière, la
|
FMI et la Banque
|
perte de crédibilité, ainsi
|
|
croissance et la diversité du
|
mondiale, et elle est mise
|
qu'un gaspillage de
|
|
Bottom up
|
secteur financier, en
|
en oeuvre de manière
|
ressources et une perte
|
|
Top down
|
appliquant des mesures
cohérentes.
|
volontaire, systématique
et cohérente.
|
d'efficacité.
|
Source : Taskinsoy John (2019), Typology of Stress
Testing
38
Section 3 : Mise en place des stress tests :
procédures et
démarches
Dans cette section, nous abordons les principales
étapes et démarches impliquées dans la mise en place des
stress tests au sein des institutions financières.
1. Les étapes clés de la mise en place des
stress tests Le processus des tests de résilience comprend
plusieurs étapes, telles que :
- Définition des objectifs : Les
objectifs du stress testing doivent être précisément
définis et compréhensibles pour les décideurs, allant
au-delà de simples contraintes réglementaires.
- Définition du périmètre :
Selon les objectifs, le stress test peut être appliqué
à l'ensemble de l'établissement ou à un
périmètre plus restreint. Un périmètre
réduit facilite l'exploitation des résultats mais peut limiter la
mesure des corrélations entre activités ou secteurs.
- Définition des scénarios :
Les chocs appliqués doivent être adaptés à
la nature de l'établissement et refléter son aversion au risque.
Ils peuvent être de différentes natures, tels que les tests de
robustesse des modèles ou les tests de stabilité
financière.
- Choix de la démarche : Le stress
testing peut être effectué selon deux approches : quantitative
basée sur des modèles ou qualitative avec l'expertise d'un groupe
d'experts.
- Analyse et décisions : L'analyse
des résultats mettra l'accent sur les tendances dégagées
et les niveaux atteints par rapport aux limites et à la perception des
risques par les dirigeants. Les décisions qui découlent de ces
exercices porteront sur les règles régissant l'activité,
comme les plans de contingence et les limites de risques.
2. Mise en oeuvre des stress tests de
crédit
Les stress tests de crédit suivent une procédure
en trois étapes pour évaluer l'impact d'un scénario
macroéconomique stressé sur la qualité des expositions de
crédit des banques. Tout d'abord, les valeurs prévisionnelles des
variables macroéconomiques sont déterminées pour un
scénario spécifié et une période donnée.
Ensuite, l'impact de ces variations sur les paramètres de risque de
crédit des banques, tels que la probabilité de défaut (PD)
et la perte en cas de défaut (LGD), est estimé. Enfin, les
paramètres de risque de crédit stressés sont
utilisés pour évaluer l'incidence du scénario de stress
sur la solvabilité des banques.
39
En pratique, la mise en oeuvre des deux premières
étapes implique généralement deux types de
modélisation distincts. Tout d'abord, pour prédire le
comportement des variables macroéconomiques, telles que la croissance du
P11B et le taux d'intérêt à long terme, sous un
scénario de stress prédéfini et sur une période
donnée, on utilise généralement un modèle macro
économétrique. Ce modèle intègre des chocs
défavorables pour une ou plusieurs variables macroéconomiques, et
les équations du modèle déterminent comment ces variables
ainsi que d'autres se comportent en réponse à ces chocs sur
l'horizon des tests de résilience. Ensuite, une deuxième
étape de modélisation est nécessaire pour estimer l'impact
des variables macroéconomiques stressées sur les
paramètres de risque de crédit des banques à l'horizon des
tests de résilience. Ces modèles de risque de crédit
consistent principalement en une ou plusieurs équations reliant les
paramètres de risque de crédit des banques aux variables
macroéconomiques.
Les variables macroéconomiques stressées,
dérivées du modèle macro économétrique, sont
utilisées comme entrées dans l'équation du modèle
de risque de crédit pour obtenir les valeurs stressées des
paramètres de risque de crédit. Enfin, ces valeurs
stressées des paramètres de risque de crédit sont
appliquées aux pertes et aux profits des banques afin d'estimer l'impact
sur leur position de solvabilité.
3. Etudes empiriques des stress tests sur le risque de
crédit
(Zeman & Jurca, 2008), ont évalué l'impact
d'un ralentissement simulé de l'économie slovaque sur le secteur
bancaire du pays. À l'aide d'un modèle de correction d'erreurs
vectorielles, ils ont constaté que, dans l'ensemble, un ralentissement
temporaire mais significatif de la croissance du P11B ne représenterait
pas une menace substantielle pour le secteur bancaire slovaque, à
condition que la politique monétaire réponde de manière
adéquate. Cette politique monétaire aurait un effet positif en
atténuant la récession et en améliorant la qualité
du portefeuille de crédit grâce à la baisse des taux
d'intérêt, ce qui allégerait le fardeau de la dette des
emprunteurs à court terme. Cependant, ils ont souligné que
l'absence de réponse adéquate aux chocs de croissance du P11B
ainsi que les risques de taux de change et de taux d'intérêt
pourraient constituer des menaces plus significatives pour le secteur bancaire
slovaque en raison de l'ouverture de l'économie du pays.
Dans l'étude de (Ben youcef, 2018), un modèle a
été proposé pour réaliser un stress test macro du
risque de crédit sur un échantillon de dix banques commerciales
tunisiennes. L'approche
40
utilisée implique d'expliquer le risque de
crédit pour chaque banque en utilisant un modèle statistique
à effets fixes. Ensuite, un stress test de résilience a
été réalisé en utilisant une simulation de Monte
Carlo pour générer des distributions de pertes de risque de
crédit pour différents scénarios, permettant ainsi de
déterminer les pertes inattendues pour chaque banque. Les
résultats de l'analyse ont révélé une relation
négative entre le risque de crédit et le taux de croissance du
PIB, ainsi que le ratio des prêts sur le total des actifs. De plus, le
ratio de rendement des actifs et la taille de la banque ont également
été identifiés comme ayant un impact négatif sur le
risque de crédit. Les résultats du test de résilience ont
montré qu'un scénario défavorable de ralentissement
économique entraîne une augmentation des pertes de crédit
les plus élevées pour toutes les banques de l'échantillon,
mais que ces pertes inattendues peuvent être couvertes par le capital
disponible des banques concernées.
Dans leur étude, (Onha, Yen, Trang, & Trung, 2018)
ont évalué la capacité des banques commerciales
vietnamiennes à faire face à une augmentation du risque de
crédit à la suite de chocs macroéconomiques. Ils ont
utilisé un modèle VAR pour estimer la relation entre les
variables macroéconomiques (PIB réel, taux de change réel,
taux d'intérêt prêteur et taux d'inflation) et ont
établi des scénarios macroéconomiques à partir de
ces estimations. Ensuite, ils ont utilisé un modèle GMM pour
estimer la relation entre le ratio de prêts non performants (risque de
crédit) et les variables macroéconomiques identifiées
précédemment. Enfin, le nouveau ratio de capital requis (CAR) a
été recalculé en tenant compte de l'augmentation du risque
de crédit et de l'augmentation des créances douteuses. Les
résultats montrent que le risque de crédit auquel les banques
commerciales sont confrontées est relativement limité tant que
leurs actifs pondérés en fonction des risques restent
inchangés. Cependant, si ces chiffres augmentent à mesure que les
banques étendent leurs prêts, le CAR de toutes les banques
diminuera considérablement, et certaines des plus grandes banques
risqueront de ne pas pouvoir répondre aux exigences de la Banque
centrale en matière de capital.
Dans son étude, (Zouali, 2015) a tenté de
développer un modèle approprié pour expliquer le risque de
défaut au sein de la banque marocaine BMCI en utilisant un modèle
VAR. Ce modèle a ensuite été utilisé pour simuler
des chocs sur l'ensemble des variables explicatives du risque de crédit
afin d'évaluer leur impact sur la solvabilité de la banque. Les
résultats du modèle indiquent que les variables PIB, inflation et
crédit immobilier sont les plus significatives. L'auteur propose que les
fonds propres de la banque BMCI absorbent ces chocs afin de
41
maintenir un ratio de solvabilité supérieur
à 8%. Cependant, il souligne que la crise immobilière a un impact
plus prononcé sur les fonds propres de la banque.
Les travaux de (Andrea, Danilo, Nicola, & Tommaso, 2023)
se concentre sur l'utilisation d'un modèle VAR bayésien pour
évaluer la suffisance en capital d'une banque à travers des tests
de résistance. L'étude vise à analyser les impacts
potentiels des chocs macroéconomiques sur la capacité de la
banque à maintenir des niveaux adéquats de capitaux
réglementaires. En utilisant des techniques statistiques basées
sur la théorie VAR bayésienne, l'article explore la relation
entre les variables macroéconomiques, les indicateurs de risque et les
mesures de capital de la banque. Cela permet d'évaluer la
résilience de la banque face à différentes conditions
économiques stressantes.
(Jacobs, Ahmet, & Frank, 2015) ont contribué
à la littérature en développant une méthodologie de
test de résistance au risque de crédit basée sur la
méthode bayésienne. Leur travail propose une approche qui peut
être mise en oeuvre par des banques de petite et moyenne taille, en
intégrant formellement des scénarios exogènes et en
quantifiant l'incertitude dans les résultats du modèle
résultant des entrées du modèle stochastique. Ils ont
également comparé leur modèle bayésien à un
modèle classique, en mettant en évidence des différences
significatives en termes de mesure de l'incertitude statistique et d'erreur
cumulée. Les résultats empiriques obtenus à partir des
mises en oeuvre du CCAR viennent appuyer leur approche. Cette contribution
à la littérature renforce la compréhension des tests de
résistance et de la validation des modèles dans le contexte de la
gestion du risque de crédit.
4. Avantage de l'application de Stress Tests avec la
modélisation BSVAR
La méthode de réalisation des stress tests
à l'aide du modèle bayésien présente
également des avantages selon plusieurs auteurs :
Selon (Pflug & Pohl, 2018), l'approche bayésienne
permet de quantifier l'incertitude liée aux scénarios de stress
en utilisant des distributions de probabilité pour les variables
clés. Cela permet d'obtenir des résultats plus robustes et de
prendre en compte les différentes sources d'incertitude dans les
prévisions des pertes potentielles. Ainsi d'après (Giudici &
Spelta, 2016), l'approche bayésienne permet d'incorporer des
connaissances expertes et des informations supplémentaires dans le
processus de modélisation des scénarios de stress. Cela permet
d'améliorer la qualité des prévisions en intégrant
des informations spécifiques au contexte et en évitant les biais
liés à une modélisation purement statistique.
42
Selon (Gael, et al., 2023), l'approche bayésienne
permet de gérer efficacement les données manquantes ou les
informations incomplètes dans les scénarios de stress. En
utilisant des techniques d'imputation bayésienne, il est possible
d'estimer les valeurs manquantes de manière robuste et d'éviter
les biais liés à des valeurs manquantes arbitraires. En outre
selon (Hegde, Hegde, Hegde, Marthanda, & Logu, 2023), l'approche
bayésienne permet de combiner de manière cohérente les
informations provenant de différentes sources, telles que des
données historiques, des données expertes et des données
économiques, pour construire des scénarios de stress plus
réalistes et plus précis. Cela permet d'obtenir des
résultats plus fiables et de prendre en compte une plus grande
variété de facteurs pertinents.
Enfin, selon (Gary, Dimitris, & Davide, 2019), l'approche
bayésienne permet de mettre à jour les scénarios de stress
au fur et à mesure que de nouvelles informations deviennent disponibles,
ce qui permet de suivre l'évolution de l'environnement économique
et d'ajuster les prévisions en conséquence. Cela permet d'obtenir
des résultats plus adaptés aux conditions actuelles et de prendre
des décisions plus éclairées.
En conclusion, l'utilisation de l'approche bayésienne
dans la réalisation des stress tests présente des avantages
significatifs, notamment en termes de quantification de l'incertitude,
d'intégration de connaissances expertes, de gestion des données
manquantes, de combinaison d'informations provenant de différentes
sources et de mise à jour des scénarios de stress en fonction des
nouvelles informations disponibles.
43
Conclusion
Dans ce chapitre, nous avons présenté le stress
test comme un outil pratique de gestion des risques, visant à quantifier
les pertes ou les risques potentiels dans des circonstances
particulières, souvent extrêmes. Ces circonstances sont
définies par des scénarios issus de l'expérience
historique (stress test historique) ou jugés possibles à l'avenir
en tenant compte de l'évolution des facteurs macroéconomiques,
socioéconomiques ou politiques (stress test hypothétique).
Les modèles de tests de résilience varient d'un
établissement à l'autre en fonction de la nature du
problème étudié et de la sélection des
scénarios de stress. En général, les stress tests jouent
deux rôles principaux : d'une part, en tant qu'outil de gestion des
risques utilisé par les banques, et d'autre part, en tant qu'instrument
de supervision macroprudentielle utilisé par les régulateurs de
différents pays, avant même que la crise ne survienne. La
flexibilité de pouvoir mettre en oeuvre différents tests en
fonction du champ d'application, du risque ou du scénario à
étudier est un avantage certain.
Enfin, nous avons mis l'accent sur la littérature des
différentes études du stress test effectuées, que ce soit
au niveau macroprudentiel ou microprudentiel. Ainsi chaque étude montre
l'utilisation d'une approche différente mais qui conduit aux mêmes
objectifs. Tandis qu'une nouvelle vision du stress test inversé qui est
déduit d'une modélisation bayésienne qui présente
une multitude des avantages du niveau économétrique et
analytique. Ce qui va faire l'objet de notre dernier chapitre qui va
développer ses approches pour crée une nouvelle dimension pour
modéliser l'intuition de l'état d'esprit des preneurs des
décisions.
44
CHAPITRE 3 : APPLICATION DU STRESS TEST DE RISQUE
DE CREDIT
45
CHAPITRE 3 : APPLICATION DU STRESS TEST DE RISQUE
DE CREDIT
Introduction
Dans le premier chapitre, nous avons abordé le risque
de crédit et les règles prudentielles au niveau international et
national. Dans le deuxième chapitre, nous avons mis en évidence
l'importance du stress test en tant qu'outil pour évaluer la
résilience d'une banque.
Dans ce chapitre, notre objectif est d'établir un
modèle de risque de crédit englobant qui prend en compte à
la fois les facteurs spécifiques à la banque et ceux liés
à l'environnement macroéconomique. Pour atteindre cet objectif,
nous avons commencé par critiquer les approches utilisées dans la
plupart des travaux réalisés, et nous nous efforçons
à chaque étape de résoudre leurs insuffisances en
améliorant la modélisation. Cela nous permettra de parvenir
à un cadre complet grâce au modèle BSVAR. En utilisant ce
modèle, nous analysons l'impact d'une mauvaise prise de décision
résultant de variations de certains facteurs, dans le but
d'évaluer le risque de crédit à travers un stress test
inversé.
Dans ce chapitre, nous le divisons en trois sections
distinctes. La première section est dédiée à la
présentation de la BFPME ainsi que de sa direction des risques. Dans la
deuxième section, nous débutons en exposant la
méthodologie choisie pour notre étude, puis nous procédons
à l'estimation des modèles, et nous clôturons notre section
par une comparaison visant à vérifier l'importance de
l'intégration de l'approche bayésienne. Enfin, la
troisième section se concentre sur l'application du stress test
inversé sur le modèle établi et l'analyse des
résultats obtenus, permettant ainsi d'évaluer l'impact de ces
réflexions sur le niveau des NPL de la banque face aux scénarios
de stress.
46
Section 1 : Présentation et organisation de la
BFPME
La section suivante sera dédiée à une
introduction générale sur la BFPME. Nous commencerons par une
brève rétrospective historique de la banque, puis nous aborderons
ses missions, ses objectifs et sa stratégie, tout en examinant
également la structure de la direction d'accueil et ses
responsabilités.
1. Présentation et historique de la BFPME
Au début des années 2000, la Tunisie a ressenti
une stagnation de son modèle économique et a décidé
de lier sa politique de développement à l'entrepreneuriat. Cette
démarche visait à atteindre des objectifs d'inclusion
financière et de développement régional, ce qui a conduit
à la création de la Banque de Financement des Petites et Moyennes
Entreprises (BFPME).
1.1. Historique de la BFPME
La BFPME a été établie le 1er mars 2005
et opère conformément à la loi n°2016-48 du 11
juillet 2016, qui régit les établissements de crédit. Elle
est en mesure de soutenir financièrement tous les projets
d'investissement des PME, qu'elles soient en phase de création ou
d'extension, pour des investissements compris entre 100 mille et 15 millions de
TND, couvrant ainsi divers secteurs économiques. À noter que
certaines exceptions s'appliquent, notamment dans le secteur du tourisme (si la
composante principale est l'hébergement) et de la promotion
immobilière (si elle est destinée à l'habitation).
La BFPME intervient en accordant des crédits à
moyen et long terme, principalement en cofinancement avec d'autres banques
locales, ce qui en fait un acteur central du segment de la mésofinance
dédiée aux PME. Elle se positionne entre la microfinance, qui
cible les TPE, et la finance bancaire destinée aux grandes
entreprises.
1.2.La stratégie de la BFPME
La BFPME assure principalement une double mission, à
savoir :
- Fournir un accompagnement aux promoteurs tout au long des
diverses étapes de la réalisation de leurs projets, y compris
l'identification de l'idée du projet, l'élaboration du business
plan, le bouclage du schéma de financement, la création juridique
de la société, ainsi que le suivi de la mise en oeuvre et du
développement de l'activité.
47
- La BFPME a pour mission de simplifier l'accès au
financement pour la création et l'extension des PME en Tunisie. À
cette fin, elle est chargée de fournir des crédits à moyen
et long terme exclusivement destinés à financer les
investissements. De plus, elle joue un rôle de passerelle vers des
instruments financiers spécifiques.
Dans le cadre de sa stratégie de développement
ambitieuse, visant à moderniser ses structures et ses méthodes de
gestion pour aligner la banque sur les normes internationales, la BFPME s'est
fixée les objectifs suivants :
- Améliorer la qualité des services et des
structures d'accueil.
- Accroître les ressources à des coûts
optimisés pour une meilleure rentabilité.
- Moderniser les outils d'intervention et de gestion.
- Mettre en place des mécanismes de contrôle et de
suivi efficaces pour garantir la fiabilité
des opérations et des données.
- Assurer une meilleure gestion et maîtrise des risques.
2. Présentation de la direction des risques
La direction des risques a pour mission de classer les divers
types de risques associés à l'activité de la banque,
d'établir les procédures et méthodes pour
l'identification, l'analyse, le contrôle et le suivi de ces risques. Elle
est également chargée d'évaluer les risques et d'estimer
la vulnérabilité de la banque ainsi que de ses performances
financières en recourant aux stress tests.
La direction des risques est rattachée au directeur
général adjoint en charge du contrôle permanent et est
supervisée par un directeur.
48
Section 2 : Modélisation du risque de
crédit
Cette section commence par présenter la
méthodologie de recherche ainsi que les variables utilisées.
Ensuite, elle passe à l'estimation des modèles de risque de
crédit. Enfin, une comparaison sera effectuée pour
démontrer l'importance de l'intégration de l'approche
bayésienne dans le contexte des modèles de la famille VAR.
1. Méthodologie de recherche
Nous commençons par la présentation et l'analyse
technique des modèles VECM et BSVAR, puis la détermination des
variables utilisées.
1.1. Présentation du modèle
VECM
Depuis la critique formulée par (Sims C. , 1980), la
modélisation Vectorielle Autorégressive (VAR) est devenue un
outil standard en économétrie pour l'analyse des séries
temporelles multivariées. Grâce à l'utilisation de
modèles vectoriels, les chercheurs peuvent examiner simultanément
plusieurs variables en interaction.
Depuis la fin des années 80, il est devenu
évident que la non-stationnarité est une caractéristique
courante des séries temporelles macroéconomiques et
financières. En effet, la plupart des séries présentent
des tendances non stationnaires. Pour résoudre ce problème,
l'économétrie des séries non stationnaires a connu un
développement majeur grâce à la théorie de la
cointégration, élaborée par (Engle & Granger, 1987),
ainsi que par (Johansen, Statistical Analysis of Cointegrating Vectors, 1988)
et (Johansen, 1991). L'attrait croissant de ce concept réside dans sa
capacité à permettre l'estimation et la mise à
l'épreuve des relations d'équilibre à long terme entre les
variables grâce à la modélisation du Vector Error
Correction Model (VECM).
1.2. Présentation du modèle BSVAR
La modélisation Structurelle Vectorielle
Autorégressive (SVAR) est un élargissement de la
modélisation VAR. Ce dernier est établi comme une démarche
a-théorique, qui se limite à l'étude de la dynamique des
variables sans aucune identification théorique. Pour faire face à
cette limite, nous soulignons l'apparition des modèles SVAR.
Certes, les modèles SVAR offrent un moyen robuste et
pratique pour la modélisation et l'interprétation des chocs
externes. Cependant, comme la plupart des modèles
économétriques,
49
le modèle SVAR repose exclusivement sur les
informations disponibles dans les données. Cela ne permet pas de tenir
compte de l'intuition et des perspectives des responsables et des
décideurs, en particulier dans les situations exceptionnelles, telles
que les périodes de crises et de chocs économiques majeurs.
Par conséquent, l'approche fréquentiste, qui ne
prend pas en compte les éléments non observables, peut limiter
l'interprétation. C'est pourquoi l'approche de l'estimation
bayésienne a été développée, notamment
à travers les modèles BSVAR. Cette approche permet à
l'économètre d'incorporer des informations supplémentaires
sur les contraintes d'identification ainsi que sur les paramètres du
modèle en se basant sur des distributions probabilistes, appelées
distributions à priori.
1.3. Présentation des données
Dans le cadre de notre étude visant à estimer le
modèle de risque de crédit, nous avons utilisé des
données spécifiques à la BFPME obtenues à partir
des états financiers publiés sur le site de la CMF, ainsi que des
données macroéconomiques provenant des sites de l'INS et de la
BCT. Nous avons veillé à rassembler un volume maximal
d'observations pour assurer la robustesse de nos modèles. En
conséquence, nous avons constitué une base de données
trimestrielle couvrant la période allant de T1 2006 à T4 2021, ce
qui nous a donné 64 observations. (Annexe1)
- La variable à expliquer :
La variable que nous utilisons pour mesurer le risque de
crédit est le ratio des prêts non performants. Cette variable est
couramment utilisée dans la littérature comme un indicateur de
mesure du risque de crédit. (Annexe2)
Figure 2 : L'évolution des prêts non
performants
100.00
|
80.00 60.00 40.00 20.00
0.00
|
|
|
Mar-06 Dec-06 Sep-07 Jun-08 Mar-09 Dec-09 Sep-10 Jun-11 Mar-12
Dec-12 Sep-13 Jun-14 Mar-15 Dec-15 Sep-16 Jun-17 Mar-18 Dec-18 Sep-19 Jun-20
Mar-21 Dec-21
|
NPL
Source : élaborer par l'auteur à l'aide de
Excel
50
D'après le graphique ci-dessus, nous constatons une
tendance à la hausse des NPL depuis la création de la banque
jusqu'à aujourd'hui. Le niveau des prêts non performants de la
BFPME a atteint un niveau élevé de 83,52 % en 2021 en raison de
la nature de son activité et de la faiblesse de son modèle
économique en tant que banque d'investissement.
- Les variables explicatives :
Pour identifier les variables explicatives du risque de
crédit, nous nous sommes inspirés des recherches
précédentes menées par (Dimitrios, Angelos, & Vouldis,
2012), (Alexandri & Santoso, 2015), ainsi que (Messai & Jouini, 2013).
Le tableau ci-dessous présente les variables explicatives que nous avons
incluses dans notre modèle.
Tableau 3 : Les variables micros et macros
économiques
|
Variables
|
Mesure
|
Description
|
|
Variables Spécifique
|
ROA
|
Rentabilité des actifs
résultat net
|
Les banques non rentables sont davantage incitées
à
sélectionner soigneusement leurs clients
afin
d'améliorer la qualité de leur portefeuille.
|
|
total actifs
|
|
PCC
|
Provisions sur
créances classés
|
Les banques ont tendance à constituer des provisions
lorsqu'elles anticipent des niveaux élevés de pertes.
|
|
Variables Macroéconomique
|
IPC
|
Indice des Prix à la Consommation
|
Permet de mesurer l'évolution du niveau moyen des prix
des biens et services consommés par les ménages et permet
d'analyser l'impact inflationniste.
|
|
IPI
|
Indice de Production Industrielle
|
C'est un instrument statistique qui mesure les
variations des quantités produites dans l'industrie.
|
|
TMM
|
Taux de Marché
Monétaire
|
C'est le taux d'intérêt sur le marché
monétaire qui présente un instrument d'indexation pour les
banques, en termes de crédit, de dépôt à terme et
d'épargne.
|
|
USD
|
Taux de Change
USD/TND
|
La dépréciation de la monnaie locale
entraîne une détérioration du portefeuille de clients
libellé en devise étrangère.
|
Source : préparer par l'auteur
2. Estimation des modèles
Pour étudier l'impact des variables spécifiques
à la banque et des variables macroéconomiques sur le risque de
crédit au sein de la BFPME, nous avons d'abord effectué plusieurs
tests à l'aide du logiciel R-CRAN avant de procéder à
l'estimation des modèles.
51
2.1. Application du modèle VECM
2.1.1. Les tests des pré-estimations - Test de la
racine unitaire :
Dans ce test, nous nous intéressons à l'analyse
du niveau d'intégration des variables. Pour ce faire, nous utilisons les
tests ADF et (Kwiatkowski, Phillips, Schmidt, & Shin, 1992) de la racine
unité sur chaque variable, en utilisant les commandes (adf.test,
kpss.test) fournies par le package « tseries » du logiciel R. Les
résultats obtenus sont les suivants :
Tableau 4 : Test de la racine unitaire
|
Test de la racine unitaire
|
|
Variable
|
ADF
|
P-value
|
KPSS
|
P-value
|
|
NPL(0)
|
-1.248
|
0.879
|
1.660
|
0.01
|
|
ROA(0)
|
-1.327
|
0.847
|
0.524
|
0.036
|
|
PCC(0)
|
-1.341
|
0.842
|
1.458
|
0.01
|
|
IPC(0)
|
-3.041
|
0.153
|
1.677
|
0.01
|
|
IPI(0)
|
-3.283
|
0.082
|
1.678
|
0.01
|
|
TMM(0)
|
-2.782
|
0.258
|
0.771
|
0.01
|
|
USD(0)
|
-2.167
|
0.507
|
1.580
|
0.01
|
|
NPL(1)
|
-2.251
|
0.01
|
0.346
|
0.1
|
|
ROA(1)
|
-3.815
|
0.023
|
0.235
|
0.1
|
|
PCC(1)
|
-4.198
|
0.01
|
1.006
|
0.1
|
|
IPC(1)
|
-4.880
|
0.01
|
0.063
|
0.1
|
|
IPI(1)
|
-4.398
|
0.01
|
0.174
|
0.1
|
|
TMM(1)
|
-3.004
|
0.01
|
0.106
|
0.1
|
|
USD(1)
|
-4.105
|
0.011
|
0.237
|
0.1
|
Source : préparer par l'auteur à l'aide de
logiciel R CRAN
Pour le test ADF l'hypothèse nulle est celle de non
stationnarité, tandis que pour le test KPSS l'hypothèse nulle est
la stationnarité. D'après les résultats illustrés
dans le tableau ci-dessus, nous remarquons que toutes les variables du
modèle sont non stationnaires en niveau, et stationnaires en
différence. Par conséquent, les variables du modèle sont
toutes intégrées d'ordre 1. (Annexe3)
- Détermination de l'ordre du retard :
Pour la détermination du nombre de retard du
modèle VAR correspondant, nous avons utilisé la commande «
VARselect » du package « vars », qui offre 4 critères de
sélection du nombre de retard, à savoir : le critère
(Akaike, 1974), le critère de (Hannan & Quinn, 1979), le
critère de (Schwarz, 1978) et le critère d'erreur de
prévision (FEP). Les résultats sont présentés dans
le tableau ci-dessous :
52
Tableau 5 : Détermination du nombre des
retards
|
Lag.max
|
AIC(n)
|
HQ(n)
|
SC(n)
|
FPE(n)
|
|
1
|
-
|
-
|
-
|
-
|
|
2
|
2
|
1
|
1
|
2
|
|
3
|
2
|
1
|
1
|
2
|
|
4
|
2
|
1
|
1
|
2
|
|
5
|
2
|
2
|
2
|
2
|
Source : préparer par l'auteur à l'aide de
logiciel R CRAN
Selon les résultats obtenus, nous constatons que le
nombre de retard optimal choisi est de 2 selon les suggestions des
critères. Par conséquent nous affirmons que nous sommes en
présence d'un modèle ??????(?? = 2).
(Annexe4)
- Test de cointégration :
L'économétrie des séries non
stationnaires a connu un développement à travers la
théorie de la cointégration, qui a été
développée par (Engle & Granger, 1987) (Johansen, Statistical
Analysis of Cointegrating Vectors, 1988) et (Johansen, 1991). Ces auteurs ont
présenté une solution plausible, dans le cas de non
stationnarité avec des variables dites intégrées d'ordre
1. Cette approche consiste à dégager des relations
d'équilibre de long terme entre les différentes variables du
modèle, appelé des relations de cointégration.
Tableau 6 : Les résultats du Test de
cointégration
|
|
Valeurs du test
|
Valeurs Critiques
|
|
H0
|
Lag = 2
|
90%
|
95%
|
99%
|
|
??
|
= ??
|
48.69
|
42.06
|
44.91
|
51.30
|
|
??
|
<= ??
|
33.93
|
36.25
|
39.43
|
44.59
|
|
??
|
<= ??
|
25.07
|
30.84
|
33.32
|
38.78
|
|
??
|
<= ??
|
15.36
|
24.78
|
27.14
|
32.14
|
|
??
|
<= ??
|
12.62
|
18.90
|
21.07
|
24.75
|
|
??
|
<= ??
|
9.92
|
12.91
|
14.90
|
19.19
|
|
??
|
<= ??
|
0.09
|
6.50
|
8.18
|
11.65
|
Source : préparer par l'auteur à l'aide de
logiciel R CRAN
D'après ces résultats, nous concluons que notre
modèle ??????(2) présente une seule
équation de cointégration, car l'hypothèse
H0: r = 1 est acceptée tandis que
r = 0 est rejeté. En d'autres termes, nos
variables intégrées d'ordre 1 sont liées entre elles en
niveau par une équation d'équilibre de long terme. (Annexe5)
53
2.1.2. Estimation du modèle VECM
En effet, l'estimation du modèle VECM permet de
déterminer le vecteur de la cointégration â. Pour ce faire,
nous nous appuyons sur les procédures d'estimation fournies par le
package «vars» du logiciel R. Ainsi, l'équation de
cointégration nous offre une forme d'équilibre de long terme,
laquelle est obtenue à partir de l'équation de
cointégration suivante (Annexe6) :
åt-1 = NPLt-1 + 2.41ROAt-1 -
7.42????????-1 + 160.74IPCt-1 -
368.55IPIt-1 - 5.33TMMt-1 -
88.61USDt-1
En se basant sur ces résultats d'estimation, nous
pouvons dériver l'équation du modèle VECM comme suit :
NPLt = -17.838 + 0.665 NPLt-1 + 0.059
ROAt-1 + 0.443 ????????-1 - 3.509 IPCt-1 - 5.066 IPIt-1
+ 0.406 TMMt-1 - 2.239 USDt-1 + 0.071 NPLt-2 -
0.230ROAt-2 + 0.363 ????????-2 - 4.832 IPCt-2 - 2.758
IPIt-2 + 0.165 ????????-2 - 1.974 USDt-2 +
åt
Les résultats de validation du modèle VECM
montrent, selon l'annexe 7, que les résidus sont stationnaires, non
corrélés et suivent la loi normale d'après les tests ADF,
Breusch-Godfrey et Jarque Bera respectivement. Enfin, les résultats du
test d'hétéroscédasticité montrent que la
probabilité associée est supérieure à 5%, ce qui
signifie l'existence d'Homoscédasticité des résidus.
(Annexe7)
2.2.Application de l'approche BSVAR
Dans le cadre de notre objectif d'étude, nous
introduirons, dans cette partie, l'approche de la statistique structurelle et
bayésienne en utilisant les mêmes variables que celles
employées dans le modèle VECM.
Dans la méthode scientifique, il existe deux types de
probabilités différents, ce qui peut créer de la confusion
parmi les chercheurs. Ce sont fondamentalement deux façons de penser
distinctes, qui visent à élaborer des opinions sur le
fonctionnement de la nature et la composition de la réalité.
La principale différence entre les deux approches
réside dans le fait que l'approche fréquentiste raisonne en
termes de vraisemblance, tandis que l'approche bayésienne raisonne en
termes de
54
plausibilité (ou crédibilité) des
hypothèses. La raison qui explique ce choix par les fréquentistes
est qu'ils estiment que l'approche bayésienne comporte deux critiques
majeures :
- Trop complexe : Ce n'est pas le cas lorsque
des logiciels et des algorithmes sophistiqués tels que le logiciel
R-CRAN sont disponibles. Pour remédier à ce problème, les
fréquentistes raisonnent en termes de vraisemblance à travers la
statistique de Fisher, qui se base sur des intervalles de confiance
fixés par les chercheurs, pouvant aller jusqu'à 10 % pour
accepter une hypothèse. Cela pose un problème majeur, en
particulier dans les cas de crises et de stress. En revanche, l'approche
bayésienne fonctionne par inférence, ce qui signifie qu'il n'y a
pas de rejet des hypothèses, mais au fil de nombreuses
itérations, on s'approche de la réalité, avec la
possibilité de prendre en compte toutes les hypothèses existantes
et/ou d'intégrer de nouvelles hypothèses.
- Trop subjectif : Cette objection ne tient
pas non plus, car la statistique fréquentiste utilise également
une forme de subjectivité, en particulier à travers le principe
de parcimonie, souvent appelé « le Rasoir d'Ockham ».
Figure 3 : Différences entre les approches
fréquentiste et bayésienne
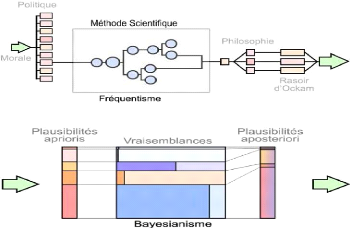
Source : Livre formule du savoir Lê Nguyên
2018
D'après (Nguyên, 2018), la statistique
bayésienne est une méthode globale qui a une grande portée
philosophique et qui contribue significativement à une réflexion
approfondie. Elle répond de manière adaptée au contexte
des tests de stress en évaluant la plausibilité des
hypothèses et en intégrant une dimension critique pour les
décideurs.
55
Cependant, avant de pouvoir procéder à ce
traitement, il est nécessaire de spécifier des contraintes
d'identification. Dans notre cas, avec un modèle à sept
variables, nous sommes amenés à introduire 21 contraintes
d'identification, conformément à la règle (??(?? -
1)/2).
Par conséquent, en s'inspirant, principalement, des
travaux de (Sims & Zha, 1998) et de (Waggoner & Zha, 2003), on
définira le cadre de notre modèle BSVAR, surtout concernant la
nature et les spécificités de la distribution à priori.
2.2.1. Spécification des contraintes
d'identification
La modélisation SVAR est une extension de la
modélisation VAR, qui est établie comme une démarche
a-théorique, se limitant à l'étude de la dynamique des
variables sans aucune identification économique. Pour remédier
à cette limitation, nous mettons en avant l'émergence des
modèles SVAR. En effet, une étape essentielle de la
modélisation SVAR consiste à incorporer des relations
instantanées qui influencent les liens entre les différentes
variables. Cette incorporation permet de passer des chocs issus d'un
modèle VAR purement subjectif à des chocs pouvant être
interprétés économiquement, comme décrit dans les
travaux de (Hamilton, 1994) et (Lütkepohl, 2005).
Dans un premier temps, pour établir nos contraintes
d'identification, nous avons examiné de nombreux articles et travaux sur
les stress tests dans différents pays. À la suite de cette revue
de littérature, nous avons constaté qu'à chaque
étude, il y avait une spécificité dans l'introduction des
contraintes, qui dépendait parfois du pays, de la banque, ou de la
période de l'étude. Face à ces variations dans les choix
effectués par les auteurs, nous avons cherché à utiliser
une méthode plus fiable, de manière à obtenir un
modèle qui se rapproche davantage de la réalité, en
fonction des données dont nous disposons.
Dans notre cas, nous utiliserons le test de Granger sur le
logiciel R, afin de spécifier toutes les relations de causalité
entre les variables du modèle. Ainsi, l'absence de la causalité
sera considérée comme une contrainte d'identification.
(Annexe8)
Tableau 7 : Les résultats du Test de
Causalité de Granger
|
H0 Fischer P-value Hypothèse retenue
|
|
ROA ne cause pas NPL
|
2.4833
|
0.0241**
|
Présence de causalité
|
|
PCC ne cause pas NPL
|
1.9822
|
0.0683*
|
Présence de causalité
|
|
IPC ne cause pas NPL
|
2.8398
|
0.0116**
|
Présence de causalité
|
|
IPI ne cause pas NPL
|
1.6057
|
0.1484
|
Absence de causalité
|
|
TMM ne cause pas NPL
|
3.8432
|
0.0271**
|
Présence de causalité
|
|
USD ne cause pas NPL
|
2.8862
|
0.0105**
|
Présence de causalité
|
56
NPL ne cause pas ROA PCC ne cause pas ROA IPC ne cause pas ROA
IPI ne cause pas ROA TMM ne cause pas ROA USD ne cause pas ROA
|
7.3922 17.872 7.2888 2.0403 1.1727 2.2921
|
0.0621* 0.0179** 0.0633* 0.0605* 0.5185 0.0358**
|
Présence de causalité Présence de
causalité Présence de causalité Présence de
causalité Absence de causalité Présence de
causalité
|
|
NPL ne cause pas PCC
|
1.1063
|
0.3864
|
Absence de causalité
|
|
ROA ne cause pas PCC
|
0.1105
|
0.9996
|
Absence de causalité
|
|
IPC ne cause pas PCC
|
2.3877
|
0.0294**
|
Présence de causalité
|
|
IPI ne cause pas PCC
|
2.1047
|
0.0529*
|
Présence de causalité
|
|
TMM ne cause pas PCC
|
0.7339
|
0.6877
|
Absence de causalité
|
|
USD ne cause pas PCC
|
2.5389
|
0.0878*
|
Présence de causalité
|
|
NPL ne cause pas IPC
|
1.0793
|
0.4051
|
Absence de causalité
|
|
ROA ne cause pas IPC
|
0.4268
|
0.9230
|
Absence de causalité
|
|
PCC ne cause pas IPC
|
0.1878
|
0.8293
|
Absence de causalité
|
|
IPI ne cause pas IPC
|
1.154
|
0.3550
|
Absence de causalité
|
|
TMM ne cause pas IPC
|
1.8866
|
0.0833*
|
Présence de causalité
|
|
USD ne cause pas IPC
|
4.1253
|
0.0212**
|
Présence de causalité
|
|
NPL ne cause pas IPI
|
1.1165
|
0.3795
|
Absence de causalité
|
|
ROA ne cause pas IPI
|
0.5768
|
0.8208
|
Absence de causalité
|
|
PCC ne cause pas IPI
|
1.5184
|
0.1768
|
Absence de causalité
|
|
IPC ne cause pas IPI
|
2.1539
|
0.0533*
|
Présence de causalité
|
|
TMM ne cause pas IPI
|
2.3861
|
0.0295**
|
Présence de causalité
|
|
USD ne cause pas IPI
|
0.7471
|
0.6761
|
Absence de causalité
|
|
NPL ne cause pas TMM
|
1.2731
|
0.2850
|
Absence de causalité
|
|
ROA ne cause pas TMM
|
0.022
|
0.9782
|
Absence de causalité
|
|
PCC ne cause pas TMM
|
1.0099
|
0.4559
|
Absence de causalité
|
|
IPC ne cause pas TMM
|
52.123
|
0.0037***
|
Présence de causalité
|
|
IPI ne cause pas TMM
|
4.2481
|
0.0190**
|
Présence de causalité
|
|
USD ne cause pas TMM
|
0.6448
|
0.7650
|
Absence de causalité
|
|
NPL ne cause pas USD
|
0.4278
|
0.9224
|
Absence de causalité
|
|
ROA ne cause pas USD
|
0.587
|
0.8127
|
Absence de causalité
|
|
PCC ne cause pas USD
|
1.402
|
0.2225
|
Absence de causalité
|
|
IPC ne cause pas USD
|
0.7544
|
0.6697
|
Absence de causalité
|
|
IPI ne cause pas USD
|
2.4226
|
0.0977*
|
Présence de causalité
|
|
TMM ne cause pas USD
|
2.6292
|
0.0808*
|
Présence de causalité
|
Source : préparer par l'auteur à l'aide de
logiciel R CRAN
Par conséquent, d'après les tests
effectués, nous retenons 21 contraintes d'identification de court terme.
La matrice des effets instantanés aura donc la forme suivante :
|
A0 =
|
11 0 0 11 0 0 11 1 0 11 1 1 01 1 0 10 0 1
|
0 0 0 0 0 0 0 0 0 1 1 0 1 1 1 1 1 1
|
1 1 1 1 0 0 1
57
2.2.2. Détermination de la distribution à
priori
Le théorème de Bayes, introduit par Thomas Bayes
et généralisé par Simon Laplace, est largement
utilisé dans de nombreuses applications en tant qu'outil puissant pour
l'inférence statistique. Conformément à la loi de Bayes,
nous avons l'équation suivante :
??(??|??) = ??(??|??) ??(??)
??(??)
Distribution à priori è x fonction de
vraisemblance y = Distribution à posteriori è ;
C?????????????? ?? ???????????? x ???????????????? ????
?????????????????????????? = C?????????????? ?? ????????????????????
Toutefois, la distribution à priori suppose une loi
définie par le modélisateur pour déterminer la
distribution à posteriori après combinaison avec l'information
disponible. L'étape la plus délicate de l'approche
bayésienne réside dans la détermination de la distribution
à priori, qui reflète l'état d'esprit des
décideurs. En effet, un mauvais choix de celle-ci peut nuire à
l'ensemble des résultats du modèle, ce qui peut ensuite
influencer les chocs du stress test. Pour cette raison, de nombreux auteurs
accordent une grande importance au choix des meilleures distributions à
priori pour obtenir de bons résultats.
Plusieurs articles de recherche ont abordé la question
des distributions à priori, ainsi que de nombreux travaux récents
sur le sujet. Parmi ces travaux, citons celui de (Waggoner & Zha, 2003),
qui suppose que la meilleure distribution à priori pour un modèle
????????(6) avec des données trimestrielles est la suivante :
??0 = 1,??1 = 0.2 ,??3 = 1,??4 = 1,??5 = 1 ???? ??6
= 1
???? : Contrôle le degré de
confiance dans les coefficients de la matrice des effets instantanés ??0
et il s'agit d'un réel appartenant à l'intervalle [0,1].
???? : Indique le niveau de confiance par
rapport à l'hypothèse proposée par Litterman, qui suppose
que chaque variable suit une marche aléatoire, c'est un réel
appartenant à [0,1].
???? : Contrôle le taux de
décroissance de la variance des données compte tenu de
l'augmentation du retard avec ??3 = 0.
???? : L'écart type autour de la
tendance déterministe avec ??4 = 0. Ce paramètre
représente la variabilité résiduelle des données
après avoir soustrait la tendance.
???? : L'écart type autour des
coefficients des variables exogènes. Si ??5 = 0, cela signifie que
l'estimation des coefficients est relativement précise. Il s'agit d'une
spécificité de la précision
58
bayésienne, donc à ne pas modifier pour limiter
les chocs à la réflexion des décideurs lors de leur
lecture des données.
???? = ?? : il s'agit des observations Dummy
pour améliorer les performances des prévisions.
???? = ?? : il s'agit de l'à priori de
la racine unitaire, ce qui permet de remettre en cause les problèmes de
la stationnarité des séries.
Ainsi, pour aboutir à la meilleure distribution
à priori, on simulera plusieurs cas des figures, selon la variation des
différents hyperparamètres, et nous choisirons l'ensemble de ces
derniers qui nous offrirons la meilleure estimation, la meilleure
prévision et la meilleure information représentative du
modèle. Pour ce faire, notre choix se basera sur les trois indicateurs
statistiques suivants :
- RMSE : la racine carrée de l'erreur quadratique moyenne
; - MAE : l'erreur absolue moyenne ;
- LogMDD : le logarithme de la densité marginale.
Par conséquent, notre procédure de choix se
déroulera comme suit :
- Nous sélectionnons la distribution qui fournit la plus
faible RMSE.
- Nous sélectionnons la distribution qui fournit la plus
faible MAE.
- Si nous obtiendrons la même distribution, alors nous
s'arrêtons.
- Si non ; nous choisirons la distribution qui a la plus grande
densité marginale.
En utilisant la commande «SZ.prior.evaluation» de
package « MSBVAR » du logiciel R, qui donne pour chaque combinaison
des hyperparamètres, les indicateurs statistiques (RMSE, MAE et
LogMDD).
En tenant compte du domaine de définition de chaque
hyperparamètres, nous ferons varier les valeurs de ces derniers,
jusqu'à l'obtention de la meilleure combinaison.
- Première simulation :
A0 = A1 = (0.1,0.2,0.3) ; A3 =
A4 = (1,2,3) ; I5 = I6 = 1
|
????
|
????
|
????
|
????
|
????
|
????
|
????
|
RMSE
|
MAE
|
logMDD
|
|
RMSE
|
0,3
|
0,3
|
1
|
3
|
0
|
1
|
1
|
2.362193
|
_
|
639.0717
|
|
MAE
|
0,3
|
0,3
|
1
|
3
|
0
|
1
|
1
|
_
|
1.265337
|
639.0717
|
Toutefois, nous remarquons que les hyperparamètres A0, A1,
A3 et A4 prend ses valeurs
possibles maximales. En d'autres termes, pour
l'hyperparamètres A0 une valeur supérieure à
0.3 pourrait nous fournir une meilleure densité à priori. Par
conséquent, nous recourons à une deuxième simulation.
59
- Deuxième simulation :
A0 = A1 = (0.3,0.4,0.5) ; A3 = (0,0.5, 1) ; A4 =
(10,20,30) ; I5 = I6 = 1
|
A??
|
A??
|
A?? A??
|
A??
|
i??
|
i??
|
RMSE
|
MAE
|
logMDD
|
|
RMSE
|
0,5
|
0,5
|
0 30
|
0
|
1
|
1
|
2.146183
|
_
|
559.7508
|
|
MAE
|
0,5
|
0,5
|
0 30
|
0
|
1
|
1
|
_
|
1.115123
|
559.7508
|
Néanmoins, la constatation que les hyperparamètres
A0, A1 et A4 atteignent leur valeur
maximale possible nous a poussés à effectuer une
troisième simulation. - Troisième simulation
:
A0 = A1 = (0.5,0.6,0.7) ; A3 = 0
; A4 = (30,60,100) ; I5 = I6 = 1
|
A??
|
A??
|
A??
|
A??
|
A??
|
i??
|
i??
|
RMSE
|
MAE
|
logMDD
|
|
RMSE
|
0,7
|
0,7
|
0
|
100
|
0
|
1
|
1
|
2.098788
|
_
|
501.2995
|
|
MAE
|
0,7
|
0,7
|
0
|
100
|
0
|
1
|
1
|
_
|
1.079721
|
501.2995
|
Cependant, il est important de noter que les
hyperparamètres A0, A1 et A4 atteignent leur valeur
maximale possible, ce qui nous a incités à
procéder à une quatrième simulation. -
Quatrième simulation :
A0 = A1 = (0.7,0.8,0.9) ; A3 = 0
; A4 = (100,200,300) ; I5 = I6 = 1
|
A??
|
A?? A??
|
A??
|
A??
|
i??
|
i??
|
RMSE
|
MAE
|
logMDD
|
|
RMSE
|
0,9
|
0,9 0
|
300
|
0
|
1
|
1
|
2.073019
|
_
|
463.8065
|
|
MAE
|
0,9
|
0,9 0
|
300
|
0
|
1
|
1
|
_
|
1.070217
|
463.8065
|
Cependant, nous avons observé que les
hyperparamètres A0, A1 et A4 atteignent leurs valeurs
maximales possibles. Par conséquent, nous avons
décidé d'effectuer une cinquième simulation.
Cinquième simulation :
A0 = A1 = (0.9, 1) ; A3 = 0 ;
A4 = (300, 400,500,600,700,800,900) ; I5 = I6 = 1
|
A?? A?? A??
|
A??
|
A??
|
i??
|
i??
|
RMSE
|
MAE
|
logMDD
|
|
RMSE
|
1 1 0
|
600
|
0
|
1
|
1
|
2.065220
|
_
|
449.6753
|
|
MAE
|
1 1 0
|
600
|
0
|
1
|
1
|
_
|
1.068554
|
449.6753
|
Cette fois, les hyperparamètres A0, A1
et A4 ont abouti à des valeurs intermédiaires ou
maximales. Par conséquent, nous arrêtons le processus de
simulation des distributions à priori. Certes, nous avons
multiplié les simulations afin de tomber sur une meilleure distribution
à priori. Mais, afin d'affirmer sur la meilleure qualité de la
distribution à priori retenue suite à la cinquième
simulation, nous comparerons tous les résultats retenus
précédemment. Nous considèrerons aussi, les
hyperparamètres de référence de l'article de Sims et Zha.
(Annexe9)
60
Tableau 8 : Les résultats des simulations pour le
choix de la distribution à priori
|
Simulation
|
????
|
????
|
????
|
????
|
????
|
????
|
????
|
RMSE
|
MAE
|
logMDD
|
|
Priori 1
|
0.3
|
0.3
|
1
|
3
|
0
|
1
|
1
|
2.362193
|
1.265337
|
639.0717
|
|
Priori 2
|
0.5
|
0.5
|
0
|
30
|
0
|
1
|
1
|
2.146183
|
1.115123
|
559.7508
|
|
Priori 3
|
0.7
|
0.7
|
0
|
100
|
0
|
1
|
1
|
2.098788
|
1.079721
|
501.2995
|
|
Priori 4
|
0.9
|
0.9
|
0
|
300
|
0
|
1
|
1
|
2.073019
|
1.070217
|
463.8065
|
|
Priori 5
|
1
|
1
|
0
|
600
|
0
|
1
|
1
|
2.065220
|
1.068554
|
449.6753
|
|
Priori SZ
|
1
|
0,2
|
1
|
1
|
0
|
1
|
1
|
2.110103
|
1.156807
|
256.6349
|
Source : préparer par l'auteur à l'aide de
logiciel R-CRAN
D'après le tableau ci-dessus, nous remarquons que la
combinaison qui nous offre le couple (RMSE, MAE) le plus faible est celle de la
cinquième simulation. Par conséquent nous retenons une
distribution à priori avec les hyperparamètres suivants :
??0 = 1,??1 = 1 ,??3 = 0,??4 = 600,??5 = 1 ???? ??6
= 1
2.2.3. Estimation du modèle BSVAR
En considérant le même modèle VECM
étudié et en introduisant la matrice des restrictions ainsi que
la distribution à priori choisie sur les paramètres, nous allons
déterminer les distributions à posteriori de chaque
paramètre du modèle SVAR. L'approche de Sims et Zha est
implémentée au niveau de la commande « szbsvar » du
package « MSBVAR » du logiciel R. Une fois que les distributions
à posteriori sont déterminées via cette procédure,
nous utilisons les procédures « gibbs.A0 » et « A02mcmc
» afin de déterminer la distribution à posteriori
complète de la matrice. (Annexe10)
Nous commençons par la présentation du
résultat graphique, qui contient les courbes des distributions a
posteriori des coefficients de la matrice, en raison de l'introduction des
contraintes de court terme. Le graphique présenté dans l'annexe
11 représente la distribution à posteriori selon l'approche de
Gibbs. Afin de mieux expliquer la signification de cette matrice, nous avons
extrait les résultats des simulations dans un fichier plat (.csv), que
nous avons ensuite converti en fichier Excel. Ensuite, nous avons
procédé à une analyse descriptive pour déterminer
la moyenne empirique ainsi que l'écart type de chaque coefficient de la
matrice des effets instantanés. Ci-dessous, nous présentons la
matrice récapitulative des informations descriptives sur la distribution
à posteriori.
61
Tableau 9 : Les moyennes et les écarts-type des
distributions à posteriori
|
NPL
|
ROA
|
PCC
|
IPC
|
IPI
|
TMM
|
USD
|
|
NPL
|
-0,65852
|
1,14834
|
_
|
_
|
_
|
_
|
_
|
|
(1,52892)
|
(1,66074)
|
|
|
|
|
|
|
ROA
|
1,08552
|
1,11938
|
_
|
_
|
_
|
_
|
_
|
|
(1,14605)
|
(1,61311)
|
|
|
|
|
|
|
PCC
|
-1,37304
(0,29447)
|
0,14720
(0,33659)
|
6,29594
(0,5312)
|
_
|
_
|
_
|
_
|
|
IPC
|
-0,53936
|
-0,11303
|
0,79840
|
5,78654
|
4,42422
|
3,06309
|
_
|
|
(0,38697)
|
(0,3411)
|
(0,87597)
|
(14,7802)
|
(15,3623)
|
(1,57875)
|
|
|
IPI
|
_
|
0,44071
|
-0,56155
|
_
|
0,06473
|
0,14051
|
-14,521
|
|
|
(0,36207)
|
(0,68539)
|
|
(11,9995)
|
(1,58542)
|
(4,2782)
|
|
TMM
|
0,04196
|
_
|
_
|
2,10889
|
15,84750
|
-1,41806
|
-0,3852
|
|
(0,41042)
|
|
|
(20,418)
|
(8,15899)
|
(2,21264)
|
(9,2289)
|
|
USD
|
-0,62389
0,32689
|
-0,29551
(0,35802)
|
-2,36066
(0,77881)
|
117,8862
(10,3075)
|
|
|
-3,34514
(2,9545)
|
Source : préparer par l'auteur à l'aide de
logiciel R-CRAN
Les résultats empiriques présentés dans
le tableau précédent nous fournissent une idée de la
nature des distributions à posteriori calculées pour chaque
coefficient de la matrice des effets instantanés. Les résultats
des distributions à posteriori des paramètres structurels seront
exposés dans l'annexe. (Annexe11)
2.3.Comparaison des performances entre les modèles
VECM et BSVAR
Dans ce cadre, pour procéder à une comparaison
des performances entre le modèle VECM et le modèle BSVAR, nous
comparons les deux modèles en s'appuyant sur le critère de
l'erreur quadratique moyenne de prévision. Ensuite, nous utiliserons le
test de Diebold- Mariano pour analyser la significativité de
différence des deux modèles en termes d'erreur de
prévision. Enfin, nous terminerons notre travail de comparaison par le
test de Harvey, Leybourne et Newbold pour voir s'il y a un modèle qui
pourrait expliquer la prévision combinée.
2.3.1. Critère de l'Erreur Quadratique Moyenne de
Prévision
Considérons deux modèles
économétriques ??1 et ??2 qui expliquent les variables ???? pour
?? ? (1, ??). Découpons l'intervalle en deux tel que : (1, ??) = (1,
??0) ? (??0, ??), nous estimons les deux modèles
considérés sur la période (1, ??0), et sur la
base des résultats, nous formons deux séries de
prévisions, ??????,1 et
??????,2sur l'intervalle (??0, ??). L'EQMP est
calculée en se basant sur les observations réelles sur
l'intervalle (??0, ??). Par conséquent, nous obtiendrons :
?????????? = v?? ((??*??,?? - ??*)2)
???????? ??* = (????0, ... , ????) ???? ??*??,?? =
(????0??,??, ??????,??).
62
Nous rappelons que notre base de données contient 64
observations, s'étalant du T1 2006 jusqu'au T4 2021. Ainsi, pour
effectuer notre démarche de comparaison, nous passons principalement par
les étapes suivantes :
- Nous estimons les deux modèles pour une série
d'observations allant du T1 2006 au T2 2019, et nous simulerons les
prévisions sur les 10 périodes restantes.
- Ensuite, pour la deuxième étape, nous
considérons pour les estimations la période du T1 2006 au T1
2018, et nous simulerons les prévisions pour les 15 périodes
restantes. - Enfin, les prévisions simulées s'étaleront
sur 20 périodes entre T1 2017 et le T4 2021. Sur la base des
différentes prévisions simulées, nous calculerons l'EQMP
variable par variable et du modèle, une valeur plus petite indique une
meilleure performance du modèle.
Tableau 10 : Les résultats de l'indice EQMP
|
EQMP
|
Différence VECM
BSVAR
|
|
VECM
|
B-SVAR
|
|
NPL
|
7.665
|
3.932
|
3.733
|
|
ROA
|
0.940
|
0.814
|
0.126
|
|
PCC
|
1.416
|
0.284
|
1.132
|
|
10 périodes
|
IPC
|
0.008
|
0.025
|
-0.017
|
|
IPI
|
0.070
|
0.129
|
-0.060
|
|
TMM
|
1.399
|
1.702
|
-0.303
|
|
USD
|
0.313
|
0.450
|
-0.137
|
|
TOTAL
|
11.810
|
7.336
|
7.475
|
|
NPL
|
14.218
|
5.798
|
8.419
|
|
ROA
|
0.761
|
1.600
|
-0.839
|
|
PCC
|
2.466
|
0.264
|
2.202
|
|
15 périodes
|
IPC
|
0.013
|
0.094
|
-0.081
|
|
IPI
|
0.063
|
0.127
|
-0.064
|
|
TMM
|
0.875
|
1.146
|
-0.271
|
|
USD
|
0.252
|
0.247
|
0.005
|
|
TOTAL
|
18.648
|
9.278
|
9.370
|
|
NPL
|
14.210
|
2.265
|
11.945
|
|
ROA
|
6.124
|
5.470
|
0.654
|
|
PCC
|
2.418
|
0.971
|
1.447
|
|
20 périodes
|
IPC
|
0.062
|
0.097
|
-0.035
|
|
IPI
|
0.057
|
0.122
|
-0.065
|
|
TMM
|
2.435
|
2.392
|
0.043
|
|
USD
|
0.259
|
0.492
|
-0.233
|
|
TOTAL
|
25.566
|
11.811
|
13.755
|
Source : préparer par l'auteur à l'aide de
logiciel R CRAN
D'après le tableau ci-dessus, nous remarquons que d'un
point de vue global, le modèle BSVAR offre dans tous les cas des
meilleures prévisions que celles produites par le modèle VECM, vu
que l'indice de l'EQMP du modèle BSVAR est plus faible que celui du
modèle VECM. Par conséquent, l'intégration de l'approche
bayésienne a amélioré la précision du
modèle.
63
Ainsi, le graphique ci-dessous nous montre la
différence entre les erreurs de prévision des NPL des deux
modèles. Nous observons une différence croissante entre les
erreurs des deux modèles, passant de 3,7% sur 10 périodes
à 11,9% sur 20 périodes. Cela prouve clairement que le
modèle BSVAR possède une meilleure robustesse et stabilité
au fil du temps. (Annexe12)
Figure 4 : EQMP des NPL
10 Période 15 Période 20
Période
16.0%
14.0%
12.0%
10.0%
NPL
8.0%
6.0%
4.0%
2.0%
0.0%
14.2% 14.2%
7.7%
3.9%3.7%
5.8%
8.4%
11.9%
2.3%
VECM BSVAR Différences
Source : préparer par l'auteur à l'aide de
logiciel R CRAN
Nous pouvons conclure que l'introduction de l'identification
structurel et l'information à priori ont améliorer le potentiel
de précision de la modélisation. En effet, la
considération d'une information supplémentaire a un effet positif
sur les prévisions des NPL. Cependant, il faut vérifier que cette
différence est significative statistiquement. Pour résoudre ce
problème, nous recourons au test de Diebold-Mariano.
2.3.2. Test de Diebold-Mariano
Le test de (Diebold & Mariano, 1995) compare la
précision de prévision de deux méthodes de
prévision. L'hypothèse nulle est, qu'ils ont la même
précision de prévision. Cette hypothèse montre que
même s'il y a une différence entre les fonctions de perte des deux
modèles, cette dernière n'est pas significative. La statistique
du test est définie par :
d1T
Ia^DW
DM=
Avant de procéder au test, nous passons par un travail
préliminaire comme suit :
- Nous gardons les séries des prévisions
utilisées pour le calcul de l'EQMP (10 périodes, 15
périodes et 20 périodes).
- Nous déterminons par la suite les fonctions de perte
L(e????).
64
- Nous calculons la série d?? de la différence
entre les deux fonctions de perte. Ainsi, nous pouvons former une matrice de
différence des fonctions de perte notée D.
- Nous déterminons la quantité d pour chaque
variable, ainsi que l'estimation de la variance de long terme de chaque vecteur
de la matrice D. A l'aide du package «sandwich» du logiciel R, on
trouve la commande «lrvar» qui nous déterminera l'estimation
de la variance de long terme de chaque vecteur d??.
- Nous déterminons la valeur de la statistique DM et
nous la comparons par rapport à la distribution normale centrée
réduite à un niveau de confiance de 95%. Par conséquent,
si |????| > 1.96, alors l'hypothèse de l'égalité entre
les fonctions de perte est rejetée avec un risque d'erreur de 5%.
Les résultats empiriques sont exposés au niveau
du tableau suivant. Si la différence entre les fonctions de perte des
deux modèles est significative, la statistique DM calculée sera
noté «*».
Tableau 11 : Les résultats du test de
Diebold-Mariano
|
NPL ROA PCC 'PC 'P' TMM USD
|
|
10 périodes
|
-10.307*
|
-1.337
|
-13.183*
|
11.420*
|
8.466*
|
10.575*
|
14.098*
|
|
15 périodes
|
-16.251*
|
13.393*
|
-21.978*
|
16.590*
|
10.947*
|
6.317*
|
-0.446
|
|
20 périodes
|
-16.835*
|
-11.350*
|
-18.349*
|
15.970*
|
10.842*
|
-6.398*
|
8.638*
|
Source : préparer par l'auteur à l'aide de
logiciel R CRAN
D'après le tableau Ci-dessus, nous remarquons qu'il y a
une différence significative entre les fonctions de perte fournies par
les deux modèles dans tous les cas des figures sauf les variables ROA
sur 10 périodes et USD sur 15 périodes. Donc nous pouvons
conclure que l'approche bayésienne a amélioré le pouvoir
prédictif de la modélisation en introduisant la distribution
à priori. (Annexe12)
Certes, dans la plupart des cas, la prévision fournie
par l'approche bayésienne est la meilleure, vu qu'elle améliore
la précision. Mais, nous pouvons tomber sur une prévision
combinée qui améliore même les prévisions de
l'approche bayésienne. Pour répondre à cette
problématique, nous recourrons au test de dominance proposé
(Harvey, Leybourne, & Newbold, 1998), pour voir si nous pouvons trouver une
meilleure prévision à partir des deux modèles, ou si un
des modèles domine l'autre et par conséquent il formera seul la
meilleure prévision.
2.3.3. Test de la dominance de prévision
Plusieurs auteurs tels que (Granger & Newbold, 1986), nous
ont fait remarquer qu'il était possible d'améliorer les
prévisions des deux modèles retenus en partant du principe de
la
65
prévision combinée. En effet, ils ont
montré l'existence d'un réel A E [0,11, tel que la
nouvelle projection ytp,c = (1 -
a.)ytp,1 + a.ytp,2.
Toutefois, si par exemple le modèle M1 est riche en
information et donne déjà la meilleure prévision, alors
nous tomberons sur un paramètre A = 0, et dans ce cas nous
dirons que le modèle M1 domine le modèle M2.
- Nous gardons les séries des prévisions
utilisées pour le calcul de l'EQMP (10 périodes, 15
périodes et 20 périodes).
- Nous calculons les écarts par rapport aux
observations réalisées (eBsvAR,t et
evECM,t)
pour déterminer finalement la fonction du test
ft = evECM,t(evECM,t - efsvAR,t)
- Nous déterminons la quantité f pour
chaque variable, ainsi que l'estimation de la variance de long terme
6^HLN de chaque vecteur de la matrice.
- Enfin, nous déterminons la valeur de la statistique
HLN = .1T-T°f avec l'hypothèse nulle
HLN
du test est H0: E(ft) = 0.
Si l'hypothèse de la domination des prévisions
fournies par l'approche VECM est valide, nous noterons la statistique HLN
calculée par «*» :
Tableau 12 : Les résultats du test de la dominance
des prévisions
|
NPL ROA PCC IPC IPI TMM USD
|
|
10 périodes
|
9.749
|
7.465
|
12.021
|
4.554
|
-6.534
|
-9.862
|
-12.943
|
|
15 périodes
|
14.384
|
-8.015
|
19.498
|
9.487
|
-7.741
|
5.808
|
14.688
|
|
20 périodes
|
15.707
|
5.060
|
12.617
|
-19515
|
-7512.8
|
-144.19
|
-427.07
|
Source : préparer par l'auteur à l'aide de
logiciel R CRAN
D'après ce tableau, nous constatons que
l'hypothèse nulle (les prévisions du modèle VECM dominent
celles du modèle BSVAR) est rejetée dans tous les cas. Par
conséquent, nous pouvons dire que les prévisions fournies par le
modèle BSVAR sont, certes, meilleures que celles fournies par le
modèle VECM, d'après les tests précédents.
Cependant, ces dernières peuvent être améliorées en
jouant sur la notion de la combinaison des prévisions. (Annexe12)
2.4. Analyse des chocs structurels et décomposition
de la variance
La logique de l'estimation par l'approche bayésienne
permet d'imposer l'aspect dynamique entre les variables qui dépend de la
distribution a postériori de chaque paramètre de l'estimation. A
l'aide de la fonction d'impulsion, nous pouvons déduire l'impact d'un
choc des variables ROA, PCC, IPC, IPI, TMM et USD sur la variable NPL.
66
D'après les graphes ci-dessous nous constatons que le
choc des variables NPL, PCC, IPC, IPI et TMM ont un effet positif sur la
variable NPL. Tandis que les variables ROA et USD ont un impact négatif
sur la variable NPL à court terme et long terme. (Annexe13)
Figure 5 : Les fonctions d'impulsion

Source : préparer par l'auteur à l'aide de
logiciel R CRAN
Le modèle BSVAR estimé va nous permettre de
faire une décomposition de la variance, l'objectif de cette
décomposition est de calculer la contribution de chacune des innovations
à la variance de l'erreur. Le tableau suivant présente les
résultats à l'étude de la décomposition de la
variance pour la série NPL :
Tableau 13 : Décomposition de la variance pour les
NPL
|
Période
|
NPL
|
ROA
|
PCC
|
IPC
|
IPI
|
TMM
|
USD
|
|
1
|
91.5026%
|
2.9532%
|
4.5647%
|
0.0073%
|
0.0019%
|
0.9649%
|
0.0051%
|
|
2
|
92.6854%
|
4.4885%
|
2.5300%
|
0.0036%
|
0.0004%
|
0.2905%
|
0.0012%
|
|
3
|
92.2199%
|
5.9327%
|
1.7150%
|
0.0022%
|
0.0003%
|
0.1290%
|
0.0005%
|
|
4
|
91.5026%
|
7.0709%
|
1.3006%
|
0.0016%
|
0.0002%
|
0.1235%
|
0.0003%
|
|
5
|
90.9724%
|
7.8099%
|
1.0549%
|
0.0012%
|
0.0002%
|
0.1607%
|
0.0003%
|
|
6
|
90.7536%
|
8.1515%
|
0.8930%
|
0.0010%
|
0.0001%
|
0.2000%
|
0.0005%
|
|
7
|
90.8380%
|
8.1548%
|
0.7774%
|
0.0008%
|
0.0001%
|
0.2280%
|
0.0006%
|
|
8
|
91.1620%
|
7.9042%
|
0.6897%
|
0.0007%
|
0.0001%
|
0.2420%
|
0.0009%
|
|
9
|
91.6466%
|
7.4871%
|
0.6199%
|
0.0006%
|
0.0001%
|
0.2442%
|
0.0012%
|
|
10
|
92.2181%
|
6.9794%
|
0.5624%
|
0.0005%
|
0.0001%
|
0.2376%
|
0.0016%
|
Source : préparer par l'auteur à l'aide de
logiciel R CRAN
Le tableau Ci-dessus indique que la variance de l'erreur de
prévision de NPL est expliquée à 91.5% à ses
propres innovations de façon instantanée. Ainsi les variations du
NPL dépendent des variations ROA, PCC, IPC, IPI, TMM et USD autour de
2.95%, 4.56%, 0.007%, 0.001%, 0.964% et 0.005% respectivement. A long terme, la
variation du NPL est expliqué à 92.21% par ses propres
innovations, et la contribution de ROA, PCC, IPC, IPI, TMM et USD se
limité à 6.979%, 0.562%, 0.0005%, 0.0001%, 0.2376% et 0.0016%
respectivement. (Annexe14)
67
Section 3 : Application du stress test sur le risque de
crédit
Dans cette section, nous avons entrepris de réaliser un
stress test inversé pour évaluer le risque de crédit au
sein de la BFPME, suite aux mauvaises décisions prises par les
responsables. Notre démarche a débuté par la
création de différents scénarios résultant de
l'à priori sur les hyperparamètres, suivie de l'analyse de leur
incidence sur le taux des prêts non performants. L'objectif était
d'évaluer l'impact des mauvaises décisions prises par le
personnel de la banque sur les NPL. Ainsi, nous avons testé la
capacité de résilience de la BFPME face au scénario le
plus pessimiste, malgré la nature de leur activité qui se limite
aux CMLT (Crédits Moyen et Long Terme) d'investissement
risqué.
1. La création des scénarios de stress
Sur la base des résultats du modèle BSVAR
obtenus précédemment, nous choisissons d'appliquer un choc pour
simuler la réaction et la prévision des responsables de la BFPME
face à l'entrée de nouvelles informations micro et
macroéconomiques. Pour ce faire, nous réaliserons plusieurs
simulations à priori afin de prévoir la réaction des
responsables, allant de la meilleure intuition à la pire décision
possible. Cela nous permettra, à chaque étape, de comprendre
l'impact de ces intuitions sur le niveau des prêts non performants.
Pour déterminer l'ampleur du choc dans la distribution
à priori, nous simulerons différents scénarios en faisant
varier les hyperparamètres. Nous choisirons ensuite la combinaison
d'hyperparamètres qui représente la pire intuition possible de la
part des décideurs en termes de prise de décision. Notre
procédure de choix se déroulera comme suit :
- Nous sélectionnerons la distribution qui fournit la RMSE
la plus élevée.
- Nous sélectionnerons la distribution qui fournit la MAE
la plus élevée.
- Si nous obtenons la même distribution, alors nous nous
arrêterons.
- Sinon, nous choisirons la distribution qui a la densité
marginale la plus faible.
En tenant compte du domaine de définition de chaque
hyperparamètre, nous ferons varier les valeurs de ces derniers
jusqu'à l'obtention de la pire combinaison.
- Première simulation :
A0 = A1 = (0.2,0.25,0.3) ; A3 =
(1, 1.5,2) ; A4 = (2,2.5,3) ; I5 = I6 = 1
68
|
A?? A?? A?? A?? A?? 12?? 12??
|
RMSE
|
MAE
|
logMDD
|
|
RMSE
|
0,2 0,2 2 2 0 1 1
|
2.676741
|
_
|
700.4254
|
|
MAE
|
0,2 0,2 2 2 0 1 1
|
_
|
1.410968
|
700.4254
|
Toutefois, nous remarquons que les hyperparamètres A0,
A1, A3 et A4 atteignent leurs valeurs maximales possibles. Par
conséquent, nous procédons à une deuxième
simulation.
- Deuxième simulation :
A0 = A1 = (0.15,0.17, 0.2) ; A3
= (2,2.2,2.5) ; A4 = (1.5, 1.7,2) ; /15 = /16
= 1
|
A??
|
A??
|
A?? A?? A??
|
12??
|
12??
|
RMSE
|
MAE
|
logMDD
|
|
RMSE
|
0,15
|
0,15
|
2.5 1.5 0
|
1
|
1
|
3.580804
|
_
|
753.9880
|
|
MAE
|
0,15
|
0,15
|
2.5 1.5 0
|
1
|
1
|
_
|
1.882709
|
753.9880
|
Pourtant, nous constatons que les hyperparamètres A0, A1,
A3 et A4 atteignent leurs valeurs
maximales possibles. Par conséquent, nous effectuons une
troisième simulation. - Troisième simulation
:
A0 = A1 = (0.1,0.12,0.15) ; A3 =
(2,2.5,3) ; A4 = (1,1.5,2) ; /15 = /16 = 1
|
A??
|
A??
|
A?? A??
|
A?? 12??
|
12??
|
RMSE
|
MAE
|
logMDD
|
|
RMSE
|
0,1
|
0,1
|
3 1
|
0 1
|
1
|
6.187913
|
_
|
816.3732
|
|
MAE
|
0,1
|
0,1
|
3 1
|
0 1
|
1
|
_
|
2.837461
|
816.3732
|
Cependant, il est à noter que les hyperparamètres
A0, A1, A3 et A4 atteignent leurs valeurs
maximales possibles. En conséquence, nous optons pour une
quatrième simulation. - Quatrième simulation
:
A0 = A1 = (0.08,0.09,0.1) ; A3 = (3,4,5) ; A4 =
(0.8,0.9, 1) ; /15 = /16 = 1
|
A??
|
A??
|
A??
|
A??
|
A??
|
12??
|
12??
|
RMSE
|
MAE
|
logMDD
|
|
RMSE
|
0,08
|
0,08
|
5
|
0.8
|
0
|
1
|
1
|
7.324767
|
_
|
845.6226
|
|
MAE
|
0,08
|
0,08
|
5
|
0.8
|
0
|
1
|
1
|
_
|
3.238978
|
845.6226
|
Néanmoins, les hyperparamètres A0,
A1, A3 et A4 continuent d'atteindre leurs
valeurs
maximales possibles. Ainsi, nous engageons une cinquième
simulation. - Cinquième simulation :
A0 = A1 = (0.06,0.07,0.08) ; A3
= (5,6,7) ; A4 = (0.6,0.7,0.8) ; /15 = /16 = 1
|
A??
|
A??
|
A??
|
A??
|
A??
|
12??
|
12??
|
RMSE
|
MAE
|
logMDD
|
|
RMSE
|
0,06
|
0,07
|
7
|
0.6
|
0
|
1
|
1
|
7.744576
|
_
|
885.4779
|
|
MAE
|
0,06
|
0,07
|
7
|
0.6
|
0
|
1
|
1
|
_
|
3.376569
|
885.4779
|
Pourtant, il apparaît que les hyperparamètres A0
A3 et A4 atteignent leurs valeurs maximales possibles. Par
conséquent, nous passons à une sixième simulation.
- Sixième simulation :
A0 = A1 = (0.05,0.06, 0.07) ; A3
= (7,9, 11) ; A4 = (0.2,0.4, 0.6) ; /15 = /16
= 1
69
|
A??
|
A??
|
A??
|
A??
|
A??
|
t??
|
t??
|
RMSE
|
MAE
|
logMDD
|
|
RMSE
|
0,06
|
0,07
|
11
|
0.2
|
0
|
1
|
1
|
7.795025
|
_
|
884.8466
|
|
MAE
|
0,06
|
0,07
|
11
|
0.2
|
0
|
1
|
1
|
_
|
3.394653
|
884.8466
|
Les hyperparamètres A3 et A4 atteignent
leurs valeurs maximales possibles. Par conséquent, nous optons pour une
septième simulation.
- Septième simulation :
A0 = A1 = (0.06,0.07) ; A3 =
(11, 13, 15,17) ; A4 = (0.05,0.1,0.2) ; I5 = I6
= 1
|
A??
|
A??
|
A??
|
A??
|
A??
|
t??
|
t??
|
RMSE
|
MAE
|
logMDD
|
|
RMSE
|
0.06
|
0.07
|
17
|
0.05
|
0
|
1
|
1
|
7.801121
|
_
|
884.7688
|
|
MAE
|
0.06
|
0.07
|
17
|
0.05
|
0
|
1
|
1
|
_
|
3.396837
|
884.7688
|
Les hyperparamètres A3 et A4
atteignent leurs valeurs maximales possibles. Par conséquent,
nous engageons une huitième simulation. -
Huitième simulation :
A0 = A1 = (0.06,0.07) ; A3 = (17,19,21,22) ;
A4 = (0.001,0.01,0.02,0.03,0.04,0.05) ; I5 = I6 = 1
|
A??
|
A??
|
A??
|
A??
|
A?? t??
|
t??
|
RMSE
|
MAE
|
logMDD
|
|
RMSE
|
0.06
|
0.07
|
21
|
0.001
|
0 1
|
1
|
7.801529
|
_
|
884.7636
|
|
MAE
|
0.06
|
0.07
|
17
|
0.001
|
0 1
|
1
|
_
|
3.396983
|
884.7636
|
Cette fois, les hyperparamètres A0, A1, A3 et A4
aboutissent à des valeurs intermédiaires. Par
conséquent, nous mettons fin au processus de simulation des
distributions à priori. Selon le tableau ci-dessus, nous notons que la
huitième simulation nous offre le couple (RMSE, MAE) le plus
élevé. (Annexe15)
A0 = 0.06,A1 = 0.07 ,A3 = 21,A4 = 0.001,I5 = 1 e?? I6
= 1 2. Les résultats des scénarios
d'intuition
Pendant chaque réflexion sur la prise de
décision à la suite de l'entrée de nouvelles informations,
nous effectuons nos estimations et prévisions pour le premier trimestre
2022. Les résultats obtenus dans le tableau ci-dessous indiquent que les
hyperparamètres de la simulation S12 nous conduisent aux niveaux les
plus élevés de NPL instantanément. (Annexe16)
70
Tableau 14: Les résultats des simulations pour
l'intuition des décideurs
|
????
|
????
|
????
|
????
|
????
|
????
|
????
|
EQM
|
MAE
|
LogMDD
|
PNL après choc
|
|
S0
|
1
|
1
|
0
|
600
|
0
|
1
|
1
|
2.065220
|
1.068554
|
449.6753
|
83.520267
|
|
S1
|
0.9
|
0.9
|
0
|
300
|
0
|
1
|
1
|
2.073019
|
1.070217
|
463.8065
|
83.523015
|
|
S2
|
0.7
|
0.7
|
0
|
100
|
0
|
1
|
1
|
2.098788
|
1.079721
|
501.2995
|
83.535041
|
|
S3
|
0.5
|
0.5
|
0
|
30
|
0
|
1
|
1
|
2.146183
|
1.115123
|
559.7508
|
83.567316
|
|
S4
|
0.3
|
0.3
|
1
|
3
|
0
|
1
|
1
|
2.362193
|
1.265337
|
639.0717
|
83.618620
|
|
S5
|
0.2
|
0.2
|
2
|
2
|
0
|
1
|
1
|
2.676741
|
1.410968
|
700.4254
|
83.766314
|
|
S6
|
0.15
|
0.15
|
2.5
|
1.5
|
0
|
1
|
1
|
3.580804
|
1.882709
|
753.9880
|
83.977492
|
|
S7
|
0.1
|
0.1
|
3
|
1
|
0
|
1
|
1
|
6.187913
|
2.837461
|
816.3732
|
84.357986
|
|
S8
|
0.08
|
0.08
|
5
|
0.8
|
0
|
1
|
1
|
7.324767
|
3.238978
|
845.6226
|
84.536934
|
|
S9
|
0.06
|
0.07
|
7
|
0.6
|
0
|
1
|
1
|
7.744576
|
3.376569
|
885.4779
|
84.657794
|
|
S10
|
0.06
|
0.07
|
11
|
0.2
|
0
|
1
|
1
|
7.795025
|
3.394653
|
884.8466
|
84.657868
|
|
S11
|
0.06
|
0.07
|
17
|
0.05
|
0
|
1
|
1
|
7.801121
|
3.396837
|
884.7688
|
84.657876
|
|
S12
|
0.06
|
0,07
|
21
|
0.001
|
0
|
1
|
1
|
7.801529
|
3.396983
|
884.7636
|
84.657876
|
Source : élaborer par l'auteur à l'aide de
R-CRAN
Cela peut être atteint si les décideurs raisonnent
de la façon suivante :
- ???? = ??.???? : Selon les résultats
obtenus, les décideurs ne possèdent qu'une faible confiance,
seulement 6 %, dans les coefficients de la matrice des effets
instantanés ??0, Cette situation s'explique par le fait qu'ils ne
comprennent pas les interactions entre les variables macroéconomiques.
Cette méconnaissance peut rapidement augmenter le niveau des PNL en
raison de l'octroi de crédits risqués dans des contextes non
favorables et en cas de chocs économiques.
- ???? = ??.???? : Pour cet
hyperparamètre, les décideurs ont un niveau de confiance de 7 %
par rapport à l'hypothèse proposée par Litterman, qui
suppose que chaque variable suit une marche aléatoire. Par
conséquent, les décideurs ne considèrent pas que chaque
variable suit une marche aléatoire, c'est-à-dire qu'ils sont
conscients que toutes les variables varient selon les mêmes tendances
à court et à long terme.
- ???? = ???? : Les résultats obtenus
confirment l'importance de ce paramètre qui contrôle le taux de
décroissance de la variance des données compte tenu de
l'augmentation du retard. Ainsi, lorsque les décideurs
considèrent que la variance se réduit suite à
l'augmentation du nombre de retards, cela signifie que les variances des
variables restent à un niveau élevé, même si nous
disposons d'un plus grand nombre d'observations. Nous pouvons également
dire que l'importance de la variance des variables ne dépend pas
seulement de l'historique des données, mais aussi de différents
facteurs non observables par un historique des données, et qui ne
doivent pas être captés par la modélisation
fréquentiste.
71
- A4 = 0. 001 : Ce paramètre
représente l'écart type autour de la tendance
déterministe, c'est-à-dire la variabilité
résiduelle des données après avoir soustrait la tendance.
Selon les résultats obtenus, nous remarquons que dans le cas où
les responsables de la BFPME considèrent qu'il n'existe pas de
variabilité résiduelle et que la tendance des NPL est statique,
un choc inattendu peut même changer la tendance prévue par la
modélisation.
Après avoir déterminé les
différents scénarios sur la réflexion des décideurs
à travers la modification des hyperparamètres à priori,
nous avons effectué des prévisions pour les scénarios
jusqu'à atteindre la limite de 100 % des NPL. Les résultats
obtenus nous ont conduits à nous arrêter au T3 2025, car les
scénarios S9, S10, S11 et S12 s'approchent de la limite de 100 % des
NPL. Ensuite, les prévisions pour le T3 2025 des différents
scénarios sont triées du scénario le plus optimiste au
scénario le plus pessimiste, comme indiqué dans la figure
ci-dessous. (Annexe17)
Figure 6 : Prévision des scénarios sur les
NPL fin 2025
Sept-25
|
S12 S11 S10 S9 S8
|
|
|
|
|
99.77902 99.77901 99.77886 99.77740 7.17190
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
scénarios
|
S7
|
|
93.30674
|
|
|
S6
|
85.57559
|
|
S5 S0
S1
S2
S3
S4
|
81.71329 81.48234 81.47706 81.44309 81.24980
79.60915
|
|
|
|
|
|
|
|
|
0.00000 20.00000 40.00000 60.00000 80.00000 100.00000
120.00000
NPL
Source : élaborer par l'auteur à l'aide de
l'Excel
La figure ci-dessus nous donne une idée sur le long
terme : la meilleure distribution à priori n'est pas
nécessairement celle qui conduit au meilleur niveau des NPL, mais
plutôt à la précision des prévisions. Le graphique
ci-dessous nous montre la classification des scénarios
extrêmes.
72
Figure 7 : Prévision cas extrême sur les
NPL
PNL fin 2025
120.00000
99.77902
100.00000
79.60915 81.48234
80.00000
60.00000
40.00000
20.00000
0.00000
NPL
S4 S0 S12
scénarios
Source : élaborer par l'auteur à l'aide de
l'Excel
Selon les résultats des prévisions des à
priori des scénarios extrêmes, nous remarquons qu'à la fin
de l'année 2025, la BFPME atteindra 100 % des NPL, ce qui poussera la
banque vers la faillite. Cela pourrait avoir des conséquences graves sur
l'écosystème en provoquant la perte d'un de ses moteurs de
développement pour la création de la croissance économique
et de la valeur ajoutée, ainsi que sur son rôle de
réduction des tensions sociales par la création d'emplois.
3. Recommandation
3.1. Recommandation statistique
L'élément crucial de notre travail réside
dans l'intégration de l'approche bayésienne pour élaborer
un stress test inversé. Cela s'accomplit en appliquant un choc à
la distribution à priori qui reflète la prise de décision.
Notre contribution majeure consiste à répondre aux critiques
formulées à l'encontre de la modélisation VECM :
- La modélisation VECM est souvent
considérée comme a-théorique, ce qui peut entraîner
des résultats difficiles à interpréter. Pour illustrer
cette critique, prenons un exemple où le ROA de la BFPME aurait un
impact sur le TMM de la BCT. Cela ne semble pas avoir de justification
économique.
- Nous avons également souligné l'importance de
l'intégration de l'approche bayésienne, qui enrichit le
modèle en informations grâce à la distribution à
priori. Cette approche a clairement amélioré la précision
des prévisions, comme en témoigne l'analyse de back testing
approfondie que nous avons réalisée dans la section
précédente.
73
- L'approche fréquentiste utilise la statistique du
test de Fisher avec un intervalle de confiance pouvant aller jusqu'à
10%. Cependant, cette approche s'oppose à la logique du stress test, qui
doit évaluer des scénarios allant au-delà de la normale,
c'est-à-dire explorer les queues de la distribution. C'est là que
la statistique bayésienne se distingue, car elle se rapproche davantage
de la réalité car il ne permet pas le rejet des
hypothèses, ainsi qu'il autorise l'ajout des nouvelles.
- Cette nouvelle perspective du stress test est fortement
recommandée pour être adoptée par le secteur bancaire, car
elle permet d'évaluer l'impact des prises de décisions
défavorables. Cette approche innovante remet en question l'approche
traditionnelle qui repose sur l'utilisation d'un nombre arbitraire
d'écart-types jusqu'à ce qu'un coefficient de solvabilité
inférieur à la réglementation de la BCT soit atteint.
- L'augmentation du nombre d'écart-types basée
sur la dernière observation peut entraîner une perte de la nature
dynamique du modèle, sans nécessité de modifier la base de
données. L'approche bayésienne offre une solution à ce
problème en permettant d'appliquer des chocs à la distribution
à priori.
3.2. Recommandation sur la réflexion des
décideurs
Dans le cas du scénario le plus pessimiste, qui
découle d'une réaction inappropriée des décideurs,
il est recommandé que lors de la prise de décisions, les
responsables tiennent compte des aspects suivants :
- Les responsables de la BFPME doivent construire de
manière objective la matrice des effets instantanés en
étudiant les causalités. Cette approche permettra de comprendre
la dynamique entre les variables macroéconomiques, améliorant
ainsi leurs réactions lors de l'octroi de crédits dans des
contextes économiques défavorables et les incitant à plus
de prudence.
- Il est nécessaire d'ajouter une tâche
périodique à la direction des risques pour réaliser des
stress tests. Cela permettra à la BFPME de suivre et anticiper les chocs
liés à la marche aléatoire des variables. Cette approche
vise à orienter les crédits accordés vers des projets
financièrement résistants aux contextes économiques
sensibles et aléatoires.
- Lors de la prise de décisions, la BFPME devrait
s'appuyer sur des éléments subjectifs de manière
scientifique, notamment dans le cadre de l'évaluation des risques
liés aux crédits accordés aux promoteurs. Il est essentiel
de noter que l'importance de la base de données ne permet pas
nécessairement de réduire les variances des variables.
74
- Les décideurs sont tenus de rester vigilants et de
procéder régulièrement à des tests de
rétroaction (back testing) afin de se prémunir contre
d'éventuelles surprises inattendues. Cette démarche leur
permettra de prendre en considération toutes les
éventualités pessimistes lors de l'octroi de crédits. En
outre, elle contribuera à mieux anticiper la variabilité
résiduelle des données après avoir soustrait la
tendance.
3.3. Recommandation stratégique de la BFPME
Selon les résultats des prévisions du
scénario le plus pessimiste, il est prévu que d'ici la fin de
l'année 2025, l'ensemble des crédits accordés par la BFPME
seront classés en tant que prêts non performants, ce qui
aggraverait la situation de la banque. Pour faire face à ce
problème, plusieurs recommandations stratégiques doivent
être prises en compte :
- La mise en place d'un plan de restructuration qui
nécessitera une recapitalisation pour sortir la banque d'une situation
critique de fonds propres négatifs.
- La BFPME devra collaborer étroitement avec les
acteurs de l'écosystème pour réduire le taux de
mortalité des PME, tout en développant de nouveaux produits et
services de financement adaptés.
- La banque pourrait chercher à attirer de nouvelles
ressources non budgétaires, telles que celles provenant du FADES, QFF,
BEI, BIRD, ou d'autres fonds à gérer par délégation
pour le compte du secteur public et privé, y compris des fonds
liés à la Responsabilité Sociétale des Entreprises
(RSE).
- La BFPME doit améliorer la gestion des
créances douteuses, ce qui lui permettra de mieux comprendre les raisons
des échecs des PMEs et de rétablir la confiance en sa
capacité à cibler efficacement et à accompagner ses
promoteurs. En outre, l'ouverture de la banque à d'autres secteurs
productifs en dehors de l'industrie pourrait contribuer à une meilleure
gestion des risques.
- L'intégration d'un système d'information
adéquat serait essentielle pour améliorer les performances de la
banque et entamer sa transformation digitale.
- Une introduction en Bourse pourrait garantir une plus grande
transparence et réduire l'influence politique directe. Elle faciliterait
également l'accès de la banque aux marchés de capitaux, ce
qui est essentiel pour son développement et sa
pérennité.
- Une attention particulière doit être
accordée à la composition du Conseil d'Administration et à
son mode de fonctionnement, car ils semblent être en contradiction avec
la stratégie de la banque et ne sont pas alignés sur les
exigences de développement.
75
Conclusion
Ce chapitre se concentre sur une étude empirique du
stress test inversé lié au risque de crédit au sein de la
BFPME. Dans un premier temps, nous avons tenté d'expliquer le risque de
crédit en utilisant à la fois des variables
macroéconomiques et des variables spécifiques à la banque.
Nous avons employé un modèle vectoriel à correction
d'erreur pour cette modélisation. Cette approche nous a permis de
comprendre la dynamique des variables économiques et de prévoir
comment elles réagiraient face à divers chocs potentiels dans
l'économie tunisienne.
Cependant, la littérature théorique et empirique
met en évidence les limites de l'approche économétrique
fréquentiste, qui repose entièrement sur les données
historiques. Pour surmonter ces limites, des études récentes
suggèrent l'intégration d'informations supplémentaires
dans la modélisation, notamment à partir d'une matrice de
restrictions et d'informations à priori. C'est dans ce contexte que nous
avons cherché à améliorer notre étude en
introduisant une distribution à priori pour la matrice des effets
instantanés avant de procéder à l'estimation du
modèle en question.
Dans ce cadre, pour procéder à une comparaison
des performances entre le modèle VECM et le modèle BSVAR, nous
avons appliqué différents tests basés sur la comparaison
des prévisions. Cependant, d'après les tests nous pouvons
conclure que les prévisions fournies par le modèle BSVAR sont
meilleures que celles fournies par le modèle VECM.
Dans un deuxième lieu, nous avons choisi les
hyperparamètres qui nous ont conduits à des réflexions
problématiques de la part des décideurs lors de l'application des
scénarios de stress test, afin de prévoir le niveau des
prêts non performants après chaque scénario proposé.
Les résultats indiquent que le niveau des prêts non performants
augmente rapidement sous le scénario de stress, ce qui conduit à
un taux de NPL qui atteint 100% vers la fin de l'année 2025. Cela
démontre l'importance d'appliquer régulièrement des stress
tests pour calibrer la réflexion des responsables et prendre des
décisions en temps opportun, ce qui permet de maintenir la
continuité de la banque.
76
CONCLUSION GENERALE
Le stress test de risque de crédit constitue un
complément important aux approches quantitatives de la gestion du risque
de crédit. Il permet à la fois de comprendre les modèles
de risque de crédit et l'analyse des portefeuilles des banques. Le
stress test fournira toujours une mesure de l'intuition qui n'est
généralement pas réalisable. L'exercice de
sélection des facteurs, de création de scénarios et
d'évaluation de l'impact de ces scénarios induit une connexion
à la fois aux modèles et aux risques du portefeuille qui est
généralement beaucoup plus riche qu'avec l'analyse quantitative
de portefeuille seule. Les scénarios fournissent des descriptions
intuitives de certaines situations qui pourraient se produire mais qui ne se
sont jamais produites auparavant, ainsi que les pertes associées
à ces situations. Cela donne un aperçu à la fois du
comportement du portefeuille et des facteurs du risque de crédit.
L'objectif de notre étude est, d'une part,
d'intégrer l'approche structurelle et bayésienne pour
modéliser le risque de crédit de la BFPME, et, d'autre part,
d'utiliser les hyperparamètres de la distribution à priori dans
la construction des scénarios de stress test inversé
appliqués au risque de crédit. Cette étude s'articule
autour de trois chapitres : le premier chapitre présente une
généralité sur les risques, en mettant
particulièrement l'accent sur le risque de crédit ; le
deuxième chapitre traite de l'aspect théorique du stress test du
risque de crédit, et le dernier chapitre a mené à la
réalisation de notre étude empirique afin de montrer l'importance
de l'inférence bayésienne dans l'élaboration d'un
modèle du risque de crédit à travers le modèle
BSVAR. Cette démarche vise à comprendre la nature de la relation
entre les variables explicatives et le ratio des prêts non performants,
tout en enrichissant le modèle grâce à l'aspect intuitif
des décideurs.
L'étude empirique met en lumière les faiblesses
de l'approche VECM, qui ne tient pas compte de l'aspect théorique des
interactions entre les variables, du caractère subjectif du principe de
parcimonie, et de l'acceptation des hypothèses à un intervalle de
confiance de 5%, ce qui va à l'encontre de l'objectif du stress test.
Pour corriger ces lacunes, nous avons tout d'abord recouru à
l'intégration de la matrice des restrictions entre les variables afin de
donner un sens économique à notre estimation, tout en
préservant la dynamique entre les variables. De plus, nous avons
également intégré l'approche bayésienne, qui permet
de résoudre plusieurs problèmes, tels que la stationnarité
des séries, le raisonnement en termes de plausibilité des
hypothèses, ce qui nous permet de prendre en compte toutes les
hypothèses sans les rejeter,
77
nous rapprochant ainsi au plus près de la
réalité. Cela a conduit à une amélioration
significative de la précision des prévisions par rapport au
modèle VECM, notamment en ce qui concerne la variable NPL sur 20
périodes, passant de 14,2% à 2,3% pour l'erreur des
prévisions.
Les back testing sont plus approfondis et portent sur toutes
les variables sur des périodes de 10, 15 et 20 périodes pour
démontrer la robustesse et la stabilité dans le temps du
modèle BSVAR. Nous avons également prouvé que les
différences des erreurs sont statistiquement significatives, montrant
que le modèle VECM ne surpasse pas celui de BSVAR. Une idée
novatrice a été d'analyser l'impact des chocs sur la
réaction des décideurs face à l'entrée de nouvelles
informations. En cherchant le niveau des hyperparamètres susceptibles de
conduire les responsables à prendre de mauvaises décisions, nous
considérons cette démarche de réflexion comme un choc
extrême, et nous évaluons ses répercussions sur les NPL.
L'avantage ici est de ne pas rechercher un nombre arbitraire
d'écart-types.
Les résultats obtenus nous conduisent à la
conclusion qu'à la fin de l'année 2025, tous les prêts de
la BFPME seront qualifiés de non performants, ce qui
accélérera la faillite de la banque. Pour faire face à ce
problème, des recommandations ont été
élaborées pour orienter les décideurs vers la prise de
décisions judicieuses.
En conclusion, l'application du stress test sur le
portefeuille de crédit de la banque se révèle très
utile, car elle peut compléter les autres méthodes de gestion.
Elle améliore la qualité des informations disponibles et
éclaire les décideurs dans l'élaboration de leur
stratégie, ou les aide à ajuster leurs plans d'action afin
d'éviter que la banque ne subisse d'importantes pertes en cas de
problèmes de gouvernance et de décisions malheureuses prises par
les responsables.
Les limites de recherche :
L'une des limites de ce travail réside dans le nombre
limité de variables choisi dans notre modèle, ce qui ne nous
permet pas d'étudier et d'expliquer la totalité du risque de
crédit. Une autre difficulté réside dans
l'interprétation des hyperparamètres pour bien comprendre
l'orientation de l'intuition des décideurs. De plus, nous n'avons pas
calculé l'impact des NPL sur le coefficient de solvabilité de la
BFPME vue l'existence d'un coefficient négatif, ainsi qu'un retard dans
la clôture des années comptable. Pour mieux évaluer le choc
sur le risque de crédit de la banque, il serait préférable
de prendre en considération une combinaison de chocs, à la fois
en termes d'écart-type et d'intuition. Il est recommandé
d'intégrer d'autres risques pour généraliser le choc, tels
que le risque de liquidité supporté par la banque.
78
BIBLIOGRAPHIE
Adamowicz, T. (2018). Types of Risk in Banking Operations :
Categorization and Definitions. Economic and Regional Studies, 11(4),
37--56.
Ahmad, F., & Bashir, T. (2013). Explanatory Power of
Macroeconomic Variable as Determinants of NPL: Evidence from Pakistan.
World Applied Sciences Journal, 22, 243-255.
Akaike, H. (1974). A new look at the statistical model
identification. IEEE Transactions on Automatic Control, 19,
716-723.
Alexandri, M., & Santoso, T. (2015). Non Performing Loan :
Impact of Internal and External Factor. International Journal of Humanities
and Social Science Invention, 4(1), 87-91.
Anand, K., Guillaume, B., & Virginie, T. (2014). Stress
testing the Canadian banking System : a systemwide approach. financial
System Review, 61-68.
Andrea, M., Danilo, R., Nicola, P., & Tommaso, F. (2023).
Advancements in Bank Stress Tests : from Bayesian Averaging to Causal AI.
Essential services for financial institutions, 3(53), 369-388.
Consulté le Mars 2023
Audu, I. (2014). Risk management in the financial service
industry. Central Bank of Nigeria Understanding Monetary Policy Series,
4(2), 1-34.
Ballester , L., Ferrer, R., & Gonzàlez, C. (2009).
interest rate risk and bank-specific characteristics. New Frontiers in
Insurance and Bank Risk Management.
Basel Committee on Banking Supervision. (2009). Principles for
sound stress testing practices. 1-26. Basel Committee on Banking Supervision.
(2018). Stress testing principles.
Ben youcef, A. (2018). Credit Risk Stress Testing of
Commercial Banks in Tunisia », , vol.1, n°1. International
Journal of Accounting and Finance Studies, 1(1).
BESSIS, J. (1995). Gestion Des Risques et Gestion
Actif-Passif des banques. Paris: Dalloz.
Blaschke, W., Jones, M., Majnoni, G., & Peria, M. (2001).
Stress Testing of Financial Systems: An Overview of Issues, Methodologies, and
Fsap Experiences. IMF Working Paper, 1(88), 1-40.
Bolt, W., & Tieman, F. (2004). Banking Competition, Risk
and Regulation. The Scandinavian Journal of Economics, 106(4),
783-804. Récupéré sur
http://www.jstor.org/stable/3441060
Bourbonnais, R. (2002). Econométrie
(éd. 4). Paris: Dunod.
Castro, V. (2013). Macroeconomic determinants of the credit
risk in the banking system : The case of the GIPSI. Economic
Modelling(31), 672-683.
Chaibi, H., & Ftiti, Z. (2015). Credit risk determinants:
Evidence from a cross-country study. Research in International Business and
Finance(33), 1-16.
79
Comité de Bâle sur le contrôle bancaire.
(2010). Bâle III : dispositif réglementaire mondial visant
à renforcer la résilience des établissements et
systèmes bancaires. 1-82.
Committee on the Global Financial System. (2005). Stress
testing at major financial institutions : survey results and practice. Bank
for International Settlements.
Diebold, F., & Mariano, R. (1995). Comparing predictive
accuracy. Journal of Business and Economic Statistics, 13(3),
253-263.
Dimitri, D. (2015). Designing Effective Macroprudential Stress
Tests: Progress so Far and the Way Forward. MF Working Paper, 15-146.
doi:
https://dx.doi.org/10.2139/ssrn.2627203
Dimitrios, P., Angelos, T., & Vouldis, L. (2012).
Macroeconomic and bank-specific determinants of non-performing loans in Greece:
A comparative study of mortgage, business and consumer loan portfolios.
Journal of Banking & Finance, 36(4), 1012-1027.
Récupéré sur
https://doi.org/10.1016/j.jbankfin.2011.10.012.
Engle, R., & Granger, C. (1987). Co-integrated variables
and Eroor-correcting models : Representation, Estimation, and Testing.
Econometrica, 55(2), 251-276.
Fofack, H. (2005). Nonperforming Loans in Sub-Saharan Africa:
Causal Analysis and Macroeconomic Implications. World Bank Policy Research
Working Paper(3769), 1-36.
Gael, M., David, T., Worapree, M., Rubén, L., Florian,
H., Gary, K., . . . Anastasios, P. (2023). Bayesian forecasting in economics
and finance : A modern review. International Journal of Forecasting.
doi:ISSN 0169-2070
Gary, K., Dimitris, K., & Davide, P. (2013). Bayesian
compressed vector autoregressions. Journal of Econometrics, 210(1),
135-154.
Gary, K., Dimitris, K., & Davide, P. (2019). Bayesian
compressed vector autoregressions. Journal of Econometrics, 210(1),
135-154. doi:
https://doi.org/10.1016/j.jeconom.2018.11.009
Giudici, P., & Spelta, A. (2016). Graphical Network Models
for International Financial Flows. Journal of Business & Economic
Statistics(34), 128-138.
Godlewski, C. (2003). Modélisation de la prévision
de la défaillance bancaire une application aux banques des pays
émergents. Université Robert Schuman, 70-98.
Granger, C. (1969). investigating causal relations by
econometrics models and cross spectral methods. Econometrica, 37(3),
424-438.
Granger, C., & Newbold, P. (1986, November). Forecasting
Economic Time Series. Academic Press(4), 352.
Hamilton, J. (1994). Time Series Analysis. Princeton.
Hannan, E., & Quinn, B. (1979). The determination of the
order of an autorégression. Journal of the Royal Statistical
Society, 41(2), 190-195.
Harvey, D., Leybourne, S., & Newbold, P. (1998). Tests for
Forecast Encompassing. Journal of Business & Economic Statistics,
16(2), 254-259.
80
Hasan, I., & Wall, L. (2004). Determinants of the loan
loss allowance: some cross-country comparison. The Financial Review,
39(1), 129-152.
Hegde, S. H., Hegde, S., Hegde, R., Marthanda, K., & Logu,
K. (2023). Performance Analysis of Machine Learning Algorithm for the Credit
Risk Analysis in the Banking Sector. International Conference on Computing
Methodologies and Communication, 57-63.
Jacobs, M., Ahmet, K., & Frank, J. (2015).
SensenbrennerStress testing and model validation : application of the Bayesian
approach to a credit risk portfolio. The journal of risk model validation,
9(3), 41-70.
Jiménez, G., Lopez, J., & Saurina, J. (2013). How
does competition affect bank risk-taking? Journal of Financial Stability,
9(2), 185-195.
Johansen, S. (1988). Statistical Analysis of Cointegrating
Vectors. Journal of Economic Dynamics and Control, 12(2-3),
231-254.
Johansen, S. (1991, Nov). Estimation and Hypothesis Testing of
Cointegration Vectors in Gaussian Vector Autoregressive Models », , ,
vol.59, n°6, pp.. Econometrica, 6(59), 1551-1580.
Kaufman, G., & Kenneth, E. (2003). What Is Systemic Risk,
and Do Bank Regulators Retard or Contribute to It ? The Independent Review,
3(7), 371-391.
Kjosevski, J., Petkovski, M., & Naumovska, E. (2019).
Bank-specific and macroeconomic determinants of non-performing loans in the
Republic of Macedonia: Comparative analysis of enterprise and household NPLs.
Economic Research, 1(32), 1185-1203.
Kwiatkowski, D., Phillips, P., Schmidt, P., & Shin, Y.
(1992). Testing the null hypothesis of stationarity against the alternative of
a unit root : How sure are we that economic time series have a unit root ?
Journal of Econometrics, 3(54).
Lièák, M. (2016). Stress testing as a risk
management method. biatec, 3(14), 3-5.
Lütkepohl, H. (2005). New Introduction to Multiple Time
Series Analysis. Springer-Verlag, 764.
Makri, V., Tsagkanos, A., & Bellas, A. (2014).
Determinants of Non-Performing Loans: The Case of Eurozone. Panoeconomicus,
2(61), 193-206.
Manove, M., Padilla, J., & Pagano, M. (2001). Collateral
versus Project Screening: A Model of Lazy Banks. The RAND Journal of
Economics, 32(4), 726-744. doi:
https://doi.org/10.2307/2696390
Mathieu, T. (2014). Implémentation du stress-test
macro-prudentiel du risque de crédit bancaire dans l'Union Economique et
Monétaire Ouest Africaine. UEMOA.
Messai, A., & Jouini, F. (2013). Les déterminants
de prêts non performants. La Revue Gestion et Organisation(5),
9-13.
Messai, A., & Jouini, F. (2013). Micro and Macro
Determinants of Non-performing Loans. International Journal of Economics
and Financial, 3(4), 852-860. Récupéré sur
https://www.econjournals.com/index.php/ijefi/article/view/517
Moussaoui, F. (2015). Le stress test. Kolea : diplôme
master statistique et économie appliqué. Finance et
actuariat.
81
Nguyên, L. (2018). La formule du savoir : Une
philosophie unifiée du savoir fondée sur le
théorème de Bayes. France: Eco science.
Nkusu, M. (2011). Non performing Loans and Macrofinancial
Vulnerabilities in Advanced. International Monetary Fund, 11(161),
1-27.
Nouy, D. (2003). L'économie du nouveau dispositif et les
conséquences de la nouvelle réglementation. Revue
d'économie financière(73).
Onha, V., Yen, V., Trang, T., & Trung, H. (2018). A
Framework for Macro Stress-Testing the Credit Risk of Commercial Banks : The
Case of Vietnam. Asian Social Science, 2(14), 1-17.
Paul, H., Matthew, J., & Graham, S. (2004). Stress Testing
Financial Systems: What to Do When the Governor Calls. IMF Working
Papers, 38.
Pflug, G., & Pohl, M. (2018). A Review on Ambiguity in
Stochastic Portfolio Optimization. Set-Valued Var(26), 733-757.
Schuermann, T. (2014). Stress testing banks. 3(30),
717-728.
Schwarz, G. (1978). Estimating the dimension of a model.
Annals of Statistics, 2(6), 461-464. Sims, C. (1980). Macroeconomics
and Reality. Econometrica, 1(48), 2-48.
Sims, C., & Zha, T. (1998). Bayesian Methods for Dynamic
Multivariate Models. International Economic Review, 4(39), 68-949.
Spuch¾áková, E., Valaková, K., &
Adamko, P. (2015). The credit risk and its measurement, hedging and monitoring.
Procedia Economics and Finance(24), 675-681.
Sylvie, C. (2005). Gestion de la banque du diagnostic
à la stratégie (éd. 4). Paris: Dunod.
Taskinsoy, J. (2013). Basel III : Road to Resilient Banking.
Impact on Turkey's Financial Sector. doi:978-3-659-30696-9.
Waggoner, D., & Zha, T. (2003). a gibbs sampler for
structural vector autoregressions. Journal of Economic Dynamics and
Control, 2(28), 349-366.
Zeman, J., & Jurca, P. (2008). Macro stress testing of the
Slovak banking sector. National bank of Slovakia working paper.
Zouali, N. (2015). Stress testing bancaire du risque de
défaut des clients Corporate de la BMCI. Institut national de
statistique et d'économie appliquée Maroc.
82
ANNEXES
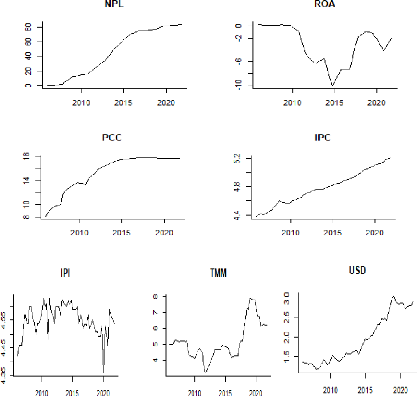
83
Annexe 1 : Analyse descriptive
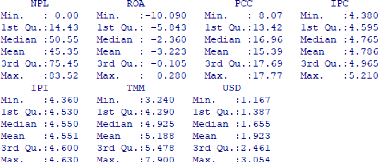
Annexe 2 : Représentation graphique
84
Annexe 3 : Test de la racine unitaire
1. Test de la racine unitaire I (0) : 1.1. Test ADF I (0)
:

1.2. Test KPSS I (0) :


85
1.3.Test ADF I (1) :

1.4.Test KPSS I (1) :

86
Annexe 4 : Détermination de l'ordre de
retard

Annexe 5 : Test de cointégration
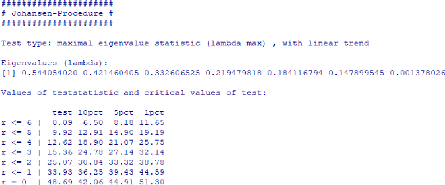
87
Annexe 6 : Estimation du modèle VECM
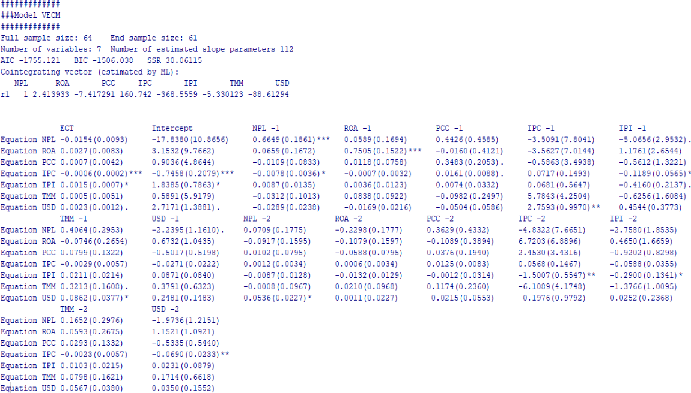
Annexe 7 : Test de validation
1. Test de stationnarité des résidus
:
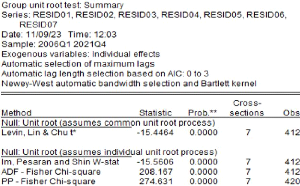
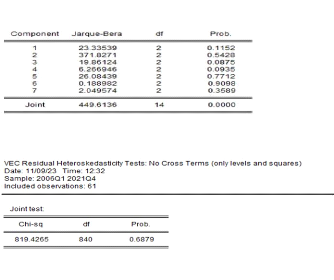
2. Test de normalité des résidus
:
3. Test
d'hétéroscédasticité
4. Autocorrélation des résidus
88
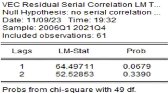
89
Annexe 8 : Test de causalité du Granger

90
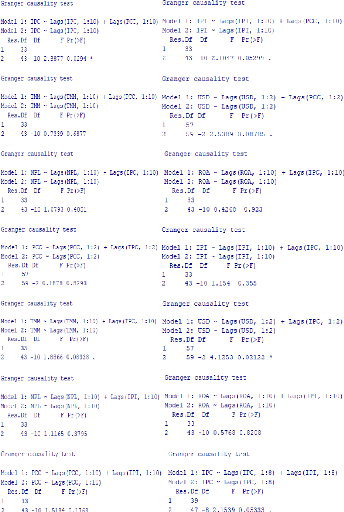
91

92
Annexe 9 : Choix de la distribution à
priori
1. Simulation 1 :
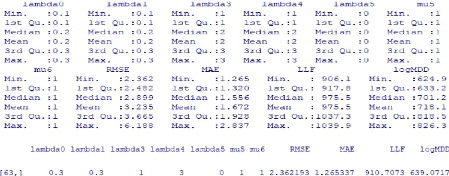
2. Simulation 2 :
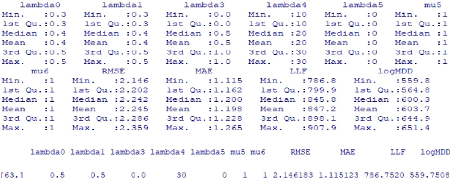
3. Simulation 3 :
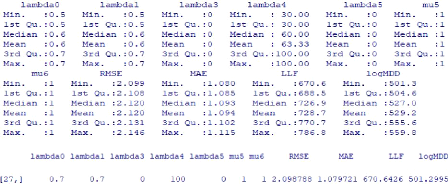
4. 93
Simulation 4 :
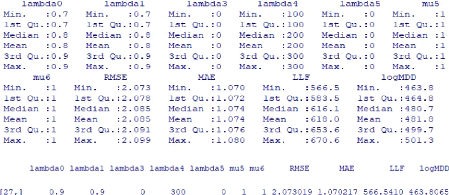
5. Simulation 5 :
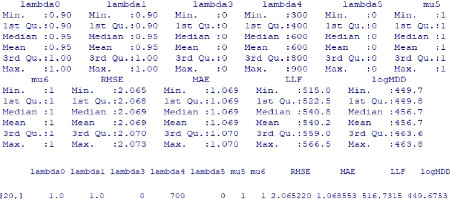
6. Simulation SZ :
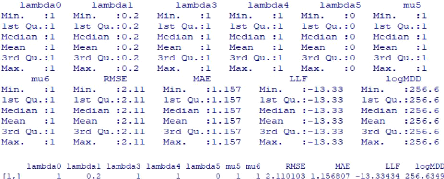
94
Annexe 10 : Estimation du modèle BSVAR
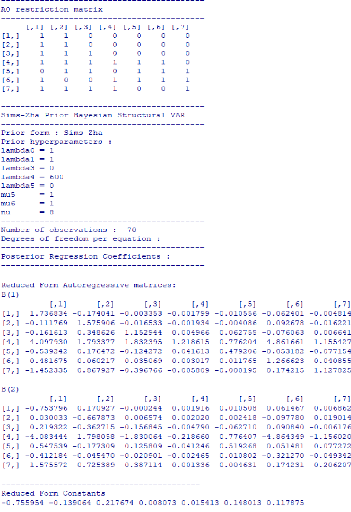
95
Annexe 11 : Les distributions à posteriori

|
NPL
|
ROA PCC IPC IPI TMM USD
|
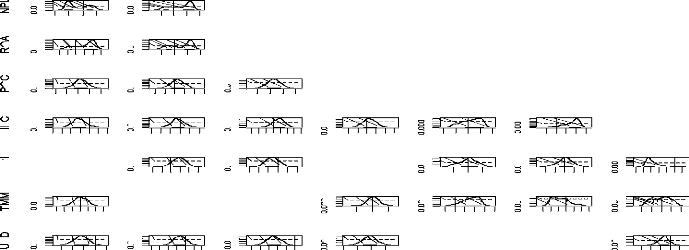
-2 0 2
-2 2 4
00 0.2 00 0.
N
-2.5 -1.0
-1.0 0.5
5 7
N 00
00
000 0.1
-2.0 -0.5 1.0
N 00 0
-1.5 0.0 -3 0 2 4
00
-40 0 40
-40 0 40
-2 2 6
30
. 3. 0
-1.0 0.5 -3 -1 1
.1
-20 20
0
0
-4 0 4
-25 -10 5
0
20
0
-1.5 0.0 1.5
0
-50 50
0
-10 10 30
0 -6 0 4
0
-20 0 20
N 00
0
0
0
N
00 0.0
-4 0 2
-2 2
-1.5 0.0 -2.0 -0.5 1.0 -5 -3 -1 80 120 -15 -5 5
96
|
Trace of earl
|
|
|
|
Density of earl
|
Trace of ears
|
fl
51
|
Density of rani
|
|
|
Trace of var9
|
|
|
Density of var9
|
|
|
|
|
|
|
o = 40041000104610444
|
|
|
|
|
|
|
|
|
0
|
200 400 600
Iterations
Trace of var2
|
300
|
1000
|
I
-4
|
I I I
-2 11 2
N = 1300 Bandwidth = 3.4371
Density of ear?
|
200 4410 FAO 1140 10110
terations
Trace of 'tari
|
-2.5 -20 -1 -1 0 -05
H =1000 Bandwiull = 0.07535
Density of rar6
|
|
0
|
200 400 600 000
Iterations
Trace of earl0
|
1000
|
-1.5 -1.3 -3.5 0.3 0.5 1.0
N =1000 Bandwidth = 0.08463
Density of var10
|
|
|
|
|
|
|
olttoesikopiwoosori
|
|
.1
|
|
|
|
|
|
|
0
|
2113 4011 6113
Iterations
Trace of var3
|
300
|
10011
|
-4
|
I I I i
-2 11 2 4
N = 1330 Bandwidth = 3.4422
Density of vara
|
t
0 200 400 600 840 1000
feratôrw
Trace ofvar?
|
-1.0 -05 0.0 0.5 141
H =1040 Bandwd0 = 006795
Density of earl.
|
1.5
|
0
|
1 i 1
200 400 600 800
Iterations
Trace of va
|
1
1000
|
|
-2 0 2 4
N = 1000 Bandwidth = 3.23
Density of var11
|
|
|
|
|
|
|
',0004),41W,00.1041141,410,
|
|
|
|
|
|
|
|
|
0
|
200 400 600
Iterations
Trace of yard
|
300
|
1000
|
|
I I I I I i
-2 -1 0 1 2 3
N =1030 Bandwidth = 3.3351
Density of yard
|
0 200 400 600 800 1000
terasoM
Trace Of 0/318
|
â
5 8 7 8
N. 1000 Sandwidtl . 0.1364
Density BFvar&
|
|
0
|
230 400 600 800
Iterations
Trace of earl?
|
1000
|
|
I I i
-40 -20 0 20 40 63
N = 1334 Bandw idth = 3.805
Density of earl?
|
|
|
|
|
|
|
|
11
|
|
|
|
|
|
|
|
0
|
2113 4011 6113
Iterations
Trace of earl3
|
800
|
1000
|
|
-2 3 2 4
N = 1330 Bandwidth = 3.4295
Density of var13
|
0 200 400 600 800 1000
ter-stems
Trace of earl?
|
-2.0 -1.5. -10 -05 9.0 0.5
H.1000 Bandwidth
· 0.09606
Density of var17
|
1.0
|
4
|
230 400 600 830
ferottns
Trace of var21
|
1030
|
|
ii
-40 -23 o- 20 40
N = 1000 Bandwidth = 4.09
Density of var21
|
|
|
|
|
|
|
|
|
|
|
|
|
o1
1
|
|
0
|
200 400 600
Iterations
Trace of var14
|
333
|
1000
|
-4
|
-2 0 2 4 6
N = 1000 Bandw idth = 0.4103
Density of va r14
|
0 200 400 600 800 1000
Iterahons
Trace of var18
|
-5 -4 -2 9 2 4
N = 1000 Bandw idth = 0.3942
Density of var18
|
6
|
0
|
200 400 600 000
Iterations
Trace of earl?
|
1000
|
1
|
-10 0 10 20 30 40
N = 1000 Bandwidth = 2.172
Density of var22
|
|
AlottiOkotworgisoopookwoo
|
|
|
|
h
|
|
|
|
|
,I
|
|
0
|
200 400 600
Iterations
Trace of earl 5
|
800
|
1000
|
-1.3
|
-0.5 0.0 0.5 1.4 1.5
N = 1000 Bandwidth = 0.0964
Density of var15
|
0 200 400 600 800 1000
Iterahans
Trace of va r19
|
-25 -20 -15 -10 -5 4 5
N = 1000 Bandwidth = 0.9595
Density of var19
|
|
0
|
200 400 600 300
Iterations
Trace of var23
|
1000
|
-4 -4 -2 0 2 4 6
N = 1000 6ondw idth = 0.5891
Density of var23
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
0
|
200 400 600
Iterations
Trace of va r16
|
800
|
1000
|
-3
|
-2 -1 0 1 2
N = 1000 Bandwidth = 0.1825
Density of sari
|
0 2010 400 600 300 1000
Iterahnns
Trace of var20
|
-1.5 -1.0 -0.5 0.0 0.5 1.0 1.5
N = 1000 Bandw idth = 0.1093
Density of var20
|
|
0
|
200 400 600 300
Iterations
Trace of var24
|
1000
|
1
|
-2[1 -110 0 10 29
N = 1000 Bandwidth = 2.457
Density of var24
|
|
|
|
|
|
|
|
|
|
|
|
|
,I
|
|
0
|
200 400 600
Iterations
|
833
|
1000
|
-40
|
-20 0 20
N = 1000 Bandwidth - 3.182
|
0 200 400 600 800 1000
Iterations
|
-50 0 50
N = 1 000 Bandwidth = 5.095
|
|
0
|
200 400 600 800
Iterations
|
1000
|
|
-1.5 -1.0 -0.5 0.0 0.5
N = 1000 Bandwidth = 3.08704
|

97
Annexe 12 : Technique de comparaison entre les deux
modèles
1. Erreur quadratique moyenne de la prévision :
1.1 VECM (10 Période) :
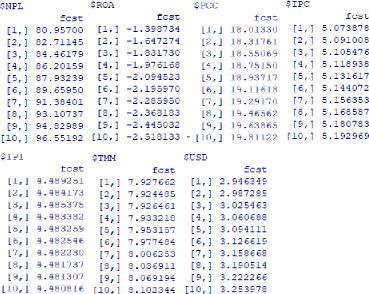

98
1.2 VECM (15 Période) :

99
1.3 VECM (20 Période) :
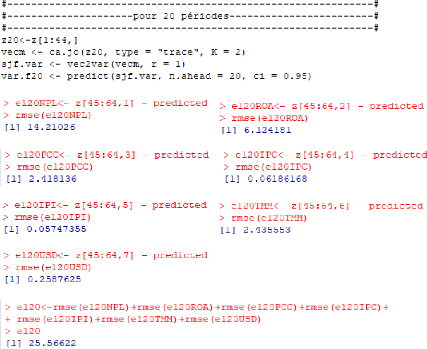
1.4 BSVAR (10 Période) :
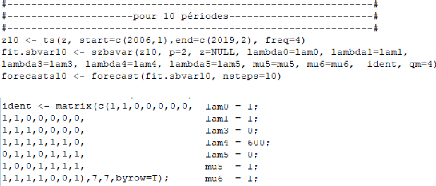

100
1.5 BSVAR (15 Période) :
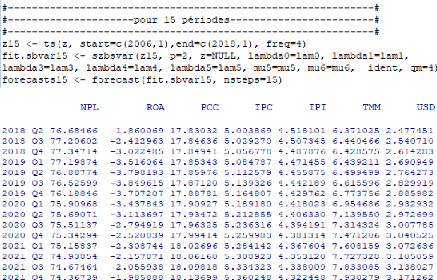
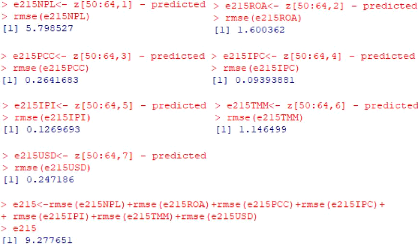
101
1.6 BSVAR (20 Période) :
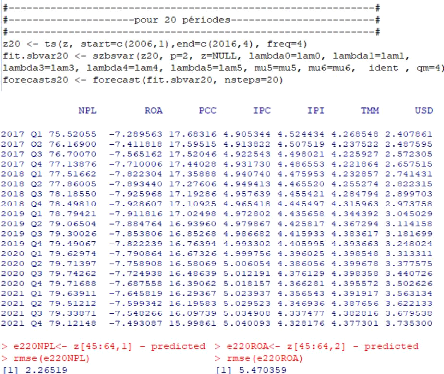

102
2. Test de Diebold-Mariano :
4. Test de la dominance de prévision
:
Annexe 13 : Les fonctions d'impulsion
Shock to
NPL
0 4 8
ROA
0 4 8
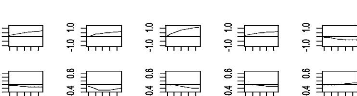
PCC
0 4 8
'PC
0 4 8
'P'
0 4 8
TMM
0 4 8
USD
0 4 8
0 4 8 0 4 8 0 4 8 0 4 8 0 4 8 0 4 8 0 4 8

0 4 8 0 4 8 0 4 8 0 4 8 0 4 8 0 4 8 0 4 8

0 4 8 0 4 8 0 4 8 0 4 8 0 4 8 0 4 8 0 4 8

0 4 8 0 4 8 0 4 8 0 4 8 0 4 8 0 4 8 0 4 8

0 4 8 0 4 8 0 4 8 0 4 8 0 4 8 0 4 8 0 4 8

103
0 4 8 0 4 8 0 4 8 0 4 8 0 4 8 0 4 8 0 4 8
104
Annexe 14 : Décomposition de la variance de
NPL
1.
Annexe 15 : Choix de scénario du
stress
Simulation 1 :
2. Simulation 2 :
3. 105
Simulation 3 :
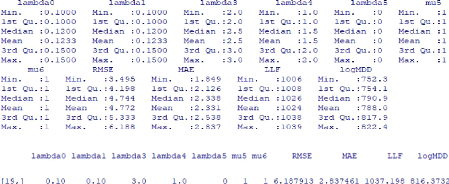
4. Simulation 4 :
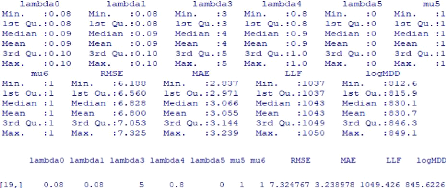
5. Simulation 5 :
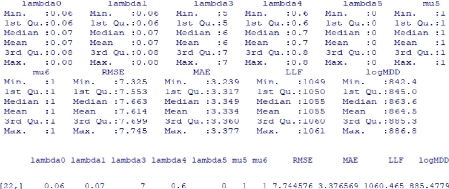
6. 106
Simulation 6 :
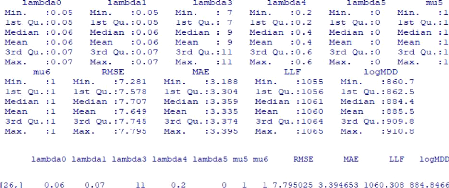
7. Simulation 7 :
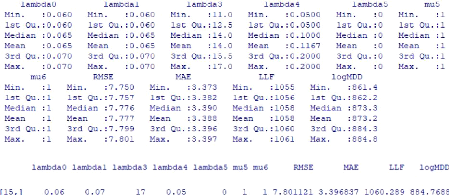
8. Simulation 8 :
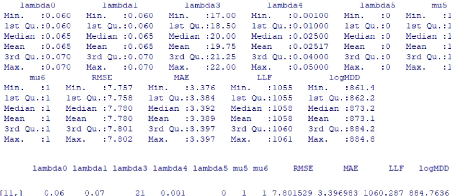
107
Annexe 16 : Prévision Court Terme

108


Annexe 17 : Prévision Long Terme

109
Sept-25
|
S12 S11 S10 S9 S8
|
|
|
|
|
99.77902 99.77901 99.77886 99.77740
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
97.17190
|
|
scénarios
|
S7
|
|
93.30674
|
|
|
S6
|
85.57559
|
|
|
S5
|
81.71329
|
|
|
|
S4
|
79.60915
|
|
|
|
|
S3 S2 S1 S0
|
81.24980 81.44309 81.47706 81.48234
|
|
|
|
|
|
|
|
|
0.00000 20.00000 40.00000 60.00000 80.00000 100.00000
120.00000
NPL
110
Date
|
S0
|
S1
|
S2
|
S3
|
S4
|
S5
|
S6
|
S7
|
S8
|
S9
|
S10
|
S11
|
S12
|
|
Déc-21
|
83,52000
|
83,52000
|
83,52000
|
83,52000
|
83,52000
|
83,52000
|
83,52000
|
83,52000
|
83,52000
|
83,52000
|
83,52000
|
83,52000
|
83,52000
|
|
Mars-22
|
83,52027
|
83,52302
|
83,53504
|
83,56732
|
83,61862
|
83,76631
|
83,97749
|
84,35799
|
84,53693
|
84,65779
|
84,65787
|
84,65788
|
84,65788
|
|
Juin-22
|
83,46403
|
83,46936
|
83,49216
|
83,54883
|
83,62983
|
83,94870
|
84,38533
|
85,17005
|
85,53935
|
85,78830
|
85,78845
|
85,78846
|
85,78846
|
|
Sept-22
|
83,37983
|
83,38666
|
83,41543
|
83,48287
|
83,57809
|
84,07282
|
84,74506
|
85,95607
|
86,52704
|
86,91140
|
86,91163
|
86,91166
|
86,91166
|
|
Déc-22
|
83,26401
|
83,27166
|
83,30346
|
83,37479
|
83,47045
|
84,14036
|
85,05722
|
86,71585
|
87,49984
|
88,02701
|
88,02733
|
88,02736
|
88,02737
|
|
Mars-23
|
83,12031
|
83,12840
|
83,16164
|
83,23367
|
83,31082
|
84,15307
|
85,32240
|
87,44921
|
88,45757
|
89,13503
|
89,13544
|
89,13548
|
89,13548
|
|
Juin-23
|
82,95434
|
82,96273
|
82,99688
|
83,06799
|
83,10262
|
84,11277
|
85,54129
|
88,15600
|
89,40005
|
90,23536
|
90,23586
|
90,23591
|
90,23591
|
|
Sept-23
|
82,77439
|
82,78299
|
82,81757
|
82,88520
|
82,84926
|
84,02140
|
85,71465
|
88,83608
|
90,32712
|
91,32791
|
91,32850
|
91,32856
|
91,32856
|
|
Déc-23
|
82,58825
|
82,59690
|
82,63106
|
82,69095
|
82,55416
|
83,88101
|
85,84329
|
89,48934
|
91,23862
|
92,41258
|
92,41326
|
92,41333
|
92,41334
|
|
Mars-24
|
82,40274
|
82,41114
|
82,44336
|
82,48941
|
82,22077
|
83,69370
|
85,92813
|
90,11571
|
92,13442
|
93,48928
|
93,49007
|
93,49015
|
93,49015
|
|
Juin-24
|
82,22292
|
82,23062
|
82,25872
|
82,28356
|
81,85255
|
83,46169
|
85,97011
|
90,71510
|
93,01437
|
94,55793
|
94,55882
|
94,55891
|
94,55892
|
|
Sept-24
|
82,05221
|
82,05862
|
82,07994
|
82,07557
|
81,45295
|
83,18727
|
85,97029
|
91,28748
|
93,87833
|
95,61844
|
95,61944
|
95,61954
|
95,61955
|
|
Déc-24
|
81,89247
|
81,89693
|
81,90856
|
81,86705
|
81,02541
|
82,87278
|
85,92974
|
91,83283
|
94,72618
|
96,67072
|
96,67183
|
96,67194
|
96,67195
|
|
Mars-25
|
81,74442
|
81,74625
|
81,74527
|
81,65926
|
80,57334
|
82,52064
|
85,84963
|
92,35113
|
95,55779
|
97,71469
|
97,71592
|
97,71604
|
97,71605
|
|
Juin-25
|
81,60791
|
81,60648
|
81,59018
|
81,45322
|
80,10015
|
82,13330
|
85,73115
|
92,84242
|
96,37307
|
98,75028
|
98,75162
|
98,75176
|
98,75177
|
|
Sept-25
|
81,48234
|
81,47706
|
81,44309
|
81,24980
|
79,60915
|
81,71329
|
85,57559
|
93,30674
|
97,17190
|
99,77740
|
99,77886
|
99,77901
|
99,77902
|
|
Date
|
S4
|
S3
|
S2
|
S1
|
S0
|
S5
|
S6
|
S7
|
S8
|
S9
|
S10
|
S11
|
S12
|
|
Sept-25
|
79,60915
|
81,24980
|
81,44309
|
81,47706
|
81,48234
|
81,71329
|
85,57559
|
93,30674
|
97,17190
|
99,77740
|
99,77886
|
99,77901
|
99,77902
|
111
TABLE DES MATIERES
REMERCIEMENTS i
DEDICACES ii
SOMMAIRE iv
LISTE DES ABREVIATIONS v
LISTE DES TABLEAUX vi
LISTE DES FIGURES vii
INTRODUCTION GENERALE 1
CHAPITRE 1 : GENERALITE SUR LE RISQUE DU CREDIT 3
Introduction 4
Section 1 : Catégorisation des risques dans le secteur
bancaire et analyse du risque de crédit 5
1. Compréhension du concept de risque 5
2. Typologie des risques dans le domaine bancaire 5
2.1. Le risque de marché 6
2.2. Le risque opérationnel 6
2.3. Risque de liquidité 7
2.4. Risque pays 7
2.5. Le risque d'insolvabilité 8
2.6. Risque systémique 8
3. Évaluation et gestion du risque de crédit 8
3.1. Définition du risque de crédit 9
3.2. Les Types du risque de crédit 9
3.2.1. Le risque de défaut 9
3.2.2. Le risque de dégradation du spread 10
3.2.3. Le risque de recouvrement 10
Section 2 : Les déterminants du risque de crédit
11
1. Facteur externe du risque de crédit 11
1.1. La croissance économique 12
1.2. Le chômage 12
1.3. Le taux d'intérêt 12
1.4. Le taux d'inflation 12
1.5. Le taux de change 13
1.6. La concentration bancaire 13
112
2. Facteurs internes du risque de crédit 13
2.1. Taille de la banque 13
2.2. La croissance du crédit 14
2.3. La rentabilité des actifs et des capitaux propres
14
2.4. Les provisions pour pertes 14
2.5. Le ratio dépôts sur crédit 15
Section 3 : La réglementation du risque de crédit
16
1. La réglementation internationale du risque de
crédit 16
1.1 La règlementation Bâle I 16
1.2 La règlementation Bâle II 18
1.2.1 Pilier I : exigences minimales en fonds propres 18
1.2.2 Le pilier II : processus de surveillance prudentielle
19
1.2.3 Le pilier III : discipline de marché 19
1.3 La règlementation Bâle III 20
2. La règlementation prudentielle en Tunisie 21
2.1 Division des risques 21
2.2 Couverture des risques 22
2.3 Classification des actifs 22
Conclusion 24
CHAPITRE 2 : LE STRESS TEST ET GESTION DES RISQUES 25
Introduction 26
Section 1 : Introduction aux Stress Tests 27
1. L'évolution des Stress Tests 27
2. Définition de stress test 28
3. Les objectifs des stress tests bancaires 29
3.1. Structure de gouvernance et Stress tests 29
3.2. Gestion des Risques et Stress Tests 30
4. Value at Risk et Stress test 30
Section 2 : Classification, méthodologies et
modèles de stress tests 32
1. Les types des stress tests 32
1.1. Test de sensibilité 32
1.2. Tests de scénarios 32
1.2.1. Les types de scénarios stress tests 32
1.2.2. La conception des scénarios stress tests 33
1.3. Approche du stress test inversé 33
2. Les approches de Stress Test 34
3. Les modèles de stress test 35
3.1. Les modèles Micro prudentiel 35
| 


