3.3.3.6. Traitement des données
Les tests statistiques ont été
effectués à l'aide des logiciels Statistica 6.0
et XL STAT 20104.5.03 avec le dénombrement, la
densité et la distribution des
fréquences permettant de statuer sur les significations
biologiques, écologiques
et environnementales des données obtenues.
VI-Aire Protégée de ressources
3.3.3.6.1. Estimation de la densité
Dans cette étude, l'abondance en richesse
biologique dans le site d'étude
est exprimée par la densité des populations.
La mesure de la densité évalue le nombre des
individus (flore et faune) données
de même taxon trouvé dans une surface
déterminée (Rabetombonirina, 2015).
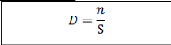
21
D : densité en fonction d'individu par km2
(ind/km2).
n : nombre d'individus comptés
S : surface totale de comptage en km2
- Pour la flore et faune (autre que la communauté
aviaire), la surface a été
comptée comme suit :
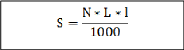
N : nombre des quadras, L : longueur du quadra, l : largeur du
quadra. N= 5, L=20 m, l=25.
-Spécifiquement pour la communauté aviaire
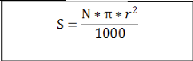
N : nombre de point d'écoute, r : rayon. Soit N=10,
ð=3.14, r=50 m. 3.3.3.6.2. Fréquence
La fréquence qui reflète l'abondance relative
est le nombre d'individus d'une espèce par rapport au nombre total
d'individus de toutes les espèces recensées exprimée en
pourcentage. Les pourcentages obtenus permettent de classer les espèces
et de déterminer leur importance au niveau de la communauté
étudiée.
Cette fréquence est donnée par la formule
suivante :
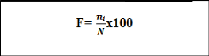
Avec F : Fréquence, ni : nombre total d'individus d'une
espèce et N : nombre total de toutes les espèces.
A partir des pourcentages calculés, les classes de
fréquence ou d'abondance ont été adoptées par
Razanakolona, 2016 sont choisies pour l'analyse dans la
présente étude.
] 0-1 %] : espèce très rare (trar) ] 1-5 %] :
espèce rare (rar) ] 5-15 %] : espèce influente (inf) ] 15 %] :
espèce abondante (ab).
3.3.3.6.3. Analyse de la diversité des oiseaux
L'indice de diversité permet d'avoir rapidement, en un
chiffre, une évaluation de la diversité du peuplement d'un site
donné. L'indice de Shannon-Weaver (Shannon et Weaver,
1963) noté h a été choisi pour
quantifier la diversité. Cet indice de diversité est le plus
utilisé pour des analyses de la diversité (Hutcheson,
1970).
22
ni : effectif de l'espèce ; N : effectif total des
individus recensés 3.3.3.6.4. Analyse statistique
3.3.3.6.4.1. La valeur moyenne
arithmétique ( )
La moyenne est calculée en faisant la somme de toutes les
mesures d'un variable d'un échantillon, puis en divisant cette somme par
le nombre des mesures des variables dans l'échantillon.
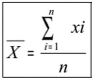
xi : Mesures d'une variable dans un échantillon n : Nombre
de mesures d'une variable dans un échantillon
23
3.3.3.6.4.2. L'écart-type ou la déviation standard
( )
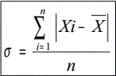
Xi = variables et n = nombre
des cas
3.3.3.6.4.3. Test de normalité
Ce test a été utilisé pour savoir la
distribution des données est normale ou anormale à partir du test
de Shapiro wilk.
-si Pt (Probabilité trouvée) est supérieure
à Ps (Probabilité Seuil)=0.05 pour une variable
trouvé, la distribution des données est normale
- si Pt (Probabilité trouvée) est inférieure
à Ps (Probabilité Seuil)=0.05 pour une variable
aperçue, la distribution des données est anormale.
Voici un exemple du procédé pour le test de
corrélation de Spearman sur la densité et la fréquence des
différents individus de communauté faunistique
recensées:
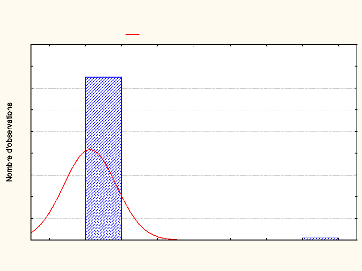
D'après le test de Shapiro-Wilk, la probabilité
trouvée (Pt) est inférieur à Probabilité seuil
(Ps) = 0.05. Donc les variables ne suivent pas la loi Gaussienne.
D'où la distribution des données est anormale (Figure
05).
40
20
90
80
70
60
50
30
10
0
-10 0 10 20 30 40 50 60 70
Histogramme : Fréquence
Shapiro-Wilk W=,14890, p=,00000
Courbe Normale Théorique
X <= Borne de catégorie

24
Figure 05 . : Fonction de densité de
probabilité à A (u=1.30, c=7.29)
(Auteur,2020)
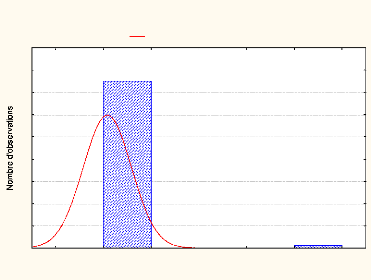
La figure 06 Ci-dessous a mentionnée
sur les résultats du test de Shapiro-Wilk, la probabilité
trouvée (Pt) est inférieure à la Probabilité seuil
(Ps) = 0.05. Donc les variables ne suivent pas la loi Gaussienne. Dou la
distribution des données est anormale.
40
90
80
70
60
50
30
20
10
0
-200 0 200 400 600 800 1000
Histogramme : Densité
Shapiro-Wilk W=,14298, p=,00000
Courbe Normale Théorique
X <= Borne de catégorie
Figure 06 : Fonction de densité de
probabilité à A (u=16.62, c=101.55)
(Auteur,2020)
25
Entant que la figure 05 et figure 06.montrant la
distribution des données de deux groupes sont anormales. Donc le test de
corrélation de Spearman à été utilisé.
3.3.3.6.4.4. Test de khi deux
Le test de Chi-deux sert à vérifier
l'homogénéité des faits observés avec ceux à
espérer pour deux ou plusieurs échantillons (Johnson,
1992). Ce test est le plus utilisé et conseillé pour les
ornithologues (Fowler et Cohen, 1985). Dans
cette étude, il a été utilisé afin de comparer la
distribution des effectifs de population de la communauté biologique
(flore et faune) dans les deux types de milieux d'étude. Pour cela, 04
groupes des animaux qui ont été recensés qui sont : les
mollusques, les insectes, les myriapodes, les poissons, les reptiles et les
oiseaux. Les végétaux ont été fusionnés en
un groupe.
Les hypothèses suivantes ont été
émises:
H0: «La répartition de la richesse biologique
visualisée dans les deux types habitats est homogènes».
: «La répartition de la richesse biologique
visualisée dans les deux types
habitats est hétérogènes».
La valeur de Chi-deux est obtenue par la formule suivante :
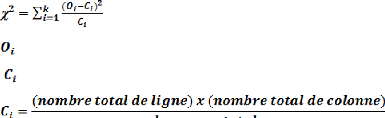
: Valeur observée.
: Valeur théorique et
Le degré de liberté se calcule comme suit:
ddl = (l - 1) (c - 1) où:
l = nombre de lignes,
c = nombre de colonnes.
Dans le cas où le degré de liberté serait
égal à un (d.d.l.=1), il faut passer
par la correction de Yate (Fowler et
Cohen, 1985) avec la formule suivante:
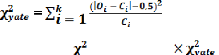
La valeur de à finale sera 2
.
Pour évaluer ce test, la valeur de Chi-deux
observée ( cal) est comparée à celle critique
( tab) en tenant compte du ddl pour un seuil de p à á
= 0,05.
Si cal > tab, la différence est significative,
l'hypothèse nulle H0 est alors
rejetée.
Si cal < tab, la différence est non significative et H0
est acceptée, c'est-à-dire, la différence entre les
résultats est significative (Schwartz, 1969).
3.3.3.6.4.5. Test de corrélation de Spearman
Ce test est réservé aux données non
paramétriques (Spearman, 1904), Il sert à
calculer le coefficient de corrélation ou à quantifier la
relation susceptible d'exister entre les échantillons à analyser.
La formule (Kendall, 1962) est la suivante:
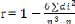
26
r: Coefficient de corrélation de Spearman
d: Différence arithmétique entre les rangs des
deux variablesn: Nombre
d'observations de l'échantillon.
La corrélation est positive si la valeur du coefficient
r est positive. Par conséquent, l'augmentation de la valeur d'une
variable pourrait entraîner l'augmentation de la valeur de l'autre. Pour
des valeurs négatives du coefficient, la corrélation étant
négative, l'augmentation de la valeur d'une variable entraînerait
la diminution de la valeur de l'autre. Toutefois, plus la valeur du coefficient
de corrélation du Spearman ne se rapproche des valeurs 1 ou -1, plus les
deux échantillons ou variables ont une corrélation étroite
(Fisher, 1921). Après le calcul de la valeur du
coefficient, le test de signification de ce coefficient nécessite une
référence au tableau de comparaison de Spearman :
27
-Si la valeur calculée est supérieure à
la valeur indiquée dans le tableau de Spearman, la corrélation
est donc significative.
-Si la valeur du coefficient de Spearman ainsi calculé
est inférieure à la valeur trouvée sur la table, la
corrélation entre les deux échantillons n'est pas
significative.
Ce test a été utile pour cette présente
étude pour comparer deux variables qui sont la densité et la
fréquence au niveau de la richesse biologique. C'est à dire, la
comparaison de la densité et fréquence au niveau de la richesse
floristique puis concernant la richesse floristique. Deux hypothèses ont
été posées.
-Hypothèses 01 :
-Ho ou Hypothèse nulle: HO: il n'existe pas
une relation entre la densité et fréquence des différents
individus de communauté faunistique recensé.
-Halt ou Hypothèse alternative: il existe une relation
entre la densité et fréquence des différents individus de
communauté faunistique recensé.
- Hypothèse 02 :
--Ho : il n'existe pas une relation entre la
densité et fréquence des différents individus de
communauté floristique recensé
- Halt : il existe une relation entre la densité et la
fréquence des différents individus de communauté
floristique recensée
Pour ces tests, le risque d'erreur de 5 % a été
adopté.
| 


