Conception et réalisation d’un quadrotor UAV.

REPUBLIQUE ALGERIENNE DEMOCRATIQUE ET POPULAIRE
Ministère de l'Enseignement Supérieur et de la Recherche Scientifique

Université des Sciences et de la Technologie Houari Boumediene

Faculté d'Electronique Et Informatique

Département Instrumentation et Automatique

Mémoire de Projet de Fin d'Etudes
Master en Electronique

Option : Ingénierie de L'Electronique et Photonique Appliquée

THEME

Conception et Réalisation d'un quadrotor UAV

Proposé par : Présenté par :

Mr. BOUDJIT KAMEL. ZITOUNI Abdelhak Amine.

Examinateurs: Président de jury:

Dr. T.BERABAR. Mr. M.Derras.

Dr. B.LEHOUIDJ.

Promotion : JUIN 2018

Remerciements

Je remercie Dieu, le tout puissant, pour m'avoir donné, le courage, la patience, la volonté et la force nécessaire, pour affronter toutes les difficultés et les obstacles, qui se sont hissés au travers de mon chemin d'études. Mes plus profonds remerciements vont à mes parents. Tout au long de mon cursus, ils m'ont toujours soutenu, encouragé et aidé. Ils ont su me donner toutes les chances pour réussir. Qu'ils trouent, dans la réalisation de ce travail, l'aboutissement de leurs efforts ainsi que l'expression de ma plus affectueuse gratitude.

J'adresse mes sincères remerciements à tous mes enseignants de L'université, notamment à mon promoteur Mr. Boudjit Kamel, d'avoir proposé le sujet sur lequel j'ai travaillé, et qui a assuré la direction et l'encadrement du travail présenté dans ce mémoire.

Je tiens aussi à exprimer mes remerciements à mon oncle Pr. Tahraoui Abdelatif (Professeur En Faculté De physique), d'avoir bien voulu de me faire profiter pleinement de ces compétences scientifiques et de ses idées durant mes années d'étude en USTHB.

Cette page ne serait être complète sans remercier mes meilleurs collègues et frères :

T. Idriss, T. Boualem, Z. Krimo, T. Zakou et sans oublier ma grande soeur Kheznadji.S, sans leurs soutiens je n'aurais sûrement pas pu mener à bien ce projet.

Enfin, Je tiens notamment, à adresser l'expression de ma sincère reconnaissance aux membres du jury d'examen, pour l'intérêt qu'ils ont porté à ce travail. Mes remerciements vont à tous ceux qui m'ont soutenu de près ou de loin à réussir ce travail.

Mes vives salutations.

Sommaire

Sommaire

Liste des figures

Introduction générale 1

Chapitre I : Généralité sur les drones 3

I.1. Introduction aux drones (U.A.V.) 3

I.2. L'historique des drones 3

I.3. Les différentes catégories des drones 4

I.3.1. Les drones militaires de longue endurance 4

· Les drones MALE « le General Atomics MQ-9 » 4

· Les drones HALE « RQ-170 Sentinel » 5

I.3.2. Les drones tactiques (Tactical Unmanned Air Vehicle) 6

I.3.3. Le drone solaire « Aquila» 7

I.3.4. Les drones miniatures 7

I.3.1. Le robot animal volant « BAT BOT B2 » 8

I.4. Domaines d'application des quadrotors 9

I.4.1. Domaine de sécurité 9

I.4.2.Domaine civil 10

I.5. Description général du quadrotor 10

I.6. Les mouvements du quadrotor 11

I.7. Conclusion 15

Chapitre II : Modélisation dynamique d'un quadrotor 16

II.1. Introduction 16

II.2. Modèle dynamique du quadrotor 16

II.2.1. Angle d'Euler 17

II.2.2. Vitesses angulaires 18

II.2.3. Vitesses linéaires 18

III.5. Contrôleur de vol du quadrotor : 43

III.5.1. Lecture des signaux du récepteur RF : 45

Sommaire

II.2.4. Effets physiques agissants sur le quadrotor 18

II.2.4.1. Les forces 18

II.2.4.2. Les moments 19

II.2.4.3. Effet gyroscopique : 20

II.2.5. Développement du Modèle mathématique selon Newton-Euler 20

II.2.5.1. Equations de mouvement de translation : 22

II.2.5.2. Equation de mouvement de rotation : 22

II.2.6. La représentation d'état du système : 24

II.7. La dynamique des rotors 25

II.3. Conclusion : 27

Chapitre III : Conception et mise en oeuvre du fonctionnement 28

III.1. Introduction : 28

III.2. Description du hardware utilisé : 28

III.2.1. Arduino Uno : 28

III.2.2. Gyroscope MPU-6050 : 29

III.2.3. Les moteurs sans balais « Brushless » : 29

III.2.4. Electronique Speed Controller « ESC » : 30

III.2.5. Batterie LIPO : 31

III.2.6. Les hélices : 32

III.2.7. Arduino Nano : 32

III.2.8. Module radio NRF24l01 2.4GHz : 33

III.2.9. Les joysticks : 34

III.2.10. La carcasse du quadrotor et du transmetteur RF: 34

III.3. Réalisation du transmetteur RF : 36

III.3.1. Schéma électronique : 36

III.3.2. Algorithme du transmetteur RF : 38

III.4. Récepteur RF 2.4 GHz : 40

III.4.1. Circuit et schéma électronique : 40

III.4.2. Algorithme du récepteur RF 2.4GHz : 41

III.4.3. Test des signaux de sortie du récepteur RF : 43

Sommaire

III.5.2. Unité de mesure de l'inertie gyroscopique MPU-6050 : 48

III.5.3. Le contrôleur PID : 53

III.5.4. Contrôle des ESC : 58

III.6. Conclusion : 63

Chapitre IV : Tests et résultats 64

IV.1. Introduction : 64

IV.2. Test des signaux du récepteur RF : 64

IV.3. Test des données angulaires du Gyroscope : 67

IV.4. Identification des gains PID : 67

IV.5. Test de vol en zone ouverte: 69

IV.6. Conclusion : 70

Conclusion générale 71

Références Bibliographiques

Annexe

Liste des figures

Liste des figures

Figure 1.1 : le General Atomics MQ-9. 5

Figure 1.2 : RQ-170 Sentinel. 5

Figure 1.3 : Le drone Tactique RQ-7 Shadow. 6

Figure 1.4 : Le drone solaire Facebook « Aquila ». 7

Figure 1.5 : Le drone miniature (nano drone UAV). 8

Figure 1.6 : Robot chauve-souris volante « BAT BOT B2 ». 8

Figure 1.7 : Les mouvements de bases du quadrotor. 10

Figure 1.8 : Illustration du mouvement vertical (Throttle). 12

Figure 1.9 : Illustration du mouvement de roulis (Roll). 12

Figure 1.10 : Illustration du mouvement de tangage (Pitch). 13

Figure 1.11 : Illustration du mouvement de lacet (Yaw). 13

Figure 1.12 : Illustration du mouvement de translation horizontale. 14

Figure 3.1 : la carte Arduino Uno. 28

Figure 3.2 : Unité de Mesure de l'Inertie gyroscopique MPU-6050. 29

Figure 3.3 : Moteur Brushless EMAX XA2212 1400Kv 30

Figure 3.4 : Composantes interne du Moteur Brushless . 30

Figure 3.5: variateur de vitesse « Hobbywing OPTO ESC 20A ». 31

Figure 3.6 : Batterie de Lithium-Polymère « LIPO » 11.1V 70C 2.2Ah. 31

Figure 3.7 : Hélices DJI 8045. 32

Figure 3.8 : Arduino Nano. 33

Figure 3.9 : NRF24l01 Radio module 2.4GHz. 33

Figure 3.10 : Joystick de haute qualité ..34

Figure 3.11 : Commandes de vol du drone .. ..34

Figure 3.12 : Les carcasses construites avec logiciel SOLID WORKS en 3D. 35

Figure 3.13 : Circuit imprimé du plat inferieur réalisé avec logiciel Eagle CAD soft. 35

Liste des figures

Figure 3.14 : Schéma électronique du transmetteur RF 2.4 GHz. 36

Figure 3.15 : Schéma du circuit imprimé du transmetteur RF 2.4 GHz. 37

Figure 3.16 : Transmetteur RF 2.4 GHz durant la réalisation. 37

Figure 3.17 : Valeurs analogiques affichées sur le moniteur série de l'Arduino IDE. 38

Figure 3.18 : Schéma électronique du récepteur RF 2.4 GHz 40

Figure 3.19 : Schéma du circuit imprimé du récepteur RF 2.4 GHz 41

Figure 3.20 : Valeurs correspondantes aux signaux PWM afficher sur le moniteur série 43

Figure 3.21 : Schéma électronique du contrôleur de vol du quadrotor. 44

Figure 3.22 : Schéma électronique global du quadrotor. 44

Figure 3.23 : Pulsations PWM de fréquence 50 Hz pour deux canaux du récepteur RF. 45

Figure 3.24 : Diagramme des broches de l'ATmega328p. 46

Figure 3.25 : Les mouvements de base. 48

Figure 3.27 : Signal de sortie du Gyro dans l'état stationnaire pour l'axe de mouvement Yaw 53

Figure 3.28 : Schéma de la boucle de contrôleur PID. 53

Figure 3.29 : Schéma montre le principe du PID utilisé dans ce contrôleur de vol. 54

Figure 3.30 : Algorithme utilisé dans le sous-programme PID du contrôleur de vol pour un axe 56

Figure 3.31 : Disposition des ESCs et direction de rotation du quadrotor 59

Figure 3.32 : Algorithme du PID conduit le quadrotor de revenir À l'état voulu 60

Figure 3.33 : Retour à l'état de consigne désiré par le pilote 0°. 60

Figure 3.34 : Simulation des impulsions PWM de fréquence 250 Hz à envoyer pour deux ESCs 61

Figure 4.1 : Image du quadrotor réalisé. 64

Figure 4.2 : Connexion du récepteur RF à l'oscilloscope digital. 65

Figure 4.3 : Signal PWM 50Hz de la commande Throttle. 65

Figure 4.4 : Largeur d'impulsion 1ms. 66

Figure 4.5 : Largeur d'impulsion 2ms. 66

Figure 4.6 : vérification des angles de Gyro sur l'Arduino IDE. 67

Figure 4.7 : Réglage des paramètres PID. 68

Figure 4.8 : Test de vol dans un espace ouvert. 69

1

Introduction générale

Introduction générale

Ces dix dernières années, les avancées technologiques et les nombreuses applications potentielles ont suscité un intérêt croissant pour la robotique aérienne. La problématique sur la programmation et le contrôl de vol des véhicules aériens sans pilote ou les drones est d'actualité. Les drones ont des applications commerciales

évidentes dans l'inspection d'ouvrages d'art comme les ponts, les barrages ou les lignes hautes tensions, l'exploration d'environnements dangereux comme des forêts en feu ou des zones radioactives, les missions militaires de reconnaissance et d'autres divers applications. La recherche dans le domaine des drones est essentiellement pluridisciplinaire, en effet elle fait intervenir des domaines très variés tels que l'aérodynamique, le traitement du signal et de l'image, la commande automatique, la télécomunication, les matériaux composites, l'informatique temps réel... etc.

Techniquement les drones n'ont pas les mêmes capacités. Tout d'abord, ils peuvent avoir toute sorte de taille qui peut aller de celle d'un avion de ligne à celle d'une mouche. il y a celle qui pèsent quelques grammes volent des centènes de mèttres à des altitudes basses et avec des durés de vole de quelque minutes et d'autres qui peuvent atteindres des tonnes, volent des centaines de kilomètres à des altitudes très élevés. Dans ce mémoire, nous nous intéressons en particulier aux robot volant de type véhicules aériens miniatures et plus particulièrement à un quadrotor (micro hélicoptère à quatre hélices). Les quadrotors ont la capacité d'effectuer un vol stationnaire, ils sont parmi les plus complexes des objets volants, La difficulté dans le pilotage de ces types des véhicules est d'assurer une bonne performance de suivi de la trajectoire voulue tout en garantissant une résistance aux perturbations aérodynamiques, parce que leur dynamique de vol est intrinsèquement non linéaire.

L'objectif de ce projet traite alors la réalisation d'un drone de type quadrotor piloté via une radiocommande, la conception du contrôleur de vol du drone se fait en utilisant des composants électroniques peu coûteux comme l'Arduino Uno et un module 3-axes gyroscope MPU6050. Le bon fonctionnement de ce système nécessite la réalisation d'une unité de commande émetteur / récepteur radio fréquence, basé d'un Arduino Nano et un module radio (NRF24L01) à 2.4 GHz pour servir à transmettre les différentes commandes au contrôleur de vol, nous voulons donc construire le Transmetteur Radio Fréquence et aussi bien le contrôleur de vol du quadrotor en se basant beaucoup plus sur la programmation des Arduino.

2

Introduction générale

Dans ce projet, le contrôleur de vol du quadrotor utilise le gyroscope pour extraire les données de mouvements du drone dans l'espace, puis les traités par l'Arduino Uno afin de contrôler les angles d'inclinaison du quadrotor. Le programme sur lequel j'ai travaillé utilise trois contrôleurs PID pour les trois axes de mouvements essentiels (PITCH), (ROLL) et (YAW). Les consignes pour le contrôleur PID sont les signaux de l'émetteur / récepteur et les variables de sortie du gyroscope. La sortie du contrôleur PID est utilisée pour contrôler la vitesse des moteurs brushless du quadrotor et pour assurer l'équilibre. Après avoir étudié des sous-programmes sur le Gyro MPU6050 et essayer de comprendre comment lire ces données angulaires à partir des registres de sortie, j'ai trouvé qu'il devait y avoir un moyen très simple de créer une IMU pour un quadrotor. L'astuce est juste d'examiner les données du gyroscope et puis j'ai essayé plusieurs façons d'obtenir le bon algorithme en se référant à l'open source. Mon mémoire est structuré comme suit :

Chapitre 1 : généralité sur les drones.

Chapitre 2 : modélisation d'un drone quadrotor.

Chapitre 3 : conception et mise en oeuvre du fonctionnement.

Chapitre 4 : teste et résultats.

Chapitre 1

généralité sur les drones

Chapitre I Généralité sur les drones

3

Chapitre I : Généralité sur les drones

I.1. Introduction aux drones (U.A.V.) :

Plusieurs termes sont utilisés pour les véhicules aériens sans pilote, qui se réfèrent généralement au même concept. Un véhicule aérien sans pilote U.A.V. (UNMANNED AIRCRAFT VEHICLE) ou R.P.A.S. (Remotely Piloted Air System), communément connu sous le nom de drone, C'est un avion qui ne porte pas d'opérateur humain à bord. Les UAV sont des composantes d'un système d'aéronef sans pilote U.A.S. (Unmanned Aircraft System); Qui comprennent un UAV, un contrôleur terrestre et un système de communication entre les deux. Les drones utilisent des forces aérodynamiques pour fournir un ascenseur de véhicule, ils peuvent voler de façon autonome et être piloté à distance, ils peuvent être récupérables grâce à un système de navigation programmable et effectuer des vols dans des différents environnements, ils sont capables aussi de porter un camera de liaison de données, permettant la transmission direct des vidéos. Le vol des drones UAV peut se fonctionner avec de différents degrés d'autonomie: soit sous contrôle à distance par un opérateur humain, soit par ordinateur embarqué de manière autonome.

Par rapport aux avions équipés, les drones UAV étaient à l'origine utilisés pour des missions trop dangereuses pour les humains. Bien qu'ils proviennent principalement d'applications militaires, leur utilisation s'étend rapidement aux applications commerciales, scientifiques, récréatives, agricoles et autres, telles que la police et la surveillance, la livraison de produits, la photographie aérienne et d'autres diverses applications. Les drones civils sont maintenant beaucoup plus nombreux que les drones militaires, avec des dépenses de plus d'un million de vends pendant ces dernières années.

I.2. L'historique des drones :

Les innovations de l'UAV ont commencé au début des années 1900 et se sont initialement concentrées sur la mise en place d'objectifs de formation pour former du personnel militaire. Le développement de l'UAV s'est poursuivi pendant la Première Guerre mondiale, lorsque Dayton-Wright Compagnie d'avion a inventé une torpille aérienne sans pilote qui exploserait à un moment préétabli. En 1920 en France, à la suite de la première guerre mondiale George Clémenceau Président de la Commission sénatoriale de l'Armée, lance un projet « d'avions sans pilote » : le capitaine Max Boucher met au point un système de pilotage automatique qui fait voler sur plus de cent kilomètres un avion Voisin BN3. Ainsi, dans les années 1920, des avions sans pilote radiocommandés voient le jour, avec les tentatives de torpilles aériennes télécommandées par des ondes de télégraphie sans fil. Le premier drone français stricto sensu a été conçu, réalisé et expérimenté dès 1923 à Etampes par l'ingénieur Maurice Percheron et le capitaine Max Boucher. Toutefois, l'armée française n'y voyait

Chapitre I Généralité sur les drones

4

pas encore d'intérêt militaire. Le drone a été développé de façon confidentielle par les Etats-Unis comme un moyen de supériorité stratégique et de rupture de capacité devant permettre la surveillance et l'intervention militaire chez l'ennemi sans encourir les risques humains que l'opinion ne supportait plus. En outre, il est utilisé pour larguer des tracts dans le cadre de la guerre psychologique. L'Allemagne nazie a produit et utilisé divers avions UAV pendant la guerre. Les moteurs à réaction sont entrés en service après la Seconde Guerre mondiale dans des véhicules tels que le GAF australien Jindivik et Teledyne Ryan Firebee de 1951, alors que des entreprises comme Beechcraft ont offert leur modèle 1001 pour la marine américaine en 1955. Néanmoins, ce ne sont que des avions télécommandés Jusqu'à la guerre du Vietnam. Les drones sont engagés pour la première fois pendant la guerre du Viet Nam, puis lors de la guerre du Kippour. Ils font désormais partie des moyens tactiques et stratégiques du champ de bataille. L'absence de pilote permet d'opérer à l'intérieur des lignes ennemies pour des missions à risque, sans crainte de pertes humaines. Après cette introduction historique nous allons à présent citer quelque type des drones actuels.

I.3. Les différentes catégories des drones :

Tous les drones n'ont pas les mêmes capacités. Selon les besoins, ils peuvent avoir toute sorte de taille qui peut aller de celle d'un avion de ligne à celle d'une mouche. La classification des drones dépend de plusieurs critères tels que leurs longueurs, leurs auteurs et leurs durées de vol. Ainsi que leurs poids changent également. On distingue donc plusieurs classes de drones [9-10] :

I.3.1. Les drones militaires de longue endurance:

Le drone militaire est utilisé pour des missions de reconnaissance, généralement à hauts risques pour les soldats. Il est très en vogue chez les grandes puissances militaires comme les Etats-Unis, la France et l'Angleterre. En effet actuellement des drones patrouillent au moyen orient pour démanteler des réseaux de terroristes. Avec des durées de vol comprises entre 12 et 48 heures, on entre ici dans la catégorie des «grands» drones, dont la taille est essentiellement dictée par une charge utile lourde et une quantité élevée de carburant, nécessaire à la mission. Cette catégorie se divise elle-même en deux parties, en fonction de l'altitude de vol des machines : comme pour les avions, plus on vole haut, plus on va vite et plus on parcourt de la distance. On distingue ainsi les drones dits «MALE» (Moyenne Altitude Longue Endurance) des drones «HALE» (Haute Altitude Longue Endurance).

· Les drones MALE « le General Atomics MQ-9 » :

Ce type de drone de combat Figure 1.1 peut atteindre une vitesse de 480km/h, il peut être commandé jusqu'à 1850 kilomètres par ses deux contrôleurs au sol ou par liaison satellite. Il pèse un peu plus de 2 tonnes et peut atteindre 15 kilomètres d'altitudes avec une autonomie de vol de 30 heures. Aussi il peut transporter six missiles et deux bombes, en temps de guerre ce type de drone est

Chapitre I Généralité sur les drones

5

utilisé pour l'espionnage mais peut également servir comme lance-missiles. Un modèle non armé mais bourré de capteurs et de caméras est également utilisé par la Nasa et destiné à des recherches scientifiques.

Figure 1.1 : le General Atomics MQ-9.

Les Américains ont d'emblée conçu des systèmes MALE à la dimension de leurs théâtres d'opérations en vue, non seulement de missions de reconnaissance, mais aussi de désignation et de destruction d'objectifs au sol.

· Les drones HALE « RQ-170 Sentinel » :

Le RQ-170 Sentinel Figure 1.2, est un véhicule aérien sans pilote de haute altitude et de longue endurance. C'est un drone furtif développé par Lockheed Martin et exploité par la Force aérienne des États-Unis (USAF), on atteint dans cette catégorie les dimensions d'un avion civil (Airbus A320 par exemple) pour des autonomies de 10 000 kilomètres et plus parcourues en volant largement au-dessus des trafics aériens courants, La masse au décollage des drones HALE peut largement dépasser les 10 tonnes, dont quelque 10% pour la charge utile.

Figure 1.2 : RQ-170 Sentinel.

Environ 90% de l'avion est composé de matériaux composites pour diminuer son poids total. Le RQ-170 peut offrir à ses opérateurs des données de renseignement en temps réel en exécutant des

Chapitre I Généralité sur les drones

6

opérations de surveillance sur une vaste zone. Ce drone peut capturer des images en temps réel puis les transférés à une station de contrôle au sol à travers des lignes de communication. Le RQ-170 a été déployé aux zones hostiles pour des missions d'observation et de renseignements et pour l'exploitation de la liberté durable, les capacités de ces drones HALE sont à rapprocher et à comparer à celles des avions pilotés du type de l'avion espion U2 (Fantôme) ou des avions de renseignement électronique Signet, ainsi qu'à celles des satellites d'observation ou d'alerte.

I.3.2. Les drones tactiques (Tactical Unmanned Air Vehicle) :

Les drones tactiques Figure 1.3 sont des drones militaires capables de s'envoler et d'atterrir sur courte distance propulsé par un moteur bicylindre. Ils sont propulsés pour le décollage par une catapulte pneumatique.

Figure 1.3 : Le drone Tactique RQ-7 Shadow.

L'atterrissage se fait à l'aide d'un parachute et de coussins gonflables de sécurité placés sous les ailes. Ils peuvent volés 5 à 8 heures et à des vitesses environ 175 km/h et volant à une altitude de 3 à 5 kilomètres, pour un rayon d'action de 30 à 500 kilomètres. On distingue plusieurs catégories des drones tactiques tels que l'AEROSTAR "AERONAUTICS DEFENSE SYSTEMS", RQ-7 Shadow, Sperwer, Hermes, Watchkeepere...etc. Ce types de drones comportent un ensemble de caméras gyrostabilisées et thermiques qui permettent la prise d'images aériennes en lumière visible et en infrarouge, il sert à la reconnaissance, la surveillance, l'acquisition de cibles et l'évaluation des dommages de combats.

Chapitre I Généralité sur les drones

7

I.3.3. Le drone solaire « Aquila» :

En juillet 2016, Facebook dévoilait son prototype de drone solaire destiné à diffuser l'Internet haut débit dans des zones non desservies ou disposant d'un accès de mauvaise qualité, le réseau social vient d'annoncer avoir accompli avec succès le premier vol d'essai d'un modèle à taille réelle.

Figure 1.4 : Le drone solaire Facebook « Aquila ».

Baptisé Aquila (nom latin signifiant « aigle ») Figure 1.4, l'engin se présente le drone avec une aile de 42 mètres d'envergure, plus grande que celle d'un Airbus A320 et pour un poids de 1468 kg. Ce drone alimenté par des cellules photovoltaïques est censé pouvoir voler durant 90 jours à des altitudes comprises entre 18 à 27 kilomètres en diffusant un accès Internet au sol dans un rayon d'un peu moins de 100 kilomètres.

Facebook indique que le drone, qui volait à une vitesse d'environ 40 km/h, dissipait un peu moins de 2000 watts. Une puissance qui, selon l'équipe en charge du projet Aquila, valide ses simulations aérodynamiques et ses choix techniques pour le système de propulsion. Aquila devrait servir à fournir une connexion internet dans les zones reculées du monde, les ingénieurs de Facebook espèrent faire voler ce type d'avion pendant plusieurs mois sans aucun ravitaillement, grâce à une très faible consommation d'énergie, l'équivalent de trois sèche-cheveux.

I.3.4. Les drones miniatures :

La course à la miniaturisation n'a de cesse d'augmenter, la catégorie des drones miniatures recouvre globalement tous les drones dont l'envergure est inférieure à 50 centimètres, on parle dans ce cas des mini-drones.

Chapitre I Généralité sur les drones

Figure 1.5 : Le drone miniature (nano drone UAV).

Ils sont généralement peu autonomes, mais qui jouent souvent le rôle de jumelles déportées, par exemple pour observer au-dessus d'un obstacle ou dans une zone à risque. Les micro-drones dont les dimensions sont inférieurs à 15 cm, pèsent environ 50 grammes avec une vitesse de croisière de l'ordre de 50 Km/h et un rayon d'action d'une dizaine de kilomètres. Ces micro-drones sont dédiés à la transmission d'images, de jour comme de nuit. Les missions envisagées sont par exemples l'évaluation de dommages ou l'observation d'une cible fixe...etc.

I.3.5. Le robot animal volant « BAT BOT B2 » :

En 2016, une équipe nord-américaine a développé un drone qui imite avec précision le vol de la chauve-souris.

Une avance qui devrait aider à étudier étroitement que possible le formidable système musculo-squelettique de cet animal, mais aussi à concevoir des robots volants plus sûrs et efficaces. Reproduire la cinématique des ailes d'un oiseau en robotique est un défi technique complexe. Mais ils ont simplement présenté la dernière version de leur drone appelé « Bat Bot B2 », Figure 1.6.

Figure 1.6 : Robot chauve-souris volante « BAT BOT B2 ».

8

Chapitre I Généralité sur les drones

9

Il pèse seulement 93 grammes pour 47 centimètres d'envergure, « Le Bat Bot » est contrôlé par des moteurs miniatures logés dans la colonne vertébrale, les ailes sont recouvertes d'une membrane en silicone de 56 microns d'épaisseur spécialement développée et qui reproduit l'élasticité naturelle des ailes des chauves-souris.

Les chercheurs disent avoir identifié cinq mouvements dominants dans l'aile battant de la chauve-souris qu'ils ont mis en oeuvre pour reproduire environ 57% de la cinématique originale. Au cours des essais, le Bat Bot B2 a volé à environ trente mètres, fait des virages inclinés et plonge. Tant de mouvements supposés reproduire en partie les techniques de chasse d'une chauve-souris.

Le but principal de ce drone est de servir à étudier plus précisément le vol de la chauve-souris. Les concepteurs du « Bat Bot » ajoutent que cette configuration offrirait également une meilleure sécurité que les drones quadri rotors dans des environnements où il y a risque de collision avec des personnes ou des objets. Le développement du « Bat Bot » continuera, dans le but notamment de reproduire la capacité des chauves-souris à se percher verticalement vers le bas.

I.4. Domaines d'application des quadrotors :

L'utilisation des quadrotors n'a cessé de progresser ces dernières années, notamment dans les applications de loisir. Mais dans les domaines professionnels cette progression est encore plus flagrante [12]. Avec ses 4 moteurs, le drone quadrotor apporte des possibilités d'embarquement de caméras, appareils photos et autres capteurs pour réaliser des missions aériennes d'acquisition de données, là où des moyens conventionnels sont trop onéreux ou trop compliqués voire impossibles à mettre en oeuvre.

Par ses capacités à rester en vol stationnaire ou à évoluer selon des trajectoires complexes, le drone quadrotor devient un outil privilégié utilisé dans plusieurs domaines tel que:

I.4.1. Domaine de sécurité :

? Les quadrotors sont utilisés par Les services de secours (police, sapeurs-pompiers et gendarmerie) pour l'évaluation des dégâts en cas de catastrophe naturelle afin de prendre des informations stratégiques sur des interventions en hauteur et délicates (exemples: victimes d'avalanches, victimes d'inondations et de tremblement de terre, repérage des feux de forêts, l'exploration des zones radioactives, les volcans etc...)

? Inspection des ouvrages d'art tels les ponts, les viaducs, les barrages.

? La surveillance maritime (voies maritimes, trafic de drogue, détection des pollutions par hydrocarbures, la surveillance urbaine, des manifestations, ainsi que les frontières).

? missions militaires de reconnaissance et support de combat.

Chapitre I Généralité sur les drones

10

I.4.2. Domaine civil :

? Dans le domaine civil, les quadri-rotors sont conçue pour explorer des situations difficiles d'accès, comme des montagnes, des canyons. Ils serviraient à faire prises de vue aériennes inédites et des vidéos pour des chaînes télé comme (des reportages sur des lieux isolés de la terre, des documentaires, films, etc..).

? Inspection des ouvrages d'art tels les ponts, les viaducs, les barrages.

? Etudes scientifiques (topographie et cartographie, Étude de l'atmosphère, des sols (géologie) et des océans).

? Transport et livraisons des produits légères sur de courtes distances comme (Les colis postaux, boites de pizza, etc...).

I.5. Description général du quadrotor :

Un quadrotor est un robot mobile aérien à quatre rotors définit par six degrés de liberté dans l'espace (3 axes X, Y, Z) Figure 17. [1-2]. Ces 4 rotors sont généralement placés aux extrémités d'une croix, et l'électronique de contrôle est habituellement placée au centre de la croix. Afin d'éviter à l'appareil de tourner sur lui-même sur son axe de lacet, il est nécessaire que deux hélices tournent dans un sens, et les deux autres dans l'autre sens. Pour pouvoir diriger l'appareil, il frauder que chaque couple d'hélice tournant dans le même sens soit placé aux extrémités opposées d'une branche de la croix. Le fonctionnement d'un quadrotor est assez particulier.

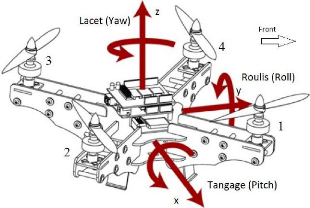
Figure 1.7 : Les mouvements de bases du quadrotor.

En faisant varier astucieusement la puissance des moteurs, il est possible de le faire monter/descendre, de l'incliner à gauche/droite (roulis) ou en avant/arrière (tangage) ou encore de le faire pivoter sur lui-même (lacet) [3], le quadrotor a six degrés de libertés, trois mouvements de rotation et trois mouvements de translation, ces six degrés doivent être commandés à l'aide de quatre déclencheurs

Chapitre I Généralité sur les drones

11

Chapitre I Généralité sur les drones

12

seulement; Donc c'est un système sous actionné (le nombre des entrées inférieure au nombre des sorties).

I.6. Les mouvements du quadrotor :

Dans les hélicoptères classiques, quand le rotor principal tourne, il produit un couple réactif qui inciterait le corps de l'hélicoptère à tourner dans la direction opposée si ce couple n'est pas contrarié. Ceci est habituellement fait en ajoutant un rotor de queue qui produit une poussée dans une direction latérale. Cependant, ce rotor avec son alimentation électrique associée ne fait aucune contribution à la poussée. Par contre, en cas de quadrotor, le rotor droit et le rotor gauche tournent dans le sens des aiguilles d'une montre et dans la direction opposée les rotors avant et arrière, ceci neutralise effectivement le couple réactif non désiré et permet au véhicule de planer sans tourner hors de la commande. D'ailleurs, différemment aux hélicoptères classiques, toute l'énergie dépensée pour contrecarrer le mouvement de rotation contribue à la force de poussée [4-11].

Les mouvements de base de quadrotor sont réalisés en variant la vitesse de chaque rotor changeant de ce fait la poussée produite. Le quadrotor incline vers la direction du rotor plus lent, qui tient compte alors de la translation le long de cet axe. Par conséquent, comme à un hélicoptère classique, les mouvements sont couplés, signifiant que le quadrotor ne peut pas réaliser la translation sans roulement ou tangage, ce qui signifie qu'un changement de la vitesse d'un rotor se traduit dans un mouvement en au moins trois degrés de liberté. Par exemple, augmentant la vitesse de propulseur gauche aura comme conséquence un mouvement de roulis (le quadrotor incline vers le rotor plus lent, vers la droite), un mouvement de lacet (l'équilibre entres les rotors qui tourne dans le sens des aiguilles d'une montre et les rotors qui tourne dans le sens inverse est perturbé ayant pour résultat un mouvement de rotation horizontal), et une translation (le mouvement de roulis incline l'armature et avec lui, l'orientation de la force de poussée). Cet accouplement est la raison pour laquelle nous pouvons commander les six degrés de liberté de quadrotor avec seulement quatre commandes (le couple appliqué par les moteurs sur chaque propulseur).

Le quadrotor a cinq mouvements principaux :

Mouvement vertical (Throttle), Mouvement de roulis (Roll), Mouvement de tangage (Pitch), Mouvement de lacet (Yaw) et Translations horizontales.

I.6.1. Le mouvement vertical (Throttle) :

Afin de planer, toute la force de portance devrait seulement être le long de l'axe z avec une grandeur exactement opposée à la force de pesanteur. D'ailleurs, la force de portance crée par chaque rotor doit être égale pour empêcher le véhicule de renverser plus. Par conséquent, la poussée produite par chaque rotor doit être identique.

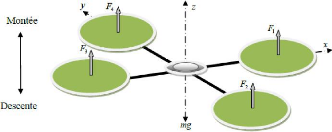
Figure 1.8 : Illustration du mouvement vertical (Throttle).

Le mouvement ascendant et descendant est obtenu par la variation de la vitesse de rotation des moteurs (par conséquence la poussée produite), si la force de portance est supérieure au poids du quadrotor le mouvement est ascendant, et si la force de portance est inférieure au poids du quadrotor le mouvement est descendant.

I.6.2. Le mouvement de roulis (Roll) :

La Figure 1.9 montre bien comment un mouvement de roulis est obtenu. Dans ce cas, on applique un couple autour de l'axe x, c'est-à-dire en appliquant une différence de poussée entre les rotors (1, 2) et les rotors (3, 4). Ce mouvement (rotation autour de l'axe x) est couplé avec un mouvement de translation selon l'axe y.

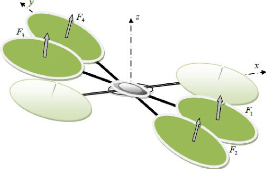
Figure 1.9 : Illustration du mouvement de roulis (Roll).

I.6.3. Le mouvement de tangage (Pitch) :

La Figure 1.10 montre comment un mouvement de tangage est obtenu. Dans ce cas, on applique un couple autour de l'axe y, c'est-à-dire en appliquant une différence de poussée entre le rotor (1, 4) et les rotors (2, 3). Ce mouvement (rotation autour de l'axe y) est couplé avec un mouvement de translation selon l'axe x.

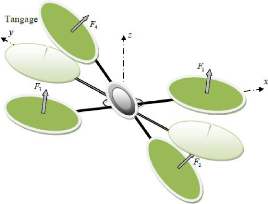
Chapitre I Généralité sur les drones

13

Figure 1.10 : Illustration du mouvement de tangage (Pitch).

I.6.4. Le mouvement de lacet (Yaw) :

La Figure 1.11 montre comment le mouvement de lacet est obtenu. Dans ce cas, nous voulons appliquer un couple autour de l'axe z, qui est fait en appliquant une différence de vitesse entre les rotors (1,3) et (2,4). Ce mouvement n'est pas un résultat direct de la poussée produit par les propulseurs mais par les couples réactifs produits par la rotation des rotors.

La direction de la force de poussée ne décale pas pendant le mouvement, mais l'augmentation de la force de portance dans une paire de rotors doit être égale à la diminution des autres paires pour s'assurer que toute la force de poussée demeure la même.

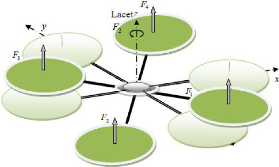
Figure 1.11 : Illustration du mouvement de lacet (Yaw).

Chapitre I Généralité sur les drones

14

I.6.5. Le mouvement de translation horizontale :

La Figure 1.12 montre comment la translation horizontale est réalisée. Dans ce cas, nous voulons appliquer une force le long de x ou de y qui est fait en inclinant le corps (par le tangage ou le roulement) et en augmentant toute la poussée produite pour garder l'importance du composant de z de la poussée égale à la force de pesanteur.

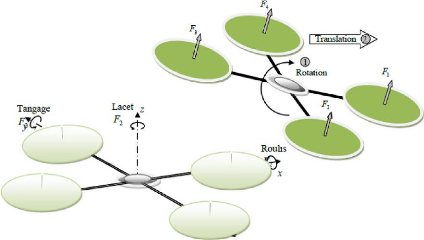
Figure 1.12 : Illustration du mouvement de translation horizontale.

Chapitre I Généralité sur les drones

15

I.7. Conclusion :

Ce chapitre permet au lecteur d'avoir des concepts préliminaires sur les différentes catégories des robots volants plus particulièrement les quadrotors et leur principe de fonctionnement. Dans le chapitre suivant nous donnons plus de détaille sur les paramètres dynamiques affectant l'orientation du quadrotor, les équations mathématiques et la modélisation de Newton-Euler.

Chapitre 2

Modélisation dynamique d'un quadrotor

Chapitre II Modélisation dynamique d'un quadrotor

16

Chapitre II : Modélisation dynamique d'un quadrotor

II.1. Introduction :

Afin de concevoir un contrôleur de vol, on doit d'abord comprendre profondément la dynamique de l'avion, par conséquent son modèle dynamique. Cette compréhension est nécessaire non simplement pour la conception du contrôleur, mais aussi pour s'assurer que le comportement de véhicule est plus proche que possible de la réalité lorsque la commande est appliquée.

Le quadrotor est classé dans la catégorie des systèmes volants les plus complexes vu le nombre d'effets physiques qui affectent sa dynamique à savoir les effets aérodynamiques, la gravité, les effets gyroscopiques, les frottements et le moment d'inertie. Cette complexité résulte essentiellement du fait que l'expression de ces effets diffère pour chaque mode de vol. En effet les modèles dynamiques du quadrotor proposés changent en fonction des taches planifiées et en fonction des milieux de navigation définis à priori par l'opérateur.

II.2. Modèle dynamique du quadrotor :

La modélisation des robots volant est une tâche délicate puisque la dynamique du système est fortement non linéaire et pleinement couplée. Afin de pouvoir comprendre au mieux le modèle dynamique développé ci-dessous, voilà les différentes hypothèses de travail :

· La structure du quadrotor est supposée rigide et symétrique, ce qui induit que la matrice d'inertie sera supposée diagonale,

· Les hélices sont supposées rigides pour pouvoir négliger l'effet de leur déformation lors de la rotation.

· Le centre de masse et l'origine du repère lié à la structure coïncident.

· Les forces de portance et de traînée sont proportionnelles aux carrés de la vitesse de rotation des rotors, ce qui est une approximation très proche du comportement aérodynamique.

Pour évaluer le modèle mathématique du quadrotor on utilise deux repères, un repère fixe lié à la terre Rb et un autre mobile Rm. Le passage entre le repère mobile et le repère fixe est donné par une matrice dite matrice de transformation T qui contient l'orientation et la position de repère mobile par rapport au repère fixe. On choisit la convention d'axes suivants :

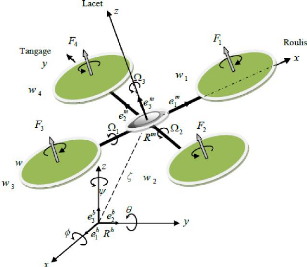
Chapitre II Modélisation dynamique d'un quadrotor

17

Figure 2.1 : Géométrie du quadrotor.

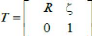
(1)

Avec R la matrice de rotation (décrit l'orientation de l'objet mobile), æ = [x Y Z]T est le vecteur de position. Pour déterminer les éléments de la matrice de rotation R, on utilise les angles d'Euler.

II.2.1. Angle d'Euler :

Au début le repère mobile est coïncide avec le repère fixe, après le repère mobile fait un mouvement de rotation autour de l'axe x d'un angle de roulis(- 2 < ç < 2), suivi d'une rotation

Autour de l'axe y d'un angle de tangage(- 2 < ç < 2), suivi d'une rotation autour de l'axe z d'angle de lacet(-7r < i < 7r). Donc on a la formule de la matrice de rotation R :

ci -si 0 ce 0 se 1 0 0

R = Rot_s (i ) × Rot_y(e) × Rot, (ç) = ~si ci 0 ~× ~0 1 0 ~× ~0 cç-sç ~ (II.2)
0 0 1 -se 0 ce 0 sç cç

R = ~ci ce sçseci - sci ???? cçseci + si sç si ce sçsesi + ci ce cçsesi - cçci ~ (II.3)
-se sçce cçce

Avec : c = cos et s = sin

Chapitre II Modélisation dynamique d'un quadrotor

II.2.2. Vitesses angulaires : Les vitesses de rotations Ù1, Ù2,Ù3dans le repère fixe sont exprimées en fonction des vitesses de rotations ?????, ?????, ????? dans le repère mobile, on a : Ù = ~Ù10 0 Ù2~ = ~^?????0~ + ????????????????(????)^-1 ~????? ~+ (????????????????(????)????????????????(????))-1 ~????0~ Ù3 0 0

(II.4)

En effet, la rotation en roulis a lieu lorsque les repères sont encore confondus. Puis, en ce qui concerne le tangage, le vecteur représentant la rotation doit être exprimé dans le repère fixe: il est donc multiplié par ????????????????(????)^-1. De même, le vecteur représentant la rotation en lacet doit être exprimé dans le repère fixe qui a déjà subites deux rotations. On arrive ainsi à:

Ù???? ????? 0 -????????????? ????? - ?????????????

Ù = ~ Ù???? ~ = ~ ?????????????

0 ~ + ~ ~ + ~ ????????????????????? ~ = ~ ????????????? + ????????????????????? ~ (II.5)

Ù???? 0 -????????????? ????????????????????? ????????????????????? - ?????????????

1 0 -????????

Ù = 0 ???????? ???????????????? ~ × ~⁽ⁱd (II.6)

0 -???????? ????????????????

Quand le quadrotor fait des petites rotations, on peut faire les approximations suivantes:

cö =cè =cø =1, et sö = sè = sø = 0.

Donc la vitesse angulaire sera:

Ù = [????? ????? ?????] (II.7)

II.2.3. Vitesses linéaires :

Les vitesses linéaires ????????????, ????????????, ???????????? dans le repère fixe en fonction des vitesses linéaires ???????????? , ???????????? , ???????????? dans le repère mobile sont données par :

18

???? ????

(II.8)

???????? ????????

???? = ~????????????~ = ???? × ~????????????~

???? ????????

????????????

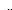
II.2.4. Effets physiques agissants sur le quadrotor :

II.2.4.1. Les forces :

Les forces agissant sur le système sont :

Le poids du quadrotor: il est donné par P = mg, où : m est la masse totale et g la gravité.

Chapitre II Modélisation dynamique d'un quadrotor

19

Les forces de poussée: qui sont des forces provoquées par la rotation des moteurs, elles sont perpendiculaires sur le plan des hélices. Ces forces sont proportionnelles au carrée de la vitesse de rotation des moteurs :

FL = bw_L² (II.9)

Avec i = 1: 4, et b est le coefficient de portance, il dépend de la forme et le nombre des pales et la densité de l'air.

Les forces de traînée : la force de traînée est le couplage entre une force de pression et la force de frottement visqueux, dans ce cas on a deux forces de traînée agissant sur le système qu'elles sont :

· La traînée dans les hélices : elle agisse sur les pales, elle est proportionnelle à la densité de l'air, à la forme des pales et au carré de la vitesse de rotation de l'hélice, elle est donnée par la relation suivante :

Th = dw² (II.10)

Avec d est le coefficient de drag il dépend de la fabrication de l'hélice.

· La traînée selon les axes (x, y, z): elle est due au mouvement du corps du quadri-rotor

F_t = Kfty (II.11)

Avec : K _ft le coefficient de traînée de translation et V la vitesse linéaire.

II.2.4.2. Les moments :

Il y a plusieurs moments agissants sur le quadrotor, ces moments sont dus aux forces de poussée et de traînée et aux effets gyroscopiques.

Moments dus aux forces de poussée :

· La rotation autour de l'axe x : elle est due au moment crié par la différence entre les forces de portance des rotors 2 et 4, ce moment est donné par la relation suivante :

M_x= l(F₄ - F₂) = lb(w₄² - w2 ²) (II.12)

Avec l, est la longueur du bras entre le rotor et le centre de gravité du quadrotor.

· La rotation autour de l'axe y : elle est due au moment crié par la différence entre les forces de portance des rotors 1 et 3, ce moment est donné par la relation suivante :

M_y= l(F3 - F1) = lb(w₃² - w₁²) (II.13)

Moments dus aux forces de traînée :

· La rotation autour de l'axe z : elle est due à un couple réactif provoqué par les couples de traînée dans chaque hélice, ce moment est donné par la relation suivante :

Chapitre II Modélisation dynamique d'un quadrotor

20

???????? = ????(????1 2 - ????2 ² + ????3 2 - ????₄²) (II.14)

(II.15)

s Moment résultant des frottements aérodynamiques, il est donné par :

???????? = ????????????Ù²

Avec ???????? ????: Le coefficient des frottements aérodynamiques et ? est la vitesse angulaire.

II.2.4.3. Effet gyroscopique :

L'effet gyroscopique se définit comme la difficulté de modifier la position ou l'orientation du plan de rotation d'une masse tournante. L'effet gyroscopique est ainsi nommé en référence au mode de fonctionnement du gyroscope, appareil de contrôle de mouvement utilisé dans l'aviation (du grec Gyro qui signifie rotation et scope, observer).

Dans notre cas il y a deux moments gyroscopiques, le premier est le moment gyroscopique des hélices, l'autre est le moment gyroscopique dû aux mouvements de quadrotor.

s Moment gyroscopique des hélices : il est donné par la relation suivante :

????????h = ? 4 Ù ? ???????? [0 0 (-1)^????+1 ????????]???? (II.16)

1

Avec ???????? est l'inertie des rotors.

s Moment gyroscopique dû aux mouvements de quadri-rotor : il est donné par la relation suivante :

???????????? = Ù ? ???? Ù (II.17)

Avec J est l'inertie du système.

II.2.5. Développement du Modèle mathématique selon Newton-Euler [5-6-7-8]:

En utilisant la formulation de Newton-Euler, les équations sont écrites sous la forme suivante:

		(II.18)	Avec æ : est le vecteur de position du quadri-rotor m : la masse totale du quadri-rotor ? : La vitesse angulaire exprimée dans le repère fixe R : La matrice de rotation ? : Le produit vectoriel

Chapitre II Modélisation dynamique d'un quadrotor

???????? ????????, ???????? ????????, ???????? ????????: Les coefficients des frottements aérodynamiques.

21

J : matrice d'inertie symétrique de dimension (3x3), elle est donnée par :

???????? 0 0

???? = ~0 ???????? 0 ~ (II.19)

0 0 ????????

????(Ù) : est la matrice antisymétrique; pour un vecteur de vélocité Ù = [????1 ????2 ????3] ???? , elle est donnée par:

0 ?Ù₃ Ù₂

????(Ù) = ~Ù3 0 ?Ù1 ~ (II.20)
?Ù2 Ù1 0

???????? : est la force totale générée par les quatre rotors, elle est donnée par :

????????= ????× [0 0 ? ????????

4 _????=1 ]???? (II.21)

???????? = ????????????2 (II.22)

???????? : La force de traînée selon les axes (x, y, z), elle est donnée par :

-???????????????? 0 0

???????? = ~0 -???????????????? 0 ~ ????? (II.23)

0 0 -????????????????

????????????????, ????????????????, ???????????????? : Les coefficients de traînée de translation, ???????? : Force de gravité, elle est donnée par :

0

???????? = ~0 ~ (II.24)
-????????

???????? : Moment provoqué par les forces de poussée et de traînée.

????(????4 - ????2)

???????? = ~????(????3 - ????1) ~ (II.25)

2

????(????₁² - ????₂² + ????₃² - ????₄)

????????: Moment résultant des frottements aérodynamiques, il est donnée par :

???????? ????????????? 2~????????

????????????????????^?

???????? ???????? ?????2

=

2 (II.26)

Chapitre II Modélisation dynamique d'un quadrotor

22

II.2.5.1. Equations de mouvement de translation :

On a:

·

???????? = ???????? + ???????? + ???????? (II.27)

On remplace chaque force par sa formule, on trouve :

????

????· ????????????????????????+ ~ ????· ~ = ~ ???????????????????????? - ????· ????????????????

???????????????? ???????????????? ~

4 ? ????=1

????????

-

???????? ????????????? ~ ???????? ????????????? ~ ???????? ???????????? ?

-

0 ~ 0 ~ ????????

(II.28)

On obtient alors les équations différentielles qui définissent le mouvement de translation :

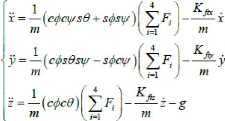
II.2.5.2. Equation de mouvement de rotation :

On a:

????Ù^? = -????????h - ????????h - ???????? + ???????? (II.30)

On remplace chaque moment par la formule correspondant, on trouve :

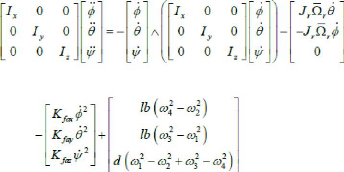
On obtient alors les équations différentielles définissants le mouvement de rotation :

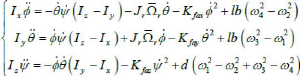
Chapitre II Modélisation dynamique d'un quadrotor

23

Avec : fr

= W1 - W2 + W3 - W4 (II.33)

En conséquence, le modèle dynamique complet qui régit le quadrotor est le suivant :

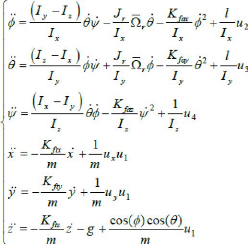
Avec :

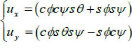
Et :

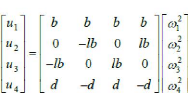
A partir de (II.35), on trouve :

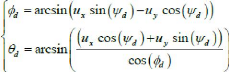
Chapitre II Modélisation dynamique d'un quadrotor

24

II.2.6. La représentation d'état du système :

Pour un système physique il existe une multitude de représentations d'état, dans notre cas on choisit le vecteur d'état comme suit [ ] :

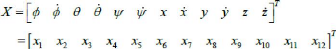
On obtient la représentation d'état suivante :

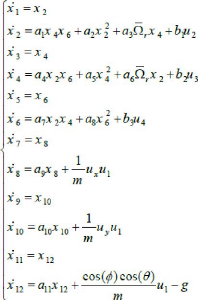
Avec :

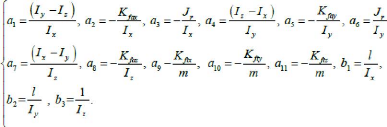
Chapitre II Modélisation dynamique d'un quadrotor

????~???? (II.43)

~?

????????

????

????????

???? =

25

II.7. La dynamique des rotors [1-2] :

Généralement les moteurs utilisés dans les quadrotors sont des moteurs à courant alternatif.

La dynamique du rotor est donc approximée à celle d'un moteur à courant alternatif, elle est donnée par les équations différentielles suivantes :

Avec : ???????? est le couple d'entrée, et ???????? = ????????????2 est le couple résistant généré par le rotor i.

Pour atteindre les objectifs de la commande d'un quadrotor, une boucle d'asservissement en vitesse est souvent nécessaire. D'abord, nous avons besoin de déterminer les vitesses désirées ????????,????

correspondantes aux valeurs des commandes fournies par le contrôleur, ces vitesses peuvent être calculées comme suit :

????~???? = ????^-1???? (II.40)

Avec: ????~???? = (????????12 , ????????22 , ????????32 , ????????4

2 ), ???? = (????₁,????₂,????₃, ????₄)^????, et ???? est une matrice non singulière, elle est obtenu à partir de (II.36).

L'objectif est de synthétisé un contrôleur pour que ???????? ? ????????,???? lorsque ???? ? 8 en utilisant les couples???????? .

On définit l'erreur de vitesse :

????~???? = ???????? - ????????,???? (II.41)
Une loi de commande est développée dans [1-2], elle est donnée par :

???????? = ???????? + ?????????????????,???? - ????????????~???? (II.42)
Avec ????????, i ?{1, 2, 3,4}sont des gains positifs.

On remplace la loi de commande dans (II.39), on obtient :

Chapitre II Modélisation dynamique d'un quadrotor

26

Cette relation représente la dynamique de l'erreur, elle nous montre la convergence exponentielle de

toi vers toi lorsquet - 00. Sa signifier la convergence des commandes du quadrotor vers ces valeurs désirées, ce qui assure la stabilité du quadrotor.

En réalité le quadrotor est commandé par les tensions d'alimentation de ces quatre moteurs. Pour commander ces moteurs, nous avons besoin d'obtenir la tension d'entrée de chaque moteur. Supposant que l'inductance du moteur est petite, et considérant que les moteurs utilisés sont identiques, nous pouvons obtenir la tension d'entrée de chaque moteur comme suit :

(II.43)

????????

KmKg

Avec : R_a est la résistance du moteur, K_m est la constant du couple de moteur, K_g est le gain du réducteur.

Vi = Ti + KmKgtoi

Chapitre II Modélisation dynamique d'un quadrotor

27

II.3. Conclusion :

Ce chapitre permet au lecteur de comprendre les bases physiques utilisées pour déterminer les équations de la cinétique et la dynamique des quadrotors, ainsi que les forces et les moments agissantes. L'utilisation du formalisme de Newton-Euler nous a permet d'établir le modèle dynamique du quad rotor. La complexité du modèle, La non linéarité, et l'interaction entre les états du système, peuvent se voir clairement. Les résultats des formules précédentes sont utilisés généralement pour établir un modèle mathématique permettant de décrire avec précision le comportement du système. Dans le prochain chapitre, je vais expliquer brièvement le hardware et le software utilisé dans la réalisation du quadrotor.

Chapitre 3

Conception et mise en oeuvre Lu

Fonctionnement

Chapitre III Conception et mise en oeuvre du fonctionnement

Chapitre III : Conception et mise en oeuvre du fonctionnement

III.1. Introduction :

Le but de ce chapitre est de donner une description globale du principe de fonctionnement des différentes parties de notre système, en expliquant le hardware que j'ai utilisé pour ce projet et comment je me suis installé avec des outils et des instruments électroniques de base pour réaliser le contrôleur de vol du drone, le transmetteur RF et le récepteur. Je vais également donner une explication détaillée sur la partie software utilisé pour ce projet, passant au processus de construction étape par étape.

III.2. Description du hardware utilisé :

Les quadrotors sont des systèmes complexes, qui exigent des composants et une instrumentation varié qui doit être à la fois de haute performance et de poids allégés. Ici on va introduire les plus importants :

III.2.1. Arduino Uno :

Un Arduino Uno Figure 3.1, c'est le composant le plus simple pour commencer avec, il me donne beaucoup de couvert pour continuer à développer mon propre contrôleur de vol du quadrotor car il s'agit d'un PCB à double face professionnelle avec des faibles interférences et bruits, donc il convient bien pour le vol. Alors je pourrais utiliser un Arduino pro mini pour cela, mais le problème c'est que l'alimentation sur un pro mini est basée d'un régulateur MIC5205, qui ne peut fournir qu'un 150mA avec un bon refroidissement. Donc pour garder les choses sur le côté sûr, j'ai utilisé un Arduino Uno pour la réalisation du contrôleur de vol.

28

Figure 3.1 : la carte Arduino Uno.

Arduino Uno, est une carte de développement "Open-Source Hardware" peu coûteuse, ce qui signifie que tout le monde est libre de télécharger les fichiers de conception et de tourner sa propre

Chapitre III Conception et mise en oeuvre du fonctionnement

29

Chapitre III Conception et mise en oeuvre du fonctionnement

Chapitre III Conception et mise en oeuvre du fonctionnement

version du conseil de développement populaire. Il est basé sur un microcontrôleur ATmega en 8-bit et Il contient tout le nécessaire pour supporter le microcontrôleur; Il suffit de le connecter à un ordinateur avec un câble USB ou de l'alimenter avec un adaptateur AC-DC ou une batterie pour le démarrer. Dans le cadre de ce projet le traitement séquentiel des instructions de programme est important, on utilise souvent les interruptions des pates d'entrés de l'Arduino Uno pour lire les signaux de commande venant du récepteur radio aussi en utilise les sorties PWM de l'Arduino Uno pour commander la rotation des moteurs brushless via les ESC. Finalement l'utilisation du protocole de communication I2C permet de lire les données provenant de Gyro, de sorte que nous pouvons agir sur la stabilité du drone.

III.2.2. Gyroscope MPU-6050 :

Nous avons seulement besoin de corriger le mouvement indésirable du quad rotor, le Gyro c'est le capteur idéal de notre projet. J'ai choisi le MPU-6050 Figure 3.2, car il est très facile à obtenir, il est également très bon marché et il détient d'un accéléromètre et un gyroscope à la fois, ceci est très pratique lors de la programmation d'une IMU. La centrale inertielle ou l'IMU est un ensemble de capteurs qui peut être installé au bord de n'importe quel corps mobile pour lire les données des mouvements de ce corps. Ce type de puce est en réalité ce qu'on appelle un micro système électromécanique ou un MEMS pour abrégé, ceci est rien d'autre que des capacités qui varient en fonction de l'accélération et de la vitesse angulaire. Donc pour notre cas, nous pourrons déterminer et traité les mouvements du quad rotor dans l'espace. L'interface du module MPU-6050 avec Arduino se fait aux broches (SCL et SDA) à l'intermédiaire d'une liaison I2C.

Figure 3.2 : Unité de Mesure de l'Inertie gyroscopique MPU-6050.

Le mouvement angulaire sur le quadrotor est partout le même. Donc, peu importe où se trouve le gyroscope. Mais c'est toujours une bonne idée de monter le gyroscope au centre de gravité du quad où les vibrations sont les plus faibles.

III.2.3. Les moteurs sans balais « Brushless » :

Dans le cadre de ce projet, j'ai besoin des moteurs de petite masse et à la fois de très haute vitesse avec un rapport couple-masse élevée. Pour cela je suis obligé de travaillé avec les moteurs sans balais ou "Brushless BLDC motor". Comme le montre la Figure 3.3.

30

Les moteurs brushless sont en fait un type de moteur synchrone à aimants permanents tourne avec un courant alternatif triphasé AC. Ils présentent de nombreux avantages par rapport aux moteurs DC classiques à savoir, leurs longues durées de fonctionnement et leurs insensibilités aux parasites en plus leurs réponses dynamiques élevées. Ce type de moteur, c'est ce qui fait tourner et générer de la poussée pour permettre au drone de voler. Dans le cas des multirotors, les moteurs génèrent une poussée vers le haut qui maintient le drone comme un quadcopter volant. Autrement dit, un moteur sans balai contient un ensemble d'électroaimants (bobines) qui sont reliés ensemble dans des paires spécifiques. Ces électroaimants sont connectés en trois sections principales, de sorte que le moteur brushless comporte trois fils sortants, Figure 3.4.

Figure 3.3 : Moteur Brushless EMAX XA2212 1400Kv. Figure 3.4 : Composantes interne du Moteur Brushless.

Le moteur sans balais se compose de deux sections principales :

· Rotor : la partie qui tourne et a les aimants montés sur un motif radial.

· Stator : la partie qui ne tourne pas, et dispose d'électroaimants.

J'utilise pour ce projet quatre moteurs de la marque EMAX XA2212 1400Kv, ces moteurs ont 27.9 mm de diamètre et 43.16 mm de longueur, ils pèsent 51g et ils consomment une puissance de 197 Watts avec un courant max de 16.4A. Le KV veut dire la vitesse de rotation du moteur pour 1 volt. Il indique le nombre de tour/minute/volt du moteur à vide. Dans notre cas, le circuit de puissance qui contient les moteurs fonctionne sur un voltage nominal de 11.1 volts, donc pour cela avec 1400 KV sous 11.1 volts chaque moteur peut effectuer jusqu'à 15540 tours/minute s'il est à vide c'est ce qui est appeler rotation par minute RPM.

III.2.4. Electronique Speed Controller « ESC » :

ESC signifie Electronique Speed Controller Figure 3.5, c'est un circuit électronique qui gère la vitesse des moteurs brushless. Sur un multi-rotor, chaque moteur obtient son propre ESC, dont chacun se connecte au contrôleur de vol. Les ESC converties les séquences des signaux de commande

31

PWM venant du contrôleur de vol ou du récepteur radio en un signal alternatif triphasé, et entraîne le moteur brushless en fournissant le niveau d'énergie électrique approprié.

Figure 3.5: variateur de vitesse « Hobbywing OPTO ESC 20A ».

Les ESCs utilisés pour ce projet sont de la série hobbykings 20A spécialement conçus pour les multirotors, ils ont un large éventail de fonctions de programmation combinés avec une courbe d'accélération linéaire. L'ESC doit supporter un ampérage au moins égal à l'ampérage max des moteurs. Généralement on prend un ESC d'ampérage un peu supérieur afin qu'il ne chauffe pas. Dans mon cas les moteurs brushless consomment 16.4A pour une max poussée « Thrust », j'ai choisie à prendre un ESC de 20A afin de garder un peu de marge de sécurité.

III.2.5. Batterie LIPO :

Notre système quadrotor besoin beaucoup d'énergie et a besoin d'une source d'alimentation puissante et en plus légère, pour cela je suis obligé de travailler avec la batterie du Lithium-Polymère Figure 3.6. Les batteries Lithium-Polymère sont des batteries chimiques très puissantes et assez légère pour le bon vol du quadrotor, en plus elle inclut un circuit de protection (PCM) qui protège la batterie contre les charges et décharges excessives et des court-circuités ou d'explosée [14].

Figure 3.6 : Batterie de Lithium-Polymère « LIPO » 11.1V 70C 2.2Ah.

J'ai utilisé pour ce projet une batterie LIPO de 3 cellules et d'une capacité de 2200mAh à 11.1 volts avec un Taux de décharge « C Rating » de 70C et un poids de 225g.

Le Taux de décharge est une façon informelle de décrire la quantité de courant que la batterie peut fournir en toute sécurité, Le C se réfère à la capacité de la batterie et à l'amplitude des heures. Dans notre cas cette batterie de 70C peut fournir jusqu'à 70 × 2.2Ah = 154 ampères dans une heure.

Chapitre III Conception et mise en oeuvre du fonctionnement

32

III.2.6. Les hélices :

Concernant les hélices, il faut les choisir en fonction de la taille des moteurs et du châssis du quadrotor utilisé. J'ai choisi les DJI 8045 comme le montre la Figure 3.7. Ces hélices sont fabriquées avec la fibre de carbone qui est une matière résistante et légère, elles ont 8 pouces (20 cm) de diamètre et un pas de tangage de 4.5 pouces (un pas de tangage signifie combien de distance que le quadrotor va aller de l'avant pour une révolution à 360 degrés de l'hélice).

Figure 3.7 : Hélices DJI 8045.

Comme déjà dit dans le chapitre 1, on prendra deux de sens horaire et deux de de sens anti horaire en direction de la palme, ces hélices seront fixé aux moteurs et leur rôle sera de brassé l'aire pour générer la force de poussée. La taille de l'hélice varie avec la puissance du moteur, pour bien comprendre voici quelques règles à respecter pour le bon choix des différents accessoires :

Plus une hélice est petite, plus elle a besoin de tourner vite pour être efficace, plus elle est grande, moins elle a besoin de tourner vite. Sur un gros modèle d'avion par exemple, une petite hélice même tournant très vite (beaucoup de KV), il ne suffira pas à le faire voler correctement (pas assez puissante). Donc il faudra l'équiper d'une grande hélice, qui aura besoin de tourner moins vite (moins de KV). Les grandes hélices consommant plus que les petites hélices, une grande hélice devra être montée sur un moteur puissant (beaucoup de watt) et vice versa. P(Watt) = U(Volt) X I(A)

I(A) : le courant max qui doit être délivré par l'ESC au moteur brushless.

U(Volt) : la tension continue de la batterie LIPO.

P(Watt) : la puissance max admise par le moteur brushless.

En général : un moteur avec fort KV, prévue pour petite hélice qui consomme peut a peu de Watts ; et inversement : moteur avec faible KV, prévu pour grande hélice qui va consommer beaucoup a beaucoup de Watts.

III.2.7. Arduino Nano :

L'Arduino Nano est une carte petite, complète et facile à utiliser basée sur l'ATmega328 Figure 3.8. Il a plus ou moins la même fonctionnalité de l'Arduino Uno, mais dans un package différent. Il ne dispose que d'une prise d'alimentation DC et fonctionne avec un câble USB Mini-B au lieu d'un câble standard pour se connecté au PC. L'Arduino Nano peut être alimenté via une alimentation externe non régulée 6-20V (broche 30) ou Alimentation externe régulée 5V (broche 27).

Chapitre III Conception et mise en oeuvre du fonctionnement

33

La source d'alimentation est automatiquement sélectionnée pour la source de tension la plus élevée. Il est généralement destiné pour des réalisations qui nécessitent la miniaturisation et à l'installation semi-permanente dans des objets ou des expositions, on l'utilise souvent dans la réalisation du transmetteur RF.

Figure 3.8 : Arduino Nano.

III.2.8. Module radio NRF24l01 2.4GHz :

Notre système quadrotor reçoit des données de contrôle en temps réel, il a donc besoin d'avoir un système radio de bonne qualité. Le transmetteur RF a besoin d'un module puissant pour envoyer le signal assez loin, mais le récepteur peut avoir un type normal d'antenne PCB. Le module radio que j'ai utilisé est celui avec l'antenne à puissance amplifiée, Figure 3.9.

Figure 3.9 : NRF24l01 Radio module 2.4GHz.

L'NRF24l01 est un module émetteur-récepteur qui utilise la bande de 2,4 GHz et peut fonctionner avec un débit de 250 Kbps à 2 Mbps à l'air libre. La consommation d'énergie de ce module est juste d'environ 12 mA au cours de la transmission et la tension de fonctionnement est de 1,9 Volts à 3,3 Volts. Le module NRF24L01 envoi et reçoit des données dans des «paquets» de plusieurs octets à la fois et la communication avec le microcontrôleur se fait via le protocole de communication SPI. L' NRF24L01 peut utiliser jusqu'à 125 canaux différents, ce qui permet d'avoir un réseau de 125 modems indépendants en un seul module. Ces unités ont beaucoup de complexité interne, mais certaines personnes talentueuses ont écrit des bibliothèques Arduino qui nous facilitent la tâche et nous donne beaucoup de liberté en programmation.

Chapitre III Conception et mise en oeuvre du fonctionnement

III.2.9. Les joysticks :

Les parties les plus importantes du contrôleur radio sont les joysticks, mieux dits, les potentiomètres. Un joystick Figure 3.10, est un dispositif de contrôle du curseur utilisé dans les jeux informatiques et la technologie d'assistance basé sur des potentiomètres. Le joystick qui a obtenu son nom du bâton de contrôle utilisé par un pilote pour contrôler les ailerons et les ascenseurs d'un avion, c'est un levier à main qui pivote sur une extrémité et transmet ses coordonnées par l'intermédiaire d'un microcontrôleur.

Les émetteurs radiocommande des quadrotors comportent deux potentiomètres de précision dans chaque joystick, dont ils varient la valeur de la résistance en fonction des accès de contrôle pour les mouvements Pitch, Roll, Yaw et Throttle, Figure 3.11.

34

Figure 3.10 : Joystick de haute qualité. Figure 3.11 : Commandes de vol du drone.

Dans ce contexte, on utilise l'Arduino Nano pour convertir le signal d'entrée de chaque potentiomètre en un signal numérique, puis le module radio NRF24101 permettra d'envoyer les variations de ces valeurs au récepteur du drone. En fait, ces valeurs numériques correspondent à la position du bâton de contrôle de chaque joystick.

III.2.10. La carcasse du quadrotor et du transmetteur RF:

Le châssis c'est l'élément central du drone qui détermine son envergure totale. La réalisation d'un quadrotor de petite taille exige l'utilisation d'un cadre léger, rigide et harmonique. Ainsi pour le transmetteur RF, il faut couvrir le circuit imprimé avec une carcasse confortable pour faciliter l'utilisation et pour le protégé. L'impression en 3D m'a permis de construire les carcasses voulus à base de nylon ultra polyamide (PLA) en utilisant les fichiers sources du logiciel SOLID WORKS [15] Figure 3.12.

Chapitre III Conception et mise en oeuvre du fonctionnement

Figure 3.12 : Les carcasses construites avec logiciel SOLID WORKS en 3D.

L'architecture du châssis du quadrotor est optimisée permettant de dégager beaucoup d'espace pour que les composants soient installés sans difficulté, pour cela j'ai construit un circuit imprimé permettant de faire le câblage des ESC et le contrôleur de vol avec la batterie plus facilement comme le montre la Figure 3.13.

Figure 3.13 : Circuit imprimé du plat inferieur réalisé avec logiciel Eagle CAD soft.

35

Chapitre III Conception et mise en oeuvre du fonctionnement

36

III.3. Réalisation du transmetteur RF :

III.3.1. Schéma électronique :

Le circuit électronique de l'émetteur radio 2,4 GHz Figure 3.14, est basé d'un microcontrôleur Atemega328, NRF24l01 et deux joysticks. Il avait 6 canaux de transmission qui corresponds aux commandes (Pitch, Roll, Yaw, Throttle et les deux commutateurs SW1 et SW2).

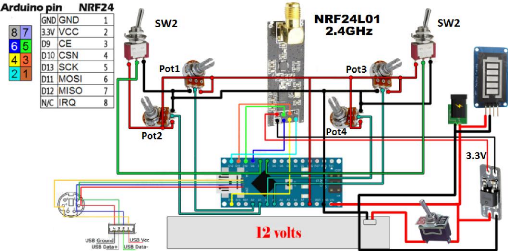
Figure 3.14 : Schéma électronique du transmetteur RF 2.4 GHz.

Au niveau de l'alimentation nous devons fournir les 12 volts de la batterie à l'entrée de l'Arduino Nano et au régulateur de tension 3.3V. Ce dernier est nécessaire pour faire chuter la tension de 12V à 3.3V, parce que le module NRF24 fonctionne à cette tension et en plus il absorbe trop de courant ainsi que l'Arduino ne pourra pas fournir autant de courant. La sortie négative de la batterie est connecté à l'une des broches GND de l'Arduino et la sortie positive à l'interrupteur ON / OFF, l'autre broche du commutateur ira directement à la broche Vin de l'Arduino et à l'entrée du régulateur de tension 3.3V. Les broches CE et CSN de la NRF24 doivent être branchées sur les pins numériques de l'Arduino Nano qui correspondent aux même sens déclaré dans le programme principale. Même pour les auteurs broches MISO, MOSOI et CLK qui sont dédiés pour la communication SPI.

Chacun des 4 potentiomètres est connecté aux entrées analogiques A0, A1, A2 et A3 de l'Arduino Nano. Nous devons d'abord fournir 5 volts à la broche droite de chaque potentiomètre et la masse à la broche gauche. De cette manière, nous aurons 0 volts aux entrées analogiques quand le potentiomètre est dans la plus basse position et 5 volts quand il est dans la plus haut et n'importe

Chapitre III Conception et mise en oeuvre du fonctionnement

quelle tension (de 0 à 5 volts) dans l'intervalle. L'Arduino Nano a un convertisseur analogique numérique (ADC) de 10 bits qui nous donnera des valeurs de 0 à 1024 unités. Les deux canaux de commutateurs SW1 et SW2 sont des canaux numériques et ne sont pas identiques à celles des potentiomètres, car ils n'ont que des valeurs de 0 et 1 logique. Le circuit imprimé double face du transmetteur RF Figure 3.15 est réalisé à l'aide du logiciel Eagle CAD soft.

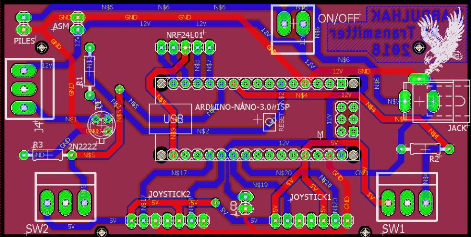
Figure 3.15 : Schéma du circuit imprimé du transmetteur RF 2.4 GHz.

Figure 3.16 : Transmetteur RF 2.4 GHz durant la réalisation.

37

Chapitre III Conception et mise en oeuvre du fonctionnement

38

III.3.2. Algorithme du transmetteur RF :

Au début, il est nécessaire de définir la librairie de l'NRF24 et l'adresse du canal de transmission radio, la même adresse doit apparaître dans les instructions du programme du récepteur pour assurer le cryptage de nos informations. Avant de commencer par le programme principal, il faut calibrer les joysticks en utilisant L'ADC de l'Arduino Nano. L'utilisation de la fonction AnalogRead permet de lire les valeurs analogiques de chaque potentiomètre des deux joysticks qui corresponds aux commandes à envoyer, puis les affichés sur le moniteur série de l'Arduino IDE à l'aide de l'instruction Serial.print (" ") en faisant varier la position des joysticks dont chaque colonne représente la valeur d'un canal "une commande" Figure 3.17.

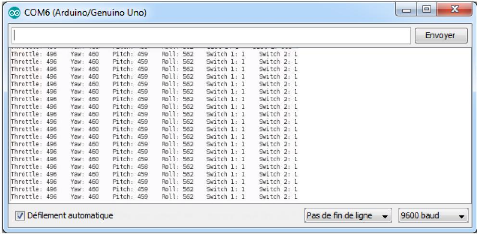
Figure 3.17 : Capture d'écran des valeurs analogiques affichées sur le moniteur série de l'Arduino IDE.

Ces valeurs analogiques sont codées sur 10 bits, de sorte que le taux des potentiomètres peut aller de 0 à 1024 en décimale. On note ensuite les valeurs correspondantes aux positions (minimal, centrale et maximal) des joysticks pour les utilisées dans le programme principal du transmetteur RF, j'ai trouvé :

Throttle = min : 115 centre : 645 max : 989 Yaw = min : 62 centre : 622 max : 980 Pitch = min : 25 centre : 594 max : 929

Roll = min : 75 centre : 612 max : 974

Comme l'NRF24l01 envoi les données dans des paquets de 8bit/s, alors l'utilisation de la fonctions prédéfinie map(, , , , ); dans le programme principale du transmetteur RF permet de coder les valeurs précédentes à des grandeurs de 8 bits (0 à 255) afin de les envoyer aux récepteur RF

en utilisant la fonction prédéfinit radio.

write(&data, sizeof(MyData)).

Chapitre III Conception et mise en oeuvre du fonctionnement

La lecture des valeurs numérique des commutateurs SW1 et SW2 sera une valeur booléenne de 0 ou 1 logique (ON/OFF). L'NRF24L01 peut envoyer jusqu'à 32 canaux différents de 8 bits chacun, dans ce cas nous enverrons que les 6 canaux de 8 bits qu'il correspond enfaite aux valeurs des commandes: (Tangage, Roulis, Lacet, Gaz et les deux switches). Le programme Principal du transmetteur RF est expliqué dans cet organigramme:

Sous-programme mapJoystickValues :

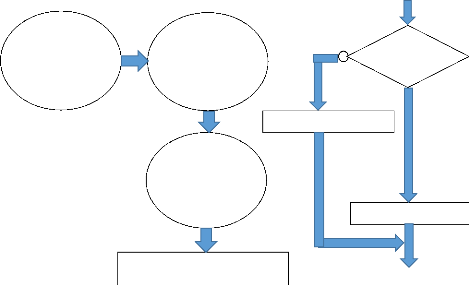
Déclaration des
librairies SPI &
NRF24l01
Pins direction

Déclaration des
variables 8 bits:
Throttle, Yaw,

Pitch, Roll,

SW1, SW2

Non

Val< centre

Oui

Void setup :

Codé val de 128 jusqu'à 255

Initialisation des instructions de la

Radio

Déclaration des
variables sur 10
bits:
min, centre,
max val

Codé val de 0 jusqu'à 128

Void loop :

Déclaration du sous-programme mapJoystickValues

Codé les valeurs de 10 bits et les Affectés aux variables à envoyer En utilisant le sous-programme mapJoystickValues Throttle = mapJoystickValues (lire de A0, 115, 645, 989) Yaw = mapJoystickValues (lire de A1, 62, 622, 980) Pitch = mapJoystickValues (lire de A2, 25, 594, 929) Roll = mapJoystickValues (lire de A3, 75, 612, 974)

SW1 = lire la valeur digitale du pin 7

SW2 = lire la valeur digitale du pin 8

39

Transmettre DATA :

radio.write

(&data,

sizeof(MyData))

Chapitre III Conception et mise en oeuvre du fonctionnement

40

III.4. Récepteur RF 2.4 GHz :

Tout émetteur a besoin d'un récepteur. Habituellement, les récepteur radio génèrent des signaux de sortie PWM qui varie de 1000 à 2000 microsecondes, parce que c'est les largeurs d'impulssion nécessaire pour le fonctionnement des ESCs. Dans ce contexte, l'utilisation des registres de Timer de l'Arduino Nano permet facilement de généré les signaux PWM pour les 6 différents canaux qui correspondent enfaite aux mêmes valeurs de 8 bits envoyés par le transmetteur.

III.4.1. Circuit et schéma électronique :

Le circuit électronique du récepteur radio 2,4 GHz est basé sur les mêmes composants que le transmetteur l'Arduino Nano, NRF24l01 et la socket-8-pin pour NRF24 qui détient d'un régulateur de 3.3v ASM1117. Les connexions de l'Arduino Nano au NRF24l01 sont les mêmes que dans le transmetteur radio, comme il est illustré dans le schéma ci-dessus Figure 3.18.

Les connexions au module radio sont les mêmes que dans le cas du transmetteur. Pour alimenter le récepteur nous pourrions obtenir 11.1 volts directement de la batterie Lipo du drone. Les broches D2, D3, D4, D5, D6 et D7 sont utilisés comme canaux de sortie PWM car ils peuvent générer ces signaux et proviennent du même registre de PORT (DDRD).

(CH1: D2, CH2: D3, CH3: D4 et CH4 : D5) sont les canaux qui corresponds respectivement aux commandes (Throttle, Yaw, Pitch et Roll) tandis que (CH5: D6) et (CH6: D7) sont les deux canaux auxiliaires numériques destinés pour les switches.

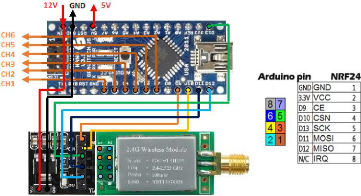
Figure 3.18 : Schéma électronique du récepteur RF 2.4 GHz

Le circuit imprimé double face du récepteur RF Figure 3.19 est réalisé à l'aide du logiciel Eagle CAD soft.

Chapitre III Conception et mise en oeuvre du fonctionnement

Figure 3.19 : Schéma du circuit imprimé du récepteur RF 2.4 GHz

III.4.2. Algorithme du récepteur RF 2.4GHz :

Nous commençons le code en initialisant la configuration de l'interruption PWM et la bibliothèque du module NRF24, au début on utilise la même adresse du canal que dans l'émetteur radio. L'Arduino nano reçoit chaque paquet de données de 8 bits dans chaque canal, ce qui nous donne des valeurs décimales au maximum de 255, pour lire ces valeurs dans l'Arduino Nano du récepteur

il suffit d'utiliser la fonction prédéfinie radio.

read(&data,

sizeof(MyData)). L'utilisation de la

fonction prédéfinie map (, , , ,);permet de codées ces valeurs de 8 bits pour que les signaux s'arrange entre 1000ìs et 2000ìs. La fonction prédéfinie du comptage writeMicroseconds (); permettent de gérer les périodes des signaux PWM avec précision.

L'algorithme du transmetteur RF est expliqué ci-dessous:

Déclaration des librairies SPI &
NRF24.
Initialisation du registre Timer à 0.
Définir la fréquence des signaux
PWM à 50 Hz.
Définir PWM_period.
Déclaration des 6 variables
« PWM_largeur » pour les sorties
(2, 3, 4, 5, 6 et 7).

Déclaration des variables de 8
bits à être reçu : Throttle, Pitch,
Roll, Yaw, SW1 et SW2.
Activer le compteur millis.
Déclaration du variable 32 bits de
comptage : « PreviousMillis ».
Définir les broches D2, D3, D4,
D5, D6 et D7 du Port D comme
sorties.

Déclaration du variable
32 bits de réception des
données :
« LastRecvTime »

41

Void setup :

Chapitre III Conception et mise en oeuvre du fonctionnement

Commencer la
communication radio

Sous-programme de réception des données

Oui

Voir si le signal radio est disponible : radio.available ( )

Lire et recevoir les données de 8 bits

Non

Void loop :

Non

Vérifier si le signal est perdu

Oui

Réinitialiser les données

Codé les valeurs reçues de 8 bits sur 1000 à 2000 et les Affectés aux
variables PWM_largeur en utilisant la fonction prédéfinie map

ch1_value = map(received_data.Throttle,0,

255,1000,2000);

ch2_value = map(received_data.Yaw,0,255,1000,2000);
ch3_value = map(received_data.Pitch,0,255,1000,2000);
ch4_value = map(received_data.Roll,0,255,1000,2000);

ch5_value = map(received_data.SW1,0,1,

1000,2000);

ch6_value = map(received_data.SW2,0,1,

1000,2000);

Générer les signaux PWM avec la fonction prédéfinie
writeMicroseconds (); pour chaque canal
channel_1.writeMicroseconds(ch1_value);
channel_2.writeMicroseconds(ch2_value);
channel_3.writeMicroseconds(ch3_value);
channel_4.writeMicroseconds(ch4_value);
channel_5.writeMicroseconds(ch5_value);
channel_6.writeMicroseconds(ch6_value);

42

Chapitre III Conception et mise en oeuvre du fonctionnement

43

III.4.3. Test des signaux de sortie du récepteur RF :

Après la construction de l'émetteur RC et du récepteur, nous devons tester les signaux de contrôle PWM sortant du récepteur car ce sont les impulsions de commande à introduire au contrôleur de vol. On peut connecter les broches numériques de sortie du récepteur RF au canal d'entré d'un oscilloscope afin que nous puissions visualiser un seul signal PWM puis on fait varier les positions des joysticks.

Pour voir la variation des quatre signaux tous à la fois, j'ai utilisé un petit programme de test pour Arduino qui apporte les valeurs des signaux de commandes PWM sur le moniteur série de l'Arduino IDE, ces valeurs vont de 1000ìs jusqu'à 2000ìs avec une impulsion centrale de 1500ìs, Figure 3.20.

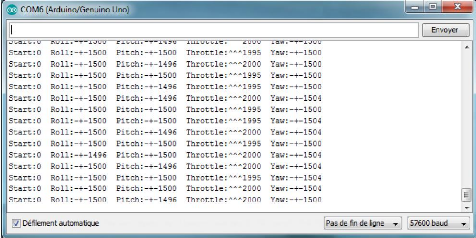
Figure 3.20 : Valeurs correspondantes aux signaux PWM afficher sur le moniteur série de l'Arduino IDE.

III.5. Contrôleur de vol du quadrotor :

Dans le schéma de la Figure 3.21, j'ai mis la diode D1 pour protéger le port USB de l'ordinateur lorsque l'Arduino est connecté à l'ordinateur lors de la programmation. Les résistances R2 = 1kÙ et R1 = 1,5kÙ divisent la tension de la batterie de vol par 2,5. De cette façon, il est possible de mesurer la tension de la batterie pendant le vol en utilisant AnalogRead à partir de la broche A0 de Arduino Uno. La LED est mise pour l'indication d'état de la batterie, elle s'allumera lorsque la tension de la batterie devienne basse.

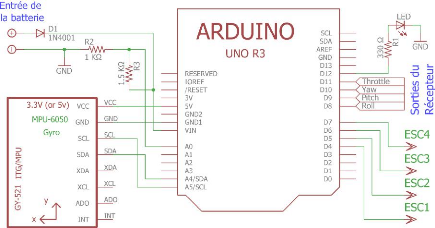
Chapitre III Conception et mise en oeuvre du fonctionnement

44

Figure 3.21 : Schéma électronique du contrôleur de vol du quadrotor.

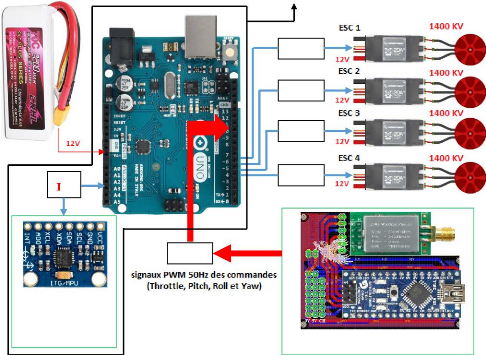
IMU

(Gyro& Accéléromètre) MPU-6050

²C

PWM

PWM

PWM

PWM

PWM

Récepteur Radio 2.4Ghz

Figure 3.22 : Schéma électronique global du quadrotor.

Chapitre III Conception et mise en oeuvre du fonctionnement

III.5.1. Lecture des signaux du récepteur RF :

Dans cette partie, je montre comment lire et calculer les largeurs des impulsions PWM venant du récepteur RF afin qu'ils puissent être utilisés pour contrôler le mouvement du quadrotor, et pour mieux comprendre le fonctionnement du contrôleur de vol, j'aime montrer au début les principes de base pour les signaux du récepteur.

Les ESC sont contrôlés par des trains d'impulsions PWM variant de 1000ìs à 2000ìs avec une amplitude de 5v, c'est à dire que la position d'arrêt de l'ESC est généralement atteinte avec une impulsion de 1000ìs et une accélération maximale est atteinte avec une impulsion de 2000ìs, la longueur de l'impulsion change lorsque nous changeons la position du joystick sur l'émetteur RC Figure 3.23. Les systèmes multicopters sont très instables et la stabilité est obtenue par d'énormes corrections par seconde, par exemple le contrôleur de vol de ce projet fait 250 correction / seconde ceci est également connu comme le taux de rafraîchissement ou la fréquence du contrôleur, en bref cela signifie que les quatres ESC sont corrigés tous les 4ms (la fréquence des signaux PWM à fournir au ESCs par le contrôleur de vol est de 250 Hz).

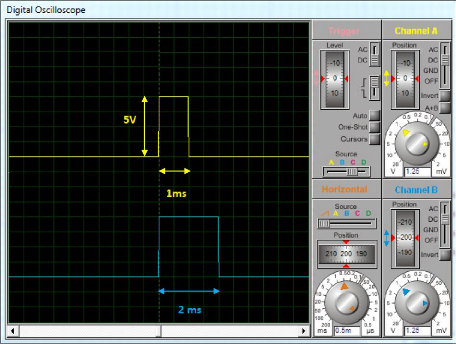
Figure 3.23 : Simulation des pulsations PWM de fréquence 50 Hz pour deux canaux du récepteur RF.

45

Chapitre III Conception et mise en oeuvre du fonctionnement

46

Dans notre cas, la fréquence des signaux PWM du récepteur RF (50 Hz) est cinq fois plus faible que la fréquence du contrôleur de vol (250 Hz), cela signifie que le quadrotor ne peut pas attendre les signaux du récepteur lors du vol.

Malgré tout cela, le processeur de l'Arduino Uno "ATmega328p" nous donne des outils pour faire résoudre à ce problème en utilisant les interruptions de changement d'état de broche «Pin Change Interrupt Register PCI0». Ça signifie que nous pouvons interrompre le programme en cours pour effectuer une tâche spéciale lorsque l'état logique de la broche numérique change, après cette interruption le processeur continue l'exécution du programme d'une façon normal. Cependant cette méthode nécessite moins de boucles CPU donc il faut garder la routine d'interruption aussi courte que possible, sinon on va gâcher l'exécution du programme en cours.

L'interruption de changement de broche « PCI0 » se déclenchera si l'une des broches PCINT7 à PCINT0 se bascule d'état, les bits (PCINT0, PCINT1, PCINT2 et PCINT3) qui correspondent au registre d'interruption « PCI0 » se réfèrent respectivement aux broches numériques (8, 9, 10 et 11) de l'Arduino Figure 3.24, selon le schéma du contrôleur de vol Figure 3.21 les entrées du récepteur sont connectées aux broches numériques 8 à 11.

Figure 3.24 : Diagramme des broches de l'ATmega328p.

Dans le programme du contrôleur de vol, on peut créer des sous-programmes d'interruption qui serait toujours exécutées chaque fois que les broches numériques 8 à 11 changent d'état logique, ceci consiste à mesurer le temps entre les fronts montants et descendants des impulsions PWM venant du récepteur. L'organigramme suivant explique une partie du sous-programme de l'interruption pour lire un seul canal « canal 1 » du récepteur, la même partie se répète pour les autres canaux sauf que les différents canaux du récepteur sont liées à des différentes broches du registre PORTB.

Chapitre III Conception et mise en oeuvre du fonctionnement

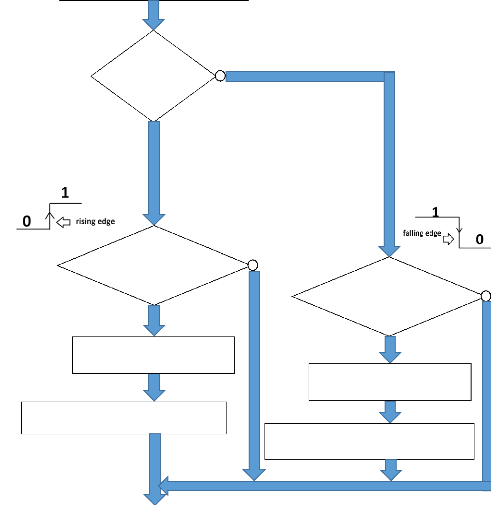
Voir si on a un front Non Voir si on a un front

Montant Descendant

Précédente_canal 1=0

La même routine se répète pour les autres canaux {canal 2 (PINB1), canal 3 (PINB2) et canal 4 (PINB3)}, le sous-programme de l'interruption est appelé chaque fois dans le programme principal du contrôleur de vol si l'une des entrées 8, 9, 10 ou 11 change d'état. Les variables d'entrées du

Affecter la variable Time 1 dans la variable Temp actuelle (Time 1 =Temp actuelle)

Se souvenir de l'état actuel du variable (Précédente_canal 1=1)

Oui

Le bit 0 du
PORTB
(PINB0=1)?

Oui

Non

Calculer la longueur de l'impulsion du canal 1 Reciver_input 1 = Temp_actuelle - Time1

Se souvenir de l'état actuel du variable (Précédente_canal 1=0)

Précédente_canal 1=1

L'entrée PINB0 se Bascule de 1 à 0

Oui

Non

47

Sous-programme d'interruption :

Activer le registre de L'interruption de changement de broche « PCI0 »

Affecter le compteur us dans la variable Temp actuelle = micros ( );

Chapitre III Conception et mise en oeuvre du fonctionnement

48

récepteur (Reciver_input 1, 2 et 4) de la routine d'interruption sont destinées pour le calcul des points de consigne (Pitch, Roll et Yaw) du contrôleur PID afin de contrôler les impulsions PWM des ESC. L'entrée « Reciver_input 3 » qui correspond à la commande «Throttle », est mise comme un signal de base pour accélérer les moteurs. Cette image Figure 3.25, représente les axes du roulis (Roll), tangage (Pitch) et lacet (Yaw) d'un aéronef.

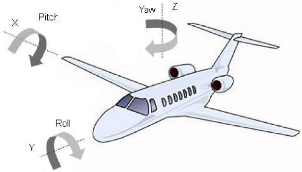
Figure 3.25 : Les mouvements de base.

L'angle de roulis positif soulève l'aile gauche et abaisse l'aile droite, l'angle de tangage positif soulève le nez et abaisse la queue et l'angle de lacet positif déplace le nez vers la droite. Ceci est la norme utilisé pour ce contrôleur de vol du quadrotor.

Pour plus d'informations sur les registres utilisés dans le programme, voir le manuel du datasheet pour l'ATMEGA328p dans l'annexe de ce mémoire.

III.5.2. Unité de mesure de l'inertie gyroscopique MPU-6050 :

Dans cette partie, je montre comment lire et traiter les données venant du Gyroscope. Plus précisément, nous allons extraire les données du Gyro afin que le contrôleur de vol puisse calculer les angles parcourus par le quadrotor pour les axes de mouvements (Pitch, Roll et Yaw) en utilisant des opérations mathématiques simples, puis les transformer en instructions algorithmiques adaptées à Arduino.

Le Gyro est un capteur de taux d'angle à trois axes (x, y et z), il mesure la vitesse angulaire en degrés par seconde de ces axes en même temps. Les données d'entrées du Gyro sont couplées linéairement avec sa sortie, signifie que la longueur de l'impulsion de sortie change proportionnellement lorsque le Gyro est tourné autour de ces axes. Pour connaître la valeur de sortie exacte de l'MPU-6050, nous devons jeter un coup d'oeil sur la fiche technique du Gyro MPU6050 mentionnée dans la page (12 of 52) de l'annexe de ce mémoire. La sortie sera de 65,5 en décimal lorsque la vitesse angulaire du Gyro est de 1°/sec, car nous utilisons 500°/sec comme vitesse angulaire maximale pour les trois axes du Gyro.

Chapitre III Conception et mise en oeuvre du fonctionnement

Par exemple si le Gyro fait tourner autour de son axe de lacet (Yaw) et que nous terminons le tour complet (360°) exactement à une minute (60 sec), la sortie du Gyro à n'importe quel moment de ce parcourt sera de 6°/sec × 65.5 = 393, car à chaque seconde le Gyro tourne 6°. Dans le programme Arduino il sera donc : Angle°/sec = sortie Gyro / 65,5. Le résultat « Angle°/sec » sera déclarée comme une variable flottante et la sortie du Gyro est une valeur signée de 16 bits (la sortie du gyroscope est une valeur de complément de 16 bits deux) qui est similaire à un entier « Int » dans l'Arduino. Cela signifie que la variable « sortie Gyro » doit être déclarée comme un entier car elle peut atteindre 32750 si la vitesse angulaire du Gyroscope atteint les 500°/sec (sortie Gyro = 500°/sec × 65.5 = 32750). La plupart des Gyro ont un petit décalage moyen (offset) qui provoque la dérive du quadrotor donc le Gyroscope doit être calibré avant d'utiliser ces données de sortie. Pour obtenir les meilleurs résultats, la sortie du Gyro doit être mise à zéro et ceci est simplement fait en prenant l'offset pour plusieurs lectures et en les soustrayant des plusieurs valeurs de la sortie du Gyro. Ceci est expliquer dans cet organigramme de boucle for (;;) qui paresse dans le void setup :

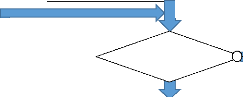
Variables entiers 16 bits : Int_cal = 0
Initialiser les Variables 8 bits : lowByte, highByte
Initialiser les Variables 64 bits : gyro_pitch,
gyro_roll, gyro_yaw, cal_axe_x, cal_axe_y,
cal axe z

Int_cal < 2000 ?

Pour exécuter Non

Le code 2000 fois Oui

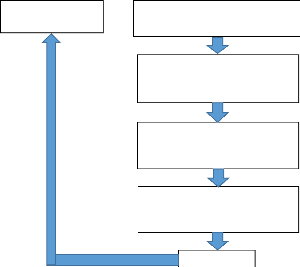
L'axe Pitch

L'axe Roll

L'axe Yaw

Ajouter la valeur lue gyro_pitch
de l'axe x du Gyro à la variable
cal_axe_x

Ajouter la valeur lue gyro_roll
de l'axe y du Gyro à la variable
cal_axe_y

Ajouter la valeur lue gyro_yaw
de l'axe z du Gyro à la variable
cal_axe_z

Incrémenter par 1
Int cal + +

Sous-programme de lecture des
données du Gyro MPU-6050

Tarder 3 ms

49

Diviser la variable
cal_axe_x par 2000 pour
obtenir l'offset de l'axe x

Diviser la variable
cal_axe_y par 2000 pour
obtenir l'offset de l'axe y

Diviser la variable
cal_axe_z par 2000 pour
obtenir l'offset de l'axe z

Reste du programme.

Chapitre III Conception et mise en oeuvre du fonctionnement

50

Cet organigramme calcule l'offset moyenne de 2000 lectures de Gyro pour les 3 axes, puis il stocke chacune de ces valeurs d'offset dans les variables (cal_axe_x, cal_axe_y et cal_axe_z). Après cette étape l'offset est soustraite de chaque mesure du Gyro dans le reste de la boucle du programme.

· Sous-programme de lecture des données du Gyro :

L'Arduino Uno du contrôleur de vol lit les données des angles parcouru par le Gyro à partir des registres de sortie d'adresses 0x69 et 0xA8 qui sont à 16 bits en utilisant le protocole de communication I²C. Par exemple pour lire l'axe « Yaw » on lit les 8 bits du poids fort du registre 16 bit à part, puis les 8 bits du poids faible et on fait un décalage pour avoir les 16 bit puis on affecte le résultat au variable « gyro_yaw ».

Toutes les autres parties intéressantes pour la communication I²C avec le Gyro sont gérées par la librairie "wire" qui nous facilitent la tâche.

L'organigramme qui explique le processus est situé dans la page suivante.

Chapitre III Conception et mise en oeuvre du fonctionnement

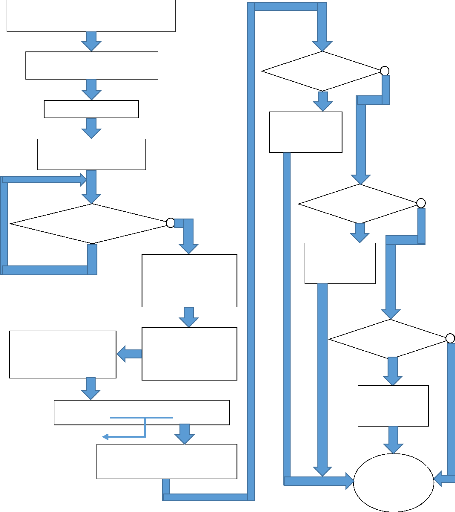
Commencer la communication I²C
avec le Gyro (registre d'adresse 0x69)

Commencer à lire du registre
d'adresse 0xA8

Fin de transmission

Demander 6 octets du
registre d'adresse 0x69

Attendre jusqu'à les 6 octets Soient reçus

Octets valables < 6 ?

Non

Oui

Réception du 1ier
Byte du poids
faible des données
angulaire lowByte

Compenser l'offset Après le calibrage Jusqu'à Int_cal = 2000

Int_cal = 2000?

Non

Oui

gyro_roll =
cal_axe_y -
gyro_roll

Int_cal = 2000?

Oui Non

gyro_pitch =
cal_axe_x -
gyro_pitch

Non

Oui

gyro_yaw =
cal_axe_z -
gyro_yaw

Fin du
sous-
programm

Int_cal = 2000?

Réception du 2nd
Byte du poids fort
des données
angulaire highByte

gyro_pitch =
(highByte X 256) +
lowByte

gyro_roll = (highByte X 256) + lowByte

Décalage de highByte

Par 8 positions

gyro_yaw = (highByte X 256) + lowByte

51

Après l'étape de calibrage, il est nécessaire de calculer l'angle total parcouru par le Gyro afin que le contrôleur de vol puisse reconnaître la position exacte du quadrotor dans l'espace. Pour cela il suffit simplement d'intégrer au fil de temps tous les valeurs de sortie Gyro (les données de la vitesse angulaire des axes Pitch, Roll et Yaw) par exemple pour l'axe Yaw :

Chapitre III Conception et mise en oeuvre du fonctionnement

52

Angle parcouruya11, =E sortie Gyroya11^, x At.

Dans le cas de notre contrôleur de vol, la fréquence de rafraîchissement est de 250 Hz, on peut donc extraire les angles parcouru par le Gyro pour chaque axe toutes les 4 ms au lieu de 1s. Cela signifie également que nous devons diviser les données de sortie Gyro sur 65,5 et ensuite diviser à nouveau sur 250 pour obtenir l'angle parcouru par le quadrotor chaque 4 ms.

J contrôleur de vol = 250 Hz - At = 4 ms

Angle parcouruyau, = 1(sortie Gyro_yau, /(250/65.5))

= E(sortie Gyro_yau, x 0.0000611)

L'intégrale en mathématique signifie la sommation d'une fonction sur un intervalle donné, donc dans le code Arduino on fait la somme de toutes les données gyroscopiques de sortie pour chaque axe à part dans un intervalle de 4ms, par exemple pour l'axe z « Yaw » se traduire par cette instruction :

Angle parcouru_yau, est : Angle_yaw_entrée += gyro_z * 0.0000611;

C.à.d. : Angle_yaw_entrée = Angle_yaw_entrée _précédente + (gyro_z x 0.0000611) Vérifions la validité de cette relation avec le dernier exemple pour une rotation complète (360°) du Gyro autour de son axe (Yaw) dans 60s, on aura :

· La sortie du Gyro en décimal à n'importe quel moment pendant la rotation est : sortie Gyroyau, = 393.

· Pendant la rotation, les données du Gyro sont ajoutées 250 fois par seconde donnant un total de 15000 lectures : ²⁵⁰lecture P/s x 60s = 15000 lecture

· Pour une minute on aura donc :

Angle parcouruyau, = 15000 lecture x 393 x 0.0000611

= 360.18° 360°

Ce qui est assez proche pour un tour complet, d'où la formule est juste.

L'inconvénient du Gyro MPU6050 c'est que le signal de sortie est très bruyant Figure 3.27.

L'utilisation d'un simple filtre complémentaire permet de réduire le bruit qui accompagne le signal

de sortie du Gyro, alors l'instruction précédente devienne:

Angle_yaw_entrée = (Angle_yaw_entrée * 0.7) + (gyro_z * 0.0000611);

C.à.d. : Angle_yaw_entrée = (Angle_yaw_entrée précédente x 0.7) + (gyro_z x 0.0000611)

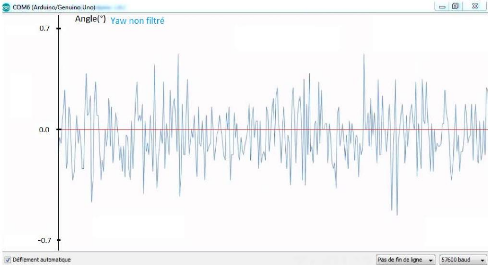
Chapitre III Conception et mise en oeuvre du fonctionnement

Figure 3.27 : Signal de sortie du Gyro dans l'état stationnaire pour l'axe de mouvement Yaw afficher sur le moniteur série de l'Arduino IDE.

Enfin, l'instruction Angle_yaw_entrée détermine le taux angulaire ou l'angle parcourus « Yaw » à introduire pour l'entrée de la boucle PID. La même instruction sera appliquer pour les autres axes de mouvement Pitch et Roll.

III.5.3. Le contrôleur PID :

Le contrôle par PID est la méthode la plus simple à programmer sur un processeur et elle est souvent employée pour les asservissements [16].

Cette méthode est basée sur une structure qui délivre un signal de commande à partir de l'erreur existante entre la référence et la mesure de son intégrale et de sa dérivée Figure 3.28.

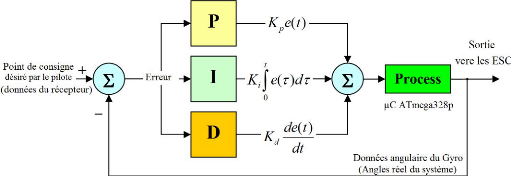
Figure 3.28 : Schéma de la boucle de contrôleur PID.

53

Chapitre III Conception et mise en oeuvre du fonctionnement

54

Chapitre III Conception et mise en oeuvre du fonctionnement

Le contrôle par PID est souvent utiliser dans l'industrie car il est très simple à mettre en place et s'avère efficace à réduire les erreurs pour la plupart des systèmes réels non linéaires. Dans notre cas le principe de base du contrôleur PID est simple, lorsque le drone se trouve déséquilibré à cause du vent ou de la turbulence, l'algorithme envoie une commande vers les ESC qui provoque une réaction dont le sens est opposé à celui qui a conduit au déséquilibre, afin que le drone retrouve l'état souhaité. Plus précisément, il faut garder les valeurs mesurées du Gyro (données angulaires réel du système) identique au point de consigne désiré par le pilote (données d'entrée du récepteur de la routine d'interruption) Figure 3.29.

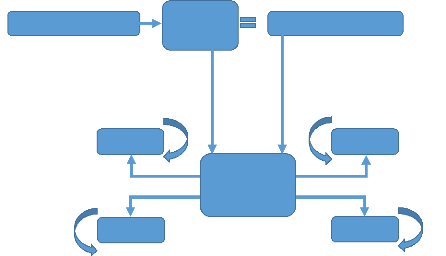
Données d'entrées du récepteur Données d'entrée du Gyro

(Reciver_input 1, 2 et 3) (Taux angulaire)

Sens antihoraire

Données du Récepteur

Sens horaire Sens antihoraire

Moteur 4

Moteur 3

Conversion en °/ sec

Contrôleur PID

Données du Gyroscope

Moteur 1

Moteur 2

Sens horaire

Figure 3.29 : Schéma montre le principe du PID utilisé dans ce contrôleur de vol.

Par exemple si le pilote ne veut aucun mouvement, le taux angulaire Gyro doit être également nul, donc l'erreur du système « ???? » pour un axe de mouvement est la différence :

???? = (Données d'entrée du Gyro - Données d'entrées du récepteur).

Le contrôleur PID calcule les corrections nécessaires pour les trois axes (Pitch, Roll et Yaw), Les consignes pour le contrôleur PID sont les signaux d'entrée du récepteur et les variables des mouvements angulaires mesurées par le gyroscope, Les sorties du contrôleur PID sont destinées pour contrôler la vitesse des moteurs du quadrotor afin d'assurer l'équilibre. L'utilisation des opérateurs mathématiques (Proportionnel, Intégrateur et Dérivateur) permet de produire une sortie de commande adéquate pour le système. Le modèle mathématique du contrôleur PID est décrit comme suit :

????????????(????)

????(????) = ????????????(????) + ???????? ? ????(????)???????? + ???????? ???????? , Tel que :

0

55

????(????) : L'erreur du système.

????(????) : Variable de sortie du PID.

???????? : Gain proportionnel.

???????? : Gain d'intégration. ???????? : Gain de dérivation.

· Effet proportionnel ???????? ???? (????) : Ce terme est proportionnel à l'erreur, il contribue à la stabilité et

à la réactivité et permet une augmentation du temps de réponse du système, en fait le contrôleur seul n'est pas tout à fait suffisant pour stabiliser le drone [17].

????

· Effet d'intégral ???????? ? ????(????)???????? : Ce terme est proportionnel à l'intégrale de l'erreur, il permet au ????

système d'atteindre le point de consigne désiré, permet aussi d'éliminé l'erreur statique du système et de diminuer l'impact des perturbations [17], il en résulte un système précis.

????????(????)

· Effet de la dérivée ???????? : Ce terme est proportionnel à la dérivée de l'erreur, il permet

^????????d'accéléré la réponse du système et d'éliminé les oscillations autours du point de consigne [17].

· Saturation du contrôleur PID et choix des gains [18] :

Pour empêcher le PID de devenir incontrôlable, il est nécessaire de limiter la sortie PID à une valeur critique qui est le point de saturation du système et ça se détermine selon les caractéristiques du système et l'algorithme du contrôleur PID utilisé. Cette limitation est souvent appliquée pour la sortie globale du contrôleur PID. Chaque quadrotor est caractérisé par ces propres gains PID, généralement les gains PID varis d'un drone à l'autre en fonction du poids et du hardware utilisé. La

mise en oeuvre de la commande PID exige d'abord une sélection adéquate des gains ???????? , ???????? et ???????? car la réponse de la sortie PID sera influencée en agissant sur ces trois gains. Pour notre système les gains seront déterminés expérimentalement.

· Algorithme PID du contrôleur de vol :

Dans le programme du contrôleur de vol, trois contrôleurs PID sont utilisés pour les trois axes de mouvement essentiels (Pitch, Roll et Yaw). Au début, il est nécessaire de transférer les variables des canaux d'entrée du récepteur (de la routine d'interruption) en degrés / seconde pour avoir les trois points de consigne de mouvement, identiques en grandeurs que les données d'entrée du Gyro. L'organigramme suivant explique l'étape de conversion des variables du récepteur en degrés / seconde pour un axe de mouvement « Roll », la même routine se répète pour les deux autres axes «Pitch et Yaw ».

Chapitre III Conception et mise en oeuvre du fonctionnement

Initialiser la variable flottante point
de consigne Roll à zéro :
Pid_Roll_consigne = 0

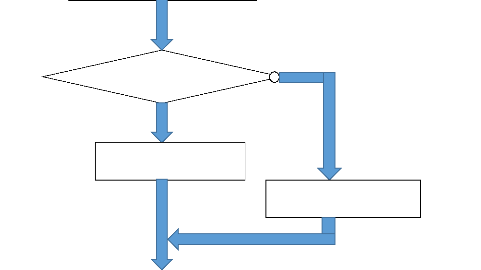
Du récepteur par 3 Permet d'obtenir

Un taux de Roll max Approximatif à 166 ° / s

Roll max = (2000 - 1500) ~ 3

La division de signal

166 ° / s

Reciver_input 1 >= 1500 ?

Pid_Roll_consigne =
(Reciver_input 1 -1500) ~ 3

Oui

1500 (en décimal) est la valeur centrale du Reciver_input 1 Qui correspond à la position centrale du joystick "canal Roll"

Non

Reciver_input 1 < 1500

Pid_Roll_consigne =
(Reciver_input 1 -1500) ~ 3

Roll max = (1000 - 1500) ~ 3

-166 ° / s

Les entrées du contrôleur PID {données du récepteur : (Pid_Roll_consigne, Pid_Pitch_consigne, Pid_Yaw_consigne) et les données angulaires du Gyro : (angle_roll, angle_pitch, angle_yaw)} sont connues, reste à déterminer les variables de sortie PID pour les mouvements (Pitch, Roll et Yaw). Dans le sous-programme PID les trois parties (proportionnel, intégral et dérivé) sont calculées simultanément et combinées à un seul signal de sortie pour chaque axe de mouvement Figure 3.30.

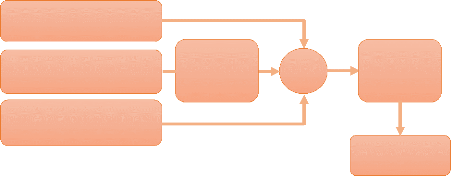
Intégral

Sortie (I) = Sortie (I) + [E × Gain (I)]

Sortie (D) = (E - E????????é????é) × Gain (D)

Proportionnel
Sortie (P) = E × Gain (P)

Dérivé

Limiter la
sortie au point
de saturation

+

Sortie PID pour un axe de mouvement

Limiter la
sortie au point
de saturation

56

Figure 3.30 : L'algorithme utilisé dans le sous-programme PID du contrôleur de vol pour un axe de mouvement.

·

Chapitre III Conception et mise en oeuvre du fonctionnement

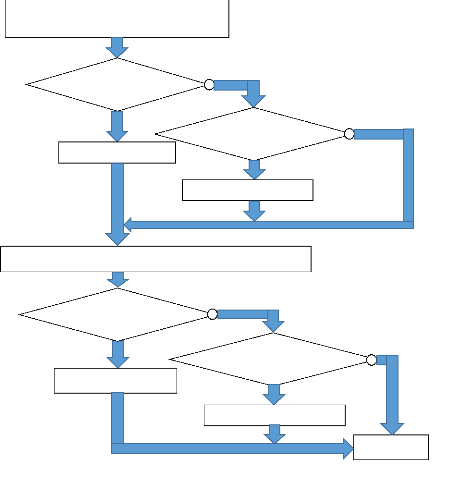
Oui

Limiter

Oui

La sortie Intégrale

Sortie i roll = 400

Sortie_ i _roll > 400

Sortie i roll = - 400

Sortie_ i _roll < -400

400 c'est la valeur max du PID

Non - 400 c'est la valeur min du PID

Limiter la sortie Intégrale

Non

Oui

Non

Oui

????????????é????é = ????

Pid_sortie_roll = (???? ???? X ????) + (Sortie_ i _roll) + ???????? X (???? - ????????????é????é)

Pid_sortie_roll = 400

Pid_sortie_roll > 400

Limiter la sortie PID globale

Pid_sortie_roll = - 400

Pid_sortie_roll < -400

Calcul du Sortie PID Pour l'axe Roll

57

Intégral de l'erreur statique ???? pour Roll: Sortie_ i _roll = Sortie_ i _roll + (???????? X ????)

Sous-programme de sortie PID :

L'organigramme suivant explique le calcul du sorties PID pour un axe de mouvement « Roll ».

La même routine se répète dans le sous-programme PID du contrôleur de vol pour les deux autres axes «Pitch et Yaw ».

Initialiser les variables flottantes à

zéro : ???? ????????????é????é Sortie_i_roll
pid sortie roll

Calcul de l'erreur statique ???? pour Roll :

???? = Angle_roll_entrée - Pid_Roll_consigne

Chapitre III Conception et mise en oeuvre du fonctionnement

Eprécé = e L'erreur actuelle e devienne l'erreur précédente Eprécé Pour le prochain calcule.

III.5.4. Contrôle des ESC :

Dans cette partie, le but est de générer les impulsions de commande à envoyer pour les quatre ESCs en fonction des variables de sorties PID, afin de contrôler la vitesse des moteurs du quadrotor. Les ESC sont connectés à l'Arduino Uno du contrôleur de vol via les broches digitales (D4, D5, D6 et D7) du registre PORTD. Au début du programme principal, ces broches numériques doivent être déclarés en tant que sorties. Après avoir calculé les variables de sortie du contrôleur PID pour les axes de commande (Pitch, Roll et Yaw), il devient possible de calculer les largeurs d'impulsion à fournir pour les ESC toutes les 4 ms afin de corriger la position du quadrotor.

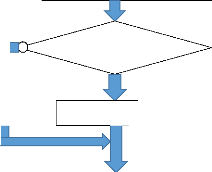
Throttle est mis comme le signal
De base pour le calcul des
Impulsions des ESCs

Affecter le signal Throttle à la variable entière d'accélération :
Accélération = Reciver_input 3

Non

Accélération> 1800

Oui

Accélération = 1800

Laisser 200us de gap pour garder le contrôle Total à plein vitesse

Calcul des impulsions de correction :

Largeurs d'impulsion esc 1 Largeurs d'impulsion esc 2 Largeurs d'impulsion esc 3 Largeurs d'impulsion esc 4

58

esc_1 = accélération - Pid_sortie_pitch + Pid_sortie_roll - Pid_sortie_yaw esc_2 = accélération + Pid_sortie_pitch + Pid_sortie_roll + Pid_sortie_yaw esc_3 = accélération + Pid_sortie_pitch - Pid_sortie_roll - Pid_sortie_yaw esc_4 = accélération - Pid_sortie_pitch - Pid_sortie_roll + Pid_sortie_yaw

Au début, il est nécessaire de déclarer le signal d'entrée du récepteur Throttle « Reciver_input 3 » comme la variable de base d'accélération. Pour assurer que les trois contrôleurs PID ont suffisamment d'espace pour corriger le quadrotor à pleine vitesse, la variable d'accélération est limitée à 1800 ìs au lieu de 2000 ìs. De cette façon, chaque contrôleur PID peut ajouter 200 ìs supplémentaires en cas de besoin. Pour calculer les impulsions des ESC, il suffit de combiner les variables de sorties PID séparées (Pitch, Roll et Yaw) et de les ajouter ou les soustraire à la variable d'accélération suivant cet algorithme :

Chapitre III Conception et mise en oeuvre du fonctionnement

59

La Figure3.31 représente les axes Roll, Pitch et Yaw du quadrotor, la correction des impulsions des ESCs se fait selon les quatre instructions de l'algorithme citées en haut.

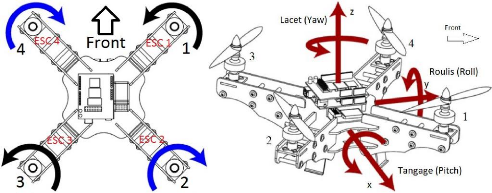
Figure 3.31 : Disposition des ESCs et direction de rotation du quadrotor

Pour l'axe de Roulis, si le quadrotor penche vers la droite en raison du vent ou de la turbulence, cela conduit le Gyro d'envoyer un angle de roulis positif (Données d'entrée Roll du Gyro> 0), lorsque le pilote ne veut aucun mouvement (le joystick de l'émetteur est en position centrale) c'est à dire la variable roulis du récepteur est de 0 ° / sec (Pid_Roll_consigne= 0°) implique que la sortie roulis du contrôleur PID est positive (Pid_sortie_roll> 0) car l'erreur????> 0. Donc pour que le quadrotor puisse revient à l'état stable 0°, la vitesse du moteur avant droit doit augmenter et ceci est fait en ajoutant la sortie du contrôleur PID Roll (Pid_sortie_roll) à l'impulsion de l'ESC 1.

Le même principe pour le tangage (Pitch), lorsque le front du drone est incliné en bas à cause d'une perturbation ou du vent, le Gyro envoie un angle de tangage négatif et la sortie du contrôleur PID Pitch devienne négative (Pid_sortie_pitch< 0), en soustrayant la sortie du PID Pitch de l'impulsion ESC 1 implique que la vitesse du moteur1 s'augmente et le quadrotor retrouve l'état stable 0°, cela est illustré dans la Figure 3.32 et la Figure 3.33 pour l'axe de roulis (Roll) et la même chose pour le tangage (Pitch).

Le même principe se répète pour chaque combinaison moteur / ESC.

Chapitre III Conception et mise en oeuvre du fonctionnement

60

Figure 3.32 : L'algorithme du PID conduit le quadrotor de revenir À l'état voulu en agissant sur les ESCs

Figure 3.33 : Retour à l'état de consigne désiré par le pilote 0°.

Selon les dernières instructions citées dans l'algorithme en haut :

Si la sortie PID Pitch est (-) : les impulsions Si la sortie PID Roll est (-) : les impulsions Si la sortie PID Yaw est (-) : les impulsions					et et et
	ESC 1		ESC 4				ESC 2		ESC 3
	ESC 3		ESC 4				ESC 1		ESC 2
	ESC 1		ESC 3				ESC 2		ESC 4
Chapitre III		Conception et mise en oeuvre du fonctionnement
Si la sortie PID Pitch est (+) : les impulsions Si la sortie PID Roll est (+) : les impulsions Si la sortie PID Yaw est (+) : les impulsions						et et et
		ESC 1		ESC 4				ESC 2		ESC 3
		ESC 3		ESC 4				ESC 1		ESC 2
		ESC 1		ESC 3				ESC 2		ESC 4

L'étape suivante consiste à envoyer les impulsions calculées aux ESC, ceci est fait en maintien les sorties numériques du PORTD (D4, D5, D6 et D7) à un niveau logique haut avec un délai de temps correspond aux largeurs d'impulsions ESC calculées précédemment. Pour avoir le front descendant des impulsions, il suffit d'exécuter une boucle « while » jusqu'à ce que les quatre bits de poids fort du registre PORTD soient à zéro, ça signifie la fin de l'impulsion ESC.

Pour s'assurer que la fréquence des signaux PWM est de 250 Hz, un temporisateur de boucle vide est employé pour s'exécuter jusqu'à ce que les 4 ms soient expirées. Finalement, il en résulte quatre trains d'impulsions PWM synchronisé avec une fréquence de 250 Hz, Figure3.34.

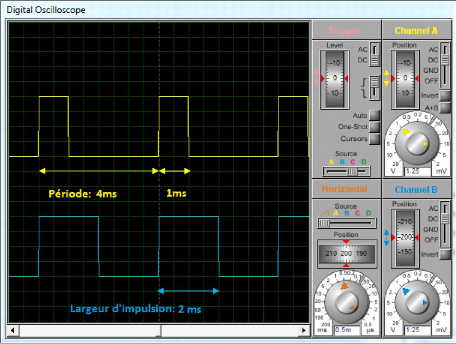
Figure 3.34 : Simulation des impulsions PWM de fréquence 250 Hz à envoyer pour deux ESCs

61

Chapitre III Conception et mise en oeuvre du fonctionnement

62

Chapitre III Conception et mise en oeuvre du fonctionnement

Toutes les données pour contrôler les moteurs sont disponibles. L'organigramme suivant explique l'algorithme utilisé pour générer des impulsions PWM aux ESC:

Initialisation des variables flottantes :
Boucle_temps, timer_ch 1, timer_ch 2,
timer_ch 3, timer_ch 4,
esc_boucle_temps

On attend jusqu'à 4000 us le TIMER microseconde Micros ( ) est utilisé pour

Sont écoulés. Calculer le temps écoulé.

Micros ( ) - boucle_temps < 4000

Non

Oui

La fréquence du contrôleur de vol est de 250Hz. Cela signifie que les ESCs ont besoin de leur Impulsions toutes les 4ms.

Stocker le temps actuel du compteur
pour la prochaine boucle :
Boucle_temps = micros ( )

Met à la fois les sorties numériques D4, D5, D6 et D7 haut : PORTD |= B11110000

Calcule des largeurs d'impulsions à Fournir pour les ESCs.

Restez dans cette boucle jusqu'à ce que D4, D5, D6 et D7 soient zéro. Non

Oui

Esc_boucle_temps = micros ( )

Stocker le temps actuel du compteur Chaque fois que la boucle est exécutée.

Si (timer_ch 1 = esc_boucle_temps) PORTD &= Si (timer_ch 2 = esc_boucle_temps) PORTD &= Si (timer_ch 3 = esc_boucle_temps) PORTD &= Si (timer_ch 4 = esc_boucle_temps) PORTD &=

	Rendre la sortie numérique
B11101111
B11011111
B10111111	À zéro pour chaque ESC si
B01111111	Le délai de temps de
	L'impulsion est expirée.

Timer_ch 1= esc_1 + Boucle_temps Timer_ch 2= esc_2 + Boucle_temps Timer_ch 3= esc_3 + Boucle_temps Timer_ch 4= esc_4 + Boucle_temps

PORTD = 16

Fin de la boucle principale void loop.

63

III.6. Conclusion :

Dans ce chapitre, les étapes de construction du quadrotor sont strictement illustré, le principe de fonctionnement du système et les instruments utilisés dans le hardware sont discutés, passant par la réalisation de l'émetteur et du récepteur puis le contrôleur de vol. Le software utilisé en transmission et en réception est présenté avec détail et les diverses étapes de programme du contrôleur de vol sont expliquées.

Chapitre 4

Tests et résultats

Chapitre IV Tests et résultats

64

Chapitre IV : Tests et résultats

IV.1. Introduction :

Dans ce chapitre, le but est de donner une description des différents tests effectués sur le système tels que le test des angles du Gyro et les signaux de sortie du récepteur RF. Je présenterai également les techniques utilisées pour définir les gaines PID adapté à ce quadrotor puis les résultats obtenus seront utilisés dans le sous-programme de contrôleur PID, afin d'avoir la stabilité désirée.

Figure 4.1 : Image du quadrotor réalisé.

IV.2. Test des signaux du récepteur RF :

Afin d'éviter tous problèmes de disfonctionnement et pour s'assurer qu'on a une bonne communication radio, il est donc nécessaire de tester les impulsions reçus par le récepteur RF du quadrotor.

On commence par alimenter le récepteur RF avec 5v séparément au circuit du contrôleur de vol, puis on connecte le canal de sortie Throttle du récepteur au canal CH1 de l'oscilloscope digital pour visualiser le signal reçue Figure 4.2.

Chapitre IV Tests et résultats

65

Figure 4.2 : Connexion du récepteur RF à l'oscilloscope digital.

Le signal PWM qui correspond à la commande Throttle apparaisse sur l'écran de l'oscilloscope avec une période de 50Hz, Figure 4.3.

Calibre de l'oscilloscope : Tension : 1 Div ? 2 volt Base de temps : 1 Div ? 2.5 ms.

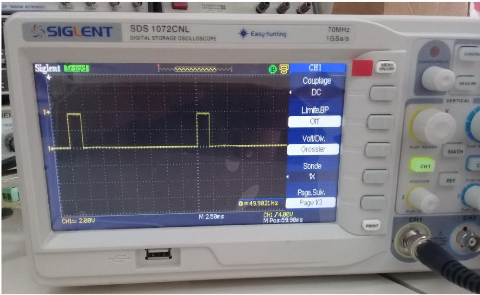
Figure 4.3 : Signal PWM 50Hz de la commande Throttle.

Chapitre IV Tests et résultats

66

En agissant sur la position du joystick de la commande Throttle du transmetteur, on voie bien que la largeur de l'impulsion PWM varie de 1ms à 2ms, Figure 4.4 et Figure 4.5. La même procédure de test est effectuée pour les signaux de commande Roll, Pitch et Yaw.

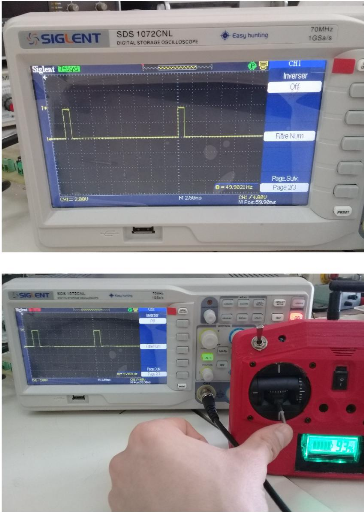
Figure 4.4 : Largeur d'impulsion 1ms.

Figure 4.5 : Largeur d'impulsion 2ms.

Chapitre IV Tests et résultats

67

IV.3. Test des données angulaires du Gyroscope :

Nous vérifions les angles de l'IMU pour éviter les problèmes de commande et les mouvements non désirés, pour ce faire j'ai introduit l'instruction Serial.print ( ); dans le sous-programme de lecture des données Gyro MPU6050. Cette instruction permet d'afficher les angles d'inclinaison du quadrotor en degré pour les axes Pitch, Roll et Yaw sur le moniteur série de L'Arduino IDE, le processus est illustré dans la Figure 4.6.

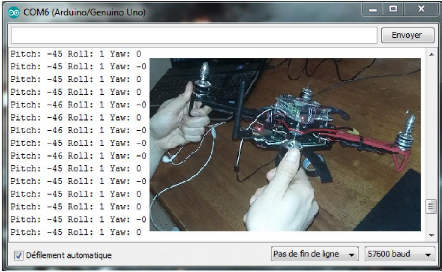
Figure 4.6 : vérification des angles de Gyro sur l'Arduino IDE.

Le quadrotor est incliné suivent les 3 axes de mouvement citées en haut. On vérifie si les angles correspondent au mouvement du quadrotor sont compatible avec la norme mentionné au Chapitre III page (48) que j'ai utilisée pour ce contrôleur de vol.

IV.4. Identification des gains PID :

Comme déjà dit dans le chapitre précédant, les gains K???? , K1 et Kd du contrôleur PID seront déterminées expérimentalement en agissant sur ces gains d'une manière à stabiliser le quadrotor pendant le vol et donc une convergence rapide de l'erreur e vers zéro.

Pour éviter les dégâts et le comportement indésirable du quadrotor, il est nécessaire de varier les gains PID avec un ordre correct [19].

C'était une pratique courante de commencer le réglage avec des valeurs de gain Kd très faible ou nulle. Mais en revanche, il est préférable de définir le gain K ???? pour les axes Pitch, Roll et Yaw à "1" et les autres à zéro, afin de voir comment le quadrotor réagit au début. Pour ajuster les gains du PID,

Chapitre IV Tests et résultats

68

on maintient le quadrotor fermement dans la main, puis on augmente le Throttle jusqu'au moment où le quadrotor commence à osciller, Figure 4.7.

Figure 4.7 : Réglage des paramètres PID.

Au début, on fixe le gain ???? ???? de 4 et le gain ???????? de 0.02 pour l'axe de mouvement lacet (Yaw), car cette configuration de base empêchera le quadrotor de flotter quand nous essayons de le faire voler, le réglage du gain ???????? pour l'axe de lacet n'est pas nécessaire parce que le lacet a une traînée des hélices donc il reste à zéro ???????? = 0.

Pour les deux axes de mouvement Pitch et Roll les gains PID seront les mêmes. On commence par incrémenter le gain ???????? avec un pas de 3, jusqu'à ce que le quadrotor semble agité. Dans ce cas j'ai trouvé ???????? = 18. On fixe ???????? à 18 puis on augmente le gain ???? ???? avec un pas de 0.2 et on continue l'incrémentation jusqu'à ce que le quadrotor cesse d'osciller. Après, on diminue le gain ???? ???? de 50% et le résultat devrait être le gain ???? ???? de base, j'ai trouvé ???? ???? = 1.3.

Enfin, nous commençons à incrémenter le gain ???????? avec un pas de 0,01 et on continue à augmenter et tester (chaque fois en introduit le nouveau gain en compilant le code du contrôleur de vol) jusqu'à ce que le quadrotor commence à osciller lentement. Quand cela arrive, on diminue le gain ???????? de 50% et le résultat devrait être le gain ???????? de base, j'ai trouvé ???? ???? = 0.04.

Chapitre IV Tests et résultats

69

Suivent ces procédure, j'ai réussi à obtenir une bonne stabilité du quadrotor pendent le vol. Les valeurs des gains PID du quadrotor pour les 3 axes de mouvement sont représentées comme suit :

·	Tangage (Pitch) :	K ????	=	1.3	K1 = 0.04	Kd = 18
·	Roulis (Roll) :	K ????	=	1.3	K1 = 0.04	Kd = 18
·	Lacet (Yaw) :	K ????	=	4	K1 = 0.02	Kd = 0

Enfin, ces gains sont introduits dans le programme principal du contrôleur de vol du quadrotor.

IV.5. Test de vol en zone ouverte:

Une fois que le drone semble assez stable pour voler en toute sécurité, nous serons capables d'effectué un premier vol prudent dans un espace ouvert, voici quelque photos du premier vol effectué dans l'USTHB Figure4.8.

Figure 4.8 : Test de vol dans un espace ouvert.

Chapitre IV Tests et résultats

70

IV.6. Conclusion :

Dans ce chapitre, les tests effectués sur le système ont été décrits à l'étape. Les gains PID ont été déterminés expérimentalement et la stabilité a été atteinte. Les tests de communication radio et d'orientation du quadrotor ont été menés. Les résultats obtenus sont bonnes.

71

Conclusion générale

Le développement des véhicules aériens sans pilote a connu une croissance rapide ces dernières années grâce aux progrès de la technologie des capteurs et actionneurs miniatures. Ces progrès ont également entraîné la production de composants et de systèmes embarqués qui représentent les outils de base pour les robots volants et la mise en oeuvre de l'intelligence artificielle, d'où l'avantage d'effectuer et de couvrir un large éventail de missions. Dans ce contexte, le travail effectué dans le cadre de ce projet consiste à réaliser un drone de type quadrotor avec une radiocommande à six canaux de transmission.

Durant cette étude, j'ai mentionné tous les étapes pour la mise en oeuvre de ce système, après une bref introduction sur les drones, avec la citation des différents normes et travaux de recherche effectués dans ce domaine, j'ai entamé à la modélisation dynamique du quadrotor, Ensuite, j'ai présenté le principe de fonctionnement des différentes parties du système à travers l'instrumentation qu'il contient le quadrotor et l'unité de la radiocommande avec l'illustration des diagrammes et des figures nécessaires. En ce qui concerne la partie software, j'ai d'abord expliqué les algorithmes utilisés dans l'émetteur et le récepteur RF afin d'avoir une réaction adéquate du quadrotor aux commandes envoyées par le pilote. Après ça, j'ai donné une explication détaillée sur les diverses étapes qui contient le programme principale du contrôleur de vol tels que:

La lecture des signaux PWM venants du récepteur.

La lecture des données angulaire venant du Gyroscope.

Le calcul des corrections PID.

Le calcul des impulsions pour chaque ESC.

L'envoie des impulsions calculées aux ESC.

Enfin, les résultats des essais effectués sur les différentes parties du système ont montré une

grande efficacité vis-à-vis des défauts, notamment en ce qui concerne le contrôleur PID qui préserve les performances du quadrotor ainsi que sa stabilité pendant la perturbation. Le seul problème que j'ai remarqué est que le quadrotor glisse un peu en vol stationnaire, ça arrive sur le quadrotor car le moteur tourne, les vibrations qui sont encore présentes sont de petites accélérations qui vont rendre l'accélération du drone un peu fiable. Donc, ce problème sera résolu avec l'utilisation des données de l'accéléromètre de l'MPU6050. Mais malheureusement, le temps ne me suffit pas pour apporter de telles améliorations à l'algorithme du contrôleur de vol. Enfin, ce projet ma permet de découvrir l'environnement des robots volant aériennes et il me permet d'amélioré mes capacités en programmation.

Références et Bibliographie

Références bibliographiques

Références Bibliographiques

> [1] A. Tayebi, and S. Mcgilvray «Attitude stabilisation of a four rotor aerial robot», Proceedings of the 43rd IEEE Conference on Decision and Control, Atlantis, Paradise Island, Bahamas, December 2004.

> [2] A. Tayebi, and S McGilvray «Attitude stabilisation of a VTOL Quadrotor Aircaft», IEEE Transactions on Control Systems Technology, Vol. 14, No. 3, pp. 562-571, May 2006.

> [3] L. Gautier, B. Hamilton, J. Hazebrouck, and T. Tourrette «Pilotage d'un quadri-rotor via un FPGA», Tuteur ESIEE engineering, Journées pédagogiques, 2008.

> [4] L. Besnard «Control of à quadrotor vehicle using sliding mode disturbance observer», Master Thesis, Alabama university, 2006.

> [5] H. Bouadi, M. Bouchoucha, and M. Tadjine «Sliding Mode Control Based on Backstepping Approach for an UAV Type-Quadrotor», International Journal of Applied Mathematics and Computer Sciences, Barcelona, Spain, Vol. 4, No. 1, pp. 12-17, 2007.

> [6] H. Bouadi, M. Bouchoucha, and M. Tadjine «Modelling and Stabilizing Control Laws Design Based on Backstepping for an UAV Type-Quadrotor» Proceeding of 6 th IFAC Symposium on IAV, Toulouse, France ,2007.

> [7] H. Bouadi, M. Bouchoucha, and M. Tadjine «Modelling and Stabilizing Control Laws Design Based on Sliding Mode for an UAV Type-Quadrotor» Engineering Letters, London, England, Vol. 15, No. 2, pp. 15-24, 2007.

> [8] H. Bouadi, and M. Tadjine «Nonlinear observer design and sliding mode control for four rotors helicopter» Proceedings of World Academy of Science, Engineering and Technology, Venise, Italy, Vol. 25, pp. 225-230, 2007.

> [9] http://drone-zone.e-monsite.com/pages/les-differents-types-de-drones.html

> [10] All the World's Rotorcraft - the biggest helicopter collection in the world, more than 700 helicoptersand autogyros.

> [11] http://www.geekmag.fr /quadricoptere-fonctionnement-configuration-et-pilotage-rc/

> [12] Conférence Mieux connaître les drones Avant-propos - Onera

> [13] Inertial Measurement Unit - Browse Our Vast Inventory - vectornav.com

> [14] https://www.mondrone.net/fabriquer-quadricoptere-la-propulsion/

> [15] https://www.thingiverse.com/

Références bibliographiques

? [16] Henri Bourlès, Systèmes linéaires - De la modélisation à la commande, Hermes Science Puplishing, 2006, 510 p. (ISBN 2746213001).

? [17] Henri Bourlès et Hervé Guillard, Commande des systèmes. Performance et robustesse, Ellipses, 2012 (ISBN 2729875352).

? [18] http://www.machinedesign.com/sensors/introduction-pid-control

? [19] https://myfirstdrone.com/blog/how-to-tune-a-quadcopter

? [20] https://github.com/

Annexe

Annexe

1. Carcasse Auto CAD :

Voici quelques photos correspondant aux fichiers source conçus avec le logiciel Auto CAD puis imprimés par une fraiseuse numérique. Cette carcasse de plexiglass transparente est mise sur la molette exacte pour protéger l'Arduino Uno du contrôleur de vol.

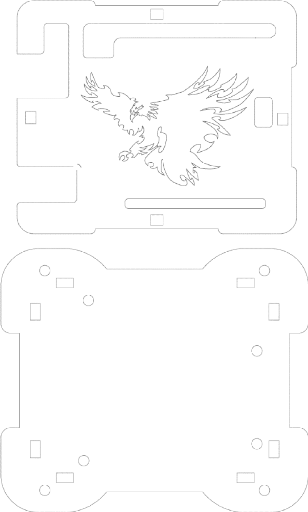
Annexe

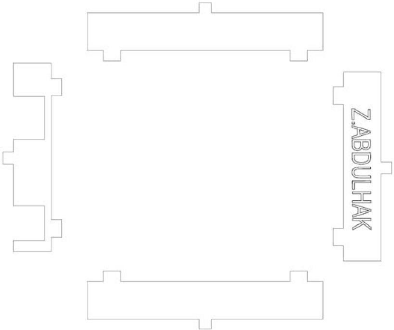
2. Caractéristiques du moteur brushless utilisé :

La description:

Nom de marque: emax

Nom de l'article: moteur brushless de xa2212

Kv: 1400kv

Diamètre: 3mm

Diamètre de l'arbre: 28.5mm

Compatible taille d'hélices: 1147.1047.9060.8040.8060

kv1400: propice pour les avions de FPV poussoir prop, ailes à grande vitesse

Annexe

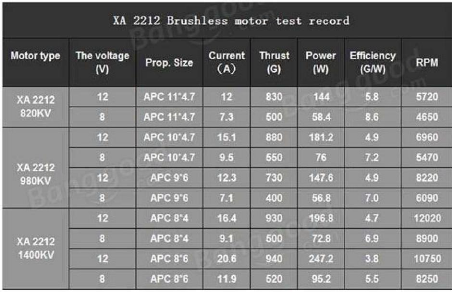
Diamètre du moteur :

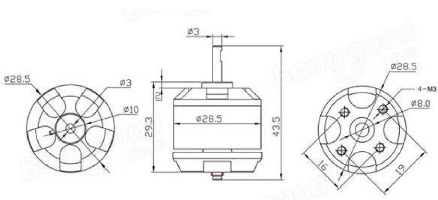
Annexe

3. Caractéristiques de l'ESC Hobbywing XRotor 20A OPTO :

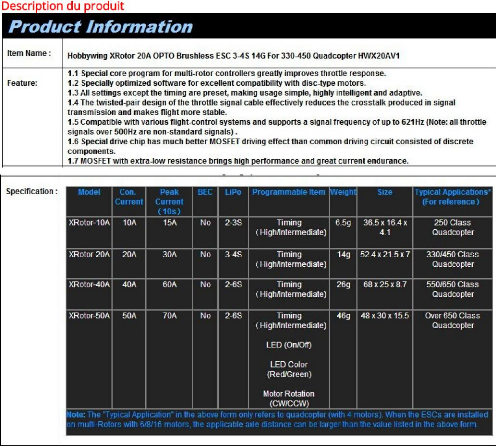
ÉÕ?ÎÑ ÑÇÚÔÊÓÇ ÉÒÌæ É?äæÑÊßáÅ ÊÇäæßã ãÇÏÎÊÓÇÈ ÑÕáÇ äã ÚÏáÇ É?ÚÇÈÑ ÑÇ?Ø äæÏÈ æ ÑÇ?Ø äæÏÈ ÉÑÆÇØ ÁÇÔäÇ æ áãÚáÇ ÇÐ äã ÏáÇ äÇß :ÕÎáã

ÉßÑÍ ?? ãßÍÊáÇ äã äßãÊáá ÒÊÑÇÛ?Ì 2.4 ÊÇÈÐÈÐ ??? áãÚÊ Éäã?Ç É?ßáÓ?áÇ Ê?ÇÕÊ?á æ?ÏÇÑ ÉÏÍææ ÑæÇÍã Ë?Ë æÐ ÈæßÓæ Ñ?Ì æä?æÏÑ?Ç áËã äãËáÇ

?? íæ?ÏÇÑáÇ

ãßÍÊáÇ ÉÏÍæ äã

?????? ÁÇÒÌ ÌÐæãä

ã?ãÕÊ

??

ÊÏÈæ ãÇÙäáÇ ÇÐ

Ð?äÊ áÍÇÑã

???? ÊÍÖæ ÉÑøßÐãáÇ åÐ ?? .ãáß

2 íáÇæÍ ÏÚÈ äÚ ÉÑÆÇØáÇ

ÏÑ ÉÑÆÇØáá

äæß? ??? íæ?ÏÇÑáÇ áÇÈÞÊÓ?Çæ áÇÓÑ?Ç

??

ÉãÏÎÊÓãáÇ

ÊÇ?ãÒÑÇæÎáÇ

ÊÍÑÔ

ÉÌãÑÈáÇ ÁÒÌá ???????

Çã

.ÉãÒ?áÇ

áÇßÔ?Çæ

É?äÇ?ÈáÇ ãæÓÑáÇ Í?ÖæÊ

ÌãÇäÑÈáÇ

???

íæÊÍÊ

íÊáÇ

ÊÇæØÎáá

????

ÇÍÑÔ

Ê?ØÚ

ßáÐ

ÏÚÈ ÑÇ?ØáÇ ÑØ äã ãÏÎÊÓãáÇ æ?ÏÇ øÑáÇ ãßÍÊã äã ÉÑÏÇÕáÇ ÑãÇæ?Ç äã

ÈÓÇäã

áÚ

ÈæßÓÑ?ÌáÇ äã ÉÑÆÇØáÇ ÇÑÍäÇ Ç?ÇæÒ ÊÇäÇ?È ÉÁÇÑÞ Þ?ÑØ äÚ ÉÑÆÇØáÇ ÇÑÍäÇ Í?ÍÕÊæ ÈÇÓÍ áËã ÉÑÆÇØáÇ ÉáÍÑ ?? ãßÍÊáá É?Ó?ÆÑáÇ ÊÇø?ãÒÑÇæÎáÇæ .ÉáÍÑáÇ ÉÁÇß ??? áæÕÍáÇæ ÉÑÆÇØáÇ ÚÖæãÊ ÁÇØÎ ?????? íæ?ÏÇÑáÇ ãßÍÊãáÇ ÑãÇæ ÊÇäÇ?ÈÈ ÇÊäÑÇÞãæ

Abstract: This work was carried out as part of the master's thesis, which the objective was the design and production of a quadrotor UAV drone with the six-channel radio controller, using only inexpensive electronic components such as the Arduino, a 3-axis gyroscope MPU6050 and a radio module (NRF24L01) at 2.4 GHz for the realization of the appropriate transmitter and RF receiver. The Both of quadrotor and transmitter frames were built with ultra polyamide nylon using a 3D printer. In this thesis, I mentioned all the stages of the implementation of this system, after a brief introduction on drones, with the citation of the different standards and research work carried out in this area, I started to model the different parts of the system through the instrumentation it contains the quadrotor and the radio control unit with the illustration of the diagrams and figures required. Regarding the programming part, I first explained the algorithms used in the RF transmitter and receiver in order to have an adequate reaction from the quadrotor to the commands sent by the pilot. After that, I gave a detailed explanation on the different stages which contains the main program of the flight controller such as: Reading the PWM signals coming from the receiver, Reading the angular data coming from the Gyroscope, Calculating the PID corrections, Calculates pulses for each ESC and sends calculated pulses to the ESCs.

Résumé: Ce travail a été réalisé dans le cadre de la thèse de maîtrise, dont l'objectif était la conception et la production d'un drone quadrotor UAV avec le contrôleur radio à six canaux, en utilisant uniquement des composants électroniques bon marché tels que l'Arduino, un gyroscope 3 axes MPU6050 et un module radio (NRF24L01) à 2,4 GHz pour la réalisation de l'émetteur et du récepteur RF appropriés. Les deux cadres du quadrotor et de l'émetteur ont été construits en nylon ultra polyamide à l'aide d'une imprimante 3D. Dans cette thèse, j'ai évoqué toutes les étapes de la mise en oeuvre de ce système, après une brève introduction sur les drones, avec la citation des différentes normes et travaux de recherche menés dans ce domaine, j'ai commencé à modéliser les différentes parties du système à travers l'instrumentation contient le quadrotor et la radiocommande avec l'illustration des schémas et figures nécessaires. Concernant la partie programmation, j'ai d'abord expliqué les algorithmes utilisés dans l'émetteur et le récepteur RF afin d'avoir une réaction adéquate du quadrotor aux commandes envoyées par le pilote. Après cela, j'ai donné une explication détaillée sur les différentes étapes qui contiennent le programme principal du contrôleur de vol telles que: lecture des signaux PWM provenant du récepteur, lecture des données angulaires provenant du gyroscope, calcul des corrections PID, calcul des impulsions pour chaque ESC et envoie des impulsions calculées aux ESC.

Zusammenfassung: Diese Arbeit wurde im Rahmen der Masterarbeit durchgeführt, deren Ziel das Design und die Produktion einer Quadrotor-UAV-Drohne mit dem Sechs-Kanal-Funkcontroller war, wobei nur kostengünstige elektronische Komponenten wie das Arduino, ein 3-Achsen-Gyroskop MPU6050 und verwendet wurden ein Funkmodul (NRF24L01) mit 2,4 GHz zur Realisierung des entsprechenden Senders und HF-Empfängers. Die Quadrotor- und Senderrahmen wurden unter Verwendung eines 3D-Druckers aus Ultra-Polyamid-Nylon hergestellt. In dieser Arbeit erwähnte ich alle Phasen der Implementierung dieses Systems. Nach einer kurzen Einführung in Drohnen und unter Berufung auf die verschiedenen Standards und Forschungsarbeiten in diesem Bereich begann ich, die verschiedenen Teile des Systems zu modellieren Die Instrumentierung enthält den Quadrotor und die Funksteuereinheit mit der Abbildung der erforderlichen Diagramme und Abbildungen. In Bezug auf den Programmierteil habe ich zunächst die im HF-Sender und -Empfänger verwendeten Algorithmen erläutert, um eine angemessene Reaktion des Quadrotors auf die vom Piloten gesendeten Befehle zu erzielen. Danach gab ich eine detaillierte Erklärung zu den verschiedenen Stufen, die das Hauptprogramm des Flugreglers enthalten, wie zum Beispiel: Lesen der vom Empfänger kommenden PWM-Signale, Lesen der vom Gyroskop kommenden Winkeldaten, Berechnen der PID-Korrekturen, Berechnen von Impulsen für jeder ESC und sendet berechnete Impulse an die ESCs.

Özet: Bu çaliþma, sadece Arduino, 3 eksenli bir jiroskop MPU6050 gibi ucuz elektronik bileþenler kullanilarak, alti kanalli radyo kontrolörü ile bir quadrotor HA uçaðinin tasarimi ve üretimi olan yüksek lisans tezinin bir parçasi olarak gerçekle°tirildi. uygun verici ve RF alicisinin gerçekle°tirilmesi için 2,4 GHz'de bir radyo modülü (NRF24L01). Dörtlü ve verici çerçevelerinin her ikisi de bir 3D yazici kullanilarak ultra poliamid naylon ile yapilmi°tir. Bu tezde, bu sistemin uygulanmasinin tüm a°amalarindan bahsetmi°tim, dronlar üzerine kisa bir giri°ten sonra, bu alanda yapilan farkli standartlarin ve ara°tirma çali°malarinin gösterilmesi ile sistemin farkli bölümlerini modellemeye ba°ladim. enstrümantasyonda gerekli diyagramlari ve °ekilleri gösteren dörtlü ve radyo kontrol ünitesini içerir. Programlama kismi ile ilgili olarak, önce kuadrotordan pilot tarafindan gönderilen komutlara yeterli bir tepki vermek için RF vericisi ve alicisinda kullanilan algoritmalari açikladim. Bundan sonra, uçu° kontrolörünün ana programini içeren farkli a°amalarda ayrintili bir açiklama yaptim: Alicidan gelen PWM sinyallerinin okunmasi, Jiroskoptan gelen açisal verilerin okunmasi, PID düzeltmelerinin hesaplanmasi, her ESC ve hesaplanan darbeleri ESC'lere gönderir.