II.5.2.4 Les types d'algorithmes de chiffrement et
déchiffrement
II.5.2.4.1 L'algorithme de chiffrement
RSA
RSA est un algorithme de chiffrement mathématiquement
significatif et important. Sa difficulté à craquer est
basée sur la difficulté de décomposer un nombre composite
en deux grands nombres premiers [65].
Parce que la factorisation du produit de deux grands nombres
Chapitre II Fonctionnement de la blockchain
[43]
premiers est assez difficile (la preuve est un peu
compliquée et nécessite des concepts tels que la factorisation en
nombres premiers, les nombres premiers et la congruence).
Le chiffrement dit asymétrique signifie que
différentes clés peuvent être utilisées pour le
chiffrement et le déchiffrement. De cette façon, la clé
publique peut être envoyée à l'expéditeur et la
clé privée est conservée sur lui-même et
déchiffrée par la clé privée. Cela garantit que
vous seul pouvez déchiffrer le message
[66].
Le 12 décembre 2009, le RSA-768 (768 bits, 232
chiffres) a également été décomposé avec
succès. À l'heure actuelle, la longueur de clé la plus
sûre est RSA-1024 ou RSA-2048.Il s'agit actuellement de l'algorithme de
cryptage le plus important de la planète
[66].
II.5.2.4.1.1 Étapes pour la
génération de clés
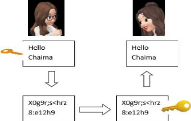
Nous utilisons un exemple pour comprendre l'algorithme RSA.
Supposons que Kawter va avoir une communication cryptée avec Chaima.
Comment peut-elle générer des clés publiques et
privées ?
Figure II- 10: Étapes pour la
génération de clés
Dans la première étape, deux
nombres premiers inégaux p et q sont choisis au hasard. Chaima a choisi
61 et 53. En pratique, plus ces deux nombres premiers sont grands, plus il est
difficile de se fissurer.
Dans la deuxième étape, le produit
n de p et q est calculé. Chaima a multiplié 61 et 53.
n = 61 × 53 = 3233
Equation II- 1: Produit de n et p.
La troisième étape,
consiste à calculer la fonction d'Euler ö (n) de n. Selon la
formule
D (n) = (p-1) (q-1)
Equation II- 2: Calcule de la fonction
d'Euler
Chaima a calculé que ö (3233) est égal
à 60 x 52, ce qui correspond à 3120.
La quatrième étape, consiste
à choisir au hasard un entier e, à condition que 1 <e
<ö (n), et e et ö (n) soient des nombres premiers.
Chapitre II Fonctionnement de la blockchain
[44]
Chaima avait choisi entre 1 et 3120 et a été
choisie au hasard 17. En pratique, 65537 est souvent
sélectionné.
Dans la cinquième étape, calculez
l'élément inverse d de e pour ö (n).
Le soi-disant "élément inverse
modulaire" signifie qu'il existe un entier d, de sorte que le reste de
ed divisé par ö (n) est 1.
ed ? 1 (mod ö (n))
Equation II- 3: Calcule d'élément
inverse d.
Par conséquent, trouver l'élément inverse
d revient essentiellement à résoudre l'équation
linéaire binaire suivante :
e.x + ö (n).y = 1
Equation II- 4: Equation linéaire binaire
Étant donné e = 17, ö (n) = 3120,
17x + 3120y = 1
Cette équation peut être résolue en
utilisant « l'algorithme euclidien étendu »,
et le processus spécifique est omis ici. En bref, Chaima a
calculé un ensemble de solutions entières comme (x,y) = (2753,
-15), c'est-à-dire d = 2753.
Jusqu'à présent, tous les calculs sont
terminés.
Dans la sixième étape, n et e
sont encapsulés dans une clé publique, et n et d sont
encapsulés dans une clé privée.
Dans l'exemple de Chaima, n = 3233, e = 17 et d = 2753, la
clé publique est donc (3233,17) et la clé privée est
(3233, 2753).
II.5.2.4.1.2 Chiffrement et
déchiffrement
Avec les clés publiques et secrètes, le chiffrement
et le déchiffrement sont possibles. (1) La clé publique
(n, e) est utilisée pour le chiffrement :
Supposons que Kawter veuille envoyer des informations
chiffrées m à Chaima, elle chiffrera m avec la clé
publique de Chaima (n, e). Notez ici que m doit être un entier (la
chaîne peut prendre des valeurs ascii ou Unicode), et m doit être
inférieur à n.
Le soi-disant "cryptage" consiste à calculer c :
La clé publique de Chaima est (3233, 17), et le m de
Kawter est supposé être 65, alors l'équation suivante peut
être calculée :
Donc, c'est égal à 2790, et Kawter envoie 2790
à Chaima.
Chapitre II Fonctionnement de la blockchain
[45]
(2) La clé privée (n, d) est utilisée
pour le déchiffrement :
Après que Chaima a obtenu 2790 de Kawter, elle a
utilisé sa clé privée (3233, 2753) pour la
décrypter. Il peut être prouvé que l'équation
suivante doit être vérifiée :
Autrement dit, le reste de la puissance de c divisé par
n est m. Maintenant, c'est égal à 2790 et la clé
privée est (3233, 2753), puis Chaima calcule :
À ce stade, le processus complet de «
chiffrement-déchiffrement » est terminé.
Nous pouvons voir que si nous ne connaissons pas d, il n'y a
aucun moyen de trouver m à partir de c. Comme mentionné
précédemment, savoir que d doit être
décomposé en n, ce qui est extrêmement difficile à
réaliser, donc l'algorithme RSA garantit la sécurité de la
communication.
Vous pourriez demander que la clé publique (n, e) ne
puisse chiffrer que des entiers m inférieurs à n, alors que faire
si vous voulez chiffrer des entiers supérieurs à n ?
Il existe deux solutions : l'une consiste à diviser le
message long en plusieurs messages courts, chacun étant chiffré
séparément, l'autre à choisir d'abord un "algorithme de
chiffrement symétrique" (tel que DES) et à utiliser la clé
de cet algorithme, chiffrez les informations, puis chiffrez la clé DES
avec la clé publique RSA.
La méthode de chiffrement à clé publique
RSA offre également une authentification à l'aide d'une signature
numérique. Notez ici qu'un algorithme différent appelé
algorithme de signature numérique (DSA) peut également être
utilisé dans de telles situations que nous verrons dans la section
suivante. RSA est largement utilisé avec HTTPS sur les navigateurs Web,
les e-mails, les VPNS et la télévision par satellite. En outre,
de nombreuses applications commerciales ou les applications dans les magasins
d'applications sont également signées numériquement
à l'aide de RSA. SSH utilise également la cryptographie à
clé publique ; lorsque vous vous connectez à un serveur SSH, il
diffuse une clé publique qui peut être utilisée pour
crypter les données à envoyer à ce serveur. Le serveur
peut ensuite décrypter les données à l'aide de sa
clé privée. L'algorithme de signature numérique DSA a
été conçu par la NSA26 dans le cadre de la
norme de signature numérique DSS et normalisé par le NIST. Notez
que son objectif principal est de signer les messages numériquement, et
non le cryptage. Juste pour paraphraser, RSA est à la fois
dédié pour la gestion des clés et l'authentification
tandis que DSA est dédié uniquement pour
l'authentification [67].
II.5.2.4.2 La signature
numérique
Lorsqu'une personne envoie des données via un document,
il devient important d'identifier son authenticité pour des raisons de
sécurité et de sûreté. Des signatures
numériques sont utilisées pour cette identification.
L'authentification des documents signifie savoir qui les a créés
et qu'ils n'ont pas interféré lors de leur transmission. Ces
signatures sont créées à l'aide de certains algorithmes.
L'algorithme de signature numérique (DSA) en
26 NSA : National
Security Agency est une agence de renseignement de niveau national du
Département de la défense des États-Unis, placée
sous l'autorité du directeur du renseignement national.
Chapitre II Fonctionnement de la blockchain
[46]
fait partie. DSA est un type d'algorithme de
chiffrement à clé publique et il est utilisé pour
générer une signature électronique
(68].
II.5.2.4.2.1 Introduction
Les signatures numériques sont idéales pour
l'intégrité et la non-répudiation. Une signature
numérique est une combinaison de hachage et de chiffrement
asymétrique. Autrement dit, un message est d'abord haché, et ce
hachage est chiffré avec la clé privée de
l'expéditeur. Cela constitue la signature, qui est envoyée avec
le message.
II.5.2.4.2.2 Fonctionnement d'algorithme de la
signature numérique
Il s'agit d'un algorithme de chiffrement à clé
publique conçu pour créer une signature électronique. Une
signature est créée « en privé » mais peut
être vérifiée « en public ». En d'autres termes,
il n'y a qu'un seul sujet qui peut créer une signature ajoutée
à un message, mais n'importe qui est en mesure de vérifier si la
signature est correcte ou non.
II.5.2.4.2.3 Schéma fonctionnel de la
signature numérique
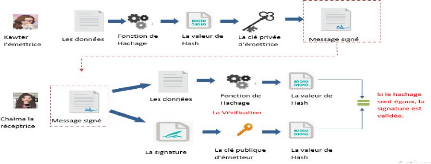
Figure II- 11: Schéma représente
comment la signature fonctionne II.5.2.4.2.4 Explication du schéma
fonctionnel
Premièrement, chaque
personne adoptant ce schéma possède une paire de clés
publique-privée en cryptographie
(69].
Les paires de clés utilisées pour le chiffrement
ou le déchiffrement et la signature ou la vérification sont
différentes pour chaque signature. Ici, la clé privée
utilisée pour la signature est appelée clé de signature et
la clé publique comme clé de vérification dans cet
algorithme.
Ensuite, les gens prennent le
signataire qui alimente les données à la fonction de hachage et
génère un hachage des données de ce message.
Maintenant, la valeur de
hachage et la clé de signature sont ensuite transmises à
l'algorithme de signature qui produit la signature numérique sur un
hachage donné de ce message. Cette signature est ajoutée aux
données, puis les deux sont envoyées au vérificateur pour
sécuriser ce message.
Ensuite, le
vérificateur alimente la signature numérique et la clé de
vérification dans l'algorithme de vérification de ce DSA. Ainsi,
l'algorithme de vérification donne une certaine valeur en sortie sous
forme de texte chiffré.
Chapitre II Fonctionnement de la blockchain
[47]
Ainsi, le vérificateur exécute
également la même fonction de hachage sur les données
reçues pour générer une valeur de hachage dans cet
algorithme.
Maintenant, pour la
vérification, la signature, la valeur de hachage et la sortie de
l'algorithme de vérification sont comparées avec chaque variable.
Sur la base du résultat de la comparaison, le vérificateur
décide si la signature numérique est valide pour cela ou non.
Par conséquent, la signature
numérique est générée par la clé
privée du signataire et personne d'autre ne peut avoir cette clé
pour sécuriser les données. Le signataire ne peut pas
répudier la signature des données à l'avenir pour
sécuriser ces données par la cryptographie.
II.5.2.4.2.5 Importance de la signature
numérique
Par conséquent, toute analyse cryptographique de la
signature numérique utilisant la cryptographie à clé
publique est considérée comme un outil très important ou
principal et utile pour assurer la sécurité des informations en
cryptographie en cryptanalyse [67].
Ainsi, outre la possibilité de fournir la
non-répudiation du message, la signature numérique fournit
également l'authentification du message et l'intégrité des
données en cryptographie.
Ceci est réalisé par la signature numérique
qui réalise :
o Authentification des messages
: Par conséquent, lorsque le vérificateur
valide la signature numérique à l'aide de la clé publique
d'un expéditeur, il est assuré que la signature n'a
été créée que par un expéditeur qui
possède la clé privée secrète correspondante et que
personne d'autre ne le fait par cet algorithme.
o Intégrité des données
: en fait, dans ce cas, un attaquant a accès aux
données et les modifie, la vérification de la signature
numérique à l'extrémité du récepteur
échoue dans cet algorithme. Ainsi, le hachage des données
modifiées et la sortie fournie par l'algorithme de vérification
ne correspondent pas à la signature de cet algorithme. Maintenant, le
récepteur peut refuser le message en toute sécurité en
supposant que l'intégrité des données a été
violée pour cet algorithme.
o Non-répudiation : Par
conséquent, c'est juste un nombre que seul le signataire connaît
la clé de signature, il ne peut que créer une signature unique
sur une donnée de ce message pour changer de cryptographie. Ainsi, le
destinataire peut présenter les données et la signature
numérique à un tiers comme preuve si un différend survient
à l'avenir pour sécuriser les données.
II.5.2.4.3 EllipticCurve Digital Signature
Algorithm
ECDSA c'est in algorithme de chiffrement à courbe
elliptique pour apprendre la signature numérique d'un
algorithme [70].
Chapitre II Fonctionnement de la blockchain
[48]
| 


