Chapitre 2- Procédure de synthèse d'une
cellule inductive
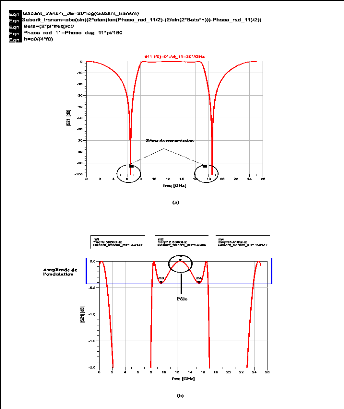
Figure 2. 5: Caractéristiques du gabarit en
transmission. (a) Zéros de transmission. (b) pôle à
f0
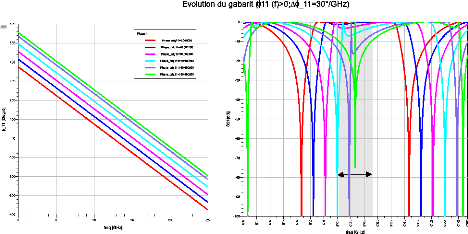
Bande
d'ntérêt
Figure 2. 6: Evolution du gabarit pour une
variation positive de ?_11 (f_0) à dispersion constante
26
Chapitre 2-Procédure de synthèse d'une
cellule inductive
Nous constatons un décalage du gabarit vers les
fréquences hautes. La bande passante se décale vers les hautes
fréquences et se déforme (l'ondulation n'est plus constante et le
pôle maximal n'est plus à ??0). Le zéro de
transmission qui précède la bande passante se rapproche
progressivement de la zone d'intérêt jusqu'à y entrer (cf.
Figure 2. 6).
La Figure 2. 7 présente une évolution
du gabarit d'amplitude pour une évolution négative de ??11(??0)
allant de 0° à -180° par pas de 40° avec une dispersion
???11 = 30°/??????.
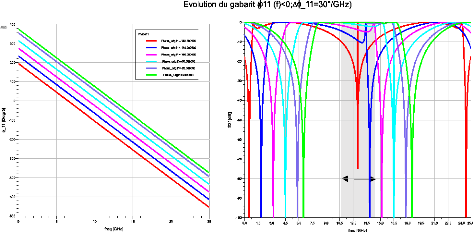
Bande
d'intérêt
Figure 2. 7: Evolution du gabarit pour une
variation négative de ?_11 (f_0) à dispersion
constante
Dans ce cas, l'effet inverse se produit. Le gabarit est
décalé cette fois ci vers les fréquences basses. La bande
passante s'éloigne de la bande d'intérêt, l'ondulation
n'est plus constante et le pôle maximal n'est plus centré à
??0. Et le second zéro de transmission se rapproche de la
zone d'intérêt jusqu'à y entrer (cf. Figure 2.
7).
A présent, on fait varier la dispersion ???11 avec une
phase à l'origine constante ??11(??0) = 0° et on obtient la
Figure 2. 8. Sur celle-ci, nous pouvons voir que la bande passante est
centrée à la même fréquence (la fréquence
centrale ??0) mais sa largeur diminue au fur et à mesure que
la dispersion augmente. Les zéros de transmission basse et haute
fréquence se rapprochent de la zone d'intérêt. L'ondulation
dans la bande passante reste constante mais sa valeur augmente avec la
dispersion (cf. Figure 2. 8).
2.2.2.4 Analyse et interprétation des résultats
En regardant la bande passante, la réponse en amplitude
du gabarit en transmission s'apparente à celle d'un filtre de type
passe-bande ou coupe bande selon la valeur de ??11(??0). Dans le cas
passe-bande, l'ondulation dans la bande passante et la présence des
zéros de transmission nous fait penser à un filtre elliptique (ou
au moins de Tchebychev si on ne prend pas compte la présence des
zéros de transmission). La présence des 3 pôles renseigne
sur l'ordre du filtre. Ainsi la synthèse des éléments du
circuit équivalent en l'occurrence l'admittance parallèle Y peut
dès lors s'opérer comme une synthèse de filtre classique.
Si le pôle de la bande passante se trouve dans la bande
d'intérêt défini, ce circuit sera synthétisé
par une synthèse de type passe-bande. Dans le cas où un des deux
zéros de transmission se trouve dans la bande d'intérêt, ce
dernier sera synthétiser par une synthèse de filtre
coupe-bande.
27
| 


