Chapitre 2- Procédure de synthèse d'une
cellule inductive
vide (cf. Figure 2. 1). On note ??11 =
??????11, le coefficient de réflexion à
l'entrée de la cellule, ??11 étant la phase à
synthétiser.
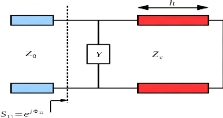
Figure 2. 1: Dipôle équivalent d'une
cellule unitaire Phoenix monocouche de réseau
réflecteur.
On cherche maintenant à relier la loi de phase à
l'amplitude du paramètre ??21 (et uniquement à celui-ci) d'un
circuit symétrique à 2 accès. On choisit le circuit
constitué par 2 cellules montées tête-bêche
créé par symétrie du premier (cf. Figure 2.
2).
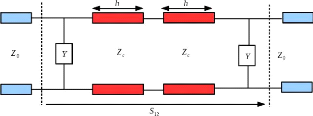
Figure 2. 2: Quadripôle équivalent
constitué de deux cellules unitaires montées
tête-bêche
En procédant par une analyse en mode pair/impaire, on
montre que le module de ??21 est directement lié à ??11 , la
phase à synthétiser par la relation suivante :
?????????????? [??????(?????? (??)
?? - ??
??????(??????))-?????? (??)]
|??????| = |?????? { ?? }| (2. 1)
La loi de phase initiale est donc transposée en un
gabarit en amplitude par la relation (2. 1). C'est le gabarit en amplitude que
nous allons utiliser pour déterminer l'inductance parallèle Y.
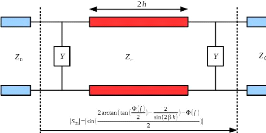
Figure 2. 3: Quadripôle
équivalent
2.2.2 Allure de la loi de phase et du gabarit en amplitude
2.2.2.1 Définition de la loi de phase
24
Chapitre 2-Procédure de synthèse d'une
cellule inductive
On considère une variation linéaire de la phase
??11 en fonction de la fréquence. Cette variation est décrite par
la relation suivante :
??11(??) = ????11(??- ??0) +
??11(??0) (2. 2)
????11(??0)
où ??11(??0) est la valeur de la phase à la
fréquence centrale ??0 et ???11 = ???? , la dispersion
de la phase en (°/GHz).
2.2.2.2 Illustration de la loi de phase et du gabarit en
transmission
Considérons la loi de phase illustrée sur la
Figure 2. 4 définie par le couple (phase à l'origine ;
dispersion) = (??11(??0); ???11) = (0°; -30°/??????) à la
fréquence centrale de la bande d'intérêt ??0=12,5GHz. La
loi équivalente sur l'amplitude du gabarit en transmission est
présentée sur la Figure 2. 5 avec une longueur de la
ligne fixée à h=??0/4 à ??0.
La réponse en amplitude présente 2 zéros
de transmissions situés de part et d'autre de la bande passante (cf.
Figure 2. 5(a)), et 3 pôles dont le pôle max est à
la fréquence centrale ??0. Cette courbe est
équivalente à la réponse d'un filtre passe-bande d'ordre 3
(3 pôles) et présente une ondulation en bande passante dont
l'amplitude est égale à 0,4137dB (cf. Figure 2.
5(b)).
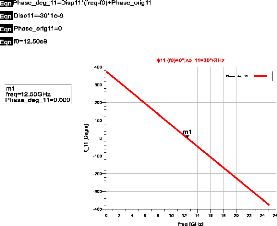
Figure 2. 4: loi de phase
2.2.2.3 Evolution du gabarit
Nous allons à présent étudier le
comportement des paramètres du gabarit (bande passante, les pôles,
les zéros de transmission, l'ondulation) en fonction d'une
évolution linéaire des paramètres de la loi de phase
(??11(??0); ???11). Nous analyserons ensuite
le comportement des paramètres du gabarit dans la bande
d'intérêt [10,5-14,5] GHz4.
La Figure 2. 6 montre l'évolution du gabarit
lorsque la phase à l'origine ??11(??0) varie de 0° à
180° par pas de 40° avec une dispersion fréquentielle
constante ???11 = -30°/??????.
4 Cette bande de fréquence
correspond à la bande Ku en liaison descendante (10,70-11,70 à
12,75 GHz) et montante (14 à 14,5). Ce spectre de fréquence est
utilisé dans les communications par satellite qui constitue
principalement le domaine d'utilisation des antennes RA.
25
| 


