Etude d'une équation hyperbolique

Faculté des Sciences

ãæ ÜÜÜÜÜÜ áÚáÇ ?? ÜÜÜÜÜÜÜÜÜ ??

Faculté des Sciences
Département de Mathématiques

Mémoire

Présentée en vue de l'obtention du diplôme de
Licence en Mathématiques appliquées

Etude d'une Equation Hyperbolique

Domaine : M.I.
Option : Mathématiques Appliquées.

Par : Mohssin Bayoud

Encadré par : Khaled ZENNIR M.A. U S T O

Devant le jury :

Président : Rabah KHMIS M.C. U. SKIKDA

Examinateur : Ahlem BOUAKKAZ M.A. U. SKIKDA

Année : 2011/2012

Etude d'une équation Hyperbolique

Par: Mohssin BAYOUD Encadré par: Khaled ZENNIR

Département de mathématiques
Université 20 Aout 55 SKIKDA
Faculté des sciences

Juin 2012

2

Table des matières

1	Préliminaire			1
	1.1	Qu'est qu'une équation différentielle partielle ?		2
		1.1.1	Equation différentielle ordinaire (EDO)	2
		1.1.2	Equation aux dirévées partielles (EDP)	2
		1.1.3	Classification des EDPs linéaires du second ordre	3
		1.1.4	Probléme bien posé .	3
	1.2	Quelques notions autour des dériveés partielles		4
		1.2.1	Dérivées directionnelles .	4
		1.2.2	Les applications de classe C'	4
		1.2.3	Conditions de Derechlet et de Numamm	6
	1.3	Espaces métriques, espaces topologiques		6
		1.3.1	Norme, distance, topologie	6
		1.3.2	Continuité, complétude, compacité	7
	1.4	Espaces fonctionnelle		10
		1.4.1	Les espaces L^p 10
		1.4.2	Espaces de Sobolev	11
		1.4.3	Les espaces L^p(0,T,X)	12
2	Equation des ondes sur un axe (Dans )			13
	2.1	Equation des cordes vibrantes		14
		2.1.1	Le modèle physique	14
		2.1.2	Solution de l'équation (Solution générale avec la méthode de D'Alembert) . .	15
		2.1.3	Existence d'une solution par la méthode de séparation des variables	19
		2.1.4	Energie	22
		2.1.5	Unicité d'une éventuelle solution par considération de l'énergie	23
		2.1.6	Vitesse de propogation	24
		2.1.7	Dérivation d'une équation des ondes	24

3 Equation des ondes en dimension ii (Dans II1ⁿ) 27

3.1 Solution de l'équation 28

3.1.1 Formulation variationnelle 28

3.1.2 Existence et unicité 30

3.2 Applications 33

Notations

R^N : L'éspace Euclidien avec la norme 1,51 = 1(si, · · ·,^5N)1 =

X N i=i

)112 s2 : i

a : Domaine borné de R^N.

F, 8a : Frontière topologique de a: x = (xi, x2, xN) : Point de R^N. Vu : Gradient de u :

0 a )

Vu = ( u ..,

0x1 " ax u .

Au : Laplacien de u est l'opérateur du second ordre sur R^N :

82 82

Au = div(Vu) = ax2 u + ... + u.

aX²

1 N

q : Conjugué de p, c -- -- d :

1

q

=1.

+

1

p

D(a) : Espace des fonctions indéfiniment différentiable sur a 2 C"°(a) et a support compacte dans a:

D'(a) : Espace de distribution .

11x1l_x : La norme de x dans X .

1

p

:

II/11p = (1₁ I f(x)I^P)

(a) = {u 2 L^P (a) , Vu 2 (L^P (a))/ .

1

P :

= (Ilur_p+ 11Vur_p)

1/Ii0 "^P (a) : La ferméture de D (a) dans W^1,P (a).

H : Espace de Hilbert.

H1 0= W 1;2

0 :

u : a x R^#177; --> Rⁿ. au

rat = at :

Opérateur de dérivation : Soit a un ouvert de IV , a 2 IT' et

f : a R,

alors :

^1111ff(x))( ( 0 )1 l( ( 0 ^nnD^af(x)) == ::: f(x) ^@x1 1 :::@x^n @x1 @xn )n

iv

Si X est un espace de Banach

_I ~

_fT

L1 (0, T ; X) = f : (0, T ) - X est mesurable ; f(t) p X dt < oc :

0

_I )

L°° (0, T ; X) = f : (0, T ) X est mesurable ;ess - sup f(t) p X < oc :

tE(0,T)

Bx = {x E X; x < 1} : La boule unitée.

Résumé
Dans ce travail, nous allons essayer de développer quelques techniques classiques
pour résoudre une équation hyperbolique.
Commençons par les deux méthodes (séparation de variables et D'Alembert)
pour une équation des ondes dans II1.
Ensuite on va voire l'idée de la formulation variationnelle pour montrer l'existence
de la solution faible d'une équation des ondes dans II1ⁿ_; ii ~ 1.

vi

Introduction

Les équations aux dérivées partielles, qui seront notées en abrégé "EDP" dans la suite, constituent une branche importante des mathématiques appliquées. Elles sont utilisées dans la modélisation de nombreux phénomènes de natures différentes.

Le but principal de résoudre ces équations est d'essayer d'apprendre quelques informations sur le processus physique que l'équation est estimée a modéliser. Il est de base a l'importance des équations différentielles que même les plus simples équations correspondent aux modèles physiques utiles. La compréhension d'un processus complexe par nature, est généralement réalisée en combinant on constituant sur des modèles plus simples et plus fondamentales. Ainsi, une connaissance approfondie de ces modèles, les équations qui les décrivent, et leurs solutions, est la première indispensable étape vers la solution des problèmes plus complexes et réalistes.

Les équations aux dérivées partielles avec le temps t en tant qu'une des variables indépendantes forment des équations d'évolutions en temps (Hyperboliques et paraboliques), elles résultent non seulement de beaucoup de champs des mathématiques, mais également d'autres branches de la science telles que la physique, la mécanique et la science des matériaux. Par exemple, équations de Navier-Stokes et d'Euler de la mécanique liquide, équations de réaction-diffusion des transferts thermiques et sciences biologiques, Klein....

Les équations aux dérivées partielles Hyperboliques servent a représenter des processus dynamiques que l'on rencontre notamment dans l'étude des structures fiexibles.

Dans ce travail, que nous présentons sous forme d'un mémoire de Licence en Mathématiques, nous étudions un problème de type Hyperbolique (l'équation typique est une equation des ondes).

Une équation différentielle du second ordre se produisant fréquemment en mathématiques appliquées est l'équation d'onde. La resolution de l'équation des ondes était l'un des problèmes mathématiques majeurs de la première moitié du XV III^em siècle.

Elle a été étudiée par D'Alembert en 1746, également elle a attirée l'attention d'Euler (1748), Daniel Bernoulli (1753), et Lagrange (1759). Des solutions ont été obtenus dans plusieurs formes différentes, et vante les mérites et les relations entre, ces solutions ont été débattues, parfois avec véhémence, dans une série de documents. Les principaux points en litige portaient sur la nature d'une fonction, et les types de fonctions qui peuvent être représentés par des séries trigonométriques. Ces questions n'ont pas été résolus jusqu'a le XIX^em siècle.

Une certaine forme de cette équation, on une généralisation de celui-ci, presque inévitablement se pose dans toute analyse mathématique des phénomènes impliquant la propagation des ondes dans un milieu continu. Par exemple, les études des ondes acoustiques, des vagues d'eau, les ondes électromagnétiques et les ondes sismiques sont toutes basées sur cette équation.

Peut-être la situation la plus facile se produit dans les vibrations mécaniques. Supposer qu'un fil élastique de longueur L est tendu entre deux supports de même niveau horizontal, de telle sorte que l'axe x s'étend le long de la chaine. La corde élastique peut être considérée comme une corde de violon, un hauban, on peut-être une ligne électrique. Supposer que la chaine est mise en mouvement (par pincement, par exemple) de sorte qu'il vibre dans un plan vertical, et u(x, t) représentent le déplacement verticale subie par la chalne au point x a l'instant t. Si les effets d'amortissement, comme l'air la résistance, sont négligés, et si l'amplitude du mouvement n'est pas trop grand, alors u(x, t) satisfait l'équation aux dérivées partielles suivante

a²uxx = utt (1)

dans un domaine 0 < x < L, t > 0. L'équation (1) est connue comme l'équation des ondes. La constante a² dans (1) est donnée par

a2 = T/p, (2)

on T est la tension (force) dans la chalne, et p est la masse par unité de longueur du matériau de chalne. Il s'ensuit que a l'unité de longueur/ heure, qui est, de la vitesse de propagation des ondes le long de la chaine. Pour décrire le mouvement de la chalne complète, il est nécessaire également de préciser des conditions initiales et limites pour le déplacement u(x, t). Les extrémités sont supposées rester fixes, et donc les conditions aux limites sont

u(0,t) = 0,u(L,t) = 0,t ~ 0. (3)

Comme l'équation (1) est de second ordre pour la variable t, il est plausible de prescrire deux conditions initiales.

Elles sont la position initiale de la corde,

u(x,0) = uo(x),0 x L, (4)

et la vélocité,

ut(x,0) = ui(x),0 x L, (5)

on u0 et ui sont des fonctions données.

Pour les équations (3), (4) and (5), il est également nécessaire d'exiger que

u0(0) = u0(L) = 0,u1(0) = u1(L) = 0. (6)

Le problème mathématique est alors de déterminer la solution de l'équation d'onde (1) que satisfis également les conditions aux limites (3) et les conditions initiales (4) et (5). Ce problème est un problème de valeur initiale dans les variables t temps, et un problème de valeur limite dans l'espace de la variable x.

Il peut être considéré comme un problème aux limites dans la semi-finis bande 0 < x < L, t > 0 du plan xt. Une condition est imposée a chaque point sur les côtés semi-infinis, et deux sont imposées a chaque point d'extrémité.

Il est important de réaliser que l'équation (1) régit un grand nombre de problèmes d'ondes autres que les vibrations transversales d'une corde élastique. Par exemple, il est seulement nécessaire d'interpréter la fonction u et la constante a appropriées a des problèmes portant sur des vagues d'eau dans un océan, ces ondes acoustiques on électromagnétiques dans l'atmosphère, on des ondes élastiques dans un corps solide. Si plus d'une dimension de l'espace est important, alors l'équation (1) doit être légèrement généralisée.

L'équation d'onde a deux dimensions est

a2 (uxx + uyy) = utt: (7)

Cette équation se poserait, par exemple, si l'on considérait le mouvement d'une feuille mince et élastique, comme une peau de tambour.

De même, dans les trois dimensions de l'équation d'onde est

a2 (uxx + uyy + uzz) = Utt. (8)

Dans le cas de ces deux dernières équations, les conditions aux bords et les conditions initiales doivent également être convenablement généralisée.

En dimension supérieure l'équation suivante

Utt(X, t) - Iu(x, t) = f(x, t), (9)

représente l'équation des ondes dans Rⁿ_; elle modélise la propagation des ondes on de vibration, avec les conditions initiales

u(x,0) = u0(x),vt(x,0) = U1(X)

et les conditions aux bords

u(x,t) = 0,

on le Laplacien dans Rⁿ et la fonction f(x, t) donnée. Par exemple, la propagation au cours

du temps du déplacement vertical d'une membrane élastique, ou bien de l'amplitude d'un champ électrique de direction constante. L'inconnue dans cette équation est la fonction u(x, t).

Plan de mémoire

On a structuré ce mémoire en trois grands chapitres :

Chapitre0l :

Dans ce premier chapitre on rassemble toutes les notions et résultats de base que nous utiliserons par la suite. Ces notions et ces résultats représentent un outil important pour l'étude de ce type de problème.

Chapitre02 :

Ce chapitre traite l'une des premières équations aux dérivées partielles mises en évidence (Equation des cordes vibrantes), qui a été étudier premièrement par D'Alembert. Une corde qui est un milieu continu unitaire unidimensionnel ayant une longueur fini ou infini.

Chapitre03 :

Dans ce dernier chapitre on traite un exemple un peut plus complequé de problèmes d'évolutions de type hyperbolique. Il s'agit d'une équation des ondes dans Rⁿ pour les conditions aux limites de Dirichlet qui modélise la propagation des ondes oil de vibration.

Dans ce chapitre, nous allons rappeler les notions essentielles, de même quelques résultats fondamentaux, qui concernent les espaces métriques, topologiques, les espaces I^I (~) , les espaces de Sobolev, espaces fonctionnelles et d'autres théorèmes classiques. Ces notions et ces résultats représentent un outil utile pour l'étude de ce type de problème.

1.1 Qu'est qu'une équation différentielle partielle ?

1.1.1 Equation différentielle ordinaire (EDO)

Définition 1.1.1 Une équation différentielle est une relation entre une variable indépendente x oIl (t), une fonction inconnue y = f(x) et ces dérivées

y⁰,y⁰⁰,y⁰⁰⁰,......., y^Th.

On peut écrire symboliquement une (ED) comme suit:

F(x, y, y^', y⁰⁰,...., yⁿ) = 0,

ou

dy d^Yy d^Thy

F (x, dx^, dx2 , ...., dx ) - 0.

Si y = f(x) une fonction d'une seule variable indépendente (x). Alors l'équation est dite équation différentielle ordinaire (EDO).

1.1.2 Equation aux dirévées partielles (EDP)

Définition 1.1.2 Soit u une fonction définie sur Rⁿ a valeur dans R

u : Rⁿ -p R

Une équation aux dérivées partielles (EDP) pour la fonction u est une relation entre u les variables x1, x2,.....x et un nombre fini de dérivées partielles de u.

F(xi, x2,......x_v,, u, D1u, D2u,.....D_nu, D1D2u, ...D1D_nu, .., D^au, ...), (1.1)

ou

a = (ai, a2,.......a_n) 2 Nⁿ.

Definition 1.1.3 On dit que u est une solution de l' EDP dans une région C Rⁿ, si aprés

substitution de u et de ses dérivées partielles, F s'annule pour tout

(x1,x2,.....x_n) 2 ~.

Definition 1.1.4 Soit = ]a, b[ x ]c, d[ dans ², et

f : ~ ~ R² ! R

une application. Soit (x0, yo) E , et

fi : ]a;b[ -- R

l'application définie par

fi (x) = f (x,yo)

on dit que f admet une dérivée partielle par rapport a la première variable en (x0, yo) lorsque fi est dérivable en x0. On note 8if (x0, yo) ou encore 8 f (xo, yo) le nombre fi (x0). De la même maniêre, si elle existe, on note 82f (x0, yo) la dérivée partielle de f par rapport a la deuxiême variable en (xO,yO).

1.1.3 Classification des EDPs linéaires du second ordre

Ce paragraphe est destiné a distinguer trois types d'équations, qui se révélent différentes tant du points de vue mathématique(propriétés des solution, méthodes de démonstration) que physique. Etudions le cas des EDP dépendant de deux variables réelles.

Définition 1.1.5 L'équation aux dériivées partielles (1.1) donnée :

8²u

a8x2 + b 82u (1.2)

8x8y + c82u

8y2 + a8u

8x + / 8u

8y + 'yu = F (x, y)

est dite de type :

-Hyperbolique lorsque

A = b² - 4ac > 0,

-Parabolique lorsque

A = b² - 4ac = 0,

-Elliptique lorsque

A = b² - 4ac < 0,

oIl A = b² - 4ac est la discriminant de l'équation (1.2).

1.1.4 Probléme bien posé:

Le nombre de solutions d'une EDP peut être trés grand. Rappelons le cas des équations différentilles linéaires homogenes a coefficients constants. Pour l'équation

a_nu⁽ⁿ⁾(x) + a_n_iu^(n_1)(x) + ... + aiu^'(x) + aou(x) = 0, (1.3)

on rappellera plus loin que l'ensemble des solutions est un espace vectoriel on dimension m : la
solution générale dépend de m (m est l'ordre de l'équation). On obtient une solution unique lorsque

l'on fixe n conditions supplémentaires du type

u(0) = _yo,u/(₀) = _yi, ..., u(n_1)(0) = yn_i, (1.4)

Considérons une équation aux dérivées partielles sur un domaine Q avec eventuellement des conditions auxiliaires sur la solution, on dit que le probléme est bien posé si on a :

- Existence d'une solution du probléme.

- Unicité de cette solution.

- Stabilité par rapport aux données du probléme (Conditions initiales et aux bords). Si la solution se change beaucoup quand les données se changent peu on dit que le probléme est sensible aux données.

1.2 Quelques notions autour des dériveés partielles

1.2.1 Dérivées directionnelles :

Soit

f : 12--> IR

une application, (xo, yo) un point de Q et u = (ui, u2) un vecteur de 118².

On appelle dérivée directionnelle de f en (x0, y0) dans la direction de u la dérivée en s = 0, si elle existe, de la fonction d'une variable

fu:s^-->f(xo,yo) + su).

On la note alors

auf(xo, yo).

1.2.2 Les applications de classe Ck

Soit Q un ouvert non vide de Tⁿ, pour tout

k E N = N U I+oo},

on définit l'espace C^k(Q) comme suit :

C^k(Q) = If : Q ----> IR ou C : D^af E C(Q),Va E Nⁿ; lal < k} .

Autrement dit : une fonction

f : 12--> IR,

est dite de classe C^k sur Q si toute ses derivées partielles jusqu'a l'ordre k existent et sont continues.

C^k(Q) = f : Q ~! R

ou C : f 2 C^k(Q), et toutes les derivées partielles l'ordre k se prolonge continument a Q.

^C°°(Q) = krOCk (Q)

et

^C°°(Q) = krOCk (Q)

Théorème 1.2.1 Si f est de classe C²dans Q, alors on a :

a2xyf =@2 _yxf_; dans Q.

on note aussi les dirévées secondes	82		82
	ax^e '		Oxoy' :::

Théorème 1.2.2 (de trace) Soit Q un ouvert borné régulier de classe C^l,ou bien

Q = Rⁿ +:

On définit l'application trace 'Yo

H¹(Q) n C(Q) L²(0Q) n C(0Q)

70(v) = van.

Cette application _'Yo se prolonge par continuité a une application linéaire continue de H¹(Q) dans L²(0Q), not& encore 70.

En particulier, il existe une constante c > 0 telle que, pour tout fonction v 2 H¹(Q),on a

IlvIlL2(an) ~ kvkH1(~)

Théorème 1.2.3 (Krein Rutman) On suppose que l'ouvert Q est connexe. Alors la premiére valeur propre Aiest (i.e le sous espace propre correspondent est de demension1) et le premier vecteur propre peut etre choisi positife presque partout dans Q:

1.2.3 Conditions de Derechlet et de Numann

Les conditions de Dirichlet imposent à la solution u d'être continue sur l'adhérence de ~, c'est-à-dire sur Q et sa frontière, et d'être alors égale à une fonction donnée sur la frontière de ~.

Les conditions de Neumann imposent à la solution u d'être continue sur l'adhérence de ~, c'està-dire sur Q et sa frontière, et d'admettre en tout point de la frontière de Q, une dérivée Ou/ON suivant le vecteur normal N orienté vers l'extérieur de la frontière de Q (supposée suf fisamment régulière) égale à une fonction donnée.

1.3 Espaces metriques, espaces topologiques

1.3.1 Norme, distance, topologie

Definition 1.3.1 Soit X un espace vectoriel reel, une norme sur X est une application x' Ixk de X dans R^#177;, telle que :

(N1) Ixk = 0 <=> x = O.

(N2) IlAx11 = IAj Ixk , vx 2 X, VA 2 R.

(N3) Ilx + yll < 1xk + Ilyll ,Vx,y 2 X (inegalite triangulaire ).

Definition 1.3.2 Soit X un espace vectoriel reel, un espace norme est un couple (X,11.11) , oh I.k est une norme sur X.

Definition 1.3.3 Soit X un ensemble non vide. Une distance sur X est une application

(x, y) i-- d (x, y)

de X x X dans R^#177; telle que :

(D1) d (x,y) = 0 <=> x = y.

(D2) d (x, y) = d (y,x) ,Vx,y 2 X.

(D3) d (x, y) < d (x, z) +d (y, z) , Vx, y, z 2 X (inegalite triangulaire).

Definition 1.3.4 Un espace metrique est un couple (X, d), ofi d est une distance sur X.

Definition 1.3.5 Soient E un ensemble quelconque et P (E) la famille de toutes les parties de E . On dit qu'une sous famille T de P (E) est une topologie sur E si elle satisfait les trois conditions suivantes :

(A1) E 2 T,0 2 T.

(A2) r est stable par réunion (fini ou non) c'est-à-dire :

U8 (~j)j EI C r : i El	~i 2 r. (1.5)
(A3) r est stable par intersection finie c'est-à-dire : fl 8 (~j)i EJ C r : j EJ		~i 2 r. (1.6)

Le couple (E, r) s'appelle espace topologique. les éléments de r sont dits ensembles ouverts de(E, r).

1.3.2 Continuité, complétude, compacité

Définition 1.3.6 Soient (X, d) , (Y, D) deux espaces métriques. Une application

f : X ~! Y

est continue au point a 2 X, si pour tout € > 0, il existe 8 > 0 tel que

D (f (x),f (y)) < (1.7)

dés que

d (x,y) < 8 (1.8)

On dit aussi que a est un point de continuité de f.

f est continue si f est continue en tout point de X.

L'ensemble des fonctions continues de (X, d) vers (Y, D) est noté C ((X, d) , (Y, D)) ofi tout simplement C (X, Y ).

Proposition 1.3.1 Soient (X, d) , (Y, D) deux espaces métriques et

f : (X,d) ~! (Y, D)

une application alors f est continue en point a 2 X si et seulement si pour toute suite (U_n) converge vers a donc la suite f (U_n) converge vers f (a).

Théorème 1.3.1 Soient (X, d) , (Y, D) deux espaces métriques et f : (X, d) -p (Y, D) une application, alors les assertions suivantes sont equivalentes :

i) f est continue sur X

ii) L'image réciproque par f de tout ouvert de Y est ouverte dans X.

iii) L'image réciproque par f de tout fermé de Y est fermée dans X.

Proposition 1.3.2 Soient (X,11.11_x) , (Y, 11.11_y ) deux espaces normés, et f application linéaire

f : (X,11.11_x) -! (Y , 11.11_y )

Les propriétés suivantes sont équivalentes :

a) f est continue.

b) f est continue en 0.

c) il existe c > 0, tel que

11f (x)11_y < c11x11_x ,Vx E X,

si de plus est de dimension finie, alors toute application linéaire

f : (X,1111x) -> ( X,1111y)

est continue.

Definition 1.3.7 Soit (X, d) un espace métrique, une suite (x_n) E X est de Cauchy si et seulement si pour tout E > 0, il existe n_o > 0, tel que d (x_n, x_m) < E dés que n,m > n_o.

Definition 1.3.8 Soit (X, d) est un espace métrique.

* Une partie A de X est bornée s'il existe a E X et r > 0 tels que

d (a, x) < r, Vx E A.

* Une suite (x_n) C X est bornée s'il existe a E X et r > 0 tels que d (a, x_n) < r, Vn E N.

Definition 1.3.9 Un espace (X, d) est complet si et seulement si toute suite de Cauchy (x_n) E X est convergente.

Soient (X, d) un espace métrique et A C X.

Proposition 1.3.3 On a

a) Si (A, d) un espace complet, alors A est un fermé de X .

b) Si (X, d) un espace complet et A est un fermé de X ,alors (A, d) est complet.

Corollaire 1.3.1 Dans un espace métrique A, A complet <=:- A est fermé.

Definition 1.3.10 Soient (X, d) , (Y, D) deux espaces métriques et

f : X ~! Y

est bornée si son image f (x) est bornée.

Cb (X, Y ) = {f : (X, d) - (Y, D) , f est continue et bornée}

.

Proposition 1.3.4 Si (Y, D) un espace complet, alors Cb (X, Y ) est un espace complet.

Definition 1.3.11 Un espace (X, d) est compact si et seulement si pour tout recouvrement ouvert (Ui)i 2I de X,

(i.e.Uiouvert et X = Ui _2iUi ), on peut extraire un sous recouvrement finie c'est-à-dire il existe une famille J c I tel que

UX = Uj.

j EJ

Corollaire 1.3.2 Un espace (X, d) est compact si et seulement si pour tout famille fermé (F j)j 2I de X, telle que

n i El

Fi = ?,

il existe une famille finie J c I , telle que

flj EJF3 = ø.

Definition 1.3.12 Un espace métrique (X, d) est compact si et seulement si toute suite (x_n) c X admet une sous suite convergente.

Proposition 1.3.5 Soit (X, d) un espace compact, et A c X, alors A est compact si et seulement si A fermé dans X.

Proposition 1.3.6 Soient (X, d) , (Y, D) deux espaces métrique, f est une application continue de X dans Y . Si X est compact, alors f (X) est un compact.

Proposition 1.3.7 Un espace compact est bornée et complet.

Definition 1.3.13 Soit (X, d) un espace métrique, une partie A de X est relativement compact si et seulement si toute suite de A admet une valeur d'adhérence dans X.

Definition 1.3.14 (Espace de Banach) Un espace (X, k.k) est de Banach si et seulement si X est complet pour la distance associe à k.k.

1.4 Espaces fonctionnelle

1.4.1 Les espaces LP

On donne ici quelques definitions et proprietes elementaires.

Definition 1.4.1 Soit Q un ouvert de TV et 1 < P < oo, on definit L^P (Q) un espace de Lebesgue par :

L^P (Q) =

{

f : Q --p IV, f est mesurable et I n

If (x)I^P dx < oo

}

· (1.9)

pour P =118 et 0 < P < oo , on definit Mf M_P par :

Mf Mp = (I If (x)I^P dx ~

1 P

·

(1.10)

Si P = oo, nous avons :

·

If (x)I < c p.p sur Q

L°° (Q) = {f : Q --> IR, f est mesurable,il existe une constante c telle que

On note

MfM°° = inf {c, If (x)I < c}

Theoreme 1.4.1 (Inegalite de Holder).

Soint f E L^P (Q) et g E L^q (Q) avec 1 < P < oo ,alors f g E L¹ (Q) et

I If gI < Mf M_i, MgM_q .

Theoreme 1.4.2 (Inegalite de Young) Soient f E L^P (R) et g E L^q (118) avec 1 < p < oo ,1 < q < oo et 1 r

=

1 p

+

1 q

-- 1> 0.Alors

f * g E L^r (118) et Mf * gM,^r(R) < Mf MLP (R) MgMyi(R) -

Lemme 1.4.1 (de Gronwall)

Soient :

0 une fonction E L°° (0, T ), 0 (t) > 0 ,p.p.t E [0, T ]. ,u une fonction E L^l (0,T ) , ,u(t) > 0,p.p. t E [0, T ] .

On suppose

(t) < 0 ,u (s) q (s) ds + C, p.p.t 2 [0, T ]. (C = constante) .

Alors

(t) < C exp (I,u (s) ds) , p.p. t 2 [0, T ]. On désigne par (f, g) le produit scalaire dans L² (a), i.e.

t

(f, g) = I

f (x) g (x)dx,

et également le produit de dualité entre f 2 D^'(a) (espace des distributions sur a) et g 2 D(a) (espace des fonctions C sur a et a support compact dans a).

Theoreme 1.4.3 L^P (a) est un espace de Banach muni de la norme 11.11p, pour tout 1 < P < 1 .

1.4.2 Espaces de Sobolev

On introduit l'espace H ^m (a) comme etant l'espace des fonctions v 2 L² (a) dont toutes les deriyees partielles d'ordre inferieure ou egale m -prises au sens des distributions sont dans L² (a) Ces espace jouent dans analyse des equations aux deriyees partielles un role fondamental.

Les espaces de Sobolev d'ordre m : [ H ^m (a)]

Definition 1.4.2 Soit a est un ouvert non vide de Rⁿ, et m 2 N. On appelle espace de sobolev d'ordre m sur a l'espace

Hm (a) =

{

u 2 L^2(a) : D^au 2 L^2(a) # calcules au sens des distributions

, Va 2 N^n; <m

9 >= ;>

Remarque 1.4.1 Pour m = 1,

H1 (a) =	8 <>>> >>>:	ou u 2 L^2(a) : 2 L^2(a) uxi # calcules au sens des distributions			,1 <i <n	9 >>>= ;>> >
mull,n(g = (E f 1D^au (x)1^2 dx) jj~m ~			1 2	0 1 @ X = kD^~uk^2 A 2 jj~m			1 2	. (1.11)

et la norme associée a ce produit scalaire

Définition 1.4.3 On introduit ensuite :

H1 ₀(l) = adh^~erence de D(l) dans H ¹ (~)

= sous - espace deH ¹ (~) des fonction "nulles" sur [1 = ô: (1.12)

Théorème 1.4.4 (Formule de Green) pour tout u 2 H ² (~) , v 2 H ¹ (~) on a

f-

ZLuv dx = ~

ZVu Vv dx - ~

@u v dO (1.13) @~

@u

ot @~

est la dérivée normale de u à 11' dirigée vers l'extérieur .

1.4.3 Les espaces Lp(O, T, X)

Définition 1.4.4 Soit X un espace de Banach, on désigne par L (0, T, X) l'espace du foncton

mesurable :

f : ]0,T [ i~! X

(1.14)

t F! f (t)

0 ZT

@0

tel que

₁

A ¹

kf (t)MP _x dt = fMLP (O;T;X) < oc, (1.15)

pour tout 1 P < 1

@f

Lemme 1.4.2 Soit f 2 L (0, T, X) et 2 L (0, T, X), pour 1 P oc, nous avons f
@t

continue de [0, T ] dans X , c'est-à-dire f 2 C ¹ (0, T, X)

Chapitre 2

Equation des ondes sur un axe (Dans R)

Les équations aux dérivées partielles sont d'intérêt répandu en raison de leur raccordement avec des phénomènes dans le monde physique. Nous commençons en examinant ce raccordement dans un problème physique simple.

L'exemple le plus simple, même d'un point de vu historique, d'un problème qui inclut l'équation d'ondes est fourni par l'étude de la vibration d'une corde, comme une corde de violon ou de guitare. Nous allons étudié un système on l'inconnu u(x, t) est le déplacement et nous devons analyser la nature des forces sur la corde (des forces internes et externes).

2.1 Equation des cordes vibrantes

Il s'agit de l'une des premières équations aux dérivées partielles mises en évidence. Elle fut étudiée dés la premiére moitie du XVIII^e siècle par D'Aleynbert :

82 u(x_; t) - C2 82

8xxu(x, t) = f(x,t) (2.1)

@tt

ou c désigne la vitesse de propagation de l'onde dans la corde et u(x, t) l'ordonnée du points d'abscisse x de la corde a l'instant t (cette ordonnée étant mesurée par rapport a la position d'équilibre supposée d'ordonnée nulle).

2.1.1 Le modèle physique

Une corde est un milieu continu unitaire unidimensionnel ayant une longueur fini ou infini, elle posséde généralement des propriétées d'élasticité et peut être tendue a des extrémités, et être amenée a une longueur supérieur a sa longueur de repos, dans ce cas, elle posséde une tension interne, dont l'effet est d'attirer, toute portion de la corde tendue, la position d'équilibre correspend a la ligne droite, joignant les deux extrémités.

La corde tendue peut être modilisé au niveau microscopique par la juxtaposition de ressorts de taille infinité simale couples, autre proches voisins et exerçant, l'un sur l'autre de force de rappel l'orsqu'on écarte une portion de la corde de sa position d'équilibre, elle subit immédiatement les forces de rappel des portions voisines et il en résulte, un mouvement ocullatoire autour de la position d'équilibre qui crée une onde qui se propage, sur toute la corde.

On peut distinguer deux cas :

Un mouvement transversal ou orthogonal a la position d'équilibre et un mouvement longitidinal a la corde.

On considère une corde de longueur L, de densitè constante, élastique, tendue avec une force F0 et en position d'équilibre rectiligne a l'instant t = 0 les points de la corde écartés de leurs positions d'équilibre accquiérent une certaine vitesse, supposons que l'axe des x coincide avec la corde en équilibre.

Le probléme des petites vibration transversales des points pour t > 0, si les extémités de la corde sont :

(a) Fixées régidemant.

(b) Libres, qu'elles peuvent se déplacer librement suivants des droites paralléles a la direction de l'écart.

(c) Fixées élastiquement, chaque extrémité prouve de la part de l'appui une réaction proportionnelle a l'écart et de sens opposé.

(d) Transversal selon des lois données.

Se ramene a l'équation des cordes vibrantes

@2 u(x_; t) - c2 82

8xxu(x, t) = f(x,t) (2.2)

@tt

avec c est la vitesse de propagation des ondes

_4!

F0

2

C = ~

p : est la densité liniaire de la corde.

2.1.2 Solution de l'équation (Solution générale avec la méthode de D'Alembert)

Cas d'une corde infinie

On suppose la corde vibrante infinie et on assimile la position d'équilibre de celle-ci a la droite réelle 1 on se propose d'étudier l'équation avec les conditions initiales suivantes, supposées réalisées pour tout nombre réel x.

u(x,O) = f(x) (2.3)

et

a u(x_; 0) = g(x)

@t

Ces conditions signifient que la corde a été lachée avec vitesse initiale a partir d'une position définie par la donnée de la fonction f, que l'on suppose de classe C² sur 1 .

On va résoudre l'équation des ondes

@2 u(x_; t) - c2 82

8xxu(x, t) = 0 (2.4)

@tt

c'est a dire trouver les fonctions u(x, t), définies et de classe C² sur 1² qui vérifient cette égalité. En utilisant la méthodes des caractéristiques :

L'équation des caractéristique associée a (2.4) est :

cw² -- bw + a = 0

{

<=>
<=>
<=>

alors

dx

W = dt

w2 -- e2 = 0

{

dx

W = dt {W = #177;C

dx

W = dt

dx dt dx dt

= +c = --c

{ x -- ct = c1

(2.5)

x + ct = c2

Les deux équations (2.5) sont les deux familles de courbes caractéristiques.

On reprend la méthode du changement de coordonnées. Soit

f

a = x -- ct 0 = x+ct'

et

v : (a, 0) i! u(x,t).

On note que :

u(x, t) = v(x + ct, x -- ct).

82

U(X, t) -- C^{2 (92}

Ott Oxx U(X_' t) = 0 (2.6)

OtU = U_aat + UsOt = --CU_a + CUs

0

0

Otto = --c(--cu_aa + cu_as) + c(--cus_a + cuss) = C²U_aa -- 2c²U_as + C²Uss

a

(9X

u

=

U_a + Us

a

u = u_aa + u_as + us_a + uss = u_aa + 2u_as + uss

axx

Subtituant ces équations dans l'équation (2.4) on obtient :

(2.4) .<=> ouaa -- ₂0_uas + ouss -- ouaa -- 2c²uo -- c²uso = 0

4 --4c²u_as = 0

<=> u=0

u_a = F(a) , F : fonction arbitraire.

u = I F(a)da + (~)
u(a,0) = (I)(a) + (Q),

0,111 : deux fonctions arbitraires donc :

u = u(x, t) = 0(x -- ct) + (x + ct) (2.7)

(2.7) est dite formule D'Alembert

D'aprés la condition initiale

u(x, 0) = f(x),

on a

f(x) = 0(x) + (x),

0

d'aprés la condition initiale

at u(x_' 0) = g(x),

on a

@ at

u(x_' t) = -- &^'(x -- ct) + c ' (x + ct)

g(x) = --&^'(x) + c '(x)

<=>

f f(x) = 4)(x) + (x) g(x) = --c(^'(x) + c ^'(x)

<=>

f f(x) = 4)(x) + (x)

^1c g(x) = --0^'(x) + ' (x) (2.8)

On derive la première equation de (2.8) par rapport a x

<=>

f 1(x) = 0'(x) + ' (x)

1 ¹_cg(x) = --0'(x) + ^'(x)

<#. 1

'11^'(x) = 2 f^' (x) + ₂¹_cg(x)

(2.9)

1

0'(x) = 1 2.'(x) -- ₂¹_cg(x)

On integre (2.9) sur Q, pour trouver

W(X) = 2.f (X) + 2c fx^x0

{

x) =¹₂^- f(x)

, 21 0 fxx ₀g(x)dx + cl, x 2 R

(

g( (2.10)

x)dx + c₂, x E IR

La somme des deux equations dans (2.10), nous donne

f(x) = f(x) + ci + c2 4--> ci + c2 = 0

Alors :

x--ct x+ct

1 1 u(x, t) = 2f(x -- ct) 2c	I xo	1 1 g(x)dx + c2 + 2f(x + ct) + 2c			I xo	g(x)dx + Cl
1 1 u(x,t) = 2(f(x -- ct) + f(x + ct)) + 2c			I x_ot	g(x)dx. (2.11)

Donc la solution est

x+ct

Cas d'une corde finie

On suppose la corde vibrante finie de longueur L, et on assimile la position d'équilibre de celle-ci au segment [0, L]. On se propose ici d'étudier l'équation avec les conditions initiales suivantes, réalisées pour tout nombre réel x :

u(x,0) = f(x)
8u @t (x, 0) = 0

qui signifient que la corde a été lâchée sans vitesse initiale a partir d'une position définie par la donnée de la fonction f, que l'on suppose de classe C² sur [0, L] (ou même de classe C¹ et de classe C2 par morceaux);

Les conditions aux limites suivantes, réalisées pour tout nombre réel positif t :

u(0,t) = u(L,t) = 0

qui signifient que la corde est fixée a ses deux extrémités. Pour t = 0, on a donc :

f(0) = f(L) = 0. (2.12)

On étudie les problèmes d'existence et d'unicité de la solution u d'une telle e.d.p.

2.1.3 Existence d'une solution par la méthode de séparation des variables

Indiquons tous d'abord l'idée de la méthode.

On commence par rechercher des solutions multiplicatives non nulles de la forme

u(x, t) = X(x) x T(t)

qui vérifient les conditions aux limites2.12 Ici, de telles solutions vérifient donc :

X(x)T⁰⁰(t) = c²X⁰⁰(x)T(t).

Puisque l'on recherche des solutions non nulles, il existe a priori des nombres réels x0 et to pour lesquels :

X(x0) =6 0

et

T(t0) =6 0.

On en déduit, quitte a fixer x = x0, puis t = t0, l'existence de constantes A et telles que l'on ait pour t ~ 0 et 0 x < L :

X⁰⁰(x) = AX(x);

T⁰⁰(t) = T(t).

En reportant réciproquement dans l'équation, on voit que, en fait:

~ = c²A

et pour tenir compte des conditions aux limites, il faut enfin bien sur que :

u(0) = u(L) = 0.

(On est ainsi amené a résoudre un problème, ici trés simple, de Sturm-Liouville; on verra que cela est général dans cette méthode de séparation des variables).

· Si le nombre A est nul, alors :

X(x) = ax + b

et puisque u(0) = u(L) = 0, on a a = b = 0 et X est la solution nulle, ce qui est exclu.

· Si le nombre A est strictement positif, on a :

/ /

X(x) = ach( Ax) + /3sh( Ax)

et puisque X(0) = X(L) = 0, on a a = /3 = 0 et X est la solution nulle, ce qui est exclu.

· Si le nombre A est strictement négatif, on a :

_{J J}

X(x) = A cos( --Ax) + B sin( --Ax)

puisque X(0) = 0, on a A = 0 et puisque X(L) = 0, on a B = 0, donc encore X = 0, sauf s'il existe un nombre entier naturel non nul ii telque

u(x, t) =	+ . E n=1		, L L nilx nilct, Bn sin( )cos( )
2 B= ^n L		L I 0		f (x)sin(nilL x )dx
A =					_n^2il^2
					L2 '

auquels cas on obtient alors les solutions suivantes :

.

X (x) = A_n sm(

nfi

L x );

).

T(t) = B_n cos(^nilct) + C_ri sin( mild

L L

L'équation étant linéaire, les combinaisons linéaires des solutions précédentes sont encore solutions de réquation. L'idée est de ne pas se borner nécessairement a des "combinaisons linéaires finies" pour obtenir une solution.

Posons donc, de fawn purement formelle (on peut faire A_n, = 1) :

u(x, t) = E sin( nilx \

L i (B_n cos( nilct ) + C_m sin( nilct

L L )).

Les conditions de Chauchy portant sur u(x, 0) et at (x, 0) seront formellement vérifiées en choisissant
ot

les coefficients C_n nuls et les coefficients B_n tels que :

f (x) = E B_n sin(n L ilx ).

Un tel développement est celui d'une fonction impaire et 2L périodique sur R , que l'on obtient en prolongeant la fonction f par imparité sur [_L, L], puis par 2L-périodicité. La fonction f ainsi prolongée est clairement de classe C¹ sur R. Elle est a priori de classe C² sur R privé de l'ensemble LZ des multiples de L, sauf si elle vérifie la conditon supplémentaire

p(0) = f (L) = 0,

auquel cas elle est alors de classe C² sur R .

On en déduit qu'elle est développables en série de Fourier et que sa série de Fourier converge normalement vers f .

Si l'on pose pour t > 0 et 0 < x < L :

on voit que la série définissant u est normalement convergente sur [0, L]x[0, +oo], donc continue, et l'on vérifie aisément, a l'aide des formules de trigonométrie et du développement en série de Fourier de f, que l'on a :

2

·

u(x,t) = [f(x + ct) + fx ct)]

La fonction u obtenue ci-dessus est donc de classe C² sur [0, L] x [0, +oo] et solution de l'équation des cordes vibrantes si :

p(₀) = f(L) = 0.

Sinon, elle n'est de classe C² et solution de l'équation des cordes vibrantes que sur l'ensemble [0, L] x [0, +oo] privé des segments se droite d'équations

x #177; ct = kL

avec t > 0, 0 < x < L et k E Z.

2.1.4 Energie

Definition 2.1.1 Soit u une solution de l'équation des ondes. On appelle énergie de u la quantité

E(t) = ^P2 .1 R

( u(x , t))^2 dx + Ot 2 ^T I R

a (axu(x,t))^2dx

Il faut noter que, pour ce qui concerne les constantes p et r qui sont strictement positives, nous avons gardé ici la définition physique de l'énergie de la corde vibrante : la premiére intégrale est la partie énergie cinétique (₂¹mv²) et la deuxiéme est la partie énergie potentielle, qui correspond à la tension multipliée par l'allongement de la corde élastique (i I 1 + (1u)² 1 , ¹₂(1u)²). Là encore l'hypothése de petitesse des oscillations permet de simplifier considérablement l'étude !

2.1.5 Unicite d'une eventuelle solution par consideration de l'energie

Supposons que l'on dispose de deux solutions u1 et u2 de l'équation (qui peut ici etre homogene ou avec second membre, ce qui ne change rien a la démonstration), vérifiant les memes conditions initiales et les memes conditions aux limites.

Posons u = ui -- u2 et introduisons la fonction d'énergie suivante :

E(t) = 1 2

L I 0

( c2 1 (@u @t (x; t)^2 + (@u @x(x; t)2)dx

Les hypotheses faites autorisent la dérivation de E sous le signe intégral, et on a, puisque

u = ui -- U2

est aussi solution de l'équation des cordes vibrantes :

E'(t) =

L I 0

1 OU 0^2U OU 0^2U ( c2 ( at (x, 0 ate (x, 0 + (ax (x, 0 atax(x, t))dx

=

L

_I

0

OU 0²U

((at (X, 0 0X2 02u (X, t) + (_0x (X, t) 0t0x (X, t))dX.

L'expression sous le signe intégral est une dérivée et on a

ou

at (0_' t) = at ou (L_' t) = 0

par dérivation des relations

u(0,t) = u(L,t) = 0,

ce qui donne :

L

E^'(t) = [ox 0u (x, t)O at (x, 01 = 0.

0

Par conséquent, la fonction t --p E(t) est constante et, en fait, nulle puisque E(0) = 0 et du fait que, ui et u2 vérifiant les memes conditions initiales, leur différence u vérifie :

- D'une part,

ou

at (x_' 0) = 0,

- D'autre part, u(x, 0) = 0.

@u

Donc, par dérivation, @x(x; 0) = 0.

puisque E(t) = 0 on a donc pour t > 0 et 0 < x < L

@u @u

_8x(x,t) = at (x,t) = 0:

La fonction u est par conséquent constante sur [0, L] x [0, +oc], et en fait nulle puisque u(x, 0) = 0. ainsi,on a bien u1 = u2 et l'unicité annoncée.

2.1.6 Vitesse de propogation

On vient de voir que l'effet d'une position ço(x) a l'instant t = 0 est une paire d'ondes et qui se propagent dans les deux directions a vitesse c. Si l'on a une vitesse (x) a l'instant t = 0, on obtient une onde qui s'étale dans les deux directions, a une vitesse inférieure ou égale a c. Dans tous les cas rien ne se propage a vitesse plus grande que c. Autrement dit la valeur de la solution u au point (x, t) ne dépend que des valeurs de en x - ct et en x + ct, et des valeurs de sur l'intervalle [x - ct, x + ct]. Pour le voir il suffit de reprendre l'expression de la solution donnée dans le théorème de D'Alembert.

2.1.7 Derivation d'une equation des ondes

Dans ce paragraphe nous dérivons l'équation d'ondes en une dimension de l'espace pendant qu'elle s'applique aux vibrations transversales d'une corde élastique, oil cable, la corde élastique peut être considérée comme une corde de violon, un cable de haubanage, oil probablement une ligne d'énergie électrique. La même équation, cependant, avec les variables correctement interprétées, se produit dans beaucoup d'autres problèmes de vague ayant seulement une variable significative de l'espace. Considérons une corde élastique parfaitement flexible étirée étroitement entre les appuis fixés au même evel de horizontall. Soit les abscisses du l'axe x liés le long de la corde avec les points des etrimités x = 0 et et x = L. Si la corde est mise en marche a temps itial t = 0 et ensuite laissée calme, elle vibrera librement dans un plan vertical a condition que atténuant des effets, tels que la résistance d'air, sont négligées. Pour déterminer l'équation régissant ce mouvement nous considérerons les forces agissant sur un petit élément de la corde du x de longueur se trouvant entre les points x et x + x. Nous supposons que le mouvement de la corde est petit, et par conséquent, chaque point sur les mouvements de corde seulement dans une ligne verticale. Notons par u(x, t) le déplacement vertical du point x dans le temps t. Laissez la tension dans la corde, qui agit toujours dans la direction tangentielle, soit notée par T(x, t), et on note par p le poid par unité de longueur de la corde.

L'application de la loi de Newton, au l'élément x de la corde, déclare que la force externe est
nette, due a la tension aux extrémités de l'élément, doit être égale au produit du poid de l'élément

et de l'accélération du centre du son poid. Puisqu'il y a pas d'accélération horizontal, les composants horizontaux doivent satisfaire

T (x + x, t) cos (0 + 0) - T (x, t) cos 0 = 0. (2.13)

Si on note par H le composant horizontal de la tension, alors en vertue de (2.13), H est indépendant de x.

D'autre part, les composants verticaux satisfont

T (x + x, t) sin (0 + 0) - T (x, t) sin0 = p xutt (x, t). (2.14)

on x est la coordonnée du centre du poid de l'élément de la corde a étudier. Clairement, x se situe
dans l'intervalle x < x < x + x. On suppose que le poid de la corde est négligeable, qui a été
négligé dans (2.14). Si la composante vertical T est notée par V , alors (2.14) peut être écrit comme

V (x + x,t) - V (x,t)	= putt (x, t).
x

pasons a la limite quand x -p 0, nous donne

V_x (x,t) = putt (x,t). (2.15)

Pour exprimer (2.15) entièrement en terme u nous notons

V (x, t) = H(t) tan 0 = H(t)u (x, t).

donc (2.15) devient

(Hu_x) = putt,

comme H est independent de x,

Huxx = putt. (2.16)

Pour un petit mouvement de la corde, on peut remplacer H = T cos 0 par T. Alors (2.16) prend son forme usuelle

a²uxx = utt, (2.17)

ou

a2 = T/p. (2.18)

Nous supposerons plus loin que a est une constante, bien que ceci ne soit pas exigé dans notre dérivation, même pour des petits mouvements. L'équation (2.17) s'appelle l'équation d'ondes pour une dimension spaciale. Puisque T a la dimension de la force, et p represente le poid, il suit que la constante a est la dimension de la vitesse. Il est possible d'identifier a comme la vitesse avec laquelle

Chapitre 2. Equation des ondes sur un axe (Dans II1) 26

une petite perturbation (vague) se déplace le long de la corde. Selon (2.18), la vitesse de vague a se change directement avec la tension dans la corde, mais inversement avec la densité du matériel de corde. Ces faits sont en accord avec l'expérience.

Il y a de diverses généralisations de l'équation d'ondes (2.17). Une équation importante est connue comme l'équation de télégraphe et a la forme

utt + Cut + ku = a²uxx + F(x, t), (2.19)

on c et k sont des constantes non négatives. Les termes ku, cut et F(x, t) résultent d'une force d'at-
ténuation visqueuse, d'une force de reconstitution élastique, et d'une force externe, respectivement.

Chapitre 3

Equation des ondes en dimension ri

(Dans RTh)

Ici on s'interres par une équation des ondes pour les conditions aux limites de Dirichlet suivante :

8 <>>> >>>:

@2 @t2 u(x; t) - ~u(x,t) = f(x,t), avec x E ~ u(x, t) = 0, avec x E %1 a u(x, 0) = u0(x), u(x, O) = u1(x); avec x E ~ ôt

(3.1)

oil est un ouvert borné de Rⁿ de frontière 8, t ~ 0 et i le Laplacien dans Rⁿ et la fonction f(x,t) donnée.

Le problème aux limite (3.1) modélise la propagation des ondes ou de vibration. Par exemple,
la propagation au cours du temps du déplacement vertical d'une membrane élastique, ou bien de
l'amplitude d'un champ électrique de direction constante. L'inconnue u(x, t) ici une fonction scalaire.

Motivation

Ce chapitre est consacré a l'analyse mathématique d'un probléme d'évolution en temps. Nous allons plus particuliérement analyser une équation hyperbolique, l'exemple typique est (3.1), sur laquelle nous nous concentrons.

Le plan de ce chapitre est le suivant, nous démontrons l'éxistence et l'unicité de la solution de l'équation des ondes on utilisons un nouveau concept de formulation variationnelle. Nous utilisons pour cela des bases Hilbertiennes de fonctions propres.

Nous insistons aussi sur la notion d'estimation d'énergie qui exprime un bilan d'énergie physique et qui justifie en partie les espaces utilisées.

3.1 Solution de l'équation

Dans cette section, au premier lieu on établit une formulation variationnelle, deuxièment, on démontre l'existence et l'unicité de la solution de cette formulation variationnelle en utilisant une base Hilbertienne de fonctions propres, en suite on montre que cette solution variationnelle vérifie bien le problème aux limites.

3.1.1 Formulation variationnelle

L'objectif dans cette action est de transformer l'équation aux derivées partielles dans (3.1) a une équation différentielle ordinaire.

L'idée est d'écrire une formulation variationnelle qui ressemble a une équation différentielle ordinaire du deuxiéme ordre.

Pour cela, nous multiplions l'équation des ondes (3.1) par une fonction test v(x) qui ne dépend pas du temps t (dépend seulement de la variable spatiale x)

v(x)utt(x, t) - v(x)~u(x, t) = v(x)f(x, t) (3.2)

Intégrons (3.2) sur , on trouve

fv(x)LIu(x, t)dx = v(x)f(x, t)dx

~ ~

fv(x)utt(x, t)dx -

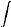
Il est clair que l'espace faible "naturel" pour la fonction test v(x) est H¹ 0(1).

On introduit alors le produit scalaire de L²(~) et la forme bilinéaire a(w, v) définis par

(w,v)L2(n) = I ~ et a(w,v) = f n

w(x)v(x)dx Vw(x).Vv(x)dx.

On utilise l'intégration par partie et le faite que

I v(x)Au(x,t)dx = (v(x), Au(x,t))L2(n)

et

I v(x)utt(x, t)dx = (v(x), utt(x, t))L²(1) .

Et a cause de la condition aux limites nous demandons a ce que v s'annule sur le bord de l'ouvert ~, apres les calculs :

(v(x)^,Au(x^,t))L²(n) = -- (Vv(x),Vu(x,t))L²(n)

= --a(v(x), u(x, t))

et comme v ne dépend que de x

d²

(v(x), utt(x,t))L202) = dt2 ^(u(t), v)

on obtient,

dt^2 I ~

u(x ,t)v(x)dx + I V u(x ,t).V v (x)dx = I sz n

f(x,t)v(x)dx. (3.3)

Soit un temps final T > 0 (éventuellement égal a +oo), on se donne le terme source

f _E L²(]0, T[; L²(Q)).

On se donne aussi des conditions initiales uo E 1¹₀ et ui E L²(Q).

La formulation variationnelle déduite (3.3) est donc : trouver une solution u dans

C([O, T] ; 1¹₍(Q) n C^l([O, T] ; L²(Q))

tellque

<> ₈

>: u(t = 0) = uo, dt (t = 0) = u1

dt2 (u(t), v)L²(n) + a(u(t), v) = (f(t), v)L²0-0v E 1/(1^-(Q),0 < t < T,

d²

du (3.4)

les données initiales ont bien un sens dans 3.4 grace au choix de l'espace d'énergie C([0,7¹];11^-j(Q)n C¹([0, T] ; L²(Q)) pour la solution u, c -- b -- d : u0 E 1¹₀(Q) et u1 E L²(Q).

Nous justiferons encore ce choix, en établissant son lieu avec des égalités d'énergie.

Finalement, la dérivée en temps dans la formulation variationnelle3.4, doit etre prise au sens faible puisqu'a priori la fonction t --p (u(t),v)L2(n) n'est qu'une fois dérivable en temps puisqu'elle appartient a C¹(0, T).

3.1.2 Existence et unicite

Un resultat general

Pour démontrer l'existence et l'unicité de la solution variationnelle 3.4 nous revenons encore pour "diagonaliser" l'opérateur Laplacien et nous ramener a la résolution, d'une famille de simples équations diférentielles ordinaires du deuxiéme ordre.

La première étape de la preuve de l'existence consiste a bien choisir l'espace on chercher la solution de l'équation. L'exigence minimale pour cet espace est la continuité de u(t, x) par rapport au temps. Soit V et H deux espaces de Hilbert tels que V C H avec injection dense et compacte (typiquement V = 1¹0(Q) et H = L²(Q). L'espace le plus faible qui satisfait l'exigence précédente est

C ([0, T] ; Hj(Q) x L²(Q)) oft 1¹₀(Q) x L²(Q) est l'espace de l'energie pour (3.1).

Theoreme 3.1.1 Soient V et H deux espaces de Hilbert tels que V C H avec injection compacte et V est dense dans H . Soit a(u, v) une forme bilinéaire symétrique continue et coercive dans V. Soit un temps final T > 0, une donnée initiale (u0, u1) E V x H, et un terme source f E L²(]0, T[; H). alors le probléme

d^2 dt2(u(t), v)H + a(u(t), v) = (f(t), v)HVv E V, 0 < t < T, (3.5) du u(t = 0) = u0, dt (t = 0) = '1,

(ou l'équation de (3.5) a lieu au sens faible dans ]0, T[) a une unique solution u E C([O, T] ;V n C¹([0, T] ; H). De plus, il exitiste une constante c > 0 (qui ne dépend que de Q et T) telleque

M¹MC([0,T];V ) + MuMc¹([0,T];i) < c(Mu0MV + ^Mu1M" + M.ML2(]0,7[;H))- (3.6)

Remarque 3.1.1 L'estimation d'énergie 3.6 prouve que la solution de 3.5 dépend continument des données, et donc que le probleme hyperbolique 3.5 est bien posé au sens de Hadamard.

Preuve Dans une premiére étape, on montre que toute solution u est une série de fonctions propres. Dans deuxiéme étape, nous démontrons la convergence de cette série dans les espaces C([0, T] ; V ) et C¹([0, T]; H).

Etape1

supposons que u E C([0, T] ; V ) n cⁱ([0, T] ; H) est solution de 3.5. Introduisons la base hilbertienne (uk)k>1 de H composée des fonctions propres de la formulation variationnelle qui vérifient

uk E V, et

a(uk, v) = A/c _(uk,v)HVV E V.

On écrit

u(t) = X+ k=1 ak(t)uk

avec

ak(t) = (u(t), uk)H :

En choisissant v = uk dans 3.5 et en notant

Ok(t) = (f(t), uk)H = (ul, uk)H ;

on obtient

( d2ak dt2 + f`kak =13k dans ]0, T[

a

k(t = 0) = dd

a

t k(t = 0) =

ak(t) = a?, cos(wkt) + ak

Wk

sin(wkt) + 1

wk

_Zt 3k(s) sin(wk(t -- s))ds (3.8)

0

ce qui donne une formule explicite pour la solution u (qui est donc unique). Etape2

Pour démontrer que la série

X+ j=1

(~0 _k cos(wjt) + wj

a j

1

_Zt

0

1

(3.7)

k:

(Attention a une confusion possible dans les notations : la donnée initiale u1 n'a rien a voir la

fonction propre uk pour k = 1.)

Posant wk = 2.k, l'unique solution de 3.7 est

(s) sin(wi(t -- s))ds)ui (3.9)

sin(wit) +

w
·

converge dans C([0, T] ; V ) n C¹([0, T] ; H) on va montrer que la suite

k

Wk = ai(t)ui

j=1

des sommes partielles de cette série est de Cauchy.

Dans V nous considérons le produit scalaire a(u, v) pour lequel la famille (u3) est orthogonale par orthogonalité dans H et dans V de (ui), on obtient pour 1 > k, et tout temps t,

~ ~ a(wl -- wk, wl ~wk) + ~ ~

~ ~~ 2 / d ~ X~^2 dt(wl ~ wk) ~ ~ ~ = (j jj(t)j^2 + ~d~j ~ dt (t) ~ ) H j=k+1

Or, en multipliant 3.7 par ddat k et en intégrant en temps, on obtient

~~~~

dai dt (t)

~~~~

2

~~~^0 + j jj(t)j^2 = ~~~^1 j(t) ~~2 + ^2 j(t) ~~ + 2 j

Zt 0

~j(s)^d~j dt (s)ds.

De la formule 3.8 on infére que

~~~~

dai dt t)

~~~~+ ~~ ~ wj ~~~0a3'1 +

Zt 0

i(s)ds.

En combinant ces deux résultats on en déduit

~~~~	dai dt (t)	~~~~	2	~~2 + 2 + j jj(t)j^2 ~ 2j ~~~^0 ~~~1 ~~2 + 2t j j					Zt 0	,3i(s)1^2 ds. (3.10)
Comme uo 2 V, u1 2 H et f 2 L^2(10,T[; H), on a Na^2 y = a(uo, uo) =							X+ j=1	~~2 < +1; j ~~~^0 j
2 11^7.^10111/ =					X+ j=1	~~ai 1^2 < +cc, 3

11./11²L²a0,7^,[;H) -- +co _f 10i(s)1²ds < +Do,

j=1

ce qui implique que la série, dont le terme général est le membre de gauche de 3.10, est convergente, c'est-à-dire que la suite w^k vérifie

~

~ ~ ~

lim max( _~w^l(t) ~ wk(t) ~2 ~

V + ~

~

d ~2

_dt(w^l(t) wk(t)) ~) = ⁰,

H

autrement dit, elle est de Cauchy dans ([0, ; H) et dans C([0, T] ; V).

Comme ces espaces sont complets, la suite de Cauchy w^k converge et on peut définir sa limite u. En particulier, comme (wk(0), dwk

dt (0)) converge vers (uo, ui) dans V x H, on obtient les conditions

initiales voulues.

D'autre part, il est clair que u(t), en tant que somme de la série3.9 vérifie la formulation variationnelle 3.5 pour chaque fonction test v = uk.

Comme ( _uk?Ak) est une base hilbertienne de V, u(t) vérifie donc la formulation variationnelle 3.5 pour tout v E V, c'est-à-dire que u(t) est bien la solution recherchée de 3.5.

Par ailleurs, on a en fait montré que

~ ~ a(wl -- wk, wl -- wk) + ~ ~

d 2 dt(wl -- w^k) < C (11uo11V + 117411H + T 11f11/,20,71;0, H

et l'estimation d'énergie 3.6 s'obtient alors facilement en prenant k = 0 et en faisant tendre l vers l'infini.

3.2 Applications

Nous appliquons maintenant le résultat abstrait du Théoréme à l'équation des ondes et nous prouvons que cette approche variationnelle a bien permis de résoudre l'équation aux dérivées partielles d'origine.

Théorème 3.2.1 Soit Q un ouvert borné régulier de R^N, et un temps final T > 0.

On considére une donnée initiale (uo, ui) E Hj(Q)xL²(Q) et un terme source f E L²(]0,T[; L²(Q)). alors l'équation des ondes

ou

8 <>>> >>>:

2 Ot2u(x, t) -- Au(x, t) = f(x, t), p.p. dans Q x ]0, T[ u(x, t) = 0 p.p. sur (Q x ]0, T[ u(x,0) = uo(x), :u(x,0) = ui(x), p.p. dans Q x ]0, T[

(3.11)

admet une unique solution u E C([0, T] ; Hj,(Q))nC^l([0, T] ; L²(Q)). De plus, il existe une constante c > 0 (qui ne dépend que de Q et de T ) telle que, pour tout t E [0, T]

I

(

~~~~

at (x, t)

~~~~

2

+ 1Vu(x, t)1^2)dx < c(f n

(1ui(x)1^2 + 1Vuo(x)1^2)dx +

t I 0

I

1f(x, s)1^2 dxds) (3.12)

Preuve Nous appliquans le Théoréme (3.2.1) à la formulation variationnelle 3.4 de l'équation des ondes obtenue à la sous-section (3.2.1) ses hypothése sont facilememt vérifiées avec H = L²(Q) et V = Hj(Q)).

Il reste à montrer que l'unique solution u E C([0, T] ; Hj(Q))nC¹([0, T] ; L²(Q)) de cette formulation variationnelle est bien une solution de 3.11.

Tout d'abord, la condition aux limites de dirichlet se retrouve par application du Théoreme (1.2.2)
de trace à u(t) E H(1^-(Q) pour tout t E [0, T] , et la condition initiale est justifiée par la continuité

de u(t) en t = 0 comme fonction a valeurs dans 1/(1(Q) et de _dtdu en t = 0 comme fonction a valeurs

)

dans L²(Q).

Si la solution u est suf fisamment réguliere, par intégration par partie la formulation variationnelle3.4 est équivalente a

I

2

( Ot2u(x, t) -- Au(x, t) -- f)vdx = 0

pour tout v(x) E C^l_c(Q) et presque tout t E ]0, T[ .on en déduit l'équation de 3.11. Si la solution u n'est pas plus réguliére que ce qui est donné par le Théoreme (3.2.1) on obtient tout de méme l'équation au sens "presque partout" en reprenant les arguments de la démonstration du Théoreme (3.3.1) (que nous ne détallons pas) .

On note 8 = (Ou ' --Vu) la fonction a valeurs victorielles dans 118ⁿ⁺¹, et on peut montrer qu'elle ot

ou

admet une divergence faible en "espace-temps" qui est justememt -- Au qui appartient donc a

ot

L²(]0, T[; L²(Q)).

En l'absence de forces, f = 0 on peut améliorer l'estimation d'énergie (3.12) et obtenir une propriété de conservation de l'énergie totale qui est trés importante du point de vue des applications. l'énergie totale est ici la somme de deux termes d'une part l'énergie cinétique l_at^au_a1² et d'autre part l'énergie mécanique 1Vu1² . Proprietes

Reversibilite en temps

Nous examinons maintenant les principales propriétées qualitatives de la solution de l'équation des ondes, la propriété la plus frappante, est la réversibilité en temps de cette équation.

Proposition 3.2.1 soit Q un ouvert borné régulier de 118ⁿ, et un temps final T > 0.Soit (vo, vi) E 1/(1^-(Q) x L²(Q), et un terme source f E L²(]0, T[; L²(Q)). Alors l'équation des ondes rétrograde en temps (intégrée en remontant le temps a partir de T).

8 <>>> >>>:

2 Ot2v(x,t) -- Av(x,t) = f(x,t), p.p. dans Q x ]0, T[ v(x, t) = 0 p.p. sur 9Q x ]0, T[ u(x, T) = vo(x), :u(x,T) = vi(x), p.p. dans Q

(3.13)

admet une unique solution v E C([0,t];1/j(Q)) n C¹([0, t] ; L²(Q)). De plus u(x, t) est la solution de l'équation des ondes (8.3) et si vo(x) = u(x, t) dans 1/(1^-(Q) et vi(x) = _a^u_t (x,t) dans L²(Q), alors on a v(x, t) = u(x, t).

Chapitre 3. Equation des ondes en dimension ii (Dans II1ⁿ) 35

Preuve On fait le changement d'inconnue w(x, t) = v(x, T - t) et 3.13 devient une équation des ondes "progrissive" avec donnée initiale en t = 0, comme l'équation "usuelle" 3.1 comme la dérivée en temps est d'ordre 2, il n'y a pas de changememt de signe dans l'équation aprés ce changememt d'inconnue).

Par application du Théorème (3.3.1), le problème 3.13 admet une unique solution. Si v0(x) = u(x, t)

@u

et V1(X) = 8t (x,t), la solution u(x,t) de 3.1 est aussi de 3.13. Par unicité on en déduit v(x,t) =

u(x, t).

Le caractére réversible en temps de l'équation des ondes a de nombreuses conséquences. La plus importante est qu'il n'y a aucun effet régularisant pour l'équation des ondes. En effet,si c'était le cas, en changeant le sens du temps, on obientdrait un effet "dérégularisant" contraductoire. Par conséquent, il n'y a ni gain ni perte de régularité pour la solution de l'équation des ondes par rapport aux données initiales. On peut tout au plus aflirmer, comme dans le cas elliptique, que la régularité de la solution de l'équation des ondes est directememt liée a celle des données.

Conclusion et discussion

Il n'y a pas de principe de maximum pour l'équation des ondes, en l'absence de terme source ( f = 0), même si la viteese initiale est nulle ( u = 0) et si la donnée initiale est positive ( u0 ~ 0), la solution u peut changer de signe au cours du temps.

Cette absence de principe de maximum est conforme a l'intuition physique. Imaginons une corde ou une membrane élastique : si on la déforme initiallement dans une position au dessus de son plan de repos, elle va vibrer et passer alternativement en dessus et au dessous de ce plan (autrememt dit u change de signe).

Mathématiquement, ce centre-exemple peut s'écrire simplement sous la forme suivante. Soit w(x) la premiére fonction propre du laplacien dans un dommaine bornée connexe avec condition aux limites de dirichlet. D'aprés le Théorème (1.2.3). On peut normaliser w de telle maniére que w(x) ~ 0 dans , en notant A = w² la premiére valeur propre associée a w, il est facile de vérifier que u(x, t) = cos(wt)w(x) change de signe au cours du temps tout en étant la solution unique dans C([0, T] ; H¹ ₀( ))flC¹([0, t] ; L²( )) de l'équation des ondes 3.11 sans terme source et avec les données initiales.

@

u(x,0) = w(x), u(x, 0) = 0 dans .

8t

Il n'y a donc pas non plus de comportement asymptatique en temps long pour l'équation des ondes en domaine bornée.

Autrememt dit, même si le terme source f ne dépend pas du temps, la solution u converge pas vers une limite stationnaire lorsque le temps t tend vers l'infini.

En particulier, si f = 0, l'infiuence des conditions initiales est la meme a tout temps puisque l'énergie est conservée et ne décroit pas.

Le meme contre exemple u(x, t) = cos(wt)w(x) permet de voir qu'il n'y a pas de limite stationnaire mais des oscillations qui perdurent sans amortissememt.

Cela n'est évidemment pas le cas pour l'équation des ondes amortie.

Dans un mot sous forme d'une conclusion, on peut souligner que nous avons montré quelques éclairassions sur l'équation des ondes. Ce la est suffi sant pour un étudiant en licence, débutant dans l'étude de ces formes d'équations, on nous avons commencé le travail par une discussion et développement du cours pédagogique des EDPs pour le parcours de licence en mathématique appliquées, et nous avons essayé de le compléter, soudain nous nous retrouvons dans une étude approfondie d'un problème mathématique relativement simple, c'est le prolongement en dimension Ti.

Il y a d'autres problèmes du même type, mais dans des conditions diffi ciles comme le cas non linéaire on au moine semi linéaire en prenant en considération les effets d'amortissement. Laissons ce projet devrait être achevé en master en utilisant les connaissances acquises est en mesure d'aller plus loin que ce la.

Si le cas, dans les études de doctorat, et avec ce bagage, on peut plonger directement dans la recherche des problèmes ouverts dans ce domaine, l'existence des solutions et l'interaction entre les différents termes de dissipations non linéaire ainsi que le comportement de la solution s'il existe, cette étude est extrêmement compliquée.

Bibliographie

[1] Georges Koeper, "EQUATIONS AUX DERIVEES PARTIELLES", univ- Paris 5-2001.

[2] Gerard DEBEAUMARCHE (Professeur de mathématiques spéciales au lycée Clemenceau de Reims), "Introduction aux équations aux dérivées partielles linéaires",

[3] S. GOCOUNOV, "équations de la phisique mathématique", Edition MIR Moscou 1973.

[4] Haim Brezis, "Functional analysis, sobolev spaces and PDE", Springer

[5] B. Helfer, "Introduction aux Equationsaux D'erivées Partielles", Université Paris-Sud, 2007.

[6] Imane BELKHEIR et Khaled ZENNIR, "Théorèmes du point ffxe et ses applications", Mémoire de Licence en Mathématiques, USTO 2010.

[7] Lawrence c. Evans, "Partial Differential Equations", AMS

[8] Peter J. Olver, "Applied Mathematics", University of Minnesota.

[9] Ravi P. Agarwal and Donal O'Regan, "NONLINEAIRE ANAlYSIS",VOLUME 9, Series in Mathematical Analysis and Applications, Boca Raton London New York Singapore,2005.

[10] REINHARD (H.). "Equations aux dérivées partielles", Dunod.

[11] B.Said-Houari et N. Tatar, "Etude de l'interaction enter un terme dissipatif et un terme d'explosion pour un probleme hyperbolique", 2003. Memoire de magister en mathématiques, Université de Annaba.

[12] Khaled ZENNIR et B.Said-Houari , "Existence and asymptotic behavior of solutions of a non linear viscoelastic hyperbolic equation", Memoire de magister en Mathématiques, 2008, Université de Annaba.