2.4.2.2.1- Etude de la
saisonnalité
Un préalable avant l'étude de la
stationnarité des séries chronologiques est celle de la
saisonnalité. En effet, il est nécessaire de corriger les
séries de type infra-annuelle des variations saisonnières avant
de les étudier. La dessaisonalisation se fera ici à partir de la
Méthode des Moyennes Mobiles (MAM) à partir du logiciel Eviews
5.0. Dans la littérature, il existe généralement trois
(03) types de modèle visant à décrire la
saisonnalité:
v Le modèle additif : 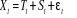
v Le modèle multiplicatif : 
v Le modèle mixte : 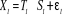
2.4.2.2.1.1- Le test de
Buys-Ballot
Le test de Buys-Ballot est fondé sur les
méthodes analytiques prenant en compte le calcul des moyennes  et les écarts types et les écarts types  pour chaque période (année). pour chaque période (année).
Pour ces paires d'observations , nous estimons par la méthode des MCO les paramètres a et
b de l'équation , nous estimons par la méthode des MCO les paramètres a et
b de l'équation . Si le coefficient . Si le coefficient  n'est pas significativement différent de 0 (test de Student)
alors on accepte l'hypothèse d'un schéma additif ; dans le
cas contraire, nous retenons un schéma multiplicatif. n'est pas significativement différent de 0 (test de Student)
alors on accepte l'hypothèse d'un schéma additif ; dans le
cas contraire, nous retenons un schéma multiplicatif.
2.4.2.2.2-Etude de la
stationnarité
2.4.2.2.2.1- Le Test de
Dickey-Fuller Augmenté
Les données de l'étude sont des séries
temporelles. On est donc amené à étudier leurs
caractéristiques stochastiques afin de déterminer si elles sont
stationnaires ou non. Par définition une série temporelle est
stationnaire lorsque sa moyenne et sa variance sont des constantes dans le
temps et si la valeur de la covariance entre deux périodes de temps ne
dépend que de la distance ou écart entre ces deux périodes
et non pas du moment auquel la covariance est calculée. Plus
précisément, il s'agit de faire le test de racine unitaire sur
ces séries. Pour cela, on effectuera le test amélioré de
Dickey Fuller. Ce test permet, non seulement de détecter l'existence
d'une tendance (test de racine unitaire), mais aussi de déterminer la
meilleure manière de rendre stationnaire une chronique.
La mise en oeuvre de ce test (Dickey Fuller Augmenté)
passe par l'estimation MCO des trois modèles de base que sont :
Modèle 1: Modèle sans
constante ni tendance déterministe.
Xt = ëXt-1 + 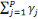 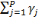  Xt-j + åt Xt-j + åt
Modèle 2 : Modèle avec
constante et sans tendance déterministe
Xt = ëXt-1 + á +
 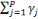 Xt-j + åt Xt-j + åt
Modèle 3 : Modèle avec
constante et tendance.
Xt = ëXt-1 + á
+ât +   Xt-j + åt Xt-j + åt
Dans ces trois modèles, åt est
l'erreur à l'instant t, Xt est la valeur de la série
à la période t et åt~BB (0, 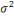 ) )
On teste alors l'hypothèse nulle Ho contre
l'hypothèse alternative H1 en se référant aux
valeurs tabulées par l'ADF. Les hypothèses du test sont
formulées comme suit :
H0 : présence de
racine unitaire (ë = 0)
H1 : absence de racine
unitaire (ë < 0)
La règle de décision est la suivante :
· si la valeur calculée de la t-statistique
associée à ë est inférieure à la valeur
critique tabulée, on rejette l'hypothèse nulle de racine
unitaire : la série étudiée est donc
stationnaire ;
· si la valeur calculée de la t-statistique
associée à ë est supérieure à la valeur
critique tabulée, on ne rejette pas l'hypothèse nulle de non
stationnarité.
Il convient en effet d'appliquer le test de Dickey-Fuller sur
un des trois modèles. Pour cela, on adopte une approche
séquentielle en trois étapes.
1ère
étape :
On estime le modèle 3. On commence par tester la
significativité de la tendance en se référant aux tables
de l'ADF. Deux cas peuvent se présenter :
*si la tendance n'est pas significative, on passe à
l'étape 2 ;
*si la tendance est significative, on teste l'hypothèse
nulle de racine unitaire en comparant la t-statistique de ë aux autres
valeurs tabulées par l'ADF. On a deux possibilités :
· si l'on ne rejette pas l'hypothèse nulle,
Xt est non stationnaire. Dans ce cas, il faut la différencier
et recommencer la procédure de test sur la série en
différence première ;
· si l'on rejette l'hypothèse nulle, Xt
est stationnaire en trend. Dans ce cas, la procédure de test
s'arrête et l'on peut travailler sur la série Xt (mais
en enlevant le trend).
2ème
étape :
Cette étape ne doit être appliquée que si
la tendance dans le modèle précédent n'est pas
significative. On estime le modèle 2 et on commence par tester la
significativité de la constante :
*si la constante n'est pas significative, on passe à
l'étape 3 ;
*si la constance est significative, on teste
l'hypothèse nulle de racine unitaire :
· si l'on ne rejette pas l'hypothèse nulle,
Xt est non stationnaire. Dans ce cas, il faut le
différencier et recommencer la procédure du test sur la
série en différence première ;
· si l'on rejette l'hypothèse nulle, Xt
est stationnaire et la procédure de test s'arrête. On peut
alors travailler directement sur la série traitée.
3ème
étape :
Celle-ci ne doit être abordée que si la constante
dans le modèle précédent n'est pas significative. On
estime alors le modèle 1 et on teste l'hypothèse nulle de racine
unitaire en utilisant les valeurs critiques :
*si l'on ne rejette pas l'hypothèse nulle, Xt
est non stationnaire ; il faut donc la différencier et tester
la stationnarité de la série en différence
première ;
*si l'on rejette l'hypothèse nulle, la série est
donc stationnaire et la procédure de test s'arrête.
| 


